Abstract
With the development of the social economy and the improvement of electrification, cables and wires play an important role in people’s lives and industrial development. Meanwhile, the large-scale laying of cables has also made them a fire hazard that cannot be ignored in land construction such as residential buildings, utility tunnels, nuclear power plants, refineries, marine systems such as submarines and ships, and airborne systems such as spacecrafts and aircrafts. In this work, studies on fire the characteristics of cables and wires over the last decades have been reviewed. Based on different experimental forms and objects (laboratory wires and commercial cables), this paper summarizes the theories of the fire dynamics in wire combustion, including the models of ignition and flame propagation, the criteria for blowing off and quenching, and the critical conditions for dripping behavior. The effects of materials, layouts, and environments on wire combustion phenomena such as airflow, ambient pressure, oxygen, gravity, and orientation angle have been discussed in detail according to the theories of heat transfer and combustion. In addition, test standards and studies on the fire behavior and release of toxic gases of commercial cables have also been fully described. Through the summary of the above content, it is expected to build a preliminary theoretical framework and future research directions for researchers in the field of cable fires.
1. Introduction
In the face of the current socio-economic development situation, the demand for cables in the fields of electric power transportation and information transmission is increasing, especially in power supply systems, nuclear power stations, utility tunnel systems, and other industrial and mining enterprises. The use of cables is significant. As the lifeblood of national power and communication, the large number of combustible components contained in the cable itself make it a fire safety hazard. According to the U.S. Fire Administration statistics, the estimate of residential building fires due to electrical malfunction was over 20,000 per year for the 10-year period of 2012 to 2021 []. In the event of a fire in a place where a large number of cables are laid, the potential hazards brought by it are mainly manifested in the following aspects [,]:
- First, the cable sheath and insulating materials are flammable, which can be ignited in high-temperature situations;
- Secondly, under good ventilation conditions, cable fires can accelerate their spread along the cables. Due to the fact that cables are mostly connected to important places, once a fire spreads to important places, the loss is significant;
- Third, the burning process of cables can release toxic and corrosive gases such as hydrogen chloride and carbon monoxide, which can cause significant damage to people and equipment;
- Fourth, the process of cable burning is often accompanied by a large amount of smoke, greatly affecting the escape and rescue work.
Since the cable fire accident of the Browns Ferry nuclear power plant in 1975, scholars have gradually begun to pay attention to the fire characteristics of cables, but have been more inclined to industrial testing. Until the early 1980s, Bakhman et al. [,] began to use PMMA and PE-wrapped copper and glass rods as simplified laboratory wires to study the phenomenon of wire combustion. After that, Fernandez-Pello et al. [] used a thermogravimetric analyzer and an experimental apparatus consisting of a gas-fired radiant panel, a specimen holder frame to study the ignition delay time and flame propagation rate of several different wires under different external radiation effects. They classified these types of wires into fire risk levels based on their combustion performance and flame propagation ability. At the same time, Tewarson, A. et al. [] and Babauskas, V. et al. [] also conducted studies on the fire behavior and test methods of commercial cables. During this period, few scholars used the method proposed by Bakhman to study the combustion behavior of wires until the late 1990s. Since 1998, domestic and foreign scholars have re-used laboratory wires to conduct a large number of studies on the ignition [,,,,,,,,,], propagation [,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,], extinction [,,,,,,,], and dripping [,,,,,,,,,,] behaviors of wires, as well as the impact of environmental factors and wire configuration in wire combustion. In addition to the bench-scale laboratory wire fire tests and the small-scale commercial cable tests such as the FPA (fire propagation apparatus) and cone calorimeter mentioned above, medium- and large-scale experiments also run through the development of cable fire research, providing many simulation methods and empirical formulas for real-world cable fire behavior [,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,]. The above-mentioned studies will be elaborated in Section 2 and Section 3.
After decades of development, research on the behavior of cable and wire fires has yielded significant results. Therefore, this work will systematically summarize the research results of many scholars over the past decades based on different experimental scales and experimental objects in the hope of establishing a relatively complete research framework and summarizing the issues to be resolved.
2. Wire Combustion Characteristics
In wire fire experiments, coaxial peeled wires or self-made wires are widely used, which are only composed of an insulating layer and a wire core. Commonly used insulation and wire core materials are polyethylene (PE), ethylene-tetrafluoro-ethylene (ETFE) and copper (Cu), iron (Fe), nickel–chromium alloy (NiCr), aluminum (Al), and stainless steel (SS).
The research on wire fires is usually divided into different categories according to its development process: ignition, flame propagation, melt and drip, extinction. Therefore, the above research sites are reviewed separately in the following paragraphs, and the effects of environmental factors and wire configurations on different combustion processes are also discussed.
2.1. Ignition
Compared with other polymer fuels, due to the unique nature of the wire core, there are three ignition models for wires:
- (1)
- Piloted ignition under external heat sources like other fuels [];
- (2)
- Spontaneous combustion of the insulation layer caused by overcurrent [,,,];
- (3)
- Arc ignition [].
2.1.1. Piloted Ignition by External Heating
The external heat source ignition process is usually as follows: The external heat source heats the insulation. When the insulation surface temperature rises to the pyrolysis temperature, the surface precipitates the pyrolysis gas and mixes with the air. As the mixture reaches the ignition limit, it is ignited when encountering a hot surface, hot spot, spark, or flame. The typical external heat source ignition phenomenon is shown in Figure 1. As shown in Figure 1, for different insulation materials, there are differences in the form of the flame after piloted ignition. The flame of polyethylene insulation after being ignited by an external heat source is usually presented as a candle-like stable flame, while it is presented as a multi-point jet flame with insulation shrinkage and swelled for polyvinyl chloride insulation. This is because the surface of PVC insulation will be charred when it is heated, while PE insulation will not. A similar combustion phenomenon was found in Gong’s research [], reporting that the PVC sheath under external heating swelled and shrank under five stages before being ignited: inert, fluctuation, rapid swelling, shrinkage, end stable, and a flame appearing as a jet flame.

Figure 1.
Ignition phenomenon of the NiCr-PE wire (dc = 0.7 mm, δp = 0.15 mm). Reprinted from Ref. [] with the permission of Elsevier.
There are usually three heat transfer protocols in the piloted ignition process of wire due to external heating:
- (1)
- The external radiation directly heats the insulation layer, and the core acts as a heat sink [,,];
- (2)
- External radiation directly heats the core, and the core acts as heat source [,];
- (3)
- Internal Joule heat and external radiation joints heat the insulation [,].
Under this ignition mode, the following assumptions can be made []:
- (1)
- The contact thermal resistance between the insulation layer and the wire core are ignored;
- (2)
- The materials are isotropic;
- (3)
- The phase transitions and deformations are ignored;
- (4)
- The radial heat transfer is ignored.
Based on the above assumptions, a one-dimensional heat transfer model can be established. The energy conservation equation of the insulation and the core are as follows []:
where x is along the wire axis, and , c, A, T, and k are the density, specific heat, cross-section area, temperature, and thermal conductivity, respectively. The subscripts p and c represent the insulation and the metal core. represents the Joule heating, which can be calculated by . represents the heat conduction between the core and the wire. represents the external radiation heat flux. The dot and apostrophe of the physical quantities mentioned in this article indicate only the variable in time and space.
The three heat transfer protocols have different boundary conditions, and the forms of Equations (1) and (2) will also change.
For protocol (1), Joule heat needs to be removed first, and secondly, the core acts as a heat sink, so the heat conduction value is negative. In this case, the energy required for pyrolysis and ignition comes from the net heat flux, which is the external heat flux minus the heat conduction of the insulation to the core. When the external heat source with length L is heated locally, there is a critical heat flux for the piloted ignition of the wire as follows [,]:
where and represent the ignition temperature and the wire balance temperature. represents the heat loss from the wire surface in the heating zone.
When the external heating is global, the prediction model of ignition delay time under the global external heating can be derived by referring to the classical thermally thin solid ignition model [,] as follows:
where , is the pyrolysis temperature of the insulation, and is the net heat flux. , and represent the pyrolysis time, the mixing time, and the gas-phase chemical time, respectively. If there is a piloted source such as a laser spark, electrical spark, flame, or hot surface that is close to the gas mixture, and are usually much smaller than . Hence, the ignition delay time of the piloted ignition is usually characterized by the pyrolysis time, while the gas-phase kinetic effects can be ignored.
As for Protocols (2) and (3), the difference mainly lies in the source of the net heat flux. For the former, mainly comes from the difference between the heat conduction of the core and the heat loss of the outer surface of the insulation, while for the latter, it is from the joint heating of the internal and external heat sources.
Figure 2 shows two examples (external coil heat and external radiation with laser spark) of the ignition delay time changing with the external heating [,]. As shown in Figure 2, the core material, insulation size, internal current, external heat flux, and environment conditions (oxygen and gravity conditions) all affect the ignition delay time of the wire.
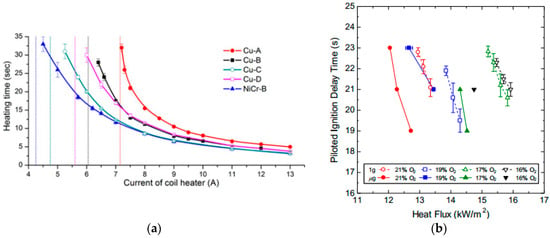
Figure 2.
Ignition characteristics under external heating. (a) External coil heat (A, B, C, D represent the wires with different diameters and insulation thickness). Reprinted from Ref. [] with the permission of Elsevier; (b) external radiation with laser spark. Reprinted from Ref. [] with the permission of Elsevier.
It is obvious and common sense that with the increase of external heat flux, the piloted ignition delay time will be significantly reduced. However, at a high heat flux, it will gradually stabilize, and when the core is energized, the increase in current will reduce the critical ignition heat flux to a certain extent. Additionally, piloted ignition will be more difficult to achieve, and the ignition delay time will be longer for the wire with the higher thermal conductivity core, larger diameter, and thinner insulation []. This can be explained by Equations (3) and (4). As for the gravity and oxygen concentration, microgravity and a high oxygen concentration significantly increase the risk of wire fire. The mechanisms of influence will be discussed at the end of Section 2.1.2.
2.1.2. Overcurrent Ignition
Overcurrent ignition caused by short circuit and overload is another important model, which may be more in line with the actual wire and cable fire. When excess current passes through the core, considerable Joule heat is generated. Under the significant amount of Joule heat, the core is rapidly heated to show a red-hot glow. The heat generated by the core is transferred to the insulation through thermal conduction, and the insulation rapidly heats up to the melting temperature and further heats up to the pyrolysis temperature. The pyrolysis gas is produced at the interface between the core and the insulation. After the gas mixes with air (released after the insulation is melted and broken for PE insulation [,], bursting jetting from the bubble containing volatile compounds after the insulation breakdown for FEP insulation [], released after the swelled insulation breakdown for PVC []), the mixture oxidizes and exotherms, which eventually leads to gas-phase thermal explosion [,], spontaneous ignition, or assisted ignition by the exposed high-temperature core [].
The research on wire overcurrent ignition started from a series of combustion studies in microgravity to improve the fire safety of spacecrafts. Kong and his team [,,,,] were pioneers in the study of overcurrent ignition. Different from previous microgravity combustion experiments, Kong et al. adopted a functional simulation method to make the Grashoff number () of the environment the same as that of the microgravity environment by adjusting the pressure and the height of the passage in the ground conditions so as to simulate the buoyancy level of the microgravity environment. The focus of their studies was to achieve pre-ignition characteristics of energized wire (the law of temperature evolution before ignition, the characteristics of flue gas transport, and the ignition delay time) that were similar to that in microgravity via functional simulation. During the same period, Fujita and Shimizu et al. [,,] conducted studies on short-term overcurrent ignition and long-term sustained overcurrent ignition in a microgravity environment achieved using tower drop and parabolic flight, respectively. Based on their research results, as shown in Figure 3, it can be found that there are significant differences in the ignition behavior of wires under microgravity and normal gravity conditions due to the absence of buoyancy-induced convection. In a microgravity environment, when a short-term overcurrent is introduced, the ignition point usually occurs on the surface of the wire core and then develops into a tubular flame around the wire core, shown in Figure 4. However, for a long-term overload current supply under normal gravity, the ignition point is usually far away from the wire. However, it was found that this phenomenon can also be observed for a short-term and small overcurrent under microgravity conditions in a subsequent study []. But the former phenomenon is unique to microgravity environments. Additionally, another phenomenon that is unique to microgravity environments is that ignition can occur after the current supply ends; that is, delayed ignition.


Figure 3.
Ignition behavior. Reprinted from Ref. [] with the permission of Elsevier. (a) Short-term excess current in microgravity; (b) continuous excess current in 0.8G0.

Figure 4.
Tubular flame. Reprinted from Ref. [] with the permission of Elsevier.
It is found that for both Studies by Kong’s and Fujita’s research teams on overcurrent ignition of polymer-insulated wires under microgravity conditions, the fire risk of wires under microgravity conditions is higher than that in normal gravity. As shown in Figure 5, because of the elimination of the nature convection in microgravity, which results in a longer residence time of the flammable mixture and a reduction in heat loss (compared with the normal gravity environment, there is no natural convection heat loss), the ignition limit (current and limit oxygen concentration) is more extensive in microgravity than in normal gravity.
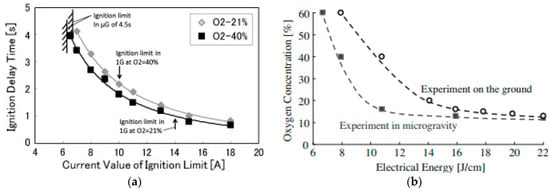
Figure 5.
(a) Current value of ignition limit. Reprinted from Ref. [] with the permission of Elsevier; (b) the limit oxygen concentration under microgravity and normal gravity conditions. Reprinted from Ref. [] with the permission of Elsevier.
In addition to microgravity studies, other scholars have also studied the effects of airflow environment [], pressure [], and inclination angles [] under normal gravity conditions on the ignition of wires under overcurrent conditions. These studies all show that the gas-phase kinetic effects cannot be ignored for the ignition behavior of wires under overcurrent conditions. Meanwhile, due to the large amount of Joule heat brought by the overcurrent, the pyrolysis time is greatly reduced compared with the external heat source, which is comparable to the mixing time and chemical reaction time. This means that all the three times of Equation (4) need to be considered.
For overcurrent ignition, will be changed to the following equation:
can be calculated as follows []:
where and represent the diffusion coefficient and boundary layer thickness. is the Lewis number. is nature convective heat transfer coefficient, which should be changed to the mixed convective heat transfer coefficient if there is external airflow.
The gas-phase chemical time consists of two parts: chemical induction time and chemical reaction time:
can be expressed as follows [,]:
where c is a proportionality constant, E is the gaseous reaction activation energy, n is the reaction order, A is the pre-exponential factor, and is coefficient and calculated as . is the spontaneous temperature. is the reaction heat, and X represents the volume fraction.
can be expressed as follows []:
It can be seen from Equations (3)–(9) that changes in gravity, pressure, oxygen concentration, air flow, and tilt angle affect different components of the ignition delay time. For example, convective heat loss is positive with the heat transfer coefficient h, which is positive with . Due to , . With the decreasing ambient pressure p, the pyrolysis time decreases according to Equation (5).
2.1.3. Arc Ignition
Arc failures can be induced in several ways [,,]: (1) when the surface of the cable insulation layer forms a conductive path due to carbonization, moisture, pollution, and other factors, a high-temperature arc may be formed on the surface of the cable insulation layer; (2) the high temperature generated by the fire or the formed arc will cause the surrounding air to ionize, and the conductive gas may lead to the formation of a new arc once it is in contact with other circuits; (3) the high temperature generated by fire or the formed arc will lead to the pyrolysis of the insulation layer, reducing its insulation and eventually leading to the formation of an arc. The arc temperature is about 6500 K at the lowest current of the arc and gradually rises to tens of thousands of Kelvin at a high current [], which is much higher than the ignition temperature of any polymer.
Previous research on arc faults usually focuses on the detection method of arc faults. Only a few scholars have studied the arc ignition characteristics of wires and cables. Currently, two methods are usually adopted to study the ignition and thermal characteristics of wire arcs: arc fault simulation [,,,] and overload-induced arc [,], as shown in Figure 6.
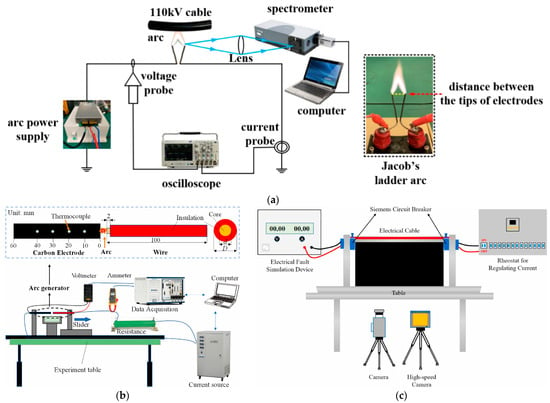
Figure 6.
Arcing mode. (a) Jacob’s ladder arc. Ref. []; (b) series arc generator by fixed electrode and movable electrode. Reprinted from Ref. [] with the permission of Elsevier; (c) overload-induced arc. Reprinted from Ref. [] with the permission of Elsevier.
The two experimental methods have their own characteristics. For the former, the thermal behavior and ignition behavior under the action of a continuous arc can be studied. For the latter, we can study the ignition characteristics of an open arc caused by a direct current. It can be confirmed that for both modes, a Joule heating effect and arc ignition effect exist simultaneously. For arc fault simulation, the ignition and non-ignition heat transfer models are shown in Figure 7. The model satisfies the following assumptions []: (1) Both the carbon electrode and polymer sheath are isotropic, meet the properties of thermally thin materials, and ignore the contact thermal resistance. (2) The thermal inertia of the polymer sheath is much smaller than that of the carbon electrode. (3) The deformation of the electrode and sheath, axial heat conduction, heat absorption, and heat release of sheath pyrolysis are ignored. (4) The arc flow is in a state of local thermodynamic equilibrium, regardless of the chemical reactions involved in the arc. (5) The heat flux density of the cylindrical arc space in each circular cross section along the radius (r) distribution approximately fits the Gauss surface heat source model and is independent of the time of arc discharge and the direction of arc length. Additionally, the current range has little effect on the radius size of heating area formed by arc heat source. In this model, the externally wrapped polymer receives energy from the arc at the point of arc generation while receiving Joule heat from the current and heat conduction of the arc through the electrode away from the arc. The equilibrium temperature of the carbon electrode and ignition delay time of the sheath can be expressed by Equation (10) and Equation (11), respectively.
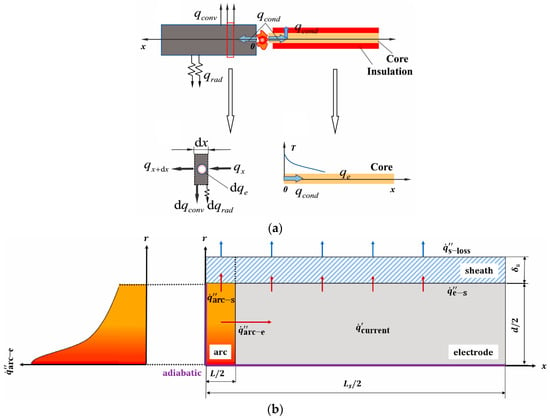
Figure 7.
Heat transfer model. (a) Non-ignition (the red square represent control body). Reprinted from Ref. [] with the permission of Elsevier; (b) ignition. Reprinted from Ref. [] with the permission of Elsevier.
For overload-induced arc, the ignition process is very similar to the overcurrent ignition process. The difference is that the overcurrent ignition source is the spontaneous ignition of the pyrolysis mixture or high-temperature core-assisted ignition, but for the former, the pyrolysis mixture is ignited by the arc. Additionally, for multi-core wires, multiple arc breakdown will occur before the core fuses due to the high temperature [,], as shown in Figure 8. This means that there will be several ignition points and that the Joule heating effect will persist, which indicates that the actual cable and wire fire scenario may be much more dangerous than the single-core wire overcurrent or arc ignition.

Figure 8.
Multiple breakdown arc at 48A. Reprinted from Ref. [] with the permission of Elsevier.
2.1.4. Ignition to Flame Propagation Transition
Regardless of the mode of ignition, it is not always possible to maintain combustion and spread after ignition. This may be due to heat sink of the high thermal conductance core, the inadequate heating energy, or the poor oxygen concentration leading to the reaction rate being too low. In this case, the combustion cannot be sustained [,]. Under external heating without an internal current, it is necessary for steady flame propagation that the preheating length by the igniter (Lig), defined as the length from the center of heating region to the temperature point being , should be larger than the preheating length of the steady flame (Ls~) []. The transition under arc ignition or overcurrent ignition also needs to be studied because the flame spread distance varies with the overload current value after the core fusing under Joule heat and flame heating [,].
2.1.5. Pyrolysis Model
In all the kinds of ignition models discussed above, only the gas–solid phase heat transfer is usually considered, and the pyrolysis process of the material is ignored. In this year’s research, more scholars began to consider the pyrolysis model within the ignition model, such as Guo’s simulation of two ignition modes of continuous electric wires under microgravity conditions [], L. Courty’s simulation of the mass loss of wires and cables under the action of external heat sources [], etc. In the fire community, the commonly used pyrolysis models are mainly the pyrolysis models of FDS, Thermakin, and GPYRO. A brief description of the governing equations of the simplified pyrolysis model will be given in the following paragraphs [].
Condensed-phase mass conservation:
Condensed-phase species conservation:
Condensed-phase energy conservation:
where , , , .
The pyrolysis kinetic parameters such as A, E, n, and ΔH can be obtained from thermogravimetric analysis experiments. Scholars have conducted many studies on the pyrolysis characteristics of commonly used cable and wire materials such as PE [,,], XLPE [,,], EVA [,], PUR [,,], and PVC [,,,], and the relevant literature can be consulted according to the specific material.
2.2. Fire Spread
After the insulation is ignited, the fire spread phenomenon can occur after meeting the conditions described in Section 2.1.4, the rate of which is another key to assessing the fire risk of wires. According to the interaction between air flow and fire spread, fire spread can be divided into opposed-flow fire spread and concurrent-flow fire spread []. The fire spread can also be divided into vertical fire spread, horizontal fire spread, and inclined fire spread according to the direction of fire spread. A schematic diagram is shown in Figure 9. The classical fire spread formula can be used to qualitatively express different fire spread behaviors.
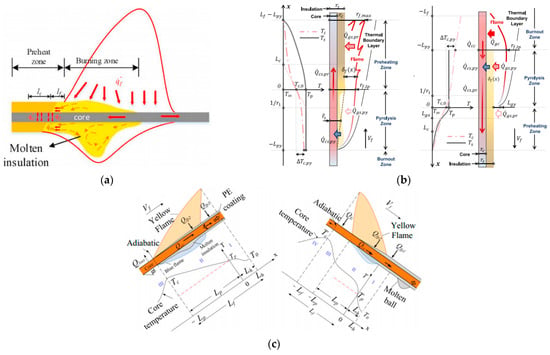
Figure 9.
Schematic diagram of fire spread. (a) Horizontal fire spread. Reprinted from Ref. [] with the permission of Elsevier. (b) Vertical fire spread: upward fire spread (left) and downward fire spread (right). Reprinted from Ref. [] with the permission of Elsevier. (c) Inclined fire spread: upward fire spread (left) and downward fire spread (right). Reprinted from Ref. [] with the permission of Elsevier.
In general, the process of flame propagation over the wire is generally considered as a series of steps that heat the polymer insulator to the characteristic temperature (i.e., the pyrolysis temperature Tp) at the pyrolysis front through inner core conduction and gas-phase flame feedback. As can be seen from Figure 8, regardless of the type of fire spread, the thermal effect affecting the flame spread in the control body comes from the following parts: the burnout zone, the combustion zone/pyrolysis zone, and the preheating zone [,,,]:
- (1)
- the heat feedback of the flame to the preheating zone (including the convection component and the radiation component);
- (2)
- the heat feedback from the core to the insulation in the preheating zone the heat feedback from the core to the insulation in the preheating zone (and joule heat generated by the energized core if the wire is energized);
- (3)
- the molten insulation in the liquid phase and Marangoni convection (and the heat loss of dripping behavior if the molten insulation drips);
- (4)
- the heat loss from the sample surface (convection and radiation).
One of the most important parameters to evaluate fire spread is the fire spread rate. According to the heat balance equation, the expression of the fire spread rate can be qualitatively given as follows:
where the subscripts f, c, m, and p represent the flame, core, molten insulation, and insulation surface, respectively. l is the characteristic length of each heat transfer component.
Equation (15) is a simplified fire spread model that only considers the heat transfer effect. The phase transition, chemical reaction process, and unstable fire spread behavior in the actual wire fire spread process will affect the fire spread rate. Therefore, under different experimental designs, the results are difficult to uniformly analyze using Equation (15). In this case, only the research results of various scholars are summarized, and the influence mechanism of each factor will be analyzed based on a simple theoretical analysis based on previous studies.
2.2.1. The Metal Core
Different from other combustibles, wire fire has a unique phenomenon of core heat conduction. In the process of wire fire spreading, there are two states of heat sink under the burnout and burning zone and heat source under the preheat zone in different areas of wire fire [,], as shown in Figure 10. The competition mechanism of the heat sink and heat source is significantly different for different core materials and fire spread forms. The horizontal flame spread increases with wire conductance [], while the vertical downward flame spread decreases with wire conductance [], as shown in Figure 11b. This is mainly because the heat transfer from the wire core plays an important role in horizontal fire spread. With the increase in thermal conductivity, the preheating effect of the core is enhanced, and the fire spread rate increases. When the vertical fire spreads, the molten insulation will slide downward due to gravity, and the convection effect from Marangoni is enhanced, while the heat source effect of the wire core is weakened. At the same time, the heating of the burnout zone of the flame increases and the heat sink effect of the core with a high thermal conductivity is enhanced, so the fire spread rate decreases with the increase in thermal inertia.
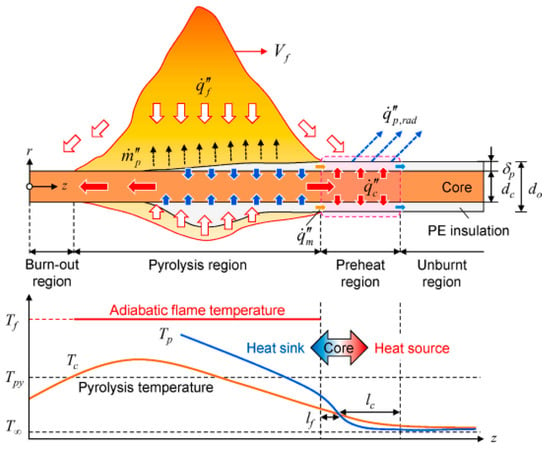
Figure 10.
The heat sink and heat source of the core. Reprinted from Ref. [] with the permission of Elsevier.
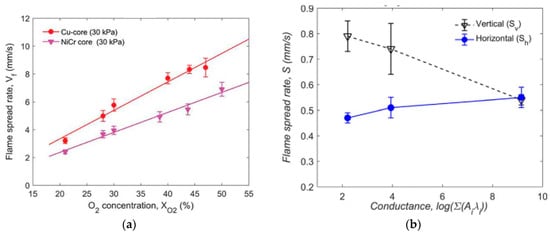
Figure 11.
Fire spread rate under different cores. (a) Horizontal fire spread rate over NiCr and Cu wires under different oxygen concentrations. Reprinted from Ref. [] with the permission of Taylor & Francis. (b) Flame spread rate over LDPE wires as a function of the cross-section’s thermal conductance. Reprinted from Ref. [] with the permission of Elsevier.
2.2.2. Inclination Effect
As the angle changes, the position relationship between the flame and the wire will change, thus changing the heat transfer mechanism []. The research on the inclination effect was first carried out by Hu [], according to which it was found that for a copper conductor with high thermal conductivity, the fire spread speed increased with the increase in the absolute angle. However, for a nickel–chromium conductor with a low thermal conductivity, it almost remained unchanged at −90 °C~+15 °C, and +15 °C~+75 °C increased with the increase in the angle, as shown in Figure 12. However, he did not propose an analysis of the inclination effect, but instead carried out theoretical calculations based on the flame characteristic lengths at different angles: the flame wrapping width Wf and pyrolysis length Lp, combined with a heat transfer analysis. Lu [] proposed in his study on the interaction between inclination angle and horizontal wind that when the flame becomes longer and tilts toward the wire, the width of the combustion zone will also increase. The former enhances the convective heat flow of the flame to the preheating zone, while the latter increases the core temperature, which also explains the inclination effect to a certain extent. Zhang [] elaborated the inclination effect by considering the influence of inclination angle on net heat flow and expressed the positive heat flow of the negative angle and positive angle as shown in Equation (16) and Equation (17), respectively.
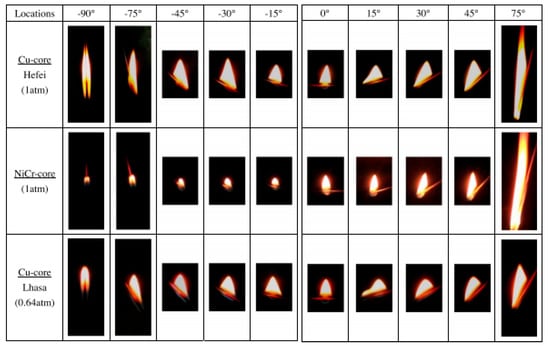
Figure 12.
Fire spread over Cu and NiCr wires at different inclination angles. Reprinted from Ref. [] with the permission of Elsevier.
Here, and represent the heat flux induced by the gravity and the heat loss from the flame.
Other scholars such as Zhao [] have considered the effects of the tilt angle on the Nussel number, the characteristic convection size, and the flame preheating length. The effects of the inclination angle on flame radiation were also considered in []. The above methods can reflect the inclination effects well, but it is still necessary to systematically summarize the inclination effects.
2.2.3. Oxygen Concentration
The effects of oxygen on combustion usually entail two aspects: (1) the pyrolysis rate of the polymer is accelerated, and the pyrolysis temperature is reduced [,]; (2) The gas-phase oxidation chemical reaction rate increases (explained by Equation (20)) and the flame temperature and the heat flux of the flame increase, as shown in Figure 12. Because of the enhancement in the heat flux of the flame and the decreased pyrolysis temperature, the limit of the ignition energy of the external heating source or Joule heat is smaller [,] and the fire spread rate increases, as shown in Figure 11a and Figure 13b,c. However, for the vertical downward fire propagation of high-thermal-conductance core wire, the fire propagation rate shows a special non-monotonic change with the increase in oxygen concentration, as shown in Figure 13c. In this case, the fire spread rate presents three states with the change in oxygen concentration. The first state is a general monotone increase, which is called the “temperature-dependent regime”. The second state is due to the increase in the flame heat flux to the limit, while the flame length decreases with the increase in oxygen, resulting in a decrease in the thermal feedback from the flame received by the core. This leads to the weakening of the heat conduction of the wire core to the preheating zone, thus showing the phenomenon that the fire spread rate decreases with the increase oinoxygen concentration, which is called “negative oxygen dependence”. However, for the NiCr core with a low thermal conductivity, the heat transfer in the preheating zone is not dominant. As a consequence, the decrease phenomenon does not exist. At a high oxygen concentration, because the flame is flame, more soot is generated. Therefore, the heat radiation from the flame is enhanced, and the fire spread rate increases [].
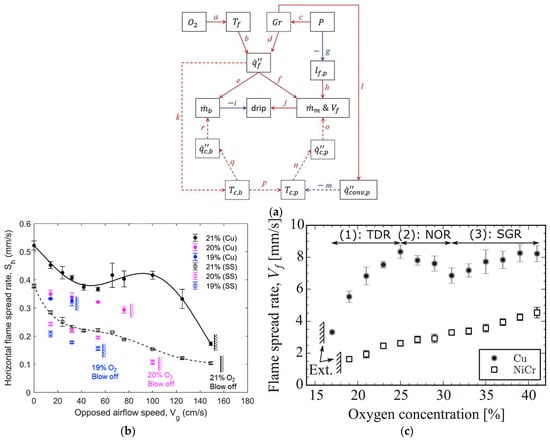
Figure 13.
Fire spread rate varies with oxygen concentration. (a) The effects of oxygen concentration and pressure. Reprinted from Ref. [] with the permission of Taylor & Francis. (b) Horizontal fire spread rate over SS (stainless steel) wire and Cu wire under different oxygen concentrations and opposed airflow speeds. Reprinted from Ref. [] with the permission of Elsevier. (c) Vertical fire spread rate over Cu and NiCr wire under different oxygen concentrations. Reprinted from Ref. [] with the permission of Elsevier.
Given the important role of oxygen in combustion, the minimum oxygen concentration at which ignition cannot occur or cannot maintain fire spread behavior after ignition—that is, the limiting oxygen concentration (LOC)—can be used as a parameter to evaluate the flammability of materials []. The LOC will change with different environments and other factors, and many studies have been carried out to study these aspects [,,,].
2.2.4. Ambient Pressure
Changes in pressure affect the process of mass transfer and convective heat transfer, and the specific performance is as follows [,,,]:
According to Equation (21), it can be inferred that with decreases in pressure, the convective heat loss decreases, making the fire spread rate increase, but the actual situation is different.
The effects of low and high pressure on the wire flame shape are shown in Figure 14. With increases in pressure, the fire spread rates are different for different cores and wire sizes, as shown in Figure 15. The increase in pressure has a negative effect on the fire spread rate of nickel–chromium alloy-core wire and has no obvious effects on the fire spread rate of iron-core wire. Meanwhile, for copper-core wire, there are different effects according to the different wire sizes. The main reason for this kind of wire core is that the wire core and the preheating effects of the flame show different behaviors under different pressures. Nakmura et al. [] proposed a “flame-driven mode” and “wire-driven mode” to explain this phenomenon, illustrated in Figure 16. However, they only considered the change in the heating length of the gas phase and the solid phase with the pressure, and both of them decreased with the pressure, which could not explain the change in the fire spread of the copper core wire with the pressure. Based on this work, Hu [] elaborated on the conversion mechanism and heat transfer mechanism of the two modes by considering the convective thermal feedback of the flame front supporting the flame-driven mode and the thermal feedback supporting the wire-driven mode and combined them with the core size. Zhao [,] also explained the effects of a high atmospheric pressure on the fire spread rate by analyzing the convection and radiant heat feedback of the flame. By considering the combustion efficiency and the characteristic scale of the wire core, Wang [] gives the expression of the change of the fire spread rate with the pressure and the wire size ().

Figure 14.
Flame shape under sub-atmospheric pressure. Reprinted from Ref. [] with the permission of Elsevier.
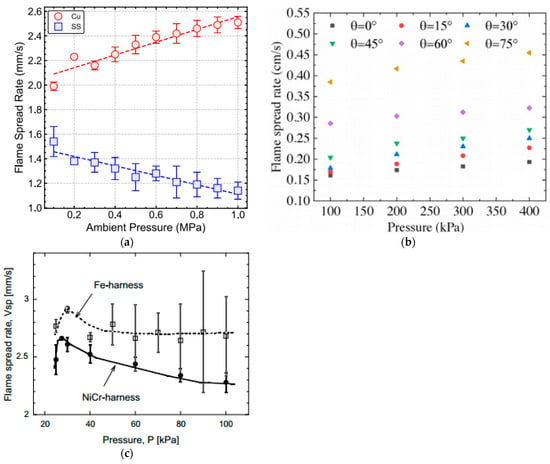
Figure 15.
Flame spread rate under various pressures over different wires. (a) Cu and SS wires under sub-atmospheric pressure. Reprinted from Ref. [] with the permission of Elsevier. (b) Cu wire versus inclination angle in high atmospheric pressure. Reprinted from Ref. [] with the permission of Elsevier. (c) Fe and NiCr wire under sub-atmospheric pressure. Reprinted from Ref. [] with the permission of Elsevier.
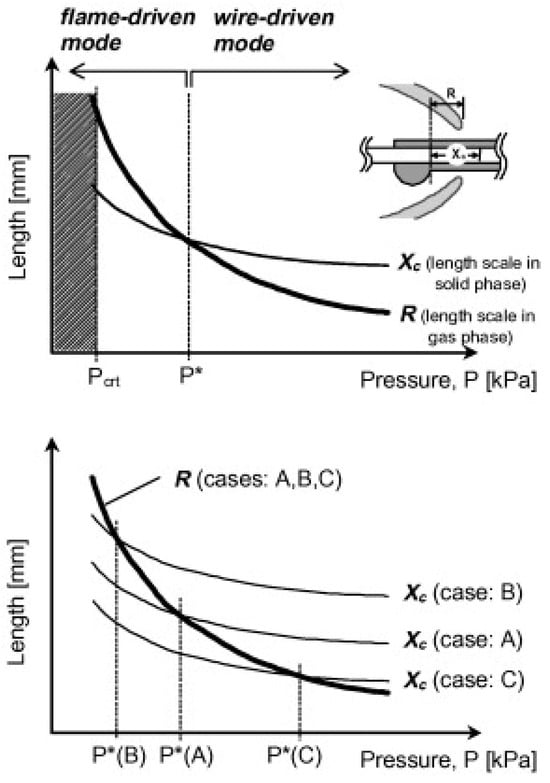
Figure 16.
The heat transfer mechanisms of “wire-driven” and “flame-driven” modes. Reprinted from Ref. [] with the permission of Elsevier.
2.2.5. Gravity
Under normal gravity conditions, the flame spreading over the wire is usually a candle-like flame due to buoyancy, while in under microgravity conditions, it appears as a symmetrical spherical flame due to the disappearance of the buoyancy effect, as shown in Figure 17. The entire flame will be wrapped around the wire due to the curvature effect of the wire []. A spherical flame also appeared under a low pressure, but the color of the flame was different, as shown in Figure 18. This shows that the gas-phase transport process under low pressure and microgravity conditions is similar, but the chemical reaction rate is different []. In the absence of buoyancy, the thickness of the meteorological boundary layer increases, causing the characteristic time of the gas relative flow and diffusion to become longer. Additionally, the gas reaction may occur at low oxygen concentrations. Therefore, the LOC to maintain fire spread under microgravity conditions is smaller than that under gravity conditions [,].
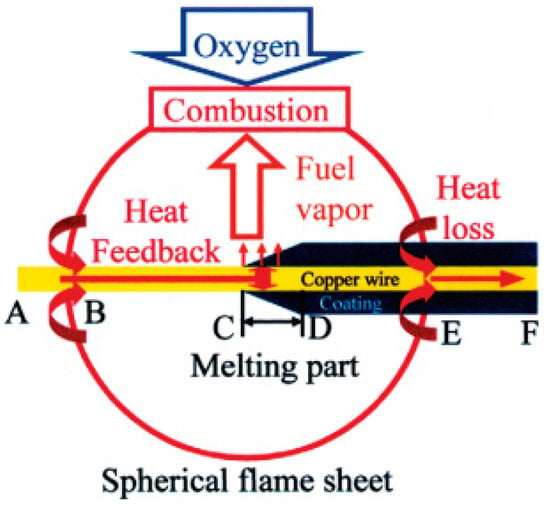
Figure 17.
The mechanism for the formation of the spherical flame in wire insulation burning under microgravity conditions. Reprinted from Ref. [] with the permission of Elsevier.

Figure 18.
Flame shape under microgravity (left) and low pressure (0.3P0) (right) conditions. Reprinted from Ref. [] with the permission of Springer Nature.
As mentioned above, there are opposed-flow fire spread and concurrent-flow fire spread modes. Under normal gravity conditions, due to the induced effect of buoyancy, the upward spread of the flame in the vertical wire is also a special down-flow fire spread. However, this fire spread cannot reach a stable state due to the melting dripping caused by gravity, which causes the flame root to remain in the initial position until the flame wraps the entire sample. This fire-spreading behavior also changes under microgravity conditions []. Meanwhile, under microgravity conditions, according to the previous analysis, the flame will wrap around the online core, and in the case of the disappearance of natural convection, the preheating length will increase compared with that under normal gravity. This enhances the flame heat feedback under microgravity conditions, while the convective heat loss disappears. Therefore, the fire spread rate is greater than that under normal gravity conditions, as shown in Figure 19.
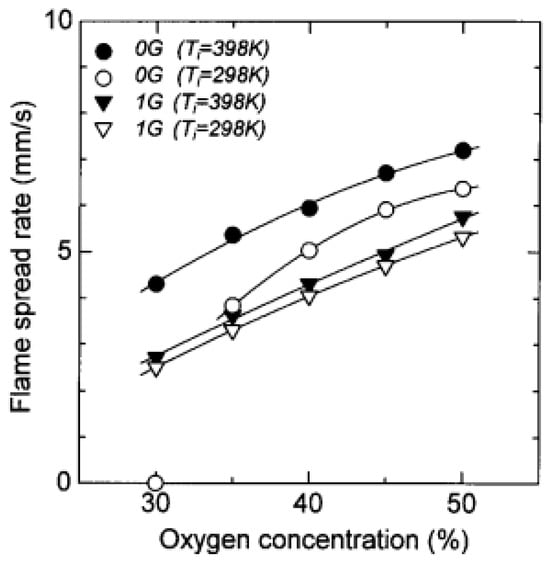
Figure 19.
Flame spread rates in microgravity conditions and at normal gravity as a function of ambient oxygen concentration. Reprinted from Ref. [] with the permission of Elsevier.
2.2.6. Airflow
According to the relationship between the direction of air flow and the direction of fire spread, it can be divided into opposed-flow, concurrent-flow, and transverse flow modes.
The influence of gas flow on the fire spread rate is mainly reflected in four aspects: preheating length, stand-off distance, flame temperature, and transport state of pyrolysis gas and oxygen. These produce four effects in the microgravity opposed-flow fire spread, resulting in three forms of change of the spread rate of opposed-flow fire spread with low-speed countercurrents, as shown in Figure 20 []. However, the flame behavior in normal gravity is different from that in microgravity due to the existence of the buoyancy effect, and the influence of opposed-flow velocity on the flame propagation rate seems to be related to the heat conduction relationship of the core from the inclined flame heat feedback [,]. The fire spread rate varies with the air flow under normal gravity in three states: (I) at a low flow velocity, the fire spread rate decreases significantly; (II) the fire spread rate changes slightly at a medium flow velocity; (III) at a high flow velocity, the fire spread rate changes rapidly. Nakamura [] explains the effects on the inbound flow and the effects of the core on the heat flow of the spreading flame. With increases in the opposed-wind velocity, the heat from the flame to the preheating zone decreases, and the heat transfer exposed to the wire core increases, thus increasing the heat transfer of the core to the preheating zone. For wire cores with a high thermal conductivity, this also means an increase in the heat loss caused by the heat sink. This explains the difference in the fire spread rate trend varying with the opposed-wind mode for different conductance cores.
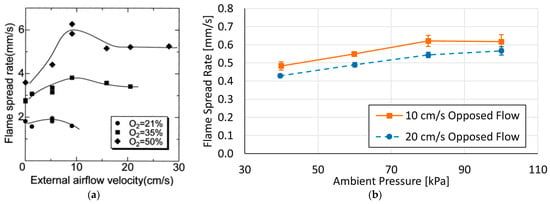
Figure 20.
Opposed flow under (a) microgravity. Reprinted from Ref. [] with the permission of Elsevier. (b) normal gravity. Reprinted from Ref. [] with the permission of Elsevier.
However, with the opposed-wind mode, it does not always appear as the opposed-flow fire spread, such as the upward fire spread under different inclinations with opposed wind. This is because under normal gravity conditions, there will be buoyancy-induced air flow in the vertical upward direction, and the component of the wire direction can offset the opposed-wind velocity. This explains why there is the transition of concurrent fire spread induced by the buoyancy and opposed fire spread induced by the high-opposed wind velocity [], as illustrated in Figure 21. At the transition of the concurrent fire spread and the opposed fire spread, the flame tends to be perpendicular to the wire, and there is a local maximum LOC because of the local minimum flame feedback and minimum heat conduction from the core.
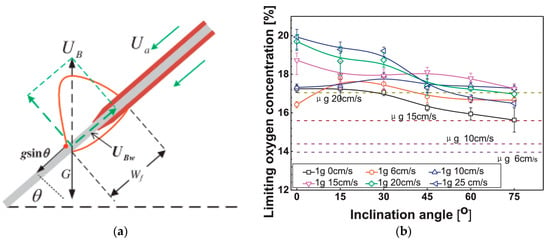
Figure 21.
Upward fire spread over inclined wires with opposed flow. Reprinted from Ref. [] with the permission of Elsevier. (a) The physical interpretation of local maximum LOC based on the balance of buoyancy-induced flow in the wire’s direction with opposed-flow speed. (b) The LOC varies with the opposed-flow velocity.
The opposite of the opposed-flow effect is concurrent flow. Compared to the opposed flame spread, the concurrent fire spread is much faster, and with the velocity of the concurrent flow increasing, the fire spread rate (FSR) increases first in a nearly linear manner and then reaches its maximum value. When it is at the blow-off velocity, the FSR decreases slightly and is eventually blown off []. The trends of FSR under different concurrent-flow velocities and the heat transfer before reaching the maximum FSP are shown in Figure 22. As for the inclination wire, the change in the FSR is similar to that for horizontal wire. However, for the horizontal wire, the flame cannot be parallel to the wire due to the role of buoyancy, while for the inclined wire, there are three kinds of positions: the flame above the wire, the flame parallel to the wire, and the flame below the wire [], as shown in Figure 23.
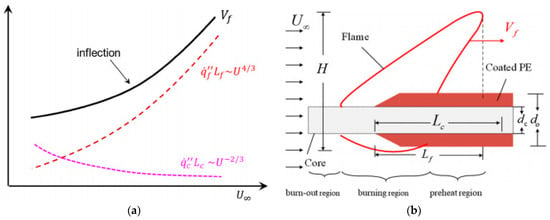
Figure 22.
The effect of the concurrent wind velocity. Reprinted from Ref. [] with the permission of Springer Nature. (a) Trends of the flame heat feedback, heat conduction from the core, and FSR. (b) Diagram of the concurrent flame spread over a thin wire.

Figure 23.
Flame behavior at different angles and parallel wind velocities. Reprinted from Ref. [] with the permission of Elsevier.
When the angle becomes 90 degrees, the opposed wind becomes the transverse wind, and the fire spread rate varies with the wind speed except periodically. Ma [] proposes a theoretical model based on two characteristic lengths (flame-base width Wf and gas-phase length Lg), which explained the trends of FSR in the four regimes, as shown in Figure 24, from the point of view of heat transfer and chemical reactions:
- (1)
- Regime A (as-phase convection-enhanced regime): The enhancement in the gas relative flow causes the enhancement of net heat flow in the low-velocity area.
- (2)
- Regime B (cooling effect-enhanced regime): The heat loss because of the heat sink of the core results in the net heat flux increasing.
- (3)
- Regime C (liquid-phase Marangoni convection effect regime): The heat flux from the molten material (liquid-phase Marangoni convection) and the solidified droplets formed downstream prevent the cooling of the naked core due to airflow, eventually causing an increase in the net heat flux.
- (4)
- Regime D (limited chemical reaction regime): The high transverse flow velocity results in the limited chemical reaction rate.
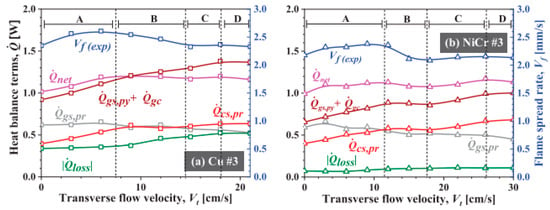
Figure 24.
Heat balance terms and FSR as a function of transverse flow velocity for Cu wire and the NiCr wire. Reprinted from Ref. [] with the permission of Elsevier.
2.2.7. Electric Current and Electric Field
The mechanism of conduction current and electric field on wire fire propagation is significantly different. The effect of current on fire spread is usually to weaken the heat sink of the core and promote its heat source. The presence of an electric field usually changes the charged particles in the reaction zone, affecting the flame shape and thus changing the heat transfer mode in the flame-spreading process. In addition, the chemical reaction rate related to the charged particles will also be affected, and the specific forms of these effects include ionic wind effects, electrophoresis effects, electrospray effects, soot deposition effects, etc.
When the current is small, the fire spread rate and the size of flame are almost always increased with increases in the current because of the enhanced preheating from the core [,,]. Additionally, because the core resistance and the convective heat loss indicated by the wire are related to the wire size (core radius and insulation layer thickness), there is usually a different trend for the fire spread rate with the increase in current, as shown in Figure 25. However, at the large currents, due to the large amount of heat production of the core, the softening of the insulation layer and the melting rate are enhanced, which promotes the generation of molten dripping. The flame height goes through three stages with the change in current: growth stage, steady stage, and drop stage, while the flame width is almost constant []. A comparison and the mechanism are shown in Figure 26c. Due to the enhanced dripping, the fire spread rate tends to remain constant at high currents, which has been explained by Tang [] based on an analysis of heat transfer.
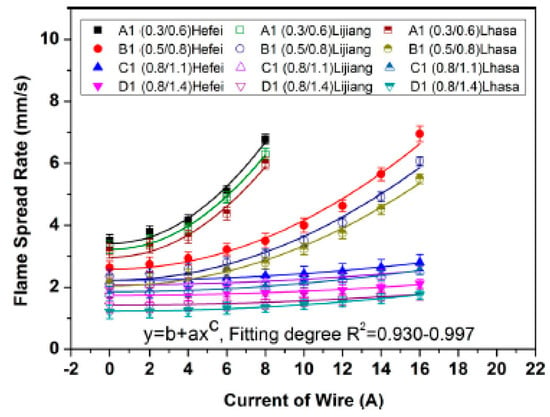
Figure 25.
Flame spread rate as a function of currents for different-sized wires (the value in the label, such as 0.3/0.6, indicates the core diameter/wire diameter). Reprinted from Ref. [] with the permission of John Wiley and Sons.
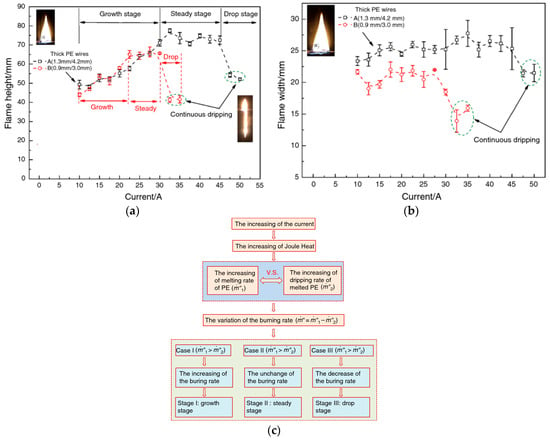
Figure 26.
The size of the flame varies with the current and the mechanism. Reprinted from Ref. [] with the permission of Springer Nature (a) Flame height; (b) flame width; (c) mechanism of flame variation with current.
As mentioned above, the effect of the electric field on wire fire propagation mainly comes from ionic wind effects, electrophoresis effects, electrospray effects, soot deposition effects, etc. At low-frequency and high-frequency regimes of the electric field, the voltage has different effects on the wire fire propagation rate, which can be divided into three regimes, within which there are several distinct regimes depending on the frequency [,], as shown in Figure 27. Additionally, the inclination angle [], core metal [], and insulation thickness [,] also affect the effect of electric fields on fire spread. Figure 28 shows the specific fire behavior under the electric field. The above studies have explained the effects of electric fields on fire propagation to some extent. However, due to the complex mechanisms of the effects of electric fields on wire fire propagation behavior, the effect mechanism has not been explained by relevant theories, which deserves further research.
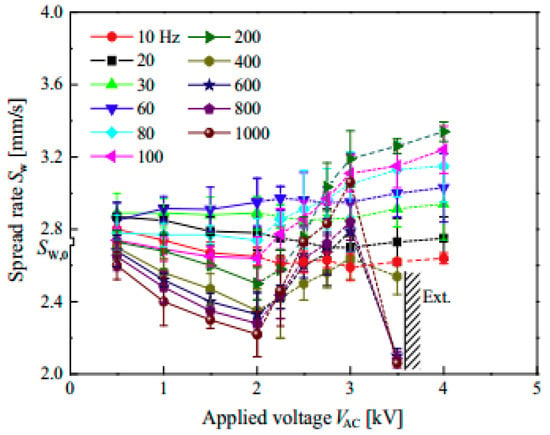
Figure 27.
Variation in fire spread and flame shape at various frequencies and voltages. Reprinted from Ref. [] with the permission of Elsevier.

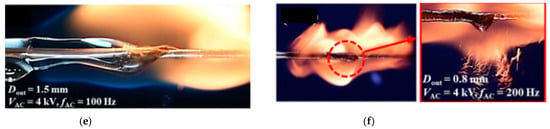
Figure 28.
Specific fire behavior under an electric field. (a) Soot deposition. Reprinted from Ref. [] with the permission of Elsevier. (b) electrospray. Reprinted from Ref. [] with the permission of Elsevier. (c) dielectrophoresis phenomenon. (d) Globular molten PE near flame front along with formation of molten-PE film. (e) Globular molten PE near flame front and twisted molten PE related to rotating phenomenon of molten PE (f) Weak vortex flames at the front and rear flame edges. Reprinted from Ref. [] with the permission of Elsevier.
2.3. Dripping
The melting rate of insulation can be represented as the sum of the burning loss and the dripping loss []:
The simple criterion for dripping is that the average melting rate is larger than the average burning rate, and the gravity of the accumulated molten ball exceeds its surface-tension [,,]:
where B is the mass transfer number, is the flame radiative loss fraction, is the equivalence ratio, is the surface re-reradiation, is the heat loss of the core, is the enthalpy of the molten PE dripping from the burning region, is the surface tension of the molten ball, and Bo is the Bond number (or Eötvös number), the critical value of which for dripping is 6. As illustrated by the above equations, variations in the oxygen concentration and pressure will change the dripping behavior, which can be expressed by Figure 13a. Fang [] finds the dripping limit and the fire spread limit under various oxygen concentrations and pressures, as shown in Figure 29.
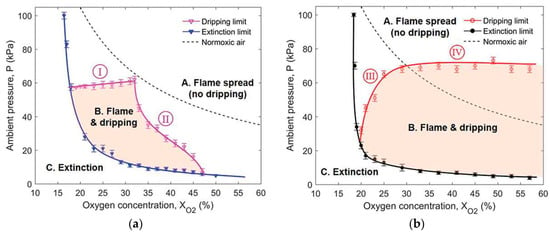
Figure 29.
Dripping and fire spread limits of (a) Cu-core wire and (b) NiCr-core wire. Reprinted from Ref. [] with the permission of Taylor & Francis.
Another important parameter is the dripping frequency , which can be expressed as follows []:
As Equation (26) illustrates, the dripping frequency is affected by the current, except for the oxygen and pressure effects on the flame feedback, which are proportional to the square of the current. Studies by He [] and Wang [] also confirm this. In addition to the above effects, the droplet behavior is also affected by the inclination angels because of the sliding over the inclination wire. The specific sliding velocity U can be described as a dimensional version of Durbin’s solution []:
where is the critical shear stress; and , and and are the advancing contact angle and the advancing contact angle of the droplet attached to the wire. It is obvious that dripping only occurs when the velocity is zero. Thus, there is a critical droplet size at U = 0 []:
Although the formation conditions of the droplet behavior and related prediction models have been studied and proposed, the droplet behavior still cannot be accurately described because the relevant parameters of the material are temperature-dependent. More studies are required to understand the complex phase change process and formation process of droplets in wire fires.
2.4. Extinction
As with other fuels, the extinction of combustion comes from two aspects: the thin combustible component and a flame that is not strong enough to pyrolyze the fuel, which represent the blowoff and quenching, respectively. The Damkohler number (Da) [,], defined as the ratio of the gas-phase residence time (tr) to the chemical reaction time (tc), or the strain rate under mixed-flow (am), defined as the ratio of the mixed flow velocity to the radius of the wire [,], are used to explain the blow off:
For quenching, the characteristic parameters are the mass transfer number (B) or Rloss [,]:
where is the mixed flow velocity of the opposed flow and natural flow, and represent the volume fraction of fuel and oxygen, R represents the characteristic radius of the wire near extinction, is the inclination angle of the wire, is the radiation loss rate from the insulation surface to the ambient condition, and is the heat loss rate of the wire.
As expressed as above, the extincition of the wire fire is determined by the oxygen, pressure, gravity, external flow, etc. Lower oxygen concentrations, pressures, and gravity can make the flame weaker or even extinct, as shown in Figure 17, because of the heat loss and burning rate, as illustrated in the preceding paragraph. Even if the flame is stronger, the external flow can bring the gas mixture away from the reaction region, which results in the extinction of the wire fire. Thicker insulation requires a higher flow velocity. In fact, blow-off and quenching could play simultaneous roles in flame extiction [], which means that the boundary between combustion and extiction can be determined by the characteristic numbers of quenching and blow-off events, as shown in Figure 30. Morever, dripping, which removes significant amounts of heat and melt insulation, can also result in extinction, and a sudden weak flame can be observed at the time after dripping []. Due to the effects of electric fields on flame and heat transfer, extinction can also be observed with increases in voltage and frequency, but this mechanism has not been clarified [,].
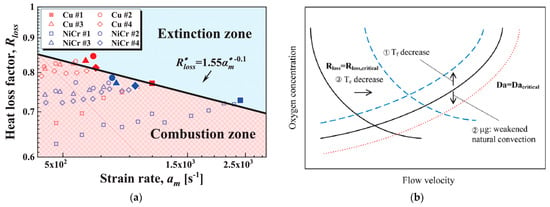
Figure 30.
The boundary between extinction and combustion. (a) Rloss vs. am. Reprinted from Ref. [] with the permission of Elsevier. (b) Rloss vs. Da. Reprinted from Ref. [] with the permission of Elsevier.
3. Real Cable Fire Research
There are two aspects of cable fire studies: the combustion characteristics of cable materials and cable tray fire behavior.
3.1. Combustion Characteristics of Cable Materials
In terms of material combustion characteristics, studies generally use cone calorimeters, OSU calorimeters, and other equipment to study the ignition time, heat release rate, effective combustion heat, and flue gas generation of the cable.
Matheson et al. [] and Barnes et al. [,] studied the combustion characteristics of halogenated and non-halogenated PVC cables and compared their fire resistance. They found that adding halogen elements improved the fire resistance of the cables, but the smoke production, toxicity, and corrosion were enhanced. Yang et al. [] used a pyrolytic combustion flow calorimeter to test the flammability of eight cable materials, analyzing the heat release rate, ignition temperature, and total heat release. Romain et al. [] also used CONE to study two kinds of halogen-free flame-retardant cables under different heat fluxes and cable spacing. The results showed that under the action of external radiation, the thermal thickness ignition model could better predict the ignition time, and the increase in cable spacing would slightly increase the ignition time. Gong [] established a ring heating experiment platform and carried out cable ignition experiments under the heating condition of a t2 heat source. He found five processes of thermal deformation of flame-retardant PVC cable before a fire: the inert stage, wave stage, expansion stage, contraction stage and stable stage. He also explained the special behavior of cable thermal expansion and ignition based on a thermogravimetric analysis.
In recent years, aging cable materials have attracted extensive attention from scholars, but the research conclusions are not the same or are even contradictory. Xie et al. [] studied the fire protection characteristics of old and new cables using TGA-FTIR and a micro-calorimeter (MCC). The experimental results showed that when the temperature was higher than 277 °C, the mass loss of the aging cable jacket was significantly greater than that of the new cable jacket. The final residual mass of the old cable was much smaller than that of the new cable. In addition, in air or nitrogen atmospheres, the initial mass loss temperature of the new and old cables under various heating rates was generally the same, but the mass loss during the pyrolysis process of the old PVC sheath was larger than that of the new sheath, and the HCl release speed was slower than that of the new sheath. However, the initial release time was earlier than that of the new sheath. The results of the MCC showed that the old jacket burned more strongly and that the heat release per unit mass was higher than the new jacket. However, in this experiment, there was no guarantee that the old and new jacket came from the same cable.
Li et al. [] used a cone calorimeter to simulate the fire characteristics of crosslinked polyethylene cables under fire conditions. The experimental results showed that with increases in aging time, the ignition time first increased and then decreased, which may be due to the volatilization of combustible components such as plasticizers and lubricants in the initial insulation layer. In the later stage, due to the decrease in the thermal stability of the insulating material, the ignition time decreased, while the heat release rate was the opposite. Zhang et al. [] used a cone calorimeter to study the effects of different aging times and types (thermal oxygen aging, hydrothermal aging, ozone aging, and xenon arc aging) on the fire resistance of two kinds of wires under a constant radiation intensity. The results showed that aging had different effects on the ignition time and heat release rate of different types of cables, but the ignition time was longer than that of non-aging cables. Among the four types of aging, the ignition time of thermal aging cables was longer than that of the other three types of aging, and the heat release rate was also higher than that of other aging modes. Kim et al. [] analyzed the fire risk in the early, middle, and late stages of combustion of cables with different aging degrees based on the fire performance index (FPI) and fire growth index (FGI). The experimental results showed that in the early stage of combustion, with the extension of aging time, FPI showed an increasing trend due to the loss of volatile components in the cables. FGI showed a downward trend, and the fire risk was low, but in the middle and late periods, HRR, THR, and MLR were greater than those of non-aged cables. The fire risk increased, and the changes in CO2, CO, and HCl with the degree of aging also varied. Fang et al. [] conducted thermogravimetric analyses, differential scanning calorimetry tests, and fire spread tests on aging wires. The results of the thermogravimetric analyses and differential scanning calorimetry tests demonstrated that the aging wires showed different pyrolysis temperatures and crystallinities at different aging temperatures. However, different pyrolysis temperatures and crystallinities have different effects on the ignition delay time of chemical kinetics under different pressures. Chemical kinetics control the ignition delay in the low-pressure region, and heat transfer controls the ignition delay in the high-pressure region. The higher the pyrolysis temperature and crystallinity, the larger the chemical kinetic control area of the wire. Wang et al. [,,,,,], combined with previous studies, conducted a comprehensive study on aging cables from the aspects of pyrolysis, fire characteristics, and flame propagation behavior and determined the reaction models and pyrolysis kinetic parameters of LDPE and PVC with different degrees of aging based on thermogravimetric experiments. Combined with Fourier infrared (FTIR), micro-scale combustion calorimetry (MCC), and cone calorimetry, it was found that aging PVC sheath was easier to pyrolyze, the combustion of which was weaker and incomplete, and at a high heat flux, the TTI and pHRR of new and old cables are not significantly different. According to the results of XPS, after thermal aging, the metal in the wire core will diffuse into the insulation layer, which plays a catalytic role in the aging and pyrolysis of the insulation layer, and the fire spread rate generally shows a downward trend with the aging time.
3.2. Cable Fire Behavior
Studies on cable fire behavior are closely related to test standards related to cable combustion performance. The major European standards are shown in Table 1.

Table 1.
Testing standards of cables.
A cable tray is a common way of laying cables in nuclear power plants, the combustion of which is also one of the most common types, as shown in Figure 31.

Figure 31.
Cable tray fire. Refs. [,].
The fire behavior of cable trays has been widely studied by scholars, and full-scale experimental studies are being led by several projects.
From 1975 to 1987, Sandia National Laboratories conducted a series of studies on cable fire behavior [], mainly including an electrical starting cable fire test in 1976, isolated cable tray fire test in 1978, cable fire test in exposed fire in 1977, cable tray fire corner effect test in 1979, flame-retardant sheathed cable test in 1978, and cable fire burning mode analysis in 1981. One of the findings was that the transverse cable bridge fire spreads upward in a “V” shape, and the “V” shape deviates from the center of gravity line at an angle of about 35°. The formation of this “V” shape spread mode is caused by the unequal horizontal spread rate of each layer of cable; that is, the spread rate of the upper layer cable is faster than that of the lower layer.
In 2000, several European national laboratories jointly carried out the FIPEC (Fire Performance of Electrical Cables) project [], which carried out cable fire experiments of different sizes. Among them, according to the actual cable installation size, the real-size cable bridge fire experiment and small-size cable material cone calorimeter experiment were carried out. The real-size experiment was carried out in a relatively narrow corridor, involving the combustion characteristics of the transverse cable bridge and the vertical cable bridge. This established a relationship with the small-size experiment, which provided a basis for the measurement of the subsequent fire heat release rate.
A German study [] carried out a vertical cable bridge fire experiment in open space to study the influence of preheating on the fire spread and burning rate of vertical cables and to simulate the different combustion characteristics of aging cables and new cables. The authors also studied the influence of natural ventilation on the fire characteristics of ordinary PVC cables and flame-retardant cables when laid vertically. The aim was to provide fire model support for nuclear power plant fire safety assessments.
In 2007, The Cable Response to Live Fire Project (CAROLEFIRE) [], including a series of 78 small-scale tests and a second series of 18 intermediate-scale open burn tests, provided data supporting the resolution of a “risk-informed approach for post-fire safe shutdown circuit inspections” and improvements to fire modeling in the area of cable responses to fires.
At the same time, the Cable Heat Release, Ignition, and Spread in Tray Installations During Fire (CHRISTIFIRE) study [,] addressed the burning behavior of a fire beyond the point of electrical failure and developed the fire model FLASH-CAT to predict the HRR of horizontal cable tray fires, vertical cable tray fires, and the corridor fires. Then, Li et al. [] and Huang et al. [] improved the model and proposed improved prediction models for the fire release rate of vertical cable bridges and the fiery release rate of horizontal cable bridges, respectively, and they carried out experimental verification.
The OECD PRIME fire research program led by the France IRSN in collaboration with 12 countries was carried out to understand the mechanisms of smoke and heat transmission in multi-chamber fire scenarios and the impact of fires on targets, which included the following []:
- (1)
- The effects of pressure induced by fires in forced ventilated enclosures;
- (2)
- The effects of oxygen depletion on the fuel mass loss rate;
- (3)
- The relative effects of heat and mass transfers from the fire compartment to an adjacent room;
- (4)
- The effects of the ventilation flow rate on the velocity profiles from the fire room to neighboring compartments;
- (5)
- Cable performance testing;
- (6)
- The effects of damper closure on the fire scenario;
- (7)
- The behavior of the activation of a sprinkler system in a fire scenario;
- (8)
- The behavior of a cable fire in confined and ventilated fire scenarios;
- (9)
- The behavior of an electrical cabinet fire in confined and ventilated fire scenarios.
In addition to the above large-scale projects on cable bridge fire research, there are also several studies on the fire characteristics of full-size cables.
Huang et al. [,,,,] carried out a series of cable tray fire experiments including room fires with vertical cable tray fires in a confined compartment, the effects of cable arrangements and the sidewall effect on the HRR of horizon cable trays. They established several models for cable tray fire prediction.
Zhang et al. [,] proposed three new approaches (improved intra-variance, integral ratio, and N-percentage methods) in a three-layer zone model to predict the stratification interface of fire smoke. Then, they developed a modified HRR prediction model in the compartment by combining the carbon dioxide measurement of HRR and the three-zone model.
Tang et al. [] studied the fire characteristic sand hazards of two typical cables used in nuclear power plants and considered the effects of the cable space, the results of which indicated that NPP flame-retardant cables have a low sustained damage, fire development rate, and overall fire risk. The distance has little effect on the burning time of the sheath, but it promotes the burning of the insulation layer. The time from the first peak to the second peak decreases with increases in the distance. Additionally, the effects of spacing on cable bridge fires are not monotonous. The combustion of cables with a spacing of 10 mm has a higher fire risk, and its quality loss rate is the largest.
The cable spacing effect with the interlayer distance was also studied by An []. The results illustrated that the larger the layer spacing, the higher the flame height and the smaller the flame width. When the distance between layers is greater than 10 cm, the flame cannot spread to the upper layer of the cable. When the layer spacing is fixed, the flame width decreases with increases in cable spacing, and the flame height increases first and then decreases. When the cable spacing is 1.0 cm, the flame height is the largest.
Except for the spacing and interlayer distance, the effects of various fire loads and ventilation speeds on the cable fire spread speed and smoke temperature in a mine was also studied, which showed that the flame-retardant cable can be ignited and continuously burnt at a certain wind speed, but the combustion can be restrained at high wind speeds.
As summarized above, a large number of scholars and projects have systematically studied horizontal and vertical cable tray fires, as well as the effects of the ventilation status, spacing, fire load, and other factors. They have proposed a large number of heat release rate or ceiling temperature prediction models. For cable tray fires, in addition to experimental studies, CFD simulations are also an important branch. The studies in this area fall into two main categories.
On the one hand, some scholars use CFD simulation software, such as FDS, to simulate real cable tray fires. Tang et al. [] simulated multi-layer cable fires using a fire dynamics simulator (FDS). The effects of the cable bridge spacing, ignition position, and tunnel ventilation speed on the fire characteristics were studied. Ferng et al. [,] used FDS to simulate cable burning and typical nuclear power plant fire scenarios and compared them with the experimental results. Qu et al. [] established a multi-physics simulation model of a double-layer cable shaft based on the theories of electromagnetism fluid mechanics and thermodynamics. They also analyzed the temperature distribution of electromagnetic flow in the cable shaft and the influence of the fire-blocking material under rated working conditions.
On the other hand, based on the experimental data, inverse modeling can be carried out using simulation software. The most influential of these studies has been the output of the OECD PRIME Fire Research Project. Sophie et al. [] used the CALIF3S/ISIS CFD software developed by IRSN and took the measured heat release rate in the experiments as the input data to simulate the fire of vertical and horizontal cable trays in the open atmosphere as well as the fire in confined and mechanically ventilated compartments. The differences between the pressure and gas temperature and the experimental results were analyzed. W. Hay et al. [] used the same method to simulate a fire in PVC cables on a long cable tray in a large mechanical ventilation facility. Daniel et al. [] and Verma et al. [] combined FLASH-CAT and FDS to propose a method for determining the HRR of cable tray fires in a confined, ventilation-controlled environment. In addition to the studies mentioned above, some researchers also used small-scale test data (from cone calorimetry) to simulate full-scale cable tray fires [,,].
3.3. The Release of Toxic Gases
As discussed in Chapter 1, toxic gases are a non-negligible potential threat to humans from cable fires. The vast majority of toxic gases in cable fires originate from the organic materials in insulation, sheathing, and other components. These toxic gases mainly include the following types [,,]: nitrogen oxides (NOx: nitrogen oxide (NO) and nitrogen dioxide (NO2)); carbon oxide (CO) and carbon dioxide (CO2); various saturated and unsaturated hydrocarbons; oxygen, hydrogen, fluorine, chlorine, sulfur, nitrogen, and bromine compounds; sulfur oxides (mainly SO2), etc. For the toxicity testing of materials, many countries and organizations have put forward standard test codes with different focuses: DIN 53436 [], NES713 [], BS 7990:2003 [], BS ISO 19703 [], IEC/TS 60695-7-51 [], etc.
The influences on the toxic gas composition in cable fires are mainly due to two aspects: the cable composition material and the type of combustion (flame-burning or smoldering). In recent years, some scholars have studied the release of toxic gases in cable fires for different cable materials and under different external conditions according to the above standard test codes or other test methods.
T. Richard et al. [] tested the yield of toxic products from five commercial cables using the steady-state tube furnace method (IEC 60695-7-50 []) and compared them with the static tube furnace method (NF X 70-100 []) and the results of large-scale cable fire experiments. The results of the steady-state tube furnace method can be used to evaluate the toxicity of combustion cables to a certain extent.
Katarzyna et al. [] studied a PVC-insulated copper electric wire with an unknown composition (PVC filled with chalk) using a steady tube furnace to examine the dependence of the amount of CO, CO2, and HCl under ventilation-controlled conditions. They showed that the values of the CO2 yields of the wire were three times and two times lower than the pure PVC and pure LDPE, respectively, while the values of the CO yield were four times higher than the pure polymers under different ventilation conditions. The value of the CO yield decreased with increasing ventilation, while the HCl yield was shown to be independent of the ventilation conditions.
Rafal et al. [] studied the effects of cable insulation materials and the type of combustion on the generation of toxic gases and the response time of fire smoke detectors in cable fires.
Hyun et al. [] conducted an experimental study of the toxicity index of non-aged to 40-year-old CR/EPR cables based on NES 713 [], which showed that the evaluation toxicity index of the aged cables was higher than that of the non-aged cable.
Min Ho and Seok Hui et al. [,] studied the combustion, smoke emission, and toxic gas emission characteristics of four flame-retardant cables and two fiber optic cables based on ISO 5660-1 [] and NES 713 []. Based on the research results, they simulated the cable laying room of a nuclear power plant and tested more advanced fire dynamics simulations in order to accurately assess the harm of toxic gases released by cable fires to humans.
In the above studies, the types and concentrations of toxic gases released by cable fires vary with different cables and environments, so it may be necessary to build a large database of toxic gases in cable fires under different conditions to achieve an accurate cable fire toxicity assessment method.
4. Conclusions
This work reviews the current research progress of laboratory wire and commercial cable fire research over the past decades. The influences of pressure, oxygen, gravity, external air flow, voltage, and current, as well as the effects of the wire placement mode on the ignition, fire spread, drip, and extinction of wires, are systematically discussed. Based on the basic research results of heat transfer and combustion, the fire behavior of wires under the above conditions was qualitative analyzed. Additionally, the ignition delay time model of three ignition modes, the flame propagation model and the critical criterion of dripping and extinction (blow off and quenching), were also discussed in detail. At the same time, for the studies of commercial cable fires, several large research projects and some researchers’ works on real cable fire behaviors, numerical simulations, and the release of toxic gases were summarized.
Although the current studies on both wires and cables have been extensive and the consideration of various influencing factors is relatively comprehensive, there are still many aspects that are worthy of further study. First of all, in the study of wire combustion, the mixing and chemical processes of the gas phase, phase transition, and flow behavior of the solid phase are usually ignored in the study of the combustion behavior of the wire itself or the influence mechanism of environmental conditions on its combustion behavior. These complex behaviors are crucial to the burning and extinguishing of wires. The neglect of these components has led to the fact that the theoretical models and empirical or semi-empirical prediction models proposed so far can only be qualitatively analyzed and cannot simulate real wire combustion. Secondly, combustion under an electric field is essential for both wires and cables, and the current study has not revealed its true mechanisms. Instead, it has only explained the burning phenomenon of wires under electric fields. Finally, there is a gap between the research of wire-burning behavior and the research of cable fire behavior, and the research conclusions of wire burning cannot be directly applied to real cable fires. Therefore, subsequent research should be gradually extended to cable fire on the basis of revealing the burning behavior of wires.
Finally, this paper only discusses the research progress on the fire and combustion characteristics of cables and wires. There are also other research fields worthy of attention, such as cable fire detection, especially with the application of artificial intelligence, which are also worthy of discussion and summary by scholars.
Author Contributions
Conceptualization, Y.Z. and S.W. (Shasha Wang); methodology, S.W. (Shijie Wang) and K.T.; investigation, Y.L.; resources, S.W. (Shijie Wang) and Y.Z.; writing—original draft preparation, F.Y.; writing—review and editing, Y.Z. and F.Y.; visualization, S.W. (Shasha Wang); supervision S.W. (Shijie Wang) and Y.Z; project administration, Y.Z and S.W. (Shasha Wang); funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (52374225, 52074202).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Symbol | Implication | Symbol | Implication |
| A | Cross-section area (m2)/pre-exponential factor | Nu | Nusselt number |
| a | Strain rate (s−1) | / | Heat flux (kW/m2) |
| B | Mass transfer number | r | Radius (m) |
| Bo | Bond number | t | Time (s) |
| c | Specific heat (kJ/kg/K)/proportionality constant | T | Temperature (K or °C) |
| D | Diffusion coefficient (m2/s)/diameter (m) | U | Sliding velocity (m/s) |
| Da | Damkohler number | x | Wire axial direction |
| E | Gaseous reaction activation energy (kJ/mol) | δ | Thickness (m) |
| f | Frequency (s−1) | Coefficient | |
| Gr | Grashoff number | Chemical reaction rate (mol/L/s) | |
| Reaction heat (kJ/mol) | X | Volume fraction (%) | |
| h | Convective heat transfer coefficient (W/(m2·K)) | Density (kg/m2) | |
| I | Electrical current (A) | Surface tension (Pa) | |
| k | Thermal conductivity (W/m/K) | Equivalence ratio | |
| L | Heating length (m) | Critical shear stress (Pa) | |
| Le | Lewis number | Angle (°) | |
| Mass loss rate (kg/s) |
References
- Residential Building Electrical Malfunction Fire Trends. Available online: https://www.usfa.fema.gov/statistics/residential-fires/electrical.html (accessed on 9 April 2024).
- Eaton, T.E. Electric Services and Building Fires. Fire Technol. 1992, 28, 70–86. [Google Scholar] [CrossRef]
- Andersson, P.; Rosell, L.; Simonson, M.; Emanuelsson, V. Small and Large Scale Fire Experiments with Electric Cables under Well-Ventilated and Vitiated Conditions. Fire Technol. 2004, 40, 247–262. [Google Scholar] [CrossRef]
- Bakhman, N.N.; Aldabaev, L.I.; Kondrikov, B.N.; Filippov, V.A. Burning of Polymeric Coatings on Copper Wires and Glass Threads: II. Critical Conditions of Burning. Combust. Flame 1981, 41, 35–43. [Google Scholar] [CrossRef]
- Bakhman, N.N.; Aldabaev, L.I.; Kondrikov, B.N.; Filippov, V.A. Burning of Polymeric Coatings on Copper Wires and Glass Threads: I. Flame Propagation Velocity. Combust. Flame 1981, 41, 17–34. [Google Scholar] [CrossRef]
- Fernandez-Pello, A.; Hasegawa, H.; Staggs, K.; Lipska-quinn, A.; Alvares, N. A Study Of The Fire Performance Of Electrical Cables. Fire Saf. Sci. 1991, 3, 237–247. [Google Scholar] [CrossRef]
- Tewarson, A.; Khan, M.M. Flame Propagation for Polymers in Cylindrical Configuration and Vertical Orientation. Symp. Int. Combust. 1989, 22, 1231–1240. [Google Scholar] [CrossRef]
- Jia, S.; Ma, Y.; Guo, Z.; Hu, L. Experimental Study of Spontaneous Ignition of Overloaded Electrical Wires under Transverse Wind. Proc. Combust. Inst. 2023, 39, 4031–4039. [Google Scholar] [CrossRef]
- Guo, F.; Kawaguchi, S.; Hashimoto, N.; Fujita, O. Effect of Pyrolysis Kinetic Parameters on the Overload Ignition of Polymer Insulated Wires in Microgravity. Proc. Combust. Inst. 2023, 39, 3939–3947. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Konno, Y.; Huang, X.; Nakaya, S.; Tsue, M.; Hashimoto, N.; Fujita, O.; Fernandez-Pello, C. Laser Piloted Ignition of Electrical Wire in Microgravity. Proc. Combust. Inst. 2019, 37, 4211–4219. [Google Scholar] [CrossRef]
- Fang, J.; Zhao, S.; Wang, J.; Xue, Y.; He, X.; Zhang, Y. Sub-Atmospheric Bursting Ignition of Fluorinated Ethylene Propylene Wire Insulation. Fire Saf. J. 2018, 100, 45–50. [Google Scholar] [CrossRef]
- He, H.; Zhang, Q.; Wang, X.; Wang, F.; Zhao, L.; Zhang, Y. The Influence of Currents on the Ignition and Correlative Smoke Productions for PVC-Insulated Electrical Wires. Fire Technol. 2017, 53, 1275–1289. [Google Scholar] [CrossRef]
- Shimizu, K.; Kikuchi, M.; Hashimoto, N.; Fujita, O. A Numerical and Experimental Study of the Ignition of Insulated Electric Wire with Long-Term Excess Current Supply under Microgravity. Proc. Combust. Inst. 2017, 36, 3063–3071. [Google Scholar] [CrossRef]
- Takano, Y.; Fujita, O.; Shigeta, N.; Nakamura, Y.; Ito, H. Ignition Limits of Short-Term Overloaded Electric Wires in Microgravity. Proc. Combust. Inst. 2013, 34, 2665–2673. [Google Scholar] [CrossRef]
- Huang, X.; Nakamura, Y.; Williams, F.A. Ignition-to-Spread Transition of Externally Heated Electrical Wire. Proc. Combust. Inst. 2013, 34, 2505–2512. [Google Scholar] [CrossRef]
- Fujita, O.; Kyono, T.; Kido, Y.; Ito, H.; Nakamura, Y. Ignition of Electrical Wire Insulation with Short-Term Excess Electric Current in Microgravity. Proc. Combust. Inst. 2011, 33, 2617–2623. [Google Scholar] [CrossRef]
- Kong, W.; Wang, B.; Zhang, W.; Ai, Y.; Lao, S. Study on Prefire Phenomena of Wire Insulation at Microgravity. Microgravity Sci. Technol. 2008, 20, 107–113. [Google Scholar] [CrossRef]
- Zhang, Y.; Fang, J.; Wang, J.; Zhang, Y.; Song, L. Lower Pressure Dripping Limits of Inclined Polyethylene-Insulated Wires during Flame Spreading under Different Oxygen Concentrations. Fire Saf. J. 2021, 120, 103108. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Nakaya, S.; Tsue, M.; Takahashi, S. Flame Spread over Polyethylene-Insulated Copper and Stainless-Steel Wires at High Pressure. Fire Saf. J. 2021, 120, 103062. [Google Scholar] [CrossRef]
- Gagnon, L.; Fernandez-Pello, C.; Urban, J.L.; Carey, V.P.; Konno, Y.; Fujita, O. Effect of Reduced Ambient Pressures and Opposed Airflows on the Flame Spread and Dripping of LDPE Insulated Copper Wires. Fire Saf. J. 2021, 120, 103171. [Google Scholar] [CrossRef]
- He, H.; Zhang, Q.; Shi, L.; Li, H.; Huang, D.; Zhang, Y. Experimental Study on the Thermoplastic Dripping and Flame Spread Behaviors of Energized Electrical Wire under Reduced Atmospheric Pressure. Polymers 2021, 13, 346. [Google Scholar] [CrossRef]
- Nagachi, M.; Citerne, J.-M.; Dutilleul, H.; Guibaud, A.; Jomaas, G.; Legros, G.; Hashimoto, N.; Fujita, O. Effect of Ambient Pressure on the Extinction Limit for Opposed Flame Spread over an Electrical Wire in Microgravity. Proc. Combust. Inst. 2021, 38, 4767–4774. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, X.; Lu, Y.; Lv, J.; Zhu, N.; Hu, L. Effect of Transverse Flow on Flame Spread and Extinction over Polyethylene-Insulated Wires. Proc. Combust. Inst. 2021, 38, 4727–4735. [Google Scholar] [CrossRef]
- Kang, M.S.; Park, S.H.; Yoo, C.S.; Park, J.; Chung, S.H. Effect of Core Metal on Flame Spread and Extinction for Horizontal Electrical Wire with Applied AC Electric Fields. Proc. Combust. Inst. 2021, 38, 4747–4756. [Google Scholar] [CrossRef]
- Guibaud, A.; Consalvi, J.-L.; Citerne, J.-M.; Legros, G. Pressure Effects on the Soot Production and Radiative Heat Transfer of Non-Buoyant Laminar Diffusion Flames Spreading in Opposed Flow over Insulated Wires. Combust. Flame 2020, 222, 383–391. [Google Scholar] [CrossRef]
- An, W.; Tang, Y.; Liang, K.; Wang, T.; Zhou, Y.; Wen, Z. Experimental Study on Flammability and Flame Spread Characteristics of Polyvinyl Chloride (PVC) Cable. Polymers 2020, 12, 2789. [Google Scholar] [CrossRef]
- Guibaud, A.; Citerne, J.-M.; Consalvi, J.-L.; Legros, G. On the Effects of Opposed Flow Conditions on Non-Buoyant Flames Spreading over Polyethylene-Coated Wires—Part II: Soot Oxidation Quenching and Smoke Release. Combust. Flame 2020, 221, 544–551. [Google Scholar] [CrossRef]
- Guibaud, A.; Citerne, J.-M.; Consalvi, J.-L.; Legros, G. On the Effects of Opposed Flow Conditions on Non-Buoyant Flames Spreading over Polyethylene-Coated Wires—Part I: Spread Rate and Soot Production. Combust. Flame 2020, 221, 530–543. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, T.; Wei, R.; Wang, J. Experimental Study of Flame Spread over PE-insulated Single Copper Core Wire under Varying Pressure and Electric Current. Fire Mater. 2020, 44, 835–843. [Google Scholar] [CrossRef]
- Konno, Y.; Hashimoto, N.; Fujita, O. Role of Wire Core in Extinction of Opposed Flame Spread over Thin Electric Wires. Combust. Flame 2020, 220, 7–15. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, J.; Chen, X.; Sheng, Y.; Lu, S.; Luo, S.; Deng, J. Influence of High Atmospheric Pressure on Flame Spread over Electric Wire at Different Inclinations. Process Saf. Environ. Prot. 2020, 136, 66–75. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, Q.; Tu, R.; Fang, J.; Wang, J.; Zhang, Y. Effects of Electric Current and Sample Orientation on Flame Spread over Electrical Wires. Fire Saf. J. 2020, 112, 102967. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, R.; He, J.; Wang, J. Melt Dripping Behavior in the Process of Flame Spread over Energized Electrical Wire at Different Pressures. Fire Mater. 2020, 44, 58–64. [Google Scholar] [CrossRef]
- Nagachi, M.; Mitsui, F.; Citerne, J.-M.; Dutilleul, H.; Guibaud, A.; Jomaas, G.; Legros, G.; Hashimoto, N.; Fujita, O. Effect of Ignition Condition on the Extinction Limit for Opposed Flame Spread over Electrical Wires in Microgravity. Fire Technol. 2020, 56, 149–168. [Google Scholar] [CrossRef]
- Konno, Y.; Kobayashi, Y.; Fernandez-Pello, C.; Hashimoto, N.; Nakaya, S.; Tsue, M.; Fujita, O. Opposed-Flow Flame Spread and Extinction in Electric Wires: The Effects of Gravity, External Radiant Heat Flux, and Wire Characteristics on Wire Flammability. Fire Technol. 2020, 56, 131–148. [Google Scholar] [CrossRef]
- Guibaud, A.; Citerne, J.-M.; Consalvi, J.-L.; Fujita, O.; Torero, J.; Legros, G. Experimental Evaluation of Flame Radiative Feedback: Methodology and Application to Opposed Flame Spread Over Coated Wires in Microgravity. Fire Technol. 2020, 56, 185–207. [Google Scholar] [CrossRef]
- Guibaud, A.; Consalvi, J.L.; Orlac’h, J.M.; Citerne, J.M.; Legros, G. Soot Production and Radiative Heat Transfer in Opposed Flame Spread over a Polyethylene Insulated Wire in Microgravity. Fire Technol. 2020, 56, 287–314. [Google Scholar] [CrossRef]
- Park, S.H.; Kang, M.S.; Cha, M.S.; Park, J.; Chung, S.H. Flame Spread over Twin Electrical Wires with Applied DC Electric Fields. Combust. Flame 2019, 210, 350–359. [Google Scholar] [CrossRef]
- Hu, L.; Zhu, K.; Lu, Y.; Zhang, X. An Experimental Study on Flame Spread over Electrical Wire with High Conductivity Copper Core and Controlling Heat Transfer Mechanism under Sub-Atmospheric Pressures. Int. J. Therm. Sci. 2019, 141, 141–149. [Google Scholar] [CrossRef]
- Zhang, Y.; Fang, J.; Wang, J.; Zhao, L.; Zhang, Y. The Effects of Angular Orientation and Ultraviolet Aging on ETFE Wire Flame Spread. Fire Mater. 2019, 43, 393–400. [Google Scholar] [CrossRef]
- Park, S.H.; Lim, S.J.; Cha, M.S.; Park, J.; Chung, S.H. Effect of AC Electric Field on Flame Spread in Electrical Wire: Variation in Polyethylene Insulation Thickness and Di-Electrophoresis Phenomenon. Combust. Flame 2019, 202, 107–118. [Google Scholar] [CrossRef]
- Lu, Y.; Huang, X.; Hu, L.; Fernandez-Pello, C. Concurrent Flame Spread and Blow-Off over Horizontal Thin Electrical Wires. Fire Technol. 2019, 55, 193–209. [Google Scholar] [CrossRef]
- Nagachi, M.; Mitsui, F.; Citerne, J.-M.; Dutilleul, H.; Guibaud, A.; Jomaas, G.; Legros, G.; Hashimoto, N.; Fujita, O. Can a Spreading Flame over Electric Wire Insulation in Concurrent Flow Achieve Steady Propagation in Microgravity? Proc. Combust. Inst. 2019, 37, 4155–4162. [Google Scholar] [CrossRef]
- Konno, Y.; Hashimoto, N.; Fujita, O. Downward Flame Spreading over Electric Wire under Various Oxygen Concentrations. Proc. Combust. Inst. 2019, 37, 3817–3824. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Konno, Y.; Huang, X.; Nakaya, S.; Tsue, M.; Hashimoto, N.; Fujita, O.; Fernandez-Pello, C. Effect of Insulation Melting and Dripping on Opposed Flame Spread over Laboratory Simulated Electrical Wires. Fire Saf. J. 2018, 95, 1–10. [Google Scholar] [CrossRef]
- Lim, S.J.; Park, S.H.; Park, J.; Fujita, O.; Keel, S.I.; Chung, S.H. Flame Spread over Inclined Electrical Wires with AC Electric Fields. Combust. Flame 2017, 185, 82–92. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, J.; Chen, X.; Lu, S. Pressure Effect on Flame Spread over Polyethylene-Insulated Copper Core Wire. Appl. Therm. Eng. 2017, 123, 1042–1049. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Huang, X.; Nakaya, S.; Tsue, M.; Fernandez-Pello, C. Flame Spread over Horizontal and Vertical Wires: The Role of Dripping and Core. Fire Saf. J. 2017, 91, 112–122. [Google Scholar] [CrossRef]
- Hu, L.; Lu, Y.; Yoshioka, K.; Zhang, Y.; Fernandez-Pello, C.; Chung, S.H.; Fujita, O. Limiting Oxygen Concentration for Extinction of Upward Spreading Flames over Inclined Thin Polyethylene-Insulated NiCr Electrical Wires with Opposed-Flow under Normal- and Micro-Gravity. Proc. Combust. Inst. 2017, 36, 3045–3053. [Google Scholar] [CrossRef]
- He, H.; Zhang, Q.; Tu, R.; Zhao, L.; Liu, J.; Zhang, Y. Molten Thermoplastic Dripping Behavior Induced by Flame Spread over Wire Insulation under Overload Currents. J. Hazard. Mater. 2016, 320, 628–634. [Google Scholar] [CrossRef]
- Citerne, J.-M.; Dutilleul, H.; Kizawa, K.; Nagachi, M.; Fujita, O.; Kikuchi, M.; Jomaas, G.; Rouvreau, S.; Torero, J.L.; Legros, G. Fire Safety in Space—Investigating Flame Spread Interaction over Wires. Acta Astronaut. 2016, 126, 500–509. [Google Scholar] [CrossRef]
- Lim, S.J.; Kim, M.; Park, J.; Fujita, O.; Chung, S. Flame Spread over Electrical Wire with AC Electric Fields: Internal Circulation, Fuel Vapor-Jet, Spread Rate Acceleration, and Molten Insulator Dripping. Combust. Flame 2015, 162, 1167–1175. [Google Scholar] [CrossRef]
- Nakamura, Y.; Azumaya, K.; Iwakami, J.; Wakatsuki, K. Scale Modeling of Flame Spread Over PE-Coated Electric Wires. In Progress in Scale Modeling; Saito, K., Ito, A., Nakamura, Y., Kuwana, K., Eds.; Springer International Publishing: Cham, Switzerland, 2015; Volume II, pp. 275–292. ISBN 978-3-319-10307-5. [Google Scholar]
- Hu, L.; Zhang, Y.; Yoshioka, K.; Izumo, H.; Fujita, O. Flame Spread over Electric Wire with High Thermal Conductivity Metal Core at Different Inclinations. Proc. Combust. Inst. 2015, 35, 2607–2614. [Google Scholar] [CrossRef]
- Takahashi, S.; Ito, H.; Nakamura, Y.; Fujita, O. Extinction Limits of Spreading Flames over Wires in Microgravity. Combust. Flame 2013, 160, 1900–1902. [Google Scholar] [CrossRef]
- Takahashi, S.; Takeuchi, H.; Ito, H.; Nakamura, Y.; Fujita, O. Study on Unsteady Molten Insulation Volume Change during Flame Spreading over Wire Insulation in Microgravity. Proc. Combust. Inst. 2013, 34, 2657–2664. [Google Scholar] [CrossRef]
- Kim, M.K.; Chung, S.H.; Fujita, O. Effect of AC Electric Fields on Flame Spread over Electrical Wire. Proc. Combust. Inst. 2011, 33, 1145–1151. [Google Scholar] [CrossRef]
- Nakamura, Y.; Yoshimura, N.; Ito, H.; Azumaya, K.; Fujita, O. Flame Spread over Electric Wire in Sub-Atmospheric Pressure. Proc. Combust. Inst. 2009, 32, 2559–2566. [Google Scholar] [CrossRef]
- Nakamura, Y.; Yoshimura, N.; Matsumura, T.; Ito, H.; Fujita, O. Opposed-Wind Effect on Flame Spread of Electric Wire in Sub-Atmospheric Pressure. J. Therm. Sci. Technol. 2008, 3, 430–441. [Google Scholar] [CrossRef]
- Nakamura, Y.; Yoshimura, N.; Matsumura, T.; Ito, H.; Fujita, O. Flame Spread over Polymer-Insulated Wire in Sub-Atmospheric Pressure: Similarity to Microgravity Phenomena. In Progress in Scale Modeling; Saito, K., Ed.; Springer: Dordrecht, The Netherlands, 2008; pp. 17–27. ISBN 978-1-4020-8681-6. [Google Scholar]
- Umemura, A.; Uchida, M.; Hirata, T.; Sato, J. Physical Model Analysis of Flame Spreading along an Electrical Wire in Microgravity. Proc. Combust. Inst. 2002, 29, 2535–2543. [Google Scholar] [CrossRef]
- Fujita, O.; Nishizawa, K.; Ito, K. Effect of Low External Flow on Flame Spread over Polyethylene-Insulated Wire in Microgravity. Proc. Combust. Inst. 2002, 29, 2545–2552. [Google Scholar] [CrossRef]
- Fujita, O.; Kikuchi, M.; Ito, K.; Nishizawa, K. Effective Mechanisms to Determine Flame Spread Rate over Ethylene-Tetrafluoroethylene Wire Insulation: Discussion on Dilution Gas Effect Based on Temperature Measurements. Proc. Combust. Inst. 2000, 28, 2905–2911. [Google Scholar] [CrossRef]
- Kikuchi, M.; Fujita, O.; Ito, K.; Sato, A.; Sakuraya, T. Experimental Study on Flame Spread over Wire Insulation in Microgravity. Symp. Int. Combust. 1998, 27, 2507–2514. [Google Scholar] [CrossRef]
- Huang, X.; Zhou, Z.; Gao, J.; Hu, J.; Wang, C.; Zhang, X. Effect of Copper Core Diameter on Heat Transfer and Horizontal Flame Spread Behaviors over Electrical Wire. Case Stud. Therm. Eng. 2021, 27, 101296. [Google Scholar] [CrossRef]
- Tang, K.; Wu, S.; Zhang, H.; Li, C.; Yuan, B.; Zhang, Y. Analysis of Heat Transfer during Flame Spread over Energized-Wire under High Currents. Int. J. Therm. Sci. 2022, 171, 107191. [Google Scholar] [CrossRef]
- Huang, X.; Zhou, Z.; Hu, J.; Shao, Y.; Liu, Z.; Liu, Y. Experimental Study on Flame Spread Characteristics of Double PE-Insulated Wires with Different Spacing Distances. Case Stud. Therm. Eng. 2022, 31, 101822. [Google Scholar] [CrossRef]
- Ma, Y.; Hu, L.; Jia, S.; Lv, J.; Xiong, S. Analysis of Upward- and Downward Flame Spread over Vertical Installed Polyethylene-Insulated Electrical Wires. Combust. Flame 2022, 238, 111896. [Google Scholar] [CrossRef]
- Kang, M.S.; Park, J.; Chung, S.H.; Yoo, C.S. Effect of the Thickness of Polyethylene Insulation on Flame Spread over Electrical Wire with Cu-Core under AC Electric Fields. Combust. Flame 2022, 240, 112017. [Google Scholar] [CrossRef]
- Li, C.; Chen, J.; Zhang, W.; Hu, L.; Cao, J.; Liu, J.; Zhu, Z.; Wu, S. Influence of Arc Size on the Ignition and Flame Propagation of Cable Fire. Energies 2021, 14, 5675. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, W.; Li, K.; Tang, K.; Liu, Z. Dripping Behavior Effects on Flame Propagation along Electrical Wires under High Currents. Fire Saf. J. 2021, 123, 103368. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J. Experimental Study on Flame Propagation over Horizontal Electrical Wires under Varying Pressure. Int. J. Therm. Sci. 2020, 156, 106492. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J. A Comprehensive Study on the Flame Propagation of the Horizontal Laboratory Wires and Flame-Retardant Cables at Different Thermal Circumstances. Process Saf. Environ. Prot. 2020, 139, 325–333. [Google Scholar] [CrossRef]
- He, H.; Zhang, Q.X.; Zhao, L.Y.; Liu, J.; Wang, J.J.; Zhang, Y.M. Flame Propagation Over Energized PE-Insulated Wire Under Low Pressure. Int. J. Comput. Methods Exp. Meas. 2017, 5, 87–95. [Google Scholar] [CrossRef]
- Wang, X.; He, H.; Zhao, L.; Fang, J.; Wang, J.; Zhang, Y. Ignition and Flame Propagation of Externally Heated Electrical Wires with Electric Currents. Fire Technol. 2016, 52, 533–546. [Google Scholar] [CrossRef]
- Fang, J.; Zhang, Y.; Huang, X.; Xue, Y.; Wang, J.; Zhao, S.; He, X.; Zhao, L. Dripping and Fire Extinction Limits of Thin Wire: Effect of Pressure and Oxygen. Combust. Sci. Technol. 2021, 193, 437–452. [Google Scholar] [CrossRef]
- Huang, X. Critical Drip Size and Blue Flame Shedding of Dripping Ignition in Fire. Sci. Rep. 2018, 8, 16528. [Google Scholar] [CrossRef] [PubMed]
- Xie, Q.; Gong, T.; Huang, X. Fire Zone Diagram of Flame-Retardant Cables: Ignition and Upward Flame Spread. Fire Technol. 2021, 57, 2643–2659. [Google Scholar] [CrossRef]
- Lee, J.; Kim, B.; Jung, Y.H.; Lee, S.; Shin, W.G. Numerical Study to Reproduce a Real Cable Tray Fire Event in a Nuclear Power Plant. Nucl. Eng. Technol. 2023, 55, 157–1584. [Google Scholar] [CrossRef]
- Pretrel, H.; Zavaleta, P.; Suard, S. Experimental Investigation of the Effects of a Sidewall and Cable Arrangement on a Horizontal Cable Tray Fire in an Open Atmosphere. Fire Mater. 2022, 47, 718–732. [Google Scholar] [CrossRef]
- Zavaleta, P.; Suard, S.; Audouin, L. Cable Tray Fire Tests with Halogenated Electric Cables in a Confined and Mechanically Ventilated Facility. Fire Mater. 2019, 43, 543–560. [Google Scholar] [CrossRef]
- Suard, S.; Van Hees, P.; Roewekamp, M.; Tsuchino, S.; Gonzalez, R. Fire Development in Multi-Compartment Facilities: PRISME 2 Project. Fire Mater. 2019, 43, 433–435. [Google Scholar] [CrossRef]
- Bascou, S.; Zavaleta, P.; Babik, F. Cable Tray FIRE Tests Simulations in Open Atmosphere and in Confined and Mechanically Ventilated Compartments with the CALIF3S/ISIS CFD Software. Fire Mater. 2019, 43, 448–465. [Google Scholar] [CrossRef]
- Klein-Heßling, W. Validation of the Lumped Parameter Code COCOSYS against Large-scale OECD PRISME 2 Fire Experiments. Fire Mater. 2019, 43, 591–609. [Google Scholar] [CrossRef]
- Plumecocq, W.; Audouin, L.; Zavaleta, P. Horizontal Cable Tray Fire in a Well-confined and Mechanically Ventilated Enclosure Using a Two-zone Model. Fire Mater. 2019, 43, 530–542. [Google Scholar] [CrossRef]
- Zavaleta, P.; Hanouzet, R.; Beji, T. Improved Assessment of Fire Spread over Horizontal Cable Trays Supported by Video Fire Analysis. Fire Technol. 2019, 55, 233–255. [Google Scholar] [CrossRef]
- Pelzer, M.; Klein-Heßling, W. Validation of COCOSYS Pyrolysis Models on OECD PRISME Fire Experiments. Fire Saf. J. 2013, 62, 174–191. [Google Scholar] [CrossRef]
- Audouin, L.; Rigollet, L.; Prétrel, H.; Le Saux, W.; Röwekamp, M. OECD PRISME Project: Fires in Confined and Ventilated Nuclear-Type Multi-Compartments—Overview and Main Experimental Results. Fire Saf. J. 2013, 62, 80–101. [Google Scholar] [CrossRef]
- Tang, K.; Zhang, Y.; Jiang, S.; Li, C.; Ma, C.; Liu, G.; Zhang, H.; Yuan, B. A Comparative Study on Fire Hazards of Cables Used in Nuclear Power Plants Based on Small- and Large-Scale Experiments. J. Therm. Anal. Calorim. 2022, 147, 14659–14671. [Google Scholar] [CrossRef]
- Yang, H.; Zou, L.; Song, Z.; Wang, X.; Sun, Y.; Duan, Y. Identification of the Ignition Point of High Voltage Cable Trenches Based on Ceiling Temperature Distribution. Symmetry 2022, 14, 1417. [Google Scholar] [CrossRef]
- Huang, P.; Ye, S.; Qin, L.; Huang, Y.; Yang, J.; Yu, L.; Wu, D. Experimental Study on the Maximum Excess Ceiling Gas Temperature Generated by Horizontal Cable Tray Fires in Urban Utility Tunnels. Int. J. Therm. Sci. 2022, 172, 107341. [Google Scholar] [CrossRef]
- Huang, X.; Zhu, H.; He, L.; Peng, L.; Cheng, C.; Chow, W. Improved Model for Estimating Sidewall Effect on the Fire Heat Release Rate of Horizontal Cable Tray. Process Saf. Environ. Prot. 2021, 149, 831–838. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Y.; Ren, Z.; Li, Z.; Cheng, C.; Chow, W. Experimental Investigation on Maximum Ceiling Jet Temperature Generated by a Vertically Spreading Cable Fire. Fire Saf. J. 2021, 120, 103125. [Google Scholar] [CrossRef]
- An, W.; Wang, T.; Liang, K.; Tang, Y.; Wang, Z. Effects of Interlayer Distance and Cable Spacing on Flame Characteristics and Fire Hazard of Multilayer Cables in Utility Tunnel. Case Stud. Therm. Eng. 2020, 22, 100784. [Google Scholar] [CrossRef]
- Ke, G.; Zimeng, L.; Jinzhang, J.; Zeyi, L.; Yisimayili, A.; Zhipeng, Q.; Yaju, W.; Shengnan, L. Study on Flame Spread Characteristics of Flame-Retardant Cables in Mine. Adv. Polym. Technol. 2020, 2020, 1–7. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Z.; Lin, Y.; Fu, M.; Chen, Y. New Approaches to Determine the Interface Height of Fire Smoke Based on a Three-layer Zone Model and Its Verification in Large Confined Space. Fire Mater. 2020, 44, 130–138. [Google Scholar] [CrossRef]
- Hehnen, T.; Arnold, L.; Mendola, S.L. Numerical Fire Spread Simulation Based on Material Pyrolysis—An Application to the CHRISTIFIRE Phase 1 Horizontal Cable Tray Tests. Fire 2020, 3, 33. [Google Scholar] [CrossRef]
- Huang, X.; Zhu, H.; Peng, L.; Zheng, Z.; Zeng, W.; Bi, K.; Cheng, C.; Chow, W. Thermal Characteristics of Vertically Spreading Cable Fires in Confined Compartments. Fire Technol. 2019, 55, 1849–1875. [Google Scholar] [CrossRef]
- Siemon, M.; Riese, O.; Forell, B.; Krönung, D.; Klein-Heßling, W. Experimental and Numerical Analysis of the Influence of Cable Tray Arrangements on the Resulting Mass Loss Rate and Fire Spreading. Fire Mater. 2019, 43, 497–513. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, K.; Duan, H.; Niu, Y.; Huang, X.; Chen, B.; Liu, Z.; Chen, Y. Modified Carbon-Dioxide Measurement to Predict the Heat Release Rate of Fire Burning in a Compartment Based on the Three-Zone Model. Fire Mater. 2019, 43, 256–265. [Google Scholar] [CrossRef]
- Huang, X.; Zhu, H.; Peng, L.; Zheng, Z.; Zeng, W.; Bi, K.; Cheng, C.; Chow, W. Burning Behavior of Cable Tray Located on a Wall with Different Cable Arrangements. Fire Mater. 2019, 43, 64–73. [Google Scholar] [CrossRef]
- Huang, X.; Ren, Z.; Zhu, H.; Peng, L.; Cheng, C.; Chow, W. A Modified Zone Model on Vertical Cable Tray Fire in a Confined Compartment in the Nuclear Power Plant. J. Fire Sci. 2018, 36, 472–493. [Google Scholar] [CrossRef]
- Huang, X.; Zhu, H.; Peng, L.; Zheng, Z.; Zeng, W.; Cheng, C.; Chow, W. An Improved Model for Estimating Heat Release Rate in Horizontal Cable Tray Fires in Open Space. J. Fire Sci. 2018, 36, 275–290. [Google Scholar] [CrossRef]
- Zavaleta, P.; Audouin, L. Cable Tray Fire Tests in a Confined and Mechanically Ventilated Facility. Fire Mater. 2018, 42, 28–43. [Google Scholar] [CrossRef]
- Li, L.; Huang, X.; Bi, K.; Liu, X. An Enhanced Fire Hazard Assessment Model and Validation Experiments for Vertical Cable Trays. Nucl. Eng. Des. 2016, 301, 32–38. [Google Scholar] [CrossRef]
- Beji, T.; Verstockt, S.; Zavaleta, P.; Merci, B. Flame Spread Monitoring and Estimation of the Heat Release Rate from a Cable Tray Fire Using Video Fire Analysis (VFA). Fire Technol. 2016, 52, 611–621. [Google Scholar] [CrossRef]
- Passalacqua, R.; Cortes, P.; Taylor, N.; Beltran, D.; Zavaleta, P.; Charbaut, S. Experimental Characterisation of ITER Electric Cables in Postulated Fire Scenarios. Fusion Eng. Des. 2013, 88, 2650–2654. [Google Scholar] [CrossRef]
- McGrattan, K.; Lock, A.; Marsh, N.; Nyden, M.; Dreisbach, J.; Stroup, D. Understanding the hazards of grouped electrical cables. In Proceedings of the 2010 14th International Heat Transfer Conference, Washington, DC, USA, 8–13 August 2010. [Google Scholar]
- McGrattan, K.B. Evaluation of Fire Models for Nuclear Power Plant Applications: Benchmark Exercise #3: International Panel Report; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2007; p. NIST IR 7338. [Google Scholar]
- Khan, M.M.; Bill, R.G.; Alpert, R.L. Screening of Plenum Cables Using a Small-Scale Fire Test Protocol. Fire Mater. 2006, 30, 65–76. [Google Scholar] [CrossRef]
- Hees, P.V.; Axelsson, J.; Green, A.M.; Grayson, S.J. Mathematical Modelling of Fire Development in Cable Installations. Fire Mater. 2001, 25, 169–178. [Google Scholar] [CrossRef]
- Alvares, N.; Fernandez-Pello, A.C. Fire Initiation and Spread in Overloaded Communication System Cable Trays. Exp. Therm. Fluid Sci. 2000, 21, 51–57. [Google Scholar] [CrossRef]
- Quintiere, J. Fundamentals of Fire Phenomena; Wiley: Hoboken, NJ, USA, 2006; ISBN 978-0-470-09113-5. [Google Scholar]
- Ge, F.; Qiu, T.; Zhang, M.; Ji, J. Experimental Research on the Thermal Characteristic of Low-Voltage Alternating Current (AC) Arc Faults. Fire Saf. J. 2023, 136, 103732. [Google Scholar] [CrossRef]
- Gong, T.; Xie, Q.; Huang, X. Fire Behaviors of Flame-Retardant Cables Part I: Decomposition, Swelling and Spontaneous Ignition. Fire Saf. J. 2018, 95, 113–121. [Google Scholar] [CrossRef]
- Miyamoto, K.; Huang, X.; Hashimoto, N.; Fujita, O.; Fernandez-Pello, C. Limiting Oxygen Concentration (LOC) of Burning Polyethylene Insulated Wires under External Radiation. Fire Saf. J. 2016, 86, 32–40. [Google Scholar] [CrossRef]
- Huang, X.; Nakamura, Y. A Review of Fundamental Combustion Phenomena in Wire Fires. Fire Technol. 2020, 56, 315–360. [Google Scholar] [CrossRef]
- Merzhanov, A.G.; Sirignano, W.A.; De Luca, L. Advances in Combustion Science: In Honor of Ya. B. Zel’Dovich; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1997. [Google Scholar]
- Buckmaster, J. The Mathematical Theory of Combustion and Explosions. Combust. Flame 1987, 67, 185. [Google Scholar] [CrossRef]
- Guo, F.; Kawaguchi, S.; Hashimoto, N.; Fujita, O. Identifying Two Ignition Modes of Polymer Insulated Wires with Continuous Excess Current in Microgravity. Fire Saf. J. 2023, 141, 103925. [Google Scholar] [CrossRef]
- Kong, W.; Lao, S.-Q.; Zhang, P.-Y.; Zhang, X.-Q. Study on Wire Insulation Flammability at Microgravity by Functional Simulation Method. Ranshao Kexue Yu Jishu J. Combust. Sci. Technol. 2006, 12, 1–4. [Google Scholar]
- Wang, K.; Wang, B.; Ai, Y.; Kong, W. Study on the Pre-Ignition Characteristics of Wire Insulation in the Narrow Channel Setup. Sci. China Technol. Sci. 2012, 55, 2132–2139. [Google Scholar] [CrossRef]
- Wang, K.; Wang, B.; Kong, W.; Liu, F. Study on the Pre-Ignition Temperature Variations of Wire Insulation under Overload Conditions in Microgravity by the Functional Simulation Method. J. Fire Sci. 2014, 32, 257–280. [Google Scholar] [CrossRef]
- Wang, K.; Xia, W.; Wang, B.; Ai, Y.; Kong, W. Study on Fire Initiation of Wire Insulation by a Narrow Channel at Low Pressure. Microgravity Sci. Technol. 2016, 28, 155–163. [Google Scholar] [CrossRef]
- Wang, W.; Lu, C.; Ji, X.; Zhao, X.; Lyu, H. Research on Overcurrent Heating Characteristics of Copper Wires at Different Inclination Angles. J. Therm. Anal. Calorim. 2023, 148, 4833–4842. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006; ISBN 978-0-471-45728-2. [Google Scholar]
- Fernandez-Pello, A.C. The Solid Phase. Combust. Fundam. Fire 1995, 2, 31–100. [Google Scholar]
- Babrauskas, V. Research on Electrical Fires: The State of the Art. Fire Saf. Sci. 2009, 9, 3–18. [Google Scholar] [CrossRef]
- Noto, F.; Kawamura, K. Tracking and Ignition Phenomena of Polyvinyl Chloride Resin under Wet Polluted Conditions. IEEE Trans. Electr. Insul. 1978, EI-13, 418–425. [Google Scholar] [CrossRef]
- Fisher, R.P.; Stoliarov, S.I.; Keller, M.R. A Criterion for Thermally-Induced Failure of Electrical Cable. Fire Saf. J. 2015, 72, 33–39. [Google Scholar] [CrossRef]
- Babrauskas, V. Ignition Handbook: Principles and Applications to Fire Safety Engineering, Fire Investigation, Risk Management and Forensic Science; Fire Science Publishers: Issaquah, WA, USA, 2003; ISBN 978-0-9728111-3-2. [Google Scholar]
- Kang, N.; Zhao, Z.; Lin, J.; Lu, S. Ignition of Silicone Rubber Sheaths by Series Arcs at Different Currents and Durations. Fire Saf. J. 2023, 136, 103753. [Google Scholar] [CrossRef]
- Du, J.-H.; Tu, R.; Zeng, Y.; Pan, L.; Zhang, R.-C. An Experimental Study on the Thermal Characteristics and Heating Effect of Arc-Fault from Cu Core in Residential Electrical Wiring Fires. PLoS ONE 2017, 12, e0182811. [Google Scholar] [CrossRef] [PubMed]
- Deng, J.; Lin, Q.-W.; Li, Y.; Wang, H.-B.; Wang, C.-P.; Zhao, Y.-H.; Lyu, H.-F.; Shu, C.-M. Ignition and Flame Spreading Features of Excessively Overloaded Polyvinyl Chloride Copper Wires. Fire Technol. 2023, 59, 3589–3607. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Y.; Gao, Y.; Sun, J.; Lyu, H.-F.; Yu, T.; Yang, S.; Wang, Y. Analysis of Overload Induced Arc Formation and Beads Characteristics in a Residential Electrical Cable. Fire Saf. J. 2022, 131, 103626. [Google Scholar] [CrossRef]
- Courty, L.; Garo, J.P. External Heating of Electrical Cables and Auto-Ignition Investigation. J. Hazard. Mater. 2017, 321, 528–536. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.E. Engineering Guide for Estimating Material Pyrolysis Properties for Fire Modeling; Worcester Polytechnic Institute: Worcester, MA, USA, 2012. [Google Scholar]
- Ogawa, S.; Mizukami, H.; Bando, Y.; Nakamura, M. The Pyrolysis Characteristics of Each Component in Municipal Solid Waste and Thermal Degradation of Its Gases. J. Chem. Eng. Jpn. 2005, 38, 373–384. [Google Scholar] [CrossRef]
- Singh, A.; Kumar, R.; Soni, P.K.; Singh, V. Investigation of the Effect of Diisocyanate on the Thermal Degradation Behavior and Degradation Kinetics of Polyether-Based Polyurethanes. J. Macromol. Sci. B Phys. 2020, 59, 775–795. [Google Scholar] [CrossRef]
- Balme, Q.; Rozaini, M.T.; Marias, F.; Lemont, F.; Charvin, P.; Sedan, J. Modeling the Rate of Batch-Mode Thermal Degradation of Polyethylene Suspended in an Oven. Waste Biomass Valoriz. 2021, 12, 4549–4566. [Google Scholar] [CrossRef]
- Suraci, S.V.; Spinazzola, C.; Fabiani, D. Analysis on the Impact of Additives on Space Charge Behavior of Thermally Aged XLPE Plaques. In Proceedings of the 2022 IEEE Conference on Electrical Insulation and Dielectric Phenomena (IEEE CEIDP 2022), Auburn, AL, USA, 6–9 October 2022; IEEE: New York, NY, USA, 2022; pp. 41–44. [Google Scholar]
- Boukezzi, L.; Rondot, S.; Jbara, O.; Boubakeur, A. Charging Kinetics of XLPE Insulation Cables Under E-Beam Irradiation in SEM: Effect of Thermal Aging. In Proceedings of the 2017 5th International Conference on Electrical Engineering—Boumerdes (ICEE-B), Boumerdes, Algeria, 29–31 August 2017; IEEE: New York, NY, USA, 2017. [Google Scholar]
- Salivon, T.; Colin, X.; Salivon, T.; Comte, R. Degradation of XLPE and PVC Cable Insulators. In Proceedings of the 2015 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Ann Arbor, MI, USA, 18–21 October 2015; IEEE: New York, NY, USA, 2015; pp. 656–659. [Google Scholar]
- Zeng, D.W.; Born, M.; Wambach, K. Pyrolysis of EVA and Its Application in Recycling of Photovoltaic Modules. J. Environ. Sci. 2004, 16, 889–893. [Google Scholar]
- Soudais, Y.; Moga, L.; Blazek, J.; Lemort, F. Comparative Study of Pyrolytic Decomposition of Polymers Alone or in EVA/PS, EVA/PVC and EVA/Cellulose Mixtures. J. Anal. Appl. Pyrolysis 2007, 80, 36–52. [Google Scholar] [CrossRef]
- Coralli, I.; Gossmann, I.; Fabbri, D.; Scholz-Boettcher, B.M. Determination of Polyurethanes within Microplastics in Complex Environmental Samples by Analytical Pyrolysis. Anal. Bioanal. Chem. 2023, 415, 2891–2905. [Google Scholar] [CrossRef] [PubMed]
- Yao, Z.; Yu, S.; Su, W.; Wu, D.; Liu, J.; Wu, W.; Tang, J. Probing the Combustion and Pyrolysis Behaviors of Polyurethane Foam from Waste Refrigerators. J. Therm. Anal. Calorim. 2020, 141, 1137–1148. [Google Scholar] [CrossRef]
- Lapcikova, B.; Lapcik, L. TG and DTG Study of Decomposition of Commercial PUR Cellular Materials. J. Polym. Mater. 2011, 28, 353–366. [Google Scholar]
- Jakic, M.; Vrandecic, N.S.; Klaric, I. Thermal Degradation of Poly(Vinyl Chloride)/Poly(Ethylene Oxide) Blends: Thermogravimetric Analysis. Polym. Degrad. Stab. 2013, 98, 1738–1743. [Google Scholar] [CrossRef]
- Krongauz, V.V.V.; DePolo, W. Kinetics of Poly(Vinyl Chloride) Thermal and Thermo-Mechanical Degradation in the Presence of Epoxidized Plasticizer. Induction Effect. J. Appl. Polym. Sci. 2023, 140, e53482. [Google Scholar] [CrossRef]
- Krongauz, V.V.; Lee, Y.-P.; Bourassa, A. Kinetics of Thermal Degradation of Poly(Vinyl Chloride). J. Therm. Anal. Calorim. 2011, 106, 139–149. [Google Scholar] [CrossRef]
- Lu, Y.; Huang, X.; Hu, L.; Fernandez-Pello, C. The Interaction between Fuel Inclination and Horizontal Wind: Experimental Study Using Thin Wire. Proc. Combust. Inst. 2019, 37, 3809–3816. [Google Scholar] [CrossRef]
- Kashiwagi, T.; Ohlemiller, T.J.; Werner, K. Effects of External Radiant Flux and Ambient Oxygen Concentration on Nonflaming Gasification Rates and Evolved Products of White Pine. Combust. Flame 1987, 69, 331–345. [Google Scholar] [CrossRef]
- Fujita, O. Solid Combustion Research in Microgravity as a Basis of Fire Safety in Space. Proc. Combust. Inst. 2015, 35, 2487–2502. [Google Scholar] [CrossRef]
- Osorio, A.F.; Mizutani, K.; Fernandez-Pello, C.; Fujita, O. Microgravity Flammability Limits of ETFE Insulated Wires Exposed to External Radiation. Proc. Combust. Inst. 2015, 35, 2683–2689. [Google Scholar] [CrossRef]
- Olson, S.L. Piloted Ignition Delay Times of Opposed and Concurrent Flame Spread over a Thermally-Thin Fuel in a Forced Convective Microgravity Environment. Proc. Combust. Inst. 2011, 33, 2633–2639. [Google Scholar] [CrossRef]
- Zhang, Y.; Tang, K.; Liu, Z.; Chen, Y. Experimental Study on Thermal and Fire Behaviors of Energized PE-Insulated Wires under Overload Currents. J. Therm. Anal. Calorim. 2021, 145, 345–351. [Google Scholar] [CrossRef]
- Kim, H.-Y.; Lee, H.J.; Kang, B.H. Sliding of Liquid Drops Down an Inclined Solid Surface. J. Colloid Interface Sci. 2002, 247, 372–380. [Google Scholar] [CrossRef] [PubMed]
- Matheson, A.F.; Charge, R.; Corneliussen, T. Properties of PVC Compounds with Improved Fire Performance for Electrical Cables. Fire Saf. J. 1992, 19, 55–72. [Google Scholar] [CrossRef]
- Barnes, M.A.; Briggs, P.J.; Hirschler, M.M.; Matheson, A.F.; O’Neill, T.J. A Comparative Study of the Fire Performance of Halogenated and Non-Halogenated Materials for Cable Applications. Part II Tests on Cable. Fire Mater. 1996, 20, 17–37. [Google Scholar] [CrossRef]
- Barnes, M.A.; Briggs, P.J.; Hirschler, M.M.; Matheson, A.F.; O’Neill, T.J. A Comparative Study of the Fire Performance of Halogenated and Non-Halogenated Materials for Cable Applications. Part I Tests on Materials and Insulated Wires. Fire Mater. 1996, 20, 1–16. [Google Scholar] [CrossRef]
- Yang, H.; Fu, Q.; Cheng, X.; Yuen, R.K.K.; Zhang, H. Investigation of the Flammability of Different Cables Using Pyrolysis Combustion Flow Calorimeter. Procedia Eng. 2013, 62, 778–785. [Google Scholar] [CrossRef]
- Meinier, R.; Sonnier, R.; Zavaleta, P.; Suard, S.; Ferry, L. Fire Behavior of Halogen-Free Flame Retardant Electrical Cables with the Cone Calorimeter. J. Hazard. Mater. 2018, 342, 306–316. [Google Scholar] [CrossRef] [PubMed]
- Xie, Q.; Zhang, H.; Tong, L. Experimental Study on the Fire Protection Properties of PVC Sheath for Old and New Cables. J. Hazard. Mater. 2010, 179, 373–381. [Google Scholar] [CrossRef] [PubMed]
- Li, J.M.; Zhang, J.Q.; Li, Q.; Guo, Z.D. Thermal Aging Effects on Fire Performance of the Cross-Linked Polyethylene Insulated Cable. Mater. Sci. Forum 2017, 898, 2399–2404. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, J.; Li, Q.; Wang, L.; Xie, H.; Fan, M. Effects of Insulating Material Ageing on Ignition Time and Heat Release Rate of the Flame Retardant Cables. Procedia Eng. 2018, 211, 972–978. [Google Scholar] [CrossRef]
- Kim, M.H.; Seo, H.J.; Lee, S.K.; Lee, M.C. Influence of Thermal Aging on the Combustion Characteristics of Cables in Nuclear Power Plants. Energies 2021, 14, 2003. [Google Scholar] [CrossRef]
- Zhang, Y.; Fang, J.; Wang, J.; Zhao, L.; Zhang, Y. Ignition and Flame Spread over Thermal Aging Electrical Wires in Subatmospheric Pressure. J. Thermoplast. Compos. Mater. 2021, 34, 1428–1439. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J. Comparative Thermal Decomposition Characteristics and Fire Behaviors of Commercial Cables. J. Therm. Anal. Calorim. 2021, 144, 1209–1218. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J. An Experimental Study on the Fire Characteristics of New and Aged Building Wires Using a Cone Calorimeter. J. Therm. Anal. Calorim. 2019, 135, 3115–3122. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, R.; Ning, X.; Xie, T.; Wang, J. Thermal Degradation Properties of LDPE Insulation for New and Aged Fine Wires. J. Therm. Anal. Calorim. 2019, 137, 461–471. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, R.; Ouyang, D.; Wang, J. Investigation on Thermal Stability and Flame Spread Behavior of New and Aged Fine Electrical Wires. J. Therm. Anal. Calorim. 2020, 140, 157–165. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, T.; Ning, X.; Liu, Y.; Wang, J. Thermal Degradation Kinetics Study of Polyvinyl Chloride (PVC) Sheath for New and Aged Cables. Waste Manag. 2019, 99, 146–153. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Wei, R.; Wang, X.; He, J.; Wang, J. Pyrolysis and Combustion of Polyvinyl Chloride (PVC) Sheath for New and Aged Cables via Thermogravimetric Analysis-Fourier Transform Infrared (TG-FTIR) and Calorimeter. Materials 2018, 11, 1997. [Google Scholar] [CrossRef]
- BS EN 50200:2015; Method of Test for Resistance to Fire of Unprotected Small Cables for Use in Emergency Circuits. British Standards Institution: London, UK, 2015.
- EN 50399; Common Test Methods for Cables under Fire Conditions—Heat Release and Smoke Production Measurement on Cables during Flame Spread Test—Test Apparatus, Procedures, Results. CENELEC: Brussels, Belgium, 2022.
- IEC 60331-1:2018; Tests for Electric Cables under Fire Conditions—Circuit Integrity—Part 1: Test Method for Fire with Dhock at a Temperature of at least 830 °C for Cables of Rated Voltage up to and Including 0.6/1.0 kV and with an Overall Diameter Exceeding 20 mm. IEC: Geneva, Switzerland, 2018.
- IEC 60331-2:2018; Tests for Electric Cables under Fire Conditions—Circuit Integrity—Part 2: Test Method for Fire with Shock at a Temperature of at least 830 °C for Cables of Rated Voltage up to and Including 0.6/1.0 kV and with an Overall Diameter not Exceeding 20 mm. IEC: Geneva, Switzerland, 2018.
- IEC 60331-3:2018; Tests for Electric Cables under Fire Conditions—Circuit Integrity—Part 3: Test Method for Fire with Shock at a Temperature of at least 830 °C for Cables of Rated Voltage up to and Including 0.6/1.0 kV Tested in a Metal Enclosure. IEC: Geneva, Switzerland, 2018.
- IEC 60332-1-2:2004; Tests on Electric and Optical Fibre Cables under Fire Conditions—Part 1–2: Test for Vertical Flame Propagation for a Single Insulated Wire or Cable—Procedure for 1 kW Pre-Mixed Flame. IEC: Geneva, Switzerland, 2018.
- McGrattan, K.B.; Lock, A.J.; Marsh, N.D.; Nyden, M.R. Cable Heat Release, Ignition, and Spread in Tray Installations during Fire (CHRISTIFIRE): Phase 1—Horizontal Trays; NIST: Gaithersburg, MD, USA, 2012. [Google Scholar]
- McGrattan, K.B.; Bareham, S.D. Cable Heat Release, Ignition, and Spread in Tray Installations During Fire (CHRISTIFIRE) Phase 2: Vertical Shafts and Corridors; NIST: Gaithersburg, MD, USA, 2013. [Google Scholar]
- Nowlen, S.P. A Summary of Nuclear Power Plant Fire Safety Research at Sandia National Laboratories 1975–1987; US Nuclear Regulatory Commission (NRC): Washington, DC, USA; Div. of Engineering; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 1989. [Google Scholar]
- Grayson, S.J.; Van Hees, P.; Green, A.M.; Breulet, H.; Vercellotti, U. Assessing the Fire Performance of Electric Cables (FIPEC). Fire Mater. 2001, 25, 49–60. [Google Scholar] [CrossRef]
- NUREG/CR-6931 Volume 1, “CAROLFIRE Test Report Volume 1: General Test Descriptions and the Analysis of Circuit Response Data, Draft for Public Comment,” and NUREG/CR-6931 Volume 2, “CAROLFIRE Test Report Volume 2: Cable Fire Response Data for Fire Model Improvement, Draft for Public Comment-Revision 1”, 30645 [E7-10611]. Available online: https://regulations.justia.com/regulations/fedreg/2007/06/01/E7-10611.html (accessed on 19 April 2024).
- Tang, Z.; Gao, K.; Shan, Y.; Zhu, C.; Liu, Z.; Liu, Z. Study of the Fire Behavior of Multilayer Cables in a Mine Tunnel. Energies 2022, 15, 2059. [Google Scholar] [CrossRef]
- Ferng, Y.M.; Liu, C.H. Investigating the Burning Characteristics of Electric Cables Used in the Nuclear Power Plant by Way of 3-D Transient FDS Code. Nucl. Eng. Des. 2011, 241, 88–94. [Google Scholar] [CrossRef]
- Lin, C.-H.; Ferng, Y.-M.; Pei, B.-S. Development of CFD Fire Models for Deterministic Analyses of the Cable Issues in the Nuclear Power Plant. Nucl. Eng. Des. 2009, 239, 338–345. [Google Scholar] [CrossRef]
- Qu, B.; Xiang, X.; Wu, S.; Li, K.; Li, X.; Zheng, Z. Simulation Analysis of Electromagnetic-Fluid-Temperature Field in Cable Shafts of High-Rise Buildings. Math. Probl. Eng. 2023, 2023, e7825964. [Google Scholar] [CrossRef]
- Hay, W.; Seguillon, J.; Boyer, G. Numerical Simulations of a PVC Cable Fire on Long Cable-Trays in a Mechanically Ventilated Large Scale Facility. Fire Saf. J. 2023, 138, 103799. [Google Scholar] [CrossRef]
- Tyas, D.; Bagshaw, D.; Plummer, J.; Nyogeri, L. Modelling the Heat Release Rate of PRISME Experimental Cable Fires in a Confined, Ventilation Controlled, Environment Using FLASH-CAT and FDS. Fire Saf. J. 2023, 139, 103828. [Google Scholar] [CrossRef]
- Verma, N.; Hostikka, S.; Vaari, J.; Korhonen, T. Adapted FLASHCAT Methodology to Model Horizontal Cable Tray Fires Using Computational Fluid Dynamics. Fire Saf. J. 2023, 138, 103814. [Google Scholar] [CrossRef]
- Beji, T.; Merci, B. Numerical Simulations of a Full-Scale Cable Tray Fire Using Small-Scale Test Data. Fire Mater. 2019, 43, 486–496. [Google Scholar] [CrossRef]
- Alonso, A.; Lázaro, D.; Lázaro, M.; Alvear, D. Numerical Prediction of Cables Fire Behaviour Using Non-Metallic Components in Cone Calorimeter. Combust. Sci. Technol. 2023, 195, 1509–1525. [Google Scholar] [CrossRef]
- Pitts, W.M. Toxic Yield; NIST: Gaithersburg, MD, USA, 2001. [Google Scholar]
- Blomqvist, P.; Rosell, L.; Simonson, M. Emissions from Fires Part I: Fire Retarded and Non-Fire Retarded TV-Sets. Fire Technol. 2004, 40, 39–58. [Google Scholar] [CrossRef]
- Blomqvist, P.; Rosell, L.; Simonson, M. Emissions from Fires Part II: Simulated Room Fires. Fire Technol. 2004, 40, 59–73. [Google Scholar] [CrossRef]
- DIN 53436; Producing Thermal Decomposition Products from Materials in an Air Stream and Their Toxicological Testing. DIN: Berlin, Germany, 2015.
- NES713; Determination of the Toxicity Index of the Products of Combustion from Small Specimens of Materials. NES: Washington, DC, USA, 1990.
- BS 7990:2003; Tube Furnace Method for the Determination of Toxic Product Yields in Fire Effluents. British Standard: London, UK, 2003.
- BS ISO 19703:2018; Generation and Analysis of Toxic Gases in Fire. Calculation of Species Yields, Equivalence Ratios and Combustion Efficiency in Experimental Fires. British Standard: London, UK, 2018.
- GSO IEC/TS 60695-7-51:2015; Fire Hazard Testing—Part 7-51: Toxicity of Fire Effluent—Estimation of Toxic Potency: Calculation and Interpretation of Test Results. IEC: Geneva, Switzerland, 2015.
- Hull, T.R.; Lebek, K.; Pezzani, M.; Messa, S. Comparison of Toxic Product Yields of Burning Cables in Bench and Large-Scale Experiments. Fire Saf. J. 2008, 43, 140–150. [Google Scholar] [CrossRef]
- IEC/TS 60695-7-50: 2002; Fire Hazard Testing Part 7-50: Toxicity of Fire Effluent Estimation of Toxic Potency Apparatus and Test Method (Inactive). IEC: Geneva, Switzerland, 2002.
- NF X70-100; Fire Behavior Tests—Analysis of Pyrolysis and Combustion Gases—Pipe Still Method. NF: La Plaine Saint-Denis, France, 2006.
- Kaczorek-Chrobak, K.; Fangrat, J. PVC-Based Copper Electric Wires under Various Fire Conditions: Toxicity of Fire Effluents. Materials 2020, 13, 1111. [Google Scholar] [CrossRef] [PubMed]
- Porowski, R.; Kowalik, R.; Ramiączek, P.; Bąk-Patyna, P.; Stępień, P.; Zielecka, M.; Popielarczyk, T.; Ludynia, A.; Chyb, A.; Gawdzik, J. Application Assessment of Electrical Cables during Smoldering and Flaming Combustion. Appl. Sci. 2023, 13, 3766. [Google Scholar] [CrossRef]
- Seo, H.J.; Kim, N.K.; Lee, M.C.; Lee, S.K.; Moon, Y.S. Investigation into the Toxicity of Combustion Products for CR/EPR Cables Based on Aging Period. J. Mech. Sci. Technol. 2020, 34, 1785–1794. [Google Scholar] [CrossRef]
- Kim, M.H.; Lee, S.H.; Jeong, S.Y.; Lee, S.K.; Lee, J.E.; Kwark, J.H.; Lee, M.C. Investigation of Combustion, Smoke, and Toxicity Characteristics of Flame-Retardant and Fiber-Optic Cables Used in Nuclear Power Plants. J. Mech. Sci. Technol. 2023, 37, 987–999. [Google Scholar] [CrossRef]
- Lee, S.H.; Kim, M.H.; Jeong, S.Y.; Lee, S.K.; Lee, J.E.; Lee, M.C. Fire Dynamics Simulation in a Cable Spreading Room of a Nuclear Power Plant Using Fire Test Results of Heat Release and Toxic Gas Emission. J. Mech. Sci. Technol. 2024, 38, 1517–1532. [Google Scholar] [CrossRef]
- ISO 5660-1:2015; Reaction-to-Fire Tests—Heat Release, Smoke Production and Mass Loss Rate. ISO: Geneva, Switzerland, 2015.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).