Abstract
This study investigated the interplay between exit selection models and local pedestrian movement patterns within floor field frameworks. Specifically, this investigation analysed the performance of a multinomial logit exit choice model, incorporating both expected utility theory and cumulative prospect theory frameworks when coupled with three distinct local-level pedestrian movement models (FF-Von Neumann, FF-Moore, and NSFF). The expected utility theory framework considers the deterministic component as a linear relationship, while the cumulative prospect theory framework further considers the decision-maker’s risky attitudes by transforming objective terms into subjective terms using a power value function. The core objective was to comprehend how local movement dynamics, as represented by the floor field models, influence decision-making during exit selection. Comparative analyses revealed intriguing variations between the three local models, despite their shared expected utility theory-based exit choice framework. These discrepancies stemmed from the diverse pedestrian trajectory behaviours generated by each model. Consequently, these local dynamics impacted the decision-maker’s assessment of critical factors, such as the number of evacuees close to the decision-maker () and the number of evacuees close to an exit (), which the exit choice model incorporates. These assessments, in turn, significantly affected higher-level decision-making. The integration of the three models with the multinomial logit exit choice model, using either cumulative prospect theory and expected utility theory frameworks, further strengthened the observed bilateral relationship. While the specific nature of this relationship varied depending on the chosen framework and its implementation details, these consistent findings demonstrate the robustness of the results. This reinforced the influence of local-level pedestrian dynamics on higher-level exit selection, highlighting the importance of accurate crowd dynamics modelling, especially when advanced exit choice models consider local movement factors.
1. Introduction
Evacuation models are crucial in the field of fire safety engineering. They enable the evaluation of safety conditions during emergencies in various environments. The process of creating these models typically involves two key steps: the selection of an exit choice and the simulation of local movement [1,2]. The selection of an exit choice is a pivotal decision-making process that dictates the route evacuees follow during an emergency. Its implementation can be influenced by a multitude of factors, including the proximity of exits, the crowd density, and an individual’s familiarity with the environment [3,4,5,6,7,8,9]. Conversely, the simulation of local movement predicts the manner in which individuals navigate within a crowd during an evacuation, taking into account elements such as individual speed, direction, and interactions with other individuals and obstacles. When combined, these components contribute to a comprehensive and realistic depiction of evacuation scenarios. Traditional exit choice models typically base their predictions on simple assumptions to determine evacuation routes [10,11]. For example, the fire safety engineering market currently offers a wide range of evacuation-modelling software, with over 70 available models. It is important to acknowledge that the core assumptions underlying many of these models were established in the late 1980s and 1990s. For instance, both Exodus [12] and Simulex [13] rely on a simplified shortest path algorithm, which identifies the most direct route between the start and end points. These models do not consider factors beyond their heuristics. Consequently, they operate in a unidirectional manner, dictating simulated movements with little feedback from the evolving pedestrian behaviour.
Recent advancements have led to the development of more sophisticated exit choice models. These models consider a broader range of factors to better simulate pedestrians’ decision-making processes. For instance, Guo and Huang’s [14] model suggests that the disutility pedestrians experience when exiting is influenced not only by the distance to the exit but also by external factors, such as the level of congestion around the exit and the width of the exit. Alizadeh [15] proposed a dynamic cellular automaton model that considers both the distance and the distribution of pedestrians in the crowd, predicting a more realistic evacuation time compared with traditional models. Lo et al. [16] proposed a game theory-based model for exit selection. In this model, factors such as crowd density, distance to the exit, and the width of the exit are considered. Pathfinder (version: 2023.3.1206) [17], which is widely used evacuation software, utilises the locally quickest method. This method assumes that the occupants are aware of all doors in their current location, any queues at those doors, and the distance to their destination from each door. Based on this information, occupants calculate travel time costs for each exit and choose the one with the minimum estimated travel time. This approach frames exit selection as an optimisation problem where individuals aim to minimise their travel time. Moreover, some researchers attempted to incorporate factors beyond physical attributes into decision-making models. These include social attributes, such as familiarity with the exit [18,19,20], herding behaviour [21,22], and the impact of cooperative or selfish behaviour [23,24,25,26]. FDS+Evac [27] utilises an exit selection algorithm rooted in game theory principles to estimate the shortest evacuation time for the exits. This algorithm considers various factors, such as the distance to the exits, congestion levels, fire-related conditions, and the visibility and familiarity of exits. Additionally, it considers psychological aspects by categorising pedestrians into different types: conservative, active, herding, and follower agents. This algorithm allows agents in FDS+Evac to continuously evaluate conditions and make dynamic decisions, contributing to its advanced exit selection capabilities. Lovreglio et al. [4] employed a random utility model (RUM) approach to develop a model for understanding and predicting human behaviour during emergency evacuations. Their model incorporates pedestrian observations and considerations of factors such as the number of people near exits, those near the decision-maker, and proximity to exits themselves to inform exit choices. Cao et al. [2] also proposed an exit choice model that takes into account the decision-maker’s current location, exits, distance from the fire to the exits, exit density, visibility, and familiarity. To further refine exit choice modelling, Lovreglio et al. [28] introduced a fire scenario model that predicts exit selection based on four factors: familiarity with the chosen exit, number of people using various exits, presence of smoke at specific exits, and exit distance. These studies collectively highlight the various trade-offs simulated pedestrians consider when making exit choices. Therefore, advanced exit choice models that incorporate the factors that are affected by local pedestrian dynamics can be expected to foster a more bidirectional relationship between exit selection and the simulated scenario as the simulation progresses. This can create a dynamic feedback loop, where evolving pedestrian behaviour can influence the simulated decision-making outputs, unlike simpler exit choice models. Consequently, for advanced exit choice models leveraging factors linked to local pedestrian dynamics, it can be expected that the local movement patterns, such as pedestrian speed and trajectory, require a high degree of accuracy in replicating real-world behaviour. Otherwise, the simulated exit selection may deviate significantly from real-world scenarios, potentially leading to inaccurate evacuation predictions. To the best of the authors’ knowledge, no prior research has explicitly investigated the impact of such a dynamic feedback loop. Whilst overcoming prediction deviations with extensive fine-tuning of the simulation parameters to fit specific data sets, this can raise concerns about the reliability of the results, particularly when the model is applied to a different evacuation scenario that was not used for the calibration. Motivated by these considerations, this study aimed to comprehensively evaluate the relationship between exit choice models and local pedestrian dynamics, especially within the context of floor field models. Floor field models typically place less emphasis on accurately capturing the intricacies of local crowd behaviour. The goal is to enhance the understanding of how the trajectories and movement behaviours of simulated pedestrians can influence the exit choice selection outputs for advanced exit choice models that incorporate factors affected by local pedestrian dynamics over time. This topic has not been explicitly addressed to date.
This study addressed this gap by conducting an in-depth analysis of the results from evacuation simulations that incorporated both exit choice and local movement models. For the exit choice model, this study utilised the multinomial logit model [29,30], which was previously used to integrate environmental- (smoke, lighting, distance to exit) and social-oriented factors. In this study, the multinomial logit model incorporated two social factors influenced by local pedestrian dynamics: the number of evacuees near the exit and near the decision-maker. Factors influenced by herding behaviour are also impacted by simulated dynamics. For local movement models, this study compared the exit choice model output with two models: the traditional floor field (FF) model [31,32] and the improved natural step length floor field (NSFF) model [33]. The FF model uses Moore or Von Neumann neighbourhoods for movement direction based on a rectangular lattice. In a Moore neighbourhood, pedestrians can move to eight surrounding cells, while Von Neumann restricts movement to four adjacent cells. The NSFF model, which was developed by the authors, allows for more realistic movement by enabling pedestrians to move in any direction and vary their step lengths. These differing trajectories and distributions will be used to highlight the bidirectional impact of movement outputs on the exit choice model.
2. Models
The evacuation model is composed of two parts: the exit choice model and the local movement model. Figure 1 depicts the evacuee’s decision-making and movement within the model. The process begins with the evacuee assessing the environment and this step is conducted at the exit selection level using the exit choice models. Following this, the evacuee approaches the exit at the local movement level guided by movement models. Upon reaching a safe zone, the evacuee successfully exits the system. Otherwise, the decision-making process is repeated to determine the next steps. The simulation continues until all evacuees have successfully exited the room.

Figure 1.
A flow chart of the evacuation model.
2.1. Exit/Route Choice Models
The logit model was implemented in numerous numerical evacuation studies to simulate and depict individual behaviour in different scenarios [3,30,34,35,36]. The model typically operates on the assumption that individuals are inclined to choose the option that yields the highest benefit or utility [37,38]. Within the utility framework, the decision-maker assigns a utility to each available option, and this utility is determined based on the relevant attributes of the option. To accommodate behavioural uncertainty, it was proposed that the utility, denoted as for the q-th alternative of the i-th decision-maker, comprises two distinct components [38]:
where is a deterministic component, whereas are regarded as random variables with a probability density function to capture the unobserved factors [39]. The inclusion of both deterministic and random elements is to reflect the predictable and unpredictable aspects of human decision-making during evacuation scenarios.
The probability of selecting each option is determined by the hypothesis regarding the distribution of the random residual. A frequently employed model for this purpose is the multinomial logit model:
In this equation, represents the probability that the agent i chooses option q, and k denotes the options within the choice set. This formula calculates the probability based on the exponentiation of a utility term for the specific option divided by the sum of similar terms for all options in the choice set.
In terms of implementation, the deterministic component of the utility function represented as can be formulated in various ways depending on the observed factors. A common approach is the expected utility theory, which is a normative model that primarily concentrates on the attributes of the options. The fundamental mathematical properties of expected utility theory are its additivity and linearity [40]. For instance, Lovreglio et al. [30] demonstrated the use of a multinomial logit model to predict exit choice behaviour during an evacuation based on the expected utility theory framework. Their model incorporated both environmental factors (such as the presence of smoke, emergency lighting, and distance to the exit) and social factors (including exit congestion, exit flow rate, and local pedestrian movement near the decision-maker). This model was calibrated using data from an online stated preference survey conducted using virtual reality (VR). The linear specification, which was used for the deterministic part of the utility value when agent i chooses exit q, follows the following formulation:
where is the weight representing the decision-maker preferences related to the corresponding factor. is the number of evacuees close to a local exit; the radius of the influence area was defined as the distance from the centre point of each exit to the midpoint between the centre points of both exits. is the flow of the evacuees through a local exit; is the number of evacuees close to the decision-maker heading towards one of the local exits; the radius of influence for evacuees was set to 5 m from the decision-maker, in accordance with Ref. [2]. is the distance of the agent from the local exits. The variables of the expected utility theory model are illustrated in Figure 2. The coefficient of each variable, as calibrated by Lovreglio et al., is presented in Table 1.
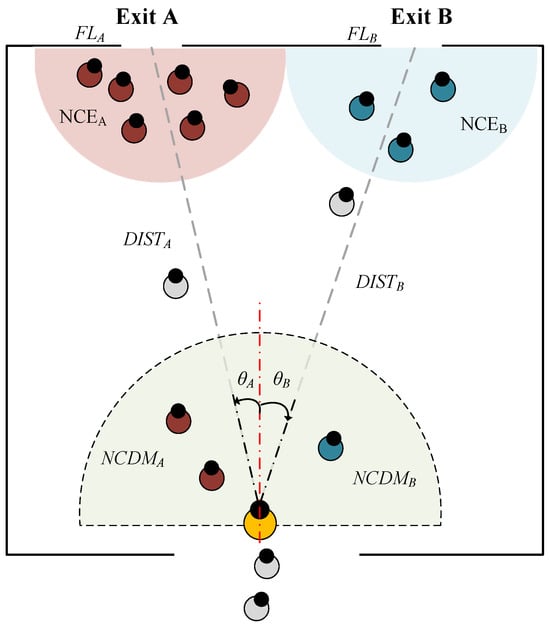
Figure 2.
A visual representation of the factors influencing exit choice models. The pedestrian, highlighted in yellow is at the decision-making point. is the number of evacuees close to a local exit; is the flow of the evacuees through a local exit; is the number of evacuees close to the decision-maker heading towards one of the local exits; is the distance of the agent from the local exits; represents the body orientation from the initial position to the exit; the subscripts A and B represent their corresponding values for the A and B exits.

Table 1.
Estimated coefficients for multinomial logit exit choice model based on expected utility theory and cumulative prospect theory [30,36].
Figure 3 illustrates the algorithm used by the decision-maker to determine which exit a nearby pedestrian is approaching. At time step , the distances to exits A and B from the pedestrian are denoted by and , respectively. At the subsequent time step t, these distances are updated to and . The difference in distance changes, compared with , indicates the pedestrian’s movement direction. A positive difference suggests the pedestrian is moving closer to exit A, implying they are heading towards exit A. Conversely, a negative difference indicates movement towards exit B. If the difference is zero, the pedestrian is considered undecided.
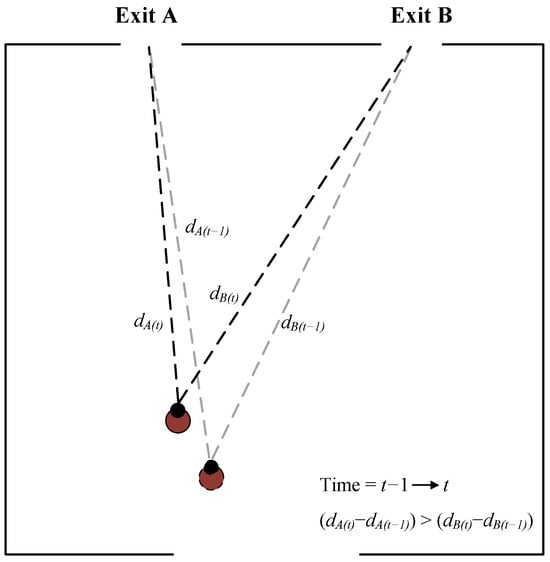
Figure 3.
Visual illustration of the algorithm decision-makers used to determine which exit a nearby pedestrian is heading to. The pedestrian, highlighted in red, indicates the same pedestrian at a different time. and represent the distances to exits A and B at time t.
It is noteworthy, however, that other studies proposed alternative implementations of the multinomial logit model. For instance, Gao et al. [36] replaced the expected utility theory with the cumulative prospect theory [41] and accentuation of differences [42] to accentuate the influence of context effects on exit choice. In their study, a power value function was used to transform the risk assessment attitude of the decision-maker into one that was more subjective-oriented:
The model proposed by Gao et al. [36] includes two parameters, and , which are used to transform each attribute of the exit into a subjective term. Here, represents the body orientation from the initial position to the exit. The result of [36] shows that had a relatively minor impact on the exit choice compared with and . This study shared similarities with the scenario presented in [36]. Both studies involved decision-making in a rectangular room with multiple exits, where exit visibility and pedestrian distribution influenced the choices. Additionally, the discrete cumulative prospect theory-based exit choice model from [36] served as the foundation for capturing individual decision-making processes when faced with multiple options. This model, which is rooted in well-established behavioural principles under choice conditions, demonstrates broad applicability across various scenarios, including the one presented here. The variables of the model are illustrated in Figure 2 and the coefficients of the model, which were derived from [36], are summarised in Table 1.
To comprehensively understand the impact of simulated pedestrians’ movement on the model outputs, both implementation versions of the multinomial logit exit choice model were considered in this study. As noted earlier, Lovreglio et al. [30] demonstrated that the expected utility theory version of the model assumes a more linear format and provides a structured representation of decision-maker preferences related to the , , , and factors. In this study, the expected utility theory framework served as the baseline for comparison. Gao et al.’s [36] proposed version of the model also considers factors such as and , but adopts a power value function format to introduce a more subjective-oriented transformation to the decision-making process. This study compared the results of this proposed framework with the expected utility theory-based baseline. Testing both implementations ensured a more robust evaluation of the multinomial logit model’s sensitivity to simulated pedestrian movements, contributing to the understanding of how the bilateral relationships can impact evacuation modelling.
While this study prioritised occupant behaviour and decision-making during an evacuation, it did not explicitly explore how fire characteristics influence exit selection. However, this study laid a foundation for future investigations that incorporate fire dynamics to improve our understanding of occupant behaviour in fire emergencies. The modelling approach utilised in this study demonstrates clear potential for adaptation to include fire-related variables. For instance, the multinomial logit exit choice model could be expanded to encompass factors like fire and smoke as decision-making considerations when evaluating the safety and accessibility of exits, ultimately altering the utility values assigned to each exit option. Similarly, local movement models could be adapted to account for the presence of fire, smoke, and other hazards when determining the probability of occupants moving towards specific target cells, paving the way for fire evacuation simulations.
2.2. Local Movement Models
This study aimed to examine the bilateral influence of the local-level movement model and the exit choice model. Three local-level models were used and their specifics are provided below.
2.2.1. Floor Field Model
Burstedde et al. [31] introduced the floor field (FF) model, employing a two-dimensional cellular automata framework for simulating pedestrian flow. This model successfully reproduced the self-organising behaviours observed in pedestrian dynamics, including phenomena such as jamming, clogging, lane formation, and oscillation at evacuation bottlenecks [43,44,45,46]. In this study, a multi-grid FF model was utilised to simulate local movement, where each pedestrian, occupying a 0.4 m × 0.4 m space, spanned a 5 × 5 grid. Each time step was 0.0615 s. Two commonly used neighbourhood rules, Moore and Von Neumann, as illustrated in Figure 4, were implemented as part of the comparative analysis.
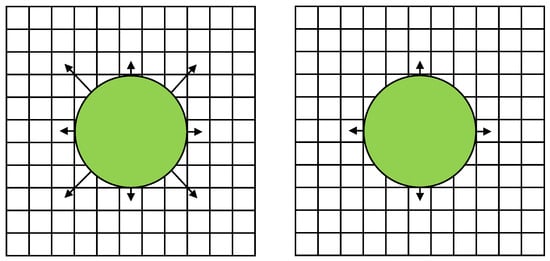
Figure 4.
Schematic diagram of Moore neighbourhood rule (left) and Von Neumann neighbourhood rule (right).
Pedestrians decide to move or remain stationary at each time step based on transition probabilities in a synchronous update approach [47]. The probability of selecting neighbouring cells for the next step, which is a key aspect of the FF model’s dynamics, is calculated via
where and represent the static and dynamic floor fields, respectively, and and are scaling factors for these fields. N is a normalisation factor that ensures the total probability sums to one, that is, . The static floor field represents a pedestrian’s behaviour of seeking the shortest route to an exit, while the dynamic floor field illustrates their tendency to trail other evacuees. Specifically, the static floor field describes the attractiveness of the exits for pedestrians, with its value being inversely related to the distance from the exits. The static floor field is a field initialised at the beginning of the model, which does not evolve over time or change due to the presence of pedestrians. Thus, cells nearer to exits are more attractive. The dynamic floor field represents the virtual trace left by pedestrians to describe the phenomenon that pedestrians tend to follow others’ traces. With each time step, the dynamic floor field value of a moving pedestrian’s original cell increases by one and the values decay with probability and diffuse with probability to one of its neighbouring cells [32,33]. The factor accounts for the presence of either an obstacle or another pedestrian in a cell, equating to zero if the cell is occupied and one otherwise.
2.2.2. Natural Step Length Floor Field Model
The natural step length floor field (NSFF) model is an extended FF model, which integrates the natural step length into pedestrian movement [33]. As shown in Figure 5, a nearly circular shape with a diameter of 0.4 m was used to represent the pedestrian by combining multiple cells. Each time step was 0.0615 s. Compared with the Moore and Von Neumann neighbourhood rules used in the traditional FF model, the NSFF model extends the interaction area to a disk with a radius determined by the natural step length. The step length is determined by the movement speed of the pedestrian. Previous research established a strong correlation between the step length and speed based on an experimental study [48].
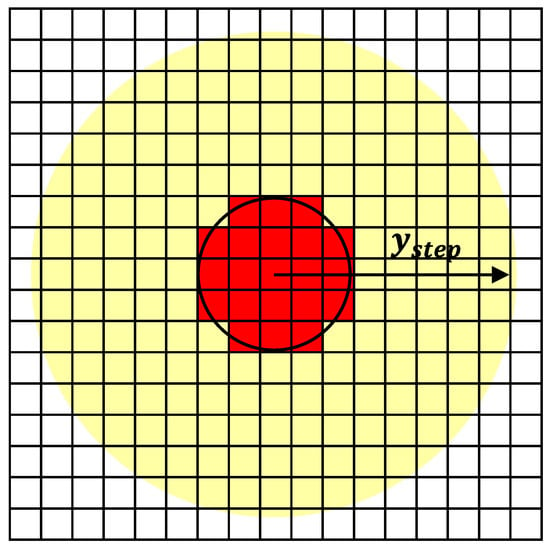
Figure 5.
Schematic diagram showing the NSFF model being used to simulate pedestrian motion. The red cells represent the body of the pedestrian, while the yellow cells denote the target cells for the pedestrian at the next time step.
In this equation, denotes the step length measured in metres (m), and v signifies the velocity expressed in metres per second (m/s). The error term is assumed to be normally distributed. The deduced regression coefficients were given as , , and .
With the introduction of the new neighbourhood rule, the potential movement targets for pedestrians have expanded, as illustrated by the yellow region in Figure 5. If the cell serves as the pedestrian’s centre, the remaining grids that depict the yellow area can be determined using the equation provided in Equation (7). r indicates the spatial resolution of 0.08 m/grid.
The NSFF model employs governing equations and collision avoidance rules that closely resemble those of the conventional FF model. Specifically, the probabilities of pedestrians moving to their target cells are determined by static and dynamic floor fields, and are calculated using Equation (8):
Here, q represents the number of grids that the pedestrian is expected to occupy in the next time step, while is the number of grids currently occupied by the pedestrian. The parameters N, , and follow the conventional definitions of the FF model (refer to Equation (5)). The factor also accounts for the presence of either an obstacle or another pedestrian in a cell; it is set to zero if the cell is occupied and one if it is unoccupied. Due to the natural step length movement, the NSFF model identifies potential target cells that the pedestrian can reach, considering not only the current and target positions but also the cells previously traversed by the pedestrian. A movement path is generated using linear interpolation [33]. The pedestrian’s body centre is placed on the cells in the movement path to check for an overlap with obstacles or other pedestrians. If any overlap is detected, the movement probability for the target cell is set to 0. A partial synchronous update scheme is used [33].
The NSFF model provides a more accurate and detailed representation of how pedestrians move compared with traditional neighbourhood rules. In the NSFF model, the pedestrian’s step length determines the disk radius, allowing pedestrians to take shorter steps in crowded areas and adapt to their surroundings. The improvisation allows the modelled pedestrians to choose from more directions for each step, unlike the traditional four-direction (Von Neumann) and eight-direction (Moore) rules, in addition to varying the stride distances for each step, which the traditional models cannot. Figure 6 presents the fundamental diagrams of these three models, which describe the relationship between speed and density. This diagram compares the simulation results with empirical data from Weidmann [49], SFPE [50], Helbing [51], Seyfried [52], and Polus [53]. Despite some variations in the exact values of the data points between the datasets, the fundamental diagrams generally exhibit similar shapes across all datasets. Given the consistency and the detailed nature of Weidmann’s fundamental diagram, it was used for the simulations performed. The choices of = 10 and = 0 in all three models aligned with established practices within the field of pedestrian dynamics, particularly studies utilising the speed–density relationship (as demonstrated in [54,55]). The parameter acts as a sensitivity coefficient, while captures the influence of pedestrian interactions on flow velocity. Setting to zero simplifies the model, allowing researchers to isolate and better understand how quantifiable static environmental features, such as the room layout and exit configurations, interact with pedestrian movement within the speed–density framework. This approach fosters comparability with existing research and facilitates a focused examination of these static interactions. All models show a decrease in speed as density increases, which is consistent with theoretical expectations. However, the FF-Von Neumann and FF-Moore models suggest higher speeds in high-density scenarios compared with the NSFF model, which differs significantly from the experimental results. This difference in modelling the relationship between pedestrian speed and density can affect evacuation dynamics and potentially influence the outcomes of exit selection.
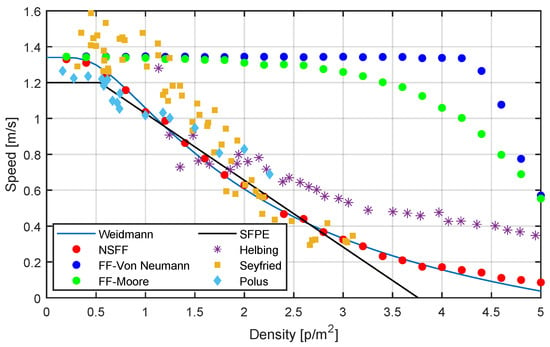
Figure 6.
Fundamental diagram of NSFF, FF-Von Neumann, and FF-Moore models compared with Weidmann [49], SFPE [50], Helbing [51], Seyfried [52], and Polus [53] models ( and ). The simulation was conducted in a corridor with a width and length of 6 m and 22 m, respectively.
3. Calibration of the Local-Level Model
The local-level movement models encompass numerous parameters that are crucial for defining the simulation precision, necessitating their calibration for accurate representations. To ensure equitable comparisons, parameters for the floor field model with the Von Neumann neighbourhood rule (FF-Von Neumann), the floor field model with the Moore neighbourhood (FF-Moore), and the natural step length floor field (NSFF) model were calibrated using identical datasets from evacuation experiments conducted by Nagai et al. [56]. They investigated the dynamic behaviour of walkers and crawlers evacuating from a channel through experiments. In these pedestrian evacuation trials, students were initially standing and positioned randomly within the channel. Separate experiments with groups of 5, 10, 20, 30, 40, and 60 pedestrians were used to investigate the effect of initial densities on the mean flow rates for walkers. Similarly, groups of 5, 10, 15, 20, and 25 pedestrians were used to examine the impact on flow rates for crawlers. The experimental scenario configuration is depicted in Figure 7, with the exit width set at 1.2 m, and the average flow rate measured across varying pedestrian densities. The density indicates the overall density in the room, which was calculated by dividing the number of pedestrians by the room area (12 ). This study only used the data collected from the walking subjects. The calibration procedures involved varied test runs to adjust the parameter values within a preliminary range of thresholds, followed by iterations with parameters that varied from lower to higher bounds. This facilitated a comparative analysis of evacuation times obtained from simulations and experiments. The search for optimal parameters and focused on maximising the R-square value. Table 2 presents the best fitting parameters and their corresponding R-square values, while Figure 8 illustrates the fitting results of the experimental data and simulation outcomes.
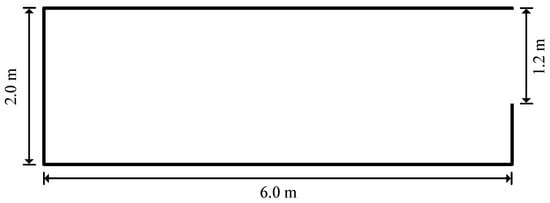
Figure 7.
Schematic illustration of the experimental setup.

Table 2.
Fitting parameters for the movement model.
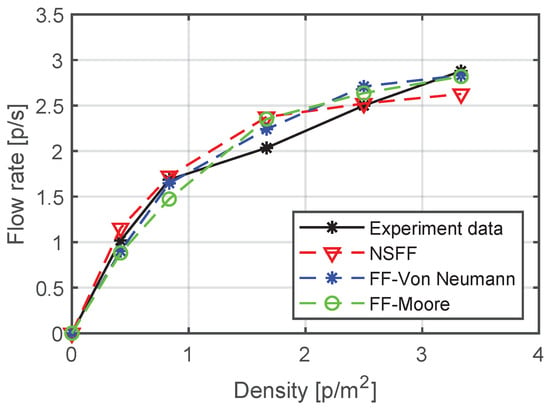
Figure 8.
Comparison of experimental data [56] and simulation results in the scenarios with a 1.2 m wide door. Following [56], the pedestrian density was converted from its original unit (pedestrians per maximum capacity) to people per square metre by dividing the number of pedestrians by the room area (12 ).
In the floor field model, the accurate representation of crowd behaviour significantly relied on the model parameters’ and scaling factors used. Here, reflects how the environmental factors, such as the layout of a space or the location of exits, influence pedestrian movement. represents the degree to which individuals follow others in a crowd. When applying the floor field model to different studies, recalibration of the and factors typically becomes necessary, as aspects of pedestrian behaviours influenced by floor fields can vary depending on the nature of the specific study and its configuration. In contrast, parameters such as and , which signify the decay and diffusion rates of the dynamic floor field, are less sensitive across different scenarios, and were therefore derived from other studies [33,54,57]. For this study, to isolate the impact of pedestrian movement on exit choice, the models were calibrated once using a fundamental speed diagram, with these constants applied across all evacuation scenarios. Recalibration was avoided to prevent masking the relationship between simulated trajectories and exit selection outcomes.
4. Simulation Results
4.1. Comparisons with Empirical Observations of the Models with Expected Utility Theory
4.1.1. Study in a Single-Room Scenario
This study investigated the impact of simulated local pedestrian dynamics on exit choice by comparing three local movement models within the same expected utility theory-based multinomial logit exit choice model. For this section of the study, to facilitate this comparison, a previously conducted evacuation experiment by Liao et al. was replicated within the simulation environment [58].
The experiment involved 18 participants (average age: 24 years, range: 18–62) navigating a single room configured with barriers (2.5 m high) and two exits (left: 0.7 m, right: 1.1 m) (see Figure 9). Participants started in a holding area connected to the room and were instructed to move freely without pushing or competition. The details of the scenario are summarised in Table 3. In the simulation, each pedestrian made a single decision regarding which of the two exits in the room to choose at the moment they enter the room. This decision was simulated for each pedestrian and remained unchanged throughout the evacuation process. The multinomial logit model based on the expected utility theory incorporated factors like , , , and in the exit selection. However, the chosen experimental setup minimised the influence of some of these factors. First, the large room and limited number of participants (18) made congestion (i.e., ) at the exits unlikely. Second, participants were initially positioned at similar distances from both exits, reducing the impact of distance (i.e., ). Consequently, the influences of and on the exit selection were minimised, leaving and as the potential drivers. While the wider right exit could influence , the limited number of participants and large room size made it unlikely for significant congestion to develop and impact exit flow rates. Hence, while could influence the exit choice, its effect was expected to be relatively constant over time. This setup then became ideal to specifically examine how the three models’ generated variations in simulated local pedestrian dynamics impact individual exit choices through their influence on . For each simulated participant entering the room, a choice between the two exits was modelled. Exit usage and evacuation time were calculated as averages across 100 repeated runs for each local movement model.
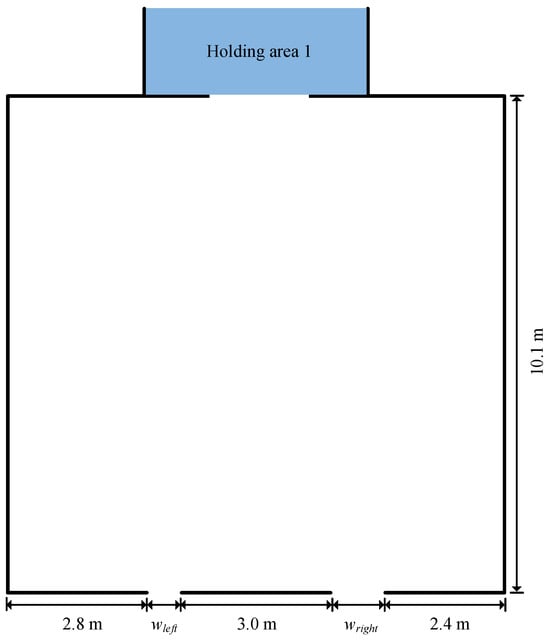
Figure 9.
Schematic illustration of the spatial configuration for the experimental scenario. and represent the widths of the left and right exits, which were 0.7 m and 1.1 m, respectively.

Table 3.
Details of the experimental scenarios. and are the widths of the left and right exits, respectively. and are the number of participants in the holding area 1 and 2, respectively.
Figure 10 depicts the trajectories of both experimentally observed and simulated pedestrians. Due to its greater flexibility in movement direction and distance, the NSFF model allowed pedestrians to follow more natural and realistic paths, closely replicating the experimental observations. The FF-Von Neumann model, in contrast, restricted movement to four cardinal directions, resulting in characteristic zig-zag trajectories. While the FF-Moore model offered eight directional choices, diagonally moving pedestrians covered a greater distance compared with horizontal or vertical movements within the same time step. To achieve consistency with other directions (where distance equals time step), the FF-Moore model needed to alternate between diagonal and non-diagonal moves to maintain the desired speed. This frequent switching led to a more random movement pattern. These distinct trajectories generated by each model thus provided a valuable tool for assessing how sensitive the multinomial logit model output was to the simulated pedestrian movements.
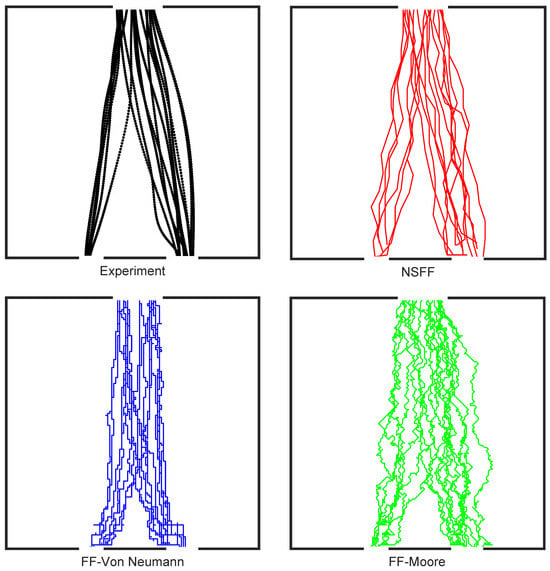
Figure 10.
Trajectories for pedestrians of the experiment and simulations for the single-room scenario.
To assess the impact of local movement patterns on exit choice, Figure 11 presents the difference utility values for , , , and across the three local movement models throughout the simulation. These metrics helped to quantify the potential impact of varying pedestrian dynamics on the exit choice. The difference utility was derived by subtracting the utility value associated with the right exit from that of the left exit for each individual (decision-maker). For example, the utility value of for the left exit of the i-th decision-maker was calculated as . Similarly, the utility value for the right exit was . The difference utility for NCE for the i-th decision-maker was then calculated as . The magnitude of this difference reflected the strength of the individual’s preference. The figure uses the time axis to represent the moment when each pedestrian made their exit decision. Within the exit choice model, pedestrians are expected to choose the exit with the higher utility value. A positive difference utility indicates a preference for the left exit, while a negative value suggests a leaning towards the right exit. Figure 11 confirmed that, as expected, and had minimal impacts on the exit choice due to the experimental setup. All models showed a preference for the wider right exit based on the factor, aligning with expectation. However, the factor revealed key differences. While all models favoured the left exit, the NSFF model exhibited a stronger bias (0.071) compared with FF-Von Neumann (0.062) and FF-Moore (0.043), highlighting the potential sensitivity of to pedestrian movement patterns.
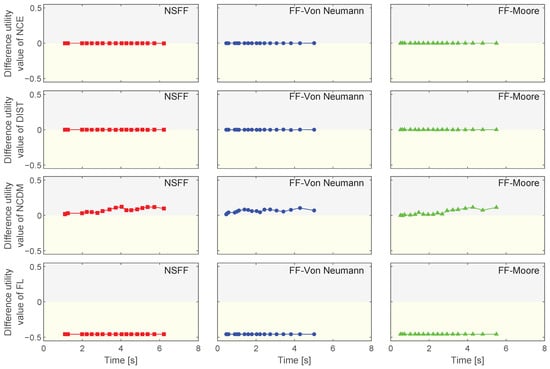
Figure 11.
Difference utilities of all the factors of each pedestrian during the whole evacuation in the single-room scenario. The difference utility was calculated by subtracting the utility value associated with the right exit from that of the left exit. A positive value indicates that the factor caused pedestrians to choose the left exit, while a negative value suggests a tendency for pedestrians to prefer the right exit. The magnitude of the difference indicates the strength of the tendency. Time in the figure represents the moment when each pedestrian makes the decision.
As noted in Section 2, the movement direction of pedestrians near the decision-maker will affect the decision-maker’s judgement for the exit selection of surrounding pedestrians. Therefore, to better understand the movement patterns generated by different models and quantify their impacts on the decision-maker’s exit selection judgement, Table 4 presents their derived consistency rates. The consistency rate reflects the consistency of simulated pedestrians’ movements towards their chosen exits throughout the evacuation. At each time step, a pedestrian’s consistency value was 1 if their movement aligned with their chosen exit, and 0 otherwise (including cases where the pedestrian did not move). The consistency rate for a pedestrian was the average of its consistency values across all time steps. Table 4 shows the average consistency rates for all pedestrians in the NSFF, FF-Von Neumann, and FF-Moore models. The NSFF model exhibited the highest average consistency (0.91), followed by the FF-Von Neumann model (0.82). The FF-Moore model had the lowest average consistency (0.61). Notably, these consistency rates aligned with the models’ biases observed in the factor. These results suggest that different trajectory patterns (e.g., zig-zag in FF-Von Neumann, random in FF-Moore) could influence the decision-maker’s judgement of , impacting the exit selection.

Table 4.
Average consistency rate between the trajectory and exit selection for the pedestrians in the NSFF, FF-Von Neumann, and FF-Moore models.
To evaluate the influence of local movement models on the exit selection, Table 5 presents the results alongside experimental observations as a benchmark. These results include left exit usage percentages and evacuation times. While all models exhibited comparable exit usage rates, the NSFF model aligned most closely with the observed exit usage. Notably, the NSFF model also achieved the evacuation time closest to the experiment (14.3 s vs. 13.8 s) when compared with the FF-Von Neumann (17.5 s) and FF-Moore models (18.3 s). These findings suggest that differing movement trajectories can influence exit choice model outputs. Although not specifically calibrated to the simulated scenario, the NSFF model, which generated more realistic movement patterns, demonstrated the best agreement with the experimental observations, highlighting the importance of incorporating realistic pedestrian dynamics in evacuation simulations.

Table 5.
Comparison results of the experiment and simulation in the single-room scenario.
4.1.2. Study in a Corridor Room Scenario
Since the simple room configuration with limited participants effectively isolated and demonstrated the impact on , further simulations were conducted in a more complex environment to assess how trajectories might affect other factors beyond . For this section of the study, a more complex experimental setup from Liao et al. [58] was leveraged to further explore the influence of simulated pedestrian trajectories on various factors that affect exit choice in a more complex scenario, as depicted in Figure 12. The participants navigated from a narrow corridor (2 m wide) into a larger room with two exits of equal width (0.8 m). The details of the scenario are summarised in Table 3. As in the previous experiment, participants were instructed to move through the setup quickly but avoid pushing or competition.
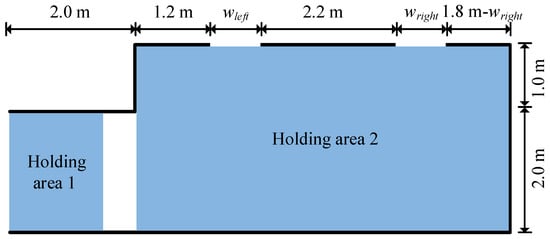
Figure 12.
Schematic illustration of the spatial configuration for the experimental corridor room scenario. and represent the widths of the left and right exits.
In the simulation, each pedestrian made a single decision regarding which of the two exits to use at the moment they entered the room from the corridor. This decision was simulated for each pedestrian and remained unchanged throughout the evacuation process. The selection of this configuration was driven by several factors. The three local movement models, as depicted in Figure 6, demonstrated unique speed–density relationships. These relationships, combined with the exit proximity to the decision-making point, potentially affected the crowd buildup near the exits, influencing the factor. Furthermore, the varying speed–density relationships were likely to alter the number of evacuees near the exits, affecting the NCE factor. Considering the identical setup across all simulations, the factor should favour the exit nearest to the pedestrians while maintaining consistency in effect. The equal-sized exits implied minimal impact on the exit choice from the factor. The anticipated differences in simulation outcomes were expected to correlate with the interplay between the and factors for the different modelled trajectories. However, this required further assessment through the simulations.
Figure 13 shows the simulated pedestrian evacuation progress in the corridor room setting using the NSFF, FF-Von Neumann, and FF-Moore models. Comparing the overall trends, the NSFF model exhibited less pedestrian clustering, while the FF-Von Neumann and FF-Moore models displayed more collective movement. This collectivity likely stemmed from their higher simulated velocities under high densities (Figure 6). Analysed individually, at t = 6 s, the NSFF model showed the fewest remaining individuals (64), with more near the right exit. This efficiency allowed initially closer pedestrians to exit quickly. By t = 9 s, the NSFF model exhibited a relatively even distribution at both exits, while the FF models showed congestion building at the left exit due to the surge of collective arrivals. From t = 12 s to t = 18 s, the NSFF avoided congestion, whereas the traditional FF models experienced considerable build-up at both exits. Notably, across all three time steps, the NSFF model consistently evacuated pedestrians faster, showcasing its higher efficiency. Throughout the simulation, the NSFF model consistently demonstrated higher evacuation efficiency, as reflected by the consistently lower number of remaining pedestrians. However, focusing at t = 18 s, while only 31 pedestrians remained in the room, a considerable number were still in the corridor for the NSFF model. Conversely, both traditional FF models demonstrated faster corridor clearance compared with the NSFF model by this point. This performance was consistent with the speed–density relationship, where the traditional FF models had higher speeds, even in high-density scenarios. This allowed them to clear the corridor more quickly. In contrast, the NSFF model exhibited lower velocities at high densities. This led to a slower corridor clearance and a more dispersed evacuation process within the room. However, with the least efficient simulated pedestrian trajectories, there was a higher number of remaining pedestrians in the room compared with the NSFF model. These variations in evacuation dynamics provide a valuable framework for evaluating their influence on exit selection decisions.
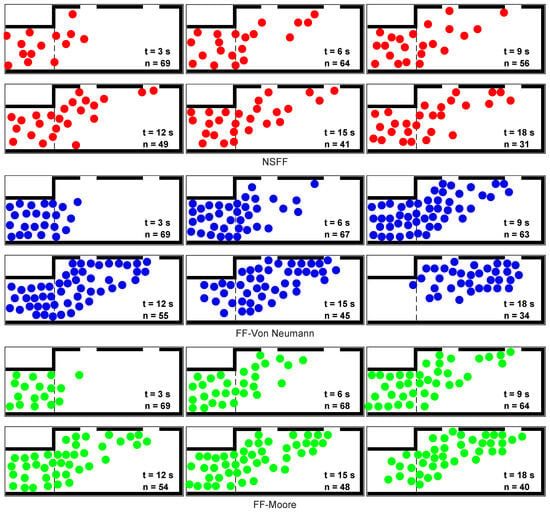
Figure 13.
The snapshots illustrate the process of pedestrian evacuation in the NSFF, FF-Von Neumann, and FF-Moore models at different times (t = 3, 6, 9, 12, 15, and 18 s). The number of remaining pedestrians in the room, denoted by n, is included in each snapshot.
Similar to the single-room scenario, this analysis examined the difference utility values to understand how the evacuees chose between the exits. A positive difference indicated a preference for the left exit, while a negative value suggested a tendency towards the right exit. A larger difference reflected a stronger influence on exit selection. The results, presented in Figure 14, aligned with expectations. The difference utility values for factors like and remained constant across all three pedestrian movement models considered. As anticipated, the factor consistently showed a positive difference of 0.12 throughout the evacuation, indicating a preference for the initially closer left exit. The factor displayed zero difference across all models, signifying that the identical size of both exits eliminated any influence of flow rate on pedestrian choice. However, the influences of and varied across the models. In the case of the factor, initially, the difference for in all models was zero, as there were no pedestrians near the exits when the first person entered the room. Due to the shorter distance, pedestrians initially favoured the left exit. As the pedestrian density at the left exit increased, the difference utility values for became negative in all models. In the NSFF model, this difference decreased continuously for around 4 s, after which it stabilised around −0.4 for the remainder of the simulation. In contrast, the traditional FF models (FF-Von Neumann and FF-Moore) exhibited a continuous decrease in the difference until approximately 6 s, reaching a minimum value near −0.8 before stabilising. These discrepancies highlight the impact of movement models on exit selection outcomes. Specifically, the NSFF model simulated less clustered pedestrian movement compared with the other models. This resulted in a more gradual build-up of evacuees near the exits, leading the difference in utility value to stabilise earlier at a comparatively lower magnitude after the initial decrease. Conversely, the FF-Von Neumann and FF-Moore models simulated a larger surge of arrivals at the left exit, causing larger negative difference utility values and influencing a higher proportion of pedestrians to choose the right exit to counter the congestion.
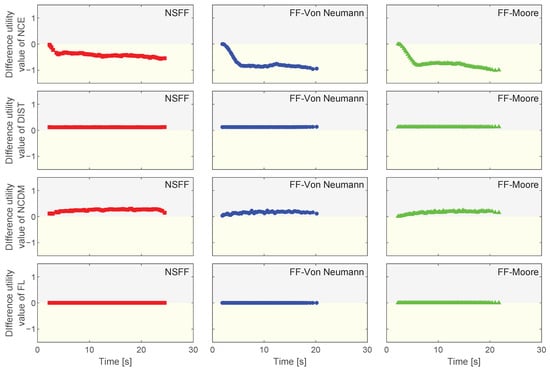
Figure 14.
Difference utility of all the factors of each evacuee during the whole evacuation in the corridor room scenario. The difference utility was calculated by subtracting the utility value associated with the right exit from that of the left exit. A positive value indicates that the factor caused pedestrians to choose the left exit, while a negative value suggests a tendency for pedestrians to prefer the right exit. The magnitude of the difference indicates the strength of the tendency. Time in the figure represents the moment when each pedestrian makes the decision.
When comparing the difference utility value for , all three models showed positive values, indicating that pedestrians were influenced to select the left exit based on this factor. This could be attributed to the presence of the crowd that already chose the left exit, accumulating near the decision point. The NSFF model exhibited the highest average difference in utility value for (0.23) compared with the FF-Von Neumann (0.17) and FF-Moore (0.18) models. This aligned with the findings from the previous section, which demonstrated that more deterministic movement models were associated with a higher difference. On the other hand, the average difference utility values for showed a stronger influence on evacuee decision-making across all models. These values were −0.41, −0.72, and −0.73 for the NSFF, FF-Von Neumann, and FF-Moore models, respectively. This suggests that for the present configuration, the near the exit played a more significant role in affecting the evacuee choice than , regardless of the movement model employed.
To assess the impact of the differing local movement models when coupled with the same exit choice model, Table 6 presents the exit selection results for different local movement models in the corridor room scenario. The models diverged from the experimental data, which are provided as a reference, with all models underestimating the left exit usage compared with the observed 54.2%. The NSFF model provided the closest prediction (48.5% left exit usage), while the FF-Moore and FF-Von Neumann models significantly underestimated the left exit selection (around 38% each). All models predicted evacuation times (28.5–30.6 s) shorter than the actual experimental time (34.4 s).

Table 6.
Comparison results of the experiment and simulation in the corridor room scenario.
For further insights, Figure 15, which compares the number of pedestrians near each exit across the three models and real-world evacuation reference data, was also derived. The results reveal a consistent trend: all models initially showed an increase in for the left exit (closer exit) at around 2.2 s, mirroring the experimental data. However, discrepancies emerged later in the simulation. The NSFF model exhibited a gradual rise in for the left exit, reaching a peak around 5 s and plateauing at a slightly higher level (seven people) compared with the experimental observations (3–5 people). Conversely, the traditional FF models showed a faster and more prolonged increase in for the left exit, exceeding experimental values and reaching up to 15 people by the end. A similar trend was also observed for the right exit. For the right exit, the experimental data indicate pedestrian arrival at around 4 s. The NSFF model aligned with this observation, with for the right exit rising steadily to reach a value of approximately 3. In contrast, the traditional FF models displayed a slower arrival time (around 6 s) and a continuous rise in for the right exit, exceeding the the experimental data (fluctuated between 0 and 4, mostly 2–4).
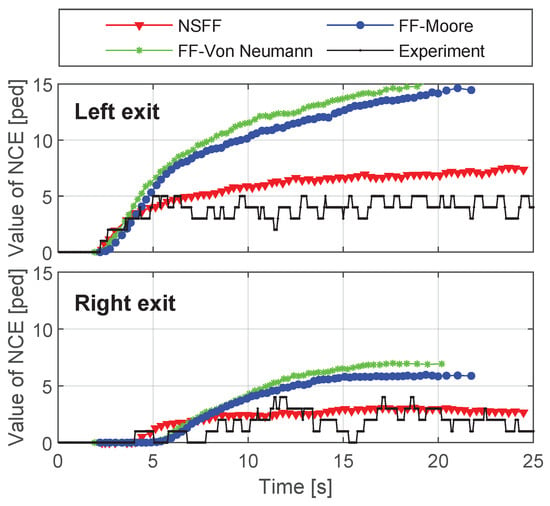
Figure 15.
Value variation of for all three models and the experiment during the whole evacuation. Note that the values for the models represent the average of 100 simulation runs.
In comparing the model outputs with the experimental data, it is essential to recognise that the NSFF model exhibited trends that aligned well with the experiment. This alignment was expected due to the model’s capability to produce realistic movement patterns. However, it is somewhat fortuitous that the NSFF model also simulated outputs with values that closely matched the experimental data, particularly as observed in the plot. Notably, the model employed constants derived from fundamental speed diagram calibration, which were not specifically tailored to this particular experiment, unlike other modelling approaches. Although further optimisation could potentially enhance alignment with the experiment, such an adjustment was not pursued, as discussed earlier.
A comparative analysis was conducted on three local-level models (FF-Von Neumann, FF-Moore, and NSFF), with each integrated with the same multinomial logit model with an expected utility theory frame across two distinct experimental scenarios. This exit choice model considered four key factors that influence pedestrian exit choices: , , , and . A linear specification was applied within the model to determine the utility value of choosing a particular exit. From the results of the single-room case, it was found that the trajectories impacted people’s assessment of within the exit choice model, thereby influencing the final exit choice outcomes. Furthermore, a notable variation was observed in the impact of across the three models in the more complicated corridor room case. From the analysis, it is evident that both individual behaviours and the dynamic performance of the crowd significantly influenced the upper-level exit choice model. This interplay highlights the importance of accurately modelling both individual and group dynamics to ensure reliable predictions of exit selection in evacuation scenarios. The NSFF model, with its accurate representation of crowd dynamics, yielded exit choice results that were closer to the experimental observations compared with the traditional FF models.
4.2. Comparisons with Empirical Observations of the Models with Cumulative Prospect Theory
To assess the generalizability of the findings, this study further explored using the cumulative prospect theory-based multinomial logit with the three different movement models. Notably, the cumulative prospect theory-based multinomial logit model (Equation (4)) employs a non-linear weighting of option probabilities and considers a reduced set of factors: and . By coupling this model with the different movement models and comparing its results with the previously obtained expected utility theory-based outcomes, it became possible to assess whether observed bilateral relationships between the exit choice and model-specific trajectories persisted under a different multinomial logit framework.
4.2.1. Study in a Corridor Room Scenario
To enable a direct comparison of the exit choice models, the corridor room scenario was again employed. Table 7 presents the results from the cumulative prospect theory-based simulations. All three models predicted a higher preference for the left exit (73–74.4%), which deviated considerably from the experimental data (54.2%). To investigate this discrepancy, Figure 16 depicts the differences in utility values for factors that influenced the exit choice ( and ). Notably, the difference in utility values for was negligible across all models. Conversely, the difference in utility for consistently favoured the left exit at around 1 for all models. This suggests that the cumulative prospect theory framework may underestimate the impact of on exit selection compared with when the expected utility theory-based framework was used.

Table 7.
Comparison results of the experiment and simulation in the corridor room scenarios.
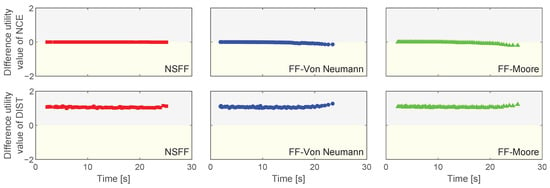
Figure 16.
Difference utility of all the factors of each evacuee during the whole evacuation in the corridor room scenario. The difference utility was calculated by subtracting the utility value associated with the right exit from that of the left exit. A positive value indicates that the factor caused the pedestrians to choose the left exit, while a negative value suggests a tendency for pedestrians to prefer the right exit. The magnitude of the difference indicates the strength of the tendency. Time in the figure represents the moment when each pedestrian made the decision.
The observed discrepancies in the factor estimation between the exit choice frameworks suggest potential differences in how they translate the actual into a corresponding utility value. To investigate this further, Figure 17 depicts the relationship between the values and their corresponding utility values within the cumulative prospect theory framework. The dashed lines represent the average for the left (black) and right (red) exits during the evacuation. The blue line shows how different values translated into utility values. Notably, in all three models, the utility values corresponding to the average at both exits were near zero. This suggests that the power function format used by the cumulative prospect theory framework was insensitive to variations in simulated crowd density near the exits. This insensitivity to lower values in the cumulative prospect theory model might have been a consequence of the calibration data. The study by Gao et al. [36] focused on values of 5 and 20. This limited range might not have provided a sufficiently diverse dataset for effective calibration across the entire spectrum, particularly in the lower range. In contrast, the expected utility theory-based model assumes a linear relationship between utility and various factors, and thus, is inherently less exposed to sensitivity variations across different data ranges.
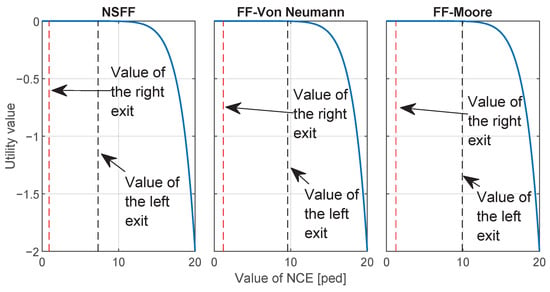
Figure 17.
The relationship between the value of and the utility value based on the cumulative prospect theory frame is indicated by the blue line. The red dashed line indicates the value of the average for the right exit, and the black dashed line indicates the value of the average for the left exit.
4.2.2. Study in a High-Density Corridor Room Scenario
To validate the hypothesis regarding the cumulative prospect theory framework’s sensitivity to values, a new simulation was conducted. This simulation replicated the corridor room scenario with modifications inspired by Liao et al. [58]. The exit dimensions were adjusted (left exit: 0.8 m, right exit: 1.2 m), and a significantly larger number of participants were included (holding area 1: 90 people, holding area 2: 48 people) to create a more crowded evacuation scenario (refer to Table 3). This increased density aimed to push the into a range where the cumulative prospect theory framework’s power function would be more sensitive.
Figure 18 depicts the difference in utility values for and in the modified corridor room scenario. As expected, the difference utility value consistently favoured the left exit (around 1) across all models. The difference utility value, however, exhibited variation. In all models, the value started at 0 and decreased negatively. The key difference lay in the average difference utility value: −1.5 for the NSFF model (moderate impact), and −3.9 and −2.6 for the FF-Von Neumann and FF-Moore models (stronger impact), respectively.
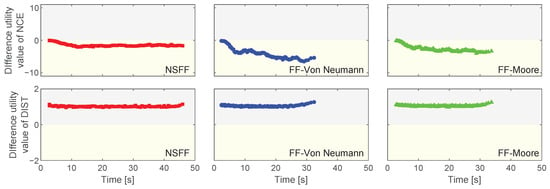
Figure 18.
Difference utility of all the factors of each evacuee during the whole evacuation in the high-density corridor room scenario. The difference utility was calculated by subtracting the utility value associated with the right exit from that of the left exit. A positive value indicates that the factor causes pedestrians to choose the left exit, while a negative value suggests a tendency for pedestrians to prefer the right exit. The magnitude of the difference indicates the strength of the tendency. Time in the figure represents the moment when each pedestrian makes the decision.
Both the experimental and simulation results are presented in Table 7. While 42.8% of participants chose the left exit in the experiment, the NSFF model provided the closest prediction (39.4% left exit usage). The FF-Von Neumann and FF-Moore models significantly underestimated the left exit selection (27.9% and 27.5%, respectively). This study confirmed that movement models significantly influence exit choice model outputs, regardless of the specific framework used, provided they remain within valid operating ranges of the exit choice models.
5. Summary and Conclusions
This study investigated the bidirectional relationship between exit choice models and local pedestrian dynamics within the context of floor field models. This study analysed the outputs of an exit choice model (multinomial logit with expected utility theory and cumulative prospect theory frameworks) when combined with three local-level pedestrian movement models (FF-Von Neumann, FF-Moore, and NSFF). Here, this study aimed to understand how local movement dynamics, as represented by the floor field models, influenced decision-making processes in exit selection.
The comparative analyses revealed that despite using the same expected utility theory-based exit choice framework, the three local models exhibited distinct performances when predicting exit selections and evacuation times. This difference stemmed primarily from the varying pedestrian trajectory behaviours generated by each model, which subsequently affected the decision-maker’s judgement of the number of evacuees close to the decision-maker heading towards one of the local exits (). Further investigation in a more complex corridor room scenario demonstrated that different trajectories and crowd dynamics (speed–density relationship) also influenced the number of evacuees close to the local exit (), impacting higher-level decision-making. This analysis highlighted that the accuracy of both the movement trajectory and crowd dynamics predicted by the local model influenced the outcomes of the higher-level exit selection process.
This study further compared the three models with the cumulative prospect theory-based exit choice model in the corridor room scenario to assess the robustness of the findings. While the expected utility theory and cumulative prospect theory model exhibited lower sensitivity to NCE variations in scenarios with a lesser number of evacuees, significant differences emerged in the high-density scenario with more people. Additionally, the NSFF model consistently demonstrated better performance compared with the traditional FF models, further corroborating that local-level pedestrian dynamics affect upper-level exit selection. This study centred on establishing the existence of a bilateral relationship between exit choice and the specific trajectories generated by different decision-making model frameworks, in addition to demonstrating that the nature of this relationship could vary depending on the implementation details of each model. It is important to recognise that both approaches have established strengths and weaknesses documented in the extensive literature on multinomial logit model variants [36,38]. Definitive performance comparisons between expected utility theory- and cumulative prospect theory-based multinomial logit models are often context dependent and require dedicated studies.
These consistent findings across different theoretical frameworks and scenarios emphasise the critical role of accurate crowd dynamics modelling in predicting exit selection behaviour, particularly with advanced exit choice models incorporating local movement factors. Traditional FF models’ limitations in accurately representing crowd dynamics led to less reliable predictions. Conversely, the NSFF model, with its more nuanced approach to pedestrian movement, provided a closer approximation to actual evacuation behaviours. This study reinforced the importance of selecting appropriate modelling approaches for evacuation simulations, particularly those that can accurately capture the complexities of crowd behaviour for reliable and effective evacuation planning and risk management.
This study shed light on the previously unexplored impact of pedestrian trajectories on simulation outcomes, particularly when combined with advanced decision-making algorithms that consider local movement dynamics. This finding underscores the potential benefits of the more accurate trajectory prediction capabilities offered by the NSFF model, which more traditional implementation of FF model cannot attain. Another under-examined feature of the NSFF model is its ability to incorporate speed variation. Traditional FF models typically reduce overall pedestrian speed by lowering the movement probability at each time step (reference [59]). This can lead to unrealistic scenarios where pedestrians stop entirely, even when their path is clear, resulting in a decrease in average speed. Conversely, the NSFF model integrates a natural step length into pedestrian movement, with the step length determined by the individual’s speed. This allows pedestrians to adjust their speed more realistically by decreasing their step size at each move, enabling a full spectrum of movement speeds. The influence of the speed variation feature within the NSFF model compared with traditional FF models warrants further investigation, particularly regarding its impact on simulation outputs. Evacuation scenarios involving dynamic elements, like smoke, fire, or crowd formation (where distributions can vary spatially), present a compelling case for such inquiry. In these dynamic environments, a crucial aspect lies in assessing how both the simulated trajectories and the incorporation of speed variation differ between models, and how these discrepancies ultimately influence the overall evacuation outcomes. Traditional FF models, which are characterised by “stop-and-go” movement patterns, may have difficulty accurately capturing the gradual reduction in pedestrian speed observed during real-world evacuations. This slowdown often occurs due to factors like smoke inhalation or navigating congested areas. The NSFF model, through its ability to model speed variation via smaller step sizes, has the potential to depict a more realistic flow of pedestrian movement, particularly near obstacles or high-density zones. By delving deeper into these nuances, researchers can not only refine the predictive accuracy of evacuation simulations but also gain valuable insights to inform the design of evacuation protocols.
Author Contributions
Conceptualization, S.X., C.W. and Q.N.C.; methodology, S.X., C.W. and Q.N.C.; writing—original draft preparation, S.X.; writing—review and editing, Q.N.C., D.G., W.W., A.C.Y.Y. and E.W.M.L.; visualization, D.G. and S.X.; project administration, Q.N.C.; funding acquisition, Q.N.C., A.C.Y.Y., E.W.M.L. and G.H.Y. All authors read and agreed to the published version of this manuscript.
Funding
This research was funded by the Australian Research Council (IC170100032).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author due to privacy restrictions.
Acknowledgments
The authors acknowledge the financial support of Wuhan ShuanglianXingxin Machinery and Equipments, China.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ronchi, E. Developing and validating evacuation models for fire safety engineering. Fire Saf. J. 2021, 120, 103020. [Google Scholar] [CrossRef]
- Cao, S.; Fu, L.; Song, W. Exit selection and pedestrian movement in a room with two exits under fire emergency. Appl. Math. Comput. 2018, 332, 136–147. [Google Scholar] [CrossRef]
- Lovreglio, R.; Fonzone, A.; Dell’Olio, L.; Borri, D.; Ibeas, A. The role of herding behaviour in exit choice during evacuation. Procedia-Soc. Behav. Sci. 2014, 160, 390–399. [Google Scholar] [CrossRef]
- Lovreglio, R.; Borri, D.; dell’Olio, L.; Ibeas, A. A discrete choice model based on random utilities for exit choice in emergency evacuations. Saf. Sci. 2014, 62, 418–426. [Google Scholar] [CrossRef]
- Kinateder, M.; Comunale, B.; Warren, W.H. Exit choice in an emergency evacuation scenario is influenced by exit familiarity and neighbor behavior. Saf. Sci. 2018, 106, 170–175. [Google Scholar] [CrossRef]
- Tong, Y.; Bode, N.W. The principles of pedestrian route choice. J. R. Soc. Interface 2022, 19, 20220061. [Google Scholar] [CrossRef] [PubMed]
- Wei, X.; Lou, Z.; Song, H.; Qin, H.; Yao, H. Exploring the impacts of exit structures on evacuation efficiency. Fire 2023, 6, 462. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, W.; Ma, Y.; Lee, E.W.M.; Shi, M. Experimental study on pedestrian behaviors during fire emergency conditions with Minecraft: Case studies in a classroom. Fire 2023, 6, 422. [Google Scholar] [CrossRef]
- Fang, Z.; Song, W.; Zhang, J.; Wu, H. Experiment and modeling of exit-selecting behaviors during a building evacuation. Phys. A Stat. Mech. Its Appl. 2010, 389, 815–824. [Google Scholar] [CrossRef]
- Pelechano, N.; Malkawi, A. Evacuation simulation models: Challenges in modeling high rise building evacuation with cellular automata approaches. Autom. Constr. 2008, 17, 377–385. [Google Scholar]
- Jiang, C.; Yuan, F.; Chow, W.K. Effect of varying two key parameters in simulating evacuation for subway stations in China. Saf. Sci. 2010, 48, 445–451. [Google Scholar] [CrossRef]
- Galea, E.; Galparsoro, J.P. A computer-based simulation model for the prediction of evacuation from mass-transport vehicles. Fire Saf. J. 1994, 22, 341–366. [Google Scholar] [CrossRef]
- Thompson, P.A.; Marchant, E.W. A computer model for the evacuation of large building populations. Fire Saf. J. 1995, 24, 131–148. [Google Scholar] [CrossRef]
- Guo, R.-Y.; Huang, H.-J. Logit-based exit choice model of evacuation in rooms with internal obstacles and multiple exits. Chin. Phys. B 2010, 19, 030501. [Google Scholar] [CrossRef]
- Alizadeh, R. A dynamic cellular automaton model for evacuation process with obstacles. Saf. Sci. 2011, 49, 315–323. [Google Scholar] [CrossRef]
- Lo, S.M.; Huang, H.C.; Wang, P.; Yuen, K. A game theory based exit selection model for evacuation. Fire Saf. J. 2006, 41, 364–369. [Google Scholar] [CrossRef]
- Pathfinder Technical Reference Manual. Thunderhead Support. Available online: https://support.thunderheadeng.com/docs/pathfinder/2023-3/technical-reference-manual/#_pathfinding (accessed on 12 April 2024).
- Sime, J.D. Movement toward the familiar: Person and place affiliation in a fire entrapment setting. Environ. Behav. 1985, 17, 697–724. [Google Scholar] [CrossRef]
- Proulx, G. A stress model for people facing a fire. J. Environ. Psychol. 1993, 13, 137–147. [Google Scholar] [CrossRef]
- Pan, X. Computational Modeling of Human and Social Behaviors for Emergency Egress Analysis; Stanford University: Stanford, CA, USA, 2006. [Google Scholar]
- Helbing, D.; Farkas, I.J.; Molnar, P.; Vicsek, T. Simulation of pedestrian crowds in normal and evacuation situations. Pedestr. Evacuation Dyn. 2002, 21, 21–58. [Google Scholar]
- Low, D.J. Following the crowd. Nature 2000, 407, 465–466. [Google Scholar] [CrossRef]
- Cirillo, E.N.; Muntean, A. Can cooperation slow down emergency evacuations? Comptes Rendus Mec. 2012, 340, 625–628. [Google Scholar] [CrossRef]
- Heliövaara, S.; Kuusinen, J.M.; Rinne, T.; Korhonen, T.; Ehtamo, H. Pedestrian behavior and exit selection in evacuation of a corridor–An experimental study. Saf. Sci. 2012, 50, 221–227. [Google Scholar] [CrossRef]
- McLean, G.A.; Funkhouser, G.E.; George, M.H.; Chittum, C.B. Aircraft Evacuations onto Escape Slides and Platforms I: Effects of Passenger Motivation; Technical Report; U.S. Department of Transportation, Federal Aviation Administration: Washington, DC, USA, 1996.
- Muir, H.; Cobbett, A. Cabin crew behaviour in emergency evacuations. In Civil Aviation Authority/Federal Aviation Administration Paper DOT; Federal Aviation Administration: Washington, DC, USA, 1995. [Google Scholar]
- tkorhon1. FDS-Evac-Guide. GitHub. Available online: https://github.com/tkorhon1/FDS-Evac-Guide (accessed on 12 April 2024).
- Lovreglio, R.; Dillies, E.; Kuligowski, E.; Rahouti, A.; Haghani, M. Exit choice in built environment evacuation combining immersive virtual reality and discrete choice modelling. Autom. Constr. 2022, 141, 104452. [Google Scholar] [CrossRef]
- Swait, J.; Louviere, J. The role of the scale parameter in the estimation and comparison of multinomial logit models. J. Mark. Res. 1993, 30, 305–314. [Google Scholar] [CrossRef]
- Lovreglio, R.; Fonzone, A.; Dell’Olio, L. A mixed logit model for predicting exit choice during building evacuations. Transp. Res. Part A Policy Pract. 2016, 92, 59–75. [Google Scholar] [CrossRef]
- Burstedde, C.; Klauck, K.; Schadschneider, A.; Zittartz, J. Simulation of pedestrian dynamics using a two-dimensional cellular automaton. Phys. A Stat. Mech. Appl. 2001, 295, 507–525. [Google Scholar] [CrossRef]
- Nishinari, K.; Kirchner, A.; Namazi, A.; Schadschneider, A. Extended floor field CA model for evacuation dynamics. IEICE Trans. Inf. Syst. 2004, 87, 726–732. [Google Scholar]
- Xing, S.; Wang, C.; Wang, W.; Cao, R.F.; Yuen, A.C.Y.; Lee, E.W.M.; Yeoh, G.H.; Chan, Q.N. A fine discrete floor field cellular automaton model with natural step length for pedestrian dynamics. Simul. Model. Pract. Theory 2023, 130, 102841. [Google Scholar] [CrossRef]
- Haghani, M.; Sarvi, M. Following the crowd or avoiding it? Empirical investigation of imitative behaviour in emergency escape of human crowds. Anim. Behav. 2017, 124, 47–56. [Google Scholar] [CrossRef]
- Haghani, M.; Sarvi, M. Stated and revealed exit choices of pedestrian crowd evacuees. Transp. Res. Part B Methodol. 2017, 95, 238–259. [Google Scholar] [CrossRef]
- Gao, D.; Lee, E.W.M.; Lee, Y.Y. The influence of context effects on exit choice behavior during building evacuation combining virtual reality and discrete choice modeling. Adv. Eng. Inform. 2023, 57, 102072. [Google Scholar] [CrossRef]
- Bruch, E.E.; Mare, R.D. Methodological issues in the analysis of residential preferences, residential mobility, and neighborhood change. Sociol. Methodol. 2012, 42, 103–154. [Google Scholar] [CrossRef] [PubMed]
- Train, K.E. Discrete Choice Methods with Simulation; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- de Dios Ortúzar, J.; Willumsen, L.G. Modelling Transport; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Grant, S.; Van Zandt, T. Expected utility theory. In INSEAD Business School Research Paper; INSEAD: London, UK, 2007. [Google Scholar]
- Tversky, A.; Kahneman, D. Advances in prospect theory: Cumulative representation of uncertainty. J. Risk Uncertain. 1992, 5, 297–323. [Google Scholar] [CrossRef]
- Spektor, M.S.; Gluth, S.; Fontanesi, L.; Rieskamp, J. How similarity between choice options affects decisions from experience: The accentuation-of-differences model. Psychol. Rev. 2019, 126, 52. [Google Scholar] [CrossRef] [PubMed]
- Kirchner, A.; Schadschneider, A. Simulation of evacuation processes using a bionics-inspired cellular automaton model for pedestrian dynamics. Phys. A Stat. Mech. Appl. 2002, 312, 260–276. [Google Scholar] [CrossRef]
- Lu, L.; Chan, C.Y.; Wang, J.; Wang, W. A study of pedestrian group behaviors in crowd evacuation based on an extended floor field cellular automaton model. Transp. Res. Part C Emerg. Technol. 2017, 81, 317–329. [Google Scholar] [CrossRef]
- Li, Y.; Chen, M.; Dou, Z.; Zheng, X.; Cheng, Y.; Mebarki, A. A review of cellular automata models for crowd evacuation. Phys. A Stat. Mech. Appl. 2019, 526, 120752. [Google Scholar] [CrossRef]
- Qiu, H.; Liang, X.; Chen, Q.; Lee, E.W.M. Effect of Different Time Step Sizes on Pedestrian Evacuation Time under Emergencies Such as Fires Using an Extended Cellular Automata Model. Fire 2024, 7, 100. [Google Scholar] [CrossRef]
- Luo, L.; Fu, Z.; Cheng, H.; Yang, L. Update schemes of multi-velocity floor field cellular automaton for pedestrian dynamics. Phys. A Stat. Mech. Appl. 2018, 491, 946–963. [Google Scholar] [CrossRef]
- Seitz, M.J.; Köster, G. Natural discretization of pedestrian movement in continuous space. Phys. Rev. E 2012, 86, 046108. [Google Scholar] [CrossRef]
- Weidmann, U. Transporttechnik der fußgänger: Transporttechnische eigenschaften des fußgängerverkehrs, literaturauswertung. IVT Schriftenreihe 1993, 90. [Google Scholar] [CrossRef]
- Hurley, M.J.; Gottuk, D.T.; Hall, J.R., Jr.; Harada, K.; Kuligowski, E.D.; Puchovsky, M.; Torero, J.L.; Watts, J.M., Jr.; Wieczorek, C.J. SFPE Handbook of fire Protection Engineering; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Helbing, D.; Johansson, A.; Al-Abideen, H.Z. Dynamics of crowd disasters: An empirical study. Phys. Rev. E 2007, 75, 046109. [Google Scholar] [CrossRef]
- Seyfried, A.; Steffen, B.; Klingsch, W.; Boltes, M. The fundamental diagram of pedestrian movement revisited. J. Stat. Mech. Theory Exp. 2005, 2005, P10002. [Google Scholar] [CrossRef]
- Polus, A.; Schofer, J.L.; Ushpiz, A. Pedestrian flow and level of service. J. Transp. Eng. 1983, 109, 46–56. [Google Scholar] [CrossRef]
- Kirchner, A.; Klüpfel, H.; Nishinari, K.; Schadschneider, A.; Schreckenberg, M. Discretization effects and the influence of walking speed in cellular automata models for pedestrian dynamics. J. Stat. Mech. Theory Exp. 2004, 2004, P10011. [Google Scholar] [CrossRef]
- Fu, Z.; Jia, Q.; Chen, J.; Ma, J.; Han, K.; Luo, L. A fine discrete field cellular automaton for pedestrian dynamics integrating pedestrian heterogeneity, anisotropy, and time-dependent characteristics. Transp. Res. Part C Emerg. Technol. 2018, 91, 37–61. [Google Scholar] [CrossRef]
- Nagai, R.; Fukamachi, M.; Nagatani, T. Evacuation of crawlers and walkers from corridor through an exit. Phys. A Stat. Mech. Appl. 2006, 367, 449–460. [Google Scholar] [CrossRef]
- Kirchner, A.; Nishinari, K.; Schadschneider, A. Friction effects and clogging in a cellular automaton model for pedestrian dynamics. Phys. Rev. E 2003, 67, 056122. [Google Scholar] [CrossRef]
- Liao, W.; Kemloh Wagoum, A.U.; Bode, N.W. Route choice in pedestrians: Determinants for initial choices and revising decisions. J. R. Soc. Interface 2017, 14, 20160684. [Google Scholar] [CrossRef]
- Weifeng, Y.; Hai, T.K. A novel algorithm of simulating multi-velocity evacuation based on cellular automata modeling and tenability condition. Phys. A Stat. Mech. Appl. 2007, 379, 250–262. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).