Experimental Study of the Influence of an Asymmetric Tunnel Structure on the Maximum Ceiling Temperature in a V-Shaped Tunnel Fire
Abstract
1. Introduction
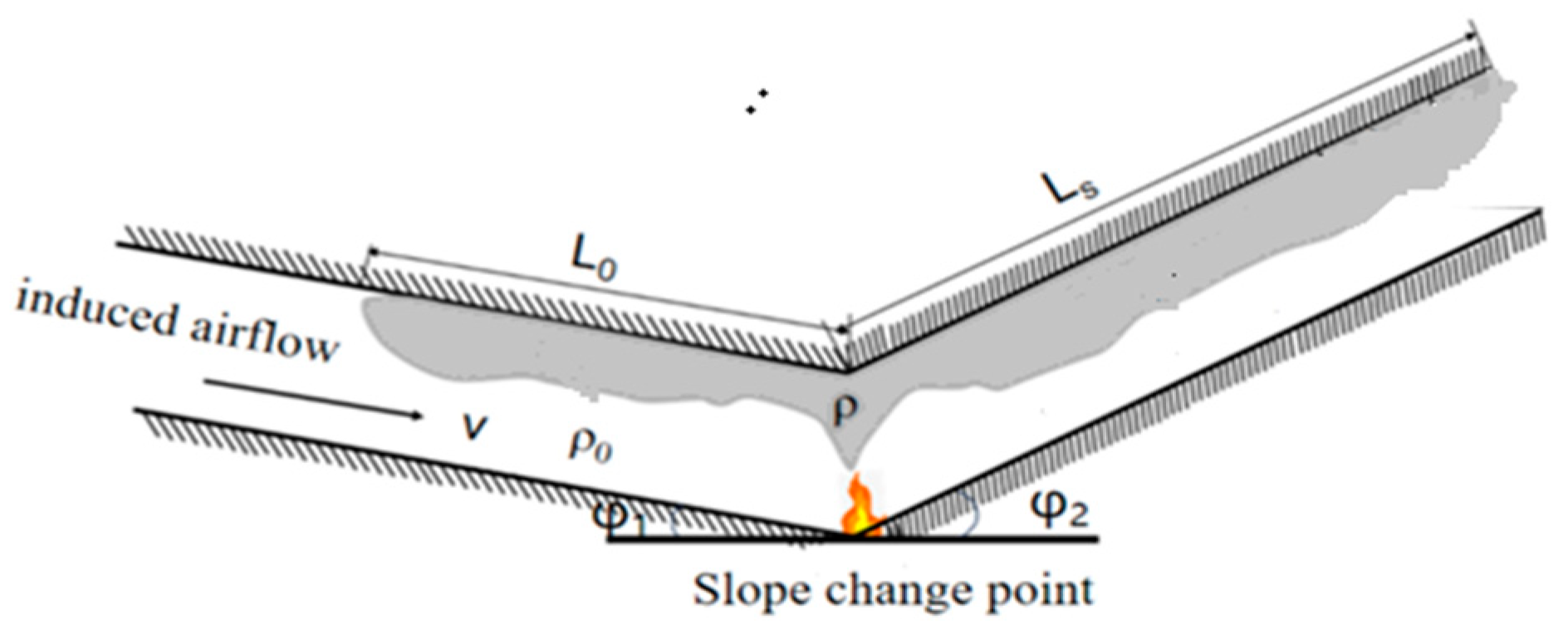
2. Theoretical Analysis
3. Experimental Study
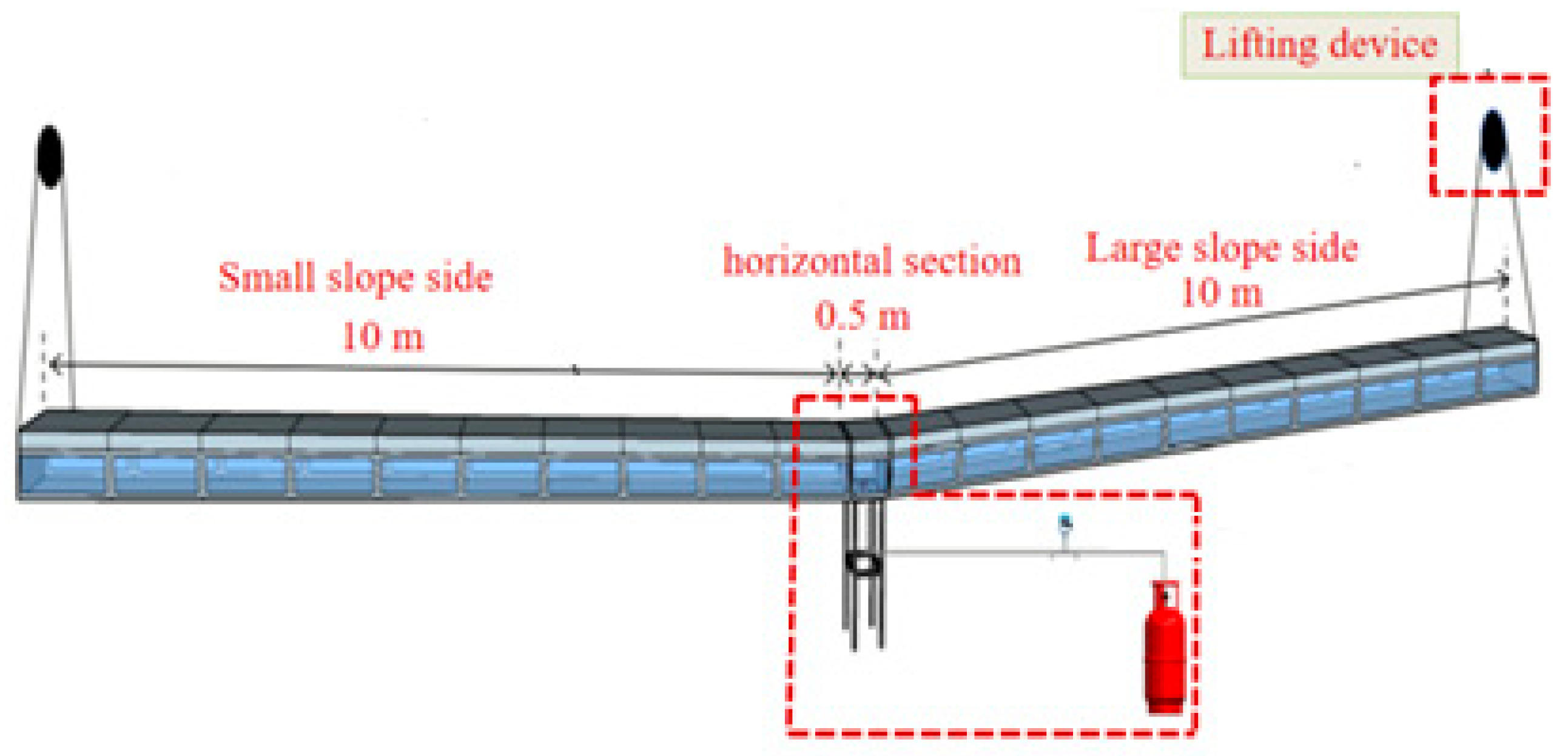
3.1. Experimental Scale-Model Tunnel
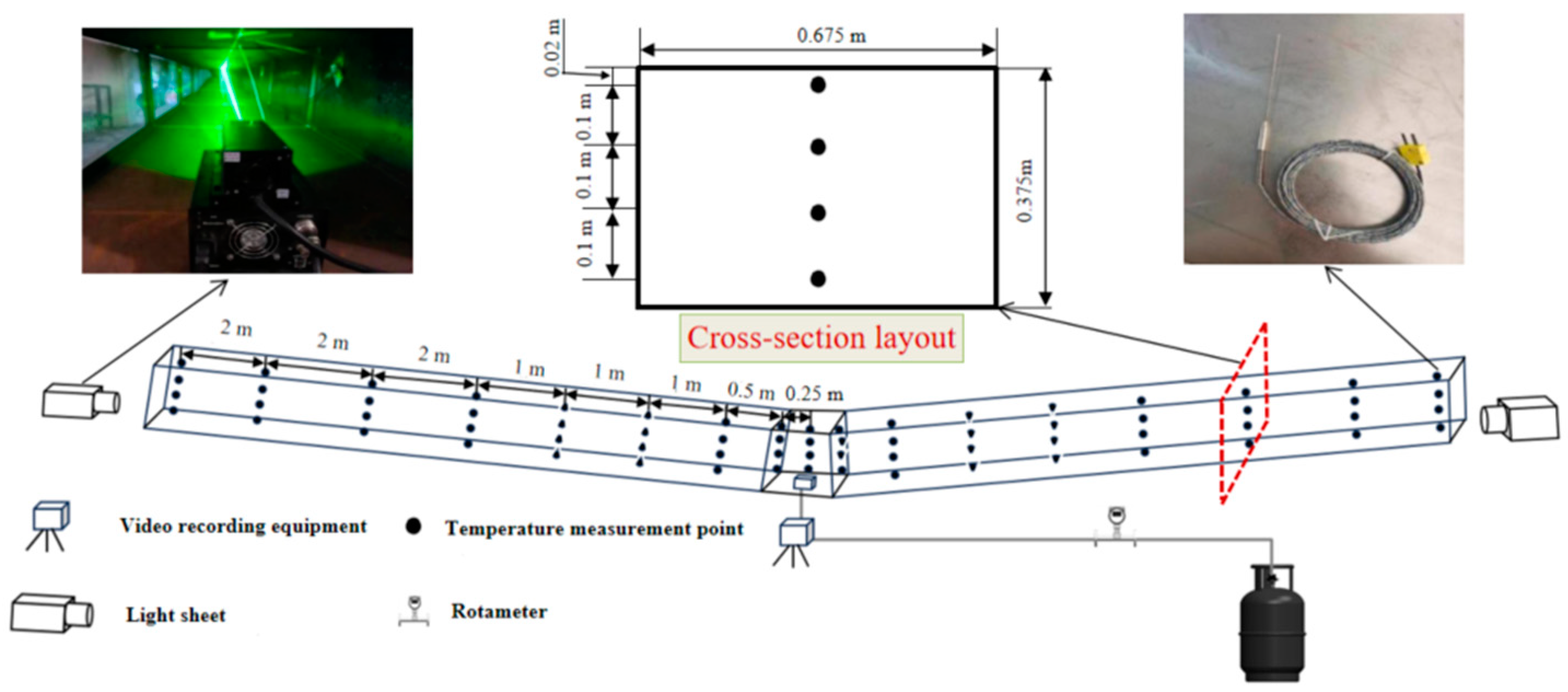
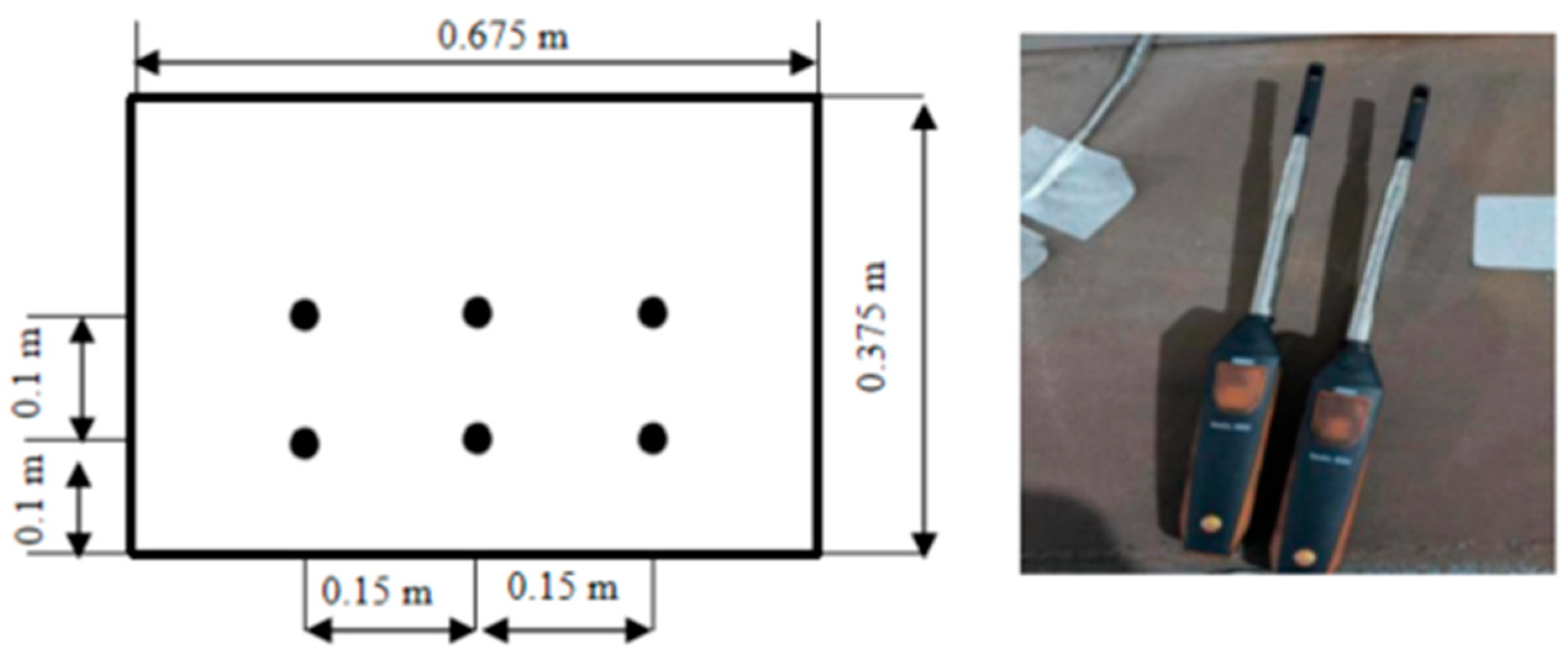
3.2. Measurement System
3.3. Experimental Conditions
4. Results and Discussion
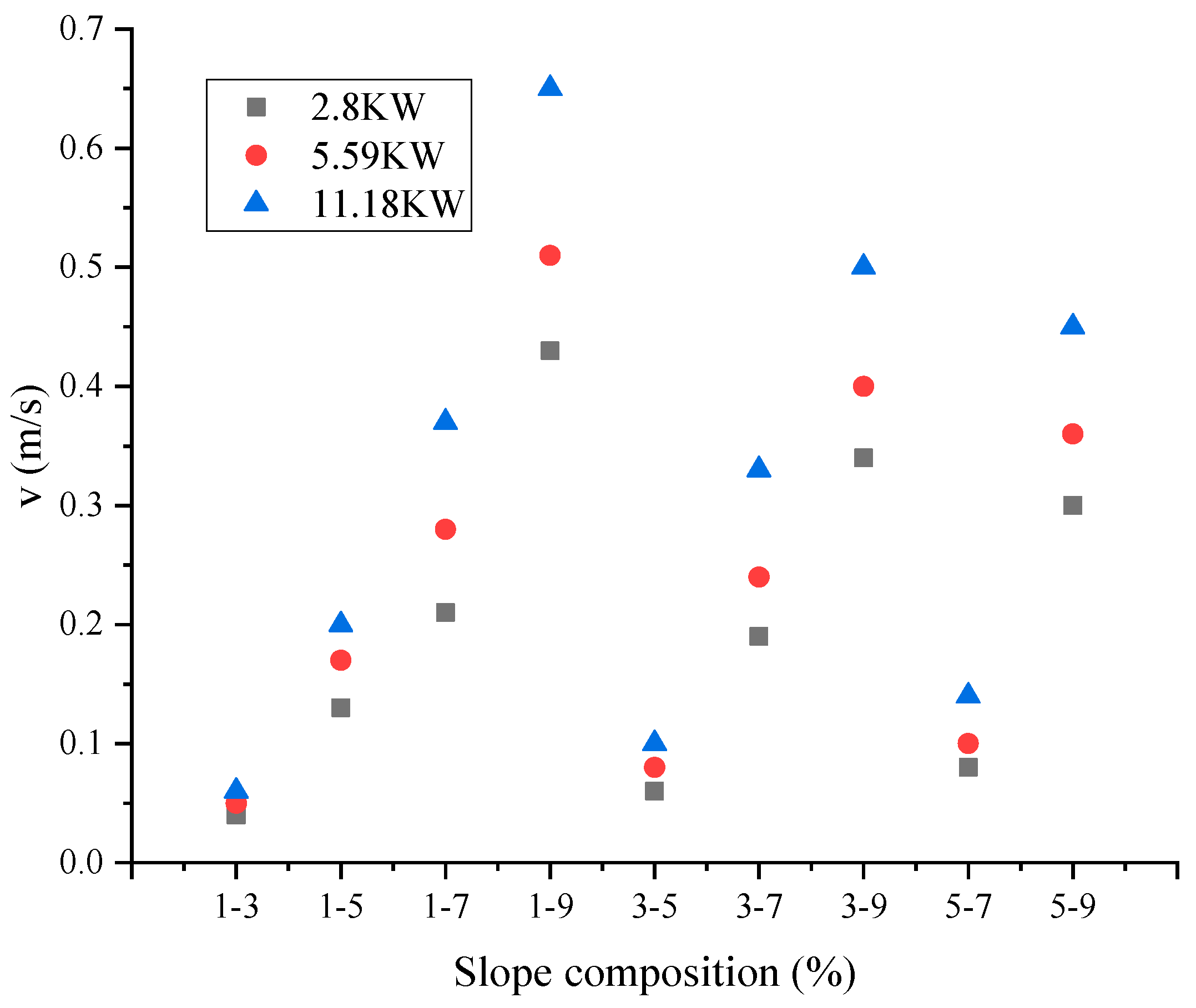
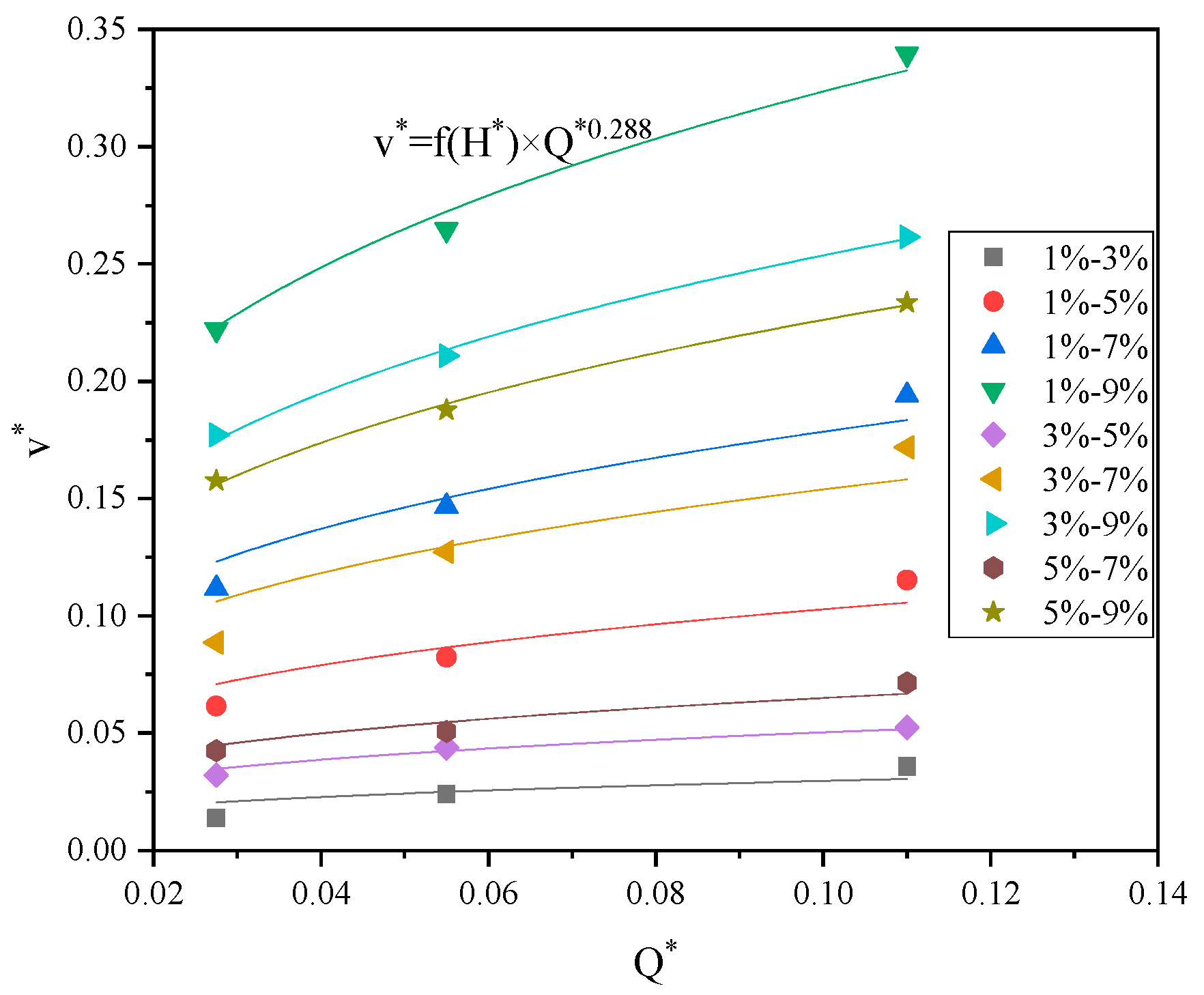
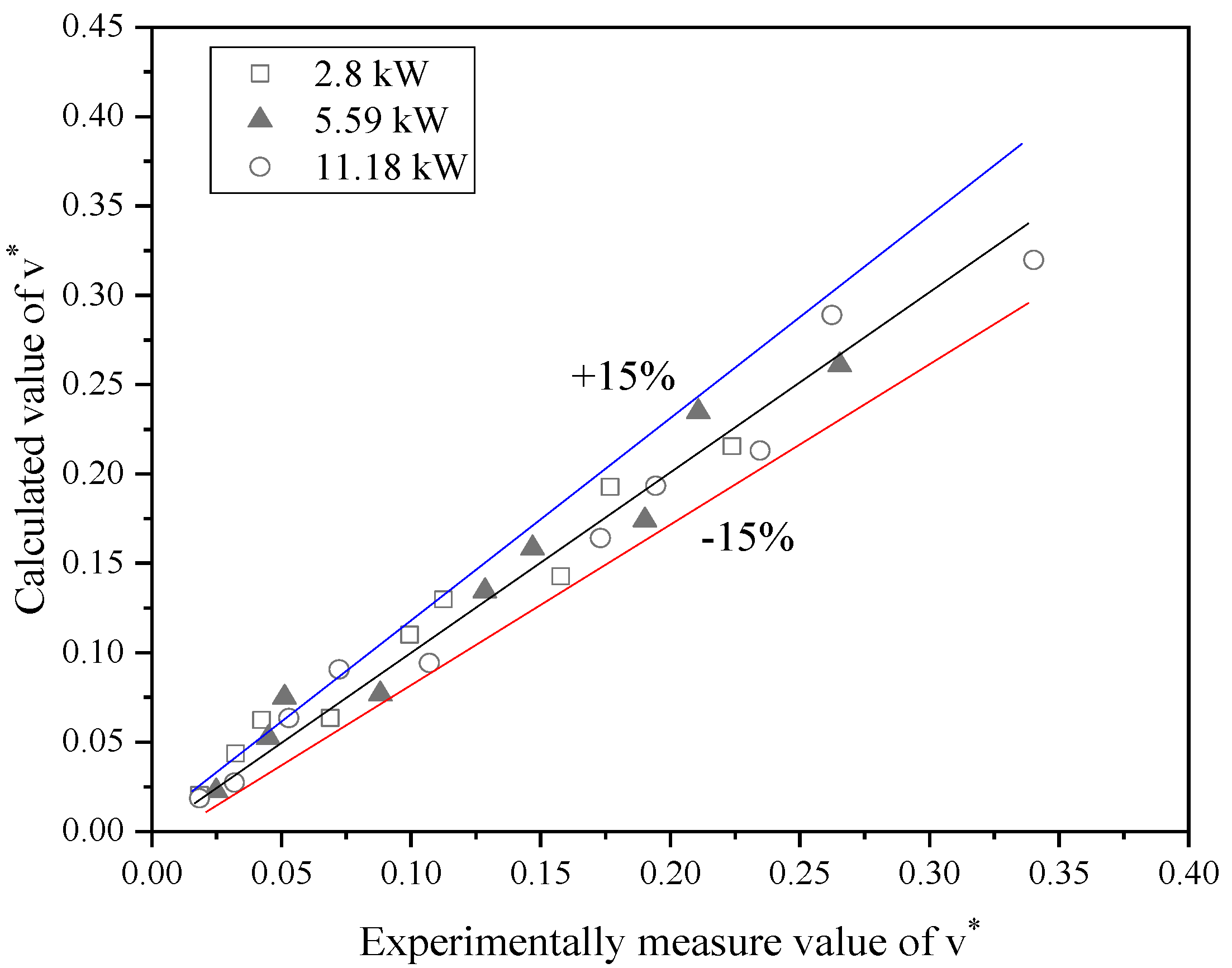
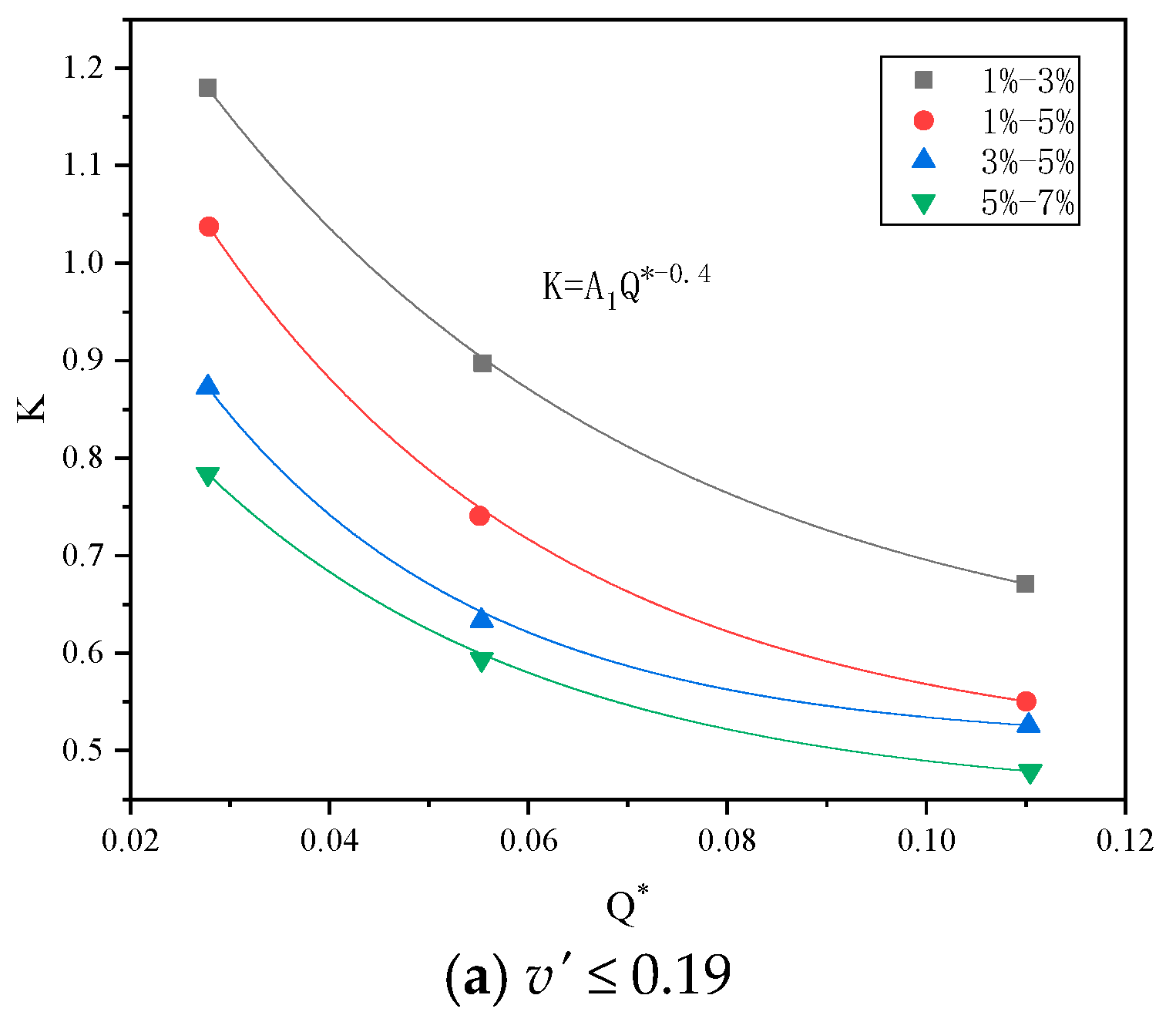
4.1. The Fire-Induced Airflow Velocity
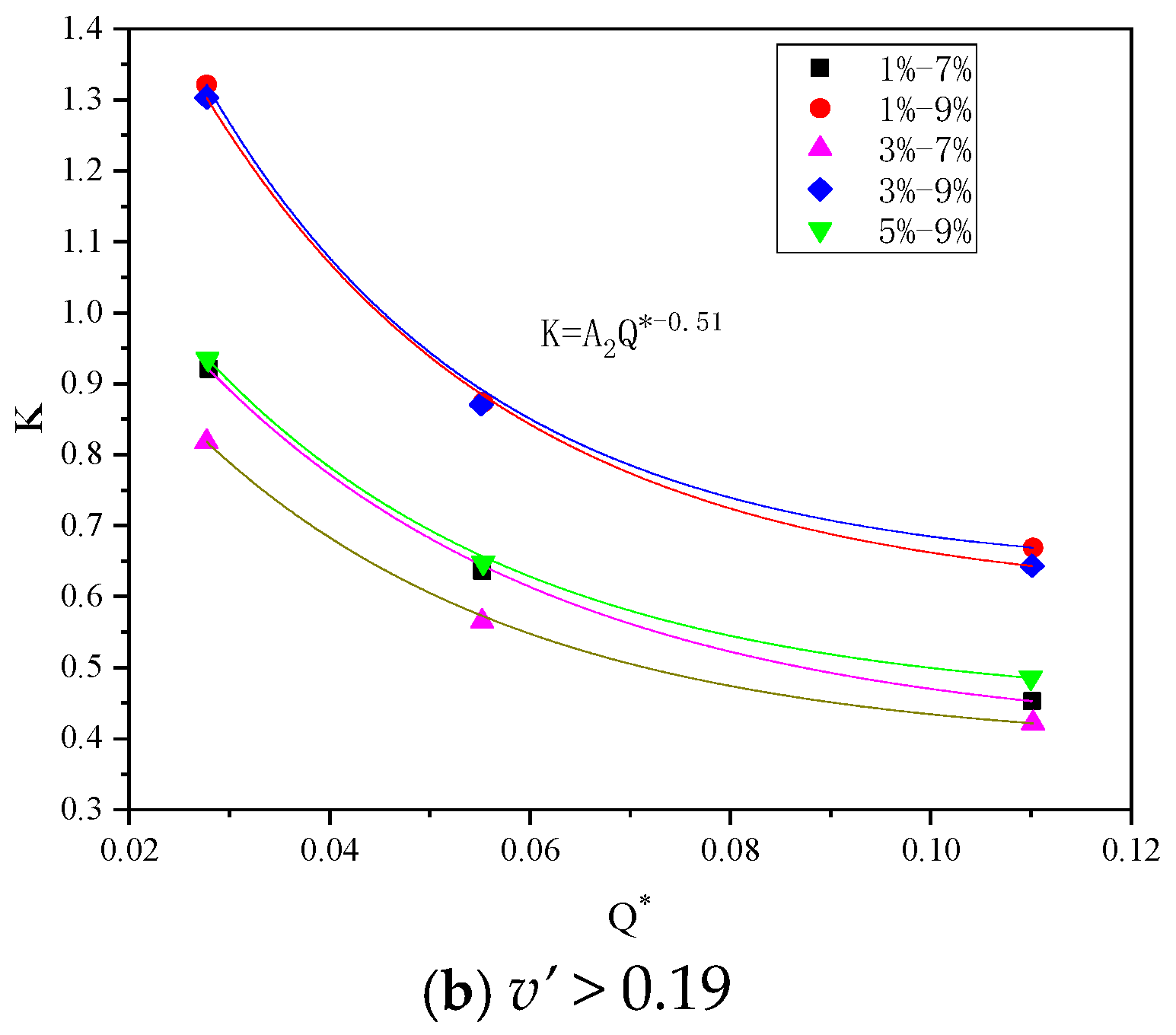
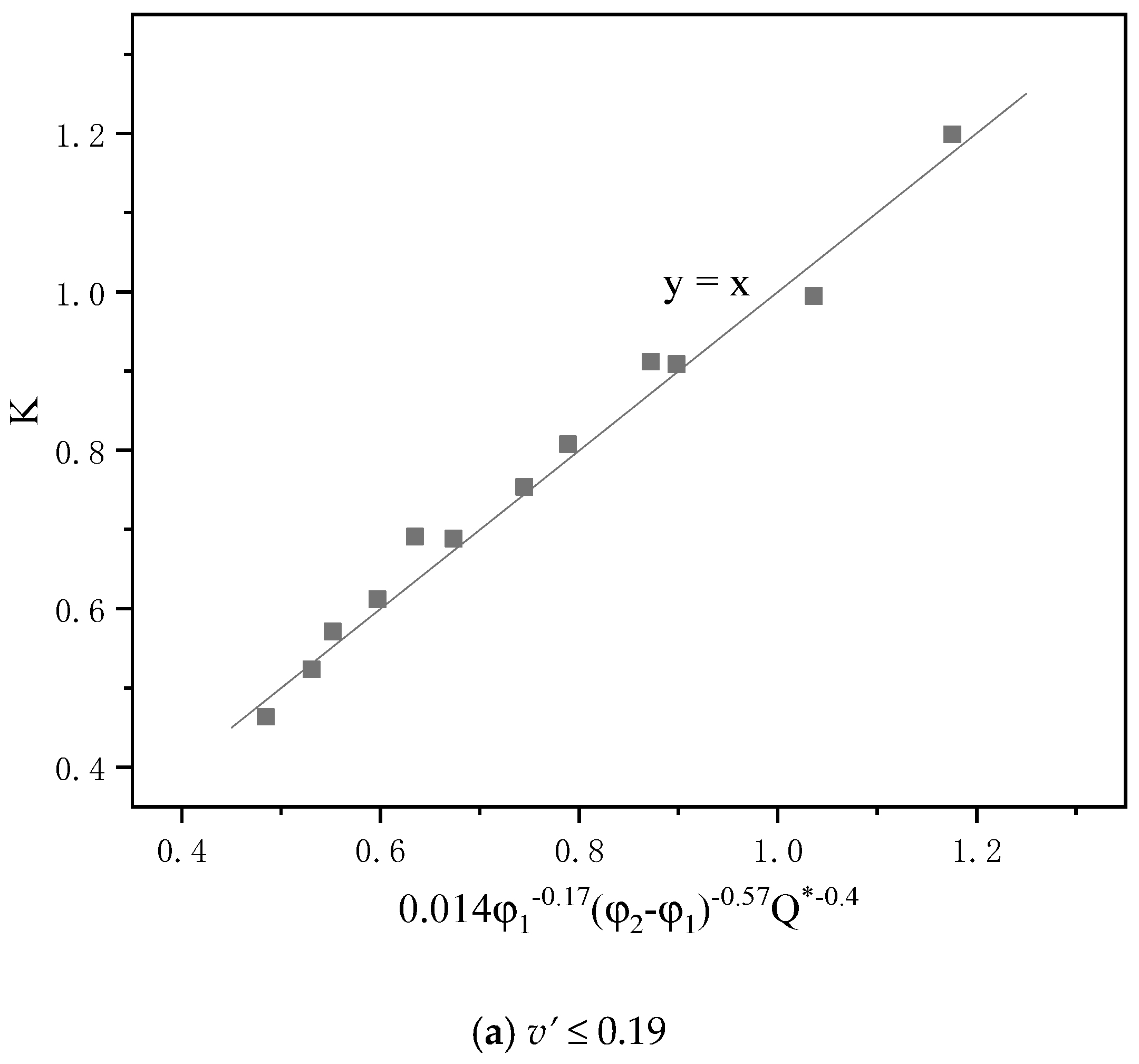
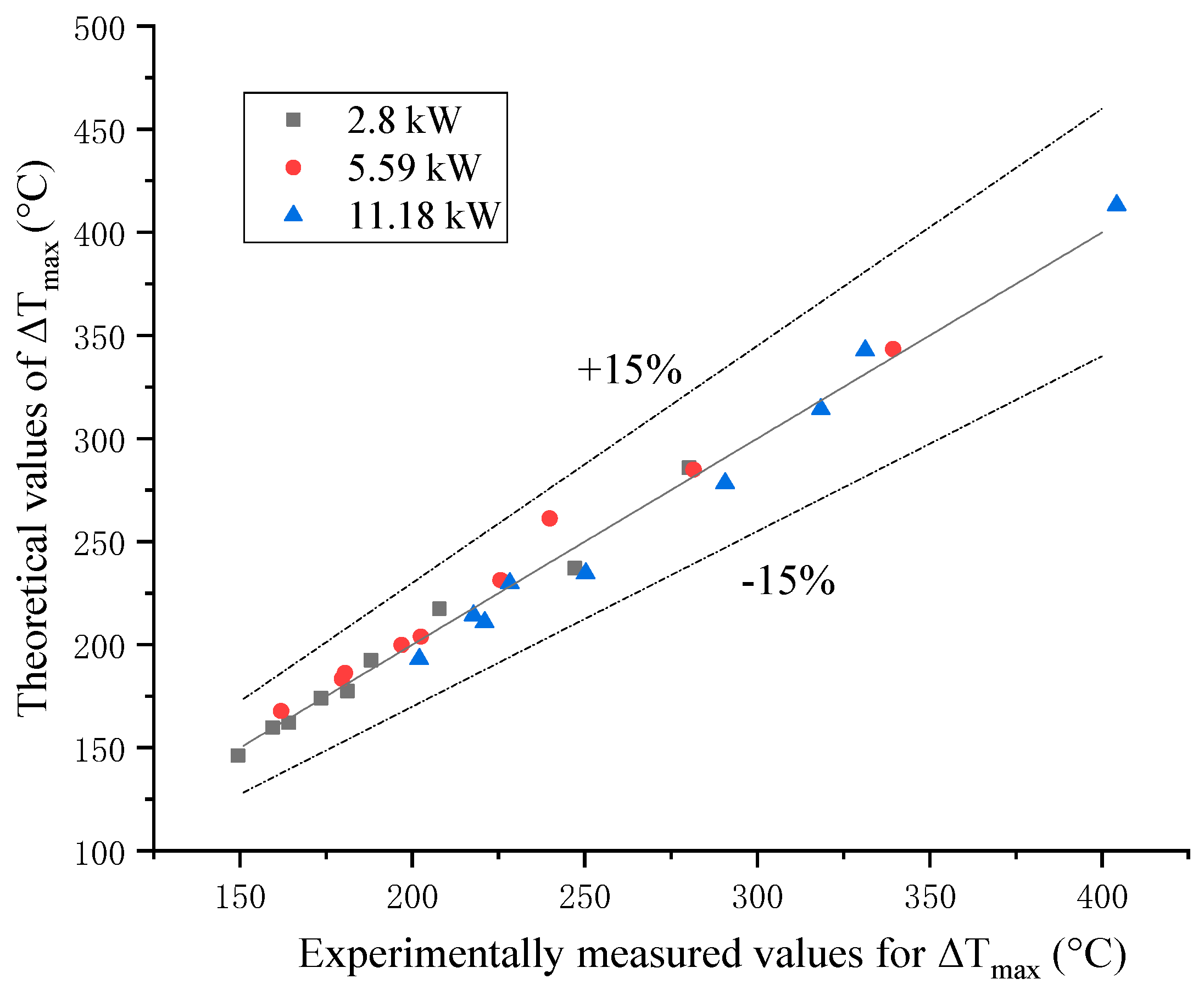
4.2. Maximum Ceiling Temperature Rise
5. Conclusions
- (1)
- Due to the thermal pressure differences between the large slope side and small slope side of the V-shaped tunnel, it is found that the fire-induced airflow flow steadily increases from the small slope side to the large slope side. The dimensionless induced airflow velocity v* is mainly related to the dimensionless fire heat release rate Q* and the dimensionless height difference H*. When the slope difference is the same, it increases with the slope of the small slope side of the tunnel. A dimensionless inlet induced airflow velocity prediction model is proposed.
- (2)
- Due to the fire-induced airflow, the fire flame is blown directly to the large slope side, the temperature decreases with the increase in the slope difference between the two sides of the tunnel, and increases with the increase in the fire HRR, and an empirical model for the maximum ceiling temperature rise is obtained.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yin, Y.; Xu, Z.; Zhao, J.; Mahmood, S.; Xie, B.; Liu, Q. The effect of width and slope in uniclinal V-shaped underground space on air transport and smoke characteristics under thermal stack effect. Therm. Sci. Eng. Prog. 2024, 51, 102599. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.F.; Cheng, C.H.; Chow, W.K. A study on the effects of the slope on the critical velocity for longitudinal ventilation in tilted tunnels. Tunn. Undergr. Space Technol. 2019, 89, 262–267. [Google Scholar] [CrossRef]
- Li, J.; Liu, W.; Li, Y.; Chow, W.K.; Chow, C.L.; Cheng, C.K. Scale modelling experiments on the effect of longitudinal ventilation on fire spread and fire properties in tunnel. Tunn. Undergr. Space Technol. 2022, 130, 104725. [Google Scholar] [CrossRef]
- Tu, D.; Li, J.; Li, Y.; Xu, D. Numerical study on the influence of the slope composition of the asymmetric V-Shaped tunnel on smoke spread in tunnel fire. Fire 2024, 7, 363. [Google Scholar] [CrossRef]
- Kurioka, H.; Oka, Y.; Satoh, H.; Sugawa, O. Fire properties in near field of square fire source with longitudinal ventilation in tunnels. Fire Saf. J. 2003, 38, 1468–1483. [Google Scholar] [CrossRef]
- Hu, L.H.; Huo, R.; Peng, W.; Chow, W.K.; Yang, R.X. On the maximum smoke temperature under the ceiling in tunnel fires. Tunn. Undergr. Space Technol. 2006, 21, 650–655. [Google Scholar] [CrossRef]
- Li, Y.Z.; Lei, B.; Ingason, H. The maximum temperature of buoyancy-driven smoke flow beneath the ceiling in tunnel fires. Fire Saf. J. 2011, 46, 204–210. [Google Scholar] [CrossRef]
- Ingason, H.; Li, Y.Z. Model scale tunnel fire tests with longitudinal ventilation. Fire Saf. J. 2010, 45, 371–384. [Google Scholar] [CrossRef]
- Li, Y.Z.; Ingason, H. The maximum ceiling gas temperature in a large tunnel fire. Fire Saf. J. 2012, 48, 38–48. [Google Scholar] [CrossRef]
- Hu, L.H.; Chen, L.F.; Wu, L.; Li, Y.F.; Zhang, J.Y.; Meng, N. An experimental investigation and correlation on buoyant gas temperature below ceiling in a slopping tunnel fire. Appl. Therm. Eng. 2013, 51, 246–254. [Google Scholar] [CrossRef]
- Oka, Y.; Sugawa, O.; Imamura, T. Correlation of temperature rise and velocity along an inclined fire plume axis in crosswinds. Fire Saf. J. 2008, 43, 391–400. [Google Scholar] [CrossRef]
- Oka, Y.; Kakae, N.; Imazeki, O.; Inagak, K. Temperature property of ceiling jet in an inclined tunnel. Procedia Eng. 2013, 62, 234–241. [Google Scholar] [CrossRef]
- Ji, J.; Wan, H.X.; Li, K.Y.; Han, J.; Sun, J. A numerical study on upstream maximum temperature in inclined urban road tunnel fires. Int. J. Heat Mass Transf. 2015, 88, 516–526. [Google Scholar] [CrossRef]
- Ji, J.; Wang, Z.Y.; Ding, L.; Yu, L.; Gao, Z.; Wan, H. Effects of ambient pressure on smoke movement and temperature distribution in inclined tunnel fires. Int. J. Therm. Sci. 2019, 145, 106006. [Google Scholar] [CrossRef]
- Zhong, M.H.; Shi, C.L.; He, L.; Shi, J.H.; Liu, C.; Tian, X.L. Smoke development in full-scale sloped long and large curved tunnel fires under natural ventilation. Appl. Therm. Eng. 2016, 108, 857–865. [Google Scholar] [CrossRef]
- Xie, E.; Zhao, W.; Xu, Z.; Zhang, X.; Wu, W.; Wang, T.; He, L. A numerical study on smoke back-layering length in V-shaped tunnels under natural ventilation. Fire Mater. 2022, 46, 1208–1221. [Google Scholar] [CrossRef]
- Jiang, X.P.; Chen, X.G.; Xiao, N.Q.; Liao, X.; Fan, C. Influence of the competitive effect of V-shaped slope tunnel on smoke characteristics. Tunn. Undergr. Space Technol. 2021, 118, 104193. [Google Scholar] [CrossRef]
- CJJ221-2015; Code for Design of Urban Underground Road Engineering. China Architecture Publishing & Media Co., Ltd.: Beijing, China, 2015. (In Chinese)



| Experimental Condition | Fire HRR | Slope Composition | Experimental Condition | Fire HRR | Slope Composition |
|---|---|---|---|---|---|
| A1 | 2.8 kW | 1–3% | C1 | 11.18 kW | 1–3% |
| A2 | 1–5% | C2 | 1–5% | ||
| A3 | 1–7% | C3 | 1–7% | ||
| A4 | 1–9% | C4 | 1–9% | ||
| A5 | 3–5% | C5 | 3–5% | ||
| A6 | 3–7% | C6 | 3–7% | ||
| A7 | 3–9% | C7 | 3–9% | ||
| A8 | 5–7% | C8 | 5–7% | ||
| A9 | 5–9% | C9 | 5–9% | ||
| B1 | 5.59 kW | 1–3% | |||
| B2 | 1–5% | ||||
| B3 | 1–7% | ||||
| B4 | 1–9% | ||||
| B5 | 3–5% | ||||
| B6 | 3–7% | ||||
| B7 | 3–9% | ||||
| B8 | 5–7% | ||||
| B9 | 5–9% |
| Slope of the Large Slope Side of the Tunnel | Slope of the Small Slope Side of the Tunnel | |||||
|---|---|---|---|---|---|---|
| 1% | 3% | 5% | ||||
| A | B | A | B | A | B | |
| 3% | 0.05745 | 0.288 | —— | —— | —— | —— |
| 5% | 0.19946 | 0.288 | 0.09766 | 0.288 | —— | —— |
| 7% | 0.34648 | 0.288 | 0.29869 | 0.288 | 0.126 | 0.288 |
| 9% | 0.62798 | 0.288 | 0.49236 | 0.288 | 0.439 | 0.288 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Q.; Li, J.; Li, Y.; Lu, H.; Zhao, H. Experimental Study of the Influence of an Asymmetric Tunnel Structure on the Maximum Ceiling Temperature in a V-Shaped Tunnel Fire. Fire 2024, 7, 483. https://doi.org/10.3390/fire7120483
Dong Q, Li J, Li Y, Lu H, Zhao H. Experimental Study of the Influence of an Asymmetric Tunnel Structure on the Maximum Ceiling Temperature in a V-Shaped Tunnel Fire. Fire. 2024; 7(12):483. https://doi.org/10.3390/fire7120483
Chicago/Turabian StyleDong, Qiwei, Junmei Li, Yanfeng Li, Huimin Lu, and Hengxuan Zhao. 2024. "Experimental Study of the Influence of an Asymmetric Tunnel Structure on the Maximum Ceiling Temperature in a V-Shaped Tunnel Fire" Fire 7, no. 12: 483. https://doi.org/10.3390/fire7120483
APA StyleDong, Q., Li, J., Li, Y., Lu, H., & Zhao, H. (2024). Experimental Study of the Influence of an Asymmetric Tunnel Structure on the Maximum Ceiling Temperature in a V-Shaped Tunnel Fire. Fire, 7(12), 483. https://doi.org/10.3390/fire7120483







