RANS Simulation of Minimum Ignition Energy of Stoichiometric and Leaner CH4/Air Mixtures at Higher Pressures in Quiescent Conditions
Abstract
1. Introduction
2. Formulation and Numerical Method
2.1. Governing Equations
2.2. Mass Conservation Equation
2.3. Momentum Equation
2.4. Species Concentration Equations
2.5. Energy Equation
2.6. Model Geometry, Initial and Boundary Conditions
2.7. Evaluation of Minimum Ignition Energy
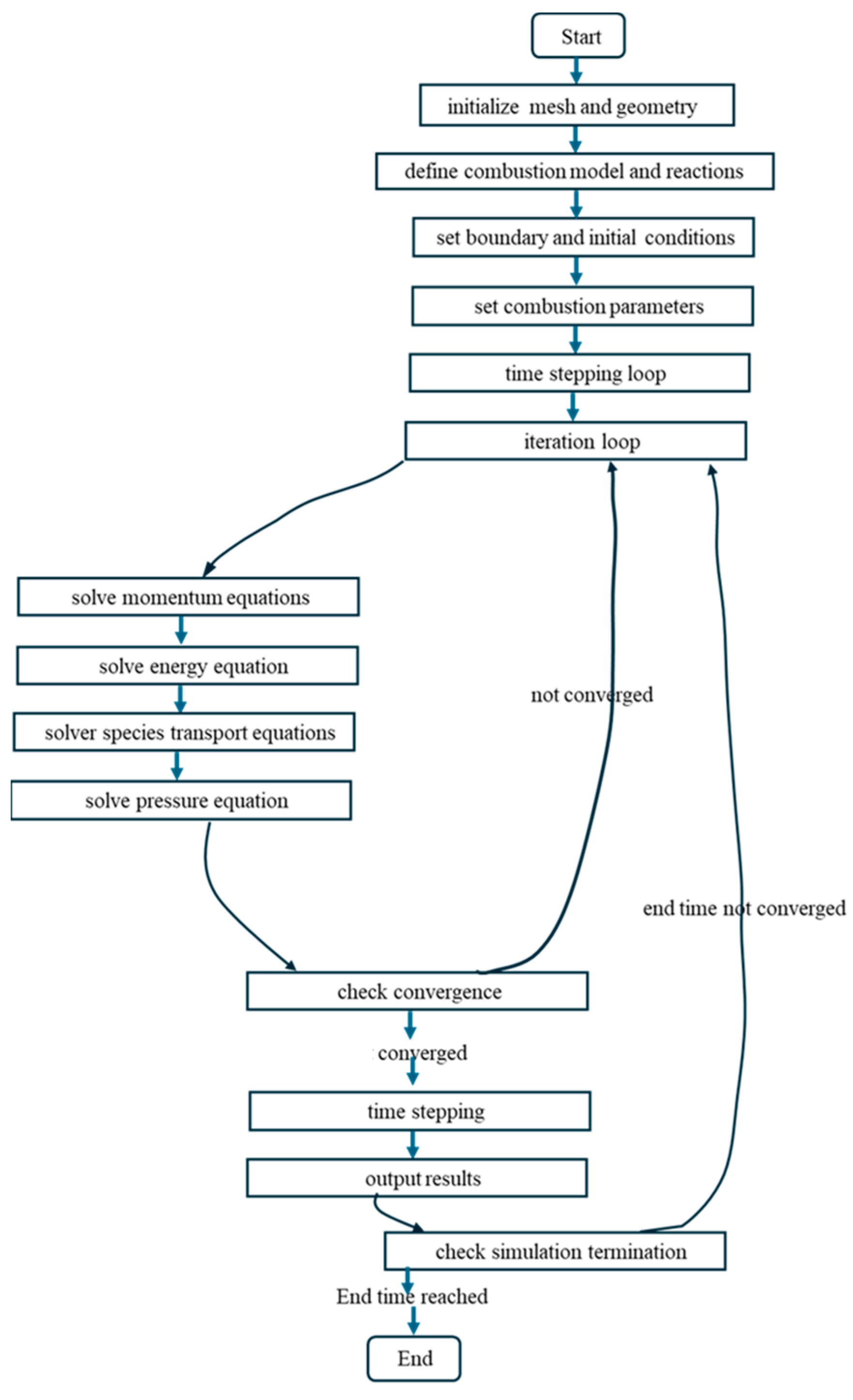
2.8. Numerical Methodology
3. Results and Discussion
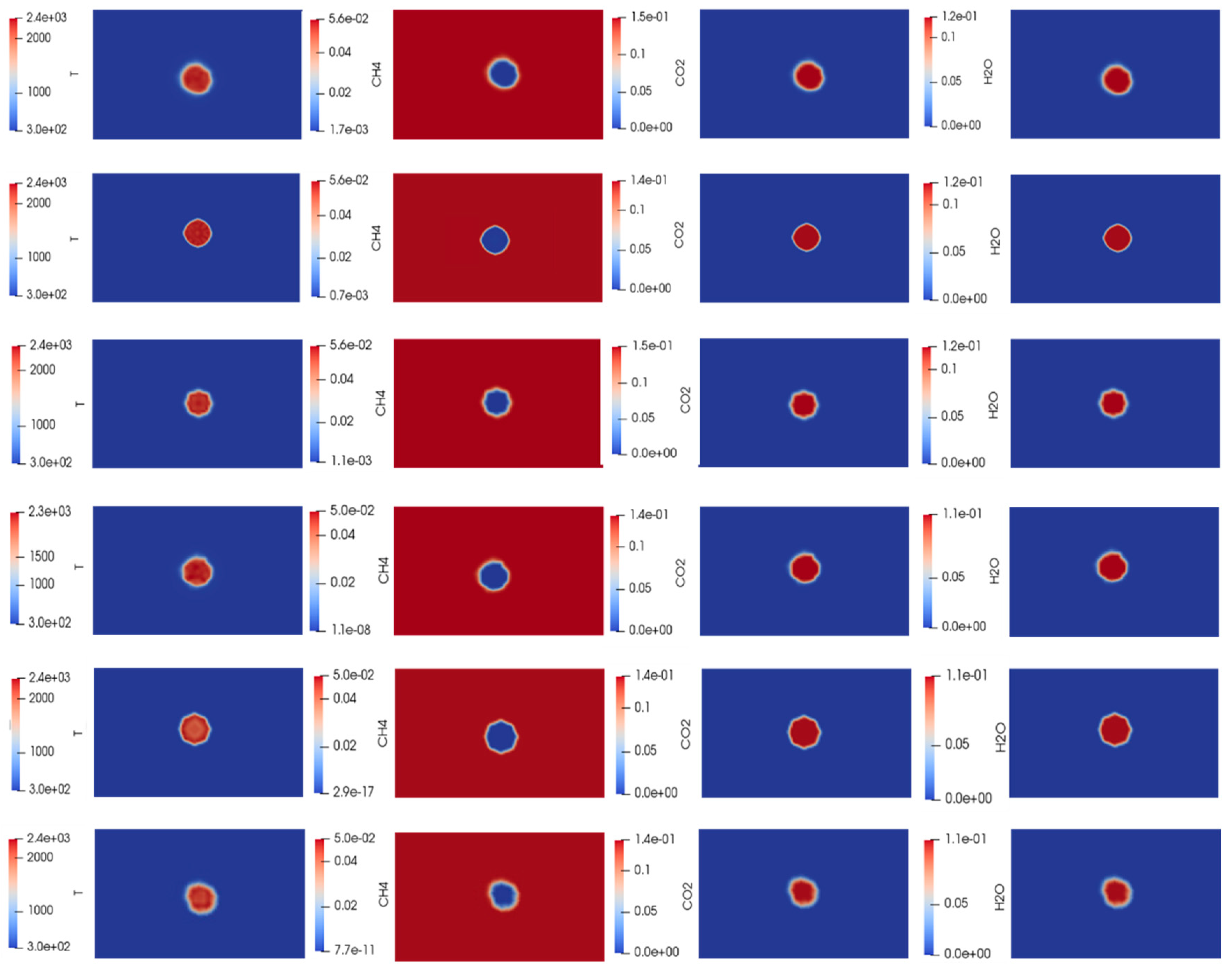
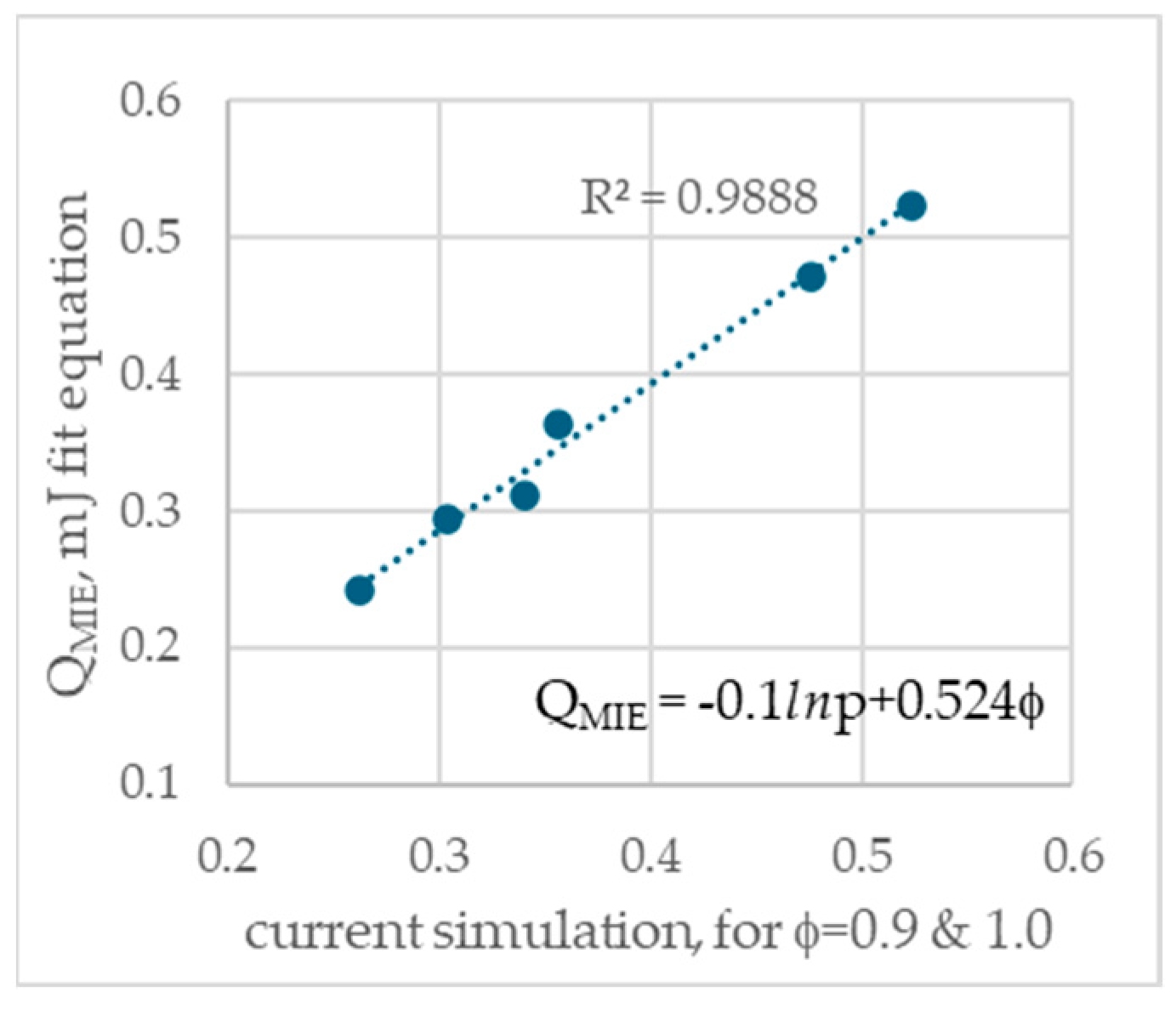
3.1. Evaluation of Minimum Ignition Energy
3.2. Comparison of MIE with Literature
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| e | Internal energy, J |
| h | Specific enthalpy, J/kg |
| K | Kinetic energy, J |
| p | Operating pressure, bar |
| pi | Initial pressure, bar. |
| Ignition source [(Emin/Vs3)/(r)3], mJ | |
| q | Minimum ignition power density, W/m3 |
| Ignition source [(Emin/Vs3)/(r)3], mJ | |
| Minimum ignition power density, W/m3 | |
| rs | Flame kernel radius, m |
| t | Computational time, s |
| Tb | Burnt temperature |
| Td | Definite ignition temperature |
| Tu | Unburned fuel mixture temperature |
| T | Temperature |
| ts | Shoot time |
| Ts | Shoot temperature |
| Tadia | Adiabatic flame temperature, K |
| Ti | Initial temperature, K |
| U | Velocity, m/s |
| The ignition kernel volume, m3 | |
| Yi | Mass fraction of ith species |
| Greek | |
| Average density of fuel/air mixture, kg/m3 | |
| Viscous stress tensor, Pa | |
| Ignition duration, ms | |
| Gradient operator, 1/m | |
| Effective thermal diffusivity, m2/s | |
| Dynamic viscosity of the fluid, kg-m/s | |
| Reaction rate of the ith species, kg/(m³s) | |
| f | Equivalence ratio (or in instances used as f) |
| Subscripts | |
| i | Initial time |
| Abbreviations | |
| MIE | Minimum ignition energy |
| LEL | Lower energy limit |
| UEL | Upper energy limit |
References
- Cui, G.; Li, Z.; Yang, C.; Zhou, Z.; Li, J. Experimental Study of Minimum Ignition Energy of Methane–Air Mixtures at Low Temperatures and Elevated Pressures. Energy Fuels 2016, 30, 6738–6744. [Google Scholar] [CrossRef]
- Sevillano, C.A.; Pesantes, A.A.; Carpio, E.P.; Martinez, E.J.; Gomez, X. Anaerobic Digestion for Producing Renewable Energy—The Evolution of This Technology in a New Uncertain Scenario. Entropy 2021, 23, 145. [Google Scholar] [CrossRef] [PubMed]
- Kundu, S.K.; Zanganeh, J.; Eschebach, D.; Mahinpey, N.; Moghtaderi, B. Explosion characteristics of methane–air mixtures in a spherical vessel connected with a duct. Process Saf. Environ. Prot. 2017, 111, 85–93. [Google Scholar] [CrossRef]
- Kundu, S.; Zanganeh, J.; Moghtaderi, B. A review on understanding explosions from methane–air mixture. J. Loss Prev. Process Ind. 2016, 40, 507–523. [Google Scholar] [CrossRef]
- Hahn, R. Sustainability Management: Global Perspectives on Concepts, Instruments, and Stakeholders, Kindle ed.; BNP Paribas: Paris, France, 2022. [Google Scholar]
- Zhao, Y.; Wang, X.; Cheng, Y.; Mei, Z.; Chen, X.; Tang, S. Ignition and combustion mechanism of alcohol/aluminum suspension nano-fluid droplets. Fuel 2024, 358, 130047. [Google Scholar] [CrossRef]
- Bjørgen, K.O.P.; Emberson, D.R.; Løvås, T. Combustion of liquid ammonia and diesel in a compression ignition engine operated in high-pressure dual fuel mode. Fuel 2024, 360, 130269. [Google Scholar] [CrossRef]
- Calcote, H.F.; Gregory, C.A.; Barnett, C.M.; Gilmer, R.B. Spark Ignition. Effect of Molecular Structure. Ind. Eng. Chem. 1952, 44, 2656–2662. [Google Scholar] [CrossRef]
- Jia, J.; Zhu, J.; Niu, W.; Zhang, J. Influence of acetylene on methane–air explosion characteristics in a confined chamber. Sci. Rep. 2021, 11, 13895. [Google Scholar] [CrossRef]
- Zeldovich, Y. Flame propagation in a substance reacting at initial temperature. Combust. Flame 1980, 39, 219–224. [Google Scholar] [CrossRef]
- Bianco, Y.; Cheng, W.; Heywood, J. “The Effects of Initial Flame Kernel Conditions on Flame Development in SI Engine. SAE Tech. Pap. 1991, 100, 1852–1862. [Google Scholar]
- Huang, C.C.; Shy, S.; Liu, C.; Yan, Y. A transition on minimum ignition energy for lean turbulent methane combustion in flame let and distributed regimes. Proc. Combust. Inst. 2007, 31, 1401–1409. [Google Scholar] [CrossRef]
- Wang, Q.; Yan, Y.; Yang, S.; Shu, C.; Jiang, J.; Wang, Q.; Yu, C.; Zhu, L. Comparative study of the effects of ignition location on the flame propagation characteristics and spectral properties of a methane–air premixed gas in a vertical pipeline. J. Energy Inst. 2024, 113, 101508. [Google Scholar] [CrossRef]
- Kravchik, T.; Sher, E. Numerical modeling of spark ignition and flame initiation in a quiescent methane-air mixture. Combust. Flame 1994, 99, 635–643. [Google Scholar] [CrossRef]
- Warnatz, J.; Maas, U.; Dibble, R.W. Combustion: Physical and Chemical Fundamentals, Modeling and Simulation, Experiments, Pollutant Formation; Textbook; 4/e; Springer: Berlin/Heidelberg, Germany, 2006; pp. 4–6. [Google Scholar]
- Scott, F.; Van Dolah, R.; Zabetakis, M. Flammability characteristics of the system H2-NO-N2O-air. Proc. Combust. Inst. 1957, 6, 540–545. [Google Scholar] [CrossRef]
- Rabl, S.; Davies, T.J.; McDougall, A.P.; Cracknell, R.F. Understanding the relationship between ignition delay and burn duration in a constant volume vessel at diesel engine conditions. Proc. Combust. Ins. 2015, 35, 2967–2974. [Google Scholar]
- The Open Source CFD Toolbox, Standard Boundary Conditions. Version v2012. Available online: https://www.openfoam.com/documentation/user-guide/ (accessed on 22 April 2024).
- Muppala, S.P.R.; Papalexandris, M.V. A Modelling Approach for Hydrogen-Doped Lean Premixed Turbulent Combustion. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Chicago, IL, USA, 5–10 November 2006; Volume 2, pp. 21–30. [Google Scholar]
- Muppala, S.P.R.; Nakahara, M.; Aluri, N.K.; Kido, H.; Wen, J.X.; Papalexandris, M.V. Experimental and analytical investigation of the turbulent burning velocity of two-component fuel mixtures of hydrogen, methane, and propane. Int. J. Hydrogen Energy 2009, 34, 9258–9265. [Google Scholar] [CrossRef]
- Han, J.; Yamashita, H.; Hayashi, N. Numerical study on the spark ignition characteristics of a methane–air mixture using detailed chemical kinetics: Effect of equivalence ratio, electrode gap distance, and electrode radius on MIE, quenching distance, and ignition delay. Combust. Flame 2010, 157, 101–113. [Google Scholar] [CrossRef]
- Yuasa, T.; Kadota, S.; Tsue, M.; Kono, M.; Nomura, H.; Ujiie, Y. Effects of energy deposition schedule on minimum ignition energy in spark ignition of methane/air mixtures. Proc. Combust. Inst. 2002, 29, 743–750. [Google Scholar] [CrossRef]
- Ghosh, A.; Munoz-Munoz, N.M.; Lactose, D.A. Minimum ignition energy of hydrogen-air and methane-air mixtures at temperatures as low as 200 K. Int. J. Hydrogen Energy 2022, 47, 53–59. [Google Scholar] [CrossRef]
- Lewis, B.; Von Elbe, G. Combustion, Flames, and Explosions of Gases; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Hankinson, G.; Mathurkar, H.; Lowensmith, B.J. Ignition energy and ignition probability of methane-hydrogen-air mixtures. In Proceedings of the 3rd International Conference on Hydrogen Safety, Ajaccio, France, 16–18 September 2009. [Google Scholar]
- Wu, C.; Schibi, R.; Mass, U. Numerical studies on minimum ignition energies in CH4/air and iso-octane/air mixtures. J. Loss Prev. Process Ind. 2021, 72, 104557. [Google Scholar] [CrossRef]
- Lu, H.; Liu, F.; Wang, K.; Xu, G.; Curran, H.J. Numerical study on the minimum ignition energy of a methane-air mixture. Fuel 2021, 285, 119230. [Google Scholar] [CrossRef]
- Kim, H.J.; Chung, S.H.; Sohn, C.H. Numerical Calculation of Minimum Ignition Energy for hydrogen and Methane Fuels. KSME Int. J. 2004, 18, 838–846. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, L.; Xu, K.; Wang, Q. Fast prediction of minimum ignition energy from molecular structure using simple QSPR model. J. Loss Prev. Process Ind. 2017, 50, 290–294. [Google Scholar] [CrossRef]
- Lewis, B.; von Elbe, G. Combustion, Flames, and Explosions of Gases, 3rd ed.; Academic Press: Orlando, FL, USA, 1987; p. 357. [Google Scholar]
- Su, Z.; Liu, L.; Li, K.; Chen, X.; Chen, T.; Huang, C. Theoretical prediction model for minimum ignition energy of combustible gas mixtures. Int. J. Hydrogen Energy 2024, 69, 103–112. [Google Scholar] [CrossRef]
- Wu, C.; Chen, Y.; Schießl, R.; Shy, S.S.; Maas, U. Numerical and experimental studies on minimum ignition energies in primary reference fuel/air mixtures. Proc. Combust. Inst. 2023, 39, 1987–1996. [Google Scholar] [CrossRef]
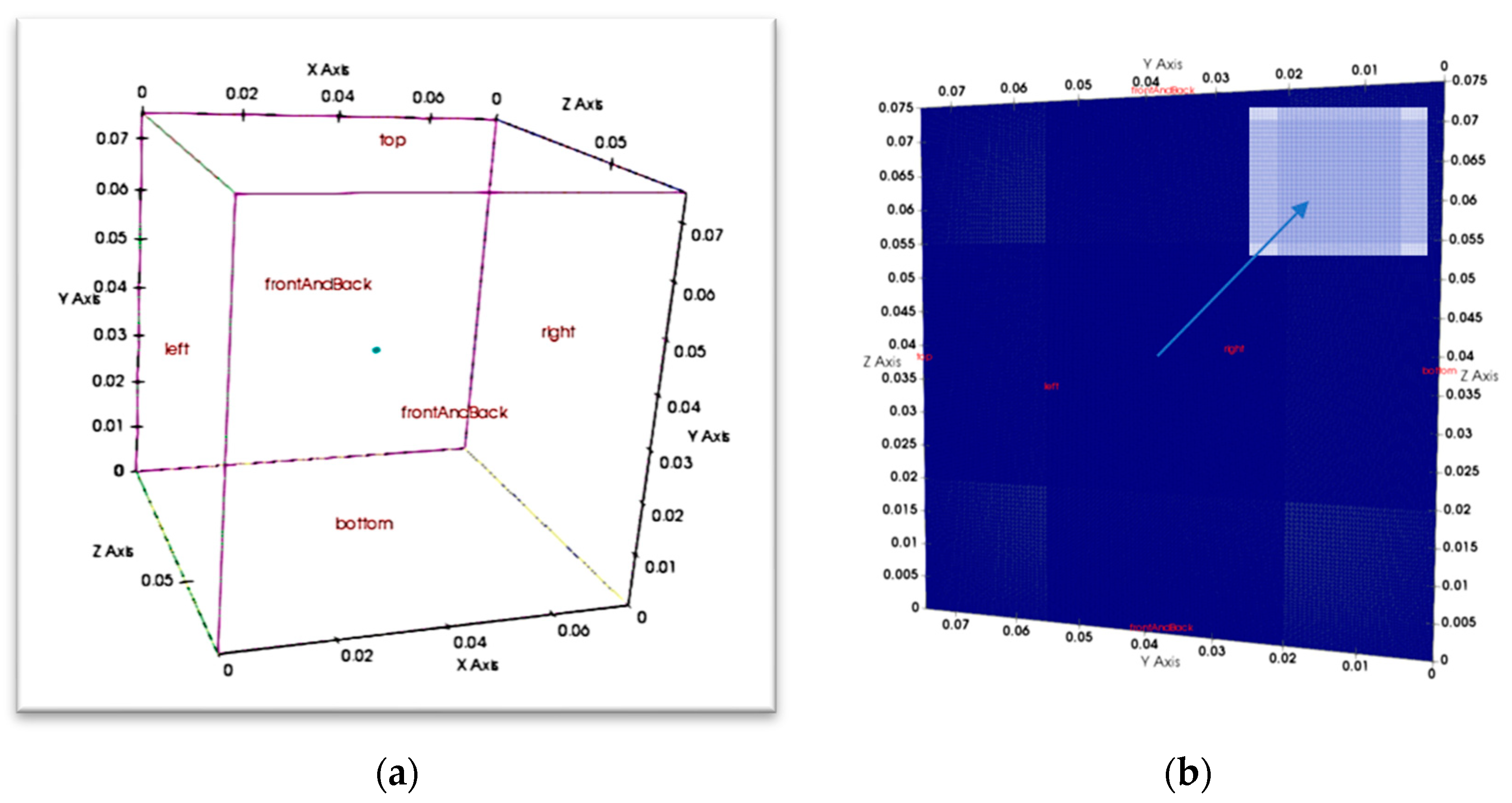
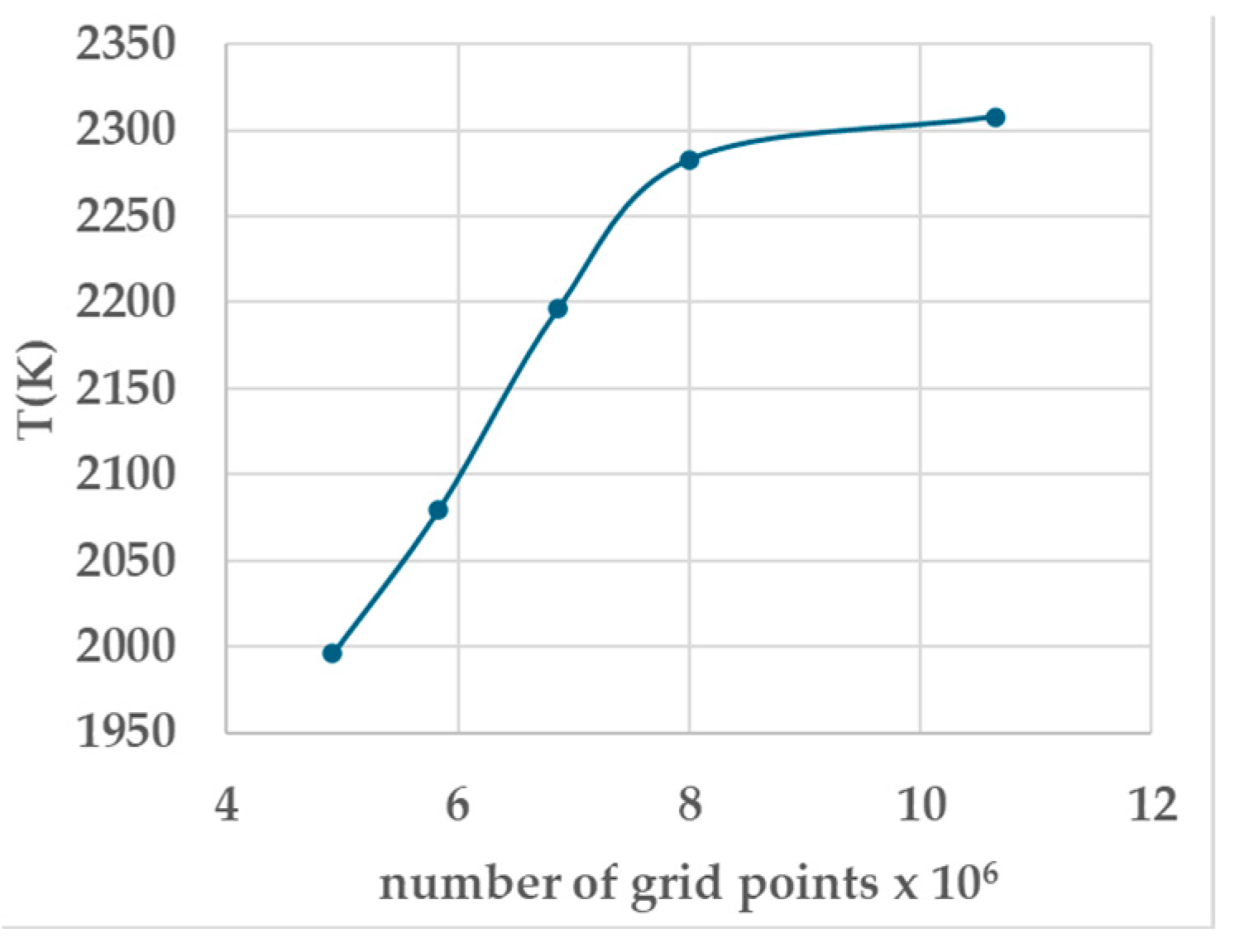

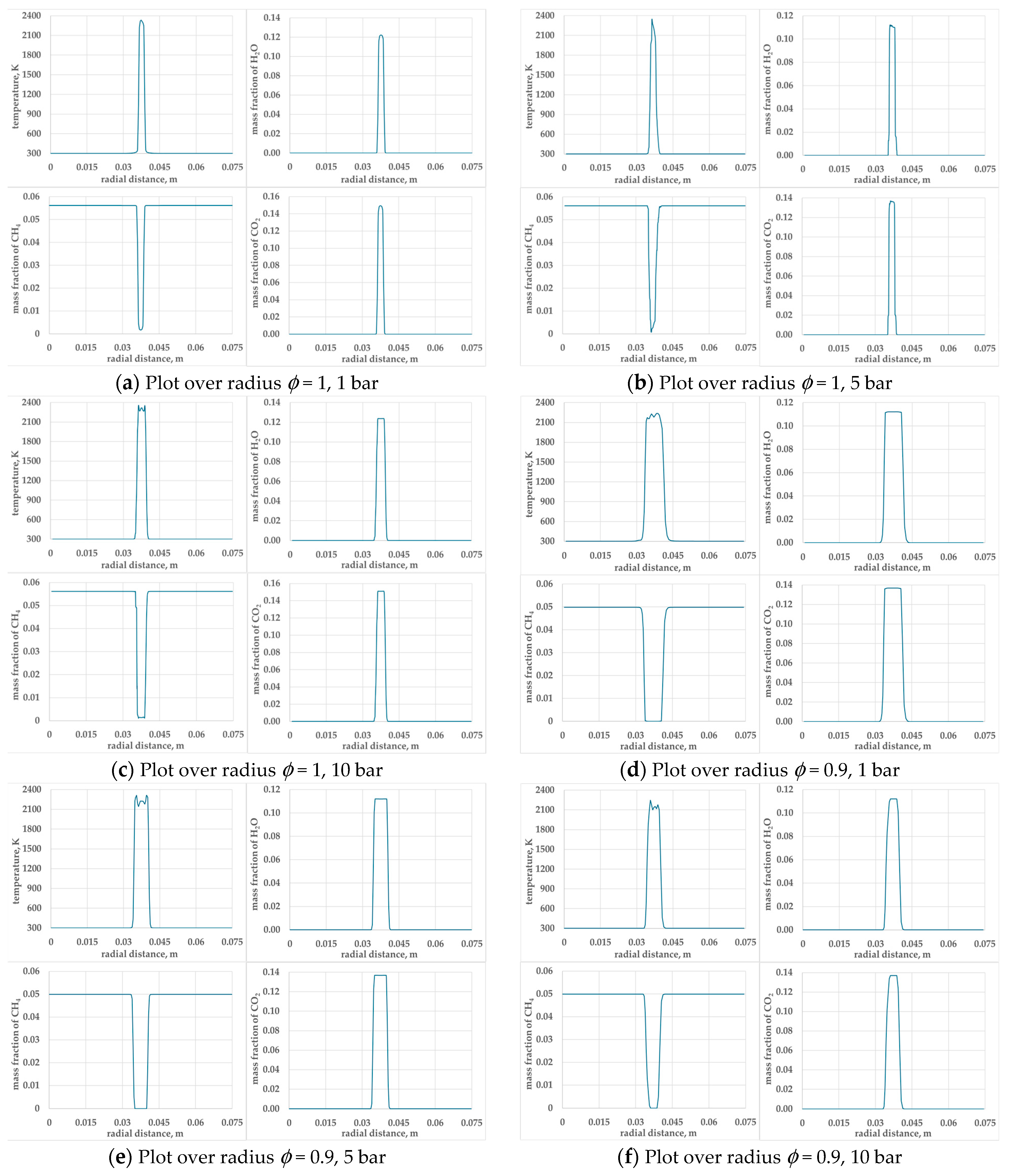

| Number of Grid Points | Number of Grids over 75 mm | Grid Size Ratio | T (K) Adiabatic Flame Temperature | Ignition |
|---|---|---|---|---|
| 4,913,000 | 170 × 170 × 170 | 0.85 | 1996 | Yes |
| 5,832,000 | 180 × 180 × 180 | 0.90 | 2080 | Yes |
| 6,859,000 | 190 × 190 × 190 | 0.95 | 2196 | Yes |
| 8,000,000 | 200 × 200 × 200 | 1.00 | 2283 | Yes |
| 10,648,000 | 220 × 220 × 220 | 1.10 | 2308 | Yes |
| Start 1. Initialize Mesh and Geometry
| 8. Solve Energy Equation (Temperature)
|
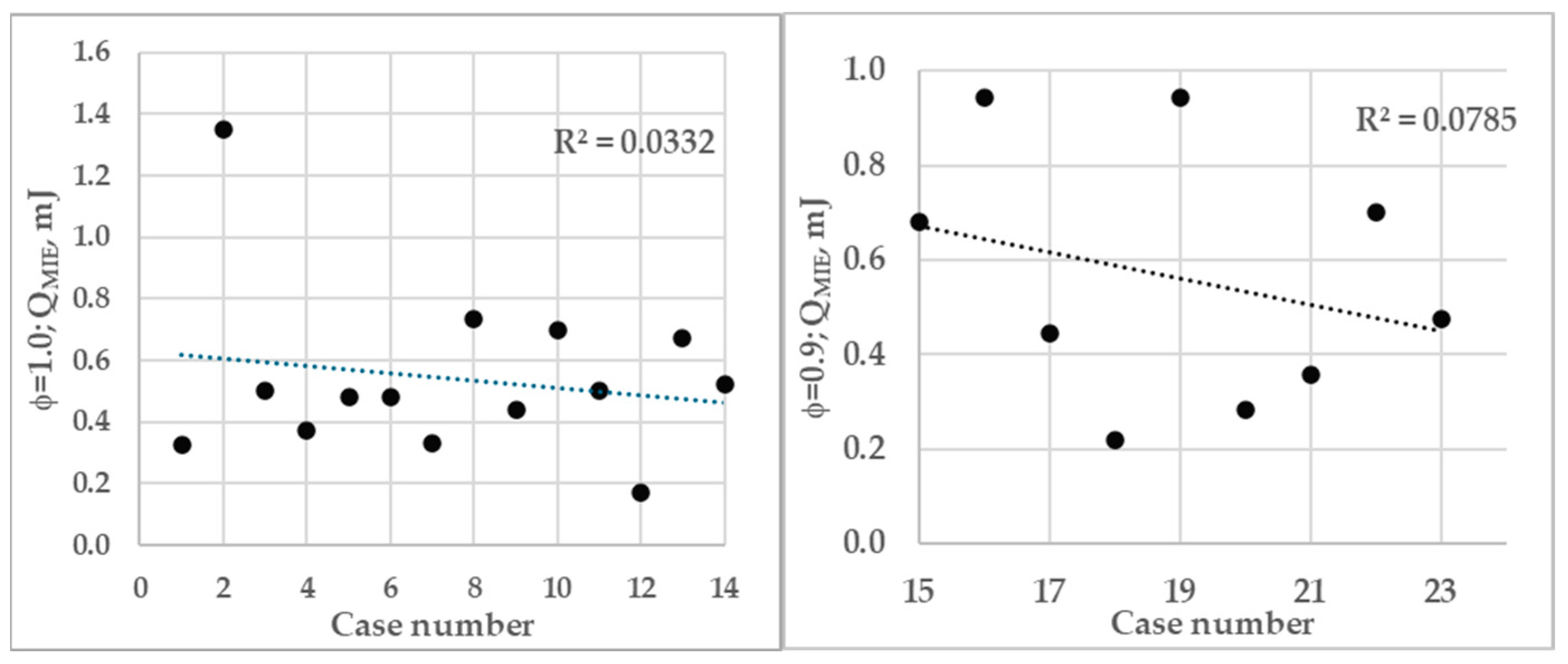
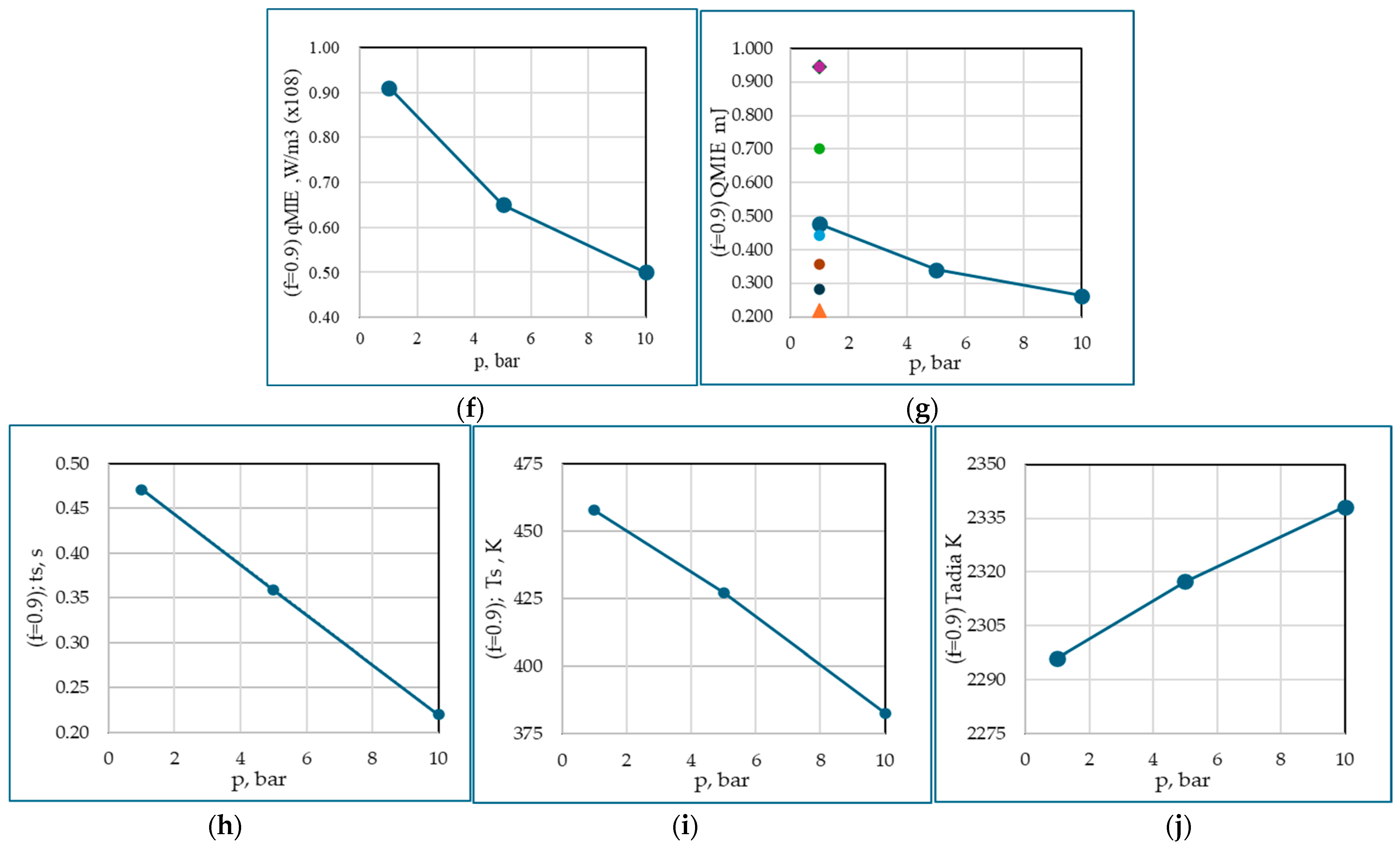
| Case Number | Author(s), Equivalence Ratio, Pressure | MIE, mJ | |
|---|---|---|---|
| 1 | Han et al. [21] ϕ = 1.0, 1 bar | Expt | 0.324 |
| 2 | Sim | 1.349 | |
| 3 | Yuasa, T. et al. [22] ϕ = 1.0, 1 bar | Expt | 0.500 |
| 4 | Sim | 0.370 | |
| 5 | Ghosh et al., [23] ϕ = 1.0, 1 bar | Expt | 0.480 |
| 6 | Calcote et al. [8] ϕ = 1.0, 1 bar | Expt | 0.480 |
| 7 | Lewis, B. and von Elbe, G. [24] ϕ = 1.0, 1 atm. | Expt | 0.330 |
| 8 | Hankinson et al. [25] ϕ = 1.0, 1 bar | Expt | 0.732 |
| 9 | Wu et al. [26] ϕ = 1.0, 1 bar | Sim | 0.441 |
| 10 | Lu, H. [27] ϕ = 1.0, 1 bar | Sim | 0.700 |
| 11 | Kim [28] ϕ = 1.0, 1 bar | Sim | 0.500 |
| 12 | Wang, B. et al. [29] ϕ = 1.0, 1 bar | Sim | 0.169 |
| 13 | Wang, B. et al. [29] ϕ = 1.0, 1 bar | Expt | 0.672 |
| 14 | Current data ϕ = 1.0, 1 bar | Sim | 0.524 |
| 15 | Hankinson et al. [25] ϕ = 0.9, 1 bar | Expt | 0.679 |
| 16 | Lewis, B. and von Elbe, G. [30]. p. 357 ϕ = 0.9, 1 bar | Expt | 0.944 |
| 17 | Wu et al. [26] ϕ = 0.9, 1 bar | Sim | 0.444 |
| 18 | Han et al. [21] ϕ = 0.9, 1 bar | Expt | 0.220 |
| 19 | Sim | 0.944 | |
| 20 | Su et al. et al. [31] ϕ = 0.9, 1 bar | Expt | 0.282 |
| 21 | Sim | 0.356 | |
| 22 | Lu, H. [27] ϕ = 0.9, 1 bar | Sim | 0.700 |
| 23 | Current data ϕ = 0.9, 1 bar | Sim | 0.476 |
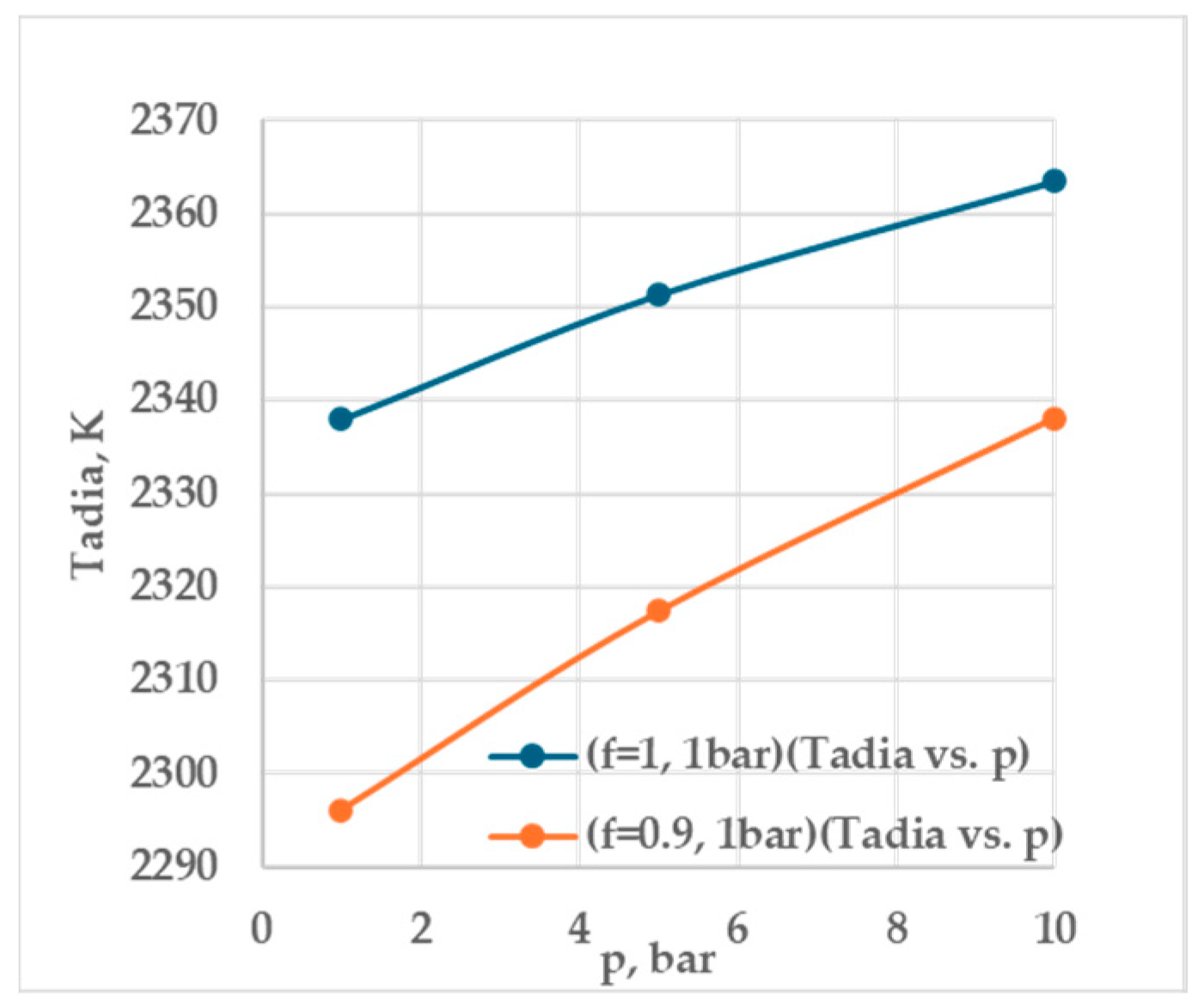
| f | p, bar | q, W/m3 (×108) | qMIE, W/m3 (×108) | Q, mJ | QMIE, mJ | ts, s | Ts, K | Tadia, K |
|---|---|---|---|---|---|---|---|---|
| equivalence ratio | initial pressure | non-ignition | ignition | non-ignition | Ignition | (shoot time) | (shoot temperature) | (adiabatic temperature) |
| 1 | 1 | 0.995 | 1.000 | 0.521 | 0.524 | 0.5082 | 481.236 | 2337.95 |
| 5 | 0.675 | 0.680 | 0.354 | 0.356 | 0.4203 | 443.176 | 2351.33 | |
| 10 | 0.575 | 0.580 | 0.301 | 0.304 | 0.2797 | 385.561 | 2363.52 | |
| 0.9 | 1 | 0.905 | 0.910 | 0.474 | 0.476 | 0.4713 | 457.803 | 2296.10 |
| 5 | 0.645 | 0.650 | 0.338 | 0.340 | 0.3589 | 427.356 | 2317.39 | |
| 10 | 0.495 | 0.500 | 0.259 | 0.262 | 0.2201 | 382.688 | 2338.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paleli Vasudevan, S.; Muppala, S.P.R. RANS Simulation of Minimum Ignition Energy of Stoichiometric and Leaner CH4/Air Mixtures at Higher Pressures in Quiescent Conditions. Fire 2024, 7, 366. https://doi.org/10.3390/fire7100366
Paleli Vasudevan S, Muppala SPR. RANS Simulation of Minimum Ignition Energy of Stoichiometric and Leaner CH4/Air Mixtures at Higher Pressures in Quiescent Conditions. Fire. 2024; 7(10):366. https://doi.org/10.3390/fire7100366
Chicago/Turabian StylePaleli Vasudevan, Sooraj, and Siva P. R. Muppala. 2024. "RANS Simulation of Minimum Ignition Energy of Stoichiometric and Leaner CH4/Air Mixtures at Higher Pressures in Quiescent Conditions" Fire 7, no. 10: 366. https://doi.org/10.3390/fire7100366
APA StylePaleli Vasudevan, S., & Muppala, S. P. R. (2024). RANS Simulation of Minimum Ignition Energy of Stoichiometric and Leaner CH4/Air Mixtures at Higher Pressures in Quiescent Conditions. Fire, 7(10), 366. https://doi.org/10.3390/fire7100366





