Sensitivity Analysis of FDS Program Parameters for Determining the Stand-Off Distances in Fire Safety Solutions for Buildings—Slovak Case Study

Abstract

Fire safety solutions for buildings in Slovakia are addressed by legislation and Slovak technical standards, which are not legally binding, but their wording is mandatory if they are referred to in an implementing regulation. Fire safety solutions for buildings in Slovakia are therefore limited mainly by legislation and technical standards. The use of fire models in fire safety solutions for buildings is common across the world, but these tools are not used in Slovakia. Their use is not prohibited by law, but it is always necessary to prove the applicability and correctness of the outputs. The paper deals with a case study of Slovak implementation of fire models when discussing the stand-off distances from fully fire-open areas. The Slovak case study addresses the fire safety solutions for buildings under the conditions of the Slovak Republic. To utilize the fire models in practice, the threshold conditions for the use of the selected FDS fire model needed to be established. This process is called a sensitivity analysis, and it is conducted based on the utilized simulation method. Based on the sensitivity analysis of FDS, the exact values of parameters can be determined, the use of which in the implementation of fire models in practice will allow accurate outputs and values of stand-off distances from fully fire-open areas in the conditions of the Slovak Republic to be obtained.

1. Introduction

Recently, there has been a significant increase in the construction of new buildings, followed by a directly proportional decrease in the number of building plots open for construction, without the issue of fire safety for different constructions being addressed. As a result, a solution regarding the problem of fire spread between neighboring buildings needs to be considered even more [1]. In order to efficiently prevent fire spread among buildings, one must know not only the distance between them but also the behavior and course of the fire itself. In fire-hazardous areas, we can determine the approximate distance needed between two buildings to prevent the spreading of fire [2]. The European Union uses Eurocodes [3,4,5,6], which deal with the design of structures and their durability under specific conditions. However, there is no uniform way of addressing fire safety solutions for buildings in the European Union or worldwide, as each country addresses the issue with its own regulations (Table 1) [7,8,9,10,11]. The fire safety of buildings in Slovakia is regulated by legal regulations and Slovak technical standards (STN) [12,13,14,15,16,17,18,19], which are not legally binding but are binding if they are referred to in the implementing regulation. All current standards are based on the publication by Reichel (1989) [20], which is principally based on the standards [21,22].

Table 1. Method of determining stand-off distances.

Country	Method of Determining Stand-Off Distances
	Standards	Use of Fire Models
European Union	Eurocodes [3,4] deal with the design of structures and their resistance under specific conditions, not the stand-off distances between structures	It is allowed
Slovak Republic	Reg. 94/2004 Coll. Decree of the Ministry of the Interior of the Slovak Republic [9] STN 92 0201- 4: Fire safety of buildings—Stand-off distances [15]	No
New Zealand	Verification method C/VM2 [23]	Yes: B-RISK [24]

In other parts of the world, stand-off distances are handled differently. In England, for example, building setbacks are determined by building type using two methods and tabulated values based on the unprotected area. In the USA, standards are applied which take into account openings and structural elements, based on radiation levels and the fire hazard classification of the building in question. Croatia sets the minimum separation distance as half the height of the building, with a minimum of 3 m. In Serbia, these distances are regulated by law and may be adjusted according to the presence of openings on facades, but may not fall below 4 m. In the Czech Republic, fire safety is governed by decrees and technical standards divided by type of building, unlike in Slovakia, where the standards are broken down by fire protection area. In New Zealand, building compliance with the law is also demonstrated by fire modeling in the B-RISK program according to the C/VM2 methodology [25].

However, a fire is influenced by various factors—furthermore, a slight change in one of them might significantly alter its course. In the conditions of the Slovak Republic, the use of fire models is not forbidden but not explicitly allowed when dealing with the fire safety of buildings; thus, their use is not legally regulated. There is also a lack of experience in the use of fire models in practice because many experts are interested in using fire models but they do not know how; they do not know how to set the correct input parameters, and therefore the use of fire models in the area of obtaining relevant information is impossible. Therefore, there are no means to effectively predict fire behavior in enclosed spaces, although it is possible to estimate it using the tools available [26]. One set of such tools are fire models. Fire models are classified as a technology which enables fire simulations [27,28], especially in enclosed spaces. This technology enables us to predict the behavior and progression of fires, allowing us to efficiently combat their outbreaks and thereby eliminate property damage and, most importantly, protect the lives and health of occupants inside said buildings.

However, in terms of fire safety solutions for buildings, the implementation of fire models in practice remains unknown in the Slovak Republic, although the only thing needed for their employment is to set the threshold conditions for the individual areas of said solutions. Then, under these conditions, similar results to those found in the prescriptive approach could be obtained. Fire model implementation in fire safety solutions for buildings is in high demand around the world. Some countries have even implemented this approach already [23,24].

Fire models are designed as fire simulation tools and are used when discussing fire safety solutions for buildings [29,30]. Fire models [31,32] are divided into two major groups, Physical and Mathematical, which are further subdivided according to their applications. There is a countless number of fire models. Each of them first and foremost aims to simulate fire and smoke transport, albeit each emphasizes different parameters of their development (Table 2) [29,31].

Table 2. Fire models.

Group of Fire Models	Fire Model	Characteristics
Mathematical	FDS	Software designed for modeling the transfer of fire and combustion products in a confined space, which is demanding to use [33].
Mathematical	PyroSim	Graphical user interface of the FDS, which is quite easy to use [34].
Mathematical	CFAST	Two-zone fire model, which divides the fire section into two zones with the assumption of a different temperature and density of combustion products in each zone [35,36].
Mathematical	Autodesk CFD Simulation	Used for the simulation of fire, smoke and human safety evaluation and monitoring of selected fire parameters [37].
Mathematical	B-RISK	Designed to model the spread of fires in buildings and monitor the activation and operation of fire equipment. The program allows visualization of geometry and simulation outputs. B-RISK operates following New Zealand building regulations [23,24].

The use of FDS has been demonstrated by Dusica Pesic [38]. The research focused on determining the optimum stand-off distance required to prevent the spread of fire between two opposing residential structures using the FDS program [38]. Pitelková et al. [39] addressed the use of CFD in predicting the fire hazard area [39]. They assessed individual user settings of simulations in FDS to change the resulting heat flux density values used to determine stand-off distances. The problem of the implementation of fire models in fire safety solutions for buildings is also being addressed in Slovakia [40,41,42,43,44,45,46,47]. Kadlic [42] paid attention to the influence of the variability and uncertainty of input parameters on the accuracy of fire model outputs. He dealt with the issue of the applicability and plausibility of fire models in engineering practice. He analyzed the input parameters and specified the ranges of values of sensitivity analysis, and he assessed the effect of uncertainty and variability in inputs on outputs [42].

The aim of the contribution of the Slovak case study is to show and verify the application of fire models, such as FDS, to determine the spacing distances for fire safety of buildings in Slovakia. Part of the objective is to develop a sensitivity analysis aimed at measuring the separation distances between buildings. Specifically, the paper deals with the influence of selected parameters of fire models on the computational time of simulations and on the size of stand-off distances. On the basis of the sensitivity analysis, the values of the input parameters are determined, which are relevant for the implementation of fire models in practice in Slovakia.

2. Materials, Methods and Results

2.1. Addressing Stand-Off Distances in FDS in General

The basis of space modeling in FDS is the creation of a computational grid. Within the application of the FDS fire model to the solution of stand-off distances, a single computational grid is sufficient. The correct setting of the initial parameters is important with respect to the heat transfer, fire and combustion product calculations, which are performed individually in cells and simultaneously in the whole computational grid at the same time, to obtain the most accurate results and visualizations [33,47].

The walls of the computational grid are defined as inert surfaces that are not subject to chemical reactions. All but one wall of the computational mesh is defined as an open surface that simulates the space of the external environment. The one wall that remains as an inert surface simulates a wall that contains fire-open areas.

Openings, called radiant surfaces, are placed in the inert surface to simulate openings in structures. The numbers and dimensions of the radiant surfaces model the actual numbers and dimensions of openings in the structure under consideration.

Fire is defined as the amount of heat escaping from the radiant surface. A fire can be simulated by adjusting the temperature (°C) or the area heat flux density (kW·m⁻²). It is possible to set these quantities as time-varying or constant-value variables. In the case of our simulations, constant values were chosen as the assumed maximum values of the quantities achieved from the whole fire progression. The determination of the radiant area values using temperature was made based on the standard temperature curve (1), which is derived from ISO 834 and can be used to convert the selected fire risk value to a constant value of the radiant surface temperature. The temperature curve is based on the equivalent fire duration, τe (min), for production buildings. For non-manufacturing buildings, pv (kg·m⁻²) is equivalent to a given value of the design fire load. The radiant area values, using the areal heat flux density, are determined from equation (2), which is based on the standard temperature curve (1) [15,48,49].

$$T_N=20+345\mathit{log} (8\mathrm{t}+1)$$

(1)

$$q={\left(T_N+273\right)}^4·5.67·{10}^{-11}$$

(2)

where

• T_N: the standard gas temperature in °C;
• t: the value of the standard fire duration time, τ_e (min), for production buildings, or, equivalent to this value, the calculated fire load for non-production buildings, p_v (kg·m⁻²);
• q: the area heat flux density (kW·m⁻²).

The stand-off distance is determined based on the quantity being measured by the measuring equipment. The FDS supports 11 types of devices that can be used to record quantities related to thermal exposure of surfaces. These devices can measure the individual components of energy transfer differently, or they may differ in their placement, either on a fixed surface or in the air. All devices are described in detail in the Fire Dynamics Simulator User’s Guide, Chapter 22.10.12, ‘Heat Flux’ [34].

The simulations were performed using Gauge Heat Flux Gas devices. These devices record both the radiant and the flow component of the heat. A Gauge Heat Flux Gas device can be placed in a free space. Any number of these devices can be placed, depending on the size of the fire-open area, and at a selected distance from the radiant area. The estimation of the distances of the devices from the radiant surface and the influence of other parameters on the results of the measurements were the subject of a sensitivity analysis (Section 2.2).

As a result of the simulations, the influence of the selected parameters on the computational time of the simulations, the accuracy of the readings and the magnitude of the stand-off distances was determined.

2.2. Sensitivity Analysis

The first step towards the successful use of fire models in determining stand-off distances from structures is to create a large number of simulations. Their task is to investigate the effect of the individual input parameters on the total computational time of the simulations and the accuracy of the distance reading. This procedure is called sensitivity analysis. The FDS program selected the parameters with the greatest influence on the computational time of the simulations, the accuracy of the readings and the size of the setback distances [33] (Table 3).

Table 3. FDS program parameters with the greatest impact on simulation computation time, readout accuracy and spacing distances.

Parameter	Characteristics
Size of Computational Cells	The size of computational cells in the computational grid.
Path Length [m]	This parameter is necessary when determining and recording the values of the radiation transfer in the fire area. When calculating the heat flux, this parameter indicates the distance between the fire and the measuring device (target).
Number of Radiation Angles	This parameter improves the spatial and temporal accuracy of the discrete radiation transfer equation, thus influencing the visualization of critical values in determining stand-off distances. The lower the number of radiation angles, the more the visualization resembles a star (a more pronounced star shape), and vice versa—the higher the number, the smoother the visualization of the critical value (resembling an oval).
Time Step Increment and Angle Increment	These parameters influence the frequency of the recorded radiation outputs. The default value of the time step increment is 3, and the angle increment is 5. Following this scenario, the radiation transfer equation is updated every 15 time steps, and the values are thus recorded.
Humidity	This parameter reaches values ranging between 0 and 100, the default value being 40%.

The sensitivity analysis focused on investigating the effects of the parameters listed in Table 3 on the total computational time of the simulations (Section 2.2.1) and on the magnitude of the spacing distances (Section 2.2.2).

2.2.1. Effect of Selected Parameters on the Computational Time of Simulations

The basic simulation space (Table 4) consisted of a computational grid that had dimensions of 3 (w) × 3 (d) × 2 (h) m. The size of the computational cells was 50 × 50 × 50 mm, with 60 computational cells (Table 4), 60 computational cells in length and 40 computational cells in height. The walls of the computational grid were defined as open surfaces, except for one, which formed an inert surface and had a heat source placed on it. The heat source was a radiant surface (dimensions 1 × 1 m) with a constant temperature of 900 °C, which is equivalent to a design fire load of p_v = 45 kg·m⁻² (the value for apartment buildings). The recording of stand-off distances was performed by Slice File Output with a height of 1 m, which is half the height of the computational grid and hence the radiant surface, and Isosurface File Output, with a value of 18.5 kW·m⁻². The Gauge Heat Flux Gas measurement devices, nine in all, were placed in free space 1.4 m from the heat source, with a mutual distance between each other of 0.2 m. The simulation time was 10 s. At approximately 6 s, the heat radiating from the source settles down. In the present experiment, the simulation time was increased to 10 s due to the margin of possible changes in the emissivity. Parameters that would not affect the computational time of the simulations, the accuracy of the readings or the size of the stand-off distances were left at preset values in the baseline model. An example input file is provided in Appendix A. Based on the example input file, all other simulations were created similarly. Figure 1 shows the basic simulation space in which the location of the radiant surface and the location of the measuring devices can be seen.

Table 4. Characteristics of the fire model for evaluating the influence of selected FDS program parameters on the computational time of simulations.

Basic Simulation Space	Values
Computational grid—dimensions	3 (w) × 3 (d) × 2 (h) m
Computational cell size	50 × 50 × 50 mm
Number of computational cells	60 (w) × 60 (d) × 40 (h)
Heat source	1 × 1 m
Position	In the center of the inert area
Fire risk (residential building)	pv = 45 kg·m−2
Heat source—radiant surface with a constant temperature	900 °C
Slice File Output	At a height of 1 m, representing the height in the middle of the computational grid (also radiant surface)
Isosurface File Output	18.5 kW·m−2
Gauge Heat Flux Gas Devices	9 pieces at a distance of 1.4 m from the heat source and with a spacing of 0.2 m between each other
Simulation time	10 s (at 6 secs, the heat emanating from the source settles) + increased to 10 s
Number of simulations	41

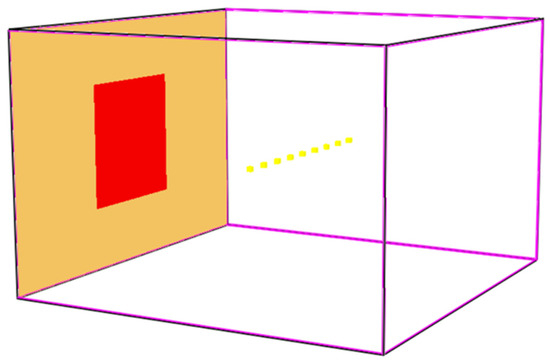
Figure 1. Basic simulation space in FDS [25].

All other fire model variations in FDS were implemented according to the above procedure and recorded in Table 4.

The Path Length parameter was the only one that did not affect the simulation time, as all five simulations took 4 min and 10 s (Table 5).

Table 5. Tested FDS program parameters indicating the influence on the time of simulations.

Tested Parameter	Range	Simulation Time		Change in Simulation Length
		Minimum	Maximum
Cell Size	10, 25, 50, 75 mm	Seconds	Days	Simulation time from seconds to days
Path Length	0.1–3 m	4:10 min	4:10 min	0%
Number Radiation Angles	100–2500	4:10 min	28 min	+600%
Time Step Increment and Angle Increment	1:1–3:5	4:10 min	17 min	+400%
Humidity	0–100%	4:10 min	5:45 min	+27%

The Number of Radiation Angles parameter had a significant effect on the computational time of the simulations. The computation time varied by up to 600% for a number of spatial angles of 2500, with a preset value of 400 (Table 5).

The Time Step Increment and Angle Increment parameters had a significant effect on the length of the simulations, up to +400%.

The Humidity parameter had a 27% effect on the computational time of the simulations.

2.2.2. Influence of Selected Parameters on the Size of Stand-Off Distances

The effect of the selected FDS parameters on the magnitude of the distance readings was considered separately for each parameter. For each parameter, a model was created (Figure 2, Table 6). In each of the following models, some input parameters were varied (Table 6). Parameters that did not change from preset values are not mentioned. Below are the parameters that did not change in any of the models but needed to be defined at the beginning:

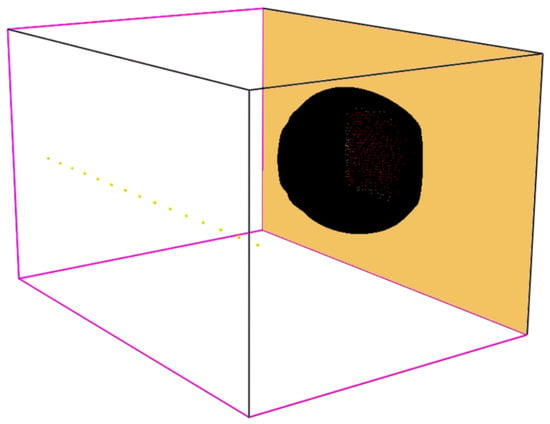
Figure 2. Basic model for sensitivity analysis of spacing distances [25].

Table 6. Characteristics of the fire model for the evaluation of the influence of selected FDS parameters on the spacing program.

	Simulation Parameters Investigated
Basic Simulation Space and Simulation Parameter Values	Time Step Increment and Angle Increment	Humidity	Path Length and Number of Radiation Angles			Computational Cell Size			Number of Measuring Devices
Time Step Increment (Table 1)	1, 2, 3	1	1			1			1
Angle Increment (Table 1)	1, 2, 3, 4, 5	1	1			1			1
Path Length	1.2	1.2	Range from 0.4 to 4.0, depending on the size of the radiant area (Table 9)			Maximum value adjusted to the largest dimensions of the computational grid **			4
Number of Radiation Angles (Table 1)	400	400	500, 1000, 1500, 2000			500			500
Computational Grid—Dimensions (m)	3 (w) × 3 (d) × 2 (h)	3 (w) × 3 (d) × 2 (h)	4 (w) × 4 (d) × 3 (h)			Depending on the sizes of the computational cells **			4 (w) × 4 (d) × 3 (h)
Computational Cell Size (mm)	50 × 50 × 50	50 × 50 × 50	25 × 25 × 25 *			25, 30, 35, 40, 45, 50 **			50 × 50 × 50
Number of Computational Cells	60 (w) × 60 (d) × 40 (h)	60 (w) × 60 (d) × 40 (h)	160 (w) × 160 (d) × 120 (h)			Depending on the sizes of the computational cells			80 (w) × 80 (d) × 60 (h)
Heat Source
Constant-temperature radiant surface (°C)	900	900	900			900			900
Fire risk—design fire load (residential buildings), pv (kg.m−2)	45	45	45			45			45
Radiant area size (m)	1 × 1	1 × 1	1 × 1	1.5 × 1.5	2 × 2	1 × 1	1.5 × 1.5	2 × 2	1 × 1	1.5 × 1.5	2 × 2
Position of the radiant area	In the center of the inert area
Recording of Stand-Off Distances
Slice File Output	At a height of 1 m (in the middle of the computational grid = radiant surface)
Isosurface File Output (kW·m−2)	18.5
Number of devices (Gauge Heat Flux Gas)	9	9	17 devices at different distances from the radiant surface			17			17/0.2 Δ 9/0.4 14/0.25 8/0.45 12/0.3 7/0.5 10/0.35
Distance between Gauge Heat Flux Gas devices (m)	0.2
Specified device clearance from the radiant surface (m)	1.6	1.6	7 position changes	7 position changes	7 position changes	Maximum value adjusted to the largest dimensions of the computational grid **			4
Basic calculation stand-off distance (m)	1.2	1.0	1.25±	1.85±	2.5±	1.25±	1.85±	2.5±	1.25±	1.85±	2.5±
Simulation time (s)	6	6	6			6			6
Number of simulations	15	11 (from 0% to 100% in 10% intervals)	84			6 ***	6	6	7 ΔΔ	7	7

* The size of the computational cells can have a significant effect on the determination of the total stand-off distance; therefore, a smaller computational cell size was chosen in order to obtain the most accurate resultant values. ** Radiation areas are explained in Table 10. *** Total of 18—6 for each size of computational cells. Δ Number of devices/distance between devices (m) (presented in Table 12). As the number of devices increases, the distance between them decreases. ΔΔ Total of 21—7 for each of the radiant surface sizes. (There was a change in the number of measuring devices and also in the distances between them (presented in Table 12).)

• The base model was always made up of five walls that formed an open surface and one wall that formed an inert surface. On this surface, there was always a radiating surface that represented a fully fire-open area. The size of the radiant surfaces and their quantity varied depending on the parameter under study, but the temperature of the radiant surface was always constant, with a value of 900 °C (Figure 2);
• The model always defined a Slice File Output, whose location was in the middle of the height of the computational grid, and an Isosurface File Output with a logging value of 18.5 kW·m⁻²;
• The measuring devices were always of the Gauge Heat Flux Gas type;
• The computational time of the simulations was set to 6 s, since the heat radiating from the source would already be steady.

All applied fire model variations for monitoring the influence of FDS program parameters on the determination of stand-off distances are listed in Table 6.

• Influence of Time Step Increment and Angle Increment parameters

The influence of the Time Step Increment and Angle Increment parameters was assessed by 15 simulations (Table 6). The Time Step Increment and Angle Increment parameters could take values from 1 to 3 and 1 to 5, respectively. All possible combinations of these two parameters were created in the simulations of Table 7.

Table 7. Results of the investigation of the influence of the Time Step Increment and Angle Increment parameters.

Combination of Parameters of Time Step Increment and Angle Increment	Stand-Off Distance [m]		Difference
	Prescriptive Approach	FDS
1-1, 1-2, 1-3, 1-4, 1-5	1.2	1.2	0%
2-1, 2-2, 2-3, 2-4, 2-5		1.2	0%
3-1, 3-2, 3-3, 3-4, 3-5		1.2	0%

Table 7 shows the results of the investigation of the influence of the selected parameters on the size of the stand-off distances in the FDS program. The given parameters did not influence the resulting spacing distances.

• Influence of the Humidity parameter

The basic simulation space for detecting the influence of the Humidity parameter was the same as in the section on the influence of the Time Step Increment (with a value of 1) and Angle Increment (with a value of 1) parameters. There were 11 simulations with a change in Humidity from 0% to 100% at intervals of 10%. Humidity had a value of 70–80% in our environment, but it varies depending on weather and season conditions. Table 8 presents the Humidity values and shows the effect on the resulting stand-off distances determined by the FDS program.

Table 8. Results of the investigation of the influence of the parameter Humidity.

Humidity [%]	Stand-Off Distance [m]		Difference
	Prescriptive Approach	FDS
0	1.20	1.35	11%
10		1.30	8%
20		1.25	4%
30, 40, 50		1.20	0%
60, 70, 80, 90		1.15	−4%
100		1.10	−9%

As the Humidity value decreased, the value of the stand-off distance read out from the simulations increased by 15 cm (11%) compared to the prescriptive procedure (specified distance of 1.2 m). Conversely, as the Humidity value increased, the total stand-off distance from the radiant surface decreased relative to the prescriptive procedure by 10 cm, or 9% (Table 8). The result is the recommendation of a preset Humidity value of 40% for calculating the stand-off distances in the FDS program, since this humidity value is preset and the stand-off distance value is the same for the standard and engineered approaches.

• Influence of Path Length and Number of Radiation Angles parameters

The basic simulation space of the influence of the Path Length and Number of Radiation Angles parameters on the magnitude of the stand-off distances is described in Table 6.

The assessment of the influence of the Path Length and Number Radiation Angles parameters was carried out in 84 simulations. In the simulations, there was a change in the size of the radiating area in three variations of Table 6 and in four variations of the values of the Number of Radiation Angles, namely, 500, 1000, 1500 and 2000 radiation angles (Table 6).

The simulation results (Table 9) showed that the parameter Number of Radiation Angles does not affect the value of the stand-off distance (Table 9). The Path Length parameter has a demonstrable effect on the total stand-off distance value. The lower the Path Length value in the FDS, the lower the resulting stand-off distance value (Table 9). At the same time, the higher the value of the Path Length parameter, the higher the value of the resulting stand-off distance. The resulting recommendation is to use higher values of this parameter in simulations. In Figure 3, one can see the difference in the rendering of the stand-off distance for different values of Number of Radiation Angles, which affect the resulting stand-off distance readings.

Table 9. Results of the investigation of the influence of the Path Length and Number of Radiation Angles parameters.

		Radiation Angles
			500		1000		1500		2000
Radiant Area	Path Length [m]	Stand-Off Distance [m]		Difference	Stand-Off Distance [m]	Difference	Stand-Off Distance [m]	Difference	Stand-Off Distance [m]	Difference
		Prescriptive Approach	FDS		FDS		FDS		FDS
1 × 1	0.50	1.25	1.20	−4%	1.20	−4%	1.20	−4%	1.20	−4%
	0.75		1.23	−2%	1.23	−2%	1.23	−2%	1.23	−2%
	1.00		1.23	−2%	1.23	−2%	1.23	−2%	1.23	−2%
	1.25		1.23	−2%	1.23	−2%	1.23	−2%	1.23	−2%
	1.50		1.23	−2%	1.23	−2%	1.23	−2%	1.23	−2%
	1.75		1.23	−2%	1.23	−2%	1.23	−2%	1.23	−2%
	2.00		1.23	−2%	1.23	−2%	1.23	−2%	1.23	−2%
1.5 × 1.5	0.40	1.85	1.75	−6%	1.75	−6%	1.75	−6%	1.75	−6%
	0.90		1.80	−3%	1.80	−3%	1.80	−3%	1.80	−3%
	1.40		1.80	−3%	1.80	−3%	1.80	−3%	1.80	−3%
	1.90		1.83	−1%	1.83	−1%	1.83	−1%	1.83	−1%
	2.40		1.83	−1%	1.83	−1%	1.83	−1%	1.83	−1%
	2.90		1.83	−1%	1.83	−1%	1.83	−1%	1.83	−1%
	3.40		1.85	0%	1.85	0%	1.85	0%	1.85	0%
2 × 2	1.00	2.50	2.35	−6%	2.35	−6%	2.35	−6%	2.35	−6%
	1.50		1.50	−5%	2.38	−5%	2.38	−5%	2.38	−5%
	2.00		2.00	−4%	2.40	−4%	2.40	−4%	2.40	−4%
	2.55		2.55	−3%	2.43	−3%	2.43	−3%	2.43	−3%
	3.00		3.00	−3%	2.43	−3%	2.43	−3%	2.43	−3%
	3.50		3.50	−3%	2.43	−3%	2.43	−3%	2.43	−3%
	4.00		4.00	−3%	2.43	−3%	2.43	−3%	2.43	−3%

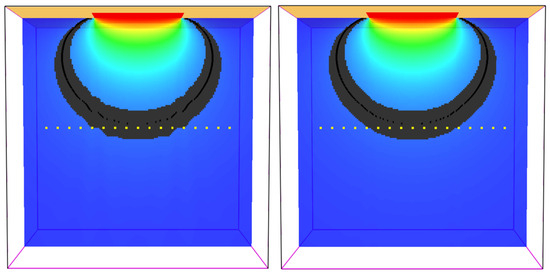
Figure 3. Difference in rendering of stand-off distances for Number of Radiation Angles: 500 (left) and 1500 (right).

• Influence of the parameter Size of computational cells

The assessment of the influence of the parameter Size of Computational Cells was carried out by 18 simulations. The simulations were divided into three basic groups according to the size of the radiating area (Table 10) and six specified simulation spaces described by the cell size (Table 11). Figure 4 shows the difference in the rendering spaces with different computational cell edge sizes, which affected the readings of the resulting stand-off distances in the sense of reading them only in the range of values of the computational cell edge.

Table 10. Simulation spaces as a function of computational cell edge size.

Computational Cell Edge Size [mm]	Computational Grid Dimensions
	Width [m]	Length [m]	Height [m]
25	4.0	4.0	3.0
30	3.99	3.99	3.0
35	3.99	3.99	2.94
40	4.0	4.0	3.0
45	3.96	3.96	2.97
50	4.0	4.0	3.0

Table 11. Results of the investigation of the influence of the parameter Computational cell edge size.

Radiant Area [m]	Computational Cell Edge Size [mm]	Stand-Off Distance [m]		Difference	Simulation Time [s]
		Prescriptive Approach	FDS
1 × 1	25	1.25	1.20	−4%	23.5
	30		1.23	−2%	11.6
	35		1.23	−2%	6.0
	40		1.24	−1%	3.1
	45		1.26	1%	2.2
	50		1.25	0%	1.3
1.5 × 1.5	25	1.85	1.85	0%	27.0
	30		1.86	1%	12.0
	35		1.89	2%	6.3
	40		1.84	−1%	3.6
	45		1.85	0%	2.3
	50		1.85	0%	1.5
2 × 2	25	2.50	2.43	−3%	30.0
	30		2.43	−3%	12.3
	35		2.42	−4%	6.6
	40		2.44	−2%	4.0
	45		2.48	−1%	2.3
	50		2.45	−2%	1.6

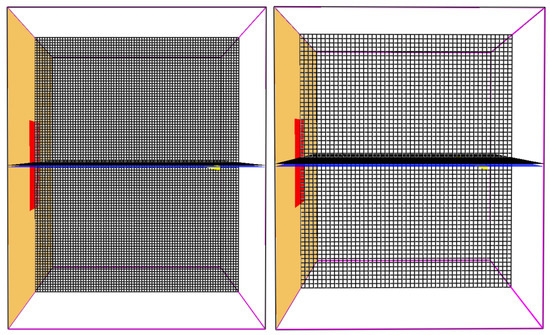
Figure 4. Rendering of the space with different computational cell edge sizes—30 mm (left) and 50 mm (right).

Table 11 shows the results of the investigation of the influence of the computational cell size parameter on the subtraction distances.

It can be concluded that the size of the computational cells had a moderate effect on the size of the resulting stand-off distances. The difference in the results of the stand-off distances may have been due to the size of the computational cells in terms of the ability to subtract the results.

The results in Table 5 show a significant effect of the size of the computational cells on the total computational time of the simulations, which can be extended from seconds to days. The above simulations of the influence of this parameter were performed with the preset values of the other parameters.

From the output files for each simulation, the total computation times of the simulations were examined according to Table 5, column 5. It is shown that the size of the computation cells can extend the computation time of simulations from 1.5 h to more than a day (20 times the increase in computation time).

It will be most appropriate to use a computational cell size of 50 mm in future simulations.

• Influence of the parameter Number of measuring devices

The assessment of the influence of the parameter Number of Measuring Devices on the size of the computational cells was carried out by 21 simulations. The simulations were divided into three basic groups according to the size of the radiating area (Table 6 and Table 7) and variations in the number of devices with adjusted distances between them.

Table 12 shows the results of the investigation of the influence of the number of measuring devices on the determination of the stand-off distances.

Table 12. Results of the investigation of the influence of the parameter Number of Measuring Devices.

Radiant Area [m]	Number of Measuring Devices	Distance Between Devices [m]	Stand-Off Distance [m]
			Prescriptive Approach	FDS
1 × 1	17	0.20	1.25	1.25
	14	0.25		1.25
	12	0.30		1.25
	10	0.35		1.25
	9	0.40		1.25
	8	0.45		1.25
	7	0.50		1.25
1.5 × 1.5	17	0.20	1.85	1.85
	14	0.25		1.85
	12	0.30		1.85
	10	0.35		1.85
	9	0.40		1.85
	8	0.45		1.85
	7	0.50		1.85
2 × 2	17	0.20	2.5	2.45
	14	0.25		2.45
	12	0.30		2.45
	10	0.35		2.45
	9	0.40		2.45
	8	0.45		2.45
	7	0.50		2.45

A significant reduction in the number of measuring devices could lead to inaccurate calculations and therefore to deviations in the determination of the stand-off distances.

At the same time, according to Table 12, the parameter number of measuring devices does not influence the calculation time of simulations.

3. Conclusions

By comparing the results of the FDS model sensitivity analysis and the prescriptive approach for the determination of stand-off distances, it can be concluded that the fire models are suitable for solving the stand-off distances from fully fire-open areas in fire safety solutions for buildings in Slovakia. A sensitivity analysis was performed to determine the parameters that affect the output data—the values of the stand-off distances.

The sensitivity analysis was carried out on the following parameters, for which the optimal parameters for effective application of the FDS program for calculation of stand-off distances were determined:

• The size of the computational cells in the computational grid → 50 mm;
• Path Length → possible maximum;
• Number of spatial radiation angles (Number of Radiation Angles) → 500;
• Time Step Increment and Angle Increment → 1:1;
• Relative humidity (Humidity) → 40%.

The results of the sensitivity analysis are processed and an accurate dynamic calculation of building stand-off distances using fire models is produced and presented in the following paper. Based on the above findings, it can be argued that each of the input parameters has a significant impact on the determination of the stand-off distance values by the fire models, on both the readout values and the total computational time of the simulations, such that it can be concluded that the correct determination of the input parameter values is always necessary and that they cannot be omitted.

On the basis of the case study and its consequences, it is also possible to consider further research on the implementation of fire models in the determination of stand-off distances from buildings, e.g., from partially fire-open areas, which in the conditions of the Slovak Republic are walls with combustible insulation material or combustible cladding. Also, in connection with the determination of fire safety as a whole, it is possible to consider the implementation of fire models in determining fire risk, fire size and evacuation solutions.