Study on the Location Determination of Building Fire Points Based on Acoustic CT Temperature Measurement
Abstract
1. Introduction
2. Principle of Temperature Field Reconstruction for Acoustic CT
3. Reconstruction Method
3.1. Acquisition of Basic Temperature Field Data
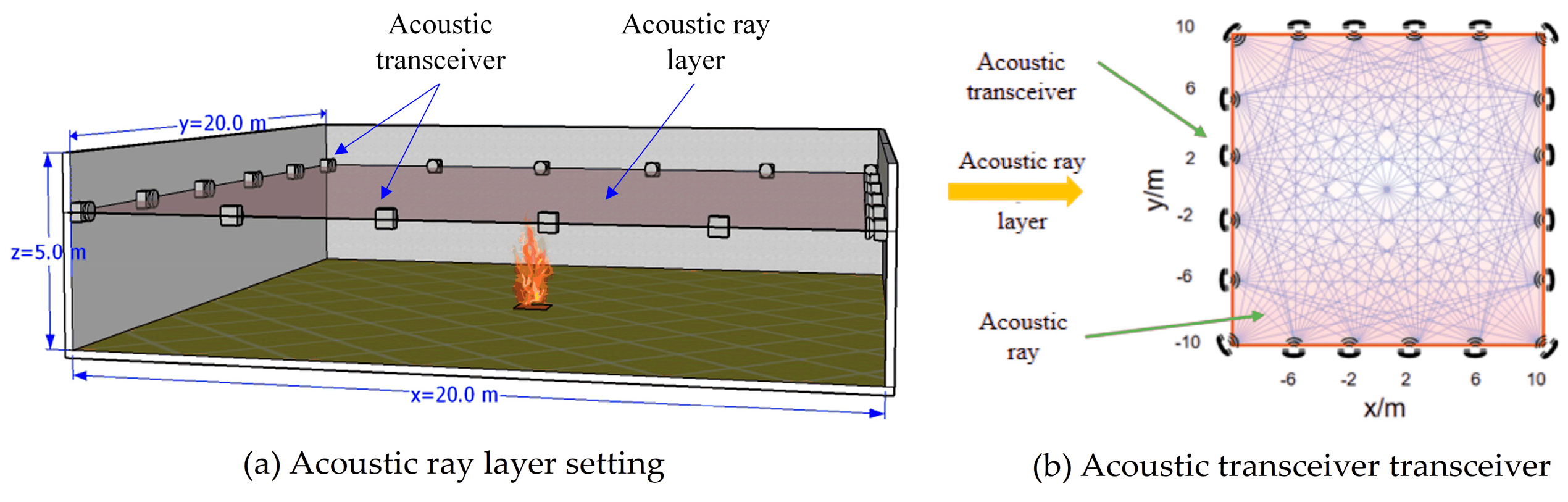
3.1.1. Establishment of Geometric Models and Setting of Key Parameters
3.1.2. Acquisition of the Time-of-Flight of Acoustic Wave Traveling
3.2. Reconstruction Scheme and the Algorithm
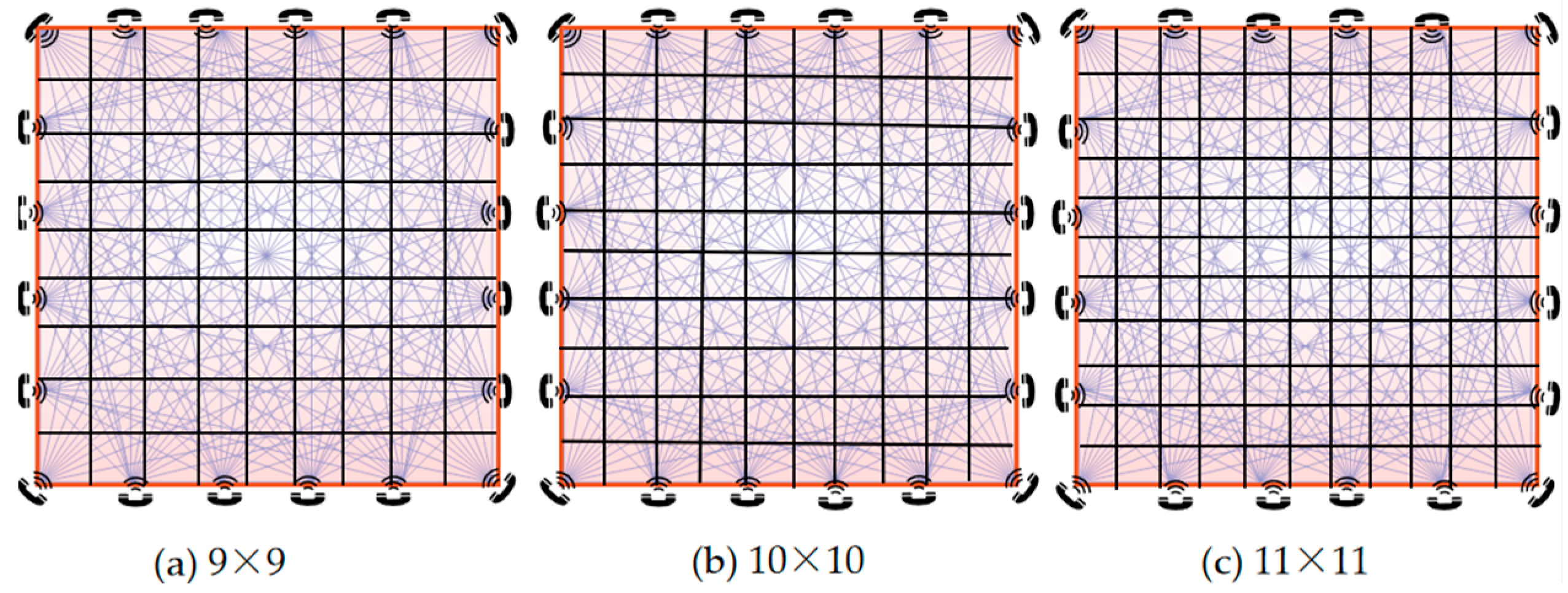
3.2.1. Arrangement of the Acoustic Transceivers and Grid Division of the Measured Cross Section
3.2.2. Solution Method of the Acoustic Matrix Equation
- (a)
- Least Squares QR-Decomposition (LSQR)
- (b)
- Simultaneous algebraic reconstruction technique (SART)
4. Analysis of Reconstruction Results
4.1. Cloud Map Comparison
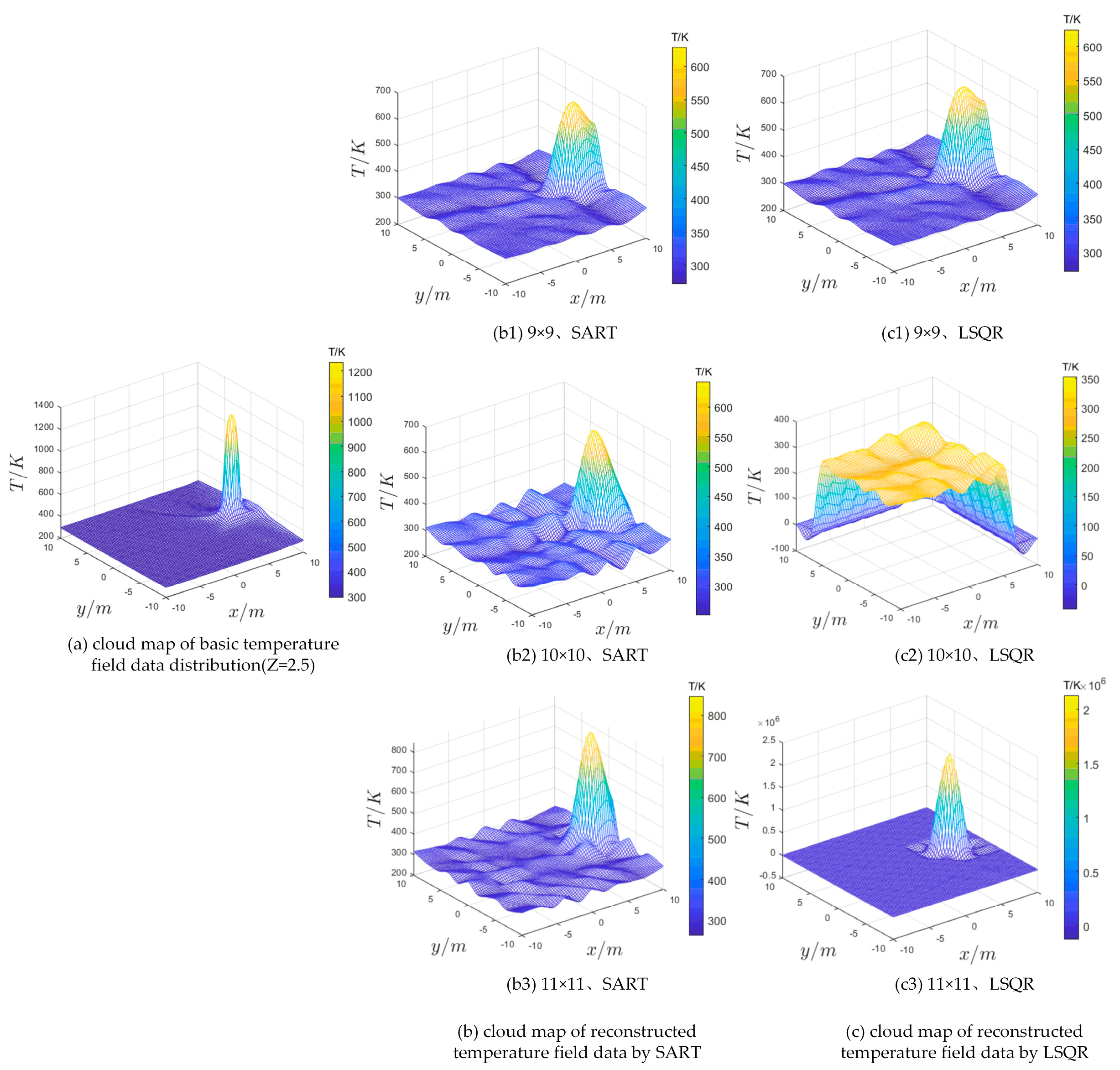
4.1.1. Reconstruction Results of Each Scheme under Fire 1 (Close to the Center)
- Under the SART, the distributional shape of the reconstructed cloud map under the three different meshing schemes is generally similar to the cloud map of basic temperature field data and shows obvious high temperature areas near the center. However, compared with the basic temperature data, the reconstruction temperature maximum of these three schemes is lower, among which the reconstruction results of the 11 × 11 grid scheme (Figure 6(b3)) are the closest to the basic temperature data.
- Under the LSQR, the reconstructed cloud map under the three different meshing schemes is significantly different from the basic temperature data cloud map in terms of the distributional shape, temperature maximum value, and coordinates of the high temperature region. Among them, the significant high temperature area appeared in the 9 × 9 grid (Figure 6(c1)) and 11 × 11 grid (Figure 6(c3)) schemes, but the latter has a large deviation from the basic temperature field in the position of the high temperature area. However, the temperature distribution of the 10 × 10 grid (Figure (6c2)) scheme was abnormal, and the reconstruction failed.
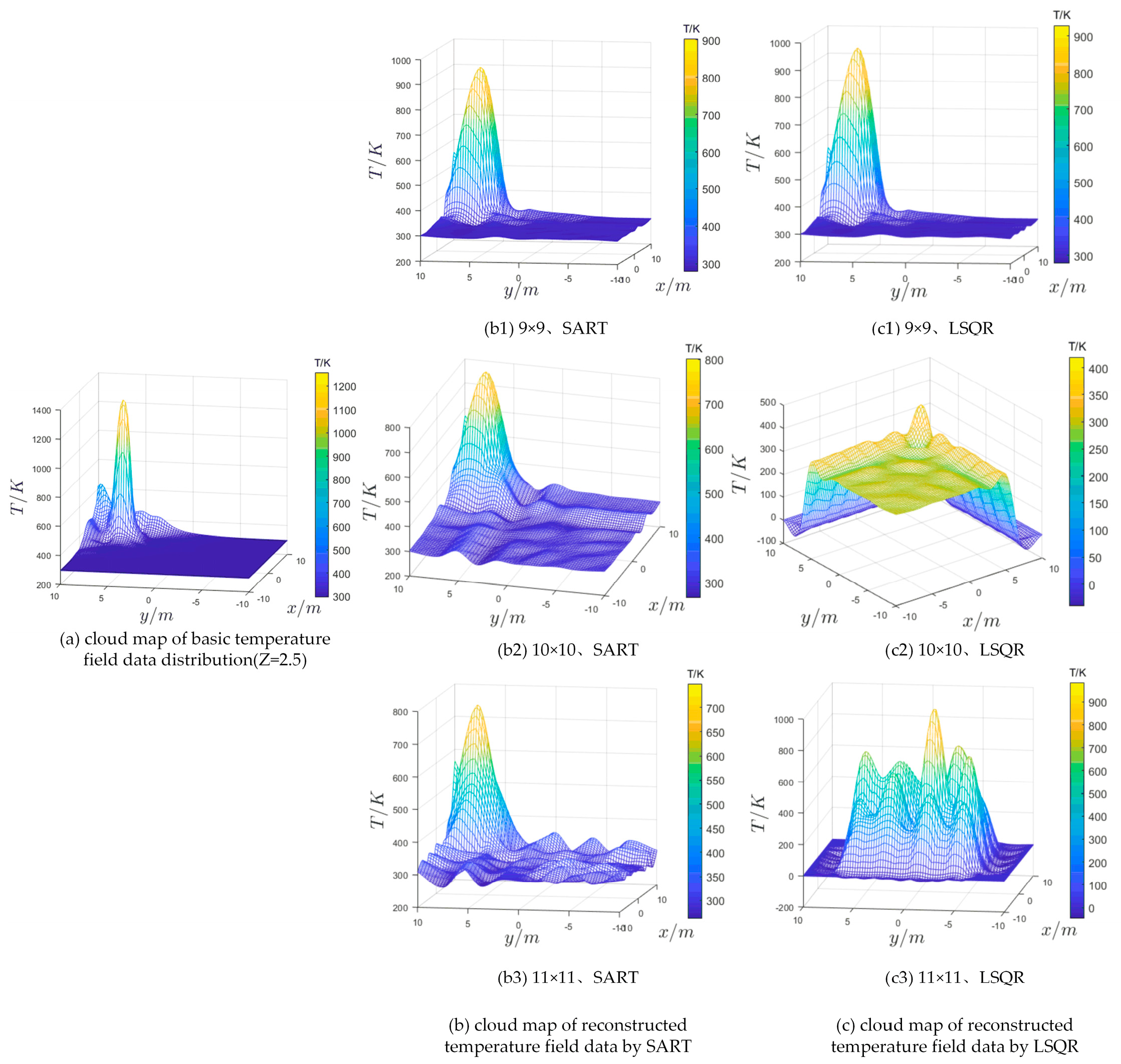
4.1.2. Reconstruction Results of Each Scheme under Fire 2 (Close to the Wall)
- Under the SART, the distributional shape of the reconstructed cloud map under the three different meshing schemes is generally similar to the basic temperature data, and it shows an obvious high temperature area in the position close to the wall. However, compared with the basic temperature data, the reconstruction maximum temperature of these three schemes is lower, among which the reconstruction results of the 11 × 11 grid scheme (Figure 7(b3)) are the closest to the basic temperature data.
- Under the LSQR, the reconstructed cloud map under the three different meshing schemes is significantly different from the basic temperature data cloud map in terms of the distributional shape, temperature maximum value, and coordinates of the high temperature region. Among them, the significant high temperature area appeared in the 9 × 9 grid (Figure 7(c1)) and 11 × 11 grid (Figure 7(c3)) schemes, but the latter has a large deviation from the basic temperature field in the position of the high temperature area. However, the temperature distribution of the 10×10 grid (Figure 7(c2)) scheme was abnormal, and the reconstruction failed.
4.1.3. Reconstruction Results of Each Scheme under Fire 3 (Close to the Corner)
- Under the SART algorithm, the distributional shape of the reconstructed cloud map under the three different meshing schemes is generally similar to the basic temperature data and shows obvious high temperature areas close to the corner. However, compared with the basic temperature data, the reconstruction temperature maximum of these three schemes is lower, among which the reconstruction results of the 9 × 9 grid scheme (Figure 8(b1)) are the closest to the basic temperature data.
- Under the LSQR, the reconstructed cloud maps under three different meshing schemes showed significant differences in the distributional shape, temperature maximum, and coordinates of the high temperature region. Among them, a significant high temperature area appeared under the 9 × 9 grid (Figure 8(c1)) grid (Figure 8(c1)) scheme, while the temperature distribution morphology in the 10 × 10 grid (Figure 8(c2)) and 11 × 11 grid (Figure 8(c3)) schemes was abnormal, and the reconstruction failed.
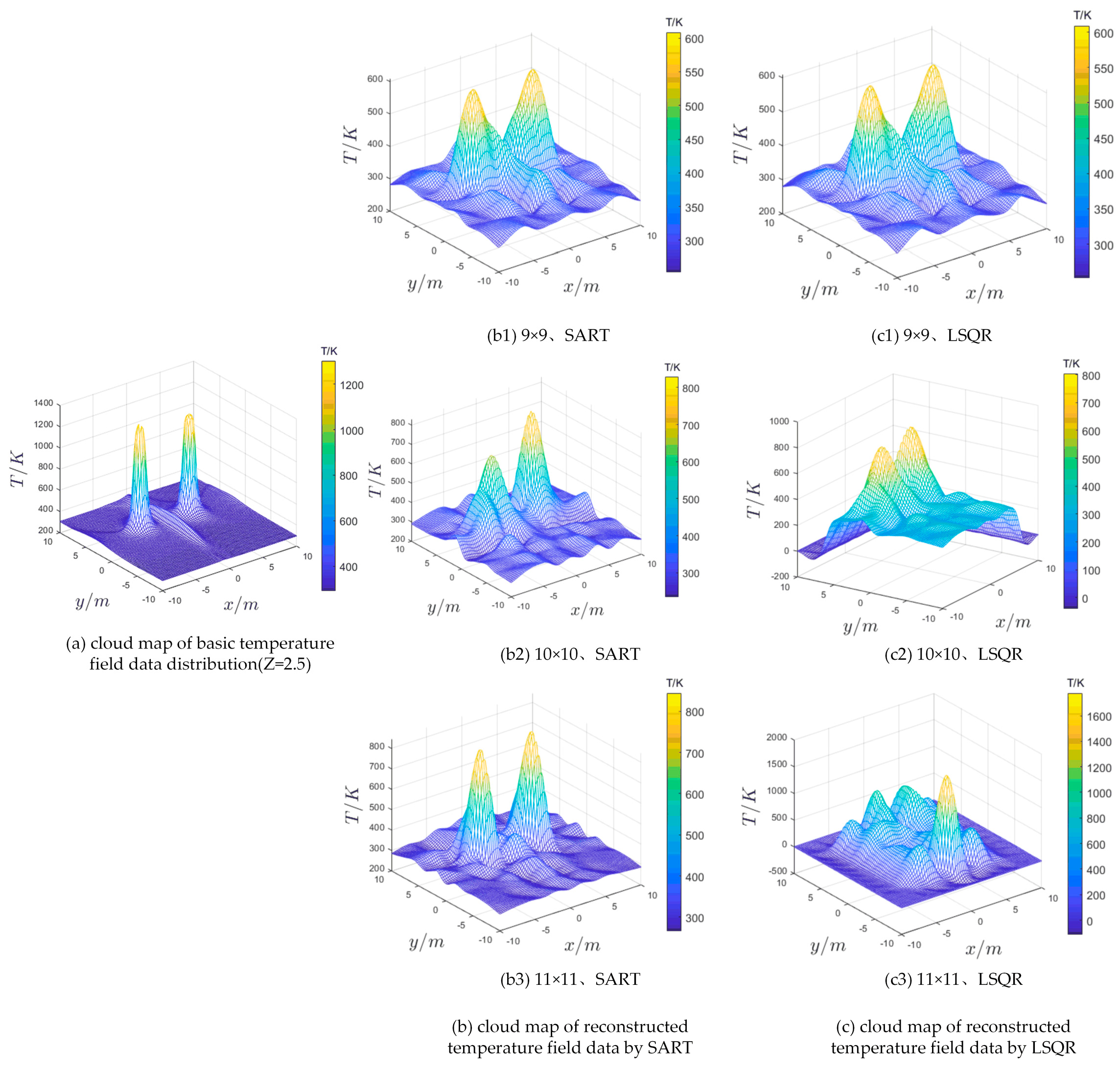
4.1.4. Reconstruction Results of Each Scheme under Fire 4 (Double Fire Source)
- Under the SART, the distributional shape of the reconstructed cloud map under three different meshing schemes is generally similar to the basic temperature data, and both fire sources show obvious high-temperature areas. However, compared with the basic temperature data, the reconstruction temperature maximum of these three schemes is lower, among which the reconstruction results of the 11 × 11 grid scheme (Figure 9(b3)) are the closest to the basic temperature data.
- Under the LSQR, the reconstructed cloud maps under three different meshing schemes showed significant differences in the distributional shape, temperature maximum, and maximum coordinates of the high temperature region. Among them, the significant high temperature area appeared in the 9 × 9 grid (Figure 9(c1)) and 10 × 10 grid (Figure 9(c2)) schemes, but the latter has a large deviation from the basic temperature field in the position of the high temperature area. However, the temperature distribution of the 11 × 11 grid (Figure 9(c3)) scheme was abnormal, and the reconstruction failed.
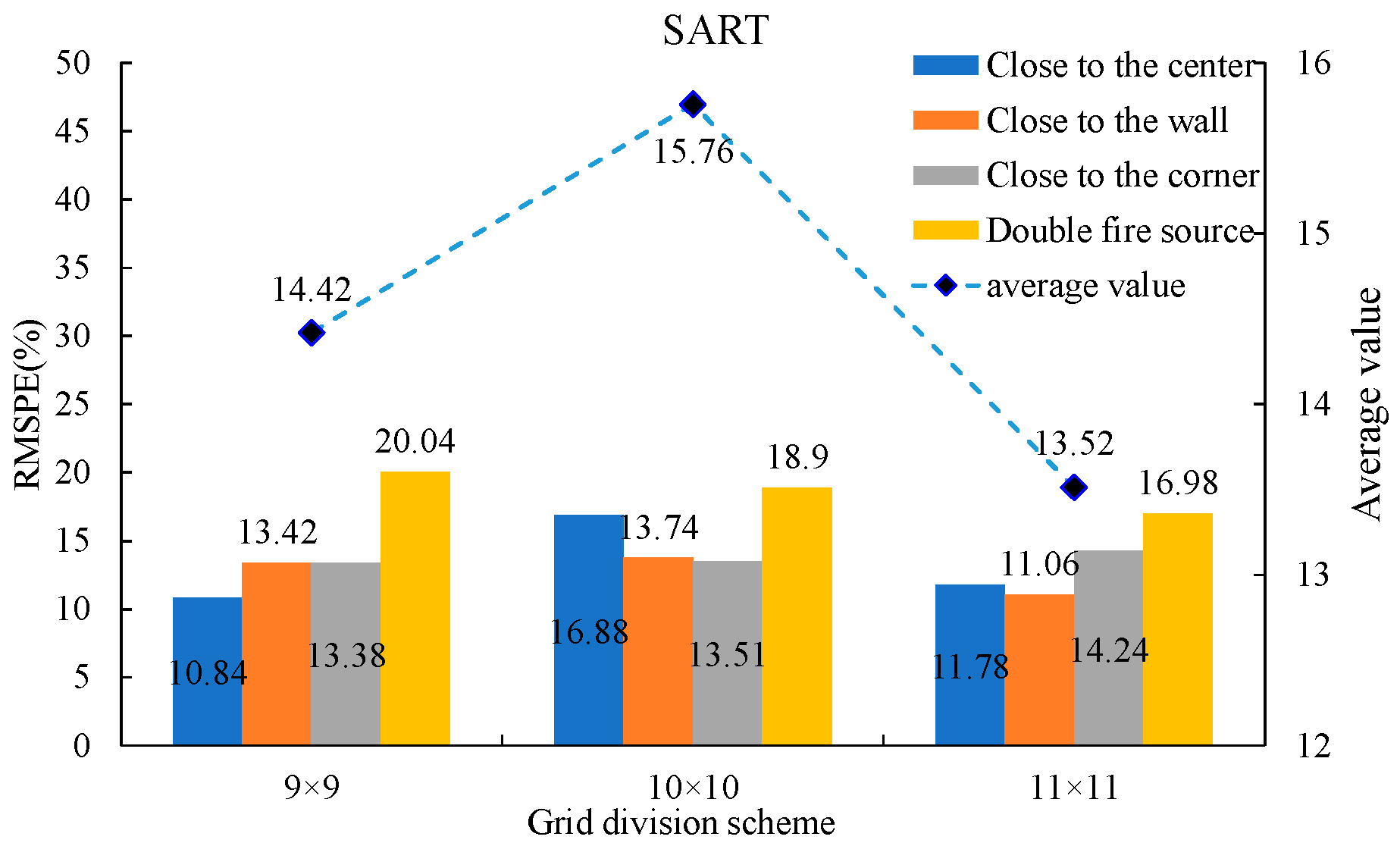
4.2. Analysis of Reconstruction Error and Reconstruction Time-Consuming
4.2.1. Error Analysis of the Reconstruction
4.2.2. Time-Consuming Analysis of the Reconstruction (Solution of the Equations)
- In terms of reconstruction time, the LSQR solution time is in the order of 10−2 s, while the SART solution time is in the order of 10−1 s, so the former has advantages in timeliness.
- Under the two algorithms, the solution time of the equation under different fire position parameters is slightly different, but the difference is not huge, and there is no obvious regularity.
- Under the two algorithms, the number of mesh divisions and the solution time have an approximately positive linear relationship. Compared with the LSQR algorithm, the computation time under the SART algorithm is more sensitive to the grid number. The grid increases, and the time consumption increase is more significant.
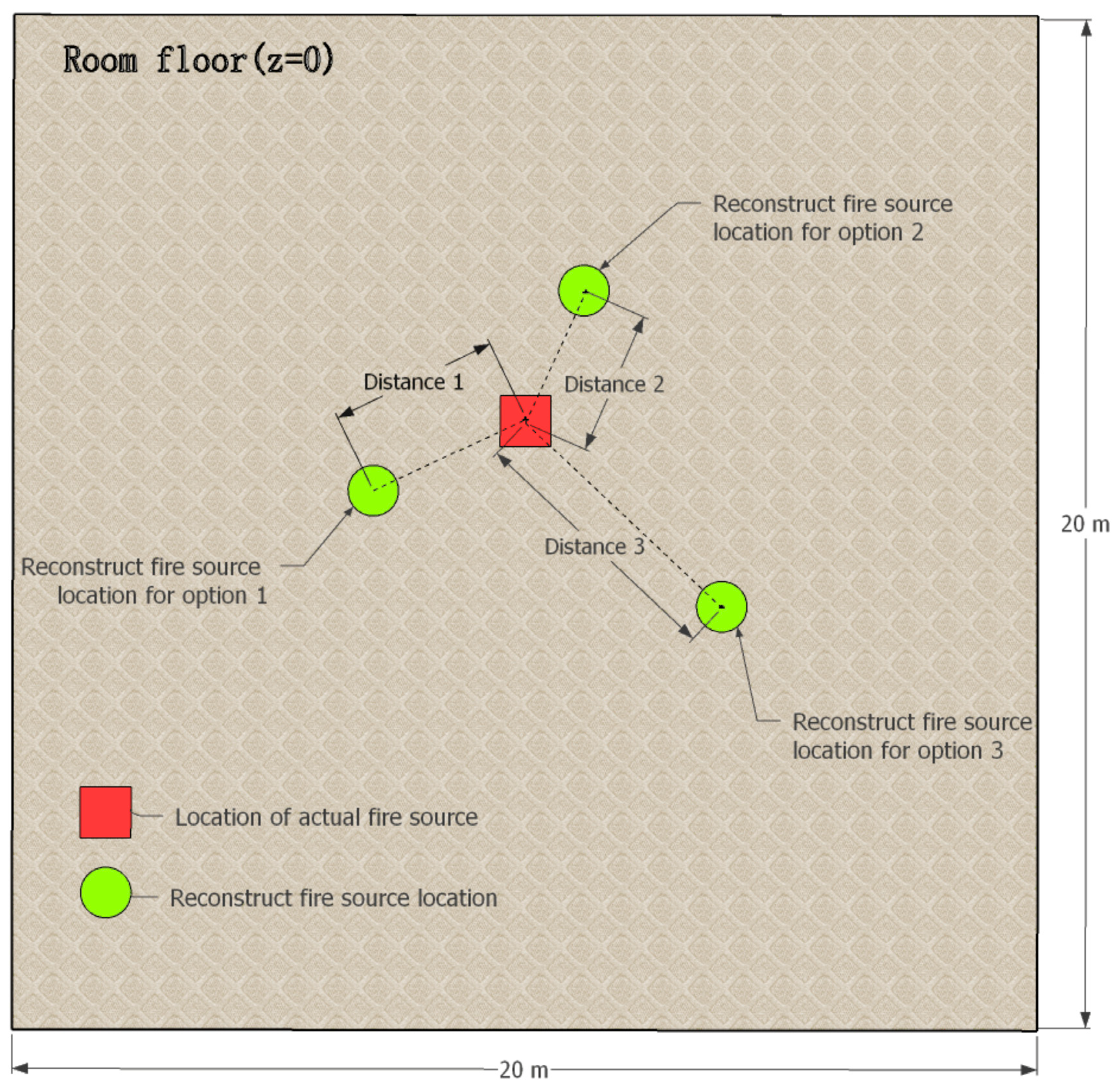
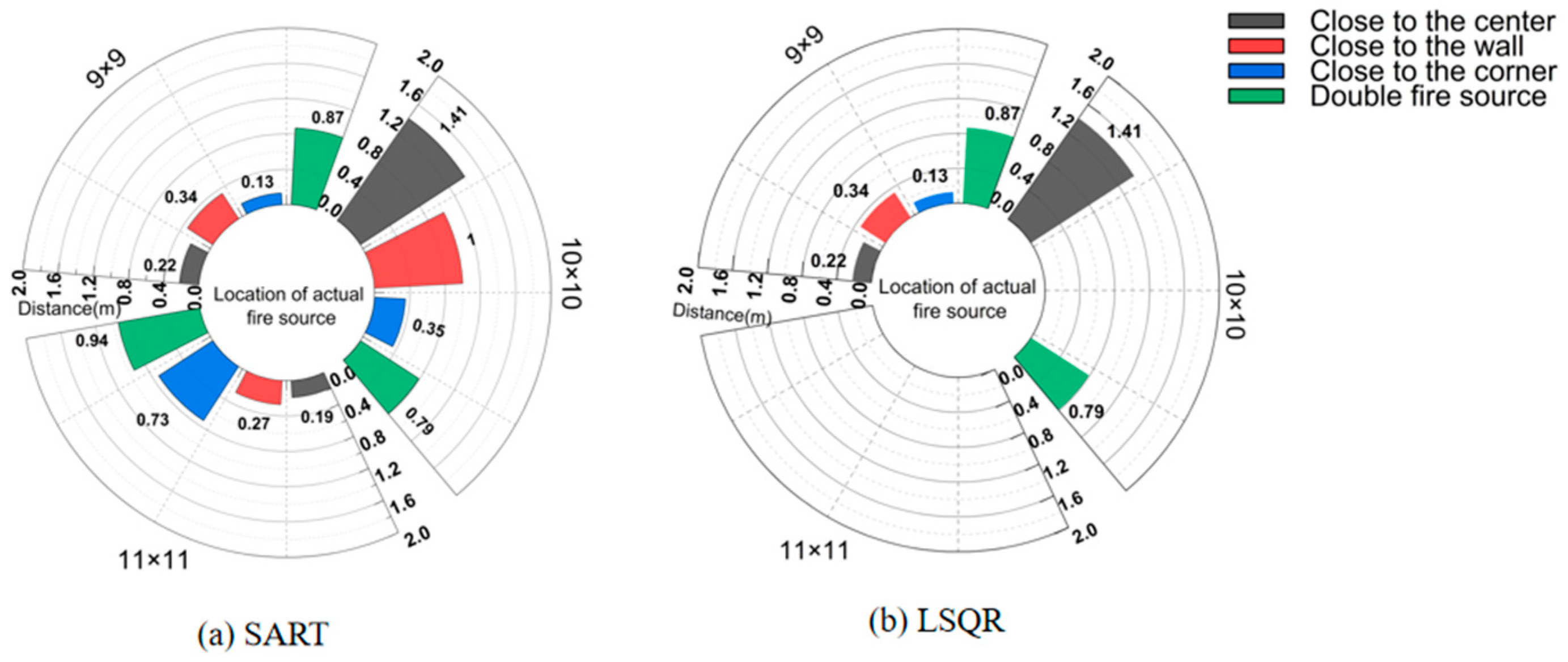
4.3. Results of Fire Source Location Determination
5. Conclusions
- Under the multi-grid division scheme, the robustness of SART is better than that of LSQR, which can better realize the temperature field reconstruction based on multiple grid schemes at different fire locations.
- In terms of reconstruction accuracy (root mean square error), SART and LSQR are basically the same under the 9 × 9 grid scheme, but in other schemes, SART is obviously better than LSQR. Under SART, the reconstruction data accuracy of the 11 × 11 grid scheme is the highest.
- In terms of reconstruction time consumption (equation solving), LSQR is better than SART overall; mesh division number has a significant positive correlation with the time consumption of equation solving.
- In terms of the determination of fire source location (peak coordinate), SART and LSQR can better realize the determination of fire source location under the 9 × 9 grid scheme. Under the SART, the three grid division schemes can determine the fire source position, but the 9 × 9 grid scheme has the highest judgment accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.W.; Cui, Y.H.; Zhou, J.G. Analysis and identification of ignition points and ignition sources. Fire Sci. Technol. 2011, 30, 973–976. [Google Scholar]
- Deng, Y.C. Investigation and analysis of a warehouse fire accident. Fire Sci. Technol. 2006, 6, 832–834. [Google Scholar]
- Florin, M.; Emilian, G.; Cornel, M.S.; Maria, P.; Loan, N.V.; Sonia, N.S.; Titus, V. FDS results for selecting the right scenario in the case of a building fire: A case study. Fire 2022, 5, 198. [Google Scholar]
- Khan, A.E.; Ahmed, A.M.; Khan, H.E.; Majumder, C.S. Fire Emergency Evacuation Simulation of a shopping mall using Fire Dynamic Simulator (FDS). J. Chem. Eng. 2017, 30, 32–36. [Google Scholar] [CrossRef][Green Version]
- Suhaimi, S.N.; Ibrahim, A.; Mustapha, S.; Adam, M.N.; Baharuddin, R.M. Development of a smoke prediction model using numerical simulations. Int. J. Comput. Aided Eng. Technol. 2021, 14, 477–492. [Google Scholar] [CrossRef]
- Li, S.F. Application and practice of drones in firefighting and rescue work. China Equip. Eng. 2023, 8, 8–10. [Google Scholar]
- Chen, B. Research on the application of firefighting drones in high-rise building fire rescue. Fire Community (Electron.) 2022, 8, 45–47. [Google Scholar]
- Li, Y.Q.; Liu, S.; Inaki, H.S. Dynamic Reconstruction Algorithm of Three-Dimensional Temperature Field Measurement by Acoustic Tomography. Sensors 2017, 17, 2084. [Google Scholar] [CrossRef]
- Zhang, S.P.; Shen, G.Q.; An, L.S.; Niu, Y.G. Online monitoring of the two-dimensional temperature field in a boiler furnace based on acoustic computed tomography. Appl. Therm. Eng. 2015, 75, 958–966. [Google Scholar] [CrossRef]
- Yan, H.; Ma, Z.; Zhou, G.Y. Acoustic tomography system for online monitoring of temperature fields. IET Sci. Meas. Technol. 2017, 11, 623–630. [Google Scholar] [CrossRef]
- Chen, Y.T.; Yan, H. Reconstruction of complex temperature field based on improved Tikhonov regularization. J. Phys. Conf. Ser. 2021, 1754, 012207. [Google Scholar] [CrossRef]
- Yan, H.; Zhuang, Q.; Wang, X.N. Simulation of acoustic CT reconstruction for temperature distribution of stored grain. J. Shenyang Univ. Technol. 2015, 37, 662–666. [Google Scholar]
- Yan, H.; Dou, H.; Chen, G.N.; Yao, L. 3D temperature field reconstruction based on the interpolation of 2D acoustic reconstructions. In Fifth International Conference on Machine Vision (ICMV 2012): Algorithms, Pattern Recognition, and Basic Technologies, Proceedings of the Fifth International Conference on Machine Vision (ICMV 2012), Wuhan, China, 20–21 October 2012; SPIE: Bellingham, WA, USA, 2013; Volume 8784, pp. 878422-1–878422-6. [Google Scholar]
- Zhong, Q.H.; Chen, Y.S.; Zhu, B.; Liao, S.H.; Shi, K.B. A temperature field reconstruction method based on acoustic thermometry. Measurement 2022, 200, 111642. [Google Scholar] [CrossRef]
- Yan, H.; Li, K.; Wang, S.H. A 3D Temperature Field Reconstruction Algorithm Based on Acoustic Travel-Time Tomography. Lect. Notes Electr. Eng. 2012, 140, 639–644. [Google Scholar]
- Song, Z.Q.; Fan, X. Detection technology and application of temperature field in boiler based on acoustic method. Boil. Technol. 2005, 1, 20–23+69. [Google Scholar]
- An, L.S.; Wang, R.; Shen, G.Q.; Zhang, S.P. Simulation study of acoustic CT algorithm for reconstructing 3D temperature field in furnace. J. Chin. Soc. Power Eng. 2015, 35, 13–18. [Google Scholar]
- Yan, H.; Chen, G.N.; Yang, Q.; Liu, L.J. Research on acoustic CT reconstruction of complex temperature fields. Acoust. J. 2012, 37, 370–377. [Google Scholar]
- Wang, S.H.; Yan, H.; Li, S. Design of layout for acoustic tomography imaging sensor. China Sci. Technol. Pap. 2014, 9, 413–416. [Google Scholar]
- Qin, H.J.; Wen, J.Q.; Gao, Z.H.; Chai, L.L.; Yao, H.W. Preliminary Study on Reconstruction of Building Thermal Field Based on Iterative Algorithm Acoustic CT. Fire 2023, 6, 199. [Google Scholar] [CrossRef]
- Wang, R. Acoustic Measurement of Three-Dimensional Temperature Field in Furnace and Its Application in Combustion Optimization; North China Electric Power University: Beijing, China, 2015. [Google Scholar]
- Ru, Y.D. Algorithm Research on Acoustic Reconstruction of Three-Dimensional Temperature Field in Furnace. Master’s Thesis, North China Electric Power University, Beijing, China, 2015. [Google Scholar]
- Huang, Z.A.; Meng, Y.R.; Yang, R.; Wang, S.Y. Numerical simulation of a cinema fire based on FDS. Int. J. Simul. Process Model. 2018, 13, 200–209. [Google Scholar] [CrossRef]
- Zhao, G.; Beji, T.; Merci, B. Study of FDS simulations of buoyant fire-induced smoke movement in a high-rise building stairwell. Fire Saf. J. 2017, 91, 276–283. [Google Scholar] [CrossRef]
- Zhao, X.L.; Wei, S.Y.; Chu, Y.Y.; Wang, N. Numerical Simulation of Fire Suppression in Stilted Wooden Buildings with Fine Water Mist Based on FDS. Buildings 2023, 13, 207. [Google Scholar] [CrossRef]
- Lu, S.L.; Li, Q.P.; Bai, L.; Wang, R. Performance predictions of ground source heat pump system based on random forest and back propagation neural network models. Energy Convers. Manag. 2019, 197, 111864. [Google Scholar] [CrossRef]
- Zhang, D.W.; Li, W.L.; Wu, X.H.; Lv, X.F. Application of simulated annealing genetic algorithm-optimized back propagation (BP) neural network in fault diagnosis. Int. J. Model. Simul. Sci. Comput. 2019, 10, 1950024. [Google Scholar] [CrossRef]
- Chen, S.X.; Xiong, H.L.; Liao, J.; Zhou, J.W.; Zuo, J.S. A joint optimization matching tracking algorithm based on CGLS and LSQR. J. Autom. 2018, 44, 1293–1303. [Google Scholar]
- Han, H.; Wu, L.N. Decision feedback equalizer based on LSQR algorithm and windowing technique. J. Circuits Syst. 2010, 15, 117–121. [Google Scholar]
- Zhang, S.; Zhou, P.; Pan, K.; Liu, Z.G.; Li, Y.D. A SART algorithm for area integral model in desktop micro-CT system. Nucl. Inst. Methods Phys. Res. A 2019, 955, 163288. [Google Scholar] [CrossRef]
- Zhu, X.Y.; Zhang, B.; Li, J.; Xu, C.L. 3D flow field reconstruction of a single optical field camera based on pre-recognition technology and SART algorithm. J. Eng. Thermophys. 2020, 41, 1445–1451. [Google Scholar]
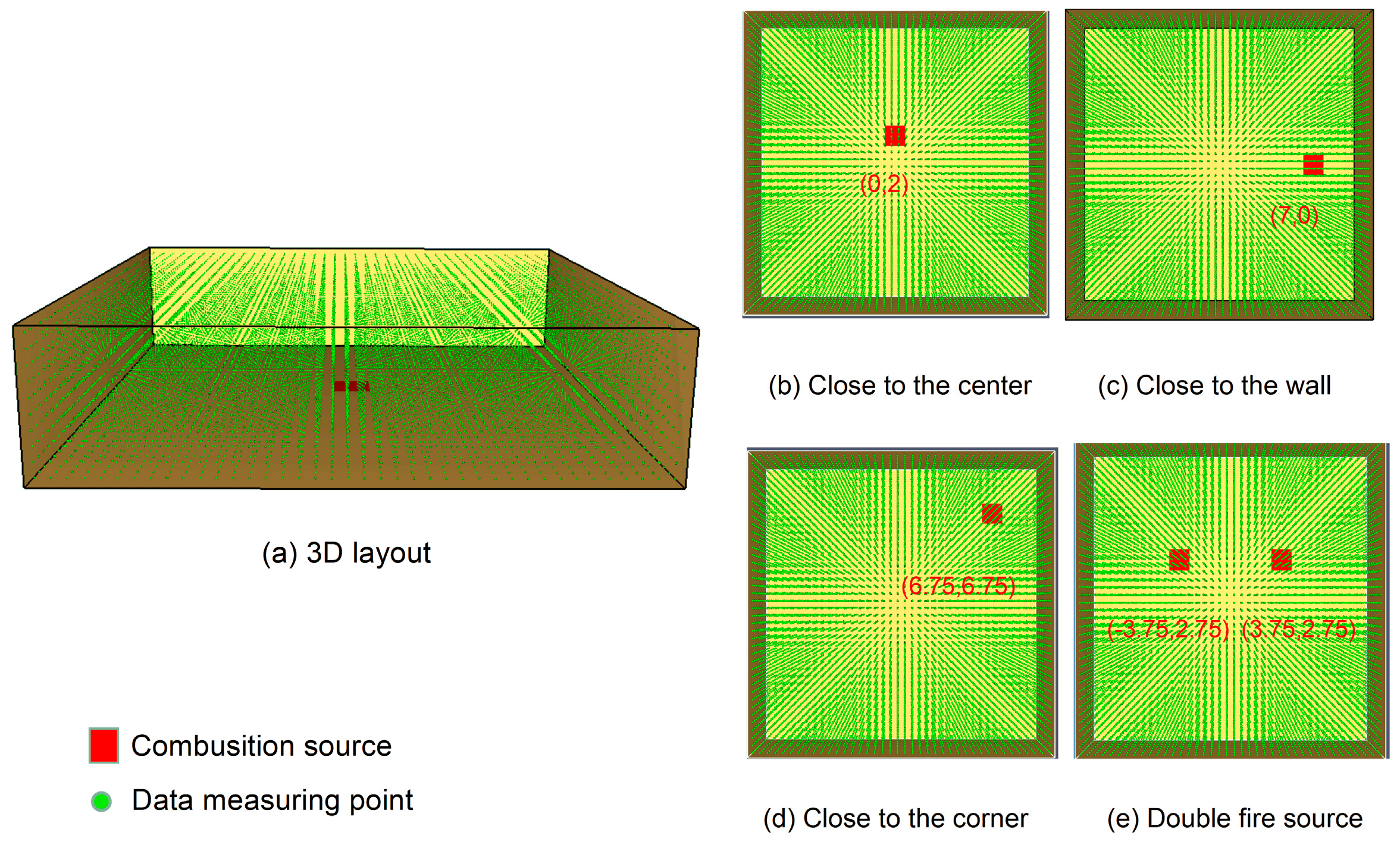

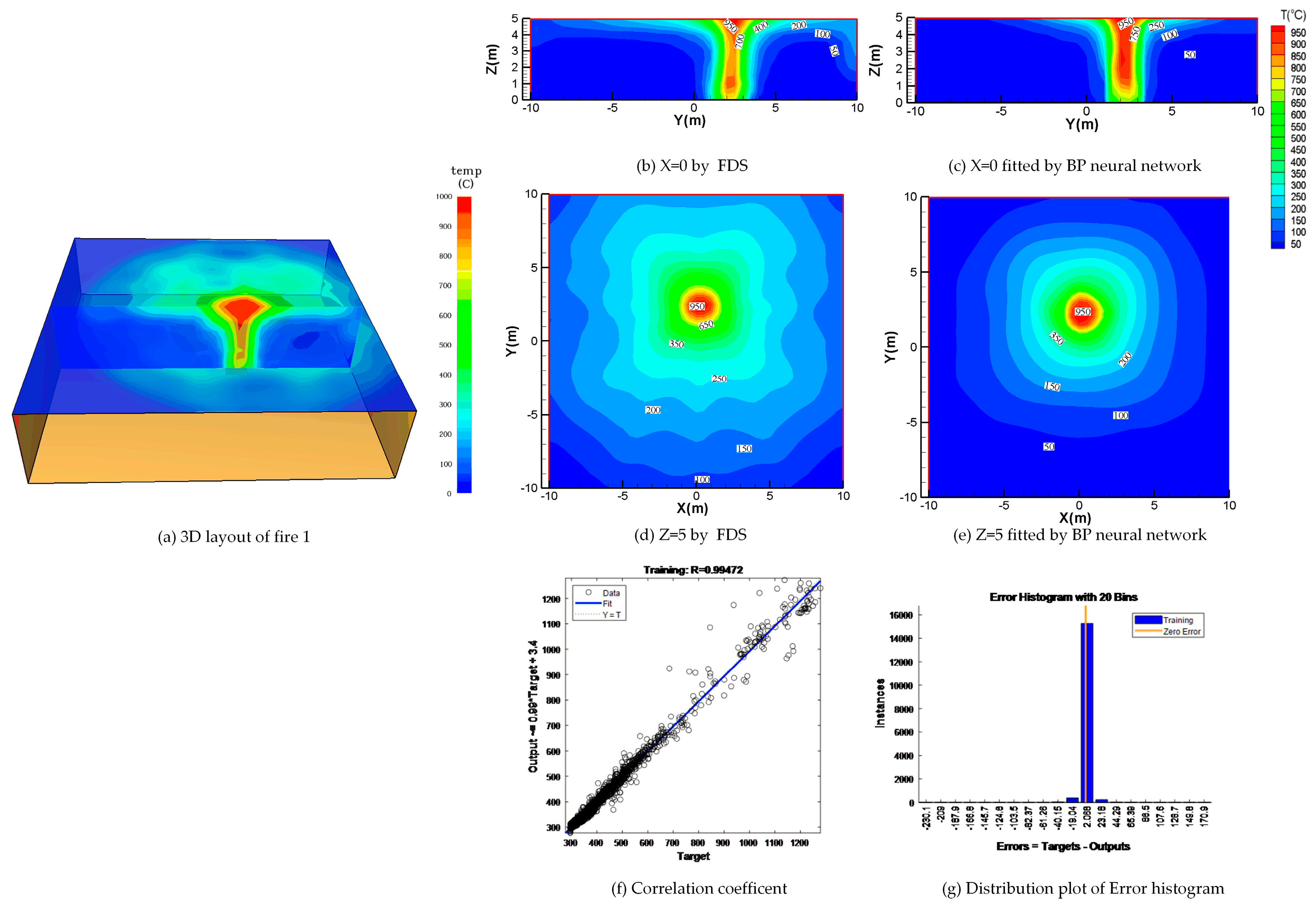




| Fire | Location of Fire Source (m) | Overall Size (m³) | Mesh Size (m³) | Fire Source Size (m2) | Initial Temperature (K) | Burning Material | Ignition Source Power (kW/m2) |
|---|---|---|---|---|---|---|---|
| Close to the center | (0,2,0) | 20 × 20 × 5 | 0.5 × 0.5 × 0.5 | 1.5 × 1.5 | 293.15 | Polyurethane _GM27 | 8000 |
| Close to the wall | (7,0,0) | ||||||
| Close to the corner | (6.75,6.75,0) | ||||||
| Double fire source | (−3.75,2.75,0), (3.75,2.75,0) |
| Fire | Coefficient of Determination R | Center Value of Error (K) | Error Distribution Proportion |
|---|---|---|---|
| Close to the center | 0.99472 | 2.068 | 93% |
| Close to the wall | 0.99507 | 6.189 | 93% |
| Close to the corner | 0.99726 | −0.951 | 93% |
| Double fire source | 0.99607 | −7.868 | 80% |
| Reconstruction Plane | Size of the Plane (m2) | Grid Division | Number of Acoustic Transceivers | Number of Valid Paths |
|---|---|---|---|---|
| Z = 2.5 | 20 × 20 | 9 × 9, 10 × 10, 11 × 11 | 20 | 130 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, H.; Chai, L.; Yang, X.; Gao, Z.; Yao, H.; Lou, Z.; Song, H.; Bai, Z.; Wen, J. Study on the Location Determination of Building Fire Points Based on Acoustic CT Temperature Measurement. Fire 2023, 6, 353. https://doi.org/10.3390/fire6090353
Qin H, Chai L, Yang X, Gao Z, Yao H, Lou Z, Song H, Bai Z, Wen J. Study on the Location Determination of Building Fire Points Based on Acoustic CT Temperature Measurement. Fire. 2023; 6(9):353. https://doi.org/10.3390/fire6090353
Chicago/Turabian StyleQin, Hengjie, Lingling Chai, Xinzheng Yang, Zihe Gao, Haowei Yao, Zhen Lou, Huaitao Song, Zhenpeng Bai, and Jiangqi Wen. 2023. "Study on the Location Determination of Building Fire Points Based on Acoustic CT Temperature Measurement" Fire 6, no. 9: 353. https://doi.org/10.3390/fire6090353
APA StyleQin, H., Chai, L., Yang, X., Gao, Z., Yao, H., Lou, Z., Song, H., Bai, Z., & Wen, J. (2023). Study on the Location Determination of Building Fire Points Based on Acoustic CT Temperature Measurement. Fire, 6(9), 353. https://doi.org/10.3390/fire6090353







