Modelling and Numerical Simulation of a Compartment Fire: Flow Rate Behaviour at Opening
Abstract
1. Introduction
2. Materials and Methods
2.1. Froude Modelling
2.2. CFD Code
2.3. Experimental Configuration
The Experimental Protocol
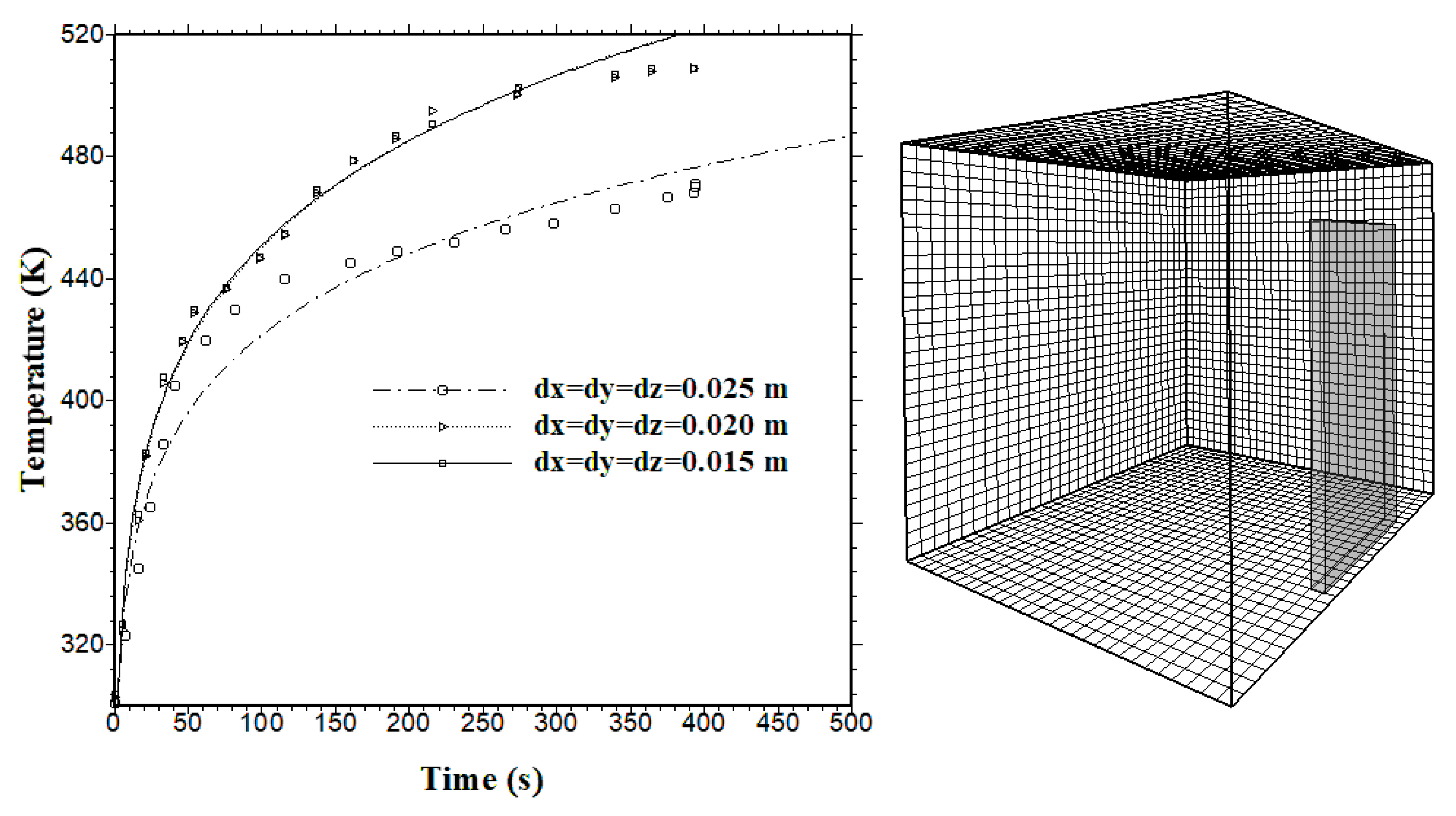
2.4. Sensitivity of the Model Mesh
3. Results and Discussion
3.1. Experimental Results and Interpretations
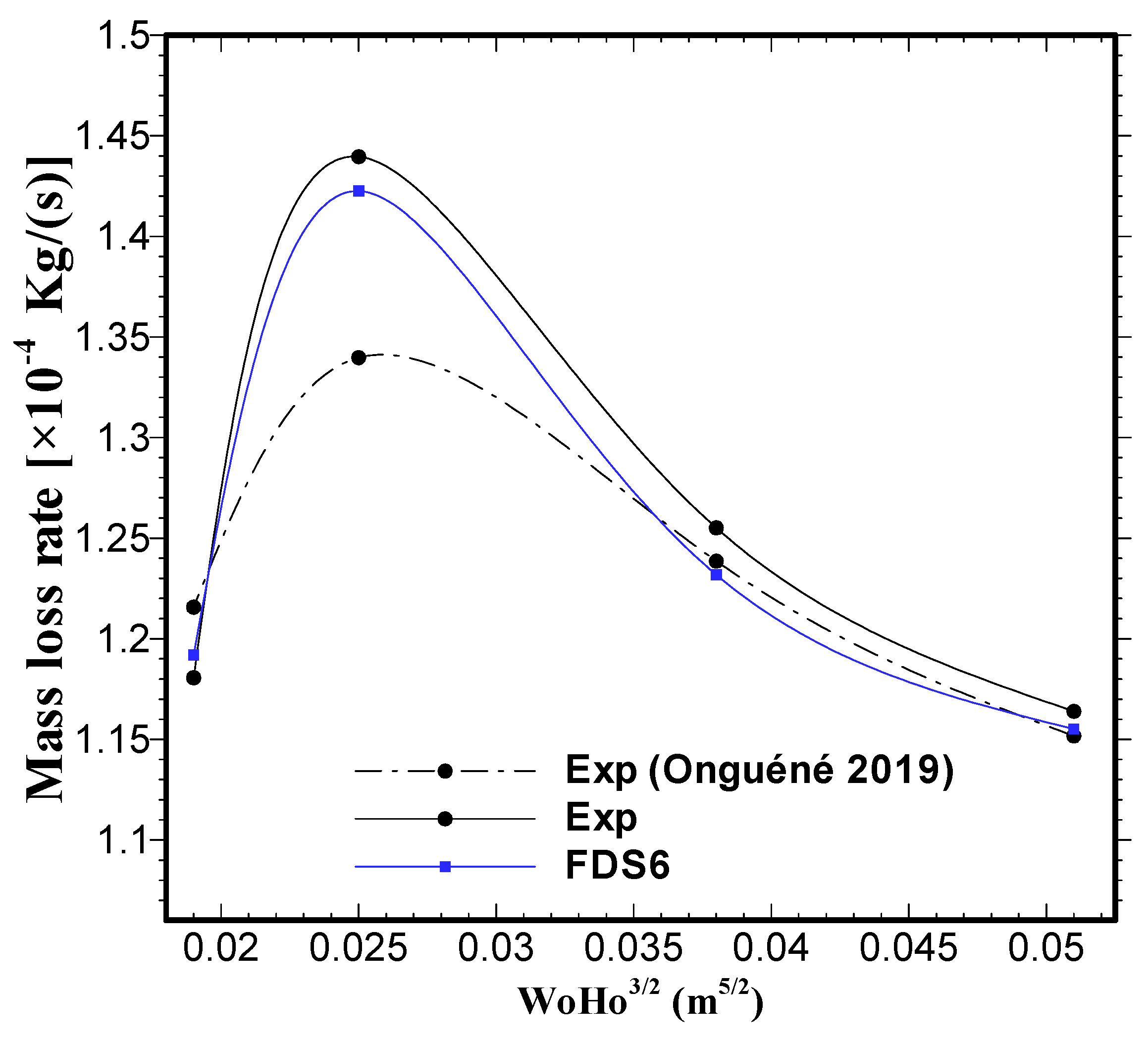
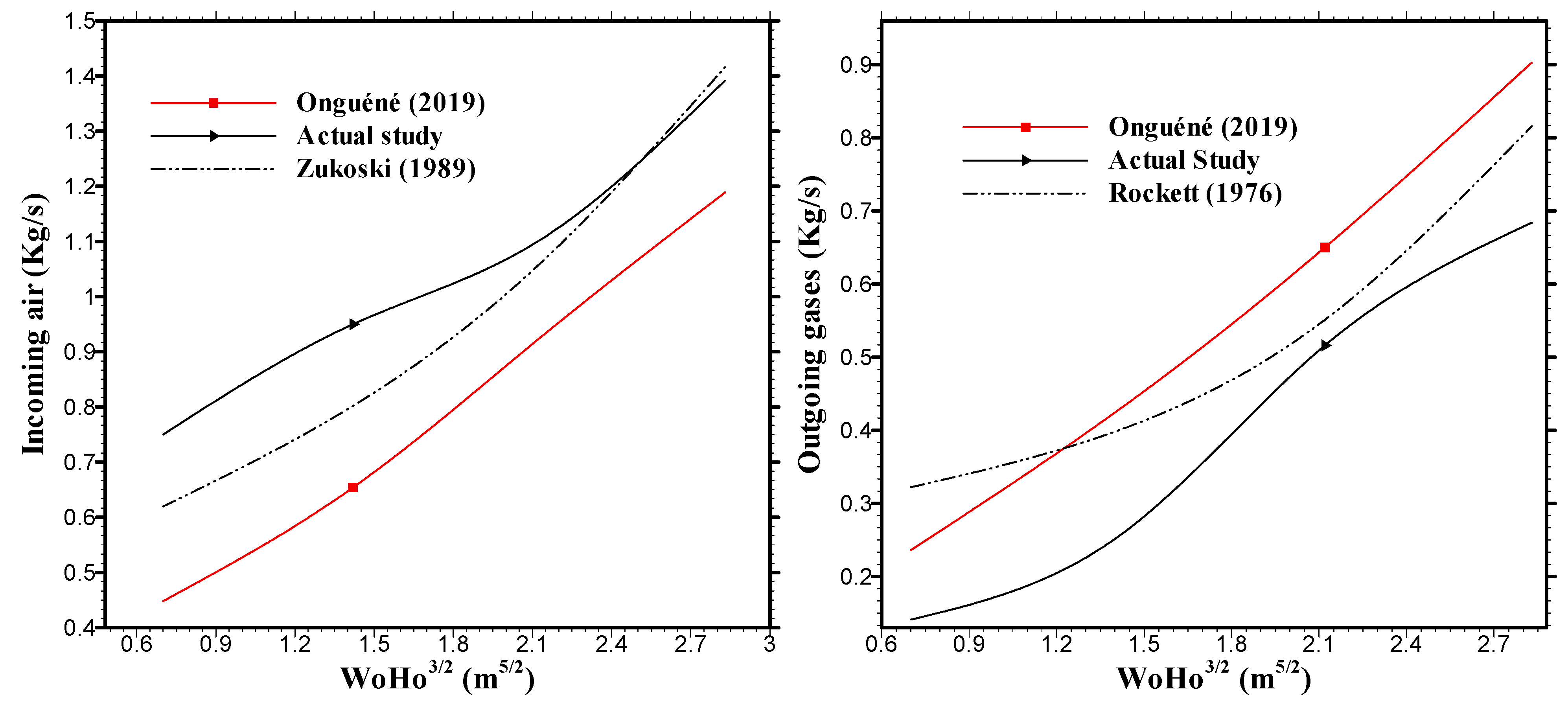
Influence of the Ventilation Factor on the Fuel Combustion Rate
3.2. Numerical Simulation
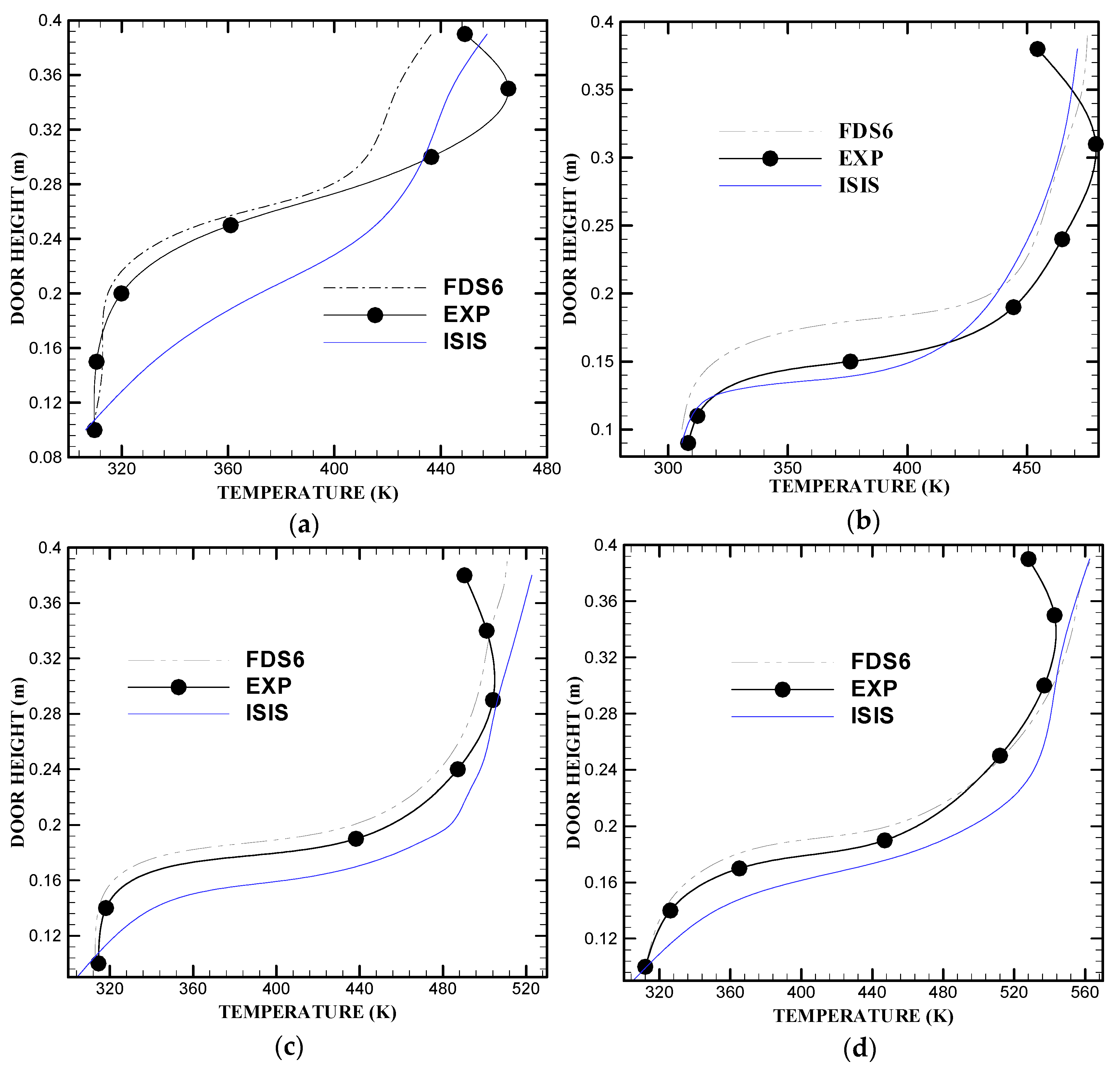
3.2.1. Temperature Profiles along the Door as the Door Width Varies
Number of benchmarks: 7
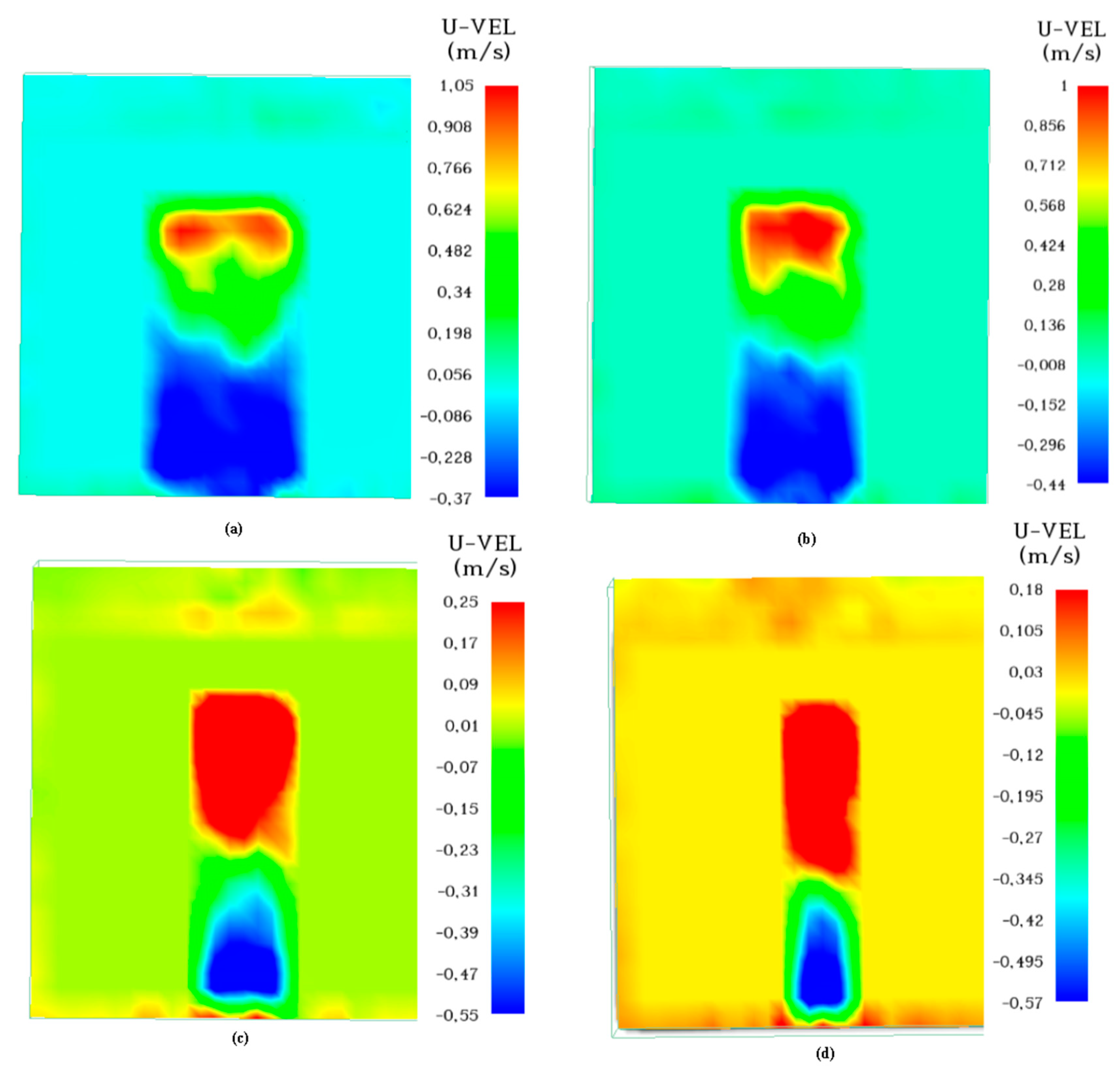
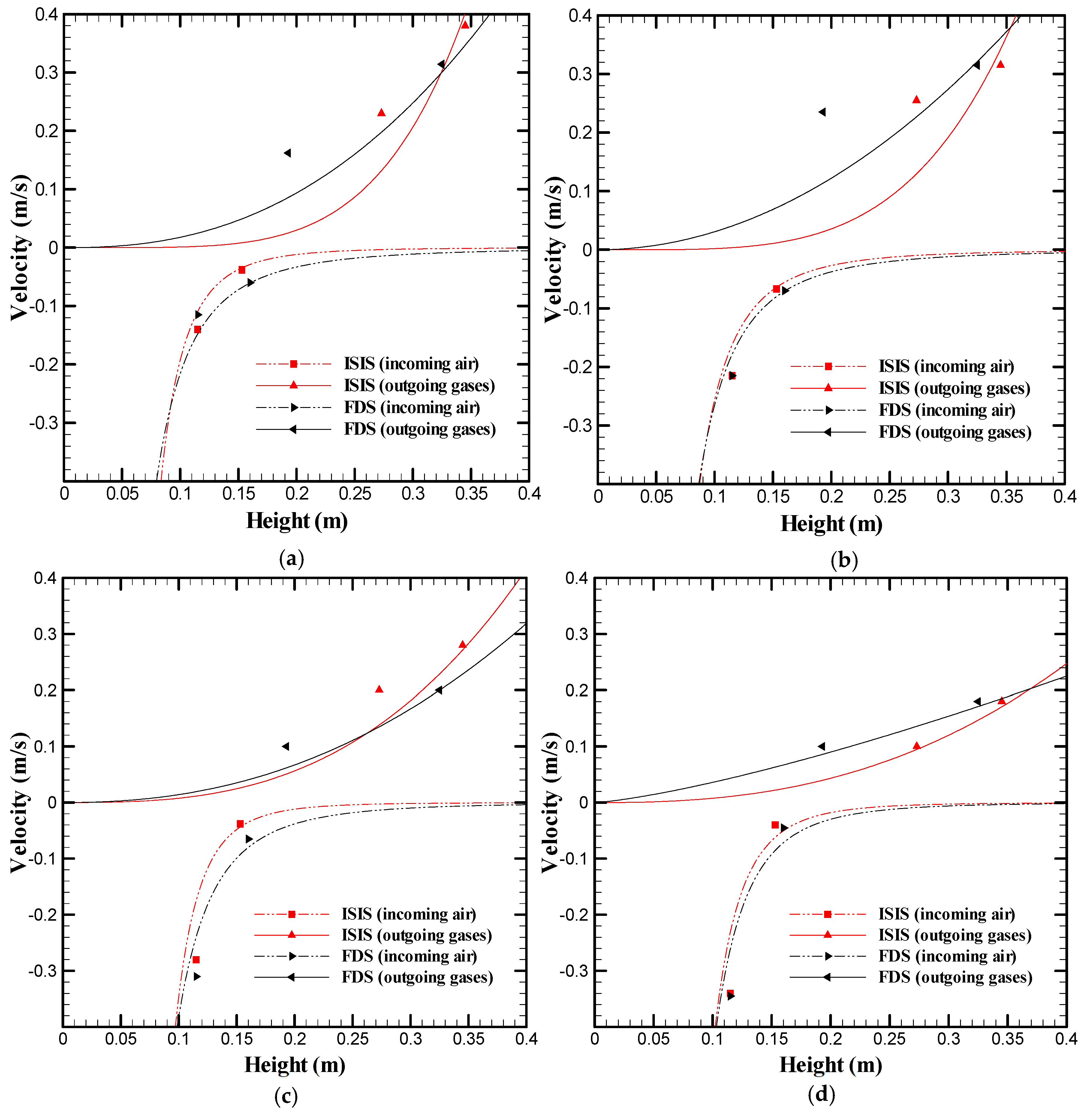
3.2.2. Velocities Fields at the Door
Number of benchmarks: 10
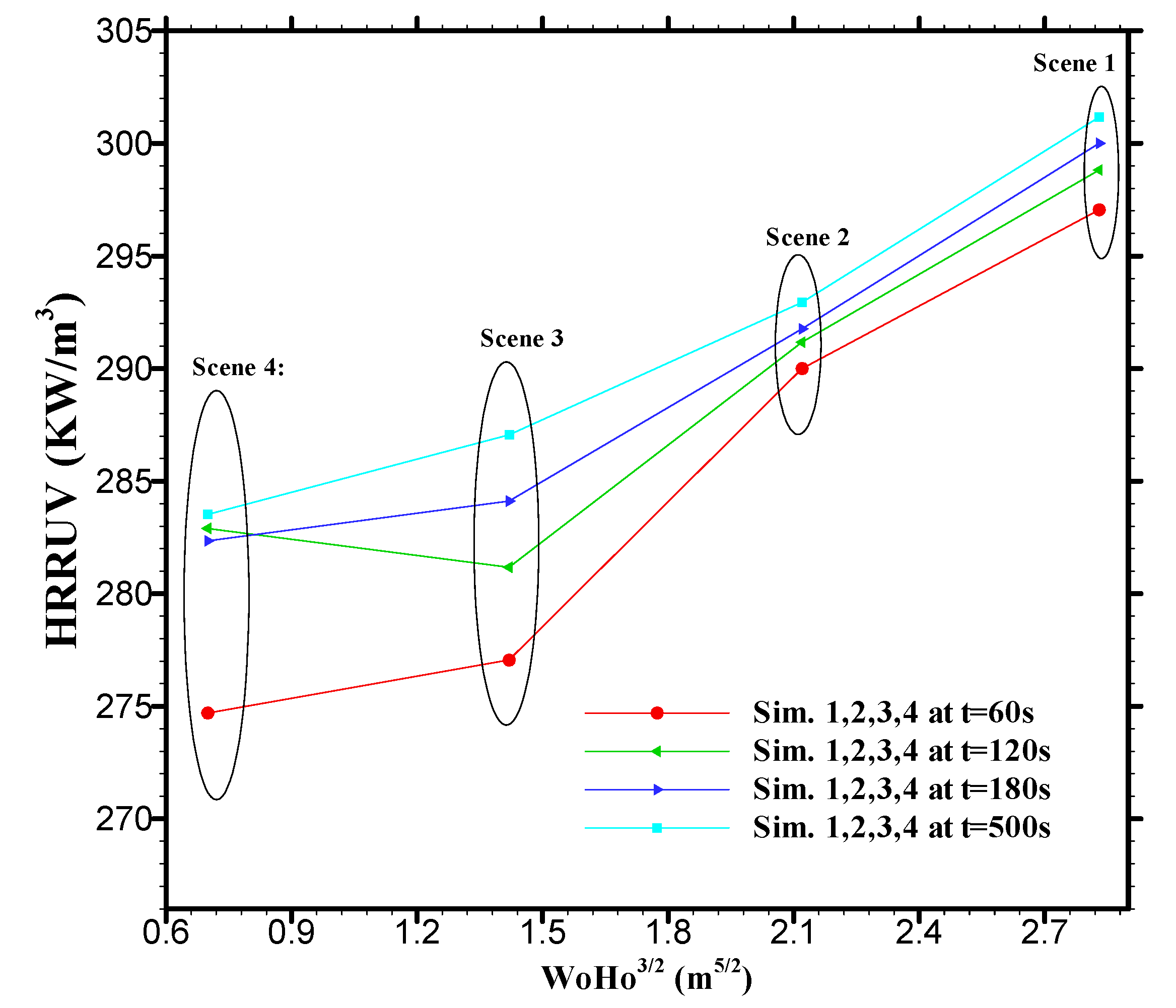
3.2.3. Influence of the Ventilation Factor on the Power Released Inside the Compartment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Ain-Aout | [m2] | Surface area of the opening of a hot air and gas compartment |
| W0 | [m] | Width of the opening |
| H0 | [m] | Height of the opening |
| Af | [m2] | Fire plane surface |
| ΔHc,eff | [KJ/Kg] | Effective heat of combustion |
| Cd | Flow coefficient (0.7) | |
| cp | [J·kg−1·K−1] | Heat capacity by mass at constant pressure |
| W | [m3] | Initial volume of fuel oil |
| D* | [m] | Characteristic diameter of the fire |
| [Kg/s] | Mass loss rate of the fuel | |
| Ta-Tg | [k] | Temperature of incoming air and hot exhaust gases |
| Hin-Hout | [m] | Height of hot gases and air |
| [Kg/m3] | Fluid density | |
| fr | Fraction of the enthalpy of combustion of vapours transferred back to the surface of the material by radiation | |
| [W/m·K] | Thermal conductivity of the wall | |
| h | [W·m2·K−1] | Convective transfer coefficient |
| Hk | [kW·m−2·K−1] | Ratio of the thermal conductivity of a material to its thickness |
| Emissivity of hot gases in the enclosure | ||
| tb | [s] | Average fire burning duration |
| Combustion efficiency | ||
| ζ = 5.67 × 10−8 | W·m−2·K−4 | Stefan–Boltzmann constant |
| g = 9.81 | m·s−2 | Gravity acceleration |
| Γ = 1.4 | Heat capacity ratio for air | |
| [m/s] | Maximal velocity of incoming gases | |
| [m/s] | Maximal velocity of outgoing gases | |
| Combustion efficiency (0.8) | ||
| [m/s] | Regression velocity | |
| L | (m) | Characteristic length |
| D | [m/s] | Characteristic velocity |
| [kg/s] | Mass flow rate of cool air | |
| [kg/s] | Mass flow rate of smoke | |
| [m/s] | Maximal velocity of incoming air | |
| [m/s] | Maximal velocity of outgoing gases | |
| W | m3 | Initial volume of fuel |
| Zn | m | Height of discontinuity |
References
- Sahu, D.; Kumar, S.; Shorab, J.; Gupta, A. Full scale experimental and numerical studies on effect of ventilation in an enclosure diesel pool fire. Build. Simul. 2017, 10, 351–364. [Google Scholar] [CrossRef]
- Peatross, M.J.; Beyler, C.L. Ventilation Effects on Compartment Fire Characterization. FIRE Saf. Sci. 1997, 5, 403–414. [Google Scholar] [CrossRef]
- Au, S.K.; Wangb, Z.-H.; Siu-Ming, L. Compartment fire risk analysis by advanced Monte Carlo simulation. Eng. Struct. 2006, 29, 2381–2390. [Google Scholar] [CrossRef]
- Kawagoe, K. Fire Behavior in Rooms; Building Research Institute: Tokyo, Japan, 1958. [Google Scholar]
- Emmons, J.; Prahl, H.W. Fire induced flow through an opening. Combust. Flame 1975, 25, 369–385. [Google Scholar]
- Zukoski, B.E.; Kubota, T.; Cetegen, B. Entrainment in fire plumes. Fire Saf. J. 1981, 3, 107–121. [Google Scholar] [CrossRef]
- Rockett, A. Fire induced gas flow in an enclosure. Combust. Sci. Technol. 1976, 12, 165–175. [Google Scholar] [CrossRef]
- Meskéoulé, F.; Ngayihi, A.; Zaida, J.T.; Mvogo, P.O.; Mouangue, R. Experimental Study on Fire Behaviour in Room following the Disposition of Openings. J. Combust. 2020. [Google Scholar] [CrossRef]
- Babrauska, V.; Peacock, R.D. Heat Release Rate: The Single Most Important Variable in Fire Hazard. Fire Saf. J. 1992, 18, 255–272. [Google Scholar] [CrossRef]
- Quintiere, J.G. Fire behavior in building compartments. Proc. Combust. Inst. 2002, 29, 181–193. [Google Scholar] [CrossRef]
- Mokhtarzadeh-Dehghan, M. Numerical simulation and comparison with experiment of natural convection between two floors of a building model via a stairwell. Int. J. Heat Mass Transf. 2011, 54, 19–33. [Google Scholar] [CrossRef]
- Mcdermott, R. Fire Dynamics Simulator Technical Reference Guide Volume 2: Verification, 6th ed.; National Institute of Standards and Technology: Gaithersburg, ML, USA, 2013.
- Mvogo, P.O.; Mouangue, R.; Zaida, J.T.; Obounou, M.; Fouda, H.E. Building fire: Experimental and numerical studies on behaviour of flows at opening. J. Combust. 2019, 2019, 2535073. [Google Scholar] [CrossRef]
- Harrack, S.H.; Koutaiba, E.M.; Mehaddi, R.; Boulet, P.; Becker, S. Impact of the room geometry on the smoke filling time due to a fire plume. J. Phys. Conf. Ser. Pap. 2018, 1107, 042022. [Google Scholar] [CrossRef]
- Harrak, S. Contributions à l’étude des écoulements de Fumées dans un Bâtiment en Situation d ’incendie Mécanique des Fluides [physics.class-ph]. Doctoral Dissertation, Université de Lorraine, Nancy, France, 2019. [Google Scholar]
- Chanson, H.; Murzyn, F. Froude similitude and scale effects affecting air entrainment in hydraulic jumps. In World Environmental and Water Resources Congress 2008: Ahupua’A; American Society of Civil Engineers: Reston, VA, USA, 2008; pp. 1–10. [Google Scholar]
- Mcgrattan, K.; Mcdermott, R.; Hostikka, S.; Floyd, J.; Vanella, M. Fire Dynamics Simulator (Version 6) User’s Guide, 6th ed.; National Institute of Standards and Technology: Gaithersburg, MA, USA, 2019. [CrossRef]
- Mcdermott, R. Fire Dynamics Simulator Technical Reference Guide Volume 1: Mathematical Model, 6th ed.; National Institute of Standards and Technology: Gaithersburg, ML, USA, 2019. [CrossRef]
- Bounagui, A.; Benichou, N.; Cartney, C.M. Optimizing the grid size used in CFD simulations to evaluate Fire Safety in House. In Proceedings of the 3rd NRC CFD Symposium on Computational Fluid Dynamics, High Performance Computing and Virtual Reality, Ottawa, ON, Canada, 4 December 2003. [Google Scholar]
- Xin, Y.; Gore, J.; Grattan, K.M. Large Eddy Simulation of Buyoant Turbulent pool Fires. In Proceedings of the 29th International Symposium on Combustion, Sapporo, Japan, 2–26 July 2002. [Google Scholar]
- Babrauskas, V. Free-burning fires. Fire Saf. J. 1986, 11, 33–51. [Google Scholar] [CrossRef]
- Jolly, S. Scale Modeling of Fires with Emphasis on room Flashover Phenomenon. Fire Saf. J. 1992, 18, 139–182. [Google Scholar] [CrossRef]
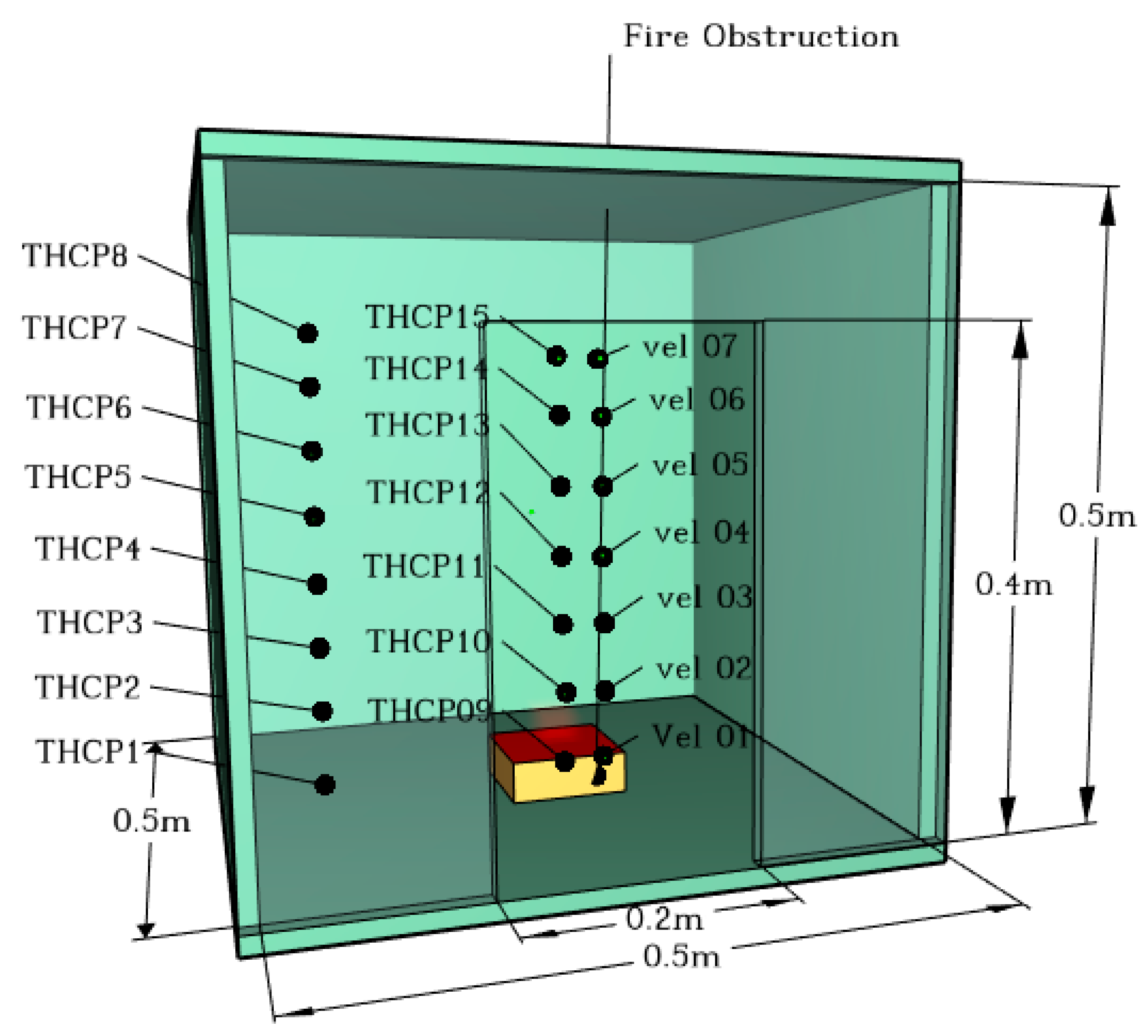

| Thermocouples/Devices for Velocity | x [m] | y [m] | z [m] |
|---|---|---|---|
| T1 | 0.35 | 0.06 | 0.06 |
| T2 | 0.35 | 0.06 | 0.12 |
| T3 | 0.35 | 0.06 | 0.17 |
| T4 | 0.35 | 0.06 | 0.22 |
| T5 | 0.35 | 0.06 | 0.27 |
| T6 | 0.35 | 0.06 | 0.32 |
| T7 | 0.35 | 0.06 | 0.37 |
| T8 | 0.35 | 0.06 | 0.41 |
| T09–Vel 01 | 0.48 | 0.22 | 0.10 |
| T10–Vel 02 | 0.48 | 0.22 | 0.15 |
| T11–Vel 03 | 0.48 | 0.22 | 0.20 |
| T12–Vel 04 | 0.48 | 0.22 | 0.25 |
| T13–Vel 05 | 0.48 | 0.22 | 0.30 |
| T14–Vel 06 | 0.48 | 0.22 | 0.35 |
| T15–Vel 07 | 0.48 | 0.22 | 0.39 |
| Case Study | Mesh Size | Temperature |
|---|---|---|
| Simulation 1 | 0.20 × 0.20 × 0.20 | 479 °C |
| Simulation 2 | 0.14 × 0.14 × 0.14 | 593 °C |
| Simulation 3 | 0.10 × 0.10 × 0.10 | 962 °C |
| Simulation 4 | 0.08 × 0.08 × 0.08 | 967 °C |
| Parameters | Simulations (1, 2, 3 and 4) |
|---|---|
| Initial temperatures (°C) | 20.0 |
| Relative humidity (%) | 40 |
| Typical simulation | LES, transient |
| The geometry of the domain (m3) | |
| Simulation time (s) | 1000 |
| Mesh sizes (m) | |
| Turbulence | Smagorinsky model |
| Smagorinsky constant | |
| Radiation loss fraction | 0.25 |
| Input | HRRUA |
| Boundary conditions | Convection–Conduction ( |
| H0 [m] | W0 [m] | [s] | ||||
|---|---|---|---|---|---|---|
| Scene 1 | 0.40 | 0.20 | 0.051 | 564 | 1.0691 | 1.1639 |
| Scene 2 | 0.40 | 0.15 | 0.038 | 523 | 1.1529 | 1.2551 |
| Scene 3 | 0.40 | 0.10 | 0.025 | 456 | 1.3224 | 1.4396 |
| Scene 4 | 0.40 | 0.075 | 0.019 | 556 | 1.0845 | 1.1806 |
| Euclidean Standard | ||||
|---|---|---|---|---|
| Greatness | Scene 1: W = 0.2 m | Scene 2: W = 0.15 m | Scene 3: W = 0.10 m | Scene 4: W = 0.075 m |
| 651.93 | 729.04 | 793.42 | 732.65 | |
| 640.98 | 724.02 | 789.42 | 733.71 | |
| 1.68 | 0.27 | 0.5 | -0.14 | |
| 0.999 | 0.998 | 0.999 | 0.999 | |
| 651.93 | 729.04 | 793.42 | 732.65 | |
| 650.31 | 667.53 | 763.11 | 763.56 | |
| 0.24 | 8.43 | 3.82 | -4.21 | |
| 0.99 | 0.997 | 0.998 | 0.999 | |
| Euclidean Standard | ||||||||
|---|---|---|---|---|---|---|---|---|
| Greatness | Scene 1: W = 0.2 m | Scene 2: W = 0.15 m | Scene 3: W = 0.10 m | Scene 4: W = 0.075 m | ||||
| Inc.air | Out.gases | Inc.air | Out.gases | Inc.air | Out.gases | Inc.air | Out.gases | |
| 0.571 | 0.19 | 0.678 | 0.299 | 0.878 | 0.137 | 0.930 | 0.161 | |
| 0.543 | 0.29 | 0.686 | 0.318 | 0.819 | 0.249 | 0.931 | 0.174 | |
| Ecart relatif ( | 2.87 | −10.12 | −0.86 | −1.87 | 5.86 | −11.19 | −0.08 | −1.36 |
| 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 | 0.97 | |
| Scene 1 | 0.051 | 4.19 | 0.28 | 0.37 | 0.12 | 0.39 |
| Scene 2 | 0.038 | 4.51 | 0.24 | 0.44 | 0.16 | 0.31 |
| Scene 3 | 0.025 | 5.17 | 0.25 | 0.55 | 0.15 | 0.25 |
| Scene 4 | 0.019 | 4.24 | 0.25 | 0.57 | 0.15 | 0.18 |
| Scene | [KW] | [m2] | [m/s] | [kg/s] | [m2] | [m/s] | [kg/s] | |
|---|---|---|---|---|---|---|---|---|
| Scene 1 | 2.83 | 235.4 | 1.35 | 0.825 | 1.392 | 0.63 | 0.869 | 0.684 |
| Scene 2 | 2.12 | 253.4 | 0.90 | 0.984 | 1.100 | 0.60 | 0.691 | 0.516 |
| Scene 3 | 1.42 | 290.4 | 0.62 | 1.226 | 0.950 | 0.37 | 0.557 | 0.257 |
| Scene 4 | 0.70 | 238.2 | 0.46 | 1.271 | 0.750 | 0.28 | 0.401 | 0.141 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iya, A.E.-k.; Epée, A.F.; Mvogo, P.O.; Zaida, J.T.; Mouangue, R. Modelling and Numerical Simulation of a Compartment Fire: Flow Rate Behaviour at Opening. Fire 2023, 6, 185. https://doi.org/10.3390/fire6050185
Iya AE-k, Epée AF, Mvogo PO, Zaida JT, Mouangue R. Modelling and Numerical Simulation of a Compartment Fire: Flow Rate Behaviour at Opening. Fire. 2023; 6(5):185. https://doi.org/10.3390/fire6050185
Chicago/Turabian StyleIya, Ahmed El-kebir, Alban Fabrice Epée, Philippe Onguéné Mvogo, Justin Tégawendé Zaida, and Ruben Mouangue. 2023. "Modelling and Numerical Simulation of a Compartment Fire: Flow Rate Behaviour at Opening" Fire 6, no. 5: 185. https://doi.org/10.3390/fire6050185
APA StyleIya, A. E.-k., Epée, A. F., Mvogo, P. O., Zaida, J. T., & Mouangue, R. (2023). Modelling and Numerical Simulation of a Compartment Fire: Flow Rate Behaviour at Opening. Fire, 6(5), 185. https://doi.org/10.3390/fire6050185






