Flaming Ignition of PMMA, Pine Wood and Pine Needle by External Radiation: Autoignition and Radiant Distance Effect
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Conditions
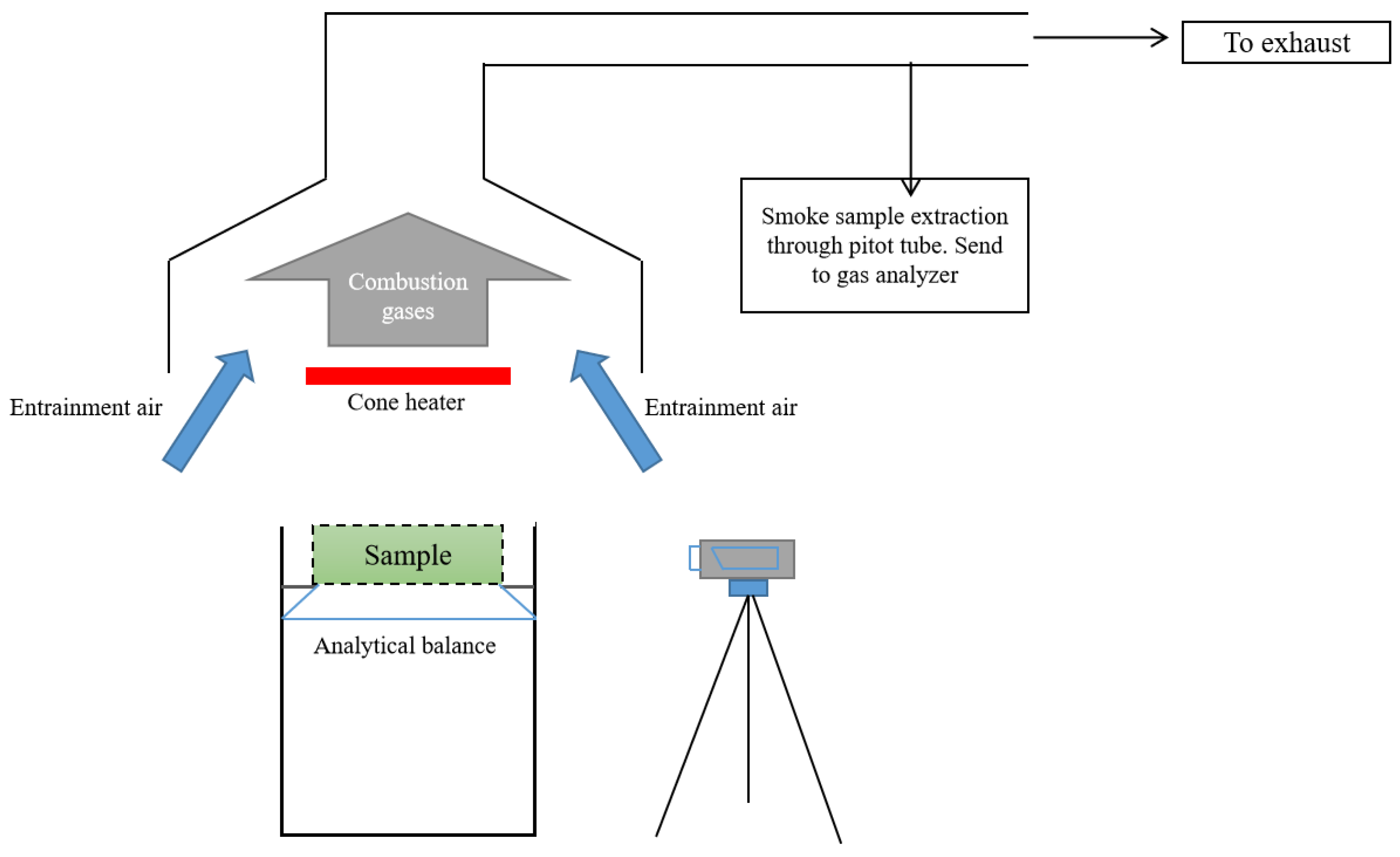
2.2. Experimental Setup
3. Results
3.1. Ignition Phenomena
3.1.1. Non-Charring Fuel (PMMA)
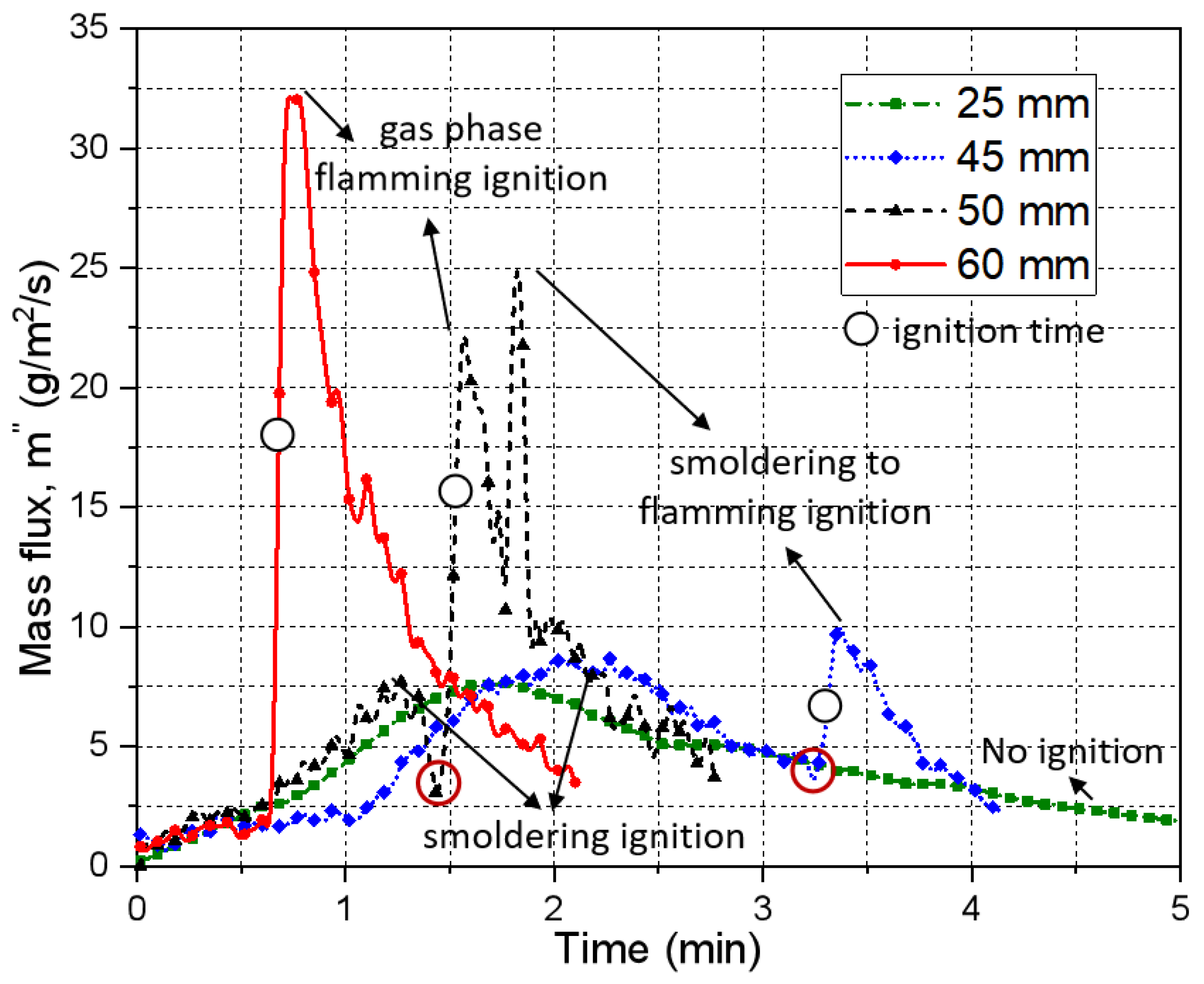
3.1.2. Porous Charring Fuel (Pine Needle)
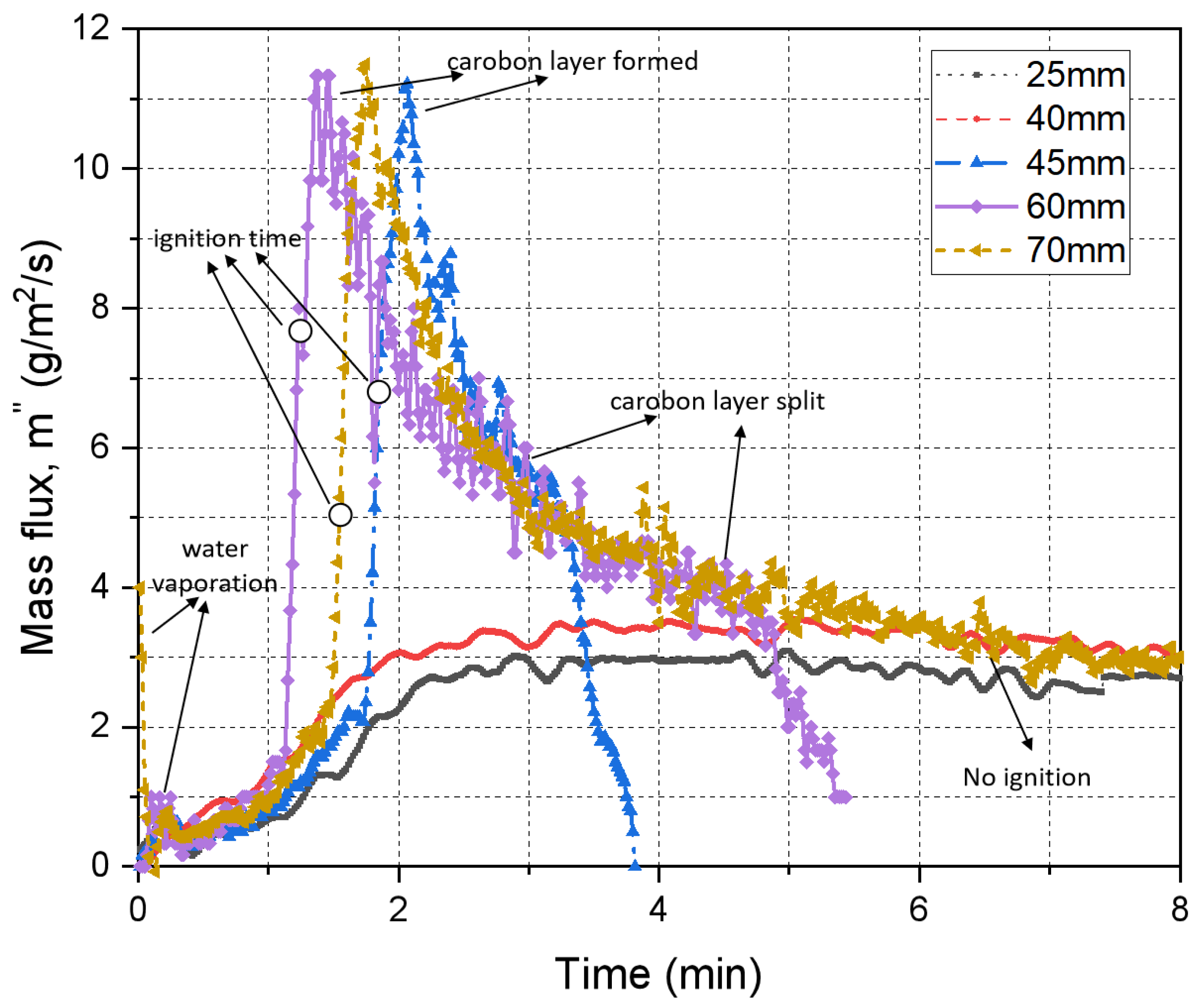
3.1.3. High-Density Charring Fuel (Wood)
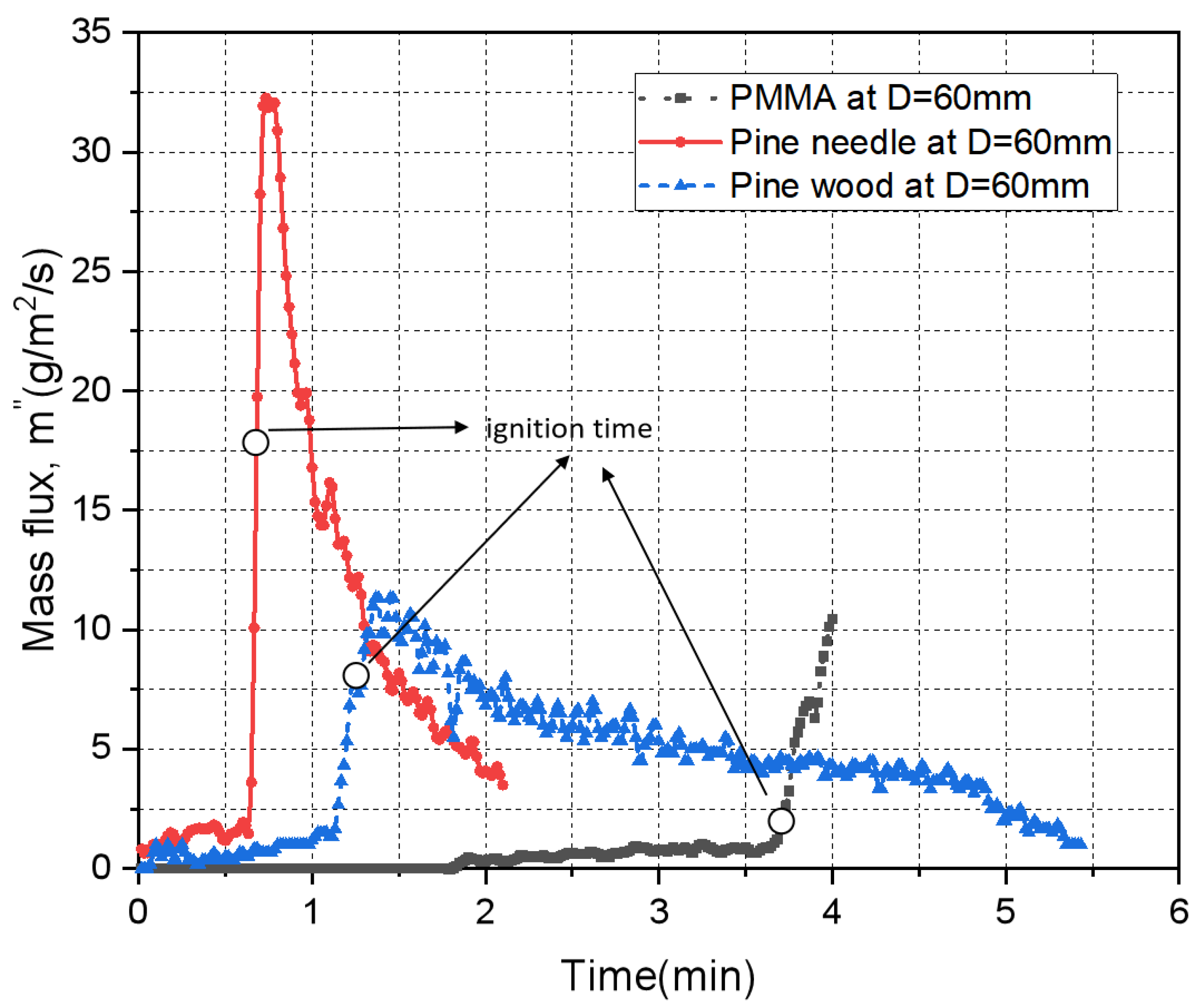
3.1.4. Fuel Type Influence
4. Discussion
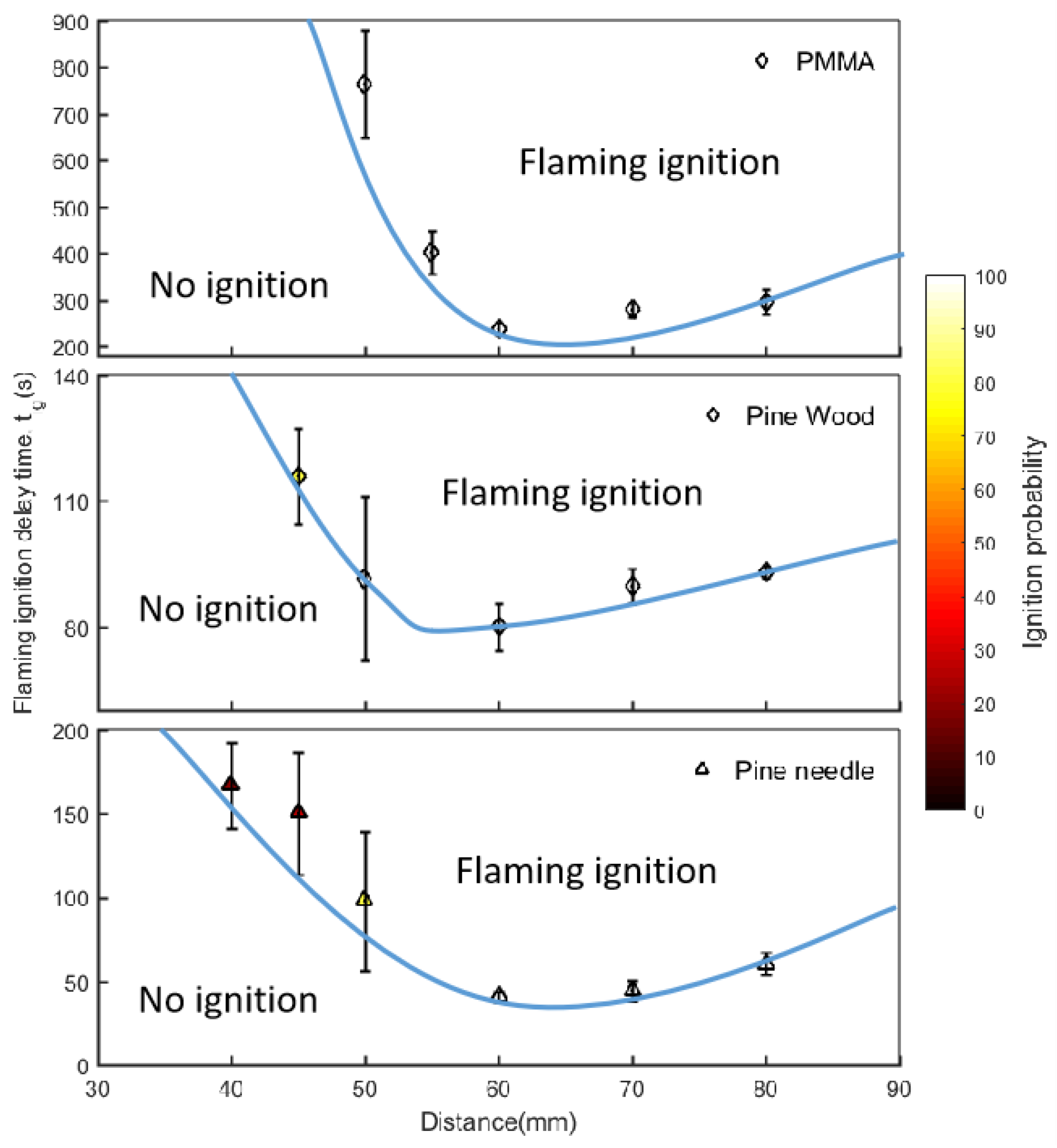
4.1. The Ignition Limit of Flaming
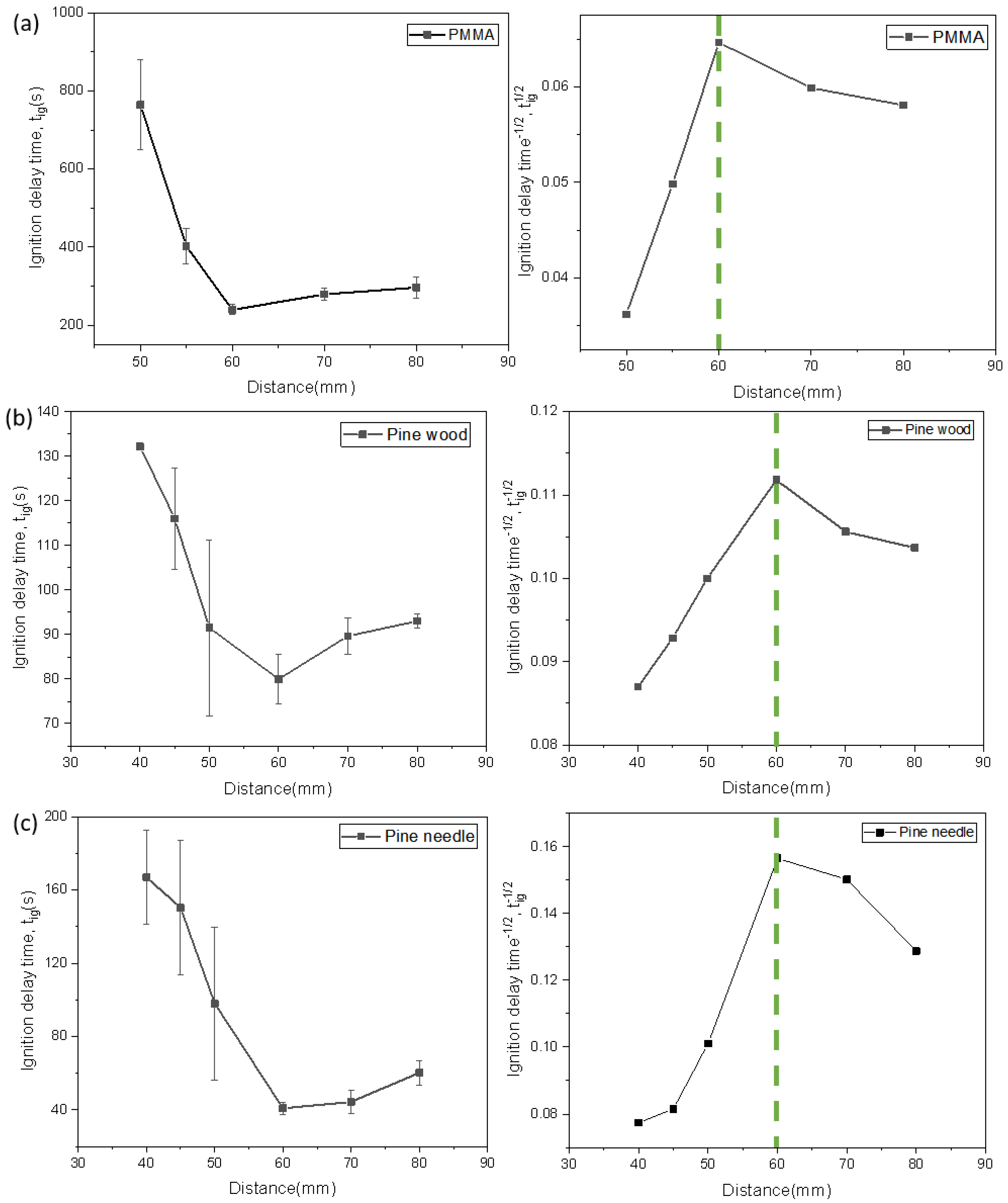
4.2. Radiant Distance Effect on the Flaming Ignition Behaviors
5. Conclusions
- (1)
- The difference in autoignition behaviors at different radiant distances is explained by the coupled effect of the different gas-phase temperatures and the concentration dilution of the combustible pyrolysis volatiles.
- (2)
- The relationship between ignition delay time, tig and distance D is an approximate inverted U-shaped curve. One marked difference between materials was the range of ignition delay time. It is also observed that all materials have a critical position of ignition delay time, where the ignition delay time is shortest. It can be seen from the experimental results that this position is 60 mm away from the cone heater.
- (3)
- For experimental results of PMMA and pine wood, when D ≤ 60 mm, the relationship between and D is linear, and the predicted results are somewhat nonlinear. When D > 60 mm, there is nonlinear relationship between D and . This also provides a theoretical prediction of the critical radiant distance.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mell, W.E.; Manzello, S.L.; Maranghides, A.; Butry, D.; Rehm, R.G. The wildland–urban interface fire problem–current approaches and research needs. Int. J. Wildland Fire 2010, 19, 238–251. [Google Scholar] [CrossRef]
- Cohen, J.D. What is the Wildland Fire Threat to Homes? School of Forestry, Northern Arizona University: Flagstaff, AZ, USA, 2000. [Google Scholar]
- Kashiwagi, T. Experimental observation of radiative ignition mechanisms. Combust. Flame 1979, 34, 231–244. [Google Scholar] [CrossRef]
- Simms, D.L.; Law, M. The ignition of wet and dry wood by radiation. Combust. Flame 1967, 11, 377–388. [Google Scholar] [CrossRef]
- Tsai, T.H.; Li, M.J.; Shih, I.Y.; Jih, R.; Wong, S.C. Experimental and numerical study of autoignition and pilot ignition of PMMA plates in a cone calorimeter. Combust. Flame 2001, 124, 466–480. [Google Scholar] [CrossRef]
- Boonmee, N.; Quintiere, J.G. Glowing and flaming autoignition of wood. Proc. Combust. Inst. 2002, 29, 289–296. [Google Scholar] [CrossRef]
- Shi, L.; Chew, M.Y.L. Experimental study of woods under external heat flux by autoignition. J. Therm. Anal. Calorim. 2013, 111, 1399–1407. [Google Scholar] [CrossRef]
- Shi, L.; Chew, M.Y.L. Fire behaviors of polymers under autoignition conditions in a cone calorimeter. Fire Saf. J. 2013, 61, 243–253. [Google Scholar] [CrossRef]
- Simeoni, A.; Thomas, J.C.; Bartoli, P.; Borowieck, P.; Reszka, P.; Colella, F.; Santoni, P.A.; Torero, J.L. Flammability studies for wildland and wildland–urban interface fires applied to pine needles and solid polymers. Fire Saf. J. 2012, 54, 203–217. [Google Scholar] [CrossRef]
- Yang, L.; Zhou, Y.; Wang, Y.; Dai, J.; Deng, Z.; Zhou, X. Autoignition of solid combustibles subjected to a uniform incident heat flux: The effect of distance from the radiation source. Combust. Flame 2011, 158, 1015–1017. [Google Scholar]
- McAllister, S.; Finney, M. Autoignition of wood under combined convective and radiative heating. Proc. Combust. Inst. 2017, 36, 3073–3080. [Google Scholar] [CrossRef]
- Tihay-Felicelli, V.; Santoni, P.A.; Barboni, T.; Leonelli, L. Autoignition of dead shrub twigs: Influence of diameter on ignition. Fire Technol. 2016, 52, 897–929. [Google Scholar] [CrossRef]
- Hadden, R.; Alkatib, A.; Rein, G.; Torero, J.L. Radiant Ignition of Polyurethane Foam: The Effect of Sample Size. Fire Technol. 2014, 50, 673–691. [Google Scholar] [CrossRef]
- Attia, N.F.; Goda, E.S.; Nour, M.A.; Sabaa, M.W.; Hassan, M.A. Novel synthesis of magnesium hydroxide nanoparticles modified with organic phosphate and their effect on the flammability of acrylonitrile-butadiene styrene nanocomposites. Mater. Chem. Phys. 2015, 168, 147–158. [Google Scholar] [CrossRef]
- Huang, G.; Chen, W.; Wu, T.; Guo, H.; Fu, C.; Xue, Y.; Wang, K.; Song, P. Multifunctional graphene-based nano-additives toward high-performance polymer nanocomposites with enhanced mechanical, thermal, flame retardancy and smoke suppressive properties. Chem. Eng. J. 2021, 410, 127590. [Google Scholar] [CrossRef]
- Fang, F.; Song, P.; Ran, S.; Guo, Z.; Wang, H.; Fang, Z. A facile way to prepare phosphorus-nitrogen-functionalized graphene oxide for enhancing the flame retardancy of epoxy resin. Compos. Commun. 2018, 10, 97–102. [Google Scholar] [CrossRef]
- Mindykowski, P.; Fuentes, A.; Consalvi, J.L.; Porterie, B. Piloted ignition of wildland fuels. Fire Saf. J. 2011, 46, 34–40. [Google Scholar] [CrossRef]
- McAllister, S.; Grenfell, I.; Hadlow, A.; Jolly, W.M.; Finney, M.; Cohen, J. Piloted ignition of live forest fuels. Fire Saf. J. 2011, 51, 133–142. [Google Scholar] [CrossRef]
- Porterie, B.; Nicolas, S.; Consalvi, J.L.; Loraud, J.C.; Giroud, F.; Picard, C. Modeling thermal impact of wildland fires on structures in the urban interface. Part 1: Radiative and convective components of flames representative of vegetation fires. Numer. Heat Tranf. A-Appl. 2005, 47, 471–489. [Google Scholar] [CrossRef]
- Consalvi, J.L.; Nmira, F.; Fuentes, A.; Mindykowski, P.; Porterie, B. Numerical study of piloted ignition of forest fuel layer. Proc. Combust. Inst. 2011, 33, 2641–2648. [Google Scholar] [CrossRef]
- Tao, J.; Wang, H. Energy uptake by wood during the ignition under external radiant heat flux. Appl. Therm. Eng. 2017, 124, 294–301. [Google Scholar] [CrossRef]
- Lamorlette, A. Analytical modeling of solid material ignition under a radiant heat flux coming from a spreading fire front. J. Therm. Sci. Eng. Appl. 2014, 6, 044501. [Google Scholar] [CrossRef]
- Vermesi, I.; DiDomizio, M.J.; Richter, F.; Weckman, E.J.; Rein, G. Pyrolysis and spontaneous ignition of wood under transient irradiation: Experiments and a-priori predictions. Fire Saf. J. 2017, 91, 218–225. [Google Scholar] [CrossRef]
- Cohen, J.D. Relating flame radiation to home ignition using modeling and experimental crown fires. Can. J. For. Res. 2004, 34, 1616–1626. [Google Scholar] [CrossRef]
- Reszka, P.; Borowiec, P.; Steinhaus, T.; Torero, J.L. A methodology for the estimation of ignition delay times in forest fire modelling. Combust. Flame 2012, 159, 3652–3657. [Google Scholar] [CrossRef]
- Zárate, L.; Arnaldos, J.; Casal, J. Establishing safety distances for wildland fires. Fire Saf. J. 2008, 43, 565–575. [Google Scholar] [CrossRef]
- Rossi, J.L.; Simeoni, A.; Moretti, B.; Leroy-Cancellieri, V. An analytical model based on radiative heating for the determination of safety distances for wildland fires. Fire Saf. J. 2011, 46, 520–527. [Google Scholar] [CrossRef]
- Billaud, Y.; Kaiss, A.; Consalvi, J.L.; Porterie, B. Monte Carlo estimation of thermal radiation from wildland fires. Int. J. Therm. Sci. 2011, 50, 2–11. [Google Scholar] [CrossRef]
- Wang, S.; Huang, X.; Chen, H.; Liu, N. Interaction between flaming and smouldering in hot-particle ignition of forest fuels and effects of moisture and wind. Int. J. Wildland Fire 2016, 26, 71–81. [Google Scholar] [CrossRef]
- Luche, J.; Rogaume, T.; Richard, F.; Guillaume, E. Characterization of thermal properties and analysis of combustion behavior of PMMA in a cone calorimeter. Fire Saf. J. 2011, 46, 451–461. [Google Scholar] [CrossRef]
- Rhodes, B.T.; Quintiere, J.G. Burning rate and flame heat flux for PMMA in a cone calorimeter. Fire Saf. J. 1996, 26, 221–240. [Google Scholar] [CrossRef]
- Gong, J.; Zhu, Z.; Zhang, M.; Zhai, C.; Wang, X. Piloted ignition of vertical polymethyl methacrylate (PMMA) exposed to power-law increasing radiation. Appl. Therm. Eng. 2022, 217, 118996. [Google Scholar] [CrossRef]
- Pandey, P.; Anbudayanidhi, S.; Mohanty, S.; Nayak, S.K. Flammability and thermal characterization of PMMA/clay nanocomposites and thermal kinetics analysis. Polym. Compos. 2012, 33, 2058–2071. [Google Scholar] [CrossRef]
- Gong, J.; Zhai, C.; Yang, L.; Wang, Z. Ignition of polymers under exponential heat flux considering both surface and in-depth absorptions. Int. J. Therm. Sci. 2020, 151, 106242. [Google Scholar] [CrossRef]
- Chen, T.B.Y.; Yuen, A.C.Y.; Wang, C.; Yeoh, G.H.; Timchenko, V.; Cheung, S.C.; Chan, Q.N.; Yang, W. Predicting the fire spread rate of a sloped pine needle board utilizing pyrolysis modelling with detailed gas-phase combustion. Int. J. Heat Mass Transf. 2018, 125, 310–322. [Google Scholar] [CrossRef]
- Lin, B.X.; Wu, Y.; Xu, M.X.; Chen, Z.G. Experimental investigation on spark ignition and flame propagation of swirling kerosene spray flames. Fuel 2021, 303, 121254. [Google Scholar] [CrossRef]
- Fang, W.; Peng, Z.; Chen, H. Ignition of pine needle fuel bed by the coupled effects of a hot metal particle and thermal radiation. Proc. Combust. Inst. 2021, 38, 5101–5108. [Google Scholar] [CrossRef]
- Thomas, J.C.; Simeoni, A.; Gallagher, M.; Skowronski, N. An experimental study evaluating the burning dynamics of pitch pine needle beds using the FPA. Fire Saf. Sci. 2014, 11, 1406–1419. [Google Scholar] [CrossRef]




| Type of Heat | Radiation Heat Flux /(kW/m2) | Distance from Heater to Fuel (mm) | Surface Temperature of Cone Center (°C) | Type of Fuel Bed | Density of Fuel Bed (kg/m3) |
|---|---|---|---|---|---|
| Radiation | 25 | 25, 40, 45, 50, 55, 60, 70, 80 | 433, 452, 470, 505, 524, 585, 633 | Pine needle | 46 |
| Pine wood | 359.2 | ||||
| PMM | 1190 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J. Flaming Ignition of PMMA, Pine Wood and Pine Needle by External Radiation: Autoignition and Radiant Distance Effect. Fire 2023, 6, 163. https://doi.org/10.3390/fire6040163
Song J. Flaming Ignition of PMMA, Pine Wood and Pine Needle by External Radiation: Autoignition and Radiant Distance Effect. Fire. 2023; 6(4):163. https://doi.org/10.3390/fire6040163
Chicago/Turabian StyleSong, Jiayun. 2023. "Flaming Ignition of PMMA, Pine Wood and Pine Needle by External Radiation: Autoignition and Radiant Distance Effect" Fire 6, no. 4: 163. https://doi.org/10.3390/fire6040163
APA StyleSong, J. (2023). Flaming Ignition of PMMA, Pine Wood and Pine Needle by External Radiation: Autoignition and Radiant Distance Effect. Fire, 6(4), 163. https://doi.org/10.3390/fire6040163









