Simulation Research on Effects of Ambient Pressure on Plug-Holing Phenomenon in Tunnel Fires with a Shaft

Abstract

This paper studied the effects of ambient pressure on the plug-holing phenomenon in tunnel fires with a shaft by a Fire Dynamics Simulator. The influence of ambient pressures on the smoke movement, temperature distribution, critical Richard number (Ri_c) and critical shaft height for plug-holing were analyzed in detail. A new prediction formula of smoke flow velocity considering different pressures was modified. A prediction formula of smoke temperature distribution beneath the ceiling under different pressures was developed. As a result, a prediction model of Richard numbers to determine whether the plug-holing occurs was proposed by combining smoke flow velocity and smoke temperature distribution. The critical Richard numbers (Ri_c) and critical shaft height (h_c) increases as the pressure decreases. Outcomes in this study can provide references for the design of a natural ventilation system in tunnel fires at a higher altitude.

1. Introduction

With the development of the economy, the demand for interconnection between cities grows rapidly. The road tunnel can greatly improve the transportation efficiency, which provides convenience to our life and production. However, owing to the long and narrow structure of tunnel, it is easy for the smoke to accumulate beneath the ceiling, which brings great difficulties and challenges for rescue work [1,2,3,4,5,6,7]. Large numbers of statistics have shown that the main reason for death and injury in a tunnel fire is the inhalation of toxic gases [8,9,10,11,12]. So, it is crucial to investigate the characteristic of smoke movement and control during fires in a road tunnel.

Nowadays, there are primarily two sorts of ventilation methods, i.e., longitudinal and natural ventilation [13]. Due to the economic and convenient advantages of a natural ventilation system, it has been applied frequently in tunnels in recent years [14,15].

So far, lots of scholars have studied the natural ventilation performance and smoke movement considering shafts settings, fire HRR and other factors. Kashef et al. [16] studied the effects of fire location on temperature distribution in naturally ventilated tunnel fires by small-size tests, and prediction formulas of the temperature distribution in the fire section and non-fire section of the tunnel were developed. Yuan et al. [17] investigated the influence of heat release rate, shaft dimension and blockage on the temperature distribution and smoke exhaust effect. The prediction models of temperature distribution and smoke exhaust volume were developed. Fan et al. [18] investigated the air entrainment in tunnel fires with shafts by conducting small-scale experiments. Results show that the process of exhausting smoke has a strong mixing between smoke and air. Xie et al. [19] investigated the effects of cross-sectional area and aspect ratio of the shaft on smoke exhaust by conducting numerical simulations. Results show that the mass flow rate of exhausted smoke decreases as the aspect ratio of the shaft increases, and mass flow rate of smoke per unit of the cross-sectional area of the shaft decreases as the cross-sectional area increases. Ji et al. [20] investigated smoke movement in the vertical shaft using different heights of the shaft by conducting small-scale experiments. Results show that the phenomenon of boundary layer separation is obvious with a smaller height of the vertical shaft, and plug-holing could occur under a higher shaft height. Further, the Ri to determine the smoke movement pattern in shaft at standard atmosphere was presented. Yao et al. [21] studied the impact of the height of a shaft on smoke exhaust capacity by FDS. It was found that a lower shaft can improve the smoke exhaust effect. Fan et al. [22] investigated the impact of shaft positions during a fire in the tunnel using natural ventilation by FDS simulations. It is found that the smoke exhausted decreases as the distance from the fire source to the shaft increases. He et al. [23] studied the impact of the height of the vertical shaft and HRR on the heat exhaust effect using FDS. Results show that the heat exhaust effect of vertical shafts decreases and then increases with increasing shaft height under a constant HRR of pool fire. Zukoski [24] studied the characteristics of smoke movement in the tunnel fires with a vertical shaft, and found that the stack effect and turbulent mixing process are responsible for the vertical motion of buoyance smoke. Vauquelin et al. [25] studied the effects of the shape of the shaft on smoke extraction efficiency by small-scale tests. Results show that a transverse rectangular shape has a positive effect on the smoke extraction effect.

However, previous experts only concentrated on the natural ventilation in the tunnel fires at standard atmosphere. Nowadays, the number of tunnels at high altitudes is more and more. For example, the average elevations of the Mila Mountain tunnel in Tibet and the Changla Mountain tunnel in Qinghai are about 4800 m (pressure: 56 kPa) and 4500 m (pressure: 58 kPa), respectively [26]. Reduced ambient pressure will directly affect the mass transport and heat transfer of smoke during tunnel fires. Previous research shows that smoke temperature was higher at a lower pressure, owing to the lower heat loss [27]. Yan et al. [28] investigated the impact of pressures on temperature distribution by conducting full-scale experiments at lower pressure. Results show that longitudinal temperature attenuation rate is faster than that at a lower pressure. Ji et al. [29] investigated the impact of pressures on the smoke movement and temperature decay in an inclined tunnel using FDS, from which the prediction formula of smoke temperature was derived. Yan et al. [30] investigated the impact of pressures on smoke movement in the shaft. Results show that critical Ri deceases as the pressure decreases. Zhang et al. [31] investigated back-layering length at lower pressure using FDS. It was found that back-layering length decreases as the pressure decreases. However, Guo et al. [32] found that back-layering length increases as pressure decreases by conducting numerical simulations. Yao et al. [33] proposed turning velocity V_T for the first time, and when $V<V_T$, back-layering length decreases as the pressure decreases. When $V_T<V<V_C$ (critical velocity), back-layering length will increase as pressure decreases.

It can be found that most research on the tunnel fires at lower pressure are about smoke temperature and movement characteristic, and few scholars have focused on the effects of ambient pressure on smoke movement patterns in the shaft. Actually, the smoke movement pattern in the shaft is an important factor that affects the smoke control effect.

This study conducted simulation research to investigate the effects of ambient pressure on plug-holing phenomenon during fires in a tunnel with a shaft. The effects of ambient pressures on smoke movement, temperature distribution and critical Richard (Ri_c) or critical shaft height for the occurrence of plug-holing were analyzed in detail. The prediction model of Richard numbers to determine whether the plug-holing occurs under different ambient pressures was proposed by combining the smoke flow velocity and smoke temperature distribution in the tunnel with a shaft.

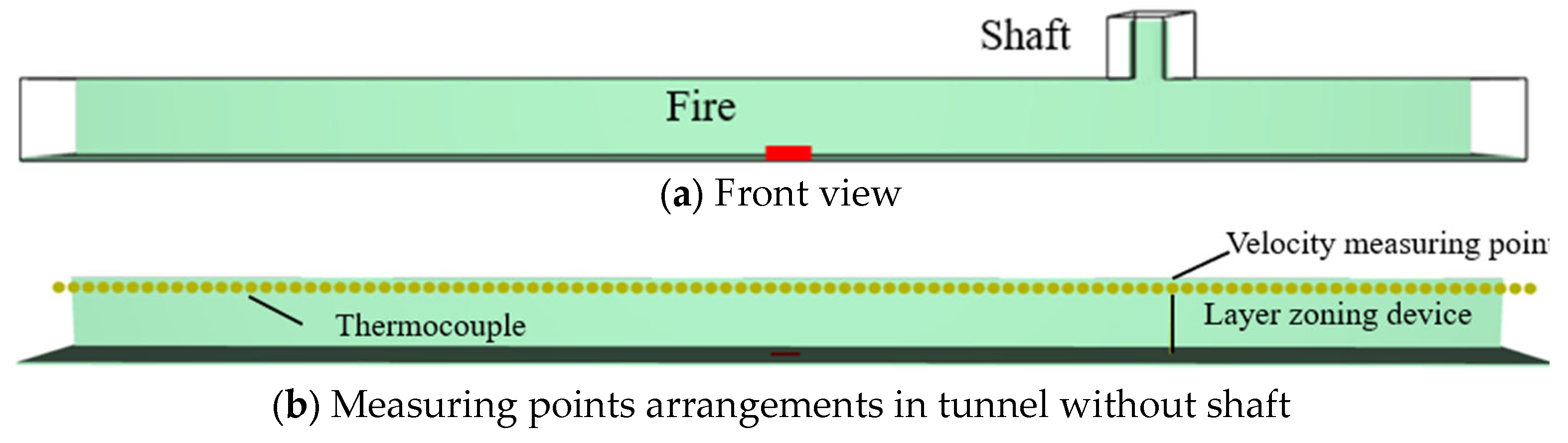
2. Numerical Modeling

Developed by the National Institute of Standards and Technology (NIST, USA), FDS numerically solves the form of the Navier–Stokes equations for thermally-driven flow, which has been widely used to investigate thermal smoke characteristics in different building fires [34]. FDS has already also been regarded as an effective tool to research the characteristics of tunnel fires [35]. For the process of fire smoke flow in a tunnel, the interaction between turbulence and buoyancy can be better solved by a large-eddy simulation (LES) [36], which was also used in the current study. The validation of FDS has been confirmed by many experiments for predicting the smoke movement. For example, Gannouni et al. [37] compared the critical velocity for stopping smoke spread upstream between the FDS numerical results and experimental measurements and found that the simulations are in acceptable agreement with the experiments. Liu et al. [38] studied the temperature distribution by FDS simulation and the full-size tests, and found that the results from the simulation agree well with the results from tests.

2.1. Fire Model Analysis

Considering the aspect ratio of the actual tunnels, a full-size tunnel with dimensions of 100 m (length) × 10 m (width) × 5 m (height) was conducted using FDS (6.5). The fire source was placed 50 m from the right entrance of the tunnel along the longitudinal center line, which is consistent with previous research [39]. The fuel is gasoline and, based on the previous studies [40,41], a single car fire is about 5 MW and a 2–3 car fire is about 10 MW. So, the heat release rate (HRR) of 5 MW was selected. The HRR of 3 MW, 7 MW and 10 MW were also selected, partially to verify the conclusion of the simulation results. The tunnel wall material was assumed to be concrete, and its default conductivity, density, and specific heat were 1.8 W/(m × K), 2280 kg/m³ and 1.04 kJ/(kg × K), respectively, which is consistent with previous research [42]. The tunnel at high altitudes is very common. The average elevations of the Changla Mountain tunnel in Qinghai, the Lana Mountain tunnel in Sichuan and the Xidu tunnel in Yunnan are about 4500 m (pressure: 58 kPa), 3000 m (pressure: 70 kPa) and 1300 m (pressure: 86 kPa), respectively. Therefore, the ambient pressure in this study changed from 100 kPa to 60 kPa.

The shaft was set 25 m from the right entrance of the tunnel with the cross-section of 2 m × 2 m, the details were shown in Figure 1a, and the shaft height changed from 0 m to 5 m. The tunnel fire tests without smoke exhaust were also set as the experimental control group. The ambient temperature was 20 °C. The boundary of the vertical shaft top and tunnel entrances were set to be open. Summary of all 54 fire cases were conducted, as shown in

Table 1. A summary of all cases.

Test No.	Ambient Pressure (kPa)	Shaft Height (m)	Fire Size (MW)
1–9	100	0,1,2,3,3.2,3.4,3.5,3.6,4	5
10–18	90	0,2,3,3.4,3.5,3.6,3.7,3.8,4
19–27	80	0,3,3.5,3.7,3.8,3.9,4,4.1,4.5
28–36	70	0,3,3.5,4,4.1,4.2,4.3,4.4,5
37–43	60	0,4,4.5,4.6,4.7,4.8,5
44–49	100,80	0	3,7,10
50–54	90	3,3.5,3.6,3.7,4	10

“0” refers to without shaft.

.

A large number of measuring points were arranged as follows: one hundred thermocouples were located 0.1 m under the tunnel ceiling along the longitudinal centerline with 1 m interval. A velocity measuring point was placed 0.1 m under the vertical shaft without smoke extraction. A layer zoning device was positioned under the shaft without smoke extraction to measure smoke layer height. Figure 1b shows the measuring points arrangements in details.

2.2. Meshes

The grid size in numerical simulation of FDS is a key parameter. Previous research has shown that the selection criterion $D^{\ast }/\delta x$ (ratio of the fire characteristic diameter to grid size) varies from 4 to 16, more accurate results of numerical simulation can be obtained [43]. $D^{\ast }$ is the characteristic fire diameter which is expressed by Equation (1) from Ref [43]:

$$D^{\ast }={(\frac{\dot{Q}}{{\rho }_a{c}_p{T}_a\sqrt{g}})}^{\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}$$

(1)

For a 5 MW fire, the characteristic diameter of the fire is 1.83 m. The optimum grid size is from 0.11 m to 0.46 m. Four grid sizes from 0.15 m to 0.4 m were selected in this study. For grid independence analysis, fire scenarios without smoke exhaust were simulated. Figure 2 displays vertical temperature distribution at 15 m and 5 m from the fire source for different grid sizes. It can be found that temperature distribution tends to be uniform as grid size decreases and there is no obvious improvement when the mesh grid size of mesh decreases to 0.20 m. So, to save computing time, the grid size of 0.20 m was chosen in this study.

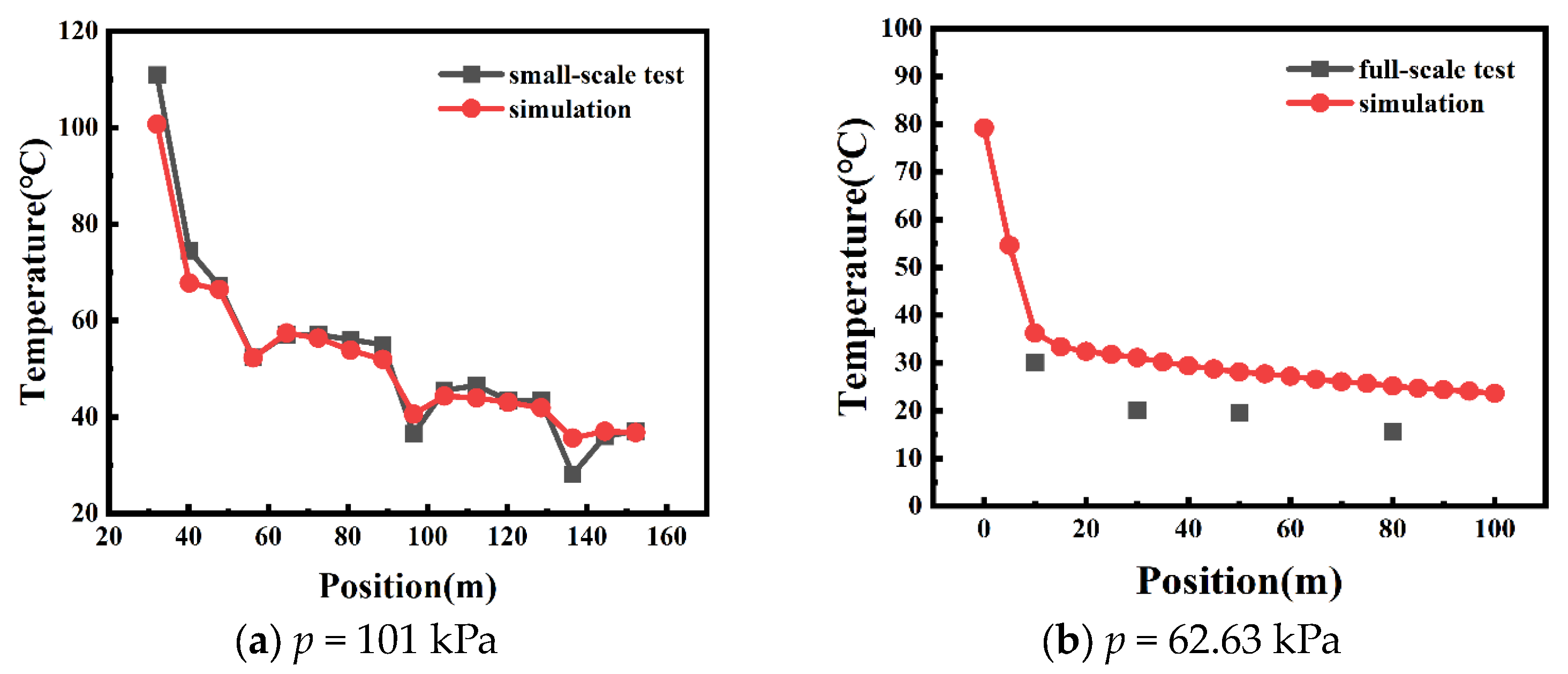
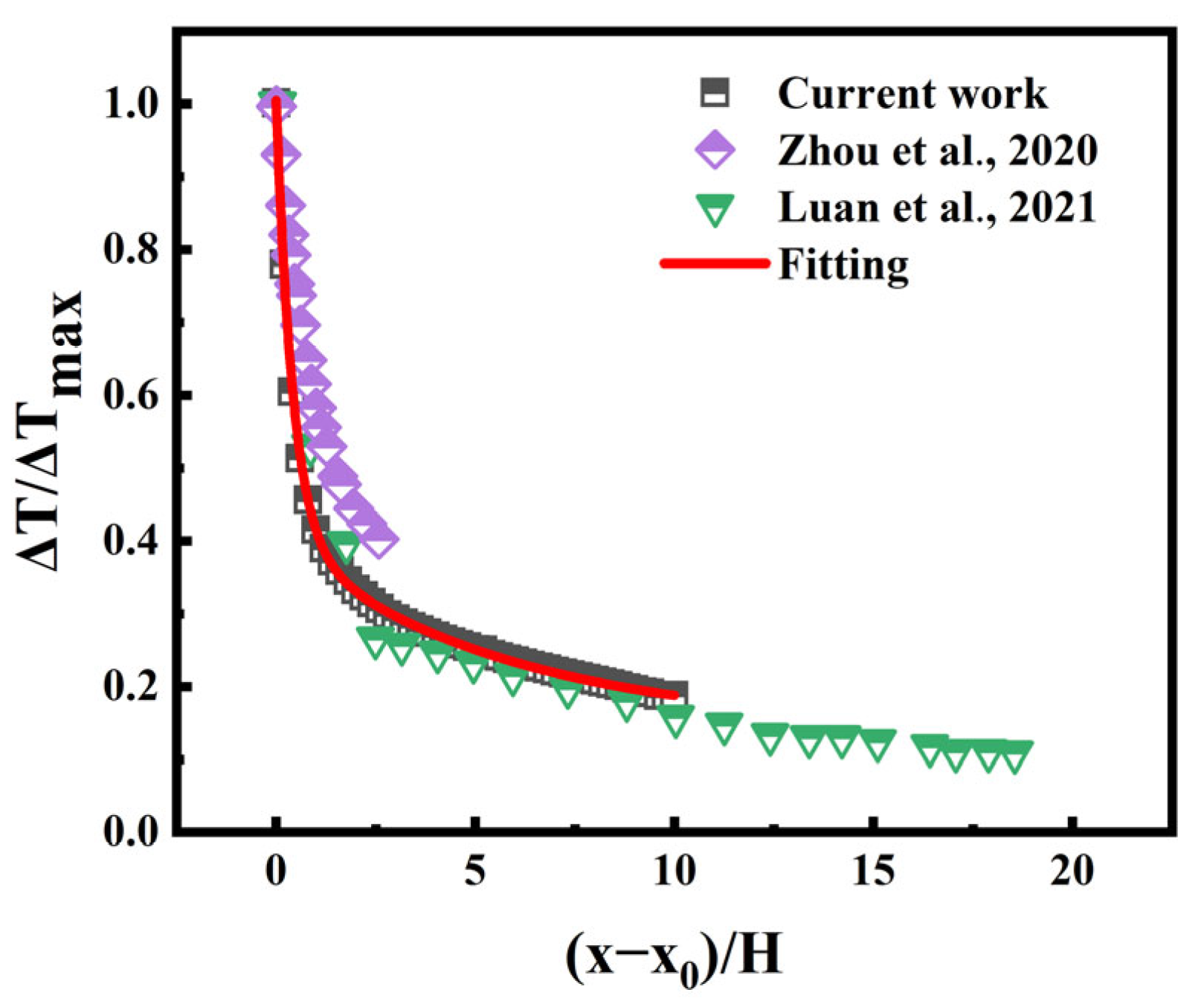
2.3. Validation

For the purpose of verifying the accuracy of the simulation, numerical simulation results were contrasted with experimental data through small-size tests conducted by Zhao et al. [44]. Tunnel size in Zhao et al.’s study [44] is 20 m (long), 2 m (wide) and 1 m (high). Fire source was placed 2.5 m from the tunnel entrance with HRR of about 54.9 kW. Three shafts were set up along the tunnel, which were located 6.5 m, 11.5 m and 16.5 m from the entrance of the tunnel. The height of the shaft is 1 m, and the width of the shaft is 0.4 m. The ventilation velocity is 1.0 m/s. Longitudinal temperature distribution under different pressures through simulation works and small-size experimental tests from Zhao et al.’s study [44] are shown in Figure 3a. The result shows that the temperature from the simulated results agrees well with that from the experiments.

To further verify the reliability of simulating smoke movement at lower pressure in FDS, the simulated results were also compared with the experimental data from Yan et al.’s study [28]. Their fire tests were implemented in the Baimang Snow Mountain Tunnel in Yunnan, China. The altitude is about 4100 m (62.63 kPa). The ventilation velocity is 0.45 m/s. HRR is 0.72 MW. Figure 3b shows the longitudinal temperature distribution between FDS simulations and full-size tests from Yan et al. [28], and it is found that the temperature from simulation results is slightly higher than that from experiments. This is because the HRR decreases after reaching the peak value during the experiment, but the value of the HRR remains constant in the simulation during the whole burning process.

3. Results and Discussion

3.1. Smoke Flow Velocity Beneath the Ceiling

The smoke flow velocity is a critical parameter in tunnel fires. Bailey et al. [45] proposed a prediction formula of smoke flow velocity:

$$v=0.7\sqrt{gd\frac{\Delta T}{T_a}}$$

(2)

where $\Delta T$ is temperature difference between hot smoke and cold air (K), d is smoke layer thickness (m). In the current study, considering the impact of pressures on smoke flow velocity, Equation (2) is rewritten as follows:

$$v=C\sqrt{gd\frac{\Delta T}{T_a}}$$

(3)

where C is the correction factor associated with ambient pressure. For a 5 MW fire,

Table 2. Parameters of smoke layer under the shaft without extraction and coefficient C.

Pressure (kPa)	Ta (K)	d (m)	ΔTs (K)	Ts (K)	v (m/s)	Coefficient C Calculated by Equation (3)
100	293	1	362	382	1.71	0.50
90			368	388	1.79	0.51
80			372	392	1.86	0.54
70			377	397	1.99	0.56
60			380	400	2.08	0.57

gives parameters of the smoke layer beneath the vertical shaft without extraction and coefficient C is calculated by Equation (3). It is found that at normal pressure, the coefficient C is 0.5, which is lower than 0.7 in Bailey et al.’s study [45]. This is because Bailey et al. [45] used the smoke layer vertical average temperature rise to obtain smoke flow velocity, while in the current study, the temperature rise $\Delta T$ refers to the maximum gas temperature rise under the tunnel ceiling, which is higher than the average temperature rise.

Figure 4 shows the correlation between C and pressure, and it is found that C decreases linearly with the pressure. Furtherly, the smoke flow velocity can be expressed by Equation (4) combining Equation (3) and Figure 4. It is found that smoke flow velocity increases as pressure decreases.

$$v=(-0.002P+0.69)\sqrt{gH\frac{\Delta T}{T_a}}$$

(4)

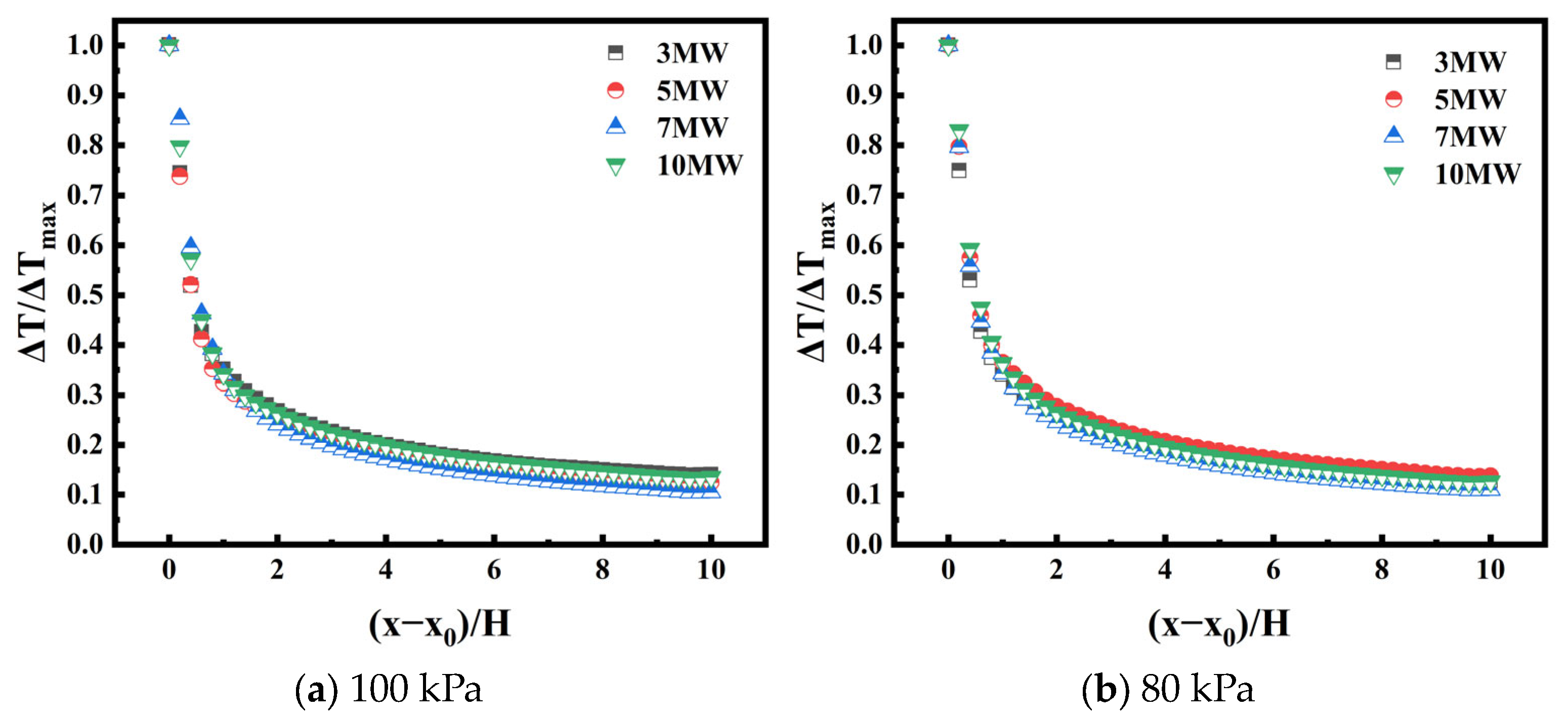
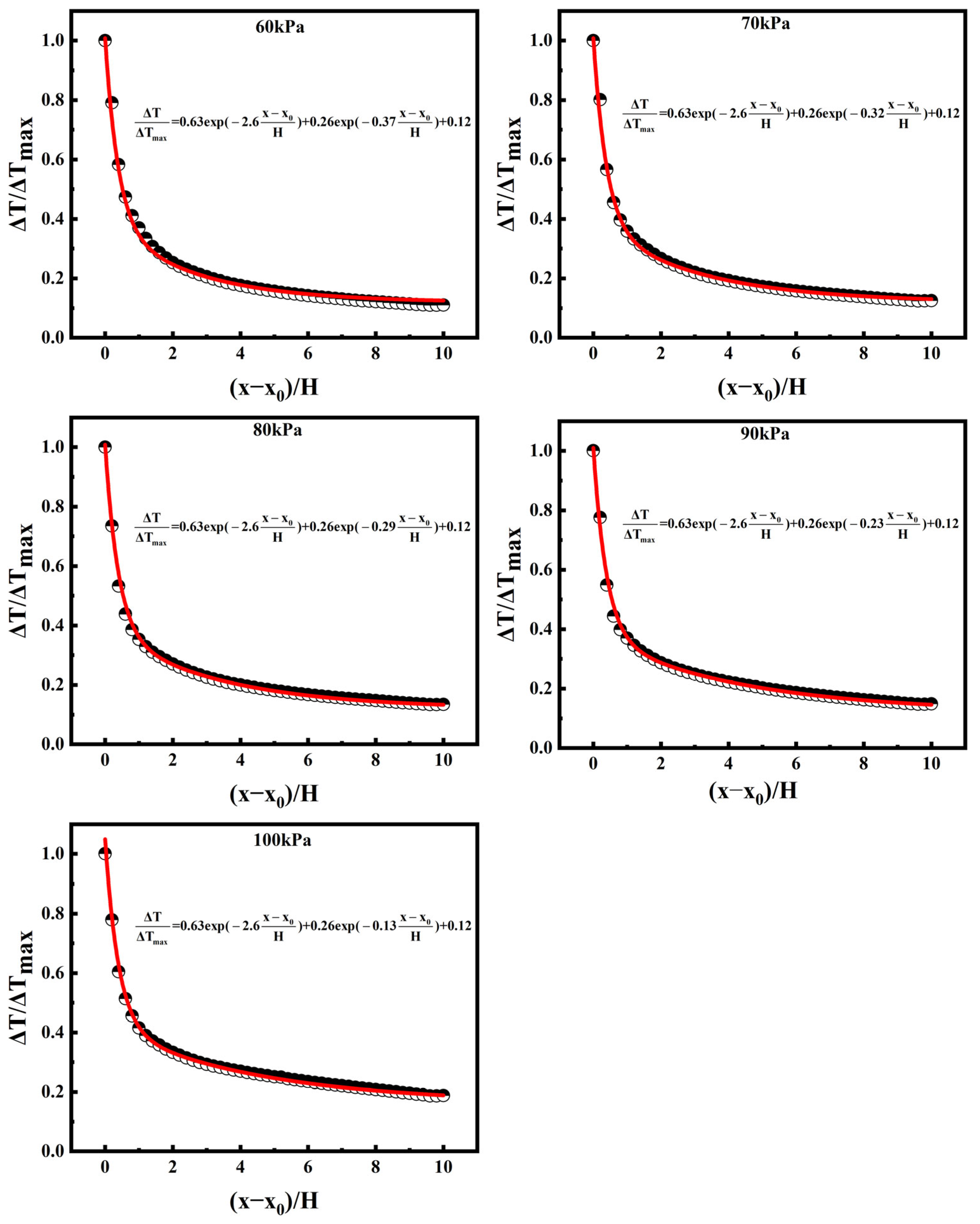
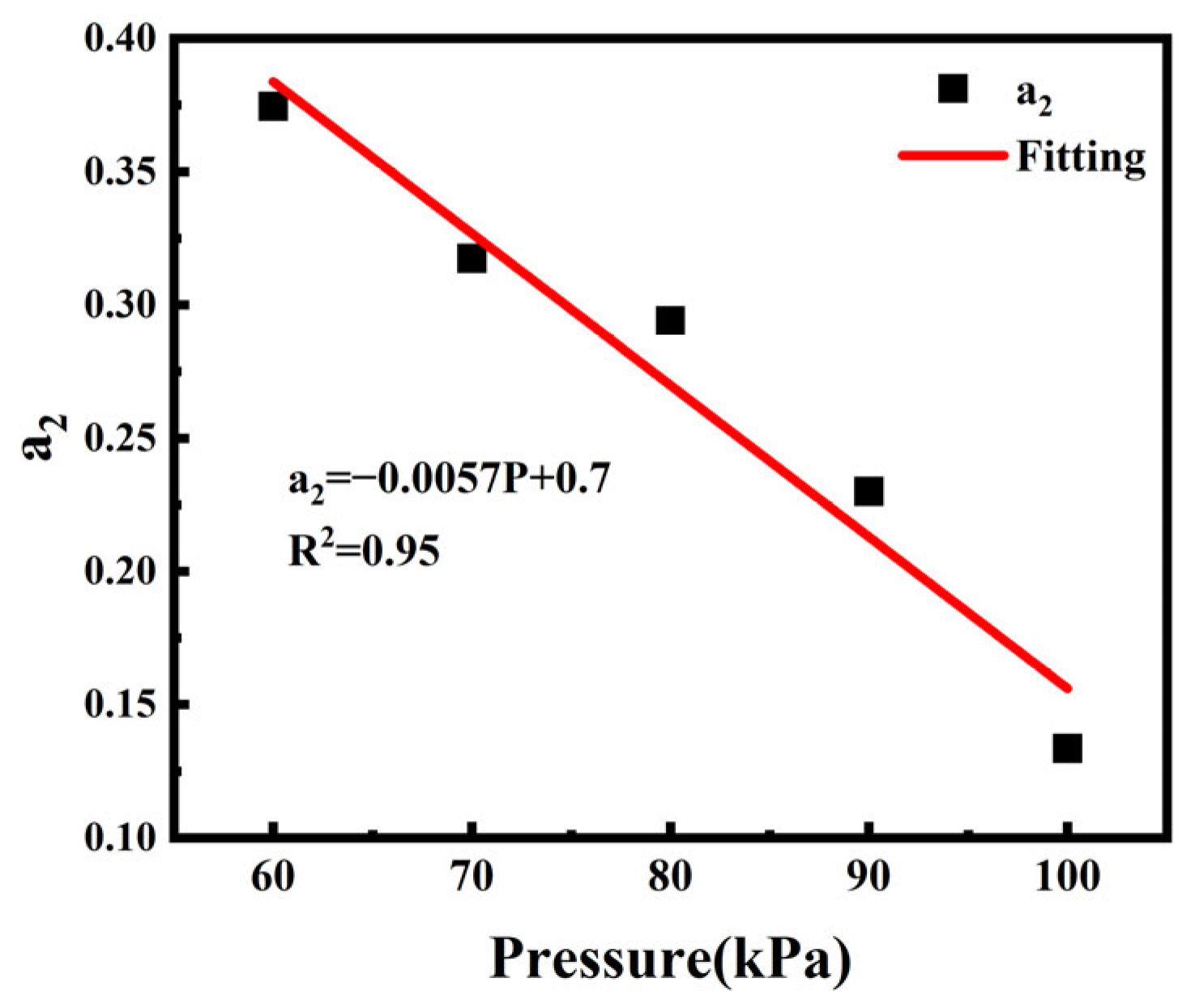
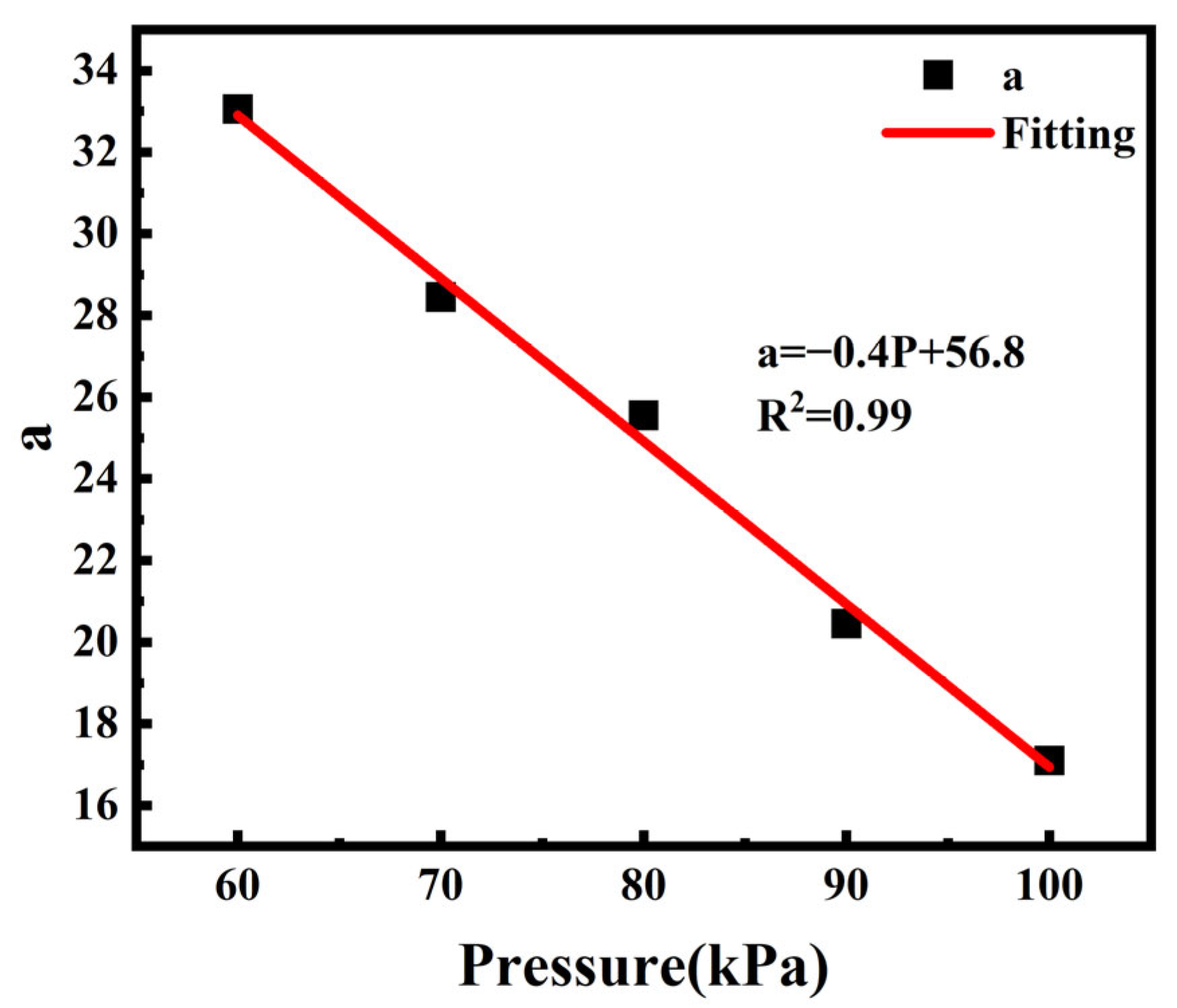
3.2. Longitudinal Temperature Distribution

Figure 5 displays that dimensionless longitudinal smoke temperature distribution under various pressures for a 5 MW fire. It is found that the longitudinal smoke temperature attenuation rate is faster at a lower pressure. The reason is that smoke flow velocity rises as pressure decreases, as shown in Table 2 and Equation (4). Liu et al. [38] also found that smoke flow velocity increases as pressure decreases for a certain HRR. In this way, smoke heat convection loss increases. Moreover, lower pressure will cause lower air density, and the air entrainment intensity of the fire plume was weakened. Consequently, the maximum smoke temperature increases significantly. This aggravates the temperature attenuation nearby the fire source.

For 100 kPa and 80 kPa of pressures, Figure 6 further displays the dimensionless smoke temperature distribution under different HRRs. It is found that the impact of HRR on the temperature distribution is very limited when the HRR ranges from 3 MW to 10 MW.

Gas temperature rise decreases exponentially with longitudinal distance. Therefore, this paper uses Equation (5) to predict smoke temperature distribution based on previous research [46,47].

$$\frac{\Delta T}{\Delta T_{\max }}=A_1\exp (-a_1\frac{x-x_0}{H})+A_2\exp (-a_2\frac{x-x_0}{H})+y_0$$

(5)

where x₀ refers to the location of fire source, x refers to the distance from fire source (m) and a₁, a₂, A₁, A₂, y₀ are coefficients.

Figure 7 displays the correlation between smoke temperature rise and the position of fire source under different pressures. It is found that the longitudinal temperature decay can be well predicted through the sum form of the double exponential relation, with correlation coefficient (R²) being above 0.98; see Equations (6)–(10) for details. Here, A₁, a₁, A₂ and y₀ is constant and a₂ decreases linearly with the pressure.

$$100 \mathrm{kPa}: \frac{\Delta T}{\Delta T_{\max }}=0.63\exp (-2.6\frac{x-x_0}{H})+0.26\exp (-0.13\frac{x-x_0}{H})+0.12$$

(6)

$$90 \mathrm{kPa}: \frac{\Delta T}{\Delta T_{\max }}=0.63\exp (-2.6\frac{x-x_0}{H})+0.26\exp (-0.23\frac{x-x_0}{H})+0.12$$

(7)

$$80 \mathrm{kPa}: \frac{\Delta T}{\Delta T_{\max }}=0.63\exp (-2.6\frac{x-x_0}{H})+0.26\exp (-0.29\frac{x-x_0}{H})+0.12$$

(8)

$$70 \mathrm{kPa}: \frac{\Delta T}{\Delta T_{\max }}=0.63\exp (-2.6\frac{x-x_0}{H})+0.26\exp (-0.32\frac{x-x_0}{H})+0.12$$

(9)

$$60 \mathrm{kPa}: \frac{\Delta T}{\Delta T_{\max }}=0.63\exp (-2.6\frac{x-x_0}{H})+0.26\exp (-0.37\frac{x-x_0}{H})+0.12$$

(10)

Figure 8 shows the correlation between coefficient a₂ and pressure P; see Equation (11) for details.

$$a_2=-0.0057p+0.7$$

(11)

Finally, the prediction formula of the dimensionless distribution of smoke temperature under different pressures can be developed combining Equations (6)–(11):

$$\frac{\Delta T}{\Delta T_{\max }}=0.63\exp (-2.6\frac{x-x_0}{H})+0.26\exp ((0.0057p-0.7)\frac{x-x_0}{H})+0.12$$

(12)

To validate the rationality of the prediction formula of dimensionless distribution of temperature, predictions from Equation (12) are compared with results from two small-scale experiments [48,49], as shown in Figure 9. The results show that the predictions from Equation (12) agree well with the simulated results from the current study and the experimental results from others’ studies.

The longitudinal temperature can be predicted by combining Equation (12) with the maximum smoke temperature over a fire source. Alpert [50] and Li et al. [51] proposed a prediction formula of the maximum smoke temperature rise through theoretical analysis and experiments, which can be described as:

$$\Delta T_{\max }=\alpha \frac{{\dot{Q}}^{2/3}}{H^{5/3}}$$

(13)

The coefficient α can be derived from experimental data and it is 16.9 in Alpert’s study [50] and 17.9 in Li et al.’s study [51].

Table 3. Coefficient α under different ambient pressures.

Pressure (kPa)	100	90	80	70	60
ΔTmax (K)	342	409	511	569	661
α (-)	17.1	20.5	25.6	28.5	33.0

shows the coefficient α under different pressures, which is obtained by combining Equation (13) and the simulation results. It is found that the coefficient α of 17.1 at normal pressure is very close to the result from Alpert [50] and Li et al. [51].

Figure 10 shows the correlation between coefficient α and pressure, and it is found that α decreases linearly with the pressure. Consequently, a maximum smoke temperature rise can be established by Equation (14) combining Equation (13) and Figure 10, and it is known that it increases with the decreasing pressure.

$$\Delta T_{\max }=(-0.4P+56.8)\frac{{\dot{Q}}^{2/3}}{H_{}^{5/3}}$$

(14)

3.3. Richard Number under Different Ambient Pressures

Smoke horizontal inertia force and vertical inertia force caused by the stack effect are two key factors to control the smoke extraction process [20]. When the shaft is high enough, and the vertical inertia force caused by the stack effect is large enough, the cold air of the lower layer will be exhausted out of the tunnel by the vertical shaft, resulting in an occurrence of plug-holing and a significant reduction of smoke exhaust efficiency. In the lower height of shaft, boundary layer separation will occur, causing the valid exhausting section to be reduced.

A dimensionless Richard number (Ri) was proposed by Ji et al. [20], determining the occurrence of the plug-holing phenomenon. Plug-holing occurs when the Ri is larger than 1.4 and this shaft height is the critical height of plug-holing (h_c), while when the Ri is less than 1.4, boundary layer separation occurs in the shaft. Ri can be thought as the ratio of vertical buoyancy force caused by the stack effect to horizontal inertia force caused by smoke. It can be written as follows [20]:

$$Ri=\frac{\Delta \rho ghA}{{\rho }_s{v}^{2}dw}$$

(15)

By introducing the ideal gas equation, which is ${\rho }_0{T}_0={\rho }_s{T}_s$, the Ri can be expressed as follows:

$$Ri=\frac{(\frac{T_s}{T_a}-1)ghA}{v^{2}dw}$$

(16)

where T_s refers to smoke temperature (K), T_a refers to environment temperature (K), h refers to shaft height (m), v refers to smoke flow velocity (m/s), d is thickness of smoke layer (m), and w refers to tunnel width (m). Obviously, Ri can be regarded as a function associated with smoke temperature and smoke flow velocity. Combined with Equations (4), (12) and (14), the Ri will be computed.

In this study, the critical Ri for plug-holing under different pressures was analyzed. The h_c according to the temperature field in the shaft under different pressures is shown in Figure 11 for a 5 MW fire. It is found that the sunken area reaches the shaft bottom (i.e., the plug-holing phenomenon occurs) when the height of the vertical shaft is 3.5 m at normal pressure, the sunken area reaches into bottom of the vertical shaft, which means the plug-holing phenomenon occurs. Otherwise, the phenomenon of boundary layer separation occurs in the shaft. Similarly, h_c in pressures of 60 kPa, 70 kPa, 80 kPa and 90 kPa is 4.7 m, 4.2 m, 4 m and 3.7 m, respectively. Namely, h_c increases with decreasing pressure. This is probably because the horizontal inertia force of smoke increases with increasing smoke flow velocity at a lower pressure, and thereby greater shaft height is required to make the plug-holing occur. Figure 12 further shows the critical shaft height according to temperature field in the shaft under different pressures for a 10 MW fire. It is found that HRR has no significant influence on h_c under different pressures.

Table 4. Critical Ri based on the simulation results.

Pressure (kPa)	Ric	hc (m)
100	1.42	3.5
90	1.46	3.7
80	1.48	4.0
70	1.49	4.2
60	1.61	4.7

shows the critical Richard number (Ri_c) under different pressures and it is calculated by Equation (16) combining with the simulated consequence in Table 2 and critical shaft height. It is found that the critical Ri is 1.42 at normal pressure, which is very close to the result of 1.4 from Ji et al. [20]. Furthermore, with the decreasing pressure, the value of Ri_c increases accordingly, which is different from Yan et al.’s study [30]. This is because in Yan et al.’s study [30], the shaft height changes from 0 m to 5 m with the interval of 0.5 m, and they do not consider critical shaft height changes under lower pressure, while in this study, the shaft height changes at an interval of 0.1 m around the critical shaft height under different pressures.

Figure 13 further shows the comparison of Ri between the results from the simulations and the results from predictions for all cases based on Equations (4), (12), (14) and (16). It is found that the predicted Richard numbers agree well with those from the simulation results.

4. Conclusions

Nowadays, the number of tunnels at high altitudes is more and more, and few scholars have focused on the effects of ambient pressure on smoke movement patterns in the shaft. This paper numerically studied the effects of ambient pressure on the plug-holing phenomenon in the shaft. A full-size road tunnel was established in FDS. The tunnel length, width and height are 100 m, 10 m and 5 m, respectively. The ambient pressure varied from 60 kPa to 100 kPa. The heat release rate varied from 5 MW to 10 MW. The shaft cross-section is 2 m × 2 m with different heights. The main findings are as follows:

(1)

The effects of different ambient pressures on the smoke flow velocity were analyzed. It is found that the smoke flow velocity increases as the ambient pressure decreases. A prediction formula of smoke flow velocity under different pressures was modified;

(2)

The effects of different ambient pressures on the temperature distribution were analyzed. It is found that the maximum smoke temperature rise increases as the ambient pressure decreases, but the temperature decays faster at a lower ambient pressure. A prediction model of smoke temperature distribution was proposed considering different ambient pressures.

(3)

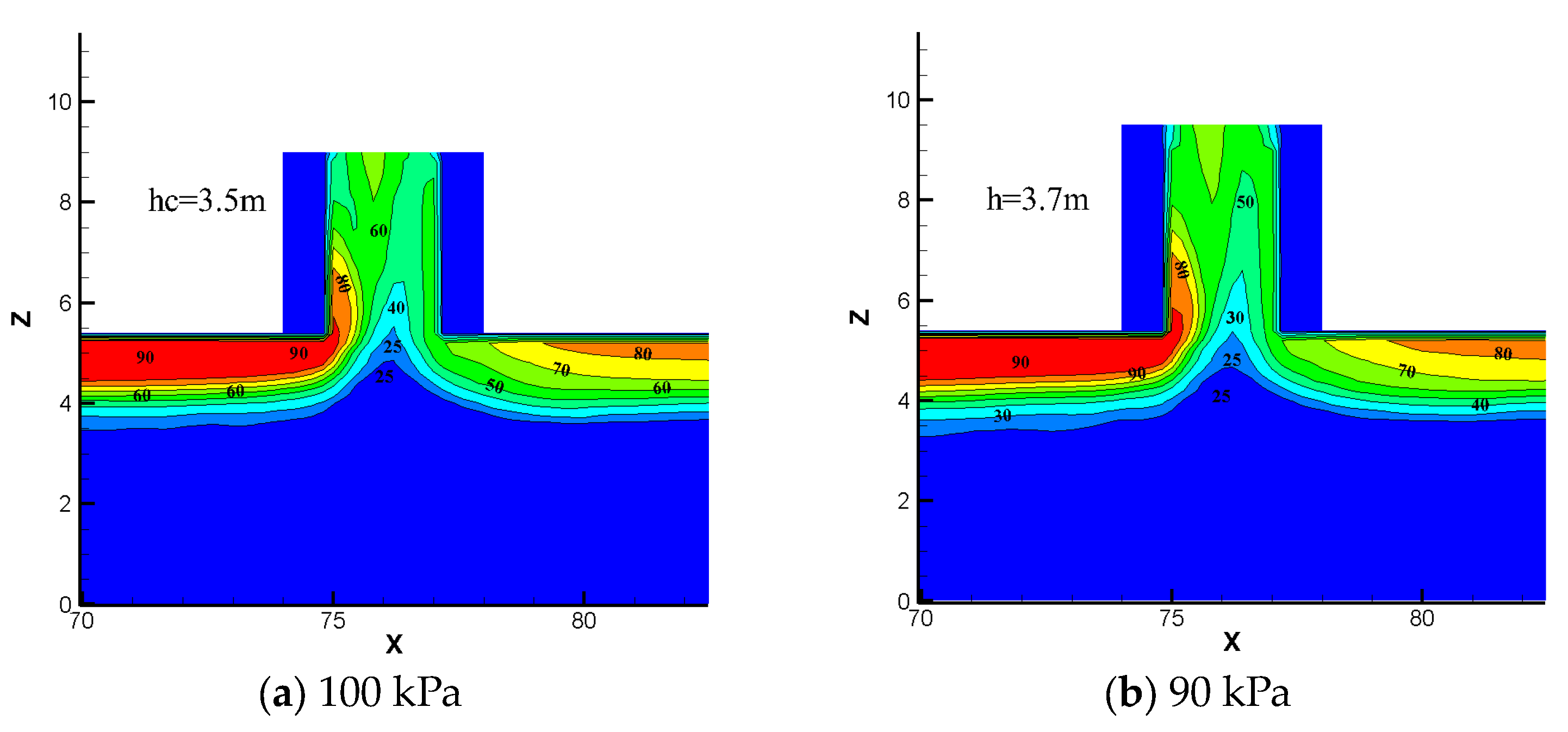
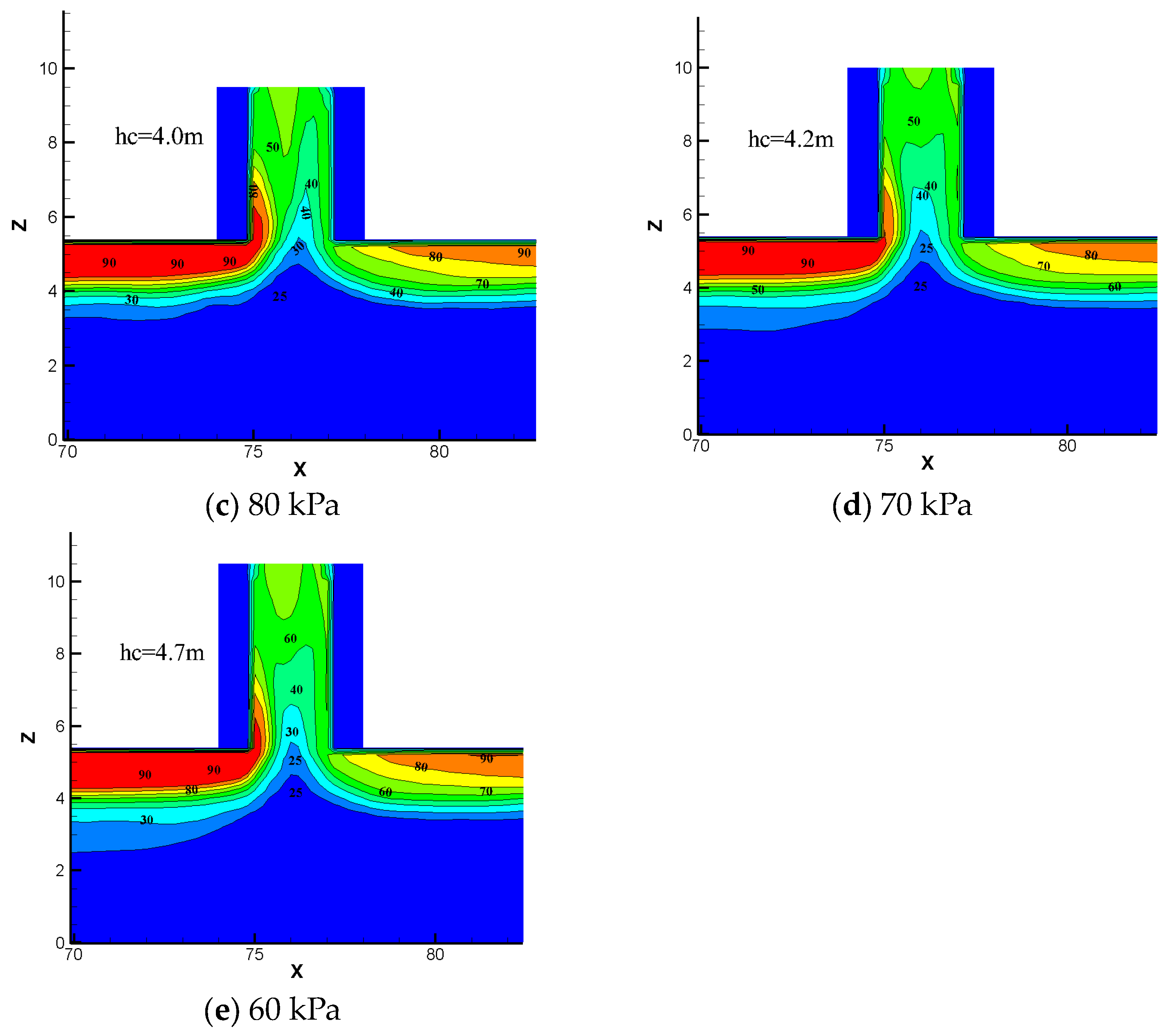
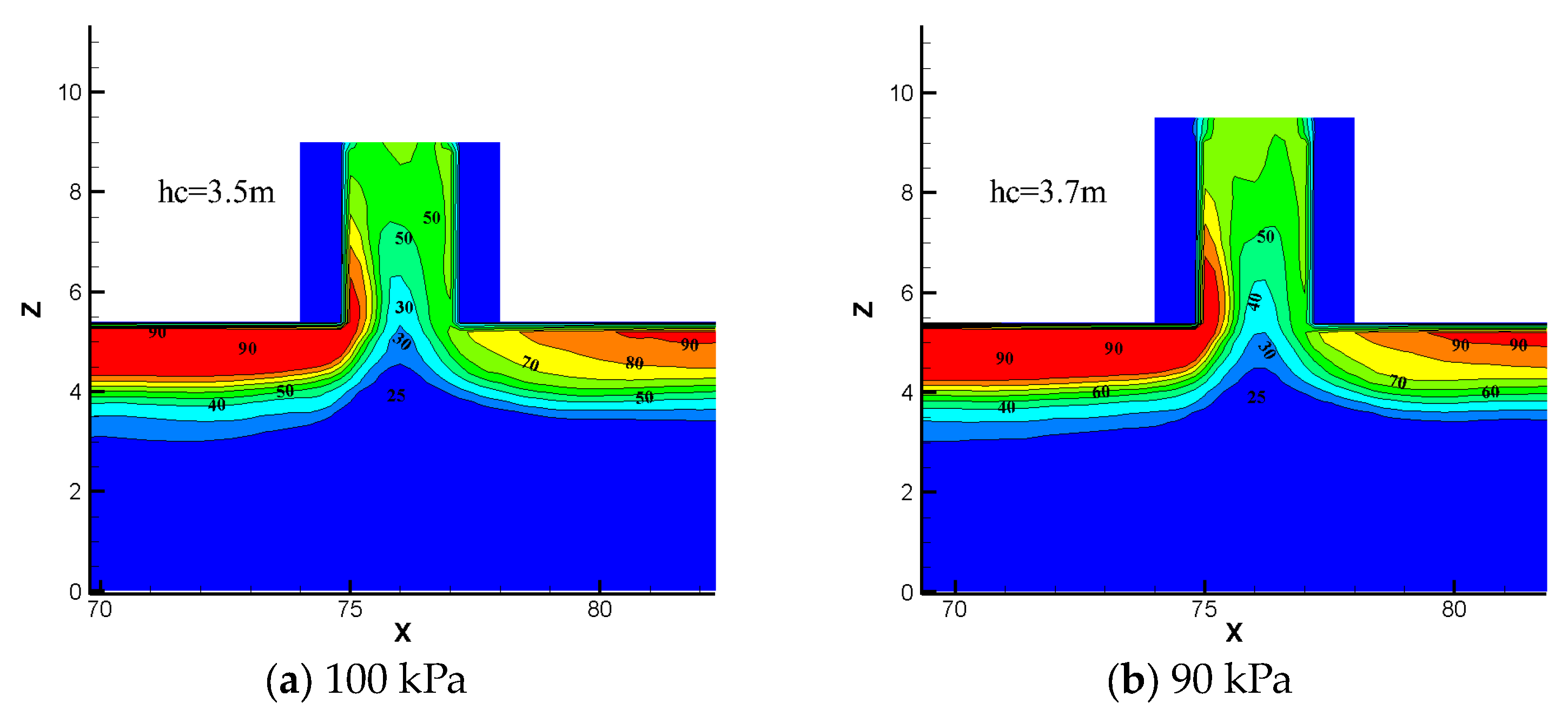
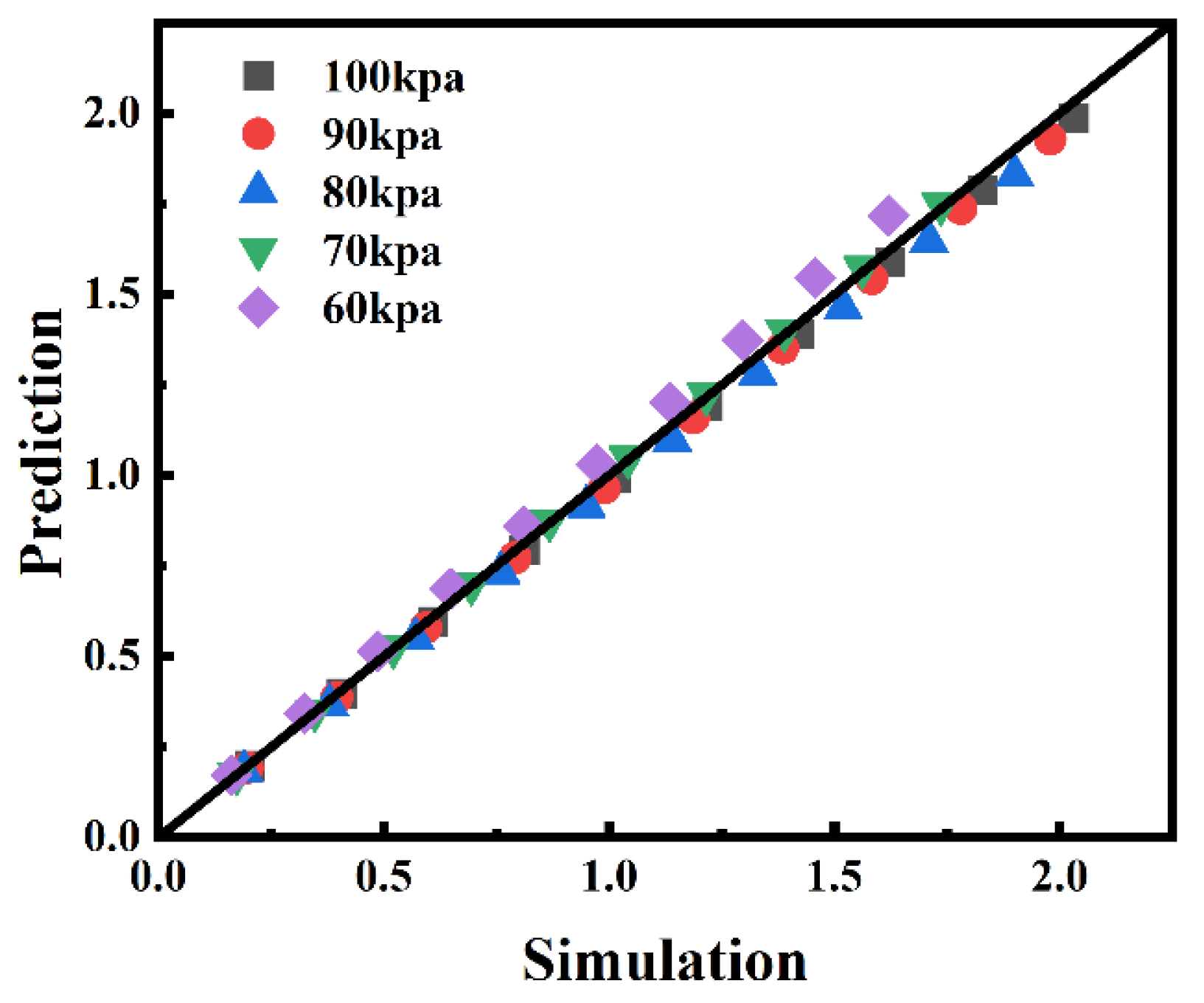
A prediction model of Richard numbers to determine whether the plug-holing occurs was proposed by combining the prediction formulas of smoke flow velocity and temperature distribution. The predicted value of the Richard number shows good agreement with the result from the simulation. The critical Richard number and the critical height of the shaft both increase as the ambient pressure decreases. For the 60 kPa, 70 kPa, 80 kPa, 90 kPa and 100 kPa of ambient pressures, the critical height of the shaft is 4.7 m, 4.2 m, 4 m, 3.7 m and 3.5 m, respectively.