A Review of Combustion and Flame Spread over Thermoplastic Materials: Research Advances and Prospects
Abstract
1. Introduction
2. Thermoplastic Materials
2.1. Thermoplastic Materials and Common Types
2.2. Thermal Characteristics of Thermoplastic Materials
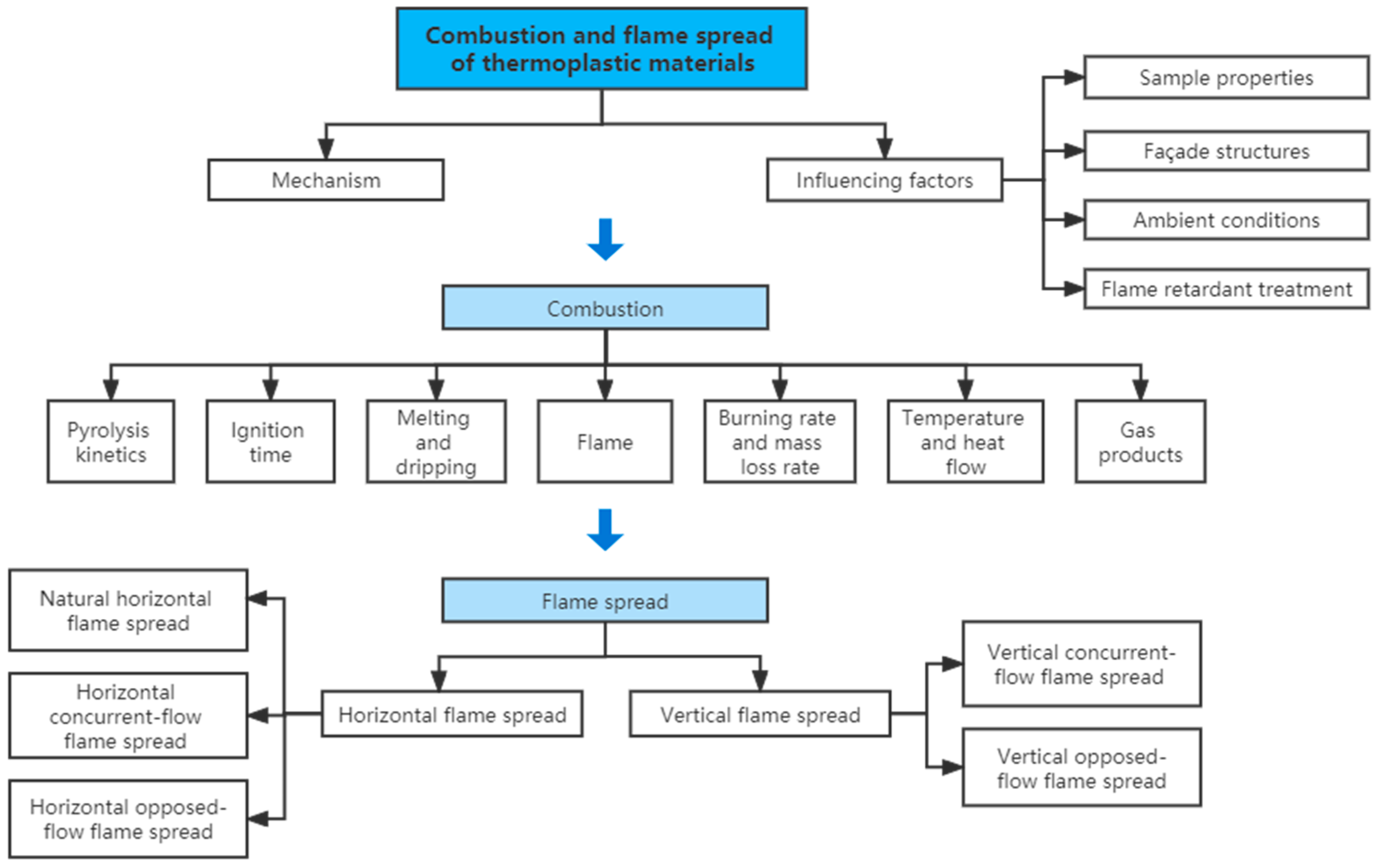
3. Combustion of Thermoplastic Materials
3.1. Pyrolysis Kinetics
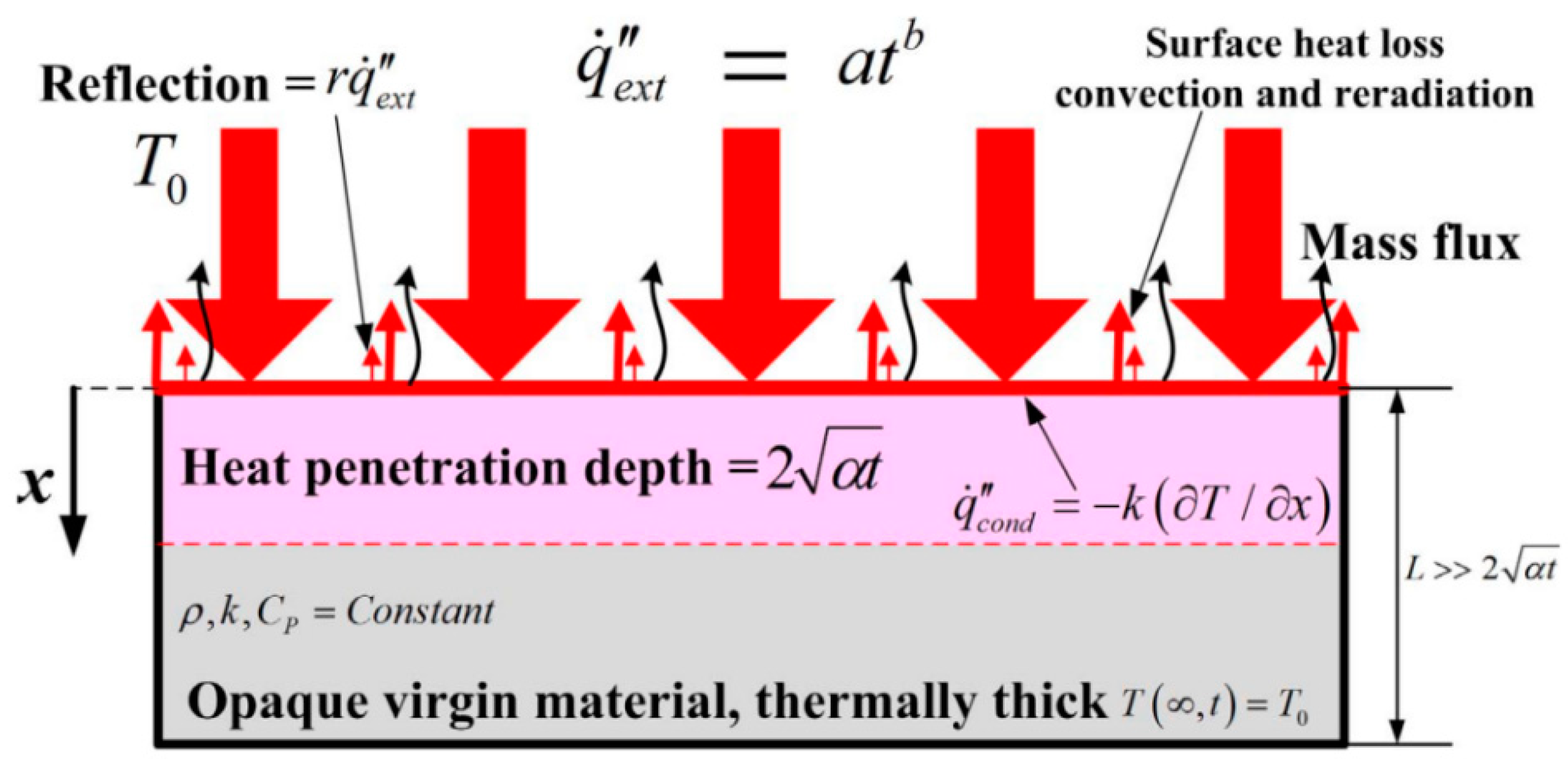
3.2. Ignition Time
3.2.1. Mechanism Analysis of Ignition
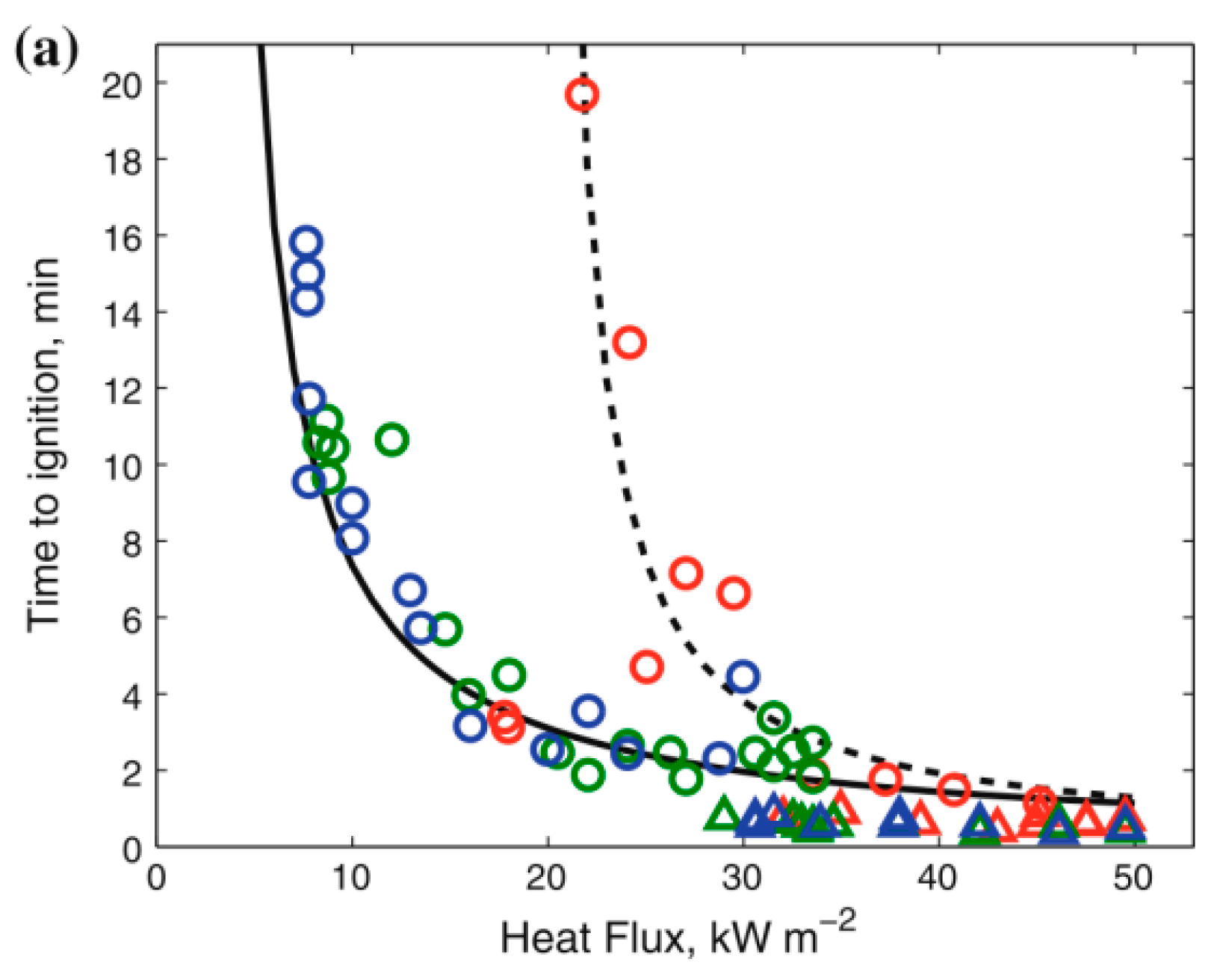
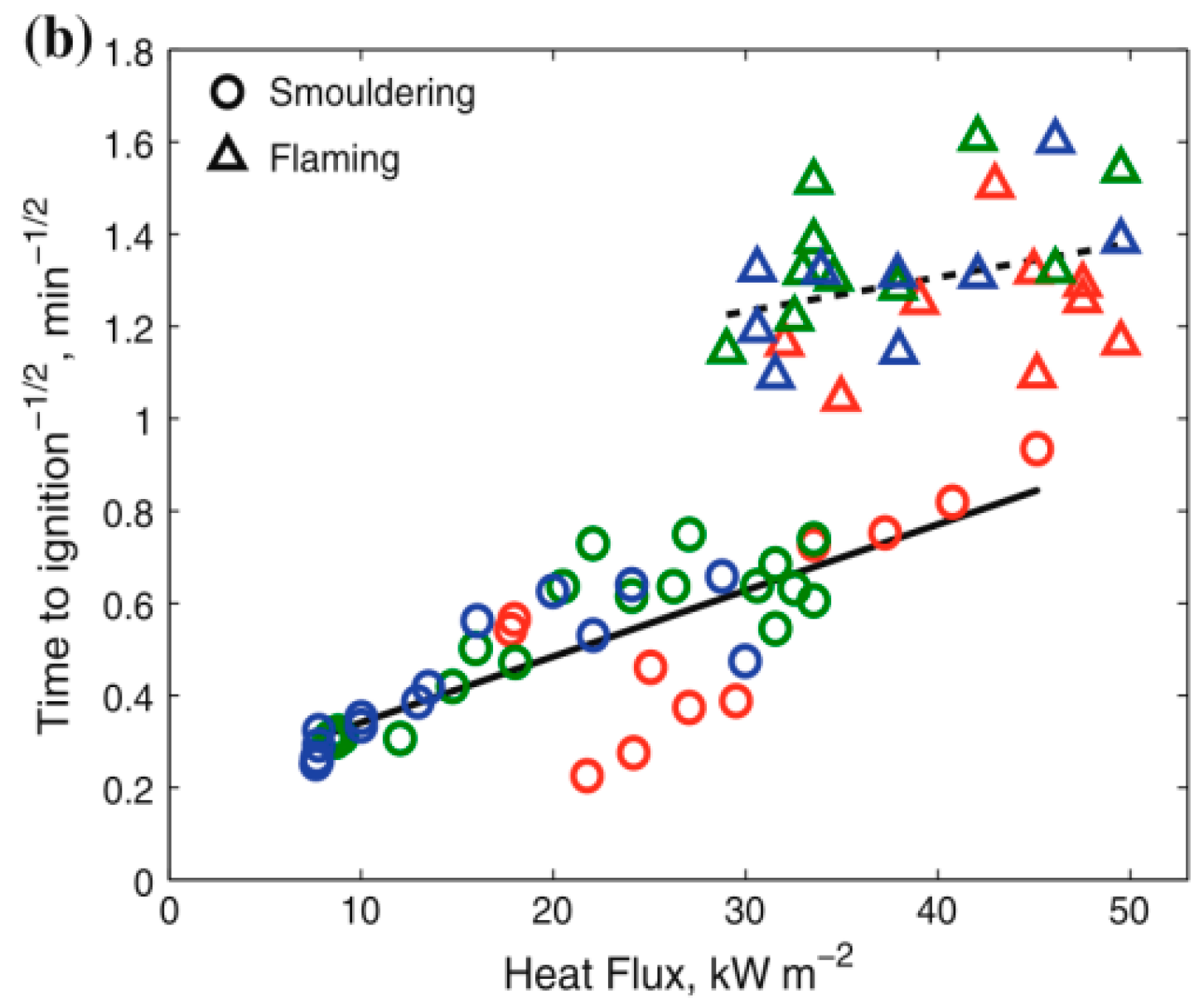
3.2.2. Influencing Factors of Ignition Time
Sample Properties
Ambient Conditions
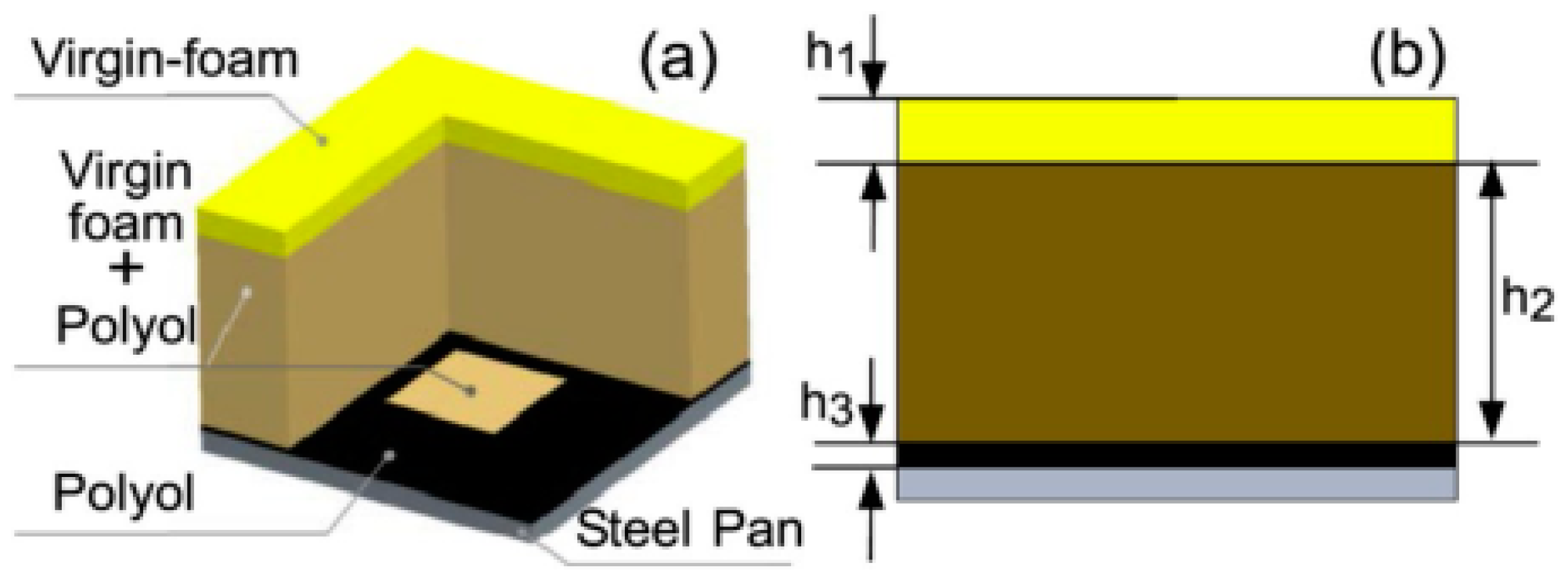
3.3. Melting and Dripping
3.3.1. Mechanism Analysis of Melting and Dripping
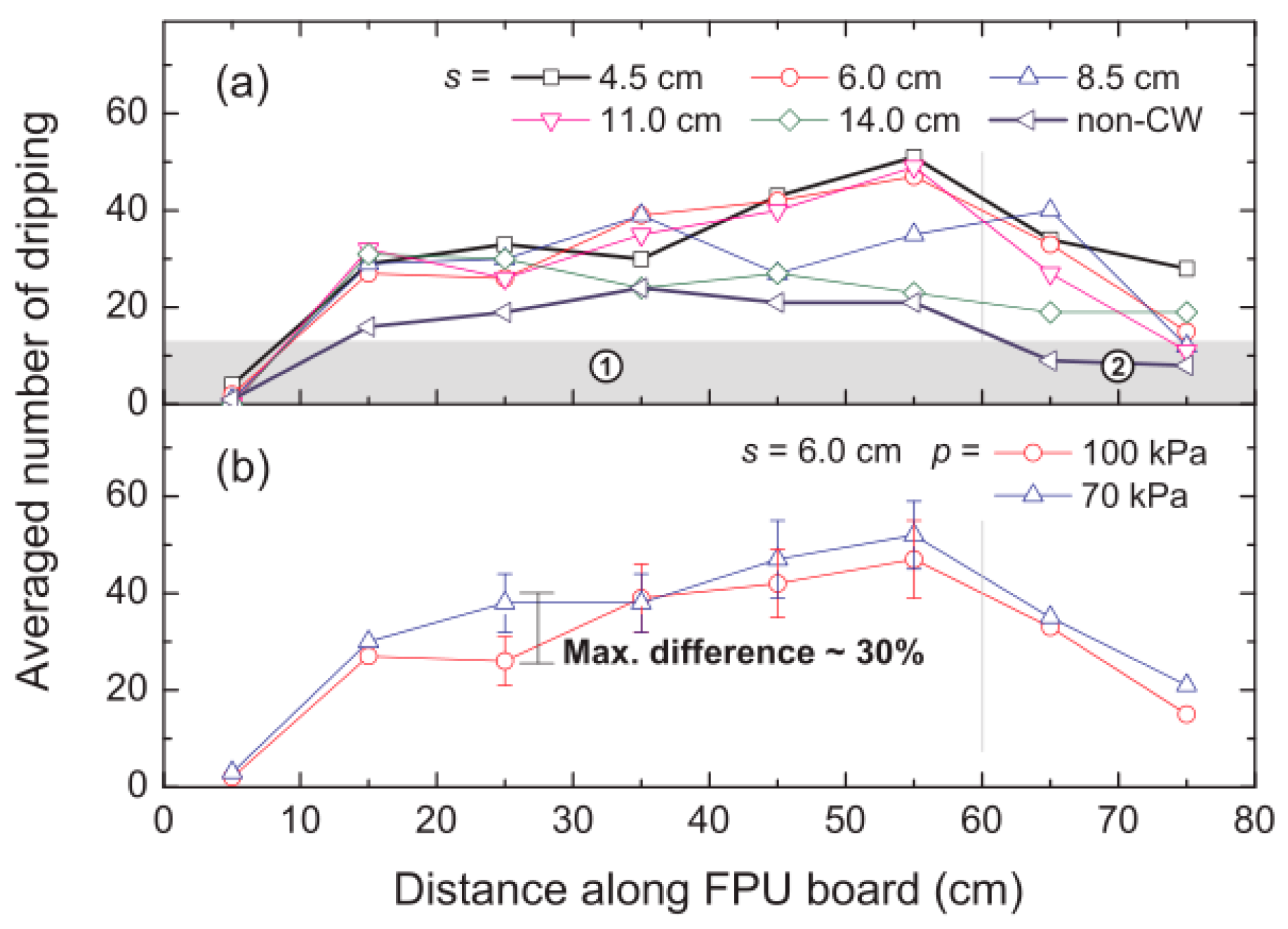
3.3.2. Influencing Factors of Melting and Dripping
Sample Properties
Façade Structures
Ambient Conditions
Flame Retardant Treatment
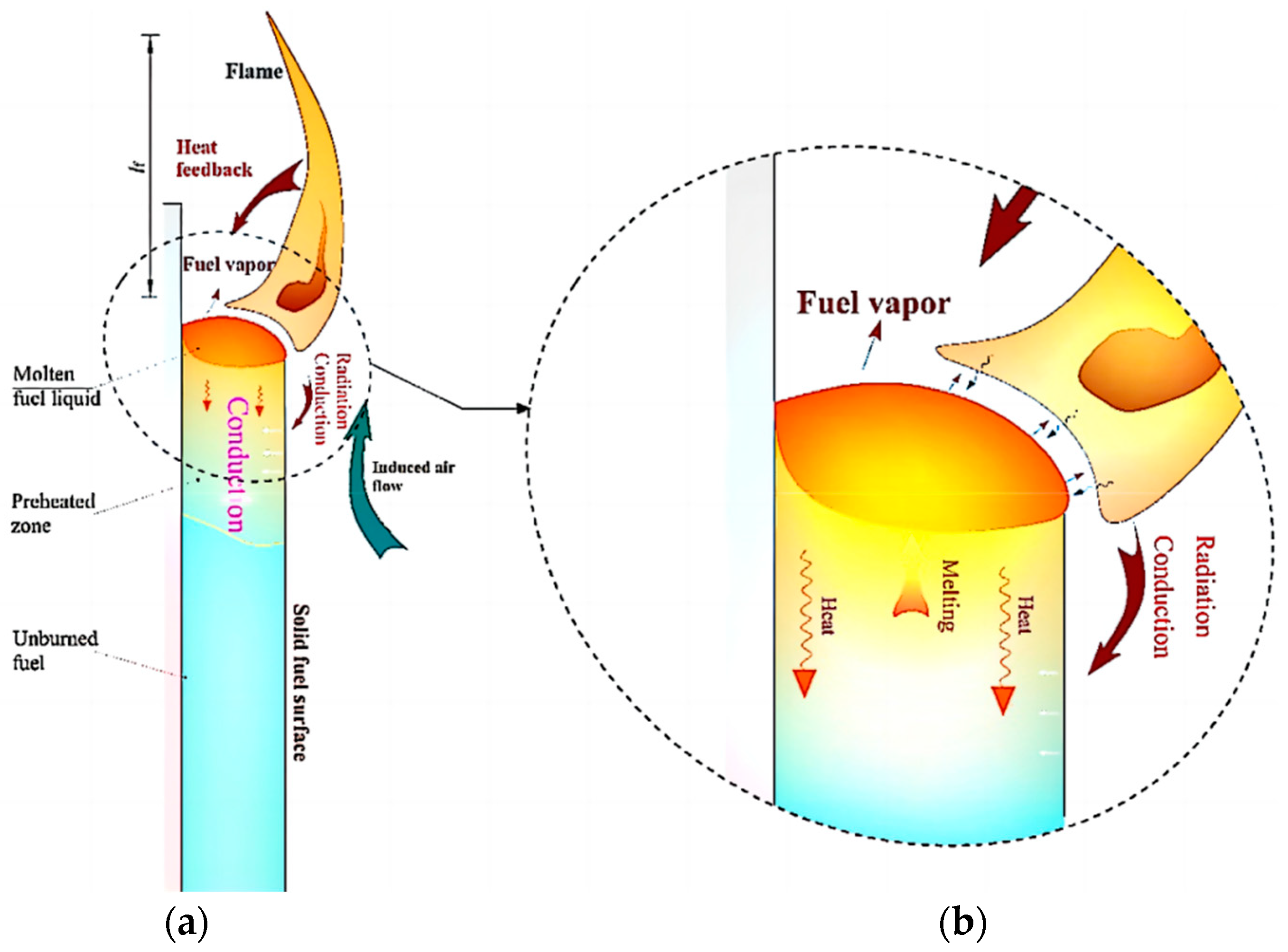
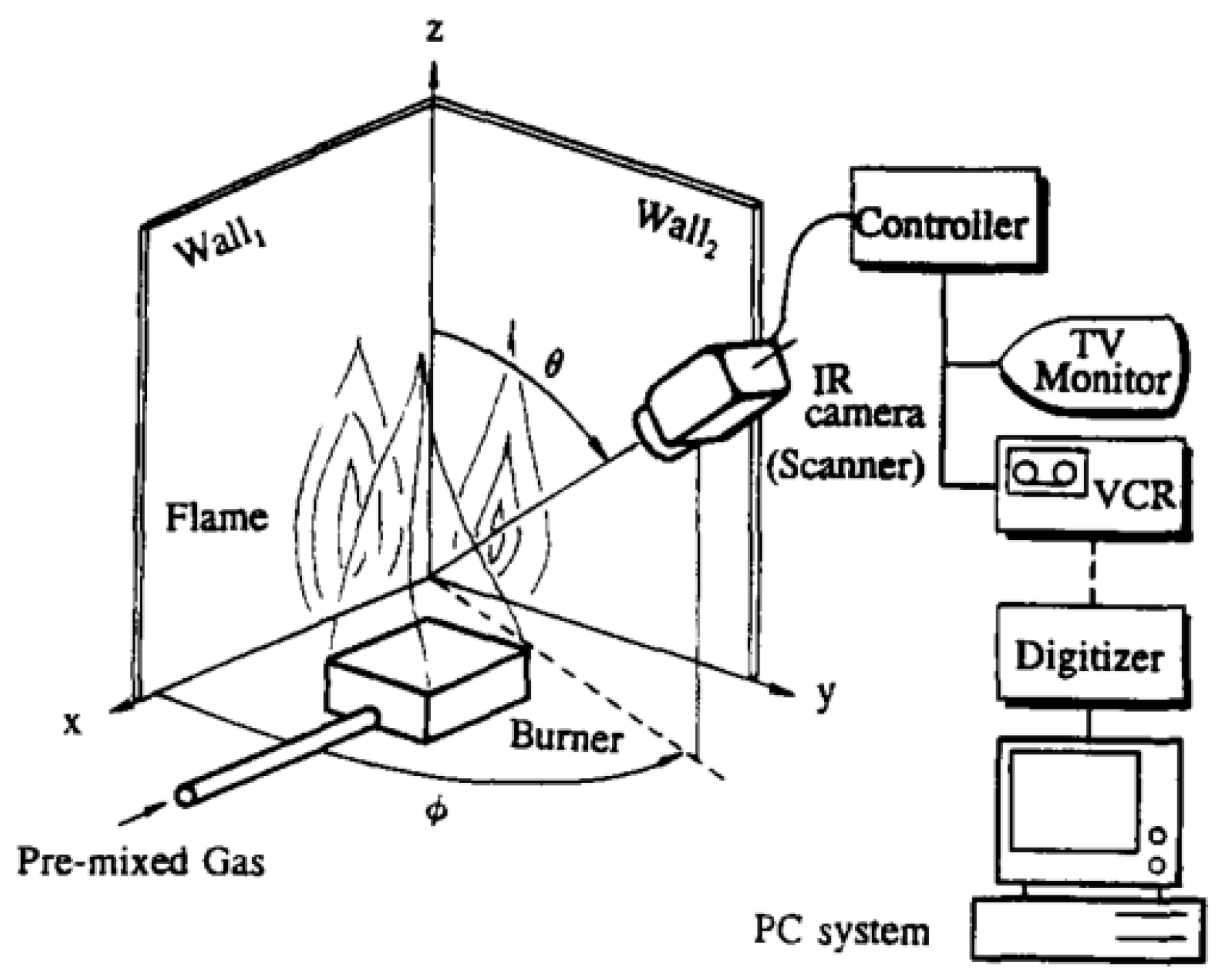
3.4. Flame Appearance
3.4.1. Mechanism Analysis of Flame Appearance
3.4.2. Influencing Factors of Flame Appearance
Sample Properties
Ambient Conditions
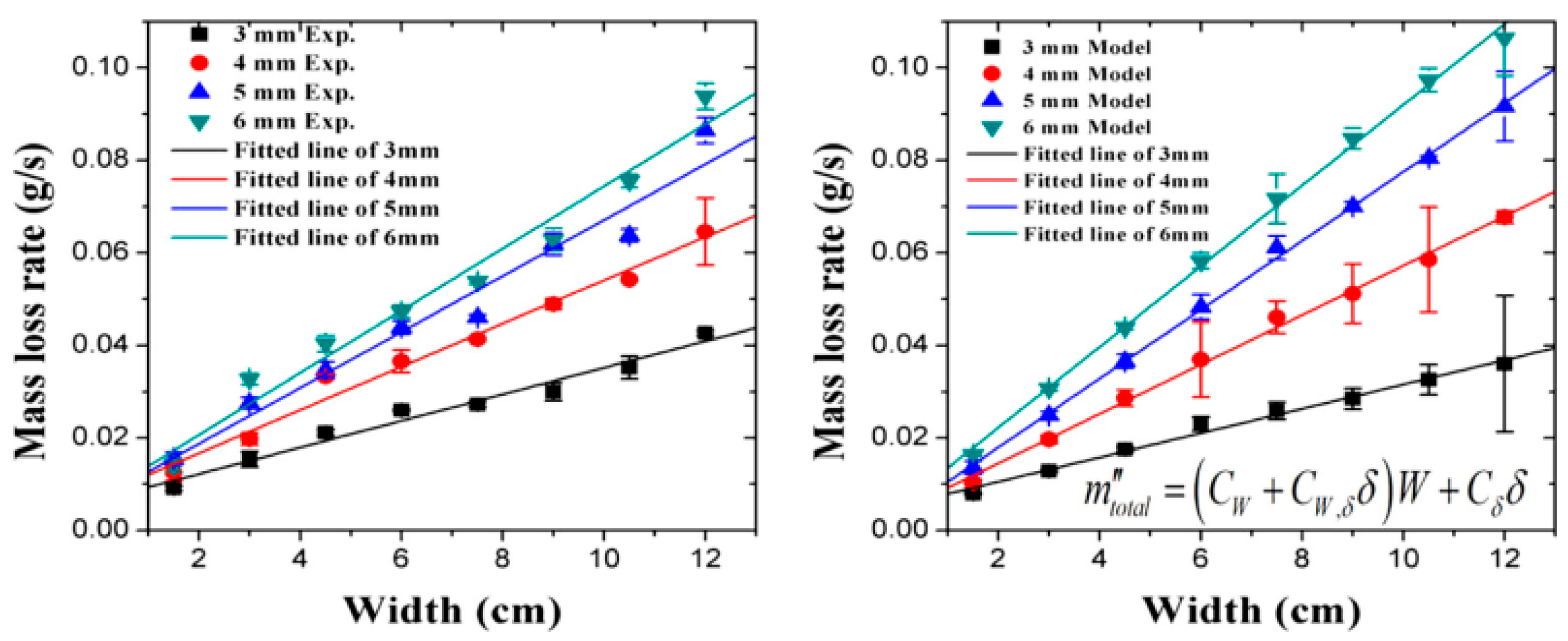
3.5. Burning Rate and Mass Loss Rate
3.5.1. Mechanism Analysis of Burning Rate and Mass Loss Rate
3.5.2. Influencing Factors of Burning Rate and Mass Loss Rate
Sample Properties
Façade Structures
Ambient Conditions
Flame Retardant Treatment
3.6. Temperature and Heat Flow
3.6.1. Mechanism Analysis of Temperature and Heat Flow
3.6.2. Influencing Factors of Temperature and Heat Flow
Sample Properties
Façade Structures
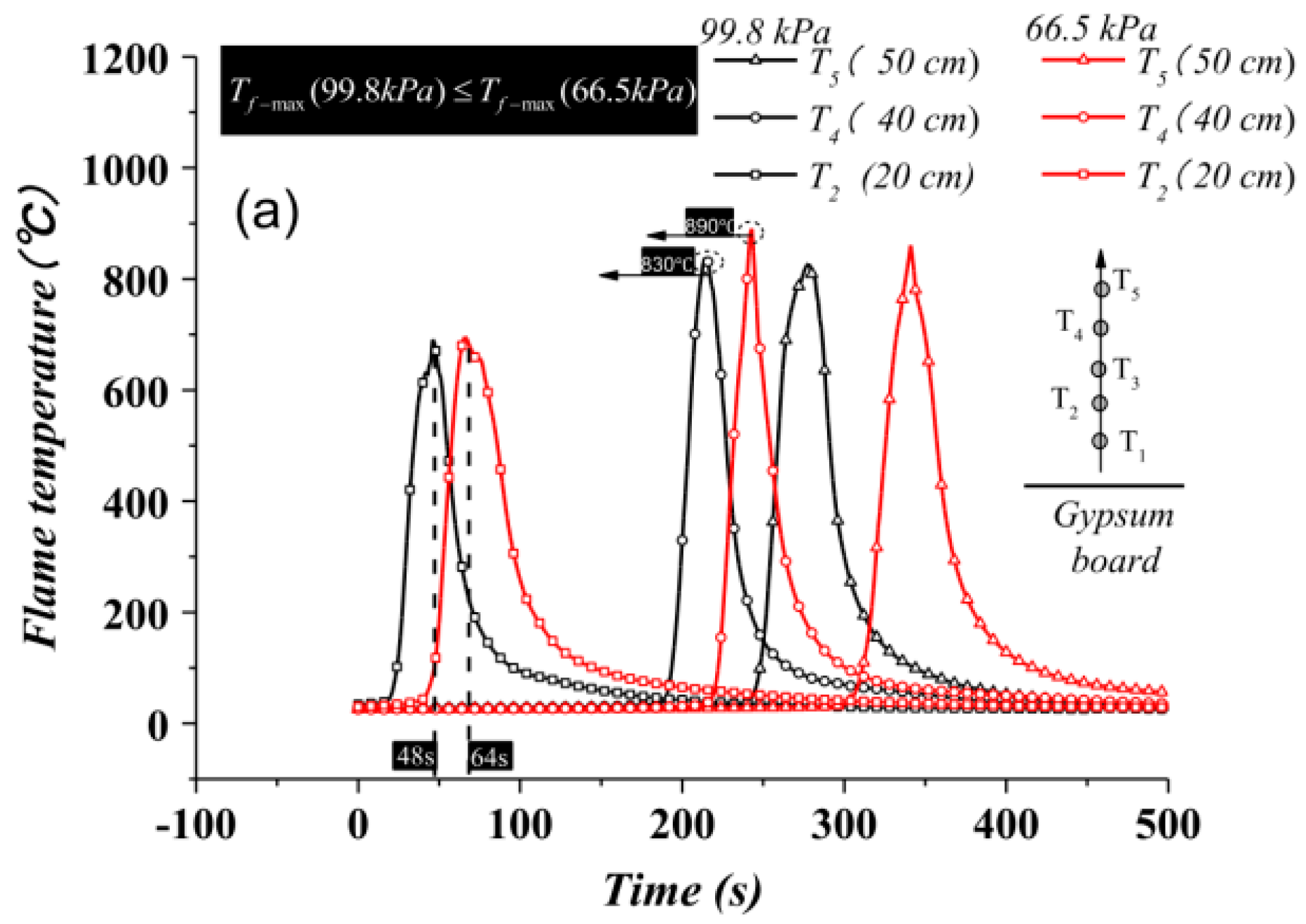
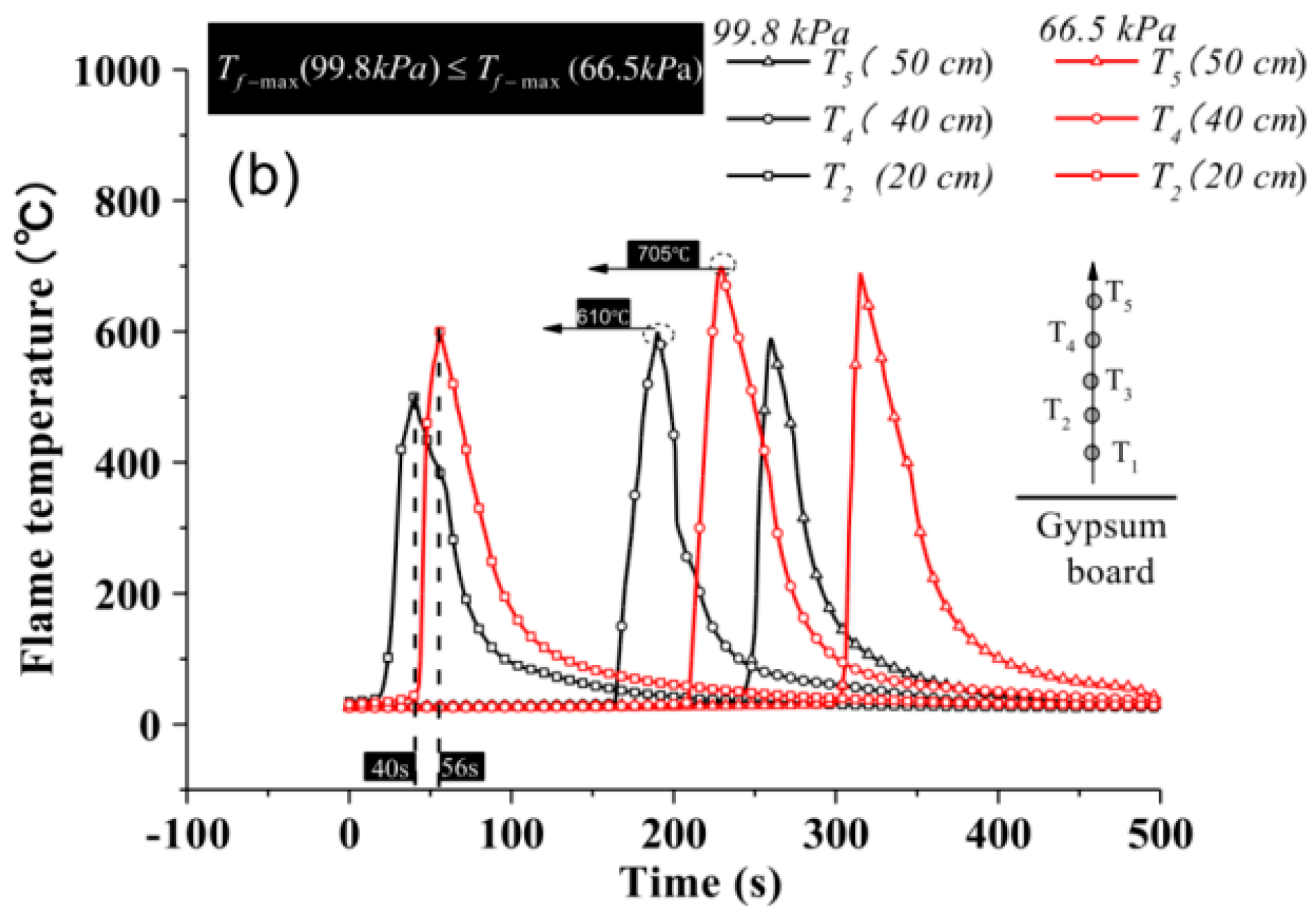
Ambient Conditions
Flame Retardant Treatment
3.7. Gas Products
3.7.1. Mechanism Analysis of Gas Products
3.7.2. Influencing Factors of Gas Products
Sample Properties
Ambient Conditions
Flame Retardant Treatment
4. Flame Spread of Thermoplastic Materials
4.1. Natural Horizontal Flame Spread
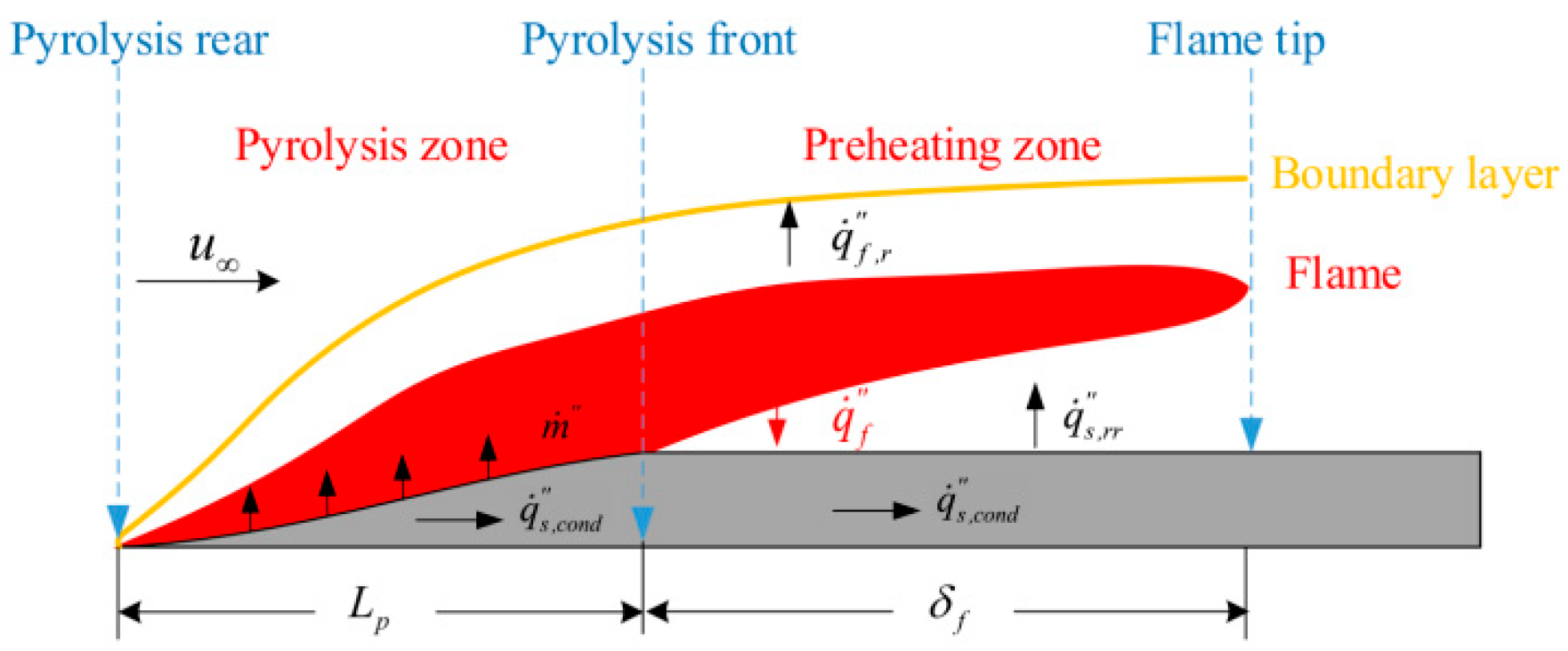
4.1.1. Mechanism Analysis of Natural Horizontal Flame Spread
4.1.2. Influencing Factors of Natural Horizontal Flame Spread
Sample Properties
Ambient Conditions
Flame Retardant Treatment
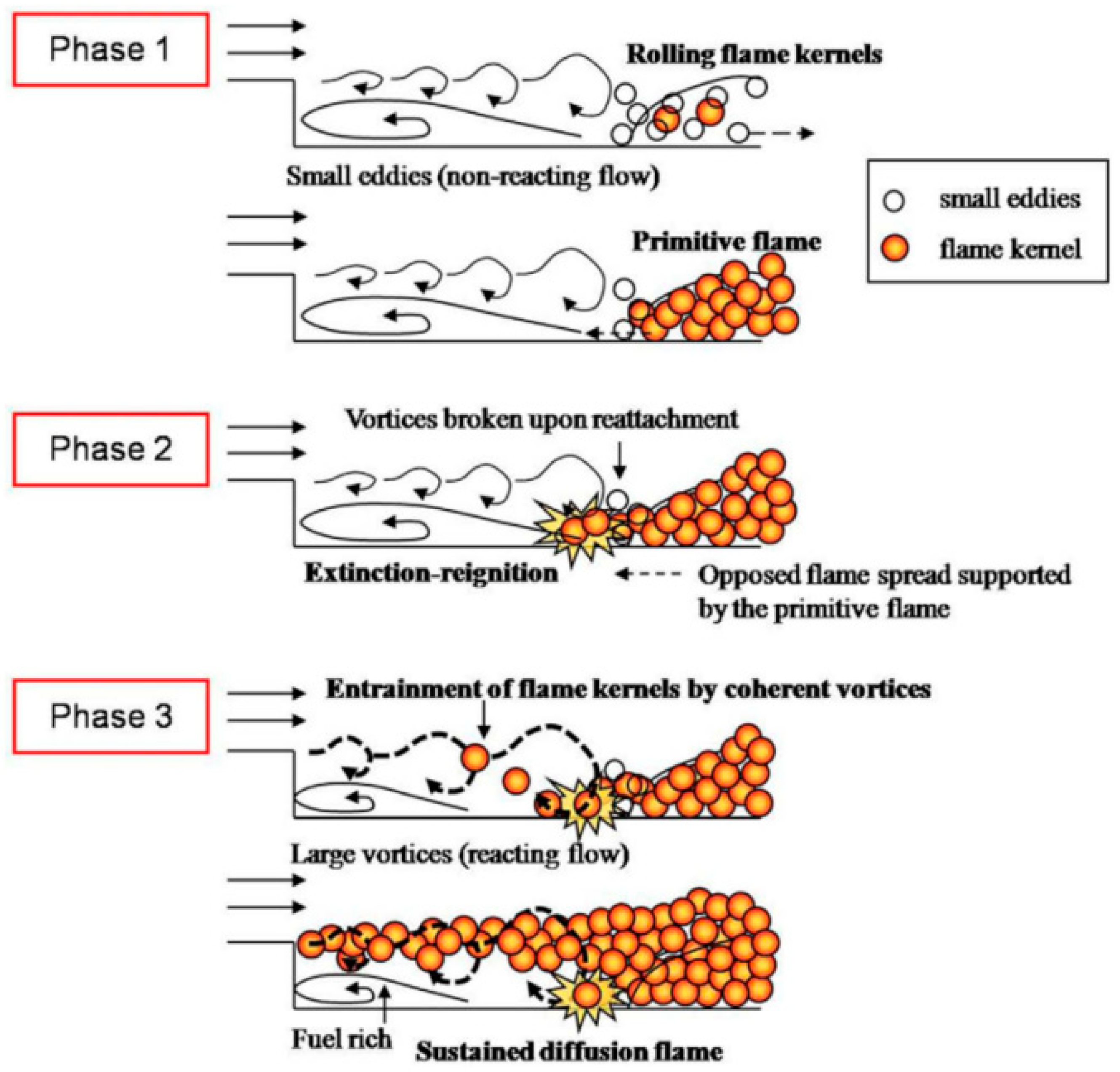
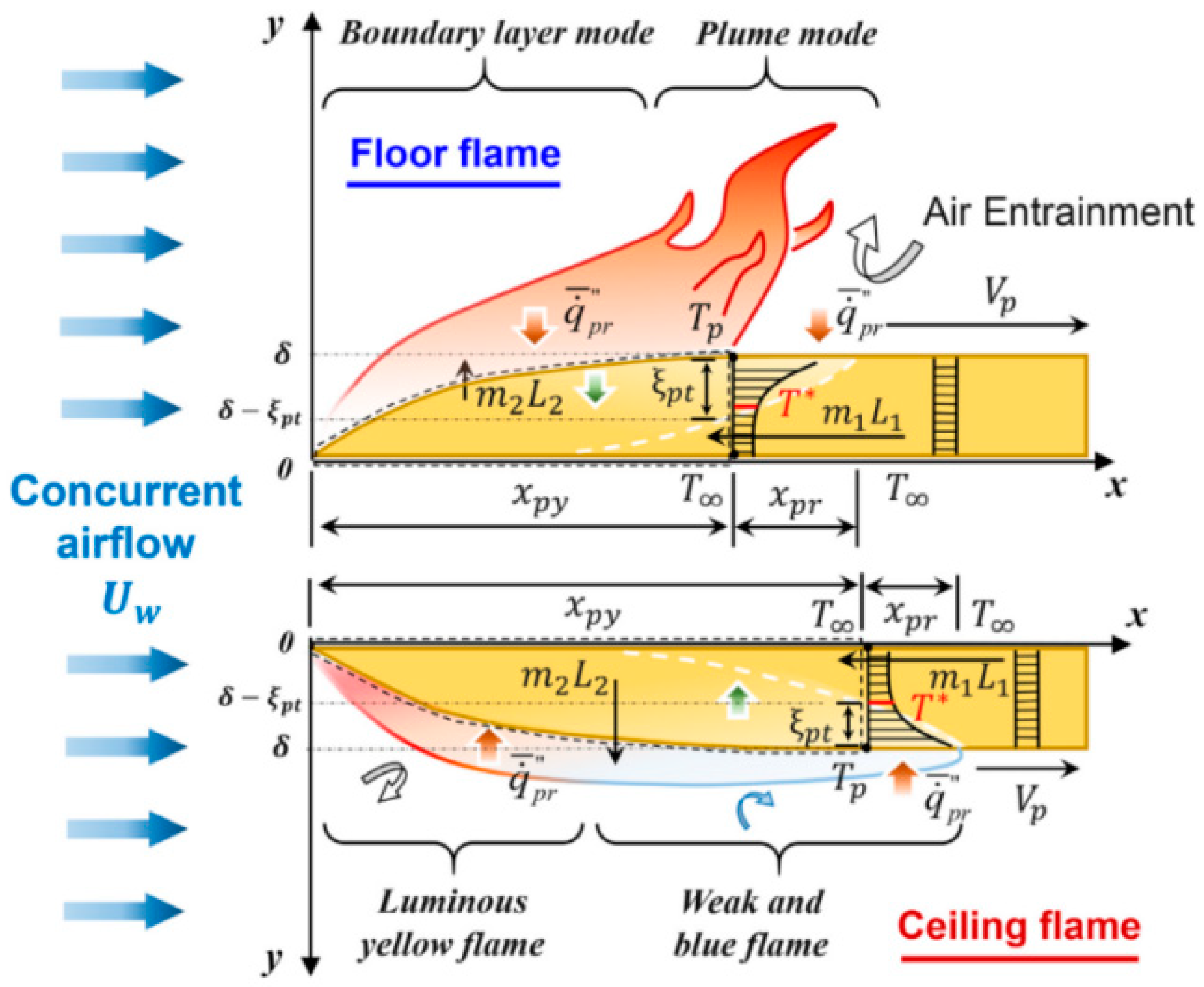
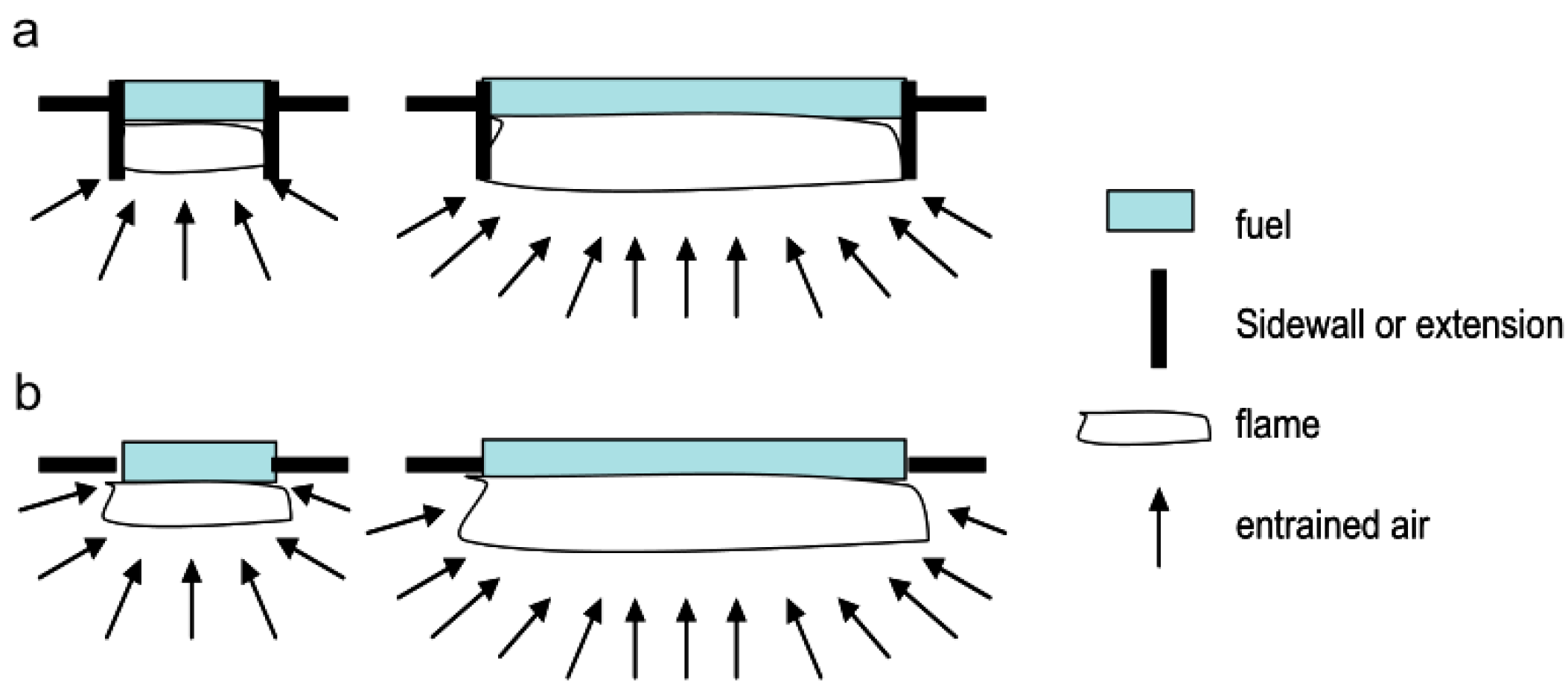
4.2. Horizontal Concurrent-Flow Flame Spread
4.2.1. Mechanism Analysis of Horizontal Concurrent-Flow Flame Spread
4.2.2. Influencing Factors of Horizontal Concurrent-Flow Flame Spread
Sample Properties
Ambient Conditions
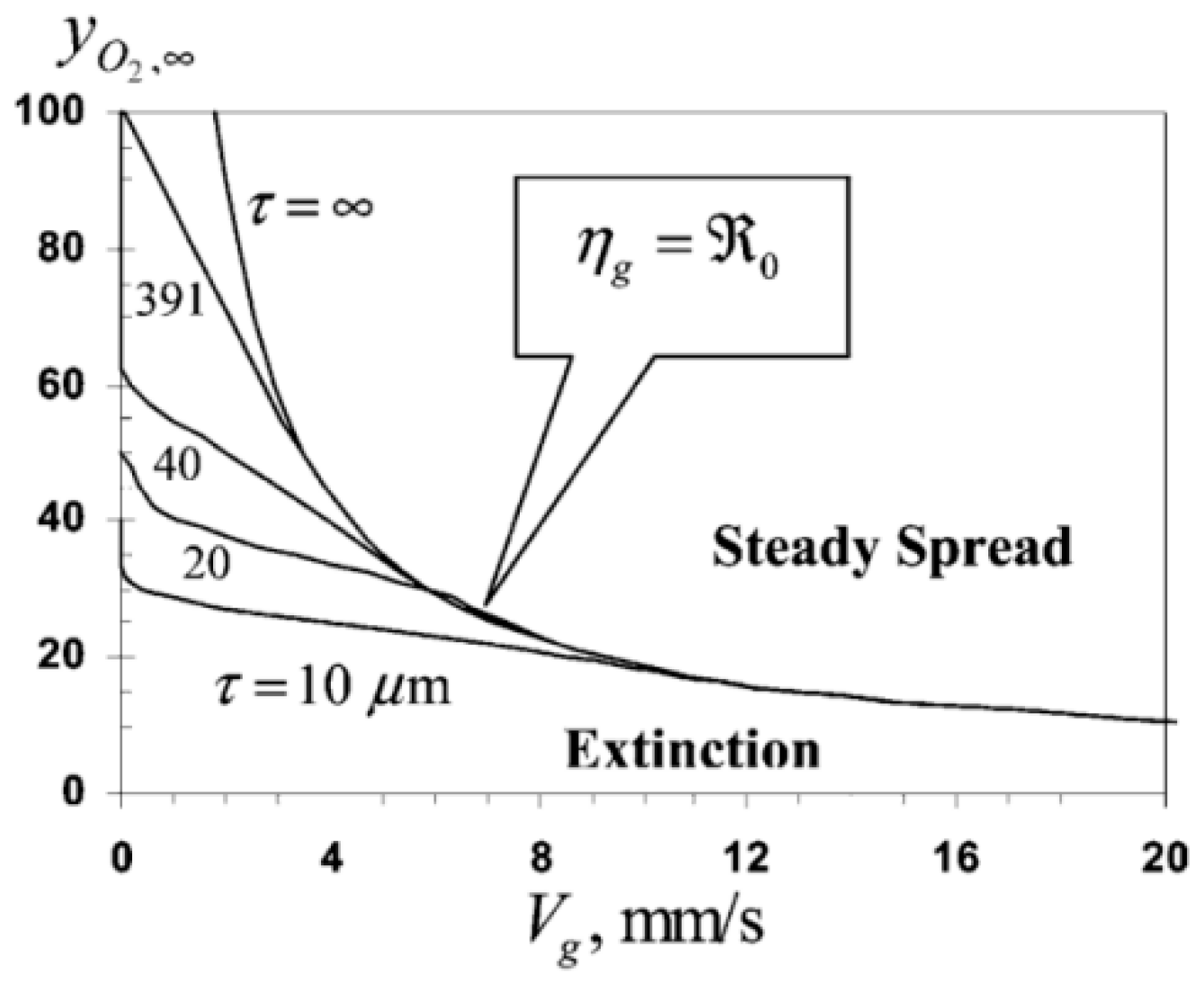
4.3. Horizontal Opposed-Flow Flame Spread
4.3.1. Mechanism Analysis of Horizontal Opposed-Flow Flame Spread
4.3.2. Influencing Factors of Horizontal Opposed-Flow Flame Spread
Sample Properties
Ambient Conditions
4.4. Vertical Concurrent-Flow Flame Spread
4.4.1. Mechanism Analysis of Vertical Concurrent-Flow Flame Spread
4.4.2. Influencing Factors of Vertical Concurrent-Flow Flame Spread
Sample Properties
Façade Structures
Ambient Conditions
4.5. Vertical Opposed-Flow Flame Spread
4.5.1. Mechanism Analysis of Vertical Opposed-Flow Flame Spread
4.5.2. Influencing Factors of Vertical Opposed-Flow Flame Spread
Sample Properties
Façade Structures
Ambient Conditions
Flame Retardant Treatment
5. Conclusions and Future Challenges
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| mass flux (g m−2 s−1) | heat of combustion (kJ mol−1) | ||
| critical mass flux (g m−2 s−1) | heat of gasification (latent plus sensible) (kJmol−1) | ||
| external heat flux (J s−1m−2) | specific heat of solid (J g−1 K−1) | ||
| heat flux (kW m−2) | specific heat (J g−1 K−1) | ||
| ignition heat flux (kW m−2) | thermal conductivity (J s−1 m−1 K−1) | ||
| heat release rate per unit width (kW m−1) | flame height (m) | ||
| initial heat flux (kW m−2) | pyrolysis height (m) | ||
| net heat flux (kW m−2) | sample thickness (m) | ||
| in-depth radiation heat flux (W m–2) | flame height | ||
| wall heat flux (kW m−2) | preheating length | ||
| Qs | solid heat release (J kg−1) | hydrodynamic diameter (m) | |
| acceleration of gravity (m/s2) | width of sample (m) | ||
| modified acceleration of gravity (m/s2) | width of sidewall (m) | ||
| width of back wall (m) | |||
| curtain wall coverage rate | width of the fuel (m) | ||
| flame pulsation frequency (Hz) | gas-phase diffusion length (m) | ||
| Strouhal number | solid length scale (m) | ||
| modified Strouhal number | flame height with flat (m) | ||
| non-dimensional radiation number | pyrolysis region height with flat (m) | ||
| non-dimensional flow velocity | flame height with concave structure (m) | ||
| universal gas constant (J K mol−1) | pyrolysis zone height with concave structure (m) | ||
| solid activation energy (J mol−1) | flame spread rate (m s−1) | ||
| activation energy (kJ mol−1) | flame spread rate in the thermal regime (m s−1) | ||
| solid heat of reaction (kJ mol−1) | flame spread rate in the radiative regime (m s−1) | ||
| de Ris flame coefficient, 4.89 at 21% O2 | velocity of opposing flow (m s−1) | ||
| ignition time (s) | dimensionless oxidizer velocity (m s−1) | ||
| residence times (s) | average wind velocity (m s−1) | ||
| scaled dimensionless heat transfer factor | initial temperature (K) | ||
| pre-exponential factor (s−1) | vaporization temperature (K) | ||
| universal gas constant (8.314 J mol−1 K−1) | characteristic flame temperature (K) | ||
| mole fraction | environmental temperature (K) | ||
| mass fraction | pyrolysis temperature (K) | ||
| environmental pressure (Pa) | ignition temperature (K) | ||
| Greek symbols | |||
| thermal diffusivity (m2/s) | Stefan–Boltzmann constant number | ||
| thermal diffusivity of gas (m2/s) | fuel half-thickness (m) | ||
| weighted thermal diffusivity (m2/s) | incline angle (°) | ||
| maximum thickness of flame (m) | solid thermal conductivity (Wm−1 K−1) | ||
| ambient gas density (kg m−3) | concave structure factor | ||
| density (kg m−3) | gas-phase conductivity (W m−1 K−1) | ||
| solid density (kg m−3) | Zel’dovich number | ||
| transition half-thickness between thin and thick fuel (m) | |||
References
- Huang, X.; Chen, G.; Liu, W.; Zhang, Y.; Sun, J. Thermal Analysis of Vertical Upward Flame Spread and Dripping Behaviors of Polystyrene Foams at Different Altitudes. J. Macromol. Sci. Part B 2017, 56, 517–531. [Google Scholar] [CrossRef]
- Tu, R.; Ma, X.; Zeng, Y.; Zhou, X.; Zhang, Q.; Wang, J.; Fang, J. Influences of sub-atmospheric pressure on downward flame spread over typical insulation material with parallel glass curtain wall structure in underground buildings. Tunn. Undergr. Space Technol. 2020, 103, 103509. [Google Scholar] [CrossRef]
- Tu, R.; Ma, X.; Zeng, Y.; Zhou, X.; He, L.; Fang, T.; Fang, J. Coupling effects of pressure and inclination on downward flame spread over flexible polyurethane foam board. Build. Environ. 2019, 164, 106339. [Google Scholar] [CrossRef]
- Gong, J.; Zhou, X.; Deng, Z.; Yang, L. Influences of low atmospheric pressure on downward flame spread over thick PMMA slabs at different altitudes. Int. J. Heat Mass Transf. 2013, 61, 191–200. [Google Scholar] [CrossRef]
- Zarzecki, M.; Quintiere, J.G.; Lyon, R.E.; Rossmann, T.; Diez, F.J. The effect of pressure and oxygen concentration on the combustion of PMMA. Combust. Flame 2013, 160, 1519–1530. [Google Scholar] [CrossRef]
- Yan, W.; Shen, Y.; An, W.; Jiang, L.; Sun, J. Experimental study on fire risk of buildings’ U-shaped exterior wall on flame propagation of insulation material on plain and plateau. J. Fire Sci. 2015, 33, 358–373. [Google Scholar] [CrossRef]
- Zhou, Y.; Bu, R.; Yi, L.; Sun, J. Heat transfer mechanism of concurrent flame spread over rigid polyurethane foam: Effect of ambient pressure and inclined angle. Int. J. Therm. Sci. 2020, 155, 106403. [Google Scholar] [CrossRef]
- Tu, R.; Ma, X.; Zeng, Y.; Zhou, X.; Zhang, Q. Influences of sub-atmospheric pressure on upward flame spread over flexible polyurethane foam board with multiple inclinations. Appl. Sci. 2020, 10, 7117. [Google Scholar] [CrossRef]
- Jiakun, D.; Delichatsios, M.A.; Lizhong, Y. Piloted ignition of solid fuels at low ambient pressure and varying igniter location. Proc. Combust. Inst. 2013, 34, 2497–2503. [Google Scholar] [CrossRef]
- McAllister, S.; Fernandez-Pello, C.; Urban, D.; Ruff, G. The combined effect of pressure and oxygen concentration on piloted ignition of a solid combustible. Combust. Flame 2010, 157, 1753–1759. [Google Scholar] [CrossRef]
- Alibert, D.; Coutin, M.; Mense, M.; Pizzo, Y.; Porterie, B. Effect of oxygen concentration on the combustion of horizontally-oriented slabs of PMMA. Fire Saf. J. 2017, 91, 182–190. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, T.; Chen, Q.; Wang, J. Numerical study on the effect of oxygen concentration on the piloted ignition of PMMA in reduced pressure atmospheres. Int. J. Numer. Methods Heat Fluid Flow 2020, 22, 3903–3917. [Google Scholar] [CrossRef]
- Tao, S.; Fang, J.; Meng, Y.; Shah, H.R.; Yang, L. Ignition risk analysis of common building material cylindrical PMMA exposed to an external irradiation with in-depth absorption. Constr. Build. Mater. 2020, 251, 118955. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, B.; Zhang, X.; Yang, Y. A comparative study on horizontal flame spread behaviors of thermoplastic polymers with different melt flow indexes under external radiation. Therm. Sci. Eng. Prog. 2022, 35, 101463. [Google Scholar] [CrossRef]
- Zhang, M.; Li, M.; Wang, Y.; Sun, J. Experimental study of thermal shrinkage and melt dripping properties of expanded polystyrene under various heat fluxes. J. Build. Eng. 2022, 60, 105179. [Google Scholar] [CrossRef]
- Zhao, K.; Zhou, X.; Yang, L.; Gong, J.; Wu, Z.; Huan, Z.; Liu, X. Width effects on downward flame spread over poly (methyl methacrylate) sheets. J. Fire Sci. 2015, 33, 69–84. [Google Scholar] [CrossRef]
- Gong, J.; Zhou, X.; Li, J.; Yang, L. Effect of finite dimension on downward flame spread over PMMA slabs: Experimental and theoretical study. Int. J. Heat Mass Transf. 2015, 91, 225–234. [Google Scholar] [CrossRef]
- Sarma, S.; Chakraborty, A.; Manu, N.M.; Muruganandam, T.M.; Raghavan, V.; Chakravarthy, S.R. Spatio-temporal structure of vertically spreading flame over non-planar PMMA surfaces. Proc. Combust. Inst. 2017, 36, 3027–3035. [Google Scholar] [CrossRef]
- Tsai, K.C. Width effect on upward flame spread. Fire Saf. J. 2009, 44, 962–967. [Google Scholar] [CrossRef]
- Pizzo, Y.; Consalvi, J.L.; Querre, P.; Coutin, M.; Porterie, B. Width effects on the early stage of upward flame spread over PMMA slabs: Experimental observations. Fire Saf. J. 2009, 44, 407–414. [Google Scholar] [CrossRef]
- An, W.; Cai, M.; Tang, Y.; Li, Q.; Wang, Z. Influence of Inclined Angle on Upward Flame Spread over Discrete Extruded Polystyrene Foam. Combust. Sci. Technol. 2022, 194, 1301–1320. [Google Scholar] [CrossRef]
- An, W.; Huang, X.; Wang, Q.; Zhang, Y.; Sun, J.; Liew, K.M.; Wang, H.; Xiao, H. Effects of sample width and inclined angle on flame spread across expanded polystyrene surface in plateau and plain environments. J. Thermoplast. Compos. Mater. 2015, 28, 111–127. [Google Scholar] [CrossRef]
- Xie, Q.; Luo, S.; Da, L. Effects of backwall on inner thermal structure in opposed-flow horizontal flame spread of thick PMMA panel. Appl. Therm. Eng. 2021, 185, 116424. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, X.; Yuan, M.; Wang, P.; Chen, J. Effect of Geometry and Dimensions on the Upward Fire Spread in U-Shaped Structures. Fire Technol. 2022, 59, 73–93. [Google Scholar] [CrossRef]
- Wang, X.; Chen, Y. Fire spread in u-shaped facade structures in high-rise buildings. In Proceedings of the 9th International Conference on Fire Science and Fire Protection Engineering, Chengdu, China, 18–20 October 2019. [Google Scholar]
- Hui, Z.; Guoqing, Z.; Yunji, G.; Zhongri, H. Dripping behavior of vertical burning thermally thin PMMA with different spacings to wall. J. Thermoplast. Compos. Mater. 2018, 31, 616–633. [Google Scholar] [CrossRef]
- Ma, X.; Tu, R.; An, W.; Xu, L.; Luo, S.; Wang, J.; Tang, F. Experimental study of interlayer effect induced by building facade curtain wall on downward flame spread behavior of polyurethane. Appl. Therm. Eng. 2020, 167, 114694. [Google Scholar] [CrossRef]
- Peng, F.; Lai, D.; Zheng, Y.; Yang, L. Effects of ceiling inclination on lateral flame spread over vertical Poly (methyl methacrylate) surface. Case Stud. Therm. Eng. 2019, 15, 100519. [Google Scholar] [CrossRef]
- Ma, X.; Tu, R.; Ding, C.; Zeng, Y.; Wang, Y.; Fang, T. Thermal and fire risk analysis of low pressure on building energy conservation material flexible polyurethane with various inclined facade constructions. Constr. Build. Mater. 2018, 167, 449–456. [Google Scholar] [CrossRef]
- Zhu, H.; Gao, Y.; Pan, R.; Zhong, B. Spacing effects on downward flame spread over thin PMMA slabs. Case Stud. Therm. Eng. 2019, 13, 100370. [Google Scholar] [CrossRef]
- Ma, X.; Tu, R.; Cheng, X.; Zhu, S.; Ma, J.; Fang, T. Experimental study of thermal behavior of insulation material rigid polyurethane in parallel, symmetric, and adjacent building façade constructions. Polymers 2018, 10, 1104. [Google Scholar] [CrossRef]
- Tsai, K.C. Influence of sidewalls on width effects of upward flame spread. Fire Saf. J. 2011, 46, 294–304. [Google Scholar] [CrossRef]
- An, W.; Sun, J.; Liew, K.M.; Zhu, G. Effects of building concave structure on flame spread over extruded polystyrene thermal insulation material. Appl. Therm. Eng. 2017, 121, 802–809. [Google Scholar] [CrossRef]
- An, W.; Yin, X.; Cai, M.; Tang, Y.; Li, Q.; Hu, X. Influence of U-shaped structure on upward flame spread and heat transfer behaviors of PMMA used in building thermal engineering. Case Stud. Therm. Eng. 2020, 22, 100794. [Google Scholar] [CrossRef]
- Chen, Z.; Chai, Q.; Liao, S.; He, Y.; Li, Y.; Wu, W.; Li, B. Application of simplified version of advanced isoconversional procedure in non-isothermal kinetic study: Thermal decomposition of NH4Co0.9Zn0.1PO4·H2O. J. Therm. Anal. Calorim. 2013, 113, 649–657. [Google Scholar] [CrossRef]
- Friedman, H.L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic. J. Polym. Sci. Part C Polym. Symp. 2007, 6, 183–195. [Google Scholar] [CrossRef]
- Ozawa, T. A New Method of Analyzing Thermogravimetric Data. Bull. Chem. Soc. Jpn. 1965, 38, 1881–1886. [Google Scholar] [CrossRef]
- Flynn, J.H.; Wall, L.A. General Treatment of the Thermogravimetry of Polymers. J. Res. Natl. Bur. Standards. Sect. A Phys. Chem. 1966, 70A, 487–523. [Google Scholar] [CrossRef]
- Wang, S.; Chen, H.; Zhang, L. Thermal decomposition kinetics of rigid polyurethane foam and ignition risk by a hot particle. J. Appl. Polym. Sci. 2014, 131, 1–9. [Google Scholar] [CrossRef]
- Li, M.; Jiang, L.; He, J.J.; Sun, J.H. Kinetic triplet determination and modified mechanism function construction for thermo-oxidative degradation of waste polyurethane foam using conventional methods and distributed activation energy model method. Energy 2019, 175, 1–13. [Google Scholar] [CrossRef]
- Coats, A.W.; Redfern, J.P. Kinetic parameters from thermogravimetric data. Nature 1964, 201, 68–69. [Google Scholar] [CrossRef]
- Coats, A.; Redfern, J.-P. Kinetic parameters from thermogravimetric data. II. J. Polym. Sci. C Polym. Lett. 1965, 3, 917–920. [Google Scholar] [CrossRef]
- Vand, V. A theory of the irreversible electrical resistance changes of metallic films evaporated in vacuum. Proc. Phys. Soc. 1943, 55, 222–246. [Google Scholar] [CrossRef]
- Pitt, G. The kinetic of the evolution of volatile products from coal. Fuel 1962, 41, 267–274. [Google Scholar]
- Li, M.; Liu, L.; Jiang, L.; Gou, F.H.; Sun, J.H. Application of distributed activation energy models to polymer pyrolysis: Effects of distributed model selection, characteristics, validation, and sensitivity analysis. Fuel 2019, 254, 115594.1–115594.18. [Google Scholar] [CrossRef]
- Liu, Z.; He, H.; Zhang, J.; Zheng, J.; Zhuang, H. Experimental investigation and numerical simulation of the combustion of flexible polyurethane foam with larger geometries. Polym Test. 2020, 81, 106270. [Google Scholar] [CrossRef]
- Lawson, D.I.; Simms, D.L. The Ignition of Wood by Radiation. Brit. J. Appl. Phys. 1952, 3, 288. [Google Scholar] [CrossRef]
- Whiting, P.; Dowden, J.M.; Kapadia, P.D.; Davis, M.P. A one-dimensional mathematical model of laser induced thermal ablation of biological tissue. Lasers Med. Sci. 1992, 7, 357–368. [Google Scholar] [CrossRef]
- Billings, M.J.; Warren, L.; Wilkings, R. Thermal Erosion of Electrical Insulating Materials. IEEE Trans. Electr. Insul. 2007, EI-6, 82–90. [Google Scholar] [CrossRef]
- Delichatsios, M.A.; Chen, Y. Asymptotic, approximate, and numerical solutions for the heatup and pyrolysis of materials including reradiation losses. Combust. Flame 1993, 92, 292–307. [Google Scholar] [CrossRef]
- Quintiere, J.; Iqbal, N. An approximate integral model for the burning rate of a thermoplastic-like material. Fire Mater. 2010, 18, 89–98. [Google Scholar] [CrossRef]
- Staggs, J. A discussion of modelling idealised ablative materials with particular reference to fire testing. Fire Saf. J. 1997, 28, 47–66. [Google Scholar] [CrossRef]
- Tewarson, A.; Pion, R.F. Flammability of plastics—I. Burning intensity. Combust. Flame 1976, 26, 85–103. [Google Scholar] [CrossRef]
- Bal, N.; Rein, G. Numerical investigation of the ignition delay time of a translucent solid at high radiant heat fluxes. Combust. Flame 2011, 158, 1109–1116. [Google Scholar] [CrossRef]
- Lautenberger, C.; Fernandez-Pello, A. Approximate Analytical Solutions for The Transient Mass Loss Rate And Piloted Ignition Time Of A Radiatively Heated Solid In The High Heat Flux Limit. Fire Saf. Sci. 2005, 8, 445–456. [Google Scholar] [CrossRef]
- Gong, J.; Li, Y.; Chen, Y.; Li, J.; Wang, X.; Jiang, J.; Wang, Z.; Wang, J. Approximate analytical solutions for transient mass flux and ignition time of solid combustibles exposed to time-varying heat flux. Fuel 2018, 211, 676–687. [Google Scholar] [CrossRef]
- Gong, J.; Stoliarov, S.I.; Shi, L.; Li, J.; Zhu, S.; Zhou, Y.; Wang, Z. Analytical prediction of pyrolysis and ignition time of translucent fuel considering both time-dependent heat flux and in-depth absorption. Fuel 2019, 235, 913–922. [Google Scholar] [CrossRef]
- Fang, J.; Meng, Y.-R.; Wang, J.-W.; Zhao, L.-Y.; He, X.-Z.; Ji, J.; Zhang, Y.-M. Experimental, numerical and theoretical analyses of the ignition of thermally thick PMMA by periodic irradiation. Combust. Flame 2018, 197, 41–48. [Google Scholar] [CrossRef]
- Yang, J.T.; Hsiao, F.C.; Lin, Y.C. Transient flame spread during convective ignition of solid fuel in a sudden-expansion combustor. Combust. Flame 2009, 156, 1917–1925. [Google Scholar] [CrossRef]
- Hadden, R.; Alkatib, A.; Rein, G.; Torero, J.L. Radiant Ignition of Polyurethane Foam: The Effect of Sample Size. Fire Technol. 2014, 50, 673–691. [Google Scholar] [CrossRef]
- Yang, J.-T.; Wu, C.Y.-Y.; Din, S.-J. Ignition Transient of a Polymethylmethacrylate Slab in a Sudden-Expansion Combustor. Combust. Flame 1994, 98, 300–308. [Google Scholar] [CrossRef]
- Brown, J.E.; Kashiwagi, T. Gas phase oxygen effect on chain scission and monomer content in bulk poly (methy1 methacrylate) degraded by external thermal radiation. Polym. Degrad. Stab. 1996, 52, 1–10. [Google Scholar] [CrossRef]
- Luo, S.; Xie, Q.; Tang, X.; Qiu, R.; Yang, Y. A quantitative model and the experimental evaluation of the liquid fuel layer for the downward flame spread of XPS foam. J. Hazard. Mater. 2017, 329, 30–37. [Google Scholar] [CrossRef] [PubMed]
- Olson, S.L.; Urban, D.L.; Ruff, G.A.; Ferkul, P.V.; Toth, B.; Eigenbrod, C.; Meyer, F.; Jomaas, G. Concurrent Flame Spread Over Two-Sided Thick PMMA Slabs in Microgravity. Fire Technol. 2020, 56, 49–69. [Google Scholar] [CrossRef]
- Zhou, Q.; Gui, W.Y.; Ma, X.; Cheng, X.; Tang, F. Experimental study of the downward flame spreading characteristics of building facade flexible polyurethane with a lateral environment wind effect. Case Stud. Therm. Eng. 2021, 26, 101090. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, J. Experimental Study on Horizontal Flame Spread of Dual-Flame Sources for Building Façade Energy Conservation FPU Foam Under the Effect of Lateral Wind. Front. Energy Res. 2022, 10, 887499. [Google Scholar] [CrossRef]
- Zhang, Z.; Wei, Z. Experiment and simulation of the effects of non-uniform magnetic field on the regression rate of PMMA. Combust. Flame 2021, 223, 337–348. [Google Scholar] [CrossRef]
- Yang, C.T.; T’ien, J.S. Numerical Simulation of Combustion and Extinction of a Solid Cylinder in Low-Speed Cross Flow. J. Heat Transfer. 1998, 120, 1055–1063. [Google Scholar] [CrossRef]
- Fukumoto, K.; Wang, C.; Wen, J. Large eddy simulation of upward flame spread on PMMA walls with a fully coupled fluid–solid approach. Combust. Flame 2018, 190, 365–387. [Google Scholar] [CrossRef]
- Zhang, Y.; Fang, J.; Shah, H.R.; Song, L. Effect of unheated segment on heat transfer over a thermally thick material under forced flow. Int. J. Therm. Sci. 2022, 178, 107585. [Google Scholar] [CrossRef]
- Xu, X.; Zhu, G.; Liu, X.; Zhang, X.; Chu, T. Experimental study on influence of air gap on upward flame spread over discrete fuel. Case Stud. Therm. Eng. 2021, 28, 101416. [Google Scholar] [CrossRef]
- Ma, X.; Tu, R.; Ding, C.; Zeng, Y.; Xu, L.; Fang, T. Experimental study on thermal safety analysis of flexible polyurethane at various facade inclined structures under low ambient pressure condition. Eng. Struct. 2018, 176, 11–19. [Google Scholar] [CrossRef]
- Trubachev, S.A.; Korobeinichev, O.P.; Karpov, A.I.; Shaklein, A.A.; Glaznev, R.K.; Gonchikzhapov, M.B.; Paletsky, A.A.; Tereshchenko, A.G.; Shmakov, A.G.; Bespalova, A.S.; et al. The Effect of Triphenyl Phosphate Inhibition on Flame Propagation over Cast PMMA Slabs. Proceedings of the Combustion Institute; Elsevier Ltd.: Amsterdam, The Netherlands, 2021; pp. 4635–4644. [Google Scholar]
- Tsai, K.C.; Drysdale, D. Flame height correlation and upward flame spread modelling. Fire Mater. 2002, 26, 279–287. [Google Scholar] [CrossRef]
- Consalvi, J.L.; Pizzo, Y.; Porterie, B.; Torero, J.L. On the flame height definition for upward flame spread. Fire Saf. J. 2007, 42, 384–392. [Google Scholar] [CrossRef]
- Yan, W.; Li, J.; Shen, Y.; Wang, K. Experimental investigations on the flame spread of building’s vertical U-shape façade. J. Therm. Anal. Calorim. 2022, 147, 5961–5971. [Google Scholar] [CrossRef]
- Zhou, J.; Mao, J.; Han, X.; Xing, Z.; Deng, Z. Experimental studies on the thickness of upward flame over poly(methyl methacrylate) slabs. Fire Mater. 2018, 42, 81–87. [Google Scholar] [CrossRef]
- An, W.; Xiao, H.; Liew, K.M.; Jiang, L.; Yan, W.; Zhou, Y.; Huang, X.; Sun, J.; Gao, L. Downward flame spread over extruded polystyrene: Effects of sample thickness, pressure, and sidewalls. J. Therm. Anal. Calorim. 2015, 119, 1091–1103. [Google Scholar] [CrossRef]
- Meng, Q.X.; Zhu, G.Q.; Yu, M.M.; Liang, Z.H. Experimental study on upward flame spread characteristics of external thermal insulation material under the influence of porosity. Case Stud. Therm. Eng. 2018, 12, 365–373. [Google Scholar] [CrossRef]
- Zhao, Z.; Tang, F.; Chen, L.; Zhang, J.; Wen, J. Effect of Parallel Curtain Walls on Upward Flame Spread Characteristics and Mass Loss Rate Over PMMA. Fire Technol. 2021, 59, 53–72. [Google Scholar] [CrossRef]
- Ma, X.; Tu, R.; Zhao, Y.; Xie, Q. Study on downward flame spread behavior of flexible polyurethane board in external heat flux. J. Thermoplast. Compos. Mater. 2015, 28, 1693–1707. [Google Scholar] [CrossRef]
- Nakamura, Y.; Kizawa, K.; Mizuguchi, S.; Hosogai, A.; Wakatsuki, K. Experimental Study on Near-Limiting Burning Behavior of Thermoplastic Materials with Various Thicknesses Under Candle-Like Burning Configuration. Fire Technol. 2016, 52, 1107–1131. [Google Scholar] [CrossRef]
- Apte, V.B.; Bilger, R.W.; Green, A.R.; Quintiere, J.G. Wind-Aided Turbulent Flame Spread and Burning Over Large-Scale Horizontal PMMA Surfaces. Combust. Flame 1991, 85, 169–184. [Google Scholar] [CrossRef]
- Zhu, H.; Zhu, G.; Gao, Y.; Zhao, G. Experimental Studies on the Effects of Spacing on Upward Flame Spread over Thin PMMA. Fire Technol. 2017, 53, 673–693. [Google Scholar] [CrossRef]
- Huang, X.; Liu, W.; Zhao, J.; Zhang, Y.; Sun, J. Experimental study of altitude and orientation effects on heat transfer over polystyrene insulation material: Ignition and combustion behaviors. J. Therm. Anal. Calorim. 2015, 122, 281–293. [Google Scholar] [CrossRef]
- Li, Y.; Liao, Y.T.T.; Ferkul, P.V.; Johnston, M.C.; Bunnell, C. Confined combustion of polymeric solid materials in microgravity. Combust. Flame 2021, 234, 111637. [Google Scholar] [CrossRef]
- Zhao, K.; Yang, L.; Tang, W.; Liu, Q.; Ju, X.; Gong, J. Effect of orientation on the burning and flame characteristics of PMMA slabs under different pressure environments. Appl. Therm. Eng. 2019, 156, 619–626. [Google Scholar] [CrossRef]
- Juste, G.L. Temperature diagnostics in downward flame spreading process on solids. Fire Saf. J. 2006, 41, 558–567. [Google Scholar] [CrossRef]
- Juste, G.L.; Contat-Rodrigo, L. Temperature field reconstruction from phase-map obtained with moiŕ deflectometry in diffusion flame on solids. Combust. Sci. Technol. 2007, 179, 1287–1302. [Google Scholar] [CrossRef]
- Korobeinichev, O.; Gonchikzhapov, M.; Tereshchenko, A.; Gerasimov, I.; Shmakov, A.; Paletsky, A.; Karpov, A. An experimental study of horizontal flame spread over PMMA surface in still air. Combust. Flame 2018, 188, 388–398. [Google Scholar] [CrossRef]
- Shaklein, A.A.; Bolkisev, A.A.; Karpov, A.I.; Korobeinichev, O.P.; Trubachev, S.A. Two-step gas-phase reaction model for the combustion of polymeric fuel. Fuel 2019, 255, 115878. [Google Scholar] [CrossRef]
- Kagan, L.; Sivashinsky, G. Pattern formation in flame spread over thin solid fuels. Combust. Theory Model. 2008, 12, 269–281. [Google Scholar] [CrossRef]
- Uchida, Y.; Kuwana, K.; Kushida, G. Experimental validation of Lewis number and convection effects on the smoldering combustion of a thin solid in a narrow space. Combust. Flame 2015, 162, 1957–1963. [Google Scholar] [CrossRef]
- Kuwana, K.; Suzuki, K.; Tada, Y.; Kushida, G. Effective Lewis number of smoldering spread over a thin solid in a narrow channel. Proc. Combust. Inst. 2016, 36, 3203–3210. [Google Scholar] [CrossRef]
- Zhang, Y.; Ronney, P.D.; Roegner, E.V.; Greenberg, J.B. Lewis number effects on flame spreading over thin solid fuels. Combust. Flame 1992, 90, 71–83. [Google Scholar] [CrossRef]
- Gao, Y.; Zhu, G.; Zhu, H.; An, W.; Xia, Y. Experimental study of moisture content effects on horizontal flame spread over thin cotton fabric. Text. Res. J. 2018, 89, 3189–3200. [Google Scholar] [CrossRef]
- Chen, X.; Liu, J.; Zhou, Z.; Li, P.; Zhou, T.; Zhou, D.; Wang, J. Experimental and theoretical analysis on lateral flame spread over inclined PMMA surface. Int. J. Heat Mass Transf. 2015, 91, 68–76. [Google Scholar] [CrossRef]
- Ma, Y.; Hu, L.; Huang, Y.; Zhu, N.; Fujita, O. Effect of sample thickness on concurrent steady spread behavior of floor- and ceiling flames. Combust. Flame 2021, 233, 111600. [Google Scholar] [CrossRef]
- Peng, F.; Zhang, X.; Zhai, C.; Li, J. Effect of ceiling height on flame spread over horizontal poly (methyl methacrylate) slabs in corridor. Case Stud. Therm. Eng. 2021, 28, 101576. [Google Scholar] [CrossRef]
- Zhou, Y.; Xiao, H.H.; Sun, J.H.; Zhang, X.N.; Yan, W.G.; Huang, X.J. Experimental study of horizontal flame spread over rigid polyurethane foam on a plateau: Effects of sample width and ambient pressure. Fire Mater. 2015, 39, 127–138. [Google Scholar] [CrossRef]
- Korobeinichev, O.P.; Paletsky, A.A.; Gonchikzhapov, M.B.; Glaznev, R.K.; Gerasimov, I.E.; Naganovsky, Y.K.; Shundrina, I.K.; Snegirev, A.Y.; Vinu, R. Kinetics of thermal decomposition of PMMA at different heating rates and in a wide temperature range. Thermochim. Acta 2019, 671, 17–25. [Google Scholar] [CrossRef]
- Stoliarov, S.I.; Raffan-Montoya, F.; Walters, R.N.; Lyon, R.E. Measurement of the Global Kinetics of Combustion for Gaseous Pyrolyzates of Polymeric Solids Containing Flame Retardants. Combust. Flame 2016, 173, 65–76. [Google Scholar] [CrossRef]
- Singh, S.; Nakamura, Y. A Numerical Study of Dripping on the Ignitability of a Vertically Oriented Thermoplastic Material Locally Heated by an Irradiation Source. Fire Technol. 2022, 58, 75–105. [Google Scholar] [CrossRef]
- Luo, S.; Xie, Q.; Qiu, R. Melting and Dripping Flow Behaviors on the Downward Flame Spread of a Wide XPS Foam. Fire Technol. 2019, 55, 2055–2086. [Google Scholar] [CrossRef]
- Luo, S.; Xie, Q.; Da, L.J.; Qiu, R. Experimental study on thermal structure inside flame front with a melting layer for downward flame spread of XPS foam. J. Hazard. Mater. 2019, 379, 120775. [Google Scholar] [CrossRef] [PubMed]
- Jian-Tao, L.I.; Yan, W.G.; Zhu, H.Y.; Wang, Q.S.; Sun, J.H. Experimental study on the fire spread in high-rise buildings with U-shaped outside-facade structure. Fire Saf. Sci. 2012, 21, 167–173. [Google Scholar]
- Jiang, Y.; Zhai, C.; Shi, L.; Liu, X.; Gong, J. Assessment of melting and dripping effect on ignition of vertically discrete polypropylene and polyethylene slabs. J. Therm. Anal. Calorim. 2021, 144, 751–762. [Google Scholar] [CrossRef]
- Sun, P.; Wu, C.; Zhu, F.; Wang, S.; Huang, X. Microgravity combustion of polyethylene droplet in drop tower. Combust. Flame 2020, 222, 18–26. [Google Scholar] [CrossRef]
- Kong, Q.; Wu, T.; Liu, H.; Zhang, Y.; Zhang, M.; Cai, Y.; Zhang, J.; Yang, L. Graphene Oxide Nanocoating Prevents Flame Spread on Polyurethane Sponge. J. Nanosci. Nanotechnol. 2017, 18, 5105–5112. [Google Scholar] [CrossRef]
- Jia, D.; Guo, X.; He, J.; Yang, R. An anti-melt dripping, high char yield and flame-retardant polyether rigid polyurethane foam. Polym. Degrad. Stab. 2019, 167, 189–200. [Google Scholar] [CrossRef]
- Günther, M.; Levchik, S.V.; Schartel, B. Bubbles and collapses: Fire phenomena of flame-retarded flexible polyurethane foams. Polym. Adv. Technol. 2020, 31, 2185–2198. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, J.; Tang, G.; Zhang, Y.; Sun, J. Effects of altitude and inclination on the flame structure over the insulation material PS based on heat and mass transfer. Int. J. Heat Mass Transf. 2015, 90, 1046–1055. [Google Scholar] [CrossRef]
- Carmignani, L.; Rhoades, B.; Bhattacharjee, S. Correlation of Burning Rate with Spread Rate for Downward Flame Spread Over PMMA. Fire Technol. 2018, 54, 613–624. [Google Scholar] [CrossRef]
- Pizzo, Y.; Consalvi, J.L.; Querre, P.; Coutin, M.; Audouin, L.; Porterie, B.; Torero, J.L. Experimental observations on the steady-state burning rate of a vertically oriented PMMA slab. Combust. Flame 2008, 152, 451–460. [Google Scholar] [CrossRef]
- Singh, A.V.; Gollner, M.J. Estimation of local mass burning rates for steady laminar boundary layer diffusion flames. Proc. Combust. Inst. 2015, 35, 2527–2534. [Google Scholar] [CrossRef]
- Consalvi, J.L.; Pizzo, Y.; Kaiss, A.; Torero, J.L.; Porterie, B. A theoretical and numerical evaluation of the steady-state burning rate of vertically oriented PMMA slabs. Combust. Theory Model. 2008, 12, 451–475. [Google Scholar] [CrossRef]
- An, W.G.; Xiao, H.H.; Sun, J.H.; Yan, W.G.; Zhou, Y.; Huang, X.J.; Wang, H.; Jiang, L. Experimental study on downward flame spread across XPS surface. Adv. Mater. Res. 2013, 753–755, 445–451. [Google Scholar] [CrossRef]
- Gou, F.H.; Xiao, H.H.; Jiang, L.; Li, M.; Zhang, M.M.; Sun, J.H. Upward Flame Spread Over an Array of Discrete Thermally-Thin PMMA Plates. Fire Technol. 2021, 57, 1381–1399. [Google Scholar] [CrossRef]
- Huang, Y.; Hu, L.; Ma, Y.; Zhu, N.; Chen, Y.; Wahlqvist, J.; Mcnamee, M.; van Hees, P. Experimental study of flame spread over thermally-thin inclined fuel surface and controlling heat transfer mechanism under concurrent wind. Int. J. Therm. Sci. 2021, 165, 106936. [Google Scholar] [CrossRef]
- Zhou, B.; Yoshioka, H.; Noguchi, T.; Wang, K.; Huang, X. Upward Fire Spread Rate Over Real-Scale EPS ETICS Façades. Fire Technol. 2021, 57, 2007–2024. [Google Scholar] [CrossRef]
- Liang, C.; Cheng, X.; Li, K.; Yang, H.; Zhang, H.; Yuen, K.K. Experimental study on flame spread behavior along poly (methyl methacrylate) corner walls at different altitudes. J. Fire Sci. 2014, 32, 84–96. [Google Scholar] [CrossRef]
- Raffan-Montoya, F.; Ding, X.; Stoliarov, S.I.; Cramer, R.H. Measurement of Heat Release in Laminar Diffusion Flames Fueled by Controlled Pyrolysis of Milligram-sized Solid Samples: Impact of Bromine- and Phosphorus-based Flame Retardants. Combust Flame 2015, 162, 4660–4670. [Google Scholar] [CrossRef]
- Ding, Y.; Stoliarov, S.I.; Kramer, R.H. Pyrolysis Model Development for a Polymeric Material Containing Multiple Flame Retardants: Relationship between Heat Release Rate and Material Composition. Combust Flame 2019, 202, 43–57. [Google Scholar] [CrossRef]
- Chu, Y.Y.; Wichman, I.S. Opposed Flow Flame Spread over Degrading Combustible Solids. Combust. Sci. Technol. 2019, 191, 1843–1865. [Google Scholar] [CrossRef]
- Vermesi, I.; Roenner, N.; Pironi, P.; Hadden, R.M.; Rein, G. Pyrolysis and ignition of a polymer by transient irradiation. Combust. Flame 2016, 163, 31–41. [Google Scholar] [CrossRef]
- Korobeinichev, O.P.; Karpov, A.I.; Bolkisev, A.A.; Shaklein, A.A.; Gonchikzhapov, M.B.; Paletsky, A.A.; Tereshchenko, A.G.; Shmakov, A.G.; Gerasimov, I.E.; Kumar, A. An experimental and numerical study of thermal and chemical structure of downward flame spread over PMMA surface in still air. Proc. Combust. Inst. 2019, 37, 4017–4024. [Google Scholar] [CrossRef]
- Kudo, Y.; Ito, A. Propagation and extinction mechanisms of opposed-flow flame spread over PMMA. Proc. Combust. Inst. 2002, 29, 237–243. [Google Scholar] [CrossRef]
- Ananth, R.; Ndubizu, C.C.; Tatem, P.A. Burning rate distributions for boundary layer flow combustion of a PMMA plate in forced flow. Combust. Flame 2003, 135, 35–55. [Google Scholar] [CrossRef]
- An, W.; Wang, Z.; Xiao, H.; Sun, J.; Liew, K.M. Thermal and fire risk analysis of typical insulation material in a high elevation area: Influence of sidewalls, dimension and pressure. Energy Convers. Manag. 2014, 88, 516–524. [Google Scholar] [CrossRef]
- Carmignani, L.; Bhattacharjee, S. Burn Angle and Its Implications on Flame Spread Rate, Mass Burning Rate, and Fuel Temperature for Downward Flame Spread over Thin PMMA. Combust. Sci. Technol. 2020, 192, 1617–1632. [Google Scholar] [CrossRef]
- An, W.; Sun, J.; Zhu, G. Experimental study on temperature field of upward flame spread over discrete polystyrene foam. J. Therm. Anal. Calorim. 2018, 131, 2647–2656. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, A.; Gao, L.; Pei, Z. Effectiveness of vertical barriers in preventing lateral flame spread over exposed EPS insulation wall. Fire Saf. J. 2017, 91, 155–164. [Google Scholar] [CrossRef]
- Li, J.; Ji, J.; Zhang, Y.; Sun, J. Characteristics of flame spread over the surface of charring solid combustibles at high altitude. Chin. Sci. Bull. 2009, 54, 1957–1962. [Google Scholar] [CrossRef]
- Thirumal, M.; Singha, N.; Khastgir, D.; Manjunath, B.; Naik, Y. Halogen-Free Flame-Retardant Rigid Polyurethane Foams: Effect of Alumina Trihydrate and Triphenylphosphate on the Properties of Polyurethane Foams. J. Appl. Polym. Sci. 2010, 116, 2260–2268. [Google Scholar] [CrossRef]
- Huang, D.; Wang, C.; Shen, Y.; Lin, P.; Shi, L. Fire behaviors of vertical and horizontal polymethyl methacrylate slabs under autoignition conditions. Process Saf. Prog. 2020, 39, e12109. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, X.; Li, L.; Lo, S.; Zhang, H. Effect of ignition condition on typical polymer’s melt flow flammability. J. Hazard. Mater. 2011, 190, 766–771. [Google Scholar] [CrossRef]
- Cheng, J.J.; Zhou, F.B. Flame-retardant properties of sodium silicate/polyisocyanate organic–inorganic hybrid material. J. Therm. Anal. Calorim. 2016, 125, 913–918. [Google Scholar] [CrossRef]
- Yan, L.; Xu, Z.; Wang, X.; Deng, N.; Chu, Z. Synergistic effects of aluminum hydroxide on improving the flame retardancy and smoke suppression properties of transparent intumescent fire-retardant coatings. J. Coat. Technol. Res. 2018, 15, 1357–1369. [Google Scholar] [CrossRef]
- Liu, H.; Yang, H.; Chen, M.; Jiang, Y.; Wan, C. An effective approach to reducing fire hazards of rigid polyurethane foam: Fire protective coating. J. Coat. Technol. Res. 2019, 16, 257–261. [Google Scholar] [CrossRef]
- Karpov, A.I.; Korobeinichev, O.P.; Shaklein, A.A.; Bolkisev, A.A.; Kumar, A.; Shmakov, A.G. Numerical study of horizontal flame spread over PMMA surface in still air. Appl. Therm. Eng. 2018, 144, 937–944. [Google Scholar] [CrossRef]
- Zik, O.; Olami, Z.; Moses, E. Fingering Instability in Combustion. Phys. Rev. Lett. 1998, 81, 3868–3871. [Google Scholar] [CrossRef]
- Zik, O.; Moses, E. Fingering instability in solid fuel combustion: The characteristic scales of the developed state. Symp. Combust. 1998, 27, 2815–2820. [Google Scholar] [CrossRef]
- Matsuoka, T.; Nakashima, K.; Nakamura, Y.; Noda, S. Appearance of flamelets spreading over thermally thick fuel. Proc. Combust. Inst. 2017, 36, 3019–3026. [Google Scholar] [CrossRef]
- Olson, S.L.; Miller, F.; Jahangirian, S.; Wichman, I.S. Flame spread over thin fuels in actual and simulated microgravity conditions. Combust. Flame 2009, 156, 1214–1226. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Q.; Zhang, Y.; Yin, Y.; Sun, J. Thickness effect on flame spread characteristics of expanded polystyrene in different environments. J. Thermoplast. Compos. Mater. 2012, 25, 427–438. [Google Scholar] [CrossRef]
- Tu, R.; Zeng, Y.; Fang, J.; Zhang, Y. The influence of low air pressure on horizontal flame spread over flexible polyurethane foam and correlative smoke productions. Appl. Therm. Eng. Des. Process. Equip. Econ. 2016, 94, 133–140. [Google Scholar] [CrossRef]
- Zhou, Y.; Xiao, H.; Yan, W.; An, W.; Jiang, L.; Sun, J. Horizontal Flame Spread Characteristics of Rigid Polyurethane and Molded Polystyrene Foams Under Externally Applied Radiation at Two Different Altitudes. Fire Technol. 2015, 51, 1195–1216. [Google Scholar] [CrossRef]
- Olson, S.L.; Baum, H.R.; Kashiwagi, T. Finger-like smoldering over thin cellulosic sheets in microgravity. Symp. Combust. 1998, 27, 2525–2533. [Google Scholar] [CrossRef]
- Kuwana, K.; Kushida, G.; Uchida, Y. Lewis number effect on smoldering combustion of a thin solid. Combust. Sci. Technol. 2014, 186, 466–474. [Google Scholar] [CrossRef]
- Wang, J.H.; Chao, C.Y.H.; Water, C.; Kowloon, B.; Kong, H. Flame Spread Over Solid Surface Coated with a Layer of Noncombustible Porous Material. J. Fire Sci. 1999, 17, 307–328. [Google Scholar] [CrossRef]
- Zhu, N.; Huang, X.; Fang, J.; Yang, L.; Hu, L. Transitional flame-spread and fuel-regression behaviors under the change of concurrent wind. Fire Saf. J. 2021, 120, 103015. [Google Scholar] [CrossRef]
- Zhao, L.Y.; Fang, J.; He, X.Z.; Wang, J.W.; Zhang, Y.M. An analysis of width effects on flame spread in conjunction with concurrent forced flow using a variable B-number. Combust. Flame 2018, 194, 334–342. [Google Scholar] [CrossRef]
- Zhou, L.; Fernandez-Pello, A.C. Turbulent, concurrent, ceiling flame spread: The effect of buoyancy. Combust. Flame 1993, 92, 45–59. [Google Scholar] [CrossRef]
- Chao, Y.H.C.; Fernandez-Pello, A.C. Concurrent Horizontal Flame Spread: The Combined Effect of Oxidizer Flow Velocity, Turbulence and Oxygen Concentration. Combust. Sci. Technol. 1995, 110–111, 19–51. [Google Scholar] [CrossRef]
- Delichatsios, M.A. Exact Solution for the Rate of Creeping Flame Spread over Thermally Thin Materials. Combust. Sci. Technol. 1986, 44, 257–267. [Google Scholar] [CrossRef]
- de Ris, J.N. Spread of a laminar diffusion flame. Symp. Combust. 1969, 12, 241–252. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Laue, M.; Carmignani, L.; Ferkul, P.; Olson, S. Opposed-flow flame spread: A comparison of microgravity and normal gravity experiments to establish the thermal regime. Fire Saf. J. 2016, 79, 111–118. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Ayala, R.; Wakai, K.; Takahashi, S. Opposed-flow flame spread in microgravity-theoretical prediction of spread rate and flammability map. Proc. Combust. Inst. 2005, 30, 2279–2286. [Google Scholar] [CrossRef]
- Hossain, S.; Wichman, I.S.; Miller, F.J.; Olson, S.L. Opposed flow flame spread over thermally thick solid fuels: Buoyant flow suppression, stretch rate theory, and the regressive burning regime. Combust. Flame 2020, 219, 57–69. [Google Scholar] [CrossRef]
- Hwang, J.J. Effect of heat-source backing on flame spread over a solid fuel in an opposed air flow. Combust. Sci. Technol. 1997, 126, 315–331. [Google Scholar]
- Bhattacharjee, S.; Simsek, A.; Miller, F.; Olson, S.; Ferkul, P. Radiative, thermal, and kinetic regimes of opposed-flow flame spread: A comparison between experiment and theory. Proc. Combust. Inst. 2017, 36, 2963–2969. [Google Scholar] [CrossRef]
- Arakawa, A.; Saito, K.; Gruver, W.A. Automated infrared imaging temperature measurement with application to upward flame spread studies. Part I. Combust. Flame 1993, 92, 222–230. [Google Scholar] [CrossRef]
- Delichatsios, M.A.; Delichatsios, M.; Chen, Y.; Hasemi, Y. Similarity solutions and applications to turbulent upward flame spread on noncharring materials. Combust. Flame 1995, 102, 357–370. [Google Scholar] [CrossRef]
- Quintiere, J.Q.; Lee, C.H. Ignitor and thickness effects on upward flame spread. Fire Technol. 1998, 34, 18–38. [Google Scholar] [CrossRef]
- Consalvi, J.L.; Pizzo, Y.; Porterie, B. Numerical analysis of the heating process in upward flame spread over thick PMMA slabs. Fire Saf. J. 2008, 43, 351–362. [Google Scholar] [CrossRef]
- Xie, W.; Desjardin, P.E. An embedded upward flame spread model using 2D direct numerical simulations. Combust. Flame 2009, 156, 522–530. [Google Scholar] [CrossRef]
- Li, M.; Wang, Y.; Jiang, L.; Gou, F.H.; Sun, J.H. Mass loss prediction of inclined fuel combustion using variable B-number theory. Fuel 2022, 310, 122446. [Google Scholar] [CrossRef]
- Ranga, H.R.R.; Korobeinichev, O.P.; Harish, A.; Raghavan, V.; Kumar, A.; Gerasimov, I.E.; Gonchikzhapov, M.B.; Tereshchenko, A.G.; Trubachev, S.A.; Shmakov, A.G. Investigation of the structure and spread rate of flames over PMMA slabs. Appl. Therm. Eng. 2018, 130, 477–491. [Google Scholar] [CrossRef]
- Zhou, Y.; Gong, J.; Jiang, L.; Chen, C. Orientation effect on upward flame propagation over rigid polyurethane foam. Int. J. Therm. Sci. 2018, 132, 86–95. [Google Scholar] [CrossRef]
- Miller, C.H.; Gollner, M.J. Upward flame spread over discrete fuels. Fire Saf. J. 2015, 77, 36–45. [Google Scholar] [CrossRef]
- Wang, Z.; Liang, W.; Cai, M.; Tang, Y.; Li, S.; An, W.; Zhu, G. Experimental study on flame spread over discrete extruded polystyrene foam with different fuel coverage rates. Case Stud. Therm. Eng. 2020, 17, 100577. [Google Scholar] [CrossRef]
- Bu, R.; Zhou, Y.; Fan, C.; Wang, Z. Understanding the effects of inclination angle and fuel bed width on concurrent flame spread over discrete fuel arrays. Fuel 2021, 289, 119924. [Google Scholar] [CrossRef]
- An, W.; Peng, L.; Yin, X.; Cai, M. Effect of shielding rates on upward flame spread over extruded polystyrene foam in vertical channel and heat transfer mechanism. Fire Mater. 2020, 44, 1118–1126. [Google Scholar] [CrossRef]
- An, W.; Li, S.; Yin, X.; Peng, L. Combustion and fire safety of energy conservation materials in building vertical channel: Effects of structure factor and coverage rate. Case Stud. Therm. Eng. 2021, 24, 100847. [Google Scholar] [CrossRef]
- Yan, W.; Jiang, L.; An, W.; Zhou, Y.; Sun, J. Large scale experimental study on the fire hazard of buildings’ U-shape façade wall geometry. J. Civ. Eng. Manag. 2017, 23, 455–463. [Google Scholar] [CrossRef]
- Huang, X.; Zhao, J.; Zhang, Y.; Zhou, Y.; Wang, Q.; Sun, J. Effects of altitude and sample orientation on heat transfer for flame spread over polystyrene foams. J. Therm. Anal. Calorim. 2015, 121, 641–650. [Google Scholar] [CrossRef]
- Liang, C.; Cheng, X.; Yang, H.; Zhang, H.; Yuen, K.K. Experimental study of vertically upward flame spread over polymethyl methacrylate slabs at different altitudes. Fire Mater. 2016, 40, 472–481. [Google Scholar] [CrossRef]
- Thomsen, M.; Fernandez-Pello, C.; Ruff, G.A.; Urban, D.L. Buoyancy effects on concurrent flame spread over thick PMMA. Combust. Flame 2019, 199, 279–291. [Google Scholar] [CrossRef]
- Urban, D.L.; Ferkul, P.; Olson, S.; Ruff, G.A.; Easton, J.; T’ien, J.S.; Liao, Y.T.T.; Li, C.; Fernandez-Pello, C.; Torero, J.L.; et al. Flame spread: Effects of microgravity and scale. Combust. Flame 2019, 199, 168–182. [Google Scholar] [CrossRef]
- Zhu, F.; Huang, X.; Wang, S. Flame Spread over Polyethylene Film: Effects of Gravity and Fuel Inclination. Microgravity Sci. Technol. 2022, 34, 26. [Google Scholar] [CrossRef]
- Bhattachariee, S.; King, M.D.; Takahashi, S.; Nagumo, T.; Wakai, K. Downward flame spread over poly(methyl)methacrylate. Proc. Combust. Inst. 2000, 28, 2891–2897. [Google Scholar] [CrossRef]
- Mamourian, M.; Esfahani, J.A.; Ayani, M.B. Experimental and scale up study of the flame spread over the PMMA sheets. Therm. Sci. 2009, 13, 79–88. [Google Scholar] [CrossRef]
- Wu, K.K.; Fan, W.F.; Chen, C.H.; Liou, T.M.; Pan, I.J. Downward flame spread over a thick PMMA slab in an opposed flow environment: Experiment and modeling. Combust. Flame 2003, 132, 697–707. [Google Scholar] [CrossRef]
- Lin, P.H.; Chen, C.H. Numerical analyses for radiative autoignition and transition to flame spread over a vertically oriented solid fuel in a gravitational field. Combust. Sci. Technol. 2000, 151, 157–187. [Google Scholar] [CrossRef]
- Delzeit, T.; Carmignani, L.; Matsuoka, T.; Bhattacharjee, S. Influence of edge propagation on downward flame spread over three-dimensional PMMA samples. Proc. Combust. Inst. 2019, 37, 3203–3209. [Google Scholar] [CrossRef]
- Gao, S.; Zhu, G.; Gao, Y.; Zhou, J. Experimental study on width effects on downward flame spread over thin PMMA under limited distance condition. Case Stud. Therm. Eng. 2019, 13, 100382. [Google Scholar] [CrossRef]
- Ma, X.; Tu, R.; Cheng, X.; Zhu, S.; Sun, Q.; Fang, T. Sub-Atmospheric Pressure Coupled with Width Effect on Downward Flame Spread over Energy Conservation Material Polyurethane Foam. J. Therm. Sci. 2020, 29, 115–121. [Google Scholar] [CrossRef]
- Ayani, M.B.; Esfahani, J.A.; Mehrabian, R. Downward flame spread over PMMA sheets in quiescent air: Experimental and theoretical studies. Fire Saf. J. 2006, 41, 164–169. [Google Scholar] [CrossRef]
- Zhou, Y.; Bu, R.; Gong, J.; Yan, W.; Fan, C. Experimental investigation on downward flame spread over rigid polyurethane and extruded polystyrene foams. Exp. Therm. Fluid Sci. 2018, 92, 346–352. [Google Scholar] [CrossRef]
- An, W.; Yin, X.; Cai, M.; Gao, Y.; Wang, H. Influence of vertical channel on downward flame spread over extruded polystyrene foam. Int. J. Therm. Sci. 2019, 145, 105991. [Google Scholar] [CrossRef]
- Pan, R.; Zhu, G.; Zhang, G.; An, W.; Zhu, H.; Yu, M. Experimental study and heat transfer analysis of downward flame spread over PMMA under the effect of wall spacing. J. Therm. Anal. Calorim. 2019, 138, 1711–1722. [Google Scholar] [CrossRef]
- An, W.; Yin, X.; Chen, S.; Zhang, G. Study on downward flame spread over extruded polystyrene foam in a vertical channel: Influence of opening area. Fire Mater. 2019, 43, 153–161. [Google Scholar] [CrossRef]
- Zhao, K.; Zhou, X.; Liu, X.; Tang, W.; Gollner, M.; Peng, F.; Yang, L. Experimental and theoretical study on downward flame spread over uninhibited PMMA slabs under different pressure environments. Appl. Therm. Eng. 2018, 136, 1–8. [Google Scholar] [CrossRef]
- Zhao, K.; Zhou, X.D.; Liu, X.Q.; Lu, L.; Wu, Z.B.; Peng, F.; Ju, X.Y.; Yang, L.Z. Prediction of three-dimensional downward flame spread characteristics over poly (methyl methacrylate) slabs in different pressure environments. Materials 2016, 9, 948. [Google Scholar] [CrossRef] [PubMed]
- Thomsen, M.; Fernandez-Pello, C.; Huang, X.; Olson, S.; Ferkul, P. Buoyancy Effect on Downward Flame Spread Over PMMA Cylinders. Fire Technol. 2020, 56, 247–269. [Google Scholar] [CrossRef]
- Thomsen, M.; Carmignani, L.; Rodriguez, A.; Scudiere, C.; Liveretou, C.; Fernandez-Pello, C.; Gollner, M.; Olson, S.; Ferkul, P. Downward Flame Spread Rate Over PMMA Rods Under External Radiant Heating. Fire Technol. 2022, 58, 2229–2250. [Google Scholar] [CrossRef]
- Sidebotham, G.W.; Olson, S.L. Microgravity opposed-flow flame spread in polyvinyl chloride tubes. Combust. Flame 2008, 154, 789–801. [Google Scholar] [CrossRef]
- Korobeinichev, O.P.; Trubachev, S.A.; Joshi, A.K.; Kumar, A.; Paletsky, A.A.; Tereshchenko, A.G.; Shmakov, A.G.; Glaznev, R.K.; Raghavan, V.; Mebel, A.M. Experimental and numerical studies of downward flame spread over PMMA with and without addition of tri phenyl phosphate. Proc. Combust. Inst. 2021, 38, 4867–4875. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Feng, Q.; Nie, Y.; Zhang, J.; Yang, L. A Review of Combustion and Flame Spread over Thermoplastic Materials: Research Advances and Prospects. Fire 2023, 6, 125. https://doi.org/10.3390/fire6030125
Chen Y, Feng Q, Nie Y, Zhang J, Yang L. A Review of Combustion and Flame Spread over Thermoplastic Materials: Research Advances and Prospects. Fire. 2023; 6(3):125. https://doi.org/10.3390/fire6030125
Chicago/Turabian StyleChen, Yanqiu, Qianhang Feng, Yifan Nie, Jiwei Zhang, and Lizhong Yang. 2023. "A Review of Combustion and Flame Spread over Thermoplastic Materials: Research Advances and Prospects" Fire 6, no. 3: 125. https://doi.org/10.3390/fire6030125
APA StyleChen, Y., Feng, Q., Nie, Y., Zhang, J., & Yang, L. (2023). A Review of Combustion and Flame Spread over Thermoplastic Materials: Research Advances and Prospects. Fire, 6(3), 125. https://doi.org/10.3390/fire6030125





