Modeling and CFD Simulation of Regression Rate in Hybrid Rocket Motors

Abstract

As the research on hybrid rocket motors advances, more accurate tools are needed to estimate the performance of the system by determining its fundamental parameters. One of them is certainly the regression rate of the solid fuel. Unfortunately, it depends on many complex physical phenomena and interactions which vary with time, space and scale, making the task of predicting its evolution very difficult. To address this issue, Computational Fluid Dynamics (CFD) was employed to investigate the inner workings of a hybrid rocket motor and develop a useful tool to help the design process and contribute to the physical understanding of the problem. By implementing a User-Defined Function (UDF) in a commercial CFD software, it has been possible to simulate the regression rate as a function of heat flux at the fuel surface. The calculation is performed by solving the energy balance at the solid–fluid interface coupled with the pyrolysis Arrhenius equation. Validation has been performed using literature data from Carmicino and Sorge. The results generally agree with the experimental regression rates within 10% of error for HDPE and 20% for HTPB. A significant discrepancy in the regression rates of these two fuels not accounted for by the classical theory was exposed.

1. Introduction

Several aspects of hybrid rockets make them an attractive technology for next-gen propulsion, such as simplicity, low cost, safety, reliability, environmental friendliness, thrust modulation and the ability to be restarted [1,2,3,4,5,6]. Nevertheless, sufficient maturity has not yet been attained and nowadays, no system has reached full operational status, even if this could happen in the near future [7,8,9,10,11,12,13]. In this frame, Computational Fluid Dynamics (CFD) is a powerful tool that can help develop a high-performance solution and increase the TRL of hybrid rocket motors in a cost-effective way [14]. CFD can, indeed, predict motor behavior, perform parametric analysis and optimization and investigate the underlying physics and local details of the system if backed up by global informations provided by experiments. By avoiding the classic trial-and-error practice and numerous expensive experiments, the cost of developing a system of this kind is lowered to much more affordable prices while also speeding up the design process.

Among all the parameters defining a hybrid rocket motor, the regression rate is one of the most difficult to predict accurately without empirical correlations [15]. It involves many complex and multiphysical phenomena, some still not well understood [16,17,18,19,20,21]. Nowadays, during a classical design process, regression rate values are usually drawn from literature [2] or proprietary data, but the combination of unknowns in the chemical composition of the fuel, the small data pool and differences in geometrical and fluid-dynamics characteristics makes the procedure quite imprecise.

Several previous attempts have been made to predict fuel regression rate through CFD simulations. Merkle and Venkateswaran [22] were able to develop a comprehensive model that included the full time-dependent Navier–Stokes equations, coupled with physical submodels and their relative transport equations which span finite rate chemistry, turbulence, gas phase radiation and fluid–solid coupling. In 2001, Akyuzlu et al. [23] published an article on a mathematical model predicting regression rate in an ablating hybrid rocket solid fuel. Serin and Gogus [24] carried out CFD simulations with a commercial package on HTPB-based hybrid rockets using O${}_2$ as oxidizer and studied the reacting flow field and the corresponding heat transfer to the solid fuel. In 2005, Antoniou and Akyuzlu [25] published a complete model to predict the entire behavior of a hybrid rocket and its performances. Cai and Tian [26] wrote an article regarding a theoretical analysis of propellant performance, solid fuel regression rate and characterization of combustion in hybrid rockets. They also added an analysis of the combusting flow using CFD. Recently, Bianchi et al. [27,28,29,30,31] performed numerical simulations of the internal flow of a GOX+HTPB hybrid rocket using a RANS solver. A detailed gas–surface interaction model based on energy and mass equations was employed. Moreover, fuel pyrolysis and heterogeneous reactions at the nozzle wall were included via finite-rate Arrhenius kinetics. Several other authors have developed similar numerical tools [32,33,34,35,36,37,38].

The University of Padua (UNIPD) has long being developing CFD tools to faithfully model hybrid motor operations as part of several programs supporting the design and testing phases [39,40,41,42,43,44]. A commercial CFD code was chosen for these scopes; while this decision reduces development costs, it also provides the opportunity to customize the setup to meet particular needs linked to the hybrid rocket combustion [45,46,47,48,49]. The self-evaluation of fuel regression rate as a function of wall heat flux was a significant advancement for UNIPD in the numerical modeling of hybrid combustion.

The usage of a special User-Defined Function (UDF), which has been created by the user in C and can be dynamically coupled with the CFD solver to expand the basic capabilities of the commercial code, has enabled the self-calculation of the regression rate.

A description of the adopted theoretical and numerical model will be given in the sections that follow. After the comparison of the numerical results with the reference experimental data, the most significant features of the flow field will be examined.

2. Theoretical Model

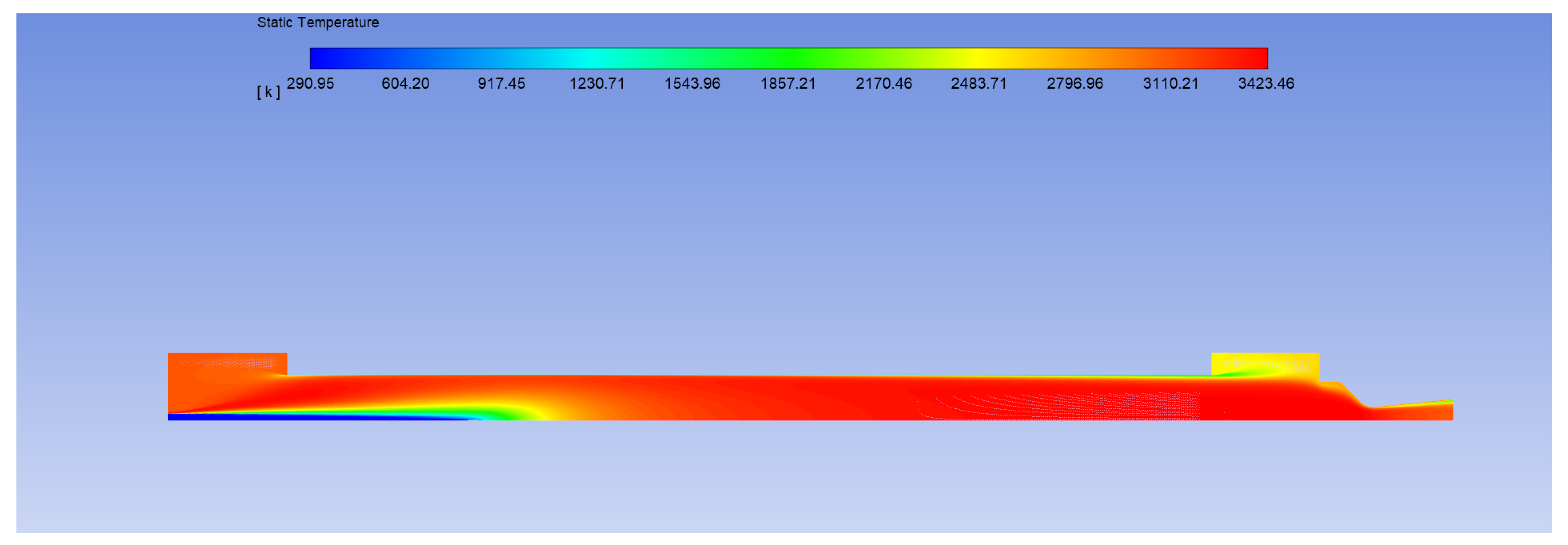
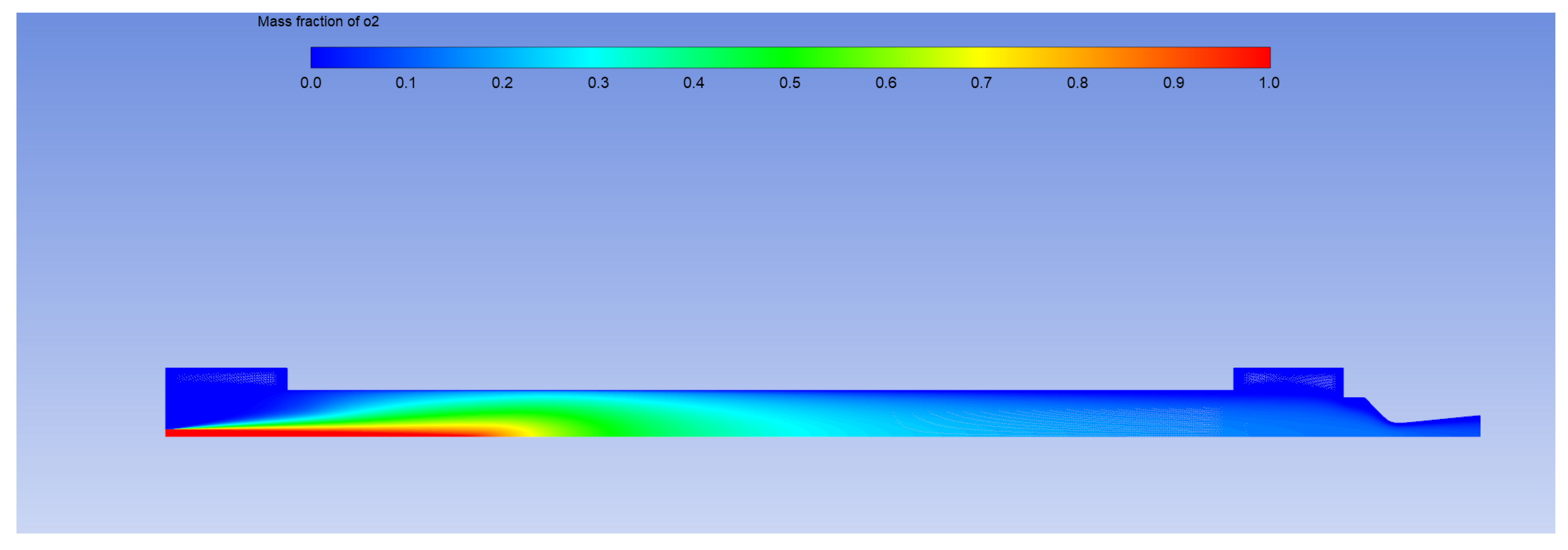
In order to accurately model the regression rate in hybrid rockets one must understand all the main phenomena in play. The obvious critical zone that must be resolved is the fluid–solid interface, where heat produced by the combustion is transferred to the solid fuel which undergoes decomposition, it is injected into the combustion chamber and burnt with the oxygen, self-sustaining the cycle.

The combustion takes place inside the boundary layer and it is the result of various processes such as:

• Kinetics of fuel pyrolysis;
• Combustion mechanisms in gaseous phase;
• Convective and radiative heat transfer in gaseous phase;
• Mass transfer of chemical species.

The result is the development of a flame which is located in a thin zone of about 10% of the boundary layer thickness (flame sheet theory) [50,51,52,53,54,55,56,57,58,59].

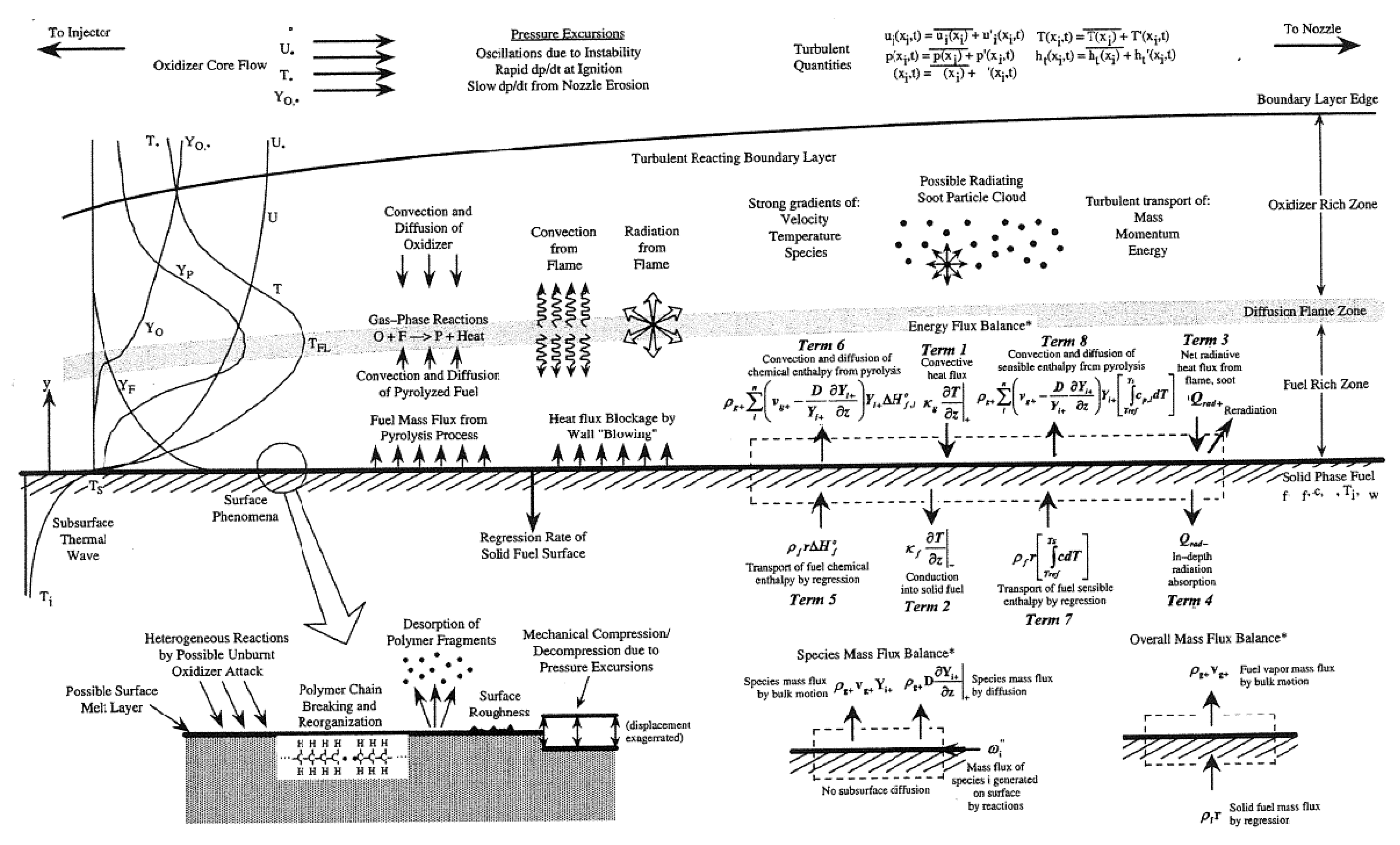
Chiaverini [60] produced an excellent image representing the contribution of all the known mechanisms that play a role in the determination of the net heat flux that goes into the solid fuel (Figure 1).

According to the above scheme, the conservation of mass and energy must be met in a control volume located right at the fluid–solid interface following the regressing surface.

The total mass balance + overall species conservation in such volume is therefore:

$$\frac{\dot{m}}{A}={\rho }_{g+}{v}_{g+}={\rho }_f\dot{r}=\sum _i^n{\omega }_i^{″}=\sum _i^n\left({\rho }_{g+}{v}_{g+}{Y}_{i+}\right)-\sum _i^n\left({\rho }_{g+}{D}_i{\left.\frac{\partial Y_{i+}}{\partial z}\right|}_{+}\right)$$

(1)

with $\rho$ being the density, v—the velocity, $\dot{m}/A$—the mass flux, $\dot{r}$—the regression rate, $D_i$, $Y_i$ and ${\omega }_i^{″}$, respectively—the mass diffusion, the concentration and the mass generation at the fuel surface of species i. The subscript g or $g+$ refers to the properties of the gas over the burning surface, while f regards the solid fuel itself. The species conservation equation for species i is instead:

$${\omega }_i^{″}=\left({\rho }_{g+}{v}_{g+}{Y}_{i+}\right)-\left({\rho }_{g+}{D}_i{\left.\frac{\partial Y_{i+}}{\partial z}\right|}_{+}\right)$$

(2)

Finally, the energy balance, considering the radiative heat transfer $Q_{rad}$ as well, is:

$$\begin{array}{c}\stackrel{\mathrm{entering}\mathrm{the}\mathrm{control}\mathrm{volume}}{\overbrace{{\rho }_f\dot{r}{h}_f-{\left.{\kappa }_g\frac{\partial T}{\partial z}\right|}_{+}+Q_{rad+}}}=\\ \underset{\mathrm{exiting}\mathrm{the}\mathrm{control}\mathrm{volume}}{\underbrace{{\rho }_{g+}{v}_{g+}{\displaystyle \sum _i^n}\left(Y_{i+}{h}_{g,i}\right)-{\rho }_{g+}{\displaystyle \sum _i^n}\left(D\frac{\partial Y_{i+}}{\partial z}{h}_{g,i}\right)-{\left.{\kappa }_f\frac{\partial T}{\partial z}\right|}_{-}+Q_{rad-}}}\end{array}$$

(3)

with

$$h_f=\Delta h_f^{\circ }+{\int }_{T_{ref}}^{T_s}cdT$$

(4)

$$h_{g,i}=\Delta h_{f,i}^{\circ }+{\int }_{T_{ref}}^{T_s}{c}_{p,i}dT$$

(5)

where $\Delta h_f^{\circ }$ and $\Delta h_{f,i}^{\circ }$ are the specific enthalpy of formation of the fuel and of the species i, respectively. Similarly, c and $c_{p,i}$ are the respective specific heats, which, integrated from the reference temperature $T_{ref}$ to the surface temperature $T_s$, give the sensible enthalpy. Finally, $\kappa$ is the thermal conductivity. As stated in Equation (3), the first series of terms represents the energy entering the volume through regression, conduction and radiation, while the second series represents the energy released through convection, diffusion of species, conduction and radiation into the solid fuel. Applying the energy equation for the solid phase in the z (normal) direction, it is possible to calculate the thermal energy that is lost from the surface due to conduction through the fuel grain while assuming that there is little variation in the fuel thermal conductivity and specific heat capacity with respect to temperature. Mathematically, it can be written in the following way:

$${\kappa }_f\frac{{\partial }^{2}T}{{\partial }^{2}z}-{\rho }_f\dot{r}c\frac{\partial T}{\partial z}=0$$

(6)

of which the general solution is:

$$T\left(z\right)=C_1+C_2{e}^{z{\rho }_f\dot{r}c/{\kappa }_f}$$

(7)

where $C_1$ and $C_2$ are integration constants. Imposing the boundary conditions $T(z=0)=T_s$ and $T(z=-\infty )=T_{ref}=298.15K$ the following exponential law can be derived:

$$T\left(z\right)=T_{ref}+(T_s-T_{ref})e^{z{\rho }_f\dot{r}c/{\kappa }_f}$$

(8)

From the above, the following equivalence is obtained by taking the first derivative at the fuel surface ($z=0$):

$$-{\kappa }_f{\left.\frac{\partial T}{\partial z}\right|}_{-}={\rho }_{f}c\dot{r}(T_s-T_{ref})$$

(9)

Additionally, the sensible contribution of fuel ablation in Equation (3) can be rewritten as follows when using an average value of c, as in Equation (6):

$${\int }_{T_{ref}}^{T_s}cdT=c(T_s-T_{ref})$$

(10)

Moreover, solid fuels are generally opaque ($Q_{rad-}\simeq 0$) and all other radiation-related phenomena have been neglected to simplify the analysis $(Q_{rad+}\simeq 0)$. Combining everything mentioned so far into Equation (3), we obtain:

$$\begin{array}{c}{\rho }_f\dot{r}\left(\Delta h_f^{\circ }+c(T_s-T_{ref})\right)-{\left.{\kappa }_g\frac{\partial T}{\partial z}\right|}_{+}=\\ {\rho }_{g+}{v}_{g+}{\displaystyle \sum _i^n}\left(Y_{i+}{h}_{g,i}\right)-{\rho }_{g+}{\displaystyle \sum _i^n}\left(D\frac{\partial Y_{i+}}{\partial z}{h}_{g,i}\right)+{\rho }_{f}c\dot{r}(T_s-T_{ref})\end{array}$$

(11)

Simplifying some recurring terms, assuming the decomposition products being composed of only one species (now the subscript i refers to the only decomposition product) and introducing the Equation (1) into the above expression, the following can be obtained:

$$\dot{Q}=-{\left.{\kappa }_g\frac{\partial T}{\partial z}\right|}_{+}={\rho }_f\dot{r}(\Delta h_{f,i}^{\circ }+{\int }_{T_{ref}}^{T_s}{c}_{p,i}dT-\Delta h_f^{\circ })={\rho }_f\dot{r}{h}_v$$

(12)

where $h_v$ is the effective enthalpy of vaporization in $[J/kg]$. In Equation (12), a polynomial expression for $c_{p,i}$ can be adopted and integrate numerically the sensible contribution.

The set of equations is completed by the pyrolysis kinetics, which allows to obtain the surface temperature by inverting the following expression:

$$\dot{r}=A{e}^{-E_a/\left(R_u{T}_s\right)}$$

(13)

where A is the pre-exponential factor, $E_a$ the activation energy and $R_u$ the universal gas constant.

3. Reference Experimental Data

The numerical model was validated using experimental data from the University of Naples in Italy. Carmicino and Sorge have tested GOX-HDPE [61,62,63] and GOX-HTPB [64] hybrid rockets at lab scale. The choice of these particular test cases among the vast array of hybrids lab-scale testing described in literature was influenced by a number of factors:

• Engine geometrical configuration and general dimensions are fully recorded and it is possible to reconstruct the fluid domain into the CFD software;
• Test results are well documented and span different operational conditions;
• Motor and injector geometry is simple and straightforward to mesh. Moreover, the axis-symmetry of the problem has been exploited to build a 2D computational grid and save computational resources;
• Oxidizer is injected into the combustion chamber in gaseous phase, so there is no need for a multi-phase simulation;
• Fuels are classic hyrbid fuels and quite common in the literature, thus, their properties are well documented and reliable. Furthermore, HTPB and HDPE are not “liquefying fuels” (whose physics is more complex [65,66,67,68,69]) and the mechanism of their pyrolysis can be modeled as a direct sublimation.

Table 1. Experimental data from literature for a lab-scale GOX-HDPE motor [61,62].

Test	${\mathit{L}}_{\mathit{g}}$ [mm]	${\mathit{D}}_{\mathit{p}0}$ [mm]	p [atm]	${\dot{\mathit{m}}}_{\mathit{ox}}$ [kg/s]	${\mathit{t}}_{\mathit{b}}$ [s]	${\mathit{G}}_{\mathit{ox}}$ [kg/sm${}^2$]	${\dot{\mathit{m}}}_{\mathit{f}}$ [kg/s]	G [kg/sm${}^2$]	O/F	${\mathit{c}}^{*}$ [m/s]	${\mathit{\eta }}_{\mathit{c}}$	${\mathit{D}}_{\mathit{p}}$ [mm]	$\dot{\mathit{r}}$ [mm/s]	${\mathit{x}}_{\mathit{max}}$ [mm]
1	560	25	15.63	0.136	24.2	99.69	0.04975	136.1	2.74	1712	0.922	41.71	0.69	280
2	560	50	16.85	0.125	54.9	27.68	0.06111	41.21	2.05	1843	0.952	75.84	0.47	320
3	560	16	17.31	0.124	58.3	63.87	0.04971	89.46	2.50	2028	1.075	49.73	0.58	280
4	560	16	15.64	0.129	43.0	87.14	0.04800	119.5	2.70	1796	0.965	43.48	0.64	-
5	560	16	15.46	0.124	40.3	92.43	0.04501	125.9	2.76	1892	1.021	41.38	0.63	260
6	560	25	25.00	0.208	42.6	84.80	0.07042	113.5	2.95	1814	0.984	55.88	0.72	320
7	560	25	18.96	0.157	50.4	66.60	0.05534	90.12	2.83	1805	0.976	54.73	0.59	-
8	560	50	22.69	0.188	40.6	47.79	0.06365	63.96	2.96	1828	0.994	70.80	0.51	280
9	560	75	22.61	0.180	31.5	28.41	0.07213	39.79	2.50	1820	0.962	89.84	0.47	400
10	560	25	20.25	0.177	21.2	126.0	0.05863	167.7	3.02	1748	0.955	42.33	0.82	320
11	560	50	20.78	0.173	33.1	47.45	0.06332	64.85	2.73	1793	0.962	68.08	0.55	240
12	560	75	13.80	0.106	15.2	20.31	0.05928	31.71	1.78	1691	0.869	81.37	0.42	320
13	560	50	10.09	0.080	26.2	28.19	0.03889	41.92	2.05	1731	0.900	60.04	0.38	320
14	560	70	15.57	0.118	36.5	20.95	0.05666	31.03	2.08	1816	0.941	84.56	0.40	-
15	560	75	15.12	0.112	22.8	20.12	0.05912	30.69	1.90	1794	0.923	84.37	0.41	380
16	560	75	15.48	0.112	25.1	19.93	0.05606	29.87	2.00	1872	0.967	84.72	0.39	280
17	560	50	12.20	0.099	24.2	34.13	0.04517	49.75	2.19	1758	0.919	60.68	0.44	240
18	560	16	11.78	0.100	44.1	78.07	0.03771	107.6	2.64	1741	0.936	40.32	0.55	300
19	560	25	11.11	0.095	44.3	54.03	0.03991	76.85	2.37	1683	0.890	47.19	0.50	-
20	560	54	11.96	0.097	50.0	23.00	0.04670	24.27	2.06	1702	0.884	73.04	0.38	260
21	560	50	9.57	0.076	61.5	18.77	0.04311	29.46	1.76	1641	0.846	71.67	0.35	200

and

Table 2. Experimental data from literature for a lab-scale GOX-HTPB motor [64].

Test	${\mathit{L}}_{\mathit{g}}$ [mm]	${\mathit{D}}_{\mathit{p}0}$ [mm]	${\mathit{t}}_{\mathit{b}}$ [s]	${\dot{\mathit{m}}}_{\mathit{ox}}$ [kg/s]	$\mathit{p}1$ [bar]	$\mathit{p}2$ [bar]	${\mathit{c}}^{*}$ [m/s]	${\mathit{\eta }}_{\mathit{c}}$	${\mathit{D}}_{\mathit{p}}$ [mm]	L/D	${\mathit{D}}_{\mathit{pf}}/{\mathit{D}}_{\mathit{p}0}$	$\dot{\mathit{r}}$ [mm/s]	O/F	${\mathit{G}}_{\mathit{ox}}$ [kg/sm${}^2$]
1	572	25	27.9	0.0320	4.6	4.5	1393	0.934	38.84	14.73	2.11	0.496	0.969	27.01
2	574	25	18.7	0.1328	16.4	16.2	1615	0.894	42.43	13.53	2.39	0.931	1.942	93.92
3	572	25	12.0	0.1924	23.7	23.5	1632	0.906	41.15	13.90	2.29	1.343	2.058	144.7
10bis	572	75	19.6	0.0697	10.2	10.0	1540	0.965	83.31	6.87	1.22	0.419	1.153	12.79
10	570	50	13.8	0.0468	7.0	6.8	1480	0.976	56.62	10.05	1.26	0.473	1.010	18.59
11	570	50	8.0	0.1886	23.9	23.7	1661	0.917	57.70	9.88	1.30	0.954	1.994	72.13
12	572	50	8.2	0.1966	24.7	24.6	1689	0.933	57.91	9.88	1.32	0.961	2.056	74.64

include all the average data used to perform the numerical validation. For more information on motor configuration, experimental findings and data processing, the reader is referred to the original papers. A useful discussion on regression rate averaging is provided in [70]. Geometrical dimensions are highlighted in Figure 2.

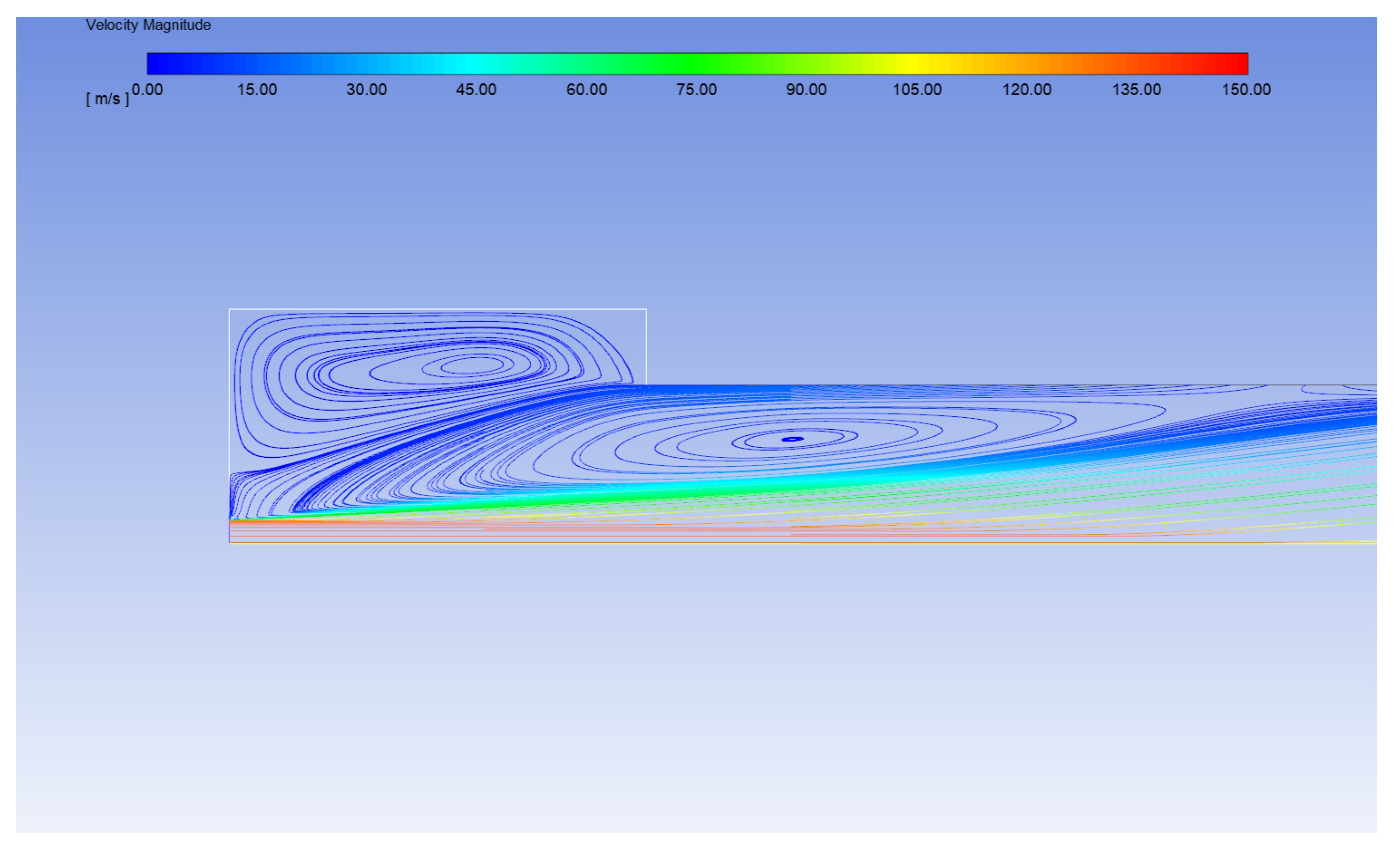
In relation to the experimental results just reported, it should be noted that, due to the unusual coupling between the oxidizer flow pattern at injection and the motor-internal geometry, the resulting average regression rate is strongly correlated with the port diameter history [62]. Thus, in order to draw a proper comparison between experimental and numerical results, not only the correspondence of oxidizer mass flux but also that of the average regression rate must be considered. 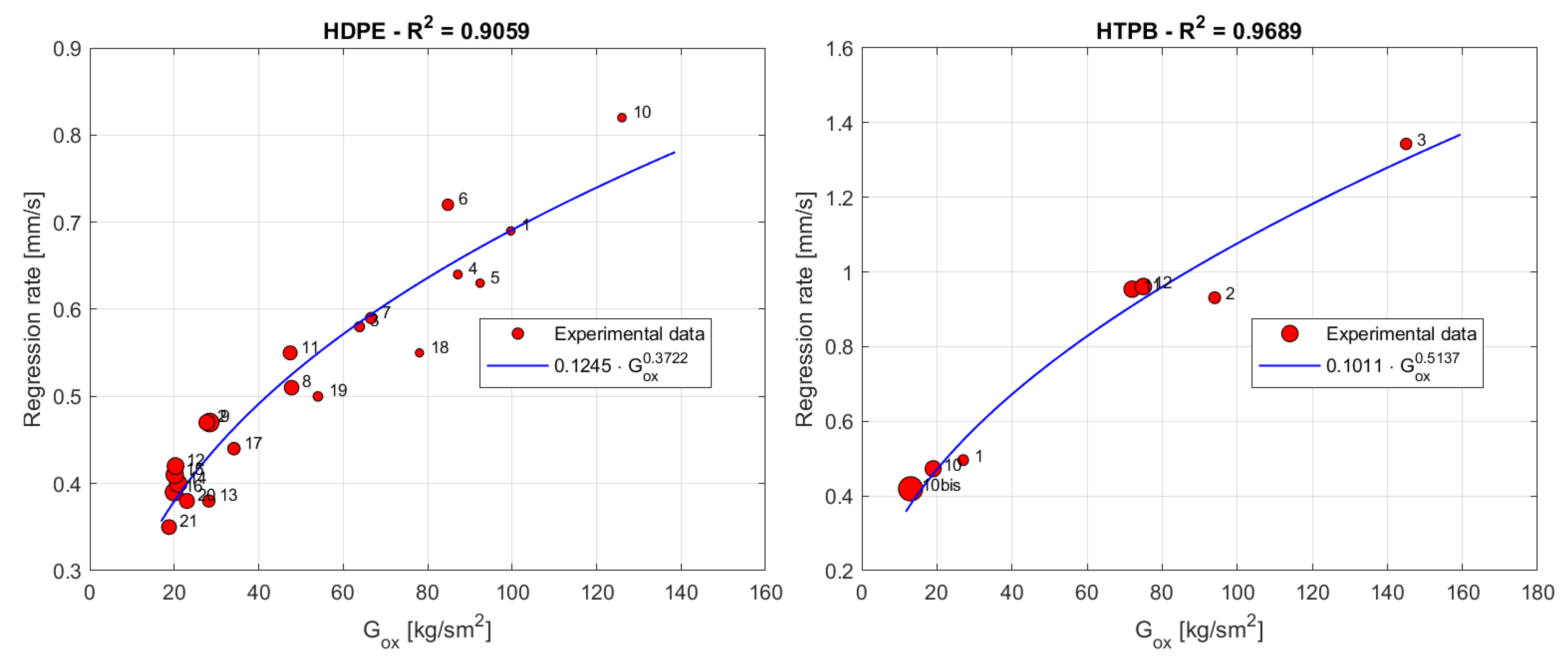Figure 3 shows the data just presented and the corresponding extrapolated regression rate laws for both fuels.

4. Fuel Characteristics

Several physical factors about the solid fuel and its constituent monomer are required to solve the system of equations comprising Equations (12) and (13). Based on the expected heat flow and fuel surface temperature in a hybrid motor, C${}_2$H${}_4$ (ethylene) and C${}_4$H${}_6$ (1,3-butadiene) are regarded as the principal constituent monomers for HDPE and HTPB, respectively [60,71].

The physical characteristics needed to implement the model are then:

• Solid fuel density: ${\rho }_f$;
• Specific enthalpy of formation of fuel monomer: $\Delta h_{f,i}^{\circ }$;
• Specific enthalpy of formation of solid fuel: $\Delta h_f^{\circ }$;
• Specific heat capacity of fuel monomer $c_{p,i}$;
• Arrhenius pre-exponential factor: A;
• Energy of activation: $E_a$.

Several sources in the literature provide these data. In general, all of the listed data for HDPE show satisfactory coherence, whereas data for HTPB show a significant variance and disagreement across the sources, particularly when it comes to the parameters of the Arrhenius equation and the specific enthalpy of formation of solid fuel [71,72,73,74,75,76]. This disparity can be explained by both the wide range of methodologies used to estimate the parameters [60,71] and the huge range of slightly different compositions that fall under the same category of HTPB.

NASA-Glenn and NIST databases [76,77] were used as references for HTPB thermochemical properties since they are comprehensive and reliable, whereas data provided by Chiaverini [60] were used for the Arrhenius equation parameters.

Regarding Arrhenius equation parameters for HDPE, the activation energy was derived from the literature [71], while a mean pre-exponential factor (generally A depends upon $\sqrt{T}$, however, this dependence is negligible in most of the cases) has been obtained using the Lengellé approach [71]:

$$\overline{A}=\sqrt{\frac{A_c{d}_p{R}_u}{E_c}}\sqrt{{\overline{T}}_s}\sqrt{1/\left(-ln\left(Y_{p,s}\right)(1-\frac{T_0}{{\overline{T}}_s}+\frac{h_D}{{\overline{c}}_{p,i}{\overline{T}}_s})-\frac{h_D}{{\overline{c}}_{p,i}{\overline{T}}_s}\right)}$$

(14)

where $A_c$ is the Arrhenius pre-exponential factor in [1/s], $E_c=2E_a$, ${\overline{d}}_p=\frac{\lambda }{{\rho }_f{\overline{c}}_{p,i}}$ and ${\overline{c}}_{p,i}$ are, respectively, the average thermal diffusivity and the specific heat capacity of the fuel monomer in the temperature range of interest and $h_D$ is heat of degradation (or pyrolysis) of the fuel, or, in other words, the heat necessary to transform the solid fuel into its associated gaseous monomer at $T_s$. Lastly, $Y_{p,s}$ is the remaining mass fraction of the polymer after the degradation, and it can be taken to be a small quantity (0.01).

Table 3. List of physical properties used in the calculation of pre-exponential factor for HDPE [71,78,79].

${\mathit{A}}_{\mathit{c}}$ [1/s]	${\mathit{E}}_{\mathit{c}}$ [J/mol]	$\mathit{\lambda }$ [J/msK]	${\mathit{\rho }}_{\mathit{f}}$ [kg/m${}^3$]	${\overline{\mathit{c}}}_{\mathit{p},\mathit{i}}$ [J/kgK]	${\overline{\mathit{d}}}_{\mathit{p}}$ [m${}^2$/s]	${\mathit{h}}_{\mathit{D}}$ [J/kg]	${\mathit{Y}}_{\mathit{p},\mathit{s}}$	${\overline{\mathit{T}}}_{\mathit{s}}$ [K]	${\mathit{T}}_0$ [K]
$2\times {10}^{16}$	251,208	0.38	960	1597	$2.46\times {10}^{-7}$	$3.19\times {10}^6$	0.01	900	300

,

Table 4. Arrhenius constants for HDPE and HTPB [71,78,79].

Fuel	$\overline{\mathit{A}}$ [m/s]	${\mathit{E}}_{\mathit{a}}$ [J/mol]	Range
HDPE	3636	125,520
HTPB	0.01104	20,543.44	T > 722 K
	3.9648	55,893.78	T < 722 K

and

Table 5. Formation enthalpies $\Delta h_{f,i}^{\circ }$ in [J/kg] for fuels and associated monomers [76,77,80].

HDPE	HTPB	${\mathit{C}}_2{\mathit{H}}_4$ (Ethylene)	${\mathit{C}}_4{\mathit{H}}_6$ (1,3-Butadiene)
−1,895,352	−310,000	1,871,447	2,033,631

contains all the numerical values of these parameters.

The density of the solid HTPB is taken as 930 kg/m${}^2$. The specific heat capacity for the gaseous monomer, $c_{p,i}$, is calculated as a fourth-order polynomial function of temperature for both HTPB and HDPE using the coefficients provided by NASA (NASA 9-Coefficient Polynomial Parametrization [77]), which are also integrated in the CFD software database.

5. Numerical Model

5.1. Combustion Model

The non-premixed combustion model [81,82,83] has been selected as a good candidate for accuracy, computational effort and reliability.

The main assumptions are:

• Infinitely fast chemical kinetics (Damkholer number Da >> 1);
• All chemical species have the same mass diffusivity (this condition is met in turbulent flows);
• Lewis Number Le = 1 (i.e., mass diffusivity = thermal diffusivity; this condition is also generally met in turbulent flows).

One of the most significant advantages of the non-premixed combustion model is its high accuracy in calculating chemical equilibrium and composition compared to fixed reaction equations models. It does, however, necessitate the calculation of a look-up table (PDF), which speeds up convergence by reducing the computational burden on each iteration but requires, on top of other obvious parameters, the definition of the Fuel Stream Rich Flammability Limit (FSRFL). This factor dictates the maximum mixture fraction for which chemical equilibrium is calculated. It is imposed as two times the stoichiometric mean mixture fraction in order to inhibit combustion in the highly fuel rich regions, as suggested by the software theory guidelines [81,82].

5.2. User-Defined Function

The implementation of a specific user-defined function (UDF) has enabled the self-calculation of regression rate: a function written by the user in C language that can be dynamically coupled with the CFD solver to expand the standard features of the commercial code. In general, UDFs can be used to specify customized model parameters, initialize a solution or improve post-processing, as well as to define specific boundary conditions, material properties and source terms for the given flow regime.

UDF is called at each iteration of the CFD simulation: based on the convective heat flux provided cell by cell at the gaseous interface, the system formed by Equations (12) and (13) is solved to obtain the new fuel mass flux and fuel surface temperature to be used as boundary conditions for the next iteration (Algorithm 1). While the temperature is directly assigned to the fuel surface, the fuel mass flux is injected into the domain through a wall+source boundary condition. In addition to a mass source, velocity, energy and mean mixture fraction, sources were defined following the expressions in Equations (15)–(18). There are two reasons for this choice: correct imposition of turbulence boundary conditions and automatic resolution of the problem of diffusion at the fuel surface, as suggested by Equation (1) (for a mass-flow inlet, the mean mixture fraction has to be defined).

• Continuity equation [84]:

  $$\begin{array}{c}\frac{\partial \rho }{\partial t}+\overrightarrow{\nabla }·(\rho \overrightarrow{v})=S_m\mathrm{with}{S}_m={\rho }_{inj}{v}_{inj}\end{array}$$

  (15)
• Conservation of momentum in y direction [84]:

  $$\begin{array}{c}\frac{\partial \left(\rho v\right)}{\partial t}+\overrightarrow{\nabla }·(\rho v\overrightarrow{v})=-\overrightarrow{\nabla }p+\overrightarrow{\nabla }·\overrightarrow{\overrightarrow{\tau }}+S_v\mathrm{with}{S}_v={\rho }_{inj}{v}_{inj}^2=S_m{v}_{inj}\end{array}$$

  (16)
• Energy conservation [85]:

  $$\begin{array}{c}\frac{\partial \left(\rho E\right)}{\partial t}+\overrightarrow{\nabla }·\left(\rho \overrightarrow{v}E\right)=-\overrightarrow{\nabla }·\left(\overrightarrow{v}p\right)+\overrightarrow{\nabla }·\left(k_{eff}\overrightarrow{\nabla }T-{\displaystyle \sum _j}{h}_i{\overrightarrow{J}}_i+{\overrightarrow{\overrightarrow{\tau }}}_{eff}·\overrightarrow{v}\right)+S_h\\ \mathrm{with}{h}_i={\int }_{T_{ref}}^T{c}_{p,j}dTE={\displaystyle \sum _i^n}{h}_i-\frac{p}{\rho }+\frac{v^2}{2}\\ \\ S_h={\rho }_{inj}{v}_{inj}{E}_i=S_m{E}_i\end{array}$$

  (17)
• Mean mixture fraction equation in the “Non-Premixed Combustion” model [86]:

  $$\begin{array}{c}\frac{\partial (\rho \overline{f})}{\partial t}+\overrightarrow{\nabla }·\left(\rho \overrightarrow{v}\overline{f}\right)=-\overrightarrow{\nabla }·\left(\frac{{\mu }_t}{{\sigma }_t}\nabla \overline{f}\right)+S_{\overline{f}}\\ \\ \mathrm{with}{S}_{\overline{f}}={\rho }_{inj}{v}_{inj}\overline{f}=S_m\overline{f}\mathrm{if}\mathrm{pure}\mathrm{monomer}\mathrm{injection}\overline{f}=1\end{array}$$

  (18)

Algorithm 1: Pseudo-code version of UDF’s main operations to calculate regression rate cell by cell.

5.3. Computational Domain

The mesh is composed of quadrilateral cells and tailored to achieve the appropriate dimension along the walls as well as a smooth transition between sections with varying refinement. In order to determine the final mesh design, a sensitivity study was conducted and the mesh was refined until the change in combustion chamber pressure was under 1%, resulting in a final number of cells in the order of $1\times {10}^5$–$2\times {10}^5$. The element thickness at the grain surface is 1 $\mathsf{\mu }$m, whereas the thickness on the other walls is 1 or 2 orders of magnitude higher. Finally, the boundary conditions are depicted in Figure 4 and are the same for all simulations. On the oxidizer inlet, a mass flow inlet condition was imposed, on the walls—an adiabatic no-slip condition was selected, the axis line was set as the axis of symmetry, the UDF was implemented on the fuel surface and the outlet was defined as a pressure outlet.

5.4. Other Settings

Additional important options are mentioned below.

• The simulation is steady-state, with the motor operating at the mean port diameter. Each simulation was executed with a fixed regression rate and brought to convergence to correctly and precisely initialize the domain before activating the UDF. In the case of an imposed regression rate, the spatial mean of the experimental data was employed;
• The mean port diameter of the fuel grain is considered to be constant along the axial direction. This way, any unevenness of the regressing fuel surface is neglected;
• The $k-\omega SST$ turbulence model [87,88,89] with Low-Re correction was employed, and the solution was derived using a double-precision and second-order upwind discretization scheme;
• Convergence was tracked using both equation residuals (<${10}^{-4}$) and specific parameter variations with iterations (for example, pressure, temperature, and axial velocity);
• Radiation was not included in the simulations for the sake of simplicity. The lack of this model could play a non-negligible role in determining the correct regression rate for HTPB as a result of its soot-producing characteristics [60,90]. Therefore, it must be taken into consideration that there could be a significant underestimation in the average regression rate in comparison with the experimental findings, particularly for low oxidizer mass fluxes [60]. Strand et al. [91] found that the radiative flux can account for more than 50% of the total heat flux. However, Marxman analysis [53] indicates that a radiative transfer in the order of one-half of the convective heat transfer results in a smaller (about 10%) net increase in regression rate due to the blocking effect.

6. Results and Discussion

Comparison with Experimental Data

A handful of cases were selected for the simulation. The subset was chosen so as to span multiple port diameters and oxidizer mass fluxes to ensure adequate coverage of data. Then, each numerical result was compared to the associated experimental one in terms of mean regression rate and chamber pressure.

Table 6. Numerical results of GOX-HDPE motor tests.

Test	${\overline{\mathit{D}}}_{\mathit{p}}$ [mm]	${\dot{\mathit{m}}}_{\mathit{ox}}$ [kg/s]	${\mathit{G}}_{\mathit{ox}}$ [kg/sm${}^2$]	${\dot{\mathit{r}}}_{\mathit{exp}}$ [mm/s]	${\dot{\mathit{r}}}_{\mathit{CFD}}$ [mm/s]	$\dot{\mathit{r}}$ Error	${\mathit{p}}_{\mathit{exp}}$ [bar]	${\mathit{p}}_{\mathit{CFD}}$ [bar]	p Error	${\mathit{c}}_{\mathit{CFD}}^{*}$ [m/s]	${{\mathit{\eta }}_{\mathit{c}}}_{\mathit{CFD}}$
5	41.38	0.124	92.43	0.630	0.613	−2.71%	15.67	14.74	−5.95%	1773	0.957
7	54.73	0.157	66.60	0.590	0.642	8.78%	19.21	19.40	0.99%	1806	0.976
10	42.33	0.177	126.0	0.817	0.821	0.44%	20.51	20.94	2.09%	1785	0.975
17	60.68	0.099	34.13	0.441	0.417	−5.60%	12.37	12.49	0.99%	1773	0.926
19	47.19	0.095	54.03	0.501	0.465	−7.25%	11.25	11.11	−1.26%	1693	0.895

and

Table 7. Numerical results of GOX-HTPB motor tests.

Test	${\overline{\mathit{D}}}_{\mathit{p}}$ [mm]	${\dot{\mathit{m}}}_{\mathit{ox}}$ [kg/s]	${\mathit{G}}_{\mathit{ox}}$ [kg/sm${}^2$]	${\dot{\mathit{r}}}_{\mathit{exp}}$ [mm/s]	${\dot{\mathit{r}}}_{\mathit{CFD}}$ [mm/s]	$\dot{\mathit{r}}$ Error	${\mathit{p}}_{\mathit{exp}}$ [bar]	${\mathit{p}}_{\mathit{CFD}}$ [bar]	p Error	${\mathit{c}}_{\mathit{CFD}}^{*}$ [m/s]	${{\mathit{\eta }}_{\mathit{c}}}_{\mathit{CFD}}$
1	38.88	0.0320	26.96	0.496	0.409	−17.56%	4.51	4.04	−10.3%	1364	0.914
2	42.42	0.1328	94.00	0.931	0.915	−1.69%	16.16	16.91	4.66%	1720	0.952
3	41.13	0.1924	144.8	1.343	1.152	−14.24%	24.56	23.89	2.91%	1754	0.973
10	56.62	0.0468	18.59	0.473	0.291	−38.52%	6.86	6.06	−11.6%	1623	0.915
12	58.00	0.1966	74.41	0.961	0.970	0.96%	24.56	24.79	0.95%	1721	0.950

report the numerical values calculated as surface weighted average for regression rate and mass-flux weighted average of total throat pressure for combustion chamber pressure.

Figure 5 presents graphically the CFD results compared to the previous experimental data, while the regression rate profiles of the simulated cases are plotted in Figure 6. From the latter, a peak is clearly visible, corresponding to the impingement of the oxidizer jet from the conical injector, supporting the statement that regression rate varies heavily with longitudinal coordinate and that CFD can capture this phenomenon.

Additionally, the temperature field, $O_2$ mass fraction and prechamber pathlines of a sample test (Test 7—HDPE,) are displayed in Figure 7, Figure 8 and Figure 9. The slightly lower temperature in the radial periphery of the postchamber is due to a recirculation of fuel and combustion products being trapped in that region. Samples of some significant variables were taken from vertical lines (with y = 0 being the symmetry axis) located at x = 300, 400, 500 and 600 mm and are shown in Figure 10, Figure 11 and Figure 12. Other simulations, both with HDPE and HDPE, show similar results. When this is combined with the uniformity of temperature and velocity profiles in Figure 10 and Figure 11, in comparison with Figure 13 and Figure 14, it is clear that these tests achieved excellent mixing and high combustion efficiencies, disrupting the stratified flow that is predominant in more classical designs. Unlike in [45,92], indeed, the radial profiles do not show marked peaks. The proposed explanation is the conical injector-induced turbulence, which strongly correlates with mixing and high combustion efficiencies.

The CFD results agree quite well with the experimental data, scoring in regression rate less than 10% error for HDPE and less than 20% error for HTPB (except for test 10 that has the lowest oxidizer flux). The lower accuracy of the second fuel, particularly for low fluxes, was expected due to the lack of a radiation model. HTPB is notoriously a soot producing fuel which in turns raises the radiation heat transfer contribution to non-negligible values. Regarding pressure, the results are consistent with the imposed self-calculated fuel mass flow rate, producing a combustion efficiency compatible with experimental measurements.

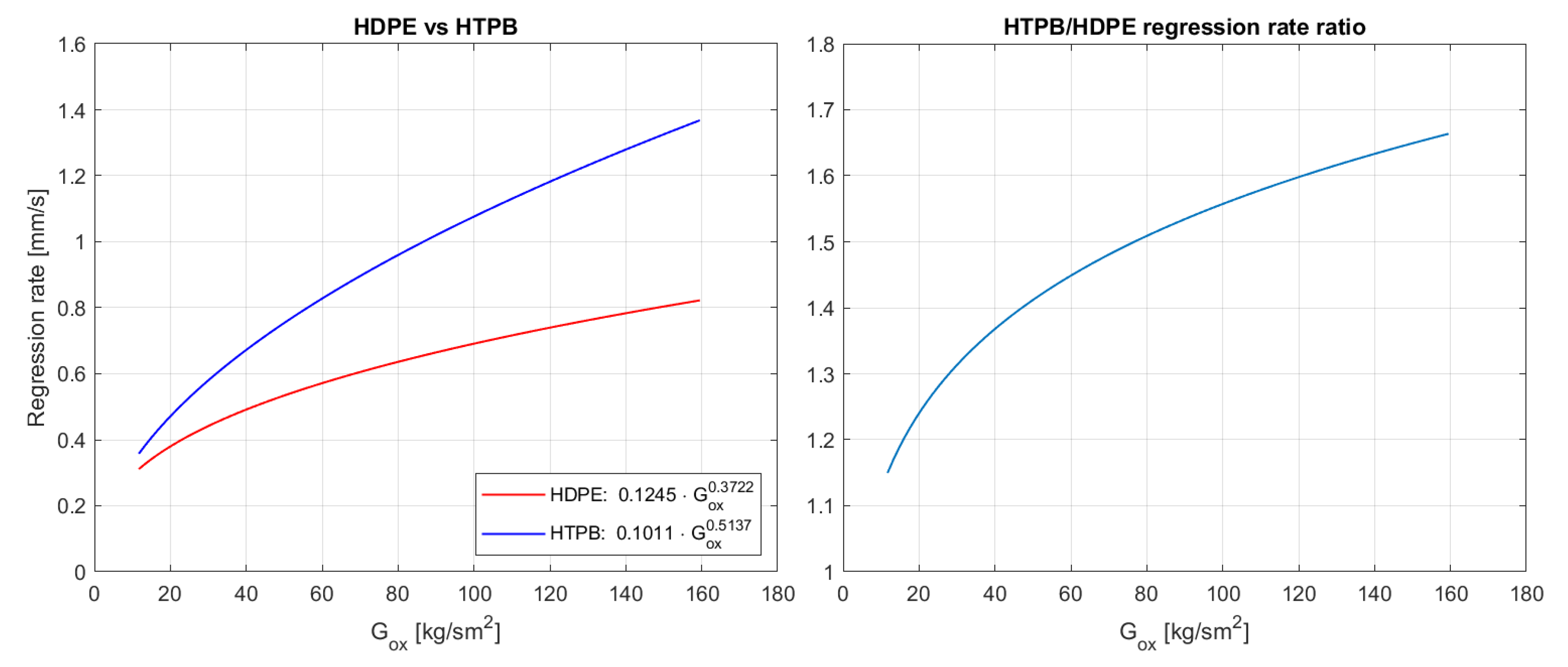
7. Regression Rate Comparison Analysis

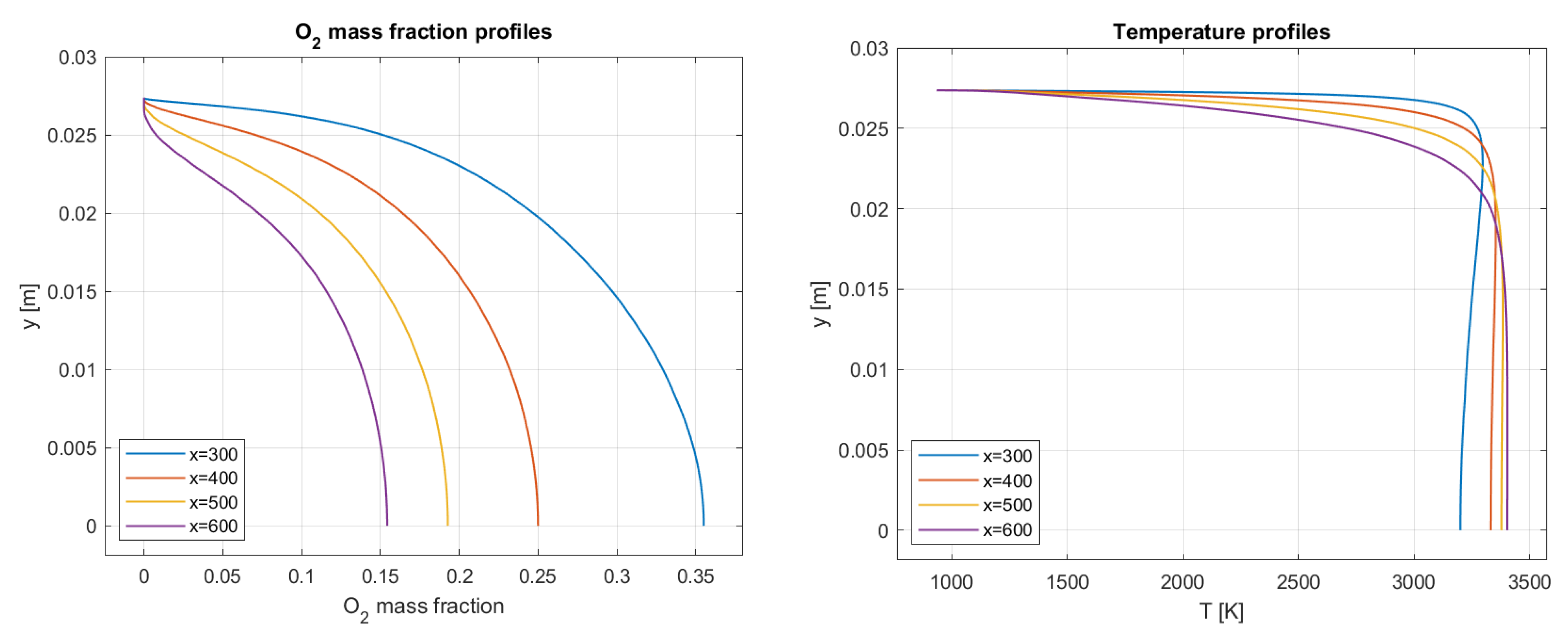
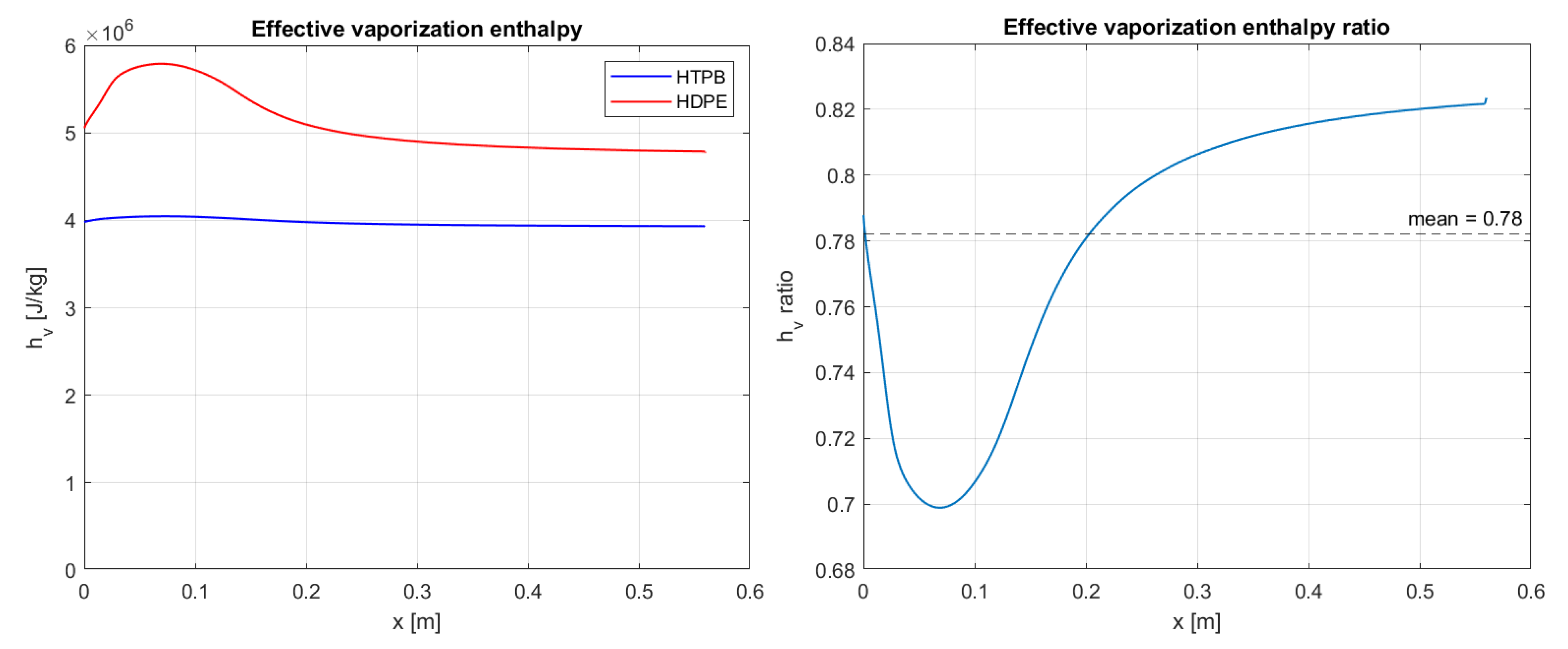
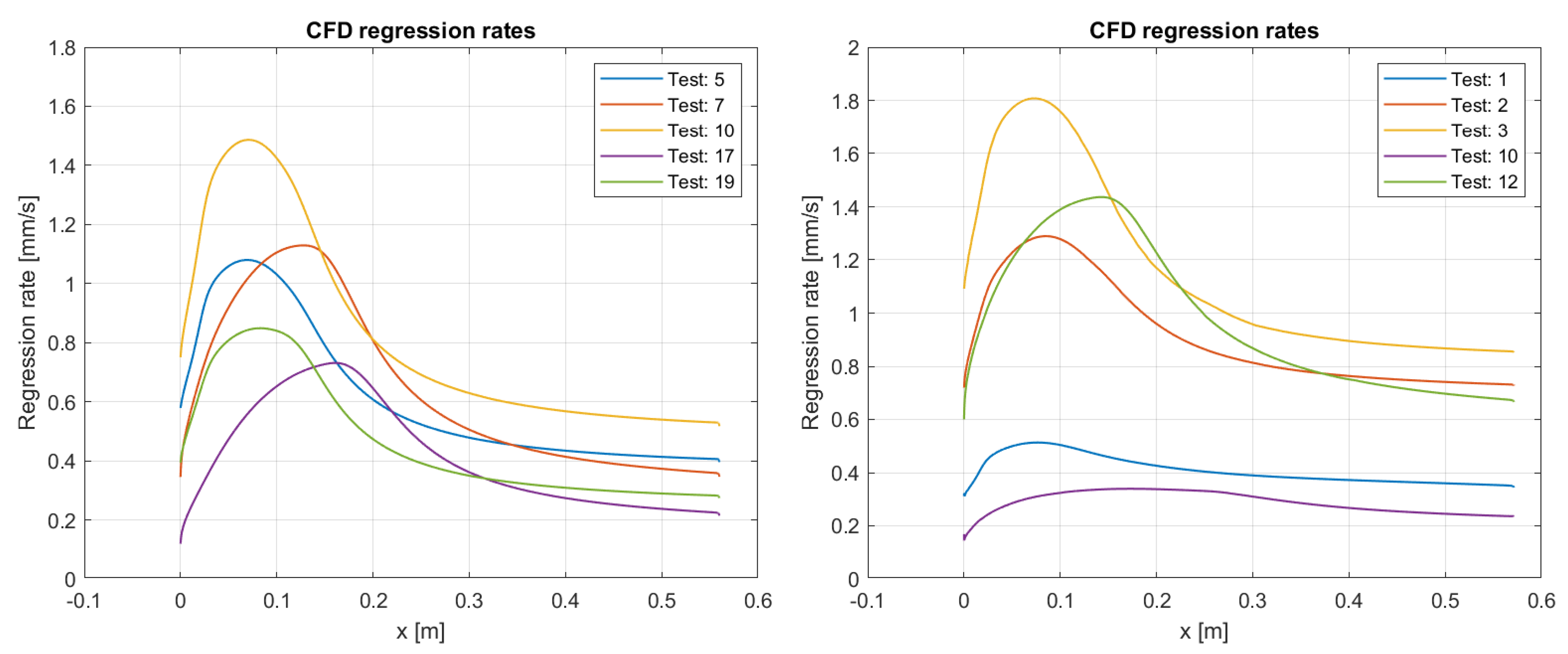
It is worth noting that these two fuels seem to display quite different regression rates despite being somewhat similar in properties. Several attempts to improve the original Marxman model have been made [75,93,94,95], but a satisfactory explanation is still lacking. As shown in Figure 15, the ratio ${\dot{r}}_{HTPB}/{\dot{r}}_{HDPE}$ varies from 1.1 to 1.7, with potentially greater values for higher oxidizer mass fluxes. Moreover, taking as samples the simulation results of Test 5 and 2, which are comparable in terms of geometric features and oxidizer mass flux, it is possible to obtain Figure 16, Figure 17 and Figure 18 as ratios of regression rates, effective vaporization enthalpy and fuel wall heat flux, respectively. The vaporization enthalpy $h_v$ at the corresponding working point is about 20% lower for HTPB. This difference, as explained below, however, is not enough to account for the observed regression rate ratio according to Marxman’s classic hybrid rocket theory [52,53,54].

Marxman’s theory states, indeed, that [52]:

$$Q\approx Q_0{B}^{-0.77}$$

(19)

The ratio between HTPB and HDPE heat flux would be:

$$\frac{Q_{HTPB}}{Q_{HDPE}}=\frac{Q_{0_{HTPB}}}{Q_{0_{HDPE}}}{\left(\frac{B_{HTPB}}{B_{HDPE}}\right)}^{-0.77}$$

(20)

Given the similarity of the combustion chemistry of the two fuels, $Q_0$ can be assumed to be nearly equal, while the ratio between the blowing coefficient B is proportional to the ratio of regression rates, producing the following expression:

$$\frac{Q_{HTPB}}{Q_{HDPE}}={\left(\frac{{\dot{r}}_{HTPB}}{{\dot{r}}_{HDPE}}\right)}^{-0.77}\approx {\left(1.57\right)}^{-0.77}\approx 0.707$$

(21)

Using the mean ratio obtained by the CFD simulation (Figure 16), the results is completely off with respect to the observed one in Figure 18, being even on the opposite direction. As noted before, $h_v$ could not explain this discrepancy, as demonstrated by the expression below [60], where again, the mean $h_v$ ratio obtained though the CFD simulation of Test 5 and 2 (Figure 17) is taken again:

$$\begin{array}{c}\dot{r}\propto B^{0.23}B=\frac{u_e\Delta h}{u_b{h}_v}\frac{{\dot{r}}_{HTPB}}{{\dot{r}}_{HDPE}}={\left(\frac{h_{v_{HDPE}}}{h_{v_{HTPB}}}\right)}^{0.23}\approx {\left(\frac{1}{0.78}\right)}^{0.23}\approx 1.06\end{array}$$

(22)

Moreover, it is unlikely that radiation could account for a substantial portion of the difference, especially when considering that it is far more significant for low values of G, while the regression rate ratio is diverging (Figure 15). This discrepancy could also be the effect of other physical properties such as density of the solid fuel and Arrhenius constants. However, it seems very unlikely that they would result in such a strong difference, especially when accounting for all the negative feedback-loops that make hybrid rocket motors safe, but at the same time, cap the $\dot{r}$ of classic fuels to low values. The source of this effect should be researched further, and the density of the decomposition products in particular is suggested [60]: lighter pyrolysis products may result in stronger blowing and blocking effects, resulting in the observed relationship between HDPE and HTPB. The primary breakdown species of a polymer is often its fundamental monomer. For the former, it is C${}_2$H${}_4$ (ethylene), with a molecular mass of 28 g/mol. When compared to 54 g/mol of C${}_4$H${}_6$ (1,3-butadiene) from HTPB, it is about twice as low. Furthermore, even if the decomposition gases are an heterogeneous mixture of very different species, the conservation of mass and atoms will produce a mean molecular mass that is around the fundamental monomer’s one (Figure 19). An investigation of this effect through a rigorous analysis will be presented in future works.

8. Conclusions and Further Developments

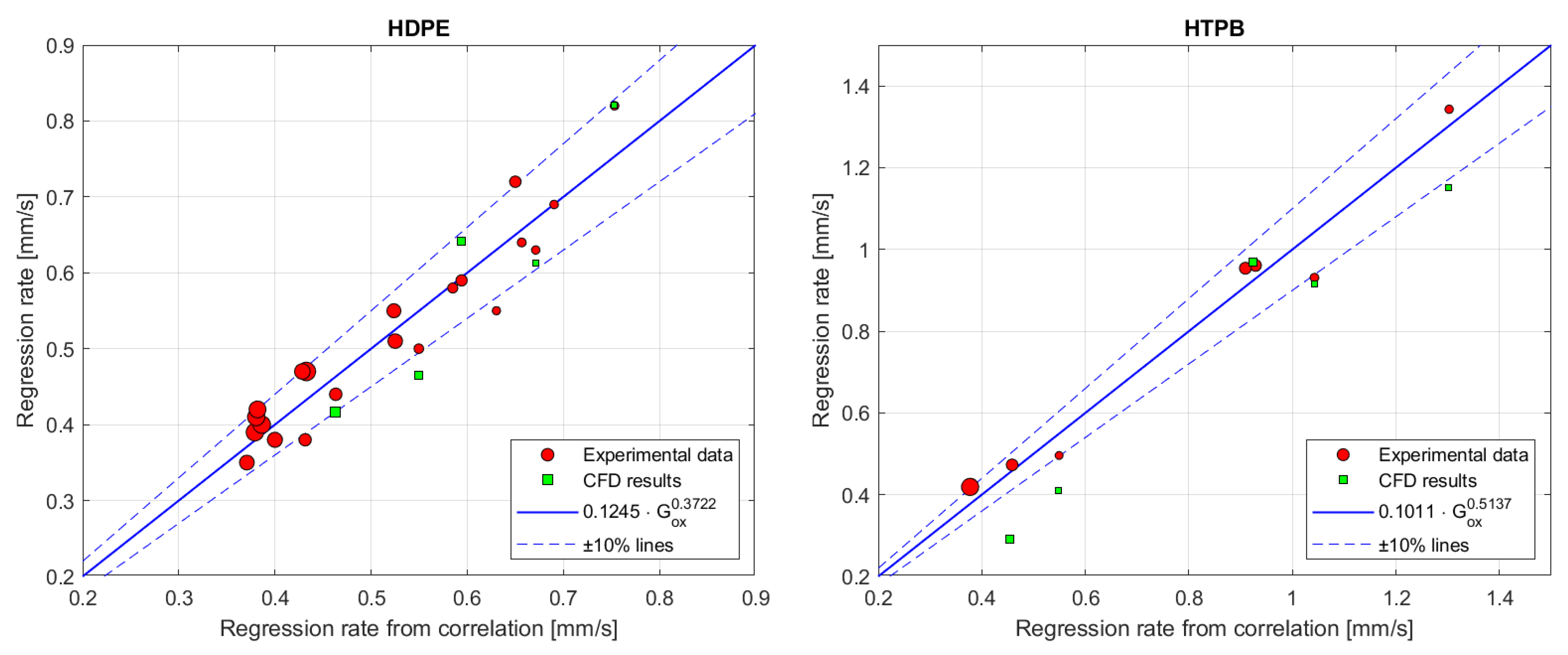
A numerical model of the ablation of classical polymeric fuels in hybrid rocket motors was implemented on a commercial CFD package using a special user-defined function that determines regression rate as a function of heat flux at the fuel surface, cell by cell. The regression rate was calculated by computing the surface energy balance in combination with the Arrhenius equation for fuel pyrolysis. A validation campaign using literature data from a cylindrical port-axial injection lab-scale motor was successfully completed. The propellant combinations GOX-HTPB and GOX-HDPE were utilized in the reference experiments, and gaseous oxygen was fed by a single hole injector. The numerically determined regression rate generally agrees within 10% of the experimental results for HDPE and 20% for HTPB, demonstrating the feasibility of tailoring a commercial software for the purpose, as well as the effectiveness, of a relatively simplified model in providing useful insight into the hybrid combustion process. CFD simulations enable the exploration of local processes inside the hybrid motor, which are frequently difficult to analyze in depth. Indeed, it has been demonstrated that a considerable local effect exists when the oxidizer flow impinges on the fuel surface, boosting the regression rate. The proposed CFD tool can be used to examine hybrid rocket regression rate behavior using parametric analysis, thus improving understanding of the ablation process and defining improved regression rate correlations. The addition of a suitable radiation model to the present UDF should improve the accuracy of the regression rate prediction, particularly for fuels that create considerable soot and/or at low oxidizer fluxes. Furthermore, it will be beneficial to adapt the model to non-classical fuels such as liquefying fuels (with the addition of an entrainment model) or fuels including energetic additions (e.g., metal particles). Finally, a discrepancy in the classic hybrid rocket theory was exposed regarding HDPE and HTPB regression rates. The proposed explanation is the difference in decomposition product density which lowers or increases the blowing effect. A detailed analysis will be conducted in future works to determine whether this effect could affect the boundary layer behavior and alter the convective heat transfer to the surface.