Shock Tube Study of Ignition Delay Times for Hydrogen–Oxygen Mixtures
Abstract
:1. Introduction
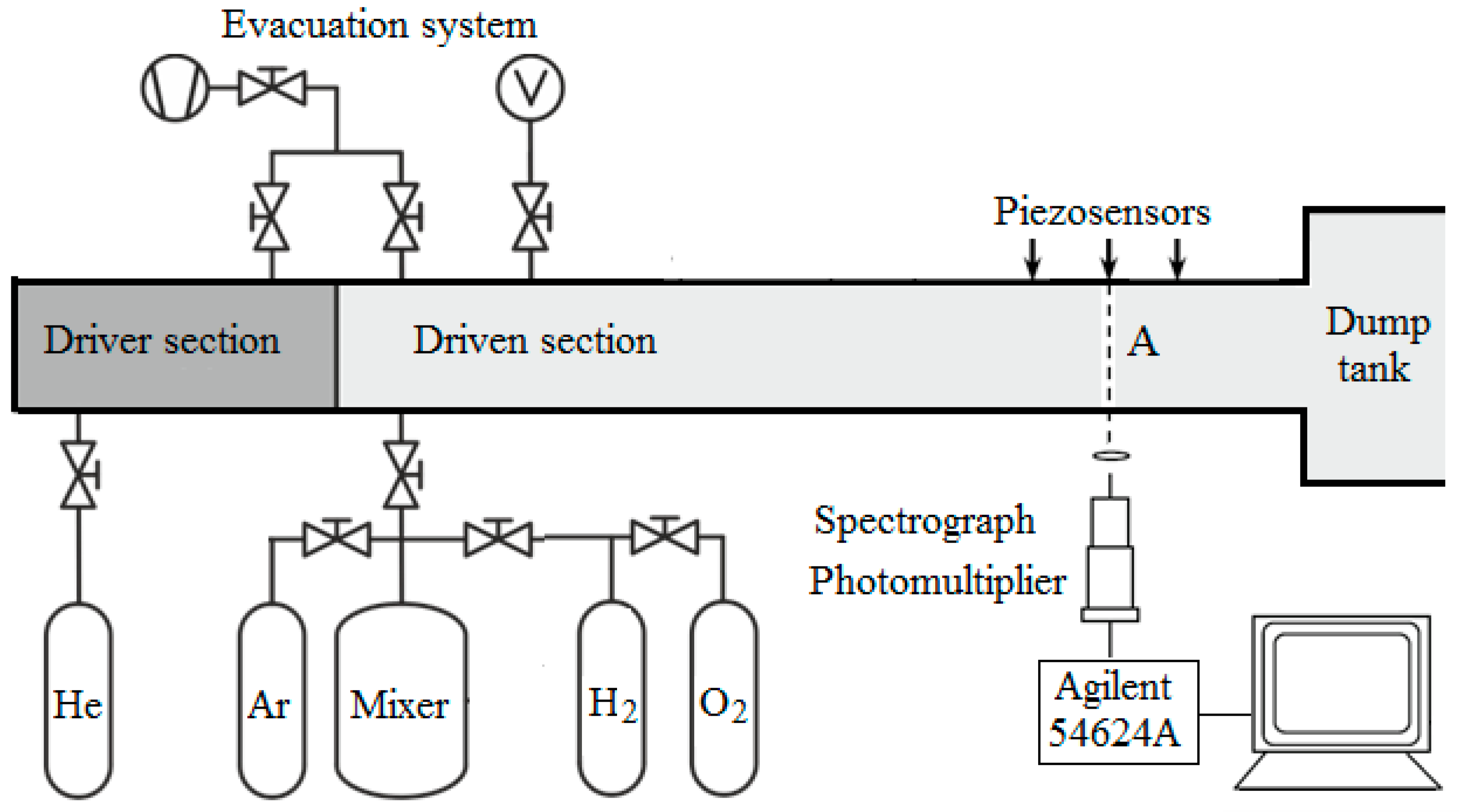
2. Experimental Procedure
3. Numerical Modeling
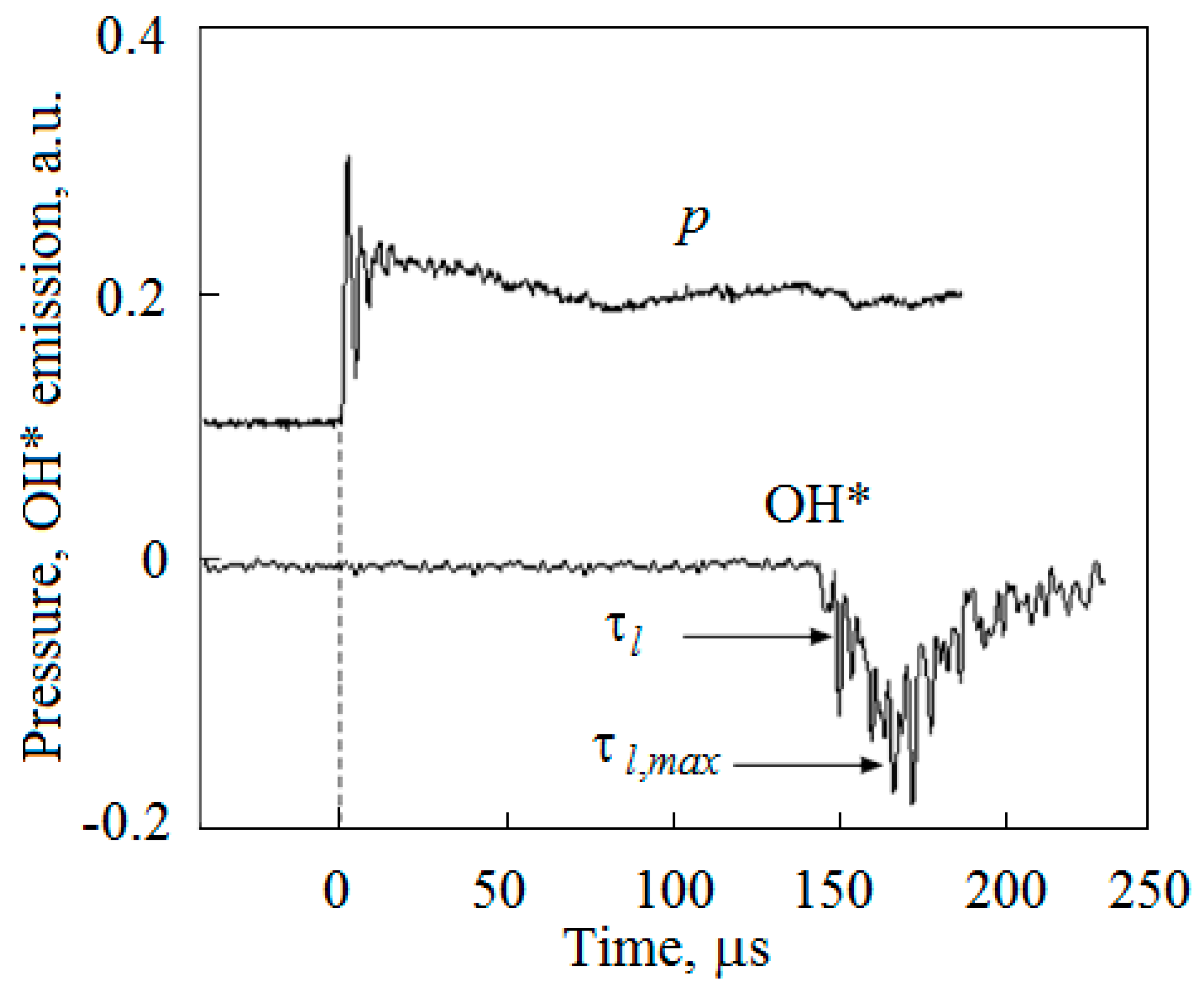
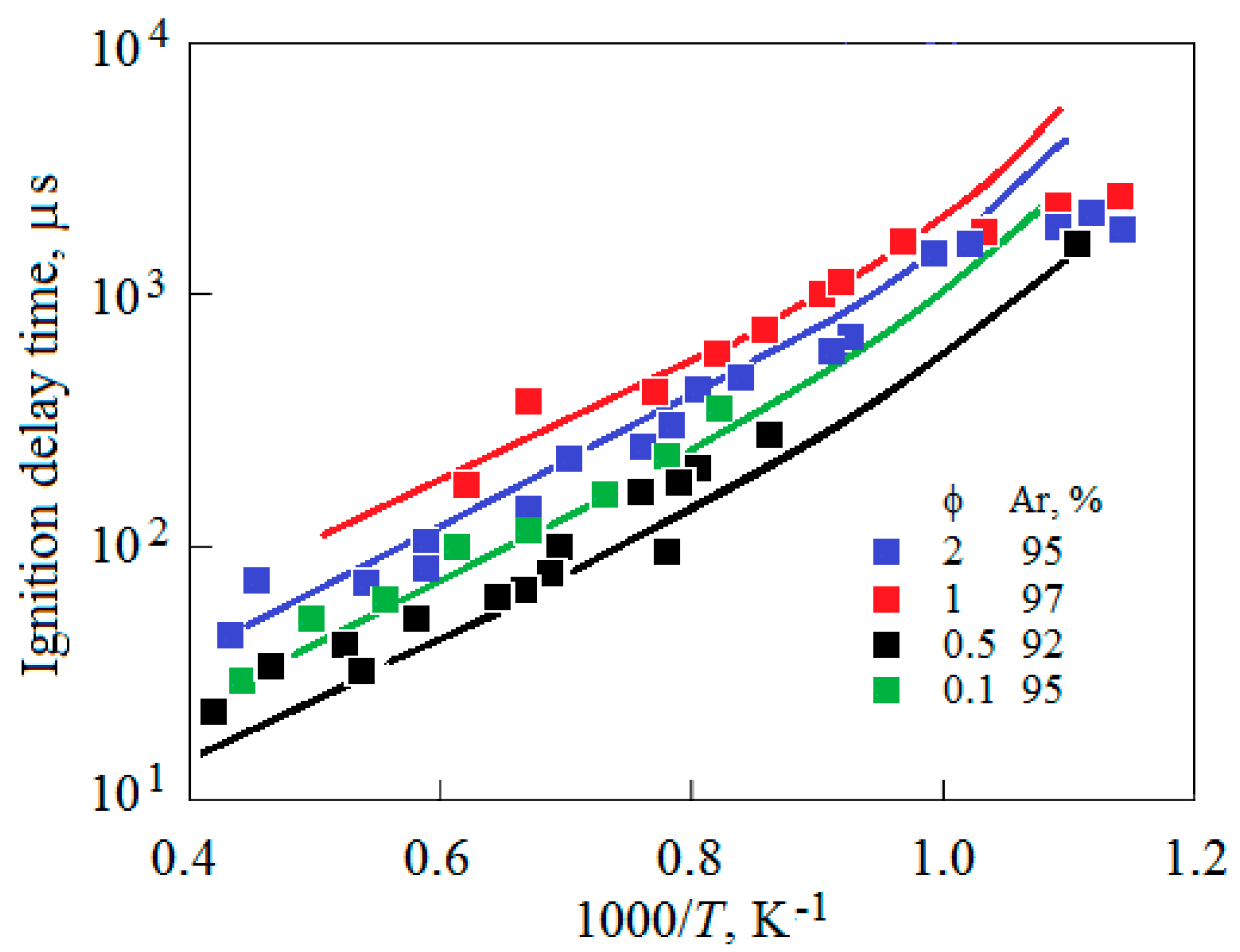
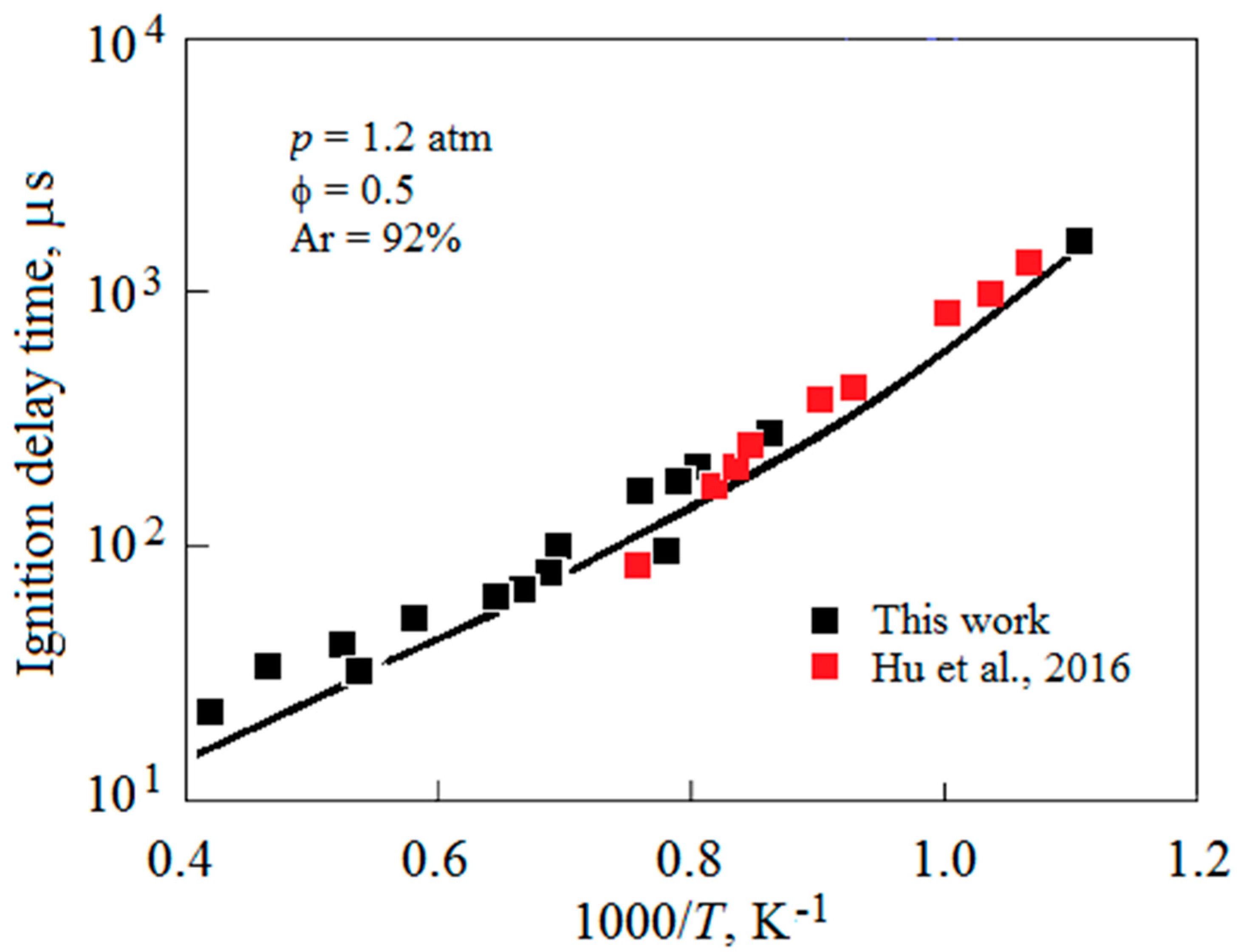
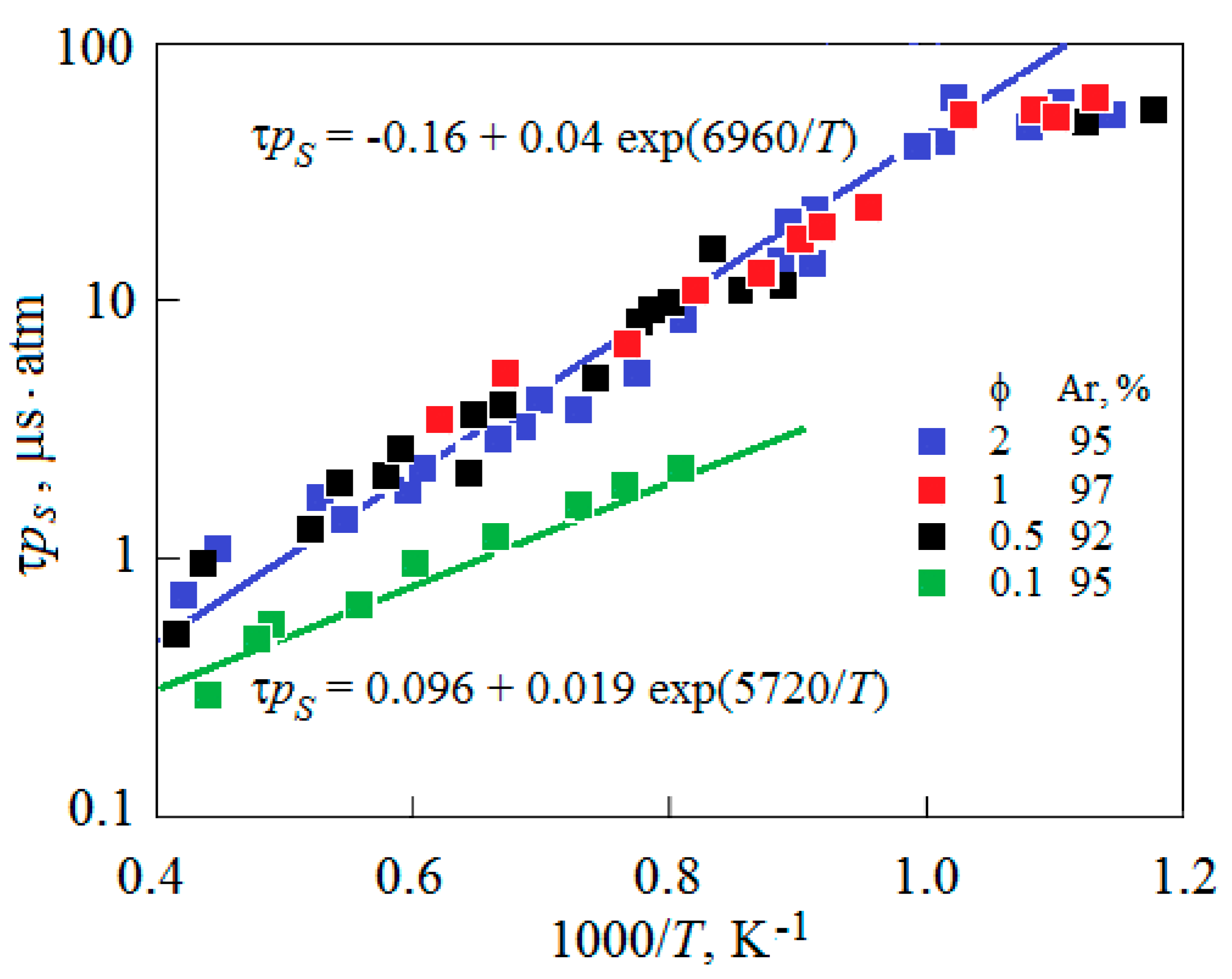
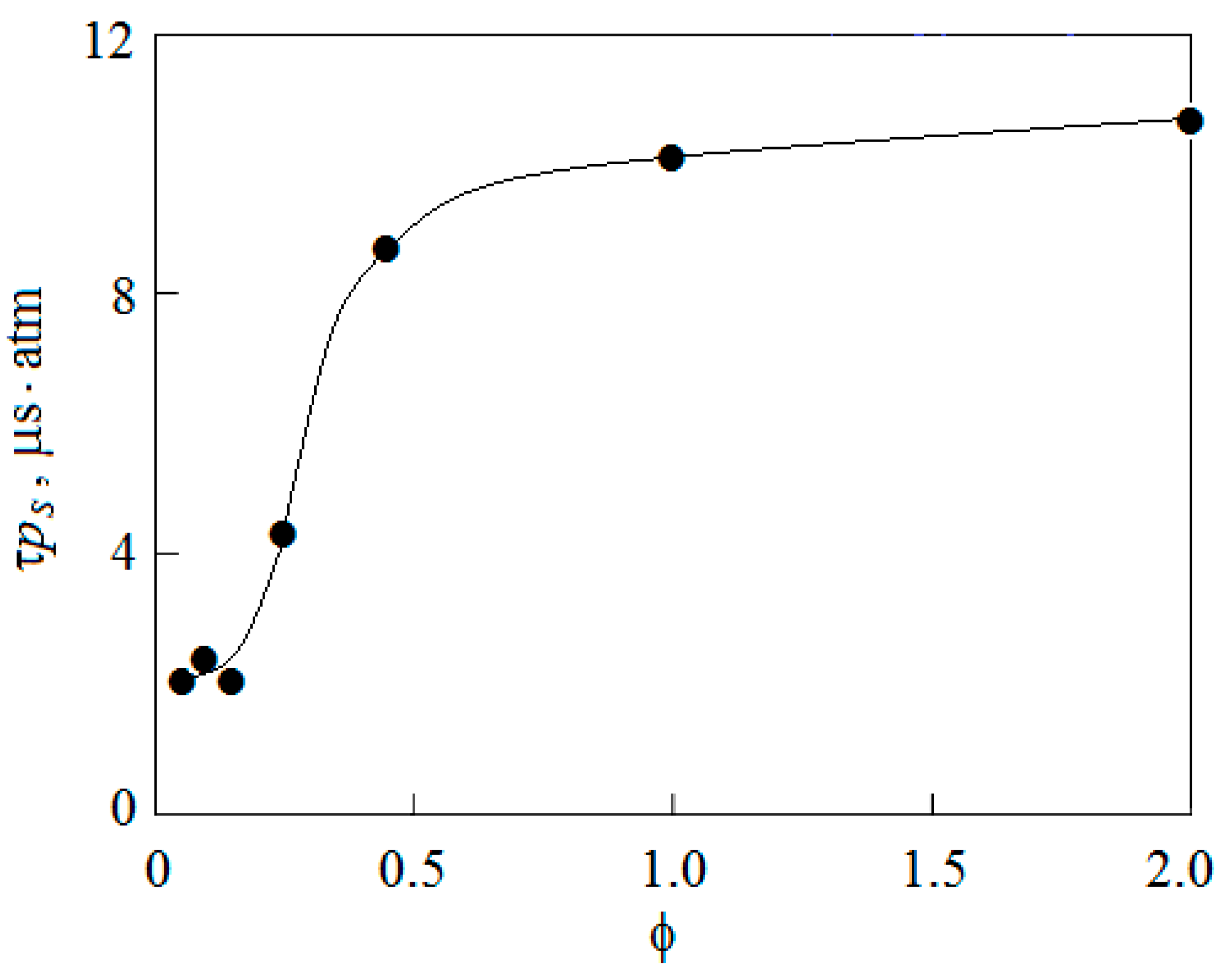
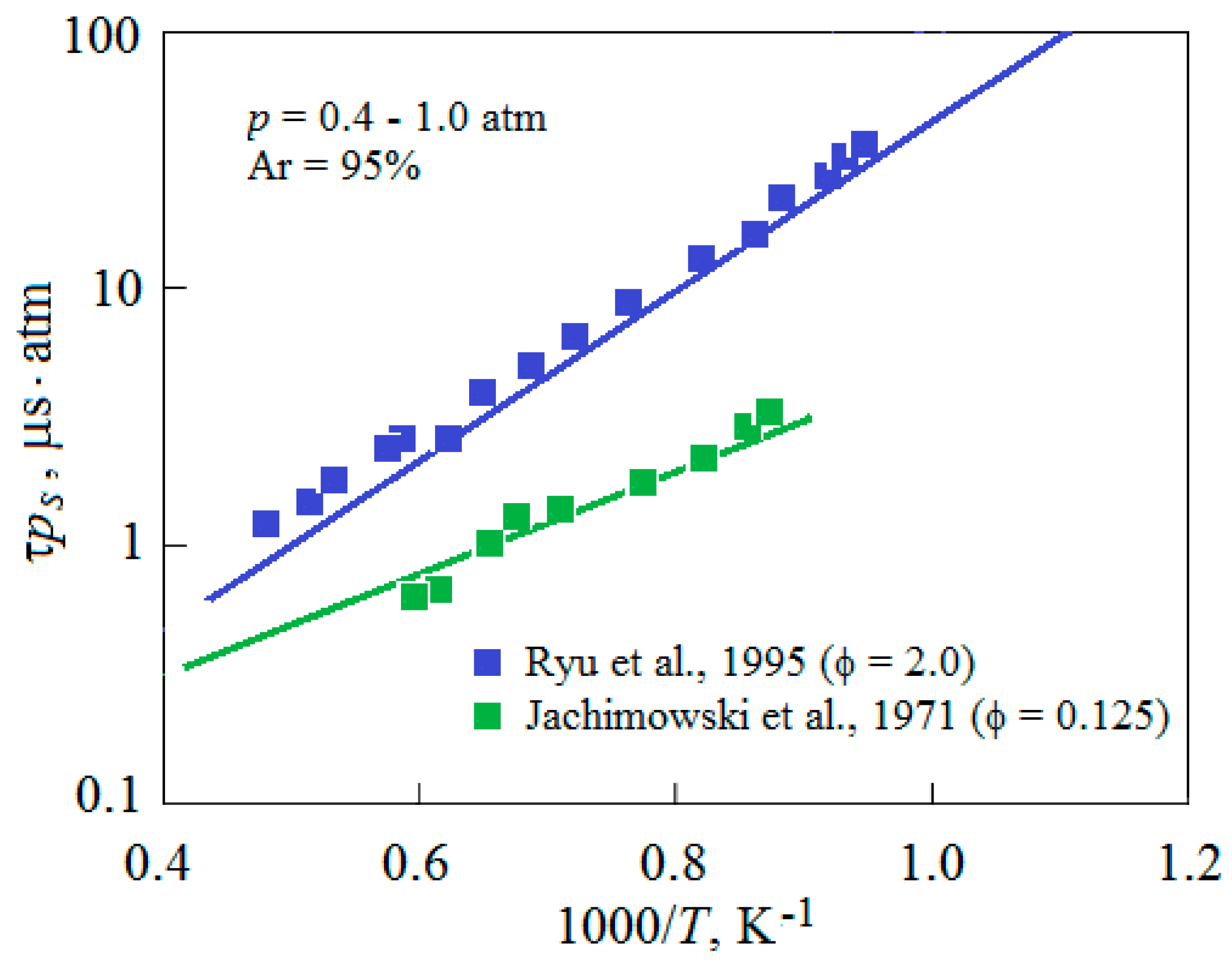
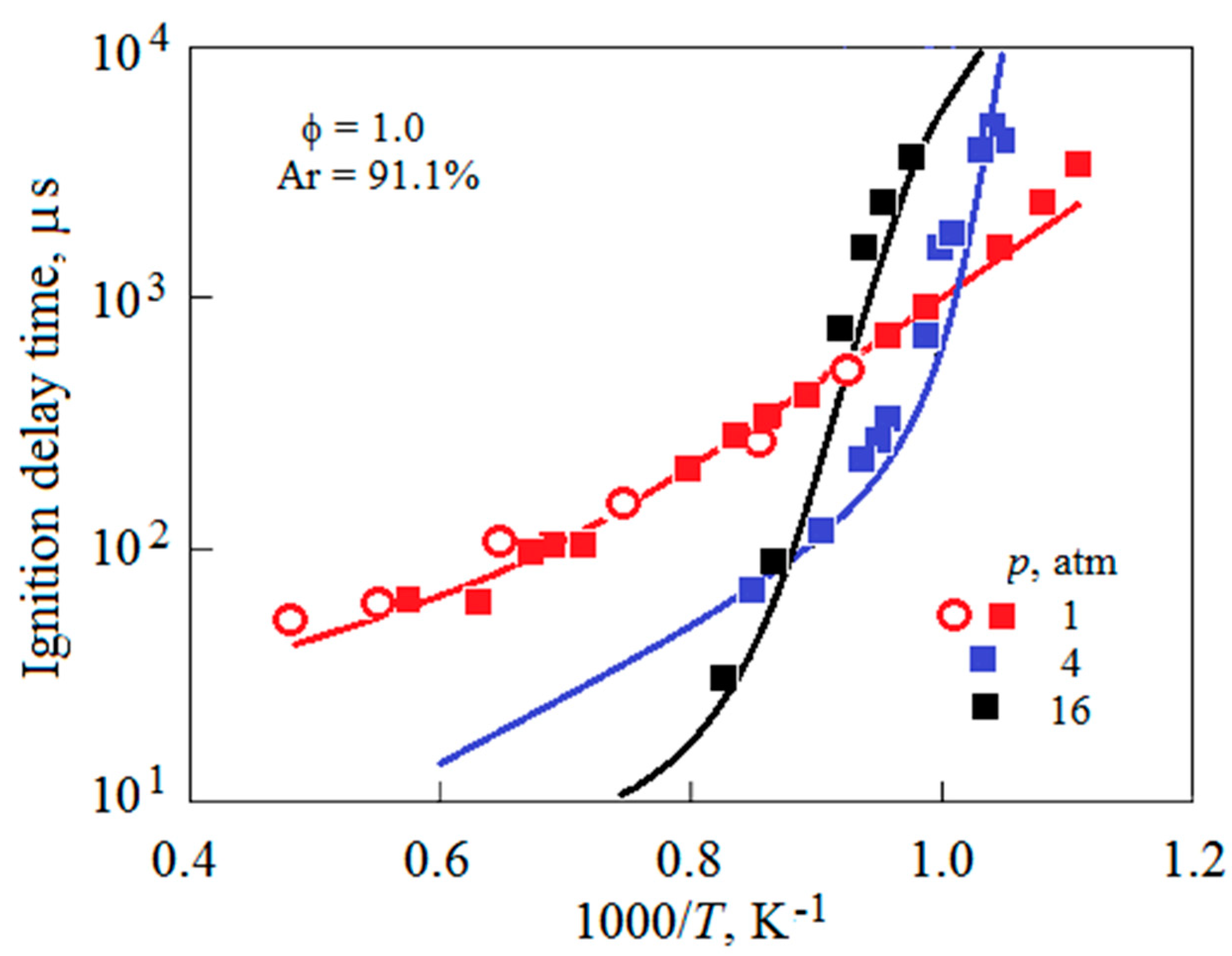
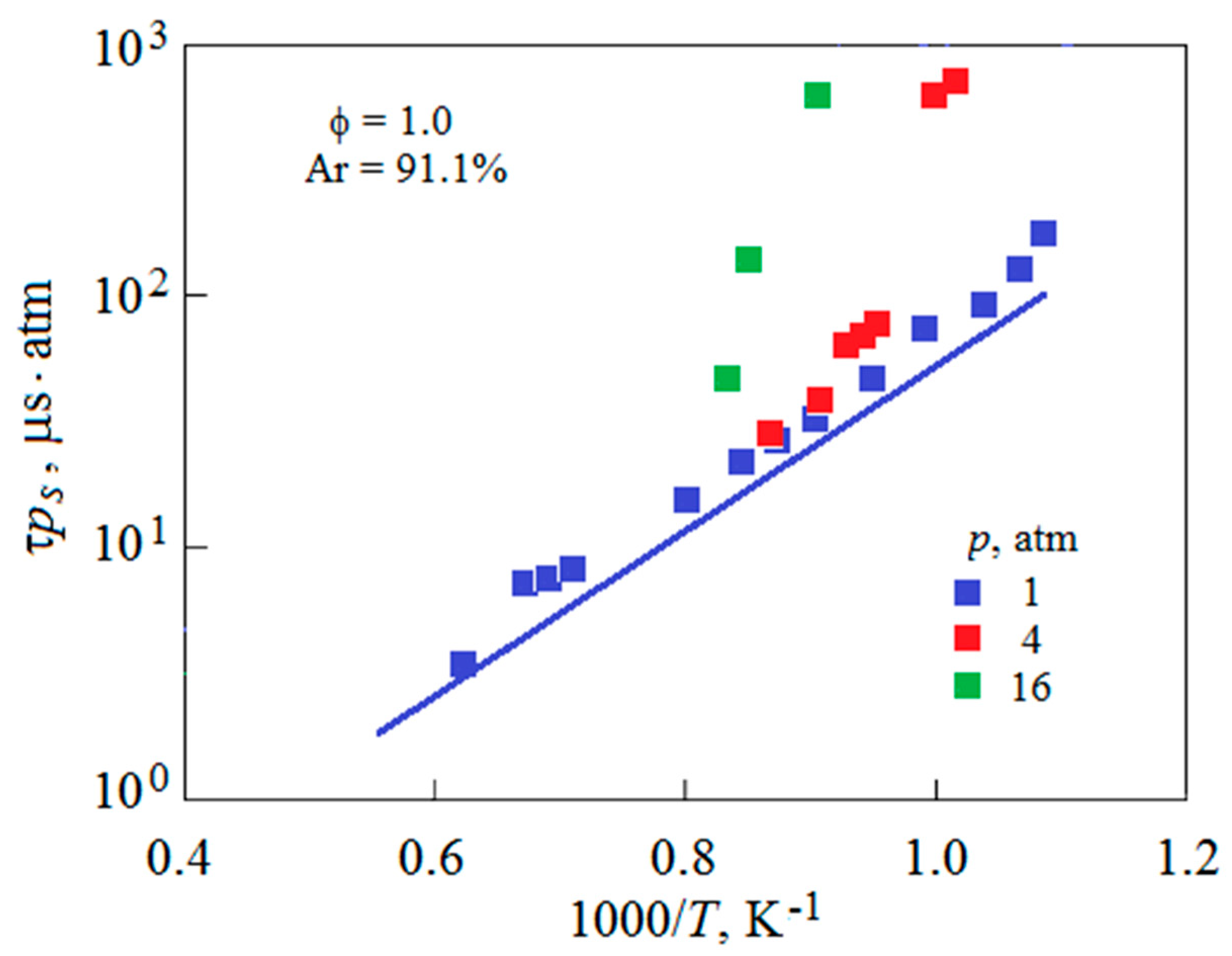
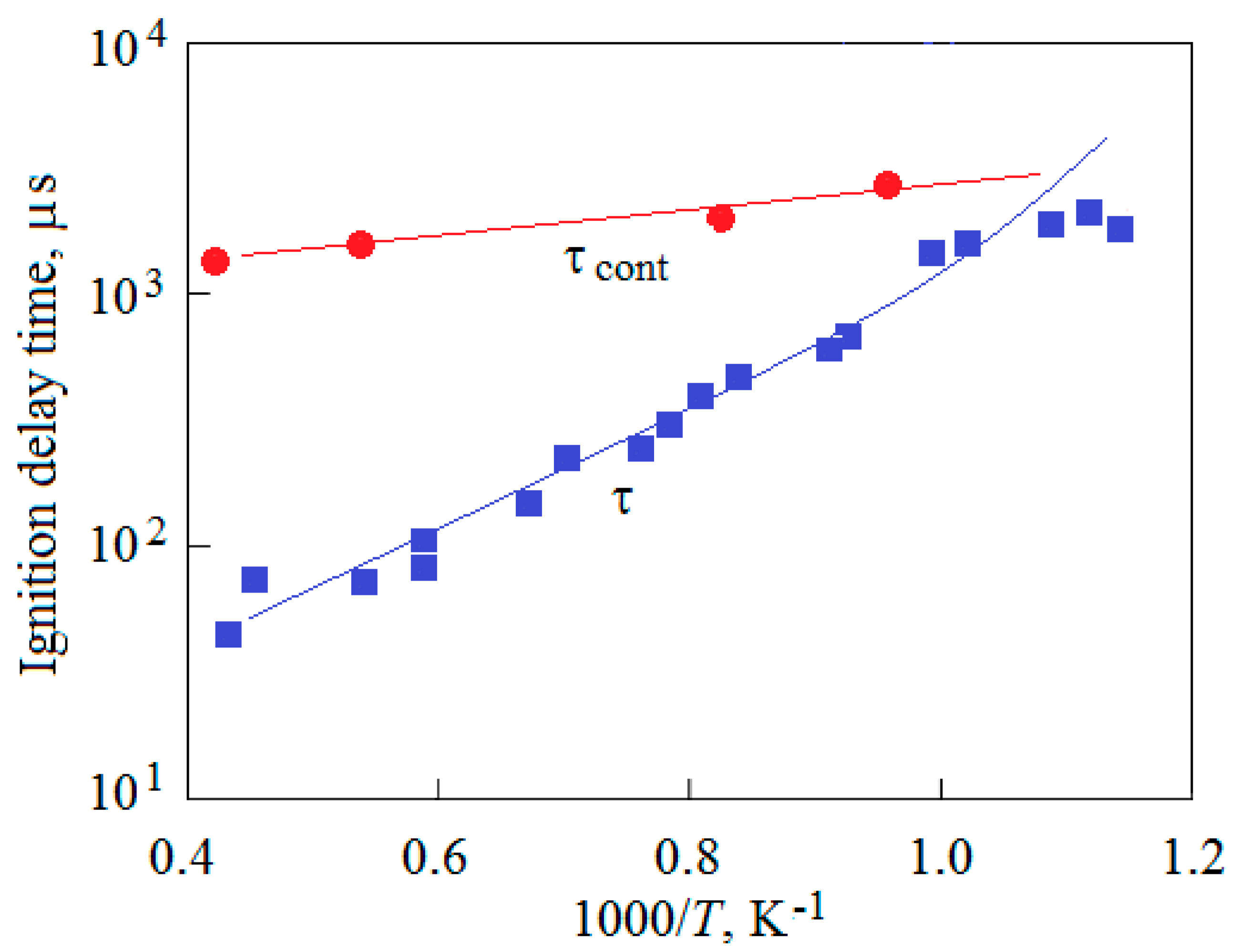
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Smirnov, N.N.; Nikitin, V.F. Modeling and simulation of hydrogen combustion in engines. Int. J. Hydrog. Energy 2014, 39, 1122–1136. [Google Scholar] [CrossRef]
- Jain, I.P. Hydrogen the fuel for 21st century. Int. J. Hydrog. Energy 2009, 34, 7368–7378. [Google Scholar] [CrossRef]
- Westbrook, C.K.; Dryer, F.L. Chemical kinetic modeling of hydrocarbon combustion. Prog. Energy Combust. Sci. 1984, 10, 1–57. [Google Scholar] [CrossRef]
- Kiverin, A.D.; Minaev, K.O.; Yakovenko, I.S. Modes of mild ignition in shock tubes: Origins and classification. Combust. Flame 2020, 221, 420–428. [Google Scholar] [CrossRef]
- Chang, X.; Bai, C.; Zhang, B.; Sun, B. The effect of ignition delay time on the explosion behavior in non-uniform hydrogen-air mixtures. Int. J. Hydrog. Energy 2022, 47, 9810–9818. [Google Scholar] [CrossRef]
- Lyu, G.; Zhong, C.; Gou, X. A pressure-ratio equivalent method for ultra-high pressure hydrogen spontaneous ignition experiment. Int. J. Hydrog. Energy 2022, 47, 22650–22661. [Google Scholar] [CrossRef]
- Böttler, H.; Chen, X.; Xie, S.; Scholtissek, A.; Chen, Z.; Hasse, C. Flamelet modeling of forced ignition and flame propagation in hydrogen-air mixtures. Combust. Flame 2022, 243, 112125. [Google Scholar] [CrossRef]
- Villenave, N.; Dayma, G.; Brequigny, P.; Foucher, F. Experimental measurements of ultra-lean hydrogen ignition delays using a rapid compression machine under internal combustion engine conditions. Fuel 2024, 355, 129431. [Google Scholar] [CrossRef]
- Smirnov, N.; Nikitin, V.; Mikhalchenko, E.; Stamov, L. Modeling a Combustion Chamber of a Pulse Detonation Engine. Fire 2023, 6, 335. [Google Scholar] [CrossRef]
- Hanson, R.K.; Davidson, D.F. Recent advances in laser absorption and shock tube methods for studies of combustion chemistry. Prog. Energy Combust. Sci. 2014, 44, 103–114. [Google Scholar] [CrossRef]
- Martynenko, V.V.; Penyaz’kov, O.G.; Ragotner, K.A.; Shabunya, S.I. High-temperature ignition of hydrogen and air at high pressures downstream of the reflected shock wave. J. Eng. Phys. Thermophys. 2004, 77, 785–793. [Google Scholar] [CrossRef]
- Pang, G.A.; Davidson, D.F.; Hanson, R.K. Experimental study and modeling of shock tube ignition delay times for hydrogen–oxygen–argon mixtures at low temperatures. Proc. Combust. Inst. 2009, 32, 181–188. [Google Scholar] [CrossRef]
- Herzler, J.; Naumann, C. Shock-tube study of the ignition of methane/ethane/hydrogen mixtures with hydrogen contents from 0% to 100% at different pressures. Proc. Combust. Inst. 2009, 32, 213–220. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, Z.; Wei, L.; Zhang, J.; Law, C.K. Experimental and modeling study on ignition delays of lean mixtures of methane, hydrogen, oxygen, and argon at elevated pressures. Combust. Flame 2012, 159, 918–931. [Google Scholar] [CrossRef]
- Hu, E.; Pan, L.; Gao, Z.; Lu, X.; Meng, X.; Huang, Z. Shock tube study on ignition delay of hydrogen and evaluation of various kinetic models. Int. J. Hydrog. Energy 2016, 41, 13261–13280. [Google Scholar] [CrossRef]
- Smirnov, N.N.; Penyazkov, O.G.; Sevrouk, K.L.; Nikitin, V.F.; Stamov, L.I.; Tyurenkova, V.V. Onset of detonation in hydrogen-air mixtures due to shock wave reflection inside a combustion chamber. Acta Astronaut. 2018, 149, 77–92. [Google Scholar] [CrossRef]
- Pavlov, V.A.; Shatalov, O.P. Measuring the ignition delay time for hydrogen-oxygen mixtures behind the front of an incident shock wave. Kinet. Catal. 2011, 52, 157–165. [Google Scholar] [CrossRef]
- A Chemical Equilibrium Program for Windows. Available online: http://www.gaseq.co.uk/ (accessed on 1 January 2005).
- Stupochenko, Y.V.; Losev, S.A.; Osipov, A.I. Relaxation in Shock Waves; Springer: New York, NY, USA, 1967. [Google Scholar]
- Gerasimov, G.Y.; Shatalov, O.P. Kinetic mechanism of combustion of hydrogen-oxygen mixtures. J. Eng. Phys. Thermophys. 2013, 86, 987–995. [Google Scholar] [CrossRef]
- Cohen, N.; Westberg, K.R. Chemical kinetic data sheets for high-temperature chemical reactions. J. Phys. Chem. Ref. Data 1983, 12, 531–590. [Google Scholar] [CrossRef]
- Tsang, W.; Hampson, R.F. Chemical kinetic data base for combustion chemistry. Part I. Methane Relat. Compd. J. Phys. Chem. Ref. Data 1986, 15, 1087–1279. [Google Scholar] [CrossRef]
- Warnatz, J.; Maas, U.; Dibble, R.W. Combustion; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Atkinson, R.; Baulch, D.L.; Cox, R.A.; Crowley, J.N.; Hampson, R.F.; Hynes, R.G.; Jenkin, M.E.; Rossi, M.J.; Troe, J. Evaluated kinetic and photochemical data for atmospheric chemistry: Volume I—Gas phase reactions of Ox, HOx, NOx, and SOx species. Atmos. Chem. Phys. 2004, 4, 1461–1738. [Google Scholar] [CrossRef]
- Baulch, D.L.; Bowman, C.T.; Cobos, C.J.; Cox, R.A.; Just, T.; Kerr, J.A.; Pilling, J.; Stocker, D.; Troe, J.; Tsang, W.; et al. Evaluated kinetic data for combustion modeling: Supplement II. J. Phys. Chem. Ref. Data 2005, 34, 757–1397. [Google Scholar] [CrossRef]
- Konnov, A.A. Remaining uncertainties in the kinetic mechanism of hydrogen combustion. Combust. Flame 2008, 152, 507–528. [Google Scholar] [CrossRef]
- Burcat, A.; Ruscic, B. Third Millennium Ideal Gas and Condensed Phase Thermochemical Database for Combustion with Updates from Active Thermochemical Tables; Tech. Rep. ANL-05/20; Argonne National Laboratory: Lemont, IL, USA, 2005. [Google Scholar]
- Kee, R.J.; Rupley, F.M.; Meeks, E.; Miller, J.A. Chemkin-III: A Fortran Chemical Kinetics Package for the Analysis of Gas-Phase Chemical and Plasma Kinetics; Tech. Rep. SAND96-8218; Sandia National Laboratories: Livermore, CA, USA, 1996. [Google Scholar]
- Hall, J.M.; Petersen, E.L. An optimized kinetics model for OH chemiluminescence at high temperatures and atmospheric pressures. Int. J. Chem. Kinet. 2006, 38, 714–724. [Google Scholar] [CrossRef]
- Pavlov, V.A.; Gerasimov, G.Y. Ignition of hydrogen–oxygen mixtures behind the incident shock wave front. J. Eng. Phys. Thermophys. 2016, 89, 587–591. [Google Scholar] [CrossRef]
- Ninnemann, E.; Koroglu, B.; Pryor, O.; Barak, S.; Nash, L.; Loparo, Z.; Sosa, J.; Ahmed, K.; Vasu, S. New insights into the shock tube ignition of H2/O2 at low to moderate temperatures using high-speed end-wall imaging. Combust. Flame 2018, 187, 11–21. [Google Scholar] [CrossRef]
- Ryu, S.O.; Hwang, S.M. Shock tube and modeling study of the H + O2 = OH + O reaction over a wide range of composition, pressure, and temperature. J. Phys. Chem. 1995, 99, 13984–13991. [Google Scholar] [CrossRef]
- Jachimowski, C.J.; Houghton, W.M. Shock-tube study of the initiation process in the hydrogen-oxygen reaction. Combust. Flame 1971, 17, 25–30. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavlov, V.; Gerasimov, G.; Levashov, V.; Kozlov, P.; Zabelinsky, I.; Bykova, N. Shock Tube Study of Ignition Delay Times for Hydrogen–Oxygen Mixtures. Fire 2023, 6, 435. https://doi.org/10.3390/fire6110435
Pavlov V, Gerasimov G, Levashov V, Kozlov P, Zabelinsky I, Bykova N. Shock Tube Study of Ignition Delay Times for Hydrogen–Oxygen Mixtures. Fire. 2023; 6(11):435. https://doi.org/10.3390/fire6110435
Chicago/Turabian StylePavlov, Valery, Gennady Gerasimov, Vladimir Levashov, Pavel Kozlov, Igor Zabelinsky, and Natalia Bykova. 2023. "Shock Tube Study of Ignition Delay Times for Hydrogen–Oxygen Mixtures" Fire 6, no. 11: 435. https://doi.org/10.3390/fire6110435
APA StylePavlov, V., Gerasimov, G., Levashov, V., Kozlov, P., Zabelinsky, I., & Bykova, N. (2023). Shock Tube Study of Ignition Delay Times for Hydrogen–Oxygen Mixtures. Fire, 6(11), 435. https://doi.org/10.3390/fire6110435




