Experimental and Numerical Analysis of Formation and Flame Precession of Fire Whirls: A Review
Abstract
1. Introduction
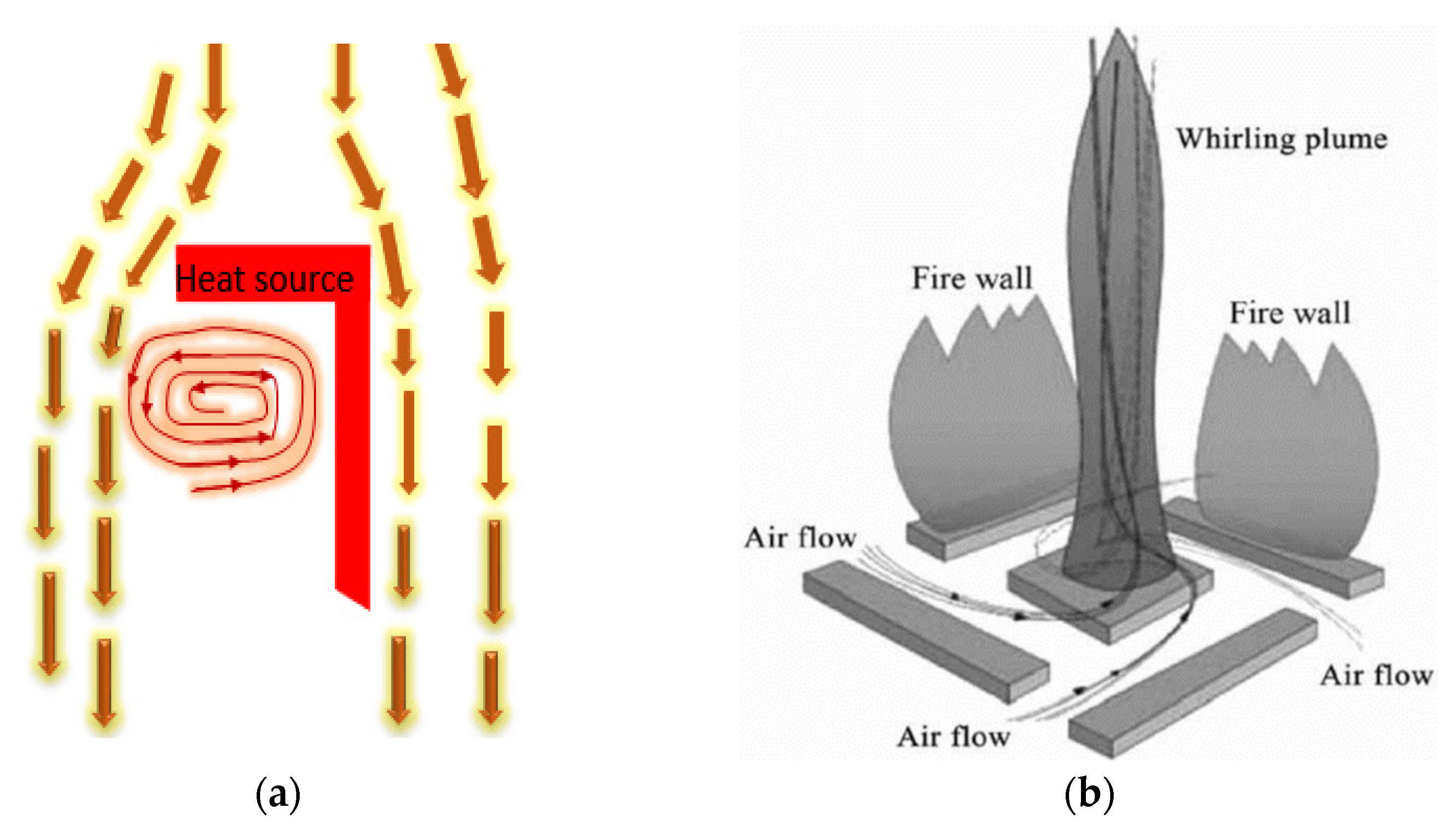
2. Fire Whirl Phenomenon
2.1. Definition, Classification, and Formation Mechanism
2.2. Source of Vorticity
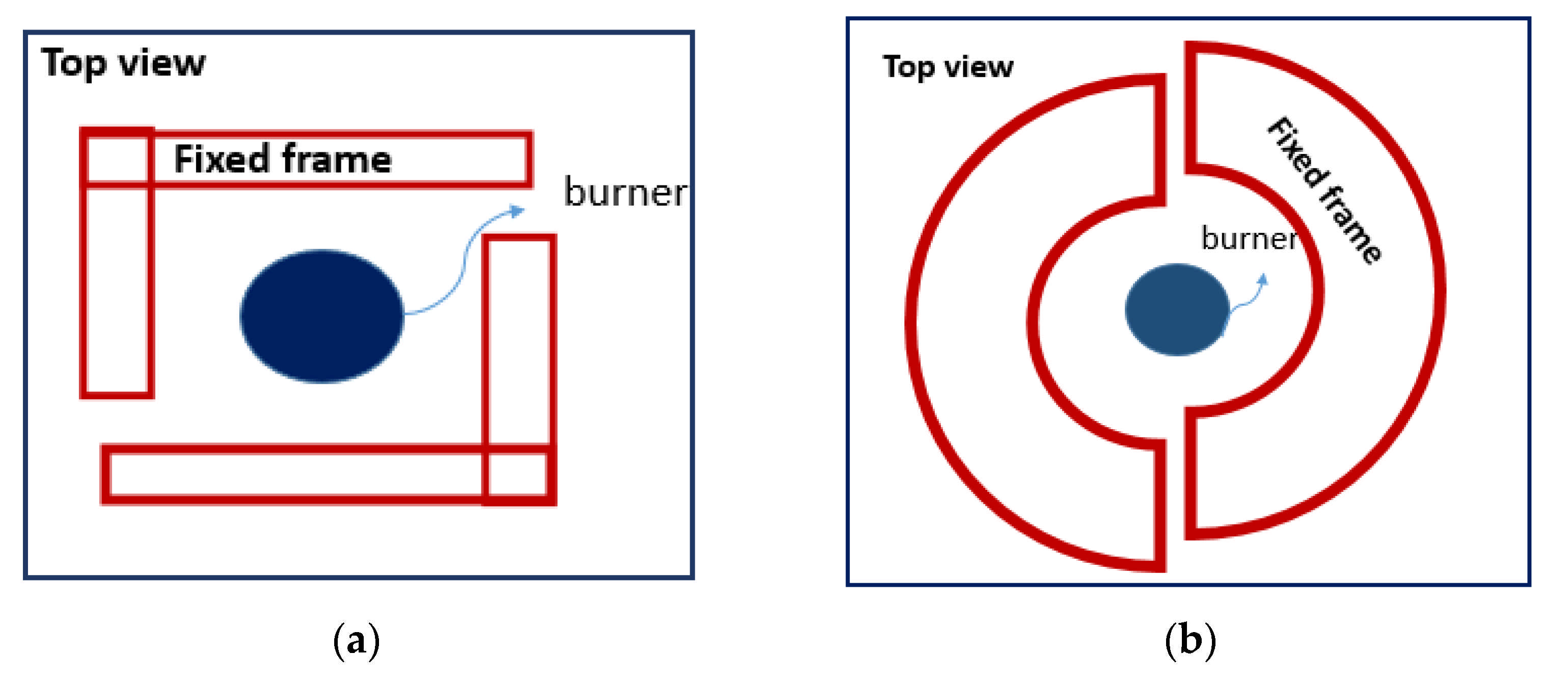
3. Experimental Arrangements (Experimental Setup, Fuels, and Burning Behavior)

4. Numerical Simulations of Fire Whirls (Turbulence Simulations, Combustion Models, Heat Transfer)
4.1. Governing Equations of Computational Fluid Dynamics for Fire Whirls
4.2. Turbulence Simulations
4.2.1. Direct Numerical Simulation (DNS)
4.2.2. Large Eddy Simulation (LES)
4.2.3. Reynolds Stress Transport Model (RST)
4.3. Combustion Models
4.3.1. Eddy Break-Up (EBU) Model
4.3.2. Mixture Fraction Combustion Model Based on the EDC
4.3.3. Gas-phase Combustion Model
4.4. Modeling of Soot Formation and Combustion
4.5. Heat Transfer of Liquid Fuel in Fire Whirl Tests
4.5.1. One-Dimensional Heat Conduction Equation
4.5.2. Radiation Heat Transfer
4.5.3. Convective Heat Transfer
4.5.4. Evaporation of Liquid Fuels
5. Review of Experimental Studies and Numerical Simulations on Fire Whirls including the Considered Models
6. Conclusions
- A successful simulation should consider both quantitative and qualitative aspects of fire whirl. The qualitative approach should include conditions incorporating transition from a buoyant diffusion gas flame to a stable fire whirl, together with stability conditions for the fire whirl.
- The qualitative features of the models used for numerical analyses should be based on the real physical nature of fire whirls.
- One of the strengths of the numerical simulation methods is that all ranges of temporal and spatial scales of turbulence in fire whirls are resolved in the computational mesh.
- While numerical studies will allow for better investigations of the fundamental mechanisms of fire whirl initiation and stability, there are currently not enough studies conducted in this area.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| specific heat capacity | |
| dynamic stress constant | |
| K | thermal conductivity |
| Nu | Nusselt number |
| heat flux | |
| Re | Reynolds number |
| T | temperature |
| temperature of grid control volume | |
| fuel surface temperature | |
| V | displacement |
| direction | |
| Y | combination fraction |
| density | |
| viscosity | |
| eddy-viscosity | |
| dissipation rate | |
| the mean strain-rate tensor | |
| Kronecker’s delta | |
| the stress tensor of SGS | |
| grid–filter scale | |
| test–filter scale | |
| dilatation dissipation | |
| soot mass function |
References
- Yuen, A.C.Y.; Yeoh, G.H.; Cheung, S.C.P.; Chan, Q.N.; Chen, T.B.Y.; Yang, W.; Lu, H. Numerical study of the development and angular speed of a small-scale fire whirl. J. Comput. Sci. 2018, 27, 21–34. [Google Scholar] [CrossRef]
- Tohidi, A.; Gollner, M.J.; Xiao, H. Fire Whirls. Annu. Rev. Fluid Mech. 2018, 50, 187–213. [Google Scholar] [CrossRef]
- Soma, S.; Saito, K. Reconstruction of fire whirls using scale models. Combust. Flame 1991, 86, 269–284. [Google Scholar] [CrossRef]
- Canberra 2003. Australian Disaster Resilience Knowledge Hub. Available online: https://knowledge.aidr.org.au/resources/bushfire-canberra-2003/ (accessed on 3 November 2019).
- Moore, T.; Contreras, T.; Murphy, K.; Butler, B.; Forthofer, J.; Bailey, K.; Meyer, R.T.; Richmond, M.; Throop, W.; Petrilli, A.; et al. Indians Fire Accident Prevention Analysis; Forest Service, Department of Agriculture, USFS Pacific Southwest Region: Vallejo, CA, USA, 2008. [Google Scholar]
- MacKinnon, E. Fire tornadoes ripped through the Australian outbackvlast week. In Life’s Little Mysteries; Business Insider: Sydney, Australia, 2012. [Google Scholar]
- Gao, Z.; Li, S.S.; Gao, Y.; Hung, H.Y.; Chow, W. Numerical studies on swirling of internal fire whirls with experimental justifications. Build. Simul. 2021, 14, 1499–1509. [Google Scholar] [CrossRef]
- Emmons, H.W.; Ying, S.J. The fire whirl. In Symposium (International) on Combustion; Elsevier: Amsterdam, The Netherlands, 1967; Volume 11, pp. 475–488. [Google Scholar]
- Varaksin, A.Y. Modeling air and fire non-stationary whirls in laboratory conditions. J. Phys. Conf. Ser. 2018, 980, 012019. [Google Scholar] [CrossRef]
- Boushaki, T. Introductory Chapter: Swirling Flows and Flames; IntechOpen: London, UK, 2019. [Google Scholar]
- Shinohara, M.; Matsushima, S. Flow Visualization Study of Stationary Fire Whirls just Downwind of Meter-Scale Turbulent Flames. Flow Turbul. Combust. 2019, 102, 313–330. [Google Scholar] [CrossRef]
- Domino, S.P. The Suitability of Hybrid Meshes for Low-Mach Large-Eddy Simulation (LES); SAND2018-TBD; Computational Thermal and Fluid Mechanics Sandia National Laboratories: Albuquerque, NM, USA, 2018. [Google Scholar]
- Wang, P.; Liu, N.; Hart, K.; Smits, A. Measurementof the flow field of fire whirl. Fire Technol. 2016, 52, 263–272. [Google Scholar] [CrossRef]
- Hartl, K.A.; Smits, A.J. Scalingof a small scale burner fire whirl. Combust. Flame 2016, 163, 202–208. [Google Scholar] [CrossRef]
- Lei, J.; Liu, N.; Zhang, L.; Satoh, K. Temperature, velocity and air entrainment of fire whirl plume: A comprehensive experimental investigation. Combust. Flame 2015, 162, 745–758. [Google Scholar] [CrossRef]
- Pirsko, A.R.; Sergius, L.M.; Hickerson, C.W. Causes and Behavior of a Tornadic Fire-Whirlwind; Pacific Southwest Forest & Range Experiment Station: Berkeley, CA, USA, 1965. [Google Scholar]
- Forthofer, J.M.; Goodrick, S.L. Review of Vortices in Wildland Fire. J. Combust. 2011, 14. [Google Scholar] [CrossRef]
- Tieszen, S.R.; Nicolette, V.F.; Gritzo, L.A.; Moya, J.L.; Holen, J.K.; Murray, D. Vortical Structures in Pool Fires: Observation, Speculation, and Simulation; SAND96-2607; Sandia National Labs: Livermore, CA, USA, 1996. [Google Scholar]
- Lei, J.; Liu, N. Reciprocal transitions between buoyant diffusion flame and fire whirl. Combust Flame 2016, 167, 463–471. [Google Scholar] [CrossRef]
- Ghodrat, M.; Shakeriaski, F.; Nelson, D.J.; Simeoni, A. Existing improvements in simulation of fire–wind interaction and its effects on structures. Fire 2021, 4, 27. [Google Scholar] [CrossRef]
- Chuah, K.H.; Kuwana, K.; Saito, K. Modeling a fire whirl generated over a 5-cm-diameter methanol pool fire. Combust Flame 2009, 156, 828–1833. [Google Scholar] [CrossRef]
- Finney, M.A.; Cohen, J.D.; Forthofer, J.M.; McAllister, S.S.; Gollner, M.J.; Gorham, D.J.; Saito, K.; Akafuah, N.K.; Adam, B.A.; English, J.D. Role of buoyant flame dynamics in wildfire spread. Proc. Natl. Acad. Sci. USA 2015, 112, 9833–9838. [Google Scholar] [CrossRef] [PubMed]
- Dobashi, R.; Okura, T.; Nagaoka, R.; Hayashi, Y.; Mog, T. Experimental Study on Flame Height and Radiant Heat of Fire Whirls. Fire Technol. 2016, 52, 1069–1080. [Google Scholar] [CrossRef]
- Zhou, K.; Liu, N.; Yin, P.; Yuan, X.; Jiang, J. Fire whirl due to interaction between line fire and cross wind. Fire Saf. Sci. 2014, 11, 1420–1429. [Google Scholar] [CrossRef]
- Hartl, K.A.; Smits, A.J. Stereo PIV measurements in fire whirls. Exp. Fluids 2019, 60, 17. [Google Scholar] [CrossRef]
- Battaglia, F.; Mcgrattan, K.B.; Rehm, R.G.; Baum, H.R. Simulating fire whirls. Combust. Theory Model. 2000, 4, 123–138. [Google Scholar] [CrossRef]
- Chuah, K.H.; Kuwana, K.; Saito, K.; Wiliams, F.A. Inclined fire whirls. Proc. Combust. Inst. 2011, 33, 2417–2424. [Google Scholar] [CrossRef]
- Lei, J.; Liu, N.; Zhang, L.; Deng, Z.; Akafuah, N.K.; Li, T.; Saito, K.; Satoh, K. Burning rates of liquid fuels in fire whirls. Combust. Flame 2012, 159, 2104–2114. [Google Scholar] [CrossRef]
- Hariharan, S.B. Experimental Investigations and Scaling Analyses of Whirling Flames. Ph.D. Thesis, University of Maryland, College Park, MD, USA, 2020. [Google Scholar] [CrossRef]
- Taghinia, J.; Rahman, M.M.; Siikonen, T. Large eddy simulation of flow past a circular cylinder with a novel sub grid scale model. Eur. J. Mech. Fluids 2015, 52, 11–18. [Google Scholar] [CrossRef]
- Fang, X.; Yuen, A.C.Y.; Yeoh, G.H.; Lee, E.W.M.; Cheung, S.C.P. Capturing the swirling vortex and the impact of ventilation conditions on small-scale fire whirls. Appl. Sci. 2020, 10, 3428. [Google Scholar] [CrossRef]
- Taghinia, J.; Rahman, M.M.; Siikonen, T.; Agarwal, R.K. One-equation sub-grid scale model with variable eddy-viscosity coefficient. Comput. Fluids 2015, 107, 155–164. [Google Scholar] [CrossRef]
- Parente, R.M.G. Direct numerical simulation and large eddy simulation. In Tackling Turbulent Flows in Engineering; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Moin, P.; Mahesh, K. Direct numerical simulation: A tool in turbulence research. Annu. Rev. Fluid Mech. 1998, 30, 539–578. [Google Scholar] [CrossRef]
- Orszag, S.A. Analytical theories of turbulence. J. Fluid Mech. 1970, 41, 363–386. [Google Scholar] [CrossRef]
- Heinz, S.; Mokhtarpoor, R.; Stoellinger, M. Theory-based Reynolds-averaged Navier–Stokes equations with large eddy simulation capability for separated turbulent flow simulations. Phys. Fluids 2020, 32, 065102. [Google Scholar] [CrossRef]
- Feng, Z.G.; Michaelides, E.E. Heat transfer in particulate flows with direct numerical simulation (DNS). Int. J. Heat Mass Transf. 2009, 52, 777–786. [Google Scholar] [CrossRef]
- Piomelli, U. Large-eddy simulation: Achievements and challenges. Prog. Aerosp. Sci. 1999, 35, 335–362. [Google Scholar] [CrossRef]
- Mason, P.J. Large-eddy simulation: A critical review of the technique. Q. J. R. Meteorol. 1994, 120, 1–26. [Google Scholar] [CrossRef]
- Mahesh, K.; Constantinescu, G.; Moin, P. A numerical method for large-eddy simulation in complex geometries. J. Comput. Phys. 2004, 197, 215–240. [Google Scholar] [CrossRef]
- Herring, J.R. Subgrid Scale Modeling—An Introduction and Overview. Turbul. Shear. Flows 1979, 1, 347–352. [Google Scholar]
- Canuto, V.M.; Cheng, Y. Determination of the smagorinsky—Lilly constant CS. Phys. Fluids 1997, 9, 1368–1378. [Google Scholar] [CrossRef]
- Boussinesq, J. Theorie d l’ecoulelement tourbillant. Mém. Prés. Acad. Sci. 1877, XXIII, 46. [Google Scholar]
- Schaefer-Rolffs, U. A generalized formulation of the dynamic Smagorinsky model. Meteorol. Z. 2016, 26, 181–187. [Google Scholar] [CrossRef]
- Lilly, D.K. A proposed modification of the Germano subgrid-scale closure model. Phys. Fluids 1992, 4, 633–635. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modeling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Vreman, A.W. An eddy-viscosity subgrid-scale model for turbulent shear flow: Alge-braic theory and applications. Phys. Fluids 2004, 16, 3670–3681. [Google Scholar] [CrossRef]
- Tang, H.; Lei, Y.; Li, X.; Fu, Y. Large-eddy simulation of an asymmetric plane diffuser: Comparison of different subgrid scale models. Symmetry 2019, 11, 1337. [Google Scholar] [CrossRef]
- Spalding, D.B. Mixing and chemical reaction in steady confined turbulent flames. Symp. Combust. 1971, 13, 649–657. [Google Scholar] [CrossRef]
- Magnussen, B.F.; Hjertager, B.H. On mathematical modeling of turbulent combustion with special emphasis on soot formation and combustion. Symp. Combust. 1977, 16, 719–729. [Google Scholar] [CrossRef]
- Parente, R.M.; Pereira, J.M.C.; Pereira, J.C.F. On the influence of circulation on fire whirl height. Fire Saf. J. 2019, 106, 146–154. [Google Scholar] [CrossRef]
- Su, Y.; Chen, C.; Su, A. Simulation of high temperature air combustion with modi-fied eddy-break-up combustion model. Energy Procedia 2012, 14, 127–132. [Google Scholar] [CrossRef][Green Version]
- Panjwani, B.; Ertesvag, A.; Gruber, A.K.E.R.A.; Rian, K.E. Turbulence combustion clo-sure model based on the Eddy dissipation concept for large eddy simulation. Adv. Fluid Mech. VIII 2010, 69, 27–38. [Google Scholar]
- Diab, M.; Yip, A.; Hadavand, M.; Haelssig, J.; Pegg, M. Experimental and numerical comparison of small-scale gaseous fire whirls. J. Phys. Conf. Ser. 2018, 1107, 042032. [Google Scholar] [CrossRef]
- Syed, K.J.; Stewart, C.D.; Moss, J.B. Modelling soot formation and thermal radiation in buoyant turbulent diffusion flames. Symp. Combust. 1991, 23, 1533–1541. [Google Scholar] [CrossRef]
- Wang, J.; Niioka, T. The effect of radiation reabsorption on NO formation in CH4/air counterflow diffusion flames. Combust Theory Model. 2001, 5, 385. [Google Scholar] [CrossRef]
- Liu, F.; Guo, H.; Smallwood, G.J.; El Hafi, M. Effects of gas and soot radiation on soot formation in counterflow ethylene diffusion flames. J. Quant. Spectrosc. Radiat. Transf. 2004, 84, 501–511. [Google Scholar] [CrossRef][Green Version]
- Liu, F.; Guo, H.; Smallwood, G.J.; Gülder, Ö.L. Numerical modelling of soot formation and oxidation in laminar coflow non-smoking and smoking ethylene diffusion flames. Combust. Theory Model. 2003, 7, 301–315. [Google Scholar] [CrossRef]
- Shakeriaski, F.; Ghodrat, M. Nonlinear response for a general form of thermoelastici-ty equation in mediums under the effect of temperature-dependent properties and short-pulse heating. J. Therm. Anal. Calorim. 2020, 142, 1–12. [Google Scholar] [CrossRef]
- Ajarostaghi, S.M.; Zaboli, M.; Noorbakhsh, M. Numerical evaluation of turbu-lence heat transfer and fluid flow of hybrid nanofluids in a pipe with innovative vortex generator. J. Therm. Anal. Calorim. 2021, 143, 1583–1597. [Google Scholar] [CrossRef]
- Shakeriaski, F.; Ghodrat, M.; Escobedo-Diaz, J.; Behnia, M. Modified Green–Lindsay thermoelasticity wave propagation in elastic materials under thermal shocks. J. Comput. Des. Eng. 2020, 8, 36–54. [Google Scholar] [CrossRef]
- Zaboli, F.M.; Noorbakhsh, M.; Ajarostaghi, S.S.M. Numerical investigation on heat transfer and fluid flow in a coil tube with lobe cross section and two types of twisted tape as swirl generator. J. Therm. Anal. Calorim. 2020, 141, 1–17. [Google Scholar]
- Wrubel, M.H. Exact curves of growth. III. The schuster-schwarzschild model. Astrophys. J. 1949, 119, 51. [Google Scholar] [CrossRef]
- Siegel, R.; Howell, J.R. Thermal Radiation Heat Transfer, 4th ed.; Taylor & Francis: New York, NY, USA, 2002. [Google Scholar]
- Reddy, B.M. Numerical investigation of soot formation in turbulent diffusion flame with strong turbulence chemistry interaction. J. Therm. Sci. Eng. Appl. 2021, 8, 011001. [Google Scholar] [CrossRef]
- AshokeDe, R. Assessment of soot formation models in lifted ethylene/air turbulent diffusion flame. Therm. Sci. Eng. Prog. 2017, 3, 49–61. [Google Scholar]
- Holman, J.P. Heat Transfer, 7th ed.; McGraw-Hill: New York, NY, USA, 1990. [Google Scholar]
- Consalvi, J.L.; Pizzo, Y.; Porterie, B. Numerical analysis of the heating process in up-ward flame spread over thick PMMA slabs. Fire Saf. J. 2008, 43, 351–362. [Google Scholar] [CrossRef]
- Sibulkin, M.; Kim, J. The dependence of flame propagation on surface heat transfer II. Upward burning. Combust. Sci. Technol. 1977, 17, 39–49. [Google Scholar] [CrossRef]
- Li, S.; Yao, Q.; Law, C.K. The bottom boundary-layer structure of fire whirls. Proc. Combust. 2019, 37, 4277–4284. [Google Scholar] [CrossRef]
- Kuwana, K.; Morishita, S.; Dobashi, R.; Chuah, K.H.; Saito, K. The burning rate’s effect on the flame length of weak fire whirls. Proc. Combust. Inst. 2011, 33, 2425–2432. [Google Scholar] [CrossRef]
- Li, S.; Yao, Q.; Law, C.K. An analysis of the stabilization of fire whirls. Proc. Combust. Inst. 2012, 38, 4587–4594. [Google Scholar] [CrossRef]
- Zou, G.; Chow, W. Generation of an internal fire whirl in an open roof vertical shaft model with a single corner gap. J. Fire Sci. 2015, 33, 183–201. [Google Scholar] [CrossRef]
- Chow, W.K. A study on relationship between burning rate and flame height of internal fire whirls in a vertical shaft model. J. Fire Sci. 2014, 32, 72–83. [Google Scholar] [CrossRef]
- Xiaoa, H.; Gollnerb, M.J.; Oran, E.S. From fire whirls to blue whirls and combustion with reduced pollution. Proc. Natl. Acad. Sci. USA 2016, 113, 9457–9462. [Google Scholar] [CrossRef] [PubMed]
- Zhou, K.; Liu, N.; Yuan, X. Effect of wind on fire whirl over a line fire. Fire Technol. 2016, 52, 865–875. [Google Scholar] [CrossRef]
- Lei, J.; Liu, N.; Tu, R. Flame height of turbulent fire whirls: A model study by concept of turbulence suppression. Proc. Combust. Inst. 2017, 36, 3131–3138. [Google Scholar] [CrossRef]
- Wang, P.; Liu, N.; Bai, Y.; Zhang, L.; Satoh, K.; Liu, X. An experimental study on thermal radiation of fire whirl. Int. J. Wildland Fire 2017, 26, 693–705. [Google Scholar] [CrossRef]
- Pinto, C.; Viegas, D.; Almeida, M.; Raposo, J. Fire whirls in forest fires: An experimental analysis. Fire Saf. J. 2017, 87, 37–48. [Google Scholar] [CrossRef]
- Hariharan, S.B.; Anderson, P.M.; Xiao, H.; Gollner, M.J.; Oran, E.S. The blue whirl: Boundary layer effects, temperature and OH* measurements. Combust. Flame. 2019, 203, 352–361. [Google Scholar] [CrossRef]
- Wang, P.; Liu, N.; Liu, X.; Yuan, X. Experimental study on flame wander of fire whirl. Fire Technol. 2018, 54, 1369–1381. [Google Scholar] [CrossRef]
- Wang, P.; Liu, X.; Che, L. Experimental study on flame wander of smallscale fire whirl based on video image analysis. In Proceedings of the 2019 9th International Conference on Fire Science and Fire Protection Engineering (ICFSFPE), Dalian, China, 19–21 September 2019. [Google Scholar]
- Iga, Y.; Kuwana, K. Generation of Fire Whirls over a Line Fire in a Crossflow: An Ex-perimental Study on the Role of Near-ground Flow. In Proceedings of the 27th ICDERS, Beijing, China, 28 July–2 August 2019. [Google Scholar]
- Yamada, R.; Kuwana, K. Scaling laws of flow structures around geometrically similar fire whirls. J. Therm. Sci. Technol. 2019, 14, JTST0009. [Google Scholar] [CrossRef]
- Hoo, C.K.; Meng, W.X.; Yi, Y.N.; Wei, C.S. Capturing the fire whirls heights and ro-tational speed by high speed camera. INTI J. 2019, 21, 2600–7920. [Google Scholar]
- Varaksin, A.Y.; Mochalov, A.A.; Romash, M.E. Experimental study of some characteristics of nonstationary wall-free fire whirls. High Temp. 2019, 57, 738–743. [Google Scholar] [CrossRef]
- Shinohara, M. Effects of wind speed and heat release rate on the vortex strength and size of fire whirls without an inner core of flame. Fire Saf. J. 2021, 120, 103045. [Google Scholar] [CrossRef]
- Hayashi, Y.; Kuwana, K.; Dobashi, R. Influence of vortex structure on fire whirl behavior. Fire Saf. Sci. 2011, 10, 671–679. [Google Scholar] [CrossRef]
- Hartl, K.; Blackburn, H.M.; Smits, A.J. Experimental and numerical studies of a laboratory fire whirl. In Proceedings of the 19th Australasian Fluid Mechanics Conference, Melbourne, Australia, 8–11 December 2014. [Google Scholar]
- Chung, J.D.; Zhang, X.; Kaplan, C.R.; Oran, E.S. Numerical simulation of a fire whirl burning gaseous heptane. In Proceedings of the AIAA Scitech Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Zhang, X.; Chung, J.D.; Kaplan, C.R.; Oran, E.S. Simulations of a triple flame and fire whirl using the BIC low-mach-number algorithm. In Proceedings of the 27th ICDERS, Beijing, China, 28 July–2 August 2019. [Google Scholar]
- Dermer, P.B.; Varaksin, A.Y.; Leontiev, A.I. The wall-free non-stationary fire whirls generation by ax-isymmetric burning of solid fuel pellets. Int. J. Heat Mass Transf. 2017, 110, 890–897. [Google Scholar] [CrossRef]
- Ghaderi, M.; Ghodrat, M.; Sharples, J. LES Simulation of Wind-Driven Wildfire Interaction with Idealized Structures in the Wildland-Urban Interface. Atmosphere 2020, 12, 21. [Google Scholar] [CrossRef]



| Smagorinsky Model (SM) [42] | is the filter width (size of mesh spacing), is the resolved strain-rate tensor | |
| Dynamic Smagorinsky Model (DSM) [44] Based on Lilly’s Idea [45] | mostly α = 2, η = 1 | The stress Lij can be expressed as the stress related to the smallest solved scales between the grid–filter scale () and test–filter scale (). |
| Wall-Adapting Local Eddy-Viscosity (WALE) Model [46] | Here, is the tensor of the velocity gradient. Cs and Cw can take different values depending on the nature of the flow, and is Kronecker Delta function | |
| Vreman Model [47] | is the filter width (size of mesh spacing), and , Cs can take different values depending on the nature of the flow | |
| Standard One-Equation Model (OM) [48] | is the SGS viscosity, Cv is a constant and always taken to be 0.1,,, and are defined in previous models. |
| References | Outcomes | Fuel Type | Schematic Diagram of Testing Equipment and Tester Equipment Details (Reproduced from Cited Work) |
|---|---|---|---|
| Dobashi et al. [23] (2015) | Middle and small-scale tests were conducted to find the mechanism of flame height growth at the fire whirls. | n-heptane |  Fire whirls were constructed on a fuel pool applying a constant-frame-type whirl producer using a pair of L-shaped covers, which produce swirling flow using dragged air. |
| Xiao et al. [75] (2016) | Proposed using the enhanced burning rate of fire whirls for oil spill remediation where the fuel is on a water surface. | n-heptane | 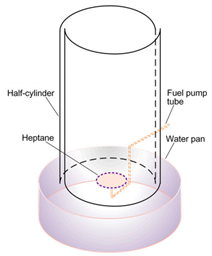 The setup contains two half-cylinders and one cylindrical stainless steel pan filled with water. Fuel is sprayed on the quiescent water surface at the center and ignited. A copper tube under the water is located to pump heptane to the water surface center and keep the fuel height constant. |
| Lei and Liu [19] (2016) | This study examined the reciprocal transition process between fire whirl and a general buoyant propane diffusion flame. | Propane | 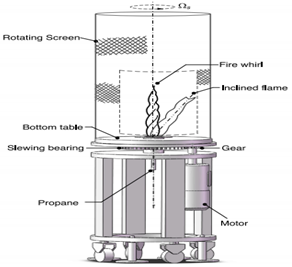 A fixed circular table was surrounded by a rotating cylindrical wire-mesh screen. A gas burner was located at the center of the table and accumulated with glass beads. The porous surface was built flat and flush with the burner rim and the surface of the table. |
| Zhou [76] (2016) | This study analyzed the fire whirls frequency on a line fire by tests under a significant range of cross wind velocities. | Heptane |  Line fire under the impact of wind was performed using a setup that contains a mechanical wind wall and a line burner placed in a sand bed. |
| Lei et al. [77] (2016) | A novel method was proposed to simulate the flame height of turbulent fire whirls by defining a Richardson number related to the average flow quantities. | Propane and heptane |  A square channel setup built of tempered glass was used for turbulent fire whirl tests. The dragged air resulting from the flame entered the channel via four corner gaps and imposed a rotating stream to generate a fire whirl. |
| Wang et al. [78] (2017) | Fire whirl radiation was analyzed in tests performed in a fire whirl facility. | n-heptane | 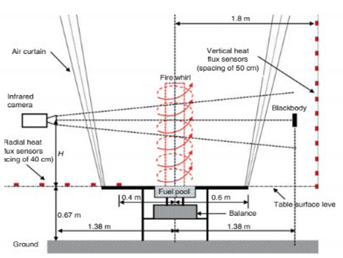 A system containing four air curtain systems was applied to generate air walls. The facility contains three parts: four air-stream channels, four air curtain mechanisms, and a basis table. |
| Pinto et al. [79] (2017) | The research work gave an analysis on the structure of fire whirls with and without a forced stream on wildfires at the scale of a laboratory. The outcomes illustrated that forced streams increase the rate of burning. | Dead Pinus pinaster, straw of Avena sativa, dead leaves of Eucalyptus globulus. |  A fire whirl generator including a vertical channel with a quadrangular part with two faces constituted of steel plate and tempered glass was regarded. There was a sheet which was covered by ceramic tiles to protect the fuel enclosure. The generator was located in the great hall of Forest Fire Reseach Laboratory. |
| Hariharan et al. [80] (2018) | Analyzed the impact of the surface boundary conditions on the transition process from a fire whirl to a blue whirl. | n-heptane | 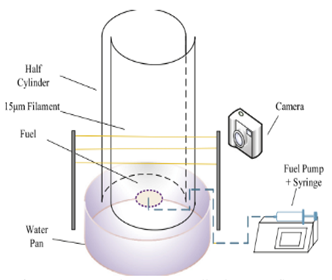 The constant-frame setup produces a naturally dragging flow resulting from buoyancy due to the burning fuel in the container. The dish represented smooth surface boundary conditions such as a flat-water surface. |
| Wang P et al. [81] (2018) | The velocity field was evaluated using stereo Particle Image Velocimetry (PIV) were investigated to track the flame displacement along the horizontal axis. | Ethanol | 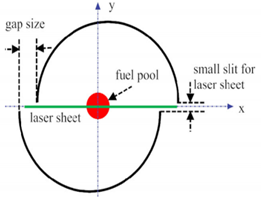 Two split cylinders located on a table surface were applied to produce small-scale fire whirls. A round pool was placed at the center of the cylinders. The tiny slit allowed the laser plate to enter the vertical sheet of the fire whirl. The velocity distribution was measured using stereo PIV. |
| Wang et al. [82] (2019) | A video camera was used to monitor the fire whirl horizontal movement due to the wandering of the flame. | Ethanol | 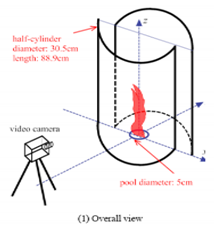 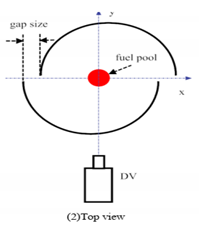 Stages: (1) transmitting the flame image to the related binary image; (2) deriving the flame contours and specifying the flame, center; (3) computing the horizontal distance from the center of the flame to the center of the fuel pool. |
| Iga and Kuwana [83] (2019) | This study analyzed the impact of near-ground flow on the frequency of fire whirl constitution. | Ethanol | 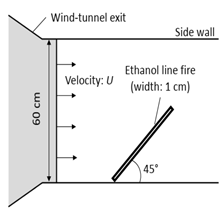 A wind tunnel was applied to produce a cross stream of velocity U, and a blocking board was located to cover the wind-tunnel exit and control its opening height (h). |
| Yamada and Kuwana [84] (2019) | This study analyzed the scale impacts on the flow structure in fire whirl with emphasis on if a dynamic similarity stays satisfied among geometrically analogous fire whirls. | Methanol |  Two half-cut cylinders with asymmetrically located slits were used to provide a rotating stream by entrainment due to upward, buoyant flow from a fire resource. |
| Hoo et al. [85] (2019) | This study analyzed the rotational velocities and the fluctuation frequencies of fire whirl. | Ethanol | 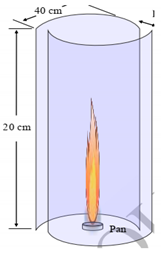 The generator of the fire whirl was a constant-frame-type including two semi-cylindrical walls located near the fuel pan, and the center of the walls of the curvature are offset by a tiny distance from the fuel pan’s center to constitute two air gaps between the walls. |
| Varaksin et al. [86] (2019) | This study presented outcomes about the procedure of non-static, wall-free fire whirl production. | Urotropine | 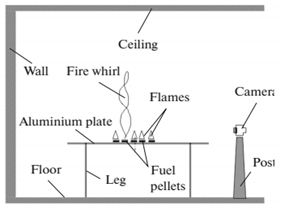 A setup is used to produce non-static, wall-free concentrated fire whirls. The table’s horizontal surface was made of an aluminum sheet with a thickness of 1.5 mm and a diameter of 1100 mm. |
| Shinohara [87] (2020) | This study investigated the impact of crosswind velocity and thermal release rate on the size, speed, and circulation of fire whirl. | Methane | 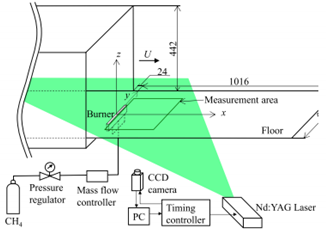 Tests were done in an open blowdown wind tunnel. The experiment section consisted of a flat floor, heat-resistant glass. The burner exit was a porous rectangular sheet built of sintered stainless-steel particles. |
| References | Outcomes | Numerical Method/Software | Fuel Type | Turbulence Model | Combustion Model | Schematic Diagram of Numerical Method | |
|---|---|---|---|---|---|---|---|
| Hartl et al. [89] (2014) | Demonstrated the feasibility of applying DNS for modeling swirling buoyant turbulent plumes. | Spectral element–Fourier method | dimethyl ether | DNS | None, heat input using flux boundary conditions | 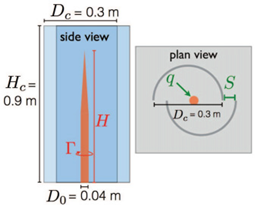 | |
| Yuen et al. [1] (2018) | Showed that liquid fuel simulations can estimate the rate of evaporation. | Finite difference method | Ethanol | LES (Smagorinsky model) | Mixture fraction simulation (Gas-phase combustion model) | 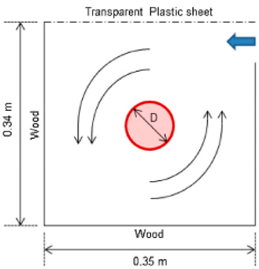 | |
| Diab et al. [54] (2018) | Investigated the dynamics of propane gas fire whirls in a small-scale, constant-frame, square-based system. | Finite volume (ANSYS Fluent 17.1) | Propane | LES (four different SGS models, including Deardorf, WALE) | Mixture fraction simulation (based on the EDC (Eddy Dissipation Concept) | 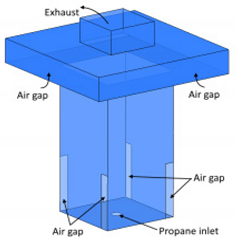 | |
| Parente et al. [51] (2019) | Studied the ability of the RST to measure physical behaviour of fire whirls (for example, the effects of used swirl generator on the flame height). | Star-CCM+ software | Propane | RST | Eddy Break-Up |  | 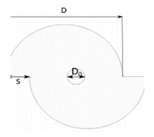 |
| Fang et al. [31] (2020) | Illustrated the capability of the generic LES model in capturing the dynamic response of fire whirl. | ANSYS Fluent | Propane | LES (Smagorinsky–Lilly model) | Combination fraction | 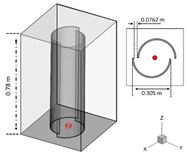 | |
| Chung et al. [90] (2020) | Illustrated that the blue whirl is made of various flame regimes: lean, premixed rich, and a diffusion flame. | The algorithm of Barely implicit correction (BIC) | Ethanol and heptane | --- | Superimposed thermal release rate | 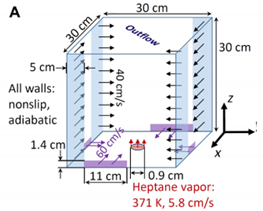 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghodrat, M.; Shakeriaski, F.; Nelson, D.J.; Simeoni, A. Experimental and Numerical Analysis of Formation and Flame Precession of Fire Whirls: A Review. Fire 2021, 4, 43. https://doi.org/10.3390/fire4030043
Ghodrat M, Shakeriaski F, Nelson DJ, Simeoni A. Experimental and Numerical Analysis of Formation and Flame Precession of Fire Whirls: A Review. Fire. 2021; 4(3):43. https://doi.org/10.3390/fire4030043
Chicago/Turabian StyleGhodrat, Maryam, Farshad Shakeriaski, David James Nelson, and Albert Simeoni. 2021. "Experimental and Numerical Analysis of Formation and Flame Precession of Fire Whirls: A Review" Fire 4, no. 3: 43. https://doi.org/10.3390/fire4030043
APA StyleGhodrat, M., Shakeriaski, F., Nelson, D. J., & Simeoni, A. (2021). Experimental and Numerical Analysis of Formation and Flame Precession of Fire Whirls: A Review. Fire, 4(3), 43. https://doi.org/10.3390/fire4030043








