Calculation of Critical Water Flow Rates for Wildfire Suppression
Abstract
:1. Introduction
2. Materials and Methods
- Water is applied to fuel surfaces not yet involved in fire, preventing pyrolysis and the production of combustion gases;
- Water is applied directly into the flames, cooling the flame below the critical temperature; or
- Water is applied directly to the burning fuel surface, cooling the fuel and resulting in a reduced pyrolysis rate and quenching of the flames.
- is the critical water application rate assuming no external heat flux, identified as ≈0.0129 Lm−2s−1 [1],
- is the efficiency of water application, representing the portion of water leaving the firefighting branch which actually contributes to fire extinguishment, conservatively assumed to be 0.7 [1],
- is the enthalpy change of water, identified as 2640 kJkg−1,
- is external heat flux, calculated using Equation (2),
- I is fire line intensity in kWm−1 calculated using Byram’s fire line intensity equation [25], calculated using Equation (3),
- is flame length in m, calculated using Equation (4),
- is depth of the active flame in m,
- is atmospheric transmissivity, assumed to be 1 due to the proximity of the unburned fuel in respect to the flames,
- is view factor, assumed to be 1 due to the proximity of the unburned fuel in respect to the flames,
- h is the convective heat transfer coefficient set at 0.077 kW/m2K assuming a forced convection and air velocity at 10 ms−1 [1],
- Tfuel is the fuel temperature of the fuel, assumed to be 588 K, being the ignition surface temperature for pine-needle fuel beds [1].
- W is total fuel load in tha−1, considering fine fuels typically less than 6 mm in diameter [22]
- RoS is the forward Rate of Spread corrected for slope in kmh−1, calculated using Equation (5). Noting that terrain influences RoS, slope is assumed to be flat for the purposes of the study.
- FDI is Forest Fire Danger Index, a dimensionless factor incorporating the chance of a fire starting, its Rate of Spread, its intensity and the difficulty of its suppression, according to various combinations of air temperature, relative humidity, wind speed and both the long- and short-term drought effects [26],
- w is understorey fuel load in tha−1, considering fine fuels typically less than 6 mm in diameter [22].
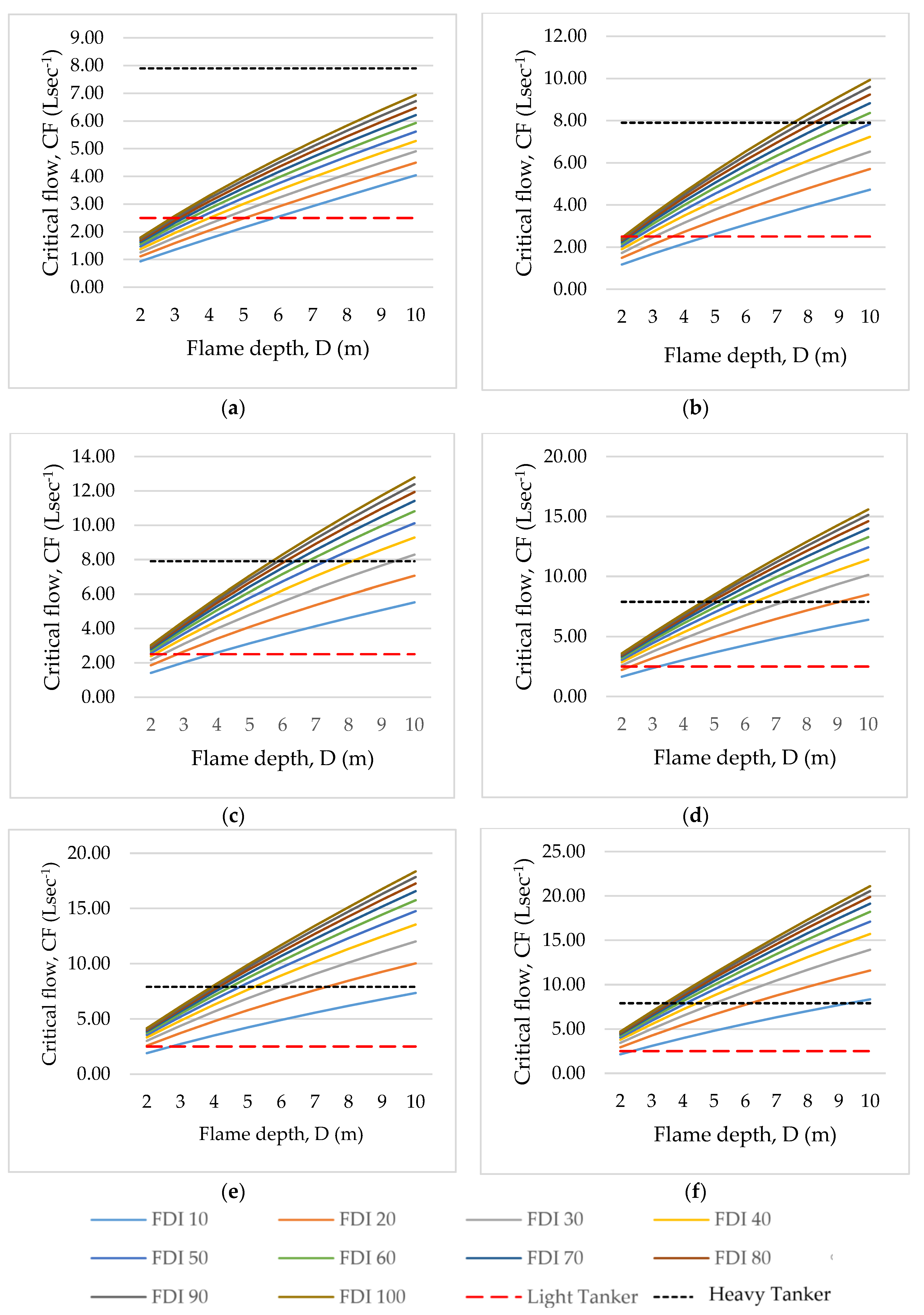
3. Results
- (1)
- The analysis incorporates the full spectrum of fire weather conditions and understorey fuel loads. Therefore the CF can be rapidly estimated by Incident Controllers without requiring current or predicted fire weather conditions (an essential component for calculating FDI) or understorey fuel loads (w) which may vary across the landscape. Both these inputs are required for calculating CF refer to Equations (1)–(5); and
- (2)
- It provides Incident Controllers both visual and mathematical tools to assess the potential suitability of suppression strategies.
4. Sensitivity
5. Validation
- (1)
- real time fire appliance and aircraft telemetry that records active fire suppression time, water application rates and location;
- (2)
- enhanced quantitative measurement of wildfire behaviour such as that available through aerial intelligence and analysis [36];
- (3)
- further experimental study in scaled controlled wildfires through natural vegetation structures with a specific focus on CF requirements.
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hansen, R. Estimating the amount of water required to extinguish wildfires under different conditions and in various fuel types. Int. J. Wildand Fire 2012, 17, 525–536. [Google Scholar] [CrossRef]
- Grimwood, P. Euro Firefighter 2; D&M Heritage Press: West Yorkshire, UK, 2017; ISBN 978-1-911148-10-4. [Google Scholar]
- Barnett, C. SFPE (NZ) Technical Publication—TP 2004/1; Society of Fire Protection Engineers: Auckland, New Zealand, 2004; Available online: http://highrisefirefighting.co.uk/docs/sfpe-TP2004-1.pdf (accessed on 3 September 2018).
- DFES. Respond to Wildfire—Participant’s Resource; revision 2.1; Department of Fire and Emergency Services: Perth, Australia, 2012.
- DFES. Advanced Bush Fire Fighting Learners Manual; revision 1.1; Department of Fire and Emergency Services: Perth, Australia, 2014.
- DCBA. Bushfire Behaviour and Suppression Manual; Department of Biodiversity, Conservation and Attractions: Perth, Australia, 2014.
- Smith, R. Fire Behaviour Formulas—A Guide for Bushfire Managers; Department of Fire and Emergency Services: Perth, Australia, 2013.
- Hirsch, K.; Martell, D. A Review of Initial Attack Fire Crew Productivity and Effectiveness. Int. J. Wildland Fire 1996, 199–215. Available online: http://www.CFs.nrcan.gc.ca/bookstore_pdfs/18905.pdf (accessed on 10 October 2017).
- EuroFire. Unit EF2: Apply Techniques and Tactics to Control Vegetation Fires; Global Fire Monitoring Centre, International Association of Fire and Rescue Services and Rural Development Initiatives, Europe, 2012. Available online: http://www.fire.uni-freiburg.de/eurofire/index.html (accessed on 10 October 2017).
- Johansson, N.; Svensson, S. Review of the Use of Fire Dynamics Theory in Fire Service Activities. Fire Technol. 2018. [Google Scholar] [CrossRef]
- Grenfell Tower Inquiry. Available online: https://www.grenfelltowerinquiry.org.uk/ (accessed on 3 September 2018).
- Top 20 Destructive Fires. Available online: http://www.fire.ca.gov/communications/downloads/fact_sheets/Top20_Destruction.pdf (accessed on 3 September 2018).
- USFS; CDFFP. California Fire Siege 2003—The Story; United States Fire Service and California Department of Forestry and Fire Protection: Sacramento, CA, USA, 2004.
- Death Toll Rises to 91 in Deadly Greece Wildfire. Available online: https://www.cbsnews.com/news/death-toll-rises-deadly-greece-wildfires-today-2018-07-29/ (accessed on 3 September 2018).
- Bushfire CRC. Victorian 2009 Bushfire Research Response Final Report; Bushfire Collaborative Research Council: Melbourne, Australia, 2009. [Google Scholar]
- Penney, G. Dynamic Risk Management in Fire and Rescue Emergency Operations. Master’s Thesis, Edith Cowan University, Perth, Australia, 2016. [Google Scholar]
- Duff, T.; Tolhurst, K. Operational wildfire suppression modelling: A review of evaluating development, state of the art and future directions. Int. J. Wildland Fire 2015, 24, 735–748. [Google Scholar] [CrossRef]
- Thompson, M.; Silva, F.R.; Calkin, D.; Hand, M. A review of challenges to determining and demonstrating efficiency of large fire management. Int. J. Wildland Fire 2017, 26, 562–573. [Google Scholar] [CrossRef]
- Särdqvist, S. Water and Other Extinguishing Agents; Swedish Rescue Services Agency: Lund, Switzerland, 2002; ISBN 91-7253-265-3. [Google Scholar]
- Penney, G. Evidence Based Practice in Fire & Rescue Operations. Tech. Rescue 2013, 65, 68–70. [Google Scholar]
- Cruz, M.; Gould, J.; Alexander, M.; Sullivan, A.; McCaw, L.; Matthews, S. Empirical-based models for predicting head-fire rate of spread in Australian fuel types. Aust. For. 2015, 78, 118–158. [Google Scholar] [CrossRef]
- Penney, G. Bushfire Fuels—Representation in Empirical and Physics Based Models. Master’s Thesis, Victoria University, Melbourne, Australia, 2017. [Google Scholar]
- Penney, G.; Habibi, D.; Cattani, M. Firefighter tenability and its influence on siege wildfire suppression. Fire Saf. J. 2019. under review. [Google Scholar]
- Cruz, M.; Sullivan, A.; Gould, J.; Sims, N.; Bannister, A.; Hollis, J.; Hurley, R. Anatomy of catastrophic wildfire: The Black Saturday East fire in Victoria, Australia. For. Ecol. Manag. 2012, 284, 269–285. [Google Scholar] [CrossRef]
- Byram, G. Combustion of forest fuels. In Forest Fire: Control and Use; Davis, K., Ed.; McGraw-Hill Book Company Inc.: New York, NY, USA, 1959. [Google Scholar]
- SAI Global. AS3959:2009 Construction of Buildings in Bushfire-Prone Areas; Standards Australia: Sydney, Australia, 2009. [Google Scholar]
- Poon, S. Predicting Radiation Exposure from an Advancing Bushfire Flame Front; Warrington Fire: Dandenong South, Australia, 2003. [Google Scholar]
- Rossi, J.; Simeoni, A.; Moretti, B.; Leroy-Cancellieri, V. An analytical model based on radiative heating for the determination of safety distances in wildland fires. Fire Saf. J. 2011, 46, 520–527. [Google Scholar] [CrossRef]
- Wotton, M.; Gould, J.; McCaw, L.; Cheney, N.; Taylor, W. Flame temperature and residence times of fires in dry eucalypt forest. Int. J. Wildland Fire 2011, 21, 270–281. [Google Scholar] [CrossRef]
- Dowdy, A.; Mills, G.; Finkele, K.; deGroot, W. CAWCR Technical Report No. 10—Australian Fire Weather as Represented by the McArthur Forest Fire Danger Index and Canadian Forest Fire Danger Index; The Centre for Australian Weather and Climate Research: Canberra, Australia, 2012; ISBN 9781921605185.
- DFES. Driver/Operator Manual Urban Tanker 3.4; 1st version; Department of Fire and Emergency Services: Perth, Australia, 2017.
- DFES. Driver/Operator Manual Light Tanker MK22; 2nd version; Department of Fire and Emergency Services: Perth, Australia, 2013.
- DFES. Operational Equipment Resource NUCOM—Delta 500 Branch; version 1.0; Department of Fire and Emergency Services: Perth, Australia, 2014.
- DFES. Operational Equipment Resource NUCOM—Task Force Tip; version 1.0; Department of Fire and Emergency Services: Perth, Australia, 2014.
- DFES. Specification FES-023 for Vehicle Crew Protection Deluge Systems; version 1.9; Department of Fire and Emergency Services: Perth, Australia, 2016.
- Parks, D.; (Department of Fire and Emergency Services, Perth, Australia); Penney, G.; (Edith Cowan University, Perth, Australia). Personal Communication, 10 August 2018.
- Noble, I.; Bary, G.; Gill, A. McArthur’s fire-danger meters expressed as equations. Aust. J. Ecol. 1980, 5, 201–203. [Google Scholar] [CrossRef]
- Cheney, N. Fire behaviour. In Fire and the Australian Biota; Australian Academy of Science: Canberra, Australia, 1981; pp. 151–175. [Google Scholar]
- Sullivan, A. Wildland surface fire spread modelling, 1990–2007. 1: Physical and quasi-physical models. Int. J. Wildland Fire 2009, 18, 349–369. [Google Scholar] [CrossRef]
- Sullivan, A. Wildland surface fire spread modelling, 1990–2007. 2: Empirical and quasi-empirical models. Int. J. Wildland Fire 2009, 369–386. [Google Scholar] [CrossRef]
- Cruz, M.; Sullivan, A.; Leonard, R.; Malkin, S.; Matthews, S.; Gould, J.; McCaw, W.; Alexander, M. Fire Behaviour Knowledge in Australia; Bushfire Cooperative Research Centre: Melbourne, Australia; ISBN 987-0-9925684-2-9.
- Gould, J.; McCaw, W.; Cheney, N.; Ellis, P.; Knight, I.; Sullivan, A. Project Vesta—Fire in Dry Eucalypt Forest: Fuel Structure, Dynamics and Fire Behaviour; CSIRO: Perth, Australia, 2007; ISBN 978-0643065345.
| Type | Name | Water Capacity (L) | Flow Rate (Ls−1) |
|---|---|---|---|
| Aircraft-Rotary 1 [36] | Dauphin Type 2 | 1000–1200 | ~333–400 |
| Aircraft-Rotary 2 [36] | Erikson S64E Aircrane | 7560 | ~1512 |
| Aircraft-Fixed wing 3 [36] | AirTractor AT802F | 3150 | ~1050 |
| Appliance 4WD 4 [32,33,34] | Light Tanker | ~500 | 2.5 |
| Appliance 4WD 4,5 [31,33,34,35] | Heavy Tanker | ~3000 | 3.8–7.9 |
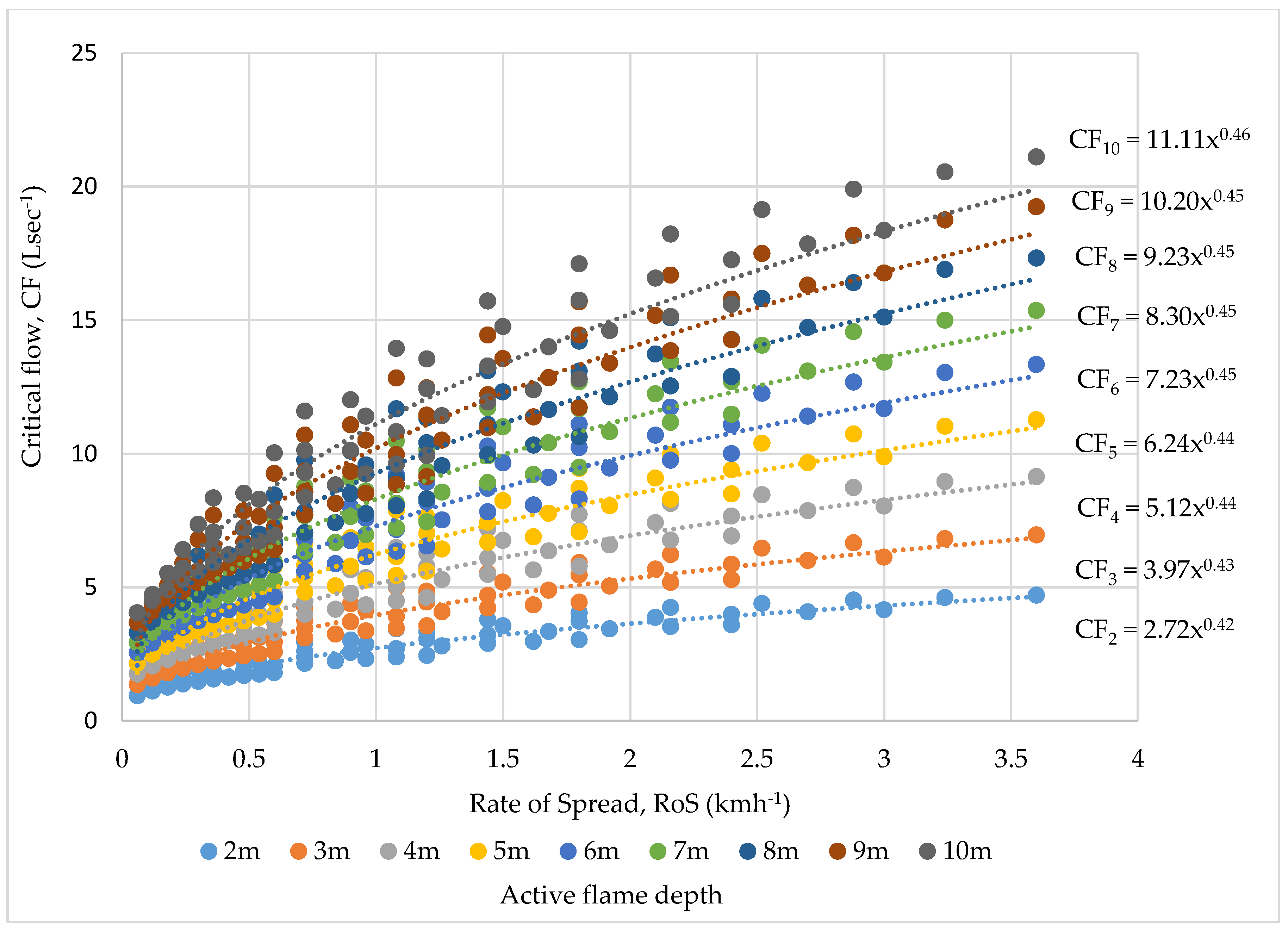
| Rate of Spread, RoS (kmh−1) | |
| Active Flame Depth (m) | Function |
| 2 | CF2 = 2.72 RoS0.42 |
| 3 | CF3 = 3.97 RoS0.43 |
| 4 | CF4 = 5.12 RoS0.44 |
| 5 | CF5 = 6.24 RoS0.44 |
| 6 | CF6 = 7.23 RoS0.45 |
| 7 | CF7 = 8.30 RoS0.45 |
| 8 | CF8 = 9.23 RoS0.45 |
| 9 | CF9 = 10.20 RoS0.45 |
| 10 | CF10 = 11.11 RoS0.46 |
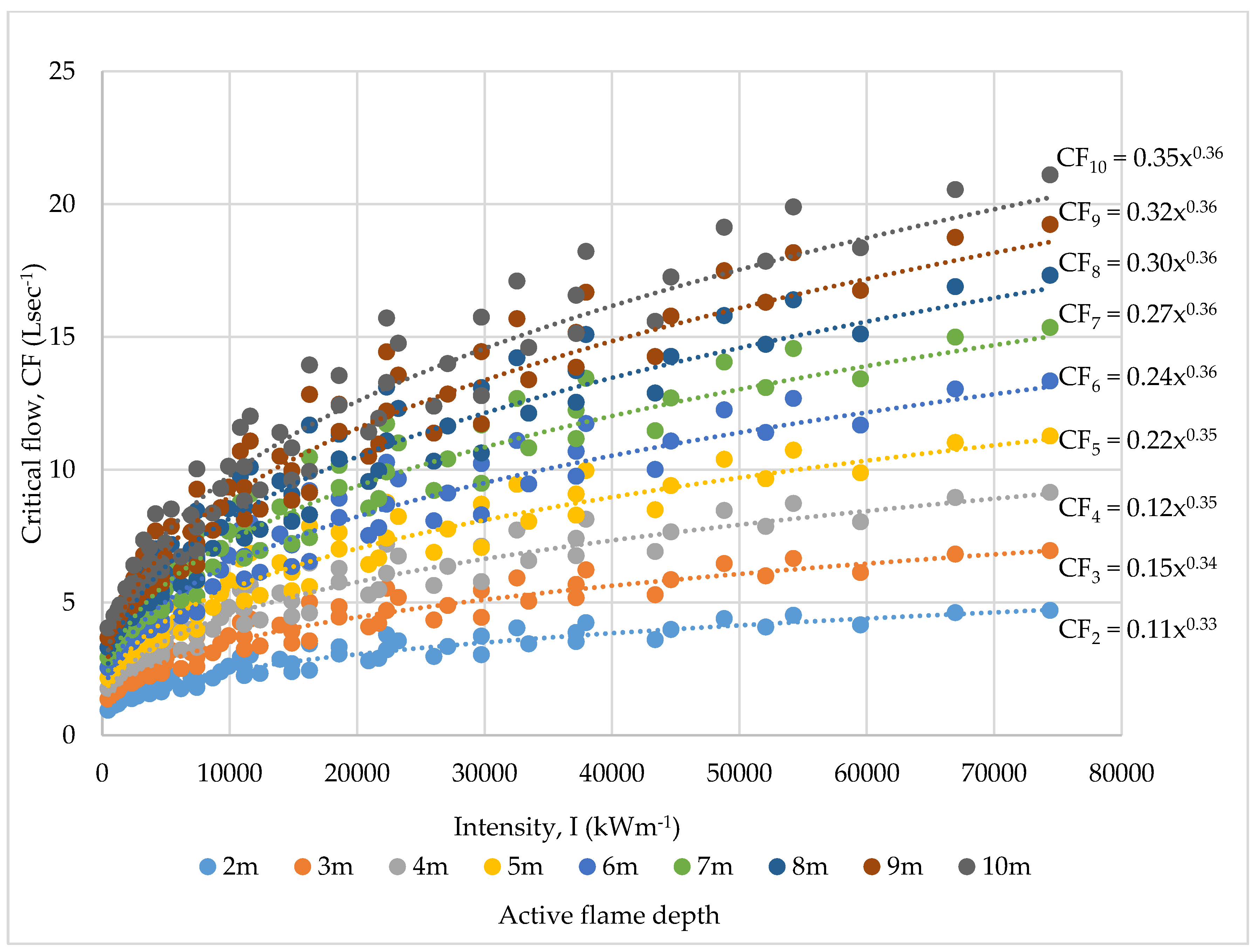
| Intensity, I (kWm−1) | |
| Active Flame Depth (m) | Function |
| 2 | CF2 = 0.11(I)0.33 |
| 3 | CF3 = 0.15(I)0.34 |
| 4 | CF4 = 0.12(I)0.35 |
| 5 | CF5 = 0.22(I)0.35 |
| 6 | CF6 = 0.24(I)0.36 |
| 7 | CF7 = 0.27(I)0.36 |
| 8 | CF8 = 0.30(I)0.36 |
| 9 | CF9 = 0.32(I)0.36 |
| 10 | CF10 = 0.35(I)0.36 |
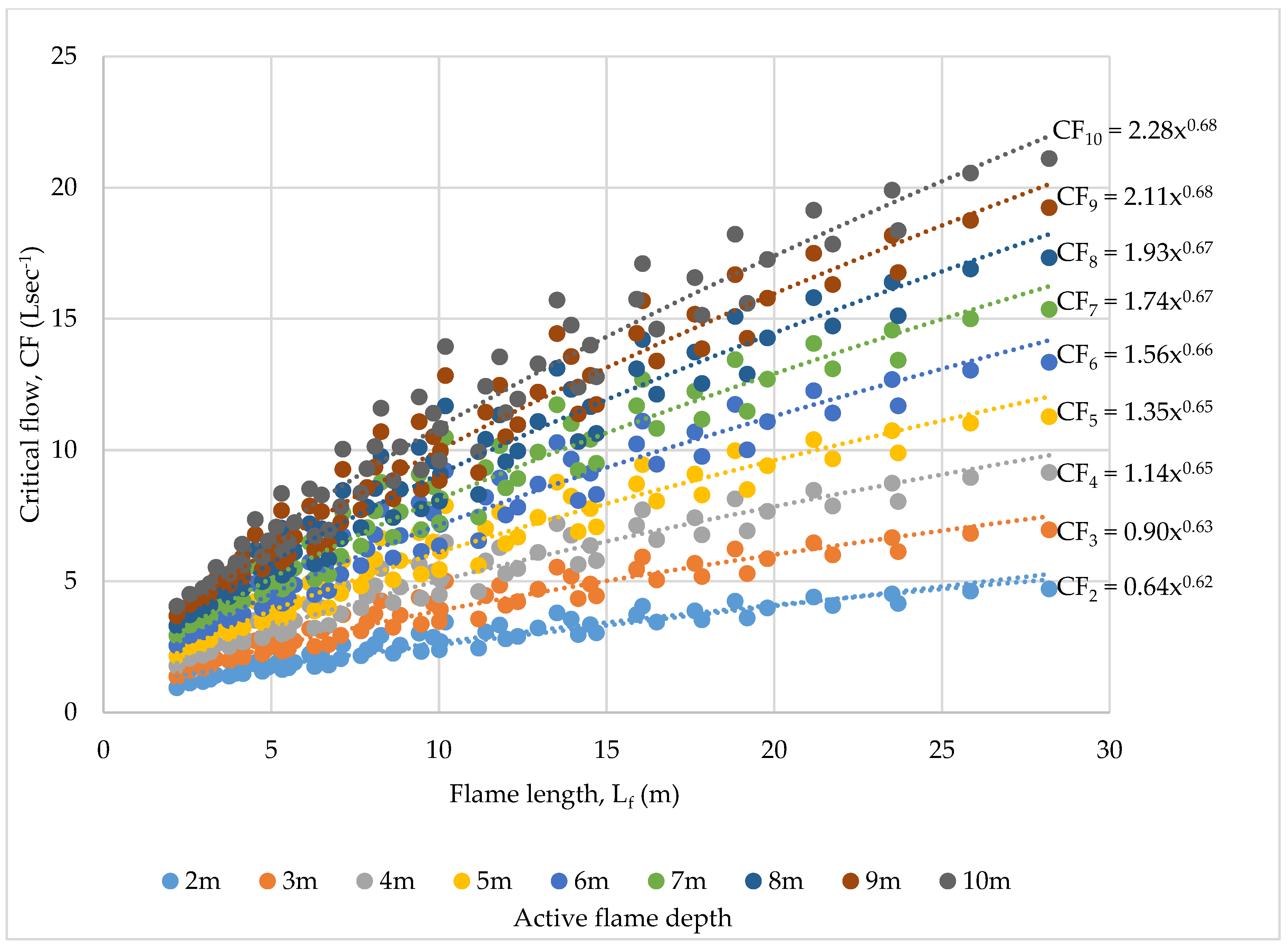
| Flame Length, Lf (m) | |
| Active Flame Depth (m) | Function |
| 2 | CF2 = 0.64 Lf0.62 |
| 3 | CF3 = 0.90 Lf0.63 |
| 4 | CF4 = 1.14 Lf0.65 |
| 5 | CF5 = 1.35 Lf0.65 |
| 6 | CF6 = 1.56 Lf0.66 |
| 7 | CF7 = 1.74 Lf0.67 |
| 8 | CF8 = 1.93 Lf0.67 |
| 9 | CF9 = 2.11 Lf0.68 |
| 10 | CF10 = 2.28 Lf0.68 |
| Input | % Change to Base Input | % Change to Critical Flow (CF) |
|---|---|---|
| h | ±20% | ±1% |
| Tg | ±20% | ±2% |
| Tfuel | ±20% | ±1% |
| ±20% | ±1% | |
| ±20% | ±1% | |
| ±20% | ±0% | |
| ±20% | ±24% | |
| ±20% | ±24% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Penney, G.; Habibi, D.; Cattani, M.; Carter, M. Calculation of Critical Water Flow Rates for Wildfire Suppression. Fire 2019, 2, 3. https://doi.org/10.3390/fire2010003
Penney G, Habibi D, Cattani M, Carter M. Calculation of Critical Water Flow Rates for Wildfire Suppression. Fire. 2019; 2(1):3. https://doi.org/10.3390/fire2010003
Chicago/Turabian StylePenney, Greg, Daryoush Habibi, Marcus Cattani, and Murray Carter. 2019. "Calculation of Critical Water Flow Rates for Wildfire Suppression" Fire 2, no. 1: 3. https://doi.org/10.3390/fire2010003
APA StylePenney, G., Habibi, D., Cattani, M., & Carter, M. (2019). Calculation of Critical Water Flow Rates for Wildfire Suppression. Fire, 2(1), 3. https://doi.org/10.3390/fire2010003





