Moisture Sorption Models for Fuel Beds of Standing Dead Grass in Alaska
Abstract
:1. Introduction
1.1. Equilibrium Moisture Content Equations
1.2. Objectives
2. Methods
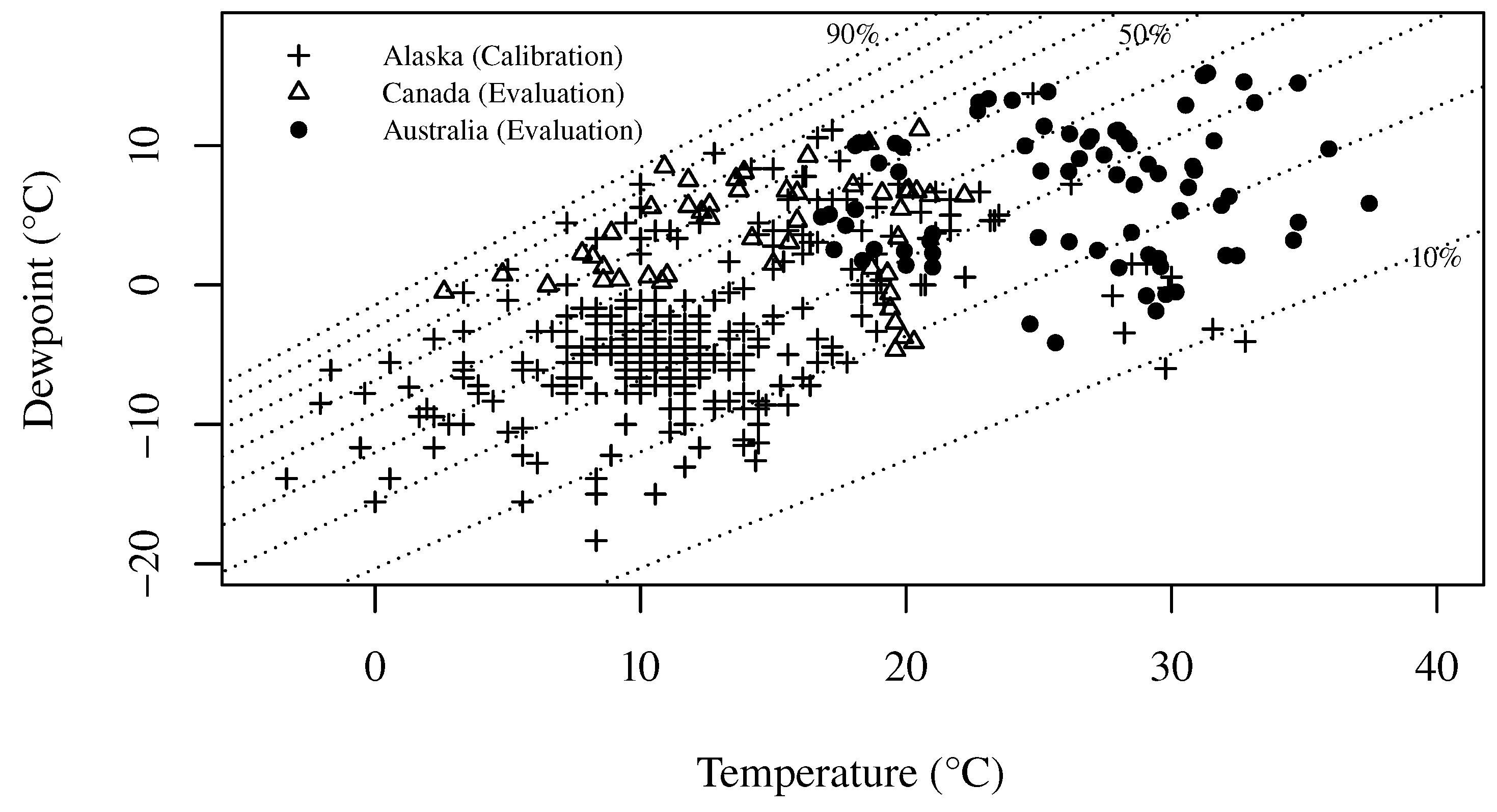
2.1. Model Calibration and Comparison
2.2. Suitability of the Models to other Biomes
3. Results
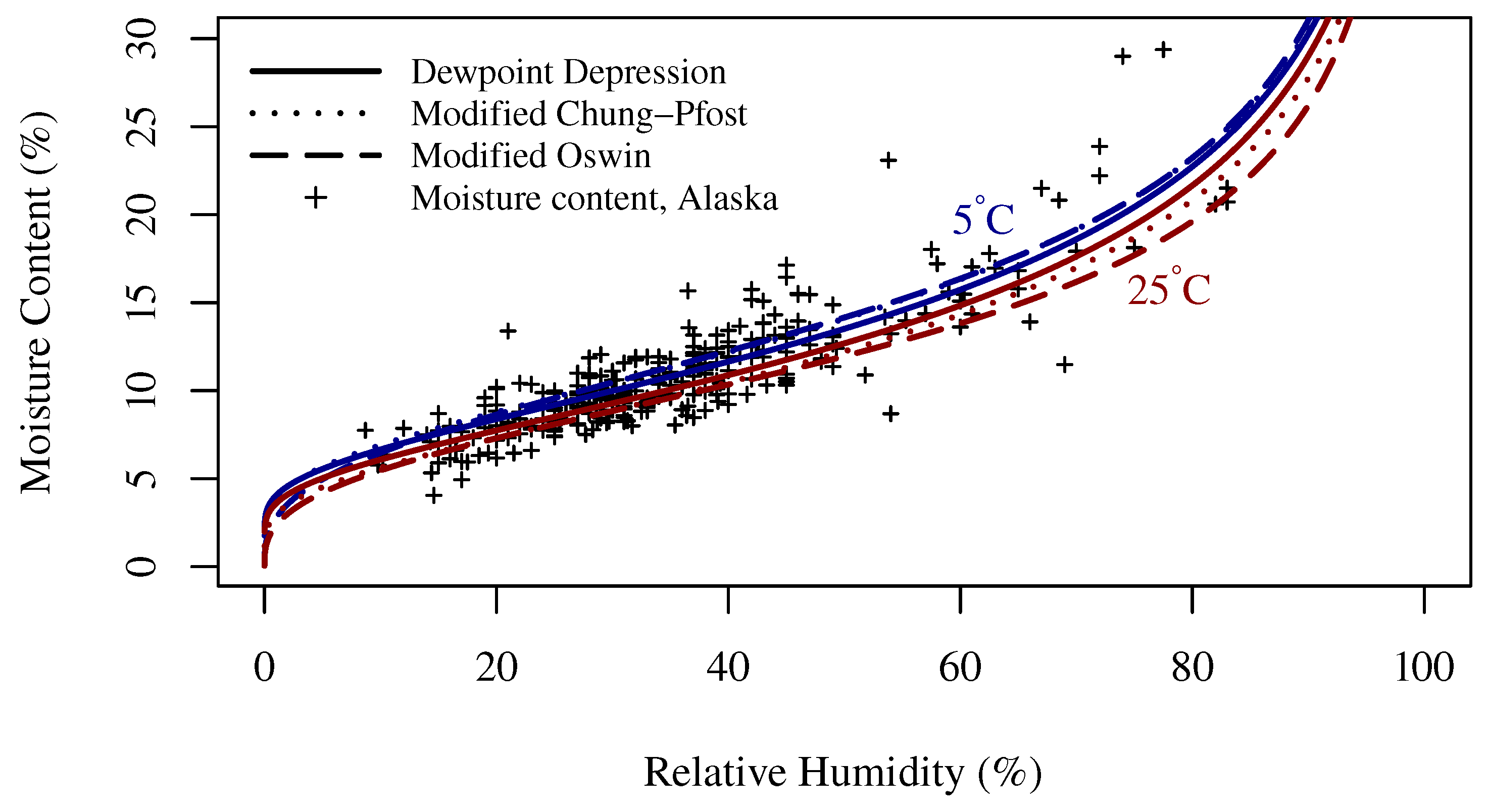
3.1. Model Calibration and Comparison
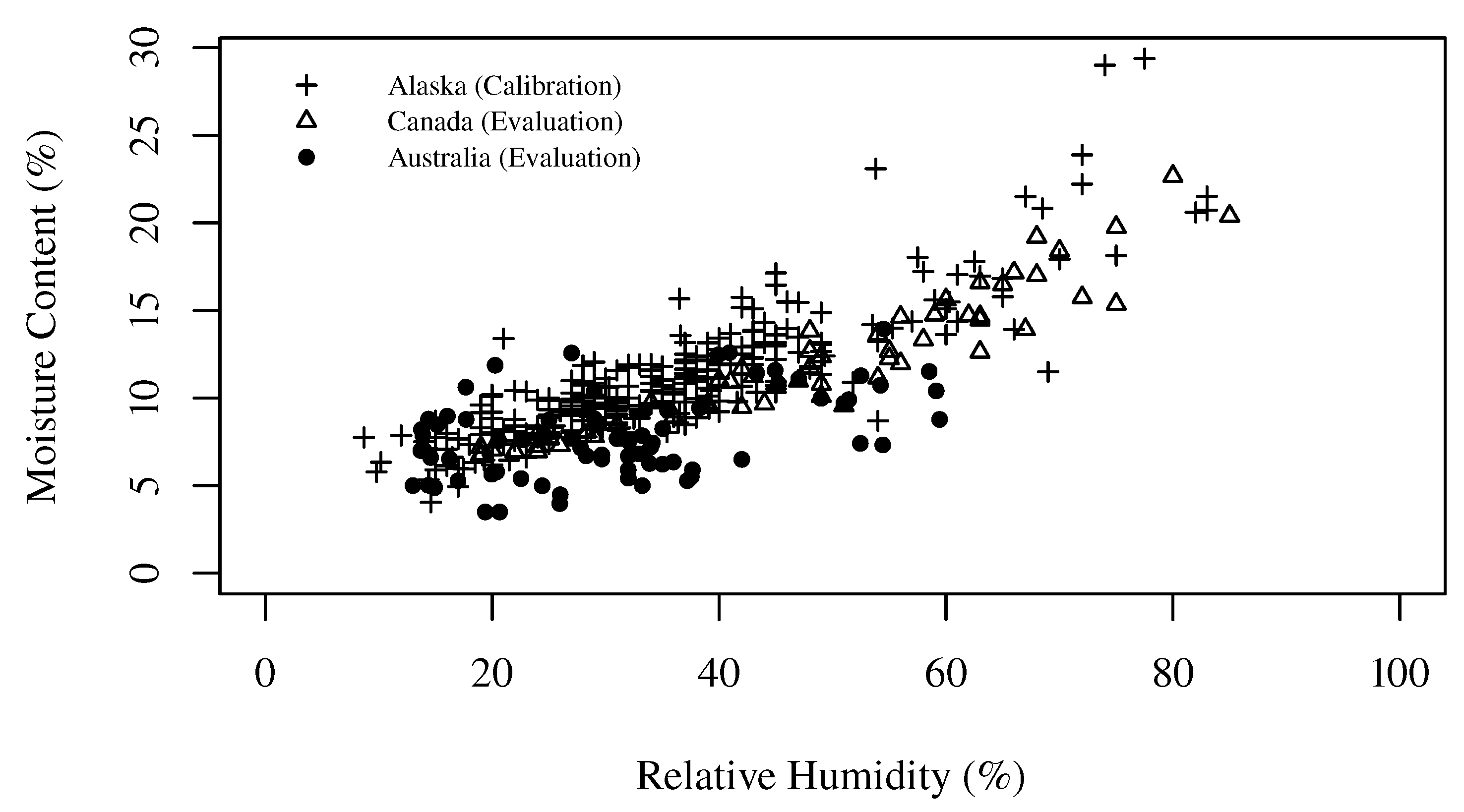
3.2. Suitability of the Models to Other Biomes
4. Discussion
4.1. Model Calibration and Comparison
4.2. Suitability of the Models to other Biomes
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Solar elevation angle () | |
| CC | Cloud cover (%) |
| Free energy () | |
| Relative Humidity (%) | |
| MAE | Mean absolute error (Units of of M) |
| MBE | Mean bias error (Units of of M) |
| MSA | Median Symmetric Accuracy (%) |
| M | Moisture content (%) |
| Moisture content, equilibrium (%) | |
| Moisture content, fiber saturation point (%) | |
| r | Correlation coefficient |
| R | Ideal Gas Constant (8.314 ) |
| RMS | Residual Mean Square |
| RMSE | Root mean squared error (Units of of M) |
| Air temperature, () | |
| Dewpoint temperature () | |
| Air Temperature, () | |
| Air temperature, reference () | |
| Wind speed, eye-level () |
Appendix A
| Site | Date & Time | () | () | (%) | () | () | CC (%) | M (%) |
|---|---|---|---|---|---|---|---|---|
| G | 2009-05-05 10:30 | 10.6 | 3.9 | 62 | 0.9 | 38 | 17.8 | |
| G | 2009-05-05 11:30 | 12.2 | 4.4 | 59 | 1.2 | 43 | 15.6 | |
| G | 2009-05-05 14:00 | 13.3 | 1.7 | 45 | 0.9 | 44 | 13.6 | |
| G | 2009-05-05 15:00 | 14.4 | 4.4 | 52 | 1.3 | 40 | 10.9 | |
| SMR | 2009-05-16 12:45 | 13.3 | −8.3 | 21 | 44 | 13.4 | ||
| SMR | 2009-05-16 14:45 | 14.4 | −8.3 | 20 | 40 | 10.2 | ||
| SMR | 2009-05-16 16:30 | 14.7 | −8.6 | 19 | 32 | 8.3 | ||
| SMR | 2009-05-16 17:00 | 14.4 | −8.9 | 19 | 29 | 9.6 | ||
| SMR | 2009-05-16 19:00 | 13.9 | −8.9 | 20 | 16 | 9.2 | ||
| CL | 2010-04-16 14:15 | 5.0 | −10.6 | 32 | 34 | 11.9 | ||
| D | 2010-04-17 11:50 | 11.1 | −7.2 | 29 | 1.3 | 35 | 12.1 | |
| D | 2010-04-17 12:40 | 12.2 | −6.7 | 29 | 0.9 | 36 | 9.7 | |
| HDZ | 2010-04-17 14:30 | 12.8 | −5.0 | 29 | 1.3 | 33 | 9.0 | |
| HDZ | 2010-04-17 16:15 | 13.3 | −6.1 | 25 | 1.8 | 25 | 8.3 | |
| CL | 2010-04-18 13:20 | 18.9 | −3.3 | 22 | 0.4 | 36 | 10.4 | |
| WR | 2010-04-20 12:05 | 8.3 | −13.9 | 20 | 37 | 8.0 | ||
| WR | 2010-04-20 15:00 | 8.3 | −15.0 | 17 | 2.0 | 32 | 7.7 | |
| WR | 2010-04-20 17:45 | 10.6 | −15.0 | 15 | 1.3 | 17 | 8.7 | |
| BAX | 2010-04-23 13:00 | 5.6 | −15.6 | 19 | 1.8 | 39 | 9.2 | |
| BAX | 2010-04-23 15:00 | 8.3 | −18.3 | 14 | 2.7 | 33 | 7.5 | |
| SMR | 2010-04-24 13:30 | 8.3 | −7.8 | 31 | 1.8 | 38 | 11.6 | |
| SMR | 2010-04-24 13:54 | 9.4 | −7.8 | 27 | 37 | 9.8 | ||
| SMR | 2010-04-24 14:45 | 9.4 | −10.0 | 25 | 1.3 | 35 | 9.8 | |
| SMR | 2010-04-24 15:50 | 11.1 | −8.9 | 24 | 30 | 9.9 | ||
| SMR | 2010-04-24 17:25 | 11.1 | −10.6 | 20 | 0.7 | 21 | 10.1 | |
| SMR | 2010-04-24 18:30 | 8.9 | −12.2 | 20 | 1.3 | 14 | 8.8 | |
| MPTR | 2010-05-03 13:30 | 11.7 | −1.1 | 37 | 1.8 | 44 | 0 | 12.5 |
| MPTR | 2010-05-03 14:20 | 12.8 | −1.1 | 35 | 1.2 | 42 | 0 | 10.3 |
| MPTR | 2010-05-03 15:20 | 16.1 | −1.7 | 29 | 1.2 | 38 | 0 | 9.7 |
| MPTR | 2010-05-03 16:20 | 15.0 | −2.2 | 31 | 2.8 | 32 | 0 | 9.8 |
| MPTR | 2010-05-03 19:30 | 13.9 | −2.8 | 30 | 1.3 | 10 | 0 | 10.6 |
| MPTR | 2010-05-03 20:30 | 15.0 | −2.8 | 31 | 3 | 9.9 | ||
| G | 2010-05-04 10:30 | 9.4 | −3.9 | 39 | 1.1 | 38 | 0 | 11.6 |
| G | 2010-05-04 11:25 | 10.6 | −3.3 | 38 | 0.7 | 42 | 0 | 11.2 |
| G | 2010-05-04 12:20 | 11.7 | −2.8 | 35 | 1.6 | 44 | 0 | 9.6 |
| G | 2010-05-04 16:45 | 15.0 | −2.2 | 31 | 2.7 | 30 | 0 | 9.3 |
| G | 2010-05-04 19:15 | 13.9 | −3.3 | 29 | 1.9 | 12 | 9.5 | |
| M | 2010-05-05 10:40 | 13.3 | −3.3 | 35 | 0.4 | 39 | 11.8 | |
| M | 2010-05-05 11:10 | 10.6 | −2.2 | 38 | 41 | 12.4 | ||
| M | 2010-05-05 11:55 | 12.2 | −2.8 | 37 | 1.2 | 44 | 12.0 | |
| CL | 2010-05-20 10:00 | 15.0 | 3.9 | 47 | 1.0 | 38 | 95 | 12.6 |
| CL | 2010-05-20 12:30 | 15.6 | 6.1 | 48 | 0.6 | 45 | 95 | 11.8 |
| CL | 2010-05-20 14:17 | 18.3 | 7.2 | 45 | 1.5 | 43 | 95 | 10.3 |
| CL | 2010-05-20 15:55 | 17.8 | 6.1 | 45 | 1.5 | 36 | 10.5 | |
| WR | 2011-04-23 11:45 | 9.4 | −6.1 | 32 | 3.6 | 38 | 10.0 | |
| WR | 2011-04-23 12:30 | 10.0 | −6.1 | 32 | 4.0 | 39 | 11.8 | |
| WR | 2011-04-23 13:21 | 10.6 | −6.1 | 30 | 3.3 | 38 | 90 | 10.0 |
| WR | 2011-04-23 15:45 | 13.3 | −5.6 | 26 | 3.4 | 30 | 25 | 9.2 |
| WR | 2011-04-23 17:15 | 13.9 | −6.1 | 25 | 2.1 | 21 | 20 | 9.8 |
| WR | 2011-04-24 13:30 | 12.2 | −6.7 | 25 | 2.3 | 38 | 0 | 9.0 |
| WR | 2011-04-24 15:30 | 12.8 | −5.6 | 25 | 1.9 | 31 | 0 | 9.9 |
| BAX | 2011-04-25 14:30 | 12.2 | −5.0 | 29 | 2.0 | 36 | 70 | 10.1 |
| BAX | 2011-04-25 17:00 | 11.7 | −6.7 | 28 | 2.7 | 23 | 60 | 9.1 |
| BAX | 2011-04-26 11:20 | 10.6 | −6.1 | 30 | 1.1 | 38 | 10 | 11.1 |
| BAX | 2011-04-26 12:45 | 11.7 | −5.6 | 27 | 1.7 | 40 | 20 | 10.3 |
| BAX | 2011-04-26 13:48 | 12.2 | −6.1 | 27 | 2.4 | 38 | 20 | 9.6 |
| BAX | 2011-04-27 10:30 | 5.0 | −1.1 | 61 | 1.4 | 35 | 17.0 | |
| BAX | 2011-04-29 12:45 | 10.0 | −5.6 | 34 | 2.8 | 41 | 35 | 11.6 |
| BAX | 2011-04-29 13:45 | 10.6 | −5.0 | 33 | 2.2 | 39 | 35 | 9.4 |
| BAX | 2011-04-29 16:10 | 10.6 | −5.0 | 31 | 1.9 | 29 | 75 | 10.0 |
| BAX | 2011-04-29 17:30 | 10.6 | −5.6 | 31 | 3.4 | 21 | 75 | 9.7 |
| BAX | 2011-04-29 18:30 | 11.1 | −5.0 | 31 | 3.8 | 14 | 25 | 9.4 |
| BAX | 2011-04-29 19:30 | 11.7 | −5.0 | 31 | 1.2 | 8 | 20 | 9.8 |
| BAX | 2011-04-30 09:55 | 7.8 | −5.0 | 40 | 1.1 | 33 | 100 | 12.5 |
| BAX | 2011-04-30 11:30 | 9.4 | −5.0 | 34 | 1.9 | 39 | 100 | 11.2 |
| BAX | 2011-04-30 12:30 | 11.1 | −6.1 | 31 | 3.3 | 41 | 100 | 9.5 |
| BAX | 2011-04-30 13:30 | 11.7 | −5.6 | 30 | 3.4 | 40 | 100 | 9.7 |
| BAX | 2011-04-30 14:45 | 11.1 | −5.6 | 30 | 4.5 | 36 | 100 | 8.9 |
| BAX | 2011-04-30 15:45 | 10.0 | −6.1 | 31 | 3.3 | 32 | 100 | 8.2 |
| BAX | 2011-04-30 17:00 | 9.4 | −6.7 | 31 | 3.6 | 24 | 100 | 9.1 |
| BAX | 2011-05-01 11:35 | 8.9 | −5.0 | 36 | 1.1 | 40 | 40 | 10.2 |
| BAX | 2011-05-01 12:20 | 11.7 | −4.4 | 30 | 0.4 | 41 | 35 | 9.4 |
| BAX | 2011-05-01 13:30 | 10.0 | −6.7 | 28 | 1.5 | 40 | 45 | 9.2 |
| BAX | 2011-05-01 14:35 | 8.3 | −1.7 | 49 | 3.2 | 37 | 70 | 11.4 |
| D | 2011-05-03 13:00 | 7.2 | −2.2 | 46 | 2.4 | 41 | 60 | 15.5 |
| D | 2011-05-03 14:00 | 8.3 | −3.9 | 40 | 2.1 | 39 | 60 | 13.4 |
| D | 2011-05-03 15:00 | 10.0 | −2.8 | 37 | 2.4 | 36 | 60 | 11.7 |
| CTR | 2011-05-05 11:20 | 9.4 | −5.6 | 34 | 0.5 | 40 | 90 | 11.9 |
| CTR | 2011-05-05 12:30 | 7.2 | −7.8 | 32 | 0.9 | 42 | 75 | 11.8 |
| CTR | 2011-05-05 13:30 | 10.0 | −7.8 | 27 | 1.3 | 42 | 60 | 11.0 |
| SMR | 2011-05-13 11:50 | 6.1 | −6.1 | 40 | 1.2 | 43 | 75 | 11.9 |
| SMR | 2011-05-13 14:00 | 8.3 | −5.0 | 37 | 1.4 | 42 | 100 | 10.8 |
| SMR | 2011-05-13 15:25 | 10.0 | −5.0 | 36 | 1.4 | 37 | 100 | 10.5 |
| SMR | 2011-05-13 16:30 | 8.3 | −5.0 | 37 | 1.7 | 31 | 100 | 10.8 |
| SMR | 2011-05-13 17:30 | 9.4 | −4.4 | 37 | 0.8 | 25 | 100 | 12.2 |
| SMR | 2011-05-13 18:45 | 10.0 | −3.3 | 39 | 1.4 | 17 | 95 | 10.6 |
| SMR | 2011-05-14 11:40 | 13.3 | −3.9 | 30 | 0.8 | 43 | 0 | 9.6 |
| SMR | 2011-05-14 12:30 | 13.9 | −5.0 | 27 | 0.9 | 44 | 0 | 9.1 |
| SMR | 2011-05-14 13:20 | 14.4 | −3.9 | 27 | 0.7 | 44 | 0 | 9.0 |
| SMR | 2011-05-14 14:30 | 14.4 | −4.4 | 26 | 1.5 | 41 | 3 | 9.3 |
| SMR | 2011-05-14 15:45 | 15.6 | −5.0 | 23 | 0.8 | 35 | 5 | 7.9 |
| SMR | 2011-05-14 16:30 | 17.2 | −4.4 | 22 | 2.0 | 31 | 5 | 7.5 |
| SMR | 2011-05-14 17:30 | 17.2 | −5.0 | 22 | 0.6 | 25 | 5 | 8.1 |
| WR | 2012-04-23 12:30 | 10.0 | −1.1 | 43 | 39 | 10 | 15.1 | |
| WR | 2012-04-23 13:34 | 8.9 | −2.8 | 41 | 0.8 | 38 | 10 | 13.7 |
| WR | 2012-04-23 14:14 | 9.4 | −3.9 | 39 | 0.8 | 36 | 12.4 | |
| WR | 2012-04-23 15:05 | 10.6 | −3.9 | 35 | 1.9 | 33 | 15 | 11.1 |
| WR | 2012-04-23 16:04 | 11.7 | −3.9 | 32 | 0.5 | 28 | 15 | 10.7 |
| CTR | 2012-04-24 13:30 | 9.4 | −4.4 | 37 | 2.4 | 39 | 20 | 8.5 |
| CTR | 2012-04-24 15:01 | 11.1 | −5.6 | 28 | 1.3 | 34 | 30 | 11.9 |
| CTR | 2012-04-24 15:55 | 11.1 | −6.7 | 25 | 1.1 | 29 | 30 | 7.4 |
| CTR | 2012-04-24 17:00 | 8.9 | −4.4 | 38 | 1.8 | 23 | 100 | 10.9 |
| CTR | 2012-04-25 13:25 | 10.6 | −4.4 | 34 | 2.0 | 39 | 40 | 10.4 |
| CTR | 2012-04-25 15:15 | 9.4 | −1.7 | 44 | 1.2 | 33 | 50 | 13.2 |
| CTR | 2012-04-25 16:30 | 9.4 | −3.3 | 39 | 1.6 | 26 | 40 | 10.1 |
| D | 2012-04-28 11:07 | 10.6 | −3.9 | 36 | 0.5 | 37 | 10.3 | |
| D | 2012-04-28 11:42 | 10.6 | −3.9 | 35 | 39 | 40 | 10.7 | |
| D | 2012-04-28 12:27 | 11.7 | −3.9 | 30 | 0.8 | 40 | 50 | 8.9 |
| D | 2012-04-28 13:17 | 12.2 | −4.4 | 31 | 1.9 | 39 | 35 | 9.9 |
| D | 2012-04-28 13:56 | 11.7 | −4.4 | 31 | 2.0 | 38 | 35 | 8.6 |
| D | 2012-04-28 14:57 | 11.7 | −4.4 | 31 | 1.7 | 35 | 90 | 9.0 |
| D | 2012-04-28 15:53 | 12.2 | −2.2 | 36 | 1.0 | 30 | 60 | 8.9 |
| D | 2012-04-28 16:57 | 11.7 | −2.8 | 33 | 0.7 | 24 | 80 | 9.3 |
| L | 2012-05-01 17:32 | −0.6 | −11.7 | 42 | 3.5 | 22 | 90 | 12.5 |
| BAX | 2012-05-03 11:21 | 1.7 | −9.4 | 43 | 0.9 | 40 | 100 | 13.9 |
| BAX | 2012-05-03 12:13 | 2.2 | −9.4 | 43 | 1.3 | 42 | 100 | 13.8 |
| BAX | 2012-05-03 13:03 | 3.3 | −10.0 | 37 | 2.1 | 42 | 100 | 13.2 |
| BAX | 2012-05-03 13:57 | 4.4 | −8.3 | 37 | 1.6 | 40 | 95 | 11.4 |
| BAX | 2012-05-03 15:12 | 6.7 | −7.2 | 37 | 1.7 | 35 | 95 | 11.2 |
| BAX | 2012-05-03 16:43 | 7.8 | −6.7 | 33 | 1.7 | 27 | 100 | 11.9 |
| BAX | 2012-05-03 17:07 | 7.2 | −6.7 | 35 | 1.7 | 24 | 100 | 11.0 |
| BAX | 2012-05-03 18:10 | 7.2 | −7.2 | 34 | 1.7 | 18 | 100 | 10.8 |
| Y-IPBC | 2012-05-04 11:00 | 5.6 | −6.1 | 42 | 1.0 | 38 | 15 | 15.8 |
| Y-IPBC | 2012-05-04 12:00 | 7.8 | −5.0 | 39 | 1.3 | 41 | 15 | 12.1 |
| Y-IPBC | 2012-05-04 13:18 | 9.4 | −7.8 | 28 | 1.9 | 41 | 20 | 10.0 |
| Y-IPBC | 2012-05-04 14:11 | 10.0 | −7.2 | 28 | 1.0 | 39 | 35 | 10.1 |
| Y-IPBC | 2012-05-04 15:06 | 10.0 | −7.2 | 28 | 0.8 | 36 | 60 | 10.9 |
| BAX | 2012-05-05 11:50 | 8.3 | −3.9 | 40 | 1.1 | 42 | 9.8 | |
| BAX | 2012-05-05 12:40 | 8.3 | −4.4 | 37 | 0.6 | 43 | 35 | 9.8 |
| BAX | 2012-05-05 13:37 | 11.1 | −4.4 | 34 | 1.8 | 42 | 50 | 10.4 |
| BAX | 2012-05-05 16:25 | 12.2 | −5.6 | 29 | 2.5 | 29 | 50 | 9.7 |
| SMR | 2012-05-08 09:40 | 6.1 | −3.3 | 48 | 0.8 | 33 | 50 | 11.8 |
| SMR | 2012-05-08 10:00 | 6.7 | −3.3 | 45 | 0.7 | 35 | 60 | 12.2 |
| SMR | 2012-05-08 12:00 | 11.1 | −2.8 | 40 | 0.7 | 42 | 75 | 11.9 |
| SMR | 2012-05-08 13:00 | 11.1 | −2.2 | 37 | 1.3 | 43 | 95 | 11.1 |
| CL | 2012-05-14 11:10 | 11.7 | −8.9 | 23 | 1.7 | 41 | 5 | 10.4 |
| CL | 2012-05-14 12:03 | 14.4 | −8.3 | 19 | 1.3 | 44 | 10 | 7.9 |
| CL | 2012-05-14 12:52 | 14.4 | −8.9 | 18 | 1.3 | 44 | 10 | 7.3 |
| CL | 2012-05-14 13:26 | 13.9 | −7.8 | 22 | 1.9 | 44 | 10 | 8.8 |
| CL | 2012-05-14 14:05 | 12.8 | −8.9 | 21 | 0.8 | 42 | 15 | 7.3 |
| CL | 2012-05-14 15:02 | 12.8 | −8.3 | 21 | 0.9 | 39 | 20 | 8.2 |
| CL | 2012-05-14 16:32 | 13.9 | −7.8 | 22 | 2.2 | 31 | 20 | 8.4 |
| L | 2012-05-22 16:23 | 22.2 | 0.6 | 25 | 1.2 | 34 | 100 | 7.4 |
| L | 2012-05-23 12:59 | 19.7 | 7.2 | 45 | 0.4 | 46 | 60 | 10.7 |
| L | 2012-05-23 13:12 | 17.2 | 6.1 | 45 | 1.3 | 46 | 60 | 13.0 |
| L | 2012-05-24 11:02 | 16.1 | 7.8 | 57 | 0.5 | 43 | 85 | 14.4 |
| L | 2012-05-24 16:16 | 21.7 | 5.0 | 33 | 0.5 | 35 | 85 | 8.8 |
| L | 2012-05-29 16:36 | 15.0 | 2.8 | 42 | 1.3 | 33 | 70 | 10.7 |
| L | 2012-05-31 15:07 | 20.7 | 0.0 | 26 | 0.6 | 42 | 100 | 8.4 |
| L | 2012-06-01 15:20 | 16.7 | 6.1 | 48 | 0.7 | 41 | 90 | 11.7 |
| L | 2012-06-05 09:31 | 17.2 | 11.1 | 67 | 0.6 | 37 | 15 | 21.5 |
| L | 2012-06-08 15:46 | 24.8 | 13.7 | 49 | 0.6 | 39 | 90 | 12.4 |
| L | 2012-06-20 15:00 | 26.2 | 7.2 | 30 | 0.5 | 44 | 10 | 8.2 |
| ED | 2013-04-20 09:35 | 0.0 | −15.6 | 29 | 0.0 | 27 | 0 | 10.2 |
| ED | 2013-04-20 13:30 | 6.1 | −12.8 | 23 | 0.8 | 36 | 0 | 8.0 |
| ED | 2013-04-20 16:30 | 5.6 | −12.2 | 25 | 0.6 | 25 | 0 | 7.8 |
| ED | 2013-04-22 08:58 | −3.3 | −13.9 | 43 | 0.0 | 25 | 0 | 11.9 |
| ED | 2013-04-23 20:15 | 5.6 | −10.3 | 31 | 0.0 | 3 | 100 | 8.5 |
| ED | 2013-05-02 20:05 | 1.9 | −8.9 | 39 | 0.0 | 6 | 70 | 13.2 |
| ED | 2013-05-03 19:33 | 0.6 | −5.6 | 65 | 0.7 | 10 | 100 | 16.8 |
| ED | 2013-05-03 20:25 | −1.7 | −6.1 | 70 | 0.6 | 5 | 100 | 17.9 |
| ED | 2013-05-04 11:40 | −2.1 | −8.5 | 60 | 0.4 | 40 | 100 | 15.5 |
| ED | 2013-05-04 14:32 | 1.3 | −7.3 | 55 | 0.3 | 38 | 100 | 14.0 |
| ED | 2013-05-04 18:29 | 3.3 | −6.7 | 49 | 0.5 | 17 | 80 | 13.1 |
| ED | 2013-05-04 21:40 | −0.4 | −7.8 | 54 | 0.0 | -1 | 0 | 8.7 |
| ED | 2013-05-05 11:00 | 2.8 | −10.0 | 40 | 0.3 | 38 | 0 | 9.2 |
| ED | 2013-05-05 14:02 | 2.2 | −11.7 | 35 | 0.3 | 40 | 0 | 9.8 |
| ED | 2013-05-05 19:50 | 3.9 | −7.8 | 40 | 0.4 | 9 | 0 | 9.2 |
| ED | 2013-05-17 08:26 | 2.2 | −3.9 | 60 | 0.5 | 28 | 100 | 15.1 |
| ED | 2013-05-17 16:51 | 3.3 | −5.6 | 49 | 0.4 | 30 | 100 | 13.2 |
| ED | 2013-05-18 17:07 | 0.6 | −13.9 | 33 | 0.4 | 28 | 0 | 9.6 |
| ED | 2013-05-18 17:13 | 16.7 | 10.6 | 69 | 0.0 | 28 | 0 | 11.5 |
| BAX | 2013-05-21 12:03 | 11.7 | −10.0 | 21 | 0.5 | 46 | 0 | 8.1 |
| BAX | 2013-05-21 13:03 | 11.7 | −13.1 | 16 | 2.7 | 46 | 3 | 8.0 |
| BAX | 2013-05-21 13:22 | 12.2 | −11.7 | 16 | 2.0 | 46 | 3 | 6.1 |
| BAX | 2013-05-21 13:30 | 13.9 | −11.5 | 15 | 1.2 | 46 | 3 | 7.1 |
| BAX | 2013-05-21 13:55 | 13.9 | −11.1 | 15 | 1.6 | 45 | 3 | 7.7 |
| BAX | 2013-05-21 14:28 | 14.3 | −12.6 | 14 | 0.6 | 43 | 5 | 7.1 |
| BAX | 2013-05-21 14:57 | 14.4 | −10.0 | 16 | 0.4 | 41 | 3 | 6.6 |
| BAX | 2013-05-21 15:27 | 14.4 | −11.3 | 16 | 1.4 | 38 | 3 | 7.1 |
| BAX | 2013-05-21 16:02 | 15.3 | −7.2 | 22 | 2.5 | 35 | 3 | 6.5 |
| BAX | 2013-05-21 17:00 | 16.4 | −7.2 | 18 | 0.5 | 29 | 3 | 6.3 |
| BAX | 2013-05-22 11:49 | 16.7 | −3.9 | 23 | 0.4 | 46 | 0 | 7.8 |
| BAX | 2013-05-22 13:03 | 16.7 | −5.6 | 20 | 1.3 | 46 | 0 | 7.2 |
| BAX | 2013-05-22 14:03 | 17.8 | −5.6 | 20 | 1.4 | 44 | 5 | 6.2 |
| BAX | 2013-05-22 15:02 | 16.7 | −5.6 | 23 | 2.8 | 40 | 5 | 6.6 |
| BAX | 2013-05-22 16:05 | 16.1 | −6.7 | 19 | 3.5 | 35 | 5 | 6.5 |
| BAX | 2013-05-22 17:05 | 15.6 | −8.6 | 18 | 3.0 | 29 | 5 | 6.0 |
| G | 2013-05-24 08:35 | 10.0 | 2.2 | 58 | 0.4 | 30 | 0 | 17.2 |
| G | 2013-05-24 11:05 | 14.4 | 3.6 | 49 | 1.1 | 45 | 5 | 12.7 |
| G | 2013-05-24 11:58 | 15.6 | 3.9 | 45 | 0.9 | 48 | 5 | 10.9 |
| G | 2013-05-24 13:00 | 16.1 | 3.6 | 43 | 1.1 | 50 | 2 | 10.3 |
| G | 2013-05-24 15:03 | 19.4 | 3.5 | 33 | 0.5 | 44 | 8 | 9.1 |
| G | 2013-05-24 15:58 | 21.1 | 3.7 | 31 | 0.5 | 39 | 15 | 8.3 |
| G | 2013-05-24 16:55 | 20.8 | 3.3 | 33 | 0.8 | 33 | 20 | 9.2 |
| G | 2013-05-24 17:55 | 21.7 | 3.9 | 32 | 1.3 | 25 | 30 | 8.0 |
| G | 2013-05-25 10:00 | 15.4 | 1.7 | 40 | 0.3 | 40 | 0 | 11.1 |
| G | 2013-05-25 11:05 | 16.1 | 2.2 | 39 | 0.7 | 45 | 1 | 10.4 |
| G | 2013-05-25 12:03 | 16.7 | 3.1 | 38 | 0.7 | 49 | 1 | 10.0 |
| G | 2013-05-25 13:02 | 18.9 | 2.2 | 32 | 0.8 | 50 | 2 | 8.8 |
| G | 2013-05-25 15:33 | 17.9 | 1.1 | 30 | 2.2 | 41 | 2 | 8.3 |
| G | 2013-05-25 16:43 | 19.2 | −1.4 | 24 | 2.9 | 34 | 5 | 7.8 |
| R-IPBC | 2013-05-26 08:50 | 11.1 | 3.9 | 61 | 0.0 | 32 | 98 | 14.4 |
| R-IPBC | 2013-05-26 10:46 | 10.0 | 3.3 | 66 | 1.6 | 44 | 85 | 13.9 |
| R-IPBC | 2013-05-26 11:47 | 11.4 | 3.3 | 54 | 1.0 | 48 | 70 | 14.2 |
| R-IPBC | 2013-05-26 14:00 | 19.1 | 0.3 | 30 | 0.9 | 48 | 60 | 10.6 |
| R-IPBC | 2013-05-26 15:03 | 16.4 | 3.1 | 36 | 1.1 | 44 | 80 | 9.1 |
| R-IPBC | 2013-05-26 16:10 | 18.3 | 3.9 | 38 | 0.4 | 38 | 80 | 8.9 |
| MPTR | 2013-05-27 16:22 | 23.5 | 5.0 | 29 | 1.2 | 37 | 1 | 8.2 |
| MPTR | 2013-05-27 16:28 | 23.2 | 4.6 | 28 | 1.2 | 36 | 1 | 7.8 |
| MPTR | 2013-05-27 16:44 | 23.3 | 4.6 | 28 | 1.0 | 34 | 1 | 7.5 |
| ED | 2013-05-29 16:33 | 29.1 | 1.5 | 17 | 0.4 | 34 | 3 | 4.9 |
| ED | 2013-05-29 16:38 | 29.9 | −0.2 | 15 | 0.3 | 33 | 3 | 4.0 |
| L | 2013-05-30 15:14 | 28.5 | 1.5 | 17 | 0.7 | 41 | 8 | 6.0 |
| L | 2013-05-30 15:19 | 30.0 | 0.6 | 15 | 0.7 | 41 | 8 | 5.9 |
| L | 2013-05-30 15:24 | 27.8 | -0.8 | 14 | 0.9 | 40 | 8 | 5.3 |
| ED | 2013-06-05 08:03 | 10.0 | 5.6 | 75 | 0.3 | 28 | 100 | 18.1 |
| ED | 2013-06-05 10:38 | 9.4 | 4.4 | 72 | 0.5 | 43 | 100 | 22.2 |
| ED | 2013-06-05 14:08 | 10.0 | 7.2 | 83 | 0.0 | 46 | 100 | 21.5 |
| ED | 2013-06-05 16:01 | 12.8 | 9.4 | 83 | 0.0 | 38 | 100 | 20.7 |
| WR | 2014-04-15 12:36 | 8.3 | −1.7 | 49 | 0.5 | 36 | 100 | 14.9 |
| WR | 2014-04-15 13:05 | 8.9 | −2.2 | 46 | 1.7 | 36 | 100 | 14.0 |
| WR | 2014-04-15 13:50 | 8.3 | −2.2 | 46 | 2.1 | 35 | 100 | 15.5 |
| WR | 2014-04-15 15:06 | 9.4 | −2.8 | 43 | 1.8 | 30 | 100 | 12.3 |
| WR | 2014-04-15 16:07 | 10.0 | −2.8 | 39 | 1.2 | 25 | 100 | 13.1 |
| WR | 2014-04-15 17:08 | 8.3 | −2.8 | 43 | 0.8 | 19 | 13.0 | |
| BAX | 2014-04-17 12:06 | 7.2 | 0.0 | 60 | 1.2 | 36 | 30 | 13.6 |
| BAX | 2014-04-17 13:14 | 7.8 | −1.7 | 54 | 2.3 | 36 | 30 | 13.2 |
| BAX | 2014-04-17 14:10 | 8.3 | −1.7 | 47 | 1.8 | 35 | 25 | 13.5 |
| BAX | 2014-04-17 15:08 | 10.0 | −2.8 | 38 | 1.5 | 31 | 20 | 11.5 |
| BAX | 2014-04-17 16:12 | 9.4 | −2.8 | 42 | 3.0 | 25 | 30 | 15.2 |
| BAX | 2014-04-17 17:05 | 8.9 | −2.2 | 43 | 2.9 | 20 | 20 | 12.3 |
| BAX | 2014-04-17 18:13 | 9.4 | −4.4 | 37 | 1.5 | 13 | 15 | 11.4 |
| BAX | 2014-04-17 18:47 | 8.3 | −5.0 | 37 | 2.1 | 9 | 15 | 12.1 |
| BAX | 2014-04-17 19:40 | 7.2 | −3.3 | 45 | 3.1 | 3 | 15 | 13.0 |
| BAX | 2014-04-18 09:10 | 3.3 | −3.3 | 63 | 1.7 | 26 | 25 | 17.0 |
| BAX | 2014-04-19 09:24 | 5.6 | −5.6 | 45 | 0.6 | 27 | 2 | 13.2 |
| BDZ | 2014-04-20 08:55 | 8.3 | −2.8 | 47 | 0.7 | 25 | 0 | 15.5 |
| BDZ | 2014-04-20 09:50 | 7.2 | −4.4 | 42 | 3.5 | 30 | 0 | 12.5 |
| BDZ | 2014-04-20 10:59 | 7.8 | −4.4 | 38 | 3.4 | 35 | 0 | 12.1 |
| BDZ | 2014-04-20 11:26 | 8.3 | −3.9 | 41 | 2.2 | 36 | 0 | 11.9 |
| BDZ | 2014-04-20 12:01 | 10.0 | −4.4 | 35 | 2.5 | 37 | 0 | 10.3 |
| BDZ | 2014-04-20 13:25 | 12.2 | −3.3 | 33 | 2.2 | 37 | 10 | 9.3 |
| BDZ | 2014-04-20 13:58 | 11.7 | −3.3 | 34 | 3.0 | 36 | 10 | 9.7 |
| BDZ | 2014-04-20 16:28 | 11.1 | −6.7 | 27 | 1.3 | 25 | 40 | 9.9 |
| BDZ | 2014-04-20 17:21 | 11.7 | −6.7 | 28 | 0.6 | 19 | 40 | 9.8 |
| BDZ | 2014-04-20 18:45 | 11.1 | −7.2 | 25 | 3.2 | 10 | 40 | 9.3 |
| BDZ | 2014-04-20 19:25 | 10.6 | −7.2 | 27 | 1.9 | 6 | 30 | 9.3 |
| CTR | 2014-04-21 09:00 | 7.2 | −4.4 | 44 | 0.0 | 25 | 0 | 14.3 |
| CTR | 2014-04-21 10:40 | 7.8 | −5.6 | 39 | 0.8 | 34 | 0 | 12.2 |
| CTR | 2014-04-21 13:34 | 12.2 | −5.6 | 28 | 1.6 | 37 | 20 | 11.0 |
| CTR | 2014-04-21 14:55 | 13.9 | −6.1 | 25 | 1.3 | 33 | 35 | 10.0 |
| CTR | 2014-04-21 15:47 | 11.7 | −7.8 | 25 | 1.0 | 29 | 45 | 7.7 |
| CTR | 2014-04-21 16:55 | 12.8 | −5.6 | 27 | 1.3 | 23 | 40 | 8.0 |
| CTR | 2014-04-21 18:00 | 11.7 | −7.2 | 25 | 1.3 | 16 | 60 | 8.1 |
| CTR | 2014-04-21 18:55 | 11.7 | −5.0 | 31 | 1.0 | 10 | 70 | 9.8 |
| CTR | 2014-04-22 08:10 | 3.3 | −6.1 | 45 | 0.3 | 21 | 5 | 17.1 |
| CTR | 2014-04-22 09:44 | 7.2 | −5.6 | 40 | 0.5 | 30 | 5 | 12.8 |
| CTR | 2014-04-22 12:10 | 11.1 | −6.7 | 29 | 1.4 | 38 | 15 | 10.8 |
| CTR | 2014-04-22 14:35 | 12.2 | −5.6 | 28 | 1.9 | 35 | 60 | 10.8 |
| CTR | 2014-04-22 18:00 | 11.7 | −7.8 | 24 | 1.7 | 16 | 75 | 8.4 |
| CTR | 2014-04-22 19:00 | 10.6 | −6.1 | 28 | 1.2 | 9 | 75 | 9.3 |
| CTR | 2014-04-23 08:55 | 3.9 | −7.2 | 45 | 0.4 | 26 | 0 | 16.4 |
| Y-IPBC | 2014-05-01 18:35 | 20.6 | 0.0 | 27 | 0.4 | 15 | 1 | 8.1 |
| ED | 2014-05-04 05:30 | 3.3 | −0.6 | 74 | 0.0 | 7 | 20 | 29.0 |
| ED | 2014-05-04 08:22 | 8.3 | 3.3 | 72 | 0.4 | 24 | 95 | 23.9 |
| SMC | 2014-05-09 08:46 | 9.4 | −1.7 | 43 | 0.5 | 28 | 0 | 12.9 |
| SMC | 2014-05-09 09:35 | 9.4 | −1.1 | 42 | 0.8 | 34 | 1 | 12.9 |
| SMC | 2014-05-09 10:52 | 10.6 | −1.1 | 42 | 2.1 | 41 | 1 | 11.9 |
| SMC | 2014-05-09 12:00 | 13.3 | −0.6 | 38 | 1.3 | 45 | 2 | 11.0 |
| SMC | 2014-05-09 13:06 | 15.0 | 1.1 | 39 | 1.5 | 46 | 2 | 9.8 |
| SMC | 2014-05-09 15:00 | 18.9 | 0.0 | 29 | 1.7 | 41 | 1 | 9.5 |
| SMC | 2014-05-09 15:57 | 18.3 | −0.6 | 28 | 1.3 | 36 | 1 | 8.7 |
| SMC | 2014-05-09 16:50 | 18.9 | −0.6 | 25 | 1.9 | 30 | 2 | 8.9 |
| SMC | 2014-05-09 17:50 | 18.3 | 0.0 | 29 | 1.4 | 23 | 2 | 8.4 |
| SMC | 2014-05-09 19:00 | 18.3 | −2.2 | 25 | 1.3 | 15 | 20 | 8.3 |
| SMC | 2014-05-09 20:00 | 18.3 | −2.2 | 24 | 1.5 | 8 | 15 | 8.3 |
| ED | 2015-05-18 06:55 | 13.9 | −0.3 | 36 | 18 | 0 | 15.7 | |
| ED | 2015-05-19 06:20 | 5.0 | 1.1 | 78 | 0.0 | 15 | 0 | 29.4 |
| ED | 2015-05-19 09:51 | 20.6 | 5.2 | 37 | 36 | 0 | 13.6 | |
| ED | 2015-05-23 16:00 | 31.6 | −3.2 | 10 | 36 | 10 | 6.3 | |
| ED | 2015-05-23 16:10 | 32.8 | −4.1 | 9 | 1.5 | 35 | 10 | 7.8 |
| ED | 2015-05-23 16:15 | 29.8 | −6.0 | 10 | 0.8 | 34 | 10 | 5.8 |
| ED | 2015-05-23 18:30 | 28.2 | −3.4 | 12 | 21 | 7.9 | ||
| ED | 2015-05-26 07:40 | 16.2 | 7.8 | 54 | 0.7 | 25 | 70 | 23.1 |
| ED | 2015-05-27 09:45 | 14.2 | 8.3 | 68 | 37 | 20.8 | ||
| ED | 2015-05-27 09:50 | 15.0 | 8.3 | 65 | 0.0 | 38 | 15.8 | |
| ED | 2015-05-27 10:45 | 17.5 | 8.9 | 58 | 0.0 | 42 | 80 | 18.0 |
| ED | 2015-05-29 06:30 | 7.2 | 4.4 | 82 | 0.0 | 18 | 90 | 20.6 |
References
- Cheney, P.; Sullivan, A. Grassfires: Fuel, Weather and Fire Behaviour, 2nd ed.; CSIRO Publishing: Collingwood, Australia, 2008. [Google Scholar]
- Henderson, S.M. A basic concept of equilibrium moisture content. Agric. Eng. 1952, 33, 29–32. [Google Scholar]
- Van Wagner, C.E. A laboratory study of weather effects on the drying rate of jack pine litter. Can. J. For. Res. 1979, 9, 267–275. [Google Scholar] [CrossRef]
- Skaar, C. Wood-Water Relations; Springer Series in Wood Science; Springer-Verlag: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Anderson, H. Predicting Equilibrium Moisture Content of Some Foliar Forest Litter in the Northern Rocky Mountains; Technical Report; Research Paper INT-429; U.S. Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1990. [Google Scholar]
- Viney, N.R. A review of fine fuel moisture modelling. Int. J. Wildland Fire 1991, 1, 215–234. [Google Scholar] [CrossRef]
- González, A.D.R.; Hidalgo, J.A.V. Modelos de Predicción de la Humedad de los Combustibles Muertos: Fundamentos y Aplicación; Monografías INIA/Serie Forestal; Monografías INIA, Instituto Nacional de Investigación y Tecnología Agraria y Alimentaria: Madrid, España, 2007. [Google Scholar]
- Matthews, S. Dead fuel moisture research: 1991–2012. Int. J. Wildland Fire 2014, 23, 78–92. [Google Scholar] [CrossRef]
- Byram, G.M.; Nelson, R.M. An Analysis of the Drying Process in Forest Fuel Material; Technical Report; e-General Technical Report SRS-200; U.S. Forest Service, Southern Research Station: Asheville, NC, USA, 2015. [Google Scholar]
- Van Wagner, C.E. Comparison of American and Canadian Forest Fire Danger Rating Systems; Technical Report; Information Report PS-X-2; Canadian Forest Service, Petawawa Forest Experiment Station: Chalk River, ON, Canada, 1966. [Google Scholar]
- McArthur, A.G. Fire Danger Rating Tables for Annual Grasslands; Commonwealth of Australia, Forestry and Timber Bureau: Canberra, Australia, 1960. [Google Scholar]
- McArthur, A.G. Weather and Grassland Fire Behaviour; Commonwealth of Australia, Department of National Development, Forestry and Timber Bureau Leaflet 100: Canberra, Australia, 1966. [Google Scholar]
- Fosberg, M.A.; Deeming, J.E. Derivation of the 1- and 10-Hour Timelag Fuel Moisture Calculations for Fire Danger Rating; Technical Report; Research Note RM-207; U.S. Forest Service, Rocky Mountain Forest and Range Experiment Station: Fort Collins, CO, USA, 1971. [Google Scholar]
- Cheney, N.P.; Just, T.E. The Behaviour and Application of Fire in Sugar Cane in Queensland; Commonwealth of Australia Department of Agriculture, Forestry and Timber Bureau, Leaflet 115: Canberra, Australia, 1974. [Google Scholar]
- Marsden-Smedley, J.B.; Catchpole, W.R. Fire modelling in Tasmanian buttongrass moorlands. III. Dead fuel moisture. Int. J. Wildland Fire 2001, 10, 241–253. [Google Scholar] [CrossRef]
- Nelson, R.M. A method for describing equilibrium moisture content of forest fuels. Can. J. For. Res. 1984, 14, 597–600. [Google Scholar] [CrossRef] [Green Version]
- Kidnie, S.A.; Cruz, M.G.; Matthews, S.; Hurley, R.J.; Slijepcevic, A.; Nichols, D.; Gould, J.S. Evaluating dead fuel moisture models for Australian grasslands. In Proceedings of the International Association of Wildland Fire, Melbourne, Australia, 11–15 April 2016. [Google Scholar]
- Cruz, M.G.; Kidnie, S.; Matthews, S.; Hurley, R.J.; Slijepcevic, A.; Nichols, D.; Gould, J.S. Evaluation of the predictive capacity of dead fuel moisture models for Eastern Australia grasslands. Int. J. Wildland Fire 2016, 25, 995–1001. [Google Scholar] [CrossRef]
- Sun, D.; Woods, J.L. The moisture content/relative humidity equilibrium relationship of wheat—A review. Dry. Technol. 1993, 11, 1523–1551. [Google Scholar] [CrossRef]
- Berry, S.L.; Roderick, M.L. Plant–water relations and the fibre saturation point. New Phytol. 2005, 168, 25–37. [Google Scholar] [CrossRef]
- Mujumdar, A.S. Handbook of Industrial Drying, 3rd ed.; CRC Press: London, UK, 2006. [Google Scholar]
- Engelund, E.T.; Thygesen, L.G.; Svensson, S.; Hill, C.A.S. A critical discussion of the physics of wood–water interactions. Wood Sci. Technol. 2013, 47, 141–161. [Google Scholar] [CrossRef]
- Halsey, G. Physical adsorption on non-uniform surfaces. J. Chem. Phys. 1948, 16, 931–937. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of gases in multimolecular layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Iglesias, H.A.; Chirife, J. Prediction of the effect of temperature on water sorption isotherms of food material. Int. J. Food Sci. Technol. 1976, 11, 109–116. [Google Scholar] [CrossRef]
- Chen, C.C. Modification of Oswin EMC/EHR equation. J. Agric. Res. China 1990, 39, 367–376. [Google Scholar] [CrossRef]
- Thompson, T.L.; Peart, R.M.; Foster, G.H. Mathematical simulation of corn drying—A new model. Trans. Am. Soc. Agric. Eng. 1968, 11, 582–586. [Google Scholar] [CrossRef]
- Chung, D.S.; Pfost, H.B. Adsorption and desorption of water vapor by cereal grains and their products Part 1: Heat and free energy changes of adsorption and desorption. Trans. Am. Soc. Agric. Eng. 1967, 10, 549–555. [Google Scholar] [CrossRef]
- Nelson, R.M. A model for sorption of water vapor by cellulosic materials. Wood Fiber Sci. 1983, 15, 8–22. [Google Scholar]
- Blackmarr, W.H. Equilibrium Moisture Content of Common Fine Fuels Found in Southeastern Forests; Technical Report; Research Paper SE-74; U.S. Forest Service, Southeastern Forest Experiment Station: Asheville, NC, USA, 1971. [Google Scholar]
- Van Wagner, C.E. Equilibrium Moisture Contents of Some Fine Forest Fuels in Eastern Canada; Technical Report; Information Report PS-X-32; Canadian Forest Service, Petawawa Forest Experiment Station: Chalk River, ON, Canada, 1972. [Google Scholar]
- Anderson, H.; Schuette, R.; Mutch, R. Timelag and Equilibrium Moisture Content of Ponderosa Pine Needles; Technical Report; Research Paper INT-202; U.S. Forest Service, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1978. [Google Scholar]
- Pfost, H.B.; Maurer, S.G.; Chung, D.S.; Milliken, G.A. Summarizing and Reporting Equilibrium Moisture Data for Grains; Technical Report; Paper No. 76-3520; American Society of Agricultural Engineers: St. Joseph, MI, USA, 1976. [Google Scholar]
- Oswin, C.R. The kinetics of package life. III. The isotherm. J. Soc. Chem. Ind. 1946, 65, 419–421. [Google Scholar] [CrossRef]
- Van Wagner, C.E. Development and Structure of the Canadian Forest Fire Weather Index System; Technical Report, Forestry Technical Report 35; Canadian Forestry Service: Ottawa, ON, Canada, 1987. [Google Scholar]
- Stocks, B.J.; Lynham, T.J.; Lawson, B.D.; Alexander, M.E.; Van Wagner, C.E.; McAlpine, R.S.; Dube, D.E. The Canadian Forest Fire Danger Rating System: An overview. For. Chron. 1989, 65, 450–457. [Google Scholar] [CrossRef]
- Van Wagner, C.E.; Pickett, T.L. Equations and Fortran IV Program for the 1976 Metric Version of the Forest Fire Weather Index; Technical Report; Information Report PS-X-58; Canadian Forest Service, Petawawa Forest Experiment Station: Chalk River, ON, Canada, 1975. [Google Scholar]
- USFS. Derivation of Spread Phase Tables National Fire-Danger Rating System; Technical Report; United States Forest Service, Division of Fire Control: Washington, DC, USA, 1966. [Google Scholar]
- Stamm, A.J.; Loughborough, W.K. Thermodynamics of the swelling of wood. J. Phys. Chem. 1935, 39, 121–132. [Google Scholar] [CrossRef]
- Warton, D.I.; Hui, F.K.C. The arcsine is asinine: The analysis of proportions in ecology. Ecology 2011, 92, 3–10. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Elzhov, T.V.; Mullen, K.M.; Spiess, A.N.; Bolker, B. minpack.lm: R Interface to the Levenberg-Marquardt Nonlinear Least-Squares Algorithm Found in MINPACK, Plus Support for Bounds; R Package Version 1.2-0; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Miller, D.M. Reducing Transformation Bias in Curve Fitting. Am. Stat. 1984, 38, 124–126. [Google Scholar] [CrossRef]
- Gregoire, T.G.; Qi, F.L.; Boudreau, J.; Nelson, R. Regression estimation following the square-root transformation of the response. For. Sci. 2008, 54, 597–606. [Google Scholar] [CrossRef]
- Cruz, M.G.; Gould, J.S.; Alexander, M.E.; Sullivan, A.L.; McCaw, W.L.; Matthews, S. A Guide to Rate of Fire Spread Models for Australian Vegetation; Technical Report; CSIRO Land and Water Flagship: Canberra, Australia; ACT, Australia and Australasian Fire Authorities Council: Melbourne, Australia, 2015. [Google Scholar]
- Morley, S.K.; Brito, T.V.; Welling, D.T. Measures of Model Performance Based on the Log Accuracy Ratio. Space Weather 2018, 16, 69–88. [Google Scholar] [CrossRef]
- Wotton, B.M. A grass moisture model for the Canadian Forest Fire Danger Rating System. In Proceedings of the Eighth Fire and Forest Meteorology Symposium, Kalispell, MT, USA, 12–15 October 2009. [Google Scholar]
- Van Wagner, C.E. Drying rates of some fine forest fuels. Fire Control Notes 1969, 30, 5–12. [Google Scholar]
| Region Dataset Type | Alaska Calibration | Canada Evaluation | Australia Evaluation |
|---|---|---|---|
| Day of the Year | 126 (104–171) | 141 (136–144) | 11 (329–116) |
| Time of Day | 14:16 (05:30–21:40) | 14:47 (07:00–21:00) | 13:45 (10:00–19:30) |
| Solar elevation angle () | 33.4 (−1.4–50) | 52.2 (−7.1–65) | |
| Solar radiation () | 474 (0–798) | 449 (11–936) | 756 (53–1392) |
| Temperature ( ) | 12.1 (−3.3–32.8) | 15.1 (2.6–22.2) | 26.3 (16.8–37.5) |
| Dewpoint ( ) | −3.5 (−18.3–13.7) | 3.5 (−4.7–11.2) | 7.3 (−4.1–15.2) |
| Relative humidity (%) | 35.4 (8.7–83) | 49.2 (19–85) | 32.9 (13–59) |
| Windspeed () | 1.3 (0–4.5) | 1.2 (0–2.5) | 2.0 (0.6–4.0) |
| Cloud Cover (%) | 39 (0–100) | ||
| Moisture Content (%) | 11.0 (4.1–29.4) | 12.3 (6.7–22.7) | 8.2 (3.5–13.9) |
| Number of observations | 293 | 54 | 75 |
| Modified Oswin | Modified Halsey | Modified Henderson | Modified hung-Pfost | Chung-Pfost | Dewpoint Depression | |
|---|---|---|---|---|---|---|
| Oswin | Halsey | Henderson | Chung-Pfost | Chung-Pfost | Depression | |
| a | 3.83 *** | 4.86 *** | 64800 *** | *** | ||
| b | *** | *** | ** | *** | *** | * |
| c | *** | *** | *** | *** | *** | |
| RMS | 0.0555 | 0.0566 | 0.0581 | 0.0554 | 0.0581 | 0.0556 |
| RSE | 0.236 | 0.238 | 0.241 | 0.235 | 0.241 | 0.236 |
| d.f. | 290 | 290 | 290 | 290 | 291 | 290 |
| Model | r | RMSE | MAE | MSA (%) |
|---|---|---|---|---|
| Dewpoint Depression | 0.872 | 1.71 | 1.16 | 8.36 |
| Modified Chung-Pfost | 0.871 | 1.71 | 1.16 | 8.64 |
| Modified Oswin | 0.871 | 1.71 | 1.16 | 8.96 |
| Modified Halsey | 0.866 | 1.74 | 1.18 | 8.77 |
| Chung-Pfost | 0.866 | 1.74 | 1.21 | 9.88 |
| Modified Henderson | 0.866 | 1.75 | 1.18 | 9.45 |
| Model | r | RMSE | MAE | MBE | MSA (%) |
|---|---|---|---|---|---|
| Canada. n = 54 | |||||
| Modified Oswin | 0.956 | 1.66 | 1.26 | +1.15 | 8.76 |
| Dewpoint Depression | 0.953 | 1.69 | 1.23 | +1.12 | 9.08 |
| Modified Chung-Pfost | 0.954 | 1.74 | 1.32 | +1.22 | 9.72 |
| Australia. n = 75 | |||||
| Dewpoint Depression | 0.517 | 2.59 | 2.13 | +1.13 | 23.5 |
| Modified Oswin | 0.513 | 2.61 | 2.17 | +1.20 | 24.8 |
| Modified Chung-Pfost | 0.511 | 2.68 | 2.23 | +1.29 | 26.4 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miller, E.A. Moisture Sorption Models for Fuel Beds of Standing Dead Grass in Alaska. Fire 2019, 2, 2. https://doi.org/10.3390/fire2010002
Miller EA. Moisture Sorption Models for Fuel Beds of Standing Dead Grass in Alaska. Fire. 2019; 2(1):2. https://doi.org/10.3390/fire2010002
Chicago/Turabian StyleMiller, Eric A. 2019. "Moisture Sorption Models for Fuel Beds of Standing Dead Grass in Alaska" Fire 2, no. 1: 2. https://doi.org/10.3390/fire2010002
APA StyleMiller, E. A. (2019). Moisture Sorption Models for Fuel Beds of Standing Dead Grass in Alaska. Fire, 2(1), 2. https://doi.org/10.3390/fire2010002





