The Effect of Electrode Geometry on Excited Species Production in Atmospheric Pressure Air–Hydrogen Streamer Discharge
Abstract
1. Introduction
2. Streamer Model and Numerical Method
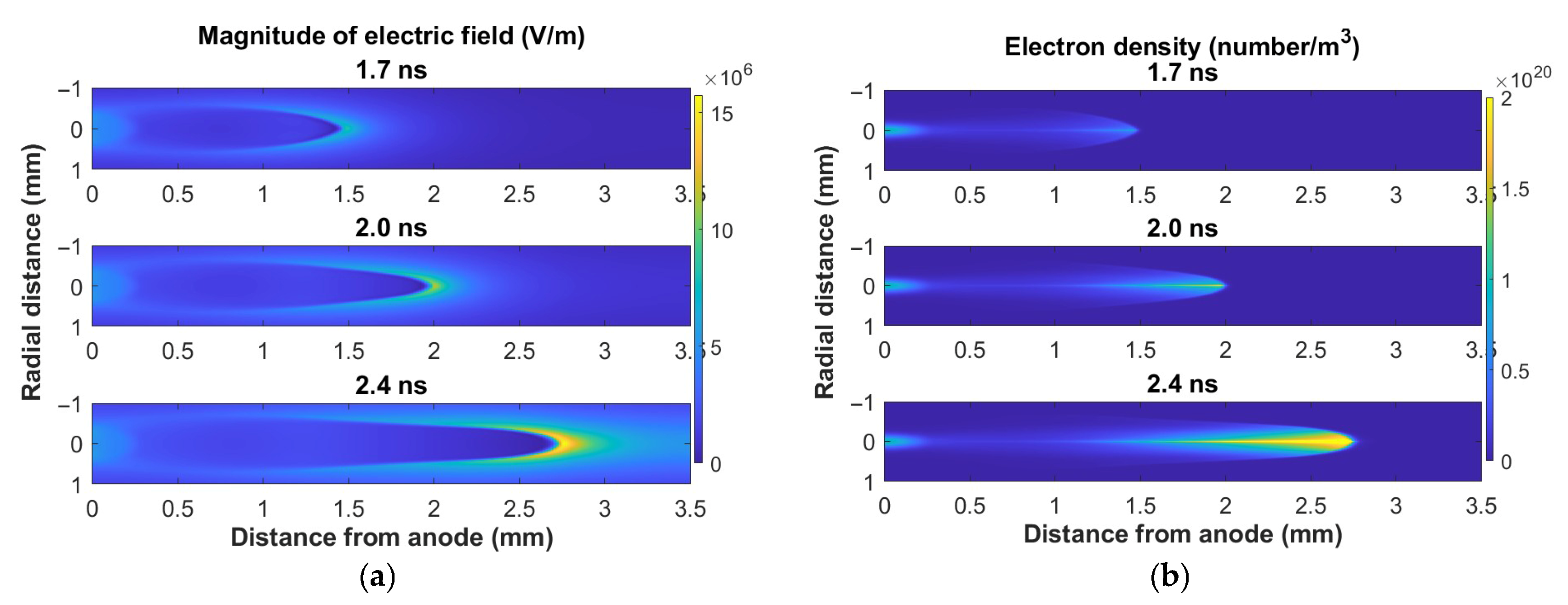
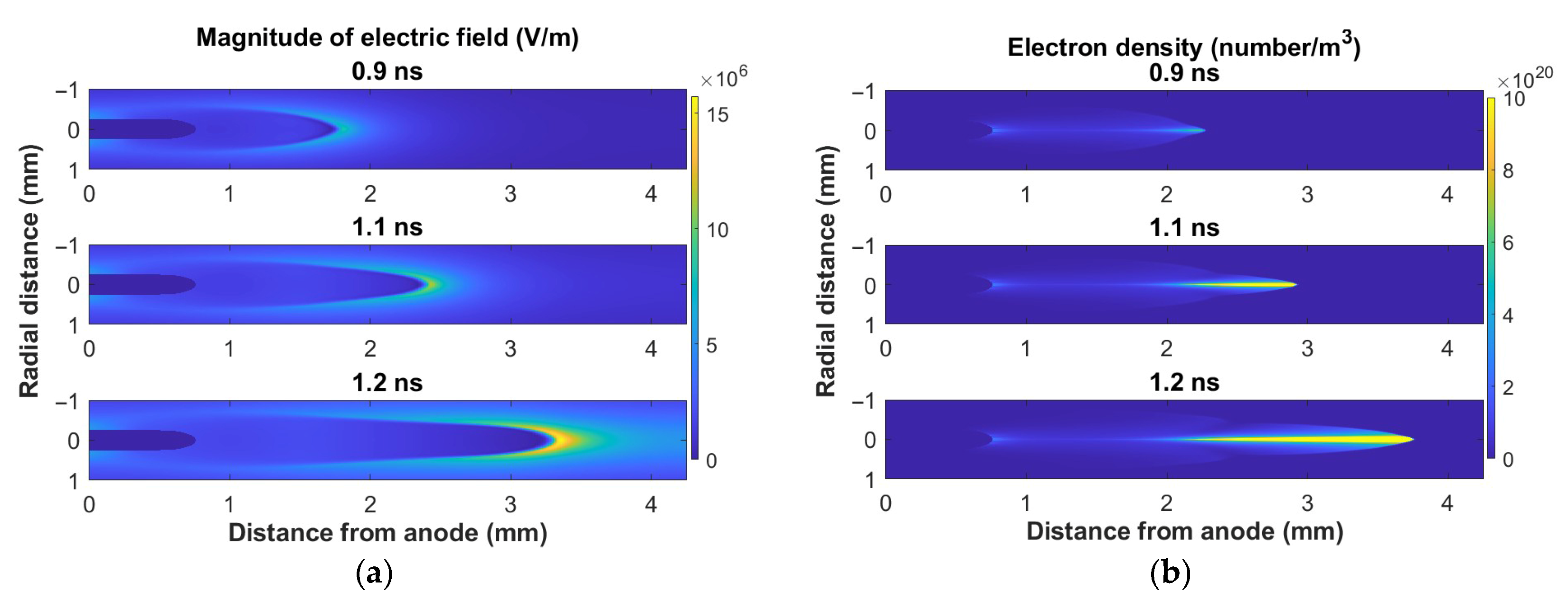
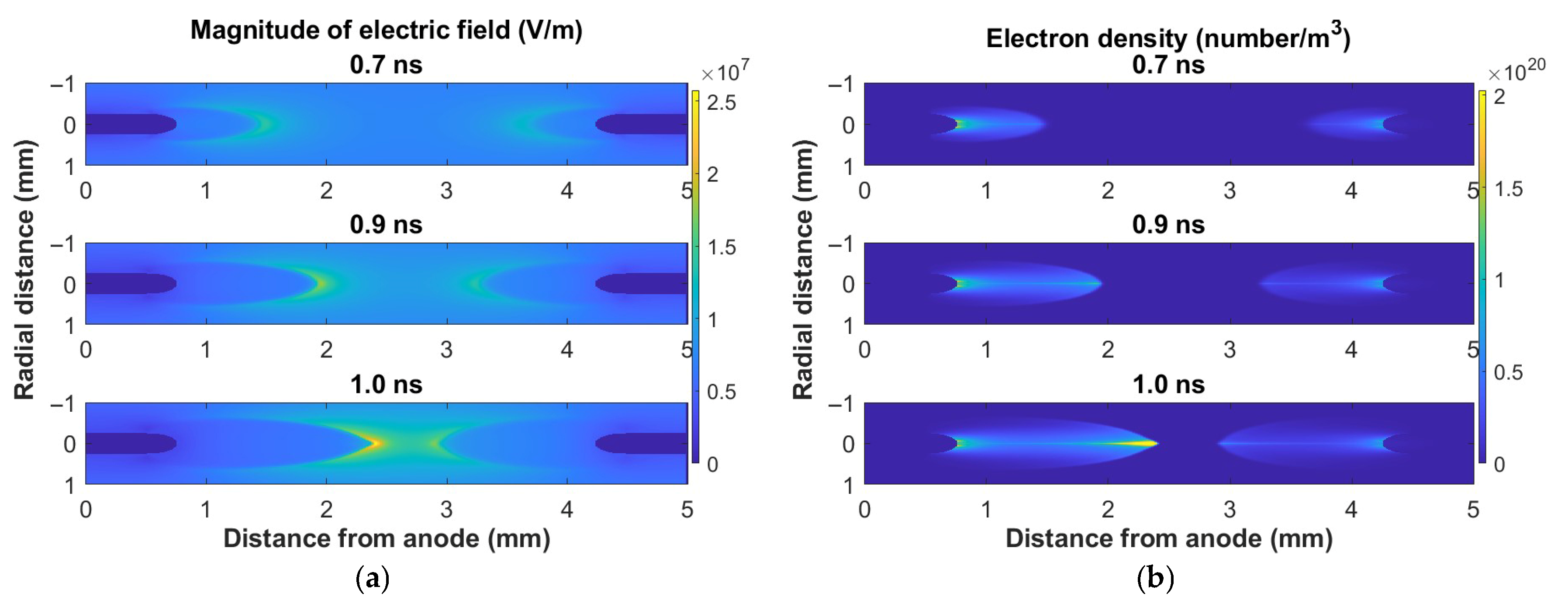
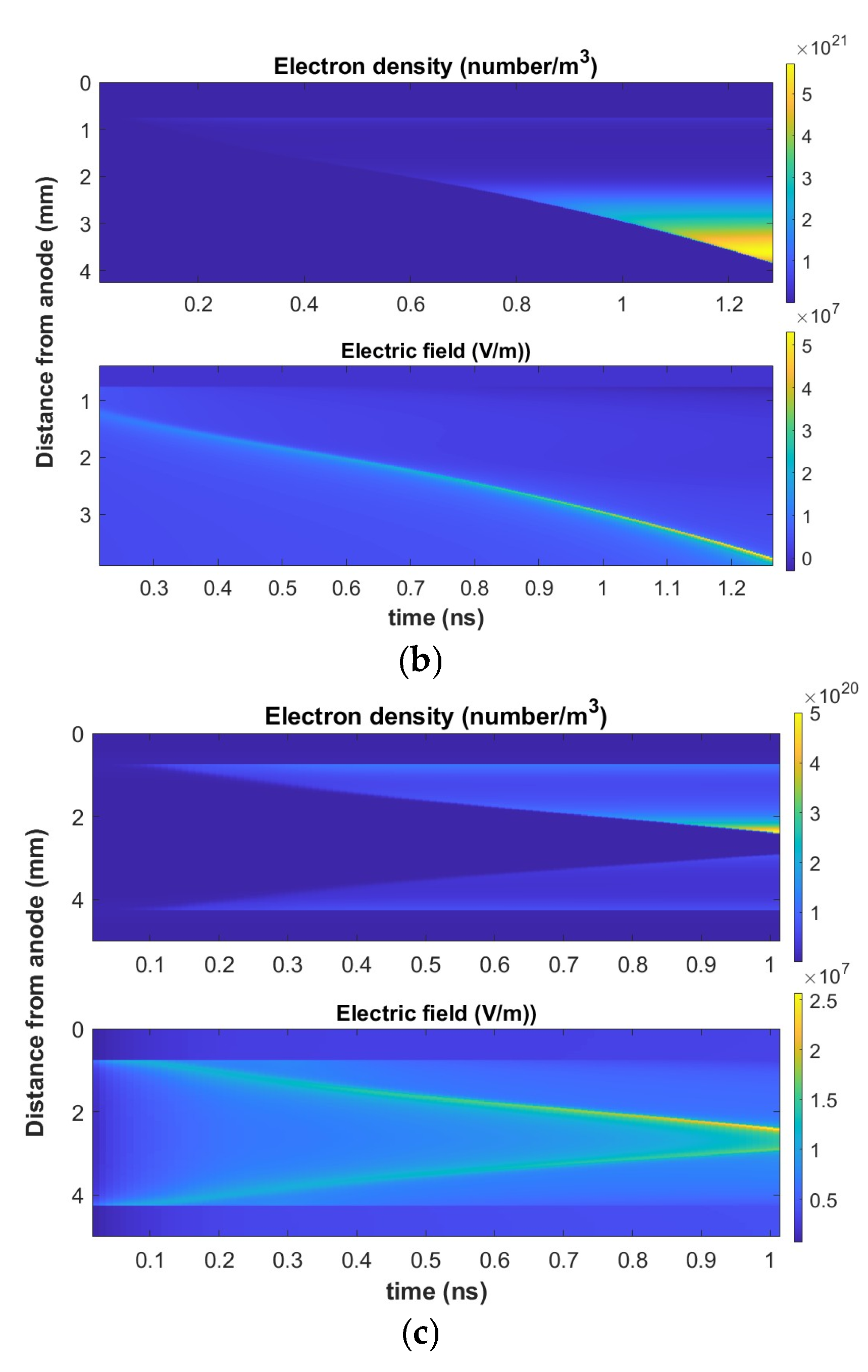
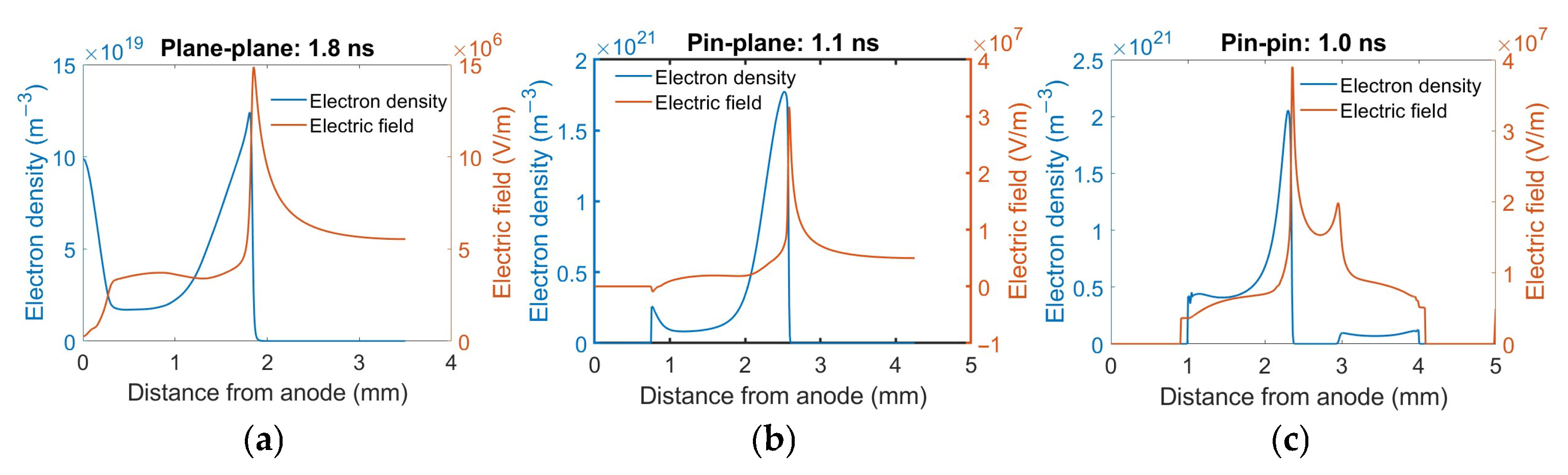
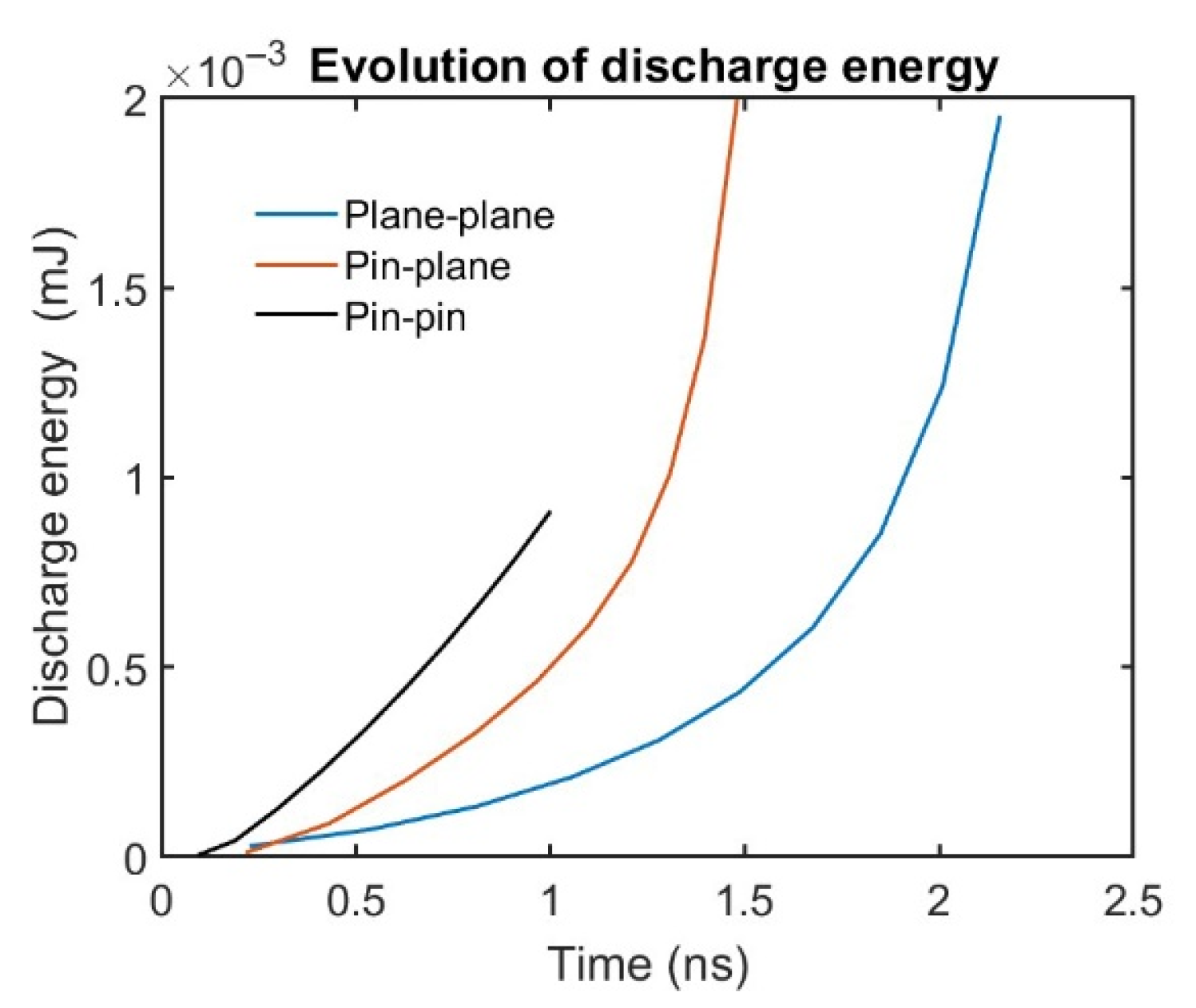
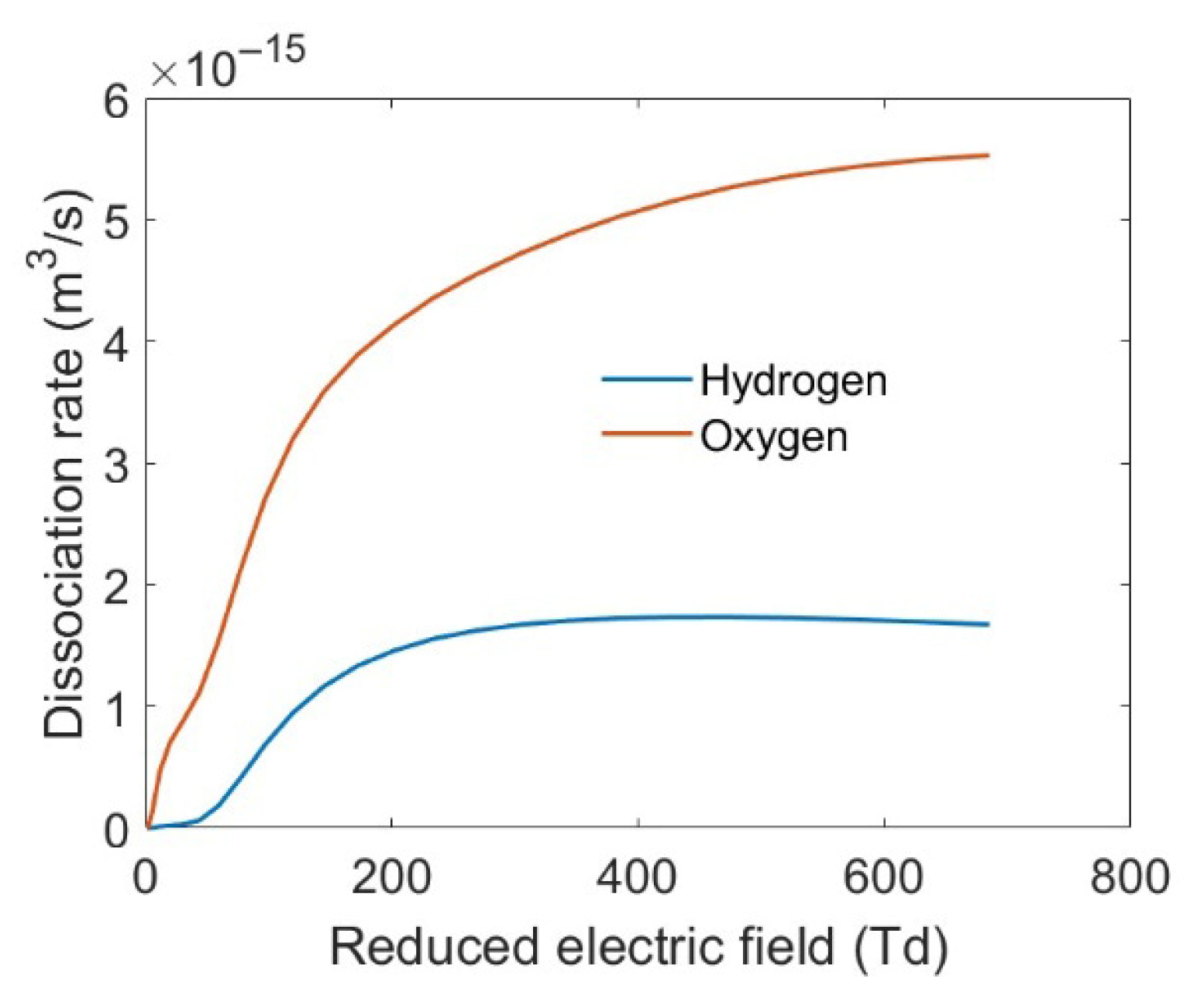
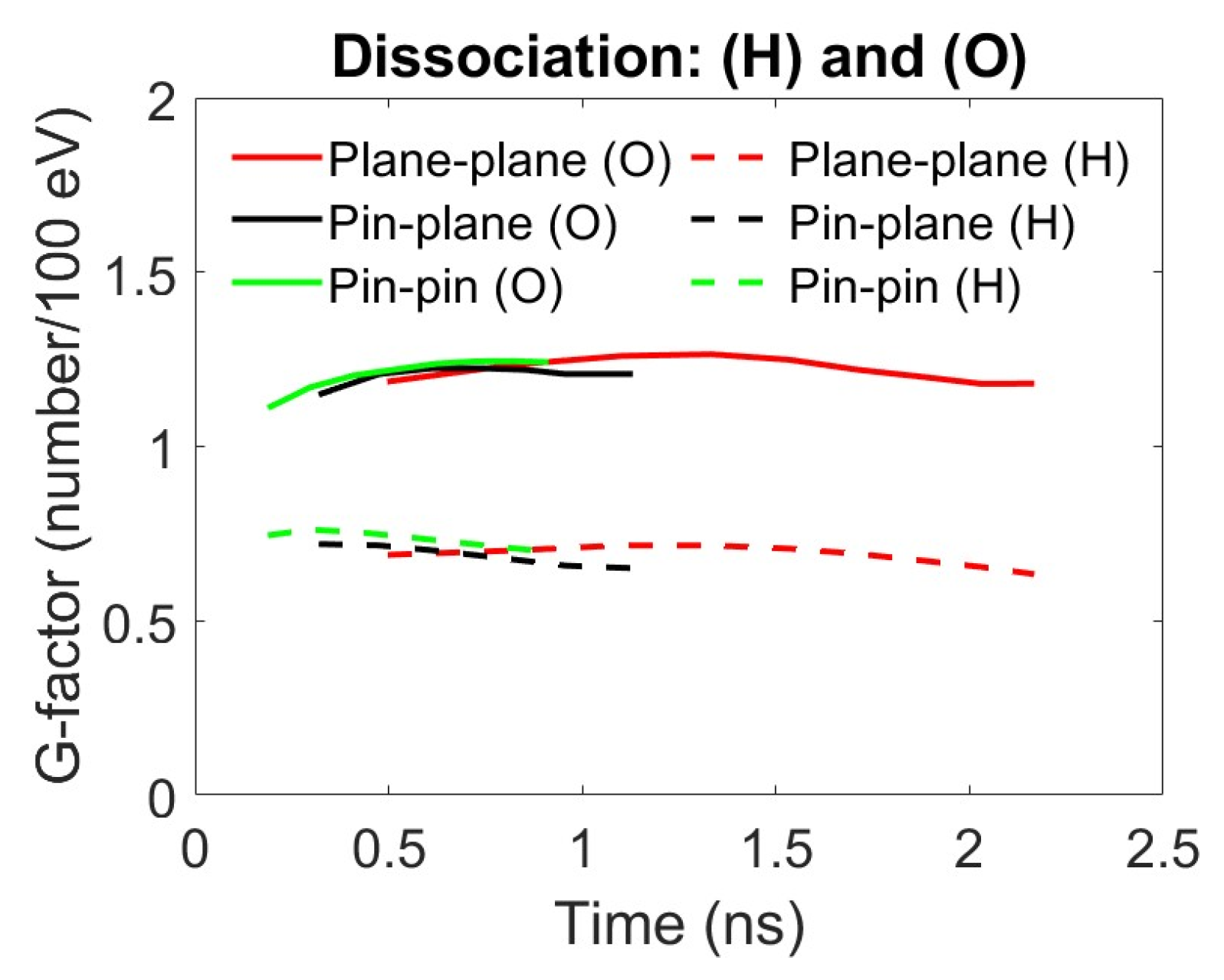
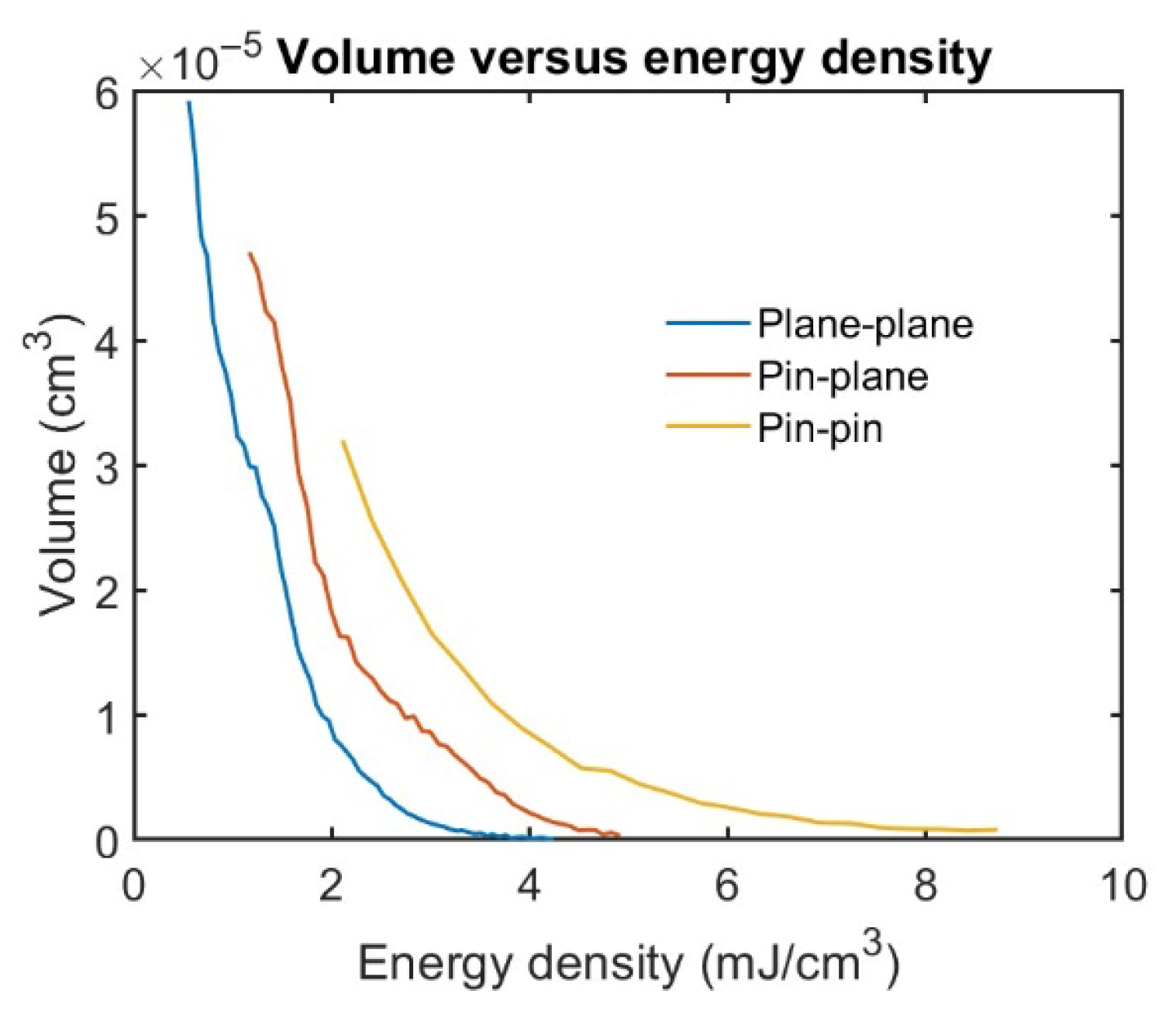
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kogelschatz, U. Dielectric-Barrier Discharges: Their History, Discharge Physics and Industrial Applications. Plasma Chem. Plasma Process. 2003, 23, 1–46. [Google Scholar] [CrossRef]
- Weltmann, K.D.; Kolb, J.F.; Holub, M.; Uhrlandt, D.; Simek, M.; Ostrikov, K.; Hamaguchi, S.; Cvelbar, U.; Cernak, M.; Locke, B.; et al. Future trends in plasma science and technology. Plasma Process Polym. 2018, 16, 1890001. [Google Scholar] [CrossRef]
- Marode, E.; Goldman, A.; Goldman, M. Non-Thermal Plasma Techniques for Pollution Control, Part A: Overview, Fundamentals and Supporting Technologies; Penetrante, B.M., Schultheis, S.E., Eds.; NATO ASI Series; Springer: Berlin/Heidelberg, Germany, 1993; p. 167. [Google Scholar]
- Taneja, T.S.; Johnson, P.N.; Yang, S. Nanosecond pulsed plasma assisted combustion of ammonia-air mixtures: Effects on ignition delays and NOx emission. Combust. Flame 2022, 245, 112327. [Google Scholar]
- Bruggeman, J.P.; Iza, F.; Brandenburg, R. Foundations of atmospheric pressure non-equilibrium plasmas. Plasma Sources Sci. Technol. 2017, 26, 123002. [Google Scholar] [CrossRef]
- Lu, X.P.; Reuter, S.; Laroussi, M.; Liu, D.W. Nonequilibrium Atmospheric Pressure Plasma Jets: Fundamentals, Diagnostics, and Medical Applications; CRC Press: Boca Raton, FL, USA, 2019; ISBN 978-0-429-62072-0. [Google Scholar]
- Zhao, Z.; He, L.; Zhang, H.; Chen, G.; Zhao, B.; Liu, X. Experimental study on working characteristics of direct current plasma jet igniter. Plasma Res. Express 2019, 1, 025015. [Google Scholar] [CrossRef]
- Dhali, S.K. Generation of Large Volume Plasma using spatially and temporally rotating electric fields. AIP Adv. 2020, 10, 035002. [Google Scholar] [CrossRef]
- Shakir, S.; Mynampati, S.; Pashaie, B.; Dhali, S.K. rf-generated ambient-afterglow plasma. J. Appl. Phys. 2006, 99, 073303. [Google Scholar] [CrossRef]
- Ganesh, S.; Rajabooshanam, A.; Dhali, S.K. Numerical Studies of Streamer to Arc Transition. J. Appl. Phys. 1992, 72, 3957–3965. [Google Scholar] [CrossRef]
- Kunhardt, E.E. Electrical breakdown of gases: The prebreakdown stage. IEEE Trans. Plasma Sci. 1980, 8, 130–138. [Google Scholar] [CrossRef]
- Kunhardt, E.E. Generation of Large-Volume, Atmospheric-Pressure, Nonequilibrium Plasmas. IEEE Trans. Plasma Sci. 2000, 28, 189–200. [Google Scholar]
- Dhali, S.K.; Williams, P.F. Two-dimensional Studies of Streamers in Gases. J. Appl. Phys. 1987, 62, 4696. [Google Scholar] [CrossRef]
- Dhali, S.K.; Pal, A.K. Numerical Simulation of Streamers in SF6. J. Appl. Phys. 1988, 63, 1355–1362. [Google Scholar] [CrossRef]
- Morrow, R. Theory of negative corona in oxygen. Phys. Rev. A 1985, 32, 1799. [Google Scholar] [CrossRef] [PubMed]
- Dhali, S.K.; Williams, P.F. Numerical Simulation of Streamer Propagation in Nitrogen at Atmospheric Pressure. Phys. Rev. A 1985, 31, 1219–1221. [Google Scholar] [CrossRef]
- Meek, J.M. Theory of spark discharge. Phys. Rev. 1940, 57, 722. [Google Scholar] [CrossRef]
- Loeb, J.B.; Meek, J.M. The mechanism of spark discharge in air at atmospheric pressure. J. Appl. Phys. 1940, 11, 438. [Google Scholar] [PubMed]
- Dhali, S.K. Generation of excited species in a streamer discharge. AIP Adv. 2021, 11, 015247. [Google Scholar] [CrossRef]
- Teunissen, J.; Ebert, U. 3D PIC-MCC simulations of discharge inception around a sharp anode in nitrogen/oxygen mixtures. Plasma Sources Sci. Technol. 2016, 25, 044005. [Google Scholar]
- Nijdam, S.; Teunissen, J.; Ebert, U. The physics of streamer discharge phenomenon. Plasma Sources Sci. Technol. 2020, 29, 103001. [Google Scholar]
- Dhali, S.K. Parametrization of Fluid Models for Electrical Breakdown of Nitrogen at Atmospheric Pressure. Plasma 2024, 7, 721–732. [Google Scholar] [CrossRef]
- Dhali, S.K. Plasma Chemistry and Applications of Atmospheric Pressure Transient Electrical Discharges. In Emerging Applications of Ions and Plasmas; Guharay, S., Wada, M., Eds.; Springer Series on Atomic, Optical, and Plasma Physics; Springer: Berlin/Heidelberg, Germany, 2025. [Google Scholar]
- Delgado, H.E.; Brown, G.B.; Bartels, D.M.; Rumbach, P.; Go, D.B. The scaling of kinetic and transport behaviors in the solution phase chemistry of plasma-liquid interface. J. Appl. Phys. 2021, 129, 083303. [Google Scholar] [CrossRef]
- Yamazawa, K.; Yamashita, H. Calculation of the electric field distribution under the point-plane gap configurations using the FEM. In Proceedings of the IEEE 1997 Annual Report Conference on Electrical Insulation and Dielectric Phenomena, Minneapolis, MN, USA, 19–22 October 1997; Volume 2, pp. 648–651. [Google Scholar] [CrossRef]
- Bourdon, A.; Péchereau, F.; Tholin, F.; Bonaventura, Z. Morphology of positive ionization waves in atmospheric pressure air: Influence of electrode set-up geometry. Plasma Sources Sci. Technol. 2021, 30, 105022. [Google Scholar] [CrossRef]
- Sato, Y.; Ishikawa, K.; Tsutsumi, T.; Ui, A.; Akita, M.; Oka, S.; Hori, M. Numerical simulations of stable, high-electron-density atmospheric pressure argon plasma under pin-to-plane electrode geometry: Effects of applied voltage polarity. J. Phys. D Appl. Phys. 2020, 53, 265204. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, P.; Verboncoeur, J.P.; Wang, X. Electrical breakdown from macro to micro/nano scales: A tutorial and a review of the state of the art. Plasma Res. Express 2020, 2, 013001. [Google Scholar] [CrossRef]
- Tarashenko, V.F.; Naidis, G.V.; Beloplotov, D.V.; Sorokin, D.A.; Lomaev, M.I.; Babaeva, N.Y. Measuring and Modeling Streamer Velocity at an Air Discharge in a Highly Inhomogeneous Electric Field. Plasma Phys. Rep. 2020, 46, 320–327. [Google Scholar] [CrossRef]
- Reyes, S.; Dhali, S.K. Streamer Discharge Modeling for Plasma-Assisted Combustion. Plasma 2025, 8, 28. [Google Scholar] [CrossRef]
- Aleksandrov, N.L.; Kindysheva, S.V.; Kochetov, I.V. Kinetics of low-temperature plasmas for plasma-assisted combustion and aerodynamics. Plasma Sources Sci. Technol. 2014, 23, 015017. [Google Scholar] [CrossRef]
- Adamovich, I.V.; Lempert, W.R. Plasma assisted ignition and high-speed flow control: Non-thermal and thermal effects. Plasma Phys. Control. Fusion 2015, 57, 01400. [Google Scholar] [CrossRef]
- Starikovskiy, A.; Aleksandrov, N. Plasma-assisted ignition and combustion. Prog. Energy Combust. Sci. 2013, 39, 61–110. [Google Scholar] [CrossRef]
- Starikovskaia, S.M. Plasma-assisted ignition and combustion: Nanosecond discharge and development of kinetic mechanisms. J. Phys. D Appl. Phys. 2014, 47, 353001. [Google Scholar] [CrossRef]
- Matveev, I.; Matveeva, S.; Gutsol, A.; Fridman, A. Non-Equilibrium Plasma Igniters and Pilots for Aerospace Application. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar] [CrossRef]
- Patel, R.; van Oijen, J.; Dam, N.; Nijdam, S. Low-temperature filamentary plasma for ignition-stabilized combustion. Combust. Flame 2023, 247, 112501. [Google Scholar] [CrossRef]
- Li, S.C.; Bai, X.; Chen, W.; Meng, L.; Li, J.; Pan, J. Numerical investigation on plasma-assisted ignition of methane/air mixture excited by the synergistic nanosecond repetitive pulsed and DC discharge. J. Phys. D Appl. Phys. 2021, 54, 15203. [Google Scholar] [CrossRef]
- Patnaik, A.K.; Adamovich, I.; Gord, J.R.; Roy, S. Recent advances in ultrafast-laser-based spectroscopy and imaging for reacting plasma and flames. Plasma Sources Sci. Technol. 2017, 26, 103002. [Google Scholar] [CrossRef]
- Eckert, Z.; Tsolas, N.; Togai, K.; Chernukho, A.; Yetter, R.; Adamovich, I.V. Kinetics of plasma-assisted oxidation of highly diluted hydrocarbon mixture excited by a repetitive nanosecond pulse discharge. J. Phys. D Appl. Phys. 2018, 51, 374002. [Google Scholar] [CrossRef]
- Pavan, C.A.; Guerra-Garcia, C. Nanosecond Pulsed Discharge Dynamics During Passage of a Transient Laminar Flow. Plasma Sources Sci. Technol. 2022, 31, 115016. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, A.; Teunissen, J. A comparison of particle and fluid models for positive streamer discharges in air. Plasma Sources Sci. Technol. 2021, 31, 015012. [Google Scholar] [CrossRef]
- Li, C.; Brok, W.J.; Ebert, U.; Van der Mullen, J. Deviation from the local field approximation in negative streamer heads. J. Appl. Phys. 2007, 101, 123305. [Google Scholar] [CrossRef]
- Dhali, S.K. Transient behavior of drift and ionization in atmospheric nitrogen discharge. Plasma Sources Sci. Technol. 2022, 31, 025014. [Google Scholar] [CrossRef]
- Markosyan, A.H.; Teunissen, J.; Dujko, S.; Ebert, U. Comparing plasma fluid models of different order for 1D streamer ionization fronts. Plasma Sources Sci. Technol. 2015, 24, 065002. [Google Scholar] [CrossRef]
- Grubert, G.K.; Becker, M.M.; Loffhagen, D. Why the local-mean-energy approximation should be used in hydrodynamic plasma descriptions instead of the local-field approximation. Phys. Rev. E 2009, 80, 036405. [Google Scholar] [CrossRef]
- Kim, H.C.; Iza, F.; Yang, S.S.; Radmilovic-Radjenovic, M.; Lee, J.K. Particle and fluid simulations of low temperature plasma. J. Phys. D Appl. Phys. 2005, 38, R283–R301. [Google Scholar] [CrossRef]
- Luque, A.; Ebert, U. Density models for streamer discharges: Beyond cylindrical symmetry and homogeneous media. J. Comput. Phys. 2012, 231, 904–918. [Google Scholar] [CrossRef]
- Zalesak, S.T. Fully Multidimensional Flux-Corrected Transport Algorithms for Fluids. J. Comput. Phys. 1979, 31, 335–362. [Google Scholar] [CrossRef]
- Boris, J.P.; Book, D.L. Flux-corrected transport. I. SHASTA, a Fluid Transport Algorithm that Works. J. Comput. Phys. 1973, 11, 38–69. [Google Scholar] [CrossRef]
- Li, J.; Dhali, S.K. Simulation of microdischarges in a dielectric-barrier discharge. J. Appl. Phys. 1997, 82, 4205–4210. [Google Scholar] [CrossRef]
- Penny, G.W.; Hummert, G.T. Photoionization measurements in air, oxygen and nitrogen. J. Appl. Phys. 1970, 41, 572–577. [Google Scholar] [CrossRef]
- Kulikovsky, A.A. The role of photoionization in positive streamer dynamics. J. Phys. D Appl. Phys. 2000, 33, 1514–1524. [Google Scholar] [CrossRef]
- Liu, N.; Pasko, V.P. Effects of photoionization on propagation and branching of positive and negative streamers in sprites. J. Geophys. Res. 2024, 109, A04301. [Google Scholar]
- Wei, W.; Li, Z.; Yang, Z. Numerical investigation of positive streamer discharge in humid air at sub-atmospheric pressure. Phys. Plasmas 2025, 32, 083906. [Google Scholar] [CrossRef]
- Hagelaar, G.J.M.; Pitchford, L.C. Solving the Boltzmann equation to obtain electron transport coefficients for fluid models. Plasma Sources Sci. Technol. 2005, 14, 722. [Google Scholar] [CrossRef]
- Phelps Database. Available online: www.lxcat.net (accessed on 30 December 2024).
- Cosby, P.C. Electron Impact Dissociation of Oxygen. J. Chem. Phys. 1993, 98, 9560–9569. [Google Scholar] [CrossRef]
- Chung, S.; Lin, C.C.; Lee, E.T.P. Dissociation of hydrogen molecule by electron impact. Phys. Rev. A 1975, 12, 1340–1349. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhali, S.K.; Reyes, S. The Effect of Electrode Geometry on Excited Species Production in Atmospheric Pressure Air–Hydrogen Streamer Discharge. Plasma 2025, 8, 42. https://doi.org/10.3390/plasma8040042
Dhali SK, Reyes S. The Effect of Electrode Geometry on Excited Species Production in Atmospheric Pressure Air–Hydrogen Streamer Discharge. Plasma. 2025; 8(4):42. https://doi.org/10.3390/plasma8040042
Chicago/Turabian StyleDhali, Shirshak Kumar, and Stuart Reyes. 2025. "The Effect of Electrode Geometry on Excited Species Production in Atmospheric Pressure Air–Hydrogen Streamer Discharge" Plasma 8, no. 4: 42. https://doi.org/10.3390/plasma8040042
APA StyleDhali, S. K., & Reyes, S. (2025). The Effect of Electrode Geometry on Excited Species Production in Atmospheric Pressure Air–Hydrogen Streamer Discharge. Plasma, 8(4), 42. https://doi.org/10.3390/plasma8040042






