Streamer Discharge Modeling for Plasma-Assisted Combustion

Abstract

Some of the popular and successful atmospheric pressure fuel/air plasma-assisted combustion methods use repetitive ns pulsed discharges and dielectric-barrier discharges. The transient phase in such discharges is dominated by transport under strong space charge from ionization fronts, which is best characterized by the streamer model. The role of the nonthermal plasma in such discharges is to produce radicals, which accelerates the chemical conversion reaction leading to temperature rise and ignition. Therefore, the characterization of the streamer and its energy partitioning is essential to develop a predictive model. We examine the important characteristics of streamers that influence combustion and develop some macroscopic parameters. Our results show that the radicals’ production efficiency at an applied field is nearly independent of time and the radical density generated depends only on the electrical energy density coupled to the plasma. We compare the results of the streamer model to the zero-dimensional uniform field Townsend-like discharge, and our results show a significant difference. The results concerning the influence of energy density and repetition rate on the ignition of a hydrogen/air fuel mixture are presented.

1. Introduction

In the last two decades, many positive results have been reported in which nonthermal plasma-assisted combustion has shown a reduction of ignition time delay, an extension of flammability limits, and flame stabilization at various fuel–air mixture flows, including supersonic flows and those with a fuel composition including hydrocarbons and hydrogen [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. Plasma-assisted combustion is an extreme nonequilibrium excitation of the gas induced by electrical discharges, in contrast to common combustion which is a thermal process requiring a high temperature for ignition. In the plasma, electrons gain energy from an external electric field and through collisions, then transfer this energy into processes that create excited radicals. Due to the slow exchange of energy to heat during the electrical discharge phase, the temperature of the heavy particles remains low compared to the electrons, leading to nonequilibrium conditions. The essence of such plasma is the nonequilibrium population of excited states which leads to an increase in reactivity and facilitates ignition and flame propagation. From this point of view, the most important question for plasma-enhanced combustion chemistry is the partitioning of the electrical discharge energy into heat and vibrational, rotational, and electronic excitation. The rate of molecule excitation by electron impact in discharge plasma depends on the electron energy. Thus, the possibility to control the electron energy means the possibility to control the direction of energy deposition and selective excitation of different states of molecules.

Improvement in fuel efficiency and the reduction of emissions from hydrocarbon combustion used for automotive and gas turbine platforms can be achieved by improved control of lean flame blowout which will lead to a reduction in the emission of greenhouse gases [15]. Low-temperature combustion was originally investigated to reduce emissions, mainly NOx and particulate matter. More recently improving efficiency and lowering fuel consumption has also been a motivating factor [15,16,17]. An electrical discharge can be the source of energy which creates a plasma and channels energy into processes that can be used to control combustion. It has been demonstrated that nonthermal plasmas have the potential to control ignition/combustion.

The existing means of creating the plasma in the combustion zone include injection from an external source, spark, dielectric barrier discharges, near-surface electric discharge, microwave discharges, repetitive pulsed discharges, and DC discharges [3,4,5,6,18]. The repetitive pulsed discharges have been shown to be the most effective in experimental demonstrations in controlling ignition and combustion characteristics. In such a discharge, the energy coupling can be controlled by the applied voltage, pulsed width and repetition rate [19]. Plasma-assisted combustion is a promising way to stabilize ignition at high altitudes and at low dynamic pressures and temperatures [7,8,9].

There is a need for fundamental understanding of the discharge physics that leads to the onset of ignition of the air–fuel mixture. There are numerous reports of the modeling and simulation of plasma-assisted combustion in hydrogen, methane, and ammonia as fuels. The majority of the reported results use zero-dimensional models to estimate radical species production. There are several reports on modeling the discharge phase as streamers to estimate radical production [20,21,22]. Bouwman et al. discuss the streamer characteristics, such as branching and the suppression of photoionization, and reactive species that are generated due to the direct electron impact of 3D particle simulations in an air–methane streamer [21]. Nagaraja et al. investigated the ignition characteristics of hydrogen–air mixtures using pulsed nanosecond dielectric barrier discharge [22]. The model was one-dimensional at low pressures, which limits its validity at or near atmospheric pressure where at least two-dimensional models are required to correctly estimate fields due to space charge. Barleon et al. investigated the impact of nanosecond repetitive pulses’ frequency on the ignition characteristics of a lean methane–air mixture using a fully coupled plasma-combustion model in cylindrical geometry. They conclude that the minimal energy to ignite decreases with increasing frequency because the plasma channel does not have the time to diffuse, and the necessary radical concentrations remain confined [20].

In this paper we investigate the modeling and simulation of the transient phase of the electrical discharge followed by adiabatic combustion to quantify a few macroscopic properties which are critical for the chemical conversion phase. Proper modeling of the discharge phase would lead to better-predictable outcomes as this phase determines the critical radical densities for chemical conversion reactions leading to ignition. As noted earlier, there are numerous reports of streamer simulations for combustion in various gas mixtures. However, this paper reports on some properties of the steamers which can be generalized for combustion studies. This will lead to predictive models for plasma enhancement with energy addition, such as the effect of specific plasma-produced species, efficient energy coupling into a high-speed and highly turbulent reactive flow, and the in situ production of elevated temperatures. [12]. The results are presented for a hydrogen/air fuel mixture. However, the proposed approach is valid for other fuel/air systems. For the successful application of this methodology to a specific application, several fundamental data sets are required, including the electron impact cross-section of the constituent gas molecules/atoms and chemical reaction rates of the neutral particles with the radicals produced by the discharge.

2. Modeling of the Transient Electrical Discharge and Combustion

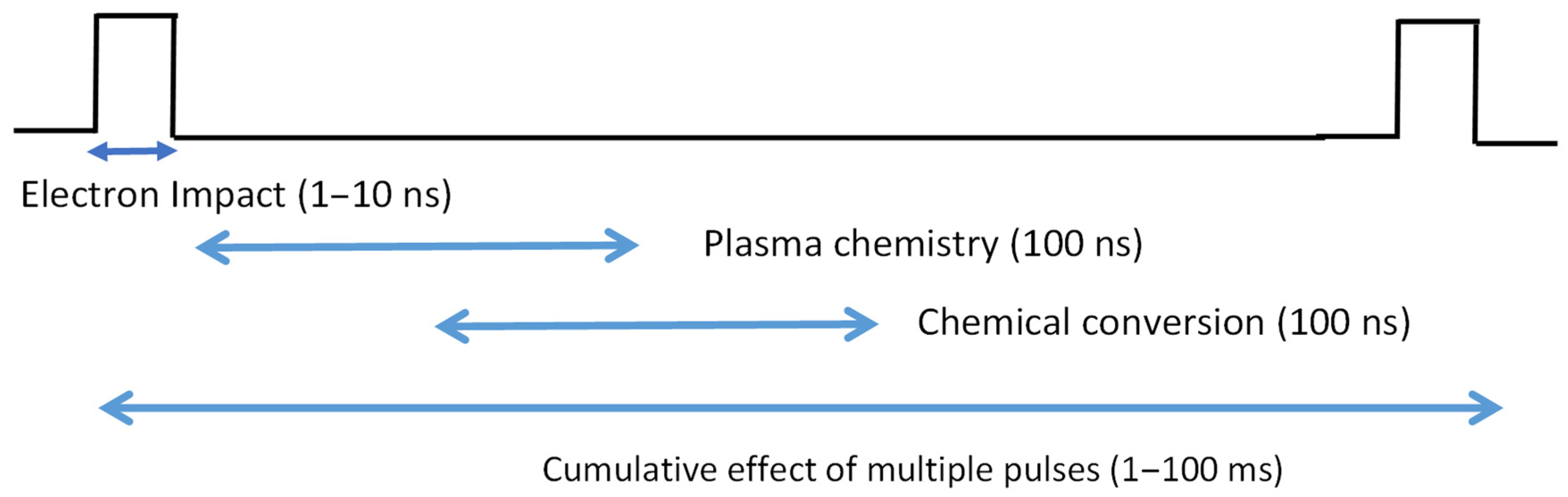
In streamer discharges the ionization front propagates at speeds several times higher than the local drift velocity and experience steep spatial gradients due to a rapid growth of ionization [23,24]. The energetic electrons in a streamer discharge at or near atmospheric pressure produce excited species and charged particles which are very reactive. The electrons see a spatially varying electric field due to the space charge created by the ionization front. This process typically is in the few nanosecond time scale. Following the electron impact process, several plasma-chemical reactions including recombination and neutral excited species reactions in the time frame of 100 ns produce the precursors for slower chemical conversion reactions. The final stage consists of the chemical conversion for the desired applications. The time frame for a repetitive pulsed nanosecond discharge for plasma-assisted combustion is shown Figure 1, where the final stage consists of the exothermic reactions initiated by the fuel and oxygen precursors.

The first step in the simulation process is to determine the radicals produced by the streamer discharge under the given conditions of the gas composition and the applied discharge voltage. Since the transport and rate coefficients are dependent on the gas composition, these quantities are determined from the solution of the Boltzmann equation with the appropriate electron impact cross-sections.

During the transient phase the heavy particles do not gain energy in the short period and the neutral gas and ions are at or near room temperature. Also, in the time scale of interest (few ns), the ions can be considered to be stationary compared to the lighter electrons. We have previously reported that at atmospheric pressure for molecular gases, the first-order model gives satisfactory results. The first-order fluid model for an attaching gas includes the following particle conservation equations [25,26,27,28]:

$${\displaystyle \frac{\partial n_e}{\partial t}}=-\nabla .{\mathsf{\Gamma }}_{\mathit{e}}\left(\mathrm{E}/\mathrm{N}\right)+n_e{\nu }_I\left(E/N\right)-n_e{\nu }_a\left(E/N\right)+S$$

(1)

$${\displaystyle \frac{\partial n_i}{\partial t}}=n_e{\nu }_I\left(E/N\right)+S$$

(2)

$${\displaystyle \frac{\partial n_n}{\partial t}}=n_e{\nu }_a\left(E/N\right)+S$$

(3)

where n_e, n_i and n_n are the electron, positive ion, and negative ion densities respectively, ν_I is the ionization frequency, and ν_a is the attachment frequency. The quantity S represents various ion/electron source or sink mechanisms such as photoionization, recombination, or remnant space charge in repetitive discharges. In the absence of a magnetic field, and assuming the velocity of the electrons is large compared to the slow species and the plasma is isothermal, the particle flux can be obtained from the momentum conservation equation and is given by [29,30]

$${\mathsf{\Gamma }}_{\mathit{e}}\left(\mathrm{E}/\mathrm{N}\right)=-n_e{\mu }_e(\mathrm{E}/\mathrm{N})\mathit{E}-D_e(\mathrm{E}/\mathrm{N})\nabla n_e$$

(4)

where µ_e is the electron mobility and D_e is electron diffusion coefficient, In the first-order fluid model, the transport and rate coefficients are determined by the local reduced electric field, E/N. In slowly varying electric field where the magnetic field can be neglected the electric field E is obtained from the solution of the Poisson equation [25,26].

$$\left\{\begin{array}{c}{𝛻}^2\mathit{\varnothing }=-q_e(n_i-n_e-n_n)/{ϵ}_o\\ E=-𝛻\varnothing \end{array}\right.$$

(5)

where q_e is the unsigned electron charge and ${ϵ}_o$ is the free space permittivity.

The discharge current can be calculated from the electron density and the drift velocity of electron in the gap from the following equation [25]:

$$I_g={\displaystyle \frac{q_e}{d}}∰-v_{ez}{n}_e{d}^{3}r$$

(6)

where d is the parallel-plate gap distance and $v_{ez}$ is the electron drift velocity in the axial direction. For all simulations presented in this article, d = 5 mm. The cumulative energy deposited in the gap which is used to determine the energy partitioning is obtained from the gap voltage, $V_g$, and the discharge current.

$$ℇ\left(t\right)={\int }_0^t{V}_g{\left(\tau \right)I}_g\left(\tau \right)d\tau$$

(7)

A generic electron impact excitation process is shown in Equation (8), where the rate coefficient $k_x$ is spatially and temporally dependent on the local electric field, E/N, obtained from the streamer simulation. At each time step, Equation (8) is used to calculate the generation of the excited species “x” from the spatial electron density distribution, which is a function of the local electric field, and the rate constants [31], as follows:

$${\displaystyle \frac{d{N}_x\left(r,z,t\right)}{dt}}=n_e(r,z,t)k_x(\mathrm{E}/\mathrm{N})M_x$$

(8)

where N_x is the excited species concentration, and $M_x$ and $k_x$ are the concentration of the neutral species and rate constant for the electron impact process respectively.

In the results presented, we bypass the avalanche phase of the streamer development by placing a neutral plasma at either electrode. A Gaussian-shaped plasma (equal number density of electrons and positive ions) is placed on one of the electrodes. The shape of the initial distribution is given as n_e(z, r) = 10¹⁸exp(−z²/0.001) * exp(−r²/0.001) m⁻³. This configuration produces a single streamer discharge whose properties are characterized in this study. The simulation is stopped when the streamer bridges the gap. The determination of spatial photoionization requires the cross-section data, which are not readily available for gas mixtures. To overcome this problem, the photoionization term “S” in Equations (1) and (2) is simulated by a very low-density spatially uniform neutral plasma. A constant background charge of 10¹¹ m⁻³ is added to simulate the photoionization. These assumptions have been widely studied and their impact on the generation and propagation of streamers is not critical for plasma generation for combustion [25,26,27,28].

The set of Equations (1)–(5) was solved numerically using the finite difference method. The model is two-dimensional with azimuthal symmetry. The Flux-Corrected Transport (FCT) method proposed by Boris and Book was used for the convective term of the electron density equation [32,33]. This method is particularly suitable for handling the steep density and field gradients encountered in streamer propagation. The details of the method as applied to streamers have been extensively reported [25,26,27,28]. The Poisson’s equation is solved for the electric potential by the Successive Over Relaxation (SOR) method [34]. This iterative method converges rapidly as there are only small perturbations in the space-charge density for the time steps used in the simulation. A detailed description of the numerical method and boundary conditions can be found in reference [35].

For combustion processes, the important precursors produced in the discharge are the dissociated products resulting from electron collision excitation to repulsive electron states. The important products include oxygen and hydrogen atoms and OH radicals. A subset of the reactions leading directly to dissociation is listed below [36,37,38,39].

$$e+O_2\underset{6.0\mathrm{e}\mathrm{V}}{\to }{O}_2{(A}^3{\Sigma }_u^{+})+e\to O{(}^{3}P)O{(}^{3}P)+e$$

(9)

$$e+O_2\underset{8.4\mathrm{e}\mathrm{V}}{\to }{O}_2\left(B^3{\Sigma }_u^{-}\right)+e\to O{(}^{3}P)+O{(}^{1}D)+e$$

(10)

$$e+H_2\underset{8.9\mathrm{e}\mathrm{V}}{\to }{H}_2\left(b^3{\Sigma }_u^{+}\right)+e\to H{(}^{1}S)+H{(}^{1}S)+e$$

(11)

$$e+H_2\underset{11.8\mathrm{e}\mathrm{V}}{\to }{H}_2\left({B\prime }^1{\Sigma }_u^{+}\right)+e\to H{(}^{1}S)+H{(}^{1}S)+e$$

(12)

$$e+H_{2}O\underset{9.13\mathrm{e}\mathrm{V}}{\to }H+OH$$

(13)

$$e+H_{2}O\underset{11.5\mathrm{e}\mathrm{V}}{\to }H+H+O$$

(14)

There are other pathways for the formation of H, O, and OH through the reaction of discharge-generated reactive species with neutrals, which are in the second time duration of afterglow plasma chemistry in the 100 ns time range shown in Figure 1. A significant fraction of the energy during the discharge phase goes into exciting the nitrogen molecular vibrational and electronic excited states, and some of these excited species can dissociate molecules. A partial list of H and O formation processes initiated by the excited nitrogen molecules produced in the discharge is shown below. This group of plasma-chemical reactions of excited radicals and neutrals consists of a total of 28 reactions, and the reactions rates can be found in reference [40].

$$N_2\left(B^3{\mathsf{\Pi }}_g\right)+O_2\underset{3\times {10}^{-10}\mathrm{c}{\mathrm{m}}^3/\mathrm{s}}{\to }{N}_2\left(\nu \right)+2O{(}^{3}P)$$

(15)

$$N_2\left(\mathrm{a}\mathrm{’}1\mathsf{\Sigma }\mathrm{u}\right)+H_2\underset{2.6\times {10}^{-10}\mathrm{c}{\mathrm{m}}^3/\mathrm{s}}{\to }{N}_2\left(\nu \right)+2H{(}^{1}S)$$

(16)

The dissociated products such as O, H, and OH undergo reactions with O₂ and H₂ during the combustion phase_. This leads to a set of chain reactions shown below [40,41,42].

$$H+O_2\to O+OH$$

(17)

$$O+H_2\to H+OH$$

(18)

$$OH+H_2\to H+H_{2}O$$

(19)

$$O+H_{2}O\to OH+OH$$

(20)

The exhaustive list of chemical conversion reactions which consists of 22 forward and 22 reverse reactions can be found in reference [40]. The chemical conversion code consists of coupled first-order nonlinear differential equations which are solved simultaneously. The reactions rates are dependent on the temperature and generally take the form of the Arrhenius equation. The hydrogen combustion mechanism has been studied extensively, and the reactions rates are well documented [40,41,42]. Since these reactions change the gas temperature, small time steps are required to calculate the change in temperature from the enthalpy of the reactants and products. These reactions are temperature-dependent and are either endothermic or exothermic. The final combustion product is H₂O and the reactions leading to H₂O formation are exothermic, resulting in an overall increase in temperature and the eventual ignition of the hydrogen/air mixture. These are relatively slow reactions compared to the discharge phase, which eventually forms water as a byproduct.

3. Results and Discussion

Most of the results presented here are for an applied step voltage of −25 kV and 25 kV across a 5 mm gap (186 Td) for cathode- and anode-directed streamers respectively. As mentioned earlier the avalanche phase of the discharge is not simulated, which typically takes a few nanoseconds. Instead, a Gaussian profile of the initial charge distribution is used to emulate the avalanche. The avalanche phase has minimal impact on radical generation which primarily takes place in the streamer phase, which has high electron densities. The gas composition is for hydrogen gas in air for an equivalence ratio of ϕ = 1, which is the ratio of hydrogen to the oxygen content in the gas that is required for complete stoichiometric combustion. When the initial charge is placed on the anode, the streamer that is formed propagates towards the cathode. 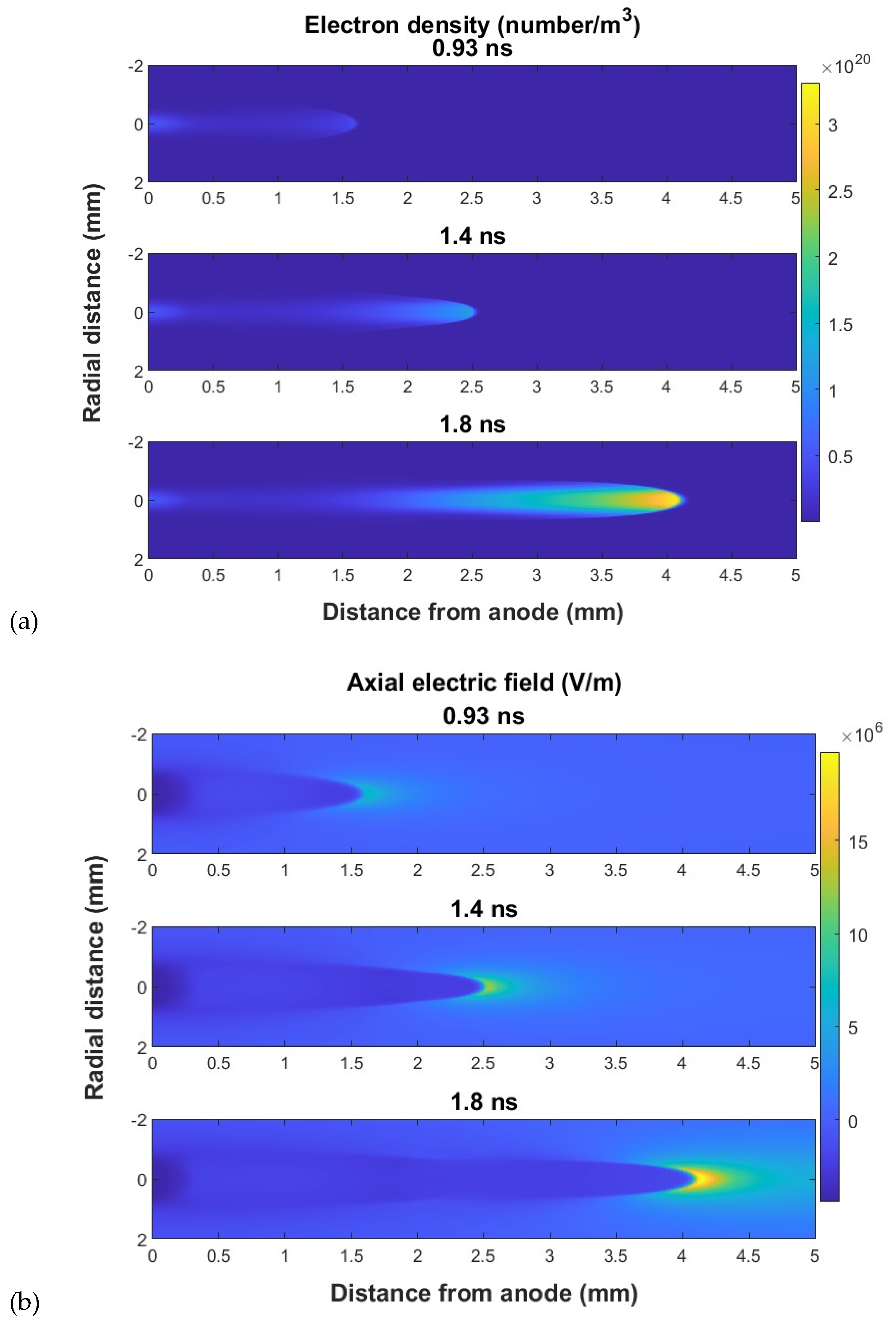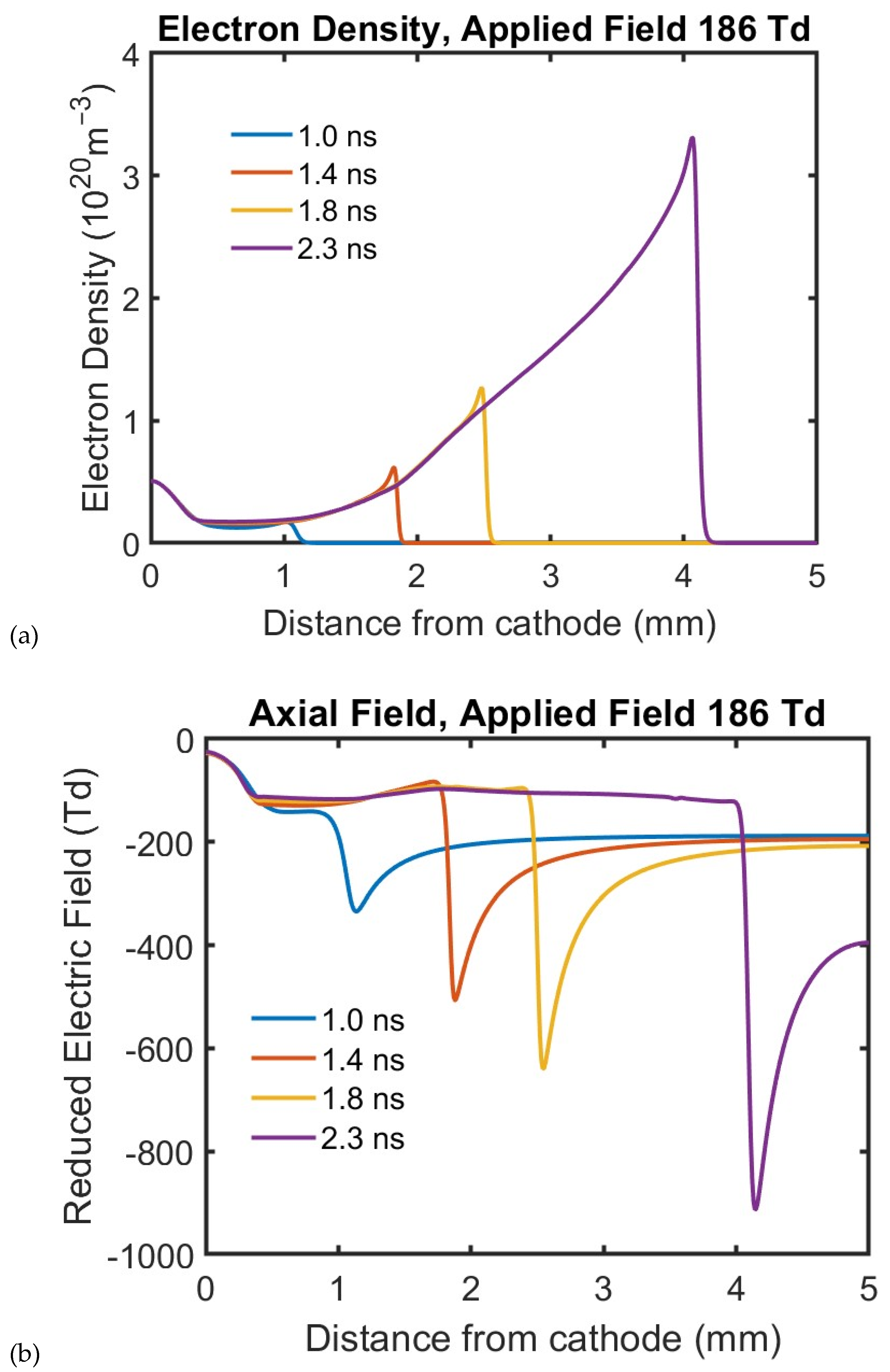Figure 2 shows the cross-sectional image of the electron density, and the electric field of a cathode-directed streamer for several instances in time as the streamer propagates. The density and the electric field show sharp gradients at the tip of the streamer. When the initial charge is placed on the cathode, an anode-directed streamer develops. The plots of the electron density and axial electric field along the axis of an anode-directed streamer are shown in Figure 3. These plots are typical of streamer propagation where the streamer tip shows high gradients for the electron density and electric field. In the streamer bulk, away from the tip, the electric field is nearly constant. The extent to which the field enhancement extends beyond the tip of the streamer depends on the radius of the tip. These plots illustrate the ionization fronts which are a characteristic of streamers.

The rate constants of electron impact processes (partial list: Equations (9)–(14)) depend on the reduced electric field (E/N) and gas composition. These rates are calculated from the electron impact cross-sections using the BOLSIG+ Boltzmann equation solver [43]. The electron impact cross-sections for the gases (N₂, O₂, H₂, and H₂O) under study are available at lxcat.net which is the most up to date database [44]. 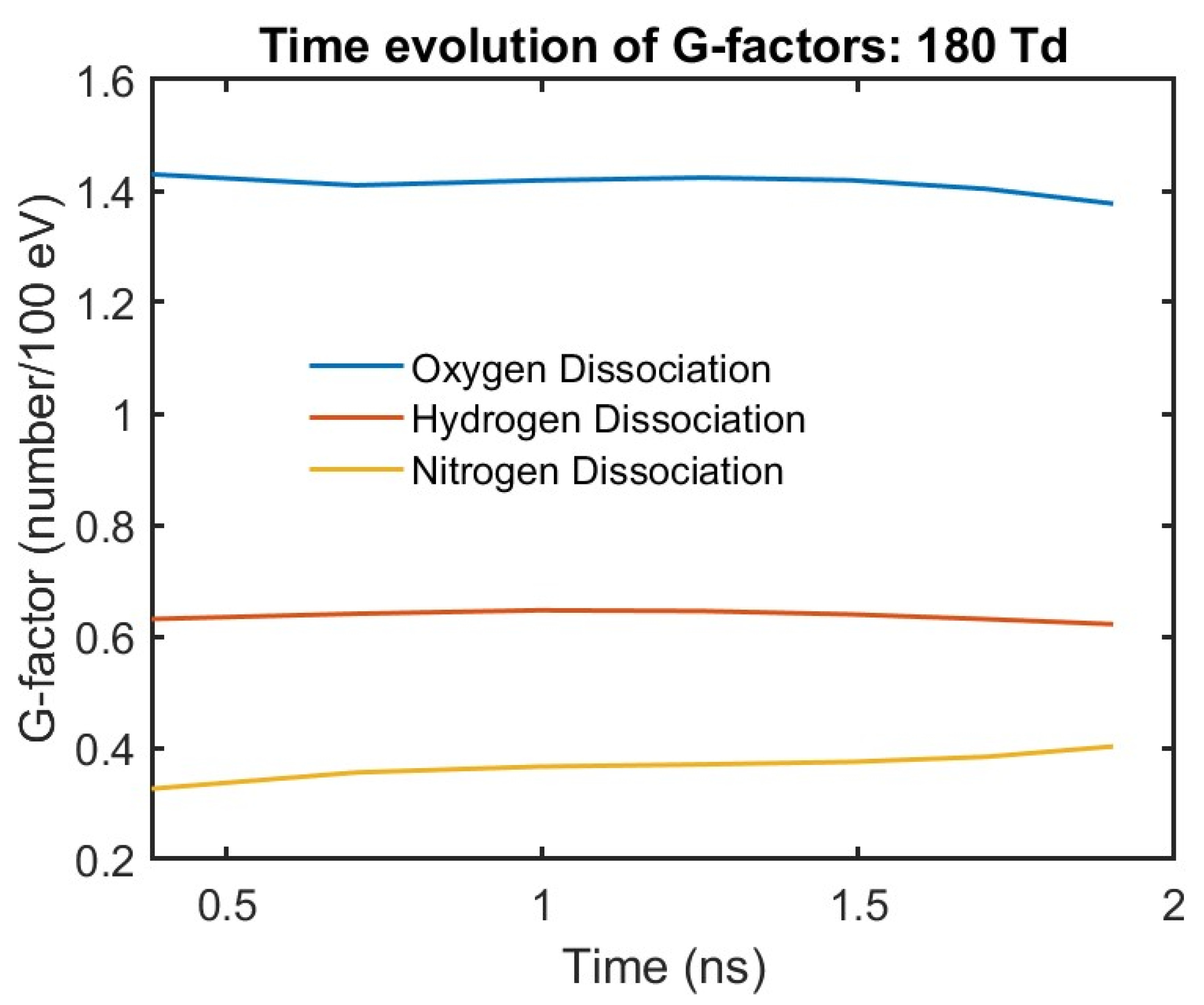All transport parameters and excitation rates as a function of the reduced electric field (E/N) are generated by BOLSIG+ for the gas composition of interest [43]. A useful measure of the efficiency of radical production is the G-factor, which is defined as the number of radicals produced for 100 eV of electrical power energy input to the discharge. Numerically the number of radicals produced in the discharge is calculated from Equation (8) and the energy input is obtained from Equation (7). This method of obtaining the G-factors gives an average estimate over the volume of the discharge. The electron impact G-factors of dissociation products as a function of time is shown Figure 4. The plot is shown starting from about 0.4 ns when the streamer is fully formed from the initial charge distribution. The G-factor of radicals is almost constant during the streamer propagation. This has also been observed in other fuel–air mixtures. Although the results shown here are for parallel-plate geometry, our preliminary results for point–plane and point–point electrode geometry show a similar trend. This may sound counter-intuitive since the electric field enhancement increases with time as shown in Figure 3b. However, at the high reduced electric field at the tip the rates for most electron impact processes start to flatten. Also, due to shielding, the bulk of the electrons are under a low electric field which favors low-threshold energy processes such as vibrational excitation. This is an important result that suggests that for a given gas composition and applied voltage, the energy partitioning is fixed, and the species’ density primarily depends on the energy deposited in the volume of gas. Therefore, the G-factor can be defined as a macroscopic property of the streamer which, once evaluated, can be used to determine the radical density from the electrical energy density of the discharge for chemical conversion simulations.

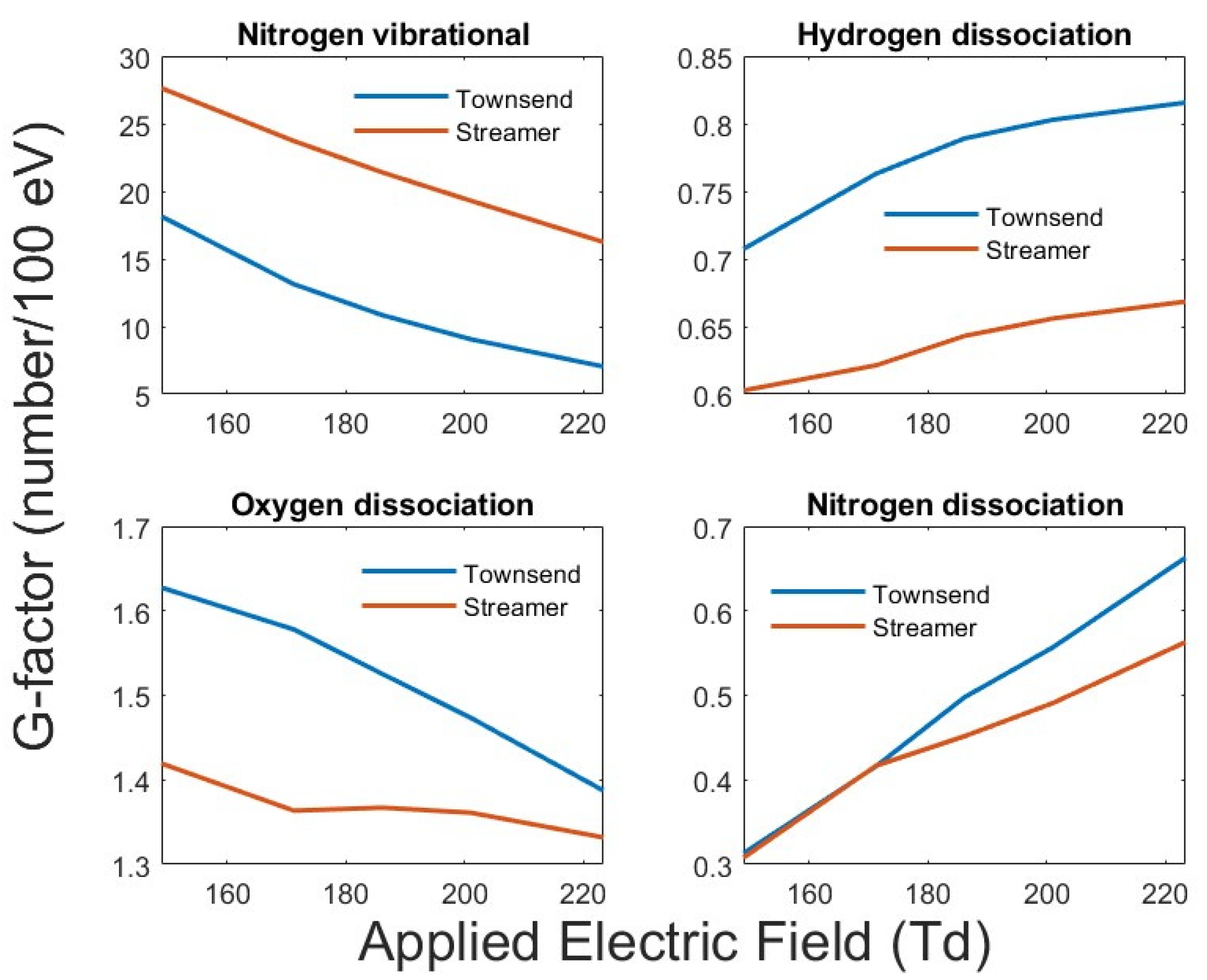
In most plasma-assisted combustion modeling in the literature, a zero-dimensional calculation is used to estimate the excited species density. This is similar to a Townsend-type discharge at low pressures where the spatial applied field does not change with time. At atmospheric pressure all discharges quicky turn into a streamer discharge from the Townsend-like avalanche phase. For comparison, the G-factors for several combustion-relevant species are shown in Figure 5 for a streamer and Townsend-type (the space-charge field is not included in the applied field) discharge for different species as a function of the applied field. For comparison, the G-factors for a Townsend-type discharge are also shown in the figure. A Townsend discharge has no space-charge field and is the same as a zero-dimensional estimation of radical production. The space charge modifies the applied field significantly as shown in Figure 2, and the radical production is spatially dependent on the local electric field. As shown in Figure 5, the zero-dimensional results can deviate significantly and overestimate the high-threshold energy radical production in the discharge phase. As the applied electric field is increased, the energy partitioning moves towards processes with higher threshold energy. As shown in the plot, the nitrogen vibrational and oxygen dissociation which have lower thresholds decrease with increasing E/N, whereas the hydrogen and nitrogen dissociations which have higher energy thresholds increase with increasing E/N.

The next set of simulations following the discharge phase were for solving the rate equation of the plasma chemistry reactions (partial list: Equations (15) and (16)) in the time scale of 100 ns. This was done for a zero-dimension time-dependent solution until a steady-state is reached. This involves the solution of a set of simultaneous first-order nonlinear differential equations for stiff problems. MATLAB R2022a has several functions for this, and we used the ode15s. This gave the final concentration of H, O, and OH radicals for the next phase of simulation.

To understand the role of electrical energy deposition which is responsible for creating the precursors necessary for combustion, we did combustion simulations for three different energy densities coupled to the discharge. The simulations were done for zero dimensions at constant pressure and the specific heats at constant pressure were used to determine the temperature. The combustion simulations were done by solving the rate equations discussed earlier for the combustion phase, which consist of 22 forward and 22 reverse reactions (partial list: Equations (17)–(20)). In practice, the electrical energy density coupled to the gas can be controlled with the applied voltage and the pulse duration of a nanosecond repetitive pulse excitation. The duration of the pulse was limited to 10 ns or less to prevent arcing. These simulations were done by initializing the densities of H and O obtained from the G-factors for different energy densities. There have been some reports of the temperature rising due to fast heating from the relaxation of excited electronic states [11]. Although a slower process, but faster than a chemical conversion reaction, in streamers we found that any significant temperature rise from the electrical energy input comes from V–T relaxation. As shown in Figure 4, at an applied field of 186 Td approximately 20% of the energy goes into nitrogen vibrational excitation. If all the vibrational (N₂, O₂ and H₂) excitations are added up it accounts for approximately 30% of the electrical energy input. Assuming a specific heat under constant pressure for the gas mixture to be 29.2 J mole⁻¹K⁻¹, for an energy density of 0.1 J cm⁻³, and if 30% of the energy goes into gas heating, we determine the temperature rise to be about 23 °C. This rise in temperature is taken into account but is not significant in determining the combustion characteristics.

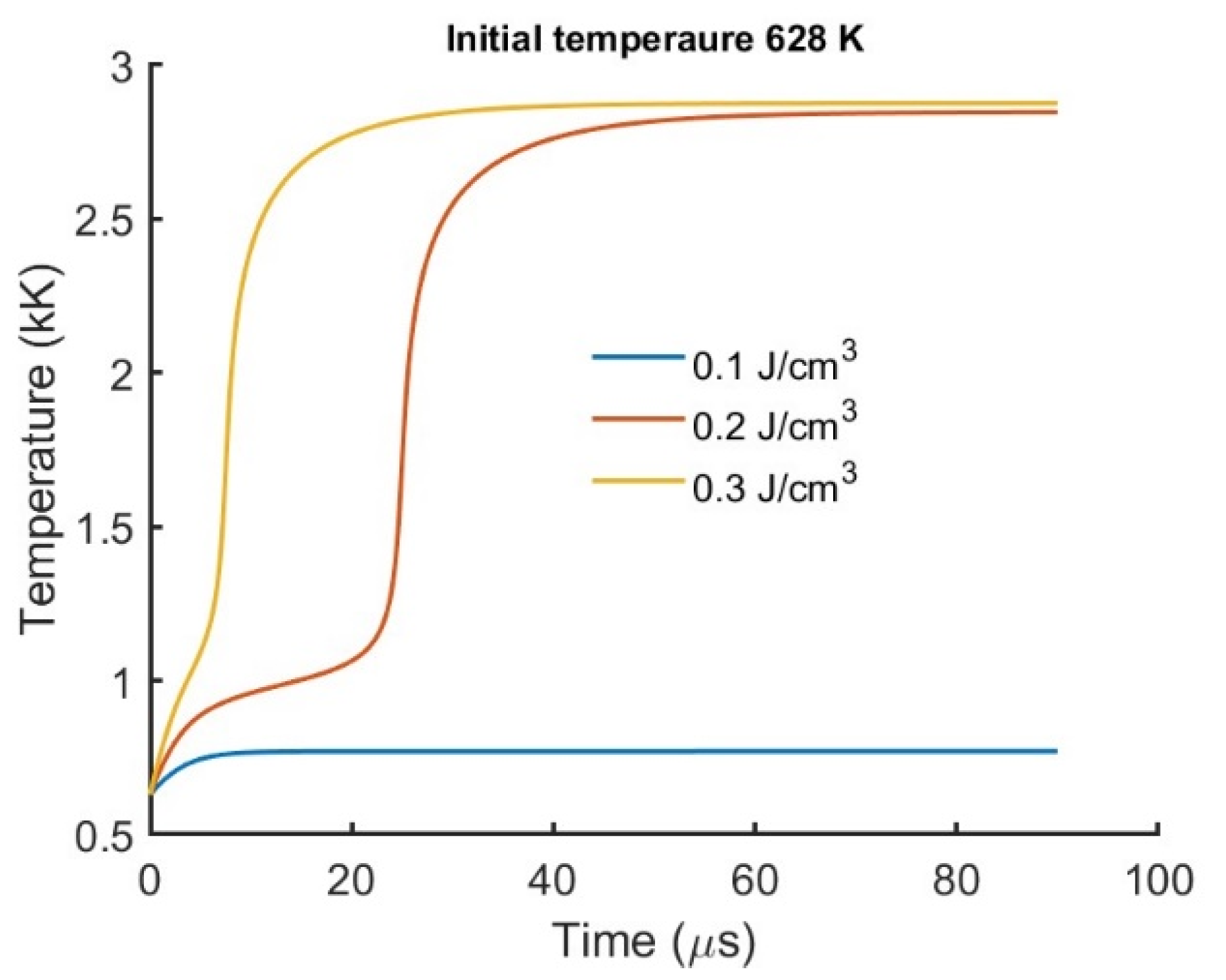
The results of the temperature rise as a function of time are shown in Figure 6. This was done for a starting temperature of 682 K, which is close to the gas temperature during the compression phase of internal combustion engine [15]. The plasma significantly reduces the ignition delay as shown in Figure 6. The higher the input energy density, the faster the ignition. 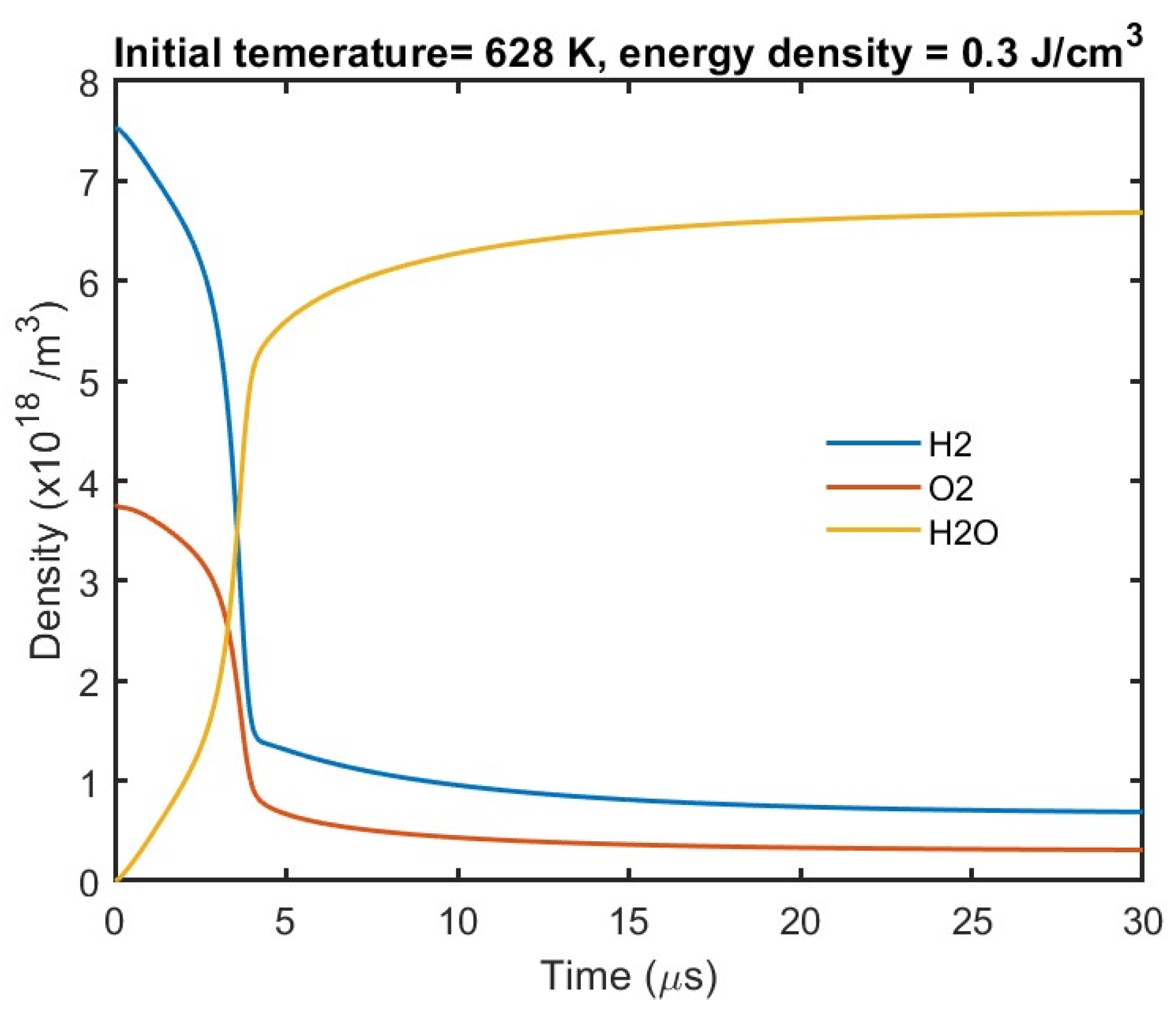The 0.2 J/cm³ and 0.3 J/cm³ energy input resulted in ignition in a few μs, but the 0.1 J/cm³ energy input did not proceed to ignition in the time range shown. The time dependance for an energy density of 0.3 J/cm³ of the reactants H₂ and O₂ and the product H₂O is shown in Figure 7. As expected, the time dependence of density follows the temperature rise shown in Figure 5.

Repetitive nanosecond pulses and dielectric barrier discharges have been studied for plasma-assisted combustion, and they have proven to be two of the most effective methods of coupling electrical energy into the combustion gas. In repetitive pulsed discharges the gas composition changes with time, which will change the electron energy distribution function. Therefore, the electron transport and rate coefficient will change, and the radical generation will be impacted. 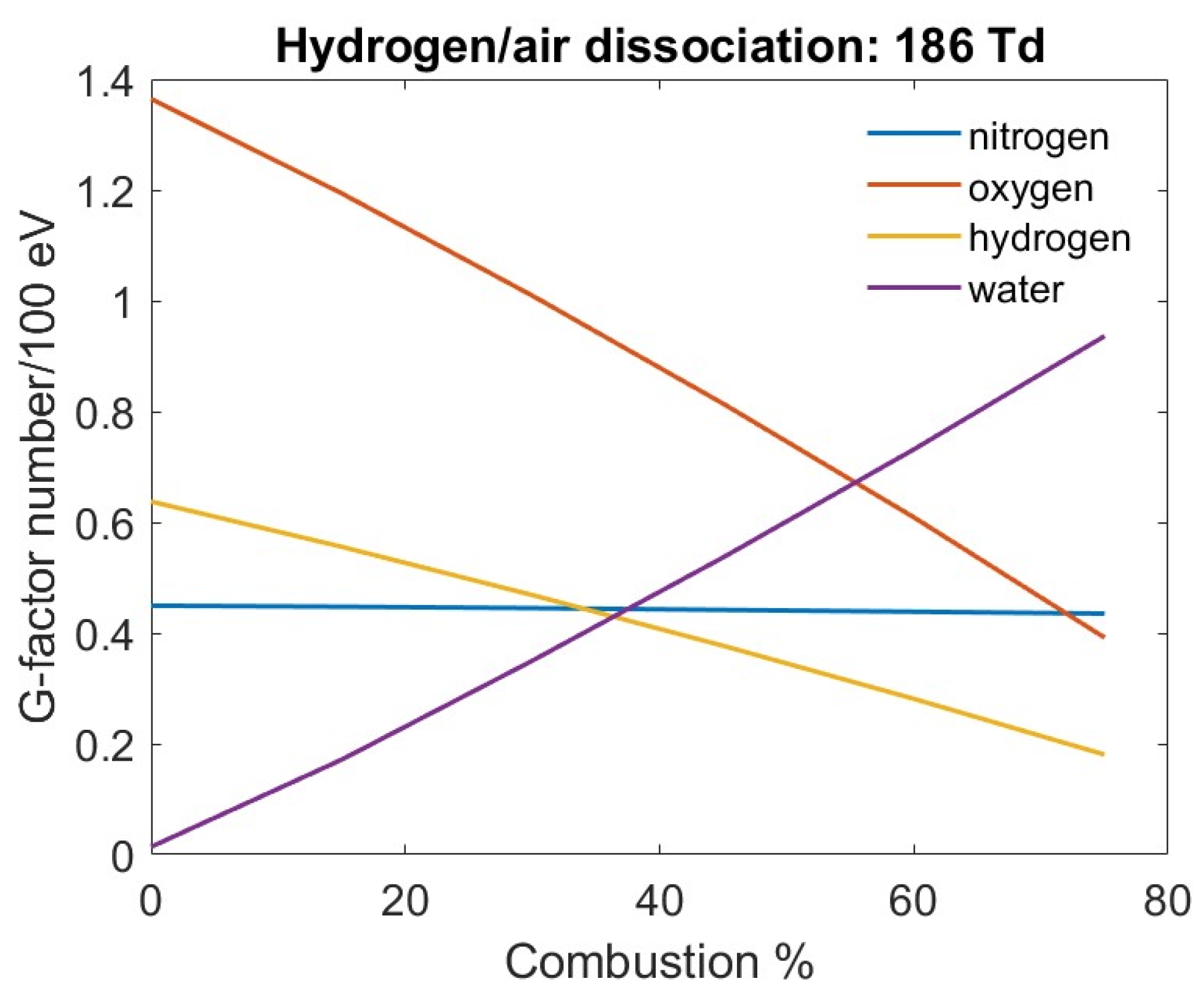Similarly, the micro-discharges in a dielectric barrier discharge can be characterized by a streamer discharge prior to the voltage collapse due to dielectric charging [35]. To correctly capture the changes as the combustion proceeds, the G-factors were calculated for partially combusted (burnt) gas compositions. Figure 8 shows the G-factors as a percentage of the completed combustion. This is determined by the fraction of H₂ remaining compared to the original concentration. Also, the burnt hydrogen is used to determine the water concentration. As the hydrogen and oxygen are depleted during combustion, the dissociation fraction also decreases. However, as the combustion proceeds, the water concentration increases and therefore the dissociation products associated with it also increase. Since the nitrogen concentration remains the same, its dissociation remains constant.

We studied the effect of the pulse repetition rate on the ignition characteristics. Figure 9 shows the onset of ignition for three different frequencies, with each pulse delivering an energy density of 0.01 J/cm³ at an applied reduced field of 186 Td. In these discharges the gas composition changes as the combustion proceeds. For these simulations, during each pulse, the G-factors used for calculating the radical densities were estimated for the composition at that instant in time from the data shown in Figure 8.

From the temperature plots (Figure 6 and Figure 9) as a function of time, as the temperature reaches about 1000 K, the combustion proceeds rapidly towards the final temperature. To reach a temperature of about 1000 K, the energy deposited is roughly about 0.3 J/cm³ for the frequencies shown in Figure 9. The slower rep rates take a proportionally longer time to get to this threshold energy density. This suggests that in the zero-dimensional case the ignition takes place when the energy deposited reaches a certain threshold. If flow is included this would give a different result as the repetition rate and residence time would determine the energy density coupled to a particular volume of gas.

4. Conclusions

The transient phase of pulsed nanosecond repetitive discharge at atmospheric pressure is best characterized by streamers. The ionization front of streamers has field enhancement, but the bulk of the streamer is shielded and has a low electric field. The gross properties are different from the zero-dimensional assumption of a uniform Townsend-type discharge. For predictive models, the discharge phase should be modelled as streamers to obtain better results. The energy density coupled to the gas is the most significant macro property of the discharge which determines the radicals produced by the discharge. The ignition characteristics are sensitive to the energy density. For a given applied field, the density of radicals produced per unit energy density input is fairly constant during the discharge phase. The energy density, which in turn depends on the pulse length, can be used to control the combustion characteristics. Therefore, an accurate estimation of the radicals produced in the discharge phase is important for predictive models. For repetitive discharges, the ignition time shows dependence on the total energy coupled to the gas during the ignition delay period.