Longitudinally Resolved Terahertz Radiation Characteristics Along Two-Color Filament in Air

Abstract

The evolution of the THz waveform generated from the two-color air filament was experimentally investigated by moving an iris along the plasma channel. By taking the differentiation of the measured THz waveforms, the local longitudinally resolved THz waves along a 54 mm-long filament were obtained. The local THz pulse underwent periodic phase shifts. A theoretical deduction indicates that the phase shifts are mainly caused by the dispersion in the plasma channel which plays a dominant role in the evolution of the local THz waveforms.

1. Introduction

In recent years, terahertz (THz) waves have attracted great attention because of their unique features, such as low photon energy, spectral fingerprints of variety of matters, and potential broad bandwidth. Thus, the THz wave has been widely used in biology, security screening, remote sensing, and communication [1,2]. However, long distance propagation of THz waves in the air is severely limited due to their strong absorption by water vapor. The THz radiation source based on a femtosecond laser filament could solve this problem [3].

However, the conversion efficiency from IR to THz from the fundamental wave (simplified as FW or single color) filament was extremely low, at ~10⁻¹⁰ [4]. In later studies, the conversion efficiency was increased by using the FW together with its second harmonic wave, SHW (also named as two-color) filamentation to generate intense THz pulses [5,6]. THz can be emitted from filaments remotely by manipulating the parameters of the laser pulse. Then, the long filament will unavoidably occur [7,8]. Focusing on the THz emission and the propagation along the long filament, several studies have been reported. In 2009, by using a heterodyne detector, which was sensitive to 0.1 THz with a bandwidth of 4 GHz, Liu et al. [9] presented the filament length dependence of the THz intensity. The observed variation in the THz intensity induced by the phase difference between the FW and SHW pulses along the laser propagation direction was proposed to be due to the dispersion and Gouy phase shift in the filament. An additional phase shift in the measured THz signal was observed around the beam focus, which is due to the Gouy phase [10]. At the same time, the THz waveform could be controlled by varying the length of the single-color filament and the CEP of the driving few-cycle laser pulses [11]. Furthermore, the THz polarization can be controlled by changing either the relative phase between the FW and the SH, and adjusting the two-color filament length, or by applying an external DC field along the single-color filament [12,13,14,15]. The spatio-temporal structure of the THz radiation can be controlled by manipulating the filament length and the initial phase difference between the two-color laser pulses [16]. Recently, Mi et al. [17] compared the relative phase between the transient current and the measured THz waveform and established a clear link between the phase dependence of plasma currents and terahertz radiation. Previous works have investigated the effect of laser properties on the terahertz radiation of the entire long filament. Nevertheless, the evolution of the longitudinally resolved THz waves along the filament has not been explored completely.

In this work, we experimentally investigated longitudinally resolved characteristics on the THz radiation by taking the differentiation of the measured THz waveforms generated from the long two-color filament. Compared with the terahertz waveform of the entire filament, which reflects the average effect of the entire filament on THz, the local terahertz waveform can more accurately reflect the effect of each part of the filament. The longitudinally resolved THz waves have periodic phase shifts along the filament. Further numerical simulation reveals that the relative phase varies in the plasma channel which leads to the rotation of the direction of the plasma current and the changes in the local THz waveform. The plasma dispersion in the relative phase between the two-color pulses made a major contribution to the variation in the local THz waveforms.

2. Methods

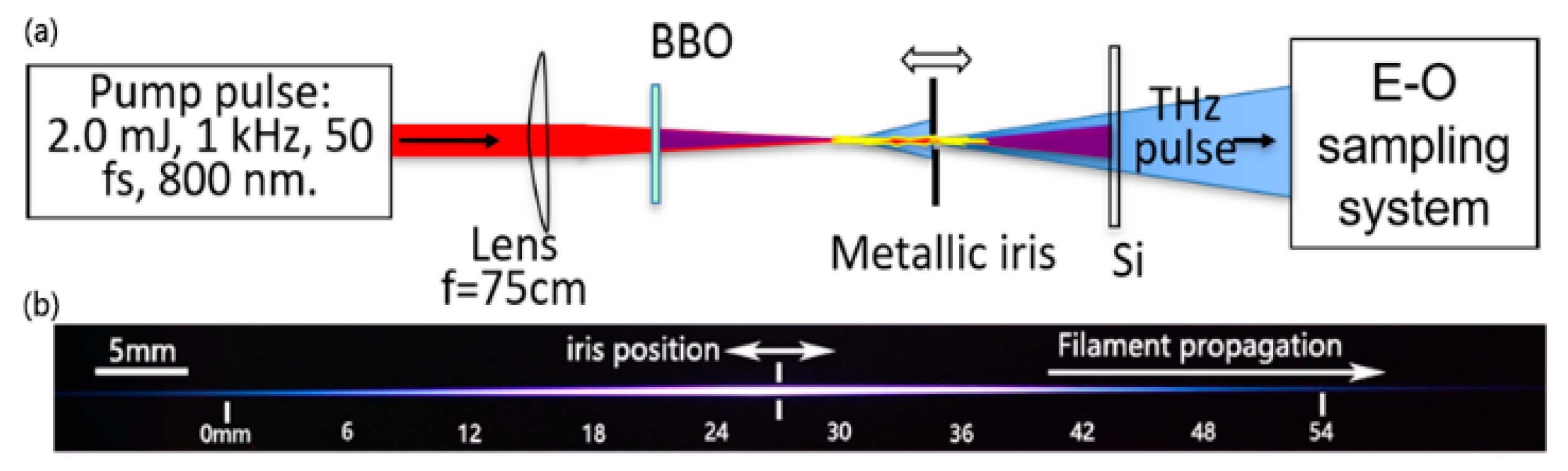
The experimental setup is illustrated in Figure 1a. A laser beam with a repetition rate of 1 kHz, wavelength centered at 800 nm, was focused by a 75 cm focal length lens. Pulse energy was 2.0 mJ, and pulse duration was 50 fs. A type-I barium borate (BBO) crystal was inserted after the lens to generate the second harmonic pulses centered at 400 nm. The BBO crystal was optimized for the most efficient THz generation when the extraordinary axis of the BBO was oriented 55° with respect to the polarization of the fundamental beam (α ≈ 55°) [18]. A filament with a length of 54 mm was created in air. The fluorescence image of the plasma channel was taken using a digital camera from the side, as shown in Figure 1b. The starting point of plasma channel was defined as “0” on the axis. Femtosecond laser pulses propagated from the left to the right in Figure 1b. In order to investigate the longitudinally resolved evolution of THz radiation along the filament, a metallic iris with 1.5 mm inner and 44 mm outer diameters aperture was inserted in the plasma channel (Figure 1a). The inner diameter of the iris ensured that the plasma formation was unchanged compared with the case without the iris, and the outer diameter was sufficiently large to block the THz signal from the filament before the iris. We confirmed that after the insertion of the iris, the radiation scattered from the plasma channel hitting the metallic iris did not generate an unwanted signal. As a result, the THz emitted from the filament segment before the iris was blocked, and the emitted THz from the filament segment (L) after the iris was collected in the forward direction through a Si filter (Figure 1a) by a pair of parabolic mirrors (2 inches diameter and with a 4 mm-diameter hole in its center, focal length f = 10 cm). According to the focal length f = 10 cm, the radius 25.4 cm of the parabolic mirrors and the filament length L = 5.4 cm, the THz radiation angle within approximate $\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n}{\displaystyle \frac{25.4}{10+5.4}}\approx 57°$ can be collected. However, the terahertz conical radiation angle is 2–10° [19]. The diameter of the parabolic mirrors is sufficiently large to collect the THz signal from the entire length of filament. Then, the THz wave was measured coherently through electric–optic sampling with a 1 mm-thick <110> oriented ZnTe crystal in the time domain. The local THz radiation from $∆L$ length plasma channel was obtained by subtracting the THz waveform of L length plasma channel from the THz waveform of the $L+∆L$ length plasma channel. By taking multiple measurements of the terahertz waveform under the same conditions, the error was calculated to be 9.8085e⁻¹¹ V. The amplitude of the local terahertz waveform signal obtained by subtracting two signals was approximately 3.2033e⁻¹⁰ V, which is 70% larger than the error.

3. Results and Discussions

The relative phase between the SHW and FW pulses when propagating in a plasma channel can be written as

$$\mathrm{\Delta }\phi =\mathrm{\Delta }{\phi }_0+\omega \left(n_{2\omega }-n_{\omega }\right)L/c+{\phi }_{Gouy}$$

(1)

The first term, $\mathrm{\Delta }{\phi }_0$, denotes the initial relative phase. The second term is the dispersion in the plasma channel, where $n_{\omega }$ and $n_{2\omega }$ are the refractive indexes of $\omega$ and $2\omega$ in the plasma, respectively. The refractive index of the pulse inside the plasma is $n_{plasma,\omega }\approx \sqrt{1-{\omega }_p^2/{\omega }^2}$, which depends on the density of the plasma. It is assumed that the filament plasma density has a Gaussian distribution, the filament is considered a combination of many short plasma channels, and the plasma density in each channel is uniform. The dispersion of the pulse during its propagation in the short channel is calculated and then summarized along the whole filament. It is only 4% less than the dispersion calculated by treating the entire filament as a homogeneous cylinder. Therefore, the filament can be assumed to be a homogeneous cylinder, the plasma density within the filament is uniform, and the refractive index is a constant. Compared with a linear refractive index, the nonlinear terms of a refractive index are extremely small and are disregarded. Even if the plasma is assumed to be a homogeneous cylinder and its density within the filament is uniform, there will still be an additional phase shift between FW and SHW. L is the effective length of plasma channel and c is the velocity of light. The third term comes from the contribution of the Gouy phase shift. The Gouy phase occurs predominantly within the Rayleigh range of the optical fields. At high laser intensities, the filamentation process completely disrupts the Gaussian optical focusing of the beams before they reach the beam waist. Thus, the Rayleigh length is no longer valid in the filament, which has to be modified according to the nonlinear propagation of the laser pulse. The modified Gouy shift is then calculated and verified by Equations (10) and (11) in Ref. [20]. The THz field can be expressed as [21]:

$$E_{THz}\left(r\right)\propto {\int }_{l_1}^{l_2}d{E}_{THz}^{local}={\int }_{l_1}^{l_2}A\mathrm{\left(}r\mathrm{\right)}sin\mathrm{[}\mathrm{\Delta }\phi \mathrm{(}r\mathrm{\left)}\mathrm{\right]}exp\mathrm{[}-i\mathrm{(}{k}_{THz}r-{\omega }_{THz}{\displaystyle \frac{r}{c}}-\mathrm{\Delta }\phi \mathrm{\left)}\mathrm{\right]}dr$$

(2)

where A is the local THz amplitude, $sin\mathrm{[}\mathrm{\Delta }\phi \mathrm{(}r\mathrm{\left)}\mathrm{\right]}$ provides a phase-dependent THz amplitude modulation along the filament direction r owing to the phase mismatch between two pulses. The last term is the phase variation due to the propagation effect in the far field, where $e^{i\mathrm{\Delta }\phi }$ is the initial phase term of the local THz radiation. From the expression of terahertz radiation, we know that the local terahertz radiation waveform is related to the initial terahertz phase $e^{i\mathrm{\Delta }\phi }$, i.e., the relative phase between two-color field.

In order to explore the influence of the relative phase of the two-color field on the local terahertz radiation waveform, two sets of experiments were performed. In the two sets of experiments, the distance from the BBO to the lens was changed and an additional phase was introduced in the relative phase. For both sets of experiments, the relative phases of the SHW and FW pulses can be expressed separately as:

$${\phi }_{Ex.1}={\phi }_0+\omega (n_{2\omega }-n_{\omega })L/c+{\phi }_{Gouy}$$

(3)

$${\phi }_{Ex.2}={\phi }_0+\omega (n_{2\omega }-n_{\omega })L/c+{\phi }_{Gouy}+\mathrm{\Delta }{\phi }_{BBO}$$

(4)

${\mathrm{\Delta }\phi }_{BBO}$ is the extra phase shift introduced by the different position of BBO crystal to the lens; it can be determined by a function of the terahertz signal versus the BBO-Lens distances. The amplitude of the measured THz signal as a function of BBO to lens distance is plotted in Figure 2. The amplitude of the THz signal was observed to oscillate in half a cycle of 34 mm. The distance between the BBO crystal and lens were arbitrarily chosen as 23.5 cm and 26.7 cm under two experimental conditions, which are marked as A and B in Figure 2, respectively. The phase shift ${\mathrm{\Delta }\phi }_{BBO}$ of two experimental conditions was about 1.06π. The conditions of the other points can also be chosen. And for two different conditions, the phase shift ${\mathrm{\Delta }\phi }_{BBO}$ will change accordingly.

To obtain the THz emission of different lengths along the filament in the far field, the iris was scanned from the tail end of the filament in a step length of 6 mm to the leading end. The THz electric field waveforms were recorded as shown in Figure 3a,d, respectively. To observe the longitudinally resolved evolution characteristics of the THz waveforms, the local THz waveforms were obtained by taking the differentiation of the measured THz signals from L and L + ∆L length plasma channels. The corresponding local THz waveforms at different positions along the plasma channel are shown in Figure 3b,e. The phase of the local THz waveforms is a phase between the envelope and carrier waves. One can clearly see that the local THz waveforms have several significant phase variations. For two conditions with different BBO–Lens distances (different initial phase), the position, and where the local waveforms undergo phase shift changes. Figure 3c,f (black dots) shows the phase obtained by a Fourier transform of the local THz waveforms measured in Figure 3b,e. It is clear that the opposite phase (crossing the phase “0”) leads to the markedly change in the longitudinally resolved THz waveforms. According to Equations (1) and (2), the phase of local terahertz waves at different positions of the filament is simulated. The simulated results at BBO–Lens distances of 23.5 cm and 26.7 cm were presented in Figure 3c,f (red square). The simulated phase shift was qualitatively consistent with the experimental results, which clearly confirms that the evolution of local THz waves is caused by the relative phase of the two-color pulses in the plasma channel. The relative phase shift including the dispersion and Gouy phase along the plasma channel leads to the rotation of the direction of the plasma current, resulting in the reshaping of the local THz waveforms. There are some small discrepancies between the experimental and simulated results, which is due to the weak signal from the short plasma channel as compared with that from the long plasma channel. However, the minimum signal of the local terahertz waveform is still 70% stronger than the background noise. Thus, it can be extracted from the noise. In the experiment, by changing the BBO-Lens distances from 23.5 cm to 26.7 cm, the obtained local terahertz phase and the simulated relative phase change still have good consistency (Figure 3f), which further validates that the origin of the relative phase $\phi$ on local terahertz waves.

In addition, the contribution of the dispersion and Gouy phase in the relative phase was simulated as shown in Figure 4a,b. The phase of the simulation results without the Gouy phase are shown as black dots. The results are mostly consistent with the results including the dispersion phase and the Gouy phase (red dots). Meanwhile, the phase of the simulation results with only the Gouy phase are shown in Figure 4c,d. The order of magnitude of the Gouy phase in the relative phase is negligible as compared with the phase of plasma dispersion, and there is no periodic structure. The result indicates that the plasma dispersion phase plays a dominant role in the variation in local terahertz waveforms. While the Gouy phase plays a negligible role for the THz from the two-color long filament.

4. Conclusions

In summary, we performed both experimental and theoretical investigations of the longitudinally resolved THz radiation from the two-color air filament. Both experimental results and simulation results indicate that the periodicity of the relative phase of a two-color pulse leads to the localized THz radiation experiencing a periodic phase shift. The Gouy phase plays a negligible role for THz generation from a two-color long filament. As for the applicability of this study, there is a huge issue with remote THz generation in a two-color scheme, caused by complications with synchronization due to the difference in refractive indexes and dispersion, etc. This study may not only help with understanding the generation mechanism of two-color filament-based THz radiation but could also benefit the THz control at a specific longitudinal position of plasma filament and its applications in longitudinally resolved THz spectroscopy and imaging.