Effects of Spiralling Trajectories on White Dwarf Spectra: Remarks on Different Calculations
Abstract
1. Introduction
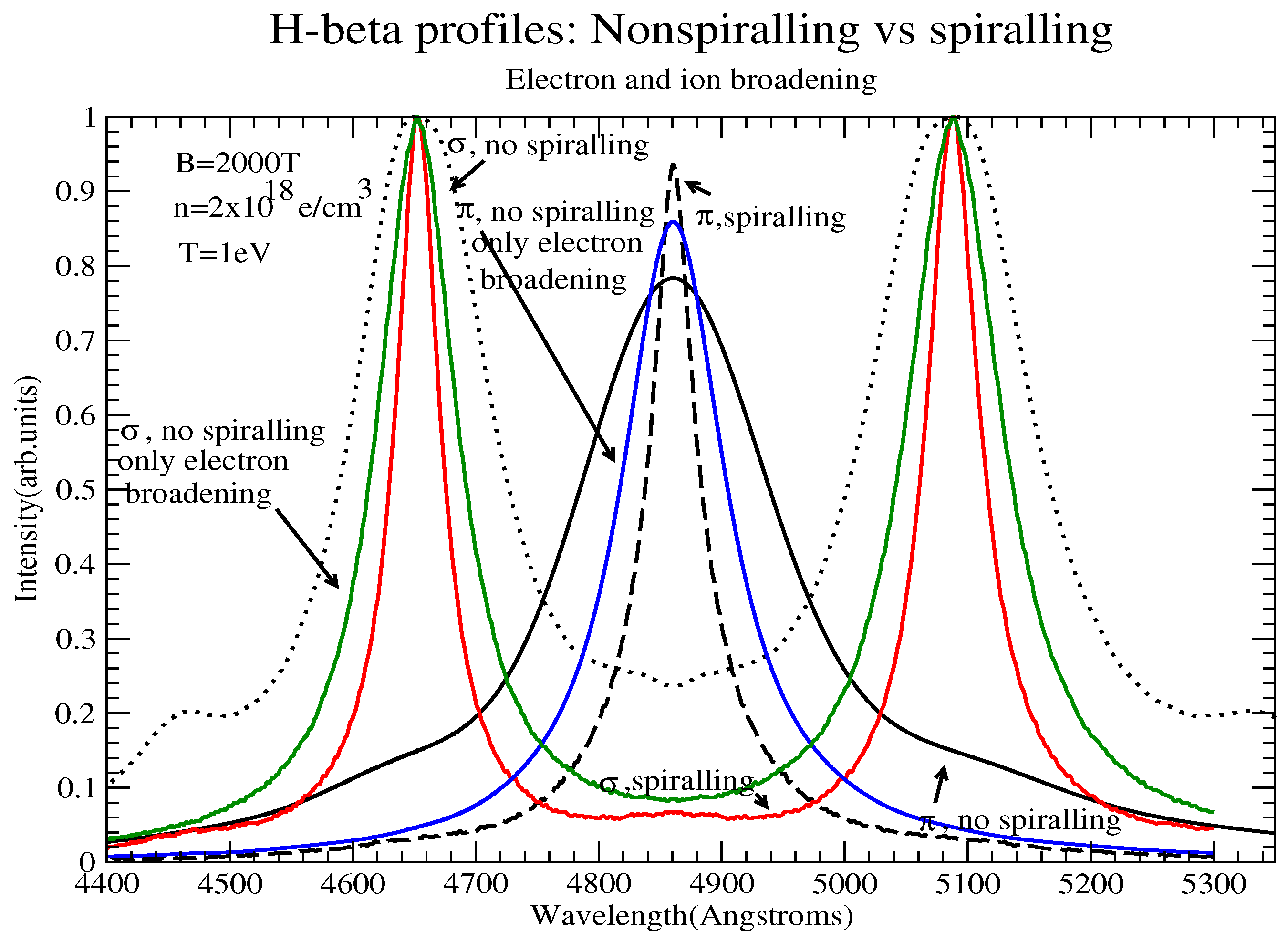
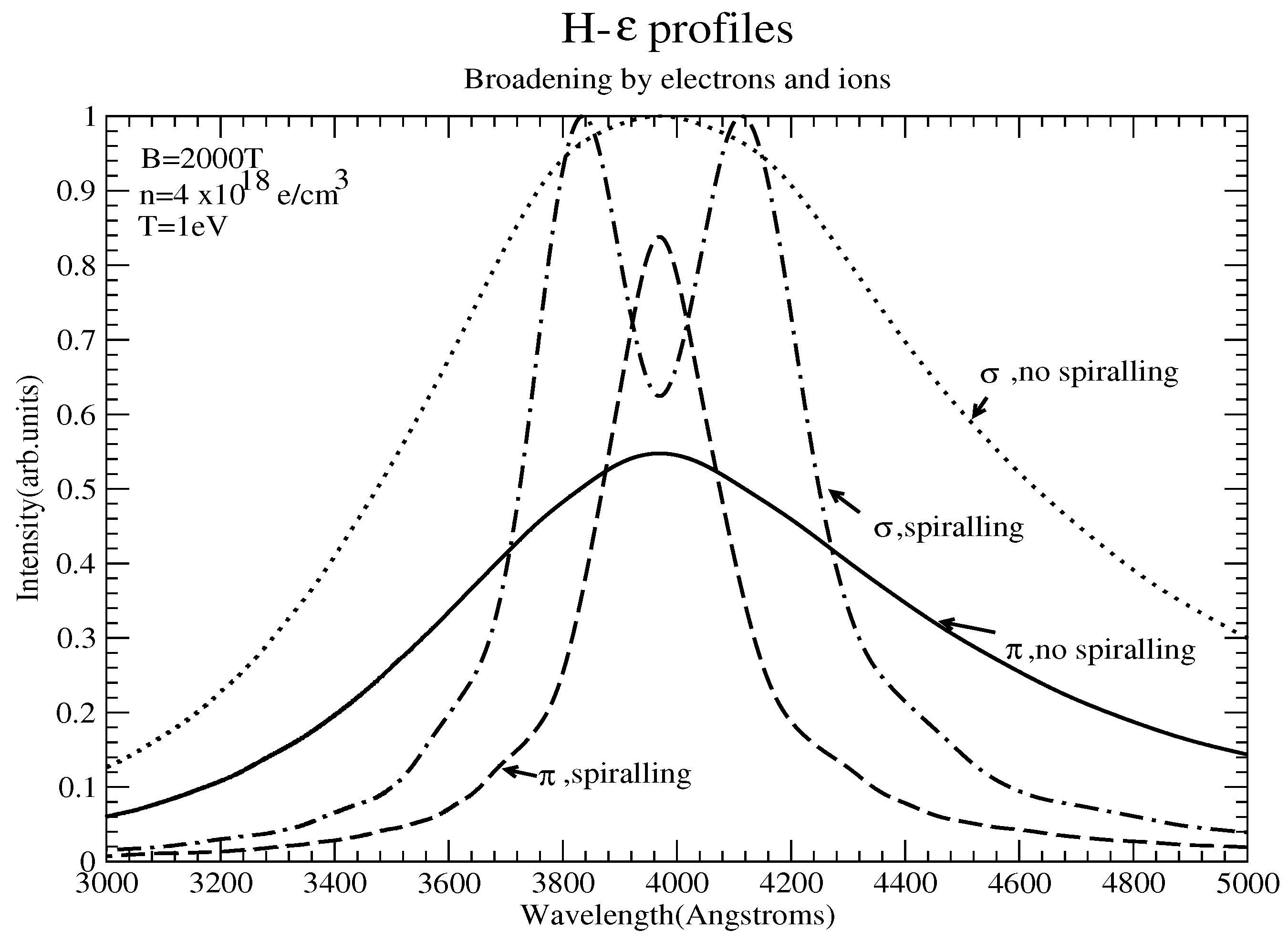
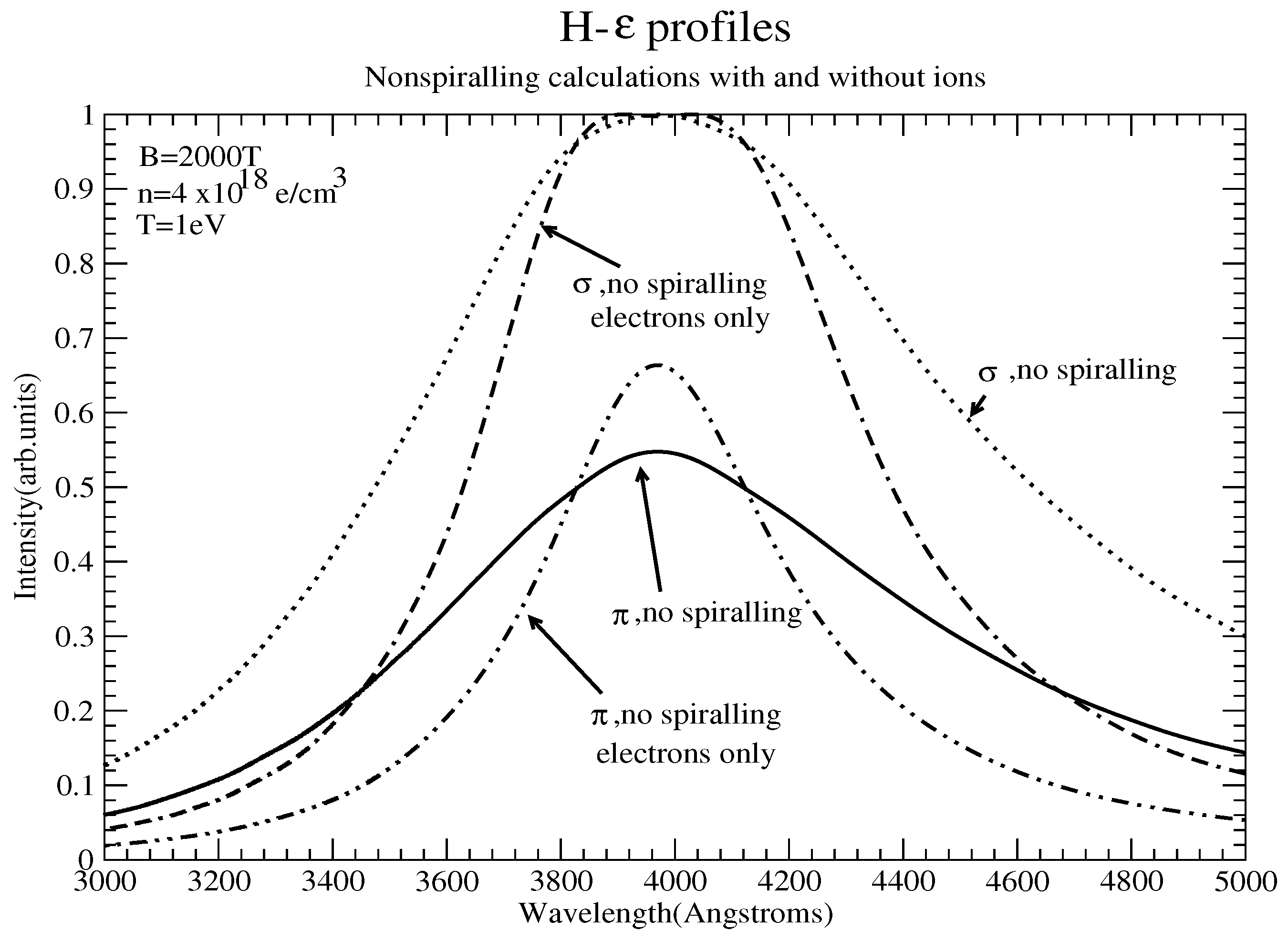
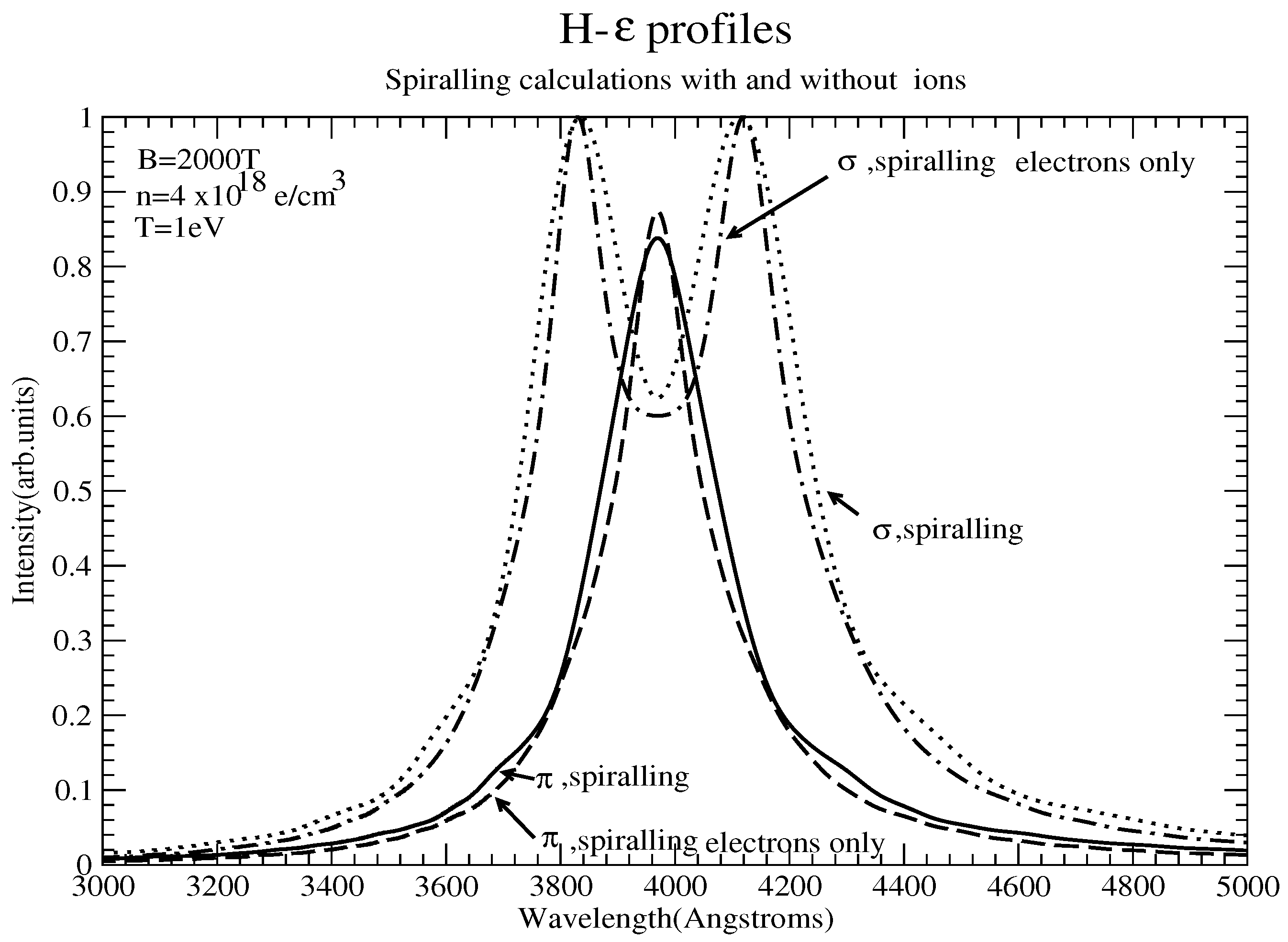
2. An Example
3. Analysis of Ref. [1]
4. Conclusions
- Ion broadening is significantly reduced due to linear Zeeman splitting, resulting in electron broadening dominating these lines. Furthermore, the nonadiabatic contribution is typically negligible; however, strong B effects may produce components with small energy separations from perturbing states, for which the nonadiabatic contribution may be quite important [5], an issue ignored in [1,2].
- Spiralling further reduces the ionic contribution, typically drastically.
Funding
Data Availability Statement
Conflicts of Interest
References
- Oks, E. Effect of Helical Trajectories of Electrons in Strongly Magnetized Plasmas on the Width of Hydrogen/Deuterium Spectral Lines: Analytical Results and Applications to White Dwarfs. Int. Rev. At. Mol. Phys. 2017, 8, 61–72. [Google Scholar]
- Oks, E. O4 -Symmetry-Based Non-Perturbative Analytical Calculations of the Effect of the Helical Trajectories of Electrons in Strongly Magnetized Plasmas on the Width of Hydrogen/Deuterium Spectral Lines. Symmetry 2024, 16, 1009. [Google Scholar] [CrossRef]
- Rosato, J.; Kieu, N.; Meireni, M.; Koubiti, M.; Marandet, Y.; Stamm, R.; Kovacević-Dojcinovic, J.; Dimitrijevic, M.S.; Popovic, L.C.; Simic, Z. A new analysis of spectral line shapes in white dwarf atmospheres. J. Phys. Conf. Ser. 2019, 1289, 012006–012008. [Google Scholar] [CrossRef]
- Rosato, J.; Kieu, N.; Hannachi, I.; Koubiti, M.; Marandet, Y.; Stamm, R.; Dimitrijevic, M.S.; Simic, Z. Stark-Zeeman Line Shape Modeling for Magnetic White Dwarf and Tokamak Edge. Atoms 2017, 5, 36. [Google Scholar] [CrossRef]
- Alexiou, S. Effects of Spiralling Trajectories on White Dwarf Spectra: High Rydberg States. Atoms 2023, 11, 141. [Google Scholar] [CrossRef]
- Alexiou, S. Line Shapes in a Magnetic Field: Trajectory Modifications I: Electrons. Atoms 2019, 7, 52. [Google Scholar] [CrossRef]
- Alexiou, S. Line Shapes in a Magnetic Field: Trajectory Modifictions II: Full Collision-Time Statistics. Atoms 2019, 7, 94. [Google Scholar] [CrossRef]
- Gomez, T.; Zammit, M.C.; Fontes, C.J.; White, J.R. A Quantum-mechanical Treatment of Electron Broadening in Strong Magnetic Fields. Astrophys. J. 2023, 951, 143. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alexiou, S. Effects of Spiralling Trajectories on White Dwarf Spectra: Remarks on Different Calculations. Plasma 2025, 8, 2. https://doi.org/10.3390/plasma8010002
Alexiou S. Effects of Spiralling Trajectories on White Dwarf Spectra: Remarks on Different Calculations. Plasma. 2025; 8(1):2. https://doi.org/10.3390/plasma8010002
Chicago/Turabian StyleAlexiou, Spiros. 2025. "Effects of Spiralling Trajectories on White Dwarf Spectra: Remarks on Different Calculations" Plasma 8, no. 1: 2. https://doi.org/10.3390/plasma8010002
APA StyleAlexiou, S. (2025). Effects of Spiralling Trajectories on White Dwarf Spectra: Remarks on Different Calculations. Plasma, 8(1), 2. https://doi.org/10.3390/plasma8010002





