Abstract
Experimental findings to contribute to the preliminary design of a metal foil pump for fuel separation in the Direct Internal Recycling loop of the DEMO fusion device are presented. In parametric studies on a small-scale superpermeation experiment with a microwave plasma source and two different metal foil materials, niobium Nb and vanadium V, a substantial increase in permeation with plasma power and with a decrease in pressure was observed. To ease operation in the typical fusion environment, in-situ heating procedures were developed to recover from impurity contamination. The temperature independence of plasma-driven permeation from 600 to 900 °C metal foil temperature was demonstrated. No proof of an isotopic effect for plasma-driven permeation of protium and deuterium could be found. The highest repeatable permeation flux achieved was 6.7 Pa∙m3/(m2∙s) or ~5.5 × 10−3 mol H/(m2∙s). The found compression ratios do safely allow the operation of the metal foil pump using ejector pumps as backing stages for the permeate. In a dedicated experimental setup, the operation of the plasma source in a strong magnetic field was tested. Parametric studies of pressure, power input, magnetic flux density, field gradient and field angle are presented.
1. Introduction
A conceptual design of a demonstration power plant for deuterium tritium, DT, magnetic confinement fusion (DEMO) is currently in development in Europe. One of the DEMO missions is the demonstration of tritium self-sufficiency [1]. Tritium is scarce on earth and a significant fraction of the tritium available for research will be consumed or decayed by the time DEMO is commissioned [2]. Tritium self-sufficiency in terms of the single-plant level is only achievable if the associated requirement on the blanket performance (tritium breeding ratio) is acceptably low. Tritium self-sufficiency in terms of global power plant rollout is only achievable if the preceding plant is able to produce sufficient fuel to start up the follower plant. Both self-sufficiency categories as well as the ease of licensing translate in the absolute need to operate a fusion power plant at the minimum tritium inventory.
The technical way to reduce inventory is a novel fuel cycle architecture based on the Direct Internal Recycling (DIR) concept [3]. It allows for a significant reduction of the tritium inventory by reducing average recycling times and, consequentially, the volume of the tritium plant. A key task of the DIR is the separation of a large fraction of unburnt fuel (deuterium and tritium) from the torus exhaust, thus bypassing the tritium plant [4]. The metal foil pump (MFP) is the prime candidate to fulfill this task and is currently in development at KIT.
The MFP can separate large fluxes of hydrogen and its isotopes from other gases in vacuum via an effect called superpermeation [5]. Its application in the MFP concept is explained in detail in [6]. Superpermeation through a metal foil occurs when there is a source of suprathermal hydrogen (for example, atomic hydrogen) on the upstream side and a surface barrier (ideally a non-metallic impurity monolayer) on the metal foil. The surface barrier inhibits the permeation of hydrogen molecules, but the energized atoms can pass through it with a very high permeation probability close to unity. When the adsorbed hydrogen atoms diffuse through the bulk, they eventually reach the downstream side, desorb and recombine to thermal molecules. Since the permeation probability of molecules is several orders of magnitude lower than that of atoms, backward permeation is suppressed and a net flux to the downstream side occurs. This flux can also be maintained against a pressure gradient, so that a pumping effect is provided. The two most promising superpermeation material candidates studied in literature are the group 5 metals Nb and V [7,8,9]. This is why these two (pure metals) have also been chosen as first materials for experimental work in the dedicated test facility HERMESplus (Hydrogen Experiment for Research on Metal foils and Superpermeability—Plasma Utilization Setup) at KIT. Our investigation focuses on the application of a linearly extended microwave plasma source [10,11], also called Plasmaline, to generate the suprathermal particles. Only hydrogen particles permeate through the foil so that the MFP is ideally suitable to separate hydrogen isotopes from the exhaust gas.
Due to its geometry, such a plasma source allows the combination of high power densities with large metal foil surfaces in a scalable way. For the application of this technology in a fusion power plant, several aspects have to be taken into account, some of which we address in this work. First of all, the magnitude of the permeation flux and its dependency on operation parameters has to be assessed and understood for scale-up. In Section 3, we present new results with substantially higher performances than those in our previous publication [12]. Second, due to its proximity to the torus, the MFP is also subjected to a strong magnetic field, which is dominated by the magnetic field lines of the poloidal field coils. In Section 3, we also show experimental results of the operation of the plasma source in strong magnetic fields (up to 250 mT) at different pressures and we introduce an approach for scaling to higher magnetic flux densities in Section 4.
In the current example design, we assume to fit an array of several cylindrical MFP modules into the rectangular DEMO pump duct [13]. Each module consists of a coaxial plasma source in the center and a surrounding, resistively heated metal foil with a thermal shield to the outside as is depicted in Figure 1. The permeate, pure hydrogenic species (namely the fuel deuterium and tritium, DT, with small amounts of protium H as an impurity), is recycled directly to the DEMO matter injection systems while the retentate, the non-permeated hydrogenic species, helium ash, impurities and plasma enhancement gases (radiative seeding), is routed to the tritium plant. In principle, the permeation flux can be controlled via the microwave power input as is shown in the results. We aim to achieve a DIR-ratio of 0.8, which is the ratio of permeated hydrogen to hydrogen entering the pump [2,14].
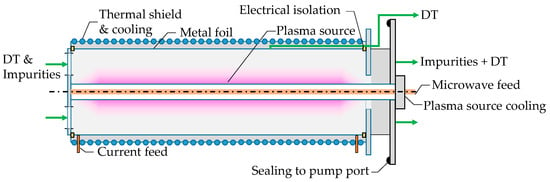
Figure 1.
Scheme of a preliminary MFP design.
2. Materials and Methods
Plasma-driven permeation (PDP) has been observed and described in the literature before [9,15,16]. Its characterization is based on a rather data-rich foundation when it comes to low pressures plasmas or hot metallic ribbon atomizers for the energization of hydrogen. However, to the authors’ current knowledge, there are no data available from other experimental work using higher-pressure (as high as up to 10–60 Pa in our application) RF plasmas as a source of suprathermal hydrogen. This is why we started with proof-of-principle experiments. Furthermore, parametric studies are required to determine the behavior and magnitude of PDP with varying pressures, plasma power and metal foil temperatures.
The experimental temperature range was chosen to be high enough to avoid damage to the foil caused by hydride formation and hydrogen embrittlement, and to reduce the hydrogen solubility (and thus the inventory) [17]. For temperatures lower than those shown, PDP fluxes decreased as the monolayer turned into an oxide. We expect that the requirements on the operation conditions in terms of sputtering yield and purity of the foil make it too challenging to sustain high PDP fluxes below 500 °C. Moreover, operation at higher temperatures improves the segregation of O to the surface, increasing sputter resistance. Finally, the heating by the chosen plasma source itself is already sufficient to make the membrane reach temperatures above 500 °C, which makes operation at this temperature range more energy-efficient than adding additional cooling necessary to establish low-temperature operation. Based on these aspects, we do not focus on low-temperature operation in this paper.
We first present performance results for the two hydrogen isotopes, protium and deuterium. In the torus exhaust, xenon, helium and argon will constitute notable impurity gases, which dilute the hydrogen gas in the MFP. Along the MFP axis, their molar fraction in the gas increases while hydrogen permeates through the foil. We investigate the effect of noble gas presence in the hydrogen plasma qualitatively via the evaluation of the relative change in PDP fluxes while seeding the plasma with Argon.
In [6], we introduce the central role of our experimental setup, HERMESplus, illustrated in Figure 2a,b, in the development of a MFP. It is equipped with a linearly extended surface wave sustained microwave plasma source at the center [10,11,18] and a 0.1 mm thin cylindrical 30 cm2 metal foil at a ~100 mm distance from the plasma source. In rectangular waveguides, a microwave of 2.45 GHz, produced by two magnetrons, is delivered to a coaxial line at the center of the plasma vessel. The inner conductor made from copper is surrounded by a dielectric tube. It is transmissive to microwaves, thus allowing the microwaves to enter the vacuum, where plasma can be ignited. This design of plasma source exhibits good scalability. HERMESplus is able to accommodate foils of different materials for comparison. A gas flow (H, D or Ar) can be admitted via calibrated mass flow controllers. The upstream chamber is continuously evacuated by a DN 100 TPU 180 H turbomolecular pump produced by Pfeiffer in Asslar, Germany and two Ecodry 25 plus roots pumps produced by Leybold in Cologne, Germany. The pumping of hydrogen can also occur through the metal foil and the downstream pump duct. The upstream pressure is continuously monitored by hot and cold cathode gauges in the low pressure regime and by two capacitance manometers (133 Pa and 1333 Pa upper range) in the operational pressure regime (~20 Pa). For the presented results, we use measurements of the capacitance manometer CM 1 by Leybold (Cologne, Germany), which is consistently in reasonable agreement with a MKS Instruments (Andover, MA, USA) 690A Baratron. With a continuous feed in operation, we regulate the pressure via a hand valve, which restricts upstream pumping. We control the metal foil temperature by manually adjusting the power input for resistive heating. The foil can also be electrically biased against the grounded vessel using the resistive heating current leads and an external power supply. The metal foil temperature is measured using a METIS M322 two-color pyrometer (500–1800 °C) produced by Sensortherm (Steinbach, Germany), which targets the bottom of the foil through a quartz window from the top of the downstream channel. The temperature variation along the axis of the foil is experimentally probed by pointing the pyrometer at the foil through one of the main vessel windows. Observed temperature differences along the foil axis are found to reduce towards lower foil temperatures. The measured difference is ~5 K at 900 °C, which is in the order of magnitude of the pyrometer’s measurement uncertainty.
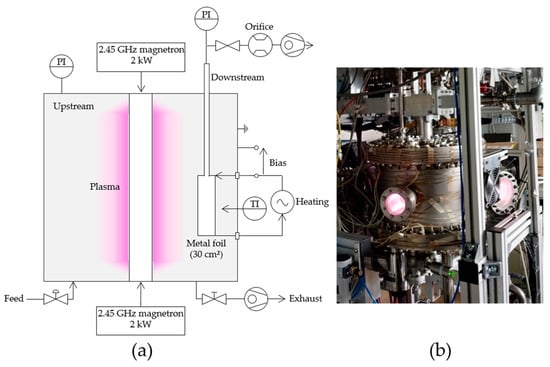
Figure 2.
Scheme (a) and photo (b) of the HERMESplus experimental setup (not in scale) with a vessel diameter of 0.3 m and a height of 0.3 m.
The downstream chamber starts at the rear side of the foil and ends at the inlet of the downstream turbomolecular pump, a DN63 HiPace80 produced by Pfeiffer (Asslar, Germany). To run compression experiments, we can close off the downstream chamber with a gate valve. In regular permeation experiments, the downstream chamber is evacuated through a precision-drilled orifice of 4.3 mm diameter and 2.1 mm length. A permeation flow is obtained via the multiplication of the downstream pressure by the effective pumping speed of the system, Seff, which is constituted by the pumping speed of the turbomolecular pump for the respective gas species (H or D), Sp,i, and the conductance through the orifice, according to
where dori is the orifice’s diameter, R is the universal gas constant, Td is the downstream temperature and Mi is the mass of the gas species. Through knowledge of the orifice’s dimensions, the gas species and the downstream pressure, the flow regime at the inlet of the orifice can be determined, to read a transmission probability, η, for the orifice from from [19] and Figure 8 therein. The downstream pressure is measured via a hot cathode gauge (A micro-ion transducer of the 355 series produced by MKS Instruments in Andover, USA) at low pressures and via three Baratron capacitance manometers (type 690A by MKS Instruments, Andover, MA, USA) at higher pressures. A gas correction factor for the measurement of the hot cathode is introduced, which puts it in line with the Baratron measurements above 1 Pa, both of which are in reasonable agreement within their individual uncertainty bars. During all experiments, the laboratory is air-conditioned, which accounts for a steady downstream chamber temperature.
In the DEMO pump duct, the MFP is subjected to a strong external magnetic field during operation. The total magnetic flux density is composed of the radial, the axial and the toroidal field component. While the first two are relatively high in value and gradient, the last is negligible in the volume not encompassed by the toroidal field coils. In the pump duct space, the absolute magnetic flux density reaches values of up to 1.2 T, radially and axially decreasing to 0.3 T, as shown in Figure 3a. The angle between Bz and Bx is displayed for the MFP location in ° in Figure 3b. Depending on the magnitude, gradient and orientation of the magnetic field, we expect that this magnetic field affects the operation of the MFP plasma. The ratio of the gyro-frequency to the collision frequency, also called the Hall parameter, is an easily obtained parameter for a first assessment of the severity of the magnetization of the plasma. We calculate this ratio to be 15,100 for electrons and 1.95 for D2+ ions in the MFP, corresponding to the largest given magnetic flux density (1.2 T) and the lowest pressure (1 Pa) in the MFP. For details and basic assumptions of the procedure behind such a calculation, the reader is referred to [20]. Hence, we can consider the electrons to be well magnetized over the entire range of the magnetic flux density in the pump cask and the pressure range during operation, giving rise to distortions due to anisotropic charge mobility. Under the assumed conditions, ions are only marginally magnetized. The description of particle movement in such a non-thermal, weakly ionized magnetized plasma is quite complicated and modeling is challenging and computationally expensive. This is especially true when we superimpose a gas flow, strong field gradients and differentiate for each MFP module position inside of the MFP cask. A contemplation of all those aspects would be unfeasible and not provide the desired certainty, which is why we relegate it to a dedicated experiment, which is to take place in the future. We note that, due to the complexity of the described problem, experimental investigation is of paramount importance to back any conclusion drawn from simulations.
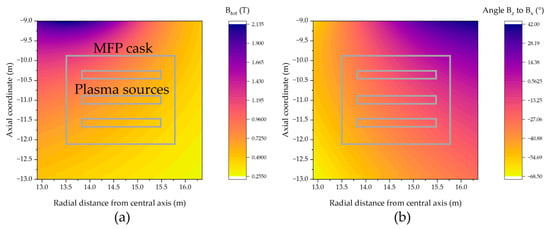
Figure 3.
Total magnetic flux density in DEMO pump duct during start of flat-top in (a) and angle between Bz and Bx in (b).
In a first approach to investigate the operation of the plasma source in a magnetic field, we use an available experimental setup, which allows for the production of operational aspects close to those in the environment in DEMO. Our investigation incorporates the assessment of the ignitability of the Plasmaline in a magnetic field, parametric studies of changes in flux density, pressure and power input and an analysis of the heat load on the plasma source itself. The FLIPS (Flexible Linear Plasma experiment Stuttgart) setup consists of a single-feed coaxial Plasmaline of 0.6 m length (up to 6 kW at 2.45 GHz) in the center of a cylindrical vacuum vessel, which is of 1170 mm length and 510 mm diameter. Along its axis, eight water-cooled copper coils are installed to produce a purely axial magnetic field. We measured the magnetic flux density with two Hall probes (A Koshava 5 probe, produced by Wuntronic in Munich, Germany and a Gaussmeter Model 425 produced by Lakeshore Cryotronics Inc. in Westerville, OH, USA) to be a homogeneous 250 mT inside the whole vessel.
The vessel features several windows and flanges for the installation of diagnostics. Those consist of optical emission spectroscopy (Compact spectrometer Jaz from Ocean Optics in Ostfildern, Germany) for the analysis of the characteristic plasma emission, infrared camera (885 model produced by Testo in Titisee-Neustadt, Germany) in front of an IR-transparent KBr window for the analysis of the plasma source dielectric tube’s temperature and optical cameras for the evaluation of the changes in plasma shape and ignitability with magnetic field. As shown in Figure 4a, we can install the Plasmaline in two orientations: parallel and perpendicular to the magnetic field. The two coils at the end of the vessel can be powered separately to achieve gradient fields along the axis of the cylindrical vessel. Both protium and deuterium can be admitted to the chamber using 1179 model mass flow controllers from MKS Instruments, Andover, USA. In all of the experiments, we feed up to 200 sccm of hydrogen and control the pressure with a 612 series butterfly valve (made by VAT group AG in Haag, Switzerland) in the exhaust pipe. Downstream the valve, an ATP 400 turbomolecular pump by Alcatel (produced in Annecy, France) and a vacuum rotary vane pump (made by Pfeiffer in Asslar, Germany) are installed. The pressure is measured using an ASD 1004 gauge made by Alcatel (Annecy, France) and a Vacuum CMR 363 gauge produced by Pfeiffer (Asslar, Germany) for the low pressures up to 1 and 11 mbar, respectively, and a Vacuum PKR 251 gauge produced by Pfeiffer (Asslar, Germany) for the full range. Figure 4b shows an image of the facility.
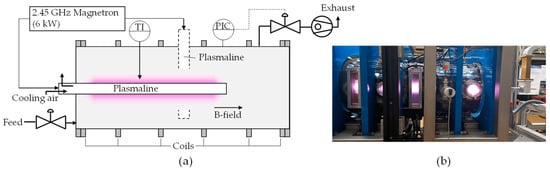
Figure 4.
Scheme (a) and photograph (b) of the FLIPS experimental setup (not in scale) with a vessel diameter of 0.51 m and a length of 1.17 m.
3. Results
In the following, we describe experimental findings obtained concerning the investigation of plasma-driven permeation and the operation of the plasma source in a magnetic field.
3.1. Plasma-Driven Permeation Experiments
This work features experiments carried out in HERMESplus via either purely gas-driven permeation (GDP), for which a pressure gradient is required, or PDP, when the plasma source is switched on. Figure 5 illustrates an example of the experimental procedure, showing the reading of the downstream hot cathode gauge. Initially, the metal foil was conditioned via 1 h pre-heating at 1050 °C to account for equal surface conditions at the start of each experiment. At t = 65 min, a flow of 35 sccm H2 was admitted to the upstream chamber. To remove impurities, it is continuously evacuated and the valve regulated so that a pressure of 20 Pa is sustained. Subsequent to hydrogen admission upstream, permeation commences and downstream pressure rises. At t ≈ 75 min, GDP is measured upon reaching steady-state and plasma is switched on, yielding an initial spike in pressure (PDP peak). After 45 min, we switch off the plasma and measur another GDP value.
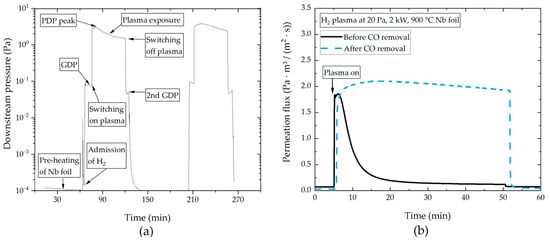
Figure 5.
Downstream pressure evolution during an exemplary experiment in (a), where GDP stands for gas-driven permeation and PDP for plasma-driven permeation; and comparison of PDP flux during plasma before and after the de-carbonization of a niobium foil in (b).
With time of plasma exposure, Figure 5a shows an initial decrease in downstream pressure compared to the peak value, i.e., a reduction in permeation. Later, X-ray diffraction (XRD) and energy-dispersive X-ray spectroscopy (EDX) surface analyses of in-vessel witnesses and plasma source components point towards a contamination of the plasma-facing surfaces with aluminum and magnesium. At the ends of the plasma column, the dielectric was encased by in-vacuum microwave conductors made from an AlMg alloy. In the tight annular gap between those components, arcs formed, which sputtered part of the outer conductor, contaminating the plasma with aluminum, potentially responsible for the degradation due to the inhibition of hydrogen transport at the inter-material boundary, which corresponds to an energy well of the hydrogen-metal system. Following this experimental finding, we modified the design to place the outer conductor inside the dielectric and remove it from vacuum. The results shown in the parametric studies were obtained with the old plasma source design but the pre-heating treatment for de-carbonization allowed for comparable foil surface conditions and repeatability, nonetheless. In these cases, we used the PDP peak value for the flux evaluation. The uncertainties in the flux measurements introduced by the gauges and measurement method were negligible in comparison to those in the variable foil surface condition.
By adding a mass spectrometer, we also detected a superimposed continuous deposition of carbon on the foil. Carbon has a substantial negative effect on plasma-driven permeation due to the obstruction of the oxygen monolayer replenishment, which is required for high steady-state fluxes. For the in situ healing of such contamination, we performed high-temperature de-carbonization treatments (at ~1400 °C) that made the foil sputter-resistant by improving the replenishment rate of oxygen to the surface from the bulk [9] and, thus, significantly improving the stability of the permeation flux during plasma exposure, as can be seen in Figure 5b. It shows a comparison of the permeation flux during plasma before and after the de-carbonization treatment. While the peak of the flux has a comparable height, the flux magnitude remains at the peak level after the treatment.
Figure 6a shows the change in the permeation flux with the plasma power, measured for a niobium foil. We obtain the plasma power by subtracting the reflected power from the input power. Only at high microwave power inputs (>2.6 kW), we observed some partial microwave power reflection. The correlation between permeation and plasma power is quite linear, with the highest PDP flux of 6.7 Pam3/(m2s) being achieved at 2.8 kW (at 25 Pa upstream pressure and 900 °C foil temperature). The change in PDP with upstream pressure for a niobium foil is depicted in Figure 6b. The plasma input power was set to 2.4 kW with 0% reflection during all measurements. The metal foil temperature was at 900 °C. We observed an increase in PDP with decreasing pressures. Momentum transfer from electrons to background gas particles happens less frequently at lower pressures, leading to a larger population of high-energy electrons and lower gas temperature. While the particle density decreases towards lower pressure, the share of high-energy collisions increases, and, according to the experimental observation, so does the absolute density of atomic hydrogen.
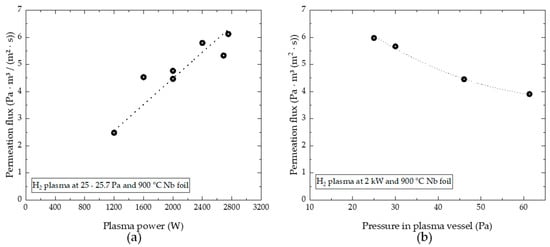
Figure 6.
PDP flux measurements over plasma power (a) and upstream pressure (b) for a niobium foil.
Figure 7a shows the correlation between temperature and GDP and PDP for protium and deuterium (adapted from [14]). The upstream pressure is 20 Pa and the plasma power is 2.0 kW. For both gases, we observed a typical increase in GDP with temperature. However, this increase was stronger for deuterium, while the GDP overall was smaller for deuterium in the tested temperature range. Taking the permeability of the two isotopes into account [17], the lower value for deuterium and the convergence for the two isotopes with higher temperatures can be explained, as the protium and deuterium permeabilities at high temperatures converge. While the high flux difference for D2 and H2 of more than one order of magnitude at lower temperatures is believed to be caused by differences in the molecular sticking coefficient. In the literature, values for the molecular sticking coefficients of the two gases on niobium strongly vary and depend on the condition of the surface and its manufacturing. Despite the decrease in H solubility with temperature, the observed GDP fluxes increased, probably due to an increase in diffusivity.
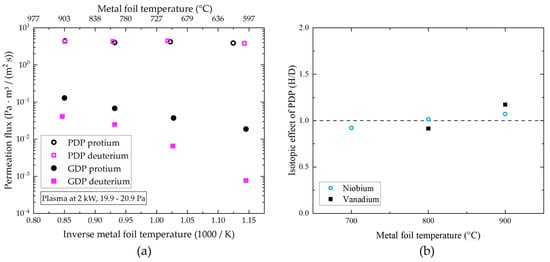
Figure 7.
PDP and GDP flux for deuterium and protium with varying metal foil temperatures of niobium foil in (a), and isotopic effect of PDP fluxes with niobium and vanadium foil (b).
The PDP behavior looks different compared to that of GDP. First, we observed an increase in permeation of about two orders of magnitude. Second, we see that for the investigated temperature range from 600 to 900 °C, permeation was reasonably independent of temperature, which is a feature of superpermeation [5]. Third and most importantly, we observed that the isotopic effect vanishes during PDP and we obtained similar permeation fluxes throughout the investigated temperature range. This indicates that atomic sticking and recombination coefficients were comparable for the two isotopes unlike the molecular sticking coefficients, as revealed by the GDP results.
Due to the explorative character of the metal foil experiments, quantitative comparisons of experimental data over long periods of time turned out to be practically unfeasible, as the operational history of the foil had a strong impact on the PDP flux magnitude and decrease during plasma. Nonetheless, we investigated two different foil materials, each with its unique operational history. A comparison of the isotopic effect of the PDP fluxes under steady-state conditions for the two investigated foil materials, Nb and V, is shown in Figure 7b. The plasma parameters of the PDP experiments shown in the figure were slightly different for the Nb and the V experiments. The Nb experiments were carried out at 2.4 kW RF power and with a +30 V bias on the membrane. The V experiments, however, were carried out with a slightly higher plasma power of 2.8 kW and +20 V for D2 plasma, at which the electron current saturated. The presented results were obtained using the modified plasma source design as described above. Post-mortem surface analyses showed that the pristine V membrane surfaces were symmetric, while the Nb, after a distinctively longer experimental period, had a thick oxide layer upstream, compromising the PDP flux magnitude overall. This explains why the PDP fluxes behind the points shown in Figure 7b) were in the range of 1.5 Pa∙m3/(m2∙s) for Nb, and in the range of 4.3 Pa∙m3/(m2∙s) for V, which is a larger difference than one would have expected simply from the difference in RF power only (compare with Figure 6a).
To obtain information on compression ratios, we carried out compression experiments by closing the gate valve to downstream pumping. These experiments were performed at 700 °C foil temperature, 20 Pa upstream pressure, and 2.4 kW plasma power with +30 V bias for the Nb foil, and at 2.8 kW with a +20 V bias for the V foil. The maximum achievable downstream pressures for the Nb foil in such experiments were 650 Pa (32.5 compression ratio) for H2 and 1000 Pa (still increasing, but halted by a downstream pressure safety limit of the setup) for D2. In the case of compression experiments with V, the same experimental conditions were applied. The downstream pressure reached the safety limit of 1000 Pa for both gases. Although the operational limit of HERMESplus did not allow the extraction of quantitative numbers on compression, it is obvious that the minimum required compression ratio of about one order of magnitude was safely met. This requirement comes from the latest configuration of the vacuum pump train in which the permeate stream is intended to be backed by an ejector pump.
The effect of noble gas presence in the torus exhaust on PDP fluxes was investigated by seeding argon to the hydrogen plasma up to a point, where its concentration made up ~10% of the molar fraction within the plasma vessel. The mixture was calibrated by measuring the two gases’ respective feeds required to reach a certain pressure (20 Pa) in the vessel at a given upstream pumping speed. The valve to upstream pumping was locked in position and so was the ratio of the pumping speeds of the two gases. Subsequently, by adapting the feeds to each other, the composition in the vessel could be controlled. Figure 8 shows the relative change in permeation fluxes through the vanadium foil during the time of noble gas admission. Initially, we observed a decline during plasma exposure due to damage to the O monolayer as explained above. However, at the time of Ar admission, the permeation flux increased spontaneously, hinting at favorable plasma conditions from which the production of suprathermal particles benefits. It is important to note that the slope of the following decline during plasma was not steeper with the Ar being present, demonstrating that there was no increased sputter damage due to the heavy argon species. However, the foil was positively biased at the point in time when steady-state fluxes were reached, repelling incoming positive ions. The positive bias protects the oxygen layer from sputtering by positive ions. On the other side, negative ions and fast electrons are accelerated towards the foil. The latter can potentially excite Ar atoms, which via the resonance transfer mechanism can produce fast H atoms that would contribute to permeation decline.
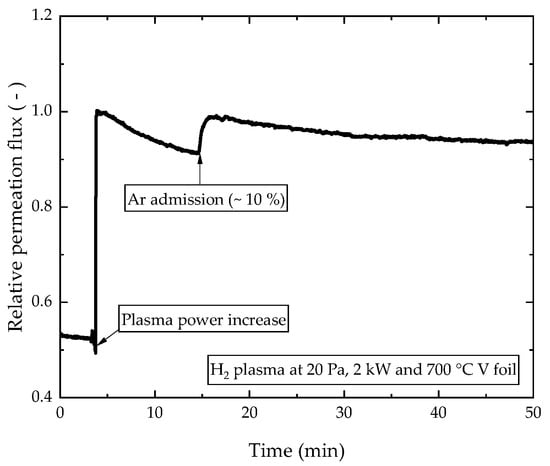
Figure 8.
Effect of noble gas (Ar) admission on PDP fluxes.
3.2. Experiments of Plasma Ignition in Magnetic Field
In this section, a summary of the parametric studies of the plasma source operation in the magnetic field of the FLIPS facility is given. Without magnetic field, we observed a rather strong expansion of the plasma with decreasing pressure, which we link to an increase in mean free path, allowing electrons to travel further before distributing their energy in collisions. As the plasma is constricted at higher pressures, the radial profiles of electron density and temperature become more steep near the dielectric tube. Figure 9 shows the plasma with 3 kW input power, no magnetic field and at different pressures. The microwave was injected from the right-hand side. All shown images in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 were obtained using cameras with varying exposure times and white balance as the main objective was set on capturing the size and shape of the plasma under different conditions.

Figure 9.
Plasma with 3 kW input power, no magnetic field and 10 Pa in (a), 20 Pa in (b), 50 Pa in (c) and 100 Pa in (d).

Figure 10.
Plasma in parallel magnetic field of 50 mT with 1 kW power at 1 Pa in (a) and 3 kW power and 50 Pa in (b), 10 Pa in (c) and 100 Pa in (d).

Figure 11.
Plasma in parallel magnetic field of 125 mT with 3 kW power at 10 Pa in (a), 20 Pa in (b), 50 Pa in (c) and 100 Pa in (d).

Figure 12.
Plasma in parallel magnetic field of 250 mT with 3 kW power input at 10 Pa in (a), 20 Pa in (b), 4 kW power input at 50 Pa in (c) and 6 kW power input at 100 Pa in (d).

Figure 13.
Plasma without magnetic field with 1 kW plasma power in (a) and with parallel magnetic field of 50 mT at 1 kW power input in (b), 87.5 mT and 1 kW in (c), 100 mT and 1 kW in (d), 125 mT and 3 kW in (e) and 250 mT and 3 kW in (f).

Figure 14.
Plasma-wall in (a) and asymmetry effect in plasma in (b) in a perpendicular configuration, and plasma in a gradient magnetic field from 60 mT at center to 30 mT towards the end in (c) and at the plasma source end in (d).
First, we operated the plasma source in the setup parallel to the magnetic field. Here, we varied pressures over a range of 1–100 Pa, with power from 1 to 6 kW and magnetic flux densities from 0 to 250 mT. We found that for both gases, H2 and D2, the behavior was the same and plasma was ignited at any magnetic field strength if sufficient microwave power was used. When varying the sequence, in which plasma power and coil current, i.e., magnetic field, were switched on, we also found no general difference. One exception to this was the ignition of plasma at low pressure. At pressures below 10 Pa, the plasma could only be ignited with magnetic field. For pressures between 5 and 10 Pa, the plasma could be sustained even if the magnetic field would be turned off again. The B field facilitates plasma ignition at low pressures due to the confinement of electrons perpendicular to the magnetic field, which decreases losses to the walls.
When applying a parallel magnetic field, we could see effects varying with magnetic field strength. Already, low magnetic flux densities of 50 mT led to a radial constriction of the plasma due to reduced electron mobility in radial direction. Cross-field diffusion of the charges was enabled via collisions with the background gas. On one hand, the increased collisionality of the plasma with pressure opposes the effect of the magnetic field’s radial constriction. On the other hand, a high pressure typically reduces the mean free path and leads to a steeper decline in emission intensity in the visual spectrum with the radial distance from the plasma source, as visible in Figure 9. Thus, such changes in the emission intensity with radial distance are barely visible in Figure 10. However, increasing pressure leads to shorter axial expansion due to the reduced magnetic confinement and the microwave power being absorbed over a shorter distance because of the higher gas and plasma density. In the images in Figure 10, the microwave power is 3 kW (except for at 1 Pa, where it was 1 kW) and plasma could be ignited at any pressure, even down to 1 Pa.
At the electron-cyclotron-resonance (ECR) field strength (87.5 mT), the gyromotion of the electrons on their helical path around the magnetic field lines is in resonance with the microwave frequency (2.45 GHz) of the plasma source. This provides a means of effective heating of the electrons via constant power absorption from the electric field without the need for collisions with background gas particles. At the ECR field strength, the plasma could always be ignited down to pressures below 1 Pa for both, parallel and perpendicular configuration. When increasing the magnetic flux density, we observed some unique visual effects that looked like standing wave formations, as visible in Figure 11. A theory with which to explain their nature is the microwave’s far propagation into the plasma due to not being completely absorbed close to the Plasmaline and, thus, creating discharges at a larger radial distance from it. A further increase in magnetic field strength to 250 mT showed similar results, as displayed in Figure 12. In both, perpendicular and parallel configuration, plasma could be ignited with 250 mT down to a pressure of 10 Pa. For the parallel setup, ignition was even possible at 1 Pa and 250 mT. However, we note that the power required for ignition increased with pressure at 250 mT. Details can be found in Table 1.

Table 1.
Results of plasma operation in magnetic field.
In Figure 13, the plasma is shown with a variation in the magnetic flux densities at a pressure of 20 Pa. Here, the plasma source and magnetic field are also parallel to each other. The shortening of the plasma at 87.5 mT is clearly visible as well as the standing-wave-like pattern at 125 mT.
For the perpendicular configuration, the ignition of plasma was slightly more challenging. We note that the used Plasmaline was significantly shorter than that in the parallel scenario, which also had some effect on the ignitability of the plasma without a magnetic field. Generally, higher powers were required to ignite the plasma than in the parallel case but with 6 kW input power, ignition was possible at 250 mT for various pressures. The perpendicular configuration gave rise to some unique effects: to some extent, there was a formation of a wall-like plasma expanding to both ends of the vacuum vessel along the magnetic field direction and an asymmetry perpendicular to the magnetic field. The two effects are visible in Figure 14a. The left-hand image in this figure was taken from a view port at the side of the cylindrical vessel, looking perpendicular to the axis of the vessel, while the right-hand photo was taken looking through a view port at one of the end flanges. The was first is caused by a reduction in the charge mobility in non-parallel directions to the magnetic field. The asymmetry grew stronger with pressure and magnetic field strength. We attribute this to a drift caused by the diffusive electron flux. Close to the plasma source, there is an electron density gradient in radial direction, which produced a net electron flux towards the dielectric tube. For two opposite sides of the plasma source, this flux was aimed in different directions with respect to the magnetic field, giving rise to drifts, which were pointed upwards on one and downwards on the other side.
In the perpendicular configuration, increasing the magnetic field strength led to a shortening of the plasma along the plasma column as most of the power was absorbed close to the front end of the coaxial line. At 250 mT, 10 Pa and 6 kW input power, for example, the plasma extended along the whole length of the vessel in the magnetic field direction but only burned halfway down the plasma source axis.
We also tested the effect of axial B-field gradients on the operation of a parallel plasma. For this, the coils at the ends of the vessel were disconnected from the high current supply. A magnetic field simulation, which we previously validated with Hall probe measurements, indicates magnetic flux densities of 200 mT at the center and 85 mT at the ends of the vessel for this coil configuration with maximum currents. In a first series of experiments, we tested a multitude of configurations of operation parameters with pressures ranging from 1 to 20 Pa and powers from 1 to 6 kW with the result that plasma could always be ignited with the magnetic field gradient—and mainly burned at the ends of the vessel. There, however, the ECR condition was satisfied, which is why we lowered the coil currents to avoid the ECR regime in the whole vessel.
In the second test series, the magnetic flux density was about 60 mT in the center, dropping to 30 mT at the ends of the vessel. We tested a pressure range of 10 to 50 Pa and found a slight increase in required power with pressure. However, 1 kW was sufficient to ignite plasma even at 50 Pa. Increasing the power led to a longer plasma column. Figure 14b shows the plasma with a parallel magnetic field gradient of 60 to 30 mT at 20 Pa and 0.68 kW input power. The results for the ignitibility of the plasma are summarized in Table 1.
The temperature of the plasma source dielectric tube was monitored with an infrared camera during all of the experiments. Convectional cooling of the plasma source was provided via the forced convection of ambient air along the inner surface of the dielectric tube using a sidechannel blower with a 20 L/s throughput. Despite the low cooling power, the dielectric tube never reached temperatures above 450 °C, even at 6 kW power input. The observed trend showed a decrease in the peak temperature with the magnetic flux density.
4. Discussion
As shown in the presented experimental data, permeation fluxes as high as 6.7 Pa∙m3/(m2∙s) have been obtained. Most PDP experiments—also in other studies not included in this paper—have been carried out in a standardized operation scheme with a power input of 2 kW at a pressure of 20 Pa and a metal foil temperature of 900 °C. In these experiments, we consistently achieved permeation fluxes of at least 4 Pa∙m3/(m2∙s) for both H2 and D2, reducing down to ~1.5 Pa∙m3/(m2∙s) until a steady state was reached. Considering this performance and a desired DIR-ratio of 0.8, one can roughly derive a first estimate of the required foil surface area in DEMO. The current range of throughput foreseen for DEMO is 265–430 Pa∙m3/s, coming from different contributions (unburnt DT, He, plasma enhancement gases, etc.) [14]. Assuming that 95% of these are hydrogenic species, the removal of 80% of such species would yield a to-be-permeated flow of 200–327 Pa∙m3/s. A simplistic scale-up from the HERMESplus fluxes would yield a required membrane surface area of 50–82 m2 for the case of observed PDP peak fluxes or 133–219 m2 for achieved steady-state fluxes. Even though the latter range is clearly seen as a very conservative limit since the geometry of the setup is far from optimized for pumping and higher performances are to be expected in a real MFP, this surface need is very well in line with the current preliminary integrated design of a number of tubular MFPs (see Figure 1) in a pump duct providing 19 m2 pumping metal foil surface per duct [13], as it corresponds to the need for 11 out of 16 available ducts for pumping in DEMO.
The permeation flux increases linearly with power until the power absorbed by the plasma saturates. Given the in-vessel plasma source length of 0.3 m with small extensions of a few cm over the outer conductor at each end in HERMESplus and a saturation power of 2.8 kW, we can approximate that for this type of Plasmaline, a power of about 8 kW per m can be coupled into hydrogen plasma at 20 Pa. We note that pressure and plasma source diameter affect this value, hence it should only be considered a first approximation for the design of the microwave power distribution system for the MFP modules in DEMO. Furthermore, the magnetic field can impact energy coupling into the plasma strongly, as will be explained more thoroughly below.
As with increasing power, permeation also increases with decreasing pressure due to increased production of suprathermal hydrogen. For hydrogen plasma, there is a lower pressure limit of plasma source ignition at ~10 Pa. However, the operational range can be significantly extended to a lower pressure via the admission of noble gases such as Ar with typically high electron densities or via the superposition of magnetic fields, as is the case in the DEMO pump duct. It is not entirely clear yet which permeation fluxes can be reached in a magnetically assisted discharge at even lower pressures around 1–5 Pa—a possible pressure range if the divertor is not operated under high neutral density. Typically, magnetically assisted microwave discharges are most stable and electron temperatures are the highest when the electron-cyclotron-resonance (ECR) condition is reached. For the given 2.45 GHz microwave, this is the case at 87.5 mT. In DEMO, as pointed out in Section 2, the flux densities are one order of magnitude larger.
The independence of the permeation flux of hydrogen on temperature and on the isotope is a very promising result considering no additional recycling or isotope rebalancing is necessary before routing to the matter injection systems. While for Nb, the theoretical value for the maximum achievable permeation flux with plasma decreases with temperature [17], experiments usually show that the achievable flux (below the theoretical limit) still increases with temperature in our setup due to the better preservation of the oxygen monolayer on the surface. For technological applications, the lower temperature range is more attractive owing to lifetime, energy efficiency and mechanical stiffness. Nevertheless, there are several shortcomings of the operation of group 5 metals at low temperatures, such as the observed reduction in oxygen surface segregation [8], or the increase in hydrogen embrittlement [17]. Recently, other groups [21] have shown interesting results with Pd-based flat membranes and inductively coupled RF plasma at low temperatures (75–200 °C). The permeation values are remarkably high, but the scalability towards fusion conditions remains unclear.
The found compression ratios of the order of 10 or more are in line with what is needed to feed a continuously working mercury-vapor-based booster ejector pump, so that in the pumping path of the permeated gas, no diffusion pumps are necessary. This is a very important confirmation of the vacuum pumping train reference concept.
The findings of plasma source ignitability in a magnetic field also require a critical discussion in view of a MFP operation in DEMO. First of all, we point out that the main species responsible for superpermeation in our plasma is neutral atomic hydrogen, which is not affected by the magnetic field itself. Furthermore, drag effects from ion movement can be neglected due to the low degree of ionization [10]. Hence, permeation flows can only be negatively affected by the magnetic field if (a) the plasma does not ignite or absorb the microwave power, (b) the plasma shape is distorted so much that it extends out of the MFP or (c) the electron energy distribution function (EEDF) changes to the disadvantage of hydrogen dissociation. With the presented experiments, we want to address cases (a) and (b), while case (c) requires sophisticated modeling of the exact DEMO magnetic field in the pump duct, which is not feasible to conduct at the current design stage.
For a parallel magnetic field, a general observation is that an increase in pressure promotes cross-field movement of the charges that opposes the constriction of the plasma usually observed with pressure. For the pressure range of interest, this effect is small as the electron gyro-frequency is still orders of magnitude larger than the collision-frequency. The length of the plasma extends significantly in the direction of the magnetic field in some configurations. We achieved plasma extension beyond the end of the Plasmaline by reducing the pressure to below 5 Pa or combining high power input and high magnetic flux densities. We explain this via the associated increase in the mean free path, which allows the particles to travel further before recombining and via the strong magnetization of the plasma with severely reduced charge losses in the radial direction. Thus, we want to emphasize that for our application, pressure and power input have a major effect on the plasma shape. Considering the magnetic field for the current fusion plasma scenario, we cannot make a definite statement on the shape and volume of the plasma or if this puts a requirement on the geometry of the MFP modules. However, we gained valuable insights into the ignitability of the plasma, which depends on the angle between electric and magnetic field and the electrons’ mobility in electric field direction.
Figure 15 presents the experimental findings as required power for plasma ignition over magnetic flux density in the parallel setup with 10 Pa pressure. The lowest magnetron power input possible was 680 W. During the experiments, we observed some variations in the required power inputs and in microwave reflection, which was probably caused by a change in the impedance of the system for different operation conditions. We see that plasma could be ignited with minimum power around the ECR field strength. When increasing the magnetic flux density, more power was required. The important transport properties, conductivity and diffusivity of electrons are complex functions of the magnetic field and depend on its direction. Hence, the extrapolation of the measurement data via a fit function of any shape is not applicable to the prediction of accurate required microwave powers to ignite the plasma at even higher magnetic flux densities.
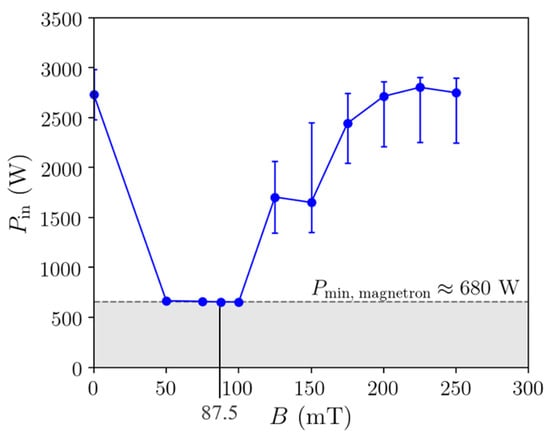
Figure 15.
Required microwave power for ignition of plasma at 10 Pa with parallel magnetic field.
To be more realistic, we will, in the following part, derive a better way of extrapolation by means of a self-consistent 2D axisymmetric hydrogen plasma simulation in COMSOL Multiphysics with a parallel configuration of the plasma source and a homogeneous magnetic field. The plasma simulation uses a fluid approximation to describe the electrons with macroscopic quantities [22]. The wave equation is solved for in the plasma domain, where resistive heating of the electron fluid succeeds based on the induced current, which can be defined through the plasma’s conductivity. The applied plasma chemistry determines the power transfer from the electron fluid to the heavy species. The simulation results, still, have to be considered a rough approximation, as a homogeneous B field leads to a different behavior from that of an inhomogeneous one at the same magnitude, as the FLIPS experiments showed with ignition at low pressure with inhomogeneous magnetic field.
Introducing an axial, homogeneous, one-directional magnetic field into the 2D plasma simulation allows us to draw some comparisons to the experiments. We consider the magnetic field in the tensors for mobility and diffusivity in the charge transport equations and in electron conductivity, which affects microwave propagation and wave heating [22]. The resistive heating term of the electrons is given by
where is the electron current density, E is the microwave electric field and σ is the electron conductivity. Without magnetic field, the electron conductivity, σ, is a scalar and resistive heating is determined via the current drive along the electric field. Since the radial component, Er, of the electric field is the strongest for the coaxial waveguide, it has the highest contribution to heating [11]. The Ez component has a minor contribution and Eφ in azimuthal direction is zero without magnetic field. With presence of a magnetic field, the conductivity has to be described as a tensor. With a one-directional magnetic field parallel to the Plasmaline, it becomes
where σ0 is the plasma conductivity without superimposed magnetic field. The induced currents are then given by
The conductivity, σzz, and the current, Jz, are parallel to B and Ez and remain unaffected by the magnetic field. The diagonal elements σrr and σφφ are also called Pedersen conductivity and are perpendicular to B but parallel to the respective component of the electric field. The off-diagonal elements (Hall current) are caused by the ExB drift and are perpendicular to B and E. In contrast to the case without magnetic field, a current is, therefore, also induced in φ-direction and there also exists an azimuthal electric field. For magnetic fields beyond the ECR field strength, the perpendicular conductivities σrr and σφφ exhibit the largest decrease. In Figure 16, we present simulation results for the ratios of parallel-to-perpendicular conductivities for hydrogen plasma at 20 Pa and 2 kW input power and their change with the magnetic field. We see that cross-field conductivity and, therefore, the plasma’s efficiency to absorb power of the radial electric component of the microwave declines quickly with B. When considering the single components, the resistive heating term can be written as
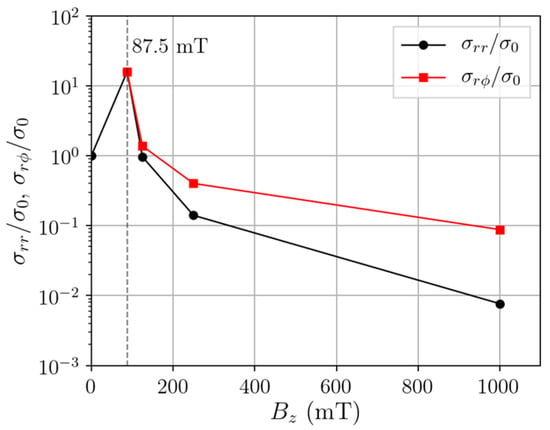
Figure 16.
Ratios of the perpendicular-to-parallel conductivities in a homogeneous, axial magnetic field.
The Hall current terms cancel each other out because of σrφ = −σφr. If only the radial component is considered, then the scaling of the resistive heating term would be , with decreasing the most out of the three conductivities with B (see Figure 16). Thus, a reduction in leads to the largest increase in required input power to obtain the same resistive heating in the plasma.
However, simulations show that a plasma can be built up at 1 T even with input powers around 2 kW. Also, the experiments do not show such an increase in required power up to 250 mT. In the simulation, we find the reason for this when looking at the directional contributions to the heating term individually. In Figure 17, we present the total absorbed power with changing parallel magnetic field strength. Peaking at 87.5 mT, the power absorbed from the perpendicular electric field component declines rapidly for higher B fields. Instead, there is a transition taking place where the plasma is heated efficiently by the parallel electric field component, which allows the plasma to be maintained even at 1 T.
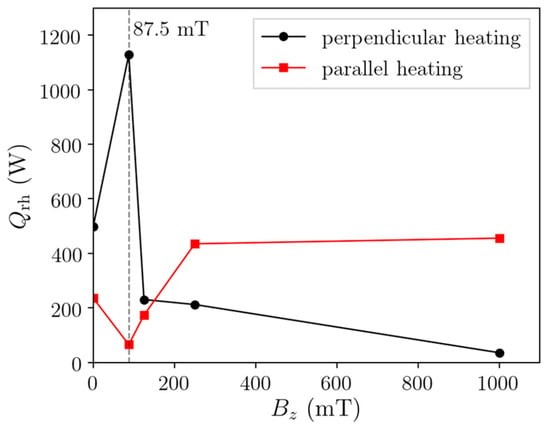
Figure 17.
Total heating contributions in parallel magnetic field plasma simulation at 2 kW input power and 20 Pa. Any remaining microwave power exits the system through the microwave port.
The parallel electric field component plays an important role at higher magnetic flux densities as the conductivity in the perpendicular direction decreases. The coupling of the axial wave component is probably also the reason why the required power for ignition in Figure 15 only increases by 1 kW from 125 to 250 mT. As pointed out before, the curved, gradient three-dimensional B-field in DEMO complicates the situation and requires consideration in an extension of our current plasma simulation. However, here, we show the principal behavior of microwave power coupling and that improvements in ignition can be made by aligning electric and magnetic fields.
One would expect the parallel configuration in FLIPS to demonstrate a worst-case scenario in terms of plasma ignition as the electric field is always perpendicular to the magnetic field. Still, we found that at the highest magnetic field strength of 250 mT, ignition was always possible in this configuration if we increased the power sufficiently, which we interpret as a reassuring result.
5. Conclusions
In this work, we describe experimental results obtained in the HERMESplus setup at KIT and in the FLIPS setup at the University of Stuttgart. We report on the handling of undesired impurities and a related modification of the plasma source design. We were able to obtain high permeation fluxes of up to 6.7 Pam3/(m2s) and investigated their dependency on pressure and power input. Not only was the achievable flux sufficient, but also the achievable compression ratio of more than one order of magnitude provided a pressure that was sufficient to use continuously in working booster ejector pumps further downstream in the vacuum pumping train. However, we note that the impact of the magnetic field on the permeation fluxes remains to be quantified.
Using conservative performance estimates, about 11 of the 16 available DEMO ducts would be required. However, we emphasize that this value cannot be linearly scaled due to multiple variables, which affect operation like changes in the pressure, effects of the magnetic field, reduction of the actual foil surface area in an integrative design and yet to be reached steady-state operation with such high flux values.
We also demonstrated the limits for power absorption of hydrogen plasma in the given coaxial discharge at 20 Pa to be approximately 8 kW per m Plasmaline, which can be taken into consideration for the design of microwave power distribution to the MFP modules. For the temperature range between 600 and 900 °C, we observed no significant isotopic effect for the PDP of protium and deuterium. In the same temperature range, the measured peak fluxes were independent of the temperature, which is proof of superpermeation.
The next step in the characterization of the PDP process and the investigation of the employed plasma source is the exploration of operation at lower pressures. In the present work, we show that PDP fluxes increase towards lower pressures. However, to achieve plasma ignition at very low pressures down to 1 Pa, the discharge requires assistance in form of a magnetic field. Thus, the HERMESplus facility will receive a major upgrade to allow for the installation of two Helmholtz coils. The new facility will be able to operate the plasma with magnetic fields of up to 100 mT in the bulk of the plasma.
The PDP experiments revealed the strong potential influence of sputtering of the oxygen monolayer by energetic plasma particles. To eliminate this, some design measures can be taken, such as the installation of a screen of the membrane from the direct line of sight of the plasma and further investigation into the characteristics of sputter-resistant foils for PDP are required.
We demonstrate the operability of the coaxial microwave plasma source in strong, homogeneous, one-directional magnetic fields of up to 250 mT with strictly perpendicular or parallel mounted plasma source. No mentionable difference in ignitability between H2 and D2 could be found. Only low cooling power was required to keep the plasma source temperature at reasonable levels during operation and maximum temperatures even decreased with magnetic field strength. Being the particle with the largest contribution to PDP flows, atomic hydrogen is not affected by the magnetic field itself; however, its production rate and its source location might be. The magnetic field helped ignite plasma at pressures below 1 Pa due to the confinement of charged particles and strongly decreased loss terms to the walls. Around the ECR magnetic field strength of 87.5 mT, the ignition of plasma was always possible even with a minimum power input of 680 W. With increasing magnetic flux density, the power input required to ignite the plasma rose. The experimentally determined increase in required power for ignition with magnetic flux density did scale much less than expected. It appears that the heating by the axial electric field, which is parallel to the magnetic field in the investigated case, increases with B.
Our findings indicate that the microwave heating at high magnetic fields works mainly via the absorption of the electric field parallel to the magnetic field. Since the Plasmaline works like a coaxial waveguide, the strongest electric field is in radial direction. Depending on the installation direction in DEMO, the microwave electric field of the Plasmaline might not be parallel to the magnetic field, which can lead to a lower ignition and heating efficiency. Therefore, a way should be found to amplify the electric field component parallel to B. This can be done, for example, by aligning the MFP to the expected magnetic field lines. Another approach is the modification of the shape of the inner conductors, possibly by adding conducting structures (rings, spirals, etc.) to their surface. It is recommended to explore this possibility in the future with corresponding experiments.
We recommend experimental investigation of the ignitibility of the plasma source in a magnetic field more representative of DEMO, with a higher field strength, strong gradients and three spatial direction components
Author Contributions
Conceptualization, Y.K., A.V.C. and C.D.; methodology, Y.K. and A.V.C.; validation, Y.K., A.V.C. and S.M.; formal analysis, Y.K., S.H. and A.S.; investigation, Y.K., A.V.C. and S.M.; resources, C.D., T.G. and M.W.; data curation, Y.K. and A.V.C.; writing—original draft preparation, Y.K.; writing—review and editing, Y.K., A.V.C., C.D., S.M., S.H., J.I. and A.S.; visualization, Y.K. and S.M.; supervision, C.D. and M.W.; project administration, C.D.; funding acquisition, C.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No 101052200—EUROfusion).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Please contact the authors via the corresponding author’s e-mail for access to the data.
Acknowledgments
This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No 101052200—EUROfusion). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them. This work has been done under the Tritium-Matter Injection-Vacuum Programme of the EUROfusion DEMO Project. We acknowledge support by the KIT-Publication Fund of the Karlsruhe Institute of Technology.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Donné, T.; Morris, W.; European Research Roadmap to the Realisation of Fusion Energy. EUROfusion. 2018. Available online: https://euro-fusion.org/wp-content/uploads/2022/10/2018_Research_roadmap_long_version_01.pdf (accessed on 18 August 2023).
- Abdou, M.; Riva, M.; Ying, A.; Day, C.; Loarte, A.; Baylor, L.; Humrickhouse, P.; Fuerst, T.F.; Cho, S. Physics and technology considerations for the deuterium-tritium fuel cycle and conditions for tritium fuel self sufficiency. Nucl. Fusion 2021, 61, 013001. [Google Scholar] [CrossRef]
- Giegerich, T.; Day, C. The KALPUREX-process—A new vacuum pumping process for exhaust gases in fusion power plants. Fusion Eng. Des. 2014, 89, 1476–1481. [Google Scholar] [CrossRef]
- Day, C.; Butler, B.; Giegerich, T.; Ploeckl, B.; Varoutis, S. A smart three-loop fuel cycle architecture for DEMO. Fusion Eng. Des. 2019, 146, 2462–2468. [Google Scholar] [CrossRef]
- Livshits, A.I.; Notkin, M.E.; Samartsev, A.A. Physico-chemical origin of superpermeability—Large-scale effects of surface chemistry on “hot” hydrogen permeation and absorption in metals. J. Nucl. Mater. 1990, 170, 79–94. [Google Scholar] [CrossRef]
- Hanke, S.; Day, C.; Giegerich, T.; Igitkhanov, J.; Kathage, Y.; Luo, X.; Varoutis, S.; Cortes, A.V.; Härtl, T.; Busniuk, A.; et al. Progress of the R&D programme to develop a metal foil pump for DEMO. Fusion Eng. Des. 2020, 161, 111890. [Google Scholar] [CrossRef]
- Hatano, Y.; Livshits, A.; Nakamura, Y.; Busnyuk, A.; Alimov, V.; Hiromi, C.; Ohyabu, N.; Watanabe, K. Influence of oxygen and carbon on performance of superpermeable membranes. Fusion Eng. Des. 2006, 81, 771–776. [Google Scholar] [CrossRef]
- Hatano, Y.; Watanabe, K.; Livshits, A.; Busnyuk, A.; Alimov, V.; Nakamura, Y.; Hashizume, K.-I. Effects of bulk impurity concentration on the reactivity of metal surface: Sticking of hydrogen molecules and atoms to polycrystalline Nb containing oxygen. J. Chem. Phys. 2007, 127, 204707. [Google Scholar] [CrossRef] [PubMed]
- Livshits, A.; Alimov, V.; Notkin, M.; Bacal, M. Hydrogen superpermeation resistant to ion sputtering. Appl. Phys. A 2005, 80, 1661–1669. [Google Scholar] [CrossRef]
- Petasch, W.; Räuchle, E.; Muegge, H.; Muegge, K. Duo-Pasmaline—A linearly extended homogeneous low pressure plasma source. Surf. Coat. Technol. 1997, 93, 112–118. [Google Scholar] [CrossRef]
- Räuchle, E. Duo-Plasmaline, a surface wave sustained linearly extended discharge. J. Phys. IV 1998, 8, Pr7-99–Pr7-108. [Google Scholar] [CrossRef]
- Peters, B.J.; Day, C. Analysis of low pressure hydrogen separation from fuel exhaust gases by means of superpermeability. Fusion Eng. Des. 2017, 124, 696–699. [Google Scholar] [CrossRef]
- Giegerich, T.; Day, C.; Gliss, C.; Luo, X.; Strobel, H.; Wilde, A.; Jimenez, S. Preliminary configuration of the torus vacuum pumping system installed in the DEMO lower port. Fusion Eng. Des. 2019, 146, 2180–2183. [Google Scholar] [CrossRef]
- Day, C.; Battes, K.; Butler, B.; Davies, S.; Farina, L.; Frattolillo, A.; George, R.; Giegerich, T.; Hanke, S.; Härtl, T.; et al. The pre-concept design of the DEMO tritium, matter injection and vacuum systems. Fusion Eng. Des. 2022, 179, 113139. [Google Scholar] [CrossRef]
- Livshits, A.I.; Sube, F.; Solovyev, M.N.; Notkin, M.E.; Bacal, M. Plasma driven superpermeation of hydrogen through group Va metals. J. Appl. Phys. 1998, 84, 2558–2564. [Google Scholar] [CrossRef]
- Bacal, M.; El Balghiti-Sube, F.; Livshits, A.I.; Notkin, M.E.; Riz, D.; Soloviev, M.N.; Kuroda, T.; Tanaka, M.Y. Plasma driven superpermeation and its possible applications to ion sources and neutral beam injectors. Rev. Sci. Instrum. 1998, 69, 935–937. [Google Scholar] [CrossRef]
- Peters, B.J. Development of a Hydrogen-Selective Vacuum Pump on the Basis of Superpermeation. Ph.D. Thesis, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2020. [Google Scholar] [CrossRef]
- Schulz, A. Investigations and applications of plasmas generated by the Duo-Plasmaline. In Proceedings of the 5th International Workshop on Microwave Discharges, Greifswald, Germany, 8–12 July 2003. [Google Scholar]
- Fujimoto, T.; Usami, M. Rarefied gas flow through a circular orifice and short tubes. J. Fluids Eng. 1984, 106, 367–373. [Google Scholar] [CrossRef]
- Callen, J.D. Fundamentals of Plasma Physics; University of Wisconsin: Madison, WI, USA, 2006. [Google Scholar] [CrossRef]
- Li, C.; Job, A.J.; Fuerst, T.F.; Shimada, M.; Way, J.D.; Wolden, C.A. Low temperature hydrogen plasma permeation in palladium and its alloys for fuel recycling in fusion systems. J. Nucl. Mater. 2023, 582, 154484. [Google Scholar] [CrossRef]
- COMSOL. Plasma Module User’s Guide. COMSOL Multiphysics. 2018. Available online: https://doc.comsol.com/5.4/doc/com.comsol.help.plasma/PlasmaModuleUsersGuide.pdf (accessed on 10 September 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).