Exospheric Solar Wind Model Based on Regularized Kappa Distributions for the Electrons Constrained by Parker Solar Probe Observations
Abstract
:1. Introduction
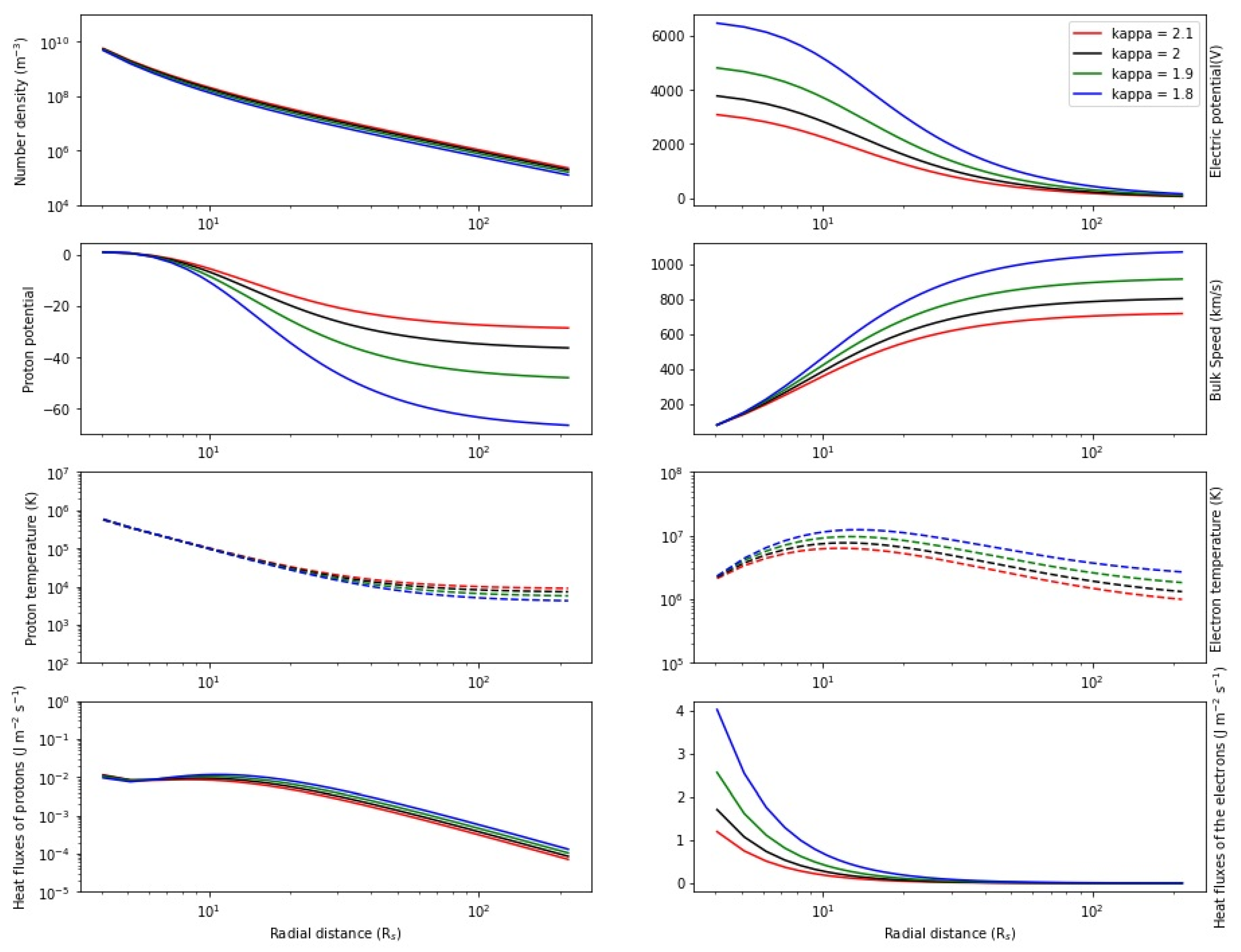
2. Exospheric Model with Regularized Kappa
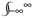 (v − u)l f(r, v, t)dv
(v − u)l f(r, v, t)dv
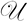 [0] (κ, α),
[0] (κ, α),
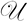 [n](κ, α) that is a ratio of two Kummer (or Tricomi) functions U. This ratio is expressed as follows:
[n](κ, α) that is a ratio of two Kummer (or Tricomi) functions U. This ratio is expressed as follows: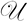 [n](κ,α) = U((3 + m)/2,(3 + m)/2 − κ,α2κ)/U((3 + n)/2,(3 + n)/2 − κ,α2κ)
[n](κ,α) = U((3 + m)/2,(3 + m)/2 − κ,α2κ)/U((3 + n)/2,(3 + n)/2 − κ,α2κ)
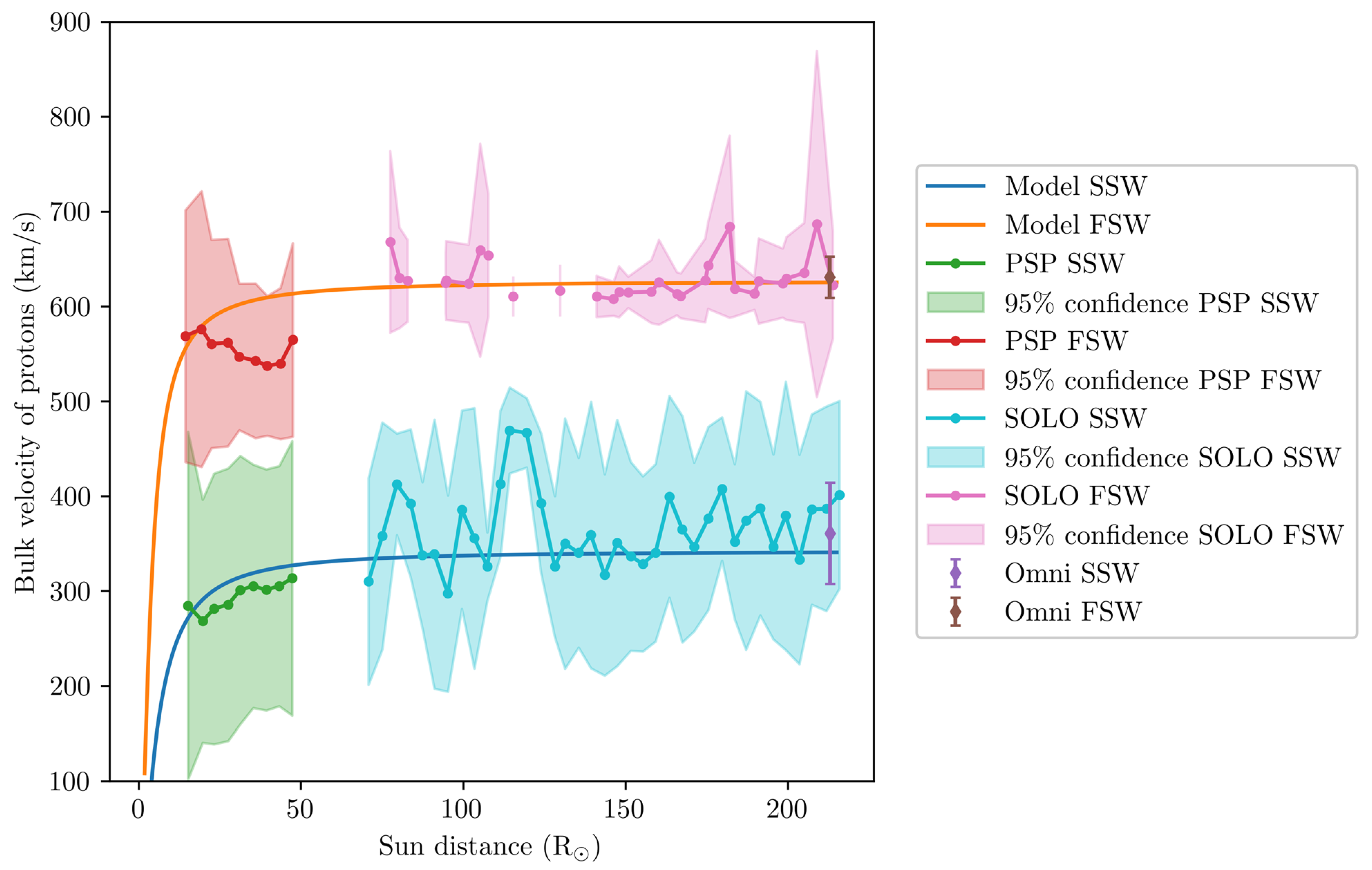
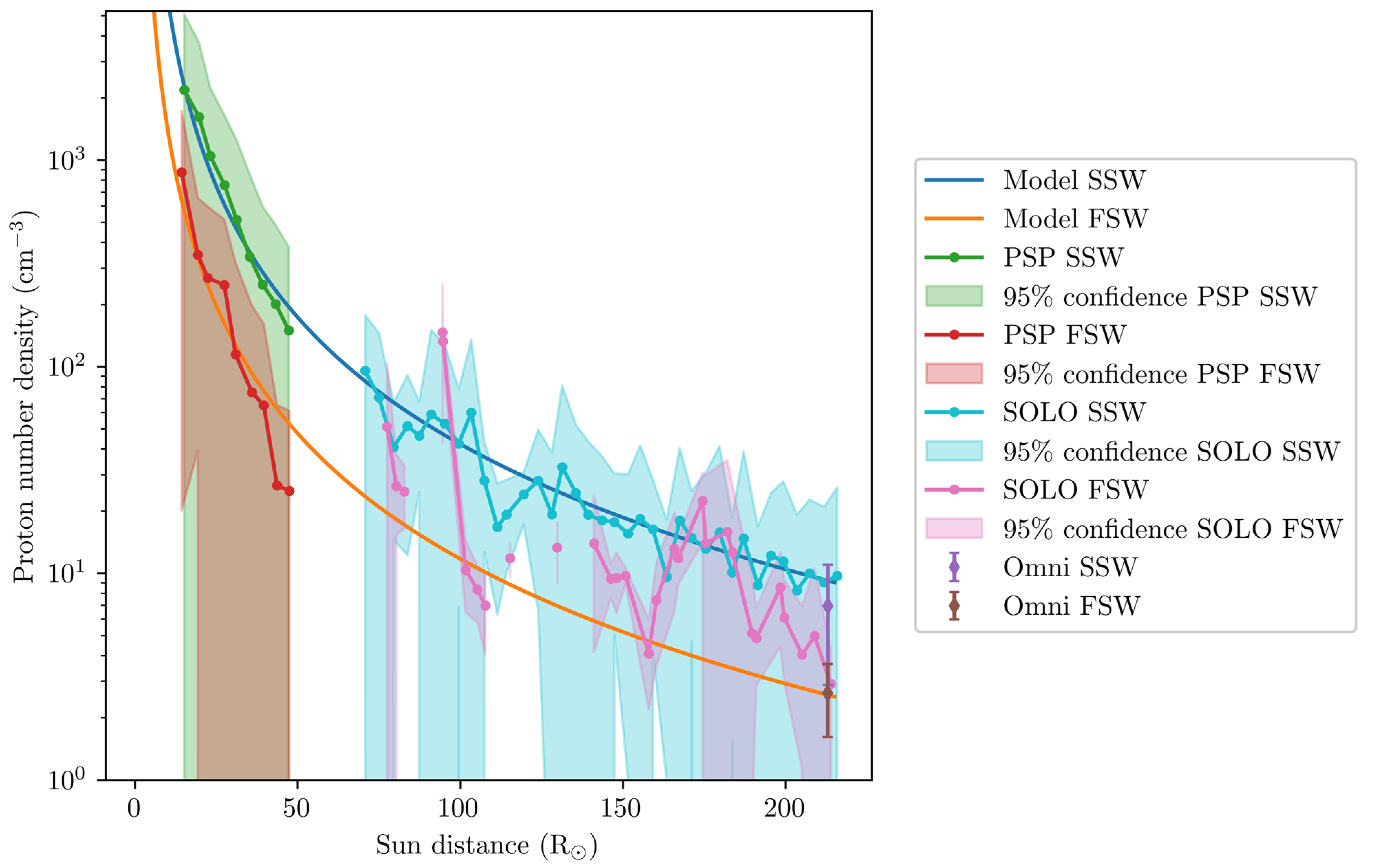
3. Comparison between the Model and New Solar Wind Observations
3.1. Averaging All Measurements with the Distance
| PSP | from 15 October 2018 | from 0.08 to 0.80 AU, |
| SOLO | from 7 July 2020 | from 0.59 to 0.99 AU, |
| OMNI | from 15 October 2018 | at 1 AU, and |
| ULYSSES (UY) | from 1 January 1995–31 December 1996 | from 1.34–1.36 AU |
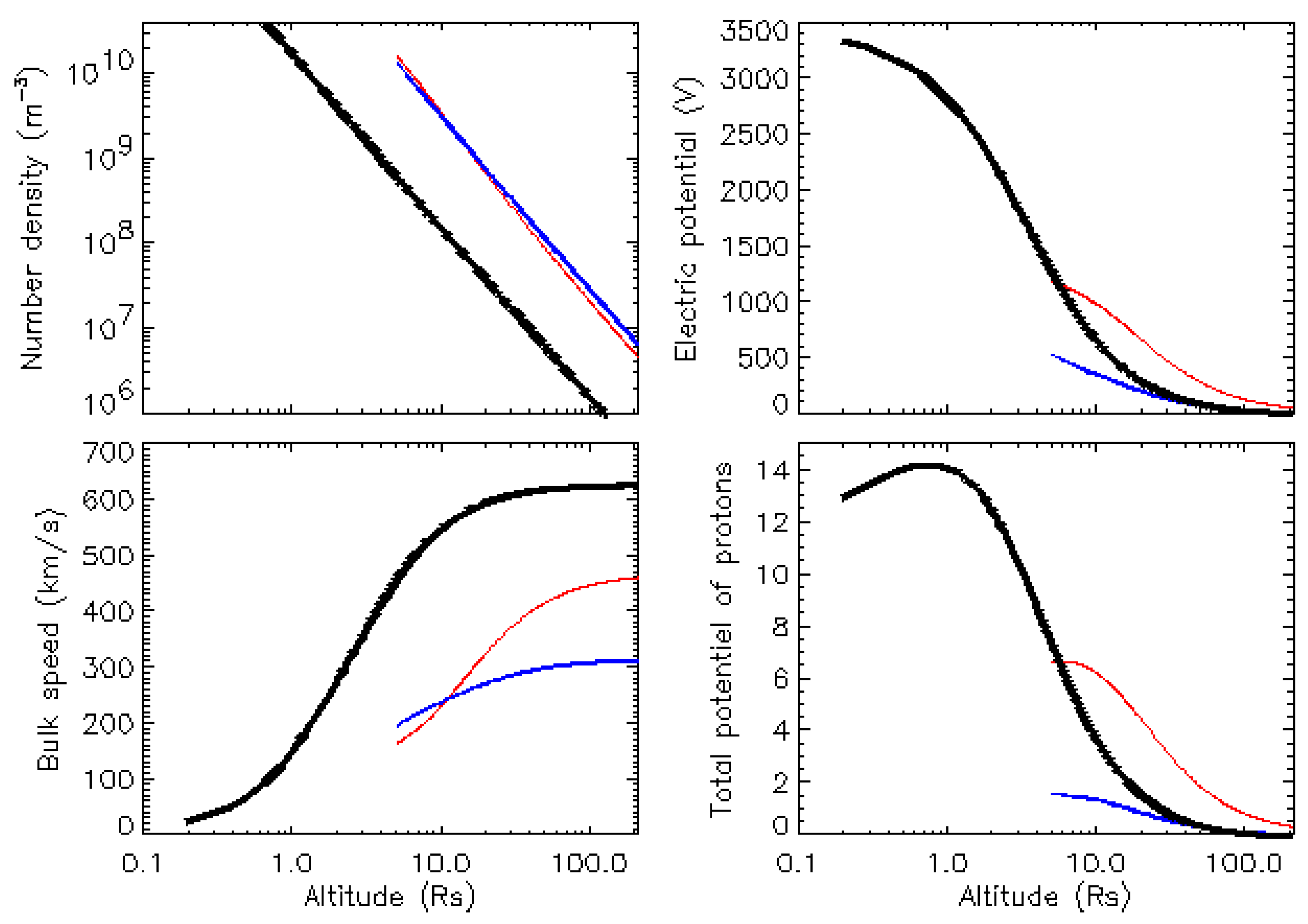
3.2. Separating Slow and Fast Wind by Considering Different Exobases
4. The Influence of the Electric Potential
5. Electron Distributions
5.1. Electron Distribution Obtained with the Exospheric Model
5.2. Electron Distribution Observed by PSP in the Velocity Plane
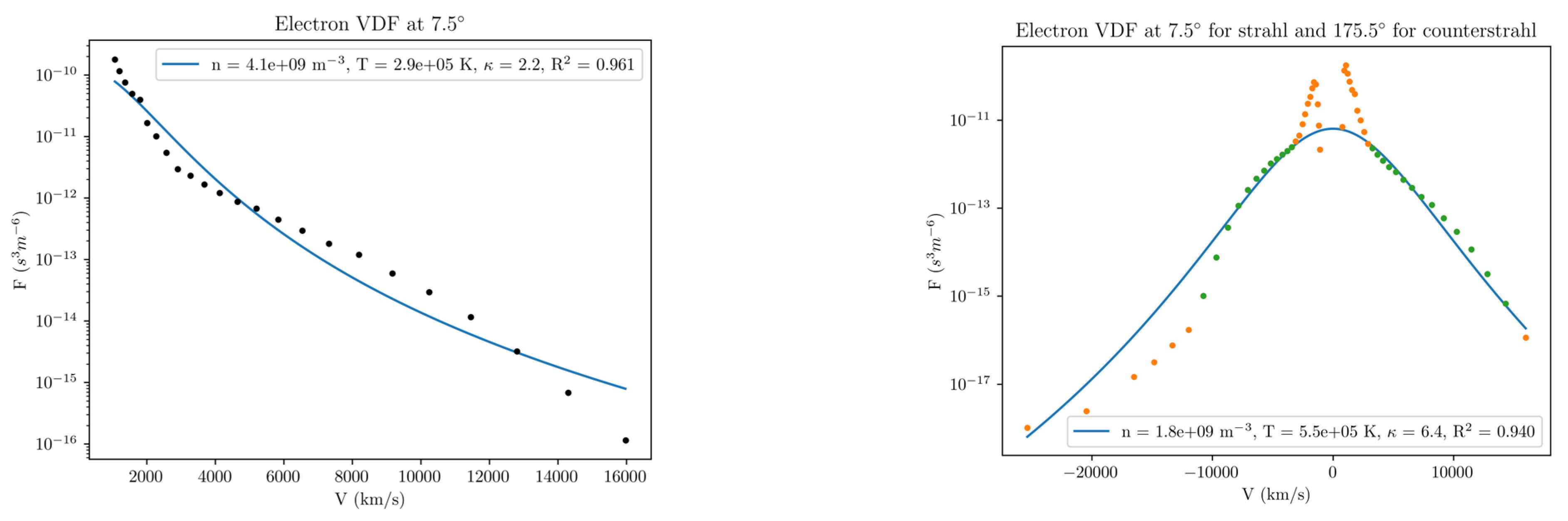
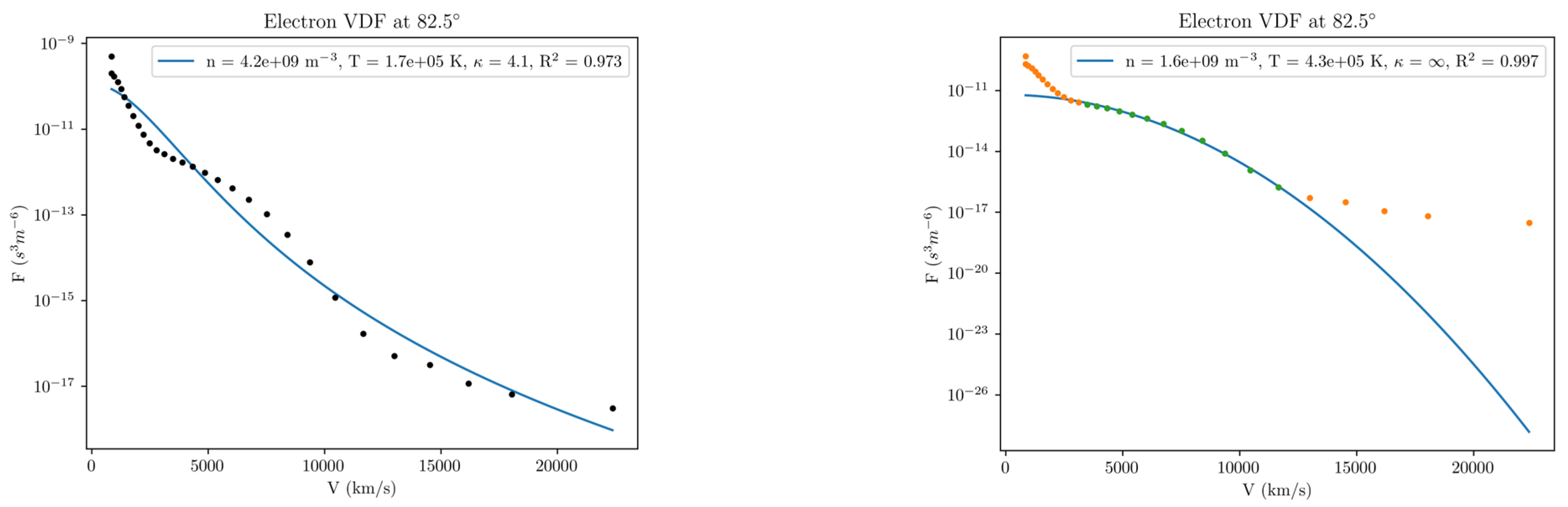
5.3. One Dimension (1D) Single Fit for the Strahl and the Halo
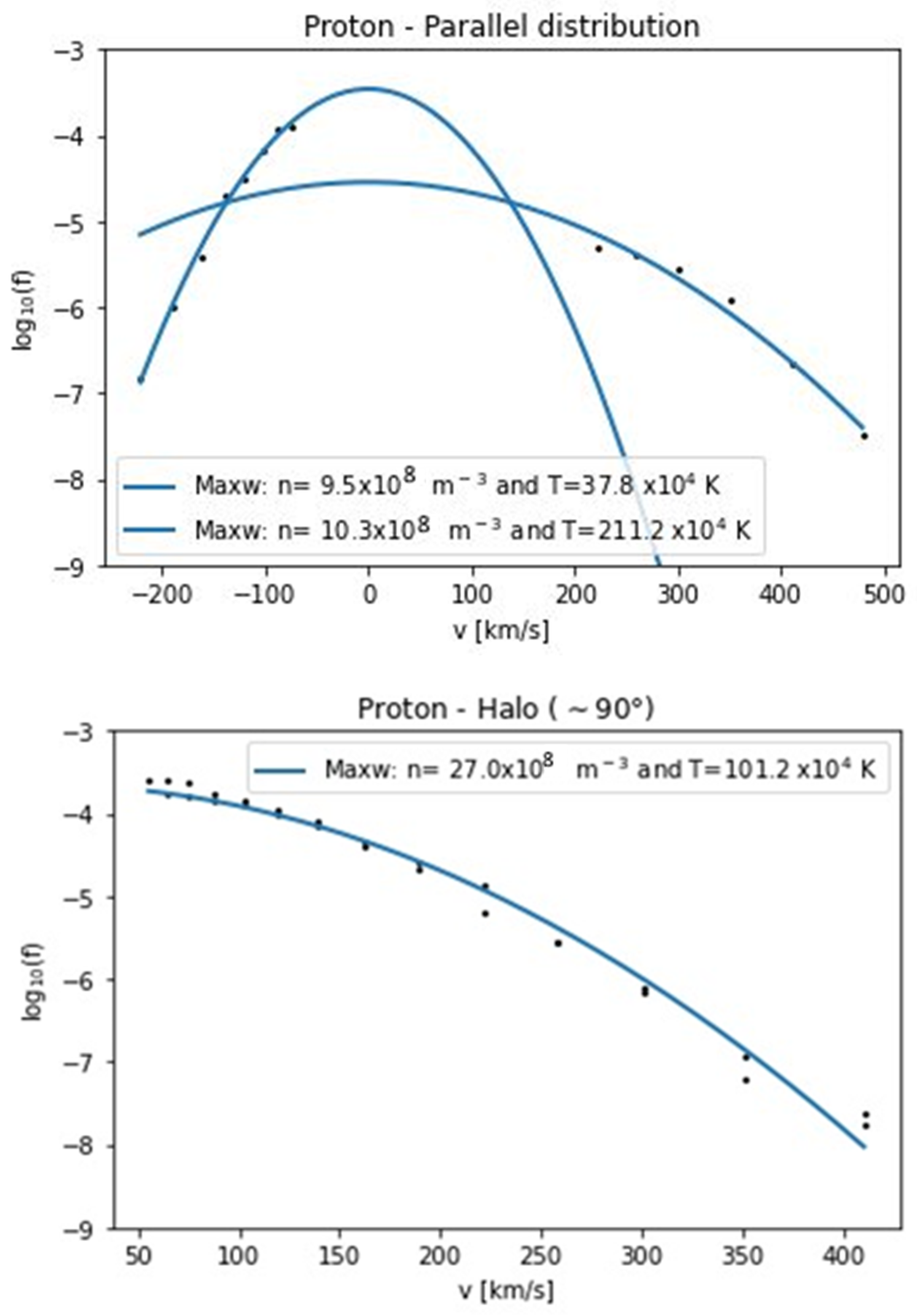
6. Proton Distribution Observed by Parker Solar Probe
6.1. Proton Distribution in the Velocity Plane
6.2. Proton Distribution Fitted by a Maxwellian
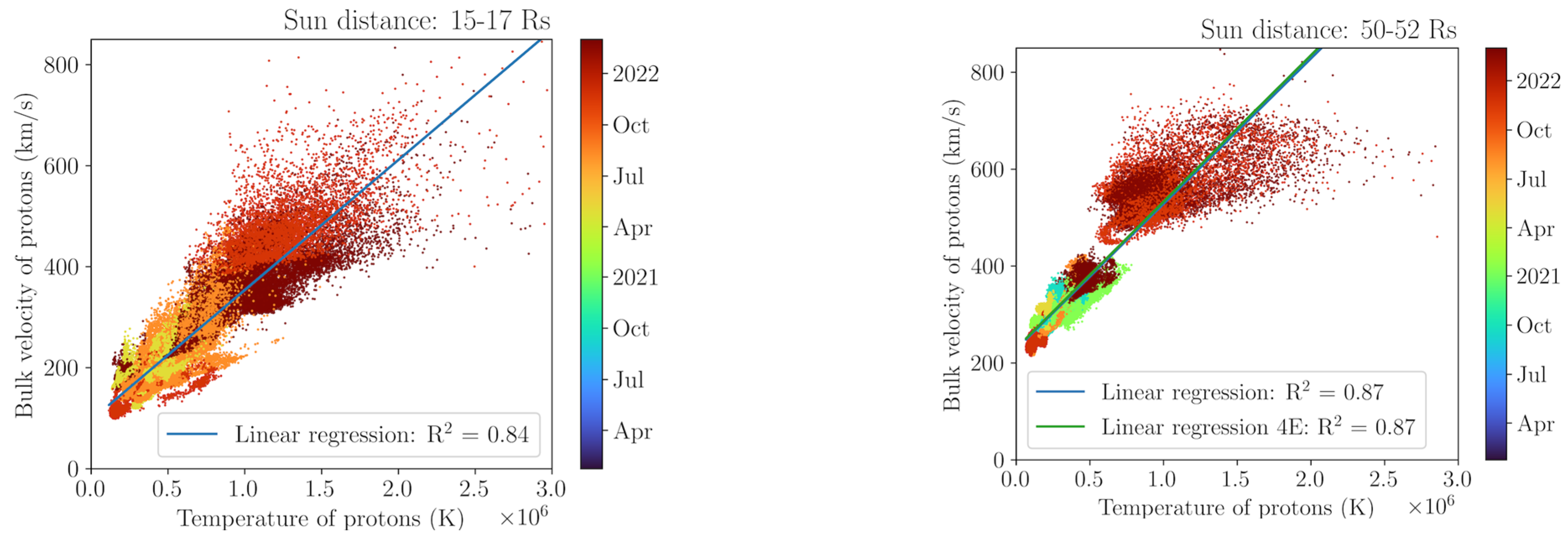
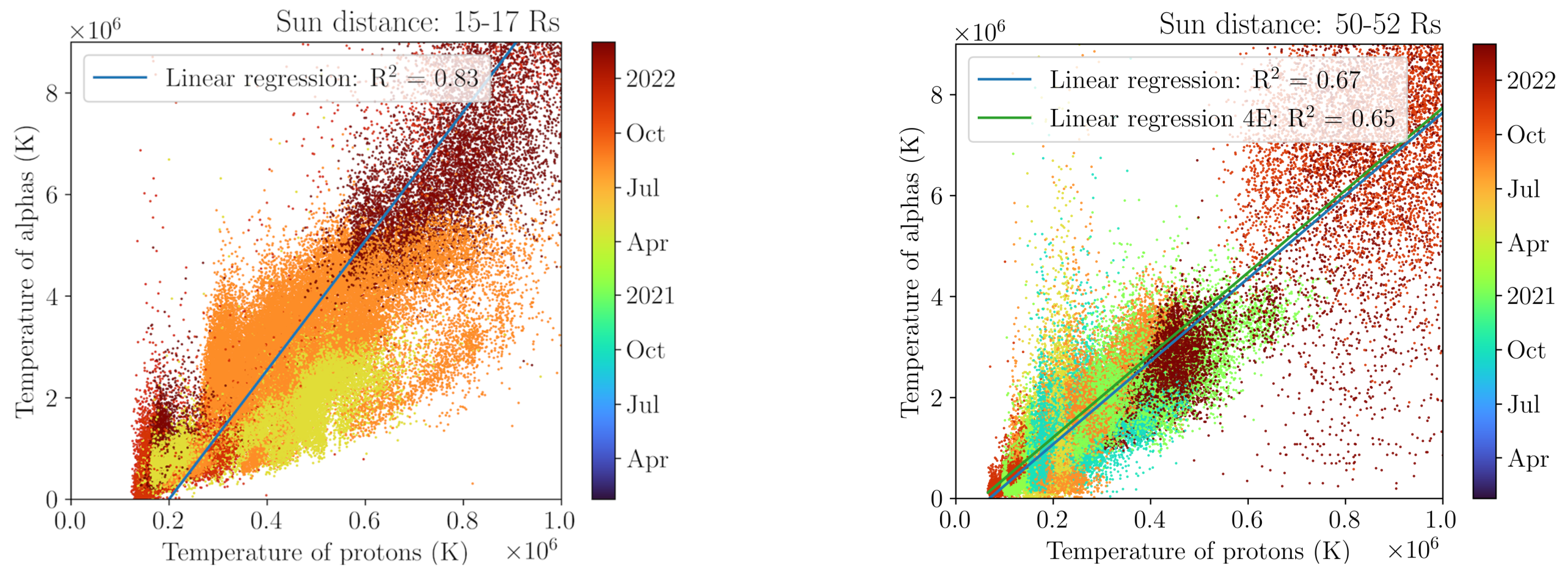
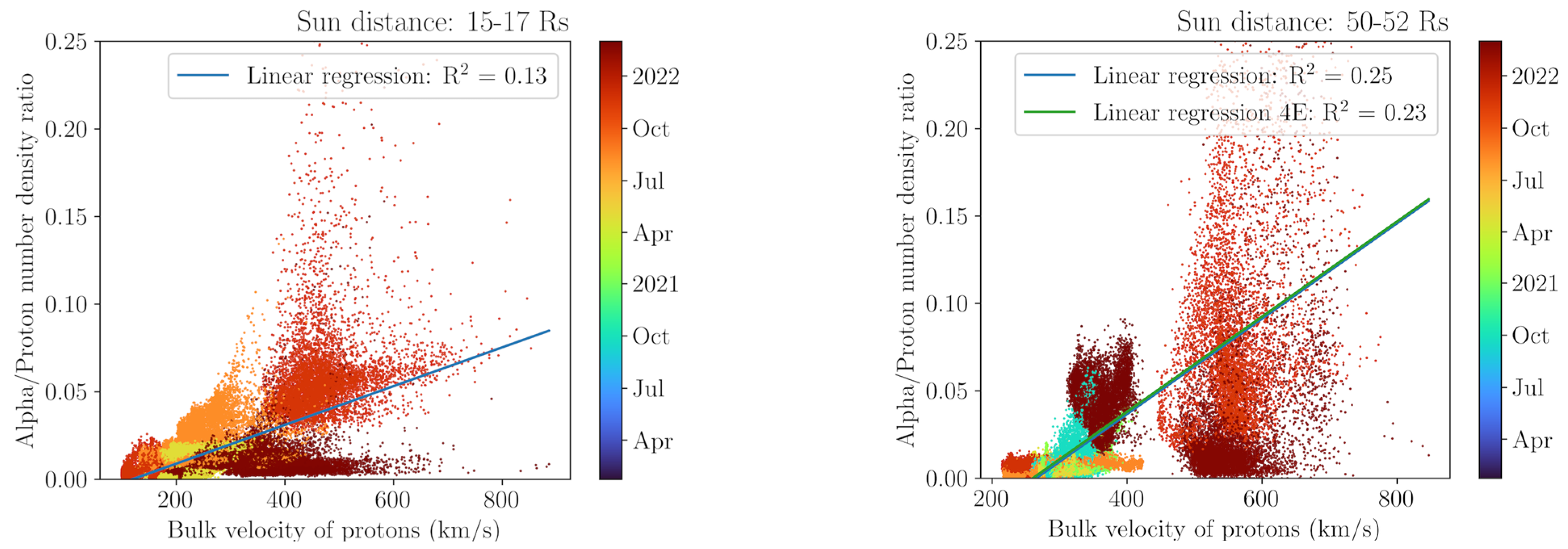
7. Correlation Proton Bulk Velocity-Temperature
8. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Parker, E.N. Dynamics of the interplanetary gas and magnetic fields. Astrophys. J. 1958, 128, 664. [Google Scholar] [CrossRef]
- Lemaire, J.; Scherer, M. Kinetic models of the solar and polar winds. Rev. Geophys. Space Phys. 1973, 2, 427–468. [Google Scholar] [CrossRef]
- Parker, E.N. Kinetic and hydrodynamic representations of coronal expansion and the solar wind. In Proceedings of the 12th International Solar Wind Conference, Saint-Malo, France, 21–26 June 2009; AIP: Melville, NY, USA, 2009. [Google Scholar]
- Pierrard, V.; Maksimovic, M.; Lemaire, J. Core, halo and strahl electrons in the solar wind. Astrophys. Space Sci. 2001, 277, 195–200. [Google Scholar] [CrossRef]
- Maksimovic, M.; Zouganelis, I.; Chaufray, J.-Y.; Issautier, K.; Scime, E.E.; Littleton, J.E.; Marsch, E.; McComas, D.J.; Salem, C.; Lin, R.P.; et al. Radial Evolution of the Electron Distribution Functions in the Fast Solar Wind between 0.3 and 1.5 AU. J. Geophys. Res. 2005, 110, A09104. [Google Scholar] [CrossRef]
- Abraham, J.B.; Owen, C.J.; Verscharen, D.; Bakrania, M.; Stansby, D.; Wicks, R.T.; Nicolaou, G.; Whittlesey, P.L.; Rueda, J.A.A.; Jeong, S.-Y.; et al. Radial Evolution of Thermal and Suprathermal Electron Populations in the Slow Solar Wind from 0.13 to 0.5 au: Parker Solar Probe Observations. Astrophys. J. 2022, 931, 118. [Google Scholar] [CrossRef]
- Scudder, J.D. Why all stars possess circumstellar temperature inversions. Astrophys. J. 1992, 398, 319–349. [Google Scholar] [CrossRef]
- Pierrard, V.; Lemaire, J. Lorentzian ion exosphere model. J. Geophys. Res. 1996, 101, 7923–7934. [Google Scholar] [CrossRef]
- Pierrard, V.; Lamy, H. The effects of the velocity filtration mechanism on the minor ions of the corona. Sol. Phys. 2003, 216, 47–58. [Google Scholar] [CrossRef]
- Pierrard, V.; Lazar, M.; Maksimovic, M. Suprathermal populations and their effects in space plasmas: Kappa vs. Maxwellian. In Kappa Distributions, from Observational Evidences via Controversial Predictions to a Consistent Theory of Nonequilibrium Plasmas; Lazar, M., Fichtner, H., Eds.; Springer/Nature-Astrophysics and Space Science Library: Cham, Switzerland, 2021; pp. 15–38. ISBN 978-3-030-82623-9, Print ISBN 978-3-030-82622-2. [Google Scholar]
- Maksimovic, M.; Pierrard, V.; Lemaire, J. A kinetic model of the solar wind with Kappa distributions in the corona. Astron. Astrophys. 1997, 324, 725–734. [Google Scholar]
- Pierrard, V.; Lamy, H.; Lemaire, J. Exospheric distributions of minor ions in the solar wind. J. Geophys. Res. 2004, 109, A02118. [Google Scholar] [CrossRef]
- Pierrard, V.; Maksimovic, M.; Lemaire, J. Self-consistent kinetic model of solar wind electrons. J. Geophys. Res. 2001, 107, 29305–29312. [Google Scholar] [CrossRef]
- Pierrard, V.; Lazar, M.; Schlickeiser, R. Evolution of the electron distribution function in the whistler wave turbulence of the solar wind. Sol. Phys. 2011, 269, 421–438. [Google Scholar] [CrossRef]
- Sun, H.; Zhao, J.; Liu, W.; Voitenko, Y.; Pierrard, V.; Shi, C.; Yao, Y.; Xie, H.; Wu, D. Electron heat flux instabilities in the inner heliosphere: Radial distribution and implication on the evolution of electron velocity distribution function. Astrophys. J. Lett. 2021, 916, L4. [Google Scholar] [CrossRef]
- Verscharen, D.; Chandran, B.D.G.; Boella, E.; Halekas, J.; Innocenti, M.E.; Jagarlamudi, V.; Micera, A.; Pierrard, V.; Vasko, I.; Velli, M. Electron-driven instabilities in the solar wind. Front. Astron. Space Sci. 2022, 9, 951628. [Google Scholar] [CrossRef]
- Zhao, J.; Lee, L.; Xie, H.; Yao, Y.; Wu, D.; Voitenko, Y.; Pierrard, V. Quantifying Wave-particle Interactions in Collisionless Plasmas: Theory and Its Application to the Alfvén-mode wave. Astrophys. J. 2022, 930, 95. [Google Scholar] [CrossRef]
- Cattell, C.; Breneman, A.; Dombeck, J.; Hanson, E.; Johnson, M.; Halekas, J.; Bale, S.D.; de Wit, T.D.; Goetz, K.; Goodrich, K.; et al. Parker Solar Probe Evidence for the Absence of Whistlers Close to the Sun to Scatter Strahl and to Regulate Heat Flux. Astrophys. J. Lett. 2022, 924, L33. [Google Scholar] [CrossRef]
- Hollweg, J.V.; Isenberg, P.A. Generation of the fast solar wind: A review with emphasis on the resonant cyclotron interaction. J. Geophys. Res. 2002, 107, 12–37. [Google Scholar] [CrossRef]
- Marsch, E. Kinetic physics of the solar corona and solar wind. Living Rev. Sol. Phys. 2006, 3, 1. [Google Scholar] [CrossRef]
- Cranmer, S.R. Self-consistent models of the solar wind. Space Sci. Rev. 2012, 172, 145–156. [Google Scholar] [CrossRef]
- Roberts, D.A. Demonstrations that the solar wind is not accelerated by waves or turbulence. Astrophys. J. 2010, 711, 1044–1050. [Google Scholar] [CrossRef]
- Isenberg, P.A.; Vasquez, B.J. A kinetic model of solar wind generation by oblique ion-cyclotron waves. Astrophys. J. 2011, 731, 88. [Google Scholar] [CrossRef]
- Cranmer, S.R.; van Ballegooijen, A.A. Can the solar wind be driven by magnetic reconnection in the Sun’s magnetic carpet. Astrophys. J. 2010, 720, 824. [Google Scholar] [CrossRef]
- Berčič, L.; Larson, D.; Whittlesey, P.; Maksimović, M.; Badman, S.T.; Landi, S.; Matteini, L.; Bale, S.D.; Bonnell, J.W.; Case, A.W.; et al. Coronal Electron Temperature Inferred from the Strahl Electrons in the Inner Heliosphere: Parker Solar Probe and Helios Observations. Astrophys. J. 2020, 892, 88. [Google Scholar] [CrossRef]
- Halekas, J.S.; Whittlesey, P.; Larson, D.E.; McGinnis, D.; Maksimovic, M.; Berthomier, M.; Kasper, J.C.; Case, A.W.; Korreck, K.E.; Stevens, M.L.; et al. Electrons in the Young Solar Wind: First Results from the Parker Solar Probe. Astrophys. J. Suppl. Ser. 2020, 246, 2. [Google Scholar] [CrossRef]
- Zhao, J.; Malaspina, M.D.; Dudok De Wit, T.; Pierrard, V.; Voitenko, Y.; Lapenta, G.; Poedts, S.; Bale, S.D.; Kasper, J.C.; Larson, D.; et al. Broadband Electrostatic Waves in the Near-Sun Solar Wind Observed by the Parker Solar Probe. Astrophys. J. Lett. 2022, 938, L21. [Google Scholar] [CrossRef]
- Rouillard, A.P.; Viall, N.; Vocks, C.; Wu, Y.; Pinto, R.; Lavarra, M.; Matteini, L.; Pierrard, V.; Sanchez-Diaz, E.; Alexandrova, O.; et al. The solar wind. In Solar Physics and Solar Wind; Raouafi, N.-E., Vourlidas, A., Eds.; Wiley: Hoboken, NJ, USA, 2021; Volume 1, pp. 1–33. 320p, ISBN 978-1-119-50753-6. [Google Scholar] [CrossRef]
- Scherer, K.; Fichtner, H.; Lazar, M. Regularized κ-distributions with nondiverging Moments. Europhys. Lett. 2017, 120, 50002. [Google Scholar] [CrossRef]
- Fichtner, H.; Lazar, M. Introduction and motivation. In Kappa Distributions, from Observational Evidences via Controversial Predictions to a Consistent Theory of Nonequilibrium Plasmas; Lazar, M., Fichtner, H., Eds.; Springer/Nature–Astrophysics and Space Science Library: Cham, Switzerland, 2021; pp. 3–12. [Google Scholar]
- Maksimovic, M.; Pierrard, V.; Riley, P. Ulysses electron distributions fitted with Kappa functions. Geophys. Res. Let. 1997, 24, 1151–1154. [Google Scholar] [CrossRef]
- Lazar, M.; Scherer, K.; Fichtner, H.; Pierrard, V. Towards a realistic macroscopic parametrization of space plasmas with regularized Kappa-distribution. Astron. Astrophys 2020, 634, A20. [Google Scholar] [CrossRef]
- Scherer, K.; Lazar, M.; Husidic, E.; Fichtner, H. Moments of the Anisotropic Regularized κ-distributions. Astrophys. J. 2019, 880, 118. [Google Scholar] [CrossRef]
- Lazar, M.; Pierrard, V.; Poedts, S.; Fichtner, H. Characteristics of solar wind suprathermal halo electrons. Astron. Astrophys. 2020, 642, A130. [Google Scholar] [CrossRef]
- McComas, D.J.; Ebert, R.W.; Elliott, H.A.; Goldstein, B.E.; Gosling, J.T.; Schwadron, N.A.; Skoug, R.M. Weaker solar wind from the polar coronal holes and the whole Sun. Geophys. Res. Lett. 2008, 35, L18103. [Google Scholar] [CrossRef]
- Pierrard, V.; Pieters, M. Coronal heating and solar wind acceleration for electrons, protons and minor ions obtained from kinetic models based on Kappa distributions. J. Geophys. Res. Space Phys. 2014, 119, 9441–9455. [Google Scholar] [CrossRef]
- Spitzer, L.; Härm, R. Transport Phenomena in a Completely Ionized Gas. Phys. Rev. 1953, 89, 977. [Google Scholar] [CrossRef]
- Halekas, J.S.; Berčič, L.; Whittlesey, P.; Larson, D.E.; Livi, R.; Berthomier, M.; Kasper, J.C.; Case, A.W.; Stevens, M.L.; Bale, S.D.; et al. The Sunward Electron Deficit: A Telltale Sign of the Sun’s Electric Potential. Astrophys. J. 2021, 916, 16. [Google Scholar] [CrossRef]
- Liu, M.; Issautier, K.; Moncuquet, M.; Meyer-Vernet, N.; Maksimovic, M.; Huang, J.; Martinovic, M.M.; Griton, L.; Chrysaphi, N.; Jagarlamudi, V.K.; et al. Total electron temperature derived from quasi-thermal noise spectroscopy in the pristine solar wind from Parker Solar Probe observations. Astron. Astrophys 2023, 674, A49. [Google Scholar] [CrossRef]
- Halekas, J.S.; Whittlesey, P.; Larson, D.E.; Maksimovic, M.; Livi, R.; Berthomier, M.; Kasper, J.C.; Case, A.W.; Stevens, M.L.; Bale, S.D.; et al. The Radial Evolution of the Solar Wind as Organized by Electron Distribution Parameters. Astrophys. J. 2022, 936, 53. [Google Scholar] [CrossRef]
- Lamy, H.; Pierrard, V.; Maksimovic, M.; Lemaire, J. A kinetic exospheric model of the solar wind with a nonmonotonic potential energy for the protons. J. Geophys. Res. Space Phys. 2003, 108, 1–11. [Google Scholar] [CrossRef]
- Kasper, J.C.; Abiad, R.; Austin, G.; Balat-Pichelin, M.; Bale, S.D.; Belcher, J.W.; Berg, P.; Bergner, H.; Berthomier, M.; Bookbinder, J.; et al. Solar wind electrons alphas and protons (SWEAP) investigation: Design of the solar wind and coronal plasma instrument suite for Solar Probe Plus. Space Sci. Rev. 2016, 204, 131–186. [Google Scholar] [CrossRef]
- Whittlesey, P.L.; Larson, D.E.; Kasper, J.C.; Halekas, J.; Abatcha, M.; Abiad, R.; Berthomier, M.; Case, A.W.; Chen, J.; Curtis, D.W.; et al. The Solar Probe Analyzers–Electrons on the Parker Solar Probe. Astrophys. J. Suppl. Ser. 2020, 246, 74. [Google Scholar] [CrossRef]
- Livi, R.; Larson, D.E.; Kasper, J.C.; Abiad, R.; Case, A.W.; Klein, K.G.; Curtis, D.W.; Dalton, G.; Stevens, M.; Korreck, K.E.; et al. The Solar Probe Analyzer–Ions on the Parker Solar Probe. Astrophys. J. 2022, 938, 138. [Google Scholar] [CrossRef]
- Wang, L.; Lin, R.P.; Salem, C.; Pulupa, M.; Larson, D.E.; Yoon, P.H.; Luhmann, J.G. Quiet-time Solar Wind Superhalo Electrons at Solar Minimum. In AIP Conference Proceedings, Proceedings of the Thirteenth International Solar Wind Conference, Big Island, HI, USA, 17–22 June 2012; American Institute of Physics: College Park: Maryland, MD, USA, 2013; Volume 1539, p. 299. [Google Scholar] [CrossRef]
- Maksimovic, M.; Walsh, A.; Pierrard, V.; Stverak, S.; Zouganelis, I. Electron Kappa distributions in the solar wind: Cause of the acceleration or consequence of the expansion? In Kappa Distributions, from Observational Evidences via Controversial Predictions to a Consistent Theory of Nonequilibrium Plasmas; Lazar, M., Fichtner, H., Eds.; Springer/Nature–Astrophysics and Space Science Library: Cham, Switzerland, 2021; pp. 39–51. [Google Scholar]
- Štverák, Š.; Maksimovic, M.; Trávníček, P.M.; Marsch, E.; Fazakerley, A.N.; Scime, E.E. Radial evolution of nonthermal electron populations in the low-latitude solar wind: Helios, Cluster, and Ulysses Observations. J. Geophys. Res. 2009, 114, A05104. [Google Scholar] [CrossRef]
- Pierrard, V.; Lazar, M.; Stverak, S. Solar wind plasma particles organized by the flow speed. Solar Phys. 2020, 295, 151. [Google Scholar] [CrossRef]
- Pierrard, V.; Lazar, M.; Stverak, S. Implications of the Kappa Suprathermal Halo of the Solar Wind Electrons. Front. Astron. Space Sci. 2022, 9, 892236. [Google Scholar] [CrossRef]
- Marsch, E. Helios: Evolution of distribution functions 0.3-1 AU. Space Sci. Rev. 2012, 172, 23–39. [Google Scholar] [CrossRef]
- Pierrard, V.; Borremans, K.; Stegen, K.; Lemaire, J. Coronal temperature profiles obtained from kinetic models and from coronal brightness measurements obtained during solar eclipses. Sol. Phys. 2014, 289, 183–192. [Google Scholar] [CrossRef]
- Voitenko, Y.; Pierrard, V. Proton beams generation by non-uniform solar wind turbulence. Solar Phys. 2015, 290, 1231–1241. [Google Scholar] [CrossRef]
- Fu, H.; Madjarska, M.S.; Li, B.; Xia, L.; Huang, Z. Helium abundance and speed difference between helium ions and protons in the solar wind from coronal holes, active regions, and quiet Sun. Mon. Not. R. Astron. Soc. 2018, 478, 1884–1892. [Google Scholar] [CrossRef]
- Pierrard, V.; Maksimovic, M.; Lemaire, J. Electron velocity distribution function from the solar wind to the corona. J. Geophys. Res. 1999, 104, 17021–17032. [Google Scholar] [CrossRef]


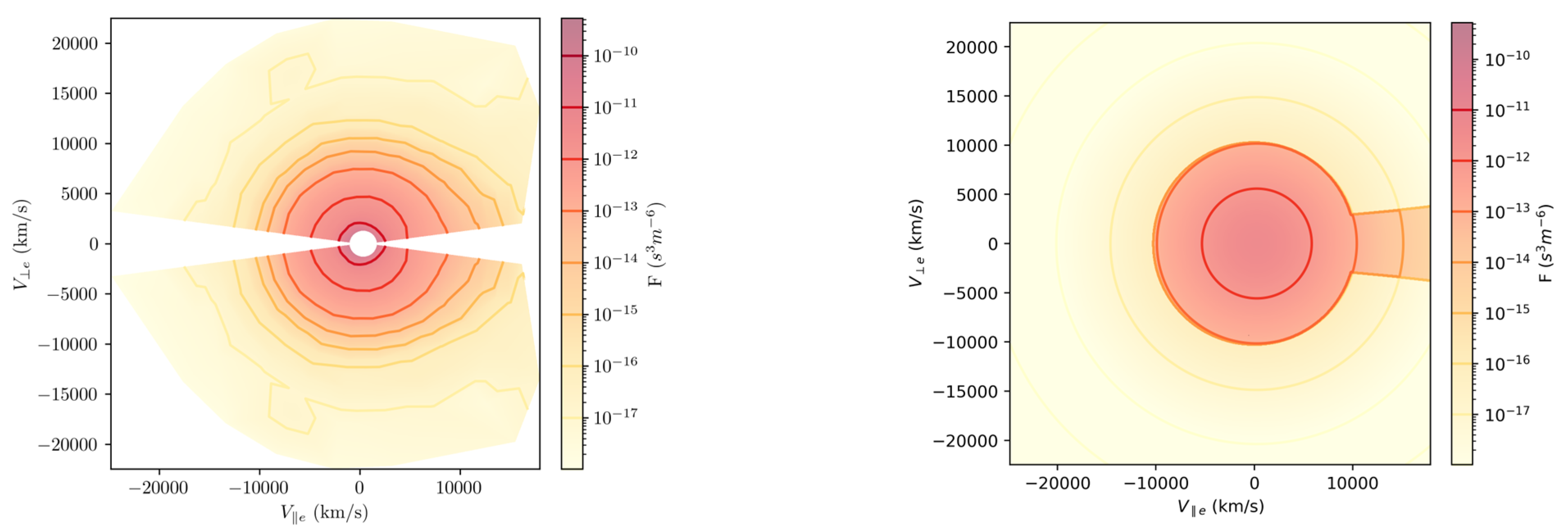
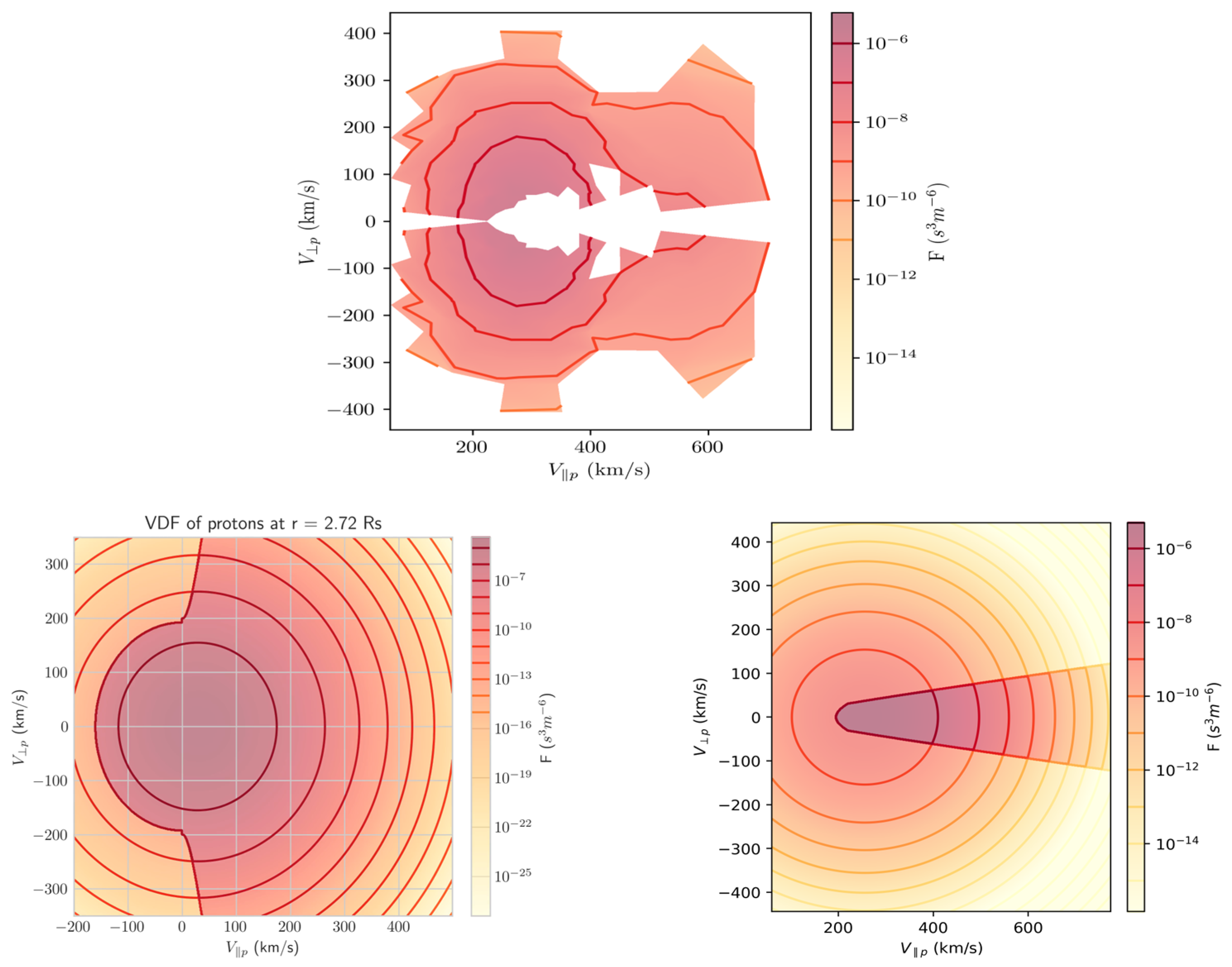
| Wind Type | Exobase Level (r0) | Density at Exobase (n0) | Temperature of Electrons at Exobase (T0e) | Temperature of Protons at Exobase (T0p) | Kappa (for Electrons) |
|---|---|---|---|---|---|
| SSW | 2.7 Rs | 4 × 1011 m−3 | 1.5 × 106 K | 1.25 × 106 K | 5 |
| FSW | 1.25 Rs | 1 × 1012 m−3 | 1.35 × 106 K | 4.06 × 106 K | 2.23 |
| Angle | n [109 m−3] (err) | Tκ [105 K] (err) | κ | R2 | |
|---|---|---|---|---|---|
| Full dataset | |||||
| 7.5° | 4.07 (0.82) | 2.86 (0.29) | 2.16 (0.36) | 0.961 | |
| 22.5° | 3.92 (0.75) | 2.55 (0.31) | 3.49 (0.51) | 0.969 | |
| 82.5° | 4.24 (0.61) | 1.76 (0.14) | 4.10 (0.31) | 0.973 | |
| 172.5° | 3.82 (0.90) | 2.39 (0.30) | 4.79 (0.51) | 0.978 | |
| Restricted dataset | |||||
| 7.5° | 1.75 (0.31) | 5.54 (0.63) | 6.41 (2.62) | 0.94 | |
| 22.5 | 1.56 (0.05) | 6.08 (0.13) | 9.22 (1.66) | 0.999 | |
| 82.5° | 1.50 (0.15) | 4.29 (0.23) | 104.3 | 0.996 | |
| 82.5° | Maxw | 1.63 (0.10) | 4.32 (0.07) | 0.997 | |
| 172.5° | 1.56 (0.25) | 4.75 (0.48) | 91.8 | 0.979 | |
| 172.5° | Maxw | 2.04 (0.19) | 4.56 (0.14) | 0.99 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pierrard, V.; Péters de Bonhome, M.; Halekas, J.; Audoor, C.; Whittlesey, P.; Livi, R. Exospheric Solar Wind Model Based on Regularized Kappa Distributions for the Electrons Constrained by Parker Solar Probe Observations. Plasma 2023, 6, 518-540. https://doi.org/10.3390/plasma6030036
Pierrard V, Péters de Bonhome M, Halekas J, Audoor C, Whittlesey P, Livi R. Exospheric Solar Wind Model Based on Regularized Kappa Distributions for the Electrons Constrained by Parker Solar Probe Observations. Plasma. 2023; 6(3):518-540. https://doi.org/10.3390/plasma6030036
Chicago/Turabian StylePierrard, Viviane, Maximilien Péters de Bonhome, Jasper Halekas, Charline Audoor, Phyllis Whittlesey, and Roberto Livi. 2023. "Exospheric Solar Wind Model Based on Regularized Kappa Distributions for the Electrons Constrained by Parker Solar Probe Observations" Plasma 6, no. 3: 518-540. https://doi.org/10.3390/plasma6030036
APA StylePierrard, V., Péters de Bonhome, M., Halekas, J., Audoor, C., Whittlesey, P., & Livi, R. (2023). Exospheric Solar Wind Model Based on Regularized Kappa Distributions for the Electrons Constrained by Parker Solar Probe Observations. Plasma, 6(3), 518-540. https://doi.org/10.3390/plasma6030036






