Abstract
The nonlinear excitations of ion acoustic (IA) structures in an electron beam embedded plasma composed of Vasyliunas–Cairns (VC) distributed hot electrons has been studied. The nonlinear Schrödinger equation (NLSE) from the Kadomtsev–Petviashvili (KP) equation with suitable transformation has been derived from rational solutions of NLSE; breathers have been studied. It has been shown that the nonthermality and superthermality of the electrons, the electron beam density, and the beam velocity alter the characteristics of different kinds of breathers. This investigation may be important in interpreting the physics of nonlinear structures in the upper layer of magnetosphere.
1. Introduction
Numerous studies have focused mainly on the investigation of different nonlinear structures in various plasma environments during the past few decades. With a variety of experiments and computer simulations revealing the basic physical phenomena of localized structures, evolution in the study of nonlinear phenomena appears to be accelerating presently. Different sorts of nonlinear homogeneous/inhomogeneous equations are developed using various techniques to explore the study of these types of structures. The KP equation [1], often known as an extension of the Korteweg–de Vries (KdV) equation, has been developed to explore two-dimensional solitary structures. For the case of one-dimensional perturbations, the soliton from KdV equation is stable if the soliton and its perturbations both are illustrated by means of KdV equation. Furthermore, the collision of two solitons is elastic, which means that their shapes and amplitudes remain unchanged after the impact. A one-dimensional soliton, however, may become unstable in the presence of two-dimensional perturbations if it propagates infinitely in two directions. The Kadomtsev–Petviashvili (KP) equation, a two-dimensional form of the KdV equation, which was derived by Kadomtsev and Petviashvili [1], determined this issue. In that study, it was demonstrated that the sign of wave dispersion affects the stability of KdV solitons with reference to two-dimensional transverse perturbations. Solitons are unstable when the wave dispersion is positive, which means that the wave frequency is monotonically increasing as function of the wave number; however, for a stable case of soliton wave, the frequency is monotonically decreasing and the dispersion of the wave is negative. Several publications [2,3,4,5,6,7] have reported the derivation of the KP equation in various plasmas to examine solitary structures. Saini et al. [3] employed the KP equation’s solution to study the propagation properties of dust acoustic (DA) solitary waves in a superthermal dusty plasma that consisted of ions and superthermal electrons. The combined effects of superthermality of electrons, ions, and dust concentration on the amplitude and breadth of DA solitary waves under transverse perturbations were investigated. Kohli et al. [5] applied the KP equation to assess the effect of ion beam and other plasma factors on the characteristics of DA solitary waves under transverse disturbances in a dusty plasma. They discovered that the variations in the values of ion density, beam density, beam velocity, and superthermality of ions and electrons had a significant impact on the amplitude, breadth, and energy of dust acoustic waves (DAWs). Ruderman [6] investigated the impact of transverse perturbations by employing the KP equation on the stability of magnetosonic solitons in a Hall plasma and demonstrated that fast and slow magnetosonic solitons are both unstable in the presence of transverse disturbances. These soliton formations are the result of the nonlinearity of medium and wave phase dispersion effects being balanced. Further, envelope solitons (localized modulated wave packets) arise if the balance between the wave group’s dispersion and the medium’s non-linearity is achieved, and their evolution is controlled by the nonlinear Schrödinger equation (NLSE).
Both the nonlinear Schrödinger equation (NLSE) and the KP equation can be used to explain the nonlinear waves in a plasma. The KP equation describes the occurrence of a non-modulated wave, also known as the KP soliton, which is a single pulse without any rapid oscillations throughout the packet. A modulated wave packet’s dynamics is monitored by the NLSE. The nonlinearities in the NLSE are balanced with the wave group dispersion, and the NLSE’s solutions exhibit a variety of nonlinear structures such as breathers, rogue waves, and envelope solitons as a result.
The NLSE, one of the most significant physics equations, is utilized to describe a wide range of nonlinear phenomena in diverse physical domains. The primary mechanism of such wave production in the framework of the NLSE is modulational instability (MI), which enables high-intensity peaks and promotes the formation and interaction of the various nonlinear phenomena (freak waves, breathers, and Peregrine solitons). Furthermore, instability induced by a modest plane wave disturbance causes amplitudes to rise exponentially until they entirely vanish. NLSE’s rational solution in the unstable area is a crucial mathematical model for the different nonlinear phenomena. Different nonlinear phenomena on a periodic background are more frequently preferable than those on a constant background. For the NLS equation and the modified Korteweg–de Vries equation, researchers have explored various nonlinear structures such as breathers and freak waves on the non-constant backdrop (such as the periodic background). The NLSE has different kinds of solutions; these describe the different kinds of nonlinear structures such as rogue waves, breather structures, envelope solitons, Peregrine soliton etc. Rogue waves are transient waves that emerge out of nowhere and were found in the ocean. Following that, the study of these waves was gradually expanded to other domains, such as optical fibres, the atmosphere, capillary water waves, superfluid helium, Bose–Einstein condensates, even in astronomical conditions, and more recently, laboratory plasma physics [8]. They are a violent event with a limited duration appearing out of nowhere. Their usual height might be more than twice as high as the waves around them. There has been a lot of interest in investigating the modulation instability of various wave modes in plasma for breather structures. Many researchers in various types of plasma have investigated the modulation instability and breather structures as one of the exciting and intriguing nonlinear phenomena [8,9,10,11,12,13,14,15,16,17]. Abdikian and Ismaeel [9] explored IA breathers and rogue waves in relativistically degenerate electron-positron plasmas and reported that the region of MI increased with increase in temperature of ions; this implies that there were high chances of existence of breather structures and amplitude of rogue waves decreased with enhancement in relativistic factor. Effects of electron trapping on IA breathers and super freak waves in degenerate quantum plasma were examined by El-Tantawy et al. [8]. They observed that an increase in temperature of degenerate trapped species leads to an increase in the area of MI of IA waves and decrease in amplitude of breather structures. MI of IA waves in Cairns distributed hot ion plasma was reported by Shan et al. [10] to explore the breather structures and it was reported that nonthermality significantly modifies the region of MI and amplitude of nonlinear structures. Employing the Gardner equation, a broad spectrum of nonlinear IA wave structures and their group dynamics are examined in a negative ion plasma by Ghosh [12]. Ullah et al. [14] studied the MI of electron acoustic waves in three component (r,q) distributed plasma. They observed that the range for area of MI highly fluctuated due to the presence of warm (r,q) distributed species. The comparison of growth rate of instability for kappa and Maxwellian case was also discussed in detail by them in their investigation. Saini and Kaur [15] investigated the propagation properties of solitary, breather, and freak waves in a degenerate quantum plasma with spin effect. They remarkably announced that the spin density polarization ratio drastically changes the properties of propagation of a nonlinear wave. The progressive nonlinear development of electron acoustic solitons into a peregrine soliton in a plasma at a fixed temperature with quantum effects was explored by Das et al. [17]. It was announced that external forcing term is responsible for this development and the properties of nonlinear wave structures showed dynamical behaviour. Therefore, studying the properties of breathers in IA plasma is highly intriguing.
The electron beam and IA waves occur side by side in space and the existence of electron beams alters the ion acoustic waves’ characteristics in a drastic way [18,19]. Numerous investigations have demonstrated that the electron beam and other physical factors have a significant impact on the propagation properties of nonlinear waves in beam plasmas [20,21,22,23,24,25,26,27,28,29,30]. The comparison of reductive perturbation technique and pseudopotential method to study the impact of electron beam in multi-species plasma comprising electrons, positrons, and negative ions was reported by Moslem [20] and indicated that effective potentials of both equations from these two methods agree to an identical extent. The impact of relativistic electron beam on propagation of solitons and double layers in a two-electron temperature plasma was explored by Sahu and Roychoudhury [22]. They discovered that the value of relativistic and beam parameters limits the region in which solitary waves may occur. To investigate the influence of beam parameters on nonlinear solitary and double-layer structures, Lakhina et al. [24] evolved out a model in four-component plasma that replicated the magnetosheath plasma and they predicted the same characteristic of electrostatic bipolar pulse by the model as the observed ones. The energy balance equation in superthermal plasma immersed with an electron beam was derived using the pseudopotential technique by Saini and Kourakis [25], who also examined how the characteristics of the electron beam and the superthermality of the electrons affected the development of arbitrary amplitude IA solitary waves. Further, the impact of finite ion temperature with beam parameters on characteristics of IA solitons in a superthermal plasma system was reported by Saberian et al. [26]. It was reported that both polarity solitons, both supersonic and subsonic speeds of solitons, exist in a particular region that is influenced by beam parameters. In order to study the effect of electron beam on the traits of IA rogue waves and on head-on collision of multi-solitons in a superthermally distributed plasma, Singla and Saini [28] adopted the Poincar–Lighthill–Kuo method and underlined the impact of the electron beam and the electrons’ superthermality on the phase shift of multi-solitons brought on by their interaction as well as on the propagation characteristics of IA solitons. In a multicomponent beam plasma, the features of electron acoustic (EA) rogue wave series were studied by Kaur et al. [30] and it was emphasized that the characteristic of EA rogue wave series drastically changed in the presence of beam. The consequences of addition of higher-order corrections to IA shocks with beam in superthermally distributed plasma were studied by Saini and Singla [29]. It was remarked that in the absence (presence) of beam, only positive (negative) polarity shocks existed and the higher orders contributed to both polarity shock waves.
Owing to wave–particle interactions, external influences, and plasma components that are no longer in equilibrium, energetic particles exist in space plasmas. These are very energetic particles with extended high-energy tails, according to several satellite data from space [31] and their velocity distribution alters the characteristics of plasma constituents that influence the nonlinear structures. The highly energetic non-Maxwellian particles are generally assumed to be described by the Kappa [32] and Cairns [33] velocity distribution functions. For analysing nonlinear processes, the more generalised version of non-Maxwellian distribution function may be the optimum distribution. So, it is preferable to employ the VC distribution (as hybrid distribution) [34] compared to a single non-Maxwellian distribution to investigate several nonlinear phenomena because at the peaks, the distribution function is well described by the Cairns distribution and along the tail, it is well-justified by the kappa distribution. The VC distribution function is represented as [2]
where , , , ; the thermal velocity of electrons is . For a realistic case, (), also for , kappa distribution exists and with & →∞, Maxwellian case is retrieved. To more accurately analyse diverse linear and nonlinear phenomena occurring in space and astrophysical circumstances, VC distribution function for plasma species has been developed [35,36,37,38]. Debnath and Bandyopadhyay [36] explored the combined effects of the Kappa and Cairns distributed electrons on the IA solitary structures in a magnetized plasma in presence of dust. It was reported that in the phase space at the vicinity of v = 0 in addition to at the tail of the distribution curve, this combined distribution can produce significantly more highly energetic particles. Another novel finding in the investigation of IA waves in magnetized dusty plasma is the production of ion acoustic supersolitons in magnetized plasma without the occurrence of an IA double layer. The dispersion and damping rate of IA waves was examined by Shahzad et al. [37] both analytically and quantitatively. They reported that the damping rate for VC distributed plasma is lower than Maxwellian one. Sarkar et al. [38] examined the role of this distribution in electron-ion plasma on electrostatic wave propagation. It was remarked that the wave is stabilised by the population of suprathermal particles, whereas the wave is destabilised by the population of nonthermal particles.
In this work, we explore the properties of IA breathers from the solutions of NLSE in a multicomponent plasma embedded with electron beam and composed of ions, VC distributed electrons, in order to provide new insight into prior studies. Our objective is to use the KP equation to derive NLSE. Then, from the solutions of this equation, the influence of different plasma factors on the propagation characteristics of IA breathers has been examined. The paper is organised as follows: Section 2 presents basic fluid equations. The KP equation and the derivation of nonlinear Schrdinger equation are described in Section 3. Section 4 presents the solution of NLSE and its analysis. The conclusions are presented in Section 5.
2. Basic Fluid Equations
A plasma made up of fluid ions and electrons that follow VC distribution and are penetrable by an electron beam is studied. The group of normalized fluid equations is denoted as [2]:
The continuity equation for ions and electrons beam is
here, . The momentum equations for ions and beam are written as
For ions:
For electron beam:
with . The Poission equation is written as
The expression of normalized VC distributed electron density is given as [2]
and
The superthermality and nonthermality (with ) of electrons are shown by the spectral index and . Here, denotes the number density of ions, beam, and superthermal electrons and is normalized by unperturbed ion density. are normalized by sound speed ). The temperature of ions and beam is represented by and with and . Time coordinate and potential function are normalized by inverse of plasma ion frequency and , respectively. The space variable is normalized by Debye length . The charge neutrality condition yields as with and .
3. The KP Equation and Derivation of Nonlinear Schrdinger Equation (NLSE)
We have employed the reductive perturbation technique, the stretching of independent variables (space and time) for transverse perturbation, to construct the KP equation which elaborates the nonlinear features of ion acoustic waves in given plasma and is:
The extended form of the perturbed quantities is [2]:
A series of equations may be obtained by replacing Equations (9) and (10) in Equations (2)–(7) and equating the coefficients of different powers on each side. The following KP equation has been obtained from the above equations [2,5]:
The nonlinear, dispersion and higher-order coefficients are stated as:
with obtained as dispersion relation; here, and . Further details can be seen in paper reported by Kohli et al. [5]. The same KP Equation (11) has been employed in this study to examine at the peculiarities of breathers. To derive NLSE from the KP equation, we have employed transformation as and . Here, F and G are direction cosines of the wave vector along the X and Y axes, respectively, so that and M is an arbitrary parameter same as the Mach number. Substituting new variables in Equation (11), we get:
where . We assume the solution of Equation (13) as [39]:
where represents the frequency and k denotes carrier wave number. The new stretched coordinates are and . For further derivation, using the procedure adopted in [4], we have determined the different quantities and NLSE as follows.
Dispersion relation is obtained from first-order approximation (l = 1, n = 1) as follows:
The group velocity is determined from first harmonic (l = 1) of second approximation (n = 2) as
The zeroth harmonic (l = 0, n = 2) gives
From the second harmonic, we get
After rigorous algebraic calculations and by eliminating higher-order terms, from n = 3, l = 1, we get the NLSE as [3]
for simplicity . The nonlinear coefficient and dispersion coefficient depend upon various plasma parameters through A and B so that it can alter the stability condition. To discuss the modulational instability, we consider a small perturbation such that ; here, the term represents nonlinear frequency shift. The amplitude of carrier wave () is greater than perturbation (). By substituting the value of in Equation (19) and from first-order quantities, we obtain
The amplitude of perturbation is assumed to be proportional to and this condition yields to
From this equation, it is disclosed that for all k only when is negative. So, is real and tends to stability of wave. On the contrary, for a positive value of , turns to imaginary (for wave number (k)< critical value and wave becomes modulationally unstable. The expression for growth rate instability for this case is given by
It acquires maximum value, i.e., at . There is much curiosity in the events that lead to breather waves becoming significant, and several explanations have been offered.The nonlinear mechanism of the self-wave interactions, such as the MI of the envelope IA waves, is a key theory and has been shown to create a massive wave in specific circumstances.
4. Various Types of Localized Solutions of the NLSE
There are various types of solutions of NLSE those describe different kinds of nonlinear waves, named freak waves, breathers, Peregrine solitons, etc. Basically, these waves are result of the wave instability; the growth of instability is nonlinear which tends to localize the energy of wave into one particular region. Generally, the first-order breather solution of Equation (20) is given as [13]
Here, and , as it is clear from these quantities, the physical behaviour of this solution depends upon the parameter R. Further, this solution has been categorized into three types of breather solutions: (i) space–time localized solution, (ii) space localized solution, (iii) time periodic solution. These solutions are illustrated as follows:
- (i)
- Space–time localized solution: The solution given by Equation (23) turns down to freak wave solution or space–time localized solution as . Peregrine was the first scientist to study the first-order freak wave as the solution of the generalised NLSE. Localized pulses of massive amplitude are produced as a result of self-modulation occurring inside the slowly evolving amplitude-modulated perturbation. Additionally, the first-order freak wave’s observed amplitude is three times that of the adjacent carrier wave, which is consistent with the NLSE’s rational inference. The expression for first-order freak waves is given asthe amplitude is maximum when and t both are zero, i.e., . Further, when a number of first-order freak waves superimpose on each other and produce a wave that remains localized in both space and time but its amplitude is more than individual waves, this is named a super freak wave. The expression for super freak wave is
- (ii)
- Space localized solution: In Equation (23) for and , , the solution will have real values localized in time and exhibit a periodic modulation in space with period (here), known as Akhmediev breather. The expression for the peak amplitude is given as
- (iii)
- Time periodic solution: In Equation (23) for , the , become imaginary and hyperbolic functions are replaced with ordinary circular functions and vice versa, the solution will have real values; the solution is periodic in time (with period ) and is known as Kuznetsov–Ma breather, given asThe peak amplitude is , for . The peak amplitude of the Kuznetsov–Ma breather is more than that of the Akhmediev breather. Thus, the characteristics of breathers depend on various plasma parameters through nonlinearity and dispersion coefficients by varying different physical parameters.
Figure 1 depicts the plot of growth rate of instability () with wave number (k) for the cases of with and without beam. It is observed that the growth rate of instability () increases to its maximum value, then starts decreasing as the value of wave number (k) increases. With increase in ratio of density of beam to ions (), nonthermality parameter () growth rate of instability decreases, and with the superthermality parameter (), it increases. It is also observed that the maximum value of growth rate for without beam is eight times lower than the case of with beam. This implies that the electron beam parameters have significant impact on the growth rate of instability.
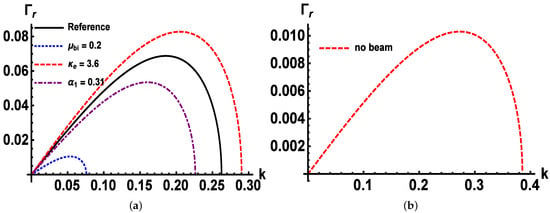
Figure 1.
The plot of growth rate of instability () with wave number (k) (a) with beam, for reference curve: , , ; (b) without beam; other parameters are , , and and .
Figure 2 reveals the first-order freak waves’ profile with/without beam. It is easily perceived that the large amount of energy is intensified in a small area in space so the amplitude of freak waves’ profile enhances vertically very high as compared to surroundings. The wave withdraws energy from other neighbouring waves and fixates it into a particular place, then become unstable and soon collapses. Figure 2a shows that with an increase in ratio of density of beam to ions (), the nonlinearity and dispersion are increased which results in an increase in amplitude and width of first-order freak waves. On increasing the ratio of temperature of beam to electrons (), nonlinearity decreases which makes the amplitude of first-order freak waves decrease. The variation of first-order freak waves’ profile with superthermality () and nonthermality () parameters with beam is illustrated in Figure 2b.
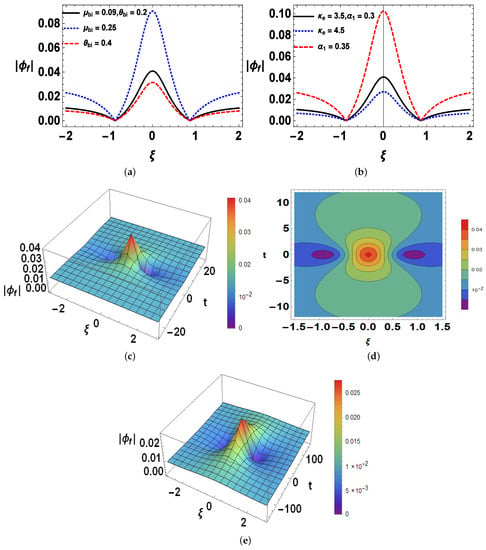
Figure 2.
The variation of first- order freak waves’ profile () with (a) ratio of density of beam to ions (), ratio of temperature of beam to electrons (); (b) superthermality parameter (), nonthermality parameter (); Solid reference curve: , , and ; (c) 3D profile; (d) contour plot; (e) without beam ().
With an increase in superthermality coefficient () (i.e., decrease in superthermality), nonlinearity decreases, and with an increase in nonthermality parameters (), nonlinearity increases; hence, the amplitude of first-order freak waves is increased. Thus, the ratio of density of beam to ions, the ratio of temperature of beam to electrons, and superthermality and nonthermality parameters greatly influence the characteristics of first-order freak waves. The three-dimensional variation and contour plot of first-order freak waves is shown in Figure 2c,d, respectively. From Figure 2e, it is observed that the amplitude of first-order freak waves is less for the case of without beam (). By virtue of dispersion of waves over a large scale, there is enhancement in profile with respect to spacial and temporal coordinates.
Further, the behaviour of second-order freak waves’ profile with respect to change in ratio of density of beam to ions (), ratio of temperature of beam to electrons (), superthermality () and nonthermality () parameters has been examined in Figure 3. From Figure 3a,b, it is evident that the amplitude of second-order freak waves is larger than the first-order freak waves due to the superposition of energies of the first-order freak waves. Also with an increase in the ratio of density of beam to ions (ratio of temperature of beam to electrons), the nonlinearity and dispersion are increased (decreased) which results in an increase (decrease) in the amplitude and width of second-order freak waves. The characteristics of second-order freak waves’ profile with superthermality () and nonthermality () parameters have been illustrated in Figure 3b. The figures epitomize that when the value of superthermality parameter () and nonthermality parameter () are raised then nonlinearity and dispersion effects are decreased for kappa but increased for nonthermal case, consequently the amplitude and width of super freak waves are reduced (enhanced) for superthermal (nonthermal) case. The three dimensional variation and contour plot of first order freak waves has been shown in Figure 3c,d respectively. There is large-scale spatial and temporal variation. From Figure 3e, it is observed that the amplitude of second-order freak waves is less for without beam (). It is emphasised that the dynamics of IA freak waves are evidently influenced by the presence of an electron beam.
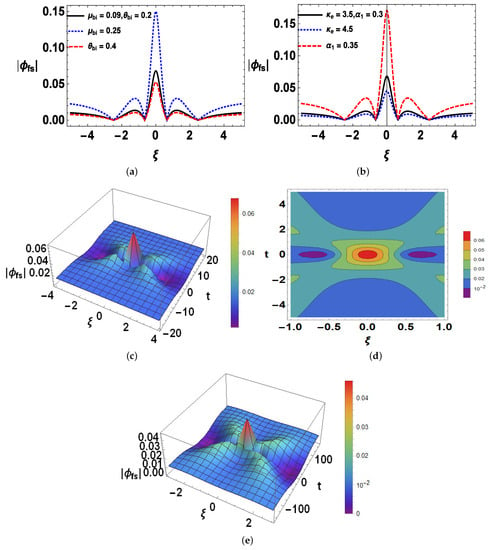
Figure 3.
The variation of super freak waves’ profile () with (a) ratio of density of beam to ions (), ratio of temperature of beam to electrons (); (b) superthermality parameter (), nonthermality parameter (); Solid reference curve: , , and ; (c) 3D profile; (d) contour plot; (e) without beam ().
Figure 4 and Figure 5 present Akhmediev breathers’ profile and Kuznetsov–Ma breathers’ profile, respectively. From Figure 4a and Figure 5a, it is depicted that on increasing the value of parameter R, the amplitude is increased. It is also reflected that Akhmediev breathers are periodic along the space coordinates (see Figure 4b) and from the Kuznetsov–Ma breathers’ profile (see Figure 5b), it is clear that these breathers are periodic in spacial and localized in temporal coordinates and their contour plots are respectively shown in Figure 4c and Figure 5c. In other words, the solution of Akhmediev breathers’ profile reduces to localized in both space and time.
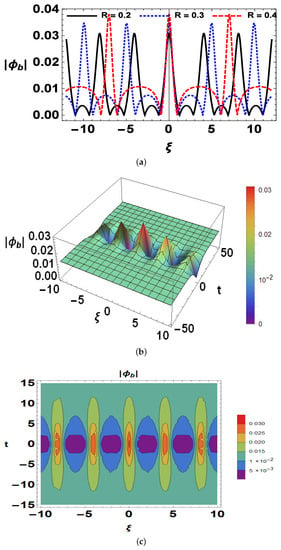
Figure 4.
The plot of Akhmediev breather’s profile () with (a) for different values of parameter R; (b) 3D plot; (c) contour plot; the other parameters are the same as given in Figure 1.
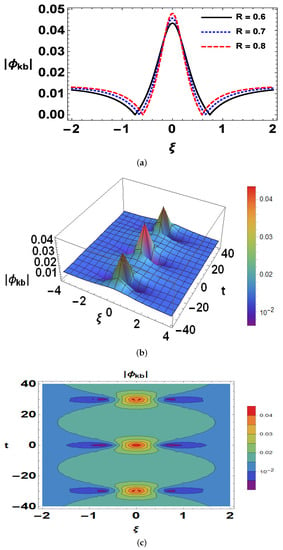
Figure 5.
The plot of Kuznetsov–Ma breather’s profile () with (a) for different values of parameter R; (b) 3D plot; (c) contour plot; the other parameters are the same as given in Figure 1.
Finally, it is highlighted that all parameters, viz., density ratio of beam to ions (), temperature ratio of beam to electrons (), superthermality (), and nonthermality () of electrons play a very significant role in the evolution of different potential IA nonlinear structures in the given plasma environment.
5. Conclusions
This study focuses on the properties of rogue waves and breathers in fluid ions as well as in electron beam and electron obeying VC distribution. From the KP equation using suitable transformation, NLSE has been derived to study the different kinds of freak waves and breathers. The combined effects of beam density as well as temperature of beam, ion temperature, superthermality, and nonthermality of electrons on breathers have been examined. The key findings are as follows:
- The amplitude of freak waves is more in the presence of beam.
- With increase in parameter R, the amplitude of breathers’ structures increases.
- The beam parameters highly modify the properties of freak waves and breathers. The increase in superthermality parameter (i.e., decrease in superthermality) and nonthermality parameters has a great impact on the amplitude of IA freak waves.
The outcomes of the present investigation may be of great importance to analyse nonlinear phenomena in plasma environments such as in the upper layer of magnetosphere where VC distributed hot electrons, hot ions, and hot electron beams may exist.
Author Contributions
Writing—original draft, M.K.; Writing—review & editing, S.S.; Supervision, N.S.S. and F.S.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors gratefully acknowledge the support for this research work from Department of Science and Technology, Govt. of India, New Delhi under DST-SERB project No. CRG/2019/003988.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kadomtsev, B.B.; Petviashivili, V.I. On the Stability of Solitary Waves in Weakly Dispersing Media. Sov. Phys. Dokl. 1970, 15, 6. [Google Scholar]
- Saini, N.S.; Kaur, M.; Singla, S. Ion-acoustic nonlinear structures in a non-Maxwellian plasma in the presence of an electron beam. J. Astrophys. Astron. 2022, 43, 65. [Google Scholar] [CrossRef]
- Saini, N.S.; Kaur, N.; Gill, T.S. Dust acoustic solitary waves of Kadomstev-Petviashvili (KP) equation in superthermal dusty plasma. Adv. Space Res. 2015, 55, 2873–2882. [Google Scholar] [CrossRef]
- El-Shewy, E.K.; Abdelwahed, H.G.; Abdo, N.F.; Shahein, R.A. Rogue waves for Kadomstev-Petviashvili solutions in a warm dusty plasma with opposite polarity. Mosc. Univ. Phys. Bull. 2016, 71, 284. [Google Scholar] [CrossRef]
- Kohli, R.; Kaur, N.; Singh, M.; Saini, N.S. Effect of ion beam on dust-acoustic waves under transverse perturbations in dusty plasma. IEEE Trans. Plasma Sci. 2016, 46, 782. [Google Scholar] [CrossRef]
- Ruderman, M.S. Kadomtsev-Petviashvili equation for magnetosonic waves in Hall plasmas and soliton stability. Phys. Scr. 2020, 95, 095601. [Google Scholar] [CrossRef]
- Kaur, M.; Saini, N.S. KP, MKP, and CKP dust ion acoustic solitons in a multispecies non-Maxwellian plasma. Phys. Plasmas 2022, 29, 033701. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Shan, S.A.; Akhtar, N.; Elgendy, A.T. Impact of electron trapping in degenerate quantum plasma on the ion-acoustic breathers and super freak waves. Chaos Solitons Fractals 2018, 113, 356. [Google Scholar] [CrossRef]
- Abdikian, A.; Ismaeel, S. Ion-acoustic rogue waves and breathers in relativistically degenerate electron-positron plasmas. Eur. Phys. J. Plus 2017, 132, 368. [Google Scholar] [CrossRef]
- Shan, S.A. Breather structures in a plasma with warm ions and Cairns electrons. Contrib. Plasma Phys. 2018, 58, 890. [Google Scholar] [CrossRef]
- Ding, C.C.; Gao, Y.T.; Li, L.Q. Breathers and rogue waves on the periodic background for the Gerdjikov-Ivanov equation for the Alfvén waves in an astrophysical plasma. Chaos Solitons Fractals 2019, 120, 259. [Google Scholar] [CrossRef]
- Ghosh, S. Nonlinear ion acoustic wave and group dynamics near critical density in a plasma with negative ion. J. Phys. Soc. Jpn. 2019, 88, 074501. [Google Scholar] [CrossRef]
- Singh, K.; Saini, N.S. Breather structures and peregrine solitons in a polarized space dusty plasma. Front. Phys. 2020, 8, 602229. [Google Scholar] [CrossRef]
- Ullah, S.; Masood, W.; Siddiq, M. Electron acoustic envelope solitons in non-Maxwellian plasmas. Eur. Phys. J. D 2020, 74, 26. [Google Scholar] [CrossRef]
- Saini, N.S.; Kaur, R. Ion-acoustic solitary, breathers, and freak waves inadegenerate quantum plasma. Waves Random Complex Media 2021. [Google Scholar] [CrossRef]
- Albalawi, W.; Jahangir, R.; Masood, W.; Alkhateeb, S.A.; El-Tantawy, S.A. Electron-Acoustic (Un)Modulated Structures in a Plasma Having (r, q)-Distributed Electrons: Solitons, Super Rogue Waves, and Breathers. Symmetry 2021, 13, 2029. [Google Scholar] [CrossRef]
- Das, A.; Ghosh, P.; Chandra, S.; Raj, V. Electron acoustic peregrine breathers in a quantum plasma with 1-D temperature anisotropy. IEEE Trans. Plasma Sci. 2022, 50, 1598. [Google Scholar] [CrossRef]
- Witt, E.; Lotko, W. Ion-acoustic solitary waves in a magnetized plasma with arbitrary electron equation of state. Phys. Fluids 1983, 26, 2176. [Google Scholar] [CrossRef]
- AI’pert, Y.L. Space Plasma; Cambridge University Press: Cambridge, UK, 1990; p. 118. [Google Scholar]
- Moslem, W.M. Propagation of ion acoustic waves in a warm multicomponent plasma with an electron beam. J. Plasma Phys. 1999, 61, 177. [Google Scholar] [CrossRef]
- Esfandyari, A.R.; Khorram, S.; Rostami, A. Ion-acoustic solitons in a plasma with a relativistic electron beam. Phys. Plasmas 2001, 8, 4753. [Google Scholar] [CrossRef]
- Sahu, B.; Roychoudhury, R. Electron-acoustic solitary waves and double layers in a relativistic electron-beam plasma system. Phys. Plasmas 2004, 11, 1947. [Google Scholar] [CrossRef]
- El-Taibany, W.F.; Moslem, W.M. Higher-order nonlinearity of electron-acoustic solitary waves with vortex-like electron distribution and electron beam. Phys. Plasmas 2005, 12, 032307. [Google Scholar] [CrossRef]
- Lakhina, G.S.; Singh, S.V.; Kakad, A.P.; Goldstein, M.L.; Vinñas, A.F.; Pickett, J.S. A mechanism for electrostatic solitary structures in the Earth’s magnetosheath. J. Geophys. Res. 2009, 114, A09212. [Google Scholar] [CrossRef]
- Saini, N.S.; Kourakis, I. Electron beam-plasma interaction and ion-acoustic solitary waves in plasmas with a superthermal electron component. Plasma Phys. Control. Fusion 2010, 52, 075009. [Google Scholar] [CrossRef]
- Saberian, E.; Esfandyari-Kalejahi, A.; Rastkar-Ebrahimzedeh, A.; Afsari-Ghazi, M. Propagation of ion-acoustic solitons in an electron beam-superthermal plasma system with finite ion-temperature: Linear and fully nonlinear investigation. Phys. Plasmas 2013, 20, 032307. [Google Scholar] [CrossRef]
- Kaur, M.; Kaur, R.; Saini, N.S. Two-dimensional ion-acoustic solitons in electron beam plasma. Afr. Rev. Phys. 2020, 15, 111. [Google Scholar]
- Singla, S.; Saini, N.S. Head-on collision of ion-acoustic multi-solitons and study of rogue waves in electron-beam superthermal plasma. Res. Phys. 2021, 22, 103898. [Google Scholar] [CrossRef]
- Saini, N.S.; Singla, S. Ion acoustic shocks with contribution of higher order effects in a superthermal beam-plasma. Chin. J. Phys. 2022, 77, 366. [Google Scholar] [CrossRef]
- Kaur, R.; Singh, K.; Saini, N.S. Electron acoustic rogue waves in Earth’s magnetosphere. J. Astrophys. Astron. 2022, 43, 62. [Google Scholar] [CrossRef]
- Livadiotis, G. Kappa Distributions: Theory and Applications in Plasmas; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Vasyliunas, V.M. A survey of low-energy electrons in the evening sector of the magnetosphere with OGO 1 and OGO 3. J. Geophys. Res. 1968, 73, 2839. [Google Scholar] [CrossRef]
- Cairns, R.A.; Mamun, A.A.; Bingham, R.; Bostroöm, R.; Dendy, R.O.; Nairn, C.M.C.; Shukla, P.K. Electrostatic solitary structures in non-thermal plasmas. Geophys. Res. Lett. 1995, 22, 2709. [Google Scholar] [CrossRef]
- Abid, A.A.; Ali, S.; Du, J.; Mamun, A.A. Vasyliunas-Cairns distribution function for space plasma species. Phys. Plasmas 2015, 22, 084507. [Google Scholar] [CrossRef]
- Ahmad, N.; Abid, A.A.; AL- Hadeethi, Y.; Qureshi, M.N.S.; Rehman, S. The effect of positive/negative ion on the dust grain charging process in a Vasyliunas-Cairns (VC)-distributed dusty plasma system. Plasma Sci. Technol. 2019, 21, 065001. [Google Scholar] [CrossRef]
- Debnath, D.; Bandyopadhyay, A. Combined effect of Kappa and Cairns distributed electrons on ion acoustic solitary structures in a collisionless magnetized dusty plasma. Astrophys. Space Sci. 2020, 365, 72. [Google Scholar] [CrossRef]
- Shahzad, M.A.; Aman-ur-Rehman; Mahmood, S.; Bilal, M.; Sarfraz, M. Kinetic study of ion-acoustic waves in non-thermal Vasyliunas-Cairns distributed plasmas. Eur. Phys. J. Plus 2022, 137, 236. [Google Scholar] [CrossRef]
- Sarkar, S.; Paul, S.; Parvin, S. Collective effect of nonthermal and suprathermal particles on electrostatic waves and instabilities in Vasyliunas-Cairns distributed plasmas. Phys. Scr. 2023, 98, 045617. [Google Scholar] [CrossRef]
- El-Labany, S.K.; Moslem, W.M.; El-Bedwehy, N.A.; Abd El-Razek, H.N. Nonplanar dust ion-acoustic solitary and shock excitations in electronegative plasmas with trapped electrons. Astrophys. Space Sci. 2012, 337, 231. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).