Abstract
A planar volume dielectric barrier discharge (DBD) in pure carbon dioxide (CO2) for the formation of carbon monoxide (CO) is examined by combined electrical and CO density measurements. The influence of the type of electrode, the barrier material, the barrier thickness, and the discharge gap on the plasma power and the CO formation is analyzed systematically. The electrical characterization by means of charge-voltage plots is based on the simplest equivalent circuit model of DBDs, extended by the so-called partial surface discharge effect and the presence of parallel parasitic capacitances. The stackable discharge arrangement in this study enables one to elucidate the influence of parasitic capacitances, which can be overlooked in the application of such plasma sources. The determination of the discharge voltage from charge-voltage plots and the validity of the so-called Manley power equation are revised by taking into account non-uniform coverage as well as parasitic capacitances. The energy yield () of CO is analyzed and compared with the literature. No correlations of with the mean reduced electric field strength or the geometric parameters of the DBD arrangement are observed.
1. Introduction
Dielectric barrier discharges (DBDs) are well-established as self-sustaining, non-thermal atmospheric pressure plasma sources in industry, e.g., for ozone generation and surface activation, in light sources, and air cleaning devices, as well as for the pumping of gas lasers [1,2]. More recently, DBDs have found application in life-science and have also been used for film deposition [3,4]. Other active fields of research are aerodynamic flow control and analytic detection devices [5,6]. A major field of research is currently the conversion of carbon dioxide (CO2) as a greenhouse gas, which is to be seen in connection with the storage of intermittent renewable energy as a so-called power-to-X (PtX) approach. The first attempts to use DBDs as plasma reactors for the conversion of CO2 date back to the 1990’s [7,8,9,10]; since about 2010, there has been renewed interest due to the energy transition, i.e., the demand of PtX technologies for the generation of fuels or chemicals [11,12]. For example, methanol or carbon monoxide (CO) is of interest as a readily storable synthetic fuel, platform chemical, or chemical feedstock for hydrocarbon and fuel synthesis, respectively.
DBDs were studied for CO2 splitting, hydrogenation, and the dry reforming of methane and methanization. Many studies include catalysts (i.e., the investigation of packed-bed DBDs) to exploit plasma-catalyst interaction for increasing the energy efficiency and/or selectivity. The latter two are insufficient in DBDs to enable industrial application. Microwave-generated plasmas (at sub-atmospheric pressure), gliding arcs, and radio-frequency-generated plasmas display much better energy efficiency and higher conversion degrees in CO2 splitting than DBDs. The advantage of DBDs is its simple and robust design. Additionally, DBDs do not require special high-voltage supplies and are not prone to significant EMC problems. Therefore, they could be attractive for decentralized power-to-X approaches. Furthermore, the DBD design allows for direct interaction with a catalyst to explore and exploit synergies [11].
CO2 splitting efficacy in DBDs was found to be determined by the electrode design and geometry, as well as by the operation parameters. Most studies were performed in coaxial DBD reactors with and without a packed bed. Paulussen et al. [13] identified the gas-flow rate as the most important parameter to optimize the CO2 conversion in an empty coaxial DBD reactor. A maximum conversion of 30% was reported. Aerts et al. presented systematic experimental studies and simulations, showing that the material of the dielectric barrier had no influence on conversion and energy efficiency (EE), while smaller discharge gaps led to an increase in conversion [14,15]. Mei et al. reported similar dependence on the discharge gap and a decrease in conversion and EE for thicker dielectric barriers [16]. The latter proposed a response surface methodology to investigate the effects of the process parameters (discharge power, gas-flow rate, and active discharge zone length) and their interactions on the reaction performance [17]. The discharge power was identified as the most important factor affecting the conversion, while EE was mostly determined by the gas-flow rate. The discharge zone length had a significant effect on EE, depending on discharge power or gas-flow rate. A similar result was reported by Niu et al. with a multi-electrode cylindrical DBD reactor [18]. Ozkan et al. reported that the barrier material as well as the high-voltage frequency have an influence on the conversion and on EE [19] (contrary to [14,20]) and that thicker barriers increase conversion and EE (contrary to [16]). Belov et al. pointed on the effect of asymmetry in such reactors [21]. When both cylindrical electrodes were covered by dielectric, a lower conversion was achieved than in the case of the asymmetric design with only one electrode covered by dielectric. The authors related these findings to the different operating regimes and current waveforms for the reactors and reported on the deposition of carbon-containing layers on the barriers [21,22], which affected the current waveforms and, thus, the chemical performance. Uytdenhouwen et al. also showed the increase in conversion and the decrease in EE with the discharge gap [23] and studied the existence of so-called partial chemical equilibria [24]. The position of these equilibria depended on reactor parameters and operating conditions (i.e., power, pressure, and gap). Adding a packed-bed in the discharge space usually increased the reactor performance. Most of the authors discuss the importance of the reduced electric field strength in the discharge gap on the chemistry.
Coaxial or cylindrical DBDs allow for a compact design without dead volumes or the slip of the reaction gas, as well as the easy inclusion of packed-beds with catalytic properties. A disadvantage is that an outer dielectric tube serves not only as the barrier of the DBD but also as the reactor housing. To ensure a mechanically robust construction, this dielectric tube therefore often has a wall thickness of more than 1 mm. However, a thinner dielectric barrier would cause a larger number of charges to be transferred to the discharge gap at the same high-voltage amplitude, thus generating more power.
Plane parallel DBDs can also be easily constructed from plate electrodes and dielectrics. Upscaling is relatively simple due to the stacking of plate electrodes and dielectrics [25,26]. Such constructions allow for more flexible choice of discharge gap and barrier thickness. For these reasons, similar DBDs are already successfully used for air-cleaning applications (e.g., deodorization) in industry [27,28]. A symmetric plane parallel volume DBD for CO2 splitting was studied by Brehmer et al. [29] and simulated by Ponduri et al. [30]. In [29], the specific input energy (), i.e., the discharge power divided by the gas flow, was identified as a universal scaling parameter, contrary to the results in coaxial reactors, e.g., [14,24]. The latter works pointed toward a more distinct effect of the gas residence time in the reactor, in particular for higher than 100 kJ/Ln. Brehmer et al. showed no effect on CO yield and EE by the variation of the discharge gap, pressure, thickness, and material of the barrier or by the frequency and duty cycle of the applied high voltage. The effect of the gap voltage and thus was also negligible in this study. The time and space (1D)-dependent model in [30] confirmed these experimental results, in particular, the linear dependence of the CO2 conversion frequency on the power per CO2 molecule. More recently, Uytdenhouwen et al. presented planar asymmetric DBD reactors with modifiable gas in and outlet designs for the dry reforming of methane [31]. The shape and size of the reaction zone and the direction of the gas flow also influenced the plasma chemistry in experiments in pure CO2. The power delivery to the reactor also largely affected the plasma chemical performance and product composition.
The mentioned non-comparability with empty coaxial DBDs and the scaling capabilities of planar DBDs motivated our work. The purpose of this paper is to present a comprehensive electrical characterization and its correlation with the plasma chemistry in a well up-scalable DBD configuration. We will show how parasitic capacitances and non-uniform plasma formation in reactors can complicate interpretation and lead to errorneous conclusions. Current research often overlooks these aspects or lacks the right approach to the problem. For this purpose, we apply the approach of the simplest equivalent circuit [32,33] and discuss the influence of geometric reactor properties such as the discharge gap, the type of electrodes, or the barrier material and thickness. We will introduce the correct determination of the so-called discharge voltage as an important mean parameter from charge-voltage (Q-V) plots under such circumstances. We will discuss the validity of the so-called Manley power equation [34] and how the discharge power is determined by the geometric reactor properties. Finally, the electrical analysis will be correlated with the splitting of CO2 to CO in a CO2 plasma. A comparison with results form literature will be made and the role of the different process and geometric parameters in DBDs will be discussed.
2. Experimental Set-Up and Procedures
The DBD configuration used in this study is a volume DBD in plane parallel arrangement as given in Figure 1. It consists of two metal electrodes (EO, area ) with an insulating plate (with relative permittivity ) in between [25]. The discharge gap g at both sides of the “floating” insulating plate is adjusted by n = 2 or 3 spacers on each side made of dielectric (with relative permittivity and area ). We vary the type of the metal electrode (grid or plate), the insulating plate and spacers material (ceramic or mica), and its thicknesses b and g. Table 1 summarizes all of the materials, dimensions, and material properties tha are relevant or varied. Such DBD arrangements can be easily upscaled to larger gas flows, namely, by stacking several electrodes and insulating plates and, thus, discharge gaps on each other [25,26,35]. However, for our study we use the most basic arrangement consisting of only two electrodes and one dielectric plate and, thus, 2 discharge gaps, similar to those in [35,36].
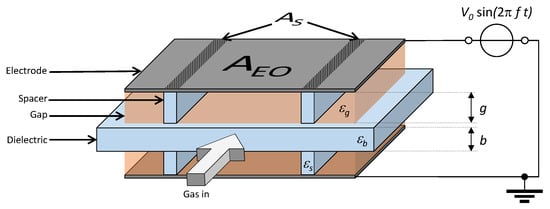
Figure 1.
Sketch of the plane parallel volume DBD arrangement with 2 discharge zones each with n= 2 spacers.

Table 1.
Parameters of DBD arrangement and operation.
The electrode arrangement is mounted in a housing made of Teflon with a cover plate made of Polycarbonate to enable visible inspection. The housing contains one centered gas in- and outlet with a diameter of 4 mm. Pure carbon dioxide with a total flow rate of 1 slm (or 1 Ln/min) is applied by a mass flow controller (EL-FLOW SELECT, Bronkhorst). For comparison, the discharge is also operated in synthetic air.
The discharge is operated with sinusoidal high voltage. The power source consists of a wave function generator (Chroma, Model 61603) and a high voltage custom-built transformer (Bremer Transformatoren GmbH). It provides a high-voltage sinusoidal waveform with a frequency f of up to 1 kHz. The high voltage and the ground connection of the electrodes are realized by a metallic screw drawn through the Teflon chamber, i.e., there is no additional high-voltage throughput. The high voltage is measured using a 1000:1 high-voltage probe (Tektronix P6015A). A polypropylene film capacitor (WIMA FKP1; 220 nF) is utilized to measure the charge transferred in the DBD. The exact values of this measurement capacitance as well as of the DBD arrangements are determined with a LCR-meter (GW Instek, Model LCR- 817). The voltage drop across the capacitor is measured via a voltage probe (Rigol, RP 2200). Both signals and are recorded with an oscilloscope (Rohde & Schwarz, HMO3004 with 4 GSa/s and 500 MHz bandwidth). In general, averaged charge and voltage slopes over 32 voltage periods are recorded. The high-voltage amplitude and the frequency f are changed to vary the plasma power P.
To study the plasma-chemical performance, the gas at the outlet was analyzed with a Micro Gas Chromatograph (MicroGC) (3000 MicroGC, Inficon). The MicroGC has 3 modules: one with a Molsieve column for the detection of permanent gases, one with a PlotQ column for the detection of CO2 and hydrocarbons from C1 to C3, and one with an OV-1 column for the detection of hydrocarbons from C3 to C6 and aromatics. Each module is equipped with a thermoconductivity detector and uses helium as the carrier and reference gas to enhance the sensitivity of the detectors. Prior to all experiments, the MicroGC was calibrated using standard gas cylinders (Alphagaz 1, AirLiquide).
In this contribution, the carbon monoxide formation is evaluated by means of two parameters, the specific input energy () and the energy yield () of CO formation. These quantities are determined as follows.
is the gas flow, given in standard liters (Ln, i.e., at 273.15 K and 1013.25 mbar) per time unit; is the carbon monoxide molar fraction; is the molar mass of CO; and is the molar volume. In most studies on CO2 splitting, the energy efficiency (EE), which relates the amount of converted CO2 with the reaction enthalpy and the dissipated energy, is discussed. However, the use the in [g/kWh] is favorable since it gives the amount of the ”target” molecule CO per energy coupled into the plasma. The second term in Equation (2) takes into account the increase in the molecular amounts due to the gross reaction CO2 → CO + O2.
EE and can be converted into one another but only if no other carbon-containing reaction products including surface depositing species than CO are present. This is not general as some authors report about carbon deposition in the reactors or unbalanced carbon in the analyzed gas, e.g., [21]. The reciprocal of can be used to calculate the energy cost () as the amount of energy per mol CO ().
3. Electrical Characterization
3.1. Q-V Plots and Equivalent Circuit
The analysis of the electrical parameters by means of Q-V plots, in particular the determination of the plasma power P, is a well-established approach for DBDs [34,37]. The interpretation of Q-V plots is based on an electrical theory that was developed for large-scale sinusoidal-driven industrial ozonizers [34] but is also applicable to DBDs in other gases and with smaller dimensions. Since it is not considering the processes at the insulator surfaces or the non-uniform breakdown, it has some limitation for miniature laboratory DBDs, which were overcome with the equivalent circuit approach [38]. The interpretation is macroscopic and one has to be careful with conclusions about the parameters within the microdischarges forming the filamentary plasma.
A typical Q-V plot measured at our DBD is shown in Figure 2b. The voltage and charge are measured over two full voltage periods, averaged over 32 samples in this example (see Figure 2a). Without plasma, the signals and are in phase, thus, the Q-V plot is measured as a line with a slope that represents the total capacitance of the discharge device. At a certain threshold of , the discharge ignites and a parallelogram-like Q-V plot is obtained. Its lower slope is the same as for the line in the non-ignited case, while the higher slope basically represents the barrier capacitance of the system. The time resolved signals in Figure 2a show that the discharge ignites when a certain value of is reached within the half-period T/2 (see the orange circles). The discharge activity stops when the peak of the applied voltage is reached. This also manifests in the reversal points of the Q-V plot. In this active phase, the charge transfer into the plasma is measured with the value .
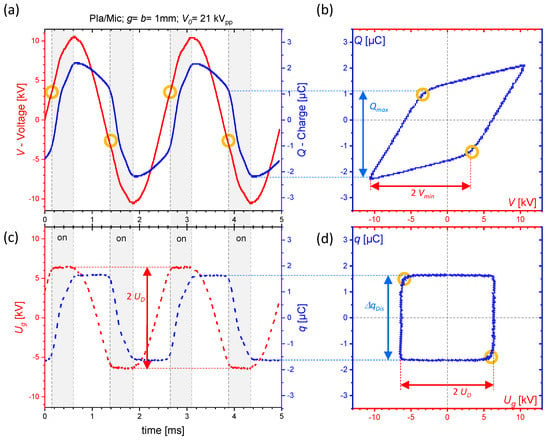
Figure 2.
(a) Typical voltage and charge signals measured for a plane-parallel volume DBD of Figure 1 in . These signals result in the parallelogram-shaped Q-V plot (b). The orange circles show the time when the plasma ignites in each half period. Processing and by Equations (8) and (7) result in the slopes of the gap voltage and the charge transferred into the plasma and as shown in (c). These signals form the “quadratic” q- plot in (d). The enclosed areas of both Q-V plots are identical and give the energy per period (about 40 mJ in this example).
The simplest lumped-element equivalent electric circuit of our DBD is shown in Figure 3, left. It is based on the circuit discussed in [33] but contains two discharge gaps. In the non-ignited case, the equivalent circuit is purely capacitive and consists of three capacitances: one resembles the barrier () and two represent the gas gaps (). The linearly arranged capacitances form the discharge cell capacitance . These capacitances are calculated as follows.
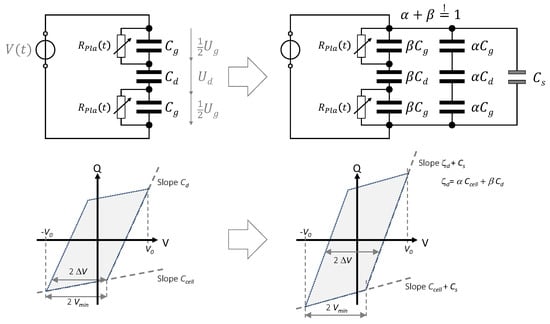
Figure 3.
Simplest equivalent circuit of the DBD arrangement in Figure 1 (left) and its extension for non-uniform plasma and the presence of a parallel parasitic capacitance (right). Measured voltages are symbolized by while apparent voltages by .
The area is either or and, indeed, the area of the spacers must be excluded from the calculation of (3) and (4). The sum of the voltages across the gas gaps and the barrier equals to the applied voltage V. The voltage drops 1/2 are too low to cause an ignition as long as . The threshold is determined by g, the pressure, and the gas composition but also depends on the properties of the dielectric barrier (b, ). For , the gap capacitances are by-passed by time-dependent resistors representing the discharge; the Q-V plot appears as a parallelogram as shown in Figure 2b and sketched below the equivalent circuit in Figure 3 (left). Its area is a measure of the supplied energy per period W, and its multiplication with the operation frequency f gives the power P. can be measured directly from the Q-V plot as the distance between the apex and the ignition point of the parallelogram (orange circles), while its slopes are (plasma-off phases) and (plasma-on phases), respectively. The voltage over the gas gaps at the inset of the plasma, the so-called discharge voltage , can be calculated from the value or directly measured from the Q-V plot as the voltage difference = in case of this simplified equivalent circuit.
It was pointed out by Peeters et al. [32] that the interpretation of Q-V plots in case of non-uniform ignition deserves special attention. In a real DBD reactor with , there will be numerous microdischarges that cover the entire electrode area cross section. However, electrode edge effects and non-perfectly aligned discharge gaps with will affect the behavior, in particular at low over-voltage [33,36,39]. This effect is called partial surface discharging and considered in the equivalent circuit in Figure 3 (right) by assuming a non-discharging areal fraction and a discharging areal fraction (with 1). Only the discharging fraction implements the resistors . Consequently, the effective (or apparent) dielectric capacitance depends on and is smaller than ; . The effect of partial surface discharging is analogous to the implementation of a parallel parasitic capacitance in the circuit. In our DBD configuration, the spacers setting the gas gap introduce an additional parallel parasitic capacitance , which is independent on and permanent. It is calculated as follows:
It must be mentioned, that such parallel capacitance is basically unavoidable in DBD set-ups as it is also caused by high-voltage throughputs, connections, and (shielded) cables in the entire circuit [40]. Furthermore, the addition of dielectric or ferroelectric packed beds in the discharge volume introduces such additional capacitances [17,23,24,41]. The equivalent circuit of surface and coplanar DBDs also contain a parallel capacitance [42,43]. The effect of parasitic (or stray) capacitances was already discussed by Falkenstein and Cogan in [44].
Applying Kirchhoff’s laws to this equivalent circuit, leads to the following expressions for the gap voltage and the transferred charge .
The Figure 2c shows and calculated by Equations (7) and (8) from the measured electrical signals for one configuration. The net charge across the gap during discharging and the plasma current were found to be independent from or [32], but has to be considered. It is also included in both slopes of the Q-V parallelogram, as shown in Figure 3, right bottom. The gap voltage is affected by both the discharge fraction and the parasitic capacitance [44]. In this macroscopic, averaged approach, the gap voltage remains constant during the plasma-on phases (at the value ), while the transferred charge is nearly constant in the plasma-off phases when there is no discharge activity. In the discharge, the amount is transferred into the plasma. Consequently, the q- plot in Figure 2d is quadratic and its area equals to . Not including and the partial surface discharging would result in incorrect values of and [32,44]. is determined as follows:
The recent application of a similar equivalent circuit for a coplanar DBD came to the same relation [42]. The determination of from is still as described in the literature, e.g., [37] (due to the parallel arrangement of the capacitances), but the parasitic capacitance should be considered for the determination of and from the slopes in the Q-V plot. Even more important is that cannot be equated with . The Equation (9) changes to the expression given in [32] for = 0. For full discharging ( = 0) only the quotient remains in the last bracket. Only for full discharging and = 0 equals as in the classical theory of Manley. This is in agreement with the equation given in [44]. For , the parasitic capacitance will have no significant influence. However, this should be checked in advance of the determination of and before drawing further conclusions from the electrical measurements. The amount of transferred charge per T/2 is determined as follows, and inserting the Equations (9) and (10) in the relation results in expression (11).
Neglecting parallel capacitances and partial surface discharging would lead to an underestimation of and an overestimation of . Nevertheless, the determination of the power from the as-measured values and would result in the same value than from the apparent discharge parameters and . The uncertainty of both calculation path is in the determination of or . If the discharge inception is not uniform, the corners of the Q-V plots (orange circles) are not pointed and W is underestimated. This is even more pronounced in surface, coplanar, and packed bed DBDs where the plasma expands over the dielectric [38,43,45]. The most precise determination is by the mathematical integration of the Q-V plot which is also used in our analysis. The results are presented in the following sub-section.
3.2. Capacitances and Discharge Power
Figure 4 presents the slopes of the Q-V plots measured at different applied voltage amplitudes for the DBD reactor with g = b = 1 mm and ceramic dielectric plate. The results obtained with grid as well as plate electrodes are shown. The lower slope (representing , orange symbols) is lower in case of the grid electrode but always constant with . The difference can be explained by a smaller effective electrode area in the case of the grid with . The larger slope (representing ) increases with and then saturates, as in [32,36,39]. This effect is attributed to the partial surface discharging. Increasing leads to a larger areal fraction of the plasma and for 17 kV equals 1. This is also seen in the top view photos (configuration Gri/Cer) on top of the diagram. It is interesting to note that the saturated values for grid and plate electrode are equal; only the increasing sections of the slopes are different. The same qualitative behavior is measured for mica as the dielectric, where the saturation is obtained at 19 kV. Similar slopes and saturation values are obtained when air is used instead of pure CO2.
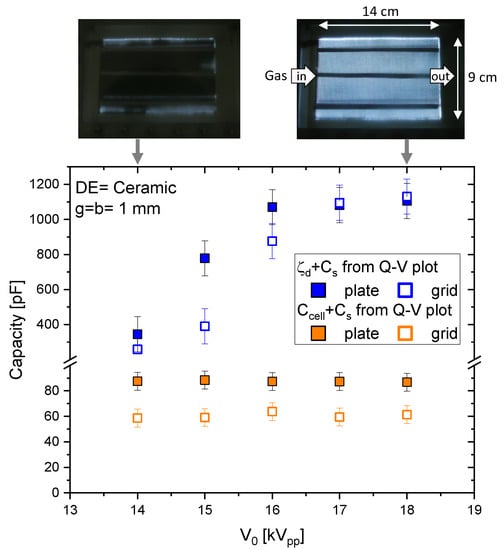
Figure 4.
The values of the slopes of Q-V plots for DBDs with g = b = 1 mm and ceramic dielectrics at different high-voltage amplitudes in pure CO2. The top of the diagram shows two top-view photos of the reactor with grid electrodes under operation at 14 and 18 kV, respectively.
In Figure 5, we summarize the values measured for the four different configurations (EO/DE) with g = b = 1 mm. The bars show the calculated values for , , and (n = 3 spacers made of ceramics in these experiments). The circle data points are the slopes of the Q-V plots measured in air and CO2. The cross is the capacitance of the electrode arrangement measured with the LCR-meter. There is a fair agreement between the values for measured in air, CO2, and without plasma operation (LCR) with the calculated values. The relative permittivity of the different gases is nearly the same and should result in the same total capacitance as measured. The lower dielectric capacitance for mica is due to the lower value of , and the lower value for grid electrodes is due to the smaller effective electrode area (see Equations (3)–(6)). The blue data points are the saturation values for the larger Q-V slopes, which are attributed to (). These values are significantly larger than the calculated values; there is no difference between plate and grid electrodes. This effect is caused by edge effects at the electrodes and the grid wires. The photos in Figure 4 also show that the visible plasma expands over the electrode boundaries. Thus, the total dielectric capacitance is determined by the area of the plasma covering the dielectric and not by the physical size of the electrodes alone.
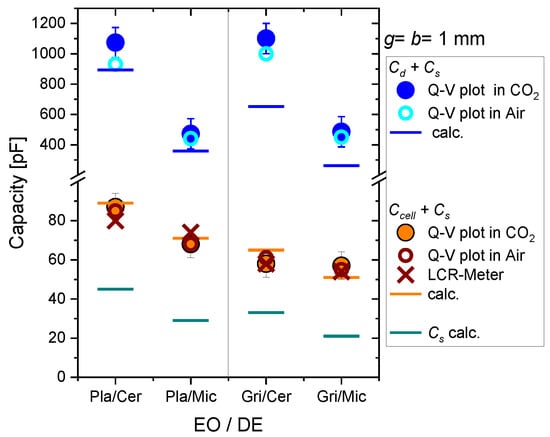
Figure 5.
Capacitances of the four different combinations of electrode and dielectric plate (DE) for = 1.
The minimum sustaining voltage as a function of measured in pure CO2 for ceramic dielectrics and g = b = 1 mm is presented in Figure 6, left. The values for are comparable at about 5.9 kV with a slightly higher uncertainty for the grid electrode because it is less rigid and plane as the plate electrode. The right diagram in Figure 6 presents the data for all four configurations. In the case of mica, a higher minimum sustaining voltage is obtained than for ceramic. This is partly explained by the larger voltage drop over the dielectric barrier (). The discharge voltage determined by Equation (9) is set by pressure, gas composition, and g but should be independent from barrier. Thus, the same value of is expected for both dielectrics. However, it is about 5.7 kV for ceramic and 6.3 kV for mica. Whether this difference of about 10% is related to the properties of the dielectric (e.g., mobility and release of deposited surface charges) or is within the uncertainties of the experiment must be elaborated in future studies. From , we calculate a mean reduced electric field strength according to
where N is the particle number density at our lab conditions (1020 hPa; 298 K). The values are about 110 Td for ceramic and 120 Td for mica. The error bars result from the uncertainties of pressure, temperature, and gap distance. Air has a similar discharge voltage at g = 1 mm (5.8 kV for ceramics; 6.3 kV for mica with = 113 Td and 121 Td, respectively).
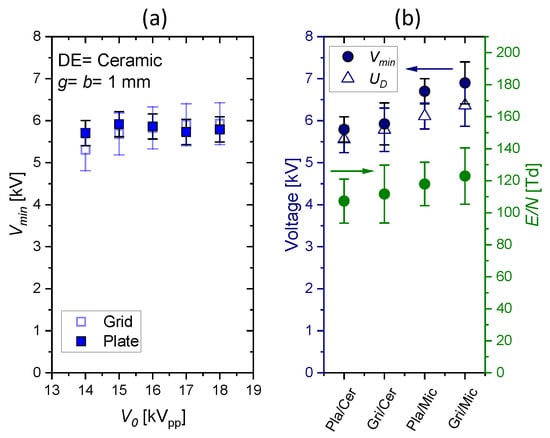
Figure 6.
Minimum sustaining voltage, discharge voltage, and mean reduced electric field strength in pure CO2.
The discharge power P is obtained from the area of the Q-V plot. The results for pure CO2 at different voltage amplitudes are presented in Figure 7. In the most basic equivalent circuit theory of the DBD, the power depends on linearly (the so-called Manley power formula). The derivation of the power equation for the extended equivalent circuit results in the following equation:
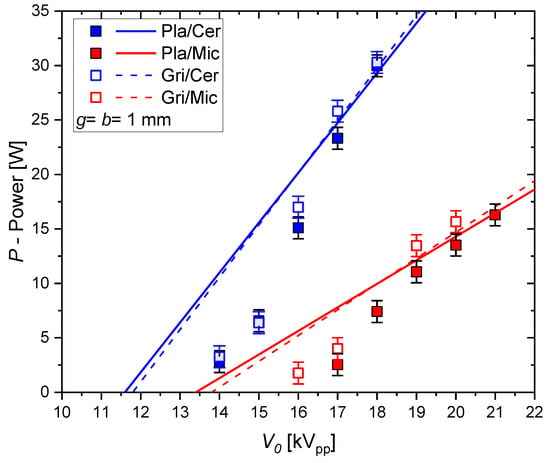
Figure 7.
Discharge power measured in pure CO2 (data points) and calculated (lines) with the classical Manley equation ( = 1; and taken from Figure 5).
The power is not affected by the parasitic parallel capacitance, but the partial surface fraction factor must be considered. The lines in Figure 7 are calculated with the classical Manley power formula (i.e., with = 1 in (13)) and with the capacitances determined from the Q-V plot. Only for the higher values of when full discharge coverage ( = 1) is achieved is a good agreement between calculated and measured values observed. For lower voltage amplitudes, the classical Manley equation overestimates the power. Taking the calculated values of instead of the measured values would underestimate the power in general as it is not taking into account the edge effects.
A significantly higher discharge power for the same applied voltage amplitude is obtained for the DBD with the ceramic dielectric. The lower voltage drop over the ceramic results in a lower minimum operation voltage. The lower and the higher results in a higher slope of . The type of electrode has no significant influence because of the similar dielectric capacitances due to the discharge expansion on the dielectric surface.
It should be noted that the coefficient is a function of the amplitude ( = f()) and that the revised Manley power formula (13) assumes a constant value of , which is confirmed by experimental data for our discharge configuration. In other DBD geometries, in particular surface DBDs or non-parallel volume DBDs, = f(), which complicates the interpretation [43,45].
3.3. Variation of DBD Geometry
In this section, we discuss the effect of changes of the geometric parameters g and b. The increase in the discharge gap results in a smaller total and parasitic capacitance, as shown in Figure 8a. The minimum sustaining voltage and the discharge voltage scale nearly linearly with g (see Figure 8b). This is in agreement with the Paschen law for air and (pressure × distance) ≥ 2 bar × mm. The mean reduced electric field strength at discharge inception decreases significantly from about 150 Td to 100 Td. An increase in with g was also obtained in [14]. The discharge power scales linearly with the voltage amplitude only for the condition as shown in Figure 9. The smallest gap width enables the highest and the maximum power at the same voltage amplitude. A uniformly covering plasma is already obtained at 13 kV. The maximum power can be achieved for the highest and the lowest g.
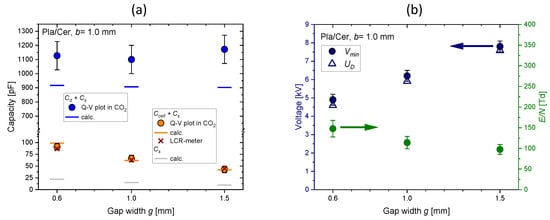
Figure 8.
(a) Dielectric, cell, and parasitic capacitances. The spacers (n = 2) are made of mica, which reduces . (b) Minimum sustaining voltage, discharge voltage, and mean reduced electric field strength for DBD reactors with different discharge gap width g measured in pure CO2.
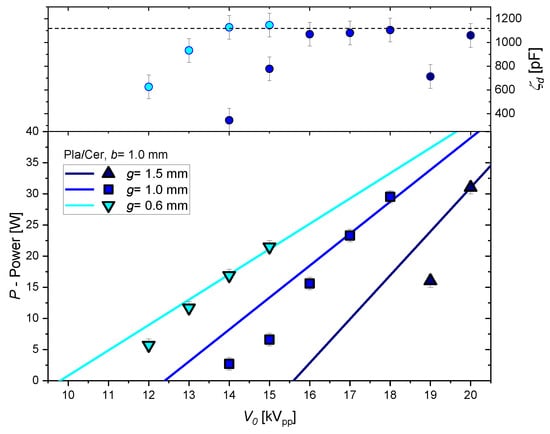
Figure 9.
Effective dielectric capacitance (top) and discharge power (bottom) as function of voltage amplitude for different discharge gap width measured in pure CO2. The lines are calculated with the classical Manley equation ( = 1).
The increase in b results in a significant decrease in the dielectric capacitance (from about 890 pF at 0.6 mm to 460 pF at 1.0 mm) (data not shown). The minimum sustaining voltage also increases with b slightly (from 6.0 to 6.8 kV), which is explainable by a higher ratio . Surprisingly, the values of and also increase (from about 109 to 115 Td), although gas, pressure, and gap width are not varied. This observation must be studied in future research.
Most of the trends can be explained by the extended equivalent circuit and the dependency of the elemental capacitances on the parameters of the DBD arrangement. The parasitic capacitances and the partial surface discharging effect have no influence on the power determined via the Q-V plot area or the product . However, and are not identical with the discharge voltage and the transfered charge per cycle . This must be taken into account for the determination of the mean reduced electric field strength or the total number of transferred charges.
The maximum P at a given can be obtained with a high and a low thickness b of the barrier. The gap distance g determines the discharge voltage and thus , which is also affected by and = f(g). The increase in the discharge voltage with g is consistent with the Paschen law in the parameter range of pressure and distance being investigated here. A high ratio decreases the voltage drop over the dielectric barrier and allows higher power at lower applied voltage amplitudes. This is well reflected in the revised Manley power equation, which shows a linear dependency on the partial surface discharging parameter . The type of electrode has no influence on , but in the case of the grid electrode, and become smaller. However, the effect on the power dissipation is not large.
For the following discussion of the carbon monoxide formation, we can rely on the measured power values for different applied voltage amplitudes. We will take into account that the DBD reactors for different parameters can operate at a different mean reduced electric field strength in a range from 100 Td to 150 Td.
4. Carbon Monoxide Formation
Figure 10 presents the measured CO fraction as a function of the . The different configurations are identified by the symbols. A linear increase in the CO fraction with is obtained. For the conditions being considered, can be confirmed as a sole scaling parameter, as obtained by Brehmer et al. [29]. Higher CO fraction is obtained with ceramic as the dielectric because of its higher discharge power; thus, is coupled into the plasma. There is no effect on the type of discharge electrode and the dielectric material on the efficiency of CO formation. It is also independent of whether the electrode surface is fully or partially covered by the plasma. The series of experiments with variation of b and g (symbols with black border) shows slightly lower concentrations in general, which is still within the uncertainty of the experiments. A significant influence of the gap or the barrier thickness cannot be detected, although the gas residence time also changes with g. The dashed light blue line corresponds to an energy yield of 30 g/kWh, and all values are presented in Figure 11.
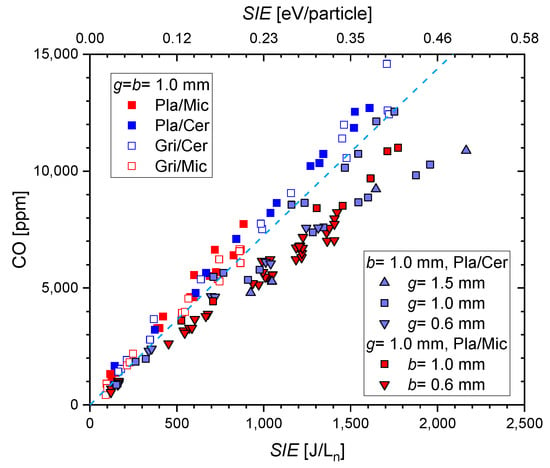
Figure 10.
CO fraction as a function of specific input energy in the different plane parallel asymmetric DBD reactors. The color represents the dielectric, full symbols are for plate electrodes, and open symbols are for grid electrodes. The data measured with different gap and dielectric thickness are included.
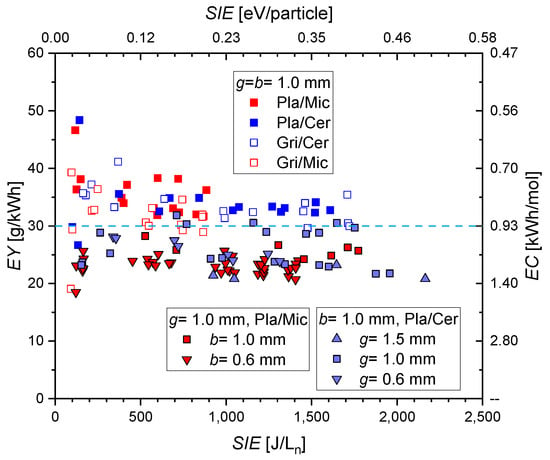
Figure 11.
Energy yield and energy cost of CO formation as a function of for the different DBD reactors. The light blue dashed line corresponds to the one in Figure 10.
Besides CO and O2, ozone (O3) is measured as a by-product. The calculated by Equation (2) does not take this into account, but the effect of O3 formation is negligible since its concentrations are a few hundred ppm only. The values of are in a range of about 20 to 50 g/kWh, but most of the values concentrate around (30 ± 8) g/kWh or at about 0.9 kWh/mol (see the dashed light blue line, this value corresponds to an EE of about 9%). Some larger (and lower ) are obtained at lower , but this seems to be caused by a higher uncertainty of measured CO fractions at lower discharge powers.
It is expected that the charge per microdischarge will change according to [46,47]. The lower b = 0.6 mm leads to a higher (factor 1.7) and a lower number of microdischarges per period for the same power. A slightly lower is obtained for this situation. The highest discharge gap of 1.5 mm also results in the lowest . However, the change of with does not show such a correlation, and the lowest discharge gap also does not result in the highest as expected. Therefore, a clear impact of electrode geometry on the efficiency of CO formation cannot be concluded from our data. The independence of the CO formation efficiency on the reactor parameters and the linear dependence of the CO fraction on the was also predicted by the numerical simulations in [30]. In conclusion, the geometric parameters of the planar DBD allow for the control of the plasma effectiveness but not of the efficacy.
In case of DBDs in pure CO2, the dominant dissociation process is direct electronic dissociation. Electron impact ionization followed by dissociative electron-ion recombination and dissociative electron attachment also contribute but to a lower extent [14,15]. The released oxygen atoms form molecular oxygen or ozone, or undergo back reaction with CO to CO2.
Since electrons are mainly responsible for dissociation, linear behavior between plasma energy and CO concentration can be expected. In Figure 12, we compare our results with the literature. We incorporate only data obtained in pure CO2 at atmospheric pressure in empty volume (coaxial or parallel) DBDs (no packed bed reactors), except the data of Schiorlin et al., which were obtained in a coplanar DBD [48]. Most authors discuss the CO2 conversion and not the CO formation, which is not essentially the same. In particular, carbon layers can be formed, which results in lower CO concentrations than predicted by the CO2 conversion. Brehmer et al. presented CO concentrations measured by quantum cascade laser absorption spectroscopy and FTIR. The other selected contributions reported on their selectivity or gave a carbon balance of their processes, which allows one to determine the CO concentration. All of the literature results (i.e., their proximate ranges) are visualized by the colored areas in the diagram. A double logarithmic scaling is chosen to enable the presentation for a wide range of concentrations (4 orders of magnitude) and (5 orders of magnitude). The dashed lines are for constant with the values given. The theoretical maximum of is marked by the red shaded line, while the stoichiometric limit of the gross reaction (CO2 → CO + O2) at 66.67% is marked by the green dashed line.
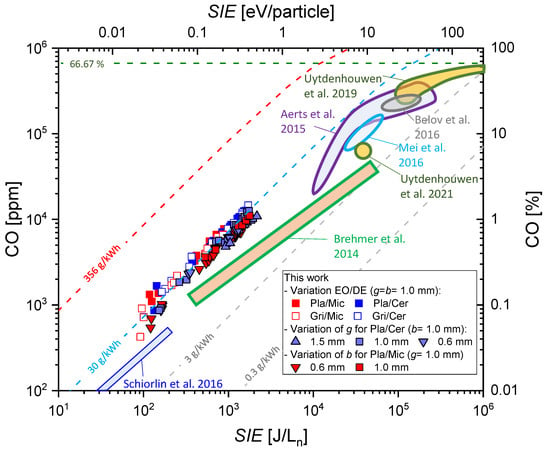
Figure 12.
CO fraction as a function of in the different DBD reactors in comparison with results from literature, namely, Brehmer et al. [29], Aerts et al. [14], Mei et al. [16], Belov et al. [21], Uytdenhouwen et al. [24,31] and Schiorlin et al. [48].
All of the results obtained with higher are for coaxial DBDs, except Uytdenhouwen et al. 2021, which was an asymmetric planar DBD with one discharge gap [31]. The experiments were operated in the power range P = 1 … 150 W but at different gas flows and lengths and volumes of the active plasma zone and thus different residence times of the gas in the plasma. The residence times span a range from 20 ms to 48 s (1 s in our reactor). The volumes of the active plasma zones are between 1 and 22.5 mL.
For lower than 10 eV/particle, this parameter is a universal scaling parameter; there is clear linear behavior with the CO concentration. For all of the data, the is in a “corridor” between 3 and 30 g/kWh, but it is not a sole scaling parameter. In the case of Brehmer et al. [29], the efficiency decreases with the , while it is almost constant at about 30 g/kWh in our reactor. The data from Schiorlin et al. [48] have been obtained for smaller and give a smaller (although nearly constant) . In this coplanar DBD reactor, the discharge was only generated at the electrode surface (the discharge expands into the gas volume a few 100 μm [49] and the majority of the flowing gas was not in direct contact with it). Furthermore, the residence times were below 1 s. Brehmer et al. measured the gas temperature in the reactor by Raman scattering and obtained about 450 K [50]. Its value was found to be determined by the wall temperature and the power per electrode area (power surface density, = ). These authors discussed the role of temperature on the chemistry and proposed a more prominent role of wall recombination (CO + O + Wall → CO2 + Wall) with higher and temperatures. Our electrode area is about 20 times higher, and the is about one order of magnitude lower than in [29]. The is also lower. However, we did not measure the gas temperature and cannot conclude whether less heating is responsible for the higher . Further studies including simulation and similarity studies are needed and remain for future work.
With higher the slope of CO formation and thus, the decrease. Due to the much lower in our experiments, we cannot obtain such saturation and reach a quasi-equilibrium as described in [14,24]. Studying whether the chemical performance is determined by the residence time in our reactor requires experiments at lower gas flow (and thus higher ). This remains for future work. Furthermore, a higher CO formation is connected with more oxygen formation, which enhances the back reaction (CO + O2 → CO2). An increase in gas temperature should be considered too. Paulussen et al. [13] showed a slight increase in CO2 conversion and CO yield by the gas temperature (up to 470 K preheated gas flow). Mei et al. measured an increase in 100 K at 28 kJ/Ln to about 430 K with a fibre optic probe [17], while Belov et al. suggested an increase up to 600 K [21]. Although these temperatures are too low for thermal dissociation, they can significantly affect the chemical kinetics and wall processes in a non-thermal plasma.
Finally, we compare the related to the mean reduced electric field strength in Figure 13. The data points are the average of the individual measured values, while the bars show the minimum and maximum values being obtained for this particular configuration. The large range of was already discussed above. However, the data points concentrate in a range of 20 … 30 g/kWh (or 0.93 kWh/mol), while a clear dependency of the on cannot be concluded. The for the highest (148 Td) appears even lower than for the configurations with g = b = 1 mm (107 … 123 Td), but that might be in the uncertainties of the gas analysis.
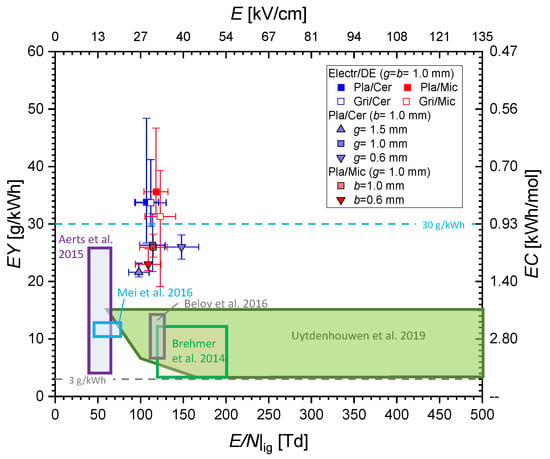
Figure 13.
Energy yield or energy cost of CO formation as a function of the reduced electric field strength or electric field strength (at ignition) in comparison with results from literature, namely, Brehmer et al. [29], Aerts et al. [14], Mei et al. [16], Belov et al. [21], and Uytdenhouwen et al. [24].
A clear dependence of the from the mean is neither obtained in our results nor reported in the literature. For lower than 30 Td, a more prominent role of vibrational excitation can be assumed [11], but these values are not covered by DBDs in pure CO2. The results in Figure 13 question the significance of the mean for the CO2 splitting in DBDs. The constant discharge voltage during the active discharge phases is only the macroscopic picture since the plasma is filamentary, i.e., consists of multiple individual microdischarges. The microdischarge development in pure CO2 is characterized by positive streamer development [51] with local values of exceeding the ignition electric field strength significantly [52,53].
5. Summary and Outlook
We introduced a stackable, and thus easily up-scalable, volume DBD reactor for the conversion of CO2 and presented its electrical properties as well as the CO formation under variation of the geometric parameters.
The systematic investigation of the electrical parameters under variation of the voltage amplitude gave (i) information about electrode coverage by the discharge and (ii) enabled one to determine the exact values of the capacitances and discharge powers. The role of the different geometric parameters on the discharge power was studied systematically. We universalized the equivalent circuit for the situation of partial surface discharging with additional dielectric material in the discharge gap, which was described by a parallel capacitance. Neglecting these issues can affect the proper determination of the gap or discharge voltage and the transferred charge. The Manley equation for the calculation of the discharge power was generalized for partial surface discharging but was found to be independent from additional parallel capacitances. This was confirmed by experimental data, which also showed that a higher dielectric permittivity and a thinner dielectric enabled a lower threshold voltage and a higher discharge power for the same voltage amplitude. The form of the electrode (grid or plate) showed no distinct effect on the power dissipation. The discharge voltage increased linearly with the discharge gap, while the mean reduced electric field strength decreased. Surprisingly, the barrier material and thickness had an effect on the discharge voltage and thus on the mean electric field strength in the gap at the microdischarge ignition.
The geometric parameters of the DBD configuration influenced the effectiveness of carbon dioxide splitting but not the efficacy. The energy yield of CO formation was not changed by the reactor construction. The distinct dependence of the energy yield of CO formation on the mean reduced electric field strength could not be concluded from the measurements. The specific input energy was identified as a sole scaling parameter in the range being studied (100 to 2000 J/Ln), which is in agreement with the literature. The comparison with the literature suggests an effect of the residence time of the gas in the active discharge zone, which must be studied further.
Future studies will use a higher number of electrodes and dielectric plates as well as different electrode sizes to explore the role of the residence time and the power surface density and to apply approaches of plasma chemical similarity similar as in [24,29,31]. Furthermore, the flow dynamics must be considered, and the studies will be extended to higher . The reactor presented here had one gas inlet, and one outlet hole of about 4 mm and the gas flow distribution was not optimized. The discussion will be extended to the role of packing materials on the discharge operation and gas residence, and, finally, the addition of catalytic materials will also be taken into account. In particular, the addition of ceria as a material with oxygen vacancies is planned [41]. Ceria can be coated on the dielectric plates, or packed bed particles with ceria on its surface can be placed in the discharge gap.
Author Contributions
Conceptualization, R.B. and V.B.; methodology, R.B., M.S. (Milko Schiorlin), M.S. (Michael Schmidt), H.H. and A.V.P.; measurements, M.S. (Milko Schiorlin); analysis, R.B., M.S. (Milko Schiorlin), V.B.; writing—original draft preparation, R.B.; writing—review and editing, V.B., M.S. (Milko Schiorlin), H.H., A.V.P. and M.S. (Michael Schmidt); visualization, R.B. and V.B.; project administration, R.B.; and funding acquisition, V.B. and R.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by German Federal Ministry of Education and Research (BMBF) under grant number 033RC030D and European Union—NextGenerationEU.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of the study will be openly available at the public repository INPTDAT (https://www.inptdat.de, accessed on 3 March 2023) after publication.
Acknowledgments
The technical help of Wolfgang Reich and Peter Gransow is kindly acknowledged. H.H. acknowledges the support of Deutsche Forschungsgemeinschaft (DFG, project MAID, grant 466331904).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DBD | Dielectric barrier discharge |
| DE | Dielectric |
| Cer | Ceramic |
| EC | Energy cost |
| EE | Energy efficiency |
| EMC | Electromagnetic compatibility |
| EO | Electrode |
| EY | Energy yield |
| Gri | Grid |
| LCR | Inductance (L), capacitance (C), and resistance (R) |
| Mic | Mica |
| Pla | Plate |
| PSD | Power surface density |
| SIE | Specific input energy |
References
- Becker, K.H.; Kogelschatz, U.; Schoenbach, K.H.; Barker, R.J. Non-Equilibrium Air Plasmas at Atmospheric Pressure; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Kogelschatz, U. Dielectric-barrier discharges: Their history, discharge physics, and industrial applications. Plasma Chem. Plasma Proc. 2003, 23, 1–46. [Google Scholar] [CrossRef]
- Laroussi, M.; Kong, M.G.; Morfill, G.; Stolz, W. Plasma Medicine—Applications of Low-Temperature Gas Plasmas in Medicine and Biology; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Massines, F.; Sarra-Bournet, S.; Fanelli, F.; Naude, N.; Gherardi, N. Atmospheric Pressure Low Temperature Direct Plasma Technology: Status and Challenges for Thin Film Deposition. Plasma Procss. Polym. 2012, 9, 1041–1073. [Google Scholar] [CrossRef]
- Moreau, E. Airflow control by non-thermal plasma actuators. J. Phys. D Appl. Phys. 2007, 40, 605. [Google Scholar] [CrossRef]
- Meyer, C.; Müller, S.; Gurevich, E.L.; Franzke, J. Dielectric barrier discharges in analytical chemistry. Analyst 2011, 136, 2427. [Google Scholar] [CrossRef] [PubMed]
- Bill, A.; Wokaun, A.; Eliasson, B.; Killer, E.; Kogelschatz, U. Greenhouse gas chemistry. Energ. Convers. Manag. 1997, 38, S415–S422. [Google Scholar] [CrossRef]
- Bill, A.; Eliasson, B.; Kogelschatz, U.; Zhou, L.M. Comparison of CO2 hydrogenation in a catalytic reactor and in a dielectric-barrier discharge. Stud. Surf. Sci. Catal. 1998, 114, 541–544. [Google Scholar]
- Eliasson, B.; Kogelschatz, U.; Xue, B.Z.; Zhou, L.M. Hydrogenation of carbon dioxide to methanol with a discharge-activated catalyst. Ind. Eng. Chem. Res. 1998, 37, 3350–3357. [Google Scholar] [CrossRef]
- Kraus, M.; Egli, W.; Haffner, K.; Eliasson, B.; Kogelschatz, U.; Wokaun, A. Investigation of mechanistic aspects of the catalytic CO2 reforming of methane in a dielectric-barrier discharge using optical emission spectroscopy and kinetic modeling. Phys. Chem. Chem. Phys. 2002, 4, 668–675. [Google Scholar] [CrossRef]
- Bogaerts, A.; Centi, G. Plasma Technology for CO2 Conversion: A Personal Perspective on Prospects and Gaps. Front. Energy Res. 2020, 8, 111. [Google Scholar] [CrossRef]
- Brandenburg, R.; Bogaerts, A.; Bongers, W.; Fridman, A.; Fridman, G.; Locke, B.R.; Miller, V.; Reuter, S.; Schiorlin, M.; Verreycken, T.; et al. White paper on the future of plasma science in environment, for gas conversion and agriculture. Plasma Process Polym. 2019, 16, e1700238. [Google Scholar] [CrossRef]
- Paulussen, S.; Verheyde, B.; Tu, X.; De Bie, C.; Martens, T.; Petrovic, D.; Bogaerts, A.; Sels, B. Conversion of carbon dioxide to value-added chemicals in atmospheric pressure dielectric barrier discharges. Plasma Sources Sci. Technol. 2010, 19, 034015. [Google Scholar] [CrossRef]
- Aerts, R.; Somers, W.; Bogaerts, A. Carbon Dioxide Splitting in a Dielectric Barrier Discharge Plasma: A Combined Experimental and Computational Study. ChemSusChem 2015, 8, 702–716. [Google Scholar] [CrossRef] [PubMed]
- Aerts, R.; Martens, T.; Bogaerts, A. Influence of Vibrational States on CO2 Splitting by Dielectric Barrier Discharges. J. Phys. Chem. C 2012, 116, 23257–23273. [Google Scholar] [CrossRef]
- Mei, D. Plasma-Catalytic Conversion of Greenhouse Gas into Value-Added Fuels and Chemicals. Ph.D. Thesis, University of Liverpool, Liverpool, UK, 2016. [Google Scholar]
- Mei, D.; He, A.-L.; Liu, S.; Yan, J.; Tu, X. Optimization of CO2 conversion in a Cylindrical Dielectric Barrier Discharge Reactor Using Design of Experiments. Plasma Process Polym. 2016, 13, 544–556. [Google Scholar] [CrossRef]
- Niu, G.; Qin, Y.; Li, W.; Duan, Y. Investigation of CO2 Splitting Process Under Atmospheric Pressure Using Multi-electrode Cylindrical DBD Plasma Reactor. Plasma Chem. Plasma Proc. 2019, 39, 809–824. [Google Scholar] [CrossRef]
- Ozkan, A.; Dufour, T.; Bogaerts, A.; Reniers, F. How do the barrier thickness and dielectric material influence the filamentary mode and CO2 conversion in a flowing DBD? Plasma Sources Sci. Technol. 2016, 25, 045016. [Google Scholar] [CrossRef]
- Chen, P.; Shen, Y.; Ran, T.; Yang, T.; Yin, Y. Investigation of operating parameters on CO2 splitting by dielectric barrier discharge plasma. Plasma Sci. Technol. 2017, 19, 125505. [Google Scholar] [CrossRef]
- Belov, I.; Paulussen, S.; Bogaerts, A. Appearance of a conductive carbonaceous coating in a CO2 dielectric barrier discharge and its influence on the electrical properties and the conversion efficiency. Plasma Sources Sci. Technol. 2016, 25, 015023. [Google Scholar] [CrossRef]
- Belov, I.; Vanneste, J.; Aghaee, M.; Paulussen, S.; Bogaerts, A. Synthesis of Micro- and Nanomaterials in CO2 and CO Dielectric Barrier Discharges. Plasma Process Polym. 2017, 14, 1600065. [Google Scholar] [CrossRef]
- Uytdenhouwen, Y.; Van Alphen, S.; Michielsen, I.; Meynen, V.; Cool, P.; Bogaerts, A. A packed-bed DBD micro plasma reactor for CO2 dissociation: Does size matter? Chem. Eng. J. 2018, 348, 557–568. [Google Scholar] [CrossRef]
- Uytdenhouwen, Y.; Bal, K.M.; Michielsen, I.; Neyts, E.C.; Meynen, V.; Cool, P.; Bogaerts, A. How process parameters and packing materials tune chemical equilibrium and kinetics in plasma-based CO2 conversion. Chem. Eng. J. 2019, 372, 1253–1264. [Google Scholar] [CrossRef]
- Müller, S.; Zahn, R.-J. Air Pollution Control by Non-Thermal Plasma. Contrib. Plasma Phys. 2007, 47, 520–529. [Google Scholar] [CrossRef]
- Brandenburg, R.; Kovacevic, V.V.; Schmidt, M.; Basner, R.; Kettlitz, M.; Sretenovic, G.B.; Obradovic, B.M.; Kuraica, M.M.; Weltmann, K.-D. Plasma-Based Pollutant Degradation in Gas Streams: Status, Examples and Outlook. Contrib. Plasma Phys. 2014, 54, 202–214. [Google Scholar] [CrossRef]
- Rafflenbeul, R. NTP-Anlagen zur Luftreinhaltung in der Abfallwirtschaft. Müll Abfall 1998, 30, 1, 38–44. [Google Scholar]
- Rafflenbeul, L.; Rafflenbeul, R. Treatment of Problematic Exhaust Air Escort Substances. Chem. Ing. Tech. 2022, 94, 471–478. [Google Scholar] [CrossRef]
- Brehmer, F.; Welzel, S.; van de Sanden, M.C.M.; Engeln, R. CO and byproduct formation during CO2 reduction in dielectric barrier discharges. J. Appl. Phys. 2014, 116, 123303. [Google Scholar] [CrossRef]
- Ponduri, S.; Becker, M.M.; Welzel, S.; van de Sanden, M.C.M.; Loffhagen, D.; Engeln, R. Fluid modelling of CO2 dissociation in a dielectric barrier discharge. J. Appl. Phys. 2016, 119, 093301. [Google Scholar] [CrossRef]
- Uytdenhouwen, Y.; Hereijgers, J.; Breugelmans, T.; Cool, P.; Bogaerts, A. How gas flow design can influence the performance of a DBD plasma reactor for dry reforming of methane. Chem. Eng. J. 2021, 405, 126618. [Google Scholar] [CrossRef]
- Peeters, F.J.J.; van de Sanden, M.C.M. The influence of partial surface discharging on the electrical characterization of DBDs. Plasma Sources Sci. Technol. 2015, 24, 015016. [Google Scholar] [CrossRef]
- Pipa, A.V.; Koskulics, J.; Brandenburg, R.; Hoder, T. The simplest equivalent circuit of a pulsed dielectric barrier discharge and the determination of the gas gap charge transfer. Rev. Sci. Instrum. 2012, 83, 115112. [Google Scholar] [CrossRef]
- Manley, T.C. The electric characteristics of the ozonator discharge. Trans. Electrochem. Soc. 1943, 84, 83–96. [Google Scholar] [CrossRef]
- Schmidt, M.; Basner, R. Brandenburg, R. Hydrocarbon Assisted NO Oxidation with Non-thermal Plasma in Simulated Marine Diesel Exhaust Gases. Plasma Chem. Plasma Proc. 2013, 33, 323–335. [Google Scholar] [CrossRef]
- Schmidt, M.; Schiorlin, M.; Brandenburg, R. Studies on the Electrical Behaviour and Removal of Toluene with a Dielectric Barrier Discharge. Open Chem. 2015, 13, 477–483. [Google Scholar] [CrossRef]
- Kogelschatz, U. Advanced Ozone Generation. In Process Technologies for Water Treatment; Stucki, S., Ed.; Springer: New York, NY, USA, 1988; pp. 87–118. [Google Scholar]
- Pipa, A.V.; Brandenburg, R. The equivalent circuit approach for the electrical diagnostics of dielectric barrier discharges: The classical theory and recent developments. Atoms 2019, 7, 14. [Google Scholar] [CrossRef]
- Reichen, P.; Sonnenfeld, A.; von Rohr, P.R. Discharge expansion in barrier discharge arrangements at low applied voltages. Plasma Sources Sci. Technol. 2011, 20, 055015. [Google Scholar] [CrossRef]
- Brandenburg, R. Dielectric barrier discharges: Progress on plasma sources and on the understanding of regimes and single filaments. Plasma Sources Sci. Technol. 2017, 26, 053001. [Google Scholar] [CrossRef]
- Hosseini Rad, R.; Brüser, V.; Schiorlin, M.; Schäfer, J.; Brandenburg, R. Enhancement of CO2 splitting in a coaxial dielectric barrier discharge by pressure increase, packed bed and catalyst addition. Chem. Eng. J. 2023, 456, 141072. [Google Scholar] [CrossRef]
- Cui, Z.; Liu, Q.; Cai, Z.; Wang, J.; Wu, Q. Modified equivalent circuit for coplanar barrier discharge considering undischarged areas. Phys. Plas 2023, 30, 013502. [Google Scholar] [CrossRef]
- Pipa, A.V.; Hink, R.; Foest, R.; Brandenburg, R. Dependence of dissipated power on applied voltage for surface barrier discharge from simplest equivalent circuit. Plasma Sources Sci. Technol. 2020, 29, 12LT01. [Google Scholar] [CrossRef]
- Falkenstein, Z.; Coogan, J.J. Microdischarge behaviour in the silent discharge of nitrogen—oxygen and water—air mixtures. J. Phys. D Appl. Phys. 1999, 30, 817–825. [Google Scholar] [CrossRef]
- Lindner, M.; Pipa, A.V.; Brandenburg, R.; Schreiner, R. Expansion of surface barrier discharge scrutinized. Plasma Sources Sci. Technol. 2022, 31, 105018. [Google Scholar] [CrossRef]
- Gibalov, V.I.; Pietsch, G.J. The development of dielectric barrier discharges in gas gaps and on surfaces. J. Phys. D Appl. Phys. 2000, 33, 2618–2636. [Google Scholar] [CrossRef]
- Höft, H.; Becker, M.M.; Kettlitz, M.; Brandenburg, R. Upscaling from single- to multi-filament dielectric barrier discharges in pulsed operation. J. Phys. D Appl. Phys. 2022, 55, 424003. [Google Scholar] [CrossRef]
- Schiorlin, M.; Klink, R.; Brandenburg, R. Carbon dioxide conversion by means of coplanar dielectric barrier discharges. Eur. Phys. J. Appl. Phys. 2016, 75, 24704. [Google Scholar] [CrossRef]
- Hoder, T.; Šíra, M.; Kozlov, K.V.; Wagner, H.-E. 3D Imaging of the Single Microdischarge Development in Coplanar Barrier Discharges in Synthetic Air at Atmospheric Pressure. Contrib. Plas. Phys. 2009, 49, 381–387. [Google Scholar] [CrossRef]
- Brehmer, F.; Welzel, S.; Klarenaar, B.L.M.; van der Meiden, H.J.; van de Sanden, M.C.M.; Engeln, R. Gas temperature in transient CO2 plasma measured by Raman scattering. J. Phys. D Appl. Phys. 2015, 48, 155201. [Google Scholar] [CrossRef]
- Brandenburg, R.; Sarani, A. About the development of single microdischarges in dielectric barrier discharges in CO2 and CO2/N2 gas mixtures. Eur. Phys. J. Spec. Top. 2017, 226, 2911–2922. [Google Scholar] [CrossRef]
- Kulikovsky, A.A. Positive streamer between parallel plate electrodes in atmospheric pressure air. J. Phys. D Appl. Phys. 1997, 30, 441. [Google Scholar] [CrossRef]
- Nijdam, S.; Teunissen, J.; Ebert, U. The physics of streamer discharge phenomena. Plasma Sources Sci. Technol. 2020, 29, 103001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).