Abstract
For the theoretical study of X and extreme-UV spectra of ions in plasmas, quantum mechanics brings more detailed results than statistical physics. However, it is impossible to handle individually the billions of levels that must be taken into account in order to properly describe hot plasmas. Such levels can be gathered into electronic configurations or superconfigurations (groups of configurations) and the corresponding calculations rely on appropriate statistical methods, for local or non-local thermodynamic equilibrium plasmas. In this article we present the basic principles of the Super-Transition-Array approach as well as its practical implementation. During the last decades, calculations performed with the SCO code (Superconfiguration Code for Opacity) have been compared to opacity measurements. The code includes static screening of ions by plasma and is well suited for studying plasma density effects (for example pressure ionization) on opacity and equation of state. The recently developed SCO-RCG code (Superconfiguration Code for Opacity combined with Robert Cowan’s “G” subroutine) combines statistical methods from SCO and fine-structure (detailed-level-accounting) calculations using subroutine RCG from Cowan’s code. SCO-RCG enables us to obtain very detailed spectra and to significantly improve the interpretation of experimental spectra. The Super-Transition-Array formalism is still the cornerstone of several opacity codes, and new ideas are emerging, such as the Configurationally Resolved-Super-Transition-Array approach or the extension of the Partially Resolved-Transition-Array concept to the superconfiguration method.
1. Introduction
Hot plasmas contain, for all their chemical constituents, atomic ions in different ionization stages, potentially spread over billions of energy levels, and subject to several atomic processes. Therefore, it is easy to understand that such systems have been studied using methods from statistical physics. This review article deals with a method of calculation of the photoabsorption cross-section in hot plasmas at local thermodynamic equilibrium (LTE). The knowledge and understanding of photoabsorption in plasmas first interested astrophysicists. Before the advent of computers, calculations relied on the hydrogenic approximation [1]. The first computers allowed the development of self-consistent models. For a long time, the field has suffered from the lack of direct experimental check of the proposed atomic models. The first experiments which made it possible to evaluate the exactness of calculations appeared at the end of the eighties. The comparisons made at that time revealed that it was necessary to take into account the real -electron states and selection rules in the modelling. Detailed-configuration-accounting methods appeared to be insufficient (see reference [2] and references therein), due to the limited number of configurations that could be taken into account. The approach described in the present article stems from intensive theoretical works generated by these comparisons. Although the superconfiguration method has been proposed in 1989 by Bar-Shalom et al. [3], it would not exist without the works of Bauche-Arnoult, Bauche and Klapisch on the statistical treatment of unresolved transition arrays between two electronic configurations (see references [4,5,6,7]). In the present article, we propose to discuss all the approximations of this method avoiding, as much as possible, technical details.
The main approximations of the superconfiguration approach in the case of absorption are described in Section 2, and the SCO code (Superconfiguration Code for Opacity) is presented in Section 3. Comparisons with experimental spectra are discussed in Section 4. With the development of more and more powerful computers, the application of precise atomic-physics methods to opacity computation became possible. This led us to develop the SCO-RCG code (Superconfiguration Code for Opacity combined with Robert Cowan’s “G” subroutine), combining statistical methods and Detailed-Level-Accounting (DLA) fine-structure calculations of atomic structure and spectra. Finally, recent works related to the Super-Transition-Array (STA) formalism are mentioned in Section 6.
2. Approximations of the Superconfiguration Method (Case of Absorption)
2.1. Photoabsorption Cross-Section
Transitions involving bound electrons play a particularly important role in emission and absorption of thermal radiation. The bound-bound absorption cross-section of ions in a plasma is given by the following formula ( is the frequency of the photon of energy :
where is the fine structure constant. n and m are the indexes of -electron quantum states and and their respective energies. In the representation, is an antisymmetric wavefunction of electrons, depending on their positions , . represents the dipolar oscillator (in the representation, ), is the population of initial state and , centered around , is the normalized line profile of transition . Except for light elements, the direct use of expression (1) is practically excluded in the case of hot plasmas because of the huge numbers of states involved in the double sum. Even the enumeration of all states is a challenging task (see Section 2.7), since the use of Equation (1) would require to solve equation:
The superconfiguration approximation consists in deriving a statistical version of Formula (1) (and of the similar formula for the emission probability). As we will see, this method offers the possibility to use Formula (1) in an efficient way, avoiding all direct sums on multi-electronic states, as well as the resolution of Equation (2).
2.2. Use of Electronic Configurations
In atomic physics, the states of the Hamiltonian are obtained from the diagonalization of this operator in a basis of states composed by one-electron wavefunctions (see, for example, reference [8]). The latest (also named “orbitals”) are wavefunctions of the one-electron Hamiltonian including the central potential, calculated in a self-consistent way, either in the framework of Hartree-Fock (or Dirac-Fock) formalism, or of another model, such as, for instance, density functional theory. In atomic physics of dense plasmas, the diagonalization of the Hamiltonian matrix is usually limited to the basis of the states associated to an electronic configuration. We denote C the configuration defined by the ensemble of one-electron subshells (non-relativistic or relativistic) and their respective occupations. A non-relativistic configuration is represented by where s runs over all bound subshells; for instance, is a configuration made of orbitals , , and populated, respectively, with 2, 2, 5 and 1 electron(s). A relativistic configuration is represented by , where . Thus, is a configuration made of orbitals , , , and , respectively, populated with 2, 2, 2, 3 and 1 electron(s). Let us remark that orbital is not entirely populated, on the contrary to relativistic orbital . Since in the case of s orbitals, the quantum number j can only take the value 1/2, it is usually omitted. Limiting oneself to states belonging to configurations, one can rewrite Equation (1) replacing the double summation over initial and final states by the double sum: . This means that all solutions of Equation (2), which would be obtained in bases composed by wavefunctions of two or more configurations, are excluded. In other words, general configuration interaction is neglected. Nevertheless, a certain kind of configuration interaction, particularly important in plasmas, can be included in an approximate way [9,10,11,12]: interaction between relativistic subconfigurations of a non relativistic configuration.
2.3. Approximation of the Probability of a State
The probability of a state with bound electrons in a plasma at local thermodynamic equilibrium can be obtained by the formula:
where represents the contribution of bound electrons to the energy of state . is the sum of the interaction energy between bound and free electrons (bf: bound-free) and the interaction energy between free electrons (ff: free-free) induced by the state . The energy dispersion of the states with respect to the value of being relatively weak, we can replace in expression (3) the energy by its average value, identical for all the states of the configuration. We can then write:
The term can be obtained as [8]:
where integer number is the population of bound subshell s; and depend on direct and exchange Slater [8] integrals calculated with wavefunctions obtained via a self-consistent calculation, restricted to the configuration C. In that framework, we have:
where is the wavefunction of subshell s, its eigen-energy and the central self-consistent potential of configuration C (the Hamiltonian used for the calculation of orbitals reads ). In the local-density approximation of the density-functional theory, the self-consistent potential is the sum of the electrostatic potential (related to the electron density through the Poisson equation) and an exchange-correlation potential. The version of the SCO code described in Section 3 relies on such an approximation. However, it is worth mentioning that Blenski et al. derived finite temperature self-consistent-field Hartree-Fock equations for atoms in plasmas based on the superconfiguration method [13,14,15]. The populations of the subshells and the interaction matrices in the Hartree-Fock equations can be expressed in terms of statistical sums. In such a way the Pauli principle and the exchange interaction are taken into account exactly [16]. This allows one to avoid problems stemming from non-integer occupation numbers in other approaches to thermal Hartree-Fock theories [17].
2.4. Probability of an Electronic Configuration in the Superconfiguration Approximation. Calculation of the Self-Consistent Potential of a Superconfiguration
The superconfiguration approximation consists in partitioning the ensemble of configurations, i.e., in gathering them into groups. A superconfiguration represents a number of configurations of the plasma and is composed by an ensemble of supershells (i.e., groups of subshells) and their respective populations. For example, superconfiguration represents all the configurations with shells , and full and a total of 20 electrons distributed in all possible ways (consistent with the Pauli exclusion principle) in the subshells and (the third supershell consists of 7 orbitals to ). As we will see in Section 2.7, contains a total of 35,413 configurations and 4.71292·10 states.
Gathering configurations into superconfigurations allows for a further simplification of the expression of the probability of a configuration. As shown by Equation (5), the Hartree-Fock energy of a configuration is a quadratic function of the subshell populations, which is not convenient for the evaluation of summations over populations. The superconfigurations will therefore be chosen in a way such that the energy of a configuration belonging to a superconfiguration can be approximated by a linear function of the subshell populations:
where represents the difference between and . The STA formalism requires the calculation of independent-electron partition functions under the constraint that a group of subshells (referred to as a supershell) has an integer number of electrons (see Section 2.7). The averages in the term are carried out upon both bound-state populations and free states. The coefficients involved in the linear function which were, originally, the one-electron eigen-energies for a configuration (see Equation (6)) are now replaced by the one-electron eigen-energies of the superconfiguration, , which are common to all the configurations belonging to superconfiguration . In other words, the superconfiguration approximation consists in replacing by in the Boltzmann factor. Each superconfiguration will therefore be characterized by a self-consistent potential and/or the one-electron states in this potential. In such a way, the probabilities of electronic states and configurations will be given in each superconfiguration by identical expressions, as for the probability of states in an ideal gas of independent electrons. Thus, in a sense, the superconfiguration approximation enables one to use the statistical mechanics of the ideal gas for the states of configurations which energies are sufficiently close to each other. This is the case when the energy dispersion of the states of a superconfiguration is small compared to the value of thermal kinetic energy . However it must be noticed that the main advantage of the superconfiguration approximation is the fact that it relies on a recursive algorithm. In practice, an efficient way to evaluate the reliability and the validity of such an approximation is to control the convergence of a photoabsorption calculation. Convergence can be considered to be achieved when, after a certain supershell subdivision, the spectrum does not change anymore. The refinement of the supershell subdivision is not required anymore (it means the number of superconfigurations to be calculated is sufficient).
Of course, in the calculation of the average energy of a configuration, required for instance for the determination of the transition energies, the quadratic terms (with respect to the subshell populations) are taken into account, and their average expressed in terms of partition functions. This means that we assume (which is reasonable), that the dependence of quantities and with respect to the populations can be neglected.
2.5. Transition Arrays between Two Configurations. Statistical Treatment of Lines
The superconfiguration formalism enables one to use a basis of one-electron wavefunctions common to superconfigurations in order to evaluate the matrix elements . Indeed, through the expression of the probability of the states, the cross-section can be expressed in a simplified way:
where represents the probability of configuration C divided by its degeneracy. Summation over states n and m becomes independent on the temperature and describes a transition array between configurations C and . The presence of dipolar operator in the matrix elements of Equation (8) enables one [8] to construct configuration from the knowledge of configuration C through the transition obeying selection rules (, or 0). In the case of ions with several open subshells, the increasing number of states n and m manifests itself by the occurrence of a large number of lines building an unresolved transition array in absorption or emission spectra. The transition arrays between two configurations were studied by Bauche-Arnoult, Bauche and Klapisch [4,5,6,7]. These authors have proposed a statistical treatment of transition arrays consisting in modelling the contribution of lines to the spectrum by “envelopes” continuous with respect to photon energy. Such an approach seems to be adequate in the case of a huge number of lines. Indeed, the widths of such lines are finite (in plasmas, “physical” broadening of lines, due to the interaction with the plasma environment made of electrons and ions, can be important because of Doppler effect, electron impact and ionic Stark effect). Subsequently, lines merge together and exhibit large unresolved structures in the spectrum. The knowledge of the first three moments (orders 0, 1 and 2) enables one to model a transition between two configurations by a Gaussian function. In the statistical approach of references [4,5,6,7], physical broadening, described by functions , is assumed to take the same value for all the lines of the transition array. Such an approximation leads us to define the three previously mentioned moments , , weighted by the line strengths:
The first three normalized moments of the Gaussian distribution can be expressed in terms of the ones of Equation (9) in the following way:
and
They correspond, respectively, to the total strength of the array, to its average transition energy and to its variance. Let us consider a transition between two configurations: C and . It can be described in terms of population numbers of the subshells by the following symbolic notation: , being the considered transition (one-electron jump). Total strength of the transitions can be evaluated [8] from one-electron states (orbitals). Therefore, the zero-order moment reads:
where is the total degeneracy of configuration C. and are the degeneracies of subshells and , respectively, and is the reduced matrix element of these two orbitals (we make the assumption, at this stage, that the basis of orbitals of C and are the same) [8].
References [4,5,6] provide analytical formulas for the first and second moments and of the transition array between two configurations. In particular, the average energy of the transition is given by: , where the first two terms correspond to pure-bound-electron energies of configurations C and (see Equation (5)) and the third term to an exact correction (sometimes referred to as the “BBK”—for Bauche, Bauche-Arnoult, Klapisch-shift). In the case of transition between two configurations , such a result can be written:
where coefficients depend on the Slater integrals [8] involving orbitals and as well as orbital quantum numbers of subshells , and s (for s different from zero). The results for the variance will not be presented here; let us only note that they involve quadratic forms with respect to populations . The formulas for the moments and , established in [4,5,6], take into account the selection rules, since the averages in Equation (9) are made on the matrix elements on the -electron states. The statistical description of “non relativistic” configurations leads (see references [4,5]) to structures named UTA (Unresolved Transition Arrays). In the framework of the configuration approximation, such a description corresponds to intermediate coupling [8]. The unresolved structures obtained in the case where the configurations are made of relativistic orbitals are named SOSA (Spin-Orbit Split Arrays) [6]. In both cases, UTA and SOSA, the total theoretical spectra are obtained as sums of weighted Gaussians, as predicted by Equation (8). The physical broadening, uniform for the configuration, can be reintroduced through a convolution leading to a Voigt profile.
2.6. Transition Arrays between Two Superconfigurations. Statistical Treatment of Lines and Configurations
The ensemble of transitions between two superconfigurations is named, in the literature, a STA (Super Transition Array). The statistical treatment of STAs relies, as in the case of UTAs or SOSAs, on the calculation of the first three moments of such superarrays and on the modelling of transitions by Gaussians built from these moments. The moments characterizing a transition are defined in a similar way as in (9):
In the case of Equation (15), the calculation must absolutely take into account the fact that the probability depends on the temperature. In order to include this dependence, we can use the main approximation of the superconfiguration method, presented in Equation (7). Such an approximation simplifies considerably the calculation.
2.7. Partition Functions of the Superconfiguration Approach
Thanks to Equations (4) and (7), the normalization coefficient of the probability (see Equation (3)), which is nothing more than the inverse of the partition function U counting all the states belonging to all the superconfigurations, becomes:
where represents the chemical potential and
being the usual binomial coefficient. The partial partition function (also named “statistical sum”) of Equation (16) reads:
where and the product runs over the supershells of . Bar-Shalom et al. have proposed to use, for the calculation of the partition function of a Q-electron supershell made of N orbitals, a recursive formula which is well-known in the thermodynamics of ideal fermions. The partition function is a linear combination of the partition functions of the same supershell (same number of orbitals N) with smaller electron numbers [18,19]:
with and
where
However, the coefficients of linear combination (19) have alternate signs which can be a source of numerical errors. In order to remedy this problem, when the number of electrons is larger than half the total degeneracy of the supershell, it has been proposed to count the holes rather than the electrons [15]. The partition function for the holes is directly related to the partition function for the electrons through the relation
where is the total degeneracy of the supershell and the number of holes. The algorithm relying on Formula (19) and using electron/hole counting enables one to perform calculations in most of the cases without any numerical errors. However, when one considers very large supershells or supershells showing large differences in the energies of their orbitals (compared to the thermal kinetic energy ), it can become numerically unstable. In the case of high-degeneracy supershells and/or at low temperature, the above relations (Equations (19) and (22)) for generating these partition functions suffer from numerical instability due to precision cancellations arising from sums of large terms of alternating sign [20]. In 2004, we proposed a robust and stable algorithm [21], relying on the calculation of partition functions by a nested recursion, building up supershells one subshell by one, at each stage from “parent” supershells (of one less subshell) with smaller numbers of electrons. All the terms entering the sums involved in this recursion are strictly positive, and cancellation effects are therefore avoided. The relation reads
The eigen-states obtained from the resolution of the Schrödinger equation are numbered by the principal n, orbital ℓ and spin s quantum numbers, as well as the magnetic moments and . Each subshell can contain states. Such a number is also the degeneracy of the subshell. In the case of Dirac equation, the degeneracy of a relativistic subshell is . The number of configurations of a system with N subshells and Q electrons is equal to the number of ways to distribute the Q electrons in the N subshells. The population i of subshell N lies between 0 and , where is the degeneracy of the subshell. For each value of i, one has to “place” the remaining electrons in the remaining subshells [22]. This yields
In the same way, the number of states of a system with N subshells and Q electrons reads
Table 1 displays the numbers of configurations and states for a supershell made of subshells to and different values of Q.

Table 1.
Number of configurations and states for different values of the number of electrons Q in the supershell .
Figure 1 displays the ratio of consecutive partition functions () versus the number of electrons for the supershell () in the case of a gold plasma (Au, ) at 100 eV and 0.01 g/cm. Electron eigen-energies have been obtained through a screened hydrogenic model with () splitting. One can check that in that case the electron-hole formalism is sufficient in order to carry out the calculation with any precision loss.
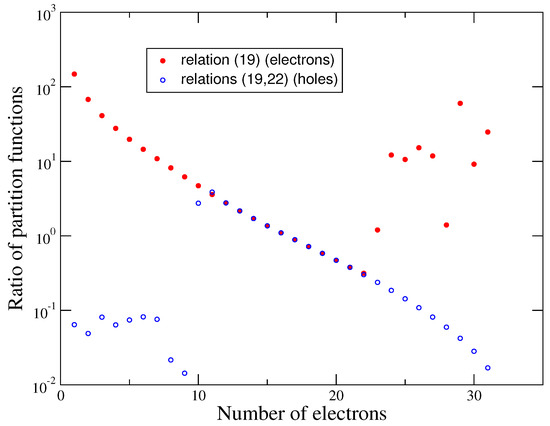
Figure 1.
Ratio of consecutive partition functions () versus the number of electrons for the supershell () in the case of a gold plasma (Au, ) at 100 eV and 0.01 g/cm. Electron eigen-energies have been obtained through a screened hydrogenic model with () splitting. Full red circles represent the results of the calculations performed using relation (19) applied to the electrons and empty blue circles represent the calculation relying on relation (19) applied to holes (22). One can check that in that case the electron-hole formalism is sufficient in order to carry out the calculation with any precision loss.
Figure 2 shows the ratio of consecutive partition functions () versus the number of electrons for the supershell () in the case of a gold plasma (Au, ) at 100 eV and 0.01 g/cm. One can check that in that case the electron-hole formalism is not sufficient in order to carry out the calculation with any precision loss. However, with the new recursion relation (23), the calculation works in all cases, even without the electron-hole formalism (which still enables to save computation time).
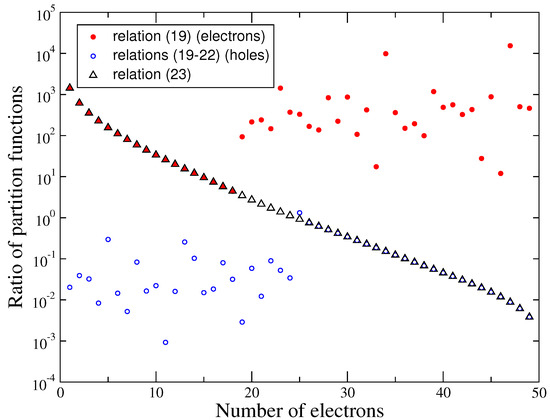
Figure 2.
Ratio of consecutive partition functions () versus the number of electrons for the supershell () in the case of a gold plasma (Au, ) at 100 eV and 0.01 g/cm. Electron eigen-energies have been obtained through a screened hydrogenic model with () splitting. Full red circles represent the results of the calculations performed using relation (19) applied to the electrons and empty blue circles represent the calculation relying on relation (22) applied to holes (19). One can check that in that case the electron-hole formalism is not sufficient in order to carry out the calculation with any precision loss. However, with the new recursion relation (23), the calculation works in all cases, even without the electron-hole formalism (which still enables to save computation time).
In a 2007 paper entitled “Further stable methods for the calculation of partition functions in the superconfiguration approach” [23], we proposed two main improvements of the initial method:
- The first improvement consists in applying the recursion relation to holes, when a supershell is more than half-filled with electrons.
- The second improvement consists in precomputing some partition functions and storing the results. It stems from the successive use of generating functions with reduced degeneracies.
The latter improvement, however, was not clearly explained, and several researchers wrote to us because they did not manage to understand how to proceed. This is mainly due to the fact that Equation (23) of reference [23] may be misleading, if not considered as incorrect. Therefore, we published recently [24] a paper in which we propose an optimization of the latter method and explain how to implement it in practice. The formalism relies on the evaluation of elementary symmetric polynomials, which opens the way to further improvements.
It is worth mentioning that we also improved the treatment of electron-electron interactions, in order to go beyond the averaging of the corresponding energy term in the Boltzmann factors (see Equation (7)). Our approach relies on the Gibbs-Bogolyubov (or Jensen-Feynman) variational approach, which enables one to include the effect of such interactions in an average manner in the one-electron energies [25,26].
3. The Opacity Code SCO
The SCO code (Superconfiguration Code for Opacity) [15,27,28], uses in practice all the formulas mentioned in Section 2 in order to evaluate the contribution to the photoabsorption cross-section of transitions involving bound electrons. The calculation of the bound-free cross-section in that code relies on the superconfiguration formalism as well. Free-free transitions (inverse bremsstrahlung) can be evaluated using the Kramers (classical) formula or via a quantum calculation using free-electron wavefunctions. One of the original features of the code is the self-consistent calculation of superconfigurations in the Wigner-Seitz (WS) cell. In such a way, the code takes into account effects due to the plasma environment, named “density effects”. The screening by the electrons is a direct consequence of the neutrality of the plasma, which ensures, adjusting the chemical potential, that the total number of electrons in the sphere (bound and free) is equal to atomic number Z.
The computation starts with an average-atom calculation. Such a model enables one to determine in a self-consistent way the average electronic structure of the plasma, i.e., the energies of the orbitals, their wavefunctions and their fractional populations, corresponding to the average configuration. The whole plasma is described by the WS sphere representing an imaginary average ion which charge is precisely the average ionization of the plasma. Then, the code determines the list of the relevant superconfigurations. Such a list is prepared on the basis of the results of the average-atom calculation (the configuration energies are estimated using the average-atom eigen-energies and wavefunctions). In the SCO code, the choice of the supershells and the creation of retained superconfigurations is automatic. Consistently with the imposed gathering criteria, the code builds the supershells containing subshells more or less dispersed on an energy scale. The supershells are populated according to the fluctuation theory of non-interacting fermions [29]. Using the eigen-energies and wavefunctions obtained from the average-atom calculation, the code determines the probabilities of the superconfigurations and retains only the required number. The electronic structure of the retained superconfigurations is obtained as a result of the self-consistent-field calculation. The superconfigurations are characterized by their self-consistent potentials (and therefore by their wavefunctions) and their free energy, which yields a more realistic evaluation of the partition functions as well as of the energy (see Section 2). The self-consistent computation of the electronic structure of a superconfiguration is similar to the average-atom one, except that in the former one has to ensure that the populations of the supershells are integers, which requires the introduction of Lagrange multipliers. The relativistic effects are included in the Pauli approximation [30] and the exchange-correlation potential at finite temperature is calculated using a fit proposed by Iyetomi and Ichimaru [31]. The choice of the number of superconfigurations (and therefore of the subdivision of supershells) is guided by the convergence of the spectrum: when the spectrum does not change anymore, the number of superconfigurations is sufficient. Such a convergence test also ensures, in an indirect way, the validity of the main approximation of the superconfigurations method consisting in averaging the quadratic terms in the Boltzmann probability of a superconfiguration (7). In addition the code includes interaction between relativistic subconfigurations of a non-relativistic configuration. Several models, proposed by Bar-Shalom et al., are implemented. They rely on analytical expressions for the correction to the intensities, owing to configuration interaction, of a super transition array [10,11,12]. Within the model described in reference [10], such formulas are obtained when the correction is small compared to the spin-orbit splitting, bypassing the need to diagonalize energy matrices. In the later works, the smallness of the correction is not assumed (in particular, the model of references [11,12] describes the limit of LS-coupling).
4. Comparisons with Experimental Spectra
4.1. Measurement of the Transmission of an Iron Plasma in the XUV Range
The experiment was performed on the ASTERIX IV laser facility by Winhart et al. [32,33]. It concerns a part of the spectrum of iron close to the absorption structure dominated by 3p-3d transitions, structure that had been measured previously by Da Silva et al. [2]. The work of reference [2] was motivated by astrophysical applications. Assuming that, during the measurement, the density and the temperature of the target are quasi-uniform, the transmission is directly related to the opacity which is nothing else than the photoabsorption cross-section per unit of mass. We show on Figure 3 that it is possible to obtain a relatively good agreement between theory and experiment concerning the position of the absorption structures. The differences between theoretical and measured transmissions can be attributed to temperature and density spatial (gradients) and temporal (non-stationarity) variations in the target during the measurement. This comparison illustrates the way the theoretical spectrum changes with the supershell splitting (see Figure 4) and with the number of superconfigurations included.
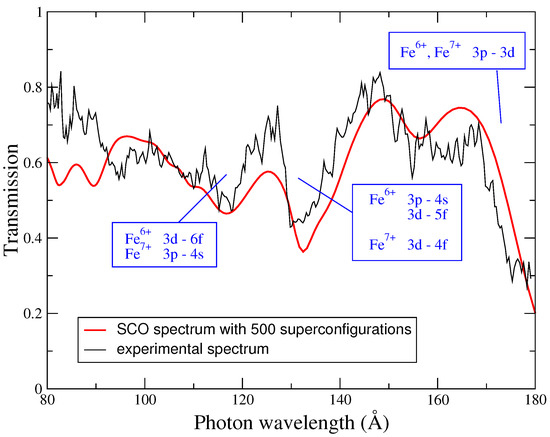
Figure 3.
Comparison between an experimental transmission spectrum (black curve) of an iron plasma (Fe, ) with a spectrum simulated by SCO code (red curve). The experiment is described in reference [32,33]. The areal mass is 20 g/cm. The best agreement has been obtained at a temperature of 22 eV and a density of 0.01 g/cm. The calculation has been carried out with 9 supershells and 500 superconfigurations.
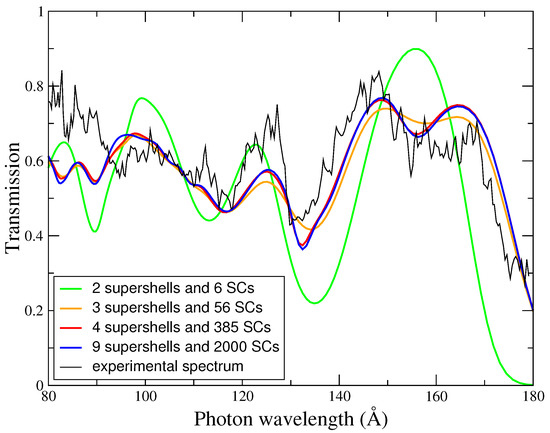
Figure 4.
Comparison between an experimental transmission spectrum (black curve) of an iron plasma (Fe, Z = 26) with a spectrum simulated by SCO code. The experiment is the same as the one in Figure 3. The figure displays 4 different calculations at a temperature of 22 eV and a density of 0.01 g/cm: the green curve corresponds to a calculation with 2 supershells and 6 superconfigurations, the yellow curve to a calculation with 3 supershells and 56 superconfigurations, the red curve to a calculation with 4 supershells and 385 superconfigurations and the blue curve to a calculation with 9 supershells and 2000 superconfigurations. This illustrates the convergence of the spectrum with respect to the subdivision in supershells and the number of superconfigurations. Beyond a threshold number of superconfigurations, the spectrum does not change much.
4.2. Transmission of a Multilayer Plasma: Aluminum and Nickel
This experiment, similar to the previous one, has been performed by the group of Chenais-Popovics [34] and addresses the theme of mixtures. The target was made of 10 alternate slices of aluminum and nickel (5 of each element) and the total areal mass of each element was 20 g/gm. In a general way, spectra of light elements are often used as “thermometers” since it is easier to determine the temperature by theoretical analysis of such elements. Figure 5 and Figure 6 show the differences between spectral structures of a low-Z element and a mid-Z element. Indeed, in the case of the aluminum spectrum, it is possible to distinguish the structures due to different ionic charges. Such a distinction is totally impossible in the case of nickel. Contributions of all ionic charges build large unresolved structures. However, it is possible to determine which transitions the main structures correspond to. Although direct information about the ionic charges seems to be lost, it is present in an implicit way in the statistics underlying the superconfiguration method.
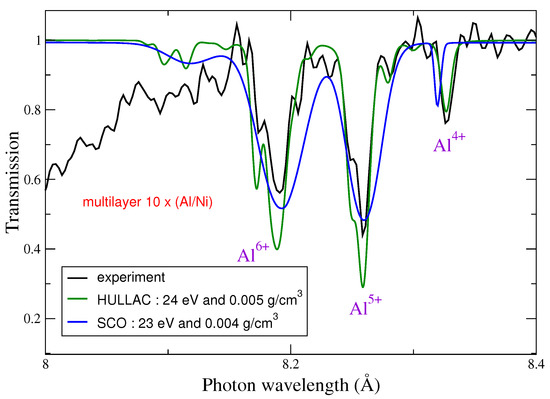
Figure 5.
Comparison between an experimental transmission spectrum (black curve) of an aluminum plasma (Al, ) of a Al/Ni multilayer, a spectrum calculated by the detailed-configuration code HULLAC (green curve) at a temperature of 24 eV and a density of 0.005 g/cm, and a spectrum calculated by the SCO code at a temperature of 23 eV and a density of 0.004 g/cm (blue curve). The experiment is described in reference [34].
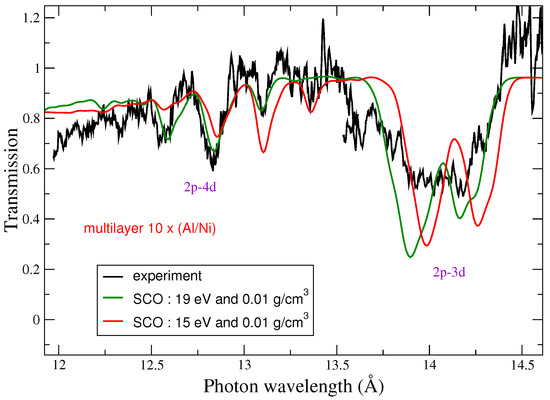
Figure 6.
Comparison between an experimental transmission spectrum (black curve) of a nickel plasma (Ni, ) of a Al/Ni multilayer, a spectrum calculated by the SCO code (red curve) at a temperature of 15 eV and a density of 0.01 g/cm, and a spectrum calculated by the SCO code at a temperature of 19 eV and a density of 0.01 g/cm (green curve). The experiment is the same as in Figure 5.
Aluminum transmission was computed with the detailed (fine-structure) code HULLAC (Hebrew University Lawrence Livermore Atomic Code) [35] and then by the superconfiguration code SCO. Figure 5 shows the measured transmission, the transmission obtained from the HULLAC code at a temperature of 24 eV and a density of 0.005 g/cm, and the transmission calculated by the SCO code at a temperature of 23 eV and a density of 0.004 g/cm. Figure 6 shows experimental and theoretical transmission spectra for nickel. Both theoretical spectra have been calculated by the SCO code and correspond to temperatures of 19 and 15 eV and to a density of 0.01 g/cm. The comparison of the 2p-3d and 2p-4d structures at 19 and 15 eV in Figure 6 illustrates the fact that the absorption structures of nickel are very sensitive to the temperature. Note that the spectra obtained with the SCO code showed a good agreement with a number of other experimental spectra, in particular the germanium spectrum obtained by Renaudin et al. [36]. The sensitivity of the absorption features calculated with SCO at the “theoretical” temperature led to an additional diagnostics in several photoabsorption experiments [37,38].
5. The Beginning of a New Story: The Birth of SCO-RCG Code
SCO-RCG [39,40,41,42] is a hybrid opacity code combining statistical modellings of transition arrays (STA, UTA, SOSA) with fine-structure calculations. The selection of transition arrays for which a detailed line-by-line treatment is possible and relevant is made according to some criteria involving the mean energy “spacing” between neighbouring lines and the mean line width in the transition array. The data required for the calculation of the detailed transition arrays (i.e., direct and exchange Slater, spin-orbit, and dipolar integrals) are provided by the superconfiguration code SCO [27], ensuring in this way a consistent modelling of the plasma screening effects on the wavefunctions. Then, the level energies and the line energies and strengths are calculated by the routine RCG, which is an ingredient of Cowan’s atomic structure code [8]. RCG proceeds to the diagonalization of the Hamiltonian. The computation starts with an usual average-atom calculation, providing the mean populations of the subshells, and from which a list of superconfigurations of the following type:
is built, where
being the last (highest-energy) subshell determined by the average-atom calculation at the given temperature and density. We then use the LTE fluctuation theory around the average-atom non-integer mean populations in order to fix the range of variation of the populations , and therefore the possible list of configurations (if is equal to zero) or superconfigurations (if is strictly positive). The superconfigurations are then sorted according to their respective Boltzmann probabilities, estimated, at this stage (they will be recalculated later with their “true” wavefunctions in their own self-consistent potential) using the average-atom wavefunctions. In the calculations presented in this paper, we kept the 1000 most probable superconfigurations. Next, a self-consistent calculation is performed for each superconfiguration which has, in such a way, its own potential and set of wavefunctions. The strength of our hybrid approach is that it makes possible the accounting for many highly excited states and satellite lines. The probabilities of those states may be small, but their number is so huge that they are likely to play a significant role in the total opacity. In SCO-RCG, the orbitals are taken individually up to a certain limit beyond which they are gathered in a single supershell. The grouped orbitals (typically, in the present calculations, the orbitals for which ) are chosen so that they weakly interact with inner ones. This is the reason why we call this supershell the “Rydberg supershell”. A DLA calculation is then carried out (when possible and necessary) for all of the transition arrays starting from that configuration. DLA calculations are performed only for pairs of configurations giving rise to less than 800,000 lines (the maximum size of a J-block inside a configuration is 4000). In other cases, transition arrays are represented statistically by Gaussian profiles in the UTA or SOSA formalisms. If the Rydberg supershell contains at least one electron, then transitions starting from the superconfiguration are treated within the STA model. In that way, no configuration is forgotten. The Rydberg supershell is pushed back in order to make its contribution as small as possible. The amount of detailed calculations in SCO-RCG is now largely dominant and subsequently the computed spectrum is less sensitive to the modelling of the remaining statistical contributions (UTA, SOSA, STA). The Partially Resolved-Transition-Array (PRTA) model [43] was also implemented in the code. It enables us to replace many statistical transition arrays by small-scale DLA calculations resulting from the withdrawal of passive subshells from the “real” configuration to form the reduced configuration. The DLA computation of the reduced configuration is carried out with the wavefunctions of the “real” configuration previously calculated. The electrostatic variance due to the passive subshells is added to each line of the DLA calculation in order to keep constant the total oscillator strength of the transition array. We extended this approach to the STA formalism of reference [3], by temporarily withdrawing the Rydberg supershell in the computation, and adding its contribution to the widths of all the lines. The contribution of the Rydberg supershell is included as a Gaussian “dressing function” [40]. We also have the possibility to replace this dressing function by a coarse-grain configurationally resolved profile, following the configurationally resolved super transition array (CRSTA) method of Kurzweil et al. [44,45,46] (see Section 6.1).
Figure 7 shows a comparison of the experimental and calculated SCO-RCG transmission spectra of Si at T = 72 eV and = 0.006 g/cm measured on the SG-II laser facility [47]. A good overall agreement is obtained, except around = 1805 eV and between 1850 and 1860 eV. The discrepancies in the latter energy window may be due to configuration interaction.
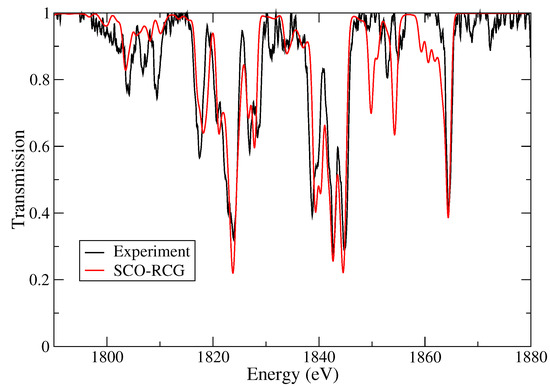
Figure 7.
Comparison of the experimental and calculated SCO-RCG (Superconfiguration Code for Opacity combined with DLA (Detailed-Level-Accounting) calculations using Robert and Cowan’s “G” subroutine) transmission spectra of Si at T = 72 eV and = 0.006 g/cm measured on the SG-II laser facility [47]. The areal mass is 23 g/cm and the resolving power E/ = 2000.
Figure 8 shows an aluminum spectrum measured by Winhart et al. on ASTERIX IV laser facility in Germany and interpreted by SCO-RCG as an average of four theoretical spectra at = 0.01 g/cm and T = 18, 20, 22 and 24 eV, respectively, in order to simulate the gradients [32].
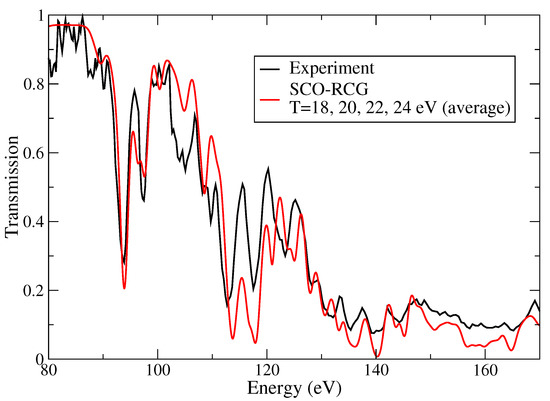
Figure 8.
Aluminum spectrum measured by Winhart et al. on ASTERIX IV laser facility in Germany and interpreted by SCO-RCG as an average of four theoretical spectra at = 0.01 g/cm and T = 18, 20, 22 and 24 eV, respectively, [32]. The areal mass is 30 g/cm.
X-ray transmission spectra of copper were measured in France at the LULI2000 laser facility (Palaiseau, France) with a target design of indirect heating by X rays [48]. The sample is a thin foil of mid-Z material inserted between two millimetre-size gold cavities heated by two 300 J frequency-doubled nanosecond laser beams. A third laser beam irradiates a gold foil to create an intense and spectrally continuous X-ray source (backlight) in order to probe the sample. Figure 9 shows an interpretation of the transmission of a multi-layer sample made of different materials: C (70 nm)/Al (38 nm)/Cu (12 nm)/Al (38 nm)/C (70 nm). Here also, the aluminum spectrum is useful to infer the plasma conditions, in the sense that the line ratios brings information about the plasma temperature, and the line width about the plasma electron density.
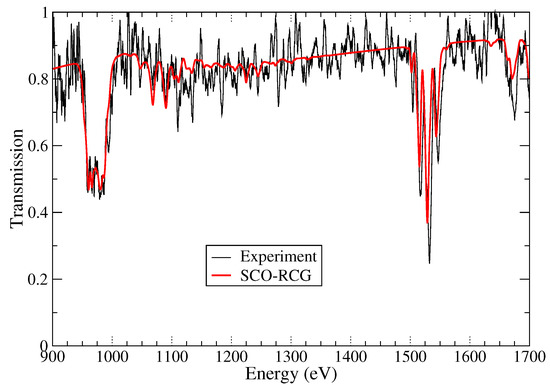
Figure 9.
Copper , n = 3, 4, ... (around 975 eV, 1075 eV, ...) and aluminum , = 2, 3, ... (around 1530 eV, 1675 eV, ...) absorption structures. Comparison between experiment and SCO-RCG calculation at T = 27 eV and = 0.01 g/cm. The areal mass of copper is equal to 15 g/cm and the areal mass of aluminum to 14 g/cm.
In 2007, Bailey et al. reported on iron transmission measurements at T = 156 eV and = 6.9·10 cm over the photon energy range 800–1800 eV [49]. The samples consisted of an Fe/Mg mixture tamped on both sides by a 10 m thick parylene-N (CH) layer. The Fe/Mg mixture was made by depositing ten alternating Mg and Fe layers. The difficulties of high-temperature opacity experiments were overcome using the dynamic Hohlraum X-ray source at the Z facility of Sandia National Laboratories in Albuquerque (New Mexico, USA). The process entails accelerating an annular tungsten Z-pinch plasma radially inward onto a cylindrical low density CH foam. A radiating shock propagates toward the cylinder axis and radiation trapped by the tungsten plasma forms a Hohlraum. A sample attached on the top diagnostic aperture is heated during ≈9 ns when the shock propagates inward and the radiation temperature rises above 200 eV. The radiation at the stagnation is used to probe the sample. As we can see in Figure 10, the agreement is much better with the fine-structure SCO-RCG computation than with the pure STA calculation performed with SCO code. The experimental spectrum was well reproduced by several fine-structure opacity codes (not only with SCO-RCG), but the features around 980 eV were not reproduced by any of the involved codes.
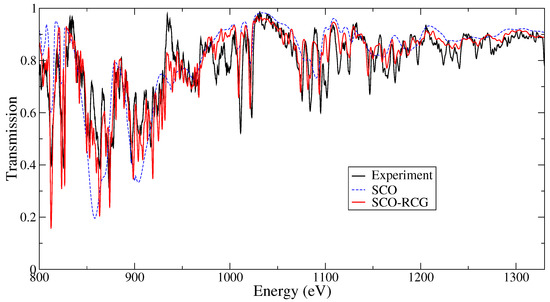
Figure 10.
Iron transmission spectrum measured by Bailey et al. on the Z facility of Sandia National Laboratories in Albuquerque (New Mexico, USA). Comparison between experiment, SCO and SCO-RCG calculations at T = 150 eV and = 0.058 g/cm. The areal mass is equal to 54 g/cm.
Interesting comparisons between detailed SCO-RCG calculations and traditional STA ones were performed recently [50]. In the same corresponding paper, germanium emission spectra were interpreted using the STA model. It is also worth mentioning that radiative properties (i.e., absorption and emission spectra) of carbon and plastic were studied by Lee et al. [51], still within the STA theory.
6. Recent Improvements of the STA Formalism
6.1. The STA Code by Krief et al.
Krief et al. [52,53,54] have recently developed a new STA code for calculating absorption and emission spectra of LTE plasmas. The code follows the prescriptions of Bar-Shalom et al. with several improvements. In particular, the authors developed a method to handle the first-order correction in the argument of the exponential in the Boltzmann populations faster by about an order of magnitude than the traditional way [52]. Their atomic code, named STAR (STA-Revised) was used to compute spectral opacities for a solar model on the basis of the recent so-called “AGSS09” composition [55]. STAR Rosseland opacities for the solar mixture showed a very good agreement with OP (Opacity Project) and OPAL (OPAcity Livermore) opacities throughout the radiation zone. Finally, an explicit STA calculation was performed with the AGSS09 photospheric mixture, including all the heavy metals and the main conclusion was that, due to their extremely low abundance, and although they are undoubtedly very good photon absorbers, the heavy elements do not affect significantly the Rosseland opacity [53,54]. The STAR code was also used to investigate the role of line shapes [56] and ion-ion correlations [57].
6.2. The Reseos Code by Ovechkin et al.
To investigate the effect of ion correlations on plasma opacities, Ovechkin et al. performed opacity calculations using an ion-correlation average-atom model, following the recent Starrett and Saumon formulation [58,59]. The model was implemented in the RESEOS code [60,61,62] that implements a generalized version of the STA approach providing a substantial acceleration of the photo-absorption and photo-ionization calculations with almost the same accuracy as that one obtained with the original superconfiguration approach. As a result, RESEOS predicts a much smaller increase of the Rosseland mean opacity due to ionic correlations (5.5%) than the above mentioned STAR code does (20%).
6.3. The Configurationally Resolved Approach of Kurzweil and Hazak
Kurzweil and Hazak developed a new method, called “Configurationally Resolved Super Transition Arrays” (CRSTA), for the calculation of the spectral opacity of hot plasmas. In the latter approach, the spectrum of each STA is computed as the Fourier transform of a single complex pseudo-partition function, which represents the exact analytical summation of the contributions of all constituting UTAs sharing the same set of one-electron states. Therefore, in such a new method, the spectrum of each STA is resolved down to the level of the (unresolved) transition arrays. It is shown that the corresponding spectrum, computed by the traditional STA method [2], is in fact just the coarse-grained Gaussian approximation of the CRSTA. The authors developed a new computer program, able to evaluate the absorption coefficient by both the new configurationally resolved and the traditional Gaussian STA model. Within the CRSTA formalism, the photoabsorption cross-section reads (without the stimulated-emission correction):
with
where
where and are the direct and exchange Slater integrals. One has also
with
and
as well as
with
It is possible to account for the homogeneous broadening and UTA widths in the framework of the CRSTA method, although the corresponding terms are not included in Equation (35).
6.4. Non-LTE Plasmas
The application of superconfigurations in a non-LTE context, i.e., in the framework of the collisional-radiative model, is presented in references [63,64,65]. Moreover, the introduction of the effective temperature of a superconfiguration enables one to simplify the calculation of emission and absorption in some non-LTE plasmas [66,67,68]. Lee et al. have investigated departures from LTE in recent interpretation of emission spectra [50].
7. Conclusions
In order to model absorption and emission of radiation by plasmas it is necessary to account for a huge number of ion configurations and to use a realistic description of their electronic structures. The superconfiguration method has been introduced by Bar-Shalom et al. in order to calculate opacities in plasmas at local thermodynamic equilibrium. This method is a statistical approach to ions allowing one to study atomic physics of dense plasmas beyond the average-atom model. Each ionic species is described by a group of superconfigurations and each superconfiguration represents in turn a certain number of configurations. The STA technique is a powerful tool to compute the emissivity and opacity of intermediate to high-Z elements where detailed-configuration-accounting methods would have a prohibitive numerical cost. In the SCO code, developed at CEA (French Alternative Energies and Atomic Energy Commission) at the end of the nineties by Blenski et al., the one-electron eigen-energies and wavefunctions were determined through a self-consistent calculation for each superconfiguration. Screening was taken into account through the neutrality of the WS sphere, the free electrons being described with the Thomas-Fermi approach [69]. A few years later, we developed a new model of plasma, providing a consistent modelling of plasma mixtures [70,71], implemented the quantum-mechanical description of continuum states, with the proper depiction of shape resonances in the density of free states [72,73], and added the capability to compute the equation of state [74,75]. In order to refine the spectra, we developed the SCO-RCG code combining statistical (UTA, SOSA, STA) methods and fine-structure calculations, using subroutines from Cowan’s code. This enabled us to obtain very detailed spectra, which were successfully compared to many recent laser and Z-pinch measurements. The STA formalism is still the cornerstone of several opacity codes, and new ideas are emerging, such as the CRSTA approach [44,45,46] or the extension to the superconfiguration approach of the PRTA model [40,76].
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The author is indebted to T. Blenski and G. Dejonghe (1954–2016) for fruitful collaborative work on the SCO code (concerning opacity, equation of state, electrical resistivity, etc.), Q. Porcherot, PhD student at the very beginning of SCO-RCG code, F. Gilleron for collaboration on many topics over the years (opacity calculations, statistics of levels and lines, spectral line shapes, etc.), J. Bauche (1940–2019) and C. Bauche-Arnoult for many discussions and common works about statistical methods in hot-plasma atomic physics, B. G. Wilson for common works on the computation of canonical partition functions, Y. Kurzweil for collaboration about the CRSTA approach and M. Krief for discussions about general features of the STA formalism. Finally, the author would like to thank all the experimentalists he collaborated with, in particular J. Bailey, S. Bastiani, C. Chenais-Popovics, M. Dozières, G. Loisel, T. Nagayama and F. Thais. This paper is dedicated to the memory of A. Bar-Shalom, J. Bauche, G. Dejonghe and R. D. Cowan.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CRSTA | Configurationally Resolved Super Transition Array |
| DLA | Detailed Line Accounting |
| HULLAC | Hebrew University Lawrence Livermore Atomic Code (LAC stands also for “Laboratoire Aimé Cotton”) |
| LTE | Local Thermodynamic Equilibrium |
| OP | Opacity Project |
| OPAL | OPAcity Livermore |
| PRTA | Partially Resolved Transition Array |
| SCO | Superconfiguration Code for Opacity |
| SCO-RCG | Superconfiguration Code for Opacity combined with Robert Cowan’s “G” subroutine |
| SOSA | Spin-Orbit Split Array |
| STA | Super Transition Array |
| STAR | Super Transition Array - Revised |
| UTA | Unresolved Transition Array |
| WS | Wigner-Seitz |
References
- Cox, A.N. Stars and Stellar Systems, Stellar Structure; Aller, L.H., McLaughlin, D.B., Eds.; The University of Chicago: Chicago, IL, USA, 1965; Volume 8. [Google Scholar]
- Da Silva, L.B.; MacGowan, B.J.; Kania, D.R.; Hammel, B.A.; Back, C.A.; Hsieh, E.; Doyas, R.; Iglesias, C.A.; Rogers, F.J.; Lee, R.W. Absorption Measurements Demonstrating the Importance of Δn = 0 Transitions in the Opacity of Iron. Phys. Rev. Lett. 1992, 69, 438–441. [Google Scholar] [CrossRef]
- Bar-Shalom, A.; Oreg, J.; Goldstein, W.H.; Shvarts, D.; Zigler, A. Super-transition-arrays: A model for the spectral analysis of hot, dense plasmas. Phys. Rev. A 1989, 40, 3183–3193. [Google Scholar] [CrossRef] [PubMed]
- Bauche-Arnoult, C.; Bauche, J.; Klapisch, M. Variance of the distribution of energy levels and of the transition arrays in atomic spectra. Phys. Rev. A 1979, 20, 2424–2439. [Google Scholar] [CrossRef]
- Bauche-Arnoult, C.; Bauche, J.; Klapisch, M. Variance of the distribution of energy levels and of the transition arrays in atomic spectra. II. Configurations with more than two open subshells. Phys. Rev. A 1982, 25, 2641–2646. [Google Scholar] [CrossRef]
- Bauche-Arnoult, C.; Bauche, J.; Klapisch, M. Variance of the distribution of energy levels and of the transition arrays in atomic spectra. III. Case of spin-orbit-split arrays. Phys. Rev. A 1985, 31, 2248–2259. [Google Scholar] [CrossRef] [PubMed]
- Pain, J.-C.; Gilleron, F. Statistical properties of levels and lines in complex spectra: A tribute to Jacques Bauche and Claire Bauche-Arnoult. AIP Conf. Proc. 2017, 1811, 050003. [Google Scholar]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Bauche-Arnoult, C.; Bauche, J.; Klapisch, M. Breakdown of jj coupling in spin-orbit-split atomic transition arrays. J. Phys. B At. Mol. Phys. 1991, 24, 1–11. [Google Scholar] [CrossRef]
- Bar-Shalom, A.; Oreg, J.; Goldstein, W.H. Configuration interaction in LTE spectra of heavy elements. J. Quant. Spectrosc. Radiat. Transf. 1994, 51, 27–39. [Google Scholar] [CrossRef]
- Bar-Shalom, A.; Oreg, J.; Klapisch, M.; Lehecka, T. Effect of configuration interaction on shift widths and intensity redistribution of transition arrays. Phys. Rev. E 1999, 59, 3512–3525. [Google Scholar] [CrossRef]
- Bar-Shalom, A.; Oreg, J.; Klapisch, M. The effect of configuration interaction on relativistic transition arrays. J. Quant. Spectrosc. Radiat. Transf. 2000, 65, 415–428. [Google Scholar] [CrossRef]
- Blenski, T.; Morel, S. Thermal Hartree-Fock theory in opacity calculation. J. Quant. Spectrosc. Radiat. Transf. 1995, 54, 65–72. [Google Scholar] [CrossRef]
- Blenski, T.; Ishikawa, K. Relation between the super-transition-array method in opacity calculations and the Hartree-Fock approximation at nonzero temperature. Phys. Rev. E 1995, 51, 1602–1604. [Google Scholar] [CrossRef] [PubMed]
- Blenski, T.; Grimaldi, A.; Perrot, F. A Hartree-Fock statistical approach to atoms in plasmas-electron and hole countings in evaluation of statistical sums. J. Quant. Spectrosc. Radiat. Transf. 1997, 58, 495–500. [Google Scholar] [CrossRef]
- Pain, J.-C. Koopmans’ theorem in the statistical Hartree-Fock theory. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 145001. [Google Scholar] [CrossRef]
- Lions, P.L. Solutions of Hartree-Fock Equations for Coulomb Systems. Commun. Math. Phys. 1987, 109, 33–97. [Google Scholar] [CrossRef]
- Busquet, M. Pressure ionization in partition function algebra. High Energy Density Phys. 2013, 9, 535–541. [Google Scholar] [CrossRef]
- Oreg, J.; Bar-Shalom, A.; Klapisch, M. Operator technique for calculating superconfiguration-averaged quantities of atoms in plasmas. Phys. Rev. E 1997, 55, 5874–5882. [Google Scholar] [CrossRef]
- Wilson, B.; Chen, M.H. A revised algorithm for the computation of super-transition array spectra of hot dense plasmas. J. Quant. Spectrosc. Radiat. Transf. 1999, 61, 813–823. [Google Scholar] [CrossRef]
- Gilleron, F.; Pain, J.-C. Stable method for the calculation of partition functions in the superconfiguration approach. Phys. Rev. E 2004, 69, 056117. [Google Scholar] [CrossRef]
- Pain, J.-C.; Gilleron, F.; Porcherot, Q. Generating functions for canonical systems of fermions. Phys. Rev. E 2011, 83, 067701. [Google Scholar] [CrossRef]
- Wilson, B.G.; Gilleron, F.; Pain, J.-C. Further stable methods for the calculation of partition functions in the superconfiguration approach. Phys. Rev. E 2007, 76, 032103. [Google Scholar] [CrossRef] [PubMed]
- Pain, J.-C.; Gilleron, F.; Wilson, B.G. Optimized recursion relation for the computation of partition functions in the superconfiguration approach. High Energy Density Phys. 2020, 37, 100891. [Google Scholar] [CrossRef]
- Faussurier, G.; Wilson, B.G.; Chen, M.H. Generalization of super-transition-array methods to hot dense plasmas by using optimum independent particle reference systems. Phys. Rev. E 2002, 65, 016403, Erratum in 2002, 65, 049901. [Google Scholar] [CrossRef]
- Pain, J.-C.; Gilleron, F.; Faussurier, G. Jensen-Feynman approach to the statistics of interacting electrons. Phys. Rev. E 2009, 80, 026703. [Google Scholar] [CrossRef] [PubMed]
- Blenski, T.; Grimaldi, A.; Perrot, F. A superconfiguration code based on the local density approximation. J. Quant. Spectroc. Radiat. Transf. 2000, 65, 91–100. [Google Scholar] [CrossRef]
- Blenski, T.; Grimaldi, A.; Perrot, F. Hartree-Fock statistical approach to atoms and photoabsorption in plasmas. Phys. Rev. E 1997, 55, R4889–R4892. [Google Scholar] [CrossRef]
- Perrot, F.; Blenski, T. Electronic structure and statistical mechanics of ionic configurations in hot plasmas. J. Phys. IV Fr. 2000, 10, 473–480. [Google Scholar] [CrossRef]
- Blenski, T.; Ishikawa, K. Pressure ionization in the spherical ion-cell model of dense plasmas and a pressure formula in the relativistic Pauli approximation. Phys. Rev. E 1995, 51, 4869–4881. [Google Scholar] [CrossRef]
- Iyetomi, H.; Ichimaru, S. Free energies of electron-screened ion plasmas in the hypernetted-chain approximation. Phys. Rev. A 1986, 34, 433–439. [Google Scholar] [CrossRef]
- Winhart, G.; Eidmann, K.; Iglesias, C.A.; Bar-Shalom, A.; Minguez, E.; Rickert, A.; Rose, S.J. XUV opacity measurements and comparison with models. J. Quant. Spectrosc. Radiat. Transf. 1995, 54, 437–446. [Google Scholar] [CrossRef]
- Winhart, G.; Eidmann, K.; Iglesias, C.A.; Bar-shalom, A. Measurements of extreme uv opacities of hot dense Al, Fe and Ho. Phys. Rev. E 1996, 53, R1332–R1335. [Google Scholar] [CrossRef] [PubMed]
- Chenais-Popovics, C.; Fajardo, M.; Thais, F.; Gilleron, F.; Gauthier, J.-C.; Eidmann, K.; Fölsner, W.; Blenski, T.; Perrot, F.; Bauche-Arnoult, C.; et al. Absorption measurements of radiatively heated multi-layered Al/Ni foils. J. Quant. Spectrosc. Radiat. Transf. 2001, 71, 249–256. [Google Scholar] [CrossRef]
- Bar-Shalom, A.; Klapisch, M.; Oreg, J. HULLAC, an integrated computer package for atomic processes in plasmas. J. Quant. Spectrosc. Radiat. Transf. 2001, 71, 169–188. [Google Scholar] [CrossRef]
- Renaudin, P.; Blancard, C.; Bruneau, J.; Faussurier, G.; Fuchs, J.-E.; Gary, S. Absorption experiments on X-ray-heated magnesium and germanium constrained samples. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 511–522. [Google Scholar] [CrossRef]
- Bailey, J.E.; Arnault, P.; Blenski, T.; Dejonghe, G.; Peyrusse, O.; MacFarlane, J.J.; Mancini, R.C.; Cuneo, M.E.; Nielsen, D.S.; Rochau, G.A. Opacity measurements of tamped NaBr samples heated by z-pinch X-rays. J. Quant. Spectroc. Radiat. Transf. 2003, 81, 31–45. [Google Scholar] [CrossRef]
- Merdji, H.; Missalla, T.; Blenski, T.; Perrot, F.; Gauthier, J.-C.; Eidmann, K.; Chenais-Popovics, C. Absorption spectroscopy of a radiatively heated samarium plasma. Phys. Rev. E 1998, 57, 1042–1046. [Google Scholar] [CrossRef]
- Porcherot, Q.; Pain, J.-C.; Gilleron, F.; Blenski, T. A consistent approach for mixed detailed and statistical calculation of opacities in hot plasmas. High Energy Density Phys. 2011, 7, 234–239. [Google Scholar] [CrossRef]
- Pain, J.-C.; Gilleron, F. Accounting for highly excited states in detailed opacity calculations. High Energy Density Phys. 2015, 15, 30–42. [Google Scholar] [CrossRef]
- Pain, J.-C.; Gilleron, F.; Blenski, T. Detailed computation of hot-plasma atomic spectra. Laser Part. Beams 2015, 33, 201–210. [Google Scholar] [CrossRef]
- Pain, J.-C.; Gilleron, F.; Porcherot, Q.; Blenski, T. The hybrid detailed/statistical opacity code SCO-RCG: New developments and applications. AIP Conf. Proc. 2017, 1811, 190010. [Google Scholar]
- Iglesias, C.A.; Sonnad, V. Partially resolved transition array model for atomic spectra. High Energy Density Phys. 2012, 8, 154–160. [Google Scholar] [CrossRef]
- Kurzweil, Y.; Hazak, G. Summation of the spectra of all partially resolved transition arrays in a supertransition array. Phys. Rev. E 2016, 94, 053210. [Google Scholar] [CrossRef] [PubMed]
- Hazak, G.; Kurzweil, Y. A Configurationally Resolved-Super-Transition-Arrays method for calculation of the spectral absorption coefficient in hot plasmas. High Energy Density Phys. 2012, 8, 290–297. [Google Scholar] [CrossRef]
- Kurzweil, Y.; Hazak, G. Inclusion of UTA widths in the Configurationally Resolved Super-Transition-Arrays (CRSTA) method. High Energy Density Phys. 2013, 9, 548–552. [Google Scholar] [CrossRef]
- Xiong, G.; Yang, J.; Zhang, J.; Hu, Z.; Zhao, Y.; Qing, B.; Yang, G.; Wei, M.; Yi, R.; Song, T.; et al. Opacity measurement and theoretical investigation of hot silicon plasma. Astrophys. J. 2016, 816, 36–46. [Google Scholar] [CrossRef]
- Dozières, M.; Thais, F.; Bastiani-Ceccotti, S.; Blenski, T.; Fariaut, J.; Fölsner, W.; Gilleron, F.; Khaghani, D.; Pain, J.-C.; Reverdin, C.; et al. X-ray opacity measurements in mid-Z dense plasmas with a new target design. High Energy Density Phys. 2015, 17, 231–239. [Google Scholar] [CrossRef]
- Bailey, J.E.; Rochau, G.A.; Iglesias, C.A.; Abdallah, J.; MacFarlane, J.J.; Golovkin, I.; Wang, P.; Mancini, R.C.; Lake, P.W.; Moore, T.C.; et al. Iron-Plasma Transmission Measurements at Temperatures Above 150 eV. Phys. Rev. Lett. 2007, 99, 265002. [Google Scholar] [CrossRef]
- Lee, T.-G.; Jarrah, W.; Benredjem, D.; Pain, J.-C.; Busquet, M.; Klapisch, M.; Schmitt, A.J.; Bates, J.W.; Giuliani, J. Super-transition-array calculations for synthetic spectra and opacity of high-density, high-temperature germanium plasmas. High Energy Density Phys. 2020, 35, 100742. [Google Scholar] [CrossRef]
- Lee, T.-G.; Busquet, M.; Klapisch, M.; Bates, J.W.; Schmitt, A.J.; Hu, S.X.; Giuliani, J. Radiative and atomic properties of C and CH plasmas in the warm-dense-matter regime. Phys. Rev. E 2018, 98, 043203. [Google Scholar] [CrossRef]
- Krief, M.; Feigel, A. The effect of first order superconfiguration energies on the opacity of hot dense matter. High Energy Density Phys. 2015, 15, 59–66. [Google Scholar] [CrossRef]
- Krief, M.; Feigel, A.; Gazit, D. Solar opacity calculations using the super-transition-array method. Astrophys. J. 2016, 821, 45–59. [Google Scholar] [CrossRef]
- Krief, M.; Feigel, A.; Gazit, D. A New Implementation of the STA Method for the Calculation of Opacities of Local Thermodynamic Equilibrium Plasmas. Atoms 2018, 6, 35. [Google Scholar] [CrossRef]
- Asplund, M.; Grevesse, N.; Sauval, A.J.; Scott, P. The Chemical Composition of the Sun. Annu. Rev. Astron. Astrophys. 2009, 47, 481–522. [Google Scholar] [CrossRef]
- Krief, M.; Feigel, A.; Gazit, D. Line broadening and the solar opacity problem. Astrophys. J. 2016, 824, 98–103. [Google Scholar] [CrossRef]
- Krief, M.; Kurzweil, Y.; Feigel, A.; Gazit, D. The effect of ionic correlations on radiative properties in the solar interior and terrestrial experiments. Astrophys. J. 2018, 856, 135–140. [Google Scholar] [CrossRef]
- Starrett, C.E.; Saumon, D. Electronic and ionic structures of warm and hot dense matter. Phys. Rev. E 2013, 87, 013104. [Google Scholar] [CrossRef] [PubMed]
- Starrett, C.E.; Saumon, D. A simple method for determining the ionic structure of warm dense matter. High Energy Density Phys. 2014, 10, 35–42. [Google Scholar] [CrossRef]
- Ovechkin, A.A.; Loboda, P.A.; Novikov, V.G.; Grushin, A.S.; Solomyannaya, A.D. RESEOS-A model of thermodynamic and optical properties of hot and warm dense matter. High Energy Density Phys. 2014, 13, 20–33. [Google Scholar] [CrossRef]
- Ovechkin, A.A.; Loboda, P.A.; Falkov, A.L. Transport and dielectric properties of dense ionized matter from the average-atom RESEOS model. High Energy Density Phys. 2016, 20, 38–54. [Google Scholar] [CrossRef]
- Ovechkin, A.A.; Loboda, P.A.; Falkov, A.L. Plasma opacity calculations using the Starrett and Saumon average-atom model with ion correlations. High Energy Density Phys. 2019, 30, 29–40. [Google Scholar] [CrossRef]
- Bar-Shalom, A.; Oreg, J.; Klapisch, M. Non-LTE superconfiguration collisional radiative model. J. Quant. Spectrosc. Radiat. Transf. 1997, 58, 427–439. [Google Scholar] [CrossRef]
- Bar-Shalom, A.; Oreg, J.; Klapisch, M. Collisional radiative model for heavy atoms in hot non-local-thermodynamical-equilibrium plasmas. Phys. Rev. E 1997, 56, R70–R73. [Google Scholar] [CrossRef]
- Peyrusse, O. A superconfiguration model for broadband spectroscopy of non-LTE plasmas. J. Phys. B At. Mol. Phys. 2000, 33, 4303–4321. [Google Scholar] [CrossRef]
- Bauche, J.; Bauche-Arnoult, C.; Fournier, K.B. Model for computing superconfiguration temperatures in non-local thermodynamic equilibrium hot plasmas. Phys. Rev. E 2004, 69, 026403. [Google Scholar] [CrossRef]
- Bauche, J.; Bauche-Arnoult, C.; Peyrusse, O. Effective temperatures in hot dense plasmas. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 55–66. [Google Scholar] [CrossRef]
- Busquet, M. Onset of pseudo-thermal equilibrium within configurations and superconfigurations. J. Quant. Spectroc. Radiat. Transf. 2006, 99, 131–141. [Google Scholar] [CrossRef]
- Feynman, R.P.; Metropolis, N.; Teller, E. Equations of State of Elements Based on the Generalized Fermi-Thomas Theory. Phys. Rev. 1949, 75, 1561–1573. [Google Scholar] [CrossRef]
- Pain, J.-C.; Blenski, T. Self-consistent approach for the thermodynamics of ions in dense plasmas in the superconfiguration approximation. J. Quant. Spectroc. Radiat. Transf. 2003, 81, 355–369. [Google Scholar] [CrossRef]
- Pain, J.-C. Sur la physique atomique des ions dans les plasmas en présence de l’écrantage. Ph.D. Thesis, Université Paris Sud XI, Orsay, France, 2002. (In French). [Google Scholar]
- Pain, J.-C.; Dejonghe, G.; Blenski, T. A self-consistent model for the study of electronic properties of hot dense plasmas in the superconfiguration approximation. J. Quant. Spectroc. Radiat. Transf. 2006, 99, 451–468. [Google Scholar] [CrossRef]
- Pain, J.-C.; Dejonghe, G.; Blenski, T. Quantum mechanical model for the study of pressure ionization in the superconfiguration approach. J. Phys. A Math. Gen. 2006, 39, 4659–4666. [Google Scholar] [CrossRef]
- Pain, J.-C. A model of dense-plasma atomic structure for equation-of-state calculations. J. Phys. B At. Mol. Opt. Phys. 2007, 40, 1553–1573. [Google Scholar] [CrossRef]
- Pain, J.-C.; Dejonghe, G.; Blenski, T. Equation of State of Dense Plasma Mixtures: Application to the Sun Center. Contrib. Plasma Phys. 2012, 52, 23–27. [Google Scholar] [CrossRef]
- Wilson, B.G.; Iglesias, C.A.; Chen, M.H. Partially resolved super transition array method. High Energy Density Phys. 2015, 14, 67–73. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).