Ion Acceleration in Multi-Fluid Plasma: Including Charge Separation Induced Electric Field Effects in Supersonic Wave Layers
Abstract
:1. Introduction
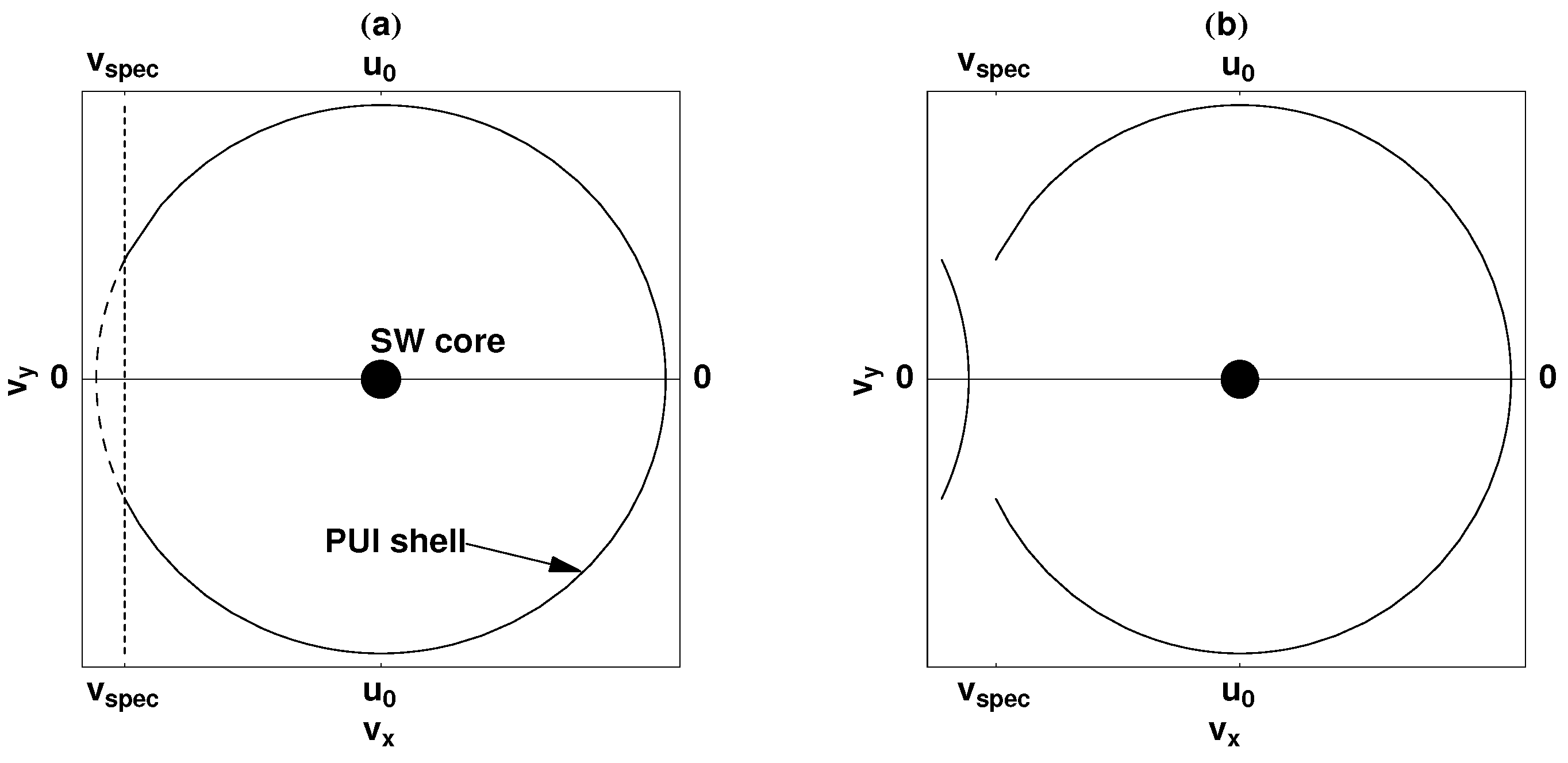
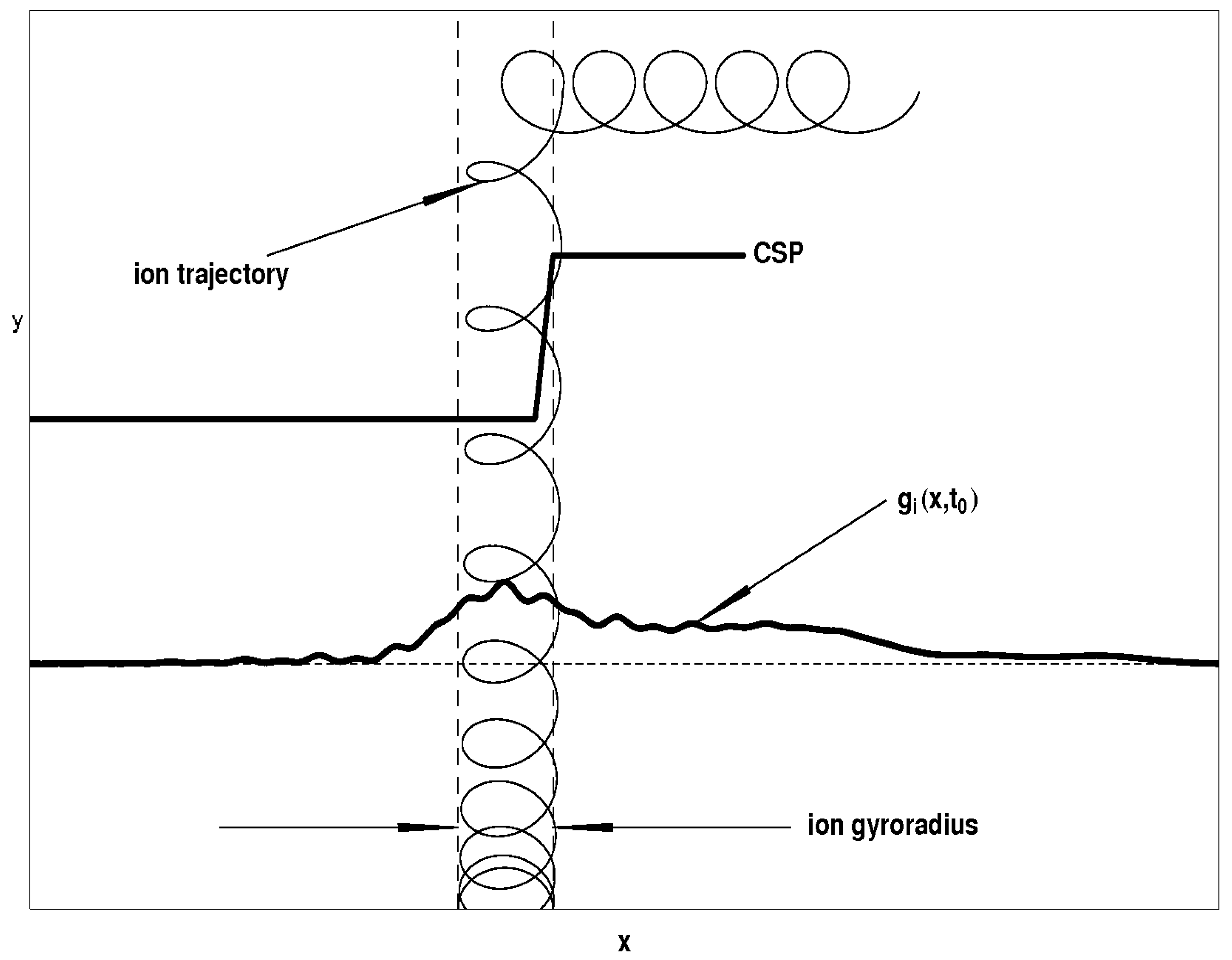
Motivation for the Development of a Multi-Fluid Plus Kinetic Ions Plasma Model
2. Materials and Methods
2.1. Two-Fluid Solar Wind Plus Kinetically Treated Shock Acceleration Candidate Kinetic Ions Numeric Model
2.1.1. Conservation Form of the Two-Fluid Plasma Equations
2.1.2. Dimensionless Forms of The Equations
2.2. Special Case: Quasi-One Dimensional, Exactly Perpendicular Shock
Steady State Equations for 1D Case with Perpendicular Magnetic Field
3. Results
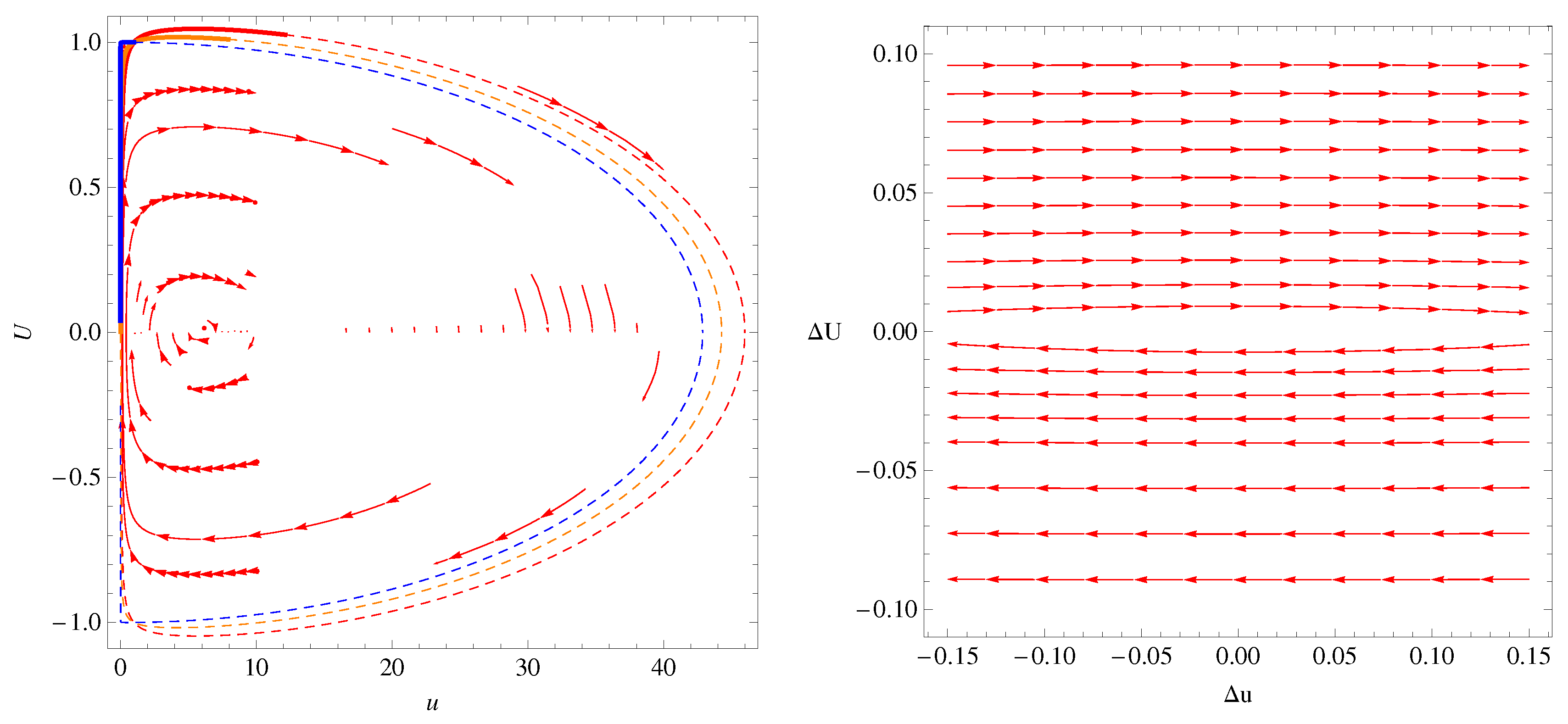
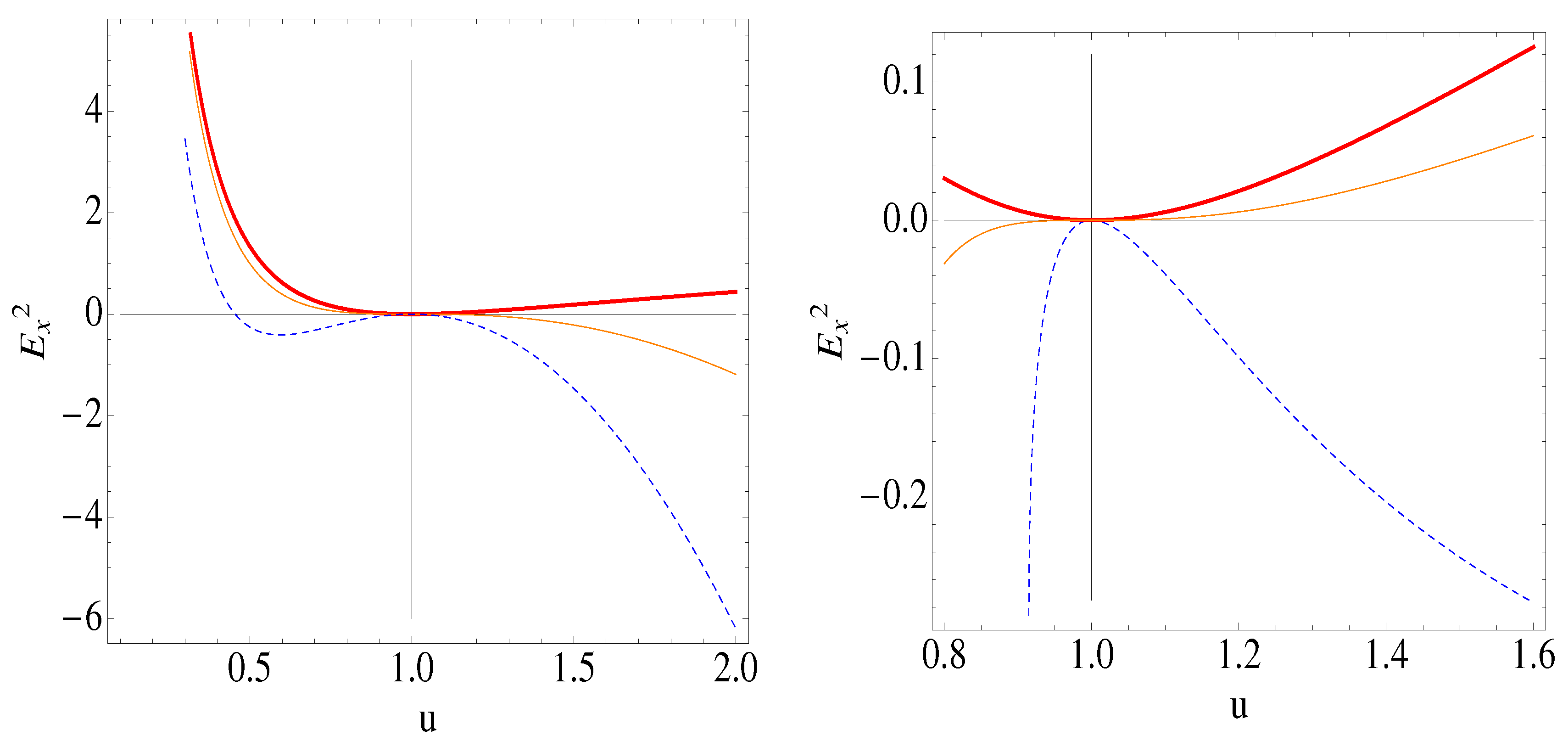
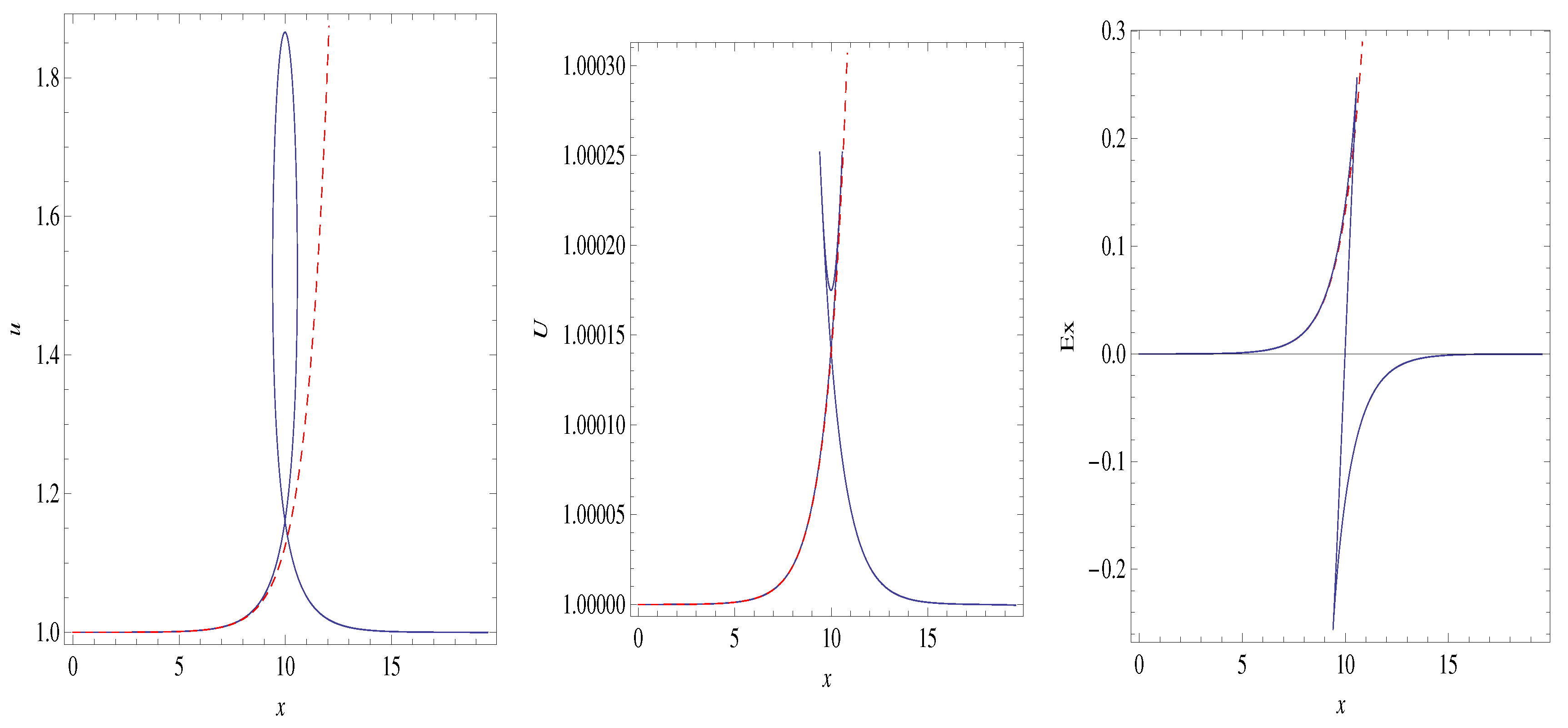
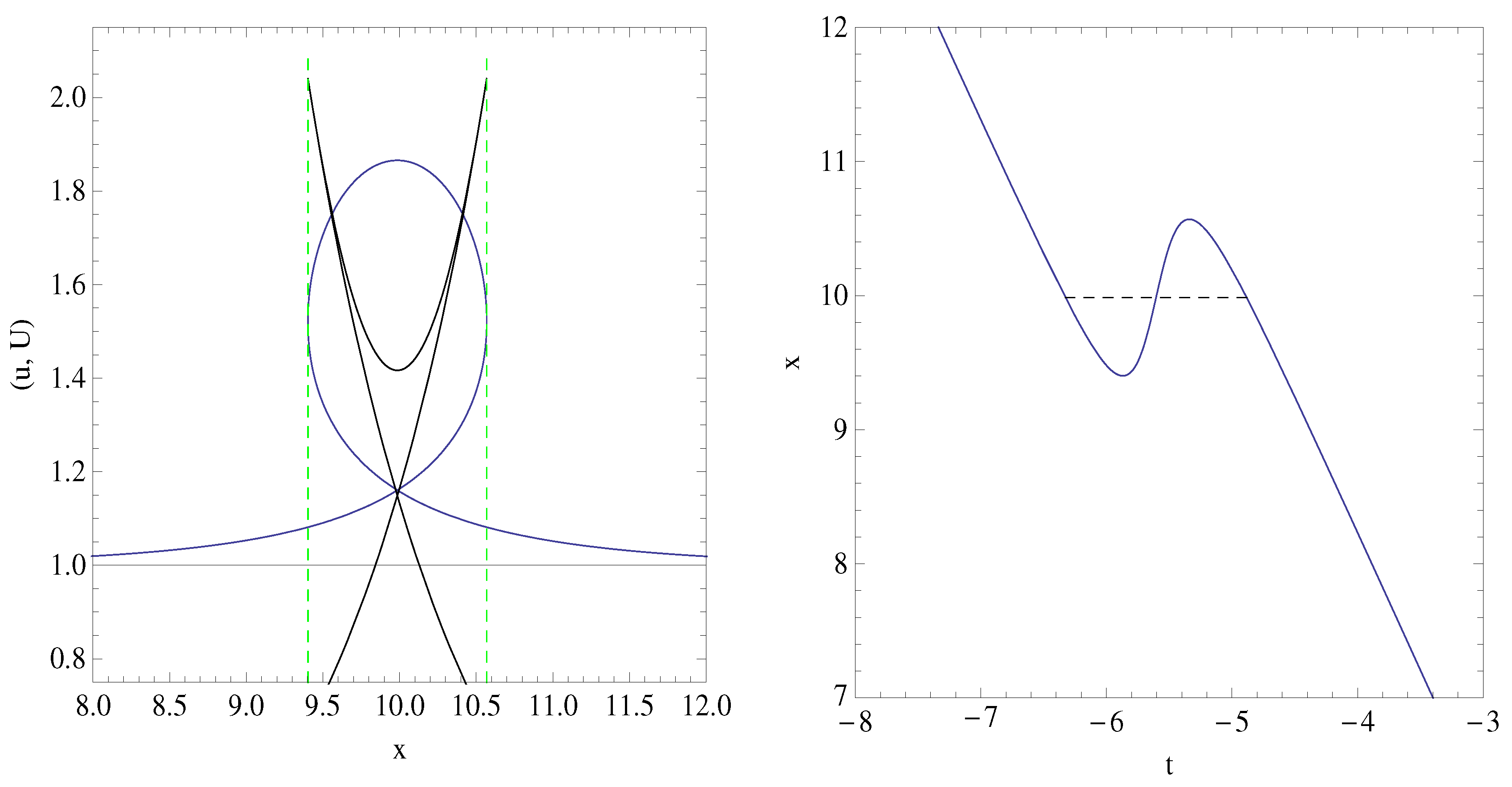
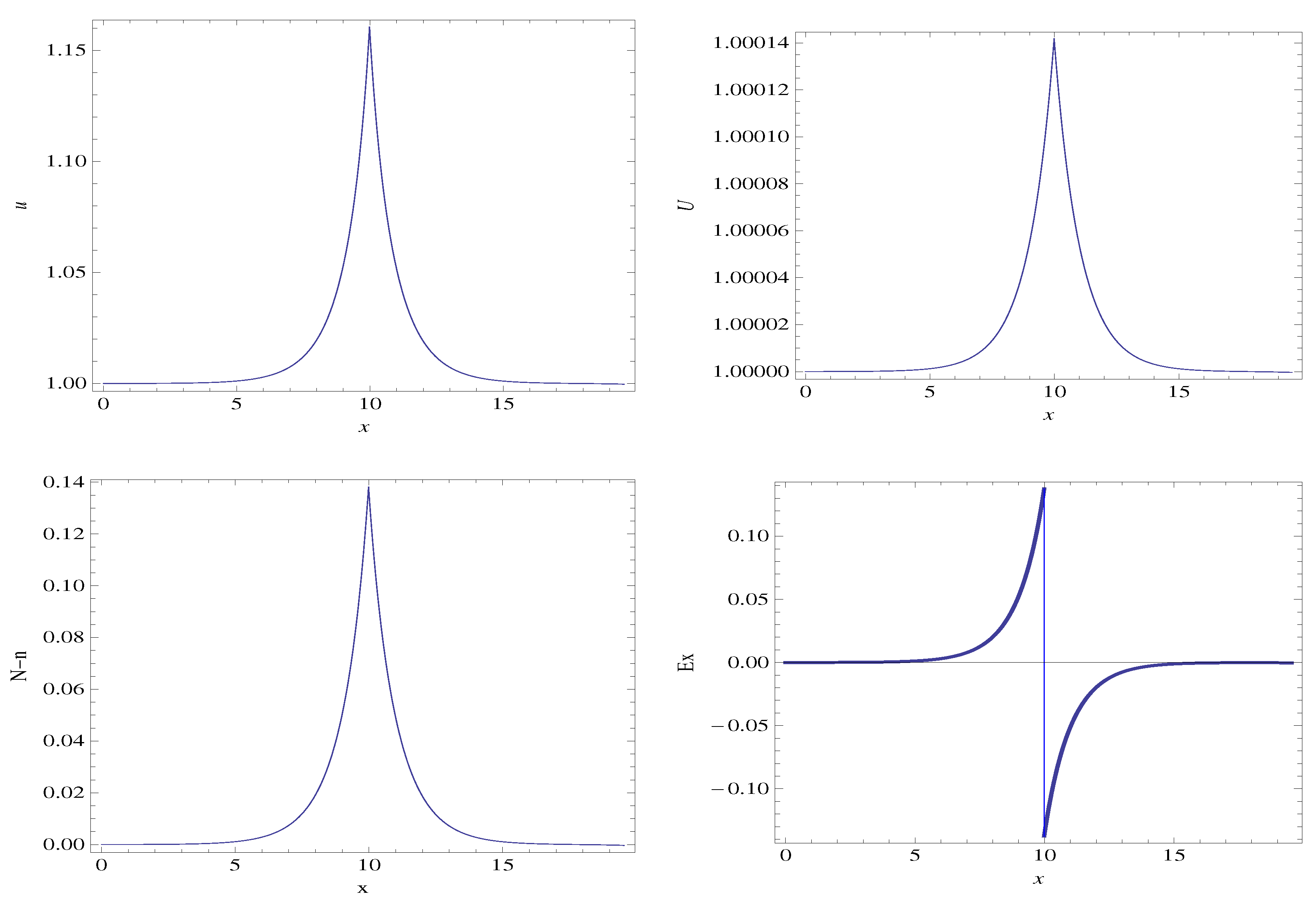
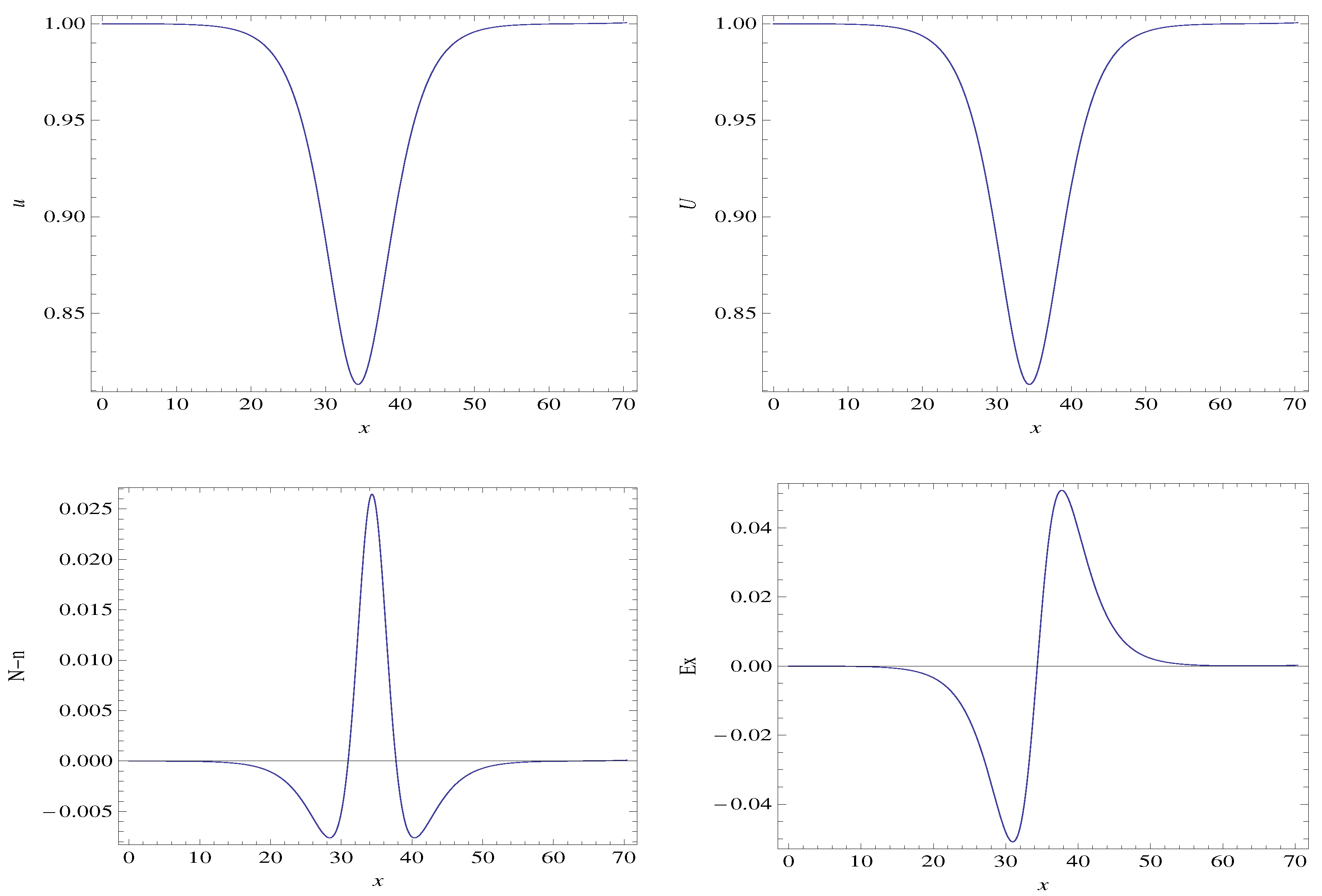
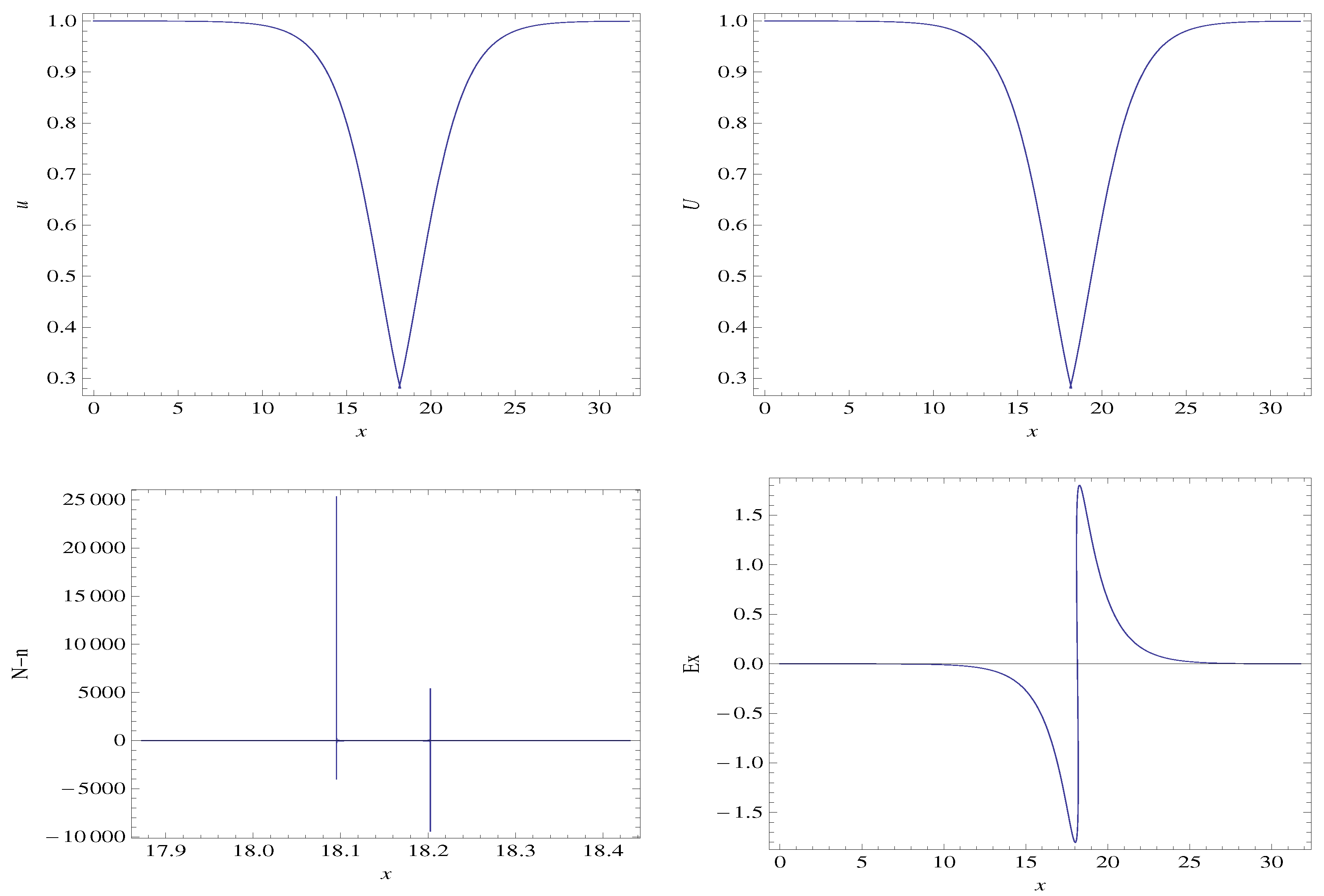
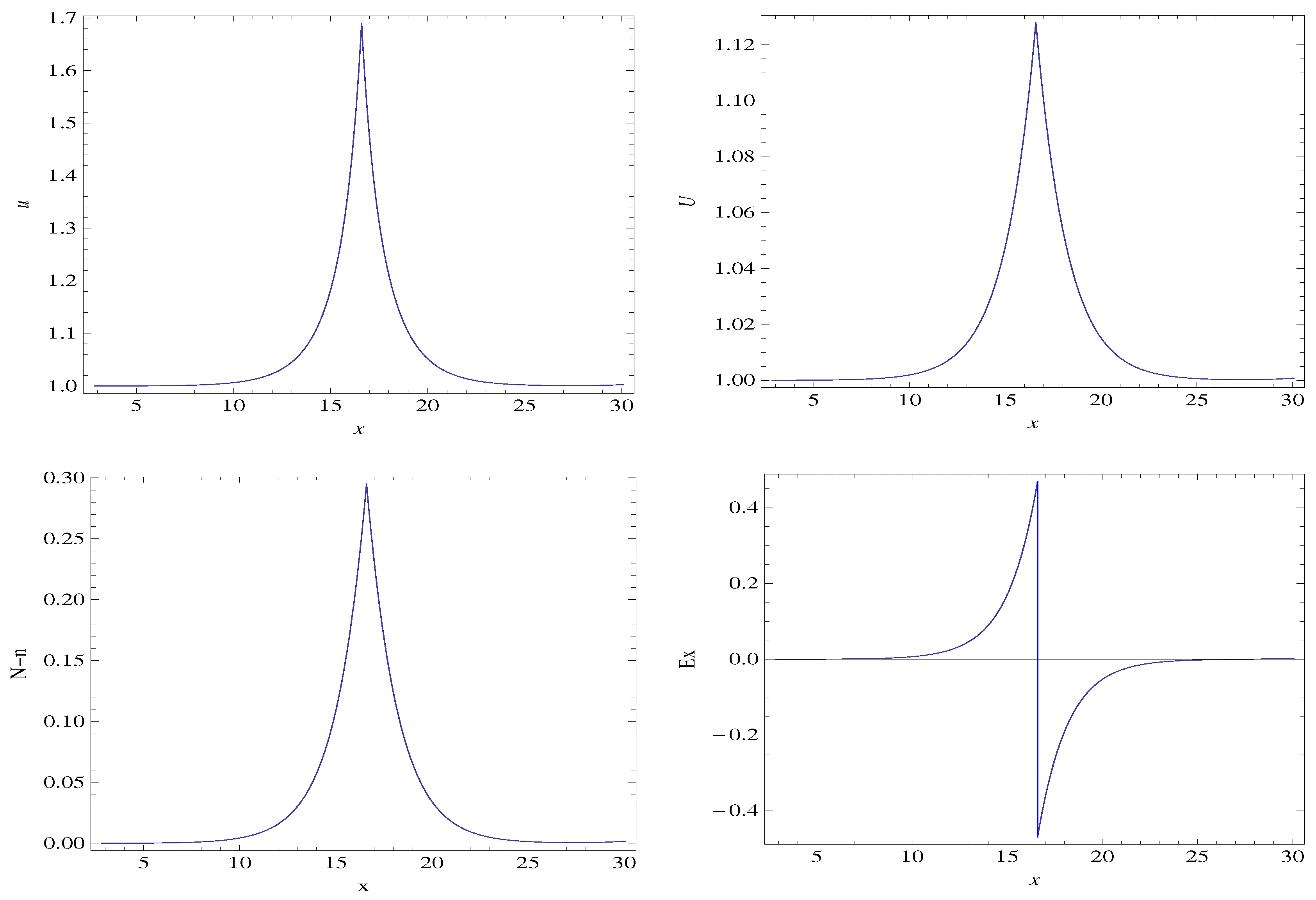
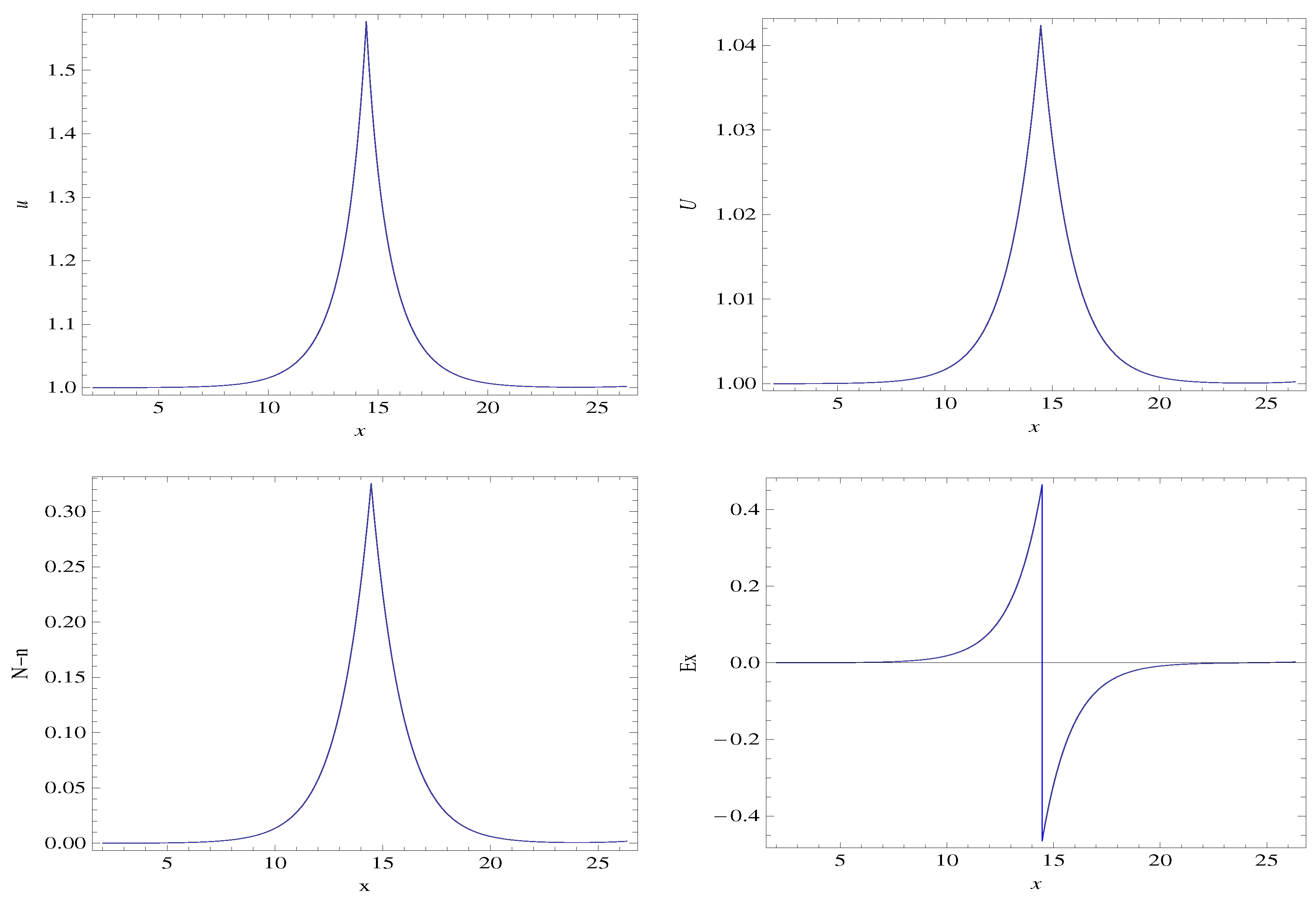
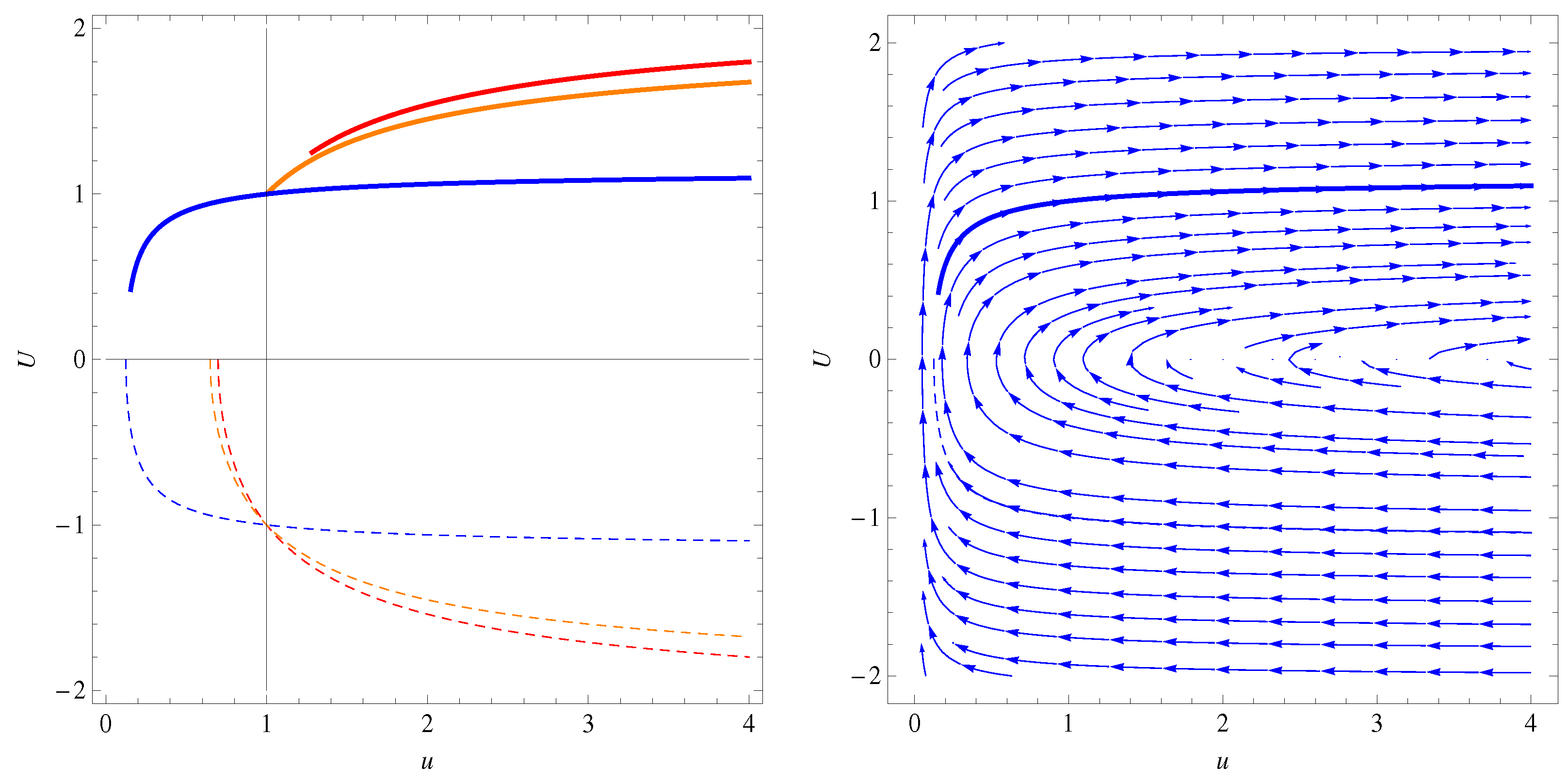
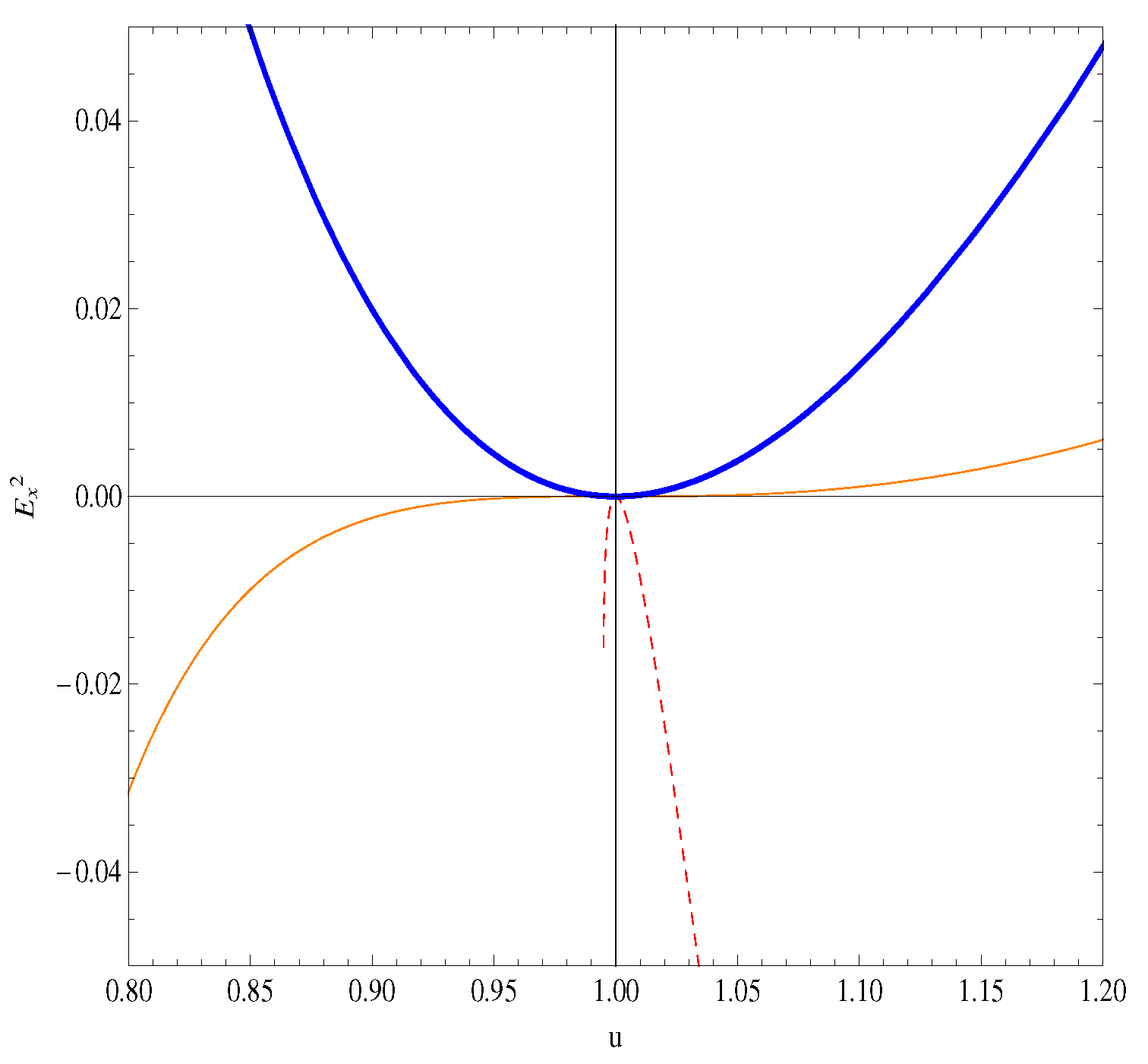
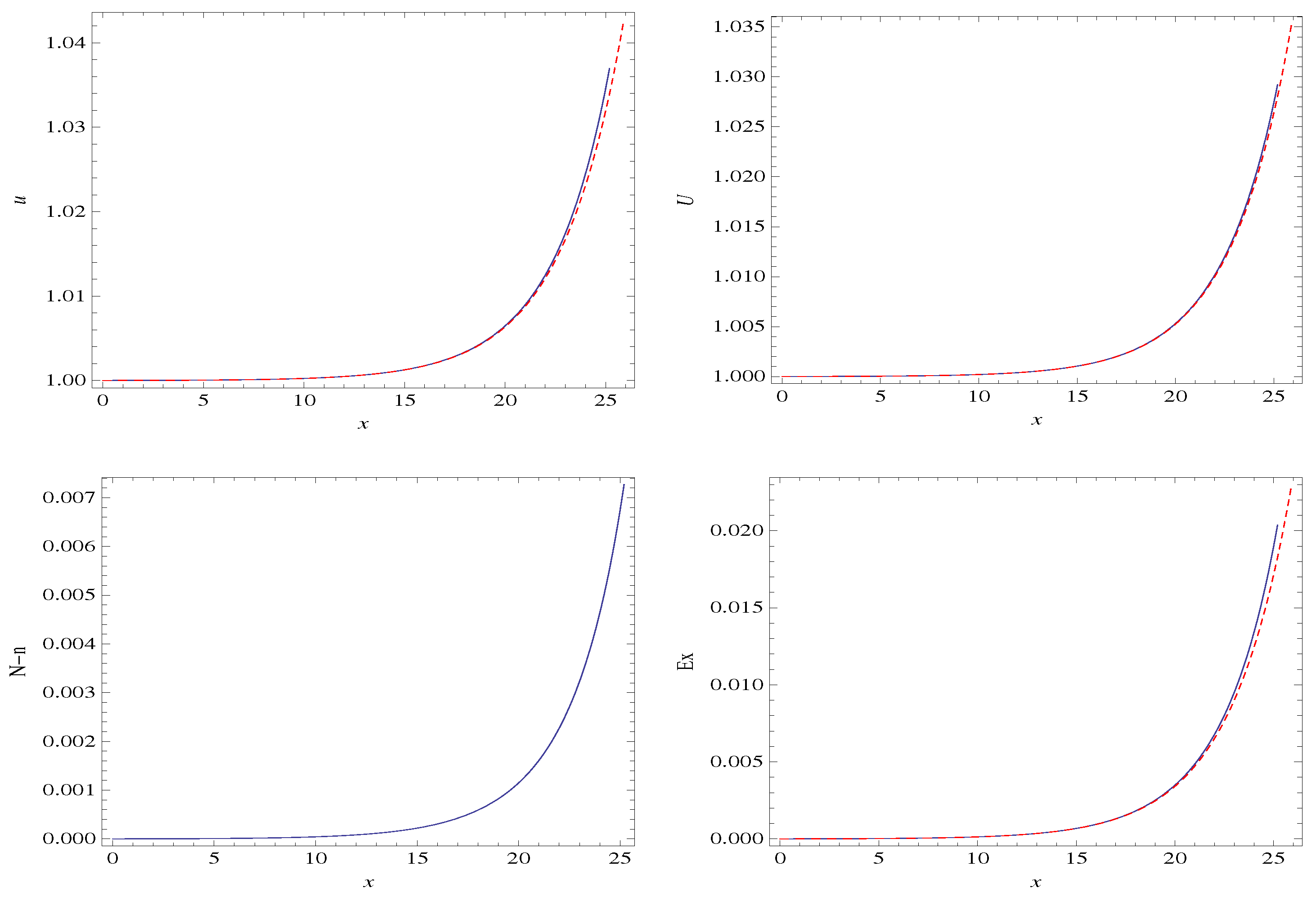
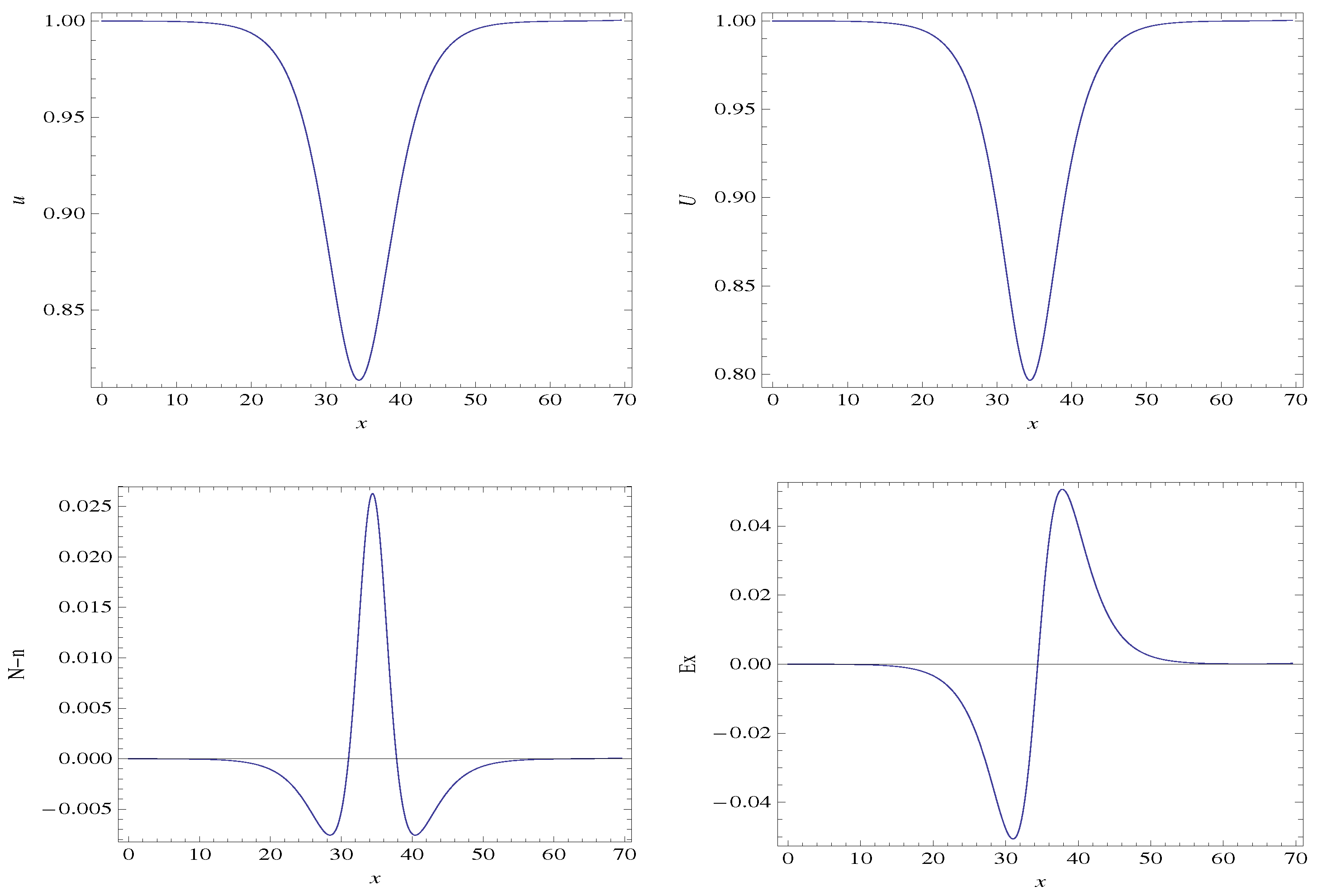
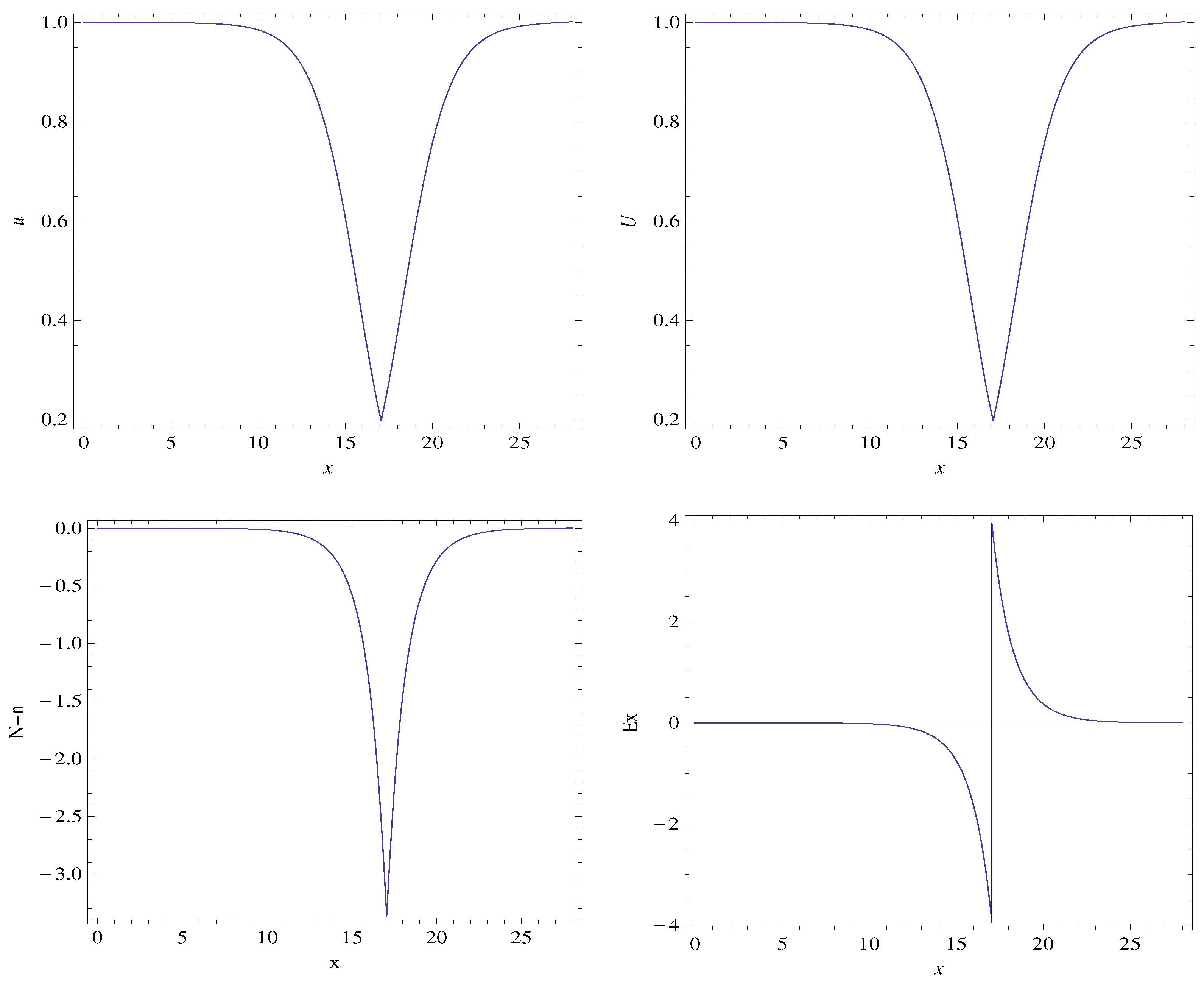
3.1. Steady State, 1D Two-Fluid Plasma System with Cold Ions
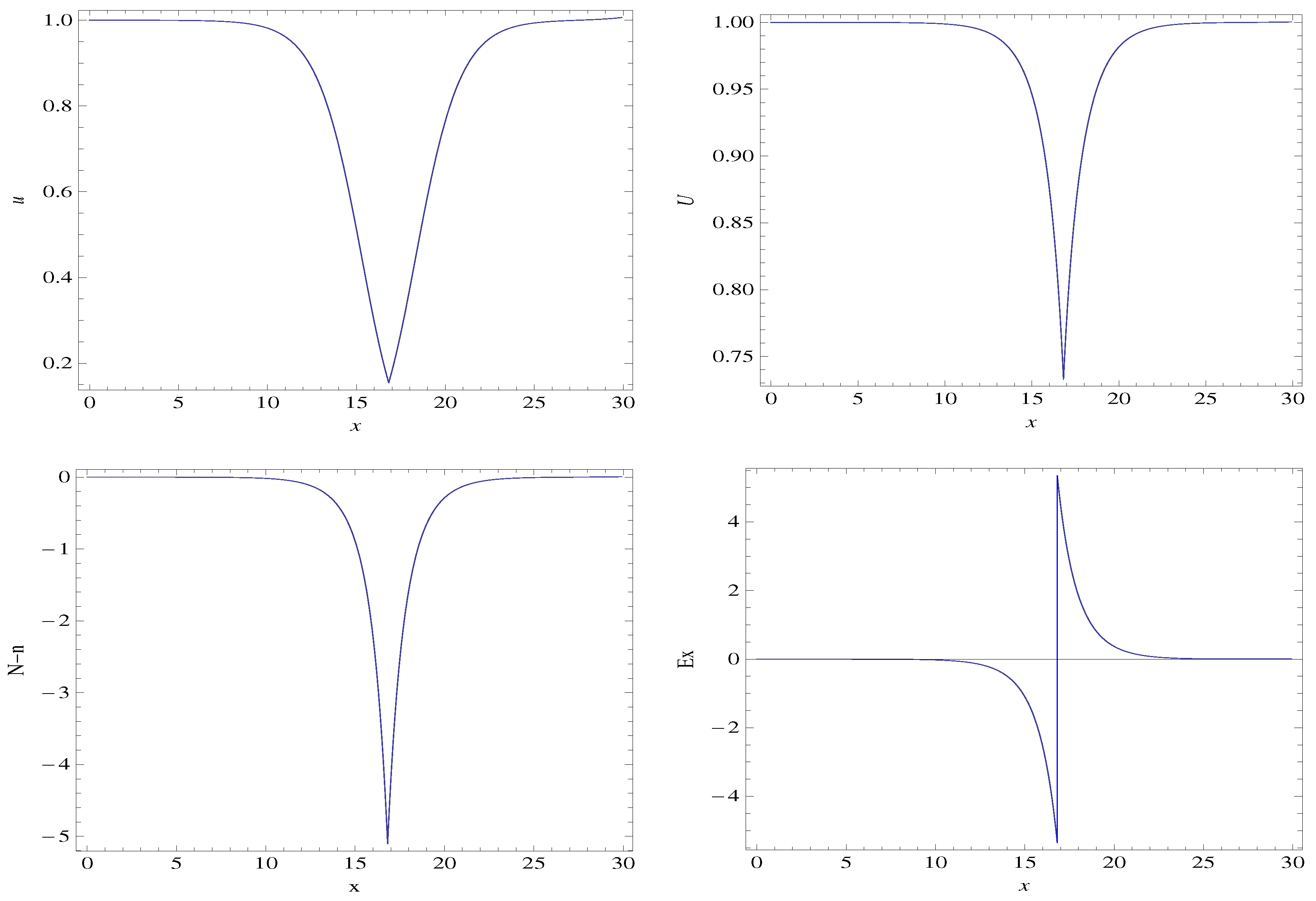
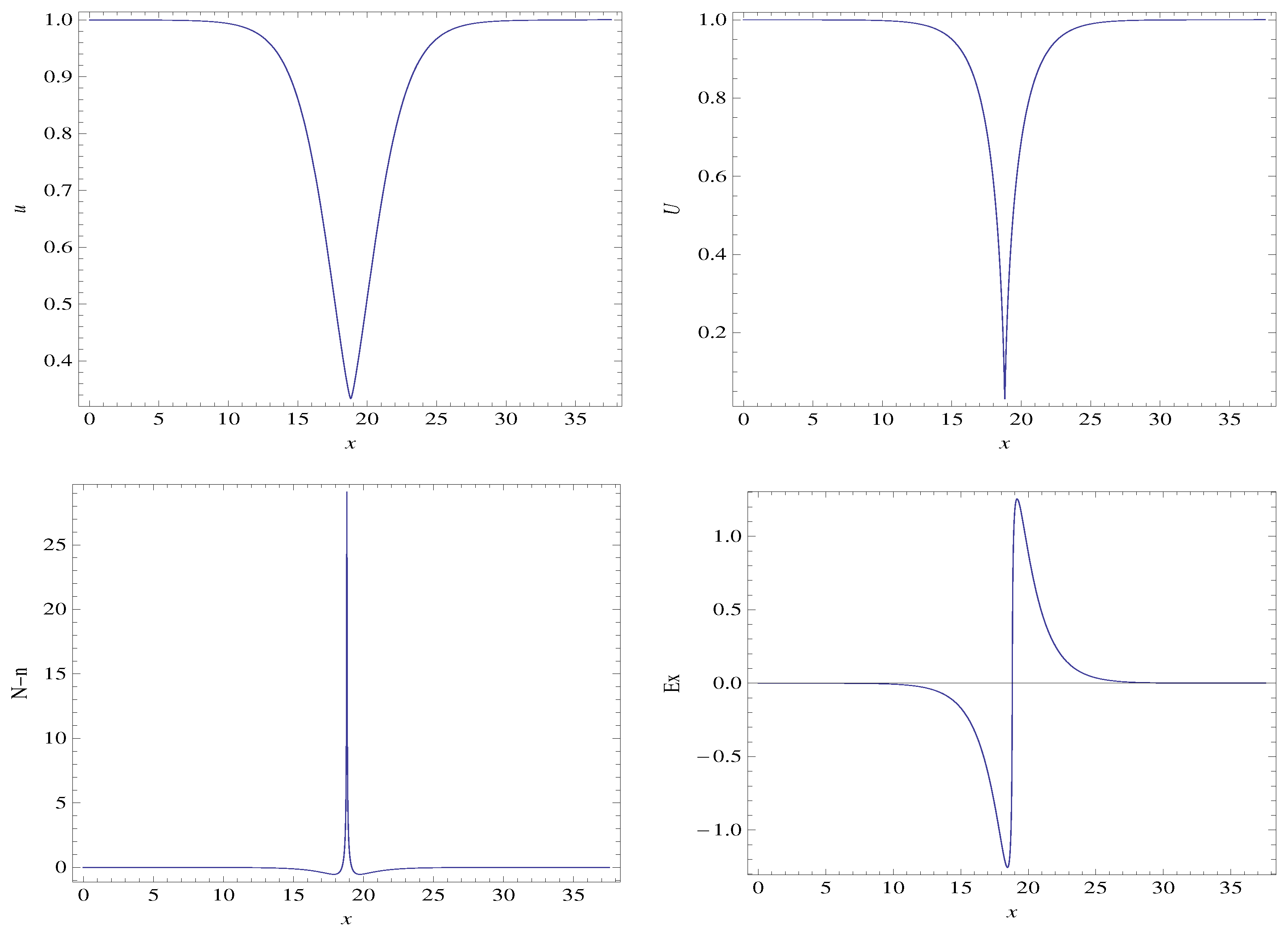
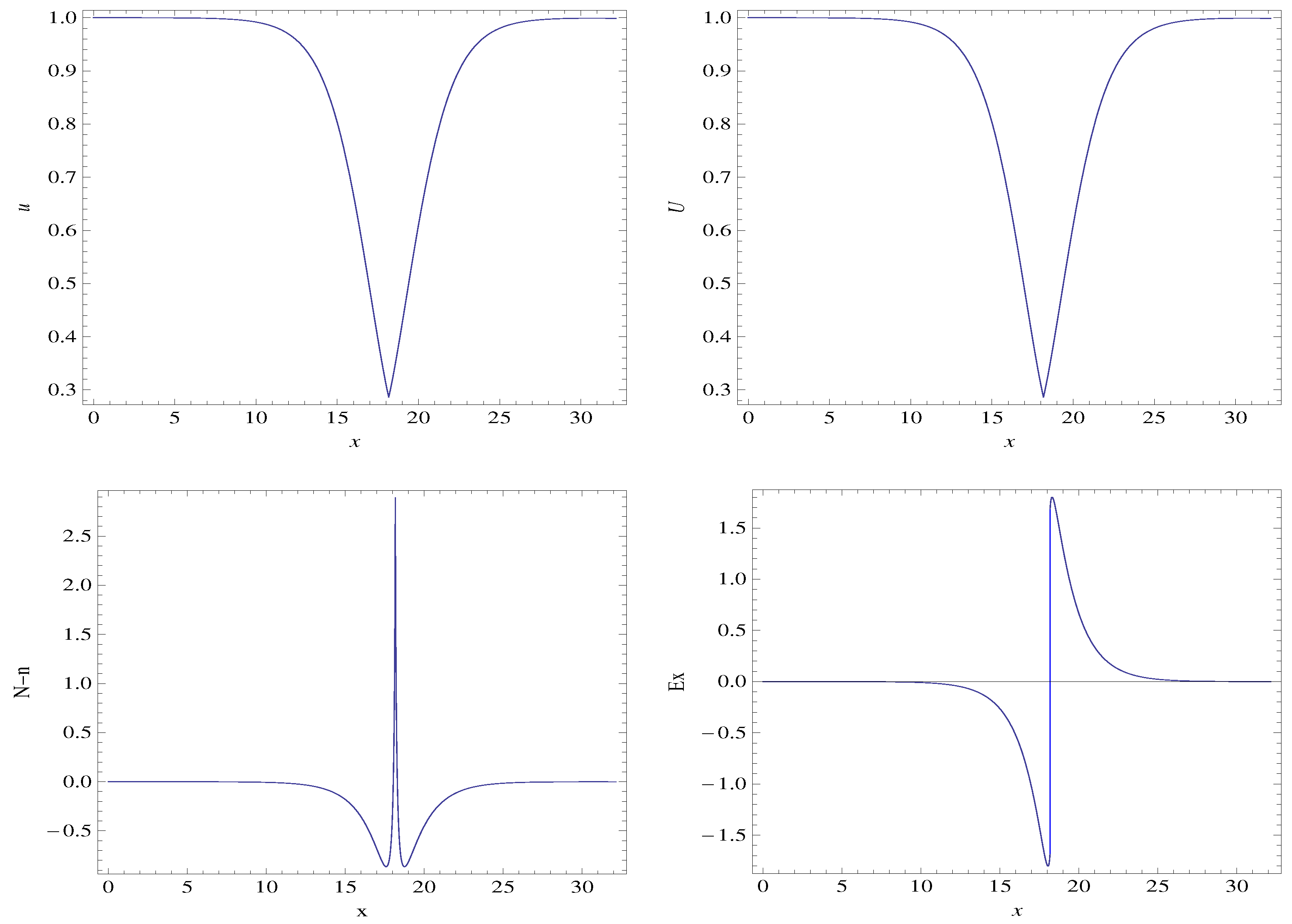
3.2. Setting the Electron Mass to Zero
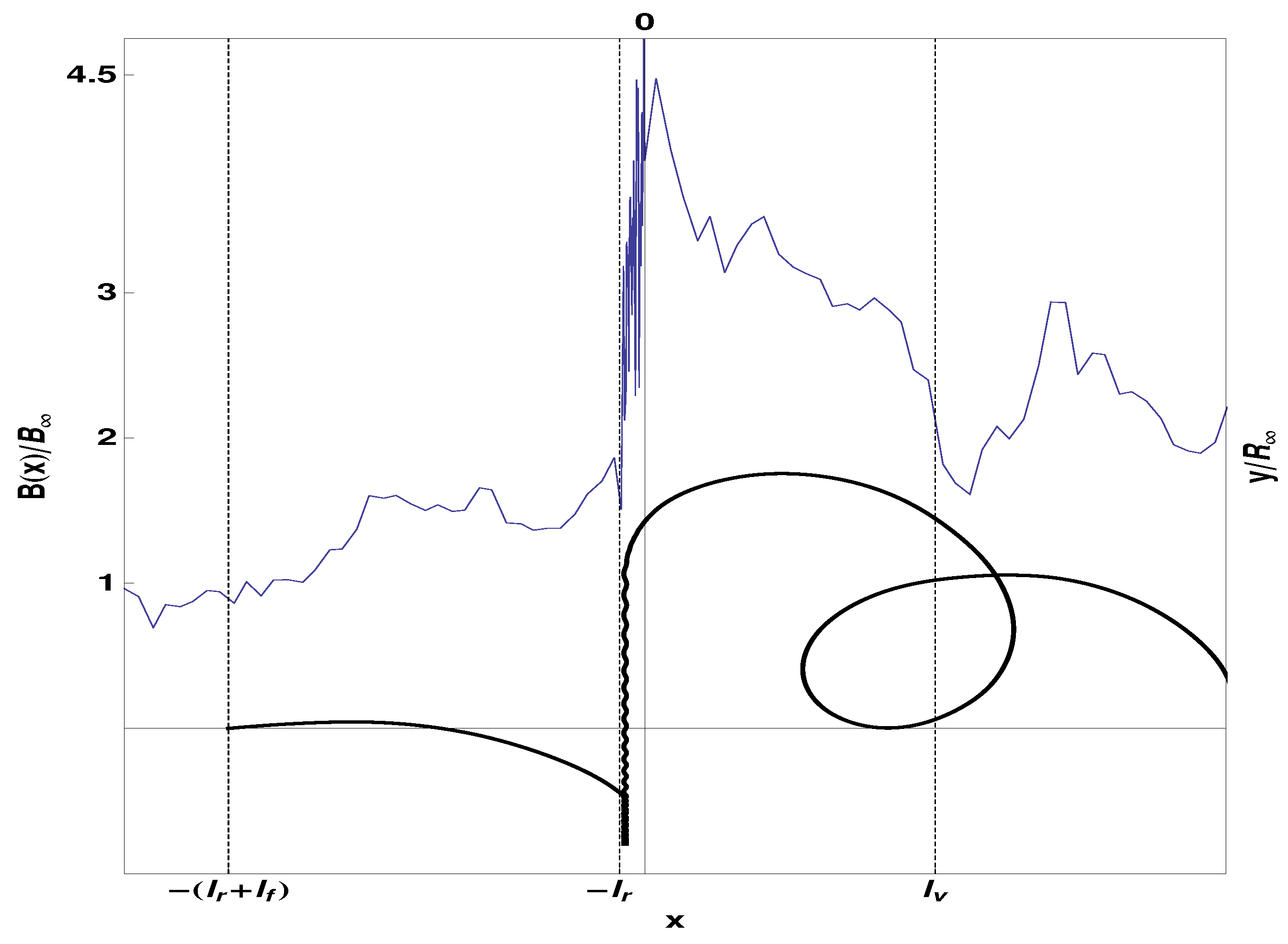
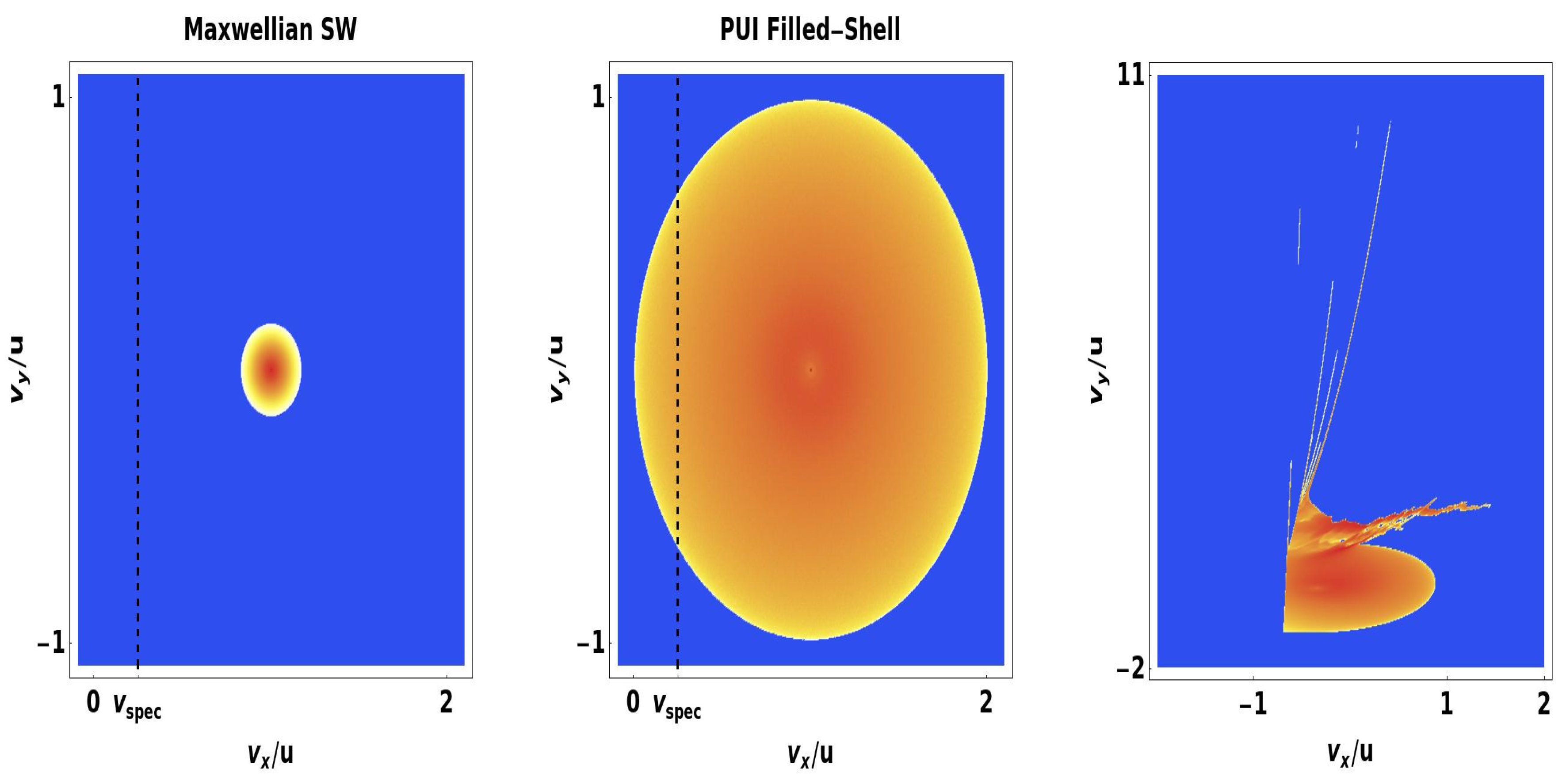
3.3. Discussion
4. Conclusions
Funding
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| MRI | multiply reflected ion |
| PUI | pickup ion |
| SW | solar wind |
| PIC | particle-in-cell |
| MHD | magnetohydrodynamics |
| ESW | electrostatic solitary wave |
| ODE | ordinary differential equation |
| SDA | shock drift acceleration |
| SSA | shock surfing acceleration |
| TS | Termination Shock |
| CSP | cross-shock potential |
| SAP | shock accelerated particle |
| B&S | Boyd and Sanderson |
| AU | astronomical unit |
| 1D | one dimensional |
| SS | steady state |
| NBS | neutral background state |
| SSS | steady state system |
References
- Burrows, R.H.; Zank, G.P.; Webb, G.M.; Burlaga, L.F.; Ness, N.F. Pickup Ion Dynamics at the Heliospheric Termination Shock Observed by Voyager 2. Astrophys. J. 2010, 715, 1109–1116. [Google Scholar] [CrossRef]
- Zank, G.P.; Pauls, H.L.; Cairns, I.H.; Webb, G.M. Interstellar pickup ions and quasi-perpendicular shocks: Implications for the termination shock and interplanetary shocks. J. Geophys. Res. 1996, 101, 457–478. [Google Scholar] [CrossRef]
- Lee, M.A.; Shapiro, V.D.; Sagdeev, R.Z. Pickup ion energization by shock surfing. J. Geophys. Res. 1996, 101, 4777–4790. [Google Scholar] [CrossRef]
- Zank, G.P.; Heerikhuisen, J.; Pogorelov, N.V.; Burrows, R.; McComas, D. Microstructure of the Heliospheric Termination Shock: Implications for Energetic Neutral Atom Observations. Astrophys. J. 2010, 708, 1092–1106. [Google Scholar] [CrossRef]
- Zank, G.P.; Burrows, R.; Oka, M.; Dasgupta, B.; Heerikhuisen, J.; Webb, G.M. Micro-Structure of the Heliospheric Termination Shock. In Proceedings of the 8th Annual International Astrophysics Conference, Kona, HI, USA, 1–7 May 2009; Ao, X., Burrows, G.Z.R., Eds.; American Institute of Physics: College Park, MD, USA, 2009; Volume 1183, pp. 156–166. [Google Scholar] [CrossRef]
- Burrows, R.H.; Ao, X.; Zank, G.P. A New Hybrid Method. In Outstanding Problems in Heliophysics: From Coronal Heating to the Edge of the Heliosphere; Hu, Q., Zank, G.P., Eds.; ASP: San Francisco, CA, USA, 2014; Volume 484. [Google Scholar]
- McKenzie, J.F. Electron acoustic-Langmuir solitons in a two-component electron plasma. J. Plasma Phys. 2003, 69, 199–210. [Google Scholar] [CrossRef]
- Burrows, R.H.; Ao, X.; Zank, G.P. Shock Surfing at a Two-Fluid Plasma Model; American Institute of Physics Conference Series; American Institute of Physics: College Park, MD, USA, 2012. [Google Scholar]
- Richardson, J.D.; Kasper, J.C.; Wang, C.; Belcher, J.W.; Lazarus, A.J. Cool heliosheath plasma and deceleration of the upstream solar wind at the termination shock. Nature 2008, 454, 63–66. [Google Scholar] [CrossRef]
- Oka, M.; Zank, G.P.; Burrows, R.H.; Shinohara, I. Energy Dissipation at the Termination Shock: 1D PIC Simulation. In Proceedings of the 2010 Huntsville Workshop, Nashville, TN, USA, 3–8 October 2010; American Institute of Physics Conference Series. Florinski, V., Heerikhuisen, J., Zank, G.P., Gallagher, D.L., Eds.; American Institute of Physics: College Park, MD, USA, 2011; Volume 1366, pp. 53–59. [Google Scholar] [CrossRef]
- Shin, K.; Kojima, H.; Matsumoto, H.; Mukai, T. Characteristics of electrostatic solitary waves in the Earth’s foreshock region: Geotail observations. J. Geophys. Res. 2008, 113, A03101. [Google Scholar] [CrossRef]
- Wilson, L.B., III; Cattell, C.; Kellogg, P.J.; Goetz, K.; Kersten, K.; Hanson, L.; MacGregor, R.; Kasper, J.C. Waves in Interplanetary Shocks: A Wind/WAVES Study. Phys. Rev. Lett. 2007, 99, 041101. [Google Scholar] [CrossRef] [Green Version]
- Bale, S.D.; Kellogg, P.J.; Larson, D.E.; Lin, R.P.; Goetz, K.; Lepping, R.P. Bipolar electrostatic structures in the shock transition region: Evidence of electron phase space holes. Geophys. Res. Lett. 1998, 25, 2929–2932. [Google Scholar] [CrossRef]
- Tidman, D.A.; Krall, N.A. Shock Waves in Collisionless Plasmas; Wiley Series in Plasma Physics; Wiley-Interscience: New York, NY, USA, 1971. [Google Scholar]
- Noguchi, K.; Tronci, C.; Zuccaro, G.; Lapenta, G. Formulation of the relativistic moment implicit particle-in-cell method. Phys. Plasmas 2007, 14, 042308. [Google Scholar] [CrossRef] [Green Version]
- Lapenta, G. Particle simulations of space weather. J. Comput. Phys. 2012, 231, 795–821. [Google Scholar] [CrossRef]
- Hoshino, M. Coupling Across Many Scales. Science 2003, 299, 834–835. [Google Scholar] [CrossRef] [PubMed]
- Webb, G.M.; Axford, W.I.; Terasawa, T. On the drift mechanism for energetic charged particles at shocks. Astrophys. J. 1983, 270, 537–553. [Google Scholar] [CrossRef]
- Pogorelov, N.V.; Zank, G.P.; Ogino, T. Three-dimensional Features of the Outer Heliosphere due to Coupling between the Interstellar and Interplanetary Magnetic Fields. II. The Presence of Neutral Hydrogen Atoms. Astrophys. J. 2006, 644, 1299–1316. [Google Scholar] [CrossRef]
- Winske, D.; Daughton, W. Generation of lower hybrid and whistler waves by an ion velocity ring distribution. Phys. Plasmas 2012, 19, 072109. [Google Scholar] [CrossRef] [Green Version]
- Boyd, T.M.M.; Sanderson, J.J. Plasma Dynamics; Barnes & Nobel, Inc.: New York, NY, USA, 1969. [Google Scholar]
- Zank, G.P. Interaction of the solar wind with the local interstellar medium: A theoretical perspective. Space Sci. Rev. 1999, 89, 413–688. [Google Scholar] [CrossRef]
- Dudík, J.; Dzifčáková, E.; Meyer-Vernet, N.; Del Zanna, G.; Young, P.R.; Giunta, A.; Sylwester, B.; Sylwester, J.; Oka, M.; Mason, H.E.; et al. Nonequilibrium Processes in the Solar Corona, Transition Region, Flares, and Solar Wind (Invited Review). Sol. Phys. 2017, 292, 100. [Google Scholar] [CrossRef]
- Yoon, P.H. Electron kappa distribution and quasi-thermal noise. J. Geophys. Res. 2014, 119, 7074–7087. [Google Scholar] [CrossRef]
- Livadiotis, G.; McComas, D.J. Understanding Kappa Distributions: A Toolbox for Space Science and Astrophysics. Space Sci. Rev. 2013, 175, 183–214. [Google Scholar] [CrossRef] [Green Version]
- McComas, D.J.; Allegrini, F.; Bochsler, P.; Bzowski, M.; Christian, E.R.; Crew, G.B.; DeMajistre, R.; Fahr, H.; Fichtner, H.; Frisch, P.C.; et al. Global Observations of the Interstellar Interaction from the Interstellar Boundary Explorer (IBEX). Science 2009, 326, 959. [Google Scholar] [CrossRef]
- Ao, X.; Burrows, R.H.; Zank, G.P.; Webb, G.M. Solitons in two-fluid plasma. In Proceedings of the 10th Annual International Astrophysics, Maui, HI, USA, 13–18 March 2011; Heerikhuisen, J., Li, G., Pogorelov, N., Zank, G., Eds.; American Institute of Physics: College Park, MD, USA, 2011; Volume 1436, pp. 5–11. [Google Scholar]
- Zank, G.P.; McKenzie, J.F. Solitons in an ion-beam plasma. J. Plasma Phys. 1988, 39, 183–191. [Google Scholar] [CrossRef]
- McKenzie, J.F. The ion-acoustic soliton: A gas-dynamic viewpoint. Phys. Plasmas 2002, 9, 800–805. [Google Scholar] [CrossRef]
- Verheest, F.; Cattaert, T.; Lakhina, G.S.; Singh, S.V. Gas-dynamic description of electrostatic solitons. J. Plasma Phys. 2004, 70, 237–250. [Google Scholar] [CrossRef]
- Chen, F.F. Introduction to Plasma Physics and Controlled Fusion; Plenum Press: New York, NY, USA, 1984. [Google Scholar]
- Verheest, F.; Hellberg, M. Electrostatic solitons and sagdeev psuedopentials in space plasmas: Review of recent advances. In Handbook of Solitons; Nova Science Publishers: New York, NY, USA, 2009; pp. 353–393. [Google Scholar]
- Webb, G.M.; Burrows, R.H.; Ao, X.; Zank, G.P. Ion acoustic traveling waves. J. Plasma Phys. 2014, 80, 147–171. [Google Scholar] [CrossRef] [Green Version]



© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burrows, R. Ion Acceleration in Multi-Fluid Plasma: Including Charge Separation Induced Electric Field Effects in Supersonic Wave Layers. Plasma 2020, 3, 117-152. https://doi.org/10.3390/plasma3030010
Burrows R. Ion Acceleration in Multi-Fluid Plasma: Including Charge Separation Induced Electric Field Effects in Supersonic Wave Layers. Plasma. 2020; 3(3):117-152. https://doi.org/10.3390/plasma3030010
Chicago/Turabian StyleBurrows, Ross. 2020. "Ion Acceleration in Multi-Fluid Plasma: Including Charge Separation Induced Electric Field Effects in Supersonic Wave Layers" Plasma 3, no. 3: 117-152. https://doi.org/10.3390/plasma3030010
APA StyleBurrows, R. (2020). Ion Acceleration in Multi-Fluid Plasma: Including Charge Separation Induced Electric Field Effects in Supersonic Wave Layers. Plasma, 3(3), 117-152. https://doi.org/10.3390/plasma3030010



