Computing the Double-Gyroaverage Term Incorporating Short-Scale Perturbation and Steep Equilibrium Profile by the Interpolation Algorithm
Abstract
:1. Introduction
2. The Basic Orders
3. QNE Incorporating the Short-Scale Perturbation and Steep Equilibrium Profile
3.1. The Particle Coordinate Density Associated with the Short-Scale Perturbation and Steep Equilibrium Profile
3.2. QNE Associated with the Adiabatic Distribution of Electron and the Steep Equilibrium Profile on Gyrocenter Coordinate Frame
3.3. Normalization
4. QNE Solver Comprising the Interpolation Algorithm to Compute DGT
4.1. The Algorithm to Compute the Interpolation Matrixes and in Finite Element Method
| Algorithm 1 Compute |
| Input: , boundary condition 1: for do 2: for do 3: get 4: get 5: get 6: for do 7: for do 8: get 9: |
4.2. Matrix Form of DGT
- Construction of the matrix such that is the vector of splines coefficients. Alternatively, can be written as . The matrix is independent of the Larmor radius or the magnetic moment , while depending on the equilibrium quantities.
- For a Larmor radius contributed by the magnetic moment , constructing the matrix which gives the contribution of the gyroaverage of the radius as the function of the splines coefficients. Here, denoting the first and the second gyroaverage, respectively.
- The first gyroaverage is given by , with .
- The second gyroaverage is written as the matrix formTo obtain the matrix form between and , the vector product is written as the product between a diagonal matrix denoted as and . Eventually, can be written as the matrix formwherePlease note that the elements of matrix only depends on the equilibrium quantities. It can be computed once for all at the beginning of the simulation.
- Then, the integral of contained by the DGT can be formulated as the discrete sum
4.3. The Fast Algorithm to Solve QNE
- Fourier transformation of the vector on the right side of QNE to get the vector on the Fourier basis.
- Obtain , and by implementing Equation (39) and get the product .
- Use the subroutine of Lapack and Blas to obtain the inverse matrix , where is of the same structure with in Equation (35a).
- Compute the vector .
- Implementing the inverse Fourier transform on the polar elements of the vector to obtain .
5. Benchmark of the Interpolation Algorithm for the Single Case
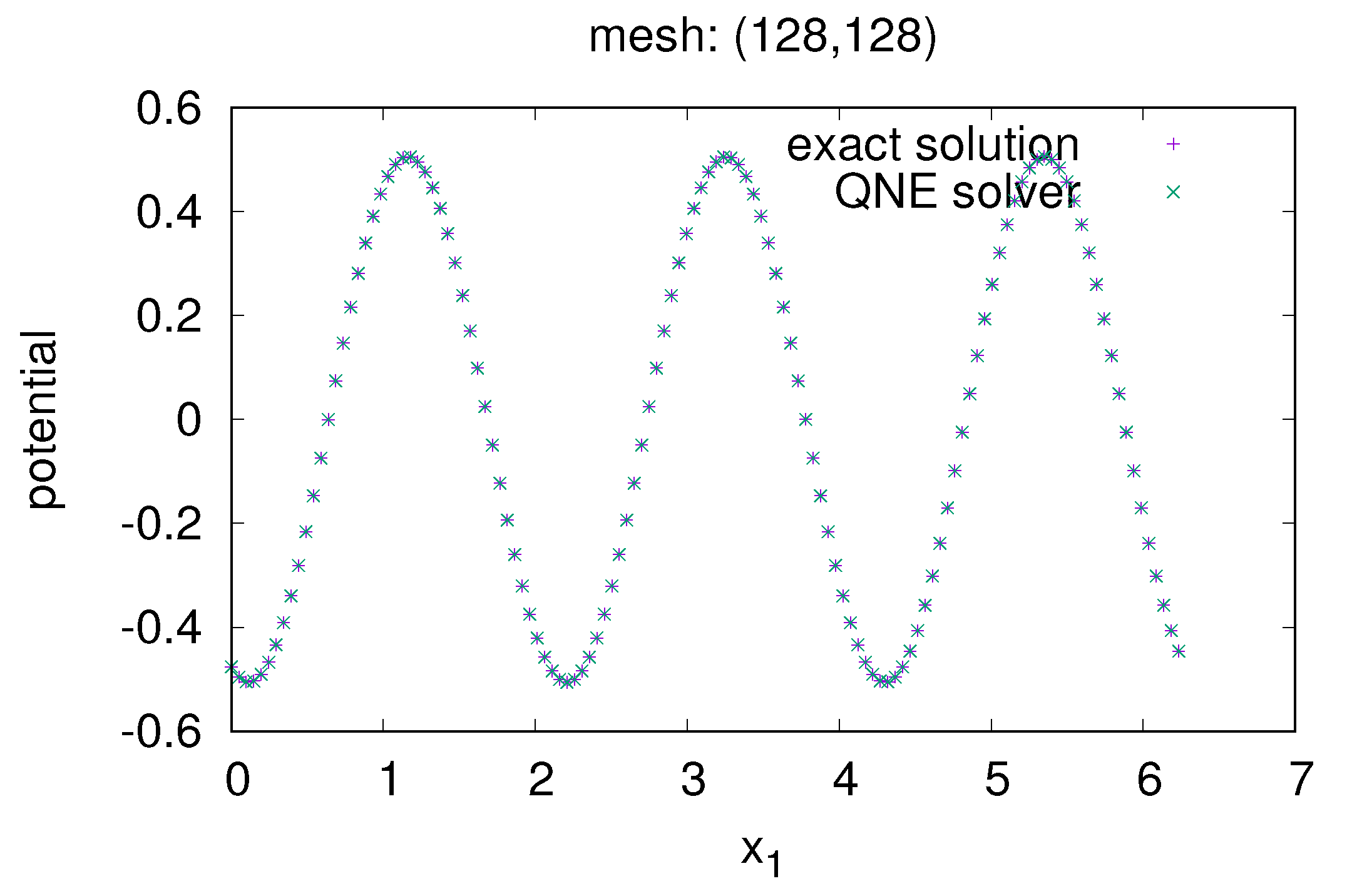
5.1. 1st Example: Double-Periodic Boundary Condition in Cartesian Coordinate
5.2. 2nd Example: Natural + Periodic Boundary Condition in Cartesian Coordinate
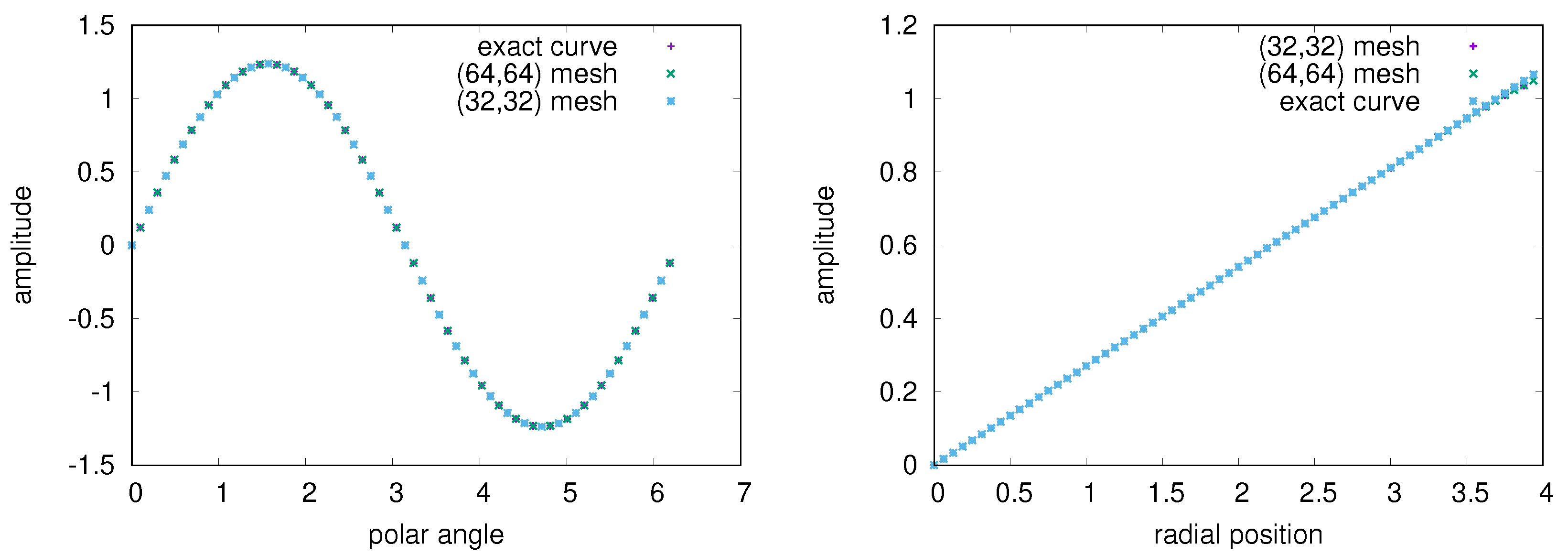
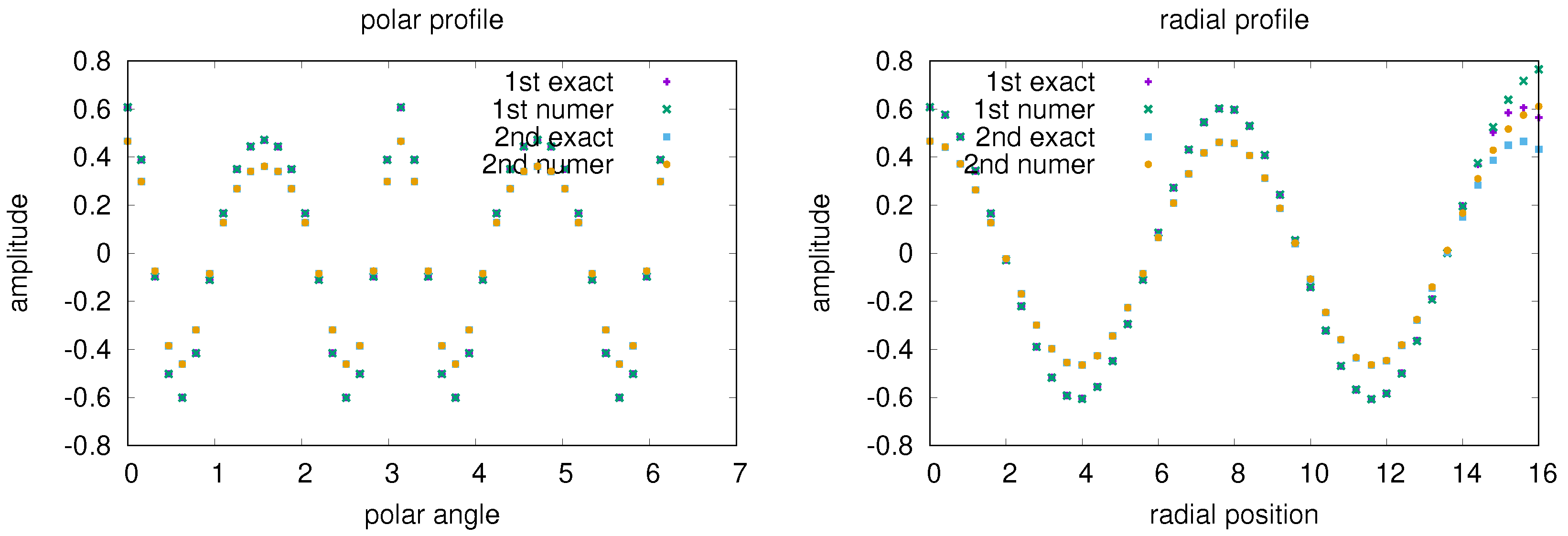
5.3. 3rd Example: Natural + Periodic Boundary Condition in the Polar Coordinate Frame
5.4. Benchmark the QNE Solver in the Cartesian Coordinate Frame and in the Polar Coordinate Frame
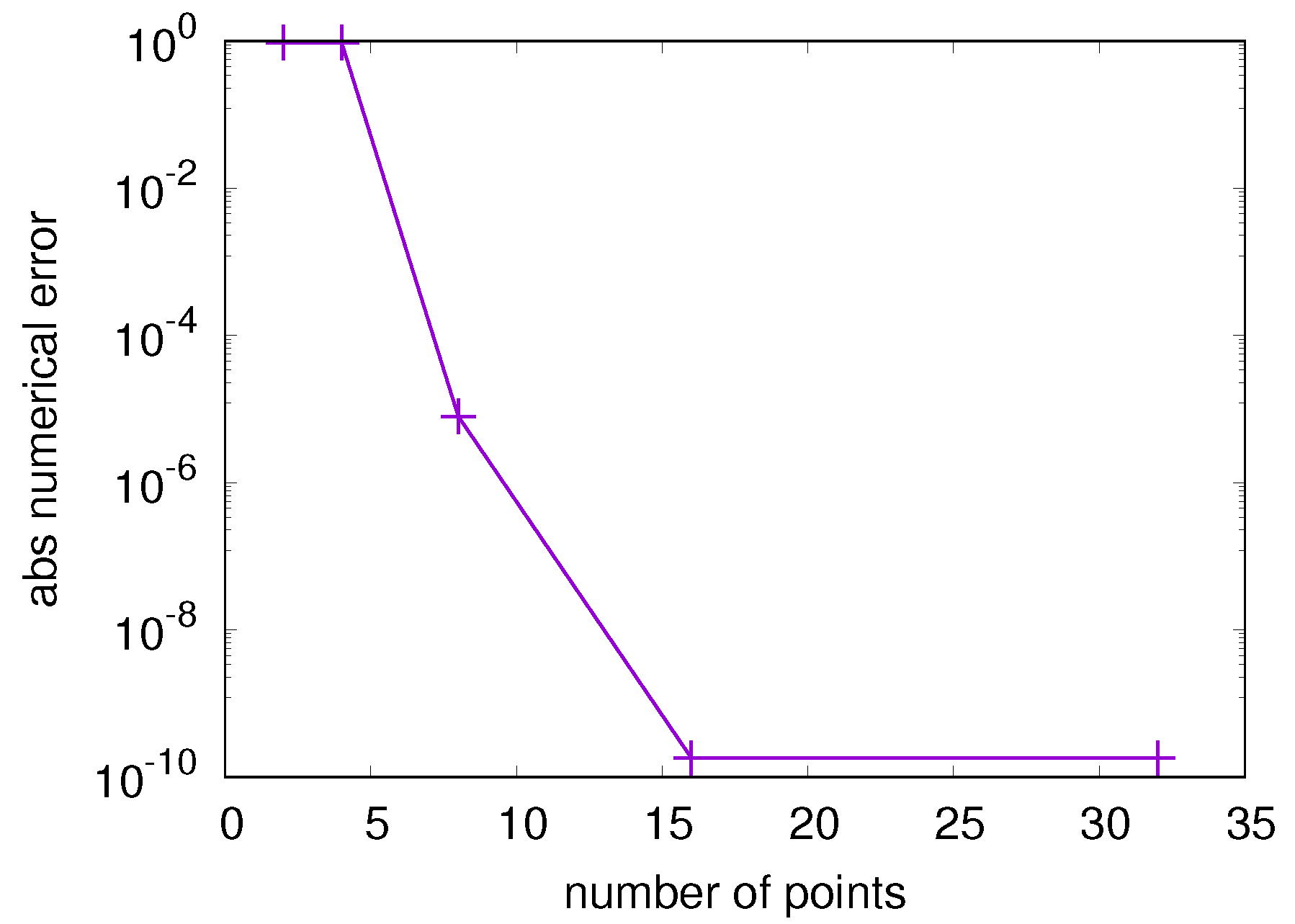
6. Benchmark of the Interpolation Algorithm for the Multiple Case
6.1. The Euler–Maclaurin-Based Quadrature Integration Algorithm
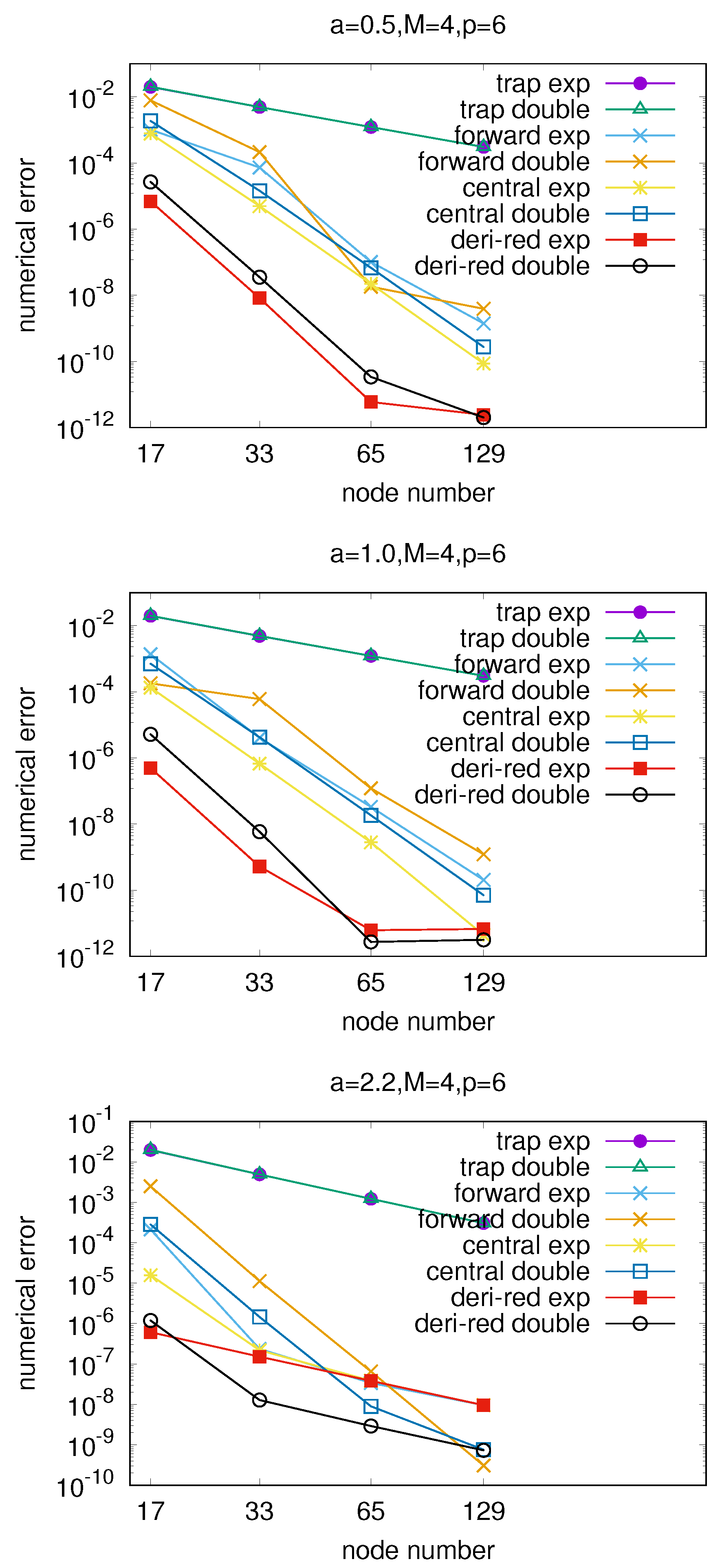
6.2. Benchmark of DGT Computed by the Interpolation Algorithm in the Polar Coordinate Frame Assisted by the Forward Scheme of the Euler–Maclaurin-Based Algorithm
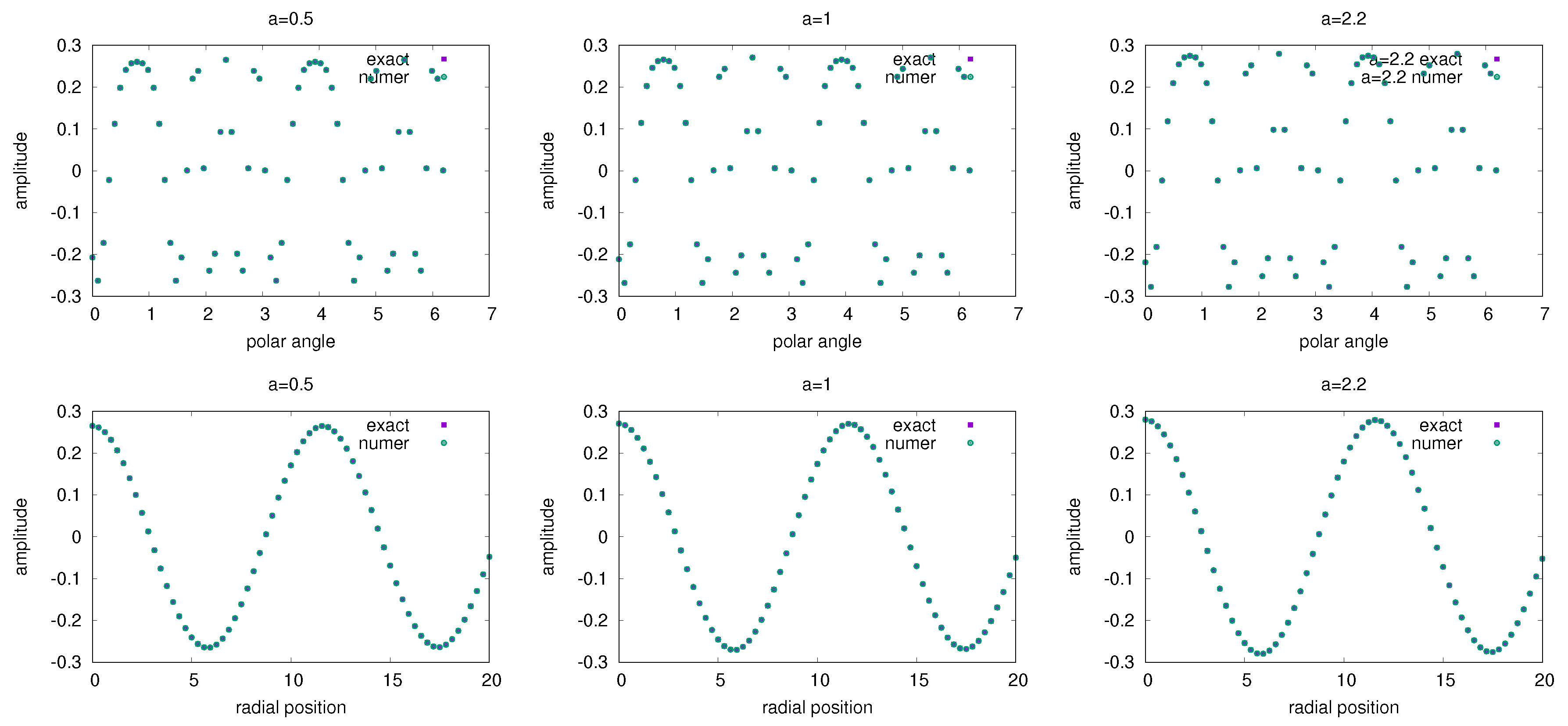
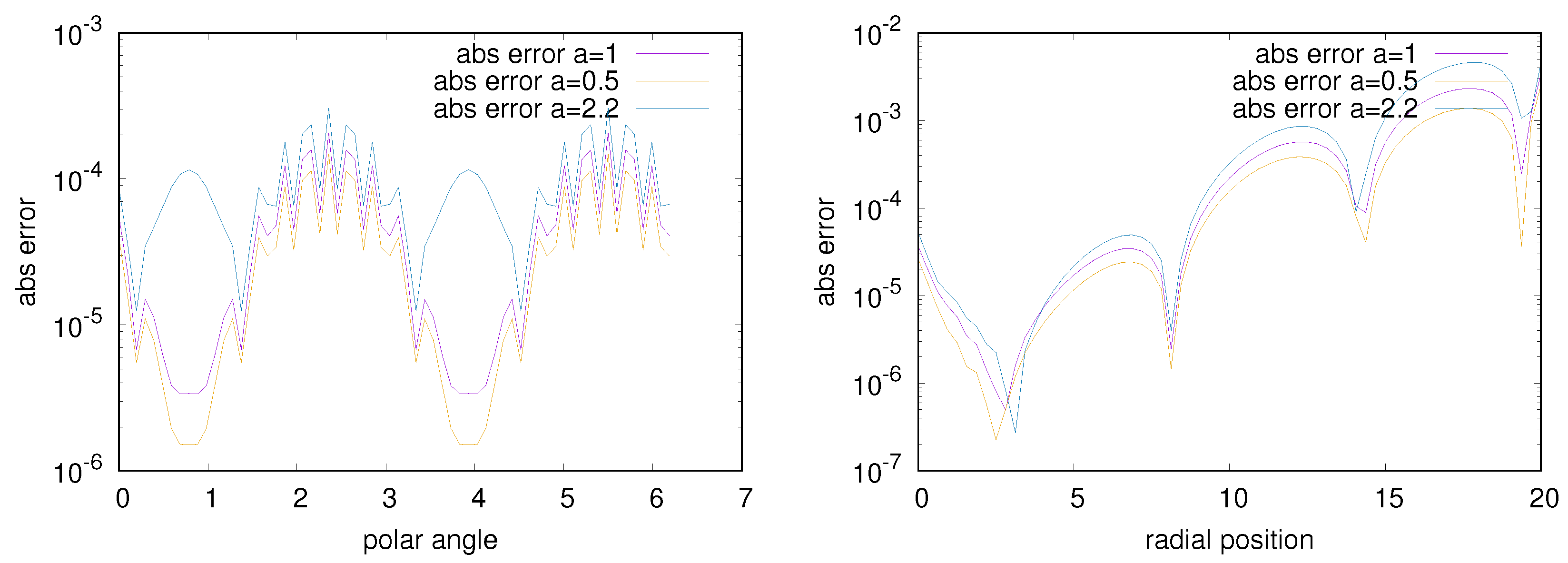
6.3. Benchmark of the QNE Solver in the Polar Coordinate Frame Assisted by the Forward Scheme of the Euler–Maclaurin-Based Algorithm
7. Application of the QNE Solver in Gyrokinetic Simulation Concerning Short-Scale Perturbation and Steep Equilibrium Profile Assisted by the Forward Scheme of the Euler–Maclaurin-Based algorithm
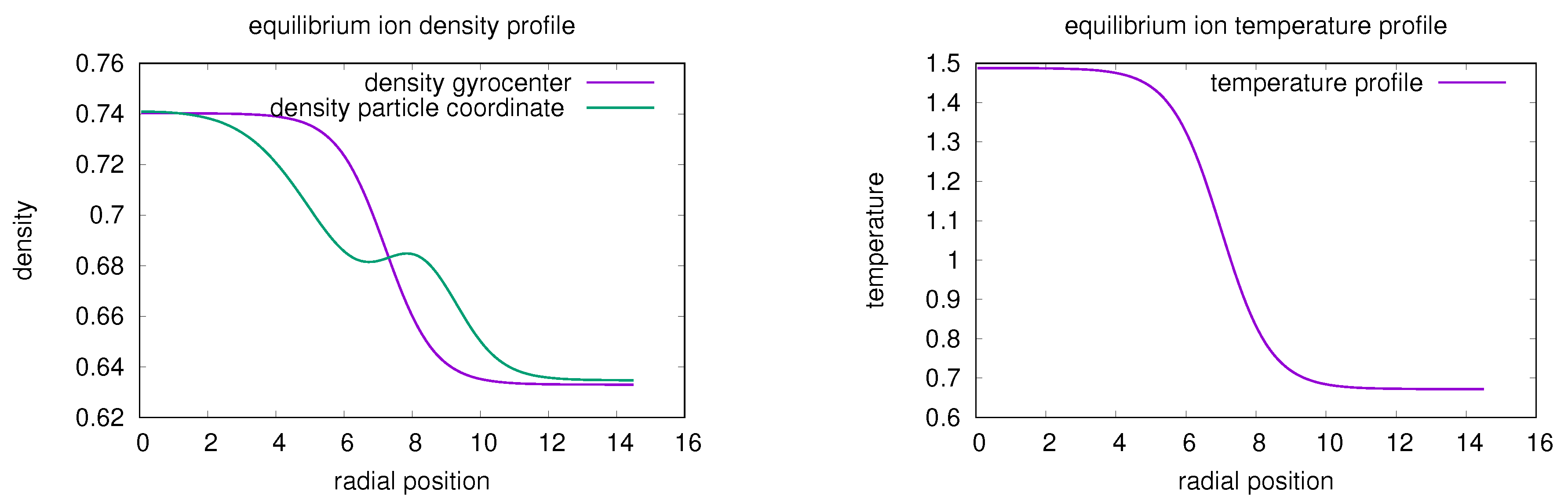
7.1. The Gyrokinetic Model with Constant Cylindrical Magnetic Field Configuration
7.2. The Parallelization
7.2.1. The Algorithm to Reduce the Distribution to the Density
- The distribution for each at time moment t is computed by Equation (54).
- The integration of the distribution of each over U is first done by the sum .
- The gyroaverage of denoted as for each is done by using the coefficient matrix with the result being , where is a vector formed by on the grids and is given asThe total density on the particle coordinate mesh contributed by the component is written as
- The equilibrium density in the particle coordinate frame obtained from the gyroaverage of the equilibrium distribution for the component is done at the beginning following the procedure and is stored for the subsequent invoking. By inheriting the symbol used in Equation (A6), the jth equilibrium density on particle coordinate spatial mesh is denoted as . Then, the perturbative density on the particle coordinate spatial mesh contributed by the component is
- The total perturbative density on the particle coordinate space computed by all is obtained by “MPI_ALLREDUCE” the as , where is the magnetic field magnitude at the node denoted by .
7.2.2. The Parallelization
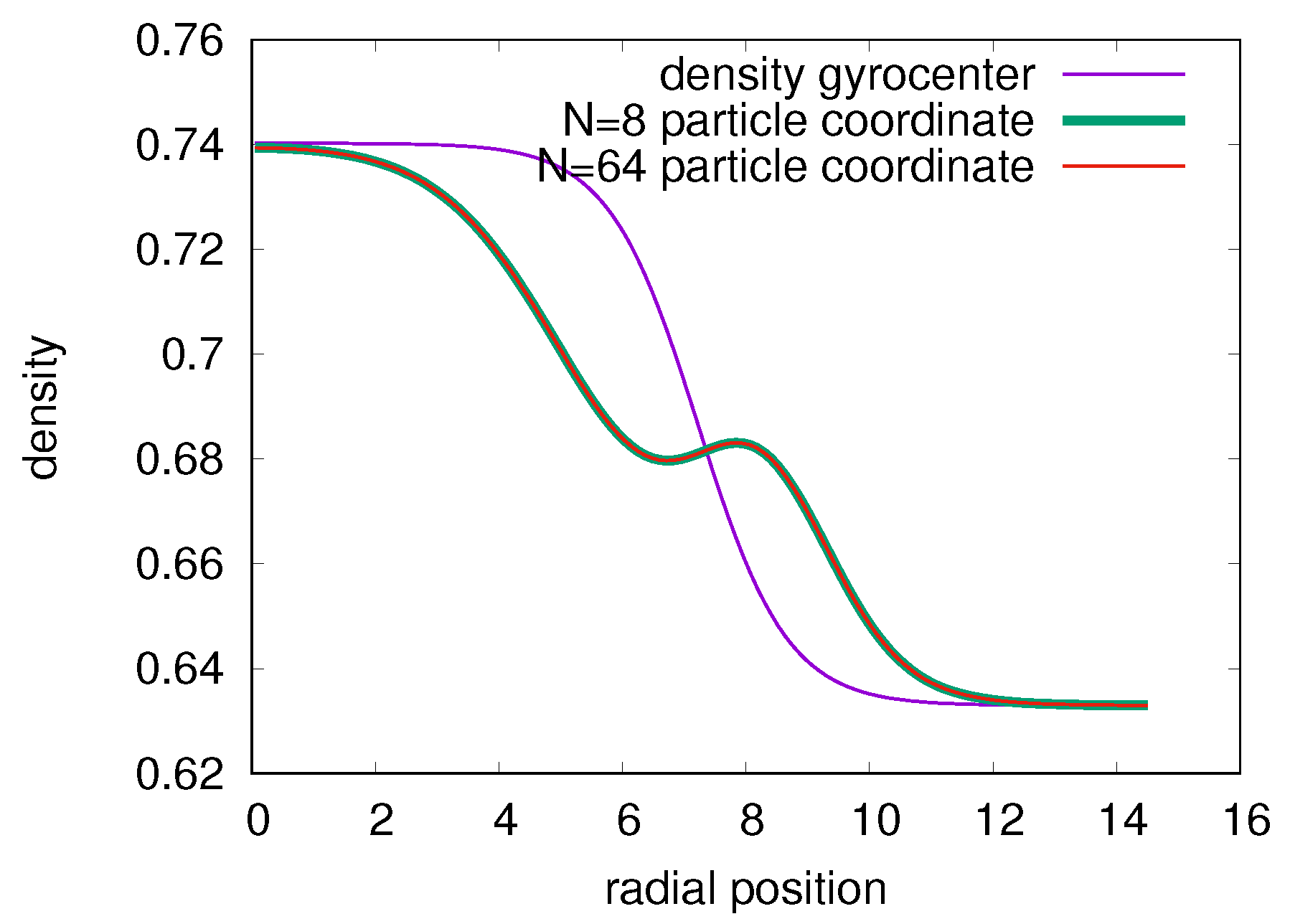
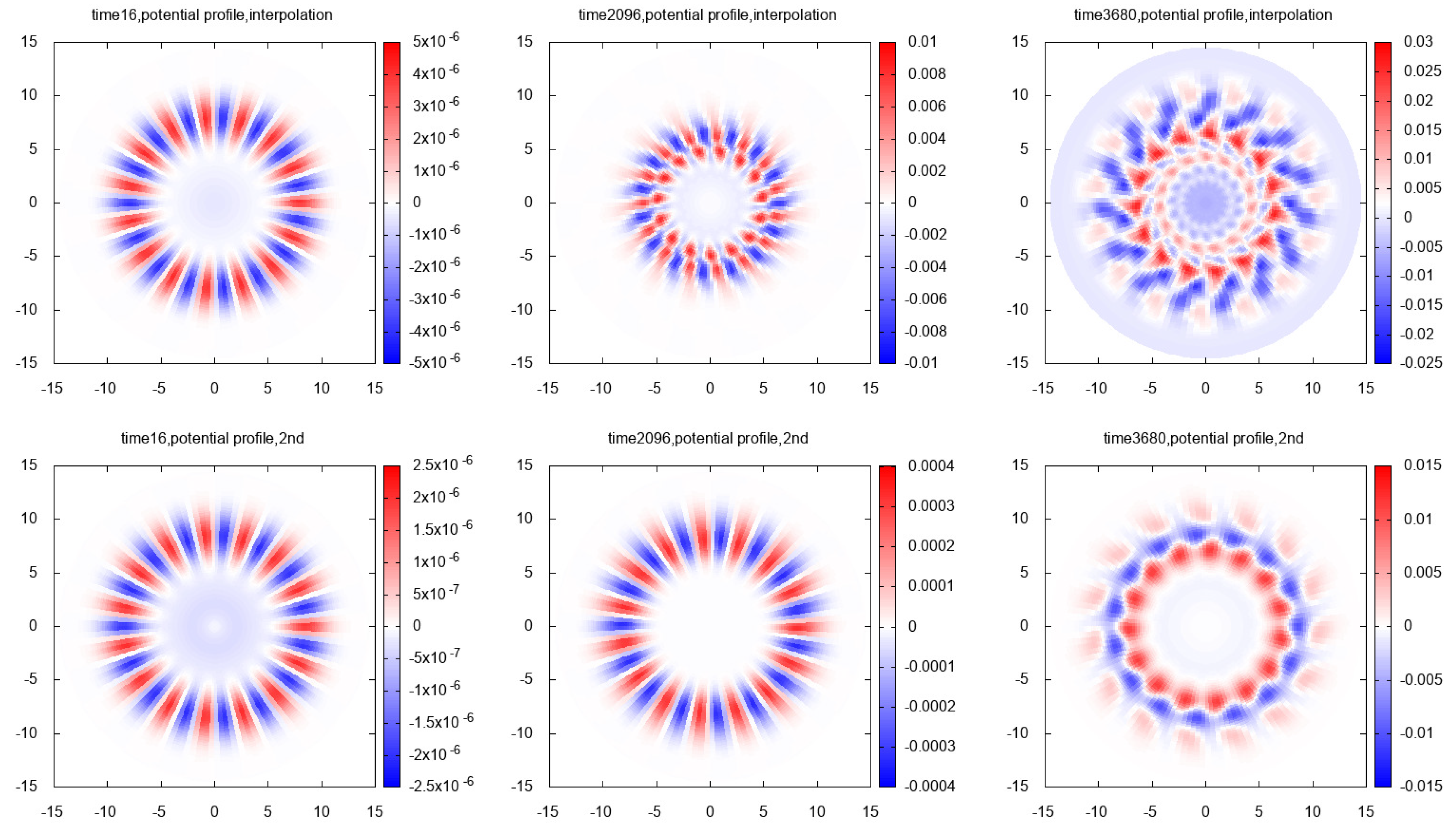
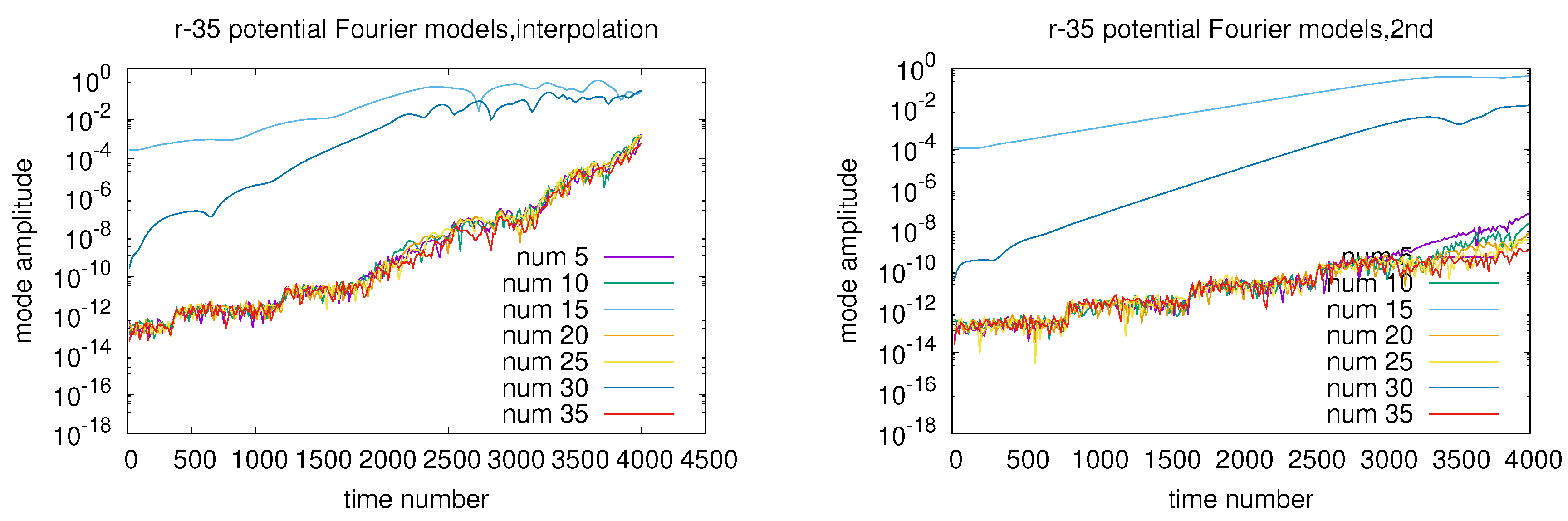
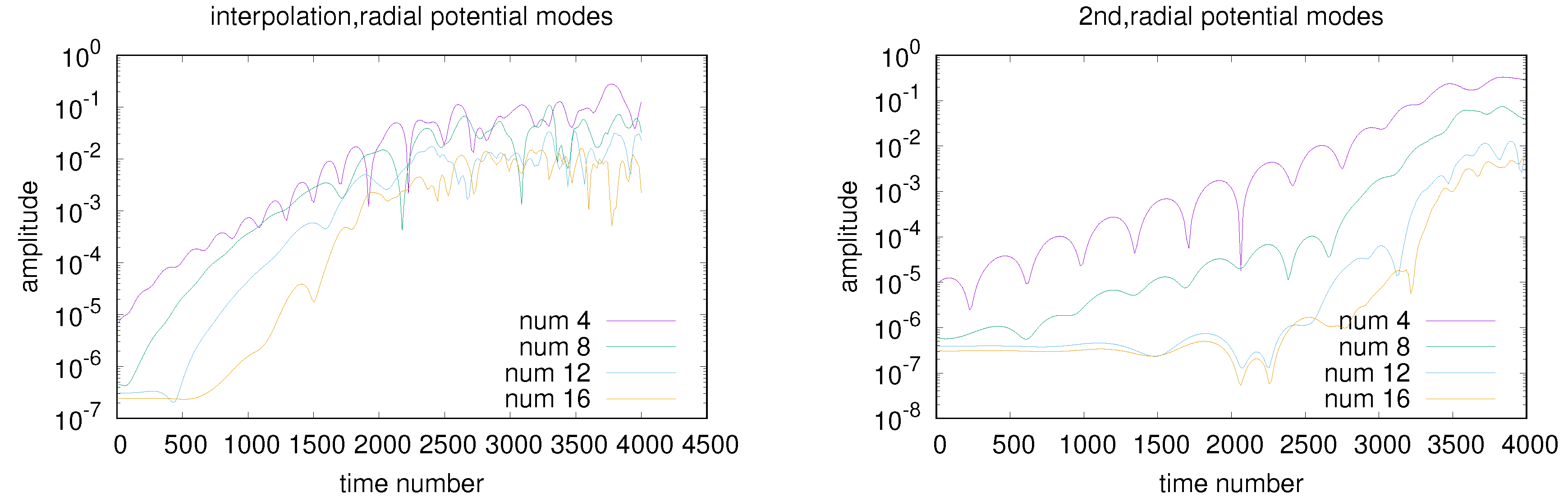
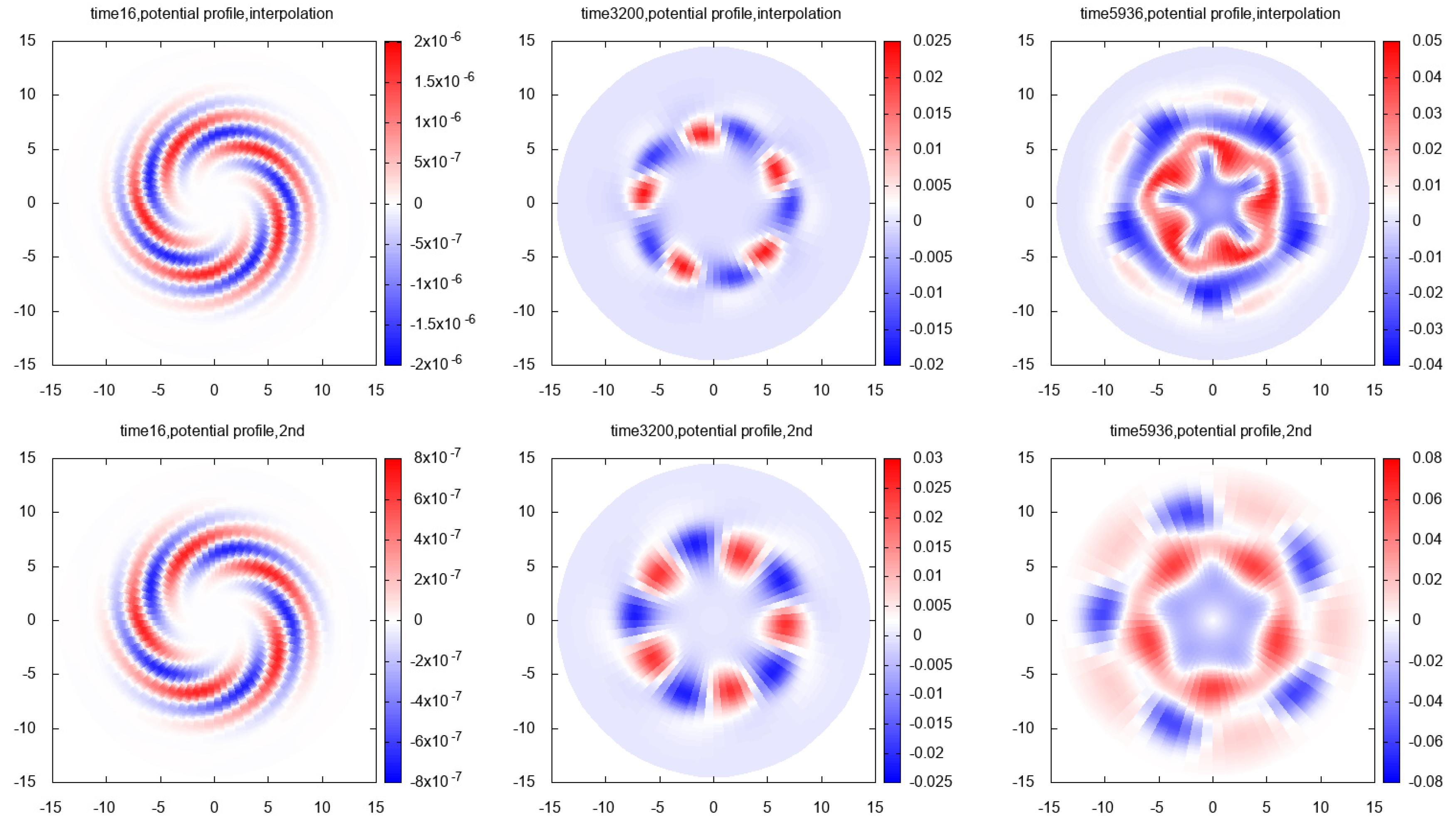
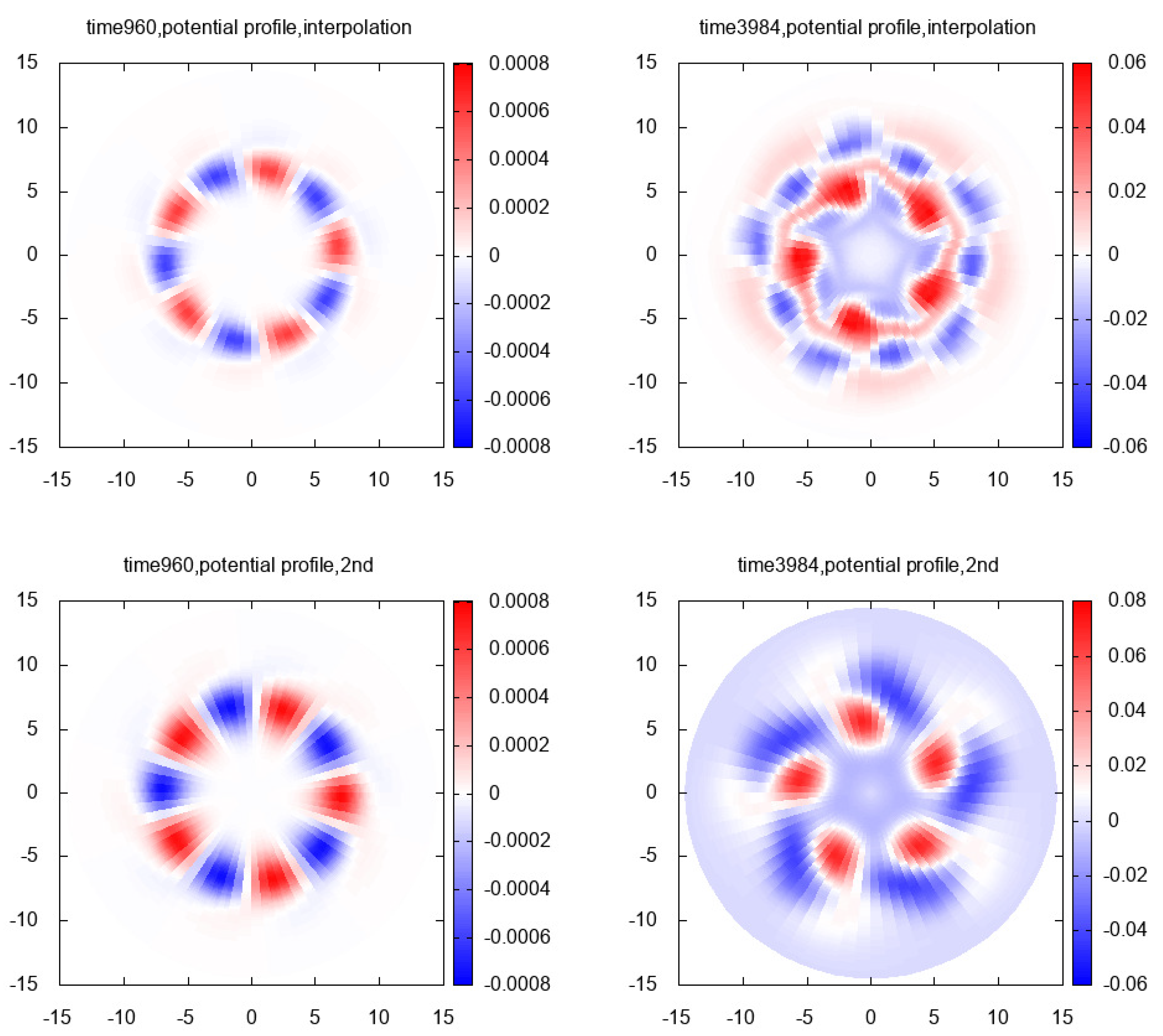
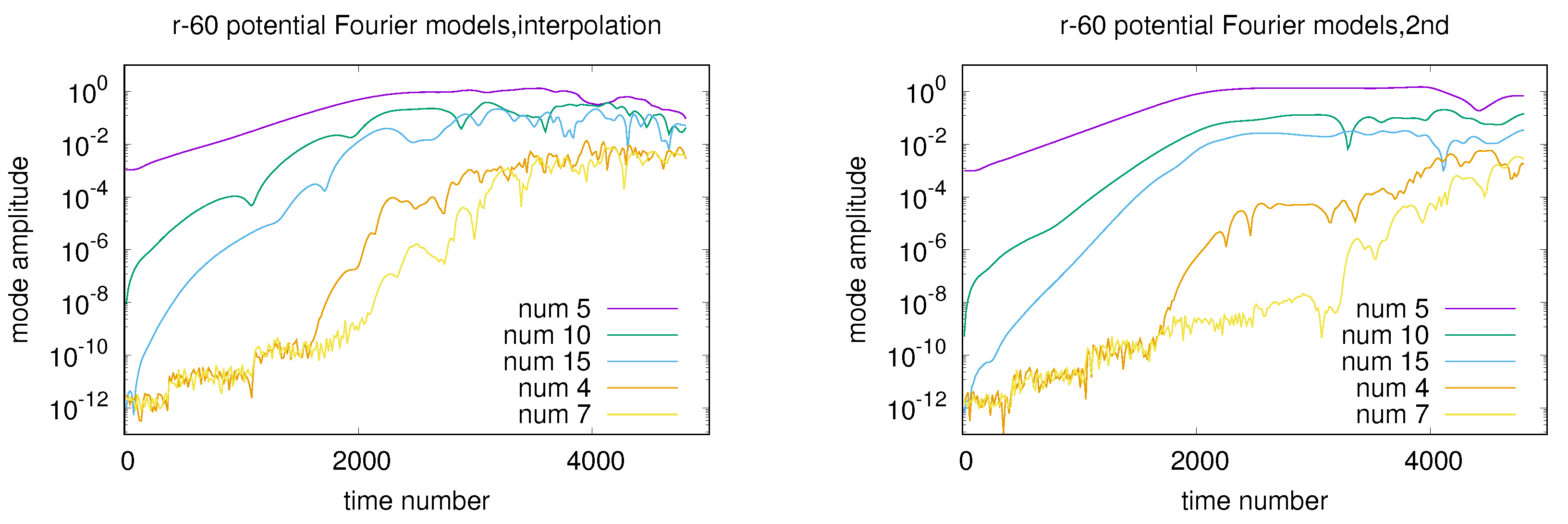
7.3. The Simulation Results
7.3.1. 1st Case:
7.3.2. 2nd Case:
7.3.3. 3rd Case:
7.3.4. 4th Case:
8. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. 2nd-Order Approximation of QNE
Appendix B. The Examples of the Exact Solution of the Gyroaverage and Double-Gyroaverage Operation
References
- Diamond, P.H.; Itoh, S.I.; Itoh, K.; Hahm, T.S. Zonal flows in plasma—A review. Plasma Phys. Control. Fusion 2005, 47, R35. [Google Scholar] [CrossRef]
- Lin, Z.; Hahm, T.S.; Lee, W.W.; Tang, W.M.; White, R.B. Turbulent Transport Reduction by Zonal Flows: Massively Parallel Simulations. Science 1998, 281, 1835–1837. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Biglari, H.; Diamond, P.H.; Terry, P.W. Influence of sheared poloidal rotation on edge turbulence. Phys. Fluids B Plasma Phys. 1990, 2, 1. [Google Scholar] [CrossRef]
- Wesson, J. Tokamaks, 3rd ed.; CLARENDON Press: Oxford, UK, 2004. [Google Scholar]
- Chen, F. Introduction to Plasma Physics and Controlled Fusion; Springer: New York, NY, USA, 2010. [Google Scholar]
- Hazeltine, R.D.; Meiss, J.D. Plasma Confinement; Addison-Wesley, Advanced Book Program: Boston, MA, USA, 1992. [Google Scholar]
- White, R.B. Theory of Tokamak Plasmas, 1st ed.; Elsevier: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Zohm, H. Edge localized modes (ELMs). Plasma Phys. Control. Fusion 1996, 38, 105. [Google Scholar] [CrossRef]
- Hayashi, N.; Takizuka, T.; Aiba, N.; Oyama, N.; Ozeki, T.; Wiesen, S.; Parail, V. Integrated simulation of ELM energy loss and cycle in improved H-mode plasmas. Nucl. Fusion 2009, 49, 95015. [Google Scholar] [CrossRef]
- Burrell, K.H.; West, W.P.; Doyle, E.J.; Austin, M.E.; Casper, T.A.; Gohil, P.; Greenfield, C.M.; Groebner, R.J.; Hyatt, A.W.; Jayakumar, R.J.; et al. Advances in understanding quiescent H-mode plasmas in DIII-D. Phys. Plasmas 2005, 12, 56121. [Google Scholar] [CrossRef]
- Hubbard, A.E. Physics and scaling of the H-mode pedestal. Plasma Phys. Control. Fusion 2000, 42, A15. [Google Scholar] [CrossRef]
- Lönnroth, J.S.; Parail, V.; Dnestrovskij, A.; Figarella, C.; Garbet, X.; Wilson, H.; Contributors, J.E. Predictive transport modelling of type I ELMy H-mode dynamics using a theory-motivated combined ballooning–peeling model. Plasma Phys. Control. Fusion 2004, 46, 1197. [Google Scholar] [CrossRef]
- Ryter, F.; Angioni, C.; Beurskens, M.; Cirant, S.; Hoang, G.T.; Hogeweij, G.M.D.; Imbeaux, F.; Jacchia, A.; Mantica, P.; et al. Experimental studies of electron transport. Plasma Phys. Control. Fusion 2001, 43, A323. [Google Scholar] [CrossRef]
- Suttrop, W. The physics of large and small edge localized modes. Plasma Phys. Control. Fusion 2000, 42, A1. [Google Scholar] [CrossRef]
- Dickinson, D.; Saarelma, S.; Scannell, R.; Kirk, A.; Roach, C.M.; Wilson, H.R. Towards the construction of a model to describe the inter-ELM evolution of the pedestal on MAST. Plasma Phys. Control. Fusion 2011, 53, 115010. [Google Scholar] [CrossRef]
- Garbet, X.; Idomura, Y.; Villard, L.; Watanabe, T.H. Gyrokinetic simulations of turbulent transport. Nucl. Fusion 2010, 50, 43002. [Google Scholar] [CrossRef]
- Lee, W.W. Gyrokinetic particle simulation model. J. Comput. Phys. 1987, 72, 243. [Google Scholar] [CrossRef]
- Lee, W.W. Gyrokinetic approach in particle simulation. Phys. Fluids 1983, 26, 556–562. [Google Scholar] [CrossRef]
- Dubin, D.H.E.; Krommes, J.A.; Oberman, C.; Lee, W.W. Nonlinear gyrokinetic equations. Phys. Fluids 1983, 26, 3524–3535. [Google Scholar] [CrossRef]
- Lin, Z.; Tang, W.M.; Lee, W.W. Gyrokinetic particle simulation of neoclassical transport. Phys. Plasmas 1995, 2, 2975–2988. [Google Scholar] [CrossRef]
- Wang, W.X.; Lin, Z.; Tang, W.M.; Lee, W.W.; Ethier, S.; Lewandowski, J.L.V.; Rewoldt, G.; Hahm, T.S.; Manickam, J. Gyro-kinetic simulation of global turbulent transport properties in tokamak experiments. Phys. Plasmas 2006, 13, 92505. [Google Scholar] [CrossRef] [Green Version]
- Jenko, F.; Dorland, W.; Kotschenreuther, M.; Rogers, B.N. Electron temperature gradient driven turbulence. Phys. Plasmas 2000, 7, 1904–1910. [Google Scholar] [CrossRef]
- Parker, S.E.; Kim, C.; Chen, Y. Large-scale gyrokinetic turbulence simulations: Effects of profile variation. Phys. Plasmas 1999, 6, 1709–1716. [Google Scholar] [CrossRef]
- Candy, J.; Waltz, R.E. An Eulerian gyrokinetic-Maxwell solver. J. Comput. Phys. 2003, 186, 545–581. [Google Scholar] [CrossRef]
- Chang, C.S.; Ku, S.; Diamond, P.; Adams, M.; Barreto, R.; Chen, Y.; Cummings, J.; D’Azevedo, E.; Dif-Pradalier, G.; Ethier, S.; et al. Whole-volume integrated gyrokinetic simulation of plasma turbulence in realistic diverted-tokamak geometry. J. Phys. Conf. Ser. 2009, 180, 12057. [Google Scholar] [CrossRef] [Green Version]
- Idomura, Y.; Ida, M.; Kano, T.; Aiba, N.; Tokuda, S. Conservative global gyrokinetic toroidal full-f five-dimensional Vlasov simulation. Comput. Phys. Commun. 2008, 179, 391–403. [Google Scholar] [CrossRef]
- Chen, Y.; Parker, S.E. A δf particle method for gyrokinetic simulations with kinetic electrons and electromagnetic perturbations. J. Comput. Phys. 2003, 189, 463–475. [Google Scholar] [CrossRef]
- Gorler, T.; Lapillonne, X.; Brunner, S.; Dannert, T.; Jenko, F.; Merz, F.; Told, D. The global version of the gyrokinetic turbulence code GENE. J. Comput. Phys. 2011, 230, 7053–7071. [Google Scholar] [CrossRef] [Green Version]
- Brizard, A.J. Nonlinear Gyrokinetic Tokamak Physics. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1990. [Google Scholar]
- Brizard, A.J.; Hahm, T.S. Foundations of nonlinear gyrokinetic theory. Rev. Mod. Phys. 2007, 79, 421–468. [Google Scholar] [CrossRef]
- Robert, G.M. Toeplitz and Circulant Matrices: A Review. Found. Trends® Commun. Inf. Theory 2006, 2, 155–239. [Google Scholar]
- SELALIB. Available online: http://selalib.gforge.inria.fr/ (accessed on 4 December 2017).
- Crouseilles, N.; Glanc, P.; Hirstoaga, S.A.; Madaule, E.; Mehrenberger, M.; Pétri, J. A new fully two-dimensional conservative semi-Lagrangian method: Applications on polar grids, from diocotron instability to ITG turbulence. Eur. Phys. J. D 2014, 68, 252. [Google Scholar] [CrossRef]
- Sonnendrücker, E.; Roche, J.; Bertrand, P.; Ghizzo, A. The Semi-Lagrangian Method for the Numerical Resolution of the Vlasov Equation. J. Comput. Phys. 1999, 149, 201–220. [Google Scholar] [CrossRef] [Green Version]
- Grandgirard, V.; Brunetti, M.; Bertrand, P.; Besse, N.; Garbet, X.; Ghendrih, P.; Manfredi, G.; Sarazin, Y.; Sauter, O.; Sonnendrücker, E.; et al. A drift-kinetic Semi-Lagrangian 4D code for ion turbulence simulation. J. Comput. Phys. 2006, 217, 395–423. [Google Scholar] [CrossRef] [Green Version]
- Grandgirard, V.; Sarazin, Y.; Garbet, X.; Dif-Pradalier, G.; Ghendrih, P.; Crouseilles, N.; Latu, G.; Sonnendrücker, E.; Besse, N.; Bertrand, P. Computing ITG turbulence with a full-f semi-Lagrangian code. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 81–87. [Google Scholar] [CrossRef] [Green Version]
- Latu, G.; Mehrenberger, M.; Güçlü, Y.; Ottaviani, M.; Sonnendrücker, E. Field-Aligned Interpolation for Semi-Lagrangian Gyrokinetic Simulations. J. Sci. Comput. 2017. [Google Scholar] [CrossRef]
- Steiner, C.; Mehrenberger, M.; Crouseilles, N.; Grandgirard, V.; Latu, G.; Rozar, F. Gyroaverage operator for a polar mesh. Eur. Phys. J. D 2015, 69, 18. [Google Scholar] [CrossRef]
- Steiner, C.; Mehrenberger, M.; Crouseilles, N.; Philippe, H. Quasi-neutrality equation in a polar mesh. Available online: https://hal.archives-ouvertes.fr/hal-01248179/document (accessed on 4 November 2015).
- Coulette, D.; Besse, N. Numerical comparisons of gyrokinetic multi-water-bag models. J. Comput. Phys. 2013, 248, 1–32. [Google Scholar] [CrossRef]








| Mesh | (16,16) | (32,32) | (64,64) |
|---|---|---|---|
| interpo, | |||
| 2nd, | 0.8738 | 0.9635 | 0.9872 |
| interpo, | |||
| 2nd, | 1.7102 | 1.8882 | 1.9352 |
| Mesh | (16,16) | (32,32) | (64,64) |
|---|---|---|---|
| interpo, | 1.3114 | ||
| 2nd, | 10.2513 | 10.8218 | 11.0119 |
| interpo, | 1.3972 | ||
| 2nd, | 115.6807 | 16.7745 | 17.1429 |
| Mesh | (32,32) | (64,64) |
|---|---|---|
| interpo, | ||
| 2nd, | 0.0 | 0.0 |
| interpo, | ||
| 2nd, | 0.0 | 0.0 |
| Mesh | (32,32) | (64,64) |
|---|---|---|
| interpo, | ||
| interpo, |
| Mesh | (32,32) | (64,64) | (128,128) |
|---|---|---|---|
| Mesh | (32,32) | (64,64) |
|---|---|---|
| 0.1186 | 0.1339 | |
| , num error | |||
| , num error | |||
| solution abs error | 1.3817 | 0.653 | 3.6886 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Mehrenberger, M.; Steiner, C. Computing the Double-Gyroaverage Term Incorporating Short-Scale Perturbation and Steep Equilibrium Profile by the Interpolation Algorithm. Plasma 2019, 2, 91-126. https://doi.org/10.3390/plasma2020009
Zhang S, Mehrenberger M, Steiner C. Computing the Double-Gyroaverage Term Incorporating Short-Scale Perturbation and Steep Equilibrium Profile by the Interpolation Algorithm. Plasma. 2019; 2(2):91-126. https://doi.org/10.3390/plasma2020009
Chicago/Turabian StyleZhang, Shuangxi, Michel Mehrenberger, and Christophe Steiner. 2019. "Computing the Double-Gyroaverage Term Incorporating Short-Scale Perturbation and Steep Equilibrium Profile by the Interpolation Algorithm" Plasma 2, no. 2: 91-126. https://doi.org/10.3390/plasma2020009
APA StyleZhang, S., Mehrenberger, M., & Steiner, C. (2019). Computing the Double-Gyroaverage Term Incorporating Short-Scale Perturbation and Steep Equilibrium Profile by the Interpolation Algorithm. Plasma, 2(2), 91-126. https://doi.org/10.3390/plasma2020009





