Next Article in Journal
Ceramic Stereolithography of Li7La3Zr2O12 Micro-Embossed Sheets for Solid Electrolyte Applications
Previous Article in Journal
A Molecular Dynamics Simulation Study of Crystalline and Liquid MgO
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Ceramics
Volume 7
Issue 3
10.3390/ceramics7030079
ceramics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effect of Prosthetic Material and Support Type on Stress Distribution of Fixed Partial Dentures: A Finite Element Study

by
Jelena Eric
1,*,
Ljiljana Bjelovic
2,
Igor Radovic
2,
Jelena Krunic
2,
Aleksandra Milic-Lemic
3,
Nidhi Gupta
1 and
Kamran Ali
1
1
College of Dental Medicine, QU-Health, Qatar University, Doha P.O. Box 2713, Qatar
2
Faculty of Medicine, University of East Sarajevo, 73300 Foca, Bosnia and Herzegovina
3
School of Dentistry, University of Belgrade, 11000 Belgrade, Serbia
*
Author to whom correspondence should be addressed.
Ceramics 2024, 7(3), 1204-1217; https://doi.org/10.3390/ceramics7030079
Submission received: 25 June 2024 / Revised: 16 August 2024 / Accepted: 6 September 2024 / Published: 8 September 2024
Browse Figures
Versions Notes

Abstract

:
Choosing an appropriate prosthetic material for the superstructure of an implant-supported or tooth-implant supported fixed partial denture (FPD) is crucial for the success of the prostheses. The objective of this study was to examine the effect of prosthetic material type and tooth-to-implant support on stress distribution of FPDs using three-dimensional finite element analysis (3D FEA). Two FEA models were generated, distinguished by their support configurations: Model I representing an FPD supported by implants, and Model II depicting an FPD supported by both a tooth and an implant. Two different restorative materials, porcelain-fused-to-metal (PFM) and monolithic zirconia, were evaluated for stress distribution under axial and oblique loads of 300 N applied to the pontic. Under both axial and oblique loading conditions, the maximum von Mises stress values were observed to be higher in the implant-abutment complex of both zirconia implant-supported and tooth-implant-supported FPDs compared to PFM FPDs. In the case of axial loading, comparable stress values were found in the cortical bone for PFM (12.65 MPa) and zirconia implant-supported FPDs (12.71 MPa). The zirconia tooth-implant-supported FPD exhibited the highest stress values in the implant-abutment system.

1. Introduction

Osseointegrated dental implants have transformed dentistry by providing a remarkable option for those who are missing teeth and enhancing their quality of life to a great extent [1,2]. However, there is an ongoing debate regarding the preference to use self-supporting implants or adjacent natural teeth as abutments [1,2,3,4]. In general, constructing fixed partial dentures (FPDs) using a combination of implants and natural teeth is not recommended [5]. On the other hand, some longitudinal studies have reported acceptable survival rates for FPDs after 5 years and suggested that tooth-implant supported FPDs with rigid connection are a viable option for partial edentulism [6,7].
The selection of an appropriate prosthetic material for the superstructure of an implant-supported FPD is crucial for the overall prognosis of the prosthesis [8,9]. In recent years, zirconia has become a popular choice due to its favorable mechanical properties and advancements in prosthodontic workflows [10]. Zirconia implant-supported single crowns are considered comparable to metal-ceramic restorations [11]. Although a higher percentage of complications have been reported with zirconia FPDs such as chipping, delamination of the ceramic veneering, and framework fracture [12], recent improvements in design and veneer application techniques have addressed these issues, increasing the resistance of the veneer layer to chipping [13,14].
In the posterior molar region, significant chewing forces are encountered, which pose potential risks to both prosthetic components and the surrounding alveolar bone integrity [15]. Such forces may potentially contribute to marginal bone resorption and compromise implant stability, thereby endangering both the implant itself and its superstructures [16]. Furthermore, the design of the prosthesis including the number of abutments, pontic length, connector design, material properties, and occlusal scheme, plays a pivotal role in determining the distribution of forces in the posterior region [17,18,19,20,21,22]. For instance, longer pontics may exert increased bending forces on the abutment teeth or implants, while variations in material stiffness can influence the transmission of forces through the prosthesis and their dispersion to the supporting structures [17,19,20].
Several studies have used finite element analysis (FEA) methodology to examine the influence of various prosthetic materials on stress distribution within the supporting structures of implant- supported FPDs [17,18,19,20,21,22]. In studies conducted by Gungor et al. (2016) and Sotto-Maior et al. (2012), no differences were observed in the distribution of loading in the bone and peri-implant tissue across various prosthetic materials [18,19]. Conversely, research by Meriç et al. (2011), Arinc et al. (2018), and Toussi et al. (2018) reported that the selection of prosthetic material does affect stress distribution at the interface between the bone and implant [20,21,22]. Furthermore, a recent systematic review demonstrated that porcelain-fused-to-metal (PFM) implant-supported prostheses have a higher survival rate compared to zirconia implant-supported prostheses [8]. Despite the contradictory findings in the literature regarding the impact of prosthetic materials on stress distribution in implant-supported FPDs, however, there remains a significant gap regarding the impact of these materials on tooth-implant-supported FPDs [23]. In this regard, understanding the influence of material type, support and pontic length on stress distribution is vital for ensuring the stability of dental prostheses under load and for making well-informed decisions regarding optimal treatment strategies. Additionally, FEA is recognized as an efficacious tool for evaluating stress distribution within restorations fabricated using different materials and designs.
The objective of this study was to examine the effect of prosthetic material type and tooth-to-implant support on the stress distribution of four-unit FPDs using three-dimensional (3D) FEA. The null hypothesis was that the zirconia tooth-implant-supported FPD would exhibit the highest stress values within the implant-abutment complex and induce non-uniform stress distribution in the supporting structures.

2. Materials and Methods

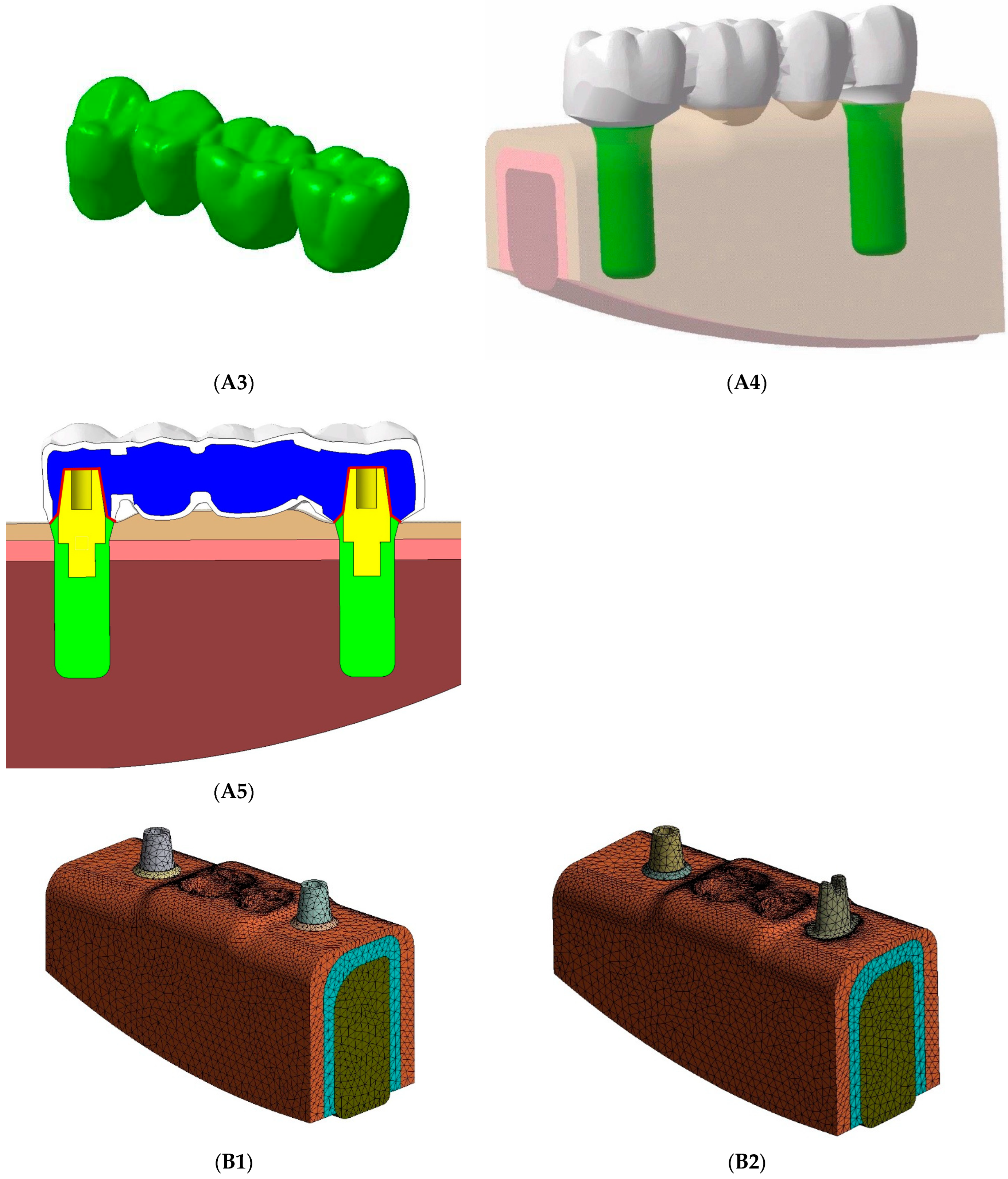
2.1. FE Model Design and Model Generation

This in vitro study was conducted following the guidelines of the Declaration of Helsinki, and the research protocol received approval from the Institutional Ethics Committee of the University of East Sarajevo (No. 01-C-284-XIV\16).
To obtain the implant-supported FPD, two implants (Straumann Standard Plus, 4.1 × 10 mm; Straumann, Basel, Switzerland) were positioned along with their corresponding abutments (non-angled titanium abutments; Straumann, Basel, Switzerland) in autopolymerizing polymethyl-methacrylate acrylic resin (PMMA) (Lucitone Fas-Por plus; Dentsply Caulk) using a surveyor (Ney 133 surveyor; Dentsply Caulk, New York, NY, USA) to ensure their axes were parallel to each other and perpendicular to the floor (Figure 1(A1)) [24]. The distance between the centers of the implants was 20 mm, to replicate a clinical scenario involving a four-unit FPD [25].
To obtain the tooth-implant-supported FPD, initially, an extracted first lower premolar was prepared following a standardized preparation protocol with a high-speed handpiece and diamond rotary cutting instruments with water cooling [26]. Subsequently, the prepared tooth was digitized using a laboratory scanner (ATOS II Rev.01, GOM mbH, Braunschweig, Germany). Following the scanning process, an implant (Straumann Standard Plus, 4.1 × 10 mm; Straumann, Basel, Switzerland) along with its abutment (non-angled titanium abutment, Straumann, Basel, Switzerland) and the tooth were embedded in PMMA (Lucitone Fas-Por plus; Dentsply Caulk). Similarly, the surveyor (Ney 133 surveyor; Dentsply Caulk) was utilized to achieve parallel implant axes (Figure 1(A2)) [24]. Following standardized protocols, implant-supported and tooth-implant supported FPDs were obtained using the traditional lost-wax technique [26]. Subsequently, the four-unit implant-supported and tooth-implant-supported PFM FPDs underwent scanning using the laboratory scanner (ATOS II Rev.01, GOM mbH, Braunschweig, Germany) (Figure 1(A3)), and the resulting computer-aided design (CAD) files were obtained and transferred to CAD software (CATIA v5; Dassault Systems, Paris, France).
3D FEA models of the implant systems were generated using the same software, based on the original geometry of the implant, abutment, and associated components. These models were constructed using solid cylinders with dimensions of 10 mm in length and 4.1 mm in diameter (Figure 1(A4)). The corresponding fastening screws, which were 7 mm long, were securely fixed into the implants. Subsequently, the implants were positioned in the first premolar and second molar locations for the implant-supported model, and in the second molar position for the tooth-implant-supported model. Additionally, a simplified 0.25-mm periodontal ligament (PDL) was created in the CAD software around the first lower premolar, according to the root-form geometry of premolars [24]. The cement used in cemented crown models was represented by a 50-µm-thick layer [19]. Furthermore, alveolar bone (including cortical and cancellous bone) and mucosa were constructed following procedures outlined in the literature [24,27,28,29]. The bone was configured with a rectangular shape, featuring dimensions of 20 mm in height, 10.7 mm in width, and 24.7 mm in lenght. It was symmetrically positioned to ensure adequate dimensions for both the implant and tooth in all directions [24].
Two FEA models were created, distinguished by their support configurations: Model I representing an implant-supported FPD and Model II depicting a tooth-implant-supported FPD. Two distinct restorative materials, PFM and monolithic zirconia, were assessed for stress distribution.
After obtaining the geometries, the models were meshed using 4-node tetrahedral solid elements in ANSYS (ANSYS, Rel. 11.0; ANSYS Inc., Houston, TX, USA). Figure 1A,B show the real and meshed models of the implant-supported and tooth-implant supported FPDs.

2.2. Material Propreties and Boundary Conditions

All materials utilized were considered homogeneous, linear elastic, and isotropic, with their mechanical properties detailed in Table 1, sourced from literature [30,31,32,33].
The boundary constraints of the models were established at the proximal and distal planes of the bone block, while mandibular movement was limited in accordance with the interaction between the mandible and the surrounding muscles. The boundary conditions were set as fixed for all axes (x, y, and z) on the bone block, ensuring zero displacement and/or rotation. To prevent interference with the stress or strain fields related to reaction forces at the bone-implant interface, constraints were imposed on nodes positioned away from the region of interest. In the mathematical model, the implant was assumed to be fully osseointegrated, while the natural tooth displayed mobility within the limits of the periodontal ligament due to its elastic modulus. Occlusal forces applied in the models consisted of axial and oblique forces of 300 N acting on the pontic, with 100 N applied to the second premolar and 200 N to the first molar in all models (Figure 1(B4)) [20,29]. The occlusal scheme utilized in this study was mutually protected occlusion with cusp-fossa contact. The oblique load was applied at a 30° angle to the long axis [21,34,35]. Bone-implant contact was presumed to be completely osseointegrated. Stress analysis was conducted using FEA software (ANSYS, Rel. 11.0; ANSYS Inc., Houston, TX, USA). Maximum von Mises stress values and stress distributions in the implants, tooth, and alveolar bone were documented for all models and compared among them. Numeric values were used because von Mises stress provides scalar values that represent the yield conditions under particular loading circumstances.

2.3. Verification and Validation of the FE Models

To validate the FE model, five different models were created for each prosthetic system, featuring varying numbers of elements and mesh densities, as outlined in previous literature [20,24,30]. A convergence test was performed to assess discretization accuracy, utilizing the maximum von Mises stresses in the cortical bone under axial loading. A tolerance of 1% was employed, where changes of less than 1% in the maximum von Mises stresses in the cortical bone indicated convergence. Following the convergence test with mesh refinements, the implant-supported FPD comprised 987,533 nodes and 681,100 elements, while the tooth-implant supported FPD consisted of 1,492,513 nodes and 932,074 elements. The tooth-implant-supported FPD required a finer mesh with a larger number of elements due to the intricate geometry of the premolar tooth and the need to accurately capture its detailed features.

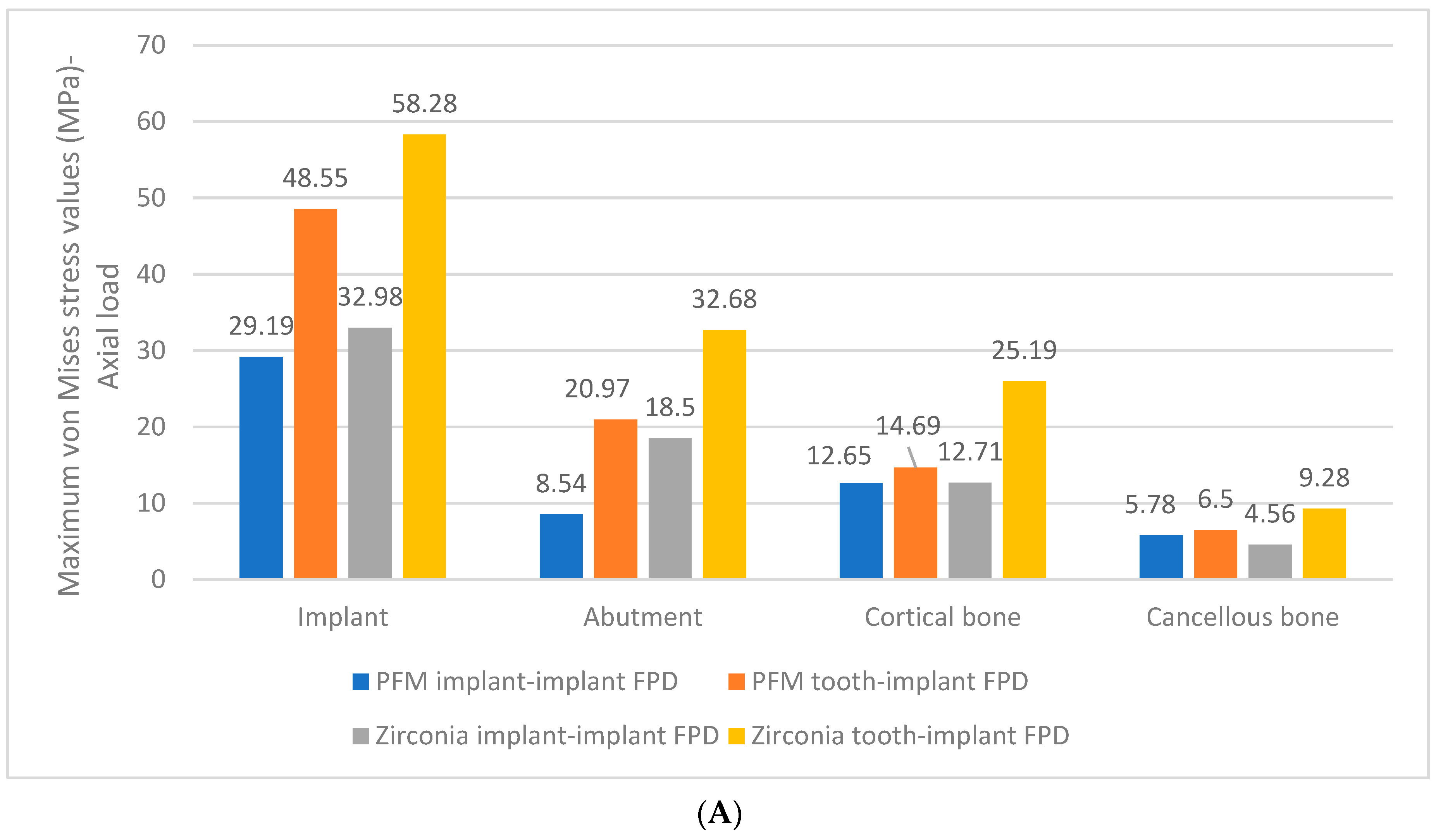
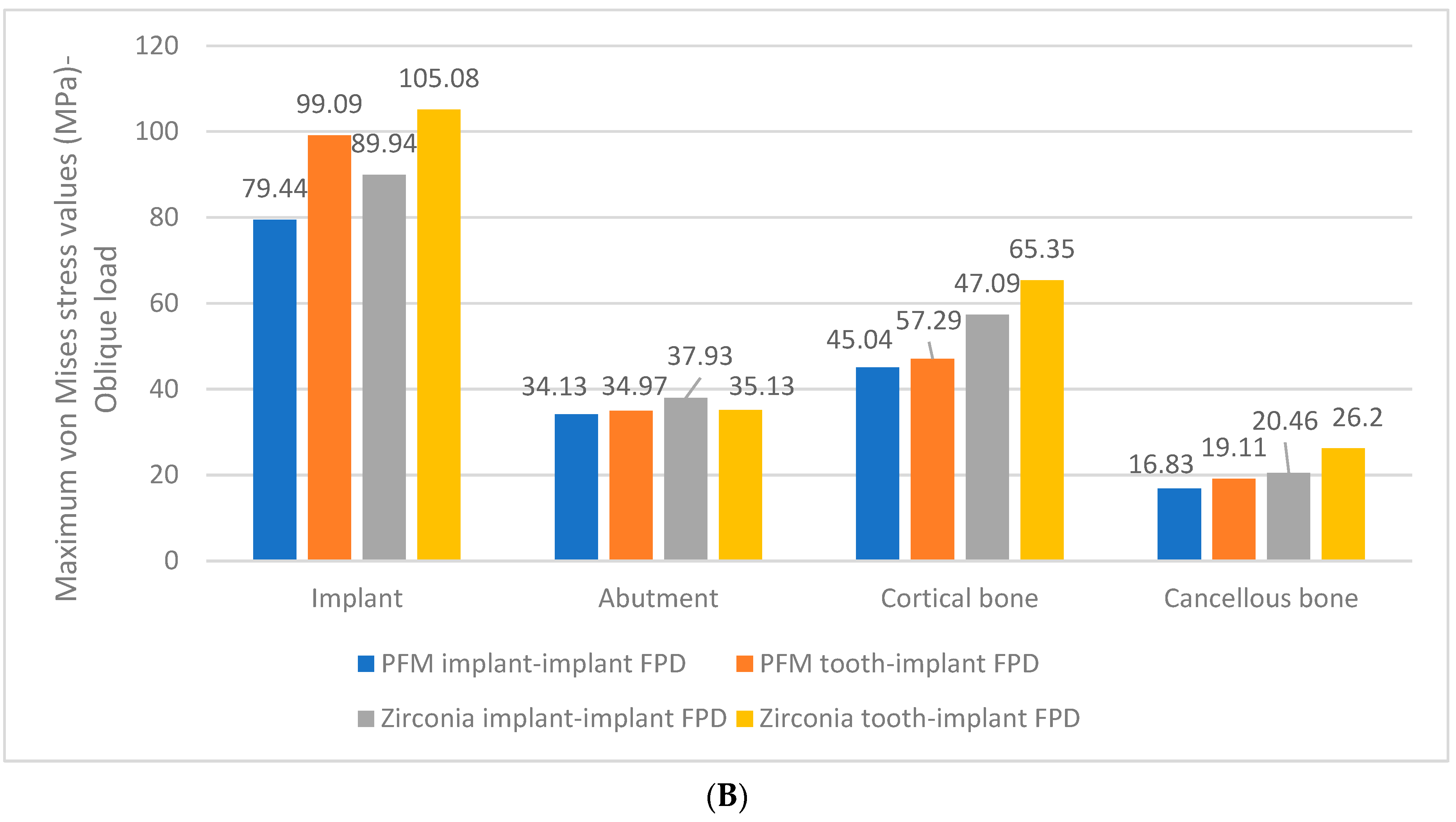
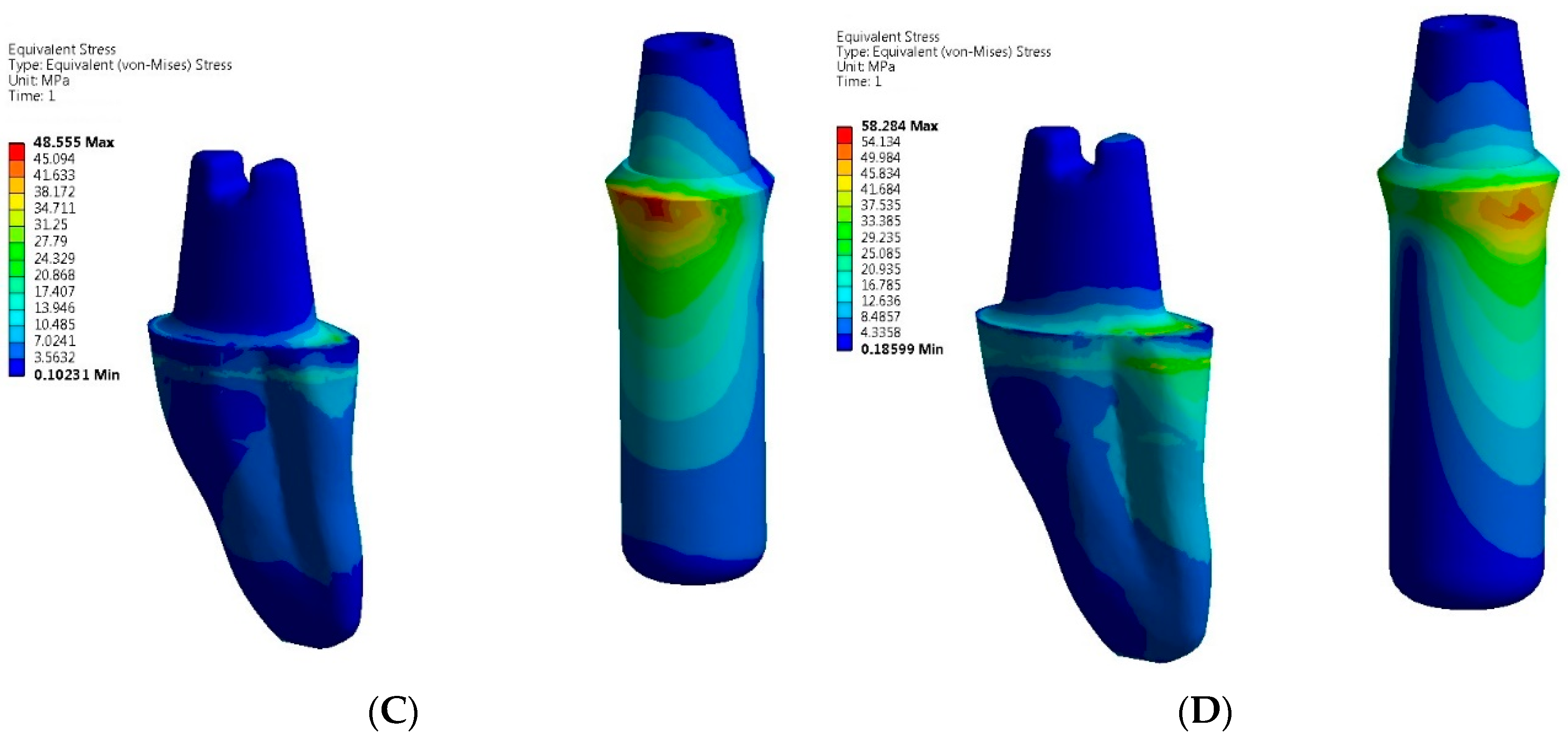
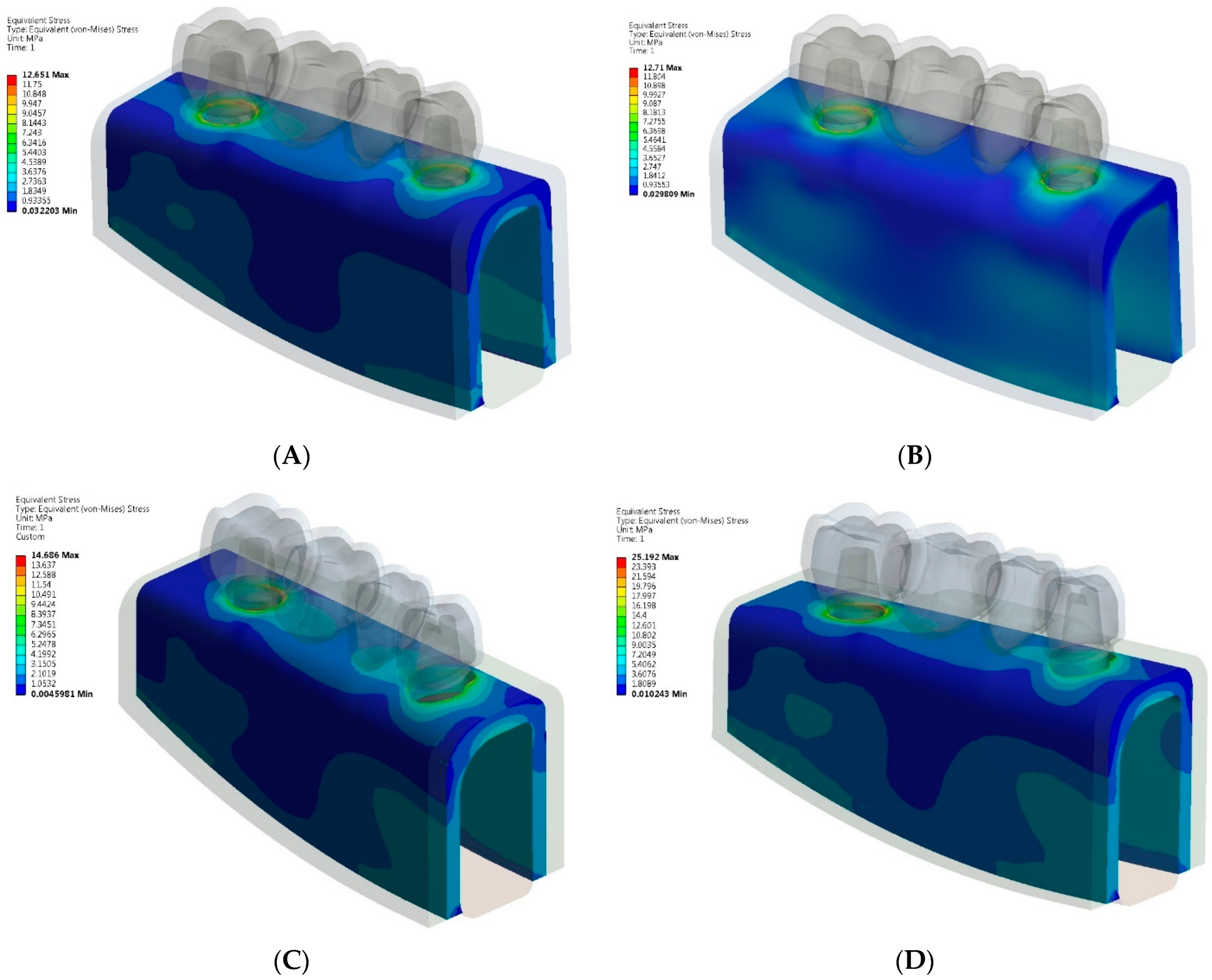
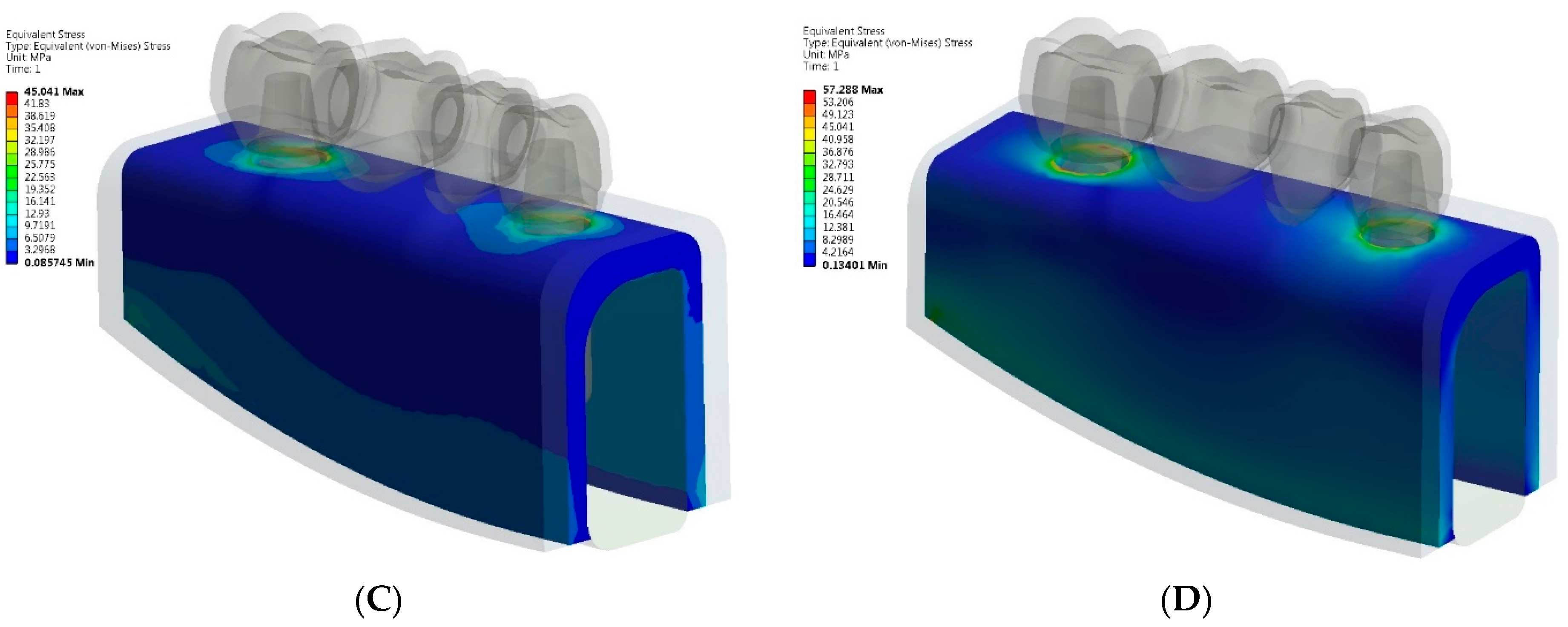
3. Results

In the models of implant-supported FPDs, the maximum von Mises stress value (32.98 MPa) in the implant-abutment complex was higher for the zirconia FPD compared to the PFM FPD under axial loading conditions (Figure 2A).
Similarly, in the models of tooth-implant supported FPDs under axial loading, a comparable stress distribution pattern was observed, with the stress value in the implant-abutment system being greater for the zirconia tooth-implant-supported FPD than for the zirconia implant-supported FPD (Figure 2A,B). However, notable discrepancies in stress values were noted under oblique loading, where the maximum von Mises stress value was approximately 2 to 2.5 times greater under oblique loading compared to axial loading (Figure 2B). Under oblique loading conditions, the maximum von Mises stress values were also increased in the implant-abutment complex for both zirconia implant-supported and tooth-implant-supported FPDs compared to PFM FPDs (Figure 2B).
Under both loading conditions, the highest stress value was localized at the neck area of implants in the zirconia implant-supported FPD, whereas the peak stress was found at the cervical region of the implant in the tooth-implant-supported FPD models (Figure 3 and Figure 4).
In both implant-supported and tooth-implant-supported FPD models, the greatest von Mises stress values in the mandibular bone were concentrated in the cortical bone around the implant neck (Figure 5 and Figure 6).
When comparing the von Mises stress values in the cortical bone under axial loading, similar maximum stress values were observed for PFM and zirconia implant-supported FPDs, while the zirconia tooth-implant-supported FPD model exhibited nearly twice the stress value in the cortical bone compared to the PFM tooth-implant-supported FPD model (Figure 2A). Conversely, under oblique loading, the greatest stress value (65.35 MPa) was located at the cortical ridge of the implant neck in the zirconia tooth-implant-supported FPD (Figure 2B). Overall, oblique occlusal force led to increased stress relative to axial loading.

4. Discussion

The findings of this research indicate that the choice of prosthetic material influences the stress distributions in the implant-abutment complex and the surrounding bone of both implant and tooth-implant-supported FPDs.
Under both axial and oblique loads of 300 N applied to the pontic, the zirconia implant-supported and tooth-implant-supported FPD models exhibited higher stress values in the implant-abutment system compared to PFM FPD models. These results align with those reported by Arinc (2018), who observed the highest stress values in the implant-abutment complex of 3-unit implant-supported FPDs in the zirconia model compared to ceramic veneered Co-Cr and composite veneer models [21]. Similarly, Toussi et al. (2018) reported that the maximum von Mises stress value in the implant of an implant-supported single crown was highest in the in-ceram zirconia model under both loading conditions [22]. In contrast, Sotto-Maior et al. [19] found that the stress concentration in the supporting structures was unaffected by the choice of restorative material, with no differences observed between metal-ceramic and all-ceramic crowns. The authors focused on a single posterior crown supported by a short implant and suggested that variations in implant length and material properties might explain discrepancies in the literature [19]. In our study, however, we observed that the choice of prosthetic material influenced stress distribution in the supporting structures of four-unit implant-supported and tooth-implant-supported FPDs. This effect can be attributed to the fact that the pontic length and material stiffness can affect stress distribution wherein materials with higher stiffness attract greater loads due to their increased resistance to deformation. Zirconia is known for its high modulus of elasticity and stiffness, which can result in less flexibility. Longer pontics may exert increased bending forces and consequently greater transmission of stress to the surrounding structures, including the implant-abutment complex.
Furthermore, our analysis revealed the greatest stress accumulation in the zirconia tooth-implant supported FPD. These findings are in line with clinical studies reporting implant survival rates of 95.4% at 5 years and 92.8% at 10 years for implant-supported FPDs, whereas tooth-implant supported restorations exhibited lower survival rates of 90.1% at 5 years and 82.1% at 10 years [36,37]. This difference in survival rates may be attributed to the biomechanical mismatch between implants and natural teeth [3,31] as well as the non-uniform distribution of occlusal forces between the tooth and the implant in tooth-implant supported FPDs, resulting in localized stress concentrations. In such FPDs, the connector may require a complex design to accommodate both the implant and the natural tooth, potentially contributing to increased stress accumulation. Moreover, zirconia and PFM possess distinct mechanical properties, with zirconia being characterized by its high stiffness, which leads to more direct and less uniform stress transmission compared to PFM.
In this study, the peak von Mises stress value was concentrated at the neck area of implants in the implant-supported FPD, whereas the highest stress value was observed at the cervical region of the implant in the tooth-implant-supported FPD models. These findings are consistent with previous studies that also reported excessive stress accumulation primarily around the neck of implants [22,31,34,38,39]. This phenomenon can be attributed to the deformation of the periodontal ligament in response to the application of a static load on the tooth. As a result, the tooth tends to sink into the alveoli, causing the fixed prosthesis to function like a cantilever on the implant, leading to stress concentration around the implant neck [22].
The analysis of stress distribution in the mandibular bone under both loading conditions revealed higher stress levels on the cortical bone near the implant neck. This observation aligns with findings from several other studies [9,17,21,34,40] and may arise from discrepancies between the elastic modulus of the implant and the bone, leading to stress shielding or concentration on the bone-implant interfaces. Additionally, similar stress values were observed in the cortical bone around the implant neck in both zirconia and PFM implant-supported FPDs. This finding is consistent with previous studies, indicating that the use of different prosthetic materials for superstructure fabrication does not significantly affect stress distribution in the supporting bone [9,18,19]. Conversely, the zirconia tooth-implant-supported FPD model exhibited higher stress values in the bone-implant interface compared to the PFM tooth-implant-supported FPD model, under both axial and oblique loading. This discrepancy may be attributed to the biomechanical mismatch of the supporting units [3,31], which affects the transmission of stresses to the underlying supporting tissue. In this regard, under functional loading, the rigid implant may absorb more force than the adjacent tooth, potentially leading to increased stress concentration at the bone-implant interface or around the implant neck. Conversely, the mobility of the natural tooth may result in altered force distribution and transmission to the surrounding bone, affecting the overall biomechanics of the prosthesis. This biomechanical mismatch between dental implants and natural teeth can disrupt the balance of forces within the supporting tissues, potentially causing variations in stress distribution and increased the risk of biomechanical complications such as bone resorption or implant failure [3,5,6,7,8].
Furthermore, the stress values induced in the supporting tissues of all models under oblique load were increased due to the lateral bending moment generated by oblique occlusal force, which substantially increased stress levels. These findings are consistent with previous studies [19,34,41] indicating that traumatic occlusion is the primary contributor to biomechanical complications, peri-implant bone loss, and eventual implant failure.
The study was designed to simulate clinical scenarios involving the use of implants alone and in combination with a tooth as support. Based on the study’s results, it can be speculated that in clinical situations where FPDs are supported by both implants and natural teeth, clinicians should focus on designing the occlusal morphology to favor dominant axial loading. Minimizing oblique loading through proper occlusal adjustments would further help counteract the unfavorable properties of the restorative material. Additionally, when deciding whether to connect a tooth and implant with an FPD, it is important to consider the choice of restorative material, as our finding suggest that a less rigid material may be beneficial in such clinical situations. Moreover, the quality and volume of the surrounding cortical bone are crucial, as increased stress at the implant-bone interface may impact long-term success.
This study showed that FEA is a valuable tool for examining stress distribution in the supporting structures of four-unit PFM and zirconia implant and tooth-implant supported FPD. However, despite providing reliable results and offering cost advantages over physical specimen testing, 3D numerical simulations do have inherent limitations. The bone structure was modeled as isotropic, homogeneous, and possessing linear elastic behavior, whereas in reality, the mandibular bone features transverse isotropy (anisotropy) and heterogeneous properties. Additionally, the implants were presumed to be perfectly osseointegrated to the bone, although achieving 100% bone-to-implant contact may not always be feasible. Future research should focus on enhancing the accuracy of simulations of the oral environment to achieve more precise outcomes. Nevertheless, this study provides important foundational data to inform future research in this field.

5. Conclusions

Considering the constraints of the present FEA research, the following conclusions were reached:
  • The greatest von Mises stress values were higher in zirconia implant and tooth-implant FPDs compared to PFM FPDs under both axial and oblique loading scenarios.
  • The zirconia tooth-implant-supported FPD demonstrated the highest recorded stress values within the implant-abutment system.
  • Peak stresses were localized at the neck of the implants in both zirconia implant and tooth-implant supported FPDs, with the highest stress values observed at these sites.
  • Comparable maximum stress levels were noted in the cortical bone for both PFM and zirconia implant-supported FPDs. However, the zirconia tooth-implant-supported FPD model demonstrated nearly double the stress value in the cortical bone relative to the PFM tooth-implant-supported FPD model.
  • Greater maximum von Mises stresses were identified in the cortical bone as opposed to the cancellous bone, irrespective of the prosthetic material used.
  • Based on the stress distribution patterns, PFM FPDs are identified as the preferred option for multiple-unit tooth-implant-supported FPDs.

Author Contributions

Conceptualization, J.E. and L.B.; Clinical relevance data acquisition, J.E. and J.K.; Methodology, J.E. and I.R.; Resources, J.E.; Writing—original draft preparation, J.E. and N.G.; Writing—review and editing, K.A. and A.M.-L. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Ethics Committee of the University of East Sarajevo (No. 01-C-284-XIV\16) for studies involving human material.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Pjetursson, B.E.; Heimisdottir, K. Dental implants–Are they better than natural teeth? Eur. J. Oral Sci. 2018, 126, 81–87. [Google Scholar] [CrossRef] [PubMed]
  2. Becker, C.M.; Kaiser, D.A.; Jones, J.D. Guidelines for splinting implants. J. Prosthet. Dent. 2000, 84, 210–214. [Google Scholar] [CrossRef] [PubMed]
  3. von Stein-Lausnitz, M.; Nickenig, H.J.; Wolfart, S.; Neumann, K.; von Stein-Lausnitz, A.; Spies, B.C.; Beuer, F. Survival rates and complication behaviour of tooth implant-supported, fixed dental prostheses: A systematic review and meta-analysis. J. Dent. 2019, 88, 103167. [Google Scholar] [CrossRef] [PubMed]
  4. Rungsiyakull, C.; Chen, J.; Rungsiyakull, P.; Li, W.; Swain, M.; Li, Q. Bone’s responses to different designs of implant-supported fixed partial dentures. Biomech. Model Mechanobiol. 2015, 14, 403–411. [Google Scholar] [CrossRef] [PubMed]
  5. Lang, N.P.; Pjetursson, B.E.; Tan, K.; Bragger, U.; Egger, M.; Zwahlen, M. A systematic review of the survival and complication rates of fixed partial dentures (FPDs) after an observation period of at least 5 years. II. Combined tooth-implant-supported FPDs. Clin. Oral Implants Res. 2004, 15, 643–653. [Google Scholar] [CrossRef]
  6. Gunne, J.; Astrand, P.; Lindh, T.; Borg, K.; Olsson, M. Tooth-implant and implant supported fixed partial dentures: A 10-year report. Int. J. Prosthodont. 1999, 12, 216–221. [Google Scholar]
  7. Olsson, M.; Gunne, J.; Astrand, P.; Borg, K. Bridges supported by free-standing implants versus bridges supported by tooth and implant. Clin. Oral Implant. Res. 1995, 6, 114–121. [Google Scholar] [CrossRef]
  8. Pjetursson, B.E.; Brägger, U.; Lang, N.P.; Zwahlen, M. Comparison of survival and complication rates of tooth-supported fixed dental prostheses (FDPs) and implant-supported FDPs and single crowns (SCs). Clin. Oral Implant. Res. 2007, 18, 97–113. [Google Scholar] [CrossRef]
  9. Vieira, F.R.; Bitencourt, S.B.; Rosa, C.D.D.R.D.; Vieira, A.B.; Santos, D.M.D.; Goiato, M.C. Influence of Different Restoring Materials on Stress Distribution in Prosthesis on Implants: A Review of Finite Element Studies. Eur. J. Dent. 2023, 17, 1–6. [Google Scholar] [CrossRef]
  10. Arena, A.; Prete, F.; Rambaldi, E.; Bignozzi, M.C.; Monaco, C.; Fiore, A.D.; Chevalier, J. Nanostructured Zirconia-Based Ceramics and Composites in Dentistry: A State-of-the-Art Review. Nanomaterials 2019, 9, 1393. [Google Scholar] [CrossRef]
  11. Sailer, I.; Strasding, M.; Valente, M.; Zwahlen, M.; Liu, S.; Pjetursson, B.E. A systematic review of the survival and complication rates of zirconia-ceramic and metal-ceramic multiple-unit fixed dental prostheses. Clin. Oral Implant. Res. 2018, 29, 184–198. [Google Scholar] [CrossRef] [PubMed]
  12. Monaco, C.; Caldari, M.; Scotti, R. Clinical Evaluation of Zirconia-Based Restorations on Implants: A Retrospective Cohort Study from the AIOP Clinical Research Group. Int. J. Prosthodont. 2016, 28, 239–242. [Google Scholar] [CrossRef] [PubMed]
  13. Rexhepi, I.; Santilli, M.; D’Addazio, G.; Tafuri, G.; Manciocchi, E.; Caputi, S.; Sinjari, B. Clinical applications and mechanical properties of CAD-CAM materials in restorative and prosthetic dentistry: A systematic review. J. Funct. Biomater. 2023, 14, 431. [Google Scholar] [CrossRef]
  14. Muller, D.; Rues, S. In vitro chipping behaviour of all-ceramic crowns with a zirconia framework and feldspathic veneering: Comparison of CAD/CAM-produced veneer with manually layered veneer. J. Oral Rehabil. 2013, 40, 519–525. [Google Scholar]
  15. Ishigaki, S.; Nakano, T.; Yamada, S.; Nakamura, T.; Takashima, F. Biomechanical stress in bone surrounding an implant under simulated chewing. Clin. Oral Implant. Res. 2003, 14, 97–102. [Google Scholar] [CrossRef]
  16. Miyata, T.; Kobayashi, Y.; Araki, H.; Ohto, T.; Shin, K. The influence of controlled occlusal overload on peri-implant tissue. Part 3: A histologic study in monkeys. Int. J. Oral Maxillofac. Implant. 2000, 15, 425–431. [Google Scholar]
  17. Ciftçi, Y.; Canay, S. Stress distribution on the metal framework of the implant-supported fixed prosthesis using different veneering materials. Int. J. Prosthodont. 2001, 14, 406–411. [Google Scholar]
  18. Gungor, M.B.; Yilmaz, H. Evaluation of stress distributions occurring on zirconia and titanium implant-supported prosthesis: A three-dimensional finite element analysis. J. Prosthet. Dent. 2016, 116, 346–355. [Google Scholar] [CrossRef] [PubMed]
  19. Sotto-Maior, B.S.; Senna, P.M.; da Silva, W.J.; Rocha, E.P.; Del Bel Cury, A.A. Influence of crown-to-implant ratio, retention system, restorative material, and occlusal loading on stress concentrations in single short implants. Int. J. Oral Maxillofac. Implant. 2012, 27, e13–e18. [Google Scholar]
  20. Meriç, G.; Erkmen, E.; Kurt, A.; Eser, A. Influence of prosthesis type and material on the stress distribution in bone around implants: A 3-dimensional finite element analysis. J. Dent. Sci. 2011, 6, 25–32. [Google Scholar] [CrossRef]
  21. Arinc, H. Effects of Prosthetic Material and Framework Design on Stress Distribution in Dental Implants and Peripheral Bone: A Three-Dimensional Finite Element Analysis. Med. Sci. Monit. 2018, 24, 4279–4287. [Google Scholar] [CrossRef] [PubMed]
  22. Toussi, C.A.; Ezatpour, H.R.; Haddania, J.; Shiri, J.G. Effect of using different metal and ceramic materials as restorations on stress distribution around dental implants: A comparative finite element study. Mater. Res. Express 2018, 5, 11. [Google Scholar]
  23. Jain, H.; Kalra, T.; Kumar, M.; Bansal, A.; Jain, D. Three-Dimensional Finite Element Analysis to Evaluate Stress Distribution in Tooth and Implant Supported Fixed Partial Denture–An In Vitro Study. Dent. J. Adv. Stud. 2020, 8, 84–91. [Google Scholar] [CrossRef]
  24. Tsouknidas, A.; Giannopoulos, D.; Savvakis, S.; Michailidis, N.; Evdokia, L.; Fytanidis, D.; Pissiotis, A.; Michalakis, K. The influence of bone’s quality on the biomechanical behavior of a tooth-implant fixed partial denture. A 3D Finite Element Analysis (FEA). Int. J. Oral Maxillofac. Implant. 2016, 31, e143–e154. [Google Scholar] [CrossRef]
  25. Rand, A.; Kohorst, P.; Greuling, A.; Borchers, L.; Stiesch, M. Stress distribution in all-ceramic posterior 4-unit fixed dental prosthesis supported in different ways: Finite element analysis. Implant Dent. 2016, 25, 485–491. [Google Scholar] [CrossRef] [PubMed]
  26. Rosenstiel, S.F.; Land, M.F.; Fujimoto, J. Contemporary Fixed Prosthodontics, 3rd ed.; Mosby: Maryland Heights, MO, USA, 2001. [Google Scholar]
  27. Stegaroiu, R.; Kusakari, H.; Nishiyama, S.; Miyakawa, O. Influence of prosthesis material on stress distribution in bone and implant: A 3- dimensional finite element analysis. Int. J. Oral Maxillofac. Implant. 1998, 13, 781–790. [Google Scholar]
  28. Tada, S.; Stegaroiu, R.; Kitamurs, E.; Miyakawa, O.; Kusakari, H. Influence of implant design and bone quality on stress/strain distribution in bone around implants: A 3-dimensional finite element analysis. Int. J. Oral Maxillofac. Implant. 2003, 18, 357–368. [Google Scholar]
  29. Huang, L.S.; Huang, Y.C.; Yuan, C.; Ding, S.J.; Yan, M. Biomechanical evaluation of bridge span with three implant abatment designs and two connectors for tooth-implant supported prosthesis: A finite element analysis. J. Dent. Sci. 2023, 18, 248–263. [Google Scholar] [CrossRef] [PubMed]
  30. Li, W.; Swain, M.V.; Li, Q.; Ironside, J.; Steven, G.P. Fibre reinforced composite dental bridge. Part II: Numerical investigation. Biomaterials 2004, 25, 4995–5001. [Google Scholar] [CrossRef]
  31. Lin, C.h.L.; Wang, J.C.h.; Chang, W.J. Biomechanical interactions in tooth–implant-supported fixed partial dentures with variations in the number of splinted teeth and connector type: A finite element analysis. Clin. Oral Implant. Res. 2008, 19, 107–117. [Google Scholar] [CrossRef]
  32. Alberto, L.H.J.; Kalluri, L.; Esquivel-Upshaw, J.F.; Duan, Y. Three-dimensional finite element analysis of different connector designs for all-ceramic implant-supported fixed dental prostheses. Ceramics 2022, 5, 34–43. [Google Scholar] [CrossRef]
  33. Ebadian, B.; Fathi, A.; Tabatabaei, S. Stress distribution in 5-unit fixed partial dentures with a pier abutment and Rigid and Nonrigid Connectors with Two Different Occlusal Schemes: A Three-Dimensional Finite Element Analysis. Int. J. Dent. 2023, 3347197. [Google Scholar] [CrossRef]
  34. Jae-Hyun, L.; Jang, H.Y.; Lee, S.Y. Finite Element Analysis of Dental Implants with Zirconia Crown Restorations: Conventional Cement-Retained vs. Cementless Screw-Retained. Materials 2021, 14, 2666. [Google Scholar] [CrossRef] [PubMed]
  35. Degirmenci, K.; Kocak-Buyukdere, A.; Ekici, B. Evaluation of reliability of zirconia materials to be used in implant-retained restoration on the atrophic bone of the posterior maxilla: A finite element study. J. Adv. Prosthodont. 2019, 11, 112–119. [Google Scholar] [CrossRef] [PubMed]
  36. Pjetursson, B.E.; Tan, K.; Lang, N.P.; Bragger, U.; Egger, M.; Zwahlen, M. A systematic review of the survival and complication rates of fixed partial dentures (FPDs) after an observation period of at least 5 years. I. Implant-supported FPDs. Clin. Oral Implant. Res. 2004, 15, 625–642. [Google Scholar] [CrossRef]
  37. Weber, H.P.; Zimering, Y. Survival and complication rates of fixed partial dentures supported by a combination of teeth and implants. J. Evid. Based Dent. Pract. 2010, 10, 58–60. [Google Scholar] [CrossRef]
  38. Gomes, E.A.; Assunção, W.G.; Tabata, L.F.; Barão, V.A.; Delben, J.A.; de Sousa, E.A. Effect of passive fit absence in the prosthesis/implant/retaining screw system: A two-dimensional finite element analysis. J. Craniofacial Surg. 2009, 20, 2000–2005. [Google Scholar] [CrossRef]
  39. Menicucci, G.; Mossolov, A.; Mozzati, M.; Lorenzetti, M.; Preti, G. Tooth-implant connection: Some biomechanical aspects based on finite element analyses. Clin. Oral Implant. Res. 2002, 13, 334–341. [Google Scholar] [CrossRef]
  40. Zhang, C.; Zeng, C.; Wang, Z.; Zeng, T.; Wang, Y. Optimization of stress distribution of bone-implant interface. Biomater. Adv. 2023, 147, 213342. [Google Scholar] [CrossRef]
  41. Alemayehu, D.B.; Jeng, Y.R. Three-Dimensional Finite Element Investigation into Effects of Implant Thread Design and Loading Rate on Stress Distribution in Dental Implants and Anisotropic Bone. Materials 2021, 14, 6974. [Google Scholar] [CrossRef]
Ceramics 07 00079 g001aCeramics 07 00079 g001bCeramics 07 00079 g001c
Figure 1. (A). Physical specimens of a 3D FE implant-supported FPD (A1) and a tooth-implant supported FPD (A2); a scan of a four-unit PFM FPD (A3); a 3D model of an implant-supported FPD (A4); and a cross-sectional view of a 3D FE PFM implant-supported FPD (A5). (B). Mesh models of a 3D FE implant-supported FPD and a tooth-implant supported FPD (B1–B3); schematic illustration of the axial and oblique loads applied to the pontic (B4). ■ mucosa; ■ cortical bone; ■ cancellous bone; ■ axial load; ■ oblique load.
Figure 1. (A). Physical specimens of a 3D FE implant-supported FPD (A1) and a tooth-implant supported FPD (A2); a scan of a four-unit PFM FPD (A3); a 3D model of an implant-supported FPD (A4); and a cross-sectional view of a 3D FE PFM implant-supported FPD (A5). (B). Mesh models of a 3D FE implant-supported FPD and a tooth-implant supported FPD (B1–B3); schematic illustration of the axial and oblique loads applied to the pontic (B4). ■ mucosa; ■ cortical bone; ■ cancellous bone; ■ axial load; ■ oblique load.
Ceramics 07 00079 g001aCeramics 07 00079 g001bCeramics 07 00079 g001c
Ceramics 07 00079 g002aCeramics 07 00079 g002b
Figure 2. Maximum von Mises stress values (MPa) in the supporting structures under 300 N axial (A) and oblique (B) loads.
Figure 2. Maximum von Mises stress values (MPa) in the supporting structures under 300 N axial (A) and oblique (B) loads.
Ceramics 07 00079 g002aCeramics 07 00079 g002b
Ceramics 07 00079 g003aCeramics 07 00079 g003b
Figure 3. Color-coded von Mises stress distributions in the implants, abutments and tooth under a 300 N axial load: (A) PFM implant FPD; (B) zirconia implant FPD; (C) PFM tooth-implant FPD and (D) zirconia tooth-implant FPD models.
Figure 3. Color-coded von Mises stress distributions in the implants, abutments and tooth under a 300 N axial load: (A) PFM implant FPD; (B) zirconia implant FPD; (C) PFM tooth-implant FPD and (D) zirconia tooth-implant FPD models.
Ceramics 07 00079 g003aCeramics 07 00079 g003b
Ceramics 07 00079 g004
Figure 4. Color-coded von Mises stress distributions in the implants-abutment complex and tooth under a 300 N oblique load: (A) PFM implant FPD; (B) zirconia implant FPD; (C) PFM tooth-implant FPD and (D) zirconia tooth-implant FPD models.
Figure 4. Color-coded von Mises stress distributions in the implants-abutment complex and tooth under a 300 N oblique load: (A) PFM implant FPD; (B) zirconia implant FPD; (C) PFM tooth-implant FPD and (D) zirconia tooth-implant FPD models.
Ceramics 07 00079 g004
Ceramics 07 00079 g005
Figure 5. Color-coded von Mises stress distributions in the peri-implant bone under a 300 N axial load: (A) PFM implant FPD; (B) zirconia implant FPD; (C) PFM tooth-implant FPD and (D) zirconia tooth-implant FPD models.
Figure 5. Color-coded von Mises stress distributions in the peri-implant bone under a 300 N axial load: (A) PFM implant FPD; (B) zirconia implant FPD; (C) PFM tooth-implant FPD and (D) zirconia tooth-implant FPD models.
Ceramics 07 00079 g005
Ceramics 07 00079 g006aCeramics 07 00079 g006b
Figure 6. Color-coded von Mises stress distributions in the peri-implant bone under 300 N oblique load: (A) PFM implant FPD; (B) zirconia implant FPD; (C) PFM tooth-implant FPD and (D) zirconia tooth-implant FPD models.
Figure 6. Color-coded von Mises stress distributions in the peri-implant bone under 300 N oblique load: (A) PFM implant FPD; (B) zirconia implant FPD; (C) PFM tooth-implant FPD and (D) zirconia tooth-implant FPD models.
Ceramics 07 00079 g006aCeramics 07 00079 g006b
Table 1. Material properties assigned to implant material, dental tissues, prosthesis and alveolar bone.
Table 1. Material properties assigned to implant material, dental tissues, prosthesis and alveolar bone.
MaterialsYoung’s Modulus (GPa)Poisson’s Ratio
Titanium1100.35
Ni-Cr alloy2040.30
Corticale bone13.70.30
Cancellous bone1.370.30
Dentin18.60.31
Periodontal ligament690.45
Feldspathic porcelain0.0690.35
Monolithic zirconia2200.30
Resin cement8.30.30
Mucosa0.340.45
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Eric, J.; Bjelovic, L.; Radovic, I.; Krunic, J.; Milic-Lemic, A.; Gupta, N.; Ali, K. Effect of Prosthetic Material and Support Type on Stress Distribution of Fixed Partial Dentures: A Finite Element Study. Ceramics 2024, 7, 1204-1217. https://doi.org/10.3390/ceramics7030079

AMA Style

Eric J, Bjelovic L, Radovic I, Krunic J, Milic-Lemic A, Gupta N, Ali K. Effect of Prosthetic Material and Support Type on Stress Distribution of Fixed Partial Dentures: A Finite Element Study. Ceramics. 2024; 7(3):1204-1217. https://doi.org/10.3390/ceramics7030079

Chicago/Turabian Style

Eric, Jelena, Ljiljana Bjelovic, Igor Radovic, Jelena Krunic, Aleksandra Milic-Lemic, Nidhi Gupta, and Kamran Ali. 2024. "Effect of Prosthetic Material and Support Type on Stress Distribution of Fixed Partial Dentures: A Finite Element Study" Ceramics 7, no. 3: 1204-1217. https://doi.org/10.3390/ceramics7030079

APA Style

Eric, J., Bjelovic, L., Radovic, I., Krunic, J., Milic-Lemic, A., Gupta, N., & Ali, K. (2024). Effect of Prosthetic Material and Support Type on Stress Distribution of Fixed Partial Dentures: A Finite Element Study. Ceramics, 7(3), 1204-1217. https://doi.org/10.3390/ceramics7030079

Article Metrics

Back to TopTop