Plasma Actuators Based on Alumina Ceramics for Active Flow Control Applications
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Microstructure of the Fabricated Ceramics
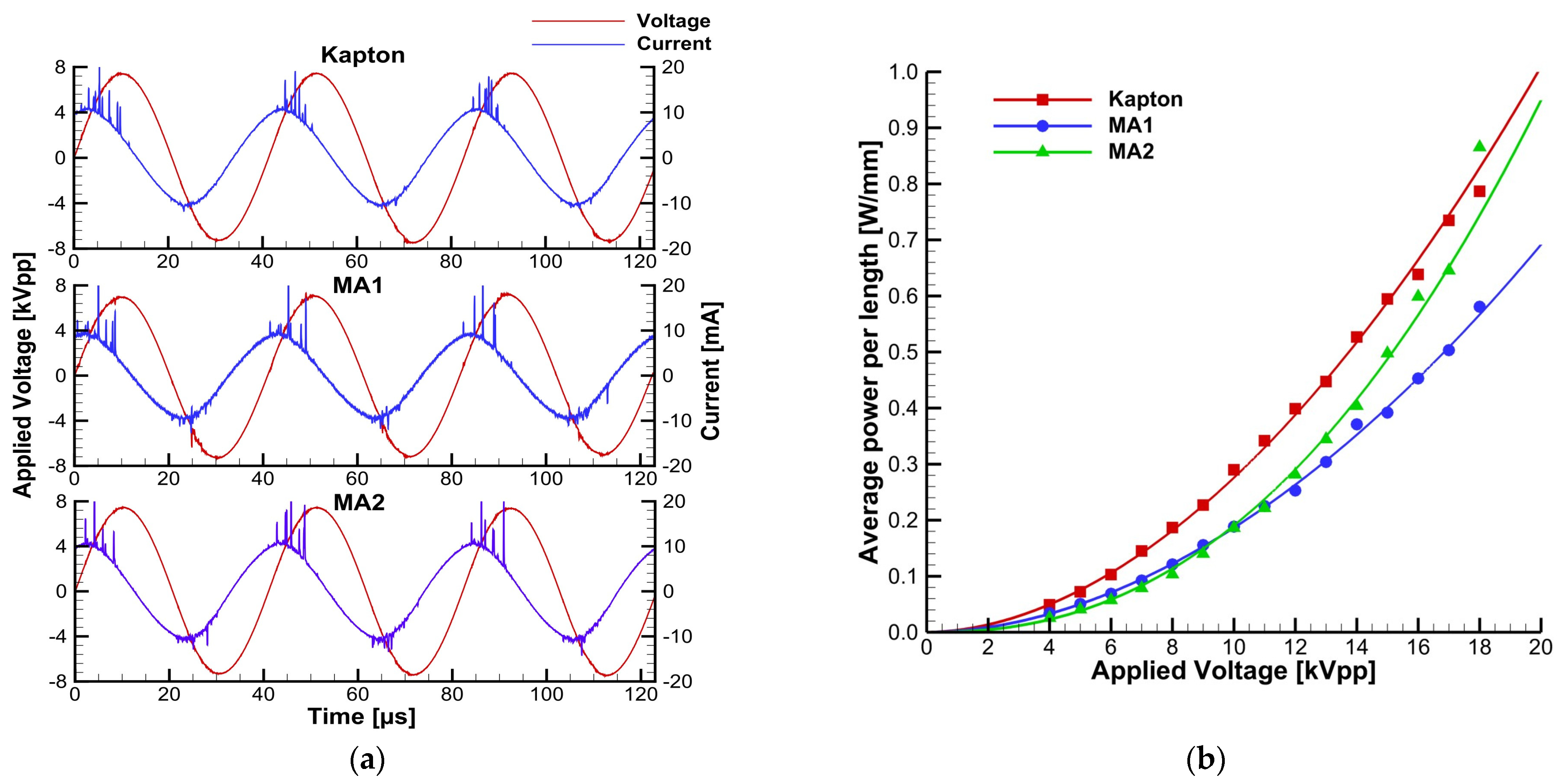
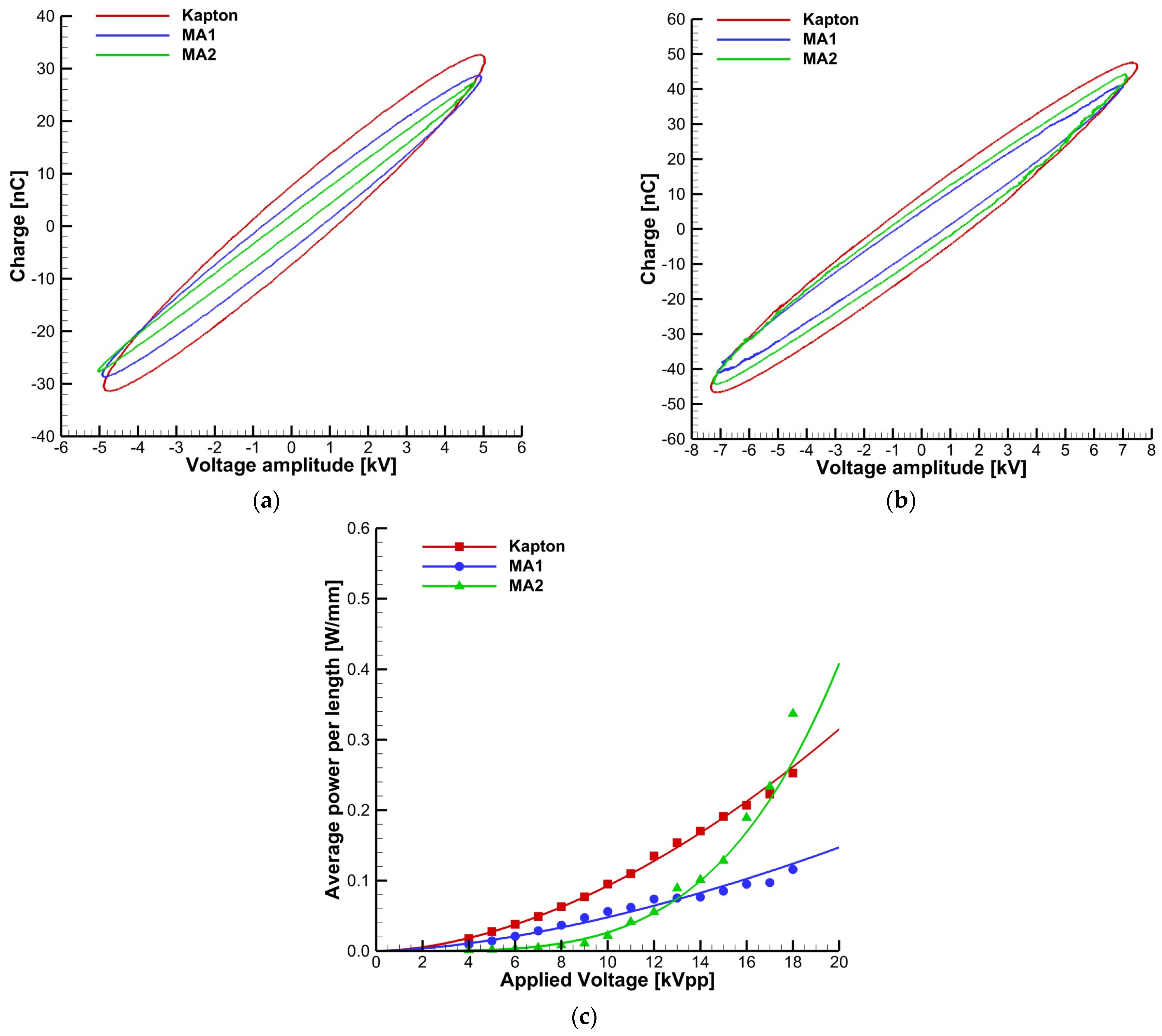
3.2. Plasma Actuators Electrical Characterization
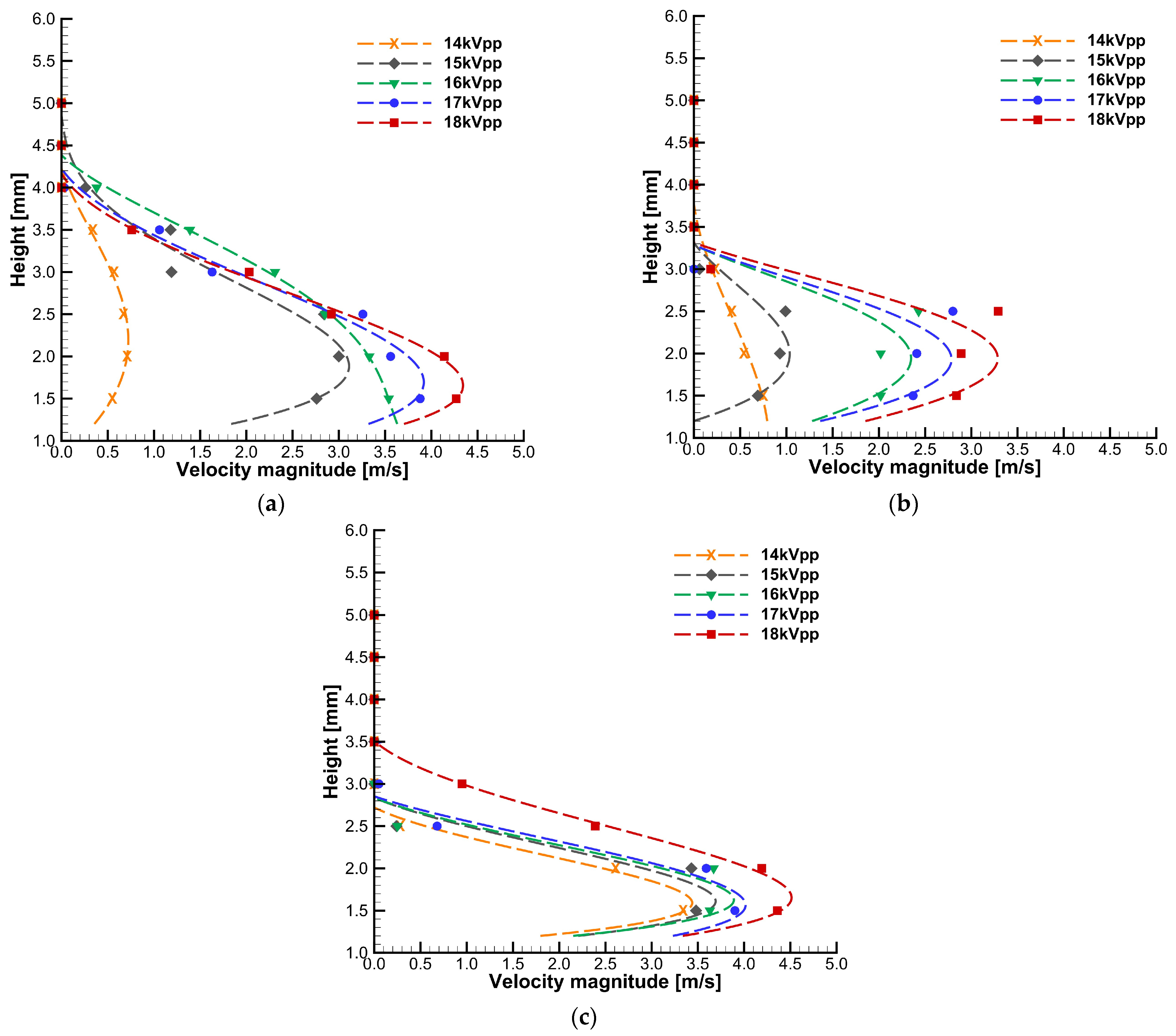
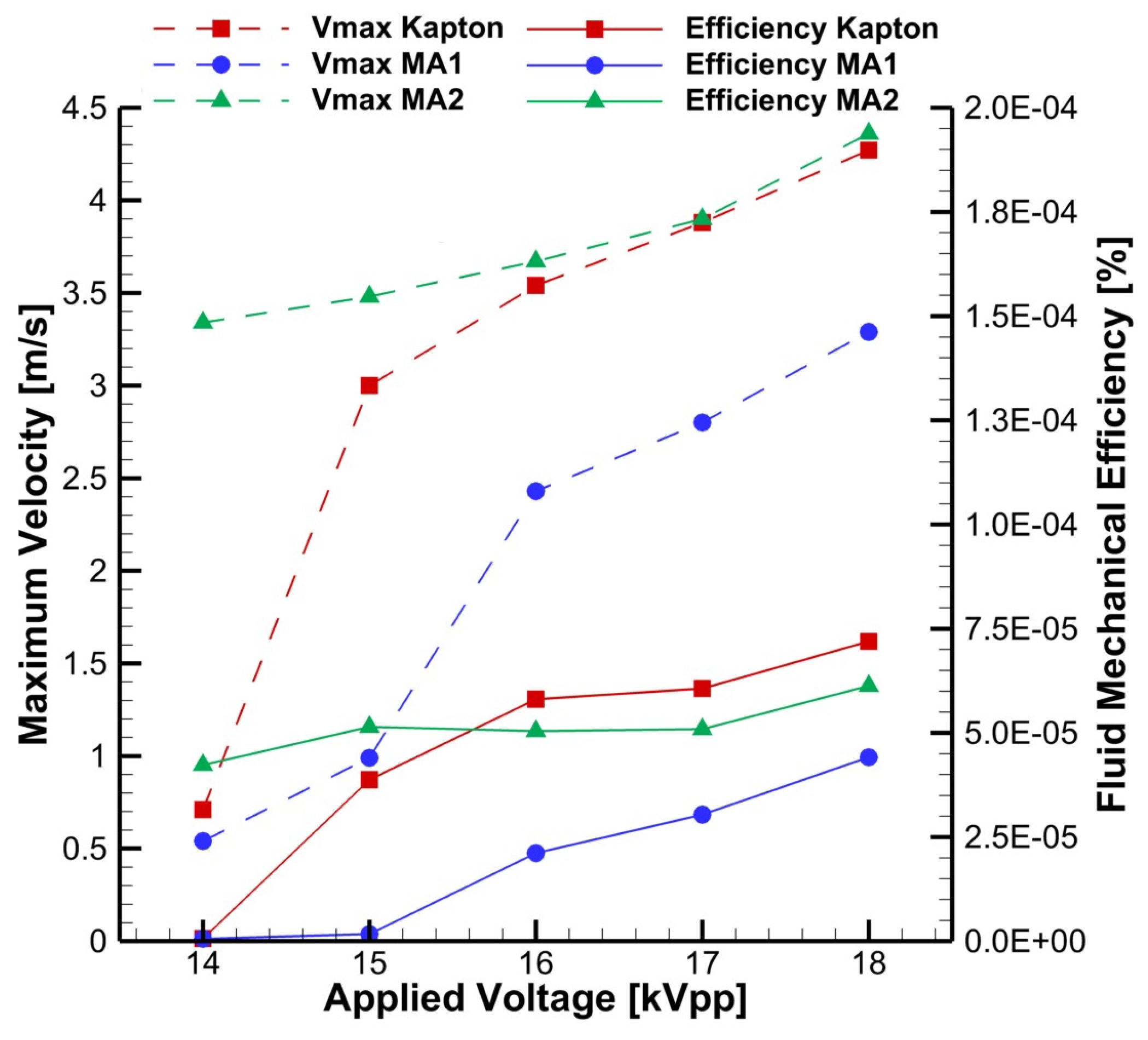
3.3. Plasma-Induced Flow Mechanical Characterization
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Clyde Warsop, Active Flow Control Using MEMS. In MEMS Aerospace Applications, RTO/NATO. Available online: https://apps.dtic.mil/sti/citations/tr/ADA425494 (accessed on 1 February 2004).
- Wang, J.; Feng, L. Introduction. In Flow Control Techniques and Applications; Cambridge University Press (CUP): Cambridge, UK, 2018; pp. 1–22. ISBN 9781107161566. [Google Scholar]
- Batikh, A.; Baldas, L.; Colin, S. Application of Active Flow Control on Aircrafts—State of the Art. 2017. Available online: https://hal.science/hal-01820331 (accessed on 20 September 2023).
- Bouremel, Y.; Li, J.; Zhao, Z.; Debiasi, M. Effects of AC Dielectric Barrier Discharge Plasma Actuator Location on Flow Separation and Airfoil Performance. Procedia Eng. 2013, 67, 270–278. [Google Scholar] [CrossRef][Green Version]
- Viguera, R.; Anzai, Y.; Sasaki, Y.; Nonomura, T. Experimental Observations of Transient Flows in Separation Control Using a Plasma Actuator. Actuators 2023, 12, 218. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, Y.; Wang, X.; Wang, W.; Tang, K.; Li, H. Turbulent boundary layer separation control using plasma actuator at Reynolds number 2000000. Chin. J. Aeronaut. 2016, 29, 1237–1246. [Google Scholar] [CrossRef]
- Visbal, M.R.; Gaitonde, D.V.; Roy, S. Control of transitional and turbulent flows using plasma-based actuators, Collection of Technical Papers. In Proceedings of the 36th AIAA Fluid Dynamics Conference and Exhibit, San Francisco, CA, USA, 5–8 June 2006; Volume 2, pp. 1087–1108. [Google Scholar] [CrossRef]
- Al-Sadawi, L.; Chong, T.P.; Kim, J.H. Aero-dynamic noise reduction by plasma actuators for a flat plate with blunt trailing edge. J. Sound Vib. 2019, 439, 173–193. [Google Scholar] [CrossRef]
- Chen, Z.; Wen, C.-Y. Flow control of a D-shaped bluff body using different DBD plasma actuators. J. Fluids Struct. 2021, 103, 103292. [Google Scholar] [CrossRef]
- Konstantinidis, E. Active Control of Bluff-Body Flows Using Plasma Actuators. Actuators 2019, 8, 66. [Google Scholar] [CrossRef]
- Grundmann, S.; Tropea, C. Experimental transition delay using glow-discharge plasma actuators. Exp. Fluids 2007, 42, 653–657. [Google Scholar] [CrossRef]
- Grundmann, S.; Tropea, C. Active cancellation of artificially introduced Tollmien–Schlichting waves using plasma actuators. Exp. Fluids 2007, 44, 795–806. [Google Scholar] [CrossRef]
- Grundmann, S.; Tropea, C. Experimental damping of boundary-layer oscillations using DBD plasma actuators. Int. J. Heat Fluid Flow 2009, 30, 394–402. [Google Scholar] [CrossRef]
- Kim, D.; Do, H.; Choi, H. Drag reduction on a three-dimensional model vehicle using a wire-to-plate DBD plasma actuator. Exp. Fluids 2020, 61, 135. [Google Scholar] [CrossRef]
- Wang, C.-C.; Wen, C.-P. Aerodynamic drag reduction for a truck model using DBD plasma actuators. Adv. Mech. Eng. 2022, 14, 16878132221087852. [Google Scholar] [CrossRef]
- Liu, Y.; Kolbakir, C.; Hu, H.; Hu, H. A comparison study on the thermal effects in DBD plasma actuation and electrical heating for aircraft icing mitigation. Int. J. Heat Mass Transf. 2018, 124, 319–330. [Google Scholar] [CrossRef]
- Li, C.; Hu, H.; Meng, X.; Cai, J.; Hu, H. Aerodynamic and Thermal Effects of Plasma Actuators on Anti-icing over an Airfoil. Lect. Notes Electr. Eng. 2019, 459, 1008–1019. [Google Scholar] [CrossRef]
- Meng, X.; Hu, H.; Li, C.; Abbasi, A.A.; Cai, J.; Hu, H. Mechanism study of coupled aerodynamic and thermal ef-fects using plasma actuation for anti-icing. Phys. Fluids 2019, 31, 37103. [Google Scholar] [CrossRef]
- Kaneko, Y.; Nishida, H.; Tagawa, Y. Visualization of the Electrohydrodynamic and Thermal Effects of AC-DBD Plasma Actuators of Plate- and Wire-Exposed Electrodes. Actuators 2022, 11, 38. [Google Scholar] [CrossRef]
- Rodrigues, F.; Abdollahzadehsangroudi, M.; Nunes-Pereira, J.; Páscoa, J. Recent Developments on Dielectric Barrier Discharge (DBD) Plasma Actuators for Icing Mitigation. Actuators 2023, 12, 5. [Google Scholar] [CrossRef]
- Xie, L.; Liang, H.; Zong, H.; Liu, X.; Li, Y. Multipurpose distributed dielectric-barrier-discharge plasma actua-tion: Icing sensing, anti-icing, and flow control in one. Phys. Fluids 2022, 34, 071701. [Google Scholar] [CrossRef]
- Thomas, F.O.; Corke, T.C.; Iqbal, M.; Kozlov, A.; Schatzman, D. Optimization of Dielectric Barrier Discharge Plasma Actuators for Active Aerodynamic Flow Control. AIAA J. 2009, 47, 2169–2178. [Google Scholar] [CrossRef]
- Hink, R.; Pipa, A.V.; Schäfer, J.; Caspari, R.; Weichwald, R.; Foest, R.; Brandenburg, R. Influence of dielectric thickness and electrode structure on the ion wind generation by micro fabricated plasma actuators. J. Phys. D Appl. Phys. 2020, 53, 405201. [Google Scholar] [CrossRef]
- Benard, N.; Moreau, E. Electrical and mechanical characteristics of surface AC dielectric barrier discharge plasma actuators applied to airflow control. Exp. Fluids 2014, 55, 1846. [Google Scholar] [CrossRef]
- Rigit, A.R.H.; La, K.C.; Bong, D.B.L. Degradation of a dielectric barrier discharge plasma actuator. In Proceedings of the IEEE International Conference on Properties and Applications of Dielectric Materials, Harbin, China, 19–23 July 2009; pp. 569–572. [Google Scholar] [CrossRef]
- Hanson, R.E.; Houser, N.M.; Lavoie, P. Dielectric material degradation monitoring of dielectric barrier dis-charge plasma actuators. J. Appl. Phys. 2014, 115, 43301. [Google Scholar] [CrossRef]
- Pons, J.; Oukacine, L.; Moreau, E.; Tatibouet, J.-M. Observation of Dielectric Degradation After Surface Dielectric Barrier Discharge Operation in Air at Atmospheric Pressure. IEEE Trans. Plasma Sci. 2008, 36, 1342–1343. [Google Scholar] [CrossRef]
- Rodrigues, F.F.; Pascoa, J.C.; Trancossi, M. Experimental Analysis of Alternative Dielectric Materials for DBD Plasma Actuators. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Pittsburgh, PA, USA, 9–15 November 2018. [Google Scholar]
- Rodrigues, F.F.; Pereira, J.N.; Abdollahzadeh, M.; Pascoa, J.; Mendez, S.L. Comparative Evaluation of Dielectric Materials for Plasma Actuators Active Flow Control and Heat Transfer Applications. In Proceedings of the ASME 2021 Fluids Engineering Division Summer Meeting, Virtual, 10–12 August 2021. [Google Scholar] [CrossRef]
- Nunes-Pereira, J.; Rodrigues, F.F.; Abdollahzadehsangroudi, M.; Páscoa, J.C.; Lanceros-Mendez, S. Improved performance of polyimide Cirlex-based dielectric barrier discharge plasma actuators for flow control. Polym. Adv. Technol. 2021, 33, 1278–1290. [Google Scholar] [CrossRef]
- Shvydyuk, K.O.; Rodrigues, F.F.; Nunes-Pereira, J.; Páscoa, J.C.; Lanceros-Mendez, S.; Silva, A.P. Long-lasting ceramic composites for surface dielectric barrier discharge plasma actuators. J. Eur. Ceram. Soc. 2023, 43, 6112–6121. [Google Scholar] [CrossRef]
- Shvydyuk, K.O.; Nunes-Pereira, J.; Rodrigues, F.F.; Silva, A.P. Review of Ceramic Composites in Aeronautics and Aerospace: A Multifunctional Approach for TPS, TBC and DBD Applications. Ceramics 2023, 6, 195–230. [Google Scholar] [CrossRef]
- C20 Standard Test Methods for Apparent Porosity, Water Absorption, Apparent Specific Gravity, and Bulk Density of Burned Refractory Brick and Shapes by Boiling Water. Available online: https://www.astm.org/c0020-00r22.html (accessed on 20 September 2023).
- Ashpis, D.E.; Laun, M.C.; Griebeler, E.L.; Zheng, B.; Ke, X.; Ge, C.; Zhu, Y.; Wu, Y.; Liu, F.; Luo, S.; et al. Progress Toward Accurate Measurement of Dielectric Barrier Discharge Plasma Actuator Power. AIAA J. 2017, 55, 2254–2268. [Google Scholar] [CrossRef] [PubMed]
- Kriegseis, J.; Grundmann, S.; Tropea, C. Power consumption, discharge capacitance and light emission as measures for thrust production of dielectric barrier discharge plasma actuators. J. Appl. Phys. 2011, 110, 013305. [Google Scholar] [CrossRef]
- Pons, J.; Moreau, E.; Touchard, G. Asymmetric surface dielectric barrier discharge in air at atmospheric pressure: Electrical properties and induced airflow characteristics. J. Phys. D Appl. Phys. 2005, 38, 3635–3642. [Google Scholar] [CrossRef]
- Rodrigues, F.F.; Pascoa, J.C. Implementation of Stair-Shaped Dielectric Layers in Micro- and Macroplasma Actuators for Increased Efficiency and Lifetime. J. Fluids Eng. 2020, 142, 104502. [Google Scholar] [CrossRef]
- Somton, K.; Dateraksa, K.; Laoratanakul, P.; McCuiston, R. Shrinkage and properties of die pressed alumina produced from different granule sources. AIP Conf. Proc. 2020, 2279, 060003. [Google Scholar] [CrossRef]
- Pribyl, R.; Stastny, P.; Pazderka, M.; Kelar, J.; Tucekova, Z.K.; Zemanek, M.; Trunec, M.; Cernak, M. Properties of MgAl2O4 doped alumina barrier layers for dielectric barrier discharge. J. Phys. D Appl. Phys. 2020, 53, 505202. [Google Scholar] [CrossRef]
- Lindner, M.; Pipa, A.V.; Brandenburg, R.; Schreiner, R. Expansion of surface barrier discharge scrutinized. Plasma Sources Sci. Technol. 2022, 31, 105018. [Google Scholar] [CrossRef]
- Synek, P.; Zemánek, M.; Kudrle, V.; Hoder, T. Advanced electrical current measurements of microdischarges: Evidence of sub-critical pulses and ion currents in barrier discharge in air. Plasma Sources Sci. Technol. 2018, 27, 045008. [Google Scholar] [CrossRef]
- Synek, P.; Akishev, Y.S.; Petryakov, A.; Trushkin, N.; Vorac, J.; Hoder, T. Electrical analysis and ultra-fast sequential imaging of surface barrier discharge with streamer-leader sequence generated with 100 kHz frequency at the water interface. Plasma Sources Sci. Technol. 2019, 28, 095018. [Google Scholar] [CrossRef]
- Roth, J.R.; Dai, X.; Rahel, J.; Shermann, D.M. The physics and phenomenology of paraelectric One Atmosphere Uniform Glow Discharge Plasma (OAUGDPTM) actuators for aerodynamic flow control. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit-Meeting Papers, Reno, NV, USA, 10–13 January 2005; pp. 14057–14068. [Google Scholar] [CrossRef]
- Wilde, N.D.; Xu, H.; Gomez-Vega, N.; Barrett, S.R.H. A model of surface dielectric barrier discharge power. Appl. Phys. Lett. 2021, 118, 154102. [Google Scholar] [CrossRef]
- Birey, H. Thickness dependence of the dielectric constant and resistance of Al2O3 films. J. Appl. Phys. 1977, 48, 5209–5212. [Google Scholar] [CrossRef]
- Wang, X.; Engel, J.; Liu, C. Liquid crystal polymer (LCP) for MEMS: Processes and applications. J. Micromech. Microeng. 2003, 13, 628–633. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Z.; Li, J.; Liu, C.; Lao, C.; Fu, Y.; Liu, C.; Li, Y.; Wang, P.; He, Y. 3D printing of ceramics: A review. J. Eur. Ceram. Soc. 2018, 39, 661–687. [Google Scholar] [CrossRef]
- Audier, P.; Fénot, M.; Bénard, N.; Moreau, E. Film cooling effectiveness enhancement using surface dielectric barrier discharge plasma actuator. Int. J. Heat Fluid Flow 2016, 62, 247–257. [Google Scholar] [CrossRef]
- Li, G.; Wang, Q.; Huang, Y.; Zhang, H. Large eddy simulation of film cooling effectiveness on a turbine vane pressure side with a saw-tooth plasma actuator. Aerosp. Sci. Technol. 2021, 112, 106615. [Google Scholar] [CrossRef]
- Liu, P.; He, L.; Zhao, B. Discharge and Optical Emission Spectrum Characteristics of a Coaxial Dielectric Barrier Discharge Plasma-Assisted Combustion Actuator. J. Spectrosc. 2020, 2020, 6034848. [Google Scholar] [CrossRef]
- Khasare, S.; Bagherighajari, F.; Dolati, F.; Mahmoudimehr, J.; Páscoa, J.; Abdollahzadehsangroudi, M. The effect of the dielectric barrier discharge plasma actuator in the control of non-reactive flow in a non-premixed bluff body burner. Phys. Fluids 2023, 35, 075135. [Google Scholar] [CrossRef]
- Ran, J.; Zhang, X.; Ge, D.; Li, X.; Li, X. Effect of Dielectric Surface Morphology on Dielectric Barrier Discharge Mode in Air at Atmospheric Pressure. IEEE Trans. Plasma Sci. 2020, 49, 214–218. [Google Scholar] [CrossRef]
- Ran, J.; Li, C.; Ma, D.; Luo, H.; Li, X. Homogeneous dielectric barrier discharges in atmospheric air and its influencing factor. Phys. Plasmas 2018, 25, 033511. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodrigues, F.F.; Shvydyuk, K.O.; Nunes-Pereira, J.; Páscoa, J.C.; Silva, A.P. Plasma Actuators Based on Alumina Ceramics for Active Flow Control Applications. Ceramics 2024, 7, 192-207. https://doi.org/10.3390/ceramics7010012
Rodrigues FF, Shvydyuk KO, Nunes-Pereira J, Páscoa JC, Silva AP. Plasma Actuators Based on Alumina Ceramics for Active Flow Control Applications. Ceramics. 2024; 7(1):192-207. https://doi.org/10.3390/ceramics7010012
Chicago/Turabian StyleRodrigues, Frederico F., Kateryna O. Shvydyuk, João Nunes-Pereira, José C. Páscoa, and Abílio P. Silva. 2024. "Plasma Actuators Based on Alumina Ceramics for Active Flow Control Applications" Ceramics 7, no. 1: 192-207. https://doi.org/10.3390/ceramics7010012
APA StyleRodrigues, F. F., Shvydyuk, K. O., Nunes-Pereira, J., Páscoa, J. C., & Silva, A. P. (2024). Plasma Actuators Based on Alumina Ceramics for Active Flow Control Applications. Ceramics, 7(1), 192-207. https://doi.org/10.3390/ceramics7010012









