Temperature-Dependent Elastic Properties of B4C from First-Principles Calculations and Phonon Modeling
Abstract
1. Introduction
2. Theory and Methodology
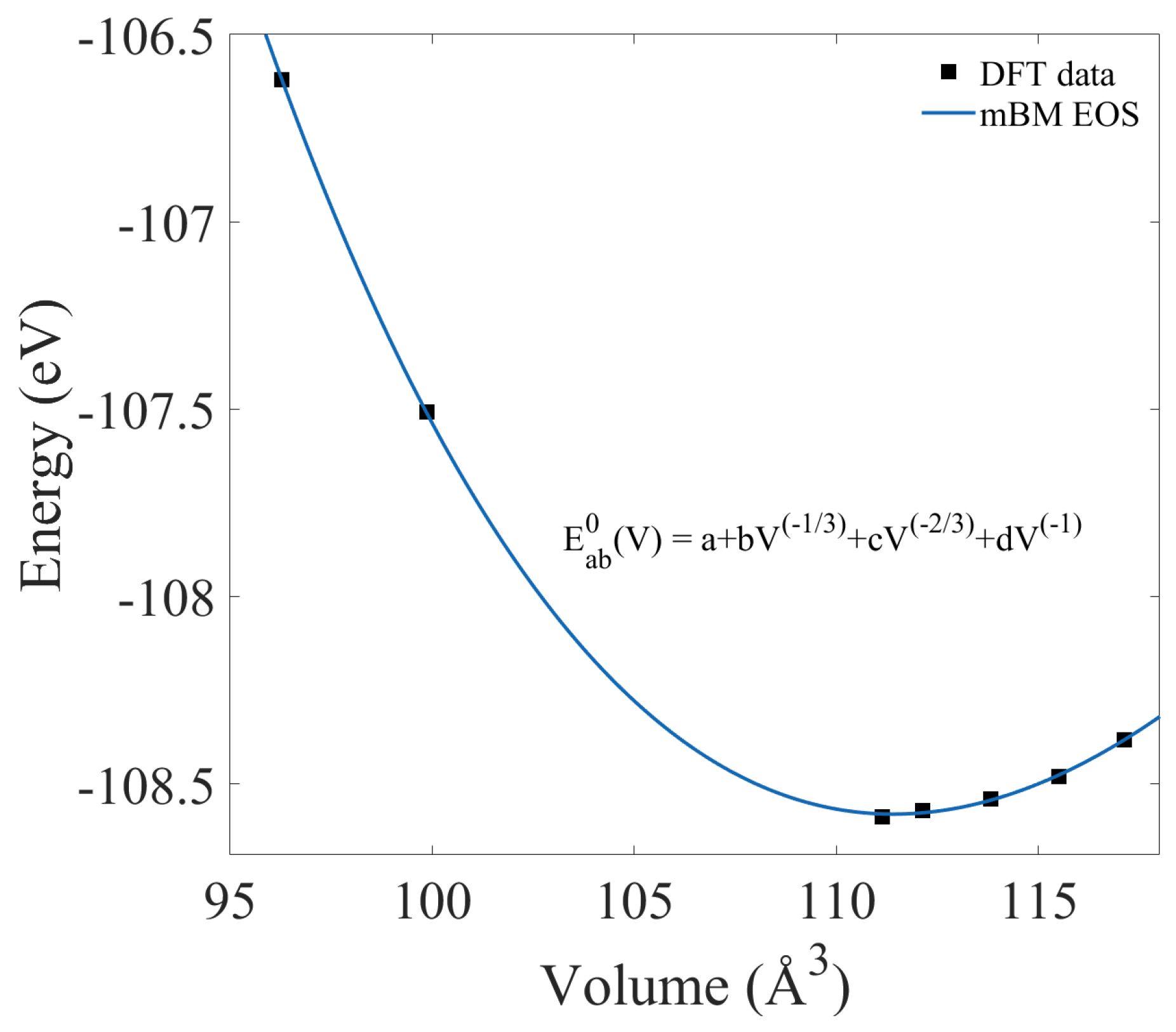
2.1. Static Energy and E-V Equation of State
2.2. Vibrational Contribution to the Helmholtz Free Energy
2.3. DFT and Phonon Calculations
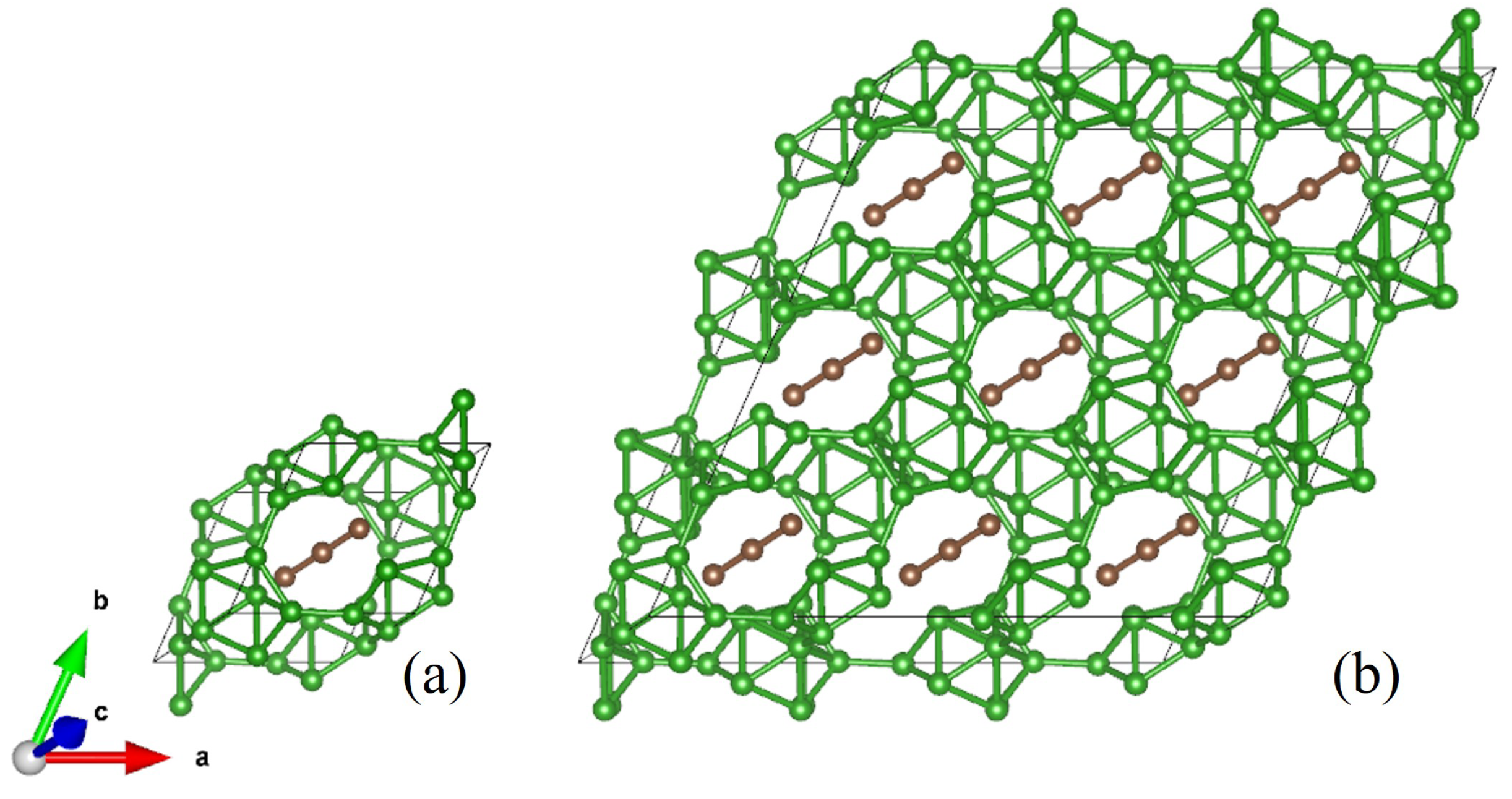
3. Results and Discussion
3.1. First-Principles Calculations’ Validation
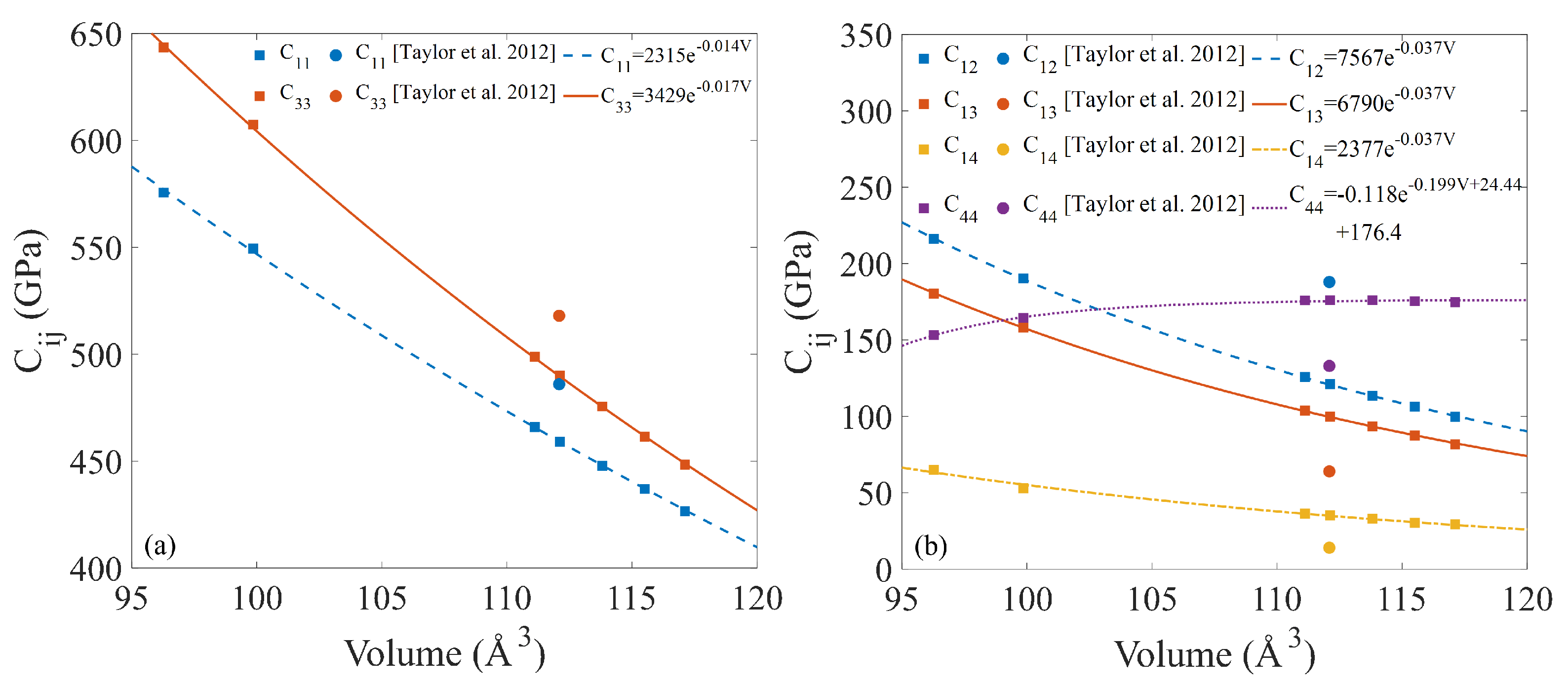
3.2. Properties from Static Calculations
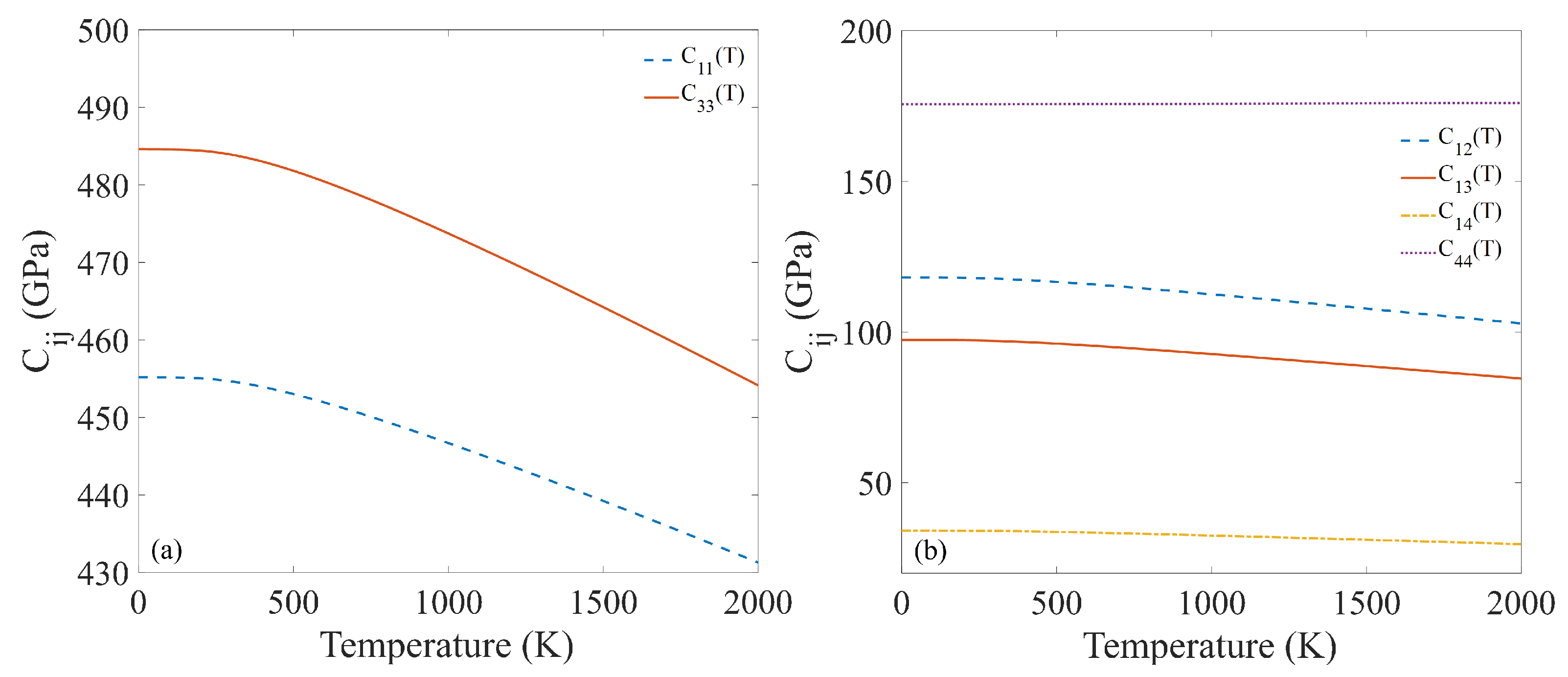
3.3. Phonon Calculation and Thermal Properties
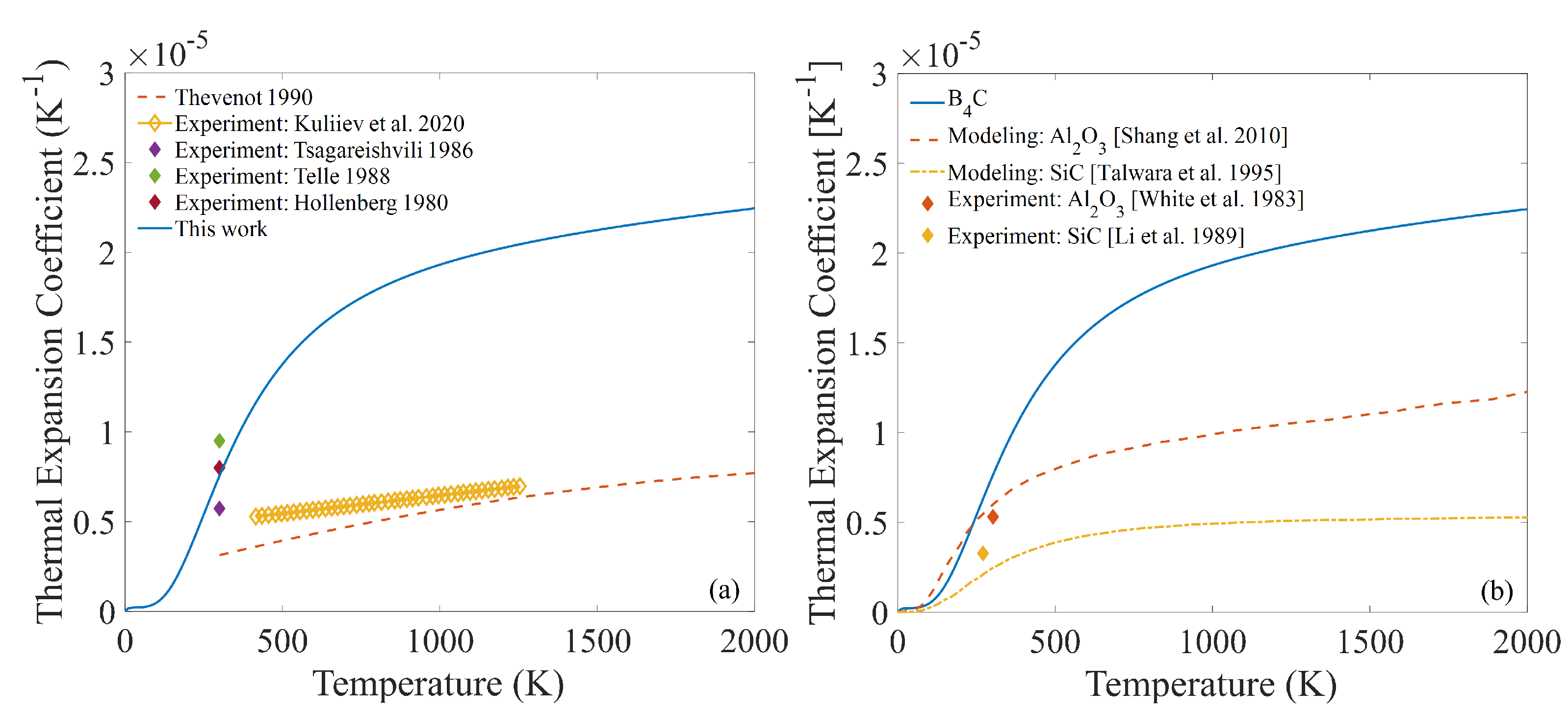
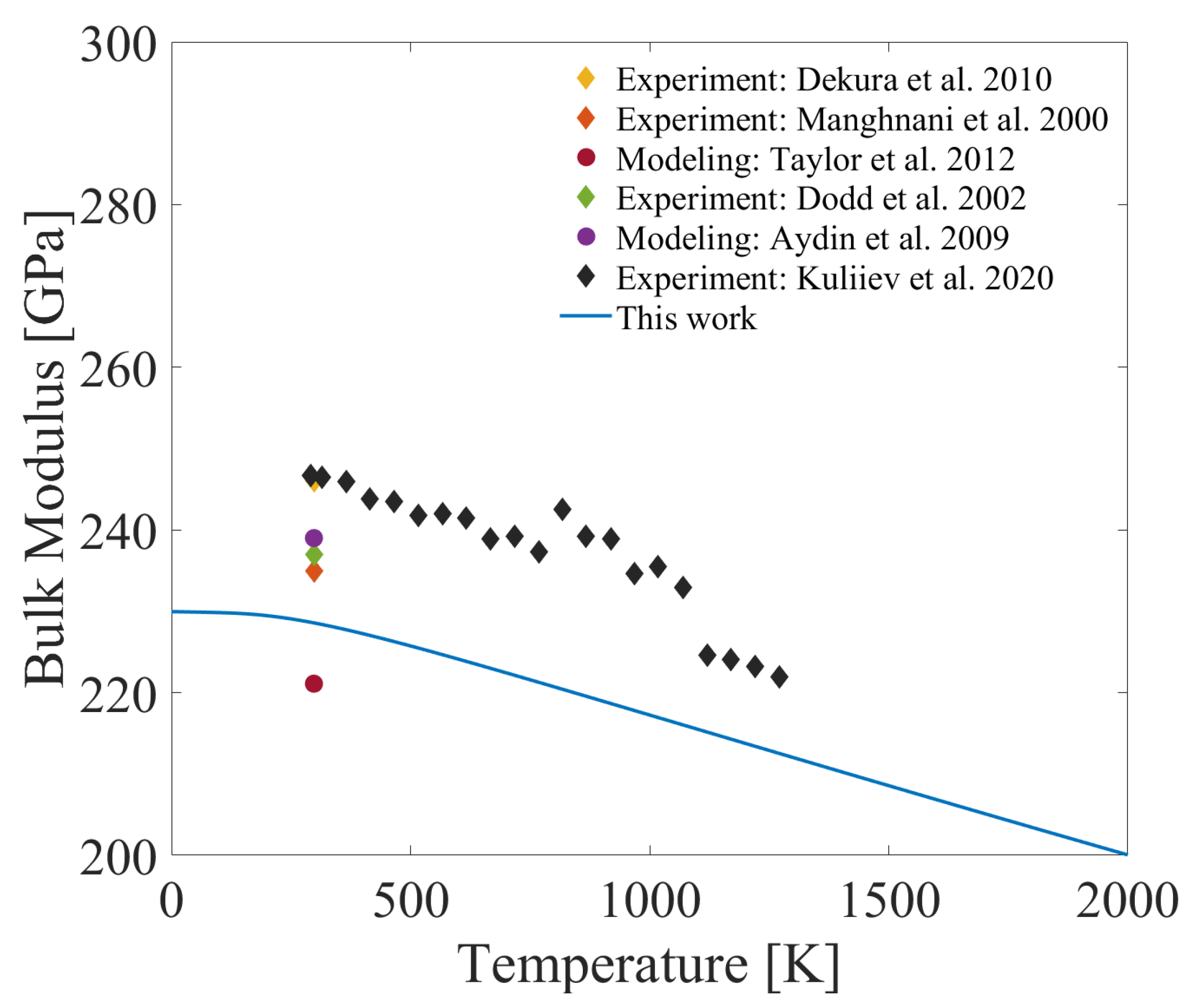
3.4. Temperature-Dependent Thermal Expansion Coefficient and Bulk Modulus
3.5. Limitations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DFT | Density Functional Theory |
| TEC | Thermal Expansion Coefficient |
| MD | Molecular Dynamics |
| EOS | Equation of State |
| BM | Birch–Murnaghan |
| mBM | Modified Birch–Murnaghan |
| DOS | Density of States |
| VASP | Vienna Ab Initio Simulation Package |
| GGA | Generalized Gradient Approximation |
| SCF | Self-Consistent Field |
References
- Roy, T.; Subramanian, C.; Suri, A. Pressureless sintering of boron carbide. Ceram. Int. 2006, 32, 227–233. [Google Scholar] [CrossRef]
- Swab, J.J.; Meredith, C.S.; Casem, D.T.; Gamble, W.R. Static and dynamic compression strength of hot-pressed boron carbide using a dumbbell-shaped specimen. J. Mater. Sci. 2017, 52, 10073–10084. [Google Scholar] [CrossRef]
- Vargas-Gonzalez, L.; Speyer, R.F.; Campbell, J. Flexural strength, fracture toughness, and hardness of silicon carbide and boron carbide armor ceramics. Int. J. Appl. Ceram. Technol. 2010, 7, 643–651. [Google Scholar] [CrossRef]
- Werheit, H.; Leithe-Jasper, A.; Tanaka, T.; Rotter, H.; Schwetz, K. Some properties of single-crystal boron carbide. J. Solid State Chem. 2004, 177, 575–579. [Google Scholar] [CrossRef]
- Matkovich, V.I.; Samsonov, G.V.; Hagenmuller, P. Boron and Refractory Borides; Springer: Berlin/Heidelberg, Germany, 1977. [Google Scholar]
- Varshney, V. Molecular dynamics methodologies for predicting thermal transport in aerospace polymers and their composites. In Hybrid Atomic-Scale Interface Design for Materials Functionality; Elsevier: Amsterdam, The Netherlands, 2021; pp. 19–34. [Google Scholar]
- El Messiry, M. Protective Armor Engineering Design; Apple Academic Press: Palm Bay, FL, USA, 2019. [Google Scholar]
- Turatti, A.M.; Pereira, A.S. Wear resistant boron carbide compacts produced by pressureless sintering. Ceram. Int. 2017, 43, 7970–7977. [Google Scholar] [CrossRef]
- Domnich, V.; Reynaud, S.; Haber, R.A.; Chhowalla, M. Boron carbide: Structure, properties, and stability under stress. J. Am. Ceram. Soc. 2011, 94, 3605–3628. [Google Scholar] [CrossRef]
- Sarıyer, D.; Küçer, R.; Küçer, N. Neutron shielding properties of concretes containing boron carbide and ferro–boron. Procedia-Soc. Behav. Sci. 2015, 195, 1752–1756. [Google Scholar] [CrossRef]
- Chevalier, J.; Gremillard, L. Ceramics for medical applications: A picture for the next 20 years. J. Eur. Ceram. Soc. 2009, 29, 1245–1255. [Google Scholar] [CrossRef]
- Levchenko, I.; Bazaka, K.; Belmonte, T.; Keidar, M.; Xu, S. Advanced Materials for Next-Generation Spacecraft. Adv. Mater. 2018, 30, 1802201. [Google Scholar] [CrossRef]
- Goldman, N. Computational Approaches for Chemistry under Extreme Conditions; Springer: Berlin/Heidelberg, Germany, 2019; Volume 28. [Google Scholar]
- Mishin, Y. Machine-learning interatomic potentials for materials science. Acta Mater. 2021, 214, 116980. [Google Scholar] [CrossRef]
- Suri, A.; Subramanian, C.; Sonber, J.; Murthy, T.C. Synthesis and consolidation of boron carbide: A review. Int. Mater. Rev. 2010, 55, 4–40. [Google Scholar] [CrossRef]
- Konovalikhin, S.; Ponomarev, V. Carbon in boron carbide: The crystal structure of B11.4C3.6. Russ. J. Inorg. Chem. 2009, 54, 197–203. [Google Scholar] [CrossRef]
- Morawiec, A. Review of deterministic methods of calculation of polycrystal elastic constants. Textures Microstruct. 1994, 22, 139–167. [Google Scholar] [CrossRef]
- Fahrenholtz, W.G.; Hilmas, G.E. Ultra-high temperature ceramics: Materials for extreme environments. Scr. Mater. 2017, 129, 94–99. [Google Scholar] [CrossRef]
- Saha, D.; Ghara, D.K.; Pal, M. Nanoporous γ-alumina based novel sensor to detect trace moisture in high temperature and high pressure environment. Sens. Actuators B Chem. 2016, 222, 1043–1049. [Google Scholar] [CrossRef]
- Medvedovski, E. Influence of corrosion and mechanical loads on advanced ceramic components. Ceram. Int. 2013, 39, 2723–2741. [Google Scholar] [CrossRef]
- Chang, J.; Chen, Z.; Hogan, J.D. Molecular Dynamics Simulations Correlating Mechanical Property Changes of Alumina with Atomic Voids under Triaxial Tension Loading. Modelling 2023, 4, 211–223. [Google Scholar] [CrossRef]
- Yang, A.; Romanyk, D.; Hogan, J.D. High-velocity impact study of an advanced ceramic using finite element model coupling with a machine learning approach. Ceram. Int. 2023, 49, 10481–10498. [Google Scholar] [CrossRef]
- Parsazadeh, M.; Fisher, G.; McDonald, A.; Hogan, J.D. Computational modelling of the effect of microstructure on the abrasive wear resistance of tungsten-carbide nickel composite coatings under sub-critical cyclic impact loading. Ceram. Int. 2022, 48, 14338–14348. [Google Scholar] [CrossRef]
- Manafi Farid, H.; McDonald, A.; Hogan, J.D. Impact Deposition Behavior of Al/B4C Cold-Sprayed Composite Coatings: Understanding the Role of Porosity on Particle Retention. Materials 2023, 16, 2525. [Google Scholar] [CrossRef]
- Gogotsi, G.; Groushevsky, Y.L.; Dashevskaya, O.; Gogotsi, Y.G.; Lavrenko, V. Complex investigation of hot-pressed boron carbide. J. Less Common Met. 1986, 117, 225–230. [Google Scholar] [CrossRef]
- Kuliiev, R.; Orlovskaya, N.; Hyer, H.; Sohn, Y.; Lugovy, M.; Ha, D.; Radovic, M.; Castle, E.G.; Reece, M.J.; Vallachira Warriam Sasikumar, P.; et al. Spark Plasma Sintered B4C—Structural, Thermal, Electrical and Mechanical Properties. Materials 2020, 13, 1612. [Google Scholar] [CrossRef]
- Dodd, S.; Saunders, G.; James, B. Temperature and pressure dependences of the elastic properties of ceramic boron carbide (B4C). J. Mater. Sci. 2002, 37, 2731–2736. [Google Scholar] [CrossRef]
- Taylor, D.E.; McCauley, J.W.; Wright, T. The effects of stoichiometry on the mechanical properties of icosahedral boron carbide under loading. J. Phys. Condens. Matter 2012, 24, 505402. [Google Scholar] [CrossRef] [PubMed]
- Manghnani, M.H.; Wang, Y.; Li, F.; Zinin, P.; Rafaniello, W. Elastic and vibrational properties of B4C to 21 GPa. Sci. Technol. High Press. 2000, 2, 25–30. [Google Scholar]
- Gieske, J.; Aselage, T.; Emin, D. Elastic properties of boron carbides. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 1991; Volume 231, pp. 376–379. [Google Scholar]
- Lee, S.; Bylander, D.; Kleinman, L. Elastic moduli of B12 and its compounds. Phys. Rev. B 1992, 45, 3245. [Google Scholar] [CrossRef] [PubMed]
- Aydin, S.; Simsek, M. Hypothetically superhard boron carbide structures with a B11C icosahedron and three-atom chain. Phys. Status Solidi (B) 2009, 246, 62–70. [Google Scholar] [CrossRef]
- Farbaniec, L.; Hogan, J.; McCauley, J.; Ramesh, K. Anisotropy of mechanical properties in a hot-pressed boron carbide. Int. J. Appl. Ceram. Technol. 2016, 13, 1008–1016. [Google Scholar] [CrossRef]
- Shang, S.L.; Zhang, H.; Wang, Y.; Liu, Z.K. Temperature-dependent elastic stiffness constants of α-and θ-Al2O3 from first-principles calculations. J. Phys. Condens. Matter 2010, 22, 375403. [Google Scholar] [CrossRef] [PubMed]
- Shang, S.L.; Wang, Y.; Kim, D.; Liu, Z.K. First-principles thermodynamics from phonon and Debye model: Application to Ni and Ni3Al. Comput. Mater. Sci. 2010, 47, 1040–1048. [Google Scholar] [CrossRef]
- Tang, B.; He, Y.; Goddard III, W.A.; An, Q. First principles predicting enhanced ductility of boride carbide through magnesium microalloying. J. Am. Ceram. Soc. 2019, 102, 5514–5523. [Google Scholar] [CrossRef]
- Shen, Y.; Reddy, K.M.; Li, J.; Chen, M.; An, Q. Atomistic origin of shear induced quasi-plastic deformation in boron carbide. Acta Mater. 2023, 249, 118828. [Google Scholar] [CrossRef]
- Kocer, E.; Ko, T.W.; Behler, J. Neural Network Potentials: A Concise Overview of Methods. Annu. Rev. Phys. Chem. 2022, 73. [Google Scholar] [CrossRef]
- Zuo, Y.; Chen, C.; Li, X.; Deng, Z.; Chen, Y.; Behler, J.; Csányi, G.; Shapeev, A.V.; Thompson, A.P.; Wood, M.A.; et al. Performance and cost assessment of machine learning interatomic potentials. J. Phys. Chem. A 2020, 124, 731–745. [Google Scholar] [CrossRef]
- Shang, S.; Wang, Y.; Liu, Z.K. First-principles calculations of phonon and thermodynamic properties in the boron-alkaline earth metal binary systems: B-Ca, B-Sr, and B-Ba. Phys. Rev. B 2007, 75, 024302. [Google Scholar] [CrossRef]
- Rou, S.; Chandran, K.R. First principles calculation of single-crystal elastic constants of titanium tetraboride (Ti3B4) and experimental validation. J. Am. Ceram. Soc. 2018, 101, 4308–4320. [Google Scholar] [CrossRef]
- Nikolussi, M.; Shang, S.; Gressmann, T.; Leineweber, A.; Mittemeijer, E.; Wang, Y.; Liu, Z.K. Extreme elastic anisotropy of cementite, Fe3C: First-principles calculations and experimental evidence. Scr. Mater. 2008, 59, 814–817. [Google Scholar] [CrossRef]
- Cheng, C.; Reddy, K.M.; Hirata, A.; Fujita, T.; Chen, M. Structure and mechanical properties of boron-rich boron carbides. J. Eur. Ceram. Soc. 2017, 37, 4514–4523. [Google Scholar] [CrossRef]
- DeVries, M.; Subhash, G.; Awasthi, A. Shocked ceramics melt: An atomistic analysis of thermodynamic behavior of boron carbide. Phys. Rev. B 2020, 101, 144107. [Google Scholar] [CrossRef]
- Pillai, H.G.; Madam, A.K.; Chandra, S.; Cheruvalath, V.M. Semiconducting B13C2 system: Structure search and DFT-based analysis. Mater. Res. Express 2019, 6, 046544. [Google Scholar] [CrossRef]
- Li, L.; Weidner, D.J.; Brodholt, J.; Alfe, D.; Price, G.D.; Caracas, R.; Wentzcovitch, R. Elasticity of CaSiO3 perovskite at high pressure and high temperature. Phys. Earth Planet. Inter. 2006, 155, 249–259. [Google Scholar] [CrossRef]
- Ritz, E.T.; Li, S.J.; Benedek, N.A. Thermal expansion in insulating solids from first principles. J. Appl. Phys. 2019, 126, 171102. [Google Scholar] [CrossRef]
- Eschrig, H. The Fundamentals of Density Functional Theory; Springer: Berlin/Heidelberg, Germany, 1996; Volume 32. [Google Scholar]
- McGaughey, A.J.; Jain, A.; Kim, H.Y.; Fu, B. Phonon properties and thermal conductivity from first principles, lattice dynamics, and the Boltzmann transport equation. J. Appl. Phys. 2019, 125, 011101. [Google Scholar] [CrossRef]
- Born, M.; Huang, K. Dynamical Theory of Crystal Lattices; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Fultz, B. Vibrational thermodynamics of materials. Prog. Mater. Sci. 2010, 55, 247–352. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.K.; Chen, L.Q. Thermodynamic properties of Al, Ni, NiAl, and Ni3Al from first-principles calculations. Acta Mater. 2004, 52, 2665–2671. [Google Scholar] [CrossRef]
- Wang, D.Y.; Yan, Q.; Wang, B.; Wang, Y.X.; Yang, J.; Yang, G. Predicted boron-carbide compounds: A first-principles study. J. Chem. Phys. 2014, 140, 224704. [Google Scholar] [CrossRef] [PubMed]
- Birch, F. Finite strain isotherm and velocities for single-crystal and polycrystalline NaCl at high pressures and 300 K. J. Geophys. Res. Solid Earth 1978, 83, 1257–1268. [Google Scholar] [CrossRef]
- Teter, D.; Gibbs, G.V.; Boisen, M.B., Jr.; Allan, D.; Teter, M. First-principles study of several hypothetical silica framework structures. Phys. Rev. B 1995, 52, 8064. [Google Scholar] [CrossRef]
- Togo, A. First-principles phonon calculations with phonopy and phono3py. J. Phys. Soc. Jpn. 2023, 92, 012001. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Blöchl, P.E.; Jepsen, O.; Andersen, O.K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223. [Google Scholar] [CrossRef]
- Heywang, W.; Zaininger, K. Silicon: The semiconductor material. In Silicon: Evolution and Future of a Technology; Springer: Berlin/Heidelberg, Germany, 2004; pp. 25–42. [Google Scholar]
- Nekrashevich, S.; Gritsenko, V. Electronic structure of silicon dioxide (a review). Phys. Solid State 2014, 56, 207–222. [Google Scholar] [CrossRef]
- Hushur, A.; Manghnani, M.H.; Werheit, H.; Dera, P.; Williams, Q. High-pressure phase transition makes B4. 3C boron carbide a wide-gap semiconductor. J. Phys. Condens. Matter 2016, 28, 045403. [Google Scholar] [CrossRef] [PubMed]
- Brown-Shaklee, H.J.; Neuman, E.W.; Fahrenholtz, W.G.; Hilmas, G.E. Optical characterization of boron carbide powders synthesized with varying B-to-C ratios. J. Am. Ceram. Soc. 2023, 106, 1932–1944. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Pulay, P. Convergence acceleration of iterative sequences. The case of SCF iteration. Chem. Phys. Lett. 1980, 73, 393–398. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.C.; Tang, G.; Geng, W.T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Togo, A.; Chaput, L.; Tadano, T.; Tanaka, I. Implementation strategies in phonopy and phono3py. J. Phys. Condens. Matter 2023, 35, 353001. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Kwei, G.H.; Morosin, B. Structures of the boron-rich boron carbides from neutron powder diffraction: Implications for the nature of the inter-icosahedral chains. J. Phys. Chem. 1996, 100, 8031–8039. [Google Scholar] [CrossRef]
- McClellan, K.; Chu, F.; Roper, J.; Shindo, I. Room temperature single crystal elastic constants of boron carbide. J. Mater. Sci. 2001, 36, 3403–3407. [Google Scholar] [CrossRef]
- Dekura, H.; Shirai, K.; Yanase, A. Metallicity of boron carbides at high pressure. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2010; Volume 215, p. 012117. [Google Scholar]
- Bylander, D.; Kleinman, L.; Lee, S. Self-consistent calculations of the energy bands and bonding properties of B12C3. Phys. Rev. B 1990, 42, 1394. [Google Scholar] [CrossRef] [PubMed]
- Project, T.M. Materials Data on B4C (mp-696746) by Materials Project (v2023.11.1). Available online: https://next-gen.materialsproject.org/materials/mp-696746 (accessed on 3 December 2023).
- An, Q.; Goddard III, W.A. Atomistic origin of brittle failure of boron carbide from large-scale reactive dynamics simulations: Suggestions toward improved ductility. Phys. Rev. Lett. 2015, 115, 105501. [Google Scholar] [CrossRef] [PubMed]
- Pavlovskii, M.S.; Andryushin, N. Calculating the Lattice Dynamics in the RFe3(BO3)4 Crystals in the Quasi-Harmonic Approximation. Phys. Solid State 2019, 61, 2019–2025. [Google Scholar] [CrossRef]
- Zhang, B.; Li, X.; Li, D. Assessment of thermal expansion coefficient for pure metals. Calphad 2013, 43, 7–17. [Google Scholar] [CrossRef]
- Shen, M.; Hansen, W.N.; Romo, P.C. Thermal expansion of the polyethylene unit cell. J. Chem. Phys. 1969, 51, 425–430. [Google Scholar] [CrossRef]
- Thevenot, F. Boron carbide—a comprehensive review. J. Eur. Ceram. Soc. 1990, 6, 205–225. [Google Scholar] [CrossRef]
- Tsagareishvili, G.; Nakashidze, T.; Jobava, J.S.; Lomidze, G.; Khulelidze, D.; Tsagareishvili, D.S.; Tsagareishvili, O. Thermal expansion of boron and boron carbide. J. Less Common Met. 1986, 117, 159–161. [Google Scholar] [CrossRef]
- Telle, R. Boride–eine neue Hartstoffgeneration? Chem. Unserer Zeit 1988, 22, 93–99. [Google Scholar] [CrossRef]
- Hollenberg, G. Thermally induced stresses and fractures in boron carbide pellets Bull. Am. Ceram. Soc. 1980, 59, 538–548. [Google Scholar]
- Wang, K.; Reeber, R. Thermal defects and thermal expansion of ionic crystals at high temperatures. Phys. Status Solidi (A) 1994, 146, 621–627. [Google Scholar] [CrossRef]
- Talwar, D.; Sherbondy, J.C. Thermal expansion coefficient of 3C–SiC. Appl. Phys. Lett. 1995, 67, 3301–3303. [Google Scholar] [CrossRef]
- White, G.K.; Roberts, R.B. Thermal expansion of reference materials: Tungsten and α-Al2O3. High Temp.-High Press. 1983, 15, 321–328. [Google Scholar]
- Li, Z.; Bradt, R. Thermal expansion and elastic anisotropies of SiC as related to polytype structure. In Proceedings of the Silicon Carbide”87, Columbus, OH, USA, 2–5 August 1989. [Google Scholar]
- Shirai, K.; Sakuma, K.; Uemura, N. Theoretical study of the structure of boron carbide B13C2. Phys. Rev. B 2014, 90, 064109. [Google Scholar] [CrossRef]
- Ektarawong, A.; Simak, S.I.; Alling, B. Structural models of increasing complexity for icosahedral boron carbide with compositions throughout the single-phase region from first principles. Phys. Rev. B 2018, 97, 174104. [Google Scholar] [CrossRef]
- Rasim, K.; Ramlau, R.; Leithe-Jasper, A.; Mori, T.; Burkhardt, U.; Borrmann, H.; Schnelle, W.; Carbogno, C.; Scheffler, M.; Grin, Y. Local atomic arrangements and band structure of boron carbide. Angew. Chem. 2018, 130, 6238–6243. [Google Scholar] [CrossRef]
- Jay, A.; Hardouin Duparc, O.; Sjakste, J.; Vast, N. Theoretical phase diagram of boron carbide from ambient to high pressure and temperature. J. Appl. Phys. 2019, 125, 185902. [Google Scholar] [CrossRef]
- Vignesh, S.; JT, W.J.; Nagaveena, S.; Sharma, K.; Khan, A. Boron carbide dispersed epoxy composites for gamma radiation shielding applications. Vacuum 2022, 205, 111474. [Google Scholar]

| (Å) | Cell Volume (Å3) | Energy per Atom (eV/atom) | ||
|---|---|---|---|---|
| Calculation | ||||
| Present work | 5.185 | 65.89 | 111.12 | −7.239 |
| Taylor et al. (2012) [28] | 5.190 | 66.01 | 112.09 | |
| Materials Project [74] | 5.180 | 65.95 | 110.65 | |
| Dekura et al. (2010) [72] | 5.110 | 66.00 | −7.231 | |
| Bylander et al. (1990) [73] | 5.182 | 65.61 | ||
| Experiment | ||||
| Kwei et al. (1996) [70] | 5.155 | 65.67 | ||
| McClellan et al. (2001) [71] | 5.190 | 65.18 |
| (GPa) | ||||||
|---|---|---|---|---|---|---|
| Present work | 465 | 125 | 103 | 36 | 498 | 175 |
| Taylor et al. (2012) [28] | 486 | 188 | 64 | 14 | 518 | 133 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheikhi, S.; Stroberg, W.; Hogan, J.D. Temperature-Dependent Elastic Properties of B4C from First-Principles Calculations and Phonon Modeling. Ceramics 2024, 7, 235-249. https://doi.org/10.3390/ceramics7010015
Sheikhi S, Stroberg W, Hogan JD. Temperature-Dependent Elastic Properties of B4C from First-Principles Calculations and Phonon Modeling. Ceramics. 2024; 7(1):235-249. https://doi.org/10.3390/ceramics7010015
Chicago/Turabian StyleSheikhi, Sara, Wylie Stroberg, and James D. Hogan. 2024. "Temperature-Dependent Elastic Properties of B4C from First-Principles Calculations and Phonon Modeling" Ceramics 7, no. 1: 235-249. https://doi.org/10.3390/ceramics7010015
APA StyleSheikhi, S., Stroberg, W., & Hogan, J. D. (2024). Temperature-Dependent Elastic Properties of B4C from First-Principles Calculations and Phonon Modeling. Ceramics, 7(1), 235-249. https://doi.org/10.3390/ceramics7010015








