External Field Assisted Freeze Casting
Abstract
:1. Introduction
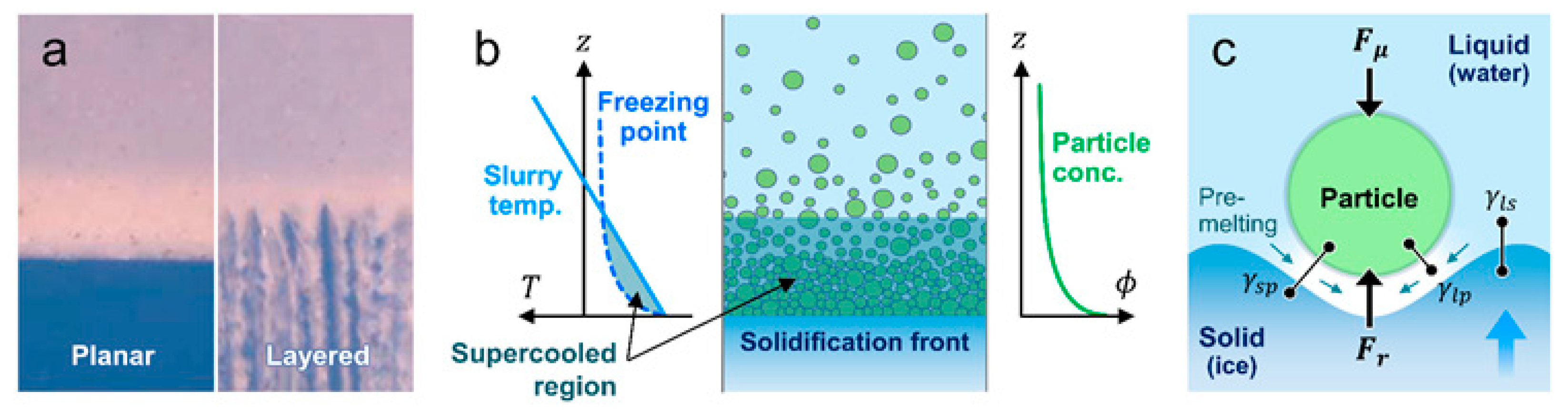
2. Constitutional Supercooling
3. Dominant Forces
3.1. Forces Exerted During Solidification
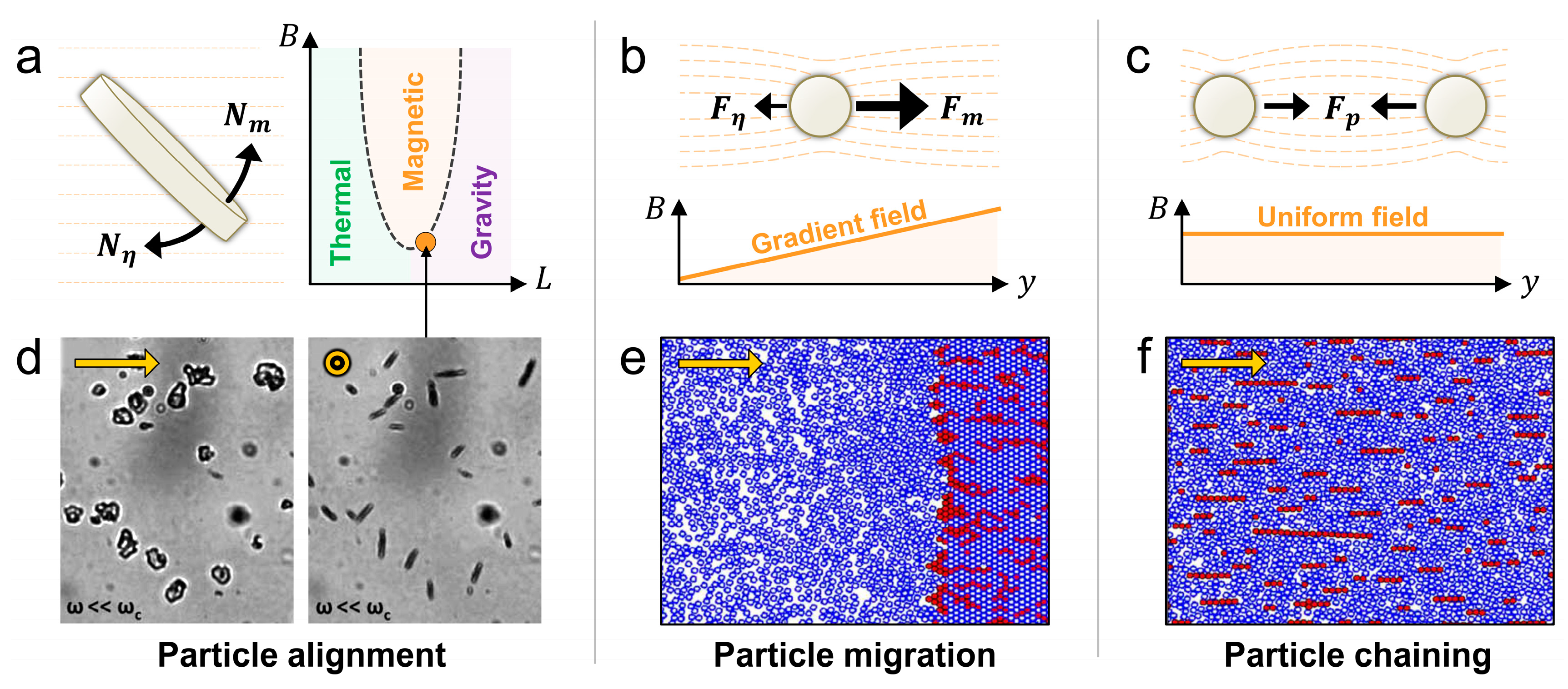
3.2. Forces Exerted by External Fields
3.2.1. Magnetic Force and Torque
3.2.2 Electric Force and Torque
3.2.3 Acoustic Force
3.3. Resistive Forces
4. Experimental Observations
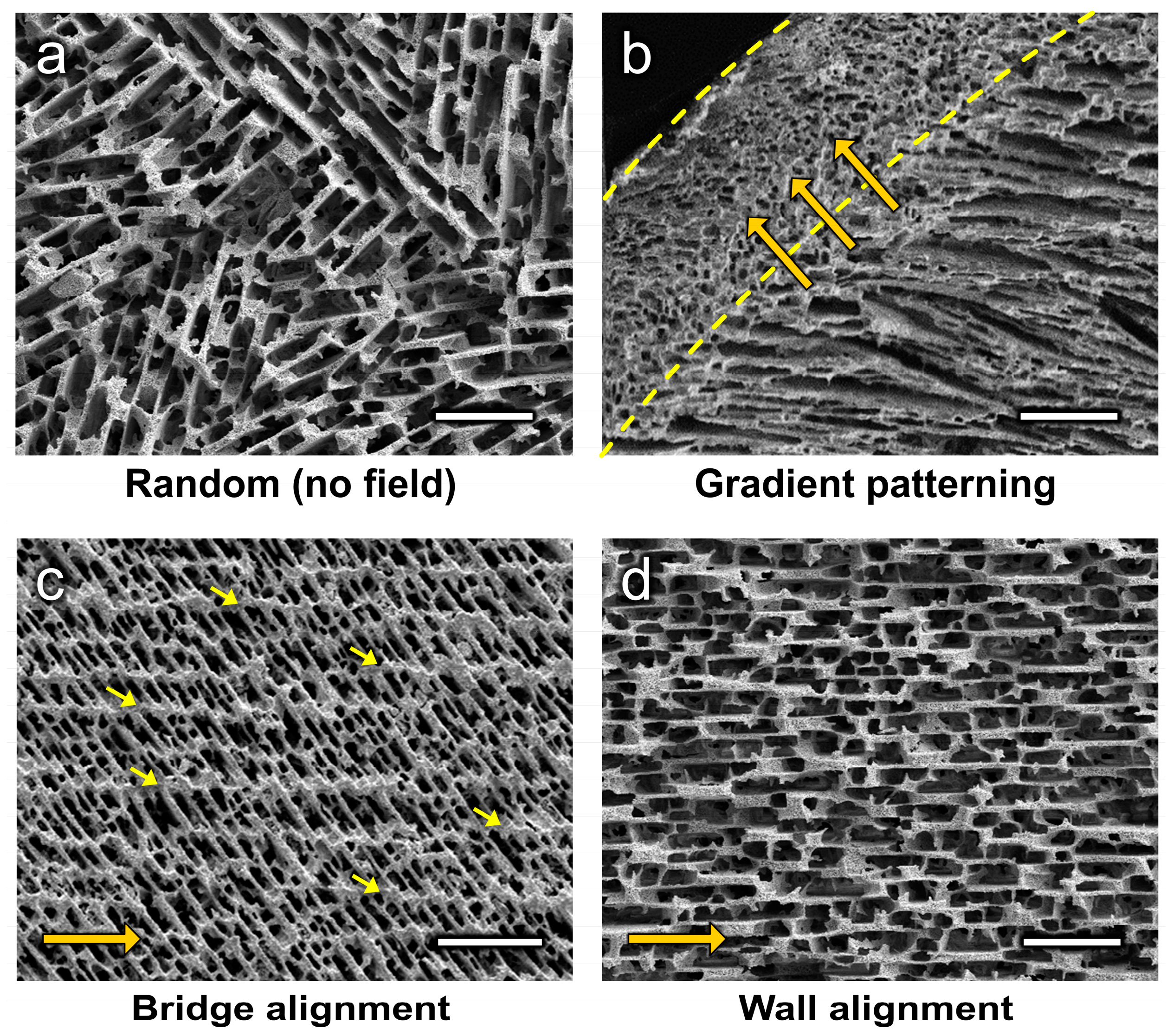
4.1. Gradient Patterning
4.1.1. Magnetic Fields
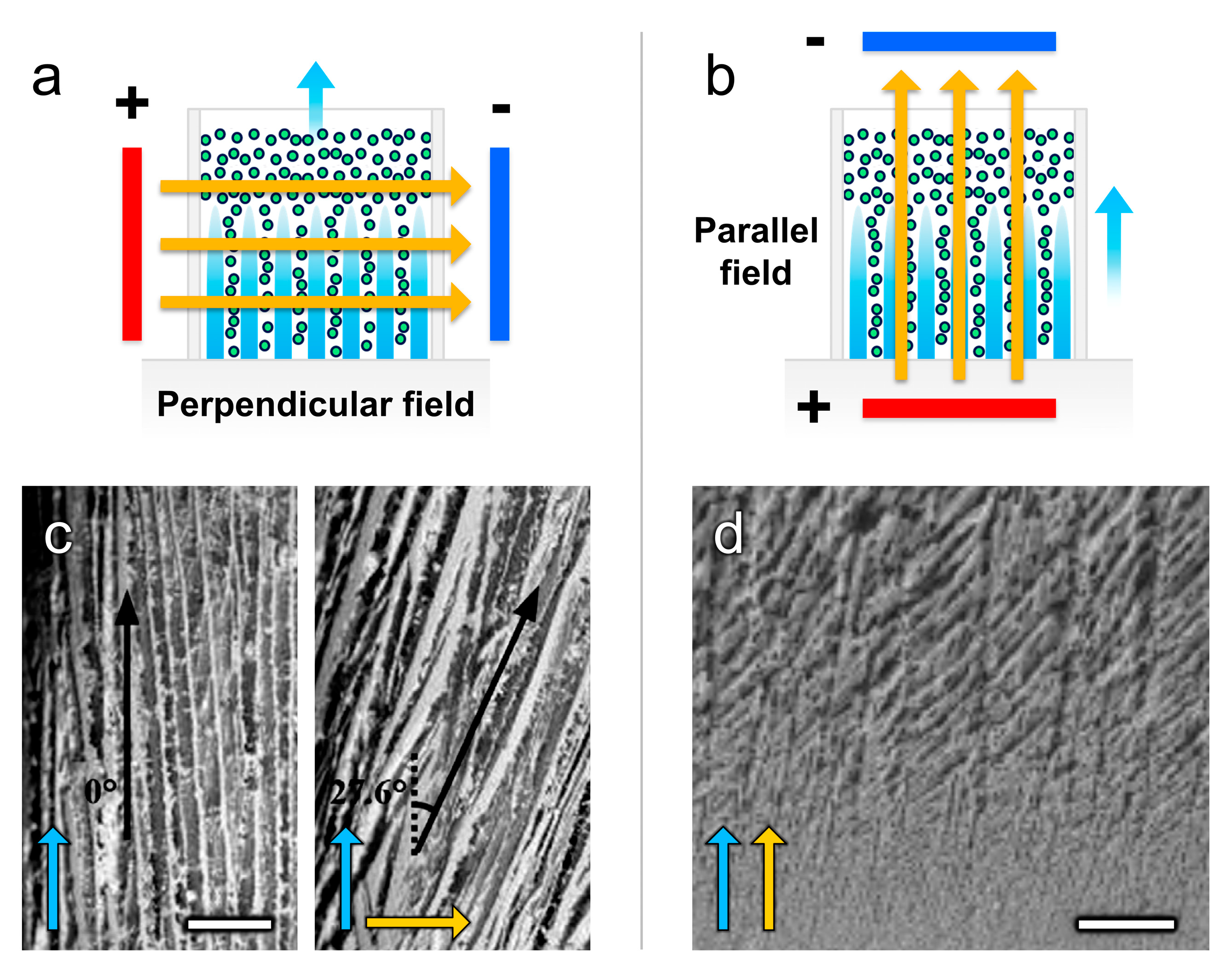
4.1.2. Electric Fields
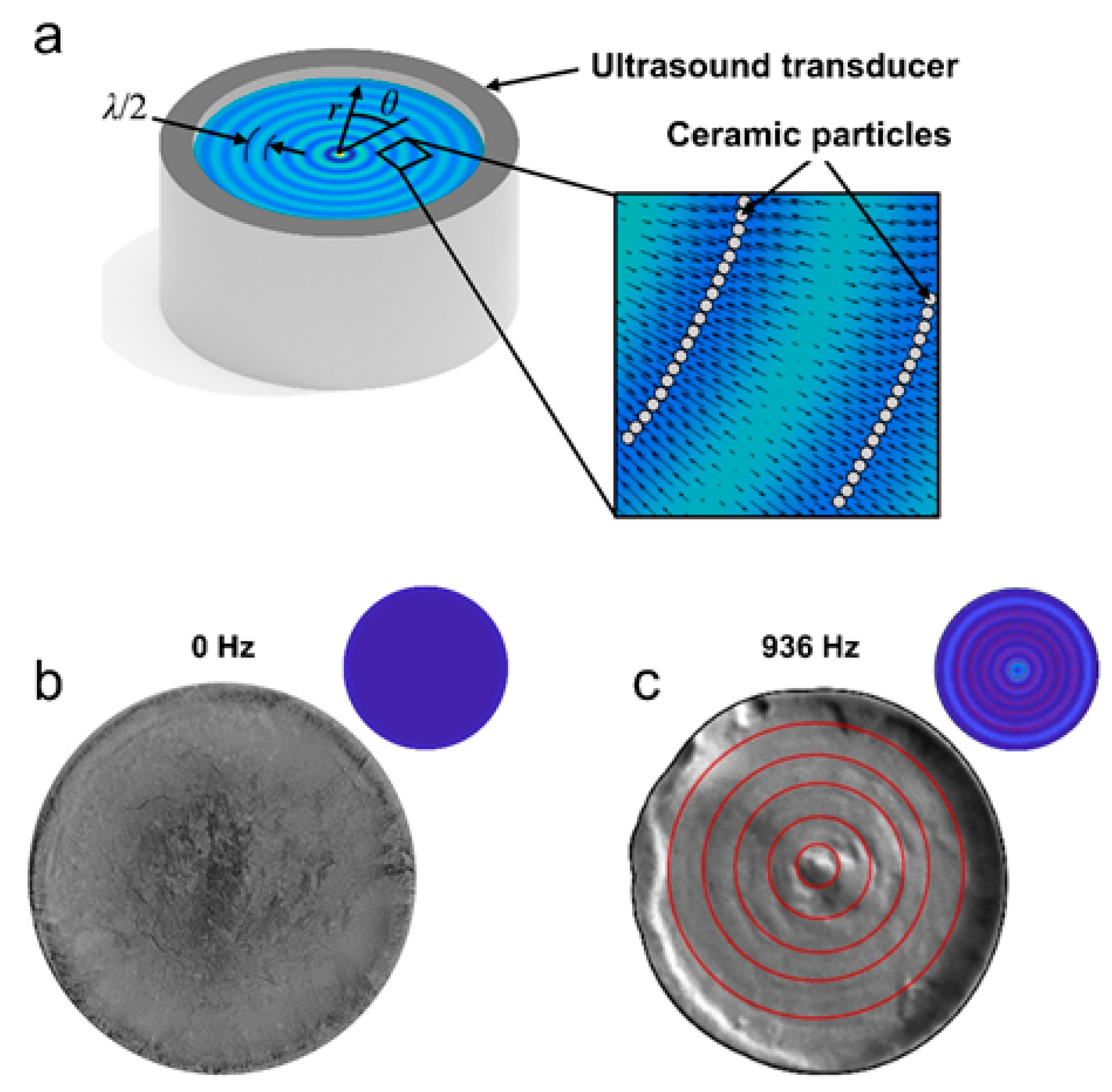
4.1.3. Acoustic Fields
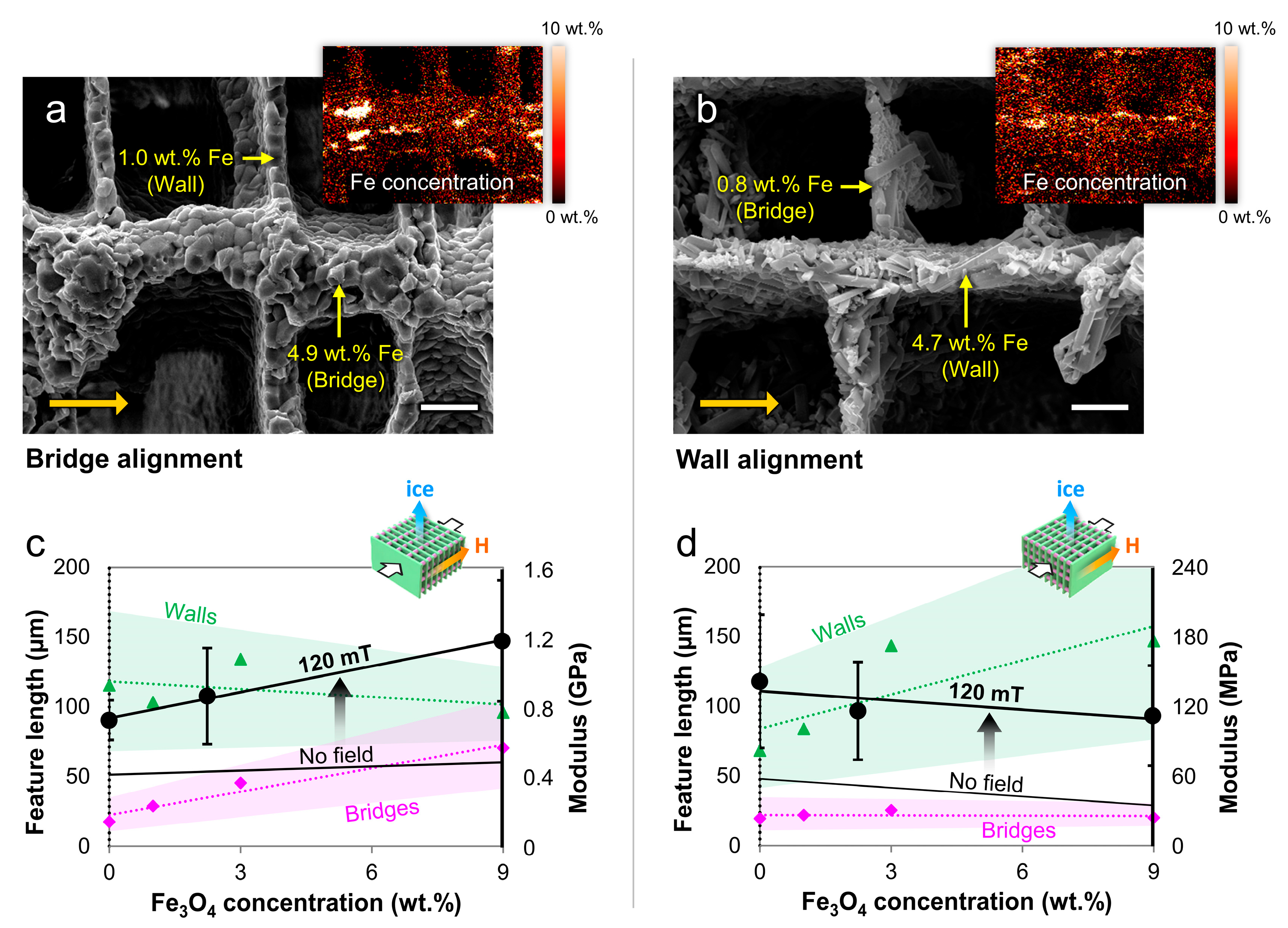
4.2. Microstructural Alignment
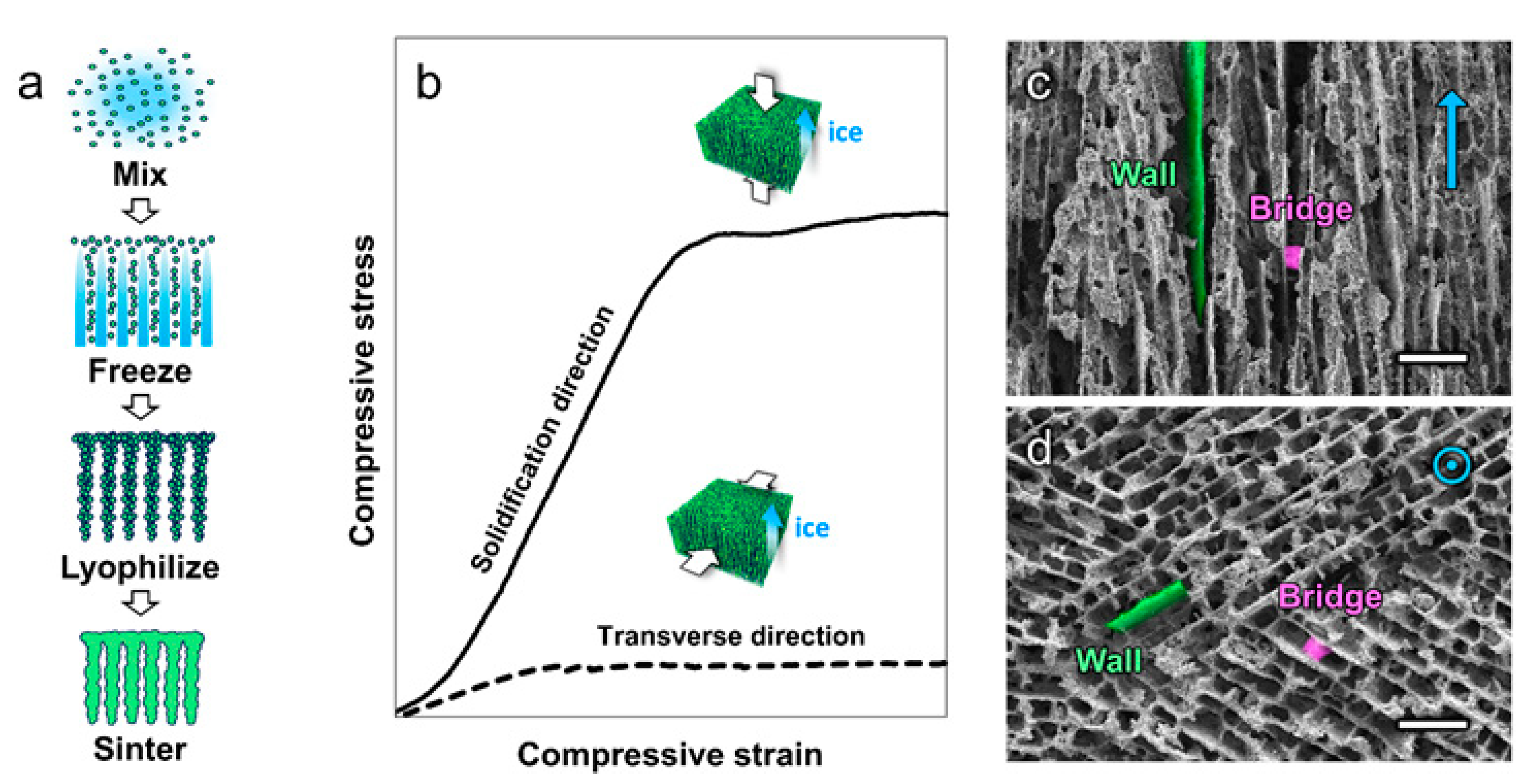
4.3. Mechanical Properties
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gibson, L.J. Cellular solids. Mrs Bull. 2003, 28, 270–274. [Google Scholar] [CrossRef]
- Gaudillere, C.; Garcia-Fayos, J.; Balaguer, M.; Serra, J.M. Enhanced Oxygen Separation through Robust Freeze-Cast Bilayered Dual-Phase Membranes. ChemSusChem 2014, 7, 2554–2561. [Google Scholar] [CrossRef] [PubMed]
- Deville, S.; Saiz, E.; Tomsia, A.P. Freeze casting of hydroxyapatite scaffolds for bone tissue engineering. Biomaterials 2006, 27, 5480–5489. [Google Scholar] [CrossRef] [PubMed]
- Touri, R.; Moztarzadeh, F.; Sadeghian, Z.; Bizari, D.; Tahriri, M.; Mozafari, M. The Use of Carbon Nanotubes to Reinforce 45S5 Bioglass-Based Scaffolds for Tissue Engineering Applications. BioMed Res. Int. 2013, 2013, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Porter, M.M.; McKittrick, J. It’s tough to be strong: Advances in bioinspired structural ceramicbased materials. Am. Ceram. Soc. Bull. 2014, 93, 18–24. [Google Scholar]
- Gurlo, A.; Bekheet, M.F.; Selve, S.; Wang, X.; Simon, U.; Bahrami, A.; Pech-Canul, M.I.; Epping, J.D.; Soltani, N. Macroporous polymer-derived SiO2/SiOC monoliths freeze-cast from polysiloxane and amorphous silica derived from rice husk. J. Eur. Ceram. Soc. 2017, 37, 4809–4820. [Google Scholar] [CrossRef]
- Soltani, N.; Martínez-Bautista, R.; Bahrami, A.; Huerta Arcos, L.; Cassir, M.; Chávez Carvayar, J. Fabrication of aligned porous LaNi0.6Fe0.4O3 perovskite by water based freeze casting. Chem. Phys. Lett. 2018, 700, 138–144. [Google Scholar] [CrossRef]
- Bahrami, A.; Simon, U.; Soltani, N.; Zavareh, S.; Schmidt, J.; Pech-Canul, M.I.; Gurlo, A. Eco-fabrication of hierarchical porous silica monoliths by ice-templating of rice husk ash. Green Chem. 2017, 19, 188–195. [Google Scholar] [CrossRef]
- Herzog, A.; Klingner, R.; Vogt, U.; Graule, T. Wood-Derived Porous SiC Ceramics by Sol Infiltration and Carbothermal Reduction. J. Am. Ceram. Soc. 2004, 87, 784–793. [Google Scholar] [CrossRef]
- Cao, J.; Rambo, C.R.; Sieber, H. Preparation of Porous Al2O3-Ceramics by Biotemplating of Wood. J. Porous Mater. 2004, 11, 163–172. [Google Scholar] [CrossRef]
- Pokhrel, A.; Seo, D.N.; Lee, S.T.; Kim, I.J. Processing of porous ceramics by direct foaming: A review. J. Korean Ceram. Soc. 2013, 50, 93–102. [Google Scholar] [CrossRef]
- Colombo, P.; Hellmann, J.R. Ceramic foams from preceramic polymers. Mater. Res. Innov. 2002, 6, 260–272. [Google Scholar] [CrossRef]
- Bose, S.; Vahabzadeh, S.; Bandyopadhyay, A. Bone tissue engineering using 3D printing. Mater. Today 2013, 16, 496–504. [Google Scholar] [CrossRef]
- Sajadi, S.M.; Owuor, P.S.; Schara, S.; Woellner, C.F.; Rodrigues, V.; Vajtai, R.; Lou, J.; Galvão, D.S.; Tiwary, C.S.; Ajayan, P.M. Multiscale Geometric Design Principles Applied to 3D Printed Schwarzites. Adv. Mater. 2018, 30, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Hench, L.L.; West, J.K. The sol-gel process. Chem. Rev. 1990, 90, 33–72. [Google Scholar] [CrossRef]
- Saboori, A.; Rabiee, M.; Moztarzadeh, F.; Sheikhi, M.; Tahriri, M.; Karimi, M. Synthesis, characterization and in vitro bioactivity of sol-gel-derived SiO2–CaO–P2O5–MgO bioglass. Mater. Sci. Eng. C 2009, 29, 335–340. [Google Scholar] [CrossRef]
- Doshi, J.; Reneker, D.H. Electrospinning Process and Applications of Electrospun Fibers. J. Electrostat. 1995, 35, 151–160. [Google Scholar] [CrossRef]
- Deville, S. Freeze-casting of porous ceramics: A review of current achievements and issues. Adv. Eng. Mater. 2008, 10, 155–169. [Google Scholar] [CrossRef]
- Mutsuddy, B.C.; Ford, R.G. Ceramic Injection Molding, 1st ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Atre, S.V.; Weaver, T.J.; German, R.M. Injection Molding of Metals and Ceramics; Metal Powder Industries Federation: Princeton, NJ, USA, 1998. [Google Scholar] [CrossRef]
- Fanelli, A.J.; Silvers, R.D.; Frei, W.S.; Burlew, J.V.; Marsh, G.B. New aqueous injection molding process for ceramic powders. J. Am. Ceram. Soc. 1989, 72, 1833–1836. [Google Scholar] [CrossRef]
- Janney, M.A.; Omatete, O.O.; Walls, C.A.; Nunn, S.D.; Ogle, R.J.; Westmoreland, G. Development of Low-Toxicity Gelcasting Systems. J. Am. Ceram. Soc. 2005, 81, 581–591. [Google Scholar] [CrossRef]
- Omatete, O.O.; Strehlow, R.A.; Walls, C.A. Drying of Gelcast Ceramics; Oak Ridge National Lab.: Oak Ridge, TN, USA, 1991. [Google Scholar]
- Chen, Y.; Xie, Z.; Yang, J.; Huang, Y. Alumina casting based on gelation of gelatine. J. Eur. Ceram. Soc. 1999, 19, 271–275. [Google Scholar] [CrossRef]
- Schilling, C.H.; Bellman, R.A.; Smith, R.M.; Goel, H.; Giesche, H. Plasticizing Aqueous Suspensions of Concentrated Alumina with Maltodextrin Sugar. J. Am. Ceram. Soc. 2004, 82, 57–66. [Google Scholar] [CrossRef]
- Russell-Floyd, R.S.; Harris, B.; Cooke, R.G.; Laurie, J.; Hammett, F.W.; Jones, R.W.; Wang, T. Application of Sol-Gel Processing Techniques for the Manufacture of Fiber-Reinforced Ceramics. J. Am. Ceram. Soc. 1993, 76, 2635–2643. [Google Scholar] [CrossRef]
- Sofie, S.W.; Dogan, F. Freeze casting of aqueous alumina slurries with glycerol. J. Am. Ceram. Soc. 2001, 84, 1459–1464. [Google Scholar] [CrossRef]
- Deville, S. Freeze-casting of porous biomaterials: Structure, properties and opportunities. Materials 2010, 3, 1913–1927. [Google Scholar] [CrossRef]
- Shaga, A.; Shen, P.; Guo, R.F.; Jiang, Q.C. Effects of oxide addition on the microstructure and mechanical properties of lamellar SiC scaffolds and Al-Si-Mg/SiC composites prepared by freeze casting and pressureless infiltration. Ceram. Int. 2016, 42, 9653–9659. [Google Scholar] [CrossRef]
- Flauder, S.; Sajzew, R.; Müller, F.A. Mechanical properties of porous β-tricalcium phosphate composites prepared by ice-templating and poly(σ-caprolactone) impregnation. ACS Appl. Mater. Interfaces 2015, 7, 845–851. [Google Scholar] [CrossRef] [PubMed]
- Colard, C.A.L.; Cave, R.A.; Grossiord, N.; Covington, J.A.; Bon, S.A.F. Conducting nanocomposite polymer foams from lce-crystal-templated assembly of mixtures of colloids. Adv. Mater. 2009, 21, 2894–2898. [Google Scholar] [CrossRef]
- Francis, N.L.; Hunger, P.M.; Donius, A.E.; Wegst, U.G.K.; Wheatley, M.A. Strategies for neurotrophin-3 and chondroitinase ABC release from freeze-cast chitosan–alginate nerve-guidance scaffolds. J. Tissue Eng. Regen. Med. 2017, 11, 285–294. [Google Scholar] [CrossRef] [PubMed]
- Plunk, A.A.; Dunand, D.C. Iron foams created by directional freeze casting of iron oxide, reduction and sintering. Mater. Lett. 2017, 191, 112–115. [Google Scholar] [CrossRef]
- Park, H.; Choi, M.; Choe, H.; Dunand, D.C. Microstructure and compressive behavior of ice-templated copper foams with directional, lamellar pores. Mater. Sci. Eng. A 2017, 679, 435–445. [Google Scholar] [CrossRef]
- Bouville, F.; Portuguez, E.; Chang, Y.; Messing, G.L.; Stevenson, A.J.; Maire, E.; Courtois, L.; Deville, S. Templated Grain Growth in Macroporous Materials. J. Am. Ceram. Soc. 2014, 1742, 1736–1742. [Google Scholar] [CrossRef]
- Naleway, S.E.; Yu, C.F.; Porter, M.M.; Sengupta, A.; Iovine, P.M.; Meyers, M.A.; McKittrick, J. Bioinspired composites from freeze casting with clathrate hydrates. Mater. Des. 2015, 71, 62–67. [Google Scholar] [CrossRef]
- Fukasawa, T.; Ando, M.; Ohji, T.; Kanzaki, S. Synthesis of porous ceramics with complex pore structure by freeze-dry processing. J. Am. Ceram. Soc. 2001, 84, 230–232. [Google Scholar] [CrossRef]
- Mazur, P. Cryobiology: The freezing of biological systems. Science 1970, 168, 939–949. [Google Scholar] [CrossRef]
- Gay, G.; Azouni, M.A. Forced migration of nonsoluble and soluble metallic pollutants ahead of a liquid—solid interface during unidirectional freezing of dilute clayey suspensions. Cryst. Growth Des. 2002, 2, 135–140. [Google Scholar] [CrossRef]
- Northcott, K.A.; Snape, I.; Scales, P.J.; Stevens, G.W. Contaminated water treatment in cold regions: An example of coagulation and dewatering modelling in Antarctica. Cold Reg. Sci. Technol. 2005, 41, 61–72. [Google Scholar] [CrossRef]
- Zhang, H. Ice Templating and Freeze-Drying for Porous Materials and Their Applications, 1st ed.; Wiley-VCH: Hoboken, NJ, USA, 2018. [Google Scholar]
- Barrow, M.; Eltmimi, A.; Ahmed, A.; Myers, P.; Zhang, H. Frozen polymerization for aligned porous structures with enhanced mechanical stability, conductivity, and as stationary phase for HPLC. J. Mater. Chem. 2012, 22, 11615. [Google Scholar] [CrossRef]
- Ghadkolai, M.A.; Creager, S.; Nanda, J.; Bordia, R.K. Freeze Tape Cast Thick Mo Doped Li4Ti5O12 Electrodes for Lithium-Ion Batteries. J. Electrochem. Soc. 2017, 164, A2603–A2610. [Google Scholar] [CrossRef]
- Choi, H.; Park, H.; Um, J.H.; Yoon, W.S.; Choe, H. Processing and characterization of titanium dioxide grown on titanium foam for potential use as Li-ion electrode. Appl. Surf. Sci. 2017, 411, 363–367. [Google Scholar] [CrossRef]
- Kang, J.S.; Noh, Y.; Kim, J.; Choi, H.; Jeon, T.H.; Ahn, D.; Kim, J.; Yu, S.; Park, H.; Yum, J.; et al. Iron Oxide Photoelectrode with Multidimensional Architecture for Highly Efficient Photoelectrochemical Water Splitting. Angew. Chem. 2017, 129, 6683–6688. [Google Scholar] [CrossRef]
- Liu, H.; Liu, X.; Mu, S.; Wang, S.; Wang, S.; Li, L.; Giannelis, E.P. A novel fabrication approach for three-dimensional hierarchical porous metal oxide/carbon nanocomposites for enhanced solar photocatalytic performance. Catal. Sci. Technol. 2017, 7, 1965–1970. [Google Scholar] [CrossRef]
- Nam, K.; Kim, H.G.; Choi, H.; Park, H.; Kang, J.S.; Sung, Y.E.; Lee, H.C.; Choe, H. Morphology and Gas-Sensing Properties of Tin Oxide Foams with Dual Pore Structure. J. Electron. Mater. 2017, 46, 3748–3756. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, M.; Chen, J.; Fan, S.; Liang, J.; Ding, L.; Chen, S. Flexible chitosan/carbon nanotubes aerogel, a robust matrix for in-situ growth and non-enzymatic biosensing applications. Sens. Actuators B Chem. 2016, 232, 750–757. [Google Scholar] [CrossRef]
- Nguyen, T.N.P.; Ulrich, J. Requirements for Designing a Freeze Casting Process for Drugs-Rheological Properties of Suspensions. Chem. Eng. Technol. 2016, 39, 1231–1236. [Google Scholar] [CrossRef]
- Mashl, S.J.; Flores, R.A.; Trivedi, R. Dynamics of Solidification in 2% Corn Starch-Water Mixtures: Effect of Variations in Freezing Rate on Product Homogeneity. J. Food Sci. 1996, 61, 760–765. [Google Scholar] [CrossRef]
- Nguyen, P.T.N.; Ulrich, J. Fast Dispersible Cocoa Tablets: A Case Study of Freeze-Casting Applied to Foods. Chem. Eng. Technol. 2014, 37, 1376–1382. [Google Scholar] [CrossRef]
- Deville, S. Freezing Colloids:Observations, Principles, Control, and Use; Springer: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Bareggi, A.; Maire, E.; Lasalle, A.; Deville, S. Dynamics of the freezing front during the solidification of a colloidal alumina aqueous suspension: In situ X-ray radiography, tomography, and modeling. J. Am. Ceram. Soc. 2011, 94, 3570–3578. [Google Scholar] [CrossRef]
- Rempel, A.W.; Worster, M.G. Interaction between a particle and an advancing solidification front. J. Cryst. Growth 1999, 205, 427–440. [Google Scholar] [CrossRef]
- Zhang, H.; Cooper, A.I. Aligned porous structures by directional freezing. Adv. Mater. 2007, 19, 1529–1533. [Google Scholar] [CrossRef]
- Zhang, H.; Hussain, I.; Brust, M.; Butler, M.F.; Rannard, S.P.; Cooper, A.I. Aligned two- and three-dimensional structures by directional freezing of polymers and nanoparticles. Nat. Mater. 2005, 4, 787–793. [Google Scholar] [CrossRef] [PubMed]
- Fu, Q.; Rahaman, M.N.; Dogan, F.; Bal, B.S. Freeze casting of porous hydroxyapatite scaffolds. I. Processing and general microstructure. J. Biomed. Mater. Res. Part B Appl. Biomater. 2008, 86, 125–135. [Google Scholar] [CrossRef] [PubMed]
- Fu, Q.; Rahaman, M.N.; Dogan, F.; Bal, B.S. Freeze casting of porous hydroxyapatite scaffolds. II. Sintering, microstructure, and mechanical behavior. J. Biomed. Mater. Res. Part B Appl. Biomater. 2008, 86, 514–522. [Google Scholar] [CrossRef]
- Deville, S.; Saiz, E.; Tomsia, A.P. Ice-templated porous alumina structures. Acta Mater. 2007, 55, 1965–1974. [Google Scholar] [CrossRef]
- Deville, S.; Saiz, E.; Nalla, R.K.; Tomsia, A.P. Freezing as a Path to Build Complex Composites. Science 2006, 311, 515–518. [Google Scholar] [CrossRef] [PubMed]
- Delattre, B.; Bai, H.; Ritchie, R.O.; De Coninck, J.; Tomsia, A.P. Unidirectional freezing of ceramic suspensions: In situ x-ray investigation of the effects of additives. ACS Appl. Mater. Interfaces 2014, 6, 159–166. [Google Scholar] [CrossRef] [PubMed]
- Scotti, K.L.; Dunand, D.C. Freeze casting—A review of processing, microstructure and properties via the open data repository, FreezeCasting.net. Prog. Mater. Sci. 2018, 94, 243–305. [Google Scholar] [CrossRef]
- Liu, X.; Rahaman, M.; Fu, Q. Oriented bioactive glass (13-93) scaffolds with controllable pore size by unidirectional freezing of camphene-based suspensions: Microstructure and mechanical response. Acta Biomater. 2011, 7, 406–416. [Google Scholar] [CrossRef]
- Porter, M.M.; Niksiar, P.; Mckittrick, J. Microstructural Control of Colloidal-Based Ceramics by Directional Solidification Under Weak Magnetic Fields. J. Am. Ceram. Soc. 2016, 1926. [Google Scholar] [CrossRef]
- Porter, M.M.; Imperio, R.; Wen, M.; Meyers, M.A.; McKittrick, J. Bioinspired scaffolds with varying pore architectures and mechanical properties. Adv. Funct. Mater. 2014, 24, 1978–1987. [Google Scholar] [CrossRef]
- Munch, E.; Saiz, E.; Tomsia, A.P.; Deville, S. Architectural control of freeze-cast ceramics through additives and templating. J. Am. Ceram. Soc. 2009, 92, 1534–1539. [Google Scholar] [CrossRef]
- Bouville, F.; Maire, E.; Meille, S.; Van de Moortèle, B.; Stevenson, A.J.; Deville, S. Strong, tough and stiff bioinspired ceramics from brittle constituents. Nat. Mater. 2014, 13, 508–514. [Google Scholar] [CrossRef] [PubMed]
- Bai, H.; Chen, Y.; Delattre, B.; Tomsia, A.P.; Ritchie, R.O. Bioinspired large-scale aligned porous materials assembled with dual temperature gradients. Sci. Adv. 2015, 1, e1500849. [Google Scholar] [CrossRef] [PubMed]
- Bai, H.; Walsh, F.; Gludovatz, B.; Delattre, B.; Huang, C.; Chen, Y.; Tomsia, A.P.; Ritchie, R.O. Bioinspired Hydroxyapatite/Poly (methyl methacrylate) Composite with a Nacre-Mimetic Architecture by a Bidirectional Freezing Method. Adv. Mater. 2016, 28, 50–56. [Google Scholar] [CrossRef]
- Bai, H.; Wang, D.; Delattre, B.; Gao, W.; De Coninck, J.; Li, S.; Tomsia, A.P. Biomimetic gradient scaffold from ice-templating for self-seeding of cells with capillary effect. Acta Biomater. 2015, 20, 113–119. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, A.; Gong, Q.; Liang, J. Carbon nanotube-chitosan composite beads with radially aligned channels and nanotube-exposed walls for bilirubin adsorption. Adv. Eng. Mater. 2015, 17, 460–466. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhao, K.; Wu, Z.P. Structure control of hydroxyapatite ceramics via an electric field assisted freeze casting method. Ceram. Int. 2015, 41, 8599–8604. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, L.; Han, J. Preparation of a dense/porous biLayered ceramic by applying an electric field during freeze casting. J. Am. Ceram. Soc. 2009, 92, 1874–1876. [Google Scholar] [CrossRef]
- Nelson, I.; Ogden, T.A.; Khateeb, S.A.; Graser, J.; Sparks, T.D.; Abbott, J.J.; Naleway, S.E. Freeze casting of surface-magnetized iron (II,III) oxide particle in a uniform static magnetic field generated by a Helmholtz coil. Adv. Eng. Mater. 2019. [Google Scholar] [CrossRef]
- Nelson, I.; Naleway, S. Intrinsic and extrinsic control of freeze casting. J. Mater. Sci. Technol. 2019. [Google Scholar] [CrossRef]
- Porter, M.M.; Yeh, M.; Strawson, J.; Goehring, T.; Lujan, S.; Siripasopsotorn, P.; Meyers, M.A.; McKittrick, J. Magnetic freeze casting inspired by nature. Mater. Sci. Eng. A 2012, 556, 741–750. [Google Scholar] [CrossRef]
- Porter, M.M.; Meraz, L.; Calderon, A.; Choi, H.; Chouhan, A.; Wang, L.; Meyers, M.A.; McKittrick, J. Torsional properties of helix-reinforced composites fabricated by magnetic freeze casting. Compos. Struct. 2015, 119, 174–184. [Google Scholar] [CrossRef]
- Frank, M.B.; Naleway, S.E.; Haroush, T.; Liu, C.-H.; Siu, S.H.; Ng, J.; Torres, I.; Ismail, A.; Karandikar, K.; Porterd, M.M.; et al. Stiff, porous scaffolds from magnetized alumina particles aligned by magnetic freeze casting. Mater. Sci. Eng. C 2017, 77, 484–492. [Google Scholar] [CrossRef] [PubMed]
- Frank, M.B.; Hei Siu, S.; Karandikar, K.; Liu, C.H.; Naleway, S.E.; Porter, M.M.; Graeve, O.A.; McKittrick, J. Synergistic structures from magnetic freeze casting with surface magnetized alumina particles and platelets. J. Mech. Behav. Biomed. Mater. 2017, 76, 153–163. [Google Scholar] [CrossRef]
- Niksiar, P.; Frank, M.; McKittrick, J.; Porter, M. Microstructural evolution of paramagnetic materials by Magnetic Freeze Casting. J. Mater. Res. Technol. In press.
- Tang, Y.F.; Zhao, K.; Wei, J.Q.; Qin, Y.S. Fabrication of aligned lamellar porous alumina using directional solidification of aqueous slurries with an applied electrostatic field. J. Eur. Ceram. Soc. 2010, 30, 1963–1965. [Google Scholar] [CrossRef]
- Ogden, T.A.; Prisbrey, M.; Nelson, I.; Raeymaekers, B.; Naleway, S.E. Ultrasound freeze casting: Fabricating bioinspired porous scaffolds through combining freeze casting and ultrasound directed self-assembly. Mater. Des. 2019, 164, 107561. [Google Scholar] [CrossRef]
- Jung, D.H.; Yang, J.H.; Jhon, M.S. The effect of an external electric field on the structure of liquid water using molecular dynamics simulations. Chem. Phys. 1999, 244, 331–337. [Google Scholar] [CrossRef]
- Pang, X.F.; Bo, D. The changes of macroscopic features and microscopic structures of water under influence of magnetic field. Phys. B Condens. Matter 2008, 403, 3571–3577. [Google Scholar] [CrossRef]
- Dalvi-Isfahan, M.; Hamdami, N.; Xanthakis, E.; Le-Bail, A. Review on the control of ice nucleation by ultrasound waves, electric and magnetic fields. J. Food Eng. 2017, 195, 222–234. [Google Scholar] [CrossRef]
- Tang, Y.; Qiu, S.; Miao, Q.; Wu, C. Fabrication of lamellar porous alumina with axisymmetric structure by directional solidification with applied electric and magnetic fields. J. Eur. Ceram. Soc. 2016, 36, 1233–1240. [Google Scholar] [CrossRef]
- Mirshahghassemi, S.; Ebner, A.D.; Cai, B.; Lead, J.R. Application of high gradient magnetic separation for oil remediation using polymer-coated magnetic nanoparticles. Sep. Purif. Technol. 2017, 179, 328–334. [Google Scholar] [CrossRef]
- Podoynitsyn, S.N.; Sorokina, O.N.; Kovarski, A.L.; Levin, I.I.; Simakin, S.B. High-Gradient Magnetic Separation of Nanoparticles with Ferromagnetic Track-Etched Membrane. IEEE Trans. Magn. 2018, 54. [Google Scholar] [CrossRef]
- Le Ferrand, H.; Bouville, F.; Niebel, T.P.; Studart, A.R. Magnetically assisted slip casting of bioinspired heterogeneous composites. Nat. Mater. 2015, 14, 1172–1179. [Google Scholar] [CrossRef]
- Martin, J.J.; Fiore, B.E.; Erb, R.M. Designing bioinspired composite reinforcement architectures via 3D magnetic printing. Nat. Commun. 2015, 6, 8641. [Google Scholar] [CrossRef]
- Kokkinis, D.; Schaffner, M.; Studart, A.R. Multimaterial magnetically assisted 3D printing of composite materials. Nat. Commun. 2015, 6, 8643. [Google Scholar] [CrossRef]
- Markx, G.H. The use of electric fields in tissue engineering: A review. Organogenesis 2008, 4, 11–17. [Google Scholar] [CrossRef]
- Demirörs, A.F.; Courty, D.; Libanori, R.; Studart, A.R. Periodically microstructured composite films made by electric- and magnetic-directed colloidal assembly. Proc. Natl. Acad. Sci. USA 2016, 113, 4623–4628. [Google Scholar] [CrossRef]
- Ran, W.; Saylor, J.R. A mechanistic explanation of the increase in particle scavenging in the ultrasonic scrubber. J. Aerosol Sci. 2015, 87, 88–101. [Google Scholar] [CrossRef]
- Santesson, S.; Nilsson, S. Airborne chemistry: Acoustic levitation in chemical analysis. Anal. Bioanal. Chem. 2004, 378, 1704–1709. [Google Scholar] [CrossRef]
- Simon, M.D.; Geim, A.K. Diamagnetic levitation: Flying frogs and floating magnets (invited). J. Appl. Phys. 2002, 87, 6200–6204. [Google Scholar] [CrossRef]
- Sirsi, S.R.; Borden, M.A. State-of-the-art materials for ultrasound-triggered drug delivery. Adv. Drug Deliv. Rev. 2014, 72, 3–14. [Google Scholar] [CrossRef] [PubMed]
- Deville, S. Ice-templating, freeze casting: Beyond materials processing. J. Mater. Res. 2013, 28, 2202–2219. [Google Scholar] [CrossRef]
- Muldrew, K.; Novak, K.; Yang, H.; Zernicke, R.; Schachar, N.S.; McGann, L.E. Cryobiology of articular cartilage: Ice morphology and recovery of chondrocytes. Cryobiology 2000, 40, 102–109. [Google Scholar] [CrossRef] [PubMed]
- Mutou, Y.; Watanabe, K.; Ishizaki, T.; Mizoguchi, M. Microscopic Observation of Ice Lensing and Frost Heaves in Glass Beads. In Proceedings of the 7th International Conference Permafrost, Yellowknife, NT, Canada, 23–27 June 1998. [Google Scholar]
- Peppin, S.S.L.; Elliott, J.A.W.; Worster, M.G. Solidification of colloidal suspensions. J. Fluid Mech. 2006, 554, 147. [Google Scholar] [CrossRef]
- Kurz, W.; Fisher, D.J. Fundamentals of Solidification; Trans Tech Publications: Aedermannsdorf, Switzerland, 1986. [Google Scholar]
- Huppert, H.E. The fluid mechanics of solidification. J. Fluid Mech. 1990, 212, 209. [Google Scholar] [CrossRef]
- Huang, T.H.; Huang, T.H.; Lin, Y.S.; Chang, C.H.; Chen, P.Y.; Chang, S.W.; Chen, C.S. Phase-Field Modeling of Microstructural Evolution by Freeze-Casting. Adv. Eng. Mater. 2017, 1700343. [Google Scholar] [CrossRef]
- Ghosh, D.; Kang, H.; Banda, M.; Kamaha, V. Influence of anisotropic grains (platelets) on the microstructure and uniaxial compressive response of ice-templated sintered alumina scaffolds. Acta Mater. 2017, 125, 1–14. [Google Scholar] [CrossRef]
- Zuo, K.H.; Zeng, Y.P.; Jiang, D. Effect of polyvinyl alcohol additive on the pore structure and morphology of the freeze-cast hydroxyapatite ceramics. Mater. Sci. Eng. C 2010, 30, 283–287. [Google Scholar] [CrossRef]
- Wu, J.; Luo, B.; Liu, X.; Zhang, L. Control of the structure and mechanical property of porous WS2 scaffold during freeze casting. J. Porous Mater. 2017, 25, 37–43. [Google Scholar] [CrossRef]
- Zuo, K.H.; Zeng, Y.P.; Jiang, D. Properties of microstructure-controllable porous yttria-stabilized ziroconia ceramics fabricated by freeze casting. Int. J. Appl. Ceram. Technol. 2008, 5, 198–203. [Google Scholar] [CrossRef]
- Wettlaufer, J.S.; Worster, M.G. Premelting Dynamics. Annu. Rev. Fluid Mech. 2006, 38, 427–452. [Google Scholar] [CrossRef]
- Peppin, S.S.L.; Worster, M.G.; Wettlaufer, J.S. Morphological instability in freezing colloidal suspensions. Proc. R. Soc. A Math. Phys. Eng. Sci. 2006, 463, 723–733. [Google Scholar] [CrossRef]
- Wang, L.; You, J.; Wang, Z.; Wang, J.; Lin, X. Interface instability modes in freezing colloidal suspensions: Revealed from onset of planar instability. Sci. Rep. 2016, 6, 23358. [Google Scholar] [CrossRef] [PubMed]
- Peppin, S.S.L.; Wettlaufer, J.S.; Worster, M.G. Experimental verification of morphological instability in freezing aqueous colloidal suspensions. Phys. Rev. Lett. 2008, 100, 1–4. [Google Scholar] [CrossRef] [PubMed]
- You, J.; Wang, L.; Wang, Z.; Li, J.; Wang, J.; Lin, X.; Huang, W. Interfacial undercooling in solidification of colloidal suspensions: Analyses with quantitative measurements. Sci. Rep. 2016, 6, 28434. [Google Scholar] [CrossRef] [PubMed]
- You, J.; Wang, L.; Wang, Z.; Li, J.; Wang, J.; Lin, X.; Huang, W. In situ observation the interface undercooling of freezing colloidal suspensions with differential visualization method. Rev. Sci. Instrum. 2015, 084901. [Google Scholar] [CrossRef]
- Gilpin, R.R. A model of the ‘liquid-like’ layer between ice and a substrate with applications to wire regelation and particle migration. J. Colloid Interface Sci. 1979, 68, 235–251. [Google Scholar] [CrossRef]
- Sadtchenko, V.; Ewing, G.E.; Sadtchenko, V.; Ewing, G.E. Interfacial melting of thin ice films: An infrared study. J. Chem. Phys. 2002, 4686. [Google Scholar] [CrossRef]
- Jellinek, H.H. Liquid-like (transition) layer on ice. J. Colloid Interface Sci. 1967, 25, 192–205. [Google Scholar] [CrossRef]
- Anderson, D.M. The interface between ice and silicate surfaces. J. Colloid Interface Sci. 1967, 25, 174–191. [Google Scholar] [CrossRef]
- Dash, J.G.; Fu, H.; Wettlaufer, J.S. The premelting of ice and its environmental consequences. Rep. Prog. Phys. 1995, 58, 115–167. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Wettlaufer, J.; Worster, M.; Wilen, L.; Dash, J. A Theory of Premelting Dynamics for all Power Law Forces. Phys. Rev. Lett. 1996, 76, 3602–3605. [Google Scholar] [CrossRef] [PubMed]
- Woodruff, D.P. The Solid-Liquid Interface; Cambridge University Press: Cambridge, UK, 1973. [Google Scholar]
- Dash, J.G.; Rempel, A.W.; Wettlaufer, J.S. The physics of premelted ice and its geophysical consequences. Rev. Mod. Phys. 2006, 78, 695–741. [Google Scholar] [CrossRef]
- Wettlaufer, J.S.; Worster, M.G. Dynamics of premelted films: Frost heave in a capillary. Phys. Rev. E 1995, 51, 4679. [Google Scholar] [CrossRef]
- Style, R.W.; Peppin, S.S.L.; Cocks, A.C.F.; Wettlaufer, J.S. Ice-lens formation and geometrical supercooling in soils and other colloidal materials. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2011, 84, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Peppin, S.; Majumdar, A.; Style, R.; Sander, G. Frost Heave in Colloidal Soils. SIAM J. Appl. Math. 2011, 71, 1717–1732. [Google Scholar] [CrossRef]
- Peppin, S.S.L.; Style, R.W. The Physics of Frost Heave and Ice-Lens Growth. Vadose Zone J. 2013, 12, 0. [Google Scholar] [CrossRef]
- Wilen, L.A.; Dash, J.G. Frost heave dynamics at a single crystal interface. Phys. Rev. Lett. 1995, 74, 5076–5079. [Google Scholar] [CrossRef]
- Jackson, K.A.; Chalmers, B. Freezing of liquids in porous media with special reference to frost heave in soils. J. Appl. Phys. 1958, 29, 1178–1181. [Google Scholar] [CrossRef]
- Everett, D.H. The thermodynamics of frost damage to porous solids. Trans. Faraday Soc. 1961, 57, 1541. [Google Scholar] [CrossRef]
- Jackson, K.A.; Uhlmann, D.R.; Chalmers, B. Frost heave in soils. J. Appl. Phys. 1966, 37, 848–852. [Google Scholar] [CrossRef]
- Rempel, A.W.; Worster, M.G. Particle trapping at an advancing solidification front with interfacial-curvature effects. J. Cryst. Growth 2001, 223, 420–432. [Google Scholar] [CrossRef]
- Liu, Z.; Muldrew, K.; Wan, R.G.; Elliott, J.A.W. Measurement of freezing point depression of water in glass capillaries and the associated ice front shape. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 2003, 67, 061602. [Google Scholar] [CrossRef]
- Kuhn, W.; Peterli, E.; Majer, H. Freezing point depression of gels produced by high polymer network. J. Polym. Sci. 1955, 16, 539–548. [Google Scholar] [CrossRef]
- Otero, L.; Rodríguez, A.C.; Pérez-Mateos, M.; Sanz, P.D. Effects of Magnetic Fields on Freezing: Application to Biological Products. Compr. Rev. Food Sci. Food Saf. 2016, 15, 646–667. [Google Scholar] [CrossRef]
- Yan, J.Y.; Patey, G.N. Heterogeneous Ice Nucleation Induced by Electric Fields. J. Phys. Chem. Lett. 2011, 2, 2555–2559. [Google Scholar] [CrossRef]
- Moore, E.B.; Molinero, V. Structural transformation in supercooled water controls the crystallization rate of ice. Nature 2011, 479, 506–508. [Google Scholar] [CrossRef] [PubMed]
- Petrenko, V.F.; Whitworth, R.W. Physics of Ice; OUP Oxford: Oxford, UK, 1999. [Google Scholar]
- Deville, S.; Maire, E.; Lasalle, A.; Bogner, A.; Gauthier, C.; Leloup, J.; Guizard, C. Influence of particle size on ice nucleation and growth during the ice-templating process. J. Am. Ceram. Soc. 2010, 93, 2507–2510. [Google Scholar] [CrossRef]
- Deville, S.; Maire, E.; Lasalle, A.; Bogner, A.; Gauthier, C.; Leloup, J.; Guizard, C. In Situ X-ray radiography and tomography observations of the solidification of aqueous alumina particles suspensions. Part II: Steady state. J. Am. Ceram. Soc. 2009, 92, 2497–2503. [Google Scholar] [CrossRef]
- Tang, Y.; Qiu, S.; Wu, C.; Miao, Q.; Zhao, K. Freeze cast fabrication of porous ceramics using tert-butyl alcohol-water crystals as template. J. Eur. Ceram. Soc. 2016, 36, 1513–1518. [Google Scholar] [CrossRef]
- Kobayashi, A.; Horikawa, M.; Kirschvink, J.L.; Golash, H.N. Magnetic control of heterogeneous ice nucleation with nanophase magnetite: Biophysical and agricultural implications. Proc. Natl. Acad. Sci. USA 2018, 115, 5383–5388. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, A.; Golash, H.N.; Kirschvink, J.L. A first test of the hypothesis of biogenic magnetite-based heterogeneous ice-crystal nucleation in cryopreservation. Cryobiology 2016, 72, 216–224. [Google Scholar] [CrossRef]
- Svishchev, I.M.; Kusalik, P.G. Electrofreezing of liquid water: A microscopic perspective. J. Am. Chem. Soc. 1996, 118, 649–654. [Google Scholar] [CrossRef]
- Gor’kov, L. On the forces acting on a small particle in an acoustical field in an ideal fluid. Sov. Phys. 1962, 6, 773–775. [Google Scholar]
- Groschl, M. Ultrasonic separation of suspended particles—Part I: Fundamentals. Acta Acust. 1998, 84, 432–447. [Google Scholar] [CrossRef]
- Torr, G.R. The acoustic radiation force. Am. J. Phys. 1984, 52, 402–408. [Google Scholar] [CrossRef]
- Uhlmann, D.R.; Chalmers, B.; Jackson, K.A. Interaction between particles and a solid-liquid interface. J. Appl. Phys. 1964, 35, 2986–2993. [Google Scholar] [CrossRef]
- Bolling, G.F.; Cisse, J. A theory for the interaction of particles with a solidifying front. J. Cryst. Growth 1971, 10, 56–66. [Google Scholar] [CrossRef]
- Gilpin, R.R. Theoretical studies of particle engulfment. J. Colloid Interface Sci. 1980, 74, 44–63. [Google Scholar] [CrossRef]
- Chernov, A.A.; Temkin, D. Capture of inclusions in crystal growth. Cryst. Growth Mater. 1977, 2, 3–77. [Google Scholar]
- Worster, M.G.; Wettlaufer, J.S. The Fluid Mechanics of Premelted Liquid Films; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Dash, J.G. Thermomolecular pressure in surface melting: Motivation for frost heave. Science 1989, 246, 1591–1593. [Google Scholar] [CrossRef]
- Rempel, A.W.; Wettlaufer, J.S.; Worster, M.G. Interfacial Premelting and the Thermomolecular Force: Thermodynamic Buoyancy. Phys. Rev. Lett. 2001, 87, 088501. [Google Scholar] [CrossRef]
- De Gennes, P.G. Wetting: Statics and dynamics. Rev. Mod. Phys. 1985, 57, 827–863. [Google Scholar] [CrossRef]
- Deryagin, B.V.; Churaev, N.V. Definition of disjoining pressure and its importance in equilibrium and flow of thin-films. Colloid J. USSR 1976, 38, 402–410. [Google Scholar]
- Park, M.S.; Golovin, A.A.; Davis, S.H. The encapsulation of particles and bubbles by an advancing solidification front. J. Fluid Mech. 2006, 560, 415. [Google Scholar] [CrossRef]
- Saint-Michel, B.; Georgelin, M.; Deville, S.; Pocheau, A. Interaction of Multiple Particles with a Solidification Front: From Compacted Particle Layer to Particle Trapping. Langmuir 2017, 33, 5617–5627. [Google Scholar] [CrossRef] [PubMed]
- Niksiar, P. Fabrication and Mechancial Properties of Micro Architectured 3D Scaffolds. PhD Thesis, Clemson University, Clemson, SC, USA, 2018. [Google Scholar]
- Erb, R.M.; Martin, J.J.; Soheilian, R.; Pan, C.; Barber, J.R. Actuating Soft Matter with Magnetic Torque. Adv. Funct. Mater. 2016, 26, 3859–3880. [Google Scholar] [CrossRef]
- Demirörs, A.F.; Pillai, P.P.; Kowalczyk, B.; Grzybowski, B.A. Colloidal assembly directed by virtual magnetic moulds. Nature 2013, 503, 99–103. [Google Scholar] [CrossRef] [PubMed]
- Le Ferrand, H. External fields for the fabrication of highly mineralized hierarchical architectures. J. Mater. Res. 2018, 1–25. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Electrodynamics; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Sommerfeld, A. Electrodynamics: Lectures on Theoretical Physics; Academic Press: Cambridge, MA, USA, 1952. [Google Scholar]
- Andersson, H.; Van den Berg, A. Microfluidic devices for cellomics: A review. Sens. Actuators B Chem. 2003, 92, 315–325. [Google Scholar] [CrossRef]
- Karpul, D.; Tapson, J.; Rapson, M.; Jongens, A.; Cohen, G. Limiting factors in acoustic separation of carbon particles in air. J. Acoust. Soc. Am. 2010, 127, 2153–2158. [Google Scholar] [CrossRef]
- Haslam, M.D.; Raeymaekers, B. Aligning carbon nanotubes using bulk acoustic waves to reinforce polymer composites. Compos. Part B Eng. 2014, 60, 91–97. [Google Scholar] [CrossRef]
- Erb, R.M.; Libanori, R.; Rothfuchs, N.; Studart, A.R. Composites reinforced in three dimensions by using low magnetic fields. Science 2012, 335, 199–204. [Google Scholar] [CrossRef]
- Erb, R.M.; Segmehl, J.; Charilaou, M.; Löffler, J.F.; Studart, A.R. Non-linear alignment dynamics in suspensions of platelets under rotating magnetic fields. Soft Matter 2012, 8, 7604. [Google Scholar] [CrossRef]
- Peng, X.; Min, Y.; Ma, T.; Luo, W.; Yan, M. Two-dimensional Monte Carlo simulations of structures of a suspension comprised of magnetic and nonmagnetic particles in uniform magnetic fields. J. Magn. Magn. Mater. 2009, 321, 1221–1226. [Google Scholar] [CrossRef]
- Peng, X.; Min, Y.; Ma, T.; Yan, M. Two-dimensional Monte Carlo simulations of a suspension comprised of magnetic and nonmagnetic particles in gradient magnetic fields. J. Magn. Magn. Mater. 2009, 321, 3250–3255. [Google Scholar] [CrossRef]
- Aoshima, M.; Satoh, A. Two-dimensional Monte Carlo simulations of a colloidal dispersion composed of polydisperse ferromagnetic particles in an applied magnetic field. J. Colloid Interface Sci. 2005, 288, 475–488. [Google Scholar] [CrossRef]
- Aoshima, M.; Satoh, A. Two-dimensional Monte Carlo simulations of a polydisperse colloidal dispersion composed of ferromagnetic particles for the case of no external magnetic field. J. Colloid Interface Sci. 2004, 280, 83–90. [Google Scholar] [CrossRef]
- Fennema, O. Water and Ice; Marcel Dekker Inc.: New York, NY, USA, 1996. [Google Scholar]
- Friedman, G.; Yellen, B. Magnetic separation, manipulation and assembly of solid phase in fluids. Curr. Opin. Colloid Interface Sci. 2005, 10, 158–166. [Google Scholar] [CrossRef]
- Cotten, G.B.; Eldredge, H.B. Nanolevel magnetic separation model considering flow limitations. Sep. Sci. Technol. 2002, 37, 3755–3779. [Google Scholar] [CrossRef]
- Ebner, A.D.; Ritter, J.A.; Ploehn, H.J.; Kochen, R.L.; Navratil, J.D. New magnetic field-enhanced process for the treatment of aqueous wastes. Sep. Sci. Technol. 1999, 34, 1277–1300. [Google Scholar] [CrossRef]
- Related, G. Cluster structures and cluster-cluster aggregations in a two-dimensional ferromagnetic colloidal system. J. Phys. A Math. Gen. Relat. Content 2000, 33, 247. [Google Scholar]
- Weis, J.J.; Levesque, D. Chain formation in low density dipolar hard spheres: A Monte Carlo study. Phys. Rev. Lett. 1993, 71, 2729–2732. [Google Scholar] [CrossRef] [PubMed]
- Jeyadevan, B.; Nakatani, I. Characterization of field-induced needle-like structures in ionic and water-based magnetic fluids. J. Magn. Magn. Mater. 1999, 201, 62–65. [Google Scholar] [CrossRef]
- Ebner, A.D.; Ritter, J.A.; Ploehn, H.J. Feasibility and limitations of nanolevel high gradient magnetic separation. Sep. Purif. Technol. 1997, 11, 199–210. [Google Scholar] [CrossRef]
- Ebner, A.D.; Ritter, J.A.; Ploehn, H.J. Magnetic hetero-flocculation of paramagnetic colloidal particles. J. Colloid Interface Sci. 2000, 225, 39–46. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Hilal, N.; Langston, P.; Starov, V. Interaction forces between colloidal particles in liquid: Theory and experiment. Adv. Colloid Interface Sci. 2007, 134, 151–166. [Google Scholar] [CrossRef] [PubMed]
- Ebner, A.D.; Ploehn, H.J.; Ritter, J.A. Magnetic field orientation and spatial effects on the retention of paramagnetic nanoparticles with magnetite. Sep. Sci. Technol. 2002, 37, 3727–3753. [Google Scholar] [CrossRef]
- Ebner, A.D.; Ritter, J.A. Retention of paramagnetic particles by magnetite particle clusters with multifunctional character. Sep. Sci. Technol. 2004, 39, 2785–2808. [Google Scholar] [CrossRef]
- Porter, M.M.; Niksiar, P. Multidimensional mechanics: Performance mapping of natural biological systems using permutated radar charts. PLoS ONE 2018, 13, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Porter, M.M. Bioinspired Design: Magnetic Freeze Casting. PhD Thesis, University of California, San Diego, CA, USA, 2014. [Google Scholar]

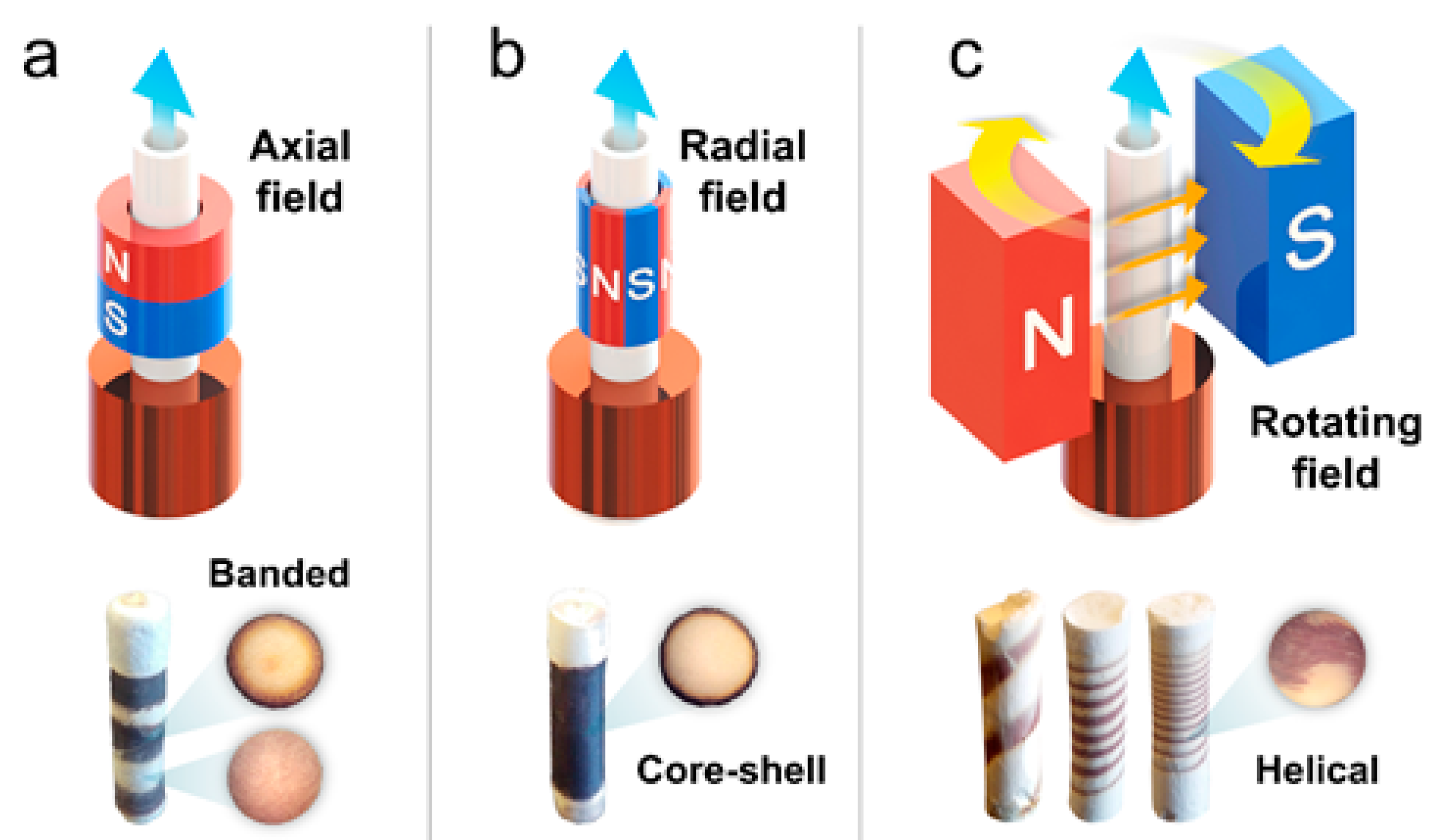
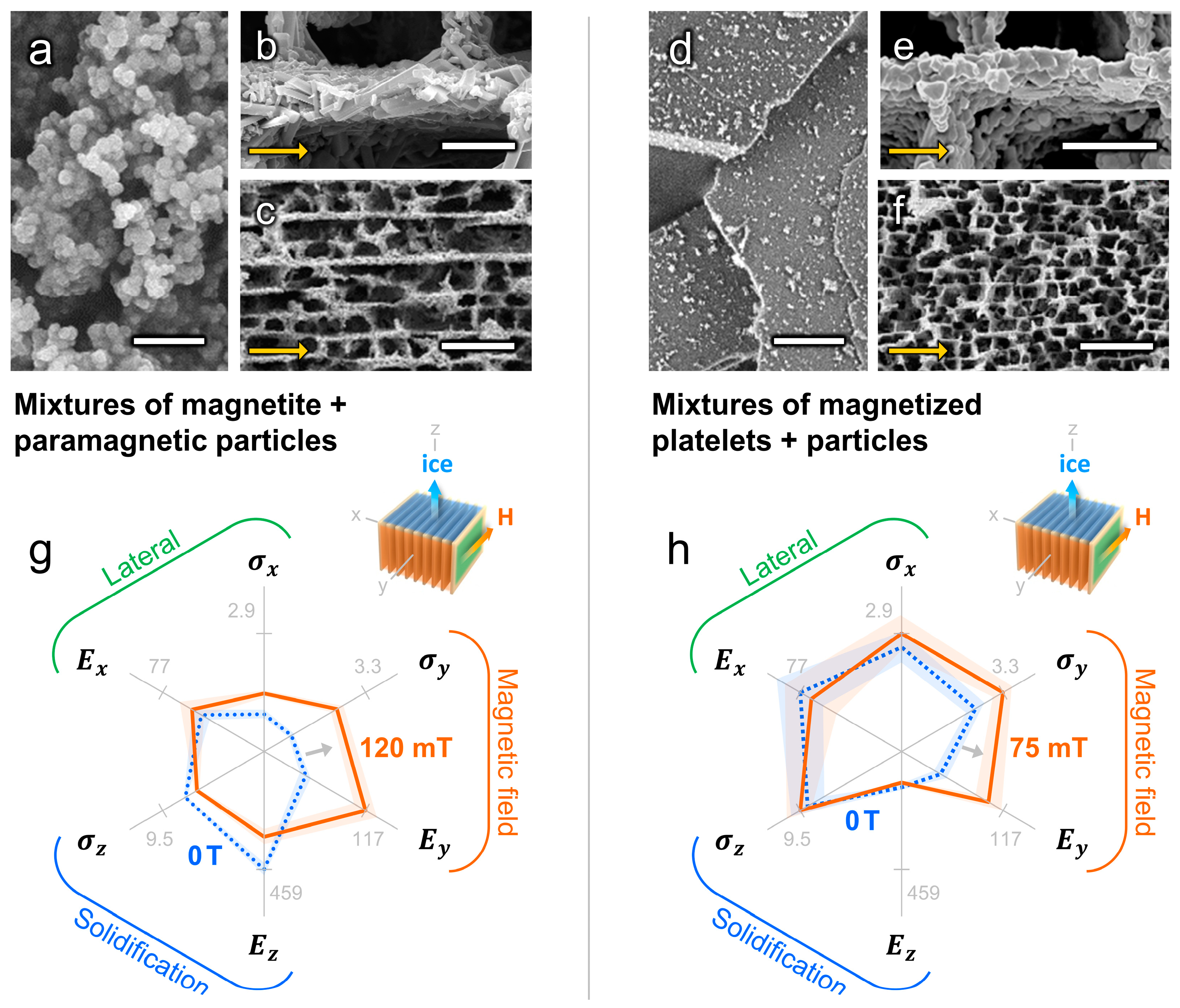
| Magnetic Freeze Casting | ||||||||
| Study | Particles | Particle Size | Susceptibility (or Magnetization) | Solvent | Additives | Freezing Rate, Direction | Field Strength, Orientation | Results Summary |
| [76] | HA ZrO2 Al2O3 TiO2 (+Fe3O4) | 1–3 µm 0.2–0.5 µm 2–5 µm 0.2–0.5 µm (<0.05 µm) | −81.5 × 10−6 cm3/mol −13.8 × 10−6 cm3/mol −37.0 × 10−6 cm3/mol +5.9 × 10−6 cm3/mol | Water | PEG, PVA, Darvan 811 | 10 °C/min, longitudinal | 0–0.12 T, transverse and rotating | Mixtures of Fe3O4 + HA, ZrO2, or Al2O3 under static and rotating transverse fields yielded biphasic iron-rich/poor structures; mixtures of Fe3O4 + TiO2 yielded wall alignment with enhanced transverse compressive properties. |
| [77] | ZrO2 (+Fe3O4) | 0.2–0.5 µm (<0.05 µm) | −13.8 × 10−6 cm3/mol | Water | PEG, PVA, Darvan 811 | 10 °C/min, longitudinal | 0–0.12 T, rotating | Mixtures of Fe3O4 + ZrO2 under rotating transverse fields yielded helix-reinforced composites with enhanced torsional properties. |
| [64] | ZrO2 (+Fe3O4) | 0.2–0.5 µm (<0.05 µm) | −13.8 × 10−6 cm3/mol | Water | PEG, PVA, Darvan 811 | 10 °C/min, longitudinal | 0–0.5 T, axial, radial and transverse | Mixtures of Fe3O4 + ZrO2 under static axial, radial, and transverse fields yielded different gradient patterns and bridge alignment with enhanced transverse compressive properties. |
| [80] | CeO2 Y2O3 (+Fe3O4) | <0.5 µm <0.5 µm (<0.05 µm) | +26.0 × 10−6 cm3/mol +44.4 × 10−6 cm3/mol | Water | PEG, PVA, Darvan 811 | 10 °C/min, longitudinal | 0–0.15 T, transverse | Mixtures of Fe3O4 + CeO2 or Y2O3 under static near-uniform fields yielded bridge alignment; under static gradient fields yielded biphasic iron-rich/poor structures. |
| [79] | Surface-magnetized Al2O3 | 0.35 µm (particles) 0.20 × 5 µm (platelets) | 2 × 10−14 emu (magnetization) 454 × 10−14 emu (magnetization) | Water | PEG, PVA, Darvan 811 | 10 °C/min, longitudinal | 0–0.075 T transverse | Mixtures of Al2O3 particles + platelets under static transverse fields yielded wall alignment with enhanced transverse compressive properties. |
| [78] | Surface-magnetized Al2O3 | 0.15–0.5 µm | 0.6–2 × 10−14 emu (magnetization) | Water | PEG, PVA, Darvan 811 | 10 °C/min, longitudinal | 0–0.15 T transverse | Uniform dispersions of Al2O3 particles under static transverse fields yielded wall alignment with enhanced compressive properties. |
| [74] | Surface-magnetized Fe3O4 | 0.25 µm | 11–16 emu/g (magnetization) | Water | PEG, PVA, Darvan 811 | 10 °C/min, longitudinal | 0–0.005 T longitudinal | Uniform dispersions of Fe3O4 particles under uniform longitudinal fields formed by Helmholtz coils yielded wall alignment and decreased porosity with enhanced compressive properties. |
| [86] | Al2O3 | 1 µm | −37.0 × 10−6 cm3/mol | Water | CMC, PAAS | −30 °C (constant), longitudinal and transverse | 0–1.28 T transverse | Uniform dispersions of Al2O3 under static fields yielded decreased pore sizes with no effect on alignment. |
| Electric Freeze Casting | ||||||||
| Study | Particles | Particle Size | --- | Solvent | Additives | Freezing Rate, Direction | Field Strength, Orientation | Results Summary |
| [73] | Al2O3 | 0.4 µm | --- | Water | Glycerol, Darvan 7-N | 6 °C/min, longitudinal | 0–90 V, longitudinal | Uniform dispersions of Al2O3 under longitudinal fields yielded dense/porous bilayered scaffolds. |
| [81] | Al2O3 | 1 µm | --- | Water | PVA, SND 6800 | 1 °C/min, longitudinal | 0–100 kV/m, transverse | Uniform dispersions of Al2O3 under transverse fields yielded inclined lamellar walls and increased pore spacing. |
| [86] | Al2O3 | 1 µm | --- | Water | CMC, PAAS | −30 °C (constant), longitudinal and transverse | 0–150 kV/m, transverse | Uniform dispersions of Al2O3 under transverse fields yielded aligned walls and increased pore sizes with enhanced compressive properties. |
| [72] | HA | --- | --- | Water + H2O2 | SND 6800 | −20 °C (constant), longitudinal | 0–90 kV/m, longitudinal | Uniform dispersions of HA in H2O2 under longitudinal fields yielded increased lamellar and spherical pore sizes. |
| Acoustic Freeze Casting | ||||||||
| Study | Particles | Particle Size | --- | Solvent | Additives | Freezing Rate, Direction | Field Frequency, Orientation | Results Summary |
| [82] | TiO2 | <0.5 µm | --- | Water | PEG, PVA, Darvan 811 | 10 °C/min, longitudinal | 0–936 kHz, radial | Uniform dispersions of TiO2 under acoustic wave fields yielded concentric ring-like structures with gradient hardness distributions. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niksiar, P.; Su, F.Y.; Frank, M.B.; Ogden, T.A.; Naleway, S.E.; Meyers, M.A.; McKittrick, J.; Porter, M.M. External Field Assisted Freeze Casting. Ceramics 2019, 2, 208-234. https://doi.org/10.3390/ceramics2010018
Niksiar P, Su FY, Frank MB, Ogden TA, Naleway SE, Meyers MA, McKittrick J, Porter MM. External Field Assisted Freeze Casting. Ceramics. 2019; 2(1):208-234. https://doi.org/10.3390/ceramics2010018
Chicago/Turabian StyleNiksiar, Pooya, Frances Y. Su, Michael B. Frank, Taylor A. Ogden, Steven E. Naleway, Marc A. Meyers, Joanna McKittrick, and Michael M. Porter. 2019. "External Field Assisted Freeze Casting" Ceramics 2, no. 1: 208-234. https://doi.org/10.3390/ceramics2010018
APA StyleNiksiar, P., Su, F. Y., Frank, M. B., Ogden, T. A., Naleway, S. E., Meyers, M. A., McKittrick, J., & Porter, M. M. (2019). External Field Assisted Freeze Casting. Ceramics, 2(1), 208-234. https://doi.org/10.3390/ceramics2010018





