Decision Support System for Wind Farm Maintenance Using Robotic Agents

Abstract

The automation of wind turbine maintenance processes is aimed at improving the operational efficiency of wind farms through timely diagnosis of technical condition, predictive identification of potential failures, and optimization of the distribution of repair and restoration procedures. In this context, the main objective of the study is to improve the reliability and efficiency of wind energy infrastructure by developing an intelligent decision support system for wind turbine maintenance. The proposed architecture includes a module for optimizing the routes of robotic agents, which implements a hybrid method based on a combination of the A* algorithm and a modified ant algorithm with dynamic pheromone updating and B-spline trajectory smoothing, as well as a module for detecting based on a modified YOLOv3 model with integrated adaptive feature fusion and bio-inspired anchor frame optimization. The choice of the YOLOv3 architecture is due to the optimal balance between accuracy and inference speed on embedded platforms of robotic autonomous agents, which ensures the functioning of the detection module in real time with limited computing resources. The results of the computational experiment confirmed a 15–20% reduction in route length and energy consumption, as well as a 41% increase in the $F1$ detection metric relative to the baseline implementation of YOLOv3 while maintaining a performance of 42 frames per second. The set of results obtained confirms the practical feasibility and integration potential of the developed architecture into the predictive maintenance and life cycle management of wind energy infrastructure.

1. Introduction

1.1. Context

The development of renewable energy sources is a priority area of global energy transformation, focused on reducing carbon emissions and creating sustainable, environmentally friendly models of electricity production. Strategic reports by the International Energy Agency (IEA) [1] and the International Renewable Energy Agency (IRENA) [2] highlight the positive dynamics of wind energy development, which is demonstrating the highest growth rates among alternative energy sources. Figure 1 presents statistical data obtained on the basis of works [3,4], visualized by the authors, demonstrating the increase in the number of wind turbines in Europe and America.

Modern wind energy complexes are characterized by a transition from autonomous wind turbine installations to a cluster organization, united into a single wind farm infrastructure [5]. At the same time, the evolution of design solutions in this area is accompanied by an increase in the installed capacity of the units, leading to an increase in the overall dimensions of the supporting elements. The increase in the size of the structure is due to the lengthening of the blades to 80–120 m and the installation of towers at a height of 120–160 m, resulting in a total wind turbine height of 190–210 m [6], complicating maintenance processes and requiring the use of specialized engineering solutions and additional organizational resources. A comparison of the dimensions of the installations with well-known architectural structures, carried out by the authors, is presented in Figure 2. It is intended to illustrate the scale of the structures, reflecting the increase in the height and mass of the elements, which leads to restrictions on access areas and increased requirements for technical maintenance equipment.

The next key factor limiting traditional maintenance methods is natural climatic conditions [7]. Wind farm locations are characterized by strong wind loads, low temperatures, sharp changes in humidity, and increased airflow turbulence [8]. Taken together, these factors increase the labor intensity of monitoring, reduce the regularity of maintenance, and increase the likelihood of hidden defects that are not detected during random checks, which increases the likelihood of unplanned downtime, leading to direct economic losses and a decrease in the overall efficiency of the power system. The combination of these limitations makes the transition to intelligent diagnostic and maintenance planning tools a necessity. Thus, the aim of this study is to improve the reliability and efficiency of wind farms under conditions of increased operational loads and meteorological instability by developing an intelligent decision support system for wind turbine maintenance.

1.2. Engineering Challenges

The development of automated wind farm maintenance systems requires the operation of autonomous robotic agents in a heterogeneous environment characterized by high density of serviced objects, aerodynamic turbulence, variable weather conditions, and limited energy resources [9], which creates requirements for the development of routing and classification algorithms that ensure stable operation in conditions of dynamic changes in the external environment and variability of operating parameters. It should be noted that autonomous robotic agents are understood to be mobile remote-control platforms equipped with sensor and navigation systems that enable movement in three-dimensional space [10].

Route optimization is a multi-criteria task aimed at minimizing the length of the trajectory, the agent’s energy consumption, and the probability of collision with the objects being inspected [9]. Solutions to this class of problems are implemented using deterministic, stochastic, and predictive algorithms. Deterministic methods (A*, Dijkstra, D*, and Theta*) provide the construction of the shortest routes on static graphs, while being characterized by low adaptability to changing environmental conditions [11,12,13,14]. In turn, stochastic algorithms (RRT, Informed-RRT, and DWA) allow for real-time agent maneuvering, accompanied by high computational complexity and reduced stability as object density increases [15,16]. Model predictive control (MPC) methods partially compensate for these limitations through predictive modeling, but are characterized by significant computational costs and limited adaptability in multi-agent scenarios [17].

The development of these areas has led to the emergence of hybrid metaheuristic approaches that combine deterministic planning principles with adaptive stochastic mechanisms that solve the problems of low adaptability, slow convergence, and high computational complexity characteristic of traditional routing methods. Thus, in studies [18,19], the authors proposed improved versions of the Hybrid RRT* and Adaptive Ant Colony Optimization (AACO) algorithms, which accelerate convergence and increase routing stability in dynamically changing environments through iterative correction of probabilistic trajectory selection rules and local restructuring of the search graph topology. However, despite the effectiveness of the solutions, these approaches remain sensitive to the parameters of the probability functions and weight coefficients, leading to a decrease in convergence stability as the search space dimension increases.

Along with the routing task, a key area of the maintenance system is the recognition and classification of defects in structural elements, which determines the effectiveness of diagnostic procedures in changing conditions of illumination, shooting angles, and partial overlaps of objects. Modern solutions to this problem are based on the use of architectures that are divided into two-stage and one-stage models.

Two-stage models include the Faster R-CNN and Mask R-CNN families, which provide high accuracy in processing static images but are characterized by high computational complexity and the inability to operate in real time. In turn, single-stage models, RetinaNet, EfficientDet, and YOLO, have high inference speed, making these methods suitable for deployment on embedded platforms of autonomous robotic agents [20].

The YOLO family of architectures outperforms RetinaNet and EfficientDet models in terms of detection accuracy, inference speed, and computational efficiency by combining object localization and classification into a single convolutional structure that provides resistance to changes in scale and viewing angle [21,22]. In turn, a comparative analysis of YOLOv3 and YOLOv10 [23] shows that YOLOv3 is characterized by the lowest computational complexity while maintaining high accuracy and stability under limited resources, whereas modifications (YOLOv5–YOLOv10) require large amounts of data and computing power with a moderate increase in detection accuracy.

1.3. Related Works

The issue of automated wind turbine maintenance using robotic agents is being actively explored in a number of areas, including routing and computer vision. In the context of routing, the development of algorithms demonstrates an evolution from deterministic trajectory construction strategies to adaptive and hybrid planning systems focused on operating in a dynamically changing environment.

In the early stages of development, approaches based on geometric decomposition of the working area and two-stage planning, including the formation of coverage zones and optimization of the sequence of visits, were used [24,25]. The application of these methods reduced route lengths, but ignoring dynamic and energy factors limited the applicability of solutions to simulation scenarios.

Further research [26,27] eliminated this shortcoming by forming energy-conscious strategies based on the integration of LiDAR systems, the MEC mechanism, and swarm intelligence principles. The application of this approach improved the positioning accuracy and movement stability of autonomous robotic agents, but the use of the described technologies led to a reduction in the maximum route length due to increased energy consumption and increased the computational complexity of the algorithms. In subsequent stages of development, architectural models are being formed that combine navigation and visual subsystems in a single computing circuit, leading to the formation of stable mechanisms for adapting trajectories based on the current technical state of objects and environmental parameters.

In [28], the authors present the BladeView architecture, which synchronizes navigation and visual models, adapting the route depending on the results of visual analysis. Such hybridization has ensured an increase in the accuracy of spatial positioning, while maintaining computational complexity and performance dependence on system scalability.

At the same time, with the development of routing strategies, there has been an intensification of research in the field of computer vision. Works [29,30] present modifications of the YOLOv3 and YOLOv5 models, integrating instance and semantic segmentation methods based on hierarchical network structures and spatial attention modules. The inclusion of these mechanisms has improved the resolution and accuracy of defect localization by refining contours and improving the separability of object classes, accompanied by an increase in computational complexity and a decrease in resistance to variations in lighting and viewing angles.

In subsequent studies [31,32], the authors proposed architectural solutions aimed at eliminating the limitations identified in previous models related to increased computational complexity and reduced resistance to external variations. The presented modifications of the YOLOv5 and YOLOv8 models were focused on optimizing the loss function, balancing weight coefficients, and integrating the PC-EMA module, which provided an increase in detection accuracy and resistance to visual data noise. However, these architectures remained dependent on the hardware configuration of computing resources and were characterized by increased resource consumption when scaled to large diagnostic systems.

An attempt to solve the resource-intensive problem is presented in [33,34], where the authors propose lightweight modifications of YOLOv8 based on the use of GhostCBS and DFSB-C2f modules, which enable the integration of models into inspection systems with a moderate reduction in accuracy. However, the presented solution demonstrates a limited ability to detect small and partially hidden defects when changing shooting angles and lighting conditions.

Summarizing the results of the studies reviewed, a set of methodological limitations emerges that hinder the practical implementation of sustainable inspection missions at wind farms. Much of the work focused on trajectory planning for autonomous aerial platforms fails to take into account energy characteristics, spatial airflow heterogeneity, and weather variability, resulting in a lack of route adaptation to turbulent zones and dynamic changes in aerodynamic loads. Approaches based on simplified heuristics or local proximity metrics do not include modeling of energy consumption during maneuvering and do not generate multi-stage optimization loops, which reduces the robustness of navigation solutions in complex terrain. In the field of defect detection, clustering and anchor frame parameterization schemes are used, relying primarily on classical k-means or fixed sets of anchor boxes, without considering small-scale blade defects and the spectral-spatial heterogeneity of visual data, limiting the accuracy of the analysis.

Given these limitations, there is a need to develop an integrated architecture that provides a coordinated solution for hybrid routing and high-precision visual defect detection within a unified decision support system for wind farm operations. The lack of comprehensive computing circuits that take into account platform energy parameters, weather impacts, adaptation of anchor parameters to small-scale damage, and the stability of detector operation under limited real-time resources significantly limits the applicability of existing approaches.

1.4. Architectural Motivation

Building on the challenges identified in the previous sections including uncertainty in spatial structure, sensitivity of visual indicators to environmental variability, and meteorological constraints that limit the execution of autonomous inspection missions the need emerges for an integrated decision support system that consolidates navigation and visual diagnostic processes. The proposed architecture is organized around two complementary functional modules. The routing module performs global trajectory generation using the A algorithm, refines the preliminary path through B-spline smoothing, and adapts the final route via a modified ant-colony mechanism that accounts for meteorological and energy-related constraints. The computer vision module is based on an enhanced YOLOv3 configuration incorporating adaptive feature-map fusion and a bio-inspired anchor-parameter optimization strategy designed to improve the detection of small-scale structural defects.

The integration of these modules forms a closed decision-making cycle that governs sensor-data processing, trajectory adaptation, visual-feature analysis, and the generation of control actions for autonomous robotic agents. This unified framework supports several key scientific contributions: the development of a hybrid routing algorithm that integrates deterministic search, curve-based smoothing, and swarm-driven adaptation; the formulation of a bio-inspired approach for adaptive anchor optimization within the detection pipeline; and the creation of an integrated DSS that enhances defect-detection robustness, increases inspection efficiency, and reduces mission-level energy expenditure. This architectural foundation establishes the structural basis for the subsequent sections detailing the algorithmic components and the experimental evaluation.

2. Materials and Methods

2.1. Route Optimization

2.1.1. Route Optimization Problem Statement

One of the main tasks in servicing wind farms is to find the shortest routes through three-dimensional space, with mandatory bypassing of a set of control points and return to the starting position. Here, the wind farm space is defined as a graph model:

$$G=(V,E),V=\{v_1,v_2,\dots ,v_n\},E\subseteq V\times V,$$

(1)

where V is a set of control points, and E is a set of edges that define permissible trajectories, taking into account geometric constraints and inaccessible areas.

The optimality of the route is determined by a set of criteria reflecting the operational characteristics of the environment: path length L, energy costs E, and weather conditions W. Thus, the routing problem is formalized as a multi-criteria cost function:

$$F=\alpha L+\beta E+\gamma W,$$

(2)

where $\alpha$, $\beta$, $\gamma$ are weighting coefficients that determine the relative importance of the corresponding criteria depending on the mission priorities. Here, E denotes the energy-related cost associated with the motion of autonomous robotic agents, accounting for velocity, altitude variation, and maneuvering load, whereas W represents the weather-induced cost reflecting local wind fields, turbulence zones, and adverse meteorological effects. The detailed mathematical definitions of E and W are provided in Equations (10) and (11).

The proposed model is the basis for developing a routing method that ensures the construction of stable and energy-efficient agent route trajectories in real conditions.

2.1.2. Method for Route Optimization

For the task formulated in Section 2.1.1, the following approach is proposed, the key feature of which is a combination of trajectory smoothing operations with a modified ant algorithm that takes into account energy constraints and weather conditions. The general scheme of the approach, visualized and compiled by the authors, is presented in Figure 3.

The presented architecture diagram of the autonomous navigation module reflects the organization of functional components that ensure the execution of inspection missions in a spatially limited environment with variable external conditions. The central link of the module is the route planning subsystem, the operation of which is based on data on weather conditions and energy constraints. Information about turbulence, precipitation, and wind load comes from the weather factor assessment module, while the calculation of the remaining resource and the cost of movement is formed in the energy consumption assessment block. These parameters jointly determine the permissible search areas and modify the probabilistic trajectory selection mechanisms within the algorithmic core.

Route construction is implemented in two stages. In the first stage, a preliminary trajectory is formed by discrete routing using the A* algorithm and subsequent smoothing using B-spline approximation. This procedure eliminates redundant nodes and sharp breaks, which reduces the duration of the mission, lowers energy consumption, and ensures smooth movement near structures. The smoothing level is adjusted adaptively depending on the density of objects, with guaranteed preservation of critical control points.

The second stage implements a modified ant algorithm that uses mechanisms for dynamic updating of the pheromone trail and the introduction of elite agents that increase the probability of selecting promising trajectories. This solution avoids premature convergence to local minima and speeds up the search for routes with minimal costs. Weather parameters, including turbulence and airflow direction characteristics, are integrated into the probabilistic decision-making model, ensuring the stability of trajectories against external disturbances.

2.1.3. Trajectory Smoothing

When implementing the first stage of route construction in three-dimensional space modeled by a graph, the A* algorithm is used, which is a modification of Dijkstra’s algorithm with a heuristic distance estimate [35]:

$$f\left(n\right)=g\left(n\right)+h\left(n\right),$$

(3)

where $g\left(n\right)$ is the length of the path to the current point n, and $h\left(n\right)$ is the heuristic distance estimate to the goal. As a result of applying the A* algorithm, a discrete trajectory is formed in the form of a sequence of graph nodes. The total length of such a trajectory is calculated as the sum of the segments between adjacent points:

$$L_t=\sum _{i=1}^{N-1}d(P_i,P_{i+1}).$$

(4)

where $d\left(P_i,P_{i+1}\right)$ is the Euclidean distance between points $P_i$ and $P_{i+1}$, N is the number of nodes on the route.

However, trajectories constructed in a standard way have a significant drawback: in particular, the discretization of space and the connection of nodes according to the principle of nearest neighbor lead to the formation of zigzag routes with sharp angles, increasing the length of the path, increasing energy consumption, and complicating traffic control. The formalization of angular trajectories is expressed as [36]

$$cos\left({\theta }_i\right)={\displaystyle \frac{(P_i-P_{i-1})·(P_{i+1}-P_i)}{|P_i-P_{i-1}\left|\right|P_{i+1}-P_i|}},i=2,\dots ,N-1,$$

(5)

where ${\theta }_i$ is the angle between consecutive segments of the route, $cos\left({\theta }_i\right)$ indicates sharp turns, indicating a decrease in the efficiency of the trajectory.

Thus, to improve route quality, a smoothing procedure is implemented to eliminate redundant points and optimize the geometry of the path:

$$L_s=\sum _{i=1}^{N-1}\parallel P_i-P_{i-1}\parallel +\kappa \sum _{i=2}^{N-1}\left(1-cos{\theta }_i\right),$$

(6)

where the first component is responsible for minimizing the length of the route, the second is responsible for reducing the total angular deviations; the parameter $\kappa >0$ determines the ratio between these criteria.

Figure 4 shows an example of a route before and after the smoothing procedure.

Thus, the use of the smoothing procedure allows reducing the number of breaks, shortening the route length, and lowering the energy costs of maneuvering while maintaining control points.

2.1.4. Ant Colony Optimization with Elite Agents

A modified ant algorithm is used in the second stage. It should be noted that the classic ant algorithm has a number of drawbacks, including slow convergence, high sensitivity to parameters, and a tendency to prematurely focus on local solutions. In this regard, the authors propose a modified ant algorithm for route optimization, which includes mechanisms for dynamic pheromone level updating and the use of elite agents. Dynamic pheromone updating is performed according to the expression

$${\tau }_{ij}(t+1)=(1-\rho ){\tau }_{ij}\left(t\right)+\Delta {\tau }_{ij}^t,$$

(7)

where ${\tau }_{ij}\left(t\right)$ is the amount of pheromone on edge $e_{ij}$ at time t, $\rho$ is the evaporation coefficient, and $\Delta {\tau }_{ij}^t$ is the change in pheromone proportional to the quality of the route found. The application of this mechanism prevents excessive accumulation of pheromones on ineffective edges, contributing to a uniform exploration of the solution space.

In turn, to accelerate convergence, “elite agents” are introduced to amplify pheromone trails on the most promising routes [37]:

$${\tau }_{ij}^{elite}(t+1)=(1-\rho ){\tau }_{ij}\left(t\right)+\epsilon ·\Delta {\tau }_{ij}^t,$$

(8)

where $\epsilon >1$ is the amplification coefficient. The concentration of pheromones increases on edges related to high-quality routes, reducing the probability of getting stuck in local minima and accelerating the search for optimal solutions. In this case, the probability of an agent moving from vertex i to vertex j is determined by the expression

$$P_{ij}={\displaystyle \frac{{\tau }_{ij}^{\alpha }·{\mu }_{ij}^{\beta }}{{\sum }_{k\in N_i}{\tau }_{ik}^{\alpha }·{\mu }_{ik}^{\beta }}},$$

(9)

where ${\mu }_{ij}$ is heuristic information, $\alpha$, $\beta$ are algorithm parameters, $N_i$ is a set of neighboring vertices. Figure 5 shows a comparison of the convergence of the classical ant algorithm and the modified approach with elite agents.

Thus, the modified ant algorithm provides faster convergence, reducing the influence of randomness and increasing the probability of selecting optimal routes in complex conditions.

2.1.5. Integration of Weather and Energy Factors

Optimizing the route of an autonomous agent in wind farms requires taking into account a combination of factors related to energy consumption and meteorological conditions that affect navigation stability and the reliability of trajectory decisions. Therefore, in this work, the criterion for evaluating the quality of energy consumption is described by the expression

$$E=\sum _{i=1}^{N-1}{c}_d·d(P_i,P_{i+1})+c_t·{\varphi }_i,$$

(10)

where $c_d$ is the specific energy consumption for overcoming a segment of length $d\left(P_i,P_{i+1}\right)$, $c_t$ is the cost of performing maneuvers, and ${\varphi }_i$ is the trajectory deviation angle. The parameters $c_d$ and $c_t$ are determined based on the technical characteristics of the agent and the results of preliminary experimental data. In turn, the influence of weather conditions is formalized using the classical function:

$$W=\sum _{i=1}^{N-1}\omega (P_i,P_{i+1}),$$

(11)

where $\omega \left(P_i,P_{i+1}\right)$ reflects the level of risk of passing through segments with increased turbulence and wind loads. The integration of the described criteria into the ant algorithm is implemented by modifying the transition probability [9]:

$$P_{ij}={\displaystyle \frac{{\tau }_{ij}^{\alpha }·{\mu }_{ij}^{\beta }·{\xi }_{ij}}{{\sum }_{k\in N_i}{\tau }_{ik}^{\alpha }·{\mu }_{ik}^{\beta }·{\xi }_{ik}}},$$

(12)

where ${\xi }_{ij}$ is a correction factor that reduces the probability of selecting routes with high energy consumption or unfavorable weather conditions.

The application of these modifications leads to a change in trajectory planning, excluding routes with excessive energy consumption and passing through high-risk areas. A visualization of the optimized route is shown in Figure 6.

Thus, the developed routing module integrates three interrelated components, whose combined implementation ensures the construction of stable, smooth, and energy-efficient agent routes adapted to real-world conditions. The procedure description of the algorithm is provided in Appendix A.

2.2. Classification with YOLO Algorithm

2.2.1. Classification with YOLO Algorithm Problem Statement

Automated maintenance of wind turbines involves implementing procedures for classifying defects in structural elements, including turbine blades and tower structures. The complexity of this task is determined by the characteristics of the input data, which are influenced by the variability of viewing angles, the influence of meteorological factors, partial overlaps of objects, and insignificant defect sizes, such as edge erosion and microcracks, occupying less than 1–2% of the area of the analyzed element, which leads to a decrease in the accuracy of standard detection algorithms [38]. In accordance with these conditions, the task of defect classification is formalized as the task of simultaneous localization and recognition of defective areas in images captured by the onboard camera system of the autonomous robotic agents [39]. Thus, let the input image I be given in the pixel space $R^{H\times W\times 3}$ and used to detect a set of objects:

$$Y={\left\{(b_i,c_i,p_i)\right\}}_{i=1}^M,$$

(13)

where $b_i$ is the coordinates of the bounding rectangle, $c_i\in C$ is the class label, $p_i\in \left[0,1\right]$ is the probability of belonging to the class. Formalization fixes the structure of the output data and sets the basis for the subsequent development of detection algorithms.

For the practical implementation of the task of defect classification and localization, the YOLOv3 architecture [9] was used, which is focused on high-speed image processing while maintaining acceptable accuracy indicators. The limitation of this approach is the use of a fixed image grid and a static set of anchor frames, which reduces the accuracy of detecting small defects in complex spatial configurations of objects, variations in geometric parameters, and the presence of partial overlaps. These limitations determine the direction of further modification of the YOLO architecture, which consists in improving the accuracy of recognizing small and partially hidden defects while maintaining real-time operation and resistance to visual data noise through dynamic updating of the set of anchor frames.

2.2.2. Modification of YOLOv3 Based on Adaptive Fusion of Multi-Scale Feature Maps

As a modification to YOLOv3, we propose integrating two complementary modules into the architecture to improve detection accuracy and model adaptability to operating conditions. The diagram of component integration into the YOLOv3 architecture is shown in Figure 7.

Let us describe the functionality of the introduced mechanisms. The first module performs adaptive feature fusion, which ensures informative merging of multi-scale maps. Unlike the rigid concatenation used in the base model, the mechanism dynamically adjusts the contribution of each feature level, improving the accuracy of image processing with minor defects and reducing information loss when processing high-detail images. The second module optimizes anchor frames by dividing the search for solutions into global and local levels. At the global level, a genetic algorithm (GA) is implemented, which explores the parameter space to find promising anchor frame configurations. At the local level, a metaheuristic bee colony algorithm (ABC) is applied, which allows refining decisions in the vicinity of the found areas. The interaction between these levels is implemented in a multi-level clustering architecture that provides a hierarchical organization of computations in order to coordinate the mechanisms of exploration and exploitation of the solution space.

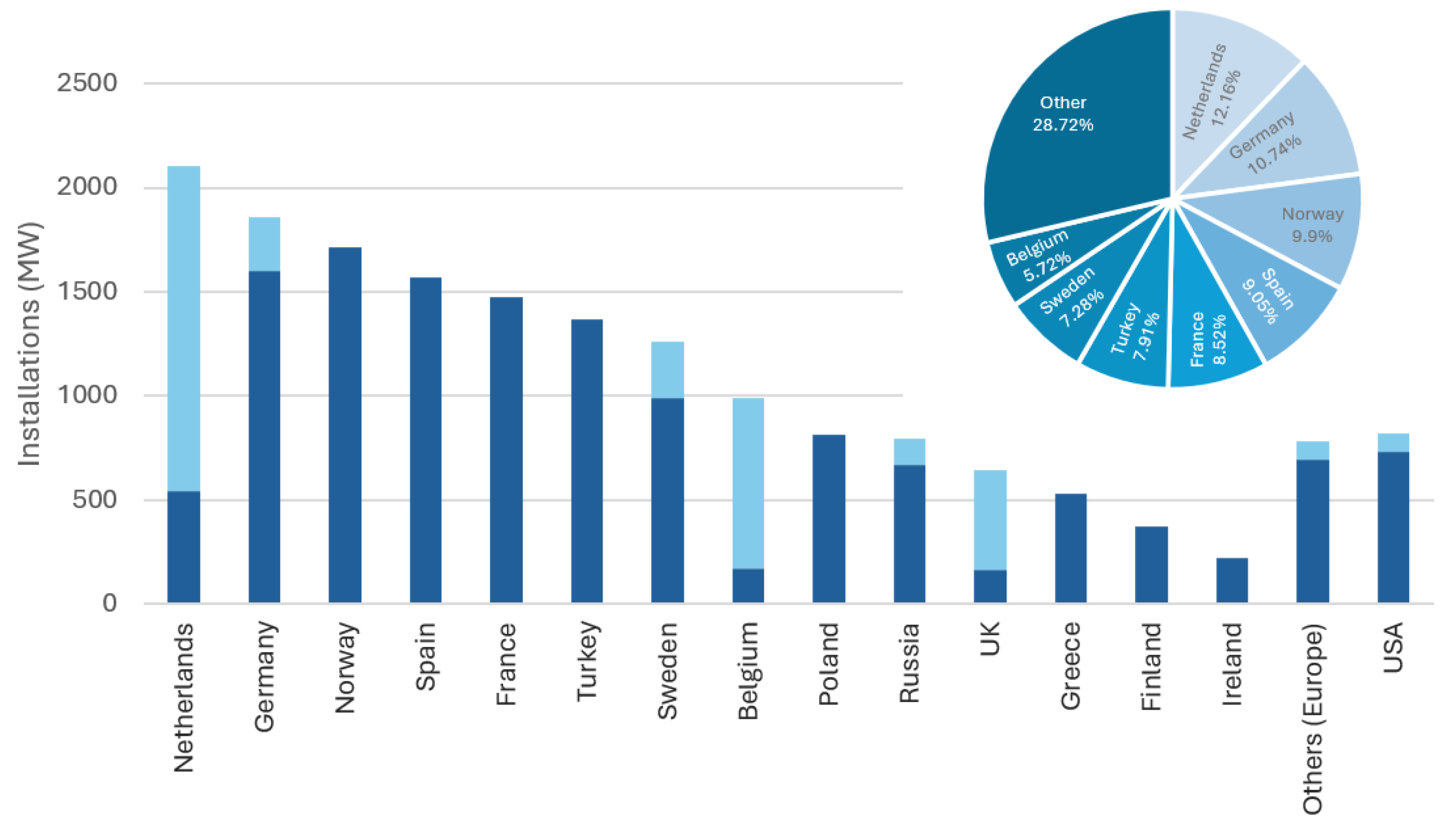
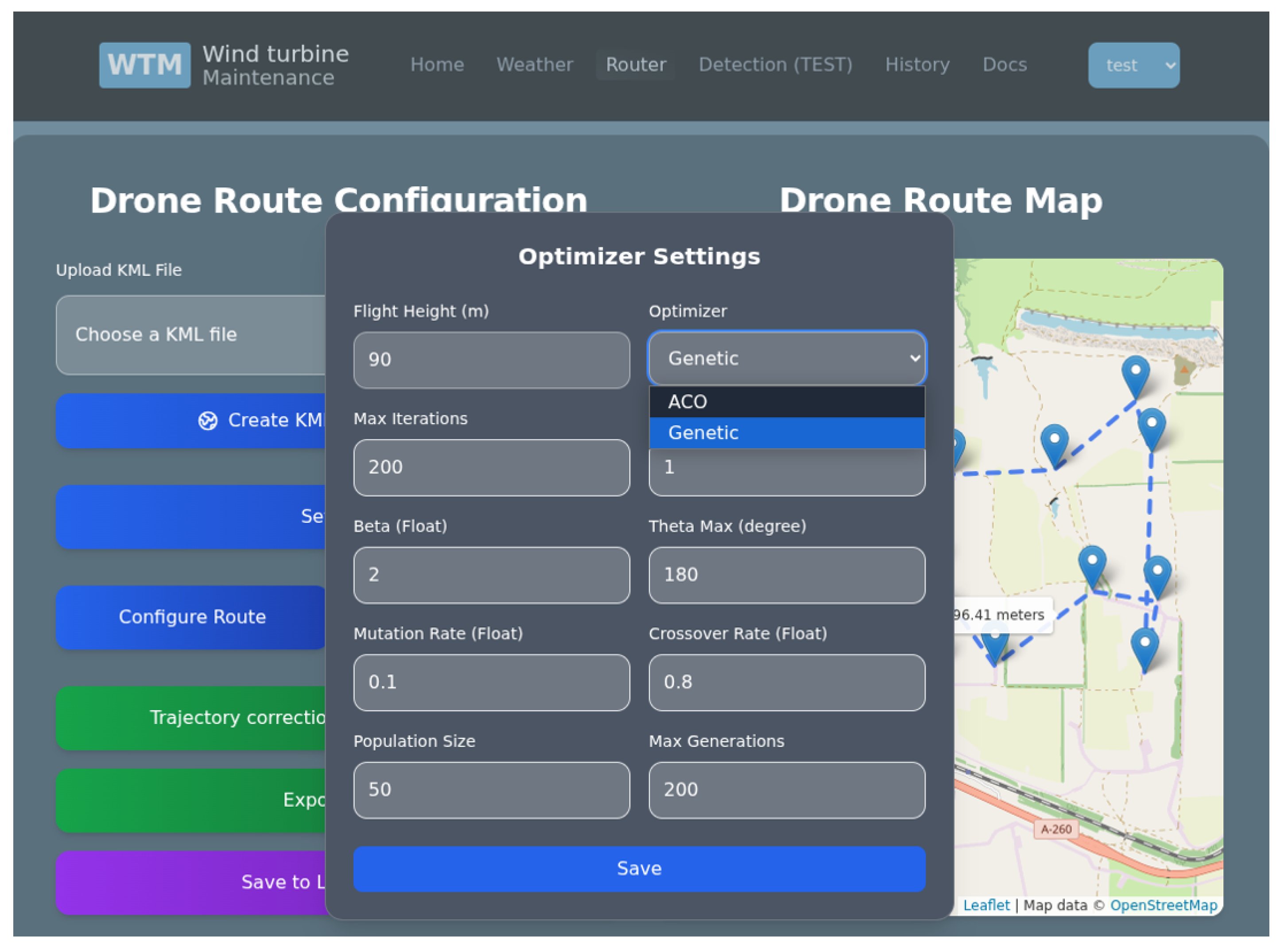
2.2.3. Proposed YOLOv3-Based Classification Method

In the YOLOv3 architecture, multi-scale feature maps are integrated using static concatenation, in which all levels ${\left\{F_l\right\}}_{l=1}^L$ are treated equally. This approach leads to the suppression of detailed features of low-level maps by signals from high-level structures, reducing the sensitivity of the model to minor defects that are critical in the maintenance of wind turbine structures.

To overcome this drawback, we propose the introduction of Adaptive Feature Fusion (AFF) [40], which provides dynamic redistribution of control coefficient weights between levels during training. Let $F_l\in R^{H_l\times W_l\times C}$ be a set of features of level l, then for each set, the global context descriptor $z_l$ is calculated by averaging over spatial dimensions:

$$z_l={\displaystyle \frac{1}{H_l{W}_l}}\sum _{i=1}^{H_l}\sum _{j=1}^{W_l}{F}_l(i,j).$$

(14)

Next, the vector $z=\left[z_1,z_2,\dots ,z_L\right]$ is fed into a trainable weight normalization mechanism, which includes a fully connected layer and a softmax function that forms the coefficients ${\alpha }_l$:

$${\alpha }_l={\displaystyle \frac{exp\left(w^{\top }{z}_l\right)}{{\sum }_{k=1}^{L}exp\left(w^{\top }{z}_k\right)}},\sum _{l=1}^L{\alpha }_l=1,$$

(15)

where w is a model parameter optimized jointly with the network. Thus, the final fusion map is calculated as a weighted combination:

$$F_{\mathrm{fusion}}=\sum _{l=1}^L{\alpha }_l·F_l.$$

(16)

As a result, the coefficients ${\alpha }_l$ are formed individually for each image, ensuring the amplification of the contribution of low-level maps in the presence of minor defects, while preserving the context of high-level structures. Unlike known attention modules (SENet, CBAM, BiFPN) [41,42,43], the proposed mechanism is focused on improving the accuracy of image processing with minor defects without losing semantic information, which is critical for wind farm maintenance tasks.

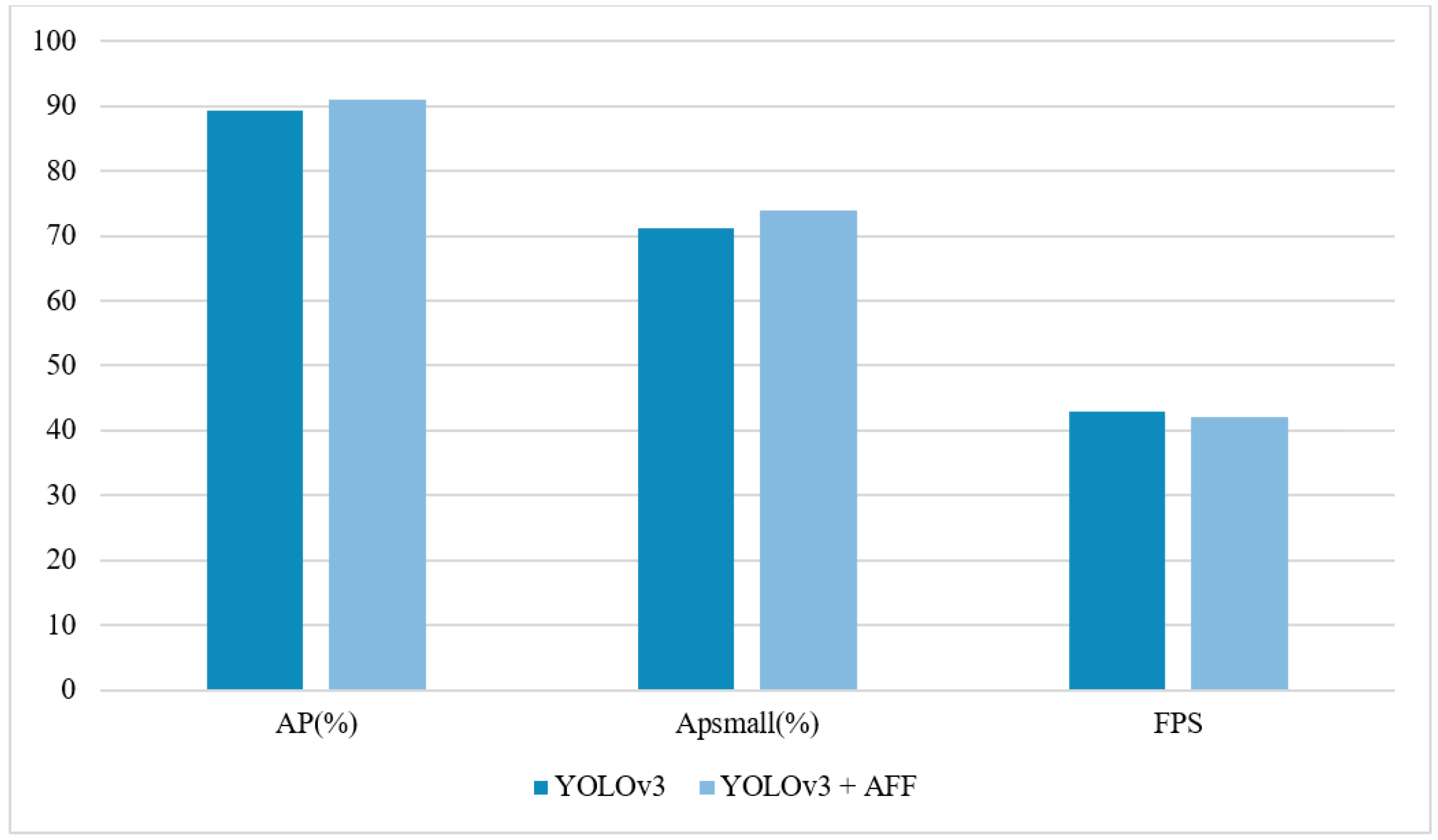
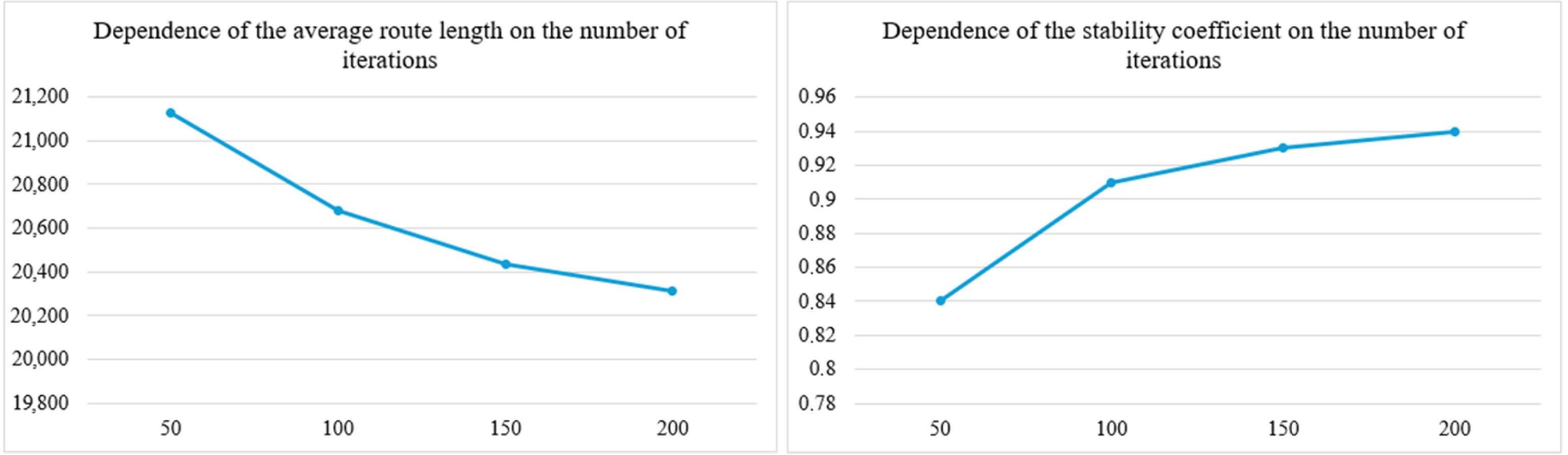
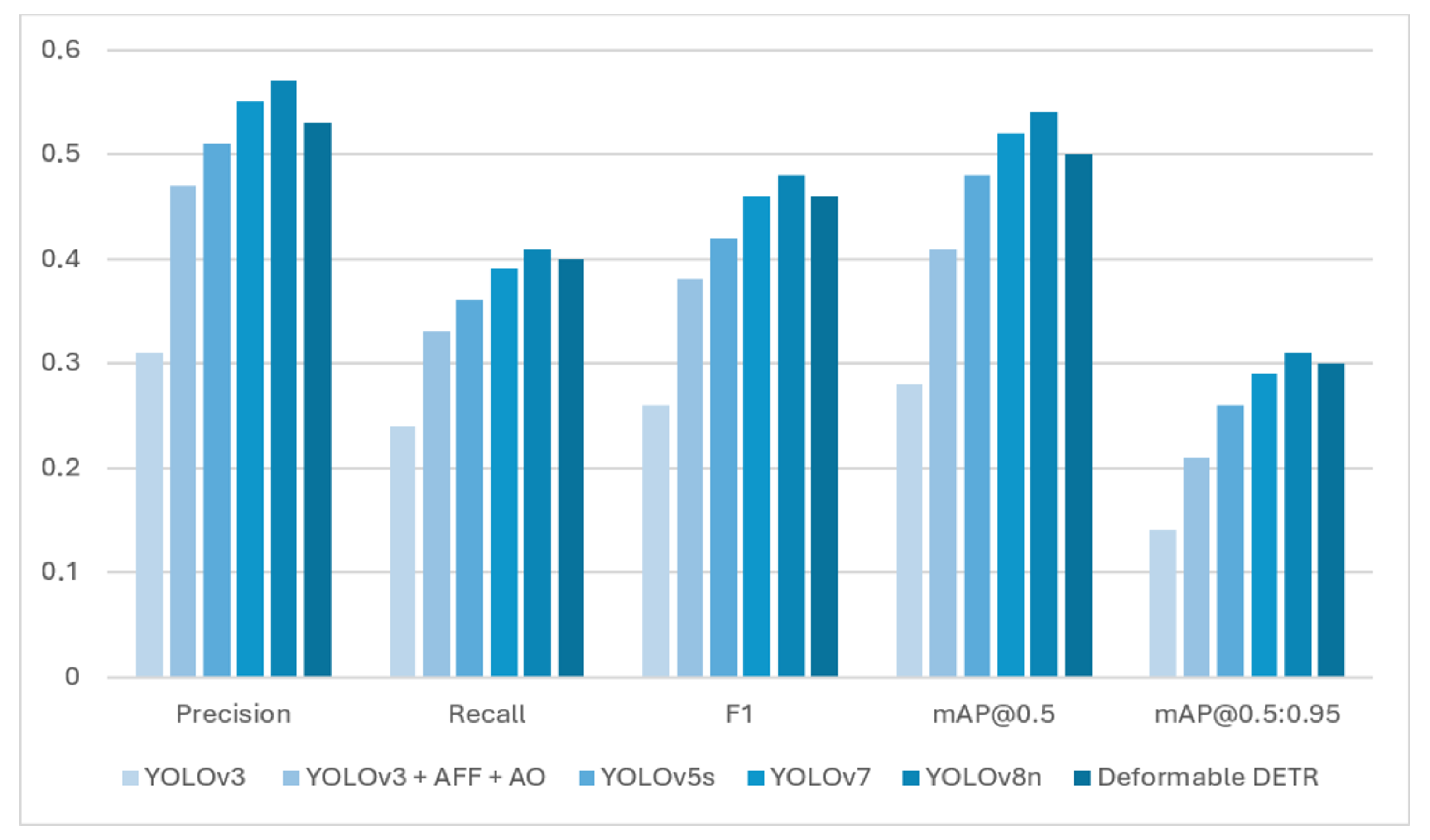
The effectiveness of the approach is confirmed by experimental results (

Table 1. Comparison of the basic model and YOLOv3 + AFF.

Model	AP (%) 1	APsmall (%) 2	FPS 3
YOLOv3	89.4	71.2	43
YOLOv3 + AFF	91.1	73.9	42

¹ AP—average precision; ² AP_small—average precision on small objects (area $<{32}^2$ pixels, as defined by COCO); ³ FPS—number of frames processed per second.

), where the average precision (AP) increased by 1.7%, and the precision for small objects (${\mathrm{AP}}_{\mathrm{small}}$) increased by 2.7% while maintaining the processing speed. The visualization of the presented results is shown in Figure 8.

The results show that AFF integration improves the detection quality of small objects without significantly reducing performance. However, the use of an additional fully connected layer increases the number of model parameters and slightly reduces the processing speed (less than 2%). It should be noted that this compromise is justified by the increase in accuracy when solving wind farm maintenance tasks.

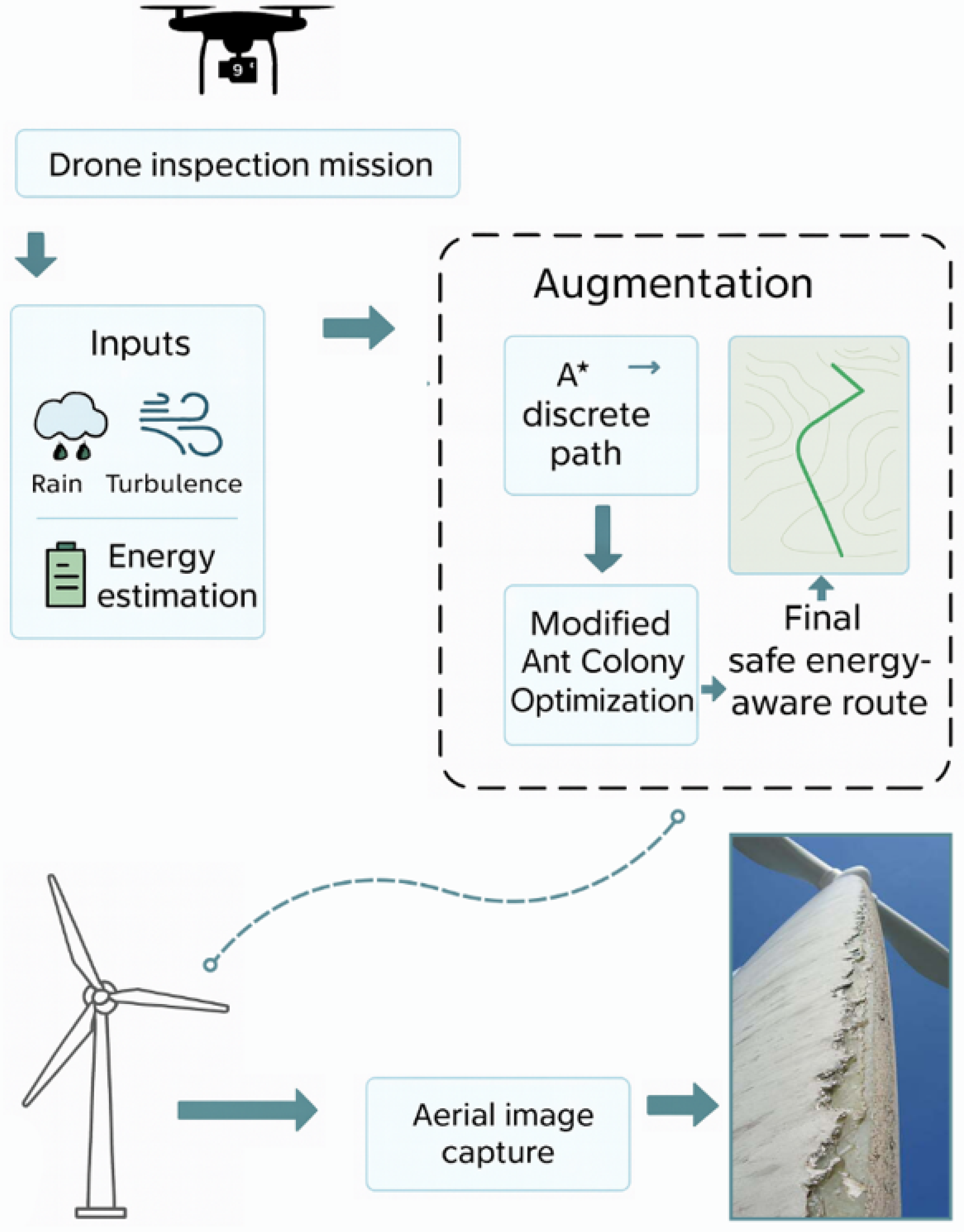
2.2.4. Bio-Inspired Anchor Box Optimization

Optimization of anchor frame parameters in object detection architectures is determined by the task of minimizing the discrepancy between anchor frames and actual bounding boxes in the training set. The k-means method used in YOLOv3 provides a basic approximation of parameters, characterized by low stability with high variability in the shapes and sizes of defects.

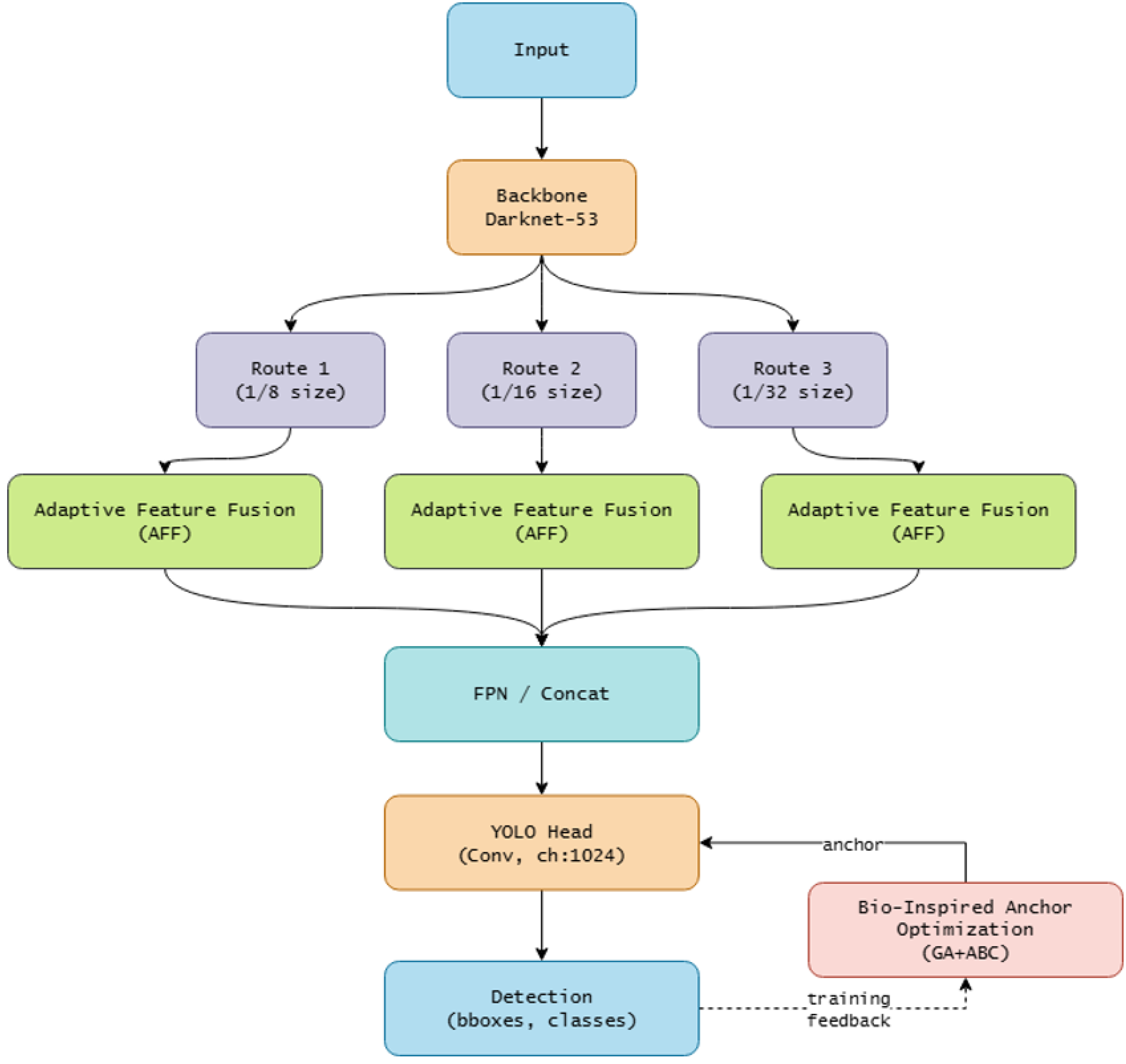
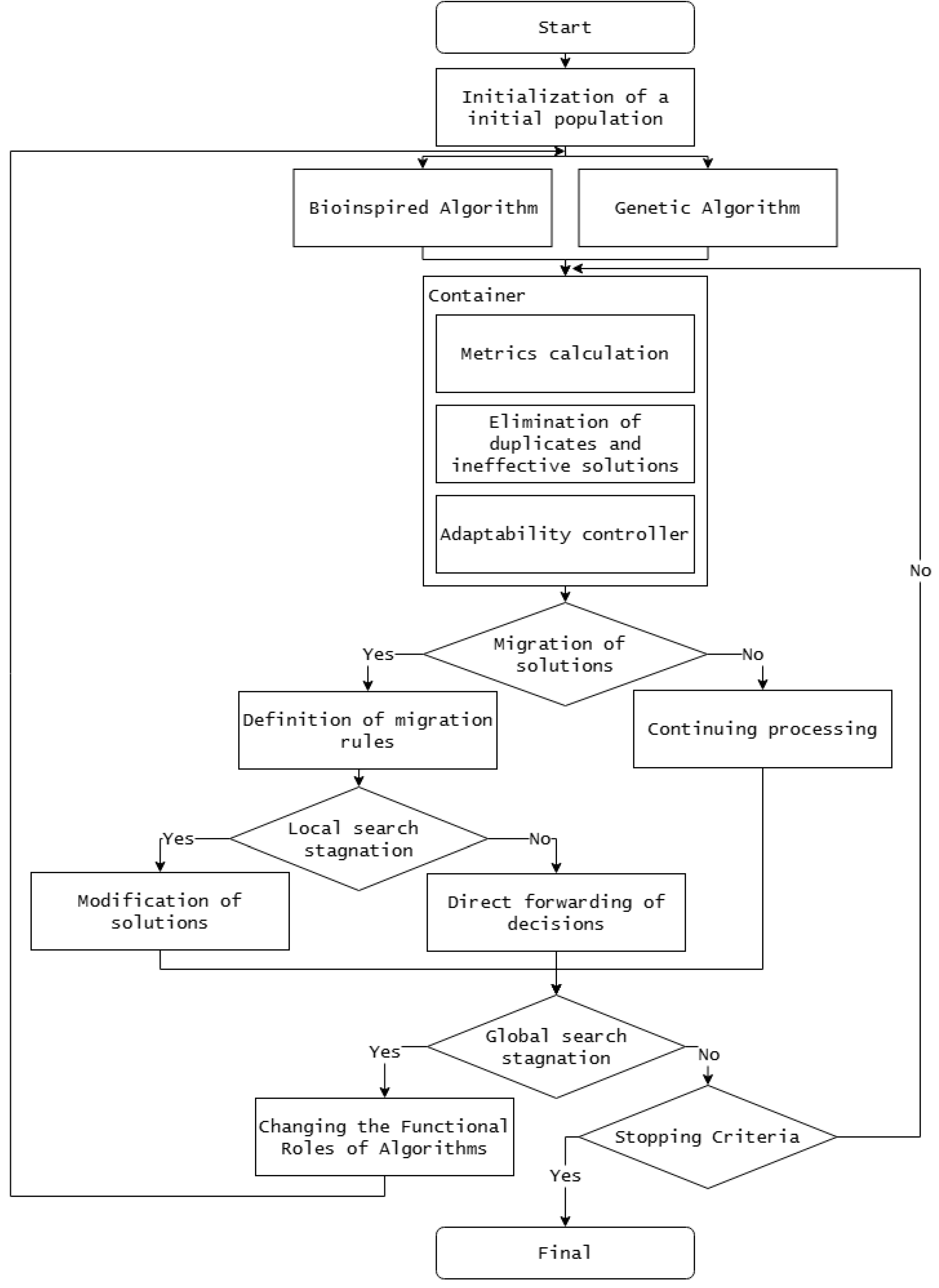
As part of this study, the authors have developed a bio-inspired optimization strategy based on the interaction of evolutionary and swarm search mechanisms operating within a hybrid-parallel architecture that ensures the coordinated execution of global search and local adaptation procedures with dynamic redistribution of computational resources. A structural diagram of the proposed architecture is shown in Figure 9.

The conceptual novelty of the proposed optimization module lies in the integration of evolutionary refinement and swarm-based diversification within a multi-level clustering framework that dynamically adapts anchor frame parameters to the geometric heterogeneity of visual defects. In contrast to traditional techniques that rely on static anchor initialization or single-stage clustering, the hybrid strategy introduces an adaptive exchange of intermediate solutions between the genetic algorithm and the bio-inspired search subsystem. This ensures a balanced combination of global exploration and local exploitation, enabling the anchor configuration to follow the real distribution of object shapes and facilitating stable optimization under high data variability [44].

Analyzing the presented architecture, we will describe the main stages. At the first stage, the initial populations are initialized, after which two complementary components are launched in parallel: a genetic algorithm that implements evolutionary parameter refinement, and a bio-inspired algorithm that ensures the generation and diversification of a set of solutions. Information exchange between algorithms is carried out through a universal container that accumulates intermediate results, calculates metrics, excludes duplicate and ineffective solutions, and forms control signals for the adaptability controller.

The adaptability controller analyzes the state of the computational process based on a set of metrics: the convergence rate $\Delta f\left(t\right)$, the population diversity $D^{\left(t\right)}$, and the decision quality improvement dynamics $P^{\left(t\right)}$. In this case, the functional roles of the algorithms change depending on the ratio of these metrics if the following condition is met:

$$\Delta f\left(t\right)<{\epsilon }_f\wedge D\left(t\right)<{\epsilon }_D,$$

(17)

where ${\epsilon }_f$, ${\epsilon }_D$ are threshold values that determine local search stagnation. A decrease in the convergence rate $\Delta f^{\left(t\right)}$ with a simultaneous decrease in diversity $D^{\left(t\right)}$ is interpreted as a sign of excessive population concentration and exhaustion of the local search potential, leading to the migration of solutions and the redistribution of the functional roles of algorithms.

Thus, a continuous self-adaptation loop is implemented, ensuring a coordinated distribution of computational resources between global and local optimization processes. Thus, at the global search stage, an evolutionary mechanism for refining anchor frame configurations is implemented by a genetic algorithm, whose main function is to explore the parameter space and generate a set of promising solutions, with each solution in the population encoded by a vector of parameters:

$$A_m^{\left(t\right)}=\left(w_{m,1}^{\left(t\right)},h_{m,1}^{\left(t\right)},\dots ,w_{m,K}^{\left(t\right)},h_{m,K}^{\left(t\right)}\right).$$

(18)

where $w_{m,k}$ and $h_{m,k}$ are the width and height of the k-th frame of the m-th solution, and K is the number of anchor frames. In turn, the quality of chromosomes is determined by the fitness function, which includes the intersection metric (IoU) and parameter variance regularization:

$$f\left(A\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N\underset{1\le j\le K}{max}\mathrm{IoU}(b_i,a_j)-\lambda ·\mathrm{Var}\left(A\right),$$

(19)

where $b_i$ is the real bounding box, $a_j$ is the anchor box, and $\lambda$ is the coefficient that regulates the ratio of approximation accuracy and solution diversity. Although the value of $\lambda$ was selected empirically, its choice was further validated by sensitivity assessments conducted in the range $[0.05; 0.2]$, which is typical for regularization principles in evolutionary swarm processes. Preliminary tests showed that $\lambda <0.1$ leads to an increase in the variance of the anchor frame parameters and a decrease in convergence stability, while $\lambda >0.15$ leads to a reordering of solutions and an outlier in IoU coverage. The value $\lambda =0.116$ was adopted as a compromise that provides a balance between the variability of candidate solutions and the stabilization of the optimization process.

The selection of parent chromosomes $A_i^{\left(t\right)}$ and $A_j^{\left(t\right)}$ is carried out in proportion to the value of the fitness function f (19), maintaining the priority of effective solutions, while new offspring are formed by means of arithmetic crossover [45]:

$$(w_{g,k}^{(t+1)},h_{g,k}^{(t+1)})=\beta (w_{i,k}^{\left(t\right)},h_{i,k}^{\left(t\right)})+(1-\beta )(w_{j,k}^{\left(t\right)},h_{j,k}^{\left(t\right)}),\beta \sim U(0,1).$$

(20)

and maintaining population diversity and preventing premature convergence is performed by a mutation operator that adds random Gaussian noise to each gene [42]:

$$(w_{g,k}^{(t+1)},h_{g,k}^{(t+1)})\leftarrow (w_{g,k}^{(t+1)},h_{g,k}^{(t+1)})+ϵ,ϵ\sim \mathcal{N}(0,{\sigma }^2).$$

(21)

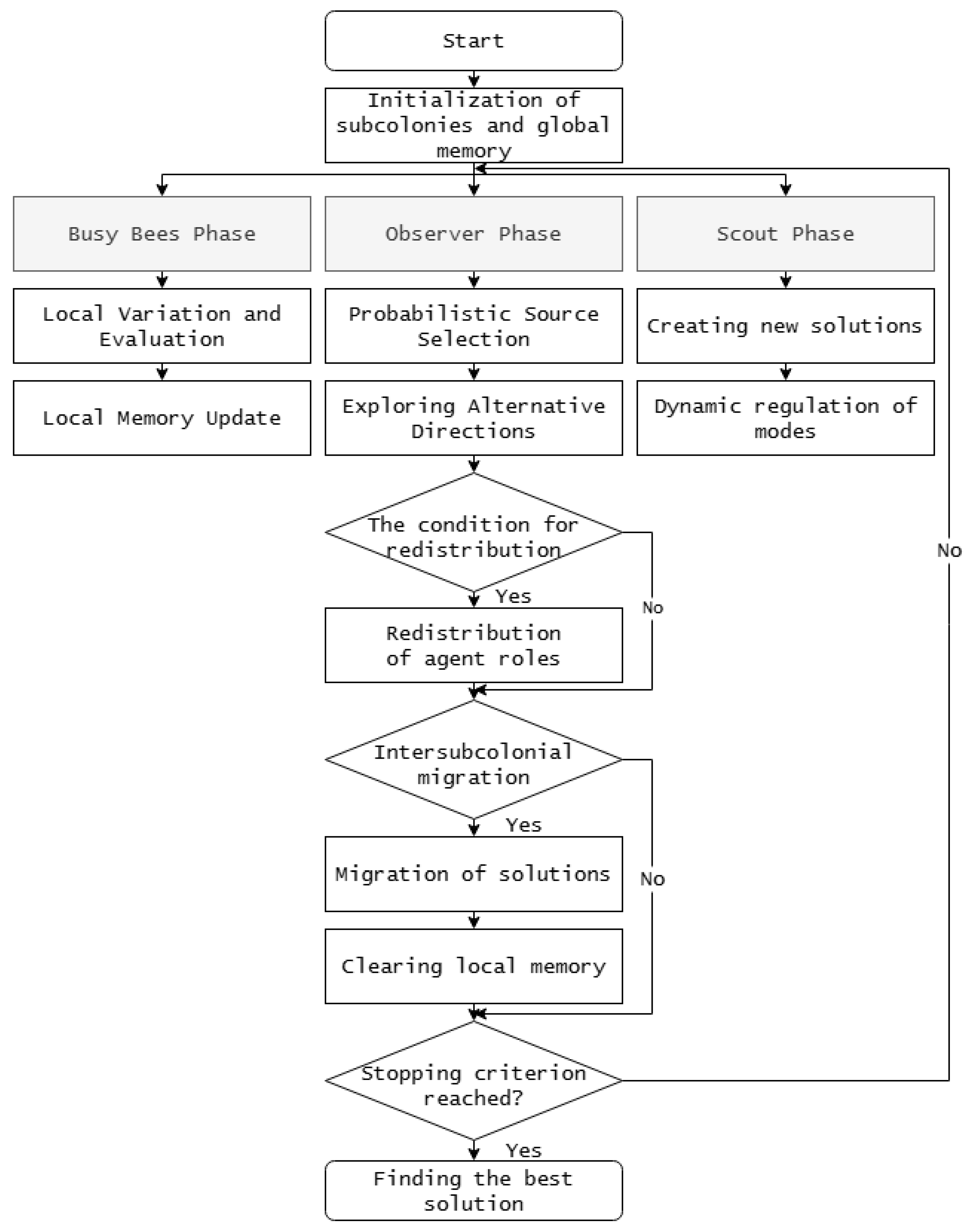
In parallel with the genetic algorithm, a modified artificial bee colony (ABC) algorithm functions, including a multi-colony structure and adaptive redistribution of agent roles. The structure of the proposed modification of the bee colony algorithm is shown in Figure 10.

Formally, the population of agents $C=C_1,C_2,\dots ,C_M$ is divided into a set of autonomous subcolonies, each of which functions in its own feature subspace. The division into subcolonies is performed by the adaptability controller based on the current diversity metric $D^{\left(t\right)}$. Within each subcolony, decisions are represented as feature vectors:

$$x_i^{\left(t\right)}=[w_1,h_1,\dots ,w_K,h_K],x_i^{\left(t\right)}\in {\Omega }_i,$$

(22)

where $w_k$, $h_k$ are the width and height of the k-th anchor frame, respectively. Three phases are implemented during the optimization process: busy bees, observers, and scouts. The busy bees phase is characterized by the execution of local variations of fixed solutions, accompanied by an evaluation of the objective function, in order to refine the parameters of the anchor frames in the vicinity of the current positions. The update of the solution is described by the expression

$$x_i^{(t+1)}=x_i^{\left(t\right)}+{\varphi }_i^{\left(t\right)}\left(x_i^{\left(t\right)}-x_r^{\left(t\right)}\right),{\varphi }_i^{\left(t\right)}\sim U(-\Phi ,\Phi ),$$

(23)

where $x_r^{\left(t\right)}$ is a randomly selected solution of the current subcolony, $\Phi$ is a parameter that regulates the scale of local changes, dynamically transformed depending on the diversity of the population:

$$\Phi ={\Phi }_{0e^{-k{D}^{\left(t\right)}}},D^{\left(t\right)}={\displaystyle \frac{1}{2}}\sum _{i=1}^n\parallel x_i^{\left(t\right)}-{\overline{x}}^{\left(t\right)}\parallel ,$$

(24)

where $D^{\left(t\right)}$ is the diversity metric, $x\left(t\right)$ is the centroid of the current solutions.

In the observer phase, a probabilistic selection of food sources is implemented, determined by the combined influence of the objective function and the uniqueness metric of solutions, which characterizes the degree of difference between individuals within the subcolony:

$$p_i={\displaystyle \frac{\eta f\left(x_i^{\left(t\right)}\right)+(1-\eta )Q_i^{\left(t\right)}}{{\sum }_{j=1}^n\left[\eta f\left(x_j^{\left(t\right)}\right)+(1-\eta )Q_j^{\left(t\right)}\right]}},$$

(25)

where $f\left(x_i^{\left(t\right)}\right)$ is the value of the objective Function (19) as applied to a particular solution, $Q_i^{\left(t\right)}$ is the uniqueness index reflecting the degree of difference between the solution and the other elements of the subcolony, determined by the inverse dependence on the average distance to neighboring solutions:

$$Q_i^{\left(t\right)}={\displaystyle \frac{1}{1+\frac{1}{|C_i|-1}{\sum }_{j\ne i}{\parallel x_i^{\left(t\right)}-x_j^{\left(t\right)}\parallel }_{{\Sigma }^{-1}}}},$$

(26)

where ${\Vert ·\Vert }_{{\Sigma }^{-1}}$ is the Mahalanobis distance, $\Sigma$ is the covariance matrix of the parameters of the current subcolony. The application of this mechanism prevents the concentration of computational resources on a limited set of solutions, supporting the diversification of search directions and increasing the probability of discovering new promising areas.

In turn, the explorer phase is activated when the efficiency of local search procedures decreases and is aimed at exploring poorly studied regions of the parametric space. New solutions are generated using the expression

$$x_i^{(t+1)}=x_{\mathrm{best}}^{\left(t\right)}+{\psi }_i^{\left(t\right)}\left(x_{\mathrm{rand}}^{\left(t\right)}-x_{\mathrm{worst}}^{\left(t\right)}\right),{\psi }_i^{\left(t\right)}\sim U(-1,1),$$

(27)

where $x_{\mathrm{best}}^{\left(t\right)}, x_{\mathrm{rand}}^{\left(t\right)}$ and $x_{\mathrm{worst}}^{\left(t\right)}$ are the best, random, and least effective solutions of the current iteration, respectively. This form of updating provides a stochastically directed shift of the search trajectory from areas of low performance to promising regions of the feature space.

At the same time, information exchange between subcolonies and the evolutionary component is carried out through the global memory of the container:

$$G^{(t+1)}={\mathrm{Top}}_P\left(G^{\left(t\right)}\cup \bigcup _{i=1}^M{C}_i^{\left(t\right)}\right),$$

(28)

$$C_i^{(t+1)}⟵C_i^{\left(t\right)}\cup \mathrm{Sample}\left(G^{\left(t\right)},\rho \right),$$

(29)

where the operator ${\mathrm{Top}}_P$ saves the P most effective solutions, $Sample\left(G^{\left(t\right)},\rho \right)$ implements the selection of elements with probability $\rho$.

After executing the GA and ABC operators, the updated solutions are consolidated into a combined set $\widetilde{P^{\left(t+1\right)}}$, from which a new population is formed:

$$P^{(t+1)}=arg\underset{\begin{array}{c}Q\subset P^{(t+1)},\left|Q\right|=M\end{array}}{max}\sum _{A\in Q}f\left(A\right).$$

(30)

Thus, the final set of solutions represents a balanced set of anchor frames, characterized by uniform distribution of parameters and resistance to stochastic disturbances, forming a consistent parametric space. The procedure description of the algorithm is provided in Appendix A.

3. Results

3.1. Experimental Setup and Data Preparation

The experimental part of the study aims to confirm the effectiveness of the developed recommendation system for servicing wind farms. Based on the developed architecture, a software environment has been implemented using Python 3.9, which provides the generation of a graph model of a wind farm, parameterization of external conditions, and visualization of motion trajectories in three-dimensional space. Within this environment, a computational experiment was conducted to verify the routing algorithm in conditions close to real operating scenarios.

The computational experiment was carried out on a computing platform equipped with an NVIDIA RTX 4070 graphics accelerator, an Intel i9-11900K processor, and 64 GB of RAM. The software environment included Windows 11, PyTorch 2.2.0, and OpenCV 4.9. The Albumentations library was used for data augmentation procedures, and YOLOv3 and modified YOLOv3-AFF models were trained using the Adam optimizer with initial parameters ${\eta }_0={10}^{-4}$, ${\beta }_1=0.9$, ${\beta }_2=0.999$, determined empirically based on a series of ten preliminary experiments with varying learning rates ${\eta }_0\in [{10}^{-5}; {10}^{-3}]$ and a step size of ${10}^{-4}$. The evaluation was based on the dynamics of the loss function reduction on the validation set and the stability of accuracy on the test sample. Training lasted 120 epochs with a batch size of 16. The stopping criterion was the stabilization of the loss function on the validation set. To ensure the comparability of the results, identical conditions and fixed weight initializations were used.

The selection of coefficients for the modified algorithms was also performed empirically. In particular, for the ant algorithm, the coefficients of pheromone influence $\alpha$ and heuristic information $\beta$ varied in the ranges $\alpha \in [0.8; 1.4]$ and $\beta \in [2.0; 3.0]$; the optimal values ($\alpha =1.1$, $\beta =2.5$) were determined based on the criterion of maximum convergence speed and minimum route length at 50 iterations. The pheromone evaporation coefficient $\rho$ was taken to be 0.35, and the amplification scale of elite agents was 1.2. In turn, for the genetic algorithm, the population size was $M=40$, the crossover probability $p_c=0.85$, and the mutation probability $p_m=0.05$. The regularization parameter $\lambda$ in the fitness Function (19) was selected based on the ratio of approximation accuracy and population diversity and was set equal to 0.116. For the modified bee colony algorithm, the number of subcolonies was set to $N=4$, the scale of local changes $\varphi$ varied in the range $[0.1; 0.5]$ and was adjusted based on the diversity metric $D^{\left(t\right)}$ according to Expression (24). The activation threshold for the scout phase was set to $\tau =10$ iterations.

The accuracy and stability of detection were evaluated on a dataset of 320 original images labeled into six defect classes: edge erosion, chips, cracks, surface contamination, tower corrosion, and fastener defects. The dataset was compiled from open sources and technical inspection archives. In addition, to increase the amount of data, synthesis was implemented through photometric transformations: rotations within 20°, scaling up to 1.2, mirror reflections, brightness and contrast changes up to 20%, addition of Gaussian noise, and partial darkening of areas to simulate object overlaps. As a result, the number of images in the training sample after augmentation increased to 4800, which provided sufficient scene diversity for training the neural model.

Note that to prevent overfitting, dropout mechanisms ($p=0.3$), five-fold cross-validation, and a weighted loss function compensating for class imbalance were used. The ratio between the training, validation, and test samples was 70%/20%/10%, respectively.

The detection results were evaluated using $Precision$, $Recall$, $meanAveragePrecision$, and F1-score metrics in accordance with COCO standards. To analyze the effectiveness of routing, the following indicators were used: average route length L, total energy consumption E, algorithm convergence time T, and trajectory stability coefficient S for variations in external parameters.

3.2. Route Optimization Experiments

The effectiveness of the modified routing algorithm was assessed using the actual coordinates of the Kamensk wind farm’s turbines, determined from satellite observations. Based on this data, a graph model of the wind farm was created, in which nodes represented inspection points and edges represented valid trajectories. Figure 11 shows the initial wind farm map with the spatial distribution of control points.

The developed system includes a route visualization module that enables parametric tuning of the optimization algorithm and displays the generated trajectories on the wind farm map. Figure 12 shows the software interface and the output of the modified ant colony algorithm, which includes a trajectory smoothing mechanism and adaptive pheromone updating.

To allow flexible configuration of the developed algorithm parameters, an optimizer configuration window is integrated into the software environment. This window allows changing the values of the $\alpha$, $\beta$ and $\rho$ parameters, the number of iterations, agents and crossover or mutation coefficients. Figure 13 shows the system configuration interface.

The computational experiment was conducted under conditions close to real-world operational scenarios, taking into account the spatial configuration of the wind turbines, flight altitude limitations, maneuvering radius, and mission execution time. The goal of the experiment was to quantitatively confirm the effectiveness of the proposed approach in comparison with existing routing solutions. The effectiveness of the generated routes was assessed based on three metrics: trajectory length L; the number of angles for which $cos\left(\theta \right)<0.85$; and integrated energy costs E. These indicators allow for an objective comparison of the effectiveness of route-building algorithms in terms of trajectory optimality, smoothness of movement, and energy costs. The results of the comparative analysis are presented in

Table 2. Comparison of the efficiency of the generated routes.

Method	Route Length, m	Number of Angles $<{150}^{\circ }$	Energy Consumption, J	Computation Time, s
A*	22,547	62	2250	78
Classical ACO	23,111	36	2440	45
A* with smoothing	21,852	39	2045	77
Proposed ACO with smoothing	20,676	19	1846	74

.

Based on the data presented in Table 2, it follows that the integration of the smoothing mechanism reduced the number of sharp bends by half compared to the A* method, thereby reducing maneuvering energy consumption and improving stability. To analyze the stability of the algorithm’s convergence, a series of additional experiments was conducted, varying the number of optimization iterations. The average route length, the standard deviation of the results, and the stability coefficient S, reflecting the degree of stability of solutions relative to the optimal value, were examined. The effect of the number of iterations on the stability of convergence is presented in

Table 3. Influence of the number of iterations on the convergence stability of the modified ACO algorithm.

Iterations	Average Route Length, m	Standard Deviation, m	Computation Time, s	Stability Coefficient, S
50	21,130	365	38	0.84
100	20,678	241	52	0.91
150	20,434	228	68	0.93
200	20,315	210	74	0.94

.

The analysis demonstrates that increasing the number of iterations to 200 stabilizes the convergence process and reduces route length variability with a moderate increase in computational load. To visualize the dynamics of these indicators, a graphical interpretation of the dependence of the average route length L and the stability coefficient S on the number of iterations of the modified ACO algorithm is presented in Figure 14 based on the data in Table 3.

The presented results demonstrate a monotonic reduction in route length with increasing iteration numbers, accompanied by an increase in the stability coefficient S from 0.84 to 0.94, confirming the effectiveness of the adaptive mechanism for regulating pheromone field parameters. After reaching 150 iterations, the reduction in route length slows, indicating the algorithm’s transition to a stable search region.

With a further increase in the number of iterations to 200, the values of L and S stabilize, indicating the development of stable convergence without signs of overfitting. The conducted computational experiment confirms that the use of a modified anti-colonial algorithm with adaptive smoothing reduces route length while maintaining energy efficiency and the stability of navigation solutions under wind turbine operating conditions.

3.3. Detection Experiments

The objective of the experimental study of the detection module is to evaluate the effectiveness of the modified YOLOv3 architecture for recognizing defects in wind turbine structural components under meteorological influences and changing lighting conditions. The computational conditions, sample structure, and training parameters fully correspond to the configuration presented in Section 3.1, ensuring the correctness of the comparison of results and the reproducibility of the experiment.

The behavior of the loss components and key detection metrics during training serves as the primary indicator of the stability and generalization ability of the modified architecture. In this regard, the training and validation dynamics of the YOLOv3-AFF-AO model are presented in Figure 15.

The graphs presented reflect the change in the loss function components and key quality metrics throughout the training process, demonstrating a steady decrease in error values for localization, classification, and focal loss distribution, accompanied by an increase in precision, recall, and integral metrics. This behavior indicates stable generalization dynamics without divergence between training and validation trajectories, confirming the absence of overfitting and the robustness of the adopted optimization strategy for varying meteorological and illumination conditions.To assess the sensitivity of the modified architecture to the decision threshold, the dependence of the $F1$ metric on the confidence parameter was analyzed, as shown in Figure 16.

It should be noted that the highest $F1$ value is observed at $confidence$ = 0.689, which was selected as the optimal threshold for subsequent experimental studies. The smooth shape of the curve and the absence of sharp fluctuations indicate a stable balance between false positives and false negatives across a wide confidence range, confirming the robustness of the modified architecture.

To quantitatively evaluate the effectiveness of the modified architecture, its performance was compared with the baseline YOLOv3 model, as well as with modern object detection architectures, including YOLOv5s, YOLOv7, YOLOv8n, and Deformable DETR. The evaluation was conducted using standard metrics: $Precision$, $Recall$, $F1$, $mAP@0.5$, and $inferencerate\left(FPS\right)$. To provide a structural comparison of accuracy- and speed-related metrics across the evaluated architectures, the numerical results presented in

Table 4. Comparison of detection performance across different models.

Model	Precision	Recall	F1	mAP@0.5	FPS
YOLOv3 (baseline)	0.31	0.24	0.26	0.28	43
YOLOv3 + AFF + AO	0.47	0.33	0.38	0.41	42
YOLOv5s	0.51	0.36	0.42	0.48	62
YOLOv7	0.55	0.39	0.46	0.52	58
YOLOv8n	0.57	0.41	0.48	0.54	65
Deformable DETR	0.53	0.40	0.46	0.50	12

were supplemented with a graphical visualization shown in Figure 17. This allows for a clearer examination of the trade-off between detection quality and inference performance.

To quantitatively evaluate the effectiveness of the modified architecture, its performance was compared with the baseline YOLOv3 model, as well as with modern detection architectures, including YOLOv5s, YOLOv7, YOLOv8n, and Deformable DETR. The evaluation was conducted using standard metrics: $Precision$, $Recall$, $F1$, $mAP@0.5$, and $inferencerate\left(FPS\right)$. The numerical results are summarized in Table 4.

To complement the numerical comparison and reveal the relative positioning of the evaluated architectures in terms of accuracy and inference speed, the summarized results were additionally visualized in Figure 17. Such visualization allows for a clearer interpretation of cross-model differences and provides an intuitive representation of the accuracy–speed trade-off that is not fully captured by the numerical table alone.

As shown by the summarized results, the modified YOLOv3-AFF-AO model demonstrates a 46% increase in the $F1$ metric relative to the baseline YOLOv3 while maintaining a comparable inference rate. Although contemporary architectures such as YOLOv8n and YOLOv7 achieve higher accuracy values, these improvements are accompanied by increased computational requirements, particularly in the case of Deformable DETR. The graphical comparison in Figure 17 confirms that the proposed modification provides a favorable accuracy–speed balance, supporting its applicability in real-time monitoring scenarios with constrained onboard resources.

To clarify the impact of the architectural components that determine the achieved results, a computational experiment was conducted to analyze the functional significance of the Adaptive Feature Fusion (AFF) and Bio-Inspired Anchor Optimization (AO) modules. The study included a series of tests with the sequential exclusion of these modules. The summarized results of the experiment are presented in

Table 5. Influence of individual modules on detection performance.

Model Configuration	Precision	Recall	F1	mAP@0.5	F1 Change, %
YOLOv3 (baseline)	0.31	0.24	0.26	0.28	–
YOLOv3 + AFF	0.39	0.29	0.33	0.35	+27%
YOLOv3 + AO	0.42	0.31	0.35	0.37	+34%
YOLOv3 + AFF + AO	0.47	0.33	0.38	0.41	+46%

.

The experimental results demonstrate that the Adaptive Feature Fusion module improves detection completeness and robustness by effectively combining features from different hierarchical levels. The Bio-Inspired Anchor Optimization module also improves object localization accuracy by adapting anchor frame sizes to the geometric characteristics and scale of defects. The combined use of these components produces a synergistic effect, resulting in increased $F1$ metrics and $mAP@0.5$.

To thoroughly analyze the effectiveness of the anchor frame adaptation mechanism and confirm the validity of the applied clustering strategy, an additional comparative study was conducted. The results are presented in

Table 6. Comparison of clustering methods for anchor boxes.

Clustering Method	Average IoU of Anchors	Average Size Deviation, %	Computation Time, s	Stability Coefficient, S
k-means	0.71	24.5	11.2	0.82
k-means++	0.74	21.7	12.9	0.85
Bio-Inspired Anchor	0.81	14.3	14.1	0.93

.

The results presented in Table 6 demonstrate that the bioinspired method provides a 10–12% increase in the average IoU coverage index, while reducing the variance of anchor frame sizes by 40%. These results indicate a more accurate match between the geometric and scaling parameters of the moorings and real objects.

As part of the experimental studies, visual verification of the detection results was performed to assess the accuracy of defect localization and classification detected by the modified YOLOv3-AFF architecture. Figure 18 shows examples of recognition of various types of defects on wind turbine blade surfaces, including coating damage, erosion zones, and cracks in structural components.

Thus, the results of the experimental studies confirm the effectiveness of the modified YOLOv3-AFF-AO architecture for detecting defects in wind turbine structural components. The implementation of the Adaptive Feature Fusion (AFF) and Bio-Inspired Anchor Optimization (AO) modules improves localization accuracy, recognition completeness, and robustness to variability in the scale and shape of objects, with a slight reduction in inference speed.

4. Discussion

The results of the study confirmed the effectiveness of the proposed architecture of an intelligent wind turbine maintenance system, which includes a hybrid routing module and a modified YOLOv3-AFF-AO detection model. The combination of the A* algorithm and the modified ant colony method resulted in a 15–20% reduction in route length and energy consumption while maintaining stable convergence ($S=0.94$). A trajectory smoothing mechanism eliminated sharp kinks and improved the smoothness of autonomous agent movement, consistent with modern research in the field of hybrid metaheuristic approaches to route planning.

In terms of defect detection, the integration of the Adaptive Feature Fusion and Bio-Inspired Anchor Optimization modules resulted in a 46% increase in the $F1$ metric and an increase in $mAP@0.5$ from 0.28 to 0.41 while maintaining high processing speed (42 FPS). These results confirm that adaptive feature fusion and bioinspired anchor frame optimization increase the model’s sensitivity to small objects and improve the alignment of localization parameters with real-world defect shapes. The developed system demonstrates robustness and reproducibility with limited data volumes, forming the basis for developing autonomous predictive maintenance solutions for wind farms and promising future research in the areas of adaptive and distributed learning.

5. Conclusions

This paper addresses the complex scientific and technical challenge of improving the efficiency and reliability of wind turbine maintenance by integrating intelligent routing algorithms for autonomous robotic agents and computer vision. A decision support system architecture has been developed that combines a routing optimization module and a module for detecting defects in wind turbine structural components.

The routing module implements a hybrid approach based on a combination of the A* algorithm and a modified ant colony algorithm with dynamic pheromone field updating and a B-spline trajectory smoothing procedure. Computational experiments confirmed a 15–20% reduction in route length and energy consumption while maintaining stability and accuracy of motion planning in a spatially constrained environment.

The detection module is implemented using a modified YOLOv3 architecture, incorporating Adaptive Feature Fusion (AFF) and Bio-Inspired Anchor Optimization (AO) mechanisms. The integration of these components resulted in a 46% increase in the $F1$ metric and a 46.4% increase in $mAP@0.5$ relative to the baseline configuration, while maintaining a high inference speed (42 FPS). Experimental results and visual verification confirmed the correct localization and classification of defects under varying illumination, viewing angles, and object scales.

Prospects for further research include expanding the training sets with synthetic data, using multispectral sensor systems to increase the information content of defect imagery, and developing predictive modules for generating maintenance schedules based on failure criticality analysis. Implementation of these areas will enhance the adaptability and predictive power of the system, ensuring its practical applicability within the framework of intelligent lifecycle management of wind energy infrastructure.