Innovative Method for Detecting Malware by Analysing API Request Sequences Based on a Hybrid Recurrent Neural Network for Applied Forensic Auditing
Abstract
1. Introduction and Related Works
- Most methods (static signatures, n-grams, visualisations) are vulnerable to obfuscation and polymorphism, which calls into question their long-term applicability.
- Existing models cope poorly with very long and sparse sequences of API calls and do not provide stable long-term dependency preservation necessary for recognising deferred or conditional actions of malicious code.
- Research rarely offers mature mechanisms for the multimodal signals’ efficient fusion (static features, dynamics, network traffic, telemetry), so models lose information content when channels are partially available.
- There are high-quality labelled and balanced datasets, acute shortages, unified benchmarks, and reproducible evaluation protocols, which hinder objective comparative analysis.
- Robustness enhancement methods (adversarial training) either worsen overall accuracy or require expensive generation of attack examples.
- Practical applicability is limited by the predictions’ interpretability problems, high computational cost, and difficulties of deployment in resource-constrained environments.
2. Materials and Methods
2.1. Developing a Mathematical Framework for Malware Detection
- 2.
- The events (intensity) arrival process, in which events have a time intensity λ(t), and, for example, in the simplest Poisson model:
- 3.
- Hidden Markov models in which a hidden state sk ∈ S (behaviour mode) is introduced. Then,
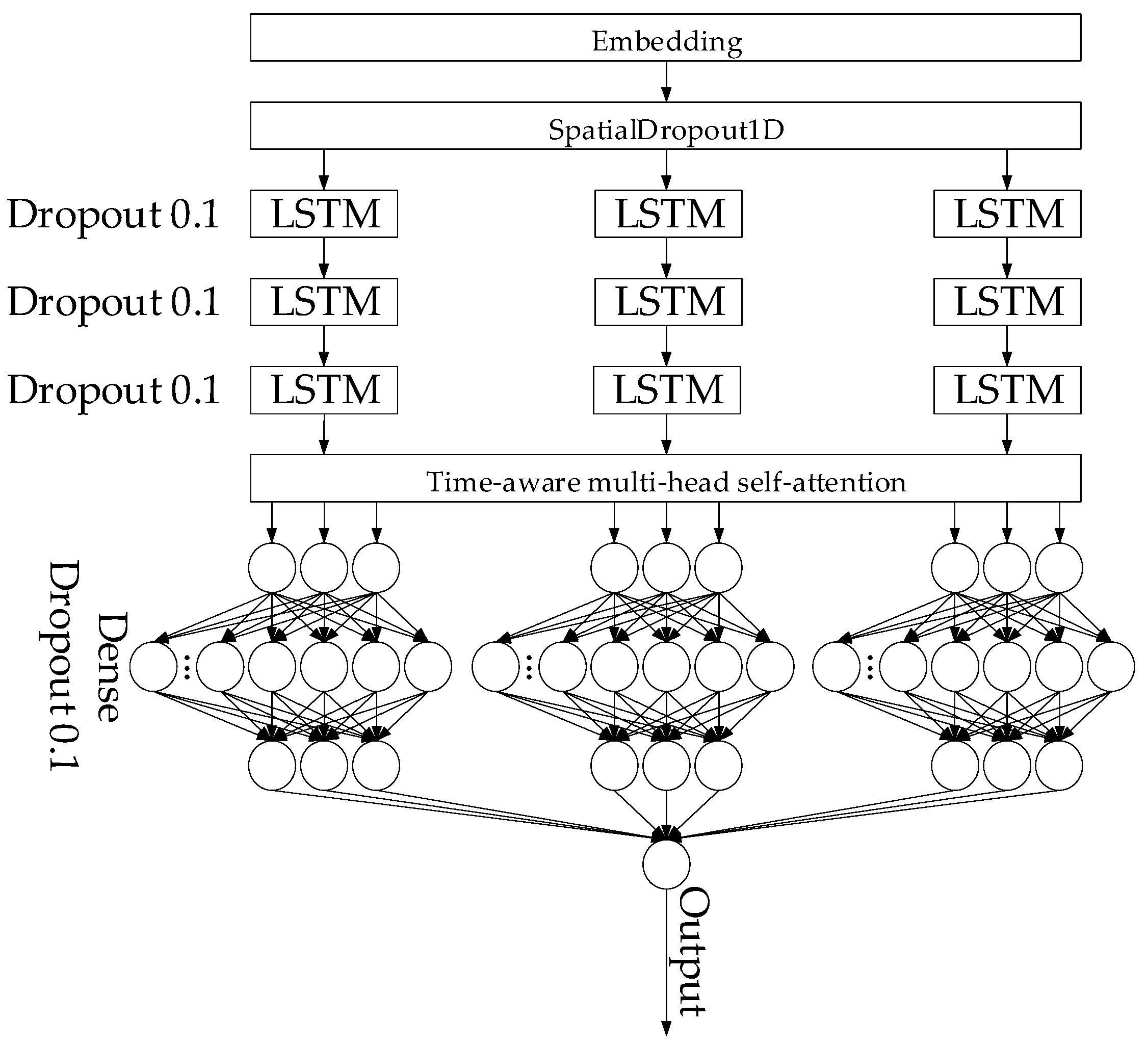
2.2. Development of a Neural Network Model for Detecting Malware
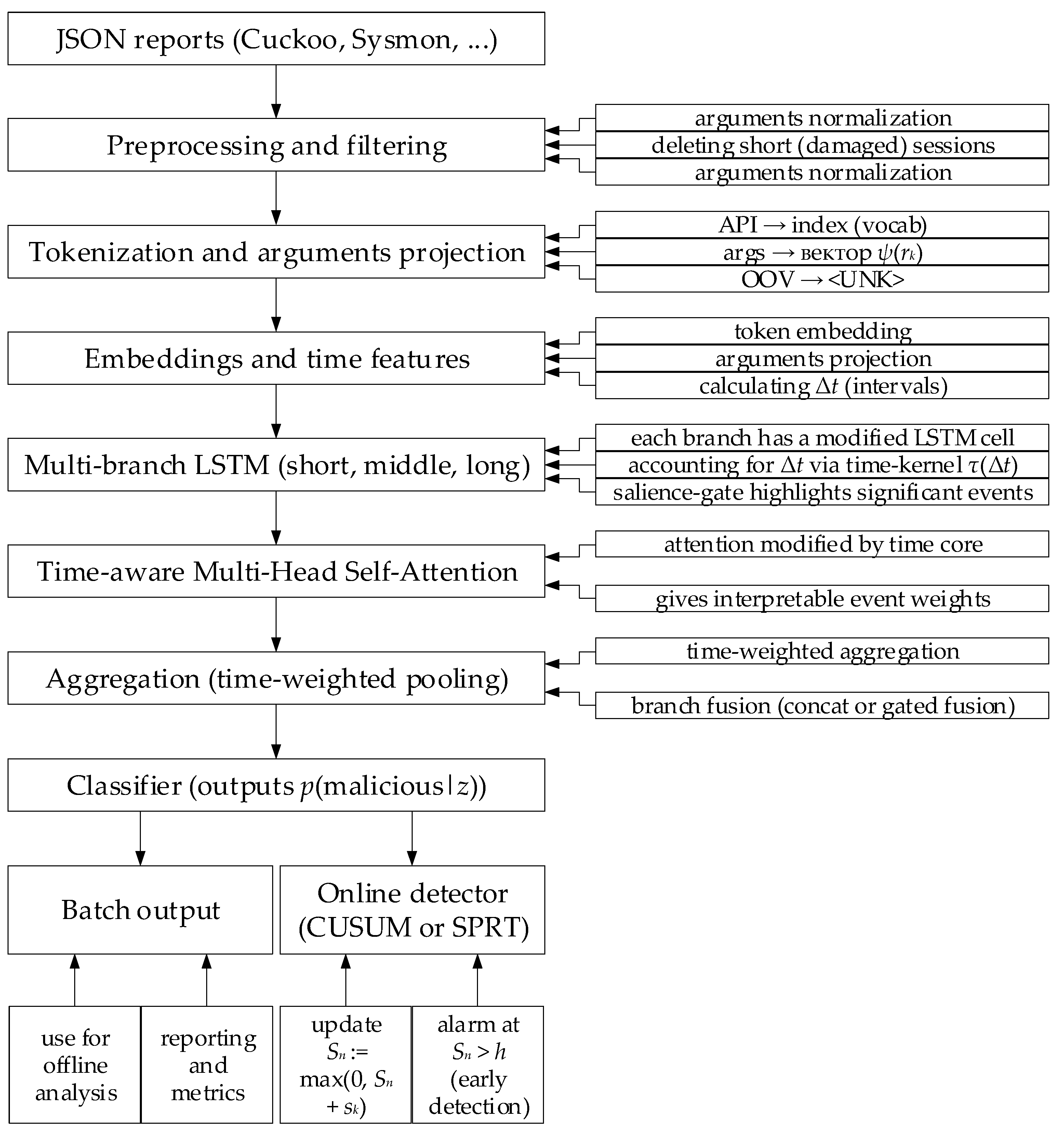
2.3. Synthesis of a Malware Detection Method for API Request Sequence Analysis
3. Case Study
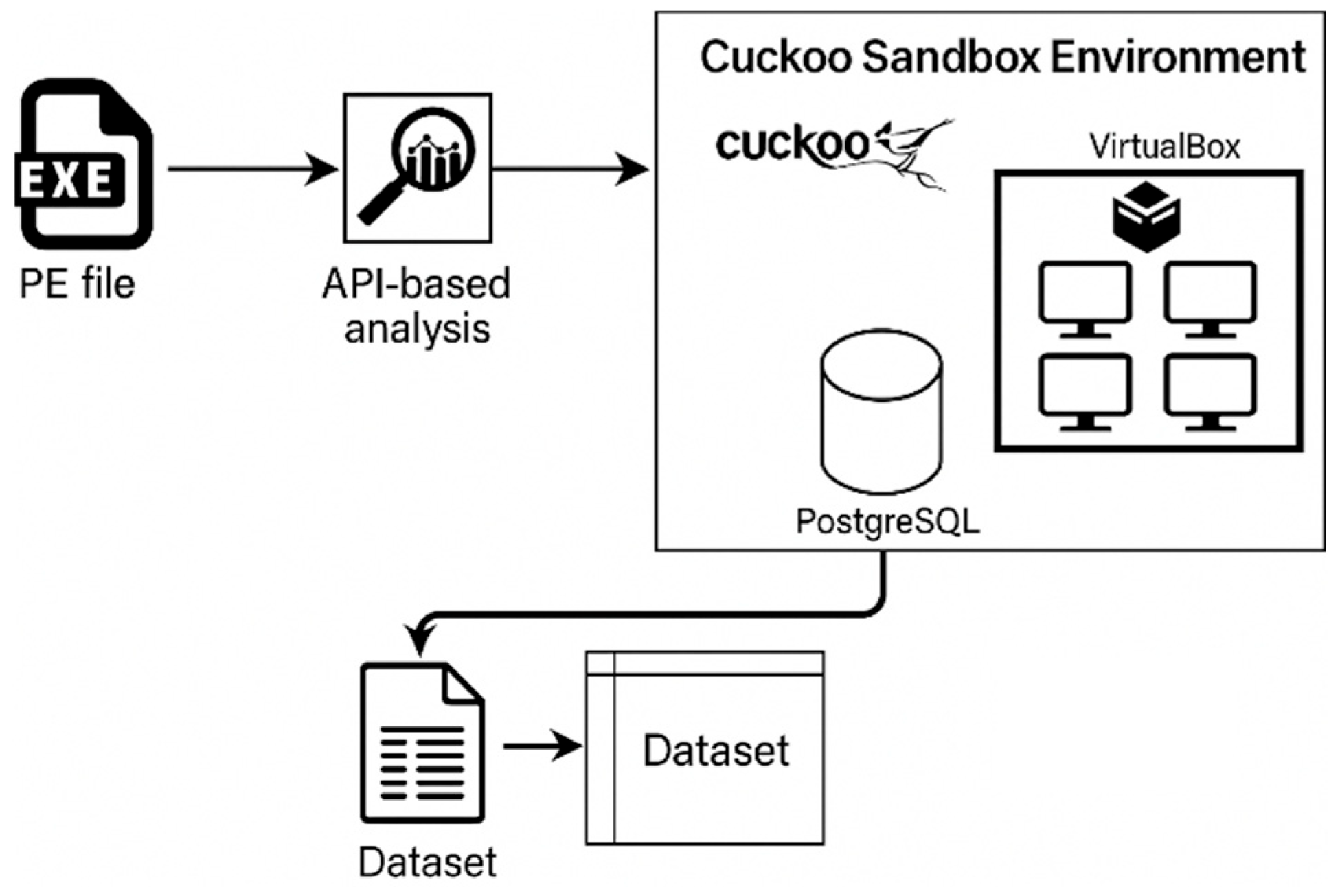
3.1. Formation and Pre-Processing of the Input Dataset
3.2. Results of the Developed Neural Network Training
3.3. Results of an Example Solution to the Detecting Malware Problem by the API Requests Analysis Sequences
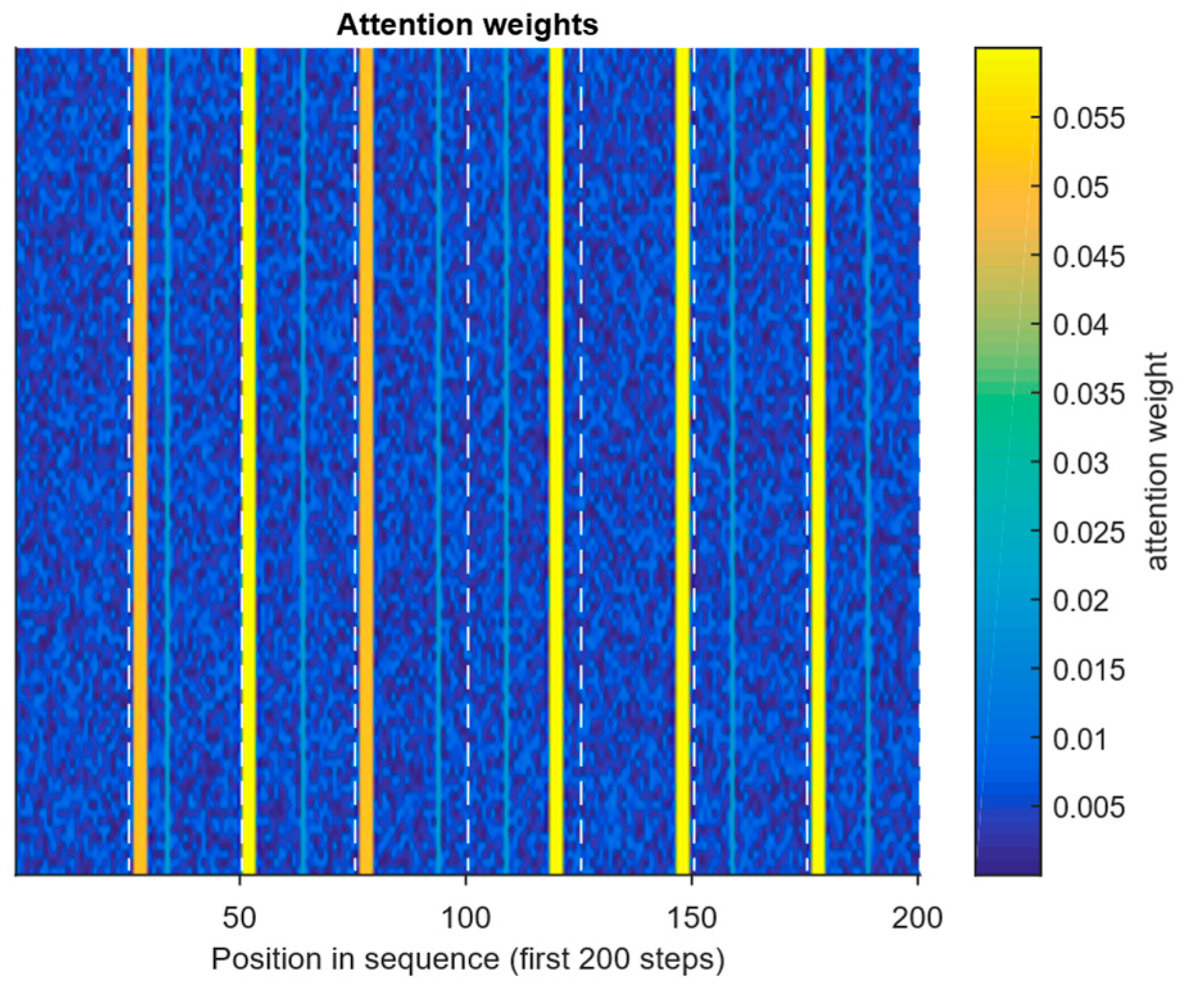
- Perturbation tests include masking and sequentially removing the top-k elements, random elements, and critical API calls; measuring the change in model confidence (a combination of sufficiency (comprehensiveness) and AOPC metrics).
- Alignment tests involve comparing the attention (or saliency) ranking with the “critical” APIs labelling (precisionk, recallk).
- Statistical correlation refers to correlating explanation ranks with the expert indicator score (IOC score).
3.4. Results of the Developed Method of Detecting Malware by API Requests, Analysing Sequences, and Computational Complexity Evaluation
3.5. Results of the Developed Method for Detecting Malware by API Requests, Analysing Sequences Implementation in Forensic Auditing
4. Discussion
- A theoretical result on the preservation of long-term memory possibility in gated recurrent cells (Theorem 1) is introduced and proved, which justifies the architectural choice.
- A multi-branch time-aware RNN architecture is proposed based on a modified LSTM with salience gates and a time kernel, integrated with time-aware multi-head self-attention for explicitly taking into account the intervals Δt and the critical steps’ interpretability.
- The sequence embedding operator Φ is formalised, and additional loss regularisers (terms) are introduced, increasing the embeddings’ interclass dispersion and resistance to noise and obfuscation.
- A hybrid detector is proposed that combines a neural network classifier with sequential criteria (LRT or CUSUM) for online response.
- A pipeline for data extraction from Cuckoo, preprocessing procedures, and augmentation techniques (adv-training) to improve robustness was implemented.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Model | MR(10) | MR(50) | MR(100) | (Timesteps) | Delayed-Task ACC (K = 100) | MSE (K = 100) |
|---|---|---|---|---|---|---|
| Standard LSTM | 0.42 ± 0.03 | 0.11 ± 0.02 | 0.03 ± 0.01 | 23 ± 2 | 0.62 ± 0.02 | 0.41 ± 0.05 |
| LSTM with regularisation (λ = 0.1, st hard) | 0.56 ± 0.02 | 0.22 ± 0.03 | 0.08 ± 0.02 | 37 ± 3 | 0.73 ± 0.02 | 0.32 ± 0.04 |
| LSTM with regularisation (λ = 0.5, st hard) | 0.63 ± 0.02 | 0.30 ± 0.03 | 0.22 ± 0.02 | 54 ± 4 | 0.79 ± 0.01 | 0.26 ± 0.03 |
| LSTM with regularisation (adaptive st via attention) | 0.60 ± 0.02 | 0.28 ± 0.03 | 0.11 ± 0.03 | 49 ± 3 | 0.77 ± 0.02 | 0.28 ± 0.03 |
References
- Yang, B.; Yu, Z.; Cai, Y. Malicious Software Spread Modeling and Control in Cyber–Physical Systems. Knowl.-Based Syst. 2022, 248, 108913. [Google Scholar] [CrossRef]
- Zhang, S.; Wu, J.; Zhang, M.; Yang, W. Dynamic Malware Analysis Based on API Sequence Semantic Fusion. Appl. Sci. 2023, 13, 6526. [Google Scholar] [CrossRef]
- Anđelić, N.; Baressi Šegota, S.; Car, Z. Improvement of Malicious Software Detection Accuracy through Genetic Programming Symbolic Classifier with Application of Dataset Oversampling Techniques. Computers 2023, 12, 242. [Google Scholar] [CrossRef]
- Amer, E.; Zelinka, I.; El-Sappagh, S. A Multi-Perspective Malware Detection Approach through Behavioral Fusion of API Call Sequence. Comput. Secur. 2021, 110, 102449. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Z.; Jiang, B.; Tse, T.H. The Impact of Lightweight Disassembler on Malware Detection: An Empirical Study. In Proceedings of the 2018 IEEE 42nd Annual Computer Software and Applications Conference (COMPSAC), Tokyo, Japan, 23–27 July 2018; pp. 620–629. [Google Scholar] [CrossRef]
- Amer, E.; Zelinka, I. A Dynamic Windows Malware Detection and Prediction Method Based on Contextual Understanding of API Call Sequence. Comput. Secur. 2020, 92, 101760. [Google Scholar] [CrossRef]
- Syeda, D.Z.; Asghar, M.N. Dynamic Malware Classification and API Categorisation of Windows Portable Executable Files Using Machine Learning. Appl. Sci. 2024, 14, 1015. [Google Scholar] [CrossRef]
- Zhang, S.; Gao, M.; Wang, L.; Xu, S.; Shao, W.; Kuang, R. A Malware-Detection Method Using Deep Learning to Fully Extract API Sequence Features. Electronics 2025, 14, 167. [Google Scholar] [CrossRef]
- Zhang, R.; Huang, S.; Qi, Z.; Guan, H. Combining Static and Dynamic Analysis to Discover Software Vulnerabilities. In Proceedings of the 2011 Fifth International Conference on Innovative Mobile and Internet Services in Ubiquitous Computing, Seoul, Republic of Korea, 30 June–2 July 2011; pp. 175–181. [Google Scholar] [CrossRef]
- Shijo, P.V.; Salim, A. Integrated Static and Dynamic Analysis for Malware Detection. Procedia Comput. Sci. 2015, 46, 804–811. [Google Scholar] [CrossRef]
- Ali, M.; Shiaeles, S.; Bendiab, G.; Ghita, B. MALGRA: Machine Learning and N-Gram Malware Feature Extraction and Detection System. Electronics 2020, 9, 1777. [Google Scholar] [CrossRef]
- Guo, W.; Du, W.; Yang, X.; Xue, J.; Wang, Y.; Han, W.; Hu, J. MalHAPGNN: An Enhanced Call Graph-Based Malware Detection Framework Using Hierarchical Attention Pooling Graph Neural Network. Sensors 2025, 25, 374. [Google Scholar] [CrossRef]
- Aggarwal, S.; Di Troia, F. Malware Classification Using Dynamically Extracted API Call Embeddings. Appl. Sci. 2024, 14, 5731. [Google Scholar] [CrossRef]
- Anil Kumar, D.; Das, S.K.; Sahoo, M.K. Malware Detection System Using API-Decision Tree. Lect. Notes Data Eng. Commun. Technol. 2022, 86, 511–517. [Google Scholar] [CrossRef]
- Cui, L.; Yin, J.; Cui, J.; Ji, Y.; Liu, P.; Hao, Z.; Yun, X. API2Vec++: Boosting API Sequence Representation for Malware Detection and Classification. IEEE Trans. Softw. Eng. 2024, 50, 2142–2162. [Google Scholar] [CrossRef]
- Yang, J.; Jiang, X.; Liang, G.; Li, S.; Ma, Z. Malicious Traffic Identification with Self-Supervised Contrastive Learning. Sensors 2023, 23, 7215. [Google Scholar] [CrossRef]
- Yang, S.; Yang, Y.; Zhao, D.; Xu, L.; Li, X.; Yu, F.; Hu, J. Dynamic Malware Detection Based on Supervised Contrastive Learning. Comput. Electr. Eng. 2025, 123, 110108. [Google Scholar] [CrossRef]
- Berrios, S.; Leiva, D.; Olivares, B.; Allende-Cid, H.; Hermosilla, P. Systematic Review: Malware Detection and Classification in Cybersecurity. Appl. Sci. 2025, 15, 7747. [Google Scholar] [CrossRef]
- Shaukat, K.; Luo, S.; Varadharajan, V. A Novel Method for Improving the Robustness of Deep Learning-Based Malware Detectors against Adversarial Attacks. Eng. Appl. Artif. Intell. 2022, 116, 105461. [Google Scholar] [CrossRef]
- Nikolova, E. Markov Models for Malware and Intrusion Detection: A Survey. Serdica J. Comput. 2023, 15, 129–147. [Google Scholar] [CrossRef]
- Abanmi, N.; Kurdi, H.; Alzamel, M. Dynamic IoT Malware Detection in Android Systems Using Profile Hidden Markov Models. Appl. Sci. 2022, 13, 557. [Google Scholar] [CrossRef]
- Maniriho, P.; Mahmood, A.N.; Chowdhury, M.J.M. API-MalDetect: Automated Malware Detection Framework for Windows Based on API Calls and Deep Learning Techniques. J. Netw. Comput. Appl. 2023, 218, 103704. [Google Scholar] [CrossRef]
- ALGorain, F.T.; Clark, J.A. Bayesian Hyper-Parameter Optimisation for Malware Detection. Electronics 2022, 11, 1640. [Google Scholar] [CrossRef]
- Vladov, S.; Shmelov, Y.; Yakovliev, R. Method for Forecasting of Helicopters Aircraft Engines Technical State in Flight Modes Using Neural Networks. CEUR Workshop Proc. 2022, 3171, 974–985. Available online: https://ceur-ws.org/Vol-3171/paper70.pdf (accessed on 6 August 2025).
- Zhang, Y.; Yang, S.; Xu, L.; Li, X.; Zhao, D. A Malware Detection Framework Based on Semantic Information of Behavioral Features. Appl. Sci. 2023, 13, 12528. [Google Scholar] [CrossRef]
- Coscia, A.; Lorusso, R.; Maci, A.; Urbano, G. APIARY: An API-Based Automatic Rule Generator for Yara to Enhance Malware Detection. Comput. Secur. 2025, 153, 104397. [Google Scholar] [CrossRef]
- Li, N.; Lu, Z.; Ma, Y.; Chen, Y.; Dong, J. A Malicious Program Behavior Detection Model Based on API Call Sequences. Electronics 2024, 13, 1092. [Google Scholar] [CrossRef]
- Li, C.; Lv, Q.; Li, N.; Wang, Y.; Sun, D.; Qiao, Y. A Novel Deep Framework for Dynamic Malware Detection Based on API Sequence Intrinsic Features. Comput. Secur. 2022, 116, 102686. [Google Scholar] [CrossRef]
- Miao, C.; Kou, L.; Zhang, J.; Dong, G. A Lightweight Malware Detection Model Based on Knowledge Distillation. Mathematics 2024, 12, 4009. [Google Scholar] [CrossRef]
- Vladov, S.; Sachenko, A.; Sokurenko, V.; Muzychuk, O.; Vysotska, V. Helicopters Turboshaft Engines Neural Network Modeling under Sensor Failure. J. Sens. Actuator Netw. 2024, 13, 66. [Google Scholar] [CrossRef]
- Han, W.; Xue, J.; Wang, Y.; Liu, Z.; Kong, Z. MalInsight: A Systematic Profiling Based Malware Detection Framework. J. Netw. Comput. Appl. 2019, 125, 236–250. [Google Scholar] [CrossRef]
- Vaddadi, S.A.; Arnepalli, P.R.R.; Thatikonda, R.; Padthe, A. Effective Malware Detection Approach Based on Deep Learning in Cyber-Physical Systems. Int. J. Comput. Sci. Inf. Technol. 2022, 14, 1–12. [Google Scholar] [CrossRef]
- Vladov, S.; Shmelov, Y.; Yakovliev, R. Modified Helicopters Turboshaft Engines Neural Network On-board Automatic Control System Using the Adaptive Control Method. CEUR Workshop Proc. 2022, 3309, 205–224. Available online: https://ceur-ws.org/Vol-3309/paper15.pdf (accessed on 12 August 2025).
- Rashid, M.U.; Qureshi, S.; Abid, A.; Alqahtany, S.S.; Alqazzaz, A.; ul Hassan, M.; Al Reshan, M.S.; Shaikh, A. Hybrid Android Malware Detection and Classification Using Deep Neural Networks. Int. J. Comput. Intell. Syst. 2025, 18, 52. [Google Scholar] [CrossRef]
- Han, W.; Xue, J.; Wang, Y.; Huang, L.; Kong, Z.; Mao, L. MalDAE: Detecting and Explaining Malware Based on Correlation and Fusion of Static and Dynamic Characteristics. Comput. Secur. 2019, 83, 208–233. [Google Scholar] [CrossRef]
- Ilić, S.; Gnjatović, M.; Tot, I.; Jovanović, B.; Maček, N.; Gavrilović Božović, M. Going beyond API Calls in Dynamic Malware Analysis: A Novel Dataset. Electronics 2024, 13, 3553. [Google Scholar] [CrossRef]
- Daeef, A.Y.; Al-Naji, A.; Chahl, J. Lightweight and Robust Malware Detection Using Dictionaries of API Calls. Telecom 2023, 4, 746–757. [Google Scholar] [CrossRef]
- Akhtar, M.S.; Feng, T. Detection of Malware by Deep Learning as CNN-LSTM Machine Learning Techniques in Real Time. Symmetry 2022, 14, 2308. [Google Scholar] [CrossRef]
- Vladov, S.; Vysotska, V.; Sokurenko, V.; Muzychuk, O.; Nazarkevych, M.; Lytvyn, V. Neural Network System for Predicting Anomalous Data in Applied Sensor Systems. Appl. Syst. Innov. 2024, 7, 88. [Google Scholar] [CrossRef]
- Kim, H.; Kim, M. Malware Detection and Classification System Based on CNN-BiLSTM. Electronics 2024, 13, 2539. [Google Scholar] [CrossRef]
- Li, W.; Tang, H.; Zhu, H.; Zhang, W.; Liu, C. TS-Mal: Malware Detection Model Using Temporal and Structural Features Learning. Comput. Secur. 2024, 140, 103752. [Google Scholar] [CrossRef]
- Qian, L.; Cong, L. Channel Features and API Frequency-Based Transformer Model for Malware Identification. Sensors 2024, 24, 580. [Google Scholar] [CrossRef]
- Lu, J.; Ren, X.; Zhang, J.; Wang, T. CPL-Net: A Malware Detection Network Based on Parallel CNN and LSTM Feature Fusion. Electronics 2023, 12, 4025. [Google Scholar] [CrossRef]
- Vladov, S.; Shmelov, Y.; Petchenko, M. A Neuro-Fuzzy Expert System for the Control and Diagnostics of Helicopters Aircraft Engines Technical State. CEUR Workshop Proc. 2021, 3013, 40–52. Available online: https://ceur-ws.org/Vol-3013/20210040.pdf (accessed on 18 August 2025).
- Ferdous, J.; Islam, R.; Mahboubi, A.; Islam, M.Z. A Survey on ML Techniques for Multi-Platform Malware Detection: Securing PC, Mobile Devices, IoT, and Cloud Environments. Sensors 2025, 25, 1153. [Google Scholar] [CrossRef]
- Lytvyn, V.; Dudyk, D.; Peleshchak, I.; Peleshchak, R.; Pukach, P. Influence of the Number of Neighbours on the Clustering Metric by Oscillatory Chaotic Neural Network with Dipole Synaptic Connections. CEUR Workshop Proc. 2024, 3664, 24–34. Available online: https://ceur-ws.org/Vol-3664/paper3.pdf (accessed on 19 August 2025).
- Vladov, S.; Shmelov, Y.; Yakovliev, R. Optimization of Helicopters Aircraft Engine Working Process Using Neural Networks Technologies. CEUR Workshop Proc. 2022, 3171, 1639–1656. Available online: https://ceur-ws.org/Vol-3171/paper117.pdf (accessed on 21 August 2025).
- Owoh, N.; Adejoh, J.; Hosseinzadeh, S.; Ashawa, M.; Osamor, J.; Qureshi, A. Malware Detection Based on API Call Sequence Analysis: A Gated Recurrent Unit–Generative Adversarial Network Model Approach. Future Internet 2024, 16, 369. [Google Scholar] [CrossRef]
- Alshomrani, M.; Albeshri, A.; Alturki, B.; Alallah, F.S.; Alsulami, A.A. Survey of Transformer-Based Malicious Software Detection Systems. Electronics 2024, 13, 4677. [Google Scholar] [CrossRef]
- Wang, Z.; Guan, Z.; Liu, X.; Li, C.; Sun, X.; Li, J. SDN Anomalous Traffic Detection Based on Temporal Convolutional Network. Appl. Sci. 2025, 15, 4317. [Google Scholar] [CrossRef]
- Ablamskyi, S.; Tchobo, D.L.R.; Romaniuk, V.; Šimić, G.; Ilchyshyn, N. Assessing the Responsibilities of the International Criminal Court in the Investigation of War Crimes in Ukraine. Novum Jus 2023, 17, 353–374. [Google Scholar] [CrossRef]
- Ablamskyi, S.; Nenia, O.; Drozd, V.; Havryliuk, L. Substantial Violation of Human Rights and Freedoms as a Prerequisite for Inadmissibility of Evidence. Justicia 2021, 26, 47–56. [Google Scholar] [CrossRef]
- Lopes, J.F.; Barbon Junior, S.; de Melo, L.F. Online Meta-Recommendation of CUSUM Hyperparameters for Enhanced Drift Detection. Sensors 2025, 25, 2787. [Google Scholar] [CrossRef] [PubMed]
- Vladov, S.; Shmelov, Y.; Yakovliev, R.; Petchenko, M.; Drozdova, S. Neural Network Method for Helicopters Turboshaft Engines Working Process Parameters Identification at Flight Modes. In Proceedings of the 2022 IEEE 4th International Conference on Modern Electrical and Energy System (MEES), Kremenchuk, Ukraine, 20–23 October 2022; pp. 604–609. [Google Scholar] [CrossRef]










| Method (Approach) | Data (Features) | Model (Architecture) | Results Obtained | Limitations | References |
|---|---|---|---|---|---|
| A combination of static disassembly and dynamics | Features from disassembled executables (IDA Pro), API call sequences | Classic classifier with API calls and sequence analysis | Practical feasibility, high results on selected datasets | Dependent on disassembly quality, static features are subject to obfuscation, and scalability and reproducibility are not always demonstrated | [5] |
| Signature-based approach based on Windows API calls | Windows API call sequences and signatures | Signature matching (classifier on signatures) | Accuracy ~75–80% by families | Vulnerable to signature changes, obfuscation, and polymorphism, weak overall generalisation | [6] |
| Detection of anomalies in system behaviour | Operational system events: registry, file (network) anomalies, telemetry | Anomaly algorithms (behaviour classifiers) | Can catch polymorphic (metamorphic) samples | Noise in telemetry, false positives; requires careful threshold tuning | [7] |
| Visualisation of behaviour (CNN networks) | Extracted API calls and signatures, encoding into images | Convolutional neural network | >90% on selected datasets | Dependent on the coding scheme, sensitive to preprocessing, and possible retraining on specific datasets | [8] |
| A hybrid approach of static and dynamic analysis | Static features and execution dynamics | Combined models (ensemble) | Improves detection completeness in some cases | Integration complexity, computational costs, and features heterogeneity | [9,10] |
| Sequence representations (n-grams, diagrams, embeddings) | API n-grams, call graphs, API vector embeddings | CNN networks, graph neural networks, embeddings and classifiers | Increases the expressiveness of features | Loss of global context (n-grams), diagram construction complexity, and need for embeddings pretraining | [11,12,13] |
| Classical ML (trees, boosting) on features | Manual feature set, behaviour aggregates | Decision Trees, Random Forest, Gradient Boosting | Stable results with limited data | Require careful feature engineering, limitations for long sequences | [14,15] |
| Self-supervised and contrastive pretraining | Unlabelled API log files, events, sequence segments | Pretraining (masked, contrastive) and fine-tuning | Reduced need for labelled data, better embeddings | Need for a large amount of unlabelled data; fine-tuning of pretraining tasks | [16,17] |
| Resistance to adversarial attacks and obfuscation | Modified and attack samples | Adversarial training, robustification techniques | Partial increase in robustness | Decreased overall accuracy, adversarial generation, and robustness assessment are of high complexity | [18,19] |
| Layer (Stage) | Training Stage Description | What Is Being Optimised |
|---|---|---|
| Input (Preprocessing) | API calls tokenisation (indexes, padding, masking, batch formation). | Preparing masks and batches (bucketing) for efficient computation. |
| Embedding | The indices are converted into dense vectors. In the forward pass, it produces embeddings, and in the backwards pass, the gradients update the embedding matrix. | We can use pre-trained embeddings or train jointly, and we can regularise with dropouts. |
| SpatialDropout1D (Regularisation) | During training, it turns off random embedding channels to reduce feature correlation. | Reduces overfitting, affects forward pass only (stochasticity). |
| Stacked LSTM (Parallel Branches) | Sequences pass through multiple LSTM layers; each cell computes hidden states (forward) and receives gradients (backprop) to update the recurrent connection weights. | Different branches can have various depths or context lengths (short-term or long-term). Use recurrent dropout and gradient clipping. |
| Per-branch Dense with Dropout | Dense layers transform high-level representations from the LSTM. Dropout extinguishes some neurons during training. | Provides a nonlinear combination of features and additional regularisation. |
| Fusion (Attention) | Merging branches (concatenation and averaging) and using an attention mechanism to weight the contributions of individual segments and branches. During training, attention weights are also optimised. | Attention increases interpretability and focuses on informative fragments. |
| Output Layer (Classification) | In the forward pass, predictions are made, and in the backwards pass, gradients are calculated for the entire network. | The activation function and output structure are selected for the task (binary or multi-class). |
| Loss and Optimiser (Outside Layers) | Based on the predictions, a loss (weighted cross-entropy, etc.) is calculated. The Adam optimiser updates all parameters based on the gradients. | Setting up LR (LR-scheduler, early stopping, checkpoints). |
| Additional: Augmentation (Adversarial) | During the training process, modified sequences (insertions, permutations, adversarials) can be added to increase robustness. | Increases resistance but requires quality control of augmentations. |
| Data Name | Data Type | Description | Value | Notes |
|---|---|---|---|---|
| sample_id | line_int | Unique record (file) identifier | file_000123 | Corresponds to one Cuckoo JSON report. |
| label | categorical | Markup: benign or malicious | malicious | The final label for training (or validation). |
| api_sequence | array_int | Indexed API calls (tokens) sequence | [12, 5, 233, 17, ...] | Tokenisation was performed using the call dictionary. Records with < 100 calls were filtered. |
| seq_length | int | Sequence length (number of API calls) | 312 | For selection: seq_length ≥ 100. |
| timestamps | array_float | Timestamps (the moment each call was executed) | [0.003, 0.052, 0.210, ...] | Used for time-aware models or Δt calculations. |
| api_args | structured JSON (dict) | Additional call attributes (arguments, PID, packet sizes, etc.) | {“pid”:1024, “arg0”:“C:\\temp\\a.exe”} | Can be partially normalised (projected) into vector rk. |
| cuckoo_metadata | dict | Cuckoo metadata: vm_id, run_id, timestamp, scenario | {“vm”:“vm01”,”run”:“r123”,”ts”:“2024-01-10T12:00Z”} | Stored in PostgreSQL JSON report. |
| raw_report_path | string (path) | Path to the original JSON report in the database (file system) | /cuckoo/reports/r123.json | For re-analysis (audit). |
| extraction_time | datetime | Extraction time (record induction) | 2024-02-01T09:00Z | Log for reproducibility. |
| notes | string | Additional notes (e.g., filtering, incomplete data) | filtered: <100 calls | Convenient for debugging the pipeline. |
| Position | Token_Index (Value) | Timestamp (Seconds) |
|---|---|---|
| 1 | 12 | 0.0018 |
| 2 | 5 | 0.0042 |
| 3 | 233 | 0.0105 |
| 4 | 17 | 0.0150 |
| 5 | 400 | 0.0203 |
| 6 | 58 | 0.0237 |
| 7 | 412 | 0.0312 |
| 8 | 233 | 0.0450 |
| 9 | 77 | 0.0521 |
| 10 | 210 | 0.0600 |
| 11 | 18 | 0.0610 |
| 12 | 305 | 0.1205 |
| 13 | 76 | 0.1210 |
| 14 | 489 | 0.2300 |
| 15 | 102 | 0.2355 |
| 16 | 12 | 0.2400 |
| 17 | 333 | 0.6000 |
| 18 | 87 | 0.6055 |
| 19 | 401 | 0.6100 |
| 20 | 5 | 0.9000 |
| Metric | Definition | Value at N = 5000 | Interpretation |
|---|---|---|---|
| Class balance | Share of benign or malicious | benign 58% (2900), malicious 42% (2100) | Moderate imbalance. Class weights or rare class oversampling during training must be taken into account. |
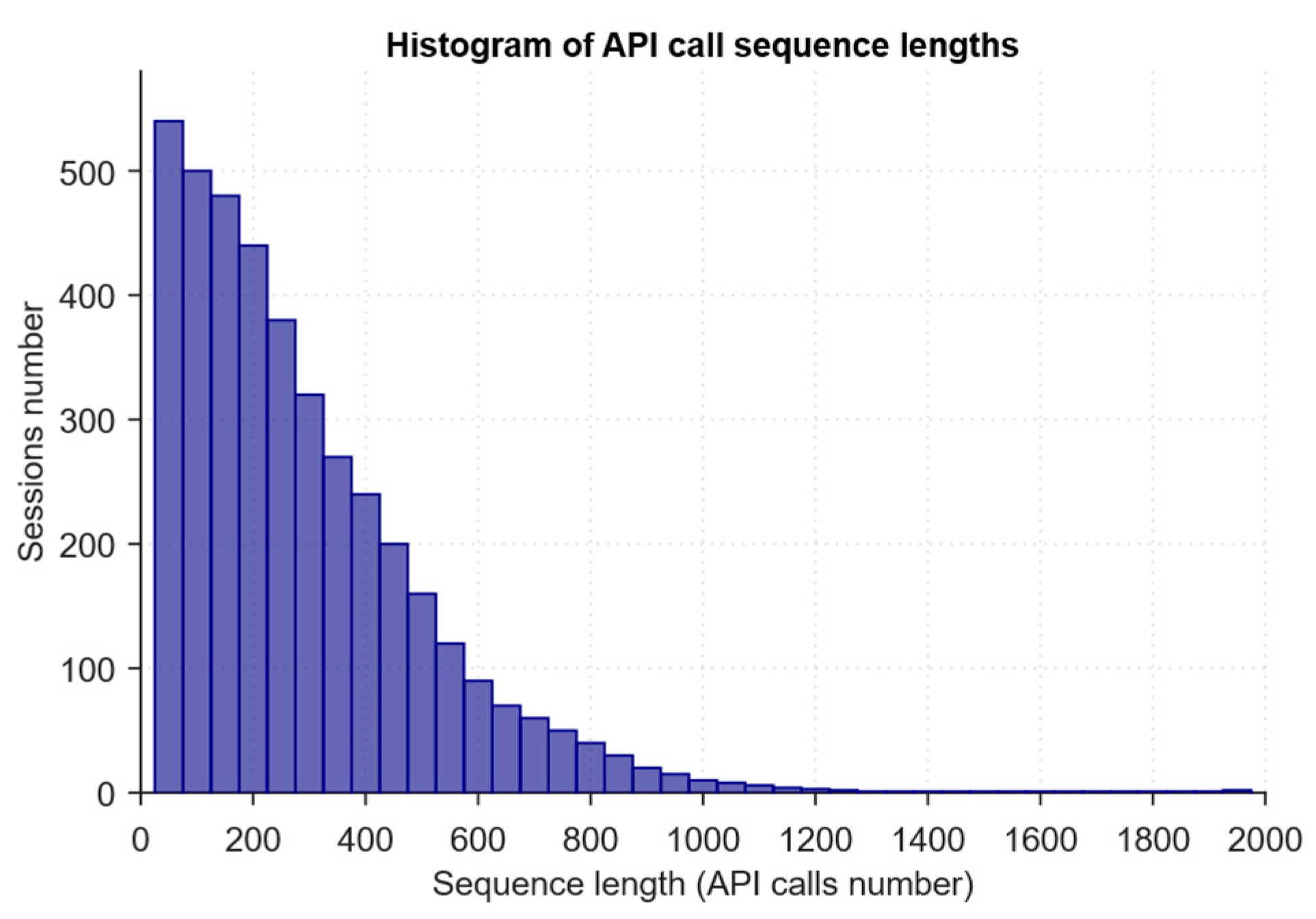
| Sequence length (seq_length): min, median, mean, max, std | API calls spread in a session | min = 100, median = 310, mean = 412, max = 2000, std = 260 | Significant length variability. Bucketing or dynamic padding control is required. However, a high CV (≈ 0.63) indicates non-uniformity of time profiles. |
| Average unique tokens per sample | How many samples cover the dictionary locally | mean = 178, std = 95 | Large variance. Some samples contain a few different APIs, while others contain many, making it difficult to generalise the model. |
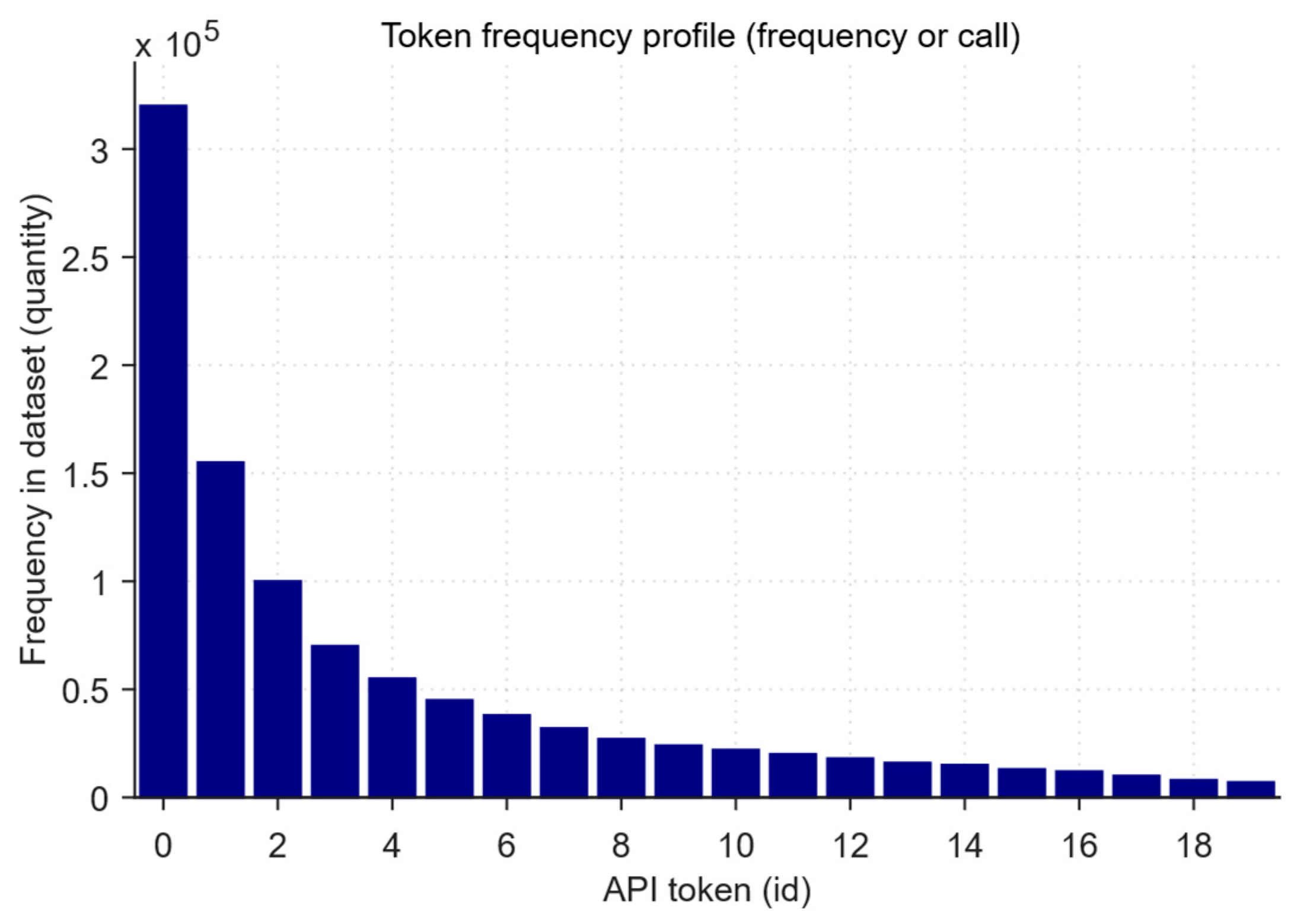
| Vocab coverage | Unique APIs found share in the dataset | ≈ 96% | Almost the entire vocabulary is used, which is positive for training embeddings. |
| Average entropy of token distribution (per-sample) | Token frequency diversity measure in a dataset (bits) | mean H ≈ 5.1 byte, std ≈ 0.9 | Moderately high diversity of calls within sessions. Low entropy in some samples indicates a few APIs’ dominance. |
| Gini coefficient of token frequencies (over the entire dataset) | Token frequency distribution unevenness | Gini ≈ 0.72 | Strong unevenness: a small number of “frequent” APIs dominate, and the majority are rare. |
| Average pairwise Jaccard similarity token-set/pair | Average intersection (union) of unique APIs between pairs of samples | mean J ≈ 0.11 | Low similarity between samples indicates high content variability and weak homogeneity. |
| Short (noisy) reports (after filtering) presence | Share of calls dropped by the rule < 100 | ~8–12% of original reports | Filtering removed some of the “noisy” short sessions, but the rest are still uneven. |
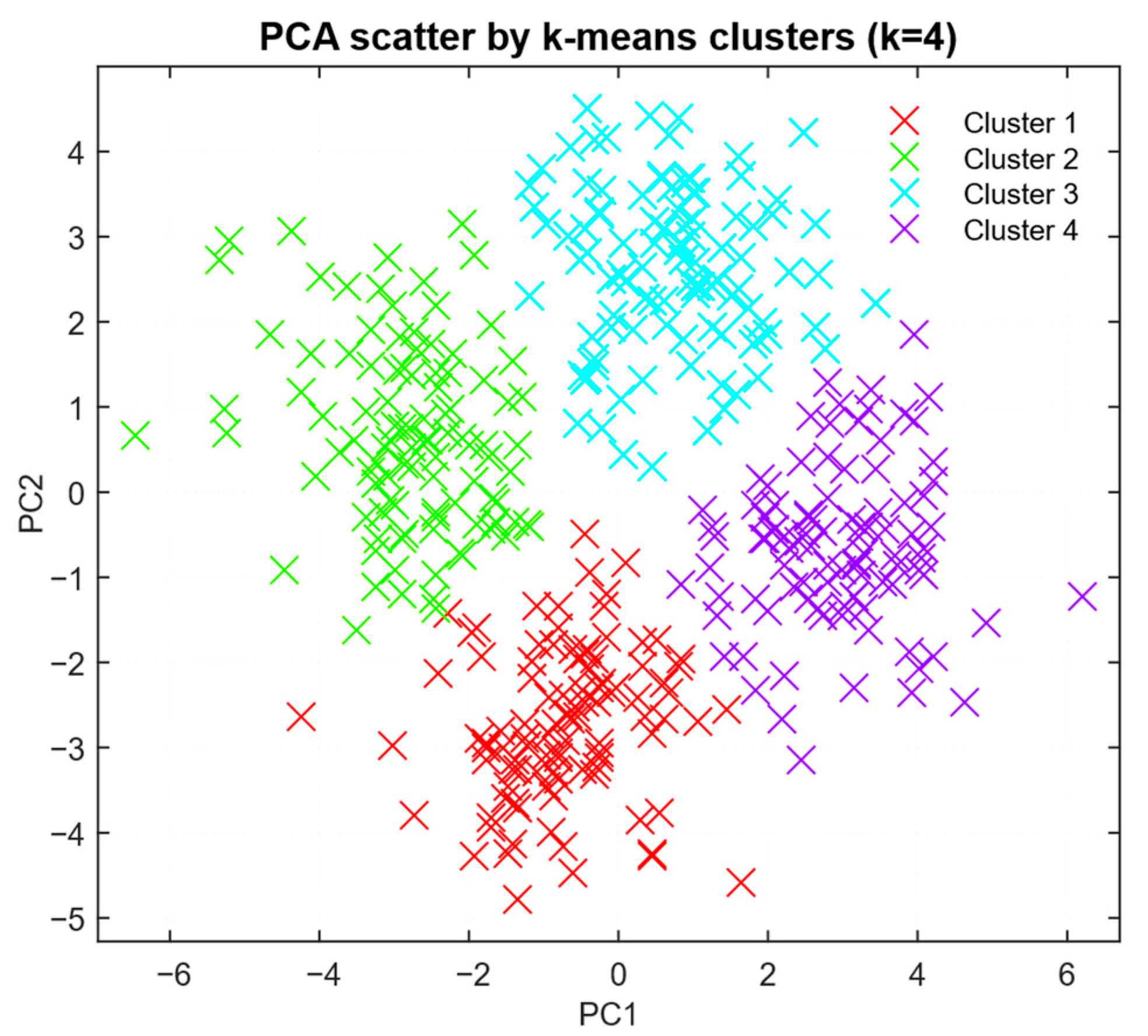
| k | Inertia (SSE) | Avg. Silhouette |
|---|---|---|
| 2 | 1.42 × 104 | 0.312 |
| 3 | 9.85 × 103 | 0.367 |
| 4 | 7.40 × 103 | 0.394 |
| 5 | 6.10 × 103 | 0.381 |
| 6 | 5.30 × 103 | 0.362 |
| Cluster | Size | Seq_Length (Centre) | Unique_Tokens (Centre) | Entropy (Centre) | Top_Token_Frac (Centre) |
|---|---|---|---|---|---|
| 0 | 810 | 220 | 85 | 4.2 | 0.34 |
| 1 | 1150 | 420 | 170 | 5.2 | 0.24 |
| 2 | 980 | 760 | 260 | 6.0 | 0.18 |
| 3 | 560 | 1350 | 410 | 7.1 | 0.12 |
| Stage | Parameter | Value |
|---|---|---|
| Preprocessing | minimum session length | 100 |
| API dictionary | 587 | |
| sliding window for online | 256 | |
| sliding step | 16 | |
| Embeddings and architecture | token embedding size | 128 |
| argument projection | 64 | |
| entry into a recurrent block | 128 + 64 = 192 | |
| Multi-branch RNN (consisting of LSTM cells) | hidden_short | 128 |
| hidden_mid | 256 | |
| hidden_long | 128 | |
| Attention | heads number | 4 |
| key size | 64 | |
| Time-kernel и salience | exponential decay | Kτ(Δt) = exp(−β · Δt) with β = 0.1 |
| salience gate coefficient | 0.5 | |
| Training and optimisation | optimiser | Adam |
| initial LR | 10−3 | |
| batch_size | 64 | |
| epochs | ≤50 | |
| early-stop patience | 5 | |
| gradient clipping | 5 | |
| L2 weight decay | 10−5 | |
| β1 | 0.9 | |
| β2 | 0.999 | |
| ϵ | 10−8 | |
| Regularisation and balancing | SpatialDropout1D | 0.15 |
| recurrent dropout | 0.1 | |
| dense dropout | 0.3 | |
| Online detector | window size for online aggregation (Nwin) | 256 |
| CUSUM threshold h | 5 (calibrated during validation to achieve target FAR) | |
| detector update rate | on every new z | |
| target FAR (benchmark) | ≈0.02 |
| Architecture | Strengths | Limitations | Metrics Values |
|---|---|---|---|
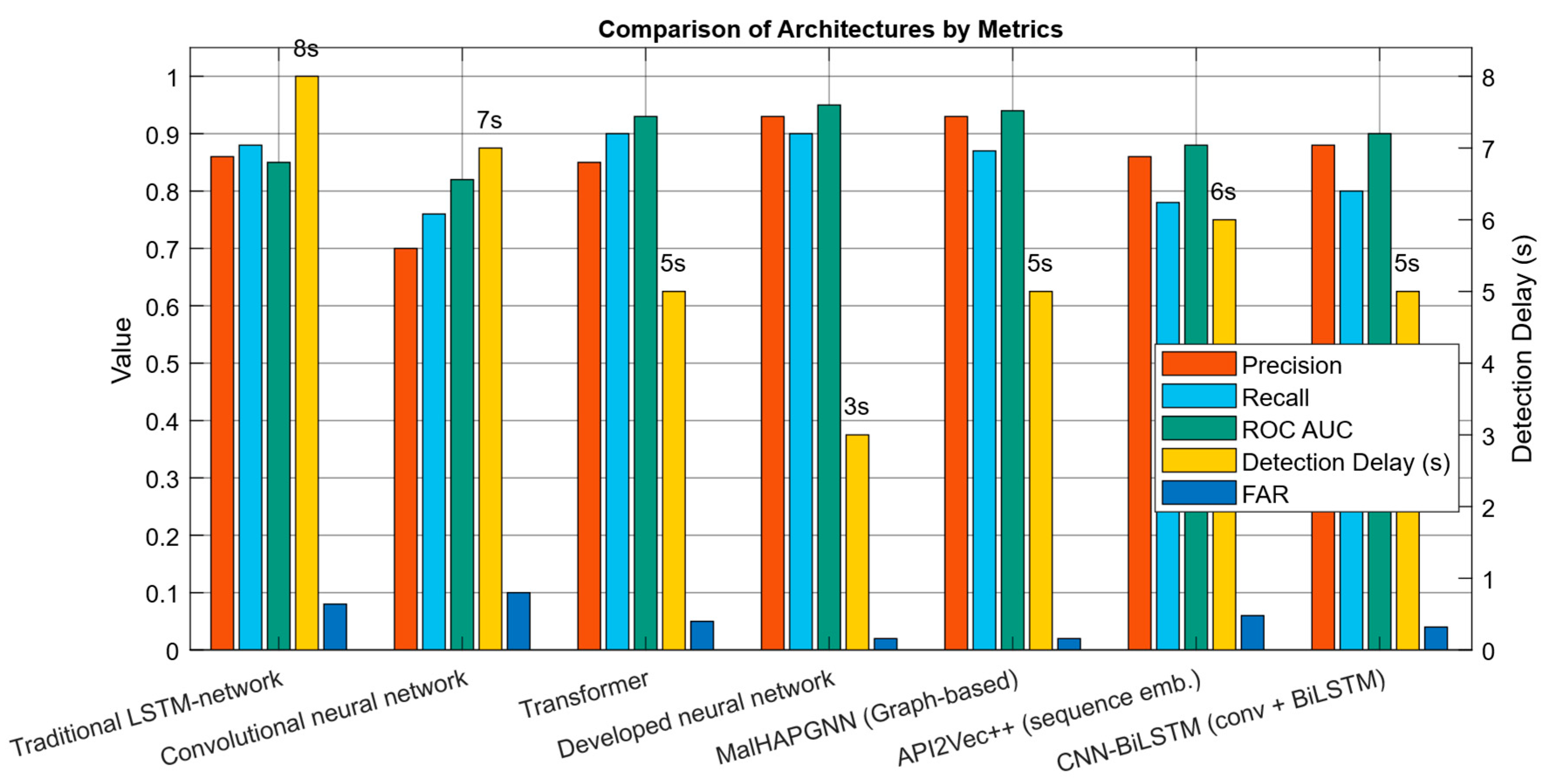
| Traditional LSTM network [38] | Simplicity, robustness, and local dependencies capture | Data loss of information over long sequences, time insensitivity | Precision ≈ 0.80, Recall ≈ 0.72, AUC ≈ 0.85, Detection delay > 8 s, FAR ≈ 0.08 |
| Convolutional neural network [11] | Good at detecting local patterns (n-grams), high speed | No long-term memory, weak Δt accounting | Precision ≈ 0.78, Recall ≈ 0.70, AUC ≈ 0.82, Detection delay ≈ 7 s, FAR ≈ 0.10 |
| Transformer (self-attention-based architecture) [16] | High accuracy, global dependencies, and explainability | High resources, poor Δt accounting without modifications | Precision ≈ 0.90, Recall ≈ 0.85, AUC ≈ 0.93, Detection delay ≈ 5 s, FAR ≈ 0.05 |
| MalHAPGNN (Graph-based, Heterogeneous API call GNN) | Takes into account the structural relationships of API calls and the graph context | Graph construction and preprocessing are more expensive and are also sensitive to noise and incomplete logs, requiring memory for large sessions | Precision ≈ 0.91, Recall ≈ 0.87, AUC ≈ 0.93, Detection delay ≈ 5 s, FAR ≈ 0.03 |
| API2Vec++ (sequence embedding with classifier) | Compact vector representations of sequences, fast inference, and classification | May lose order and spacing (unless time-aware is extended); worse with very long (or noisy) sessions | Precision ≈ 0.86, Recall ≈ 0.78, AUC ≈ 0.88, Detection delay ≈ 6 s, FAR ≈ 0.06 |
| CNN-BiLSTM (convolutions with bidirectional LSTM) | Combines local patterns (CNN) and context (BiLSTM). | More difficult to set up, higher latency than pure CNNs, sensitive to noise | Precision ≈ 0.88, Recall ≈ 0.84, AUC ≈ 0.90, Detection delay ≈ 4–6 s, FAR ≈ 0.04 |
| Developed a neural network | Balance of short and long dependencies, Δt accounting, interpretability, and low latency | More complex implementation, need to configure additional hyperparameters | Precision ≈ 0.93, Recall ≈ 0.88, AUC ≈ 0.95, Detection delay ≈ 3 s, FAR ≈ 0.02 |
| Architecture | Accuracy (%) | ROC-AUC | PR-AUC | FAR (%) | P95 Latency (Seconds) |
|---|---|---|---|---|---|
| Complete model (salience, attention, and CUSUM) | 96.4 | 0.803 | 0.866 | 2.5 | 4.2 |
| Without salience gate (attention and CUSUM) | 94.9 | 0.781 | 0.842 | 3.6 | 4.0 |
| Without attention (salience and CUSUM) | 95.1 | 0.784 | 0.845 | 3.3 | 4.1 |
| without CUSUM (salience and attention) | 95.5 | 0.789 | 0.851 | 4.8 | 3.3 |
| Method | Dataset (Amount) | Detection Mode | Accuracy | Precision | Recall | Key Numerical Indicators |
|---|---|---|---|---|---|---|
| Gated Recurrent Unit with Generative Adversarial Network [48] | ≈5000–50,000 samples | batch (offline) | 98.9% | 0.985 | 0.989 | The GAN augmentation with GRU encoder use allowed for achieving significant improvement in quality (accuracy and recall exceed 90%). |
| Early Malware Detection [49] | ≈21,000–24,000 samples | early (few-shot) | 95.4% | 0.95 | 0.92 | The fine-tuned transformer (GPT-2) with Bi-RNN and attention application is focused on early API prediction. |
| Temporal Convolutional Network with Attention [50] | ≈3000–40,000 samples | batch (near-online) | 92.2% | 0.92 | 0.90 | Parallelism and low latency, while the attention introduction allows for interpretability. |
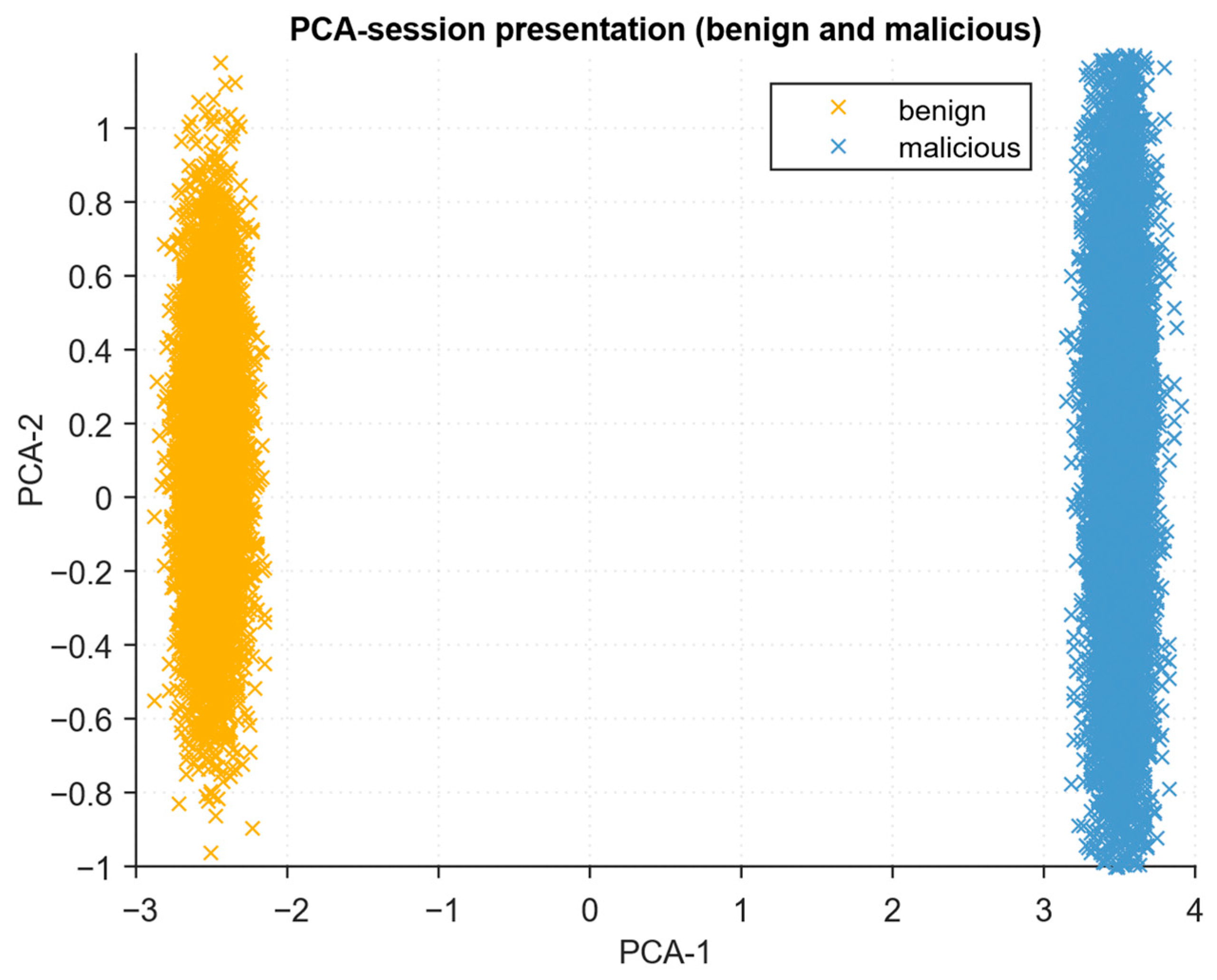
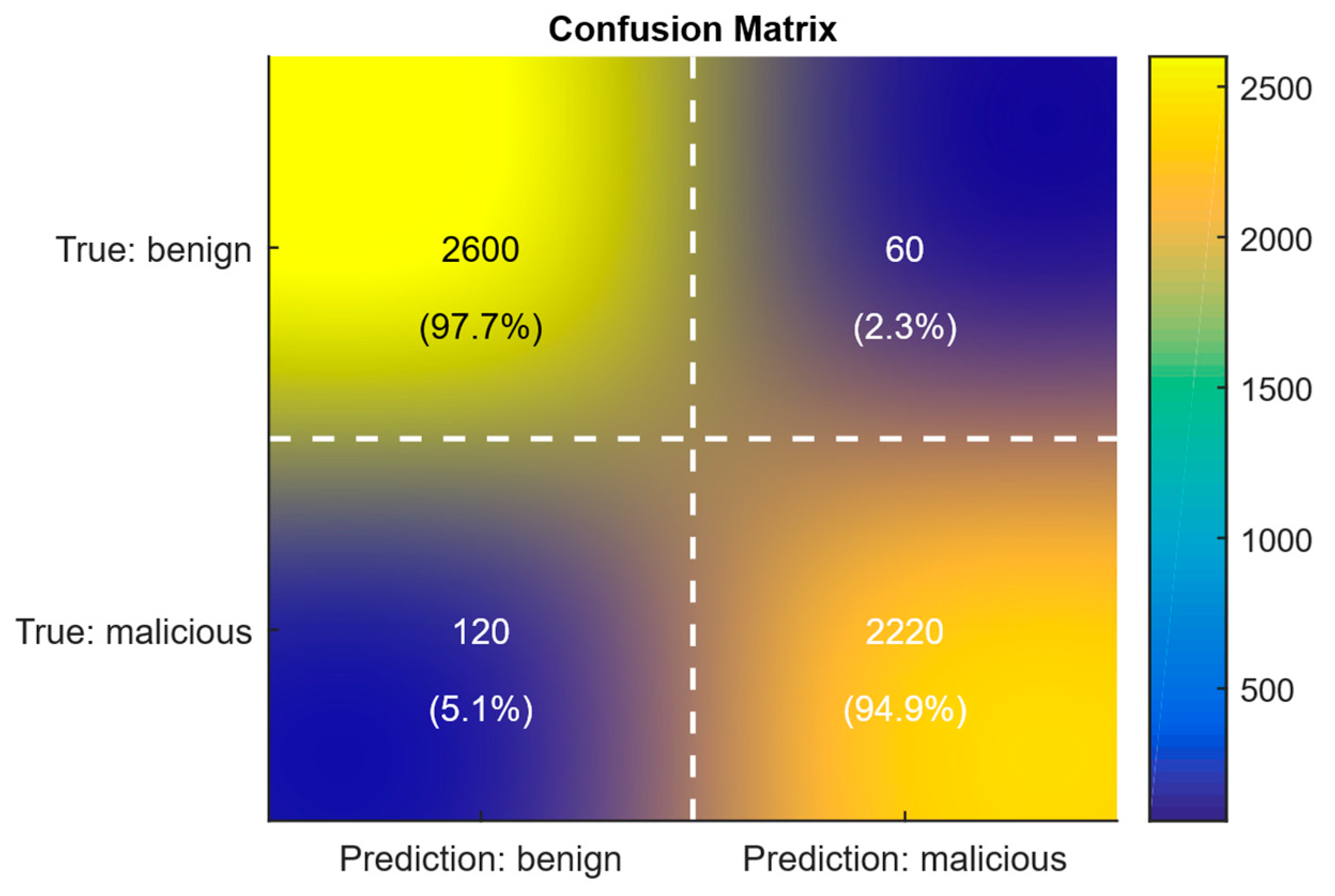
| Developed method | N = 5000, vocab = 587 | online or early (attention, salience, CUSUM) | 96.4% | 0.9737 | 0.9487 | Mean seq len = 411.32, Median = 346; Max = 2000, PCA centroid dist = 5.598, PCA silhouette = 0.948, attention peak ≈ 5%, CUSUM first alarm ≈ 180; confusion matrix TN = 2600, FP = 60, FN = 120, TP = 2220. |
| Component | Function in Forensic Audit (Benefits for the Expert) |
|---|---|
| Parser and Normaliser | Original timestamps preservation, formats unification |
| Feature Extraction | Reproducible input data preparation |
| Time-Aware Model with an Attention Mechanism | Classification, explanations (which events are essential) |
| Online CUSUM | Early detection of anomalies in real time |
| Visualisation | Triage, replay, evidence export |
| Export (Evidence Database) | Immutable reports storage, model versions, trust chain |
| Model Variant | Throughput (Batch is 256) Seq/Second | Online Latency P50, P95, and P99 (Seconds) | Peak GPU Mem (GB) | Avg GPU Mem (GB) | Accuracy (%) | FAR (%) |
|---|---|---|---|---|---|---|
| Complete model (multi-scale time-aware LSTM with attention and CUSUM) | 25,000 | 2.8, 4.2, and 6.5 | 22 | 20 | 96.4 | 2.5 |
| Knowledge Distillation (KD, 4× smaller) | 80,000 | 0.9, 1.6, and 2.8 | 8 | 6 | 94.8 | 3.5 |
| Quantised INT8 (post-train or QAT) | 60,000 | 1.1, 1.9, and 3.2 | 6 | 5 | 95.6 | 3.0 |
| Pruned (structured, ~50% FLOPs) | 45,000 | 1.2, 2.0, and 3.5 | 10 | 9 | 95.9 | 2.9 |
| Early-exit architecture (adaptive inference) | 130,000 | 0.6, 1.1, and 2.0 | 12 | 11 | 95.0 | 3.2 |
| Time, Seconds | API Event | Salience | Suggested Triage Action |
|---|---|---|---|
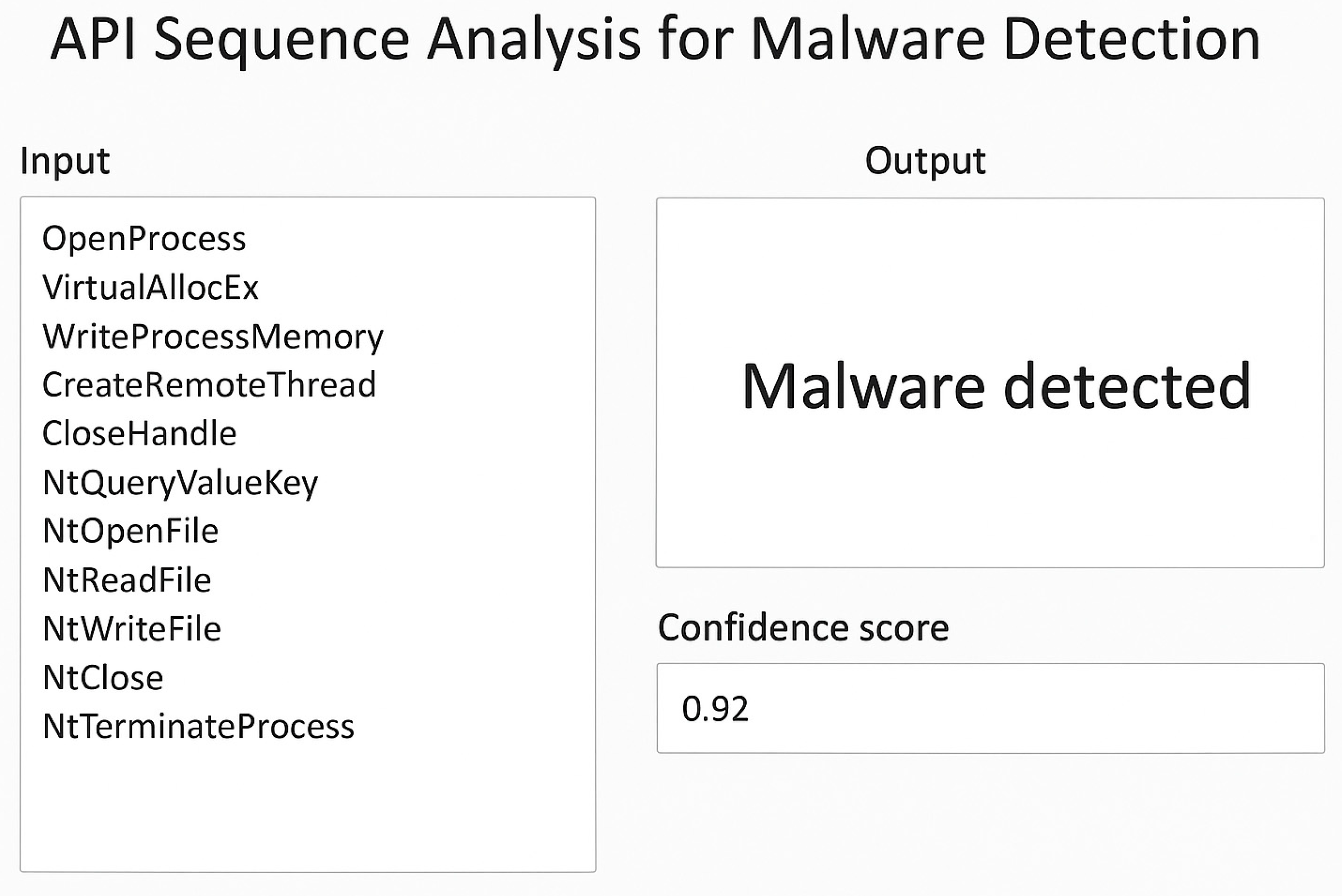
| 27.432 | create_process | 0.97 | Immediately check child processes and the command line |
| 29.011 | write_file | 0.94 | Extract file, check hashes and contents |
| 33.201 | load_library | 0.91 | Check loaded DLLs for known indicators |
| 40.512 | network_connect | 0.89 | Network metadata collection (IP, port), domain analysis |
| 66.980 | read_registry | 0.86 | Check modified registry keys and modification times |
| 82.114 | open_file | 0.83 | Compare with the allowlist, check access |
| 104.256 | query_handles | 0.79 | Evaluate which descriptors are being requested, search for anomalies |
| Number | Limitation | Brief Explanation (Impact) |
|---|---|---|
| 1 | Limited generalisability | The model was trained primarily on Windows behavioural traces (Cuckoo), which creates a decreased accuracy risk and an increase in the number of false classifications when transferred to other operating systems, alternative sandboxes, or real endpoint data without additional adaptation. |
| 2 | Vulnerability to strong obfuscation and adversarial attacks | When deliberately modifying system call sequences (polymorphism, aggressive obfuscation, targeted adversarial distortions), the probability of a false negative (FN) increases significantly, which leads to a decrease in completeness (recall) while maintaining the apparent reliability of the trace. |
| 3 | High computational requirements and online detection latencies | Using time-aware RNNs in combination with multi-head attention and sequential statistical criteria increases the load on the GPU and CPU. It may lead to latencies incompatible with high-throughput environments. |
| 4 | Dependence on data quality and relevance | The class imbalance presence, noise in the labelling, and the concept drift phenomenon (software evolution and the emergence of new types of attacks) reduce the models’ stability and require regular dataset updates and additional training to maintain high accuracy. |
| Number | Limitation | Aim | Tasks | Metrics |
|---|---|---|---|---|
| 1 | Limited generalisability (portability to other operating systems or endpoints) | Increase the models’ portability across different platforms and real endpoint data | (1) Collection of cross-platform datasets (Windows, Linux, Android) and real endpoint data; (2) Development of domain-adaptation or domain-generalisation (adversarial, MMD, meta-learning) for embeddings; (3) Validation on hold-out platforms and field sets | Increase in AUC (recall) on new platforms ≥ 10% vs. baseline; Reduced degradation during transfer (drop ≤ 5%) |
| 2 | Vulnerability to strong obfuscation and adversarial attacks | Ensure resistance to obfuscation and targeted sequence distortions | (1) Creation of attacks or obfuscations set (call proxying, noise injection, time-warp); (2) Adversarial training with adversarial augmentation (seq2seq or perturbation); (3) Certified research (verifiable) defences (robustness certificates for sequences); (4) Attack detectors integration | False-Negative reduction under attack ≥ 30% compared to the unattended model; Certified change margin (if applicable) |
| 3 | High computational requirements and online detection latency | Reduce latency and resource consumption without a significant quality loss | (1) Model bottleneck profiling; (2) Model compression research: knowledge distillation, quantisation, pruning, early-exit; (3) Online pipeline implementation and optimisation (streaming inference, batching policies); (4) Testing on target devices (edge, SIEM) | 50% latency reduction and/or 2x memory and CPU reduction with ≤ 3% accuracy loss |
| 4 | Dependence on the quality and relevance of data (concept drift) | Ensure that the model adapts to drift and changing threats | (1) Development of a drift monitoring system (statistical tests, embedding drift); (2) Continuous or incremental learning methods (continual learning, replay buffers, regularisers against catastrophic forgetting); (3) Collection automation and “new” examples annotation; (4) Regular validation and triggers for retraining | Drift response time (from detection to update) ≤ specified SLA; Maintaining metrics (AUC or recall) within specified limits when new classes appear |
| 5 | Cross-cutting activities (infrastructure, replication, open benchmarks) | Speed up research and results verification | (1) Creation of a reproducible software system or external storage devices for experiments; (2) External validation organisation | A repository with a dataset (scripts) and external replication availability; adoption of the benchmark in the community |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vladov, S.; Vysotska, V.; Varlakhov, V.; Nazarkevych, M.; Bolvinov, S.; Piadyshev, V. Innovative Method for Detecting Malware by Analysing API Request Sequences Based on a Hybrid Recurrent Neural Network for Applied Forensic Auditing. Appl. Syst. Innov. 2025, 8, 156. https://doi.org/10.3390/asi8050156
Vladov S, Vysotska V, Varlakhov V, Nazarkevych M, Bolvinov S, Piadyshev V. Innovative Method for Detecting Malware by Analysing API Request Sequences Based on a Hybrid Recurrent Neural Network for Applied Forensic Auditing. Applied System Innovation. 2025; 8(5):156. https://doi.org/10.3390/asi8050156
Chicago/Turabian StyleVladov, Serhii, Victoria Vysotska, Vitalii Varlakhov, Mariia Nazarkevych, Serhii Bolvinov, and Volodymyr Piadyshev. 2025. "Innovative Method for Detecting Malware by Analysing API Request Sequences Based on a Hybrid Recurrent Neural Network for Applied Forensic Auditing" Applied System Innovation 8, no. 5: 156. https://doi.org/10.3390/asi8050156
APA StyleVladov, S., Vysotska, V., Varlakhov, V., Nazarkevych, M., Bolvinov, S., & Piadyshev, V. (2025). Innovative Method for Detecting Malware by Analysing API Request Sequences Based on a Hybrid Recurrent Neural Network for Applied Forensic Auditing. Applied System Innovation, 8(5), 156. https://doi.org/10.3390/asi8050156








