Resilience Oriented Distribution System Service Restoration Considering Overhead Power Lines Affected by Hurricanes
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Paper Contribution
- To develop a spatiotemporal dynamic Bayesian network (DBN) model with a step-ahead predictive time horizon for probabilistic risk assessment of overhead power distribution line failures during hurricanes.
- To develop a service restoration model based on the results of the DBN failure model, incorporating two independent service restoration strategies, PSO-based reconfiguration and PSO-optimized DG placement.
- To test the scenario-wise performance of overhead line failure and service restoration models on modeled test systems.
- To assess the operational resilience of PDS using resilience metrics.
1.4. Paper Organization
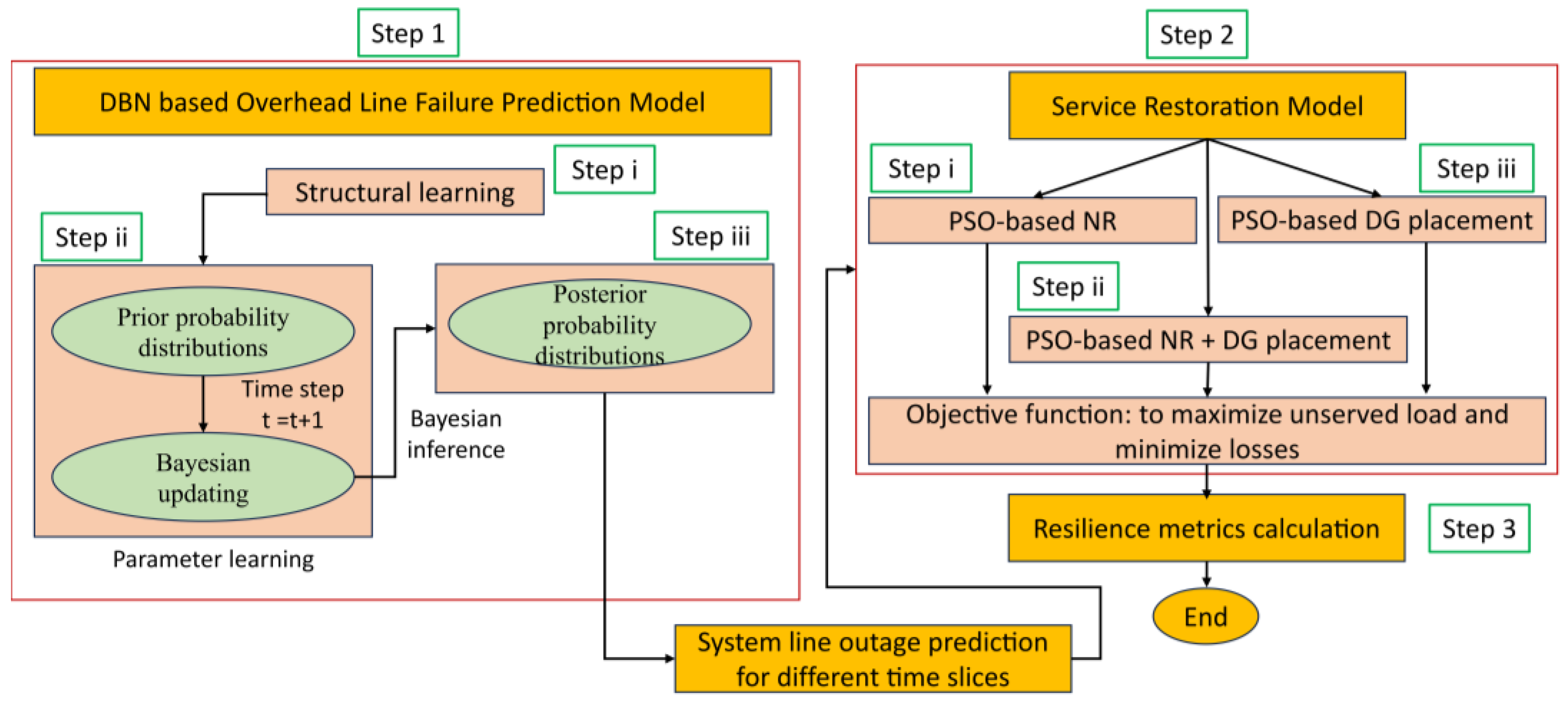
2. Materials and Methods
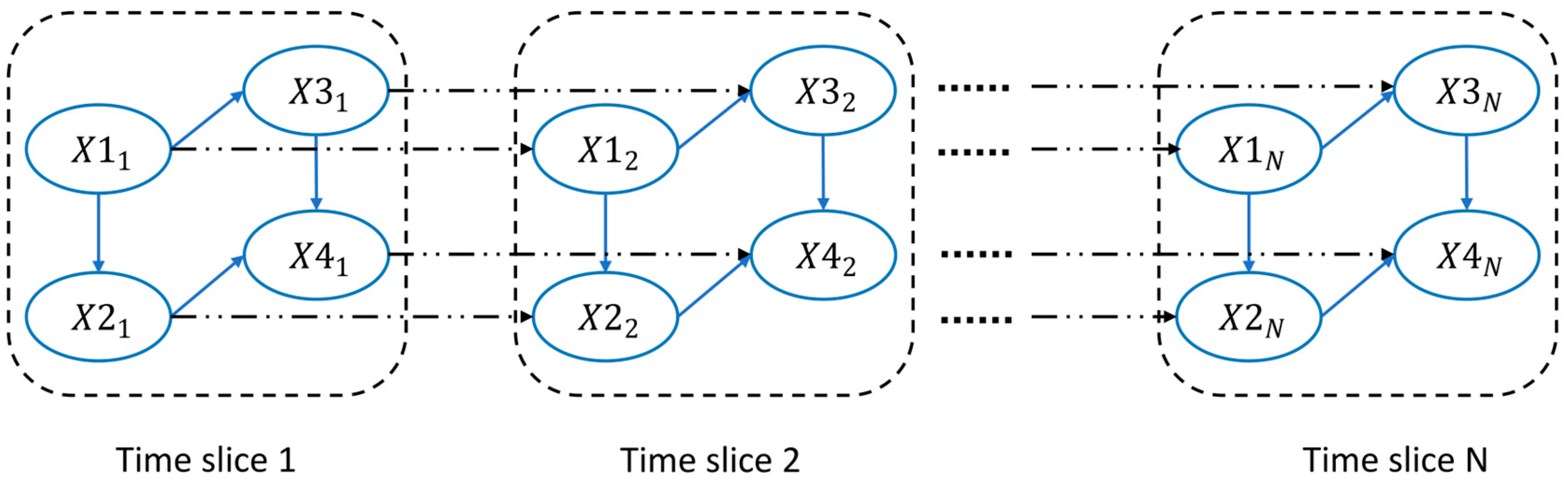
2.1. Overhead Line Failure Prediction Model (Preliminaries)
2.2. Service Restoration Model (Main Methodology)
- Balanced Three-Phase AC System: The distribution network was assumed to operate under balanced conditions, allowing the use of single-phase equivalent models for power flow analysis. Power generated should be capable of supplying the demand capacity and the system losses [40]. For this, the following equations should be satisfied for each bus in Figure 4.where is the voltage at bus , is the active power generation at bus , is the active power demand at bus , is the reactive power generation at bus , is the reactive power demand at bus , is the admittance of the line connecting buses , and is the magnitude of the admittance.∀ i ∈ 1, 2, 3…N
- Radial Topology: The restored PDS must maintain a radial structure to ensure protection coordination and avoid loop currents and should satisfy [43].where is the count of nodes in the system and is the total count of the network’s branches.
- Operational Limits: Voltage magnitudes at all buses must remain within permissible bounds. The generator voltage will be the bus/load voltage in addition to the voltage drop caused by the impedance of the line and the power flow along the line. The generator voltage must increase with increasing impedance and power flow to maintain a constant bus/load voltage. Because the resistive elements of the distribution network’s lines are higher than those of other lines, the increased active power flows have a significant effect on the voltage level. Instead of the more common number of 5 on transmission networks, this results in an X/R ratio of roughly 1 [40]. Based on the American National Standards Institute (ANSI C84.1), the voltage limits expressed in Equation (15) were to ensure voltage stability and power quality.where and are the maximum (+5% of the nominal voltage) and minimum (−5% of the nominal voltage) limits at the sending end node of the th branch, respectively.
2.3. Particle Swarm Optimization
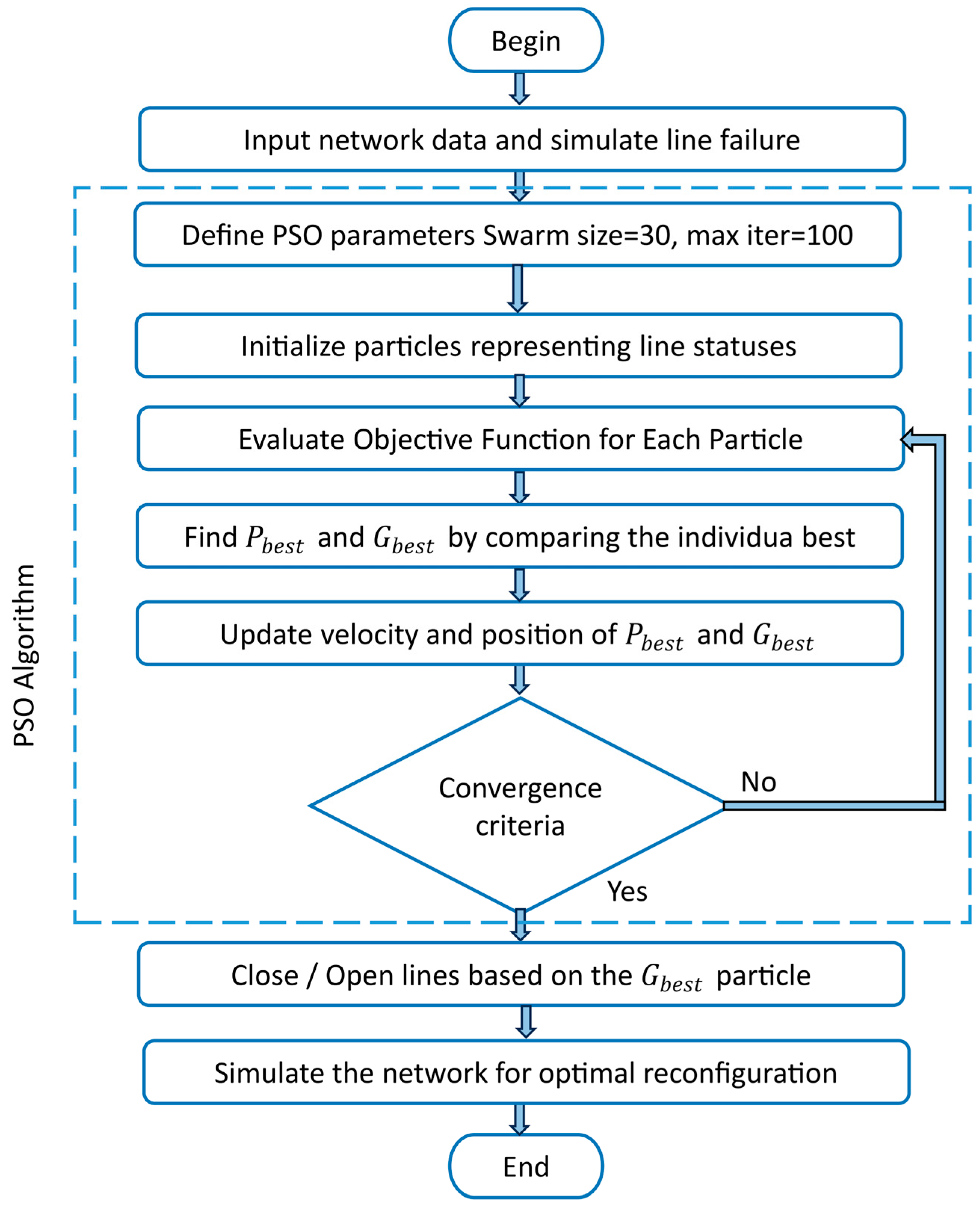
2.4. Reconfiguration of PDS
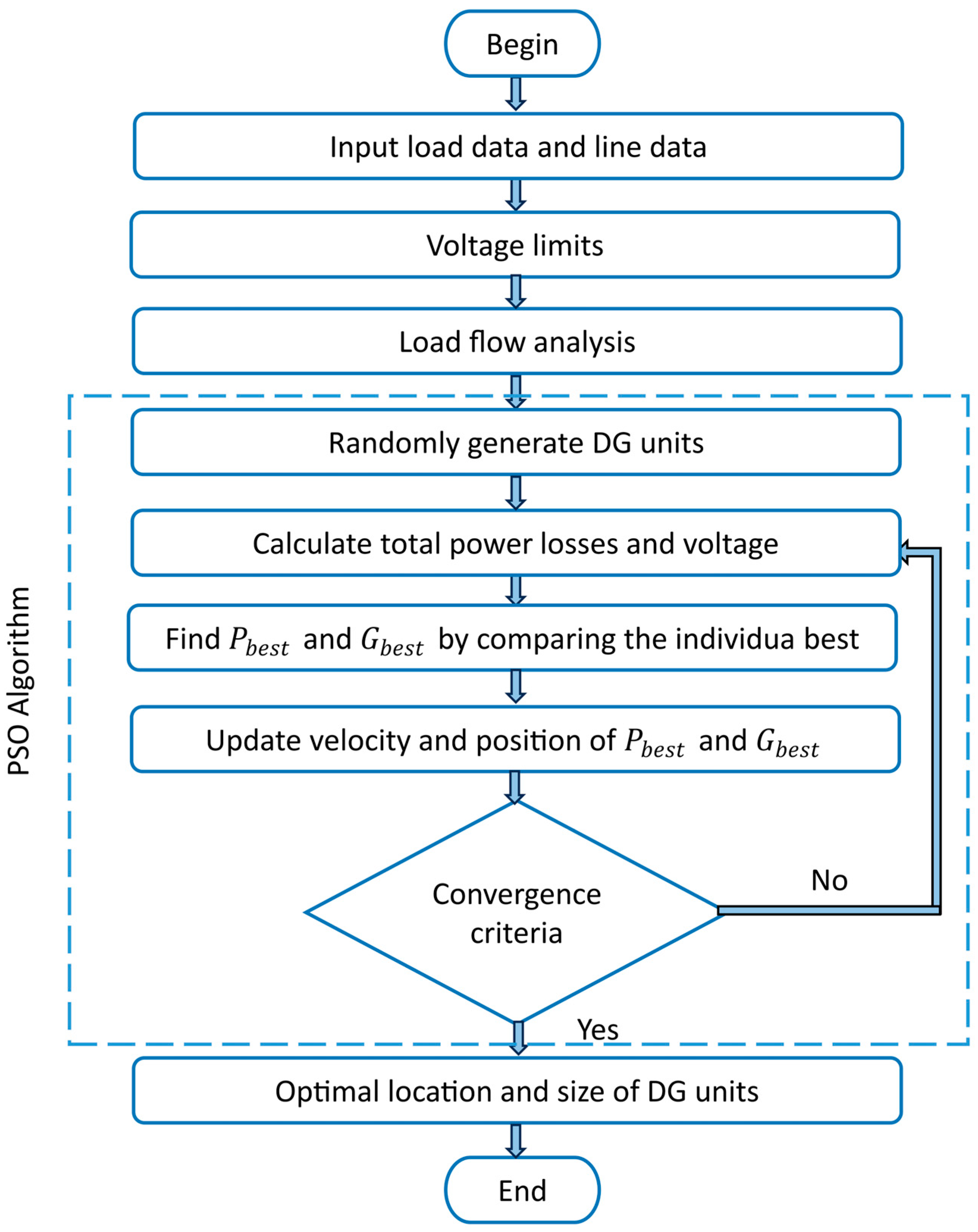
2.5. DG Units Placement
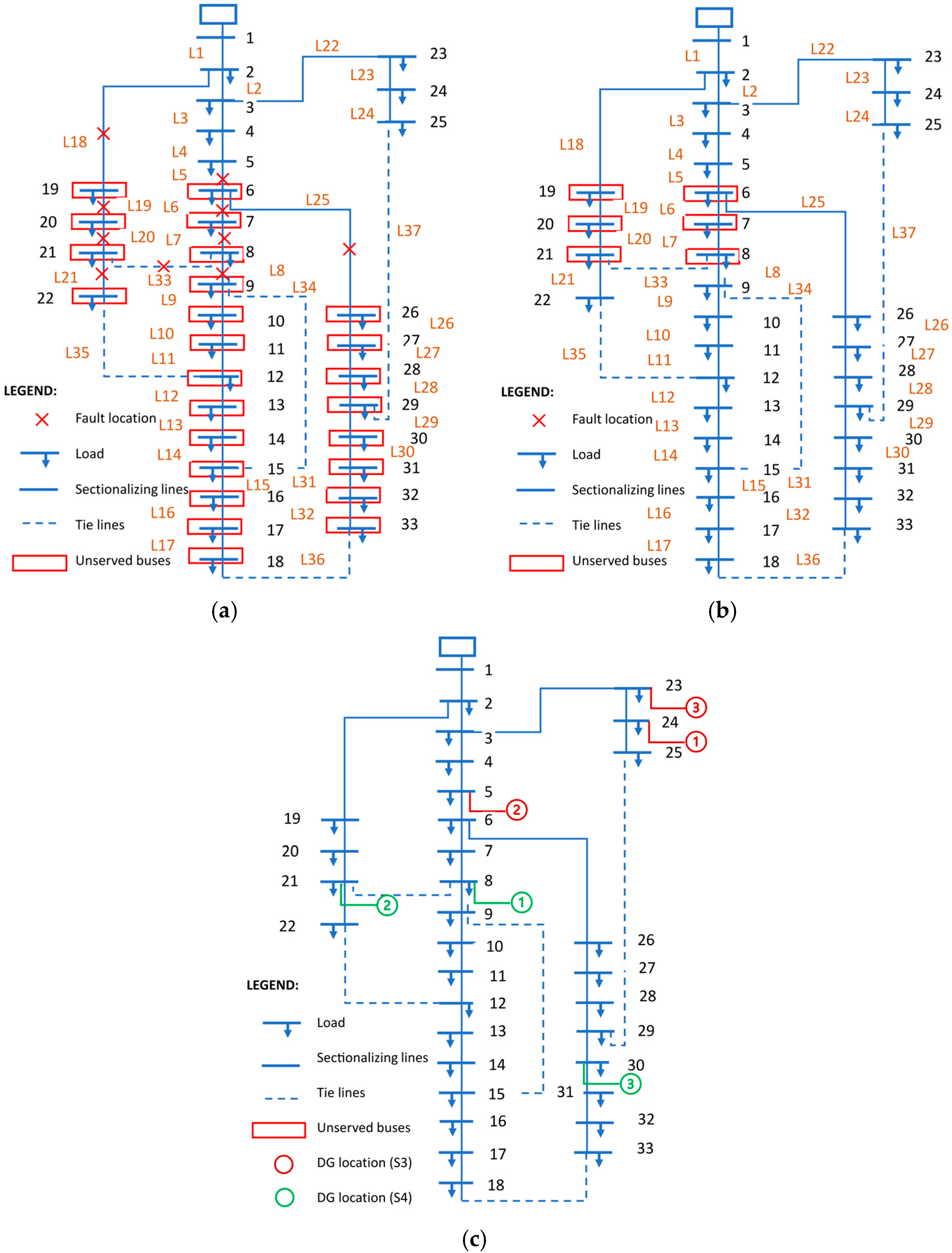
- Scenario 0—Base System: In scenario 0 (S0), the IEEE 33 bus radial PDS before the fault was investigated for the line power losses using Newton–Raphson power flow analysis.
- Scenario 1—System After the Fault: In scenario 1 (S1), the system was investigated after the occurrence of a line fault.
- Scenario 2—Reconfigured PDS: In scenario 2 (S2), the system, after a fault, undergoes the optimal reconfiguration process using the PSO algorithm.
- Scenario 3—PDS with DG Placement: In scenario 3 (S3), the system, after a fault, undergoes the optimal DG placement and sizing using the PSO algorithm.
- Scenario 4—PDS with Reconfiguration and DG Placement: In scenario 4 (S4), the system, after a fault, undergoes reconfiguration with optimal DG placement and sizing using the PSO algorithm.
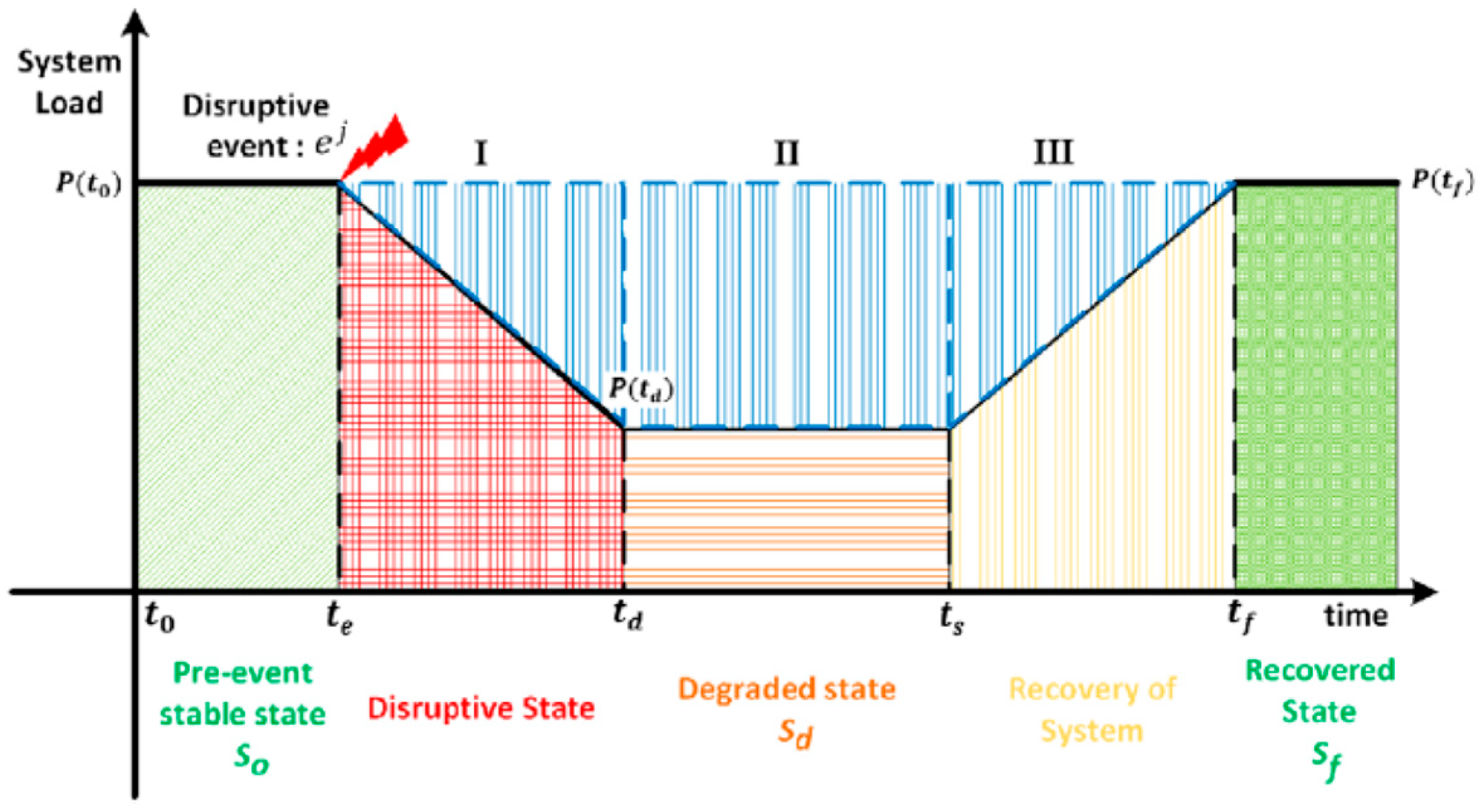
2.6. Resilience Metric
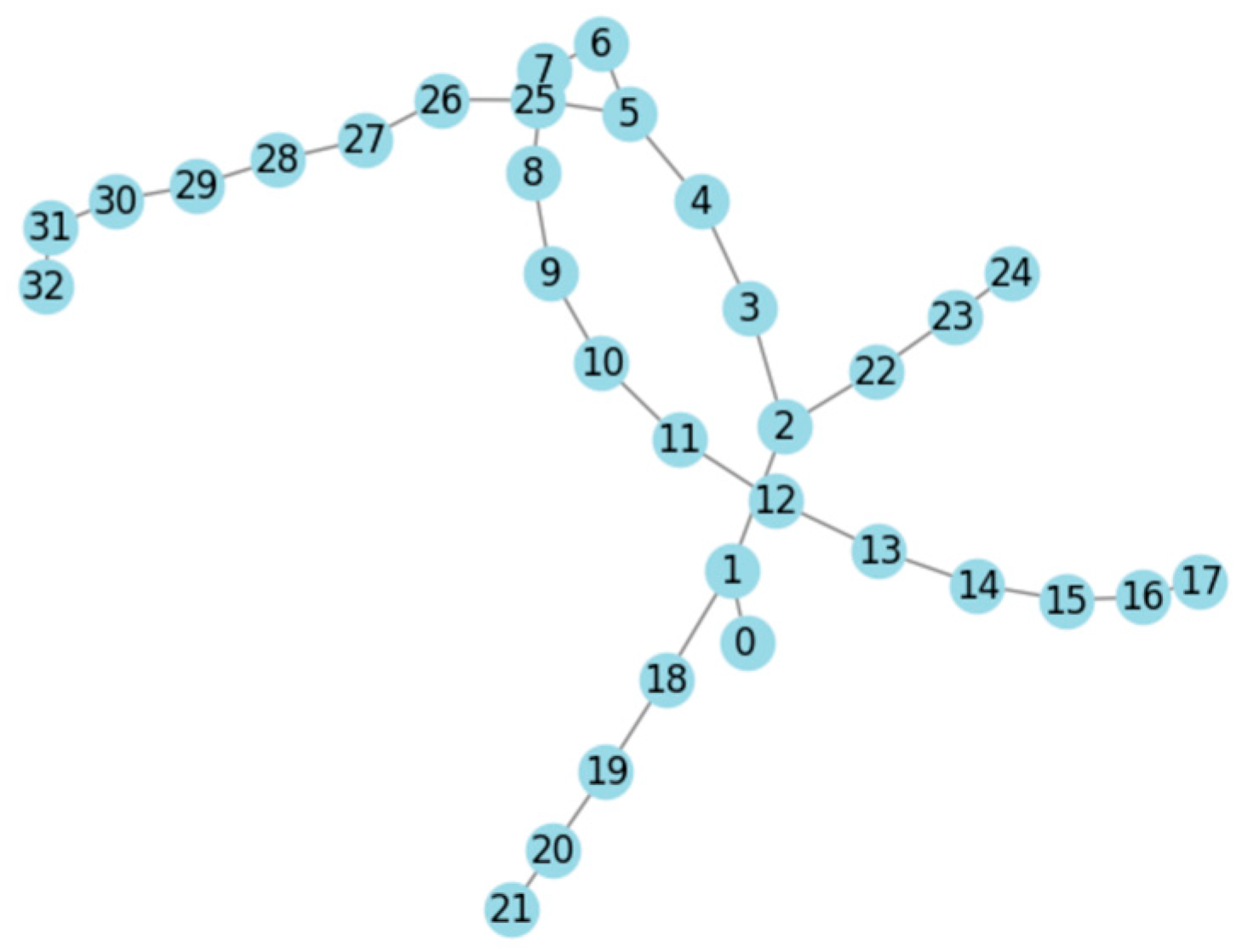
3. Case Studies
4. Results and Discussion
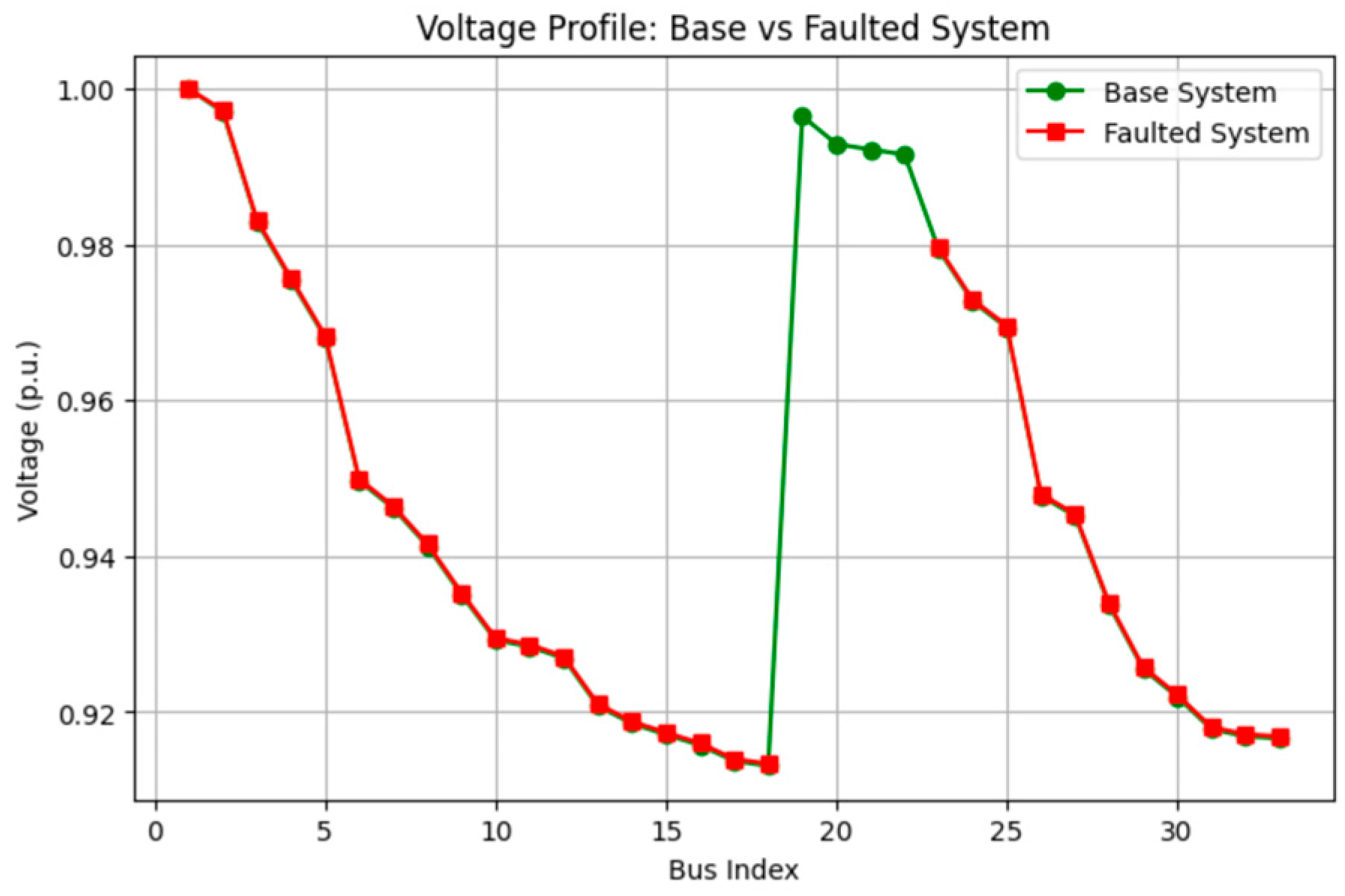
4.1. Case 0
Base System (Scenario S0)
4.2. Case 1
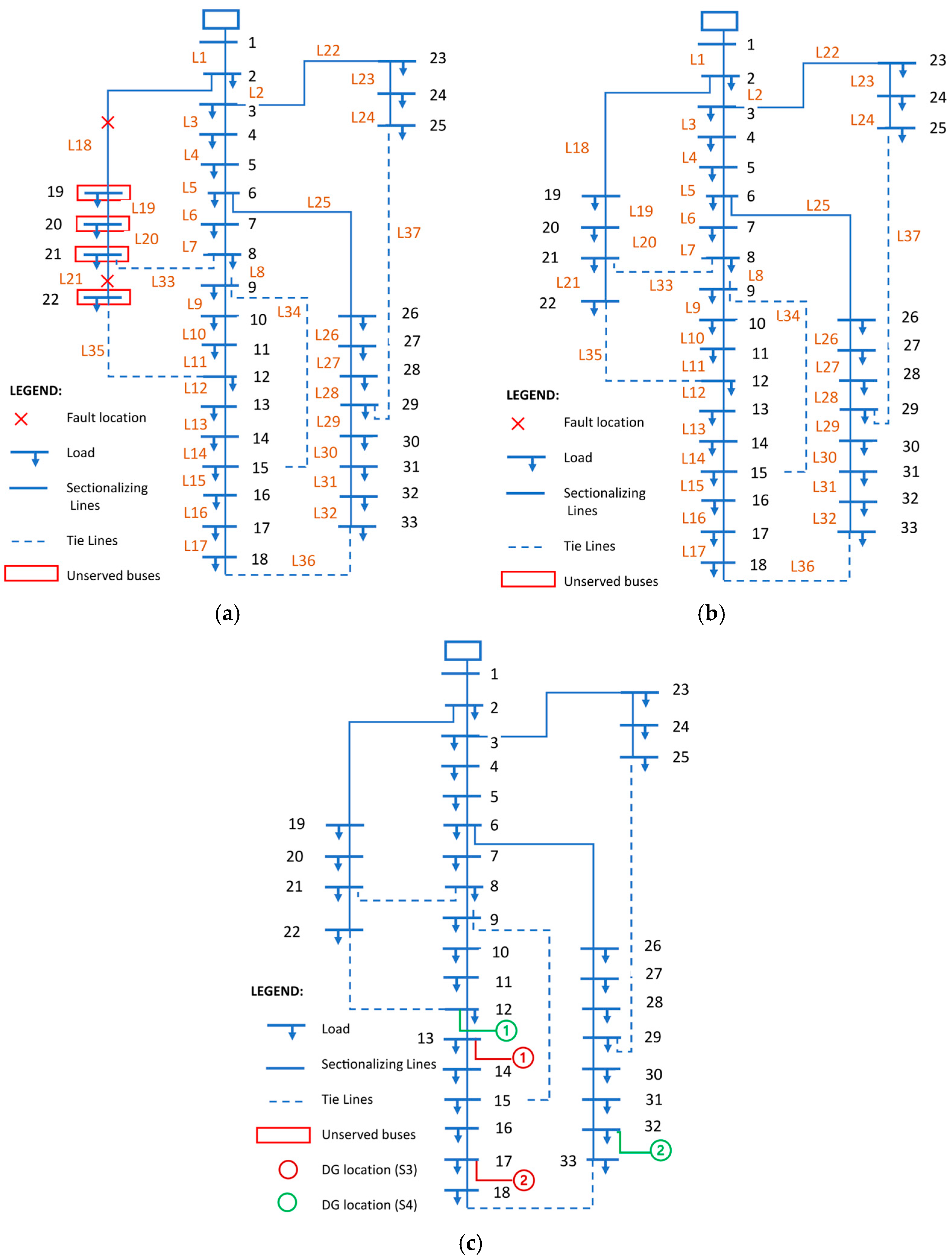
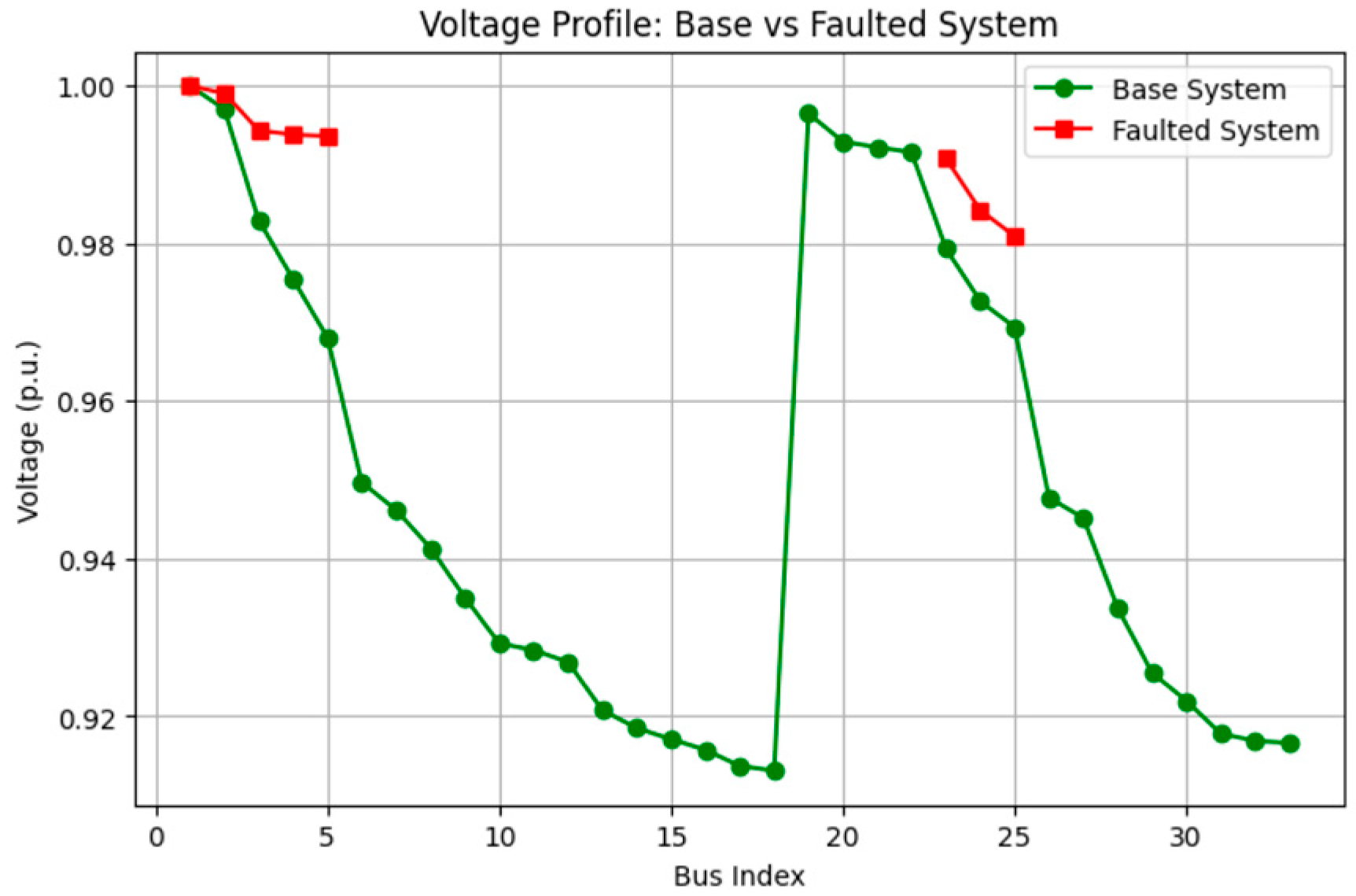
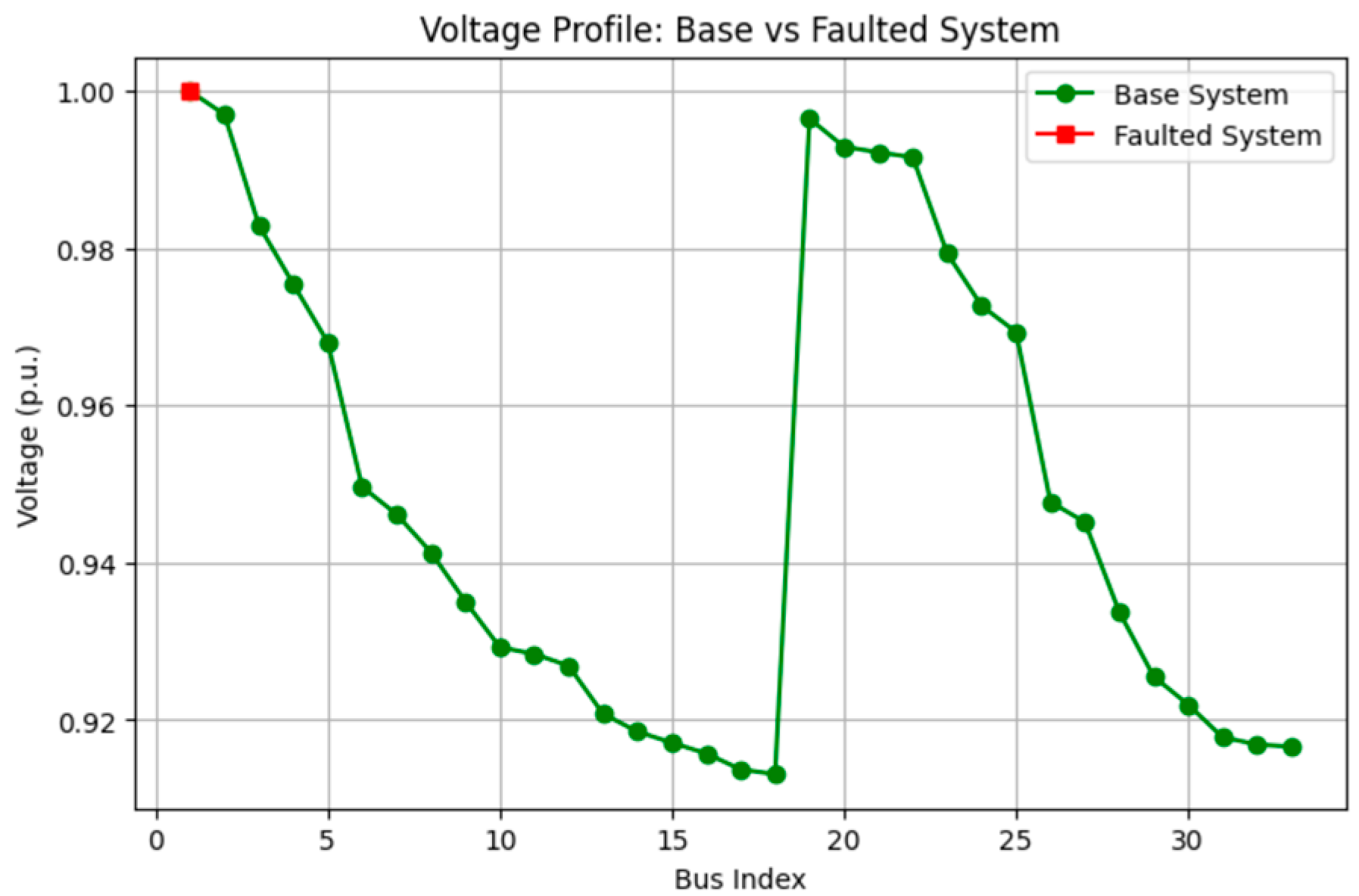
4.2.1. Faulty System (Scenario S1)
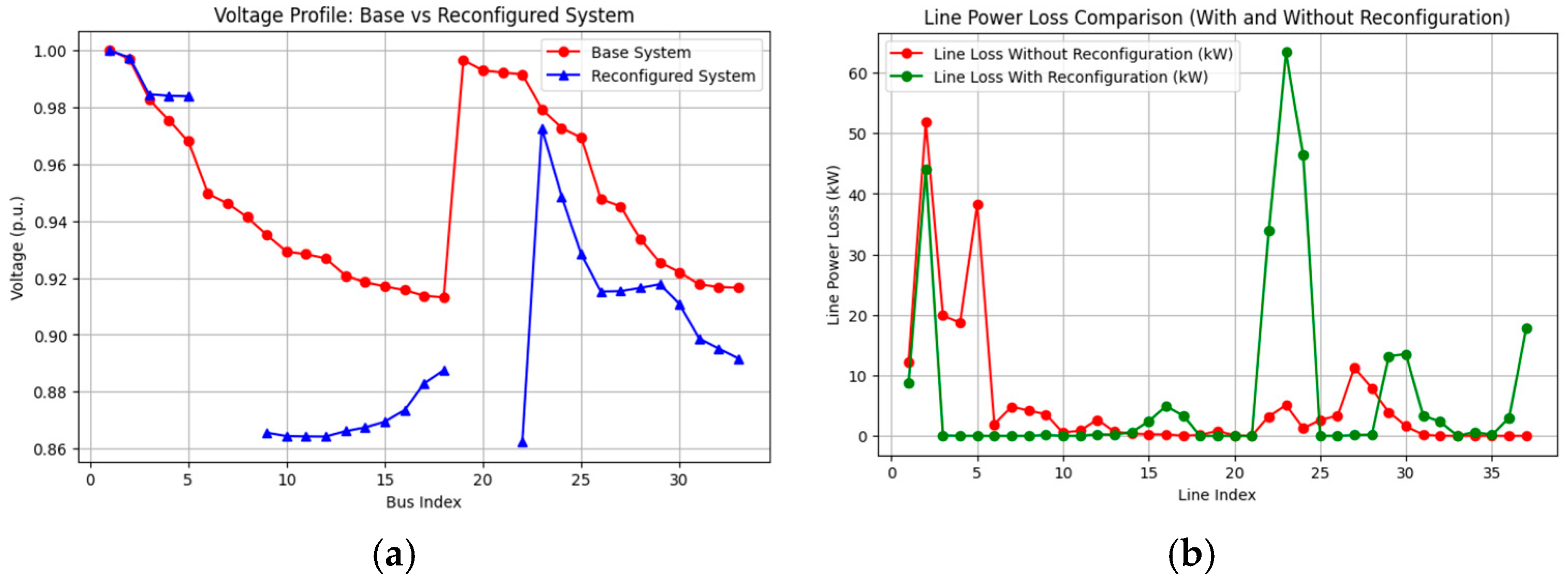
4.2.2. Only Reconfiguration (Scenario S2)
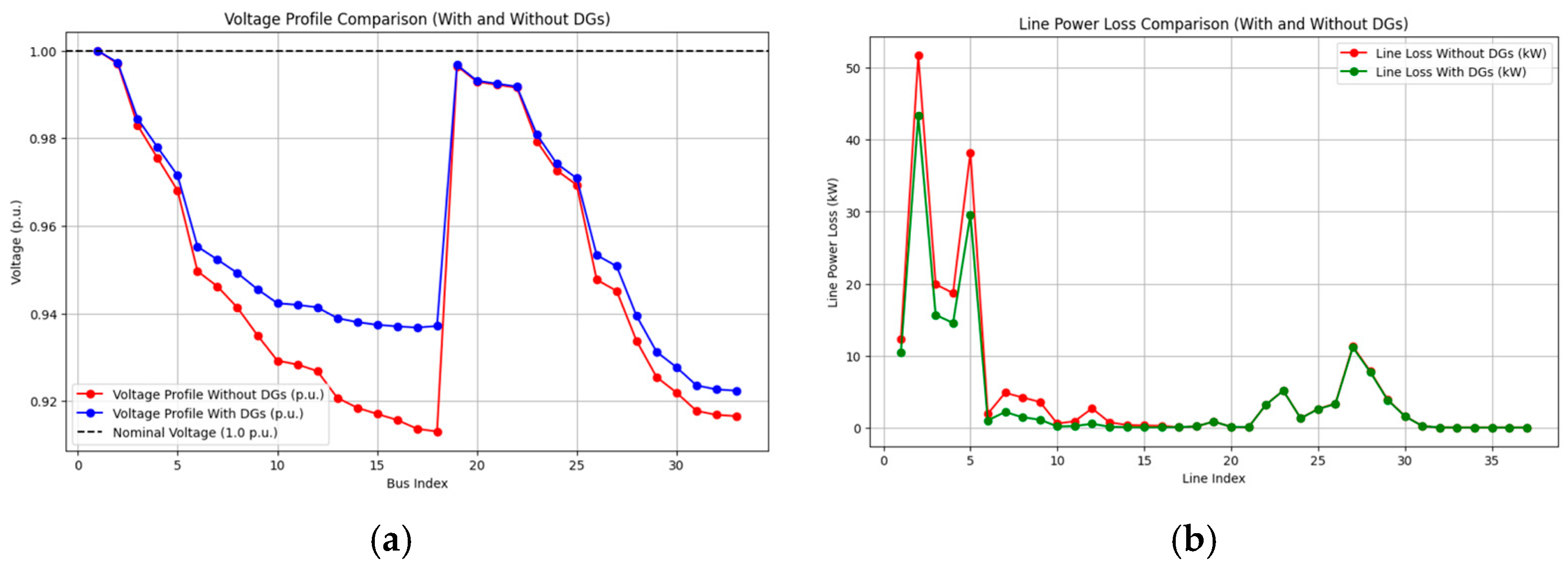
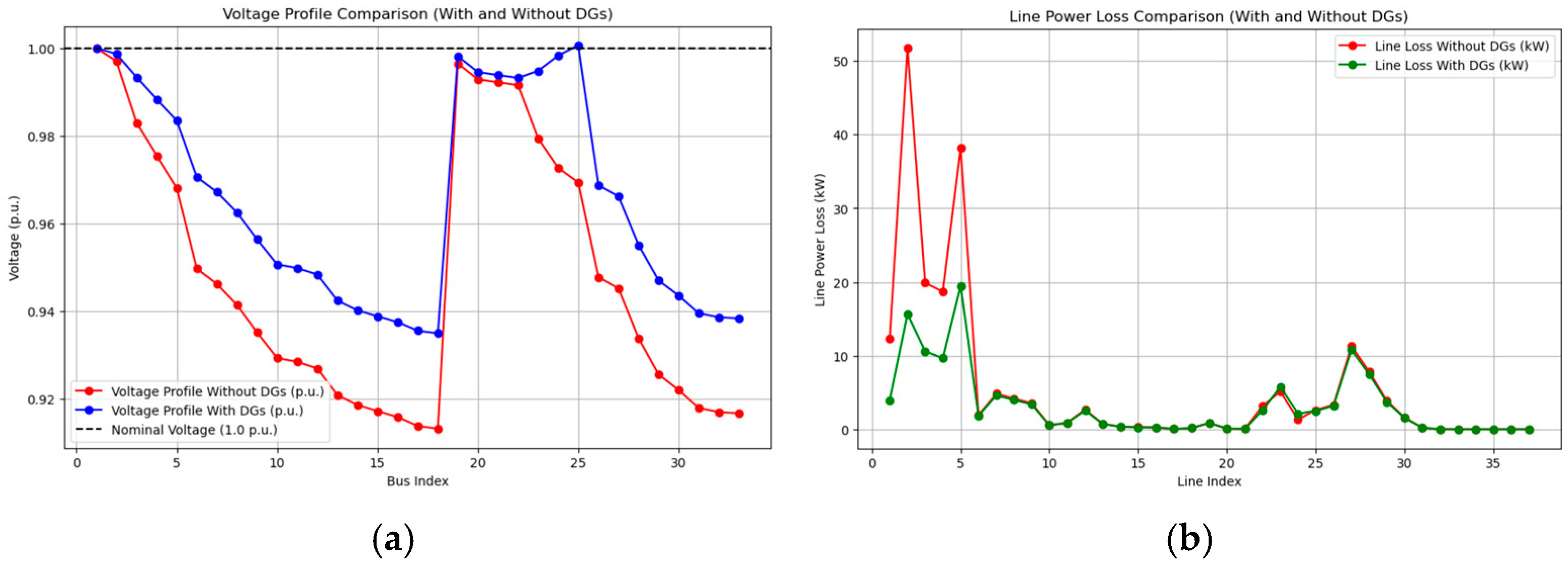
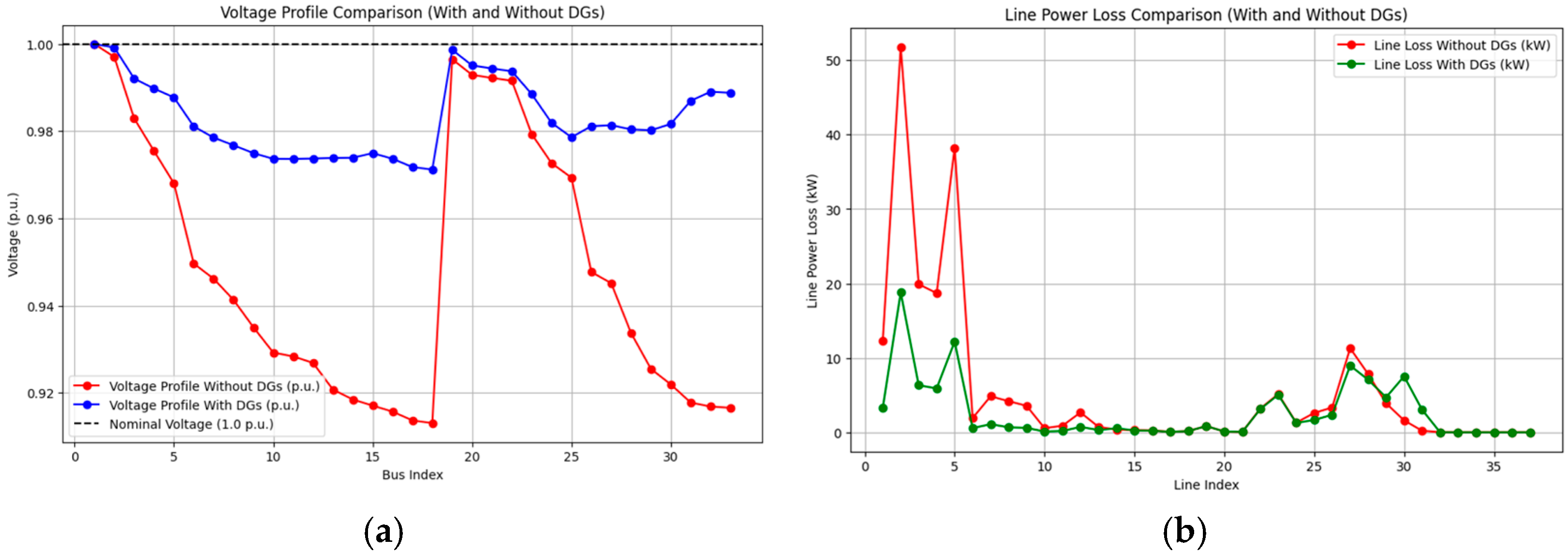
4.2.3. Only DG (Scenario S3)
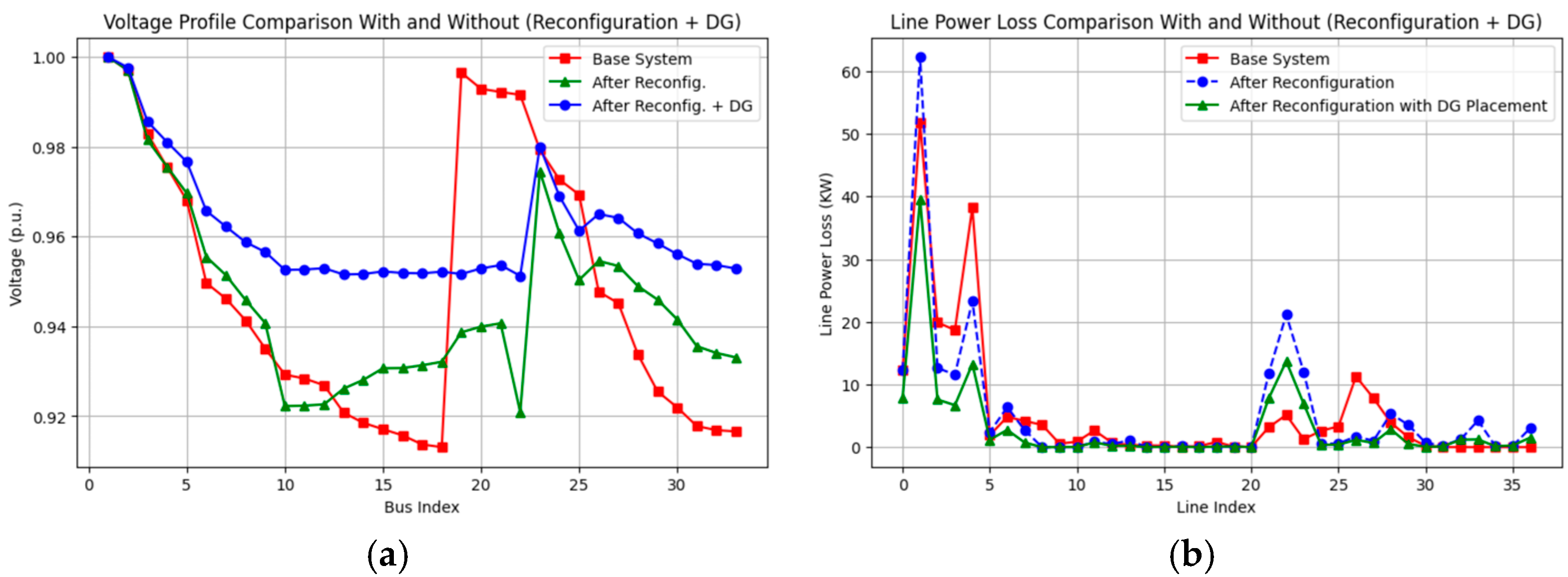
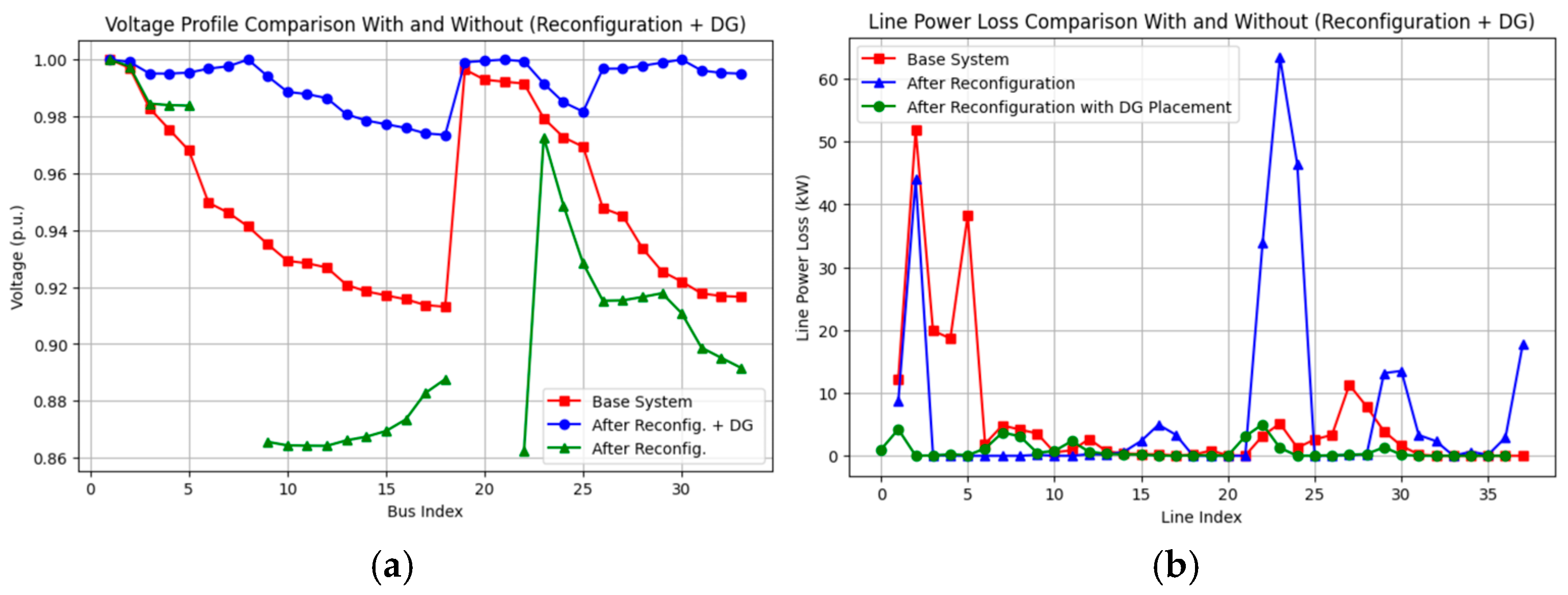
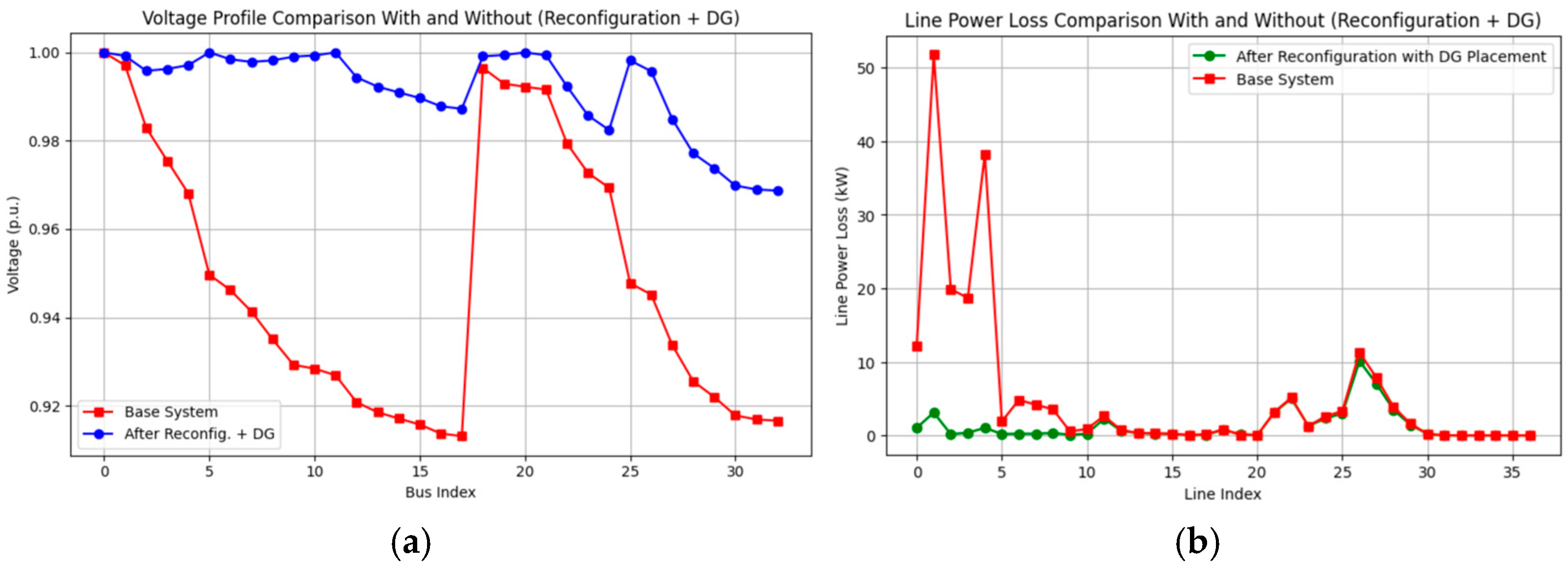
4.2.4. Reconfiguration and DG (Scenario S4)
4.3. Case 2
4.3.1. Faulty System (Scenario S1)
4.3.2. Only Reconfiguration (Scenario S2)
4.3.3. Only DG (Scenario S3)
4.3.4. Reconfiguration and DG (Scenario S4)
4.4. Case 3
4.4.1. Faulty System (Scenario S1)
4.4.2. Only Reconfiguration (Scenario S2)
4.4.3. Only DG (Scenario S3)
4.4.4. Reconfiguration and DG (Scenario S4)
4.5. Resilience Metric Results
5. Conclusions
- A dynamic Bayesian network (DBN) was used to model the evolution of overhead line failures across a predictive time horizon. The model was run for two time steps (time step was assumed to be of 1 h duration) to obtain failure probability for time instants t = 0 and t = 1, and accordingly, three different cases were considered. Case 1 depicts a minor case scenario and corresponds to region 2 affected by a category 3 hurricane (49.38–57.72 m/s) at time instant t = 0. Case 2 depicts a major case scenario and corresponds to region 2 affected by category 3 hurricanes at the time instant, i.e., t = 1. Case 3 depicts a blackout and corresponds to region 1 affected by a category 4 hurricane (57.72–69.65 m/s) at time instant t = 0. Regions 3 and 4 did not experience any outages due to category 2 and 1 hurricanes, respectively; therefore, no case was considered for regions 3 and 4. Any line found to have a failure probability greater than 0.5 using the DBN model was assumed to suffer an outage.
- Depending on the DBN’s outage predictions results, three independent restoration strategies, reconfiguration, optimal DG placement, and reconfiguration with optimal DG placement using PSO, were formulated for the IEEE 33 bus system. The objective was to ensure maximal load recovery with minimal power losses. The integration of DG only, reconfiguration only, and reconfiguration along with DG placement restored the load from 90.3% to 100% for Case 1 (t = 0). For Case 2 (t = 1), reconfiguration only restored the load from 34.994% to 80.35%, while DG only and reconfiguration with DG placement restored the load from 34.994% to 100%. For Case 3 (t = 0), reconfiguration was insufficient in restoring the load, while DG placement restored the load from 0% to 100% in scenarios 3 and 4. The case studies demonstrated that integrating DGs achieved superior restoration outcomes compared to reconfiguration alone.
- The findings of the overhead line failure model and the service restoration model were used to calculate resilience metrics. While and were derived from the resilience trapezoid framework, evaluating recovery efficiency and phased performance, provided a complementary perspective by quantifying cumulative losses across all nodes. Together, these metrics holistically assess resilience in terms of severity (), restoration success (), and phased adaptability ().
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fatima, K.; Shareef, H.; Costa, F.B.; Bajwa, A.A.; Wong, L.A. Machine Learning for Power Outage Prediction during Hurricanes: An Extensive Review. Eng. Appl. Artif. Intell. 2024, 133, 108056. [Google Scholar] [CrossRef]
- Stürmer, J.; Plietzsch, A.; Vogt, T.; Hellmann, F.; Kurths, J.; Otto, C.; Frieler, K.; Anvari, M. Protecting the Texas Power Grid from Tropical Cyclones: Increasing Resilience by Protecting Critical Lines. arXiv 2023, arXiv:2301.13793. [Google Scholar] [CrossRef]
- Daeli, A.; Mohagheghi, S. Power Grid Infrastructural Resilience against Extreme Events. Energies 2023, 16, 64. [Google Scholar] [CrossRef]
- Fatima, K.; Sefid, M.; Anees, M.A.; Rihan, M. An Investigation of the Impact of Synchrophasors Measurement on Multi-Area State Estimation in Active Distribution Grids. Aust. J. Electr. Electron. Eng. 2020, 17, 122–131. [Google Scholar] [CrossRef]
- Liu, X.; Xie, Q.; Liang, H.; Zhang, X. Post-Earthquake Recover Strategy for Substations Based on Seismic Resilience Evaluation. Eng. Struct. 2023, 279, 115583. [Google Scholar] [CrossRef]
- Salman, A.M.; Li, Y.; Stewart, M.G. Evaluating System Reliability and Targeted Hardening Strategies of Power Distribution Systems Subjected to Hurricanes. Reliab. Eng. Syst. Saf. 2015, 144, 319–333. [Google Scholar] [CrossRef]
- Zhai, C.; Chen, T.Y.; White, A.G.; Guikema, S.D. Power Outage Prediction for Natural Hazards Using Synthetic Power Distribution Systems. Reliab. Eng. Syst. Saf. 2021, 208, 107348. [Google Scholar] [CrossRef]
- Martinez-Amaya, J.; Radin, C.; Nieves, V. Advanced Machine Learning Methods for Major Hurricane Forecasting. Remote Sens. 2023, 15, 119. [Google Scholar] [CrossRef]
- Klauberg, C.; Vogel, J.; Dalagnol, R.; Ferreira, M.P.; Hamamura, C.; Broadbent, E.; Silva, C.A. Post-Hurricane Damage Severity Classification at the Individual Tree Level Using Terrestrial Laser Scanning and Deep Learning. Remote Sens. 2023, 15, 1165. [Google Scholar] [CrossRef]
- Cheng, P.-H.; Lin, C.C.-H.; Morton, Y.T.J.; Yang, S.-C.; Liu, J.-Y. A Bagged-Tree Machine Learning Model for High and Low Wind Speed Ocean Wind Retrieval From CYGNSS Measurements. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4201910. [Google Scholar] [CrossRef]
- Moeini, M.; Memari, A.M. Hurricane-Induced Failure Mechanisms in Low-Rise Residential Buildings and Future Research Directions. Nat. Hazards Rev. 2023, 24, 03123001. [Google Scholar] [CrossRef]
- Faramarzi, D.; Rastegar, H.; Riahy, G.H.; Doagou-Mojarrad, H. A Three-Stage Hybrid Stochastic/IGDT Framework for Resilience-Oriented Distribution Network Planning. Int. J. Electr. Power Energy Syst. 2023, 146, 108738. [Google Scholar] [CrossRef]
- McCann, Z.H.; Szaflarski, M. Differences in County-Level Cardiovascular Disease Mortality Rates Due to Damage Caused by Hurricane Matthew and the Moderating Effect of Social Capital: A Natural Experiment. BMC Public Health 2023, 23, 60. [Google Scholar] [CrossRef]
- Liang, D.; Ewing, B.; Cardella, E.; Song, L. Probabilistic Modeling of Small Business Recovery after a Hurricane: A Case Study of 2017 Hurricane Harvey. Nat. Hazards Rev. 2023, 24, 05022012. [Google Scholar] [CrossRef]
- Friedman, E.; Solecki, W.; Troxler, T.G.; Paganini, Z. Linking Quality of Life and Climate Change Adaptation Through the Use of the Macro-Adaptation Resilience Toolkit. Clim. Risk Manag. 2023, 39, 100485. [Google Scholar] [CrossRef]
- Fatima, K.; Shareef, H.; Bajwa, A.A. An Insight into Power System Resilience and Its Confounding Traits. In Proceedings of the 2022 International Seminar on Application for Technology of Information and Communication (iSemantic), Semarang, Indonesia, 17–18 September 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 226–231. [Google Scholar]
- Xu, Y.; Xing, Y.; Huang, Q.; Li, J.; Zhang, G.; Bamisile, O.; Huang, Q. A Review of Resilience Enhancement Strategies in Renewable Power System under HILP Events. Energy Rep. 2023, 9, 200–209. [Google Scholar] [CrossRef]
- Schmidt, D.H.; Garland, K.; Quebedeaux, L.K. Resilient Recovery Strategies: Lessons from the Local Nonprofit Sector Following Hurricane Ike. In Case Studies in Disaster Recovery; Elsevier: Amsterdam, The Netherlands, 2023; pp. 33–51. [Google Scholar]
- Hou, G.; Muraleetharan, K.K.; Panchalogaranjan, V.; Moses, P.; Javid, A.; Al-Dakheeli, H.; Bulut, R.; Campos, R.; Harvey, P.S.; Miller, G. Resilience Assessment and Enhancement Evaluation of Power Distribution Systems Subjected to Ice Storms. Reliab. Eng. Syst. Saf. 2023, 230, 108964. [Google Scholar] [CrossRef]
- Li, X.; Fu, D.; Nielsen-Gammon, J.; Gangrade, S.; Kao, S.C.; Chang, P.; Morales Hernández, M.; Voisin, N.; Zhang, Z.; Gao, H. Impacts of Climate Change on Future Hurricane Induced Rainfall and Flooding in a Coastal Watershed: A Case Study on Hurricane Harvey. J. Hydrol. 2023, 616, 128774. [Google Scholar] [CrossRef]
- Darestani, Y.M.; Shafieezadeh, A. Multi-Dimensional Wind Fragility Functions for Wood Utility Poles. Eng. Struct. 2019, 183, 937–948. [Google Scholar] [CrossRef]
- Hosseini, M.M.; Parvania, M. Quantifying Impacts of Automation on Resilience of Distribution Systems. IET Smart Grid 2020, 3, 144–152. [Google Scholar] [CrossRef]
- Lei, S.; Member, S.; Wang, J.; Member, S.; Chen, C.; Hou, Y.; Member, S. Mobile Emergency Generator Pre-Positioning and Real-Time Allocation for Resilient Response to Natural Disasters. IEEE Trans. Smart Grid 2018, 9, 2030–2041. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J. Self-Healing Resilient Distribution Systems Based on Sectionalization into Microgrids. IEEE Trans. Power Syst. 2015, 30, 3139–3149. [Google Scholar] [CrossRef]
- Fatima, K.; Idrisi, A.H.; Mourad, A.-H.I. LabView Based Conrol System Design for VTOL Aircraft System. In Proceedings of the 2020 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 4 February–9 April 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar]
- Shi, Q.; Liu, W.; Zeng, B.; Hui, H.; Li, F. Enhancing Distribution System Resilience Against Extreme Weather Events: Concept Review, Algorithm Summary, and Future Vision. Int. J. Electr. Power Energy Syst. 2022, 138, 107860. [Google Scholar] [CrossRef]
- Marnay, C.; Chard, J.S.; Hamachi, K.S.; Lipman, T.; Moezzi, M.M.; Ouaglal, B.; Siddiqui, A.S. Modeling of Customer Adoption of Distributed Energy Resources. 2001. Available online: https://escholarship.org/uc/item/5x9154mg (accessed on 1 January 2023).
- Farzin, H.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M. Role of Outage Management Strategy in Reliability Performance of Multi-Microgrid Distribution Systems. IEEE Trans. Power Syst. 2017, 33, 2359–2369. [Google Scholar] [CrossRef]
- Farzin, H.; Fotuhi-Firuzabad, M.; Moeini-Aghtaie, M. Enhancing Power System Resilience through Hierarchical Outage Management in Multi-Microgrids. IEEE Trans. Smart Grid 2016, 7, 2869–2879. [Google Scholar] [CrossRef]
- Arab, A.; Khodaei, A.; Khator, S.K.; Ding, K.; Emesih, V.A.; Han, Z. Stochastic Pre-Hurricane Restoration Planning for Electric Power Systems Infrastructure. IEEE Trans. Smart Grid 2015, 6, 1046–1054. [Google Scholar] [CrossRef]
- Gao, H.; Chen, Y.; Mei, S.; Huang, S.; Xu, Y. Resilience-Oriented Pre-Hurricane Resource Allocation in Distribution Systems Considering Electric Buses. Proc. IEEE 2017, 105, 1214–1233. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Y.; Fang, J.; He, J.; Tian, Y.; Zhang, H. Emergency Sources Pre-Positioning for Resilient Restoration of Distribution Network. Energy Rep. 2020, 6, 1283–1290. [Google Scholar] [CrossRef]
- Arif, A.; Wang, Z.; Wang, J.; Chen, C. Power Distribution System Outage Management with Co-Optimization of Repairs, Reconfiguration, and DG Dispatch. IEEE Trans. Smart Grid 2017, 9, 4109–4118. [Google Scholar] [CrossRef]
- Hughes, W.; Zhang, W.; Bagtzoglou, A.C.; Wanik, D.; Pensado, O.; Yuan, H.; Zhang, J. Damage Modeling Framework for Resilience Hardening Strategy for Overhead Power Distribution Systems. Reliab. Eng. Syst. Saf. 2021, 207, 107367. [Google Scholar] [CrossRef]
- Li, M.; Hou, H.; Yu, J.; Geng, H.; Zhu, L.; Huang, Y.; Li, X. Prediction of Power Outage Quantity of Distribution Network Users under Typhoon Disaster Based on Random Forest and Important Variables. Math. Probl. Eng. 2021, 2021, 1–14. [Google Scholar] [CrossRef]
- Shen, Y.; Gu, C.; Ma, Z.; Yang, X.; Zhao, P. A Two-Stage Resilience Enhancement for Distribution Systems under Hurricane Attacks. IEEE Syst. J. 2020, 15, 653–661. [Google Scholar] [CrossRef]
- Kahouli, O.; Alsaif, H.; Bouteraa, Y.; Ben Ali, N.; Chaabene, M. Power System Reconfiguration in Distribution Network for Improving Reliability Using Genetic Algorithm and Particle Swarm Optimization. Appl. Sci. 2021, 11, 3092. [Google Scholar] [CrossRef]
- Moradi, M.H.; Abedini, M. A Combination of Genetic Algorithm and Particle Swarm Optimization for Optimal DG Location and Sizing in Distribution Systems. Int. J. Electr. Power Energy Syst. 2012, 34, 66–74. [Google Scholar] [CrossRef]
- Bie, Z.; Lin, Y.; Li, G.; Li, F. Battling the Extreme: A Study on the Power System Resilience. Proc. IEEE 2017, 105, 1253–1266. [Google Scholar] [CrossRef]
- Haider, W.; Ul Hassan, S.J.; Mehdi, A.; Hussain, A.; Adjayeng, G.O.M.; Kim, C.H. Voltage Profile Enhancement and Loss Minimization Using Optimal Placement and Sizing of Distributed Generation in Reconfigured Network. Machines 2021, 9, 20. [Google Scholar] [CrossRef]
- Vai, V.; Suk, S.; Lorm, R.; Chhlonh, C.; Eng, S.; Bun, L. Optimal Reconfiguration in Distribution Systems with Distributed Generations Based on Modified Sequential Switch Opening and Exchange. Appl. Sci. 2021, 11, 2146. [Google Scholar] [CrossRef]
- Gallego Pareja, L.A.; López-Lezama, J.M.; Carmona, O.G. A Mixed-Integer Linear Programming Model for the Simultaneous Optimal Distribution Network Reconfiguration and Optimal Placement of Distributed Generation. Energies 2022, 15, 3063. [Google Scholar] [CrossRef]
- Gallego Pareja, L.A. ElectricalSystemsDataForReconfiguration. Available online: https://github.com/LuisGallego2019/ElectricalSystemsDataForReconfiguration (accessed on 1 January 2023).
- Bajwa, A.A.; Mokhlis, H.; Mekhlief, S.; Mubin, M.; Azam, M.M.; Sarwar, S. Resilience-Oriented Service Restoration Modelling Interdependent Critical Loads in Distribution Systems with Integrated Distributed Generators. IET Gener. Transm. Distrib. 2021, 15, 1257–1272. [Google Scholar] [CrossRef]
- Ryan, P.C.; Stewart, M.G.; Spencer, N.; Li, Y. Reliability Assessment of Power Pole Infrastructure Incorporating Deterioration and Network Maintenance. Reliab. Eng. Syst. Saf. 2014, 132, 261–273. [Google Scholar] [CrossRef]
- Hou, G.; Muraleetharan, K.K. Modeling the Resilience of Power Distribution Systems Subjected to Extreme Winds Considering Tree Failures: An Integrated Framework. Int. J. Disaster Risk Sci. 2023, 14, 194–208. [Google Scholar] [CrossRef]
- Khomami, M.S.; Sepasian, M.S. Pre-Hurricane Optimal Placement Model of Repair Teams to Improve Distribution Network Resilience. Electr. Power Syst. Res. 2018, 165, 1–8. [Google Scholar] [CrossRef]
- Ouyang, M.; Duenas-Osorio, L. Multi-Dimensional Hurricane Resilience Assessment of Electric Power Systems. Struct. Saf. 2014, 48, 15–24. [Google Scholar] [CrossRef]
- Fatima, K.; Shareef, H. Dynamic Bayesian Network Model for Overhead Power Lines Affected by Hurricanes. Forecasting 2025, 7, 11. [Google Scholar] [CrossRef]
- Omogoye, O.S.; Folly, K.A.; Awodele, K.O. Enhancing the Distribution Power System Resilience against Hurricane Events Using a Bayesian Network Line Outage Prediction Model. J. Eng. 2021, 2021, 731–744. [Google Scholar] [CrossRef]
- GeNIe Modeler by BayesFusion, LLC. Available online: https://www.bayesfusion.com/genie/ (accessed on 2 February 2024).
- Guo, Y.; Wang, H.; Guo, Y.; Zhong, M.; Li, Q.; Gao, C. System Operational Reliability Evaluation Based on Dynamic Bayesian Network and XGBoost. Reliab. Eng. Syst. Saf. 2022, 225, 108622. [Google Scholar] [CrossRef]
- Luo, D.; Xia, Y.; Zeng, Y.; Li, C.; Zhou, B.; Yu, H.; Wu, Q. Evaluation Method of Distribution Network Resilience Focusing on Critical Loads. IEEE Access 2018, 6, 61633–61639. [Google Scholar] [CrossRef]
- Almoghathawi, Y.; Barker, K. Component Importance Measures for Interdependent Infrastructure Network Resilience. Comput. Ind. Eng. 2019, 133, 153–164. [Google Scholar] [CrossRef]
- Liu, X.; Shahidehpour, M.; Li, Z.; Liu, X.; Cao, Y.; Bie, Z. Microgrids for Enhancing the Power Grid Resilience in Extreme Conditions. IEEE Trans. Smart Grid 2016, 8, 589–597. [Google Scholar] [CrossRef]
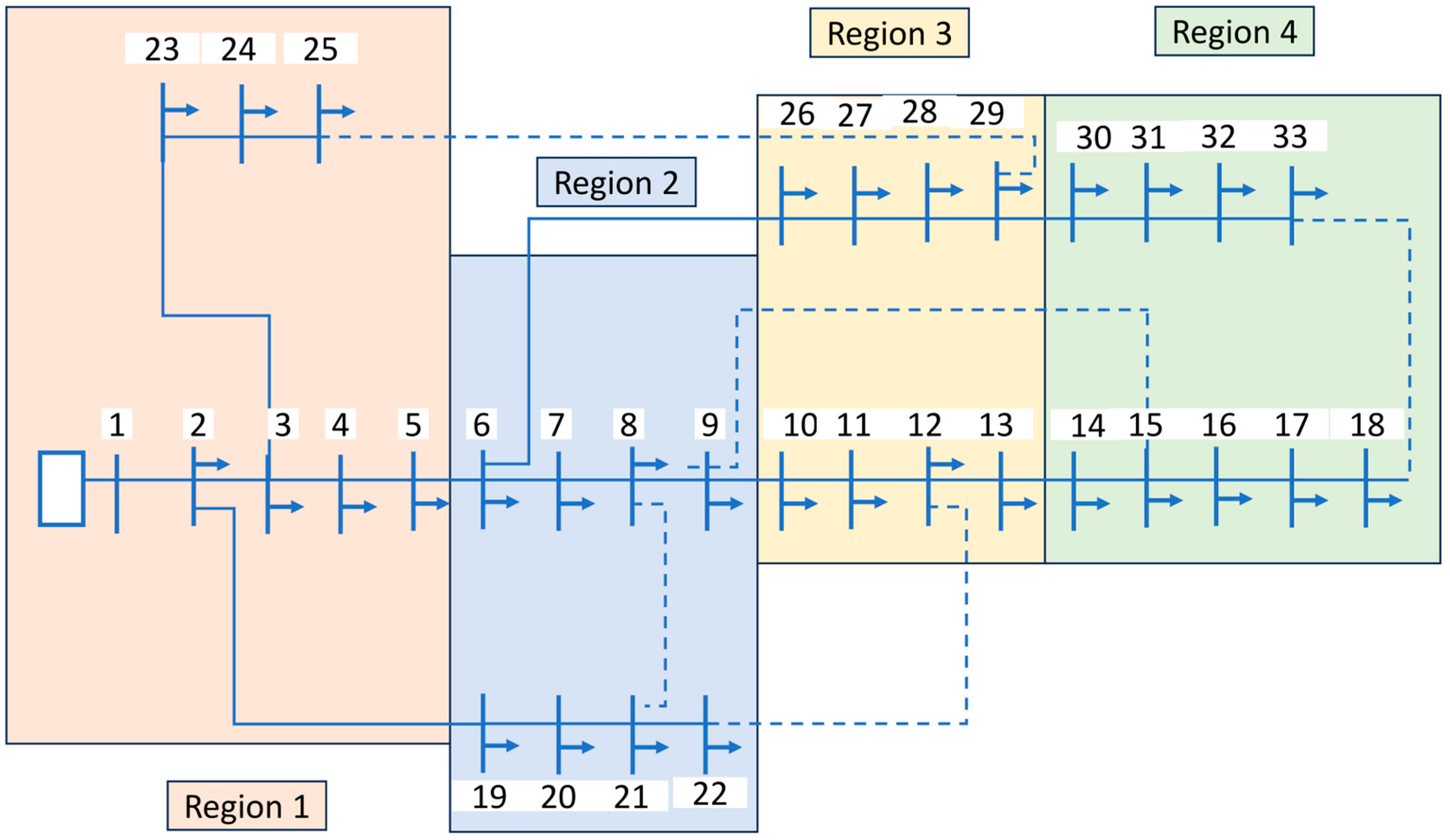
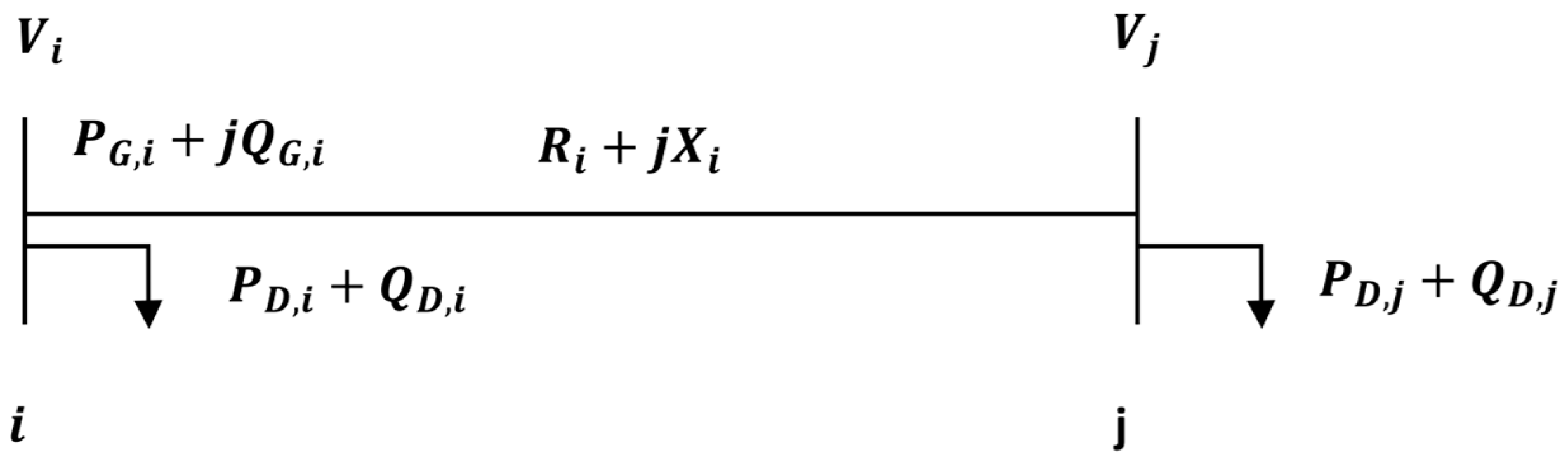

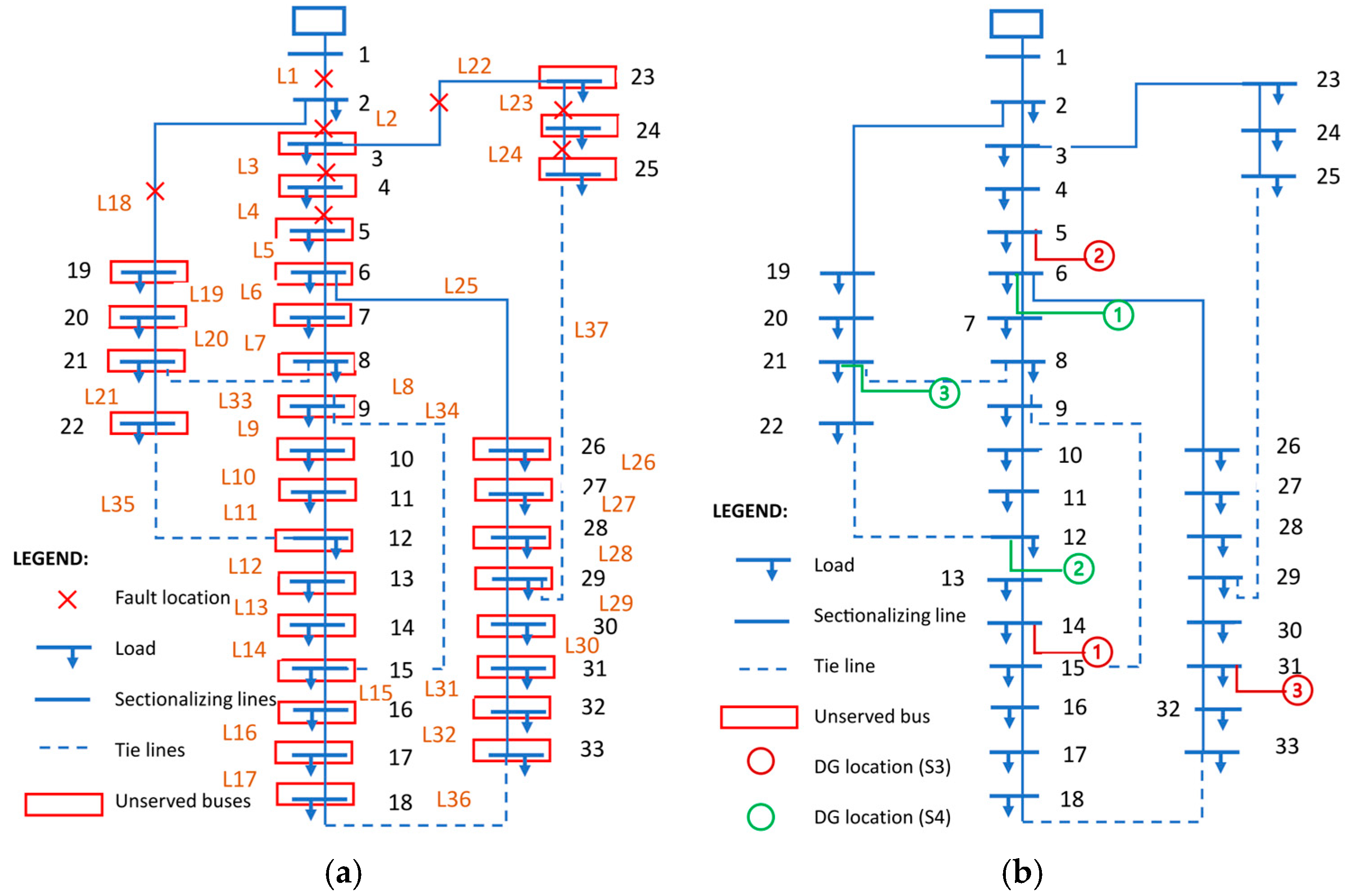

| System Lines | From Bus to Bus | HWSI (m/s) | CASE 1 (t = 0) | CASE 2 (t = 1) | CASE 3 (t = 0) |
|---|---|---|---|---|---|
| 1 | 1–2 | 58.115 | 1 | 1 | 0 |
| 2 | 2–3 | 59.903 | 1 | 1 | 0 |
| 3 | 3–4 | 61.691 | 1 | 1 | 0 |
| 4 | 4–5 | 63.479 | 1 | 1 | 0 |
| 5 | 5–6 | 50.068 | 1 | 0 | 1 |
| 6 | 6–7 | 50.962 | 1 | 0 | 1 |
| 7 | 7–8 | 51.856 | 1 | 0 | 1 |
| 8 | 8–9 | 52.750 | 1 | 0 | 1 |
| 9 | 9–10 | 42.915 | 1 | 1 | 1 |
| 10 | 10–11 | 43.586 | 1 | 1 | 1 |
| 11 | 11–12 | 44.257 | 1 | 1 | 1 |
| 12 | 12–13 | 44.927 | 1 | 1 | 1 |
| 13 | 13–14 | 33.528 | 1 | 1 | 1 |
| 14 | 14–15 | 34.422 | 1 | 1 | 1 |
| 15 | 15–16 | 35.316 | 1 | 1 | 1 |
| 16 | 16–17 | 36.210 | 1 | 1 | 1 |
| 17 | 17–18 | 37.104 | 1 | 1 | 1 |
| 18 | 2–19 | 59.903 | 0 | 0 | 0 |
| 19 | 19–20 | 54.538 | 1 | 0 | 1 |
| 20 | 20–21 | 55.433 | 1 | 0 | 1 |
| 21 | 21–22 | 56.327 | 0 | 0 | 1 |
| 22 | 3–23 | 61.691 | 1 | 1 | 0 |
| 23 | 23–24 | 67.056 | 1 | 1 | 0 |
| 24 | 24–25 | 68.844 | 1 | 1 | 0 |
| 25 | 6–26 | 50.962 | 1 | 0 | 1 |
| 26 | 26–27 | 46.268 | 1 | 1 | 1 |
| 27 | 27–28 | 46.939 | 1 | 1 | 1 |
| 28 | 28–29 | 48.056 | 1 | 1 | 1 |
| 29 | 29–30 | 37.998 | 1 | 1 | 1 |
| 30 | 30–31 | 38.892 | 1 | 1 | 1 |
| 31 | 31–32 | 39.786 | 1 | 1 | 1 |
| 32 | 32–33 | 40.680 | 1 | 1 | 1 |
| 33 | 8–21 | 52.750 | 1 | 0 | 1 |
| 34 | 9–15 | 42.915 | 1 | 1 | 1 |
| 35 | 12–22 | 44.927 | 1 | 1 | 1 |
| 36 | 18–33 | 42.468 | 1 | 1 | 1 |
| 37 | 25–29 | 49.397 | 1 | 1 | 1 |
| Case | Scenario | Objective 1 (MW) | Objective 2 (kW) | Min. Voltage (p.u.) |
|---|---|---|---|---|
| C0 | S0 | 3.715 | 202.677 | 0.9131 (Bus 18) |
| C1 | S1 | 3.355 | 188.00 | - |
| S2 | 3.715 | 197.85 | 0.9335 (Bus 22) | |
| S3 | 3.715 | 161.63 | 0.9224 (Bus 33) | |
| S4 | 3.715 | 120.06 | 0.9510 (Bus 22) | |
| C2 | S1 | 1.3 | 15.20 | - |
| S2 | 2.985 | 262.80 | - | |
| S3 | 3.715 | 119.689 | 0.9348 (Bus 18) | |
| S4 | 3.715 | 43.90 | 0.9518 (Bus 18) | |
| C3 | S1 | 0 | 0.00 | - |
| S2 | 0 | 0.00 | - | |
| S3 | 3.715 | 97.589 | 0.9712 (Bus 18) | |
| S4 | 3.715 | 27.0 | 0.9687 (Bus 33) |
| Parameter | Case | Scenario | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| Degraded | 1 | 9.69 | 9.69 | 9.69 | 9.69 |
| system | 2 | 65.006 | 65.006 | 65.006 | 65.006 |
| state (%) | 3 | 100 | 100 | 100 | 100 |
| Restored | 1 | 90.31 | 100 | 100 | 100 |
| system | 2 | 34.994 | 80.35 | 100 | 100 |
| state (%) | 3 | 0 | 0 | 100 | 100 |
| td − te(hr) | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 2 | 2 | |
| 3 | 1 | 1 | 1 | 1 | |
| tS − td(hr) | 1 | 0 | 0.01 | 0.01 | 0.01 |
| 2 | 0 | 0.01 | 0.01 | 0.01 | |
| 3 | 0 | 0.01 | 0.01 | 0.01 | |
| tf − ts(hr) | 1 | 0 | 8 | 0 | 8 |
| 2 | 0 | 10 | 0 | 10 | |
| 3 | 0 | 10 | 0 | 10 | |
| R1 | 1 | 5.319 | 5.054 | 6.186 | 8.329 |
| 2 | 65.789 | 3.805 | 8.354 | 22.779 | |
| 3 | inf | inf | 10.247 | 37.037 | |
| R2 | 1 | 0 | 1 | 1 | 1 |
| 2 | 0 | 0.6977 | 1 | 1 | |
| 3 | 0 | 0 | 1 | 1 | |
| R3 | 1 | 329.717 | 415.182 | 153.942 | 415.182 |
| 2 | 115.006 | 249.451 | 164.656 | 189.626 | |
| 3 | 150 | 150 | 200 | 300 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fatima, K.; Shareef, H.; Costa, F.B. Resilience Oriented Distribution System Service Restoration Considering Overhead Power Lines Affected by Hurricanes. Appl. Syst. Innov. 2025, 8, 149. https://doi.org/10.3390/asi8050149
Fatima K, Shareef H, Costa FB. Resilience Oriented Distribution System Service Restoration Considering Overhead Power Lines Affected by Hurricanes. Applied System Innovation. 2025; 8(5):149. https://doi.org/10.3390/asi8050149
Chicago/Turabian StyleFatima, Kehkashan, Hussain Shareef, and Flavio Bezerra Costa. 2025. "Resilience Oriented Distribution System Service Restoration Considering Overhead Power Lines Affected by Hurricanes" Applied System Innovation 8, no. 5: 149. https://doi.org/10.3390/asi8050149
APA StyleFatima, K., Shareef, H., & Costa, F. B. (2025). Resilience Oriented Distribution System Service Restoration Considering Overhead Power Lines Affected by Hurricanes. Applied System Innovation, 8(5), 149. https://doi.org/10.3390/asi8050149






