1. Introduction
The automation of farmland layout design plays a critical role in enhancing land-use efficiency, resource allocation, and digital agricultural management, making it a cornerstone of smart agriculture. Traditional design processes are often labor-intensive and repetitive, hindering both productivity and flexibility in spatial planning [
1]. To address these limitations, the integration of artificial intelligence (AI) offers a promising pathway toward more efficient and intelligent farmland design. Existing AI-based approaches, including deep learning models [
2,
3,
4,
5], typically require extensive training datasets, while heuristic algorithms [
6,
7,
8,
9,
10,
11] often treat layout units as geometric planes, resulting in increased computational cost when modifying their sizes and positions. However, these methods offer limited opportunities for expert intervention and fail to leverage the valuable domain knowledge of agricultural professionals.
This paper specifically addresses this gap by proposing an interactive approach that integrates human expertise into the layout optimization process. Recent research highlights the potential of using simple 2D graphical and topological representations to streamline complex design workflows [
12], reducing computational complexity and enhancing user interaction. Building on this insight, we propose a phased, interactive farmland layout system that incorporates a user-friendly interface and an advanced 3D visual editing environment. The system begins by preprocessing freehand boundary sketches provided by the user, then applies the Graphics-Guided Evolutionary Layout (GGEL) algorithm to efficiently generate high-quality 2D layouts while ensuring spatial feasibility. It further supports real-time user adjustments and offers procedural tools for detailed scene refinement, enabling flexible and efficient farmland planning.
Our key contributions are as follows:
We introduce a topologically aware optimization algorithm, Graphics Guided Evolutionary Layout (GGEL), which ensures fast convergence and spatial feasibility. GGEL significantly improves computational efficiency, reducing optimization time while maintaining high-quality layout solutions.
We develop an interactive layout module that allows users to dynamically modify farmland layouts. This module provides real-time feedback to ensure the final design meets specific agricultural requirements and spatial constraints.
By combining GGEL and the interactive layout module, we design a user-friendly system that enables efficient design and refinement of farmland layouts. With 95% support for creative flexibility and 90% support for usability, the system demonstrates its effectiveness in real-world applications.
Qualitative and quantitative evaluations show that our system combines topological optimization with interactive design, significantly improving the efficiency of farmland layout planning and supporting users in creating customized farmland designs. This work advances the application of artificial intelligence in smart agriculture and provides a scalable and user-friendly solution to modern agricultural challenges.
2. Related Work
Overall, our work belongs to the task of layout generation based on structured arrangements, aiming to use graph structure and heuristic algorithms to optimize scene layout, with a particular focus on automatic design of farmland layout. Significant progress has been made in the research of graph-guided generation models and heuristic algorithms, especially in urban layout [
13,
14,
15,
16], architectural layout [
5,
17,
18,
19], and other fields [
20,
21,
22,
23]. However, the research on farmland layout remains in the preliminary stage, facing challenges such as complex land shapes and dynamic demands.
2.1. Graph-Guided Generative Models
A graph is a structured data model that can represent the spatial relationships and semantic information of objects in a scene. In recent years, graph structure has been widely used in 2D layout design, which effectively captures the user’s layout intention and simplifies the input. Zhang et al. [
24] review recent work on graphic visualization and computational efficiency optimization and propose concepts of pre-layout, in-layout, and post-layout. The pre-layout method focuses on graphic data compression, the in-layout method optimizes the layout process from the computational architecture and algorithm, and the visual mapping and interactive layout adjustment are the post-layout optimization techniques. Sepulveda et al. [
25] design a Unity component that allows users to edit graphical structures on a 2D plane to generate reasonable building layouts based on room size and tightness constraints. Wu et al. [
26] introduce a deep network for generating residential building plans. Given an architectural outline as input, the position of rooms and walls is predicted via the network and then converted into a vector graphic format. The network is trained on massive, densely annotated datasets of real residential buildings. The limitations of this approach are that it is difficult for the user to control the generated layout, and the cost of data acquisition and annotation is also high due to the large dataset. Hu et al. propose a learning framework for automatic floor plan generation, Graph2Plan [
5], which takes the layout diagram provided by users as a sparse design constraint and combines it with a deep neural network to generate and model indoor room layout. However, Graph2Plan is an end-to-end model, which does not allow users to make adjustments during the design process. To enhance interaction between the model and designers at different levels, He et al. design a human-in-the-loop staged generation model called iPlan [
19], which can automatically generate layouts while interacting with users, offering a high degree of flexibility. However, both Graph2Plan and iPlan require a large amount of data for training, and their rule boundaries are highly dependent. Compared with the method combining graphs and deep learning, this study focuses on the graph-guided heuristic algorithm, which can efficiently generate layouts that meet users’ needs without large amounts of data, providing greater flexibility and controllability.
2.2. Heuristic Algorithm-Based Scene Layout
The application of a heuristic algorithm in layout optimization has achieved remarkable results, especially in reducing computation overhead and improving generation efficiency. Hu et al. [
27] optimize the layout of e-commerce warehouses with the aim of reducing picking costs. They construct attributes such as center point, length, and width for each layout entity, and then stretch and translate these layout entities as faces to complete the layout. By comparing Genetic Algorithms (GA) [
9,
10], Simulated Annealing (SA) [
8], and Particle Swarm Optimization (PSO) [
6,
7], they validate the advantages of GA in layout optimization problems. Jalayer et al. [
28] use a GA with multiple constraints as the optimization framework to automatically design cage layouts within animal shelters, minimizing the number of cages facing each other to reduce stress and ensure accessibility for staff and visitors. Garcia et al. [
29] propose a multi-objective interactive genetic algorithm, which is effective in application scenarios such as sheep slaughterhouses and carton recycling plants. In this approach, the decision-maker’s knowledge contribution to the method guides a complex search process that is adjusted to the decision-maker’s preferences. Kumar et al. propose an Entity Planning Genetic Algorithm (EPGA) [
10] that optimizes the layout design of buildings and houses by leveraging the entities structure topological relationships extracted from a Multi-Population Genetic Algorithm (MPGA). de Almeida et al. [
30] propose an evolutionary approach that enables the automated design of mass custom production of modular homes and is not constrained by size and location constraints on the search space. Coelho et al. [
11] optimize the number of light sources in indoor environments using GA to achieve adequate light intensity with the minimum number of sources. This study introduces topology awareness on the basis of heuristic algorithms, demonstrating higher computational efficiency, especially for layout problems with complex and irregular shapes.
2.3. Layout Optimization in Agriculture
The proper layout of farmland is the key to ensuring sustainable agricultural production [
31]. Ju et al. [
32] propose a genetic algorithm guided by support vector regression to solve the problem of layout optimization of farm stroke motors. Gao et al. [
33] propose a supplementary sampling layout optimization method using the spatial simulated annealing algorithm to improve farmland management and obtain the optimal sampling layout. Ye et al. [
34] propose the layout optimization of urban space and agricultural space based on spatial decision, determine the boundaries of different functional zones in agricultural space, and optimize the boundaries based on the principle of contradiction and coordination. Dadi et al. [
35] believe that planning farm layout before starting agriculture can provide higher quality services, and adopt three facility planning methods to develop sustainable layout, namely, system layout design (SLP), pin-pair exchange method (PEM), and Graph-based theory (GBT). Satake et al. [
36] compare the simulated annealing algorithm and the ramp climbing algorithm (HC) to optimize the layout of functional partitions such as cold storage, warehouse, packaging plant, and grading area in the agricultural facility site. In conclusion, optimizing the layout of functional zones in agriculture has always been a key issue, but it often faces challenges such as insufficient time efficiency and lack of interactivity during the design process. To address these issues, this study proposes a topology-aware heuristic optimization strategy and designs an interactive layout optimization system, aiming to provide a more intuitive and convenient user experience.
3. System Overview
Figure 1 presents an overview of our system. In the following, we provide an overview of each component in the system.
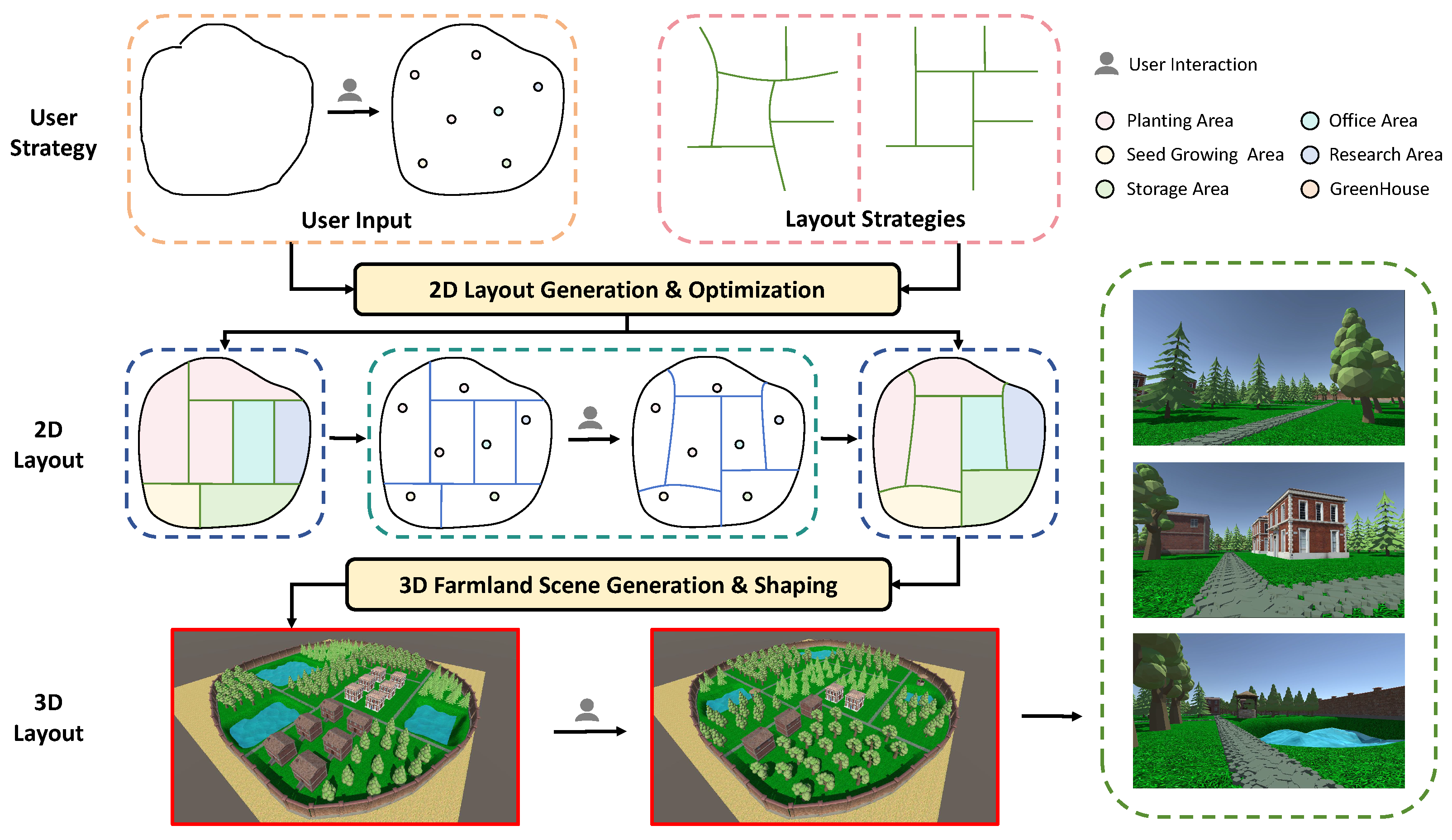
User Strategy. The system allows the user to draw and adjust the boundary sketch of the farmland scene. For functional zones, users can specify their location, quantity, and type. Our predefined functional zones include six types: planting area, seed planting area, storage area, office area, research area, and greenhouse.
2D Layout Generation and Optimization. The GGEL algorithm can quickly design the layout of the farmland scene through the topological perception of the graph. In addition, we design a layout adjustment module that allows users to visually modify the size and location of functional zones to meet customized needs.
3D Farmland Scene Generation and Edit. Based on the 2D layout, we also design a series of 3D procedural brushes, including plant brushes, construction brushes, and pond brushes, allowing users to adjust the details of the scene. Brushes can control the creation or destruction of single or multiple entities.
Agricultural Requirement and Spatial Constrains. The system’s design and optimization processes are governed by a comprehensive set of constraints, ensuring that generated layouts are spatially feasible and agriculturally viable. These constraints are derived from agronomic practices and spatial planning principles, acting as hard rules and soft objectives within our GGEL algorithm, specifically as follows: (1) Minimum Area Requirements: Each zone must satisfy a predefined minimum area to be functional; (2) the research area should be proximate to both the greenhouse and planting areas for monitoring and experimentation; (3) the greenhouse may require proximity to a water source; (4) Connectivity: All zones must be connected via a network of pathways for personnel and machinery access; (5) Shape Rules: Different areas within the boundaries hand-drawn by users all adopt regular rectangular shapes to promote efficient mechanized agricultural operations.
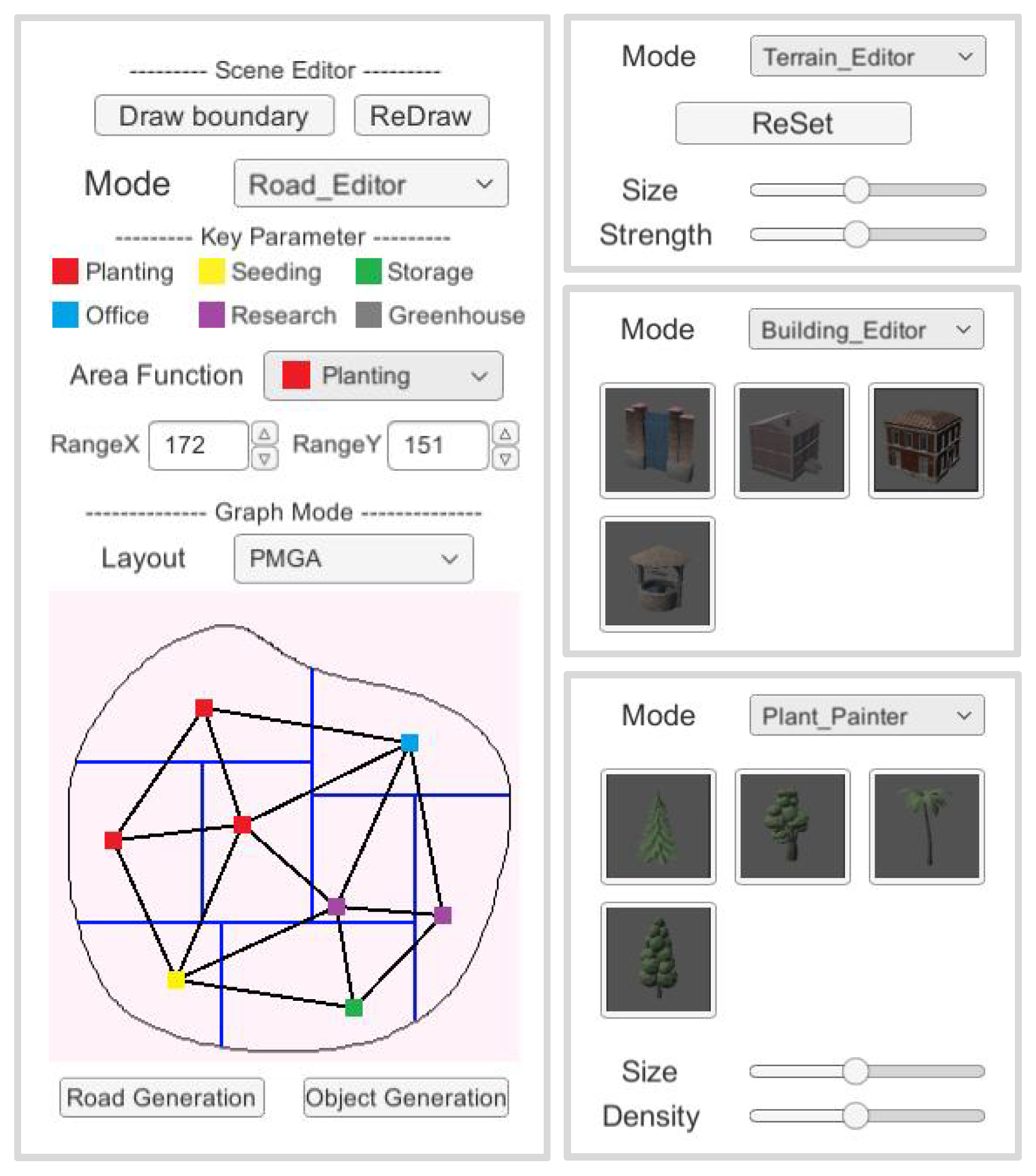
User Interface.Figure 2 presents the user interface we designed. The Scene Editor module in the main panel enables users to draw boundary sketches. The Key Parameter module displays the predefined functional areas and the coordinates of road nodes. The core module of the interface is Graph Mode, which presents the freehand boundary sketches drawn by users on the UI canvas. In the brush control panel, we offer multiple procedural 3D brushes with adjustable parameters (b).
The rest of this article is arranged as follows:
Section 4 describes user input.
Section 5 discusses 2D layout generation and optimization of farmland.
Section 6 describes the 3D detail shaping of the farmland scene.
Section 7 analyzes experimental results and user evaluations, and
Section 8 presents conclusions and future work.
4. User Input
4.1. Freehand Boundary Sketch
The boundary drawn by users is represented as a series of continuous points
, which are recorded sequentially when users draw. To address the inefficiency of directly using a large number of points, we use a sampling process to extract key points from the boundary, while effectively preserving the overall shape of the boundary. Our sampling algorithm is based on the principle that more points are sampled on segments with sharp bends and fewer points are sampled on smooth segments with low curvature. Therefore, we use curvature as the sampling weight. Given a boundary stroke composed of dense points
P, we first compute the curvature
at each point
through polynomial fitting. The curvature at a point
is calculated as follows in Equation (
1):
where
is the polynomial function obtained by fitting at the points
. Then, from the starting point
of the point set
P, we use a variable move step to access the point set
P in order to collect the key points. The moving step at point
is calculated as follows in Equation (
2):
where
=
. The default value of the constant
k is set to 10, which keeps the step size within the range of [2, 11]. Finally, we use Hermite interpolation to fit the sampled boundary points, creating a smooth boundary curve connected end to end.
Based on the sampled vertices
, we design a planar boundary optimization strategy using Laplacian deformation method, which allows users to adjust the freehand boundary by updating the position of sampling points in real time. We define Laplacian coordinates for each point, capturing the differential characteristics of the sampling point with respect to its neighbors. For each sampled point
, its Laplacian coordinate is specified in Equation (
3):
where
is the Laplacian coordinate of point
,
is the set of points adjacent to
, and
is the number of neighbors.
Additionally, we design the following objective function to minimize the difference between the coordinates of the sampled points before and after optimization. The objective function is defined in Equation (
4):
where
denotes the subset of control points subject to user-defined adjustments, and
corresponds to the designated new position for each control point
. The first term of the objective function,
, is crucial for preserving the integrity of the Laplacian coordinates, thereby maintaining the intrinsic geometric properties of the original curve. The second term,
, ensures that the modified positions of the control points align with the user-specified positions
, facilitating a controlled and precise optimization process.
4.2. Node Representation of Functional Zones
In order to simplify the layout design, each function zone is represented by a node. Users only need to mark nodes in a reasonable position to describe the distribution of function zones in the form of a graph and complete the preliminary layout planning. For each node, we encode two pieces of information: the zone type and the location. At the same time, we preset the zong constraints of each area type and the types of objects that may appear in the 3D scene to ensure the rationality and authenticity of the farmland scene.
5. 2D Layout Generation and Optimization
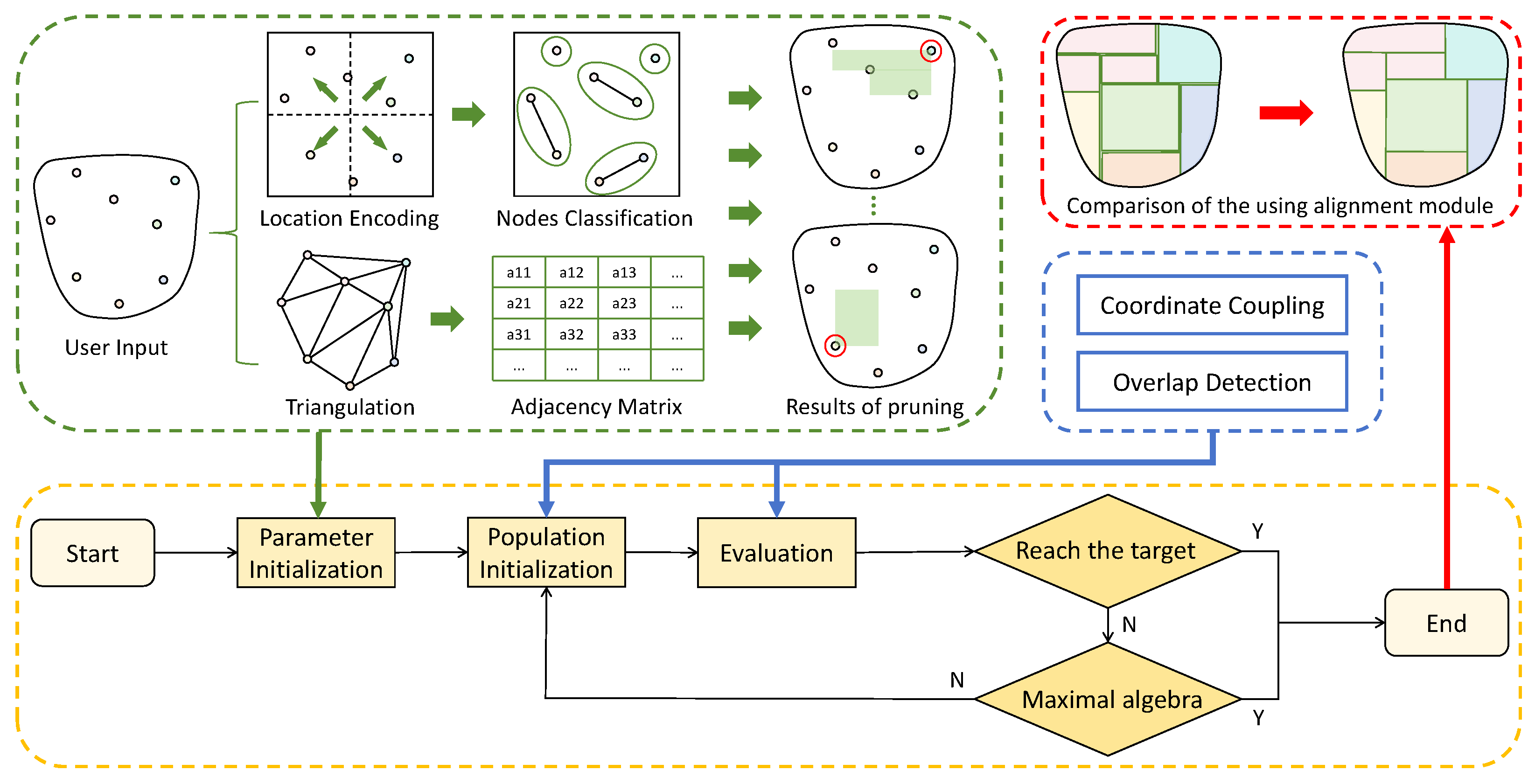
Since most of the zones in farmland have rectangular characteristics, we design a Graphics Guided Evolutionary Layout (GGEL) algorithm to better conform to the actual structure of the farmland scene. The algorithm flow is shown in
Figure 3.
5.1. Node Encoding and Graph Construction
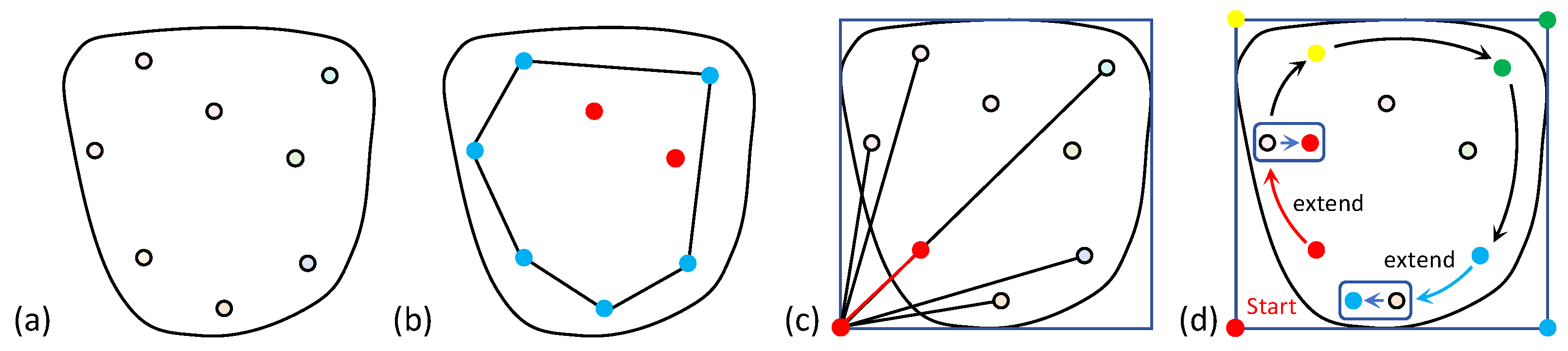
In order to clearly describe the spatial position of nodes, as shown in
Figure 4, we use the convex hull algorithm to classify nodes into external nodes and internal nodes, and then encode the orientation of the external points.
We first encapsulate the freehand boundary and nodes in the bounding box and extract the four corner coordinates of the bounding box. Then, the Euclidean distance between the external node and each corner point is calculated separately, and the node closest to each corner point is selected as the reference point. After that, the lower left reference point is taken as the starting point, and the convex hull boundary is traversed clockwise: if the external node is the reference point, the node is coded directly, otherwise the coding of the previous reference point is inherited.
Finally, we use the Delaunay triangulation to connect the nodes and construct a graph structure. At the same time, we build an adjacency matrix to record the adjacency relationship between nodes.
5.2. Layout Spatial Pruning
As shown in
Figure 5, we design the layout space pruning strategy according to the topological relationship of the graph nodes.
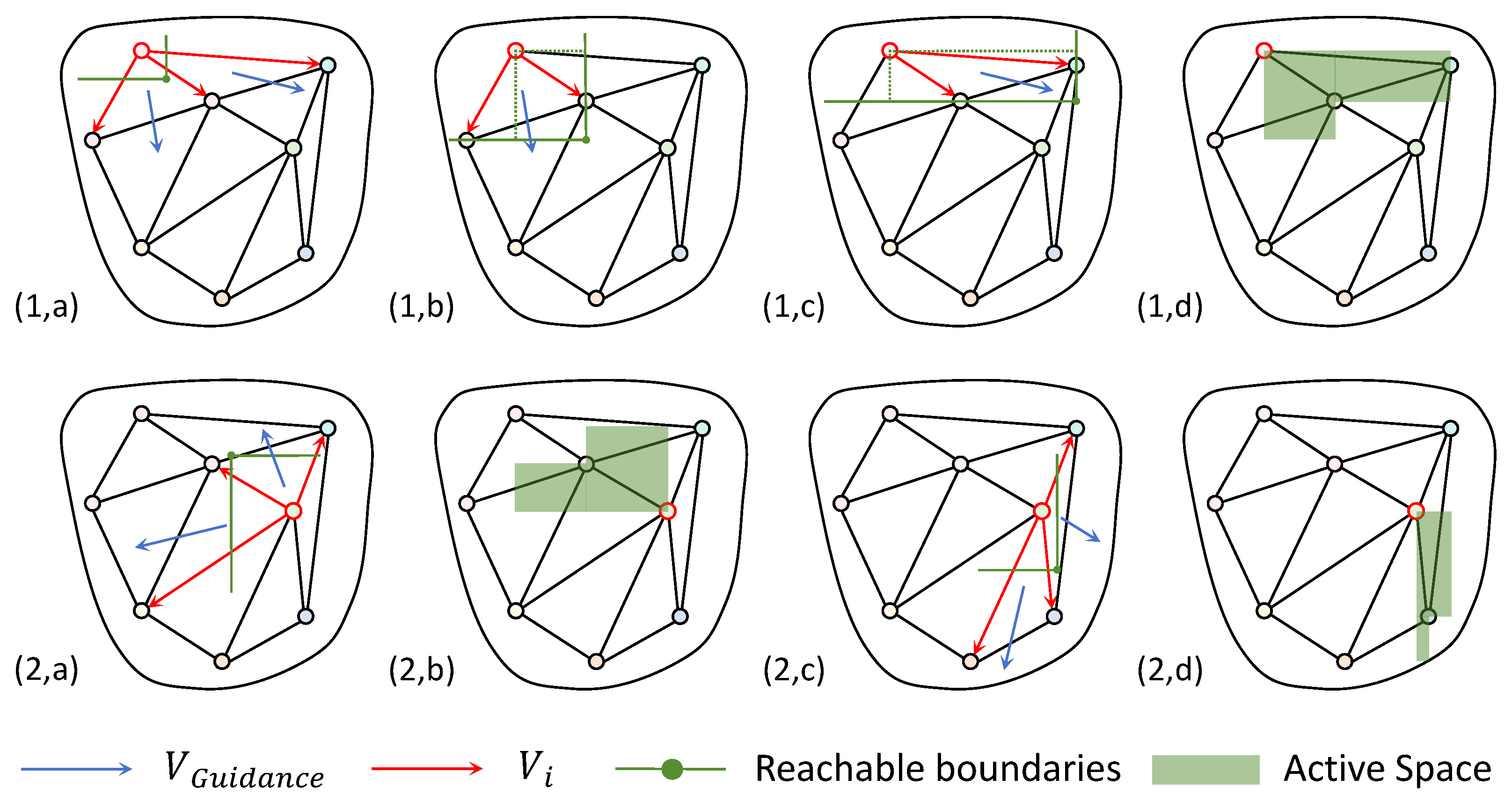
We first select two neighboring nodes of the target node and compute the normalized vector (red) starting from the target node, respectively. The resultant vector is then used as an attraction (blue) to continuously expand the activity space of the target node until it touches other nodes, reaching the farthest range of activity. Combine all the active ranges to get the layout range of the target node (green). Compared with the whole inner region of the freehand boundary, the layout range after pruning is greatly reduced, which not only improves the calculation efficiency, but also reduces the problem of overlapping functional zones.
5.3. Conditional Constraint
In order to avoid gaps or overlaps between functional zones, we design two constraint modules and one optimization module to ensure the rationality of layout generation.
Coordinate Coupling. In the process of layout generation, we detect the point coordinates in the generated layout in real time, according to the orientation of the nodes being coded, so that the last node in each direction has the same x or y coordinates as the first node in the next direction, ensuring that there is no gap between the outside area and its neighbors.
Overlap Detection. We use geometric conditions to compare the corner coordinates of any two zones, preserve the layout without overlapping regions, and further optimize the layout structure.
Zone Alignment. In order to optimize the layout, we traverse the boundary corners of the function zone in turn. If the difference between different x or y coordinate values is less than the threshold value, the corresponding coordinate values are set to be the same, effectively eliminating the gap between the regions.
5.4. Fitness Functions
We design a suitable fitness function to evaluate whether the generated layout is reasonable. In the desired optimal solution, all zones should avoid overlapping, and the total area of each zone should be equal to the area of the entire region. The fitness function is designed to minimize the area error, and the closer the value is to 0, the better the quality of the solution. The fitness function is defined as shown in Equation (
5):
where
is the set of zones.
is defined as the area where
i blocks overlap each other.
is the total area of
i blocks.
and
are weight coefficients used to adjust the impact of overlap area and total area on fitness.
OverlapArea Fitness. Functional zones should not overlap, and the fitness function of the overlap area is defined in Equations (6)–(8):
where
represents the area within the freehand boundary,
represents the vertex of
, judging the overlap according to whether
is inside
.
means there is one vertex in
, and
means there are two vertices in
.
TotalArea Fitness. Zones should be distributed as tightly as possible within the campus. Therefore, the total area fitness is defined as Equation (
9):
5.5. Interactive Layout Edit
We design an interactive editing module, which can adjust the layout according to the programmatic generated results to further optimize the overall layout. As shown in
Figure 6, users can edit road nodes independently to adjust the area. Specifically, we construct coupling matrices
and
for the
x and
y coordinates of road nodes, respectively, and assign the same labels to nodes with the same coordinate values. When a coordinate value changes, other coordinate values coupled with it in the
x or
y direction will also adapt to maintain the consistency of the layout. In addition, users can also edit the degree of curvature of regional boundaries to improve the authenticity of farmland scenes.
5.6. Experiments of EEGL
In order to prove the layout capability of EEGL in the farmland scene, we design experiments on the algorithm convergence speed and running time.
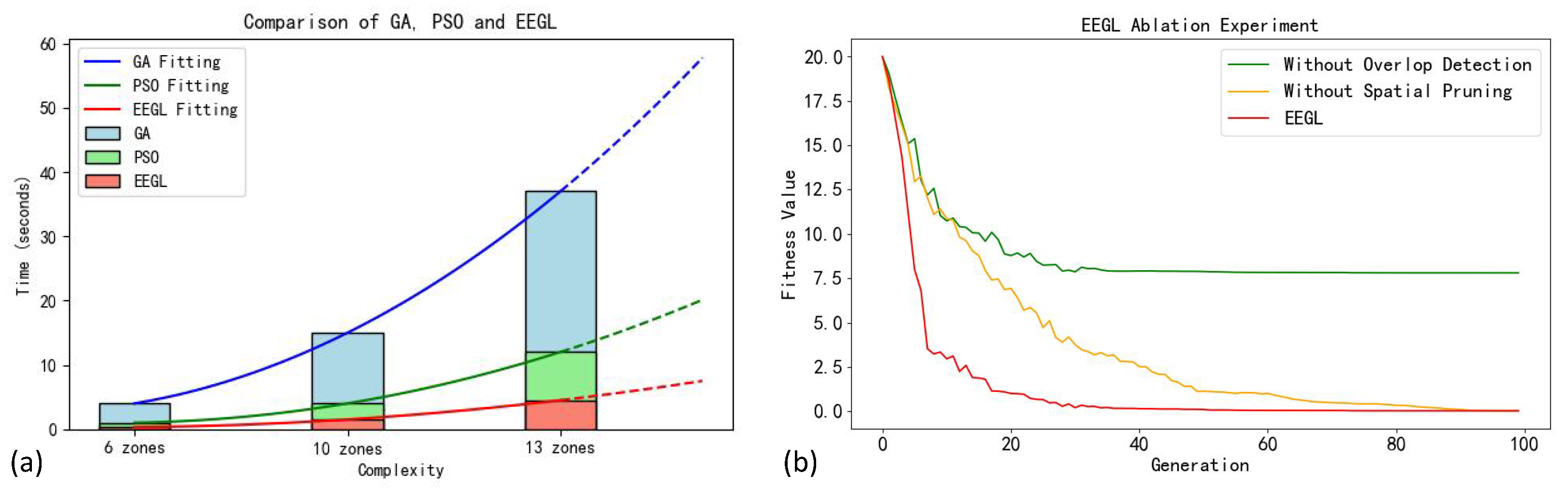
Contrast experiment for running time. We compare the operation time of EEGL, GA, and PSO under different numbers of zones. As shown in
Figure 7a, when the number of zones is small, the operation time of EEGL and PSO is similar and lower than GA. With the increase of the number of zones, the running time of EEGL increases gently and stays below 10 s, while the running time of GA and PSO increases rapidly, indicating that EEGL has the best time efficiency in large-scale farmland scene layout tasks.
Ablation experiment for convergence speed. As shown in
Figure 7b, we conduct ablation experiments on two modules of EEGL: overlap detection and spatial pruning. After removing the overlap detection module, the algorithm presents a downward trend similar to that of the complete EEGL in the initial stage, but in the later convergence process, the fitness value fails to reach the low point of the complete model, and the curve finally stabilizes at a higher fitness value. After the spatial pruning module is removed, the convergence speed of the algorithm in the early stage is significantly slowed down. Although the final fitness value can still reach a level similar to that of the complete EEGL, the convergence process is significantly prolonged. The ablation experiment results show that in the EEGL algorithm, the overlap detection module can ensure the rationality of the generated solution and reduce the unreasonable overlap between zones. The spatial pruning module greatly improves the computational efficiency and convergence speed of the algorithm. Multiple modules cooperate with each other and play an important role in the farmland scene layout task.
6. 3D Farmland Scene Generation
For different functional areas, we map the preset model to the actual layout to generate a preliminary farmland scene model. In addition, we have designed some procedural brushes that users can use to edit scene details and enhance the visualization of the model.
Plant Brush. We add four tree models to the system, allowing users to adjust the brush size and density according to their design needs, precisely controlling the distribution of vegetation.
Building Brush. There are three main buildings in the system, and users can adjust the position and orientation of individual buildings compared to plant brushes.
Pond Brush. The role of the pond brush is to change the height of the local terrain, and the user can freely adjust the size and force of the brush. In addition, we also provide a smoothness parameter to smooth terrain of different heights.
7. User Evaluation
7.1. Research Approach
The user study lasts approximately 1 h and is divided into three main parts.
System introduction. We introduce our system to each participant, and at the same time show some of the scene layouts generated by the system to give participants a clear visualization.
Task assignment. We assign each participant two tasks. Task 1: We present a farmland scene on Google Maps and ask participants to design a digital farmland scene based on the map scene. Task 2: We provide a farmland scene layout for participants to make creative designs, including but not limited to modifying boundaries, layouts, scene models, etc.
System feedback. Finally, we ask participants to complete a survey to collect their experience and feedback on using the system to assess the effectiveness of the system and user satisfaction.
We use a questionnaire to collect users’ subjective evaluations on three questions with 5-point Likert scale [where 1 = strongly disagree, 5 = strongly agree ] to evaluate the following: (1) users’ ability to successfully edit farmland scenes, (2) users’ satisfaction with the farmland scenes they created, and (3) users’ satisfaction with the real-time editing experience provided by our system.
7.2. Participant
This test involves 20 participants, aged between 20 and 50, including 13 males and 7 females. The participants come from diverse backgrounds, covering multiple professional fields. Specifically, 5 participants are graduate students in the field of computer graphics, while 4 are from non-graphics fields (including 2 from evolutionary computing and 2 from computer vision), 4 are experts in agricultural park planning, 5 are experts who are not only proficient in modeling but also possess a deep understanding of agriculture, and 2 are undergraduate students in computer science and technology. In the self-assessment of 3D modeling skills, 6 participants consider themselves novices, 6 are relatively familiar with 3D modeling, and 8 have extensive experience in 3D modeling, previously working on Unity Engine and Unreal Engine 4. Regarding the participants’ cognition of farmland scenes, 3 participants indicate that they have never seen farmland scenes, 6 have only learned about farmland scenes through videos and images, 7 have personally visited farmland scenes, and 4 are in charge of a farmland.
7.3. Research Result
In the first task, all participants successfully generated a digital farmland scene model based on a real scenario (
Figure 8). In the second task, all participants used the system to edit their own field scenes (
Figure 9). After all users complete the task, we collect the time spent by each user on each task. As first-time users of the system, they took slightly longer to complete, mainly due to differences in the level of refinement of the scene model. The results showed that the participants completed the first task in an average of 14 min and the second in an average of 6 min.
In the course of user research, we do not encounter any failures or unacceptable results. The qualitative evaluation shows that participants generally believe that our system has important practical value in the field scene design. Users also note that the system has a user-friendly interface and there is no delay during use. To further illustrate, we ask the following three questions and record participants’ responses: (1) “I can easily complete the task” (score:
= 4.50); (2) “I am satisfied with the modeling results of the farmland scene” (score:
= 4.45); (3) “I feel very creative” (score:
= 4.75).
Table 1 also provides a detailed summary of each participant’s information and the amount of time they spent on each task.
Participants also share some additional tips. Agricultural park planning experts believe that our system effectively solves practical problems in current farmland scene planning in terms of efficiency and visualization, and are highly satisfied with the layout generation results and time efficiency. In addition, two graduate students from the field of evolutionary computing showed great interest in our point mapping mechanism. Although they have no exposure to computer graphics and 3D modeling, they believe that the graph guidance has significant innovation potential and application value, and suggest further exploration of more application scenarios in the field of farmland scene designing. These recommendations are expected to significantly enhance the user experience. Based on this valuable feedback, we plan to further improve the system’s flexibility and user satisfaction.
8. Conclusions
In this paper, a farmland scene layout design system is proposed which successfully realizes the scene generation by user input and graph guidance. The experimental results of several key performance indicators show that the proposed EEGL is superior to the mainstream heuristic algorithm in convergence speed and running time, and interactive editing modules shorten the user’s time from design to implementation and enhance the convenience of the overall workflow. In addition, the scene generation quality and user experience also received positive feedback, providing a high standard and diversified digital modeling solution for modern farmland scene.
Looking forward, future work will include conducting longitudinal real-world case studies, combining Internet of Things (IoT) and unmanned aerial vehicle (UAV) technology to quantify the economic return on investment (ROI), such as evaluating the reduction in design time, improvements in space utilization and potential yield increases, and the lowering of planning costs. We will also expand the model to incorporate key agronomic factors including soil properties, fertility conditions, and crop rotation patterns, thereby enhancing the practical relevance and decision-support capability of the system in diverse agricultural settings.
Author Contributions
Methodology, G.L.; Software, G.L.; Writing—original draft, G.L.; Writing—review and editing, H.Y.; Funding acquisition, H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (No. 32472002); the Key Research and Development Program of Shaanxi province (No. 2023-YBNY-229, 2024NC-YBXM-197).
Data Availability Statement
Acknowledgments
We sincerely thank the anonymous reviewers and the editorial team for their valuable comments, which have greatly contributed to improving the quality of this article. We also thank the participants involved in software testing.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tutam, M.; White, J.A. Comparison of expected distances in traditional and non-traditional layouts. Asia-Pac. J. Oper. Res. 2024, 41, 2350024. [Google Scholar] [CrossRef]
- Tang, H.; Shao, L.; Sebe, N.; Van Gool, L. Graph Transformer GANs with Graph Masked Modeling for Architectural Layout Generation. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 4298–4313. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Lu, Z.; Xiao, J. DepthGAN: GAN-based depth generation of indoor scenes from semantic layouts. arXiv 2022, arXiv:2203.11453. [Google Scholar] [CrossRef]
- Nauata, N.; Hosseini, S.; Chang, K.H.; Chu, H.; Cheng, C.Y.; Furukawa, Y. House-gan++: Generative adversarial layout refinement network towards intelligent computational agent for professional architects. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 13632–13641. [Google Scholar]
- Hu, R.; Huang, Z.; Tang, Y.; Van Kaick, O.; Zhang, H.; Huang, H. Graph2plan: Learning floorplan generation from layout graphs. ACM Trans. Graph. (TOG) 2020, 39, 118. [Google Scholar] [CrossRef]
- Xu, L.; Xu, B.; Su, J. Facilities layout design optimization of production workshop based on the improved PSO algorithm. IEEE Access 2024, 12, 112025–112037. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Zhao, M.; Zhai, X. Optimization of planning layout of urban building based on improved logit and PSO algorithms. Complexity 2018, 2018, 9452813. [Google Scholar] [CrossRef]
- Jiang, L.; Ji, J.; Lu, Y.; Chen, Y.; Jia, Y. Mathematical modeling and simulated annealing algorithm for spatial layout problem. Clust. Comput. 2019, 22, 6383–6391. [Google Scholar] [CrossRef]
- Li, S.; Chen, S.; Zheng, Z. Intelligent indoor layout design based on interactive genetic and differential evolution algorithms. J. Adv. Comput. Intell. Intell. Inform. 2024, 28, 929–938. [Google Scholar] [CrossRef]
- Kumar, A.; Dutta, K.; Srivastava, A. Topological and Dimensional constraints based optimal placement of Layout Entities using Clustering and Genetic Algorithm. Appl. Soft Comput. 2023, 132, 109867. [Google Scholar] [CrossRef]
- Coelho, P.H.G.; do Amaral, J.F.; Guimarães, K. Use of Genetic Algorithm for Spatial Layout of Indoor Light Sources. In Proceedings of the 20th International Conference on Enterprise Information Systems (ICEIS 2018), Madeira, Portugal, 21–24 March 2018; pp. 456–460. [Google Scholar]
- Zhou, Y.; Rathore, A.; Purvine, E.; Wang, B. Topological simplifications of hypergraphs. IEEE Trans. Vis. Comput. Graph. 2022, 29, 3209–3225. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.L.; Yuan, X.F. StyleTerrain: A novel disentangled generative model for controllable high-quality procedural terrain generation. Comput. Graph. 2023, 116, 373–382. [Google Scholar] [CrossRef]
- Rogla, O.; Patow, G.A.; Pelechano, N. Procedural crowd generation for semantically augmented virtual cities. Comput. Graph. 2021, 99, 83–99. [Google Scholar] [CrossRef]
- Bulbul, A. Procedural generation of semantically plausible small-scale towns. Graph. Model. 2023, 126, 101170. [Google Scholar] [CrossRef]
- Benes, B.; Zhou, X.; Chang, P.; Cani, M.P.R. Urban brush: Intuitive and controllable urban layout editing. In Proceedings of the 34th Annual ACM Symposium on User Interface Software and Technology, Virtual, 10–14 October 2021; pp. 796–814. [Google Scholar]
- Liu, C.; Wu, J.; Furukawa, Y. Floornet: A unified framework for floorplan reconstruction from 3d scans. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 201–217. [Google Scholar]
- Wang, K.; Lin, Y.A.; Weissmann, B.; Savva, M.; Chang, A.X.; Ritchie, D. Planit: Planning and instantiating indoor scenes with relation graph and spatial prior networks. ACM Trans. Graph. (TOG) 2019, 38, 132. [Google Scholar] [CrossRef]
- He, F.; Huang, Y.; Wang, H. iPLAN: Interactive and procedural layout planning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 7793–7802. [Google Scholar]
- He, L.; Lu, Y.; Corring, J.; Florencio, D.; Zhang, C. Diffusion-based document layout generation. In Proceedings of the International Conference on Document Analysis and Recognition, San José, CA, USA, 21–26 August 2023; pp. 361–378. [Google Scholar]
- Xu, P.; Li, Y.; Yang, Z.; Shi, W.; Fu, H.; Huang, H. Hierarchical layout blending with recursive optimal correspondence. ACM Trans. Graph. (TOG) 2022, 41, 249. [Google Scholar] [CrossRef]
- Shabani, M.A.; Wang, Z.; Liu, D.; Zhao, N.; Yang, J.; Furukawa, Y. Visual Layout Composer: Image-Vector Dual Diffusion Model for Design Layout Generation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 9222–9231. [Google Scholar]
- Xiao, S.; Jiang, Z.; Yang, S. Tile Networks: Learning Optimal Geometric Layout for Whole-page Recommendation. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Virtual, 28–30 March 2022; pp. 8360–8369. [Google Scholar]
- Zhang, S.; Xu, R.; Quan, Y. Large graph layout optimization based on vision and computational efficiency: A survey. Vis. Intell. 2023, 1, 14. [Google Scholar] [CrossRef]
- Sepúlveda, G.K.; Romero, N.; Vidal-Silva, C.; Besoain, F.; Barriga, N.A. Semi-Automatic Building Layout Generation for Virtual Environments. IEEE Access 2024, 12, 87014–87022. [Google Scholar] [CrossRef]
- Wu, W.; Fu, X.M.; Tang, R.; Wang, Y.; Qi, Y.H.; Liu, L. Data-driven interior plan generation for residential buildings. ACM Trans. Graph. (TOG) 2019, 38, 234. [Google Scholar] [CrossRef]
- Hu, X.; Chuang, Y.F. E-commerce warehouse layout optimization: Systematic layout planning using a genetic algorithm. Electron. Commer. Res. 2023, 23, 97–114. [Google Scholar] [CrossRef]
- Jalayer, A.; Jalayer, M.; Khakzand, M.; Faizi, M. Automated Optimal Layout Generator for Animal Shelters: A framework based on Genetic Algorithm, TOPSIS and Graph Theory. arXiv 2024, arXiv:2405.14172. [Google Scholar] [CrossRef]
- García-Hernández, L.; Arauzo-Azofra, A.; Salas-Morera, L.; Pierreval, H.; Corchado, E. Facility layout design using a multi-objective interactive genetic algorithm to support the DM. Expert Syst. 2015, 32, 94–107. [Google Scholar] [CrossRef]
- de Almeida, A.; Taborda, B.; Santos, F.; Kwiecinski, K.; Eloy, S. A genetic algorithm application for automatic layout design of modular residential homes. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 002774–002778. [Google Scholar]
- Ying, S.; Jin, X.; Liang, X.; Han, B.; Liu, J.; Zhou, Y. Morphology’s importance for farmland landscape pattern assessment and optimization: A case study of Jiangsu, China. Appl. Geogr. 2024, 171, 103364. [Google Scholar] [CrossRef]
- Ju, X.; Liu, F.; Wang, L.; Lee, W.J. Wind farm layout optimization based on support vector regression guided genetic algorithm with consideration of participation among landowners. Energy Convers. Manag. 2019, 196, 1267–1281. [Google Scholar] [CrossRef]
- Gao, B.; Lu, A.; Pan, Y.; Huo, L.; Gao, Y.; Li, X.; Li, S.; Chen, Z. Additional sampling layout optimization method for environmental quality grade classifications of farmland soil. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5350–5358. [Google Scholar] [CrossRef]
- Ye, Y.; Sun, K.; Kuang, L.; Zhao, X.; Guo, X. Spatial layout optimization of urban space and agricultural space based on spatial decision-making. Trans. Chin. Soc. Agric. Eng. 2017, 33, 256–266. [Google Scholar]
- Dadi, P.S.; Tamilvizhi, T.; Surendran, R. Layout optimization for agriculture or small scale agrarian industry. In Proceedings of the 2022 6th International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 28–30 April 2022; pp. 174–179. [Google Scholar]
- Satake, T.; Satake, O.; Ohta, Y.; Furuya, T. Optimal Layout Design for Agricultural Facility Using Simulated Annealing. Agric. Eng. Int. CIGR J. Sci. Res. Dev. 2003, 5, 1–11. [Google Scholar]
Figure 1.
Users first sketch the boundary outline and arranges the functional zones into graph nodes. The system then generates an aligned 2D layout based on user input and layout strategy. Users can interactively edit and adjust 2D layouts. The system ultimately generates a 3D agricultural park scene from the optimized 2D layout and allows for further refinement of the scene appearance.
Figure 1.
Users first sketch the boundary outline and arranges the functional zones into graph nodes. The system then generates an aligned 2D layout based on user input and layout strategy. Users can interactively edit and adjust 2D layouts. The system ultimately generates a 3D agricultural park scene from the optimized 2D layout and allows for further refinement of the scene appearance.
Figure 2.
User Interface: The main panel provides the core area for interactive design and layout optimization, while the brush control panel offers multiple procedural 3D brushes with adjustable parameters. By selecting different editing modes from the “Mode” dropdown menu, users can freely switch between the Road Editor, Terrain Editor, Building Editor, and Plant Editor interfaces.
Figure 2.
User Interface: The main panel provides the core area for interactive design and layout optimization, while the brush control panel offers multiple procedural 3D brushes with adjustable parameters. By selecting different editing modes from the “Mode” dropdown menu, users can freely switch between the Road Editor, Terrain Editor, Building Editor, and Plant Editor interfaces.
Figure 3.
The Evolution module (yellow area) is the main part of the GGEL and controls the layout generation and optimization process. The topological awareness module (green area) processes user input by constructing a graph structure and using spatial pruning to simplify the calculation process. The constraint module (blue area) sets multiple constraints to oversee the generation of the layout. Finally, the layout results output by the algorithm are aligned (red areas).
Figure 3.
The Evolution module (yellow area) is the main part of the GGEL and controls the layout generation and optimization process. The topological awareness module (green area) processes user input by constructing a graph structure and using spatial pruning to simplify the calculation process. The constraint module (blue area) sets multiple constraints to oversee the generation of the layout. Finally, the layout results output by the algorithm are aligned (red areas).
Figure 4.
Using convex hull algorithm to distinguish between nodes and azimuth coding. (a) User input boundaries and nodes; (b) Determine the blue external nodes and the red internal nodes; (c) Use the boundary to determine the minimum bounding box and calculate the node closest to the lower left corner among the external nodes as the starting point; (d) Determine the positions of the four corners of the bounding box where the external nodes are located clockwise in sequence according to the distance.
Figure 4.
Using convex hull algorithm to distinguish between nodes and azimuth coding. (a) User input boundaries and nodes; (b) Determine the blue external nodes and the red internal nodes; (c) Use the boundary to determine the minimum bounding box and calculate the node closest to the lower left corner among the external nodes as the starting point; (d) Determine the positions of the four corners of the bounding box where the external nodes are located clockwise in sequence according to the distance.
Figure 5.
Examples of layout space pruning for external points and internal points. (1) Space pruning of external nodes, encourages nodes to explore the activity space around nodes as much as possible, where (1,a), (1,b) and (1,c) represent the guiding process and (1,d) represents the activity space of the node. (2) Space pruning of internal points, where (2,a) and (2,c) represent the guiding process while (2,b) and (2,d) represent the activity space of the node in the northwest and southeast directions respectively.
Figure 5.
Examples of layout space pruning for external points and internal points. (1) Space pruning of external nodes, encourages nodes to explore the activity space around nodes as much as possible, where (1,a), (1,b) and (1,c) represent the guiding process and (1,d) represents the activity space of the node. (2) Space pruning of internal points, where (2,a) and (2,c) represent the guiding process while (2,b) and (2,d) represent the activity space of the node in the northwest and southeast directions respectively.
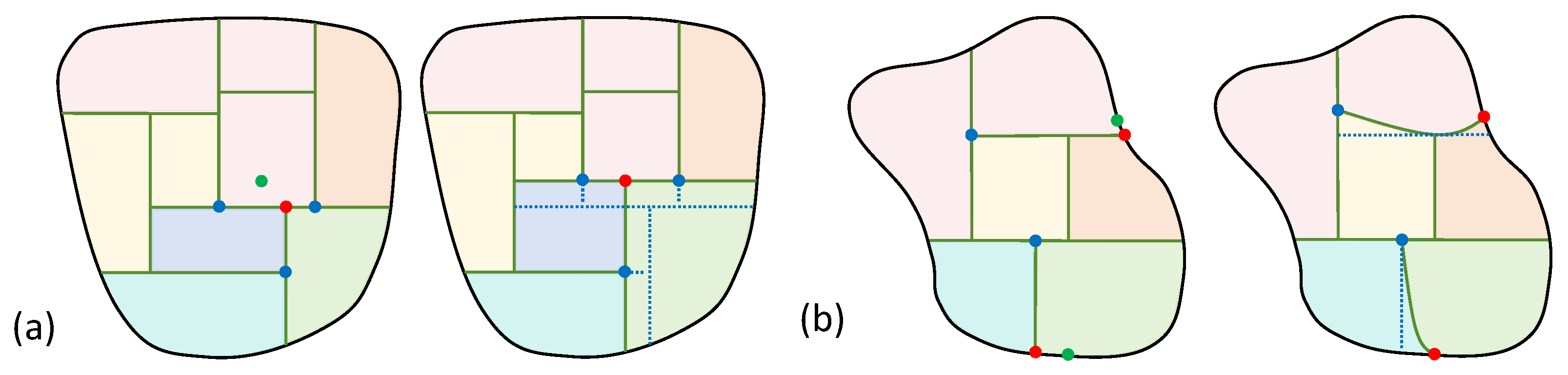
Figure 6.
Layout adjustments after programmatic generation. Among them, the red nodes are the nodes edited by the user, the green areas are the positions of the nodes after they are moved, and the blue nodes are the nodes associated with the edited nodes. (a) Internal node editing rules; (b) Boundary point editing rules.
Figure 6.
Layout adjustments after programmatic generation. Among them, the red nodes are the nodes edited by the user, the green areas are the positions of the nodes after they are moved, and the blue nodes are the nodes associated with the edited nodes. (a) Internal node editing rules; (b) Boundary point editing rules.
Figure 7.
(a) Ablation experiments of different modules in the EEGL model and (b) comparison of running time with the basic methods of GA and PSO.
Figure 7.
(a) Ablation experiments of different modules in the EEGL model and (b) comparison of running time with the basic methods of GA and PSO.
Figure 8.
The first task. The first image is an image of a farmland scene on Google Maps, where the red lines represent the external boundary, and the yellow lines represent the internal roads, while the others are designed by the participants based on that image.
Figure 8.
The first task. The first image is an image of a farmland scene on Google Maps, where the red lines represent the external boundary, and the yellow lines represent the internal roads, while the others are designed by the participants based on that image.
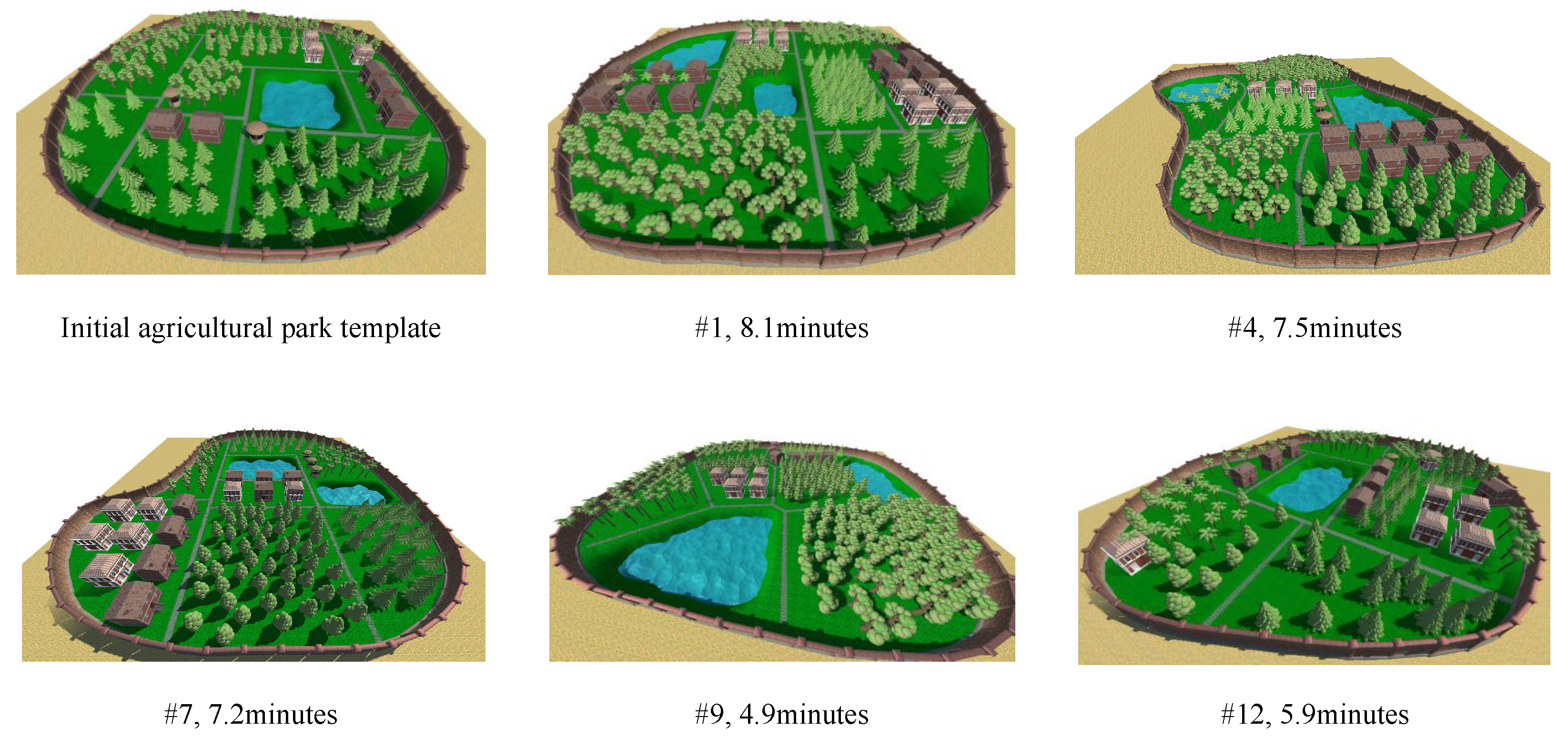
Figure 9.
The second task. The first image shows the layout of the farmland scene, while the other images show the participants’ designs. It is worth noting that User #4 modifies the boundary range, User #7 reduces the number of nodes, and User #9 changes the region boundary shape.
Figure 9.
The second task. The first image shows the layout of the farmland scene, while the other images show the participants’ designs. It is worth noting that User #4 modifies the boundary range, User #7 reduces the number of nodes, and User #9 changes the region boundary shape.
Table 1.
User information survey and the time spent on each task.
Table 1.
User information survey and the time spent on each task.
| User | Modeling | Agricultural | Task 1 | Task 2 | Q1 | Q2 | Q3 |
|---|
| ID | Experience | Cognition | Time [min] | Time [min] | | | |
|---|
| #1 | 1 | 1 | 14.8 | 8.1 | 4 | 4 | 4 |
| #2 | 0 | 0 | 11.3 | 6.9 | 5 | 3 | 4 |
| #3 | 1 | 2 | 12.7 | 5.4 | 5 | 4 | 5 |
| #4 | 1 | 2 | 13.6 | 7.5 | 4 | 5 | 5 |
| #5 | 0 | 0 | 18.3 | 6.3 | 4 | 3 | 5 |
| #6 | 0 | 2 | 16.4 | 6.2 | 4 | 5 | 5 |
| #7 | 1 | 2 | 17.9 | 7.2 | 5 | 5 | 5 |
| #8 | 0 | 1 | 15.1 | 6.8 | 4 | 4 | 5 |
| #9 | 0 | 0 | 17.6 | 4.9 | 3 | 3 | 4 |
| #10 | 2 | 2 | 12.5 | 6.9 | 5 | 5 | 5 |
| #11 | 0 | 1 | 13.6 | 4.1 | 4 | 5 | 4 |
| #12 | 2 | 3 | 12.3 | 5.9 | 5 | 5 | 5 |
| #13 | 3 | 1 | 11.8 | 4.9 | 5 | 5 | 5 |
| #14 | 3 | 2 | 10.3 | 6.1 | 5 | 4 | 5 |
| #15 | 2 | 3 | 13.7 | 6.4 | 5 | 5 | 5 |
| #16 | 3 | 1 | 13.6 | 5.4 | 4 | 5 | 4 |
| #17 | 2 | 1 | 12.3 | 5.3 | 5 | 4 | 5 |
| #18 | 1 | 3 | 16.8 | 5.9 | 5 | 5 | 5 |
| #19 | 1 | 3 | 14.1 | 7.1 | 4 | 5 | 5 |
| #20 | 2 | 3 | 15.3 | 6.8 | 5 | 5 | 5 |
| Avg | 1.25 | 1.65 | 14.20 | 6.21 | 4.50 | 4.45 | 4.75 |
| SD | 1.07 | 1.04 | 2.28 | 1.00 | 0.61 | 0.76 | 0.44 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).