Integrating Machine Learning and Sustainability in Nonwoven Production: A Case Study Using the FOREST Framework

Abstract

The environmental impact of industrial processes, especially regarding CO₂ emissions, requires innovative tools to monitor and optimize resource consumption. This study presents a data-driven approach for a carded nonwoven production line, aiming to support integration into the sustainability framework FOREST (Framework for Resource, Energy, Sustainability Treatment). Real process data from a pilot line were pre-processed, analysed, and used to train machine learning models to predict energy consumption across multiple production stages. Using techniques such as recursive feature elimination and SHAP value interpretation, the most influential parameters for each process step were identified. Extra Trees Regression proved to be the most accurate and explainable model across all scenarios. The results allow real-time estimation of the Product Carbon Footprint (PCF) based on process parameters and provide a foundation for energy optimization in nonwoven manufacturing.

1. Introduction

Carbon emissions are a significant contributing factor to climate change. The recent increase in global average temperature makes sustainability an important factor for industrial processes worldwide. Considering the role played by the generation of electricity in the emission of greenhouse gases, manufacturing processes can be made more sustainable through the reduction of energy consumption [1].

Transparency of industrial processes can be enhanced through digital solutions. Real-time data monitoring within a guiding framework supports the optimization of energy use and corresponding CO₂ emission reductions. The increased access to process information can then be leveraged for economic advantages and sustainability purposes.

The FOREST research project is a proposed framework for the connection of created process models. Using predictive models, the resulting energy consumption and greenhouse gas emissions can be tracked in real time to identify possible sustainability improvements [2]. This paper presents an algorithmic approach for the creation of data-driven models to predict the energy consumption of individual steps within a nonwoven manufacturing process. A total of nine models are trained to predict energy consumption of the eight identified steps of the examined process, with one additional model to describe the overall process. The data used to train each model must be carefully selected from the complete data set of measurements to provide accurate predictions. This paper showcases a data selection method which aims to ensure usability, relevance, and adequate representation of all data samples used for training and testing. All remaining features are ranked in order of importance as determined by a recursive feature elimination (RFE). The resulting information is used to define subsets of parameters with which the current prediction model is trained. The root mean square error (RMSE) is evaluated based on parameter subset and type of regression model. To avoid an excessive number of features, larger subsets are only used if they lead to a significant improvement in model accuracy. Shapley additive explanation (SHAP) values are applied to the created models to gain insight into the model predictions. It should be emphasized that SHAP values reflect correlations between input features and model outputs rather than causal relationships. The identified influences therefore provide transparency into model behavior but cannot be interpreted as evidence of physical causality.

2. Background

While the physical steps of the nonwoven production process are well established in industry, recent academic efforts have focused on modelling individual stages to enhance process transparency, efficiency, and sustainability. Common approaches include the use of first-principle models to simulate material flow and machine behavior [3], as well as empirical models based on statistical correlations [4]. Researchers such as [5] have used regression techniques to predict energy usage in thermobonding or needling processes, while others [6] applied machine learning methods like support vector regression (SVR) or artificial neural networks (ANNs) to estimate production quality or failure risks in continuous textile processes [7]. However, few studies have systematically compared different regression techniques with explainability in mind or embedded them within a larger digital framework that supports sustainability evaluation. The present work addresses this gap by developing interpretable machine learning models for each process step, enabling energy prediction and potential integration into a system-level digital twin architecture.

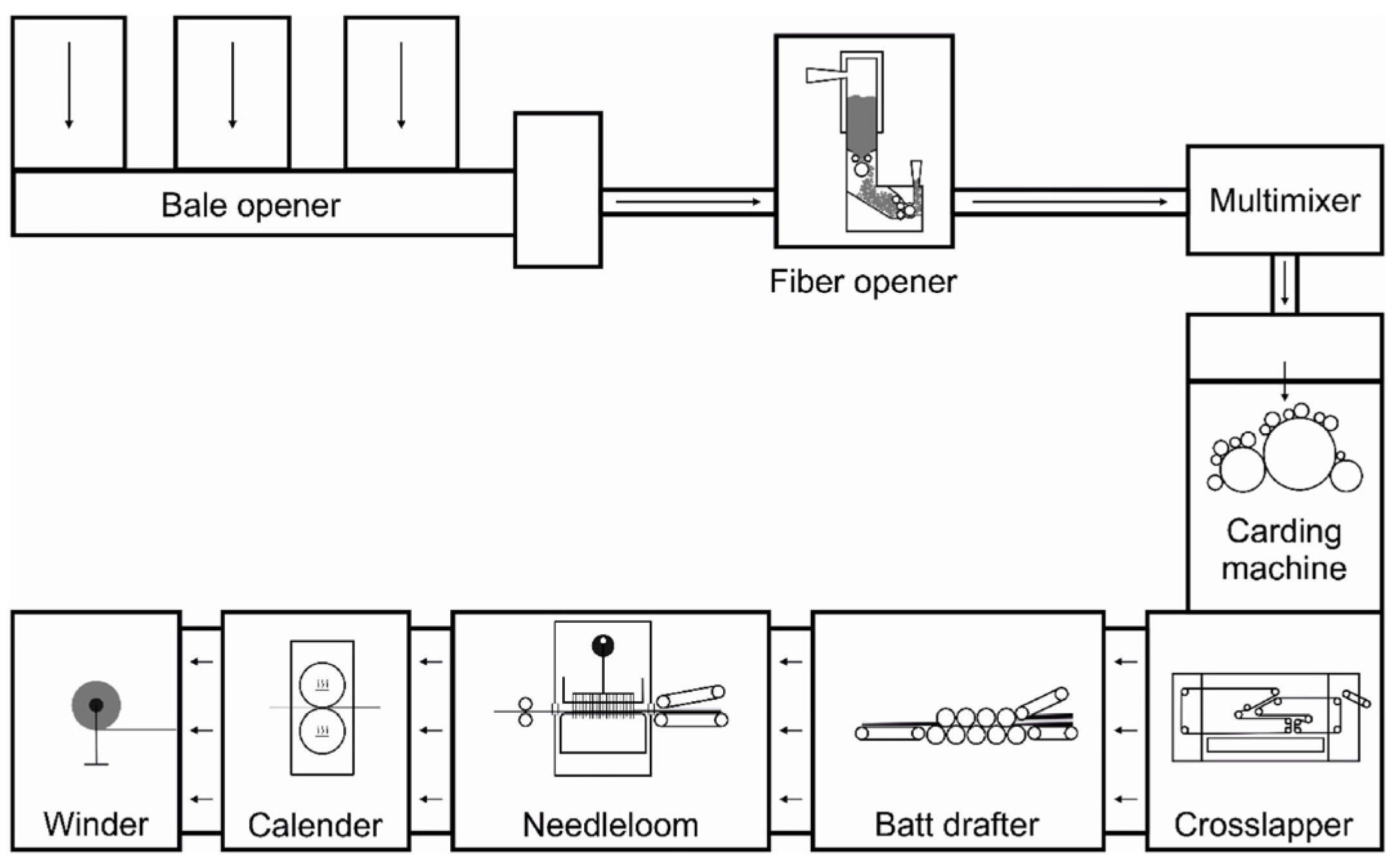
The production process is briefly outlined in Figure 1. From its delivery in bales, the nonwoven material can be followed as it undergoes every manufacturing step.

The fiber is opened and fed into a carding machine, after which it passes through a cross-lapper and a batt drafter. The resulting web is mechanically bonded by a needle-loom and thermally bonded by a calender. Finally, the finished web is laid onto a winder.

3. Materials and Methods

All models are based on process data provided by an undisclosed industry partner. The data set containing the full data of measurements from the nonwoven manufacturing process is available on request, in addition to the code used to filter the data and train the models. Python 3.13.7 libraries were used within the model creation, including lazypredict, pandas, shap, and scikit-learn [9,10,11].

Generative artificial intelligence was used during the creation of the algorithms for assistance in correcting coding and syntax errors.

3.1. Data Selection

The complete measurement data set contains recordings from a wide range of parameters. A variety of nonwoven products were manufactured during the duration of measurement. The momentary electrical energy consumption is recorded for each process step and will be used as the target variable for the corresponding machine learning model. In the data set, the energy consumptions of bale opener, fiber opener, and multimixer are combined into one step. The following section will focus on defining a procedure to extract subsets of this data which are appropriate for training and testing each of the predictive models. Criteria are defined to remove certain samples or parameters from consideration. To avoid inadvertently removing any parameters with established relevance to a model, exact parameter names can be manually entered into a list to override the automatic selection process. The override is used in this specific nonwoven manufacturing process for the recorded winding length of the winder. This parameter certainly has relevance to the behavior of the winder but would normally be removed due to its low number of recorded entries.

An immediate criterion by which to select useful data is the presence of an entry for the target value. In this case, the target value is momentary energy consumption. Since measurement samples for which this value has not been recorded cannot be used for model training or evaluation, they are consequently removed from further consideration. The process data is influenced by the current state of production. Measurements collected during cleaning or maintenance have different values compared to those recorded during production. The focus of the models created in this paper is on an accurate prediction of the production process. For this reason, the data is further reduced by discarding all samples not recorded during active production.

Each model should be trained using parameters which have relevance to the corresponding process step. In the provided data set, such information is contained within the names of the recorded parameters. This can be used to attribute parameters to a process step by manually examining recurring strings, such as “BOe” for parameters pertaining to the bale opener. The assignment is performed separately for each process step, ensuring that the resulting data sets include no parameters that do not have relevance to the respective process step. In the case of the model of the fiber transport system and that of the entire process, no strings are identified as belonging specifically to those models. Therefore, the removal of parameters from other steps is skipped, removing no parameters from consideration for either of the models.

The data used for model training should be representative of the overall process. The proportion of data samples from each manufactured product type within the data sets used for training and testing must therefore be the same as or similar to that of the overall usable data set. For this reason, the total available data of each specific product type are individually processed and split into training and test subsets. In this case, 70% of the data are allocated to training while the remaining 30% are kept for model evaluation. This 70/30 split is a widely adopted practice in machine learning as it provides a balanced compromise between sufficient data for model learning and an adequately large, independent test set for evaluating model performance and generalizability. The subsets are iteratively combined to construct the total set of training and test data to be used for the final models, thereby ensuring that the full resulting training data set contains 70% of the data for each type of product.

All remaining empty entries must be cleared from the data set before a regression model can be trained. Removing all samples containing one or more parameters with no recorded value at this stage would cause an excessive loss of otherwise usable data. Within the original data set, there are a small number of parameters for which comparatively few measurements exist. An example is the winding length of the winder mentioned in the introduction of this section. Of the 152,762 recorded samples in the original data set, only 35,397 contain any measurement for the winding length. For models where this parameter has not been previously excluded, such as the fiber transportation model or the full process model, most of the samples would be dropped based on this parameter alone. Parameters with a high number of missing entries should be removed without compromising the representative proportion of data from specific articles. To achieve this, a simple rule is defined that any parameter is only kept if it contains more than 50% non-empty entries for at least half of all product data subsets. This ensures that potentially relevant parameters can still be kept if they have very few empty entries and that data samples are not unnecessarily dropped. After the identified parameters have been removed, the remaining data set is cleared of all samples that have any empty entries.

A final step of the data selection process removes parameters where a low proportion of unique values has been recorded. The data set contains several parameters which have a value that is constant throughout the entire measurement timeframe and can thus not be meaningfully used in the creation of a model. Other parameters contain numbers corresponding to a mode of operation with no direct relation between their value and any physical quantity. A threshold of 1% is chosen to remove such parameters without overly reducing the available data. This threshold means that a parameter is kept if it contains at least one unique value for every 100 samples. The proportion of unique values is preferred over a flat variance threshold due to the difference in size of the measurements between the parameters.

This selection procedure is applied to each process step to extract fully usable data sets for the training and testing of each prospective model. The resulting data sets will be used in the following section to examine how model accuracy depends on the type of regressor trained and the subset of parameters used. These two factors will be independently examined in the following section.

3.2. Selection of Regressor Models and Parameter Subsets

A list of common scikit-learn regressor models is defined and can be iterated through using the Python library Lazy Predict. This library is chosen because it produces a table of direct comparisons between the resulting RMSE values of different regressors. Furthermore, its source code is easily modifiable to allow for comparisons between higher order linear regressions or Extra Trees Regressions of a custom maximum depth. The list of regressors examined includes:

• Ridge regression
• Lasso regression
• Linear regressions (LR) of order 1, 2, and 3
• Extra Trees Regression (ETR) of maximum depth 5, 10, 15, and unlimited

Deep learning techniques were not prioritized in this study due to the moderate dataset size and the need for interpretability. While they may provide advantages for very large datasets, ensemble tree-based methods offered the best compromise between accuracy and transparency for the available data. Future studies could explore neural networks once larger and more heterogeneous datasets are accessible. Although more complex methods such as Support Vector Regression (SVR) or Artificial Neural Networks (ANNs) are common in manufacturing applications, they were not prioritized in this study due to (i) higher computational cost for benchmarking across many parameter subsets and (ii) lower model interpretability in an industrial setting. In contrast, Extra Trees Regression (ETR) consistently yielded the lowest RMSE across tested subsets while remaining compatible with post-hoc explainability (SHAP), offering a favorable balance of accuracy, efficiency, and transparency. This motivated the choice of ETR as the default regressor for all models.

The table returned by the Lazy Predict algorithm contains the RMSE value achieved for each model. It remains necessary to further define a list of parameter subsets from which to choose a suitable subset to be used for the predictions. As the analysis of models for all possible subsets of up to 117 parameters is not computationally feasible, only the subsets containing the most important parameters are considered. Beginning with only the most important parameter, each following subset additionally includes the parameter with the next highest importance. This reduces the number of subsets to be equal to the number of parameters. It should be noted that this method can include highly correlated parameters within the same subset. The ranking order of the most significant parameters is created through a recursive feature elimination (RFE) which uses an Extra Trees Regressor to determine feature importance for all process steps with each respective set of relevant parameters. Independently of the automated ranking, factors with high expected influence on process steps are manually determined based on prior knowledge of the nonwoven manufacturing process. This information is used to validate the ranking order returned by the RFE in a manual review.

Once the relative importance of parameters has been established and deemed accurate, regression models are created from all defined subsets using all selected regressors. This is done through a further modification of code from the Lazy Predict library to iterate through all subsets of parameters for each process step. The following section will focus on selecting a suitable pair of regressor and subset from the evaluations that minimizes the RMSE without including an unnecessarily large number of parameters in the final model. The root mean square error (RMSE) is calculated as:

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2}$$

where $y_i$ represents the observed values, ${\widehat{y}}_i$ the predicted values, and n the number of samples. In this context, a small RMSE indicates that the predicted energy consumption values are close to the actual measurements, suggesting good model accuracy and reliable forecasting performance. Conversely, a large RMSE reflects a higher deviation between predictions and observations, meaning that the model has limited predictive capability and reduced applicability for forecasting.

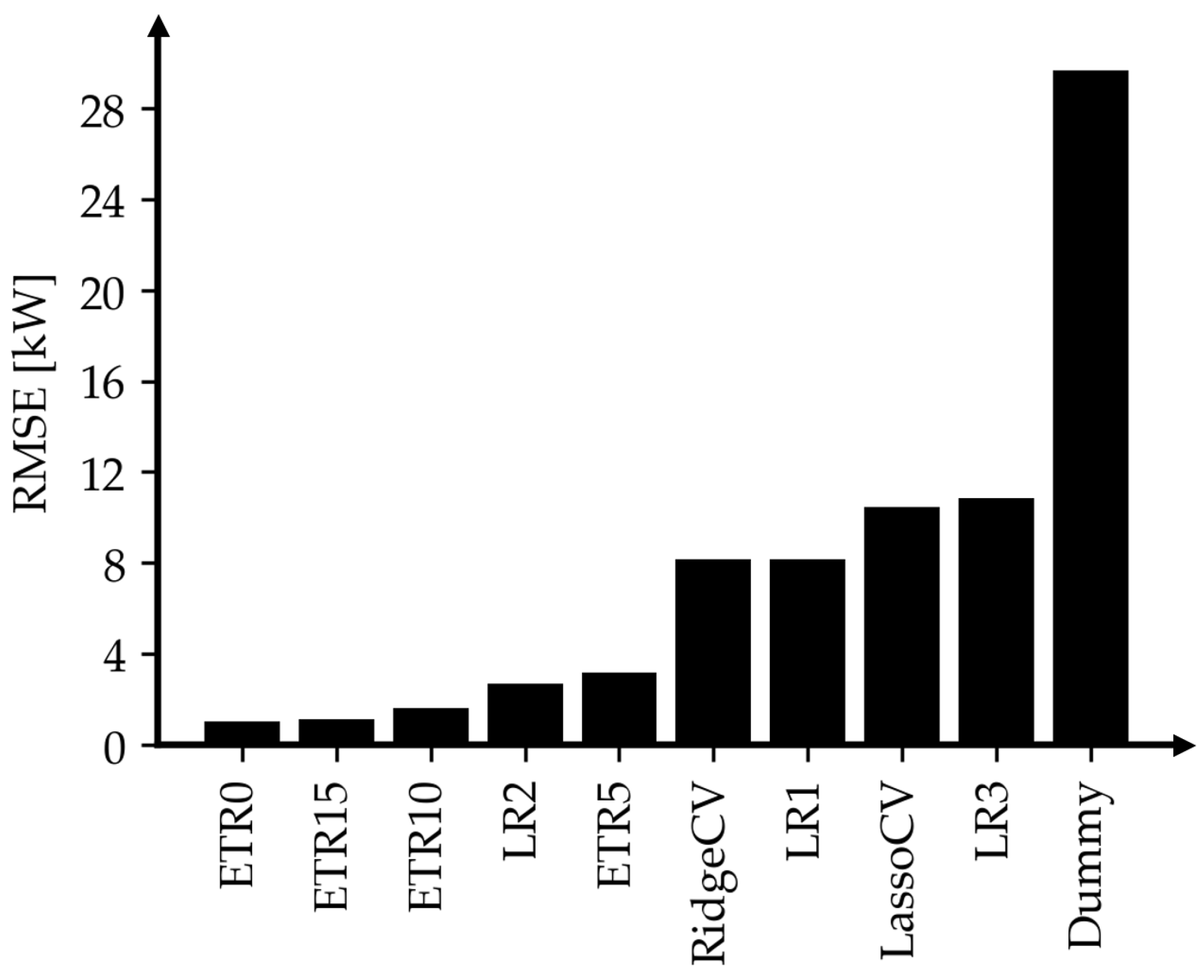
An exemplary comparison of RMSE values by regressor type for the subset containing 25 parameters can be seen in Figure 2.

By examining the regressor types in order of RMSE for all tested parameter subsets, it quickly becomes clear that an ETR has the lowest error rate in every case. In particular, the RMSE tends to be lowest with a higher limit on maximum fitting depth. However, a later explanation of the models with SHAP values is only possible for a maximum depth of up to 15 due to computational restrictions. The ETR models with this constraint still outperform other regressors for all subsets. For this reason, an ETR of maximum depth 15 is chosen as the basis of all further models.

The second degree of freedom to be fixed is the subset of parameters to be used. The RFE ranking order, and therefore the list of possible subsets, is different for all process steps. A method is devised that can be generally applied to the RMSE data of all respective subsets for all process steps with the aim of including all parameters which significantly reduce the RMSE. A significant reduction is defined as at least 1% of the RMSE of a model created using only one parameter. Beginning from the smallest error value and iteratively decreasing the number of included parameters, the first significant increase in RMSE due to an excluded parameter is marked as the number of parameters to select. This procedure is illustrated in Figure 3 for the carding machine model.

In the above example, the use of subsets with parameter counts higher than 12 have no significant impact on the achieved RMSE. The subset containing 12 parameters is therefore chosen as it is the last occurrence of an additional parameter significantly improving model performance. The resulting number of chosen parameters is compared to the total parameter count for each process step in

Table 1. Selected number of parameters with total parameter count by process step.

Process Step	Chosen Parameter Count	Chosen RMSE	Parameter Count at Minimal RMSE	Minimal RMSE
Opener	9	0.4512 kW	32	0.1974 kW
Carding machine	21	1.2168 kW	43	1.0361 kW
Cross-lapper	5	0.2289 kW	9	0.2241 kW
Batt drafter	6	0.0050 kW	7	0.0045 kW
Needle-loom	12	1.2986 kW	22	1.0974 kW
Calender	10	0.0597 kW	10	0.0597 kW
Winder	3	0.0941 kW	3	0.0941 kW
Fiber transportation	27	3.3199 kW	48	2.3916 kW
Full process	13	6.0485 kW	46	4.3924 kW

. This method reduces the number of parameters to consider without significantly raising the RMSE beyond the minimal value.

3.3. Interpretation of Created Models

Each process step has been modelled using appropriate data with a selected regressor and a suitable set of parameters. For a meaningful evaluation of the created models, the absolute RMSE values are compared with those of a dummy regressor provided by scikit-learn. The dummy regressor assumes that the target value is equal to the mean of the target value training data regardless of any given parameters. Its RMSE value can be compared with the trained regressors to account for the variance within the recorded target values and the uneven distribution of energy consumption among the steps of the process.

4. Results

The model creation process described in this paper produces nine unique Extra Trees Regression models which predict the energy consumption of each process step based on provided measurements for the input parameters.

Each model is compared to a dummy regression model of the same target value to determine the suitability of the creation process. An overview of the created models and their respective root mean square error (RMSE) value compared to the test data can be found in

Table 2. Resulting model accuracy for each modelled process step.

Process Step	Parameter Count	Dummy RMSE	Model RMSE	Proportion of RMSE Reduction
Opener	9	20.3509 kW	0.4512 kW	2.22%
Carding machine	21	29.6581 kW	1.2168 kW	4.10%
Cross-lapper	5	2.0602 kW	0.2289 kW	11.11%
Batt drafter	6	0.2542 kW	0.0050 kW	1.97%
Needle-loom	12	25.4130 kW	1.2986 kW	5.11%
Calender	10	1.3323 kW	0.0615 kW	4.62%
Winder	3	0.3104 kW	0.0941 kW	30.32%
Fiber transportation	27	61.3879 kW	3.3199 kW	5.41%
Full process	13	136.9950 kW	6.0485 kW	4.42%

.

The resulting RMSE values are further compared to the mean energy consumption for each process step in

Table 3. Model RMSE compared to mean power consumption.

Process Step	Mean Consumption	Model RMSE	Proportion of RMSE to Mean Value
Opener	26.0189 kW	0.4512 kW	1.7341%
Carding machine	36.1398 kW	1.2168 kW	3.3669%
Cross-lapper	3.4481 kW	0.2289 kW	6.6384%
Batt drafter	0.4519 kW	0.0050 kW	1.1064%
Needle-loom	30.8915 kW	1.2986 kW	4.2037%
Calender	1.6720 kW	0.0615 kW	3.6782%
Winder	1.6593 kW	0.0941 kW	5.6711%
Fiber transportation	82.4206 kW	3.3199 kW	4.0280%
Full process	183.9174 kW	6.0485 kW	3.2887%

.

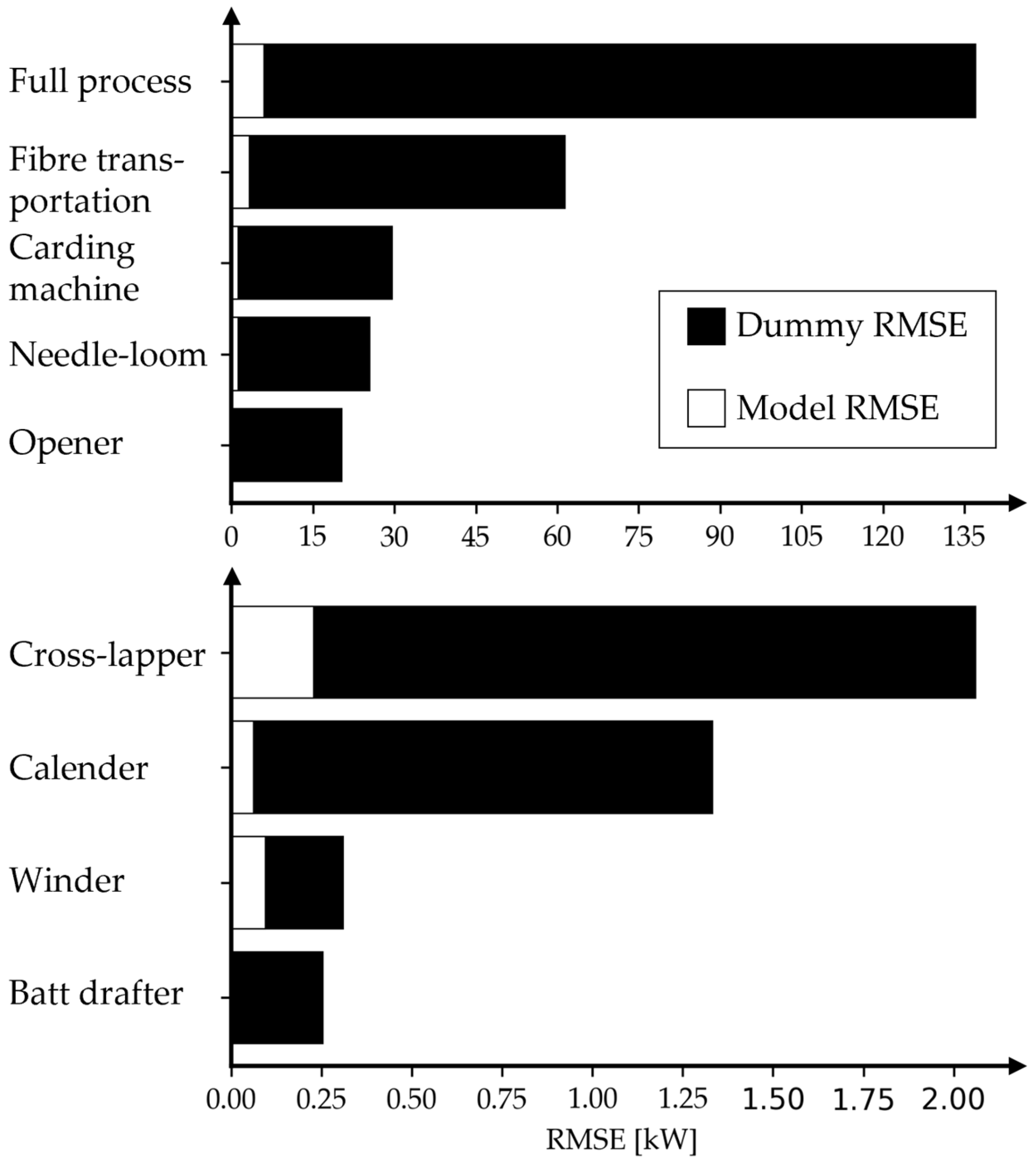
To complement the tabular results, Figure 4 illustrates the absolute RMSE values of the models in comparison to the corresponding dummy regressors, providing a visual representation of the prediction accuracy across all process steps.

Shapley additive explanations (SHAP) are used to gain further insight into the behavior of the created models. As the chosen regressor for all models was an Extra Trees Regressor, the calculations are performed using the TreeExplainer class of the shap Python library. Each set of SHAP values shows the relation between input feature values and the predicted values in the model output. It should be emphasized that SHAP values capture correlations between input features and predictions, not causal relationships. Future studies could integrate causal inference methods or controlled experiments to validate whether identified features are true causal drivers of energy consumption.

5. Discussion

The comparatively lower accuracy of the winder model underscores the impact of data limitations in industrial practice. With few process-specific parameters and a restricted number of complete samples, the model’s predictive power was constrained. Two main factors contributed to this outcome: (i) only a limited set of winder-specific parameters was available in the data set, reducing the information content for training, and (ii) comparatively few samples contained all relevant parameters, further restricting model development. These limitations reflect issues of data quality and coverage rather than shortcomings of the applied modeling approach. Nevertheless, the absolute error value of the winder model remains the third lowest among all created models, indicating that the predictions retain practical utility. To address these limitations, several strategies could be employed: (i) installing additional winder-specific sensors to capture relevant variables, (ii) improving data acquisition routines to ensure more complete and consistent sampling, (iii) applying data augmentation or transfer learning techniques to expand the training set, and (iv) integrating machine learning with first-principle models in a hybrid framework to compensate for sparse or incomplete data. Such measures would enhance prediction accuracy and support the practical deployment of the models in industrial environments.

Although the RFE method successfully identified influential features, it did not always eliminate redundancy among correlated inputs. Future work should therefore incorporate correlation analysis or dimensionality reduction techniques to streamline feature sets and further improve model efficiency. Subsets of parameters for model training derived solely from RFE may include interdependent features, inflating the number of required inputs without proportionally improving predictive accuracy. Correlation checks or dimensionality reduction could help to mitigate this issue.

While SHAP values provide transparency regarding the influence of parameters on model outputs, they should not be interpreted as evidence of causality [12]. SHAP values capture correlations between features and predictions, but they do not establish direct cause–effect relationships. This limitation is particularly evident in the full-process model, where the inclusion of broadly defined parameters introduces variables with weak causal links to total energy consumption. By contrast, the narrower parameter selection in models of individual process steps constrains the input space to more relevant features, thereby improving interpretability. Future research could validate causal relationships by combining SHAP analysis with domain-specific physical models, controlled experiments, or causal inference techniques.

Overall, the presented data selection method and modeling procedure can be adapted to similar data sets from other manufacturing processes. The workflow of systematically comparing regression models and parameter subsets is broadly applicable and can facilitate the integration of machine learning into sustainability-oriented frameworks.

Compared to first-principle models, which require detailed physical parameterization and are computationally intensive, the proposed data-driven approach enables rapid, real-time predictions based on readily available process data. Unlike empirical correlations, which are often restricted to narrow operating ranges, the machine learning models generalize across multiple conditions and production steps. Moreover, the integration of SHAP-based interpretability ensures that predictions can be linked back to influential process parameters, bridging the gap between empirical simplicity and physical transparency. These advantages highlight the potential of the presented approach to complement—and in some contexts, outperform—traditional modeling techniques for energy prediction and sustainability management.t.

6. Summary and Outlook

Each created model has an RMSE value that is substantially reduced compared to the simple RMSE of the corresponding dummy regressor. The absolute model RMSE does not exceed the order of 1 kilowatt for any model. An overview of RMSE values compared to the dummy regressor for the corresponding step can be seen in Figure 4. The exact data is recorded in Table 3.

In the case of the winder, a greater reduction may be achieved by taking more measurements specific to the corresponding process step.

The selection method for parameter subsets could take correlations of parameter values into account and remove redundant features from the models. The reduction of required measurement inputs would additionally simplify the practical application of the created models.

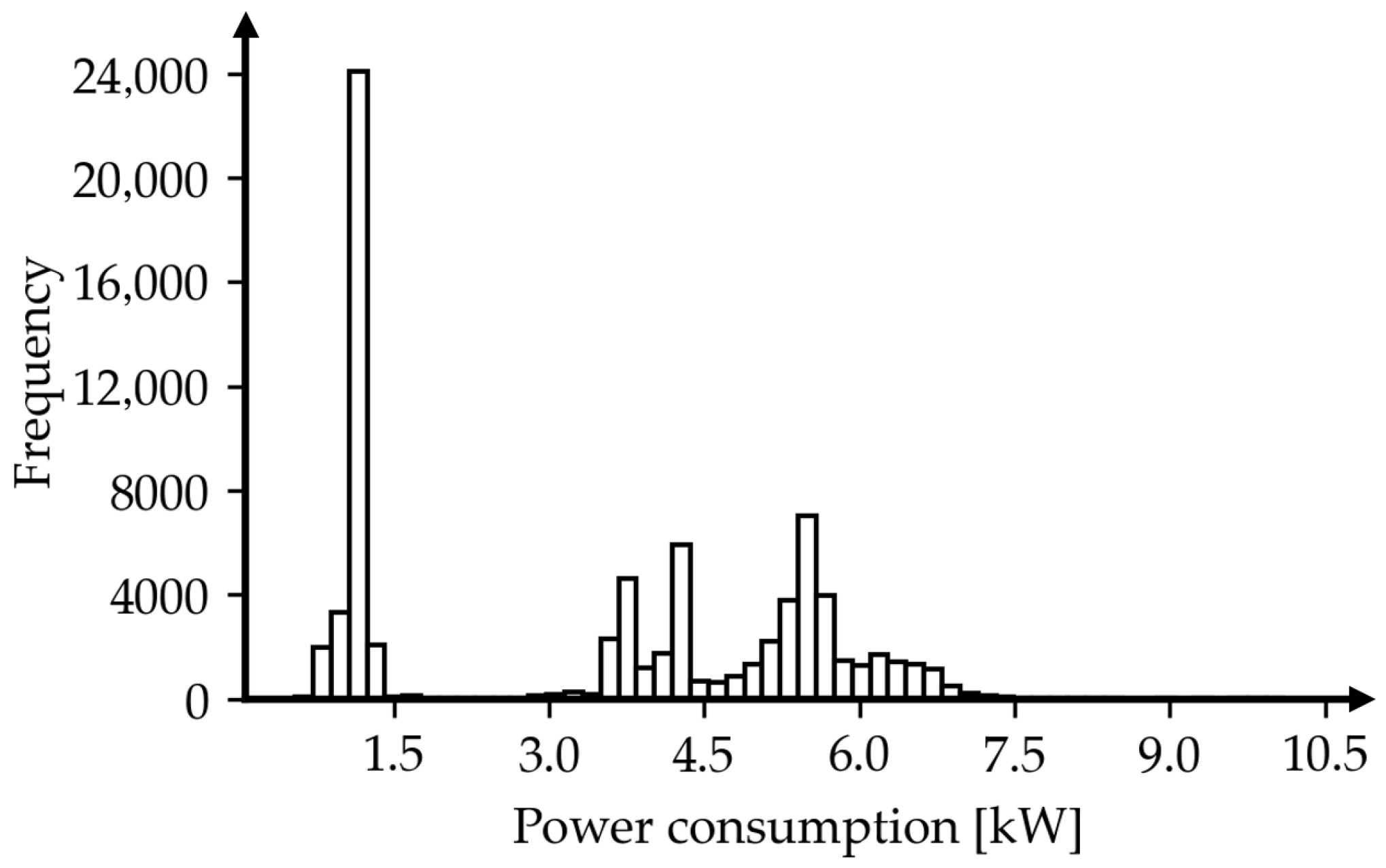
Another aspect of the filtered data set that may be considered is the distribution of values within the target column. A histogram of recorded power usage for the cross-lapper is shown in Figure 5.

Although only production data has been selected, there is a clear division of high and low values. Similar distributions are observed in the production data for all recorded measurements. To account for the distribution, a classification algorithm could be applied to the data to sort it into categories not explicitly recorded during the measurements.

The developed models can be embedded in industrial systems such as MES dashboards or PLC controllers to provide live forecasts of energy demand. Within digital twin architectures, they can be linked with sustainability indicators such as carbon footprint to support real-time optimization and scenario analysis. This integration offers industries a practical pathway to implement energy-aware and sustainable manufacturing practices. Beyond standalone model evaluation, a key opportunity lies in embedding these predictive models into existing industrial systems such as Manufacturing Execution Systems (MES), programmable logic controllers (PLCs), or digital twin platforms. Such integration would allow live predictions of energy consumption during production and enable real-time feedback loops for process optimization. For example, PLCs could directly adjust machine settings based on model forecasts, while MES dashboards could visualize predicted energy consumption to support operator decisions. Within a digital twin environment, the models could be coupled with first-principle simulations and sustainability metrics, enabling scenario testing and optimization of both energy efficiency and carbon footprint. These pathways highlight the potential of the presented approach not only as an analytical tool but as a building block for smart, energy-aware manufacturing systems. Further improvements to model accuracy could be made by incorporating results from the regression models into predictions made by first-principle models. A possible implementation is to fuse both energy consumption predictions with a weighting mechanism.

Although the workflow originates from applications in the paper industry [13], it has been successfully transferred to a nonwoven production line in this study. The generic procedures for data selection, regression benchmarking, and feature interpretation are not industry-specific and can be adapted to other manufacturing domains as long as process-specific data are available, making the approach broadly applicable to sustainability-oriented production.