Residential Load Flow Modeling and Simulation
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Research Gaps
1.4. Contributions
- Development of line models for single-phase two-wire, single-phase three-wire, and three-phase four-wire installation systems suitable for load flow calculations in various types of installations, such as smart homes across Taiwan, America, and Europe. Measurements used to determine the series and shunt parameters of residential wiring sections validate the modeling of home electrical networks.
- Prosumer-based models for single-phase and three-phase DGs, as well as Electronically Coupled Distributed Generators (ECDGs), have been developed and integrated into the load flow framework. These models incorporate advanced control strategies to represent the behavior of ECDGs more accurately within residential energy systems.
- A comprehensive load flow methodology and simulator tailored for smart home networks has been developed using the proposed network models. To achieve more realistic test scenarios, measurements of various household electrical appliances have been incorporated into the load flow simulator. The developed simulator constitutes a versatile platform for the evaluation of additional models and scenarios in the context of future experimental studies.
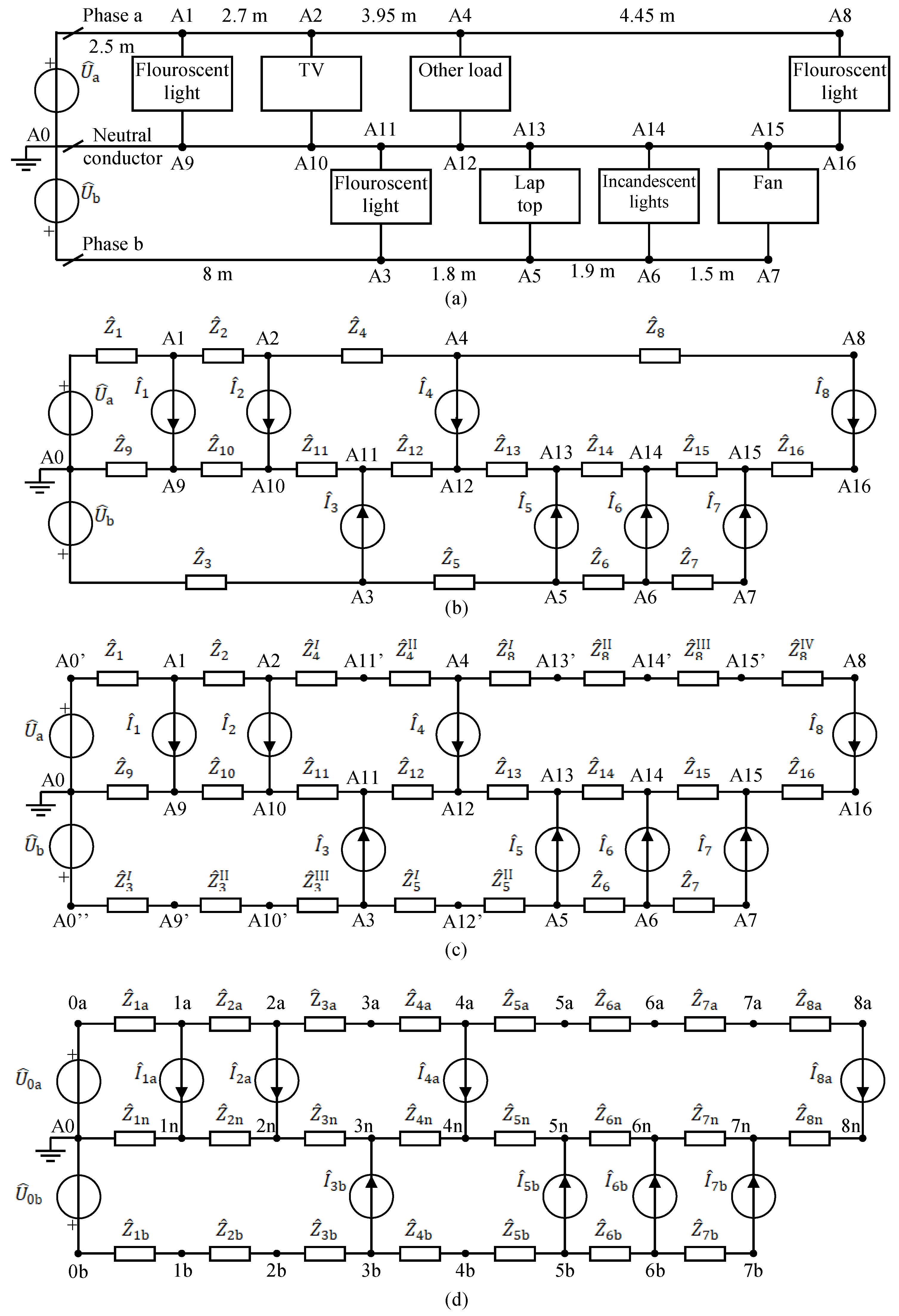
2. Home Network Models
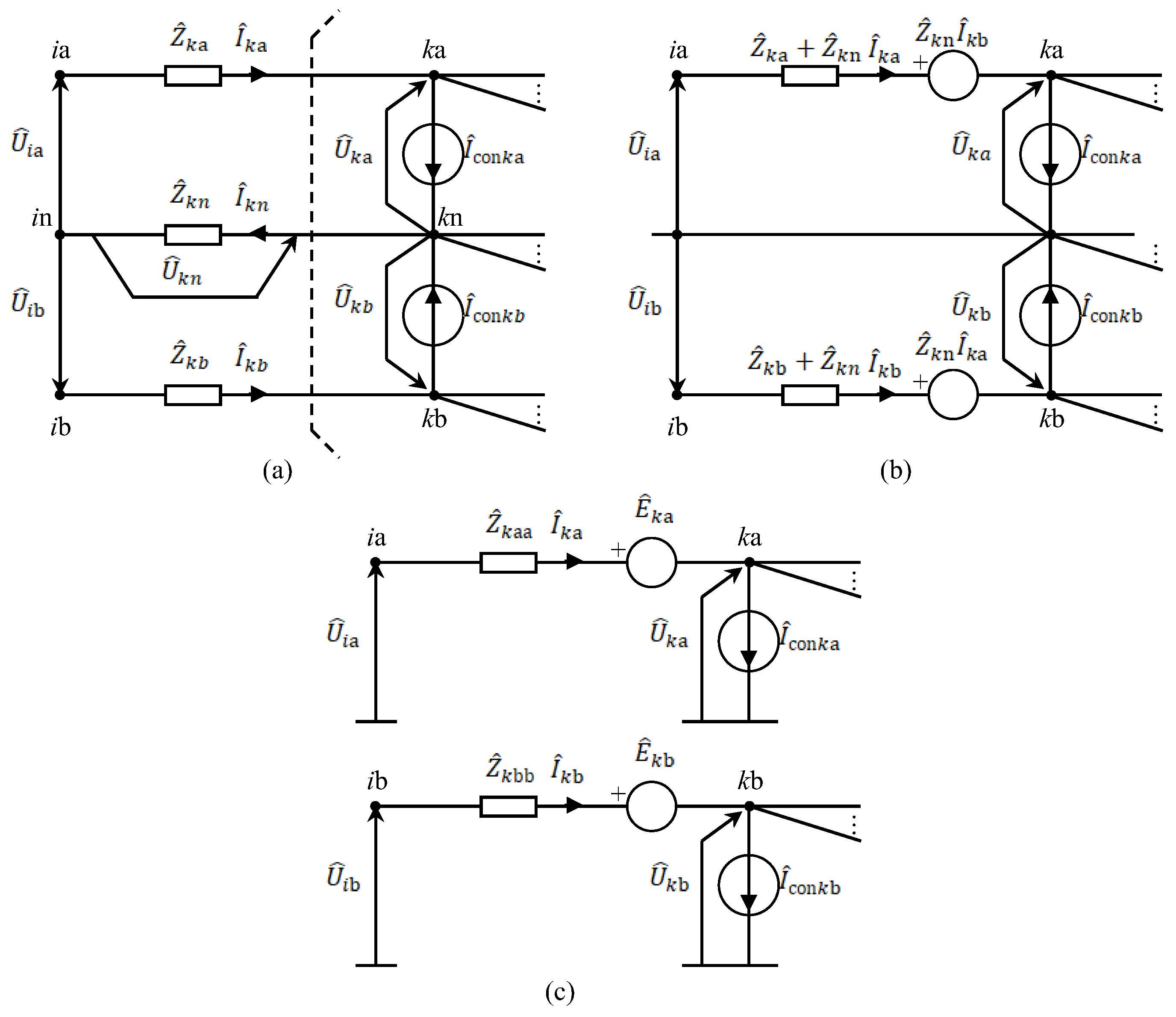
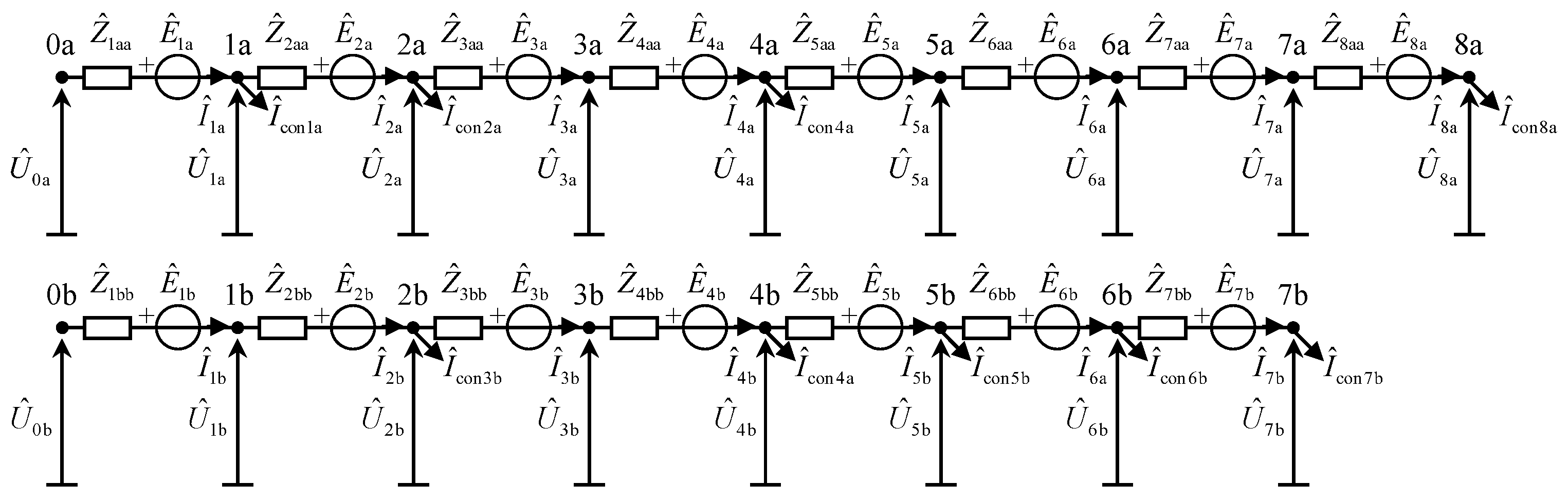
2.1. Single-Phase Three-Wire System and Consumer Model
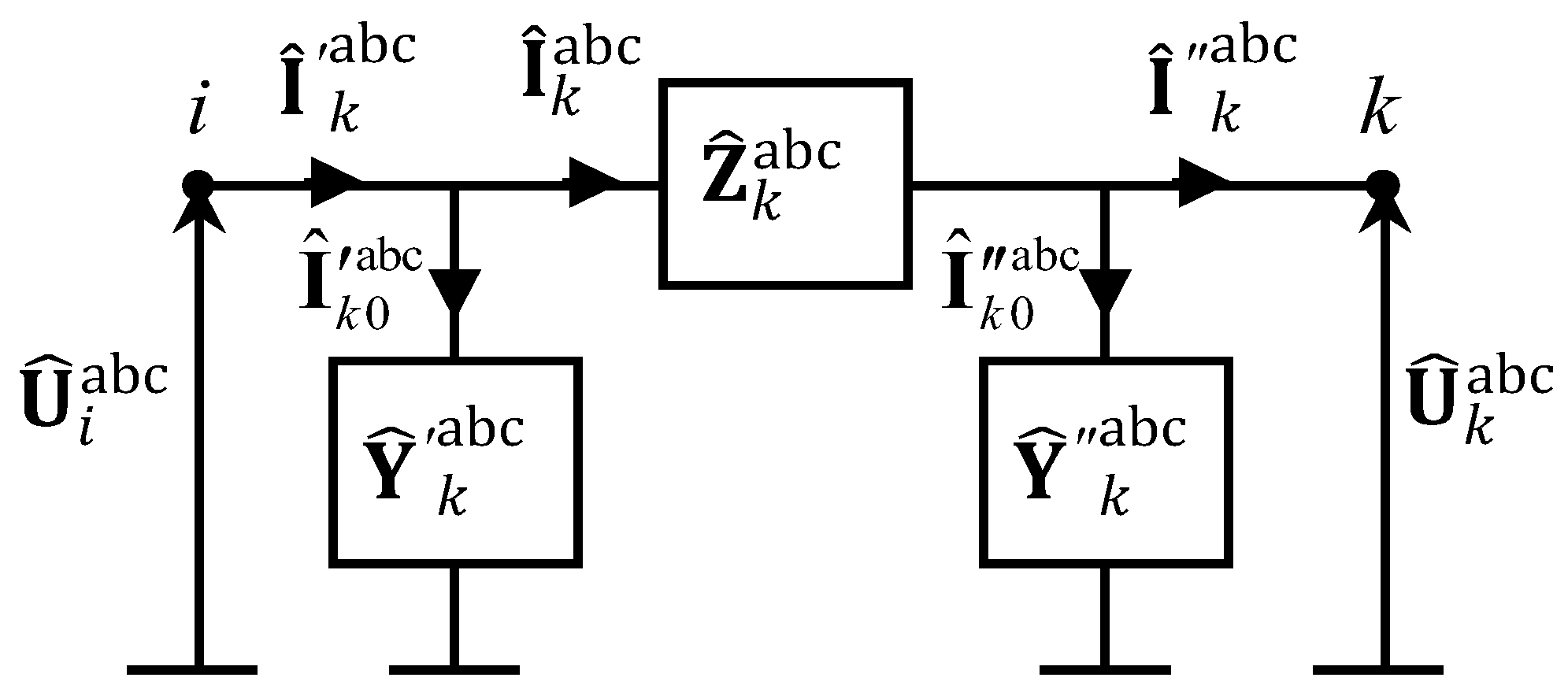
2.2. Three-Phase and Multiphase Systems
Measurement of Series and Shunt Parameter Matrices of Home Line Sections
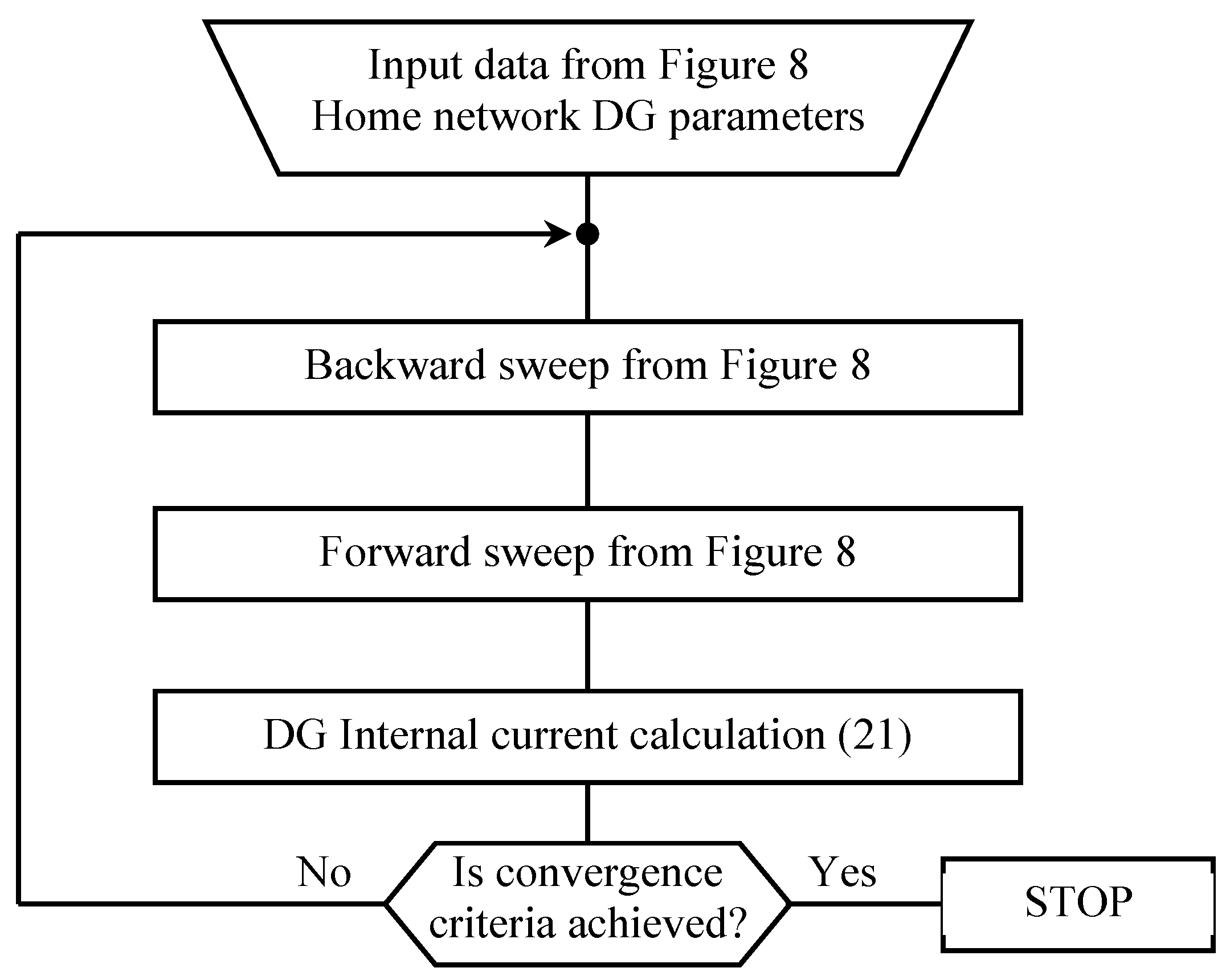
3. Home Network Load Flow Model and Calculation
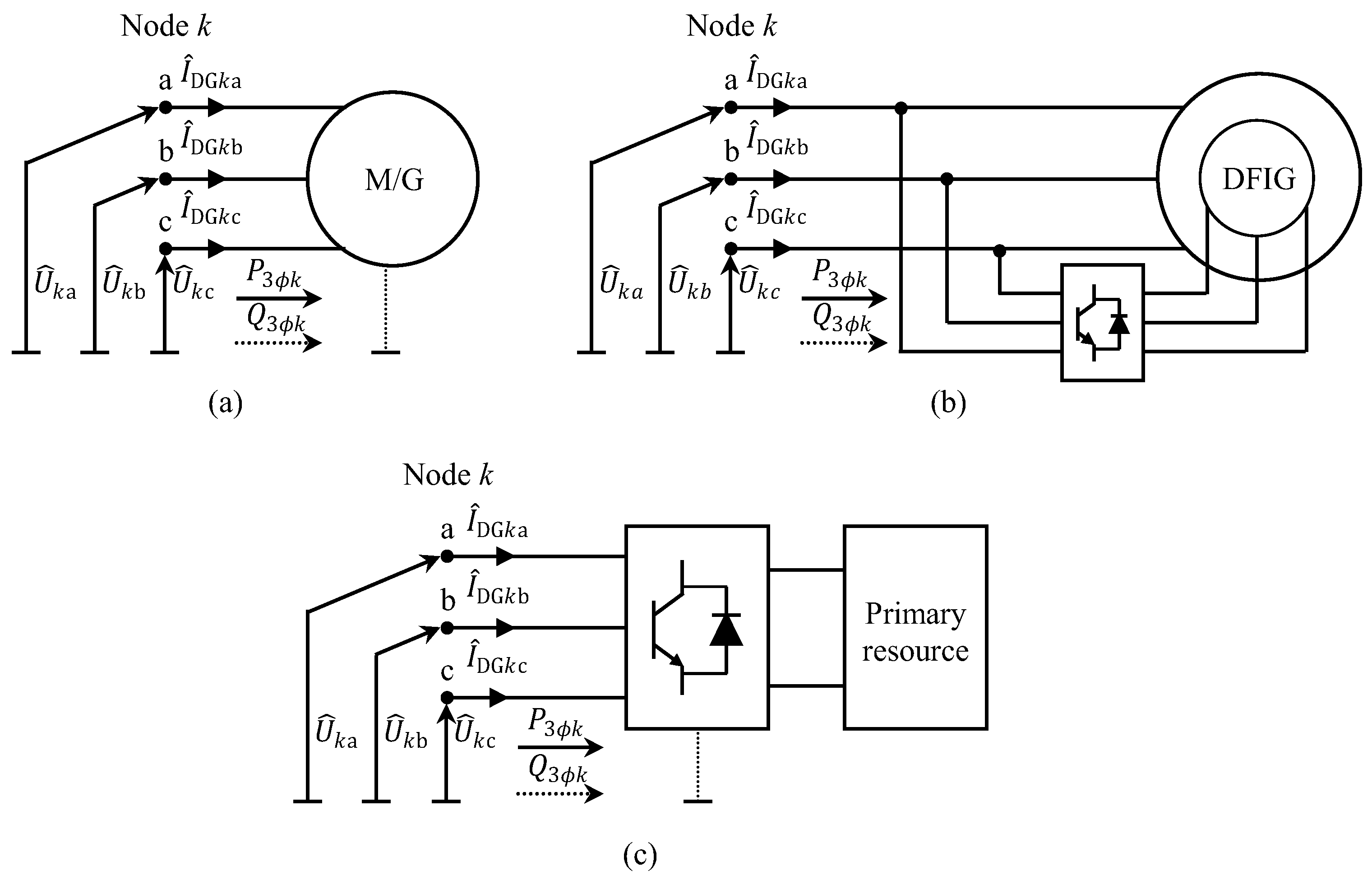
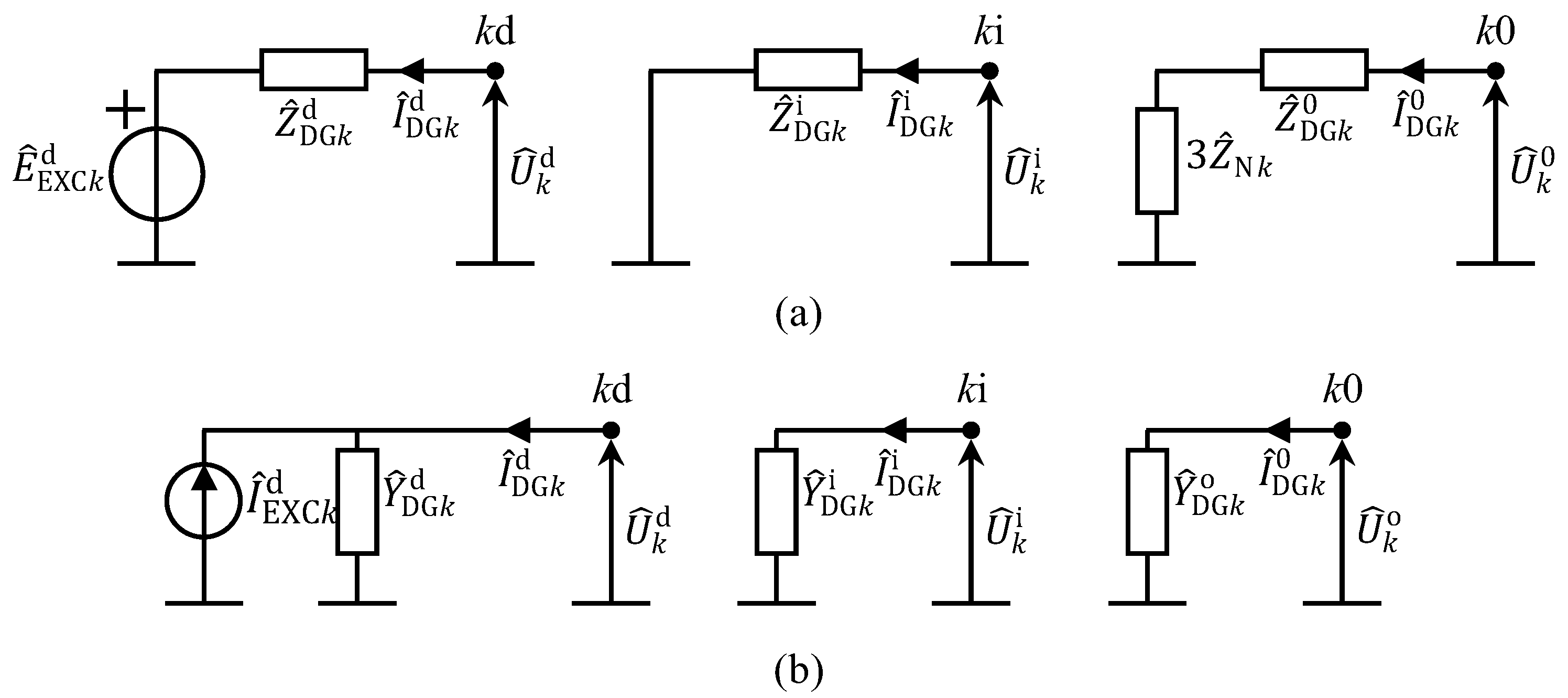
Three-Phase Distributed Generator Model Integration in Load Flow Procedure
4. Results and Discussion
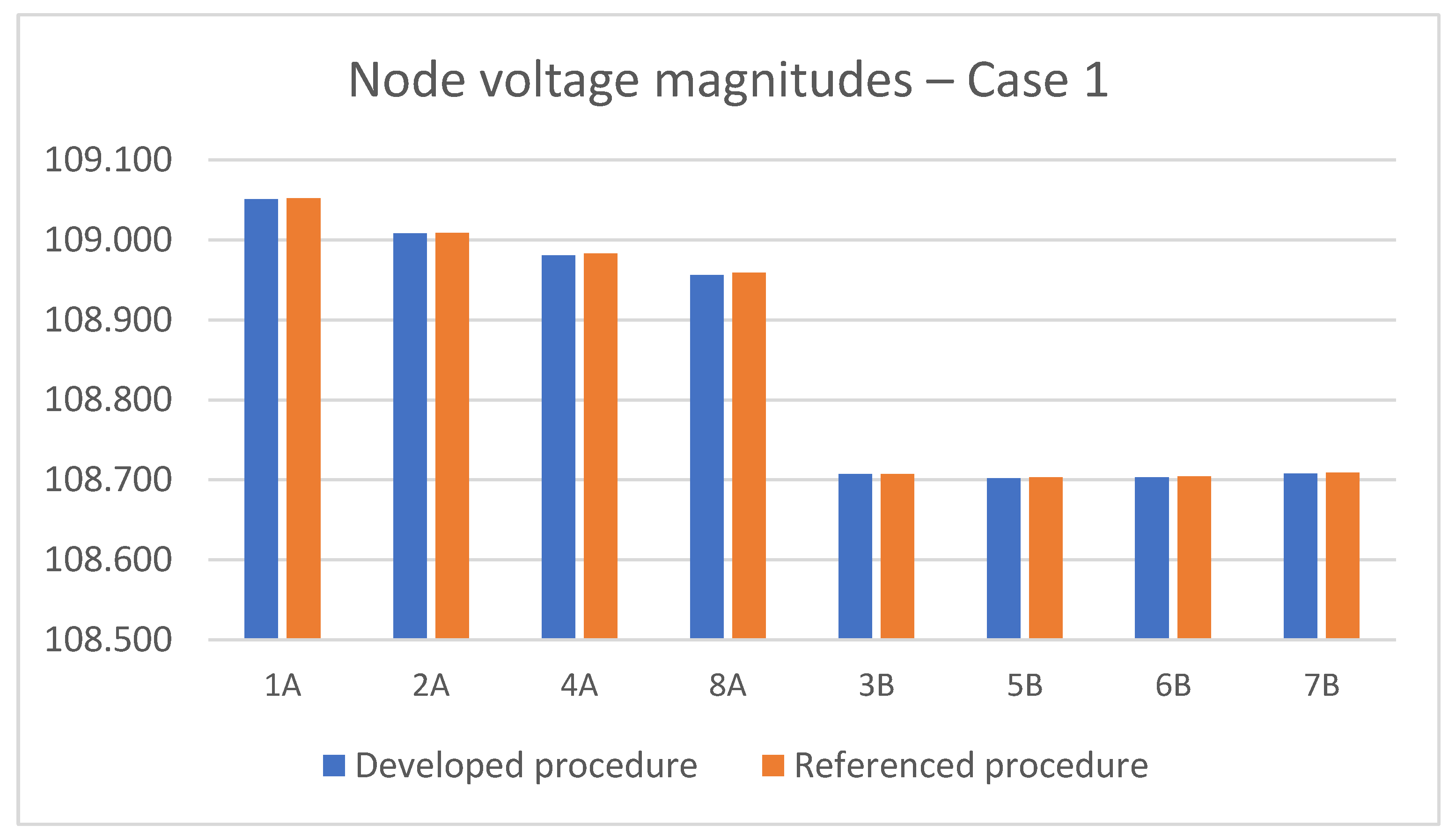
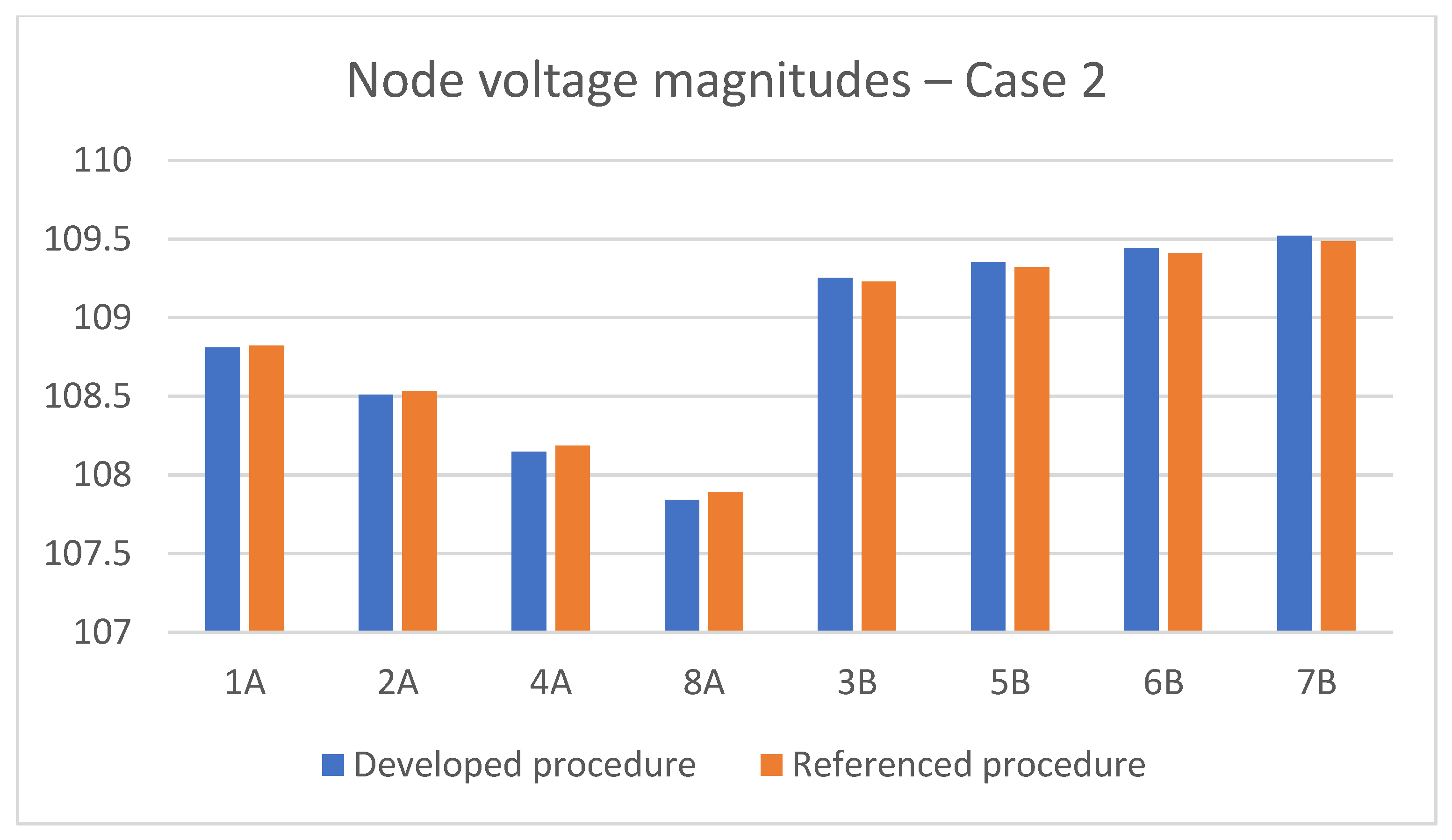
4.1. Model Verification on the Single-Phase Three-Wire Configuration
4.2. Three-Phase and Single-Phase Sections
4.3. Three-Phase European Home Network
Integration of DG in Home Network
4.4. Performance of the Developed Procedure on the Large-Scale Distribution Network
4.5. Limitations of the Proposed Methodology
- (i)
- The distribution energy resource voltage control in situation where part of the residential network forms the microgrid, operating in islanded mode.
- (ii)
- When the distribution energy resource is intermittent, the output power could be estimated using the weather, solar irradiation, ambient temperature, and wind speed model. Once these complex models are tailored for power flow model, they can be easily incorporated into the developed power flow calculation procedure since the efficiency is demonstrated in the previous subsection.
- (iii)
- Since EVs represent complex load, it is mandatory to measure their consumption at each stage of charging (grid to vehicle) or discharging (vehicle to grid) and then form the consumption diagram for this complex type of load. Based on this diagram it is possible to integrate the EV model into the load flow model and develop the load flow calculation procedure.
- (iv)
- The non-linearity loads results in a non-sinusoidal current which is periodic and needs Fourier expansion. It is possible to extend power flow models by increasing the number of relations by using the first Kirchhoff’s law for current and power balance.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations and Nomenclature
| Abbreviations | |
| HEMS | Home Energy Management Systems |
| PV | Photovoltaic |
| DG | Distributed generation |
| EV | Electric vehicle |
| ER | Energy Resources |
| BFS | Backward–Forward Sweep |
| BIBC | Bus-Injection to Branch-Current |
| BCBV | Branch-Current to Bus-Voltage |
| LV | Low voltage |
| ESS | Energy Storage Systems |
| ECDG | Electronically Coupled Distributed Generators |
| 1φ3w | Single-phase three wire system |
| 1φ2w | Single-phase two-wire system |
| 3φ4w | Three-phase four-wire system |
| 3φ5w | Three-phase five-wire system |
| DFIG | Double-Fed Induction Generator |
| PCC | Point of Common Coupling |
| TPN | Three-Phase and Neutral Distribution Board |
| DN | Distribution network |
| Nomenclature | |
| i, k | Node indices |
| , | Phase indices |
| , | Actual and nominal voltage magnitudes at load terminal |
| Specified active and reactive powers at nominal voltage | |
| , , , , | Constant impedance, current and power coefficients |
| Load power factor | |
| {in, ia, ib} | Node set indices closer to the root of American/Taiwan 1φ3w line section |
| {kn, ka, kb} | Node set indices further to the root of American/Taiwan 1φ3w line section |
| American/Taiwan 1φ3w line section impedances | |
| American/Taiwan 1φ3w section self-impedances | |
| , | American/Taiwan 1φ3w node voltages closer to the root |
| , | American/Taiwan 1φ3w node voltages further to the root |
| American/Taiwan 1φ3w inductive coupling voltages | |
| American/Taiwan 1φ3w line section currents | |
| Load current | |
| Series impedance matrix of European 3φ4w, 3φ5w, 1φ3w line sections | |
| , | Shunt admittance matrices of self and mutual capacitive phase couplings of European 3φ4w, 3φ5w, 1φ3w line sections |
| , | Node voltage vectors |
| , | Current vectors at the and at the end of European 3φ4w, 3φ5w, 1φ3w line section |
| Branch current vector of European 3φ4w, 3φ5w, 1φ3w line section | |
| , | Shunt current vectors of European 3φ4w, 3φ5w, 1φ3w line section |
| Branch impedance of Γks section | |
| Total self capacitance admittance of Γks section | |
| Mutual inductance impedance of Γks section | |
| Mutual capacitive coupling admittance of Γks section | |
| , | Node voltages of Γks section |
| Branch current of Γks section | |
| Capacitive coupling current of Γks section | |
| Induced voltage of Γks section | |
| , | Transformation matrices |
| DG Subtransient reactance | |
| , , | DG Positive, negative and zero sequence impedances |
| , , | DG Positive, negative and zero sequence impedances |
| DG Impedance between the neutral and the ground | |
| DG internal voltage source (electro motive force) | |
| DG internal current source | |
| , | Three-phase DG active and reactive powers |
| , | DG Positive, negative and zero sequence currents |
| DG phase domain self capacitive admittance | |
| DG phase domain mutual capacitive admittance | |
| DG phase coupling current | |
| DG phase current at the PCC |
References
- Leitao, J.; Gil, P.; Ribeiro, B.; Cardoso, A. A survey on home energy management. IEEE Access 2020, 8, 5699–5722. [Google Scholar] [CrossRef]
- Rathor, S.K.; Saxena, D. Energy management system for smart grid: An overview and key issues. Int. J. Energy Res. 2020, 44, 4067–4109. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, L.; Yao, G.; Bu, S. Pricing-based demand response for a smart home with various types of household appliances considering customer satisfaction. IEEE Access 2019, 7, 86463–86472. [Google Scholar] [CrossRef]
- Vojnović, N.; Vidaković, J.; Vidaković, M. Multi-threadaed unbalanced load flow of large-scale networks with advanced bus classification. Comput. Electr. Eng. 2022, 101, 108134. [Google Scholar] [CrossRef]
- Vojnović, N.; Vidaković, J.; Vidaković, M. Multi-threaded load flow of large-scale active multiphase distribution networks. Expert Syst. Appl. 2023, 1, 120313. [Google Scholar] [CrossRef]
- Strezoski, L.V.; Vojnovic, N.R.; Strezoski, V.C.; Vidovic, P.M.; Prica, M.D.; Loparo, K.A. Modeling challenges and potential solutions for integration of emerging DERs in DMS applications: Load flow and short-circuit analysis. J. Mod. Power Syst. Clean Energy 2019, 7, 1365–1384. [Google Scholar] [CrossRef]
- Liao, R.N.; Yang, N.C.; Chen, T.H. A novel and fast single-phase three-wire load flow solution for a modern home premises wiring systems. Int. J. Electr. Power Energy Syst. 2017, 1, 190–207. [Google Scholar] [CrossRef]
- Vojnović, N.; Vidaković, J.; Vidaković, M. Decoupled load flow for large-scale multiphase distribution networks. Sustain. Energy Grids Netw. 2023, 1, 101049. [Google Scholar] [CrossRef]
- Rahim, S.; Siano, P. A survey and comparison of leading-edge uncertainty handling methods for power grid modernization. Expert Syst. Appl. 2022, 204, 117590. [Google Scholar] [CrossRef]
- Tošić, S.; Vojnović, N.; Vidaković, M.; Vidaković, J.; Levi, V.; Ćetenović, D. Single and multi-threaded power flow algorithm for integrated transmission-distribution-residential networks. Comput. Electr. Eng. 2024, 120, 109735. [Google Scholar] [CrossRef]
- Shen, T.; Li, Y.; Xiang, J. A graph-based load flow method for balanced distribution systems. Energies 2018, 11, 511. [Google Scholar] [CrossRef]
- Strezoski, V.C.; Vidović, P.M. Power flow for general mixed distribution networks. Int. Trans. Electr. Energy Syst. 2015, 25, 2455–2471. [Google Scholar] [CrossRef]
- Ouali, S.; Cherkaoui, A. An improved backward/forward sweep load flow method based on a new network information organization for radial distribution systems. J. Electr. Comput. Eng 2020, 2020, 5643410. [Google Scholar] [CrossRef]
- Dkhili, N.; Eynard, J.; Thil, S.; Grieu, S. A survey of modelling and smart management tools for power grids with prolific distributed generation. Sustain. Energy Grids Netw. 2020, 21, 100284. [Google Scholar] [CrossRef]
- Koksoy, A.; Ozturk, O.; Balci, M.E.; Hocaoglu, M.H. A new wind turbine generating system model for balanced and unbalanced distribution systems load flow analysis. Appl. Sci. 2018, 8, 502. [Google Scholar] [CrossRef]
- Anirudh, C.V.S.; Seshadri, S.K.V. Enhanced modelling of doubly fed induction generator in load flow analysis of distribution systems. IET Renew. Power Gener. 2021, 15, 980–989. [Google Scholar] [CrossRef]
- Arboleya, P.; Koirala, A.; Suárez, L.; Mohamed, B.; González-Morán, C. Impact Evaluation of the New Self-Consumption Spanish Scenario on the Low-Voltage Terminal Distribution Network. IEEE Trans. Ind. Appl. 2019, 55, 7230–7239. [Google Scholar] [CrossRef]
- Qu, L.; Ouyang, B.; Yuan, Z.; Zeng, R. Steady-State Power Flow Analysis of Cold-Thermal-Electric Integrated Energy System Based on Unified Power Flow Model. Energies 2019, 12, 4455. [Google Scholar] [CrossRef]
- Sereeter, B.; Vuik, K.; Witteveen, C. Newton load flow methods for unbalanced three-phase distribution networks. Energies 2017, 10, 1658. [Google Scholar] [CrossRef]
- Murari, K.; Padhy, N.P. Graph-theoretic based approach for the load-flow solution of three-phase distribution network in the presence of distributed generations. IET Gener. Transm. Distrib. 2020, 14, 1627–1640. [Google Scholar] [CrossRef]
- Marini, A.; Mortazavi, S.S.; Piegari, L.; Ghazizadeh, M.S. An efficient graph-based load flow algorithm for electrical distribution systems with a comprehensive modeling of distributed generations. Electr. Power Syst. Res. 2019, 170, 229–243. [Google Scholar] [CrossRef]
- Hernández-Fuentes, H.E.; Soto, F.J.Z.; Martínez-Ramos, J.L. A fast non-decoupled algorithm to solve the load flow problem in meshed distribution networks. Sustain. Energy Grids Netw. 2022, 32, 100895. [Google Scholar] [CrossRef]
- Verma, R.; Sarkar, V. Application of modified Gauss-Zbus iterations for solving the load flow problem in active distribution networks. Electr. Power Syst. Res. 2019, 168, 8–19. [Google Scholar] [CrossRef]
- Feng, F.; Zhang, P. Implicit Zbus Gauss Algorithm Revisited. IEEE Trans. Power Syst. 2020, 35, 4108–4111. [Google Scholar] [CrossRef]
- Junior, H.M.; Melo, I.D.; Nepomuceno, E.G. An interval load flow for unbalanced distribution systems based on the Three-Phase Current Injection Method. Int. J. Electr. Power Energy Syst. 2022, 139, 107921. [Google Scholar] [CrossRef]
- Švenda, G.; Strezoski, V.; Kanjuh, S. Real-life distribution state estimation integrated in the distribution management system. Int. Trans. Electr. Energy Syst. 2017, 27, e2296. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, X.; Ye, X.; Pirouzi, S. Economic energy management of networked flexi-renewable energy hubs according to uncertainty modeling by the unscented transformation method. Energy 2023, 278, 128054. [Google Scholar] [CrossRef]
- Pirouzi, S. Network-constrained unit commitment-based virtual power plant model in the day-ahead market according to energy management strategy. IET Gener. Transm. Distrib. 2023, 17, 4958–4974. [Google Scholar] [CrossRef]
- Yang, N.C.; Zeng, S.T. Three-phase power flow solution for multi-grounded four-wire residential networks considering neutral grounding. Energy Build. 2024, 323, 114784. [Google Scholar] [CrossRef]
- Clarke, J.A.; Kelly, N.J. Integrating power flow modelling with building simulation. Energy Build. 2001, 33, 333–340. [Google Scholar] [CrossRef]
- Wu, J.; Lian, Z.; Zheng, Z.; Zhang, H. A method to evaluate building energy consumption based on energy use index of different functional sectors. Sustain. Cities Soc. 2020, 1, 101893. [Google Scholar] [CrossRef]
- Teki, V.K.; Maharana, M.K.; Panigrahi, C.K. Study on home energy management system with battery storage for peak load shaving. Mater. Today Proc. 2021, 1, 1945–1949. [Google Scholar] [CrossRef]
- Liao, R.N.; Yang, N.C. Evaluation of voltage imbalance on low-voltage distribution networks considering delta-connected distribution transformers with a symmetrical NGS. IET Gener. Transm. Distrib. 2018, 12, 1644–1654. [Google Scholar] [CrossRef]
- Mbungu, N.T.; Bansal, R.C.; Naidoo, R.M. Smart energy coordination of autonomous residential home. IET Smart Grid 2019, 2, 336–346. [Google Scholar] [CrossRef]
- Hannagan, J.; Woszczeiko, R.; Langstaff, T.; Shen, W.; Rodwell, J. The Impact of Household Appliances and Devices: Consider Their Reactive Power and Power Factors. Sustainability 2022, 15, 158. [Google Scholar] [CrossRef]
- Pipattanasomporn, M.; Kuzlu, M.; Rahman, S.; Teklu, Y. Load profiles of selected major household appliances and their demand response opportunities. IEEE Trans. Smart Grid 2013, 5, 742–750. [Google Scholar] [CrossRef]
- Wang, X.; Mao, X.; Khodaei, H. A multi-objective home energy management system based on internet of things and optimization algorithms. J. Build. Eng. 2021, 33, 101603. [Google Scholar] [CrossRef]
- Sangswang, A.; Konghirun, M. Optimal strategies in home energy management system integrating solar power, energy storage, and vehicle-to-grid for grid support and energy efficiency. IEEE Trans. Ind. Appl. 2020, 56, 5716–5728. [Google Scholar] [CrossRef]
- Munankarmi, P.; Wu, H.; Pratt, A.; Lunacek, M.; Balamurugan, S.P.; Spitsen, P. Home Energy Management System for Price-Responsive Operation of Consumer Technologies Under an Export Rate. IEEE Access 2022, 10, 50087–50099. [Google Scholar] [CrossRef]
- Rizvi, S.M.H.; Sajan, K.S.; Srivastava, A.K. Synchrophasor based ZIP parameters tracking using ML with adaptive window and data anomalies. IEEE Trans. Power Syst. 2021, 37, 3–13. [Google Scholar] [CrossRef]
- Jabbar, W.A.; Annathurai, S.; Rahim, T.A.A.; Fauzi, M.F.M. Smart energy meter based on a long-range wide-area network for a stand-alone photovoltaic system. Expert Syst. Appl. 2022, 197, 116703. [Google Scholar] [CrossRef]
- IEEE.Org. IEEE PES Test Feeder. Available online: https://cmte.ieee.org/pes-testfeeders (accessed on 1 May 2025).
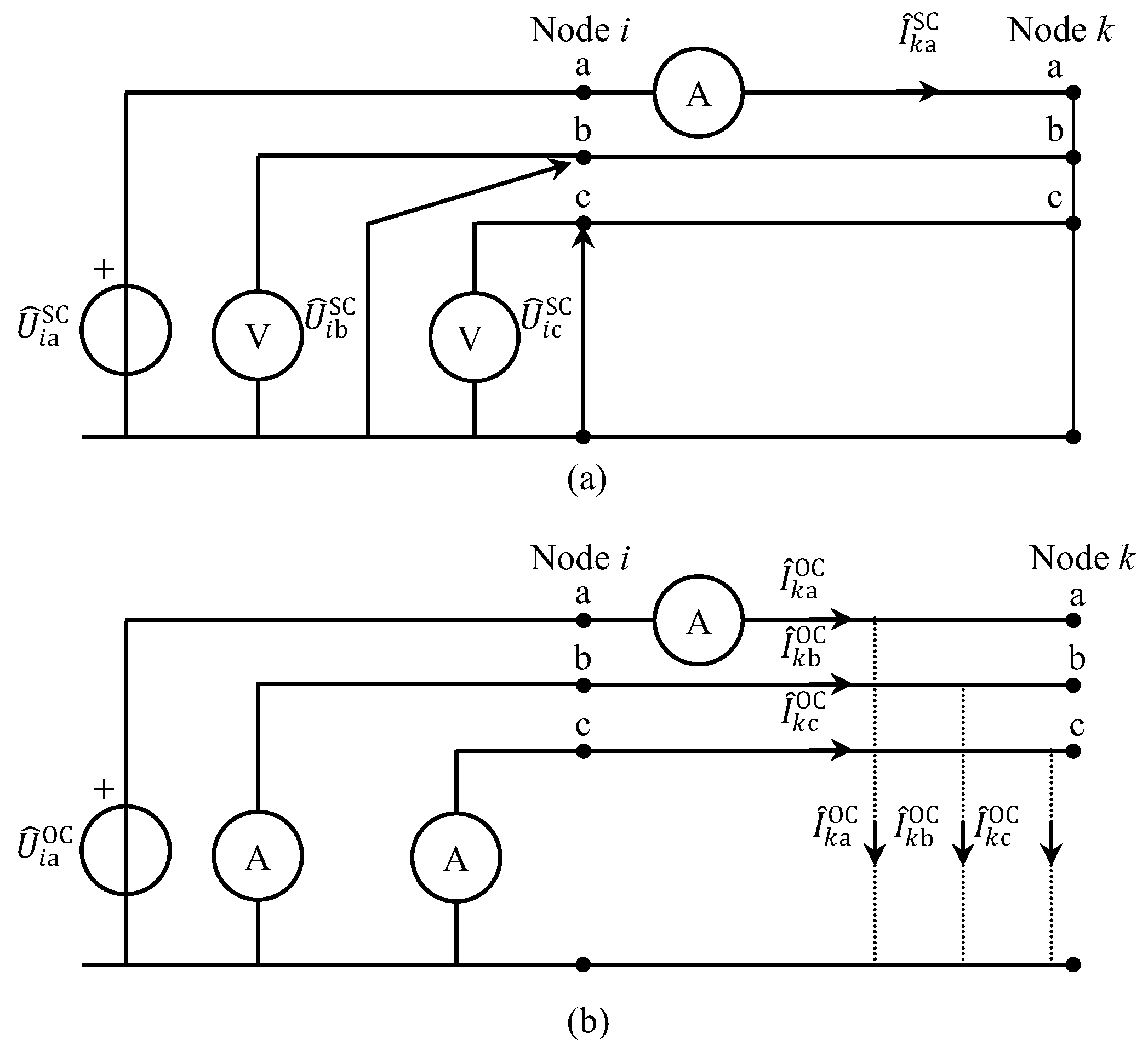
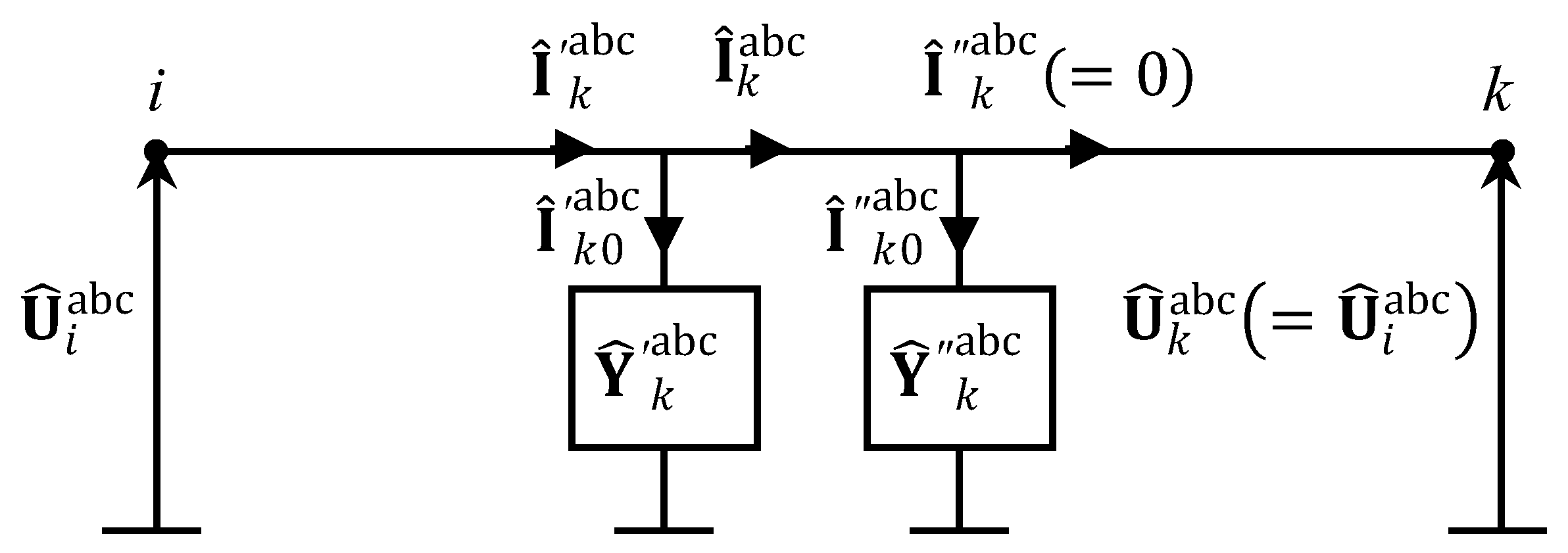
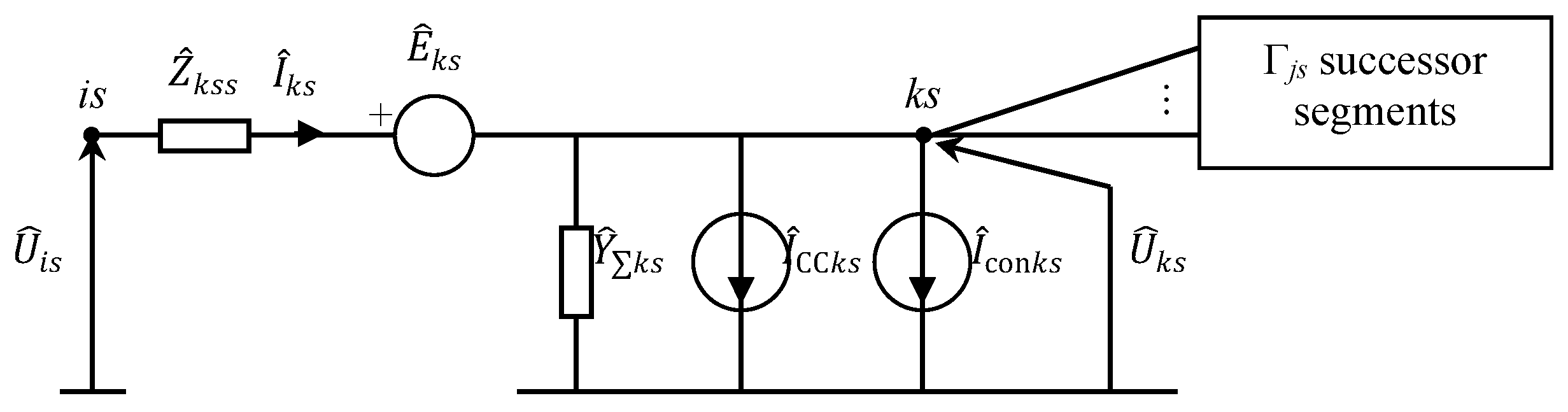
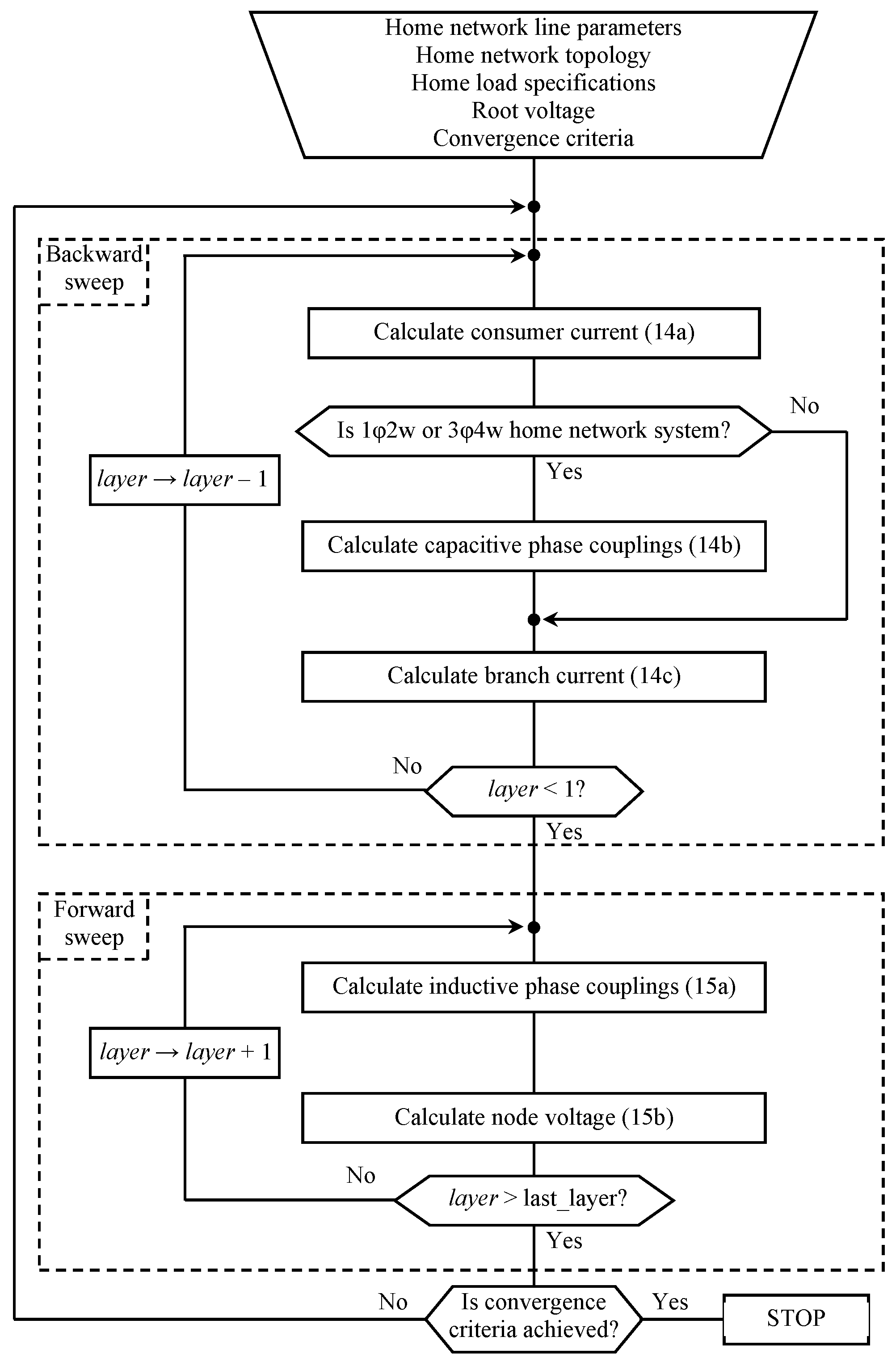
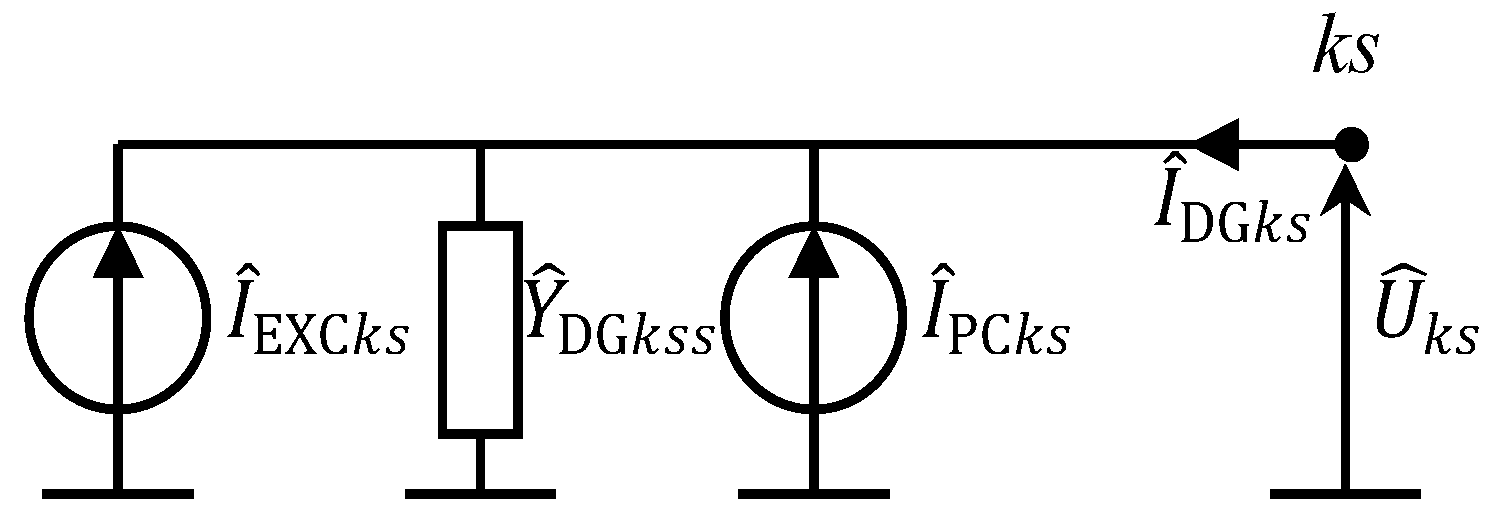
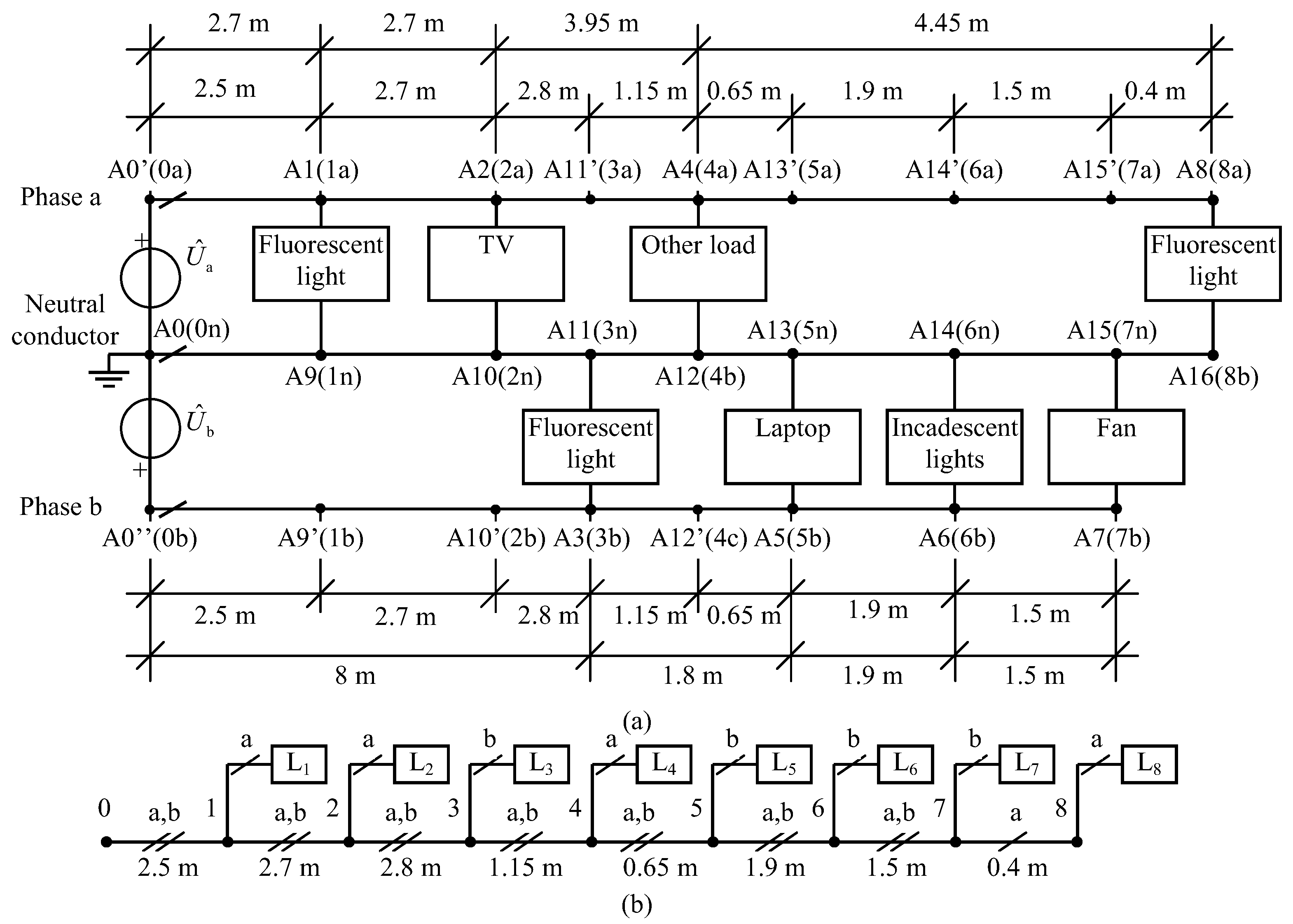
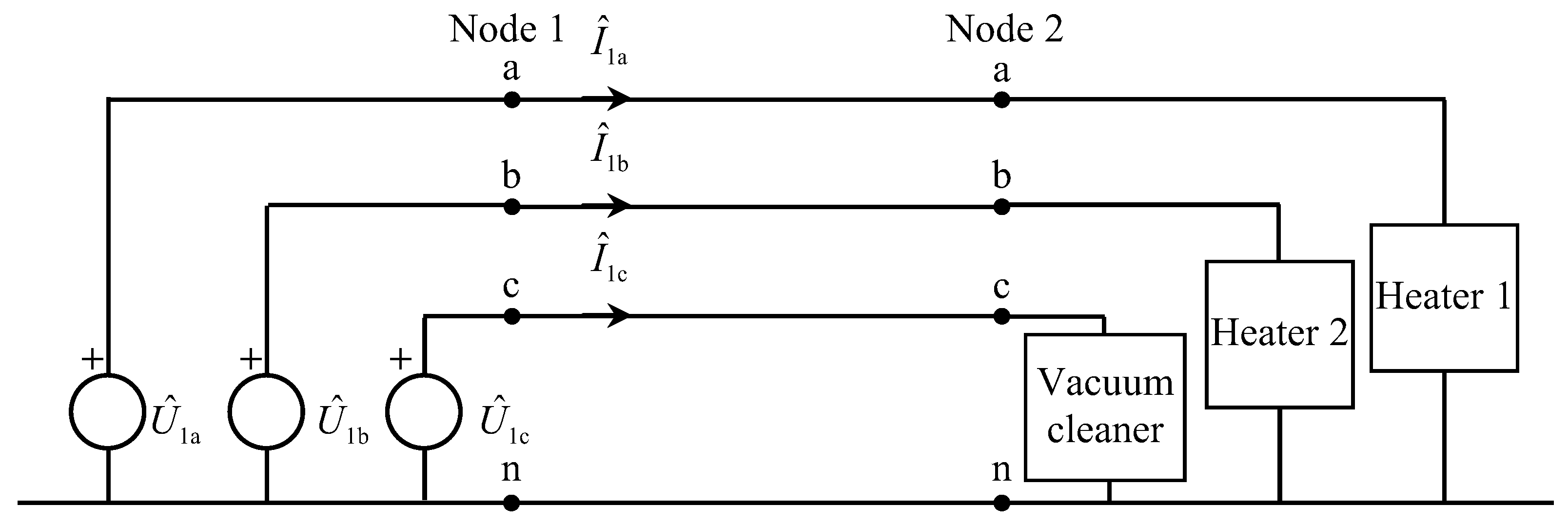

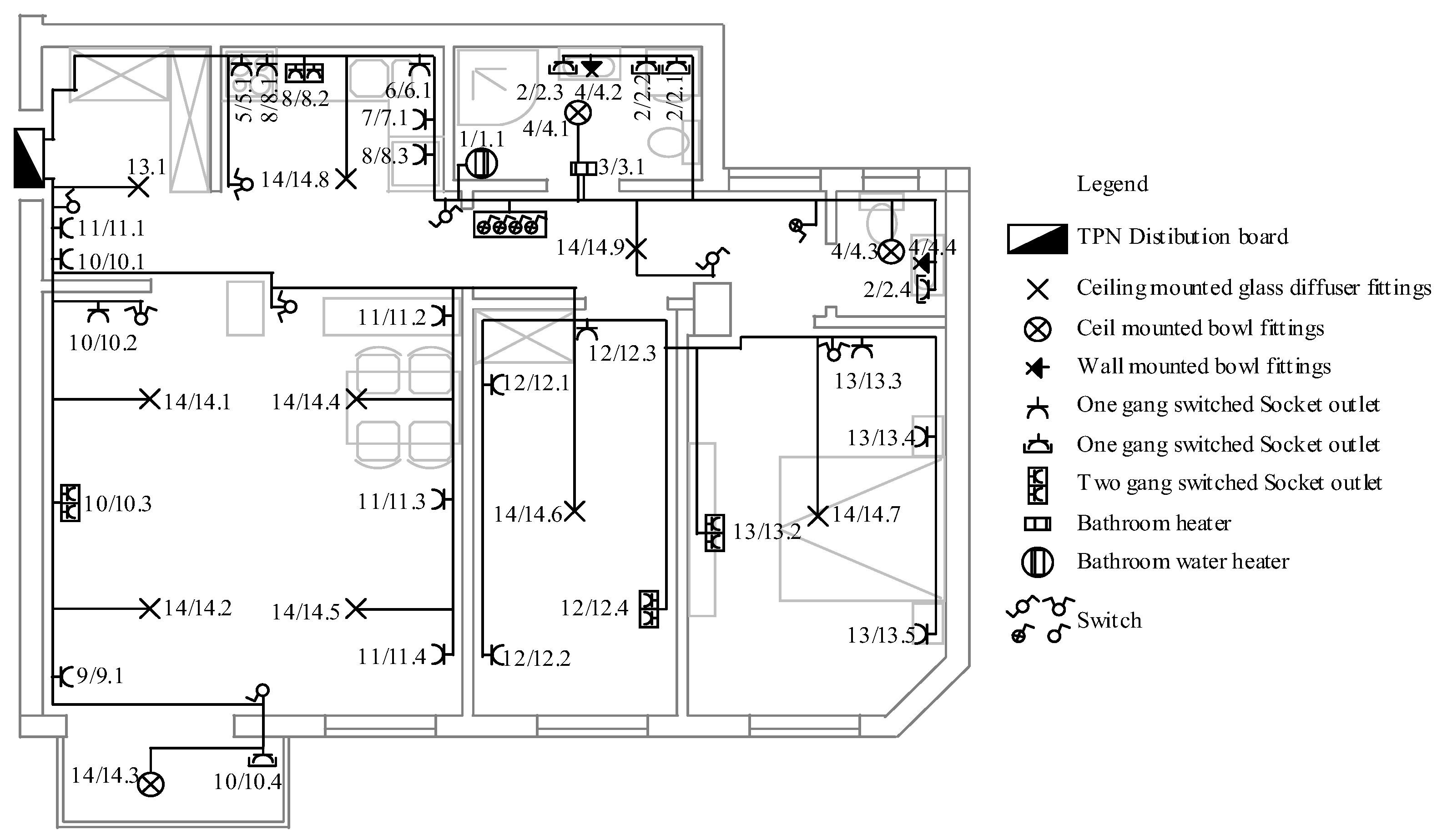

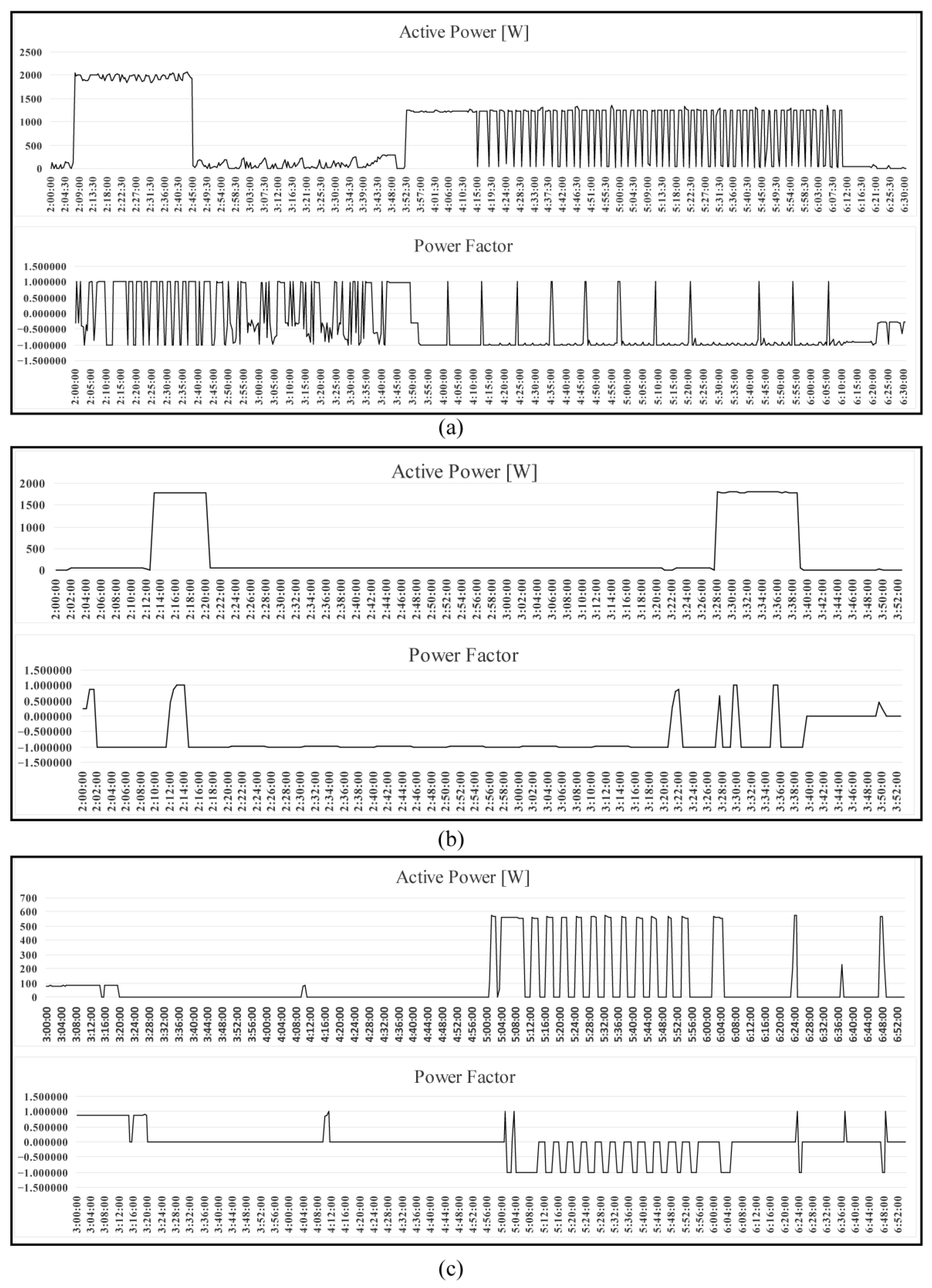
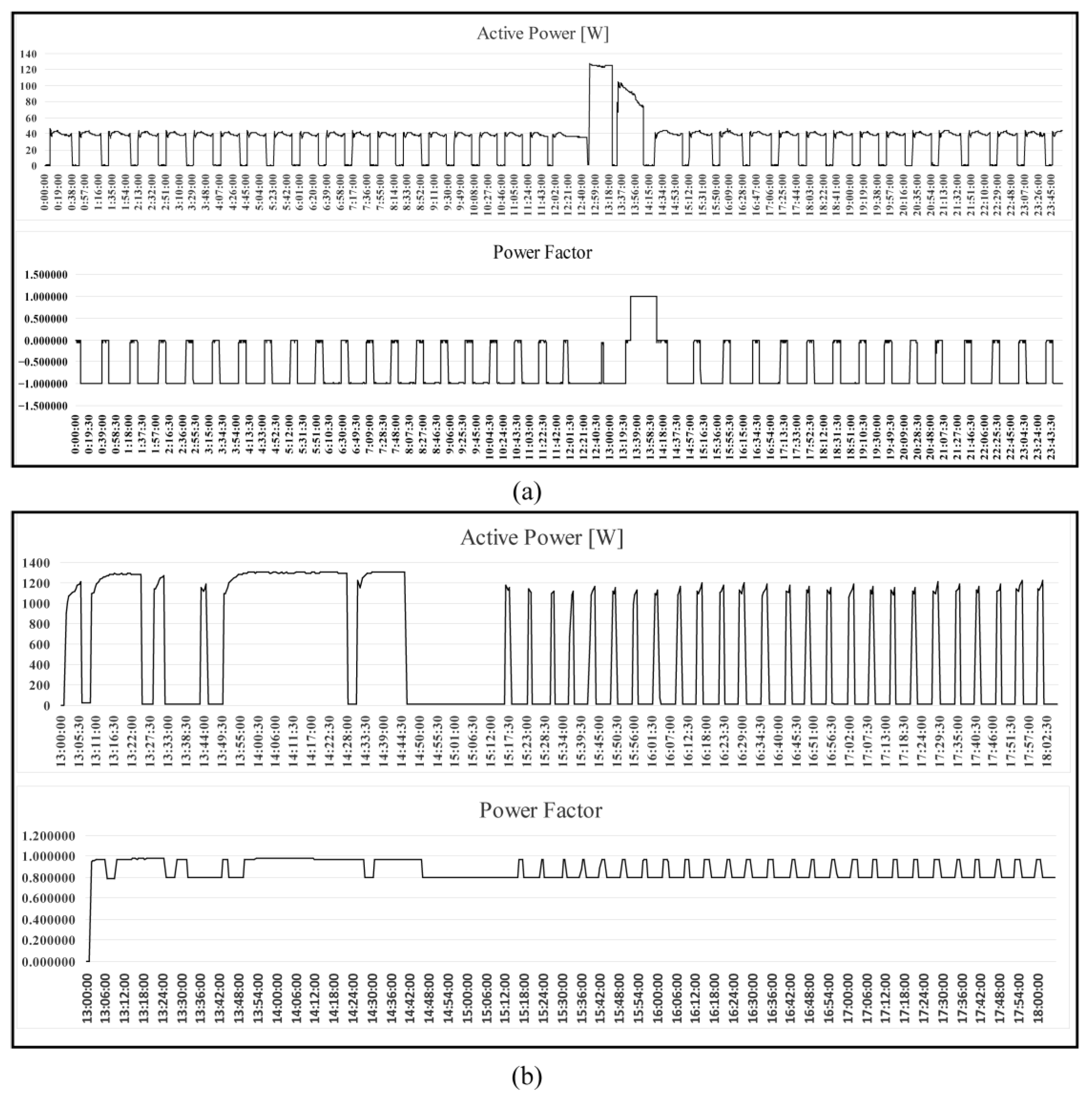

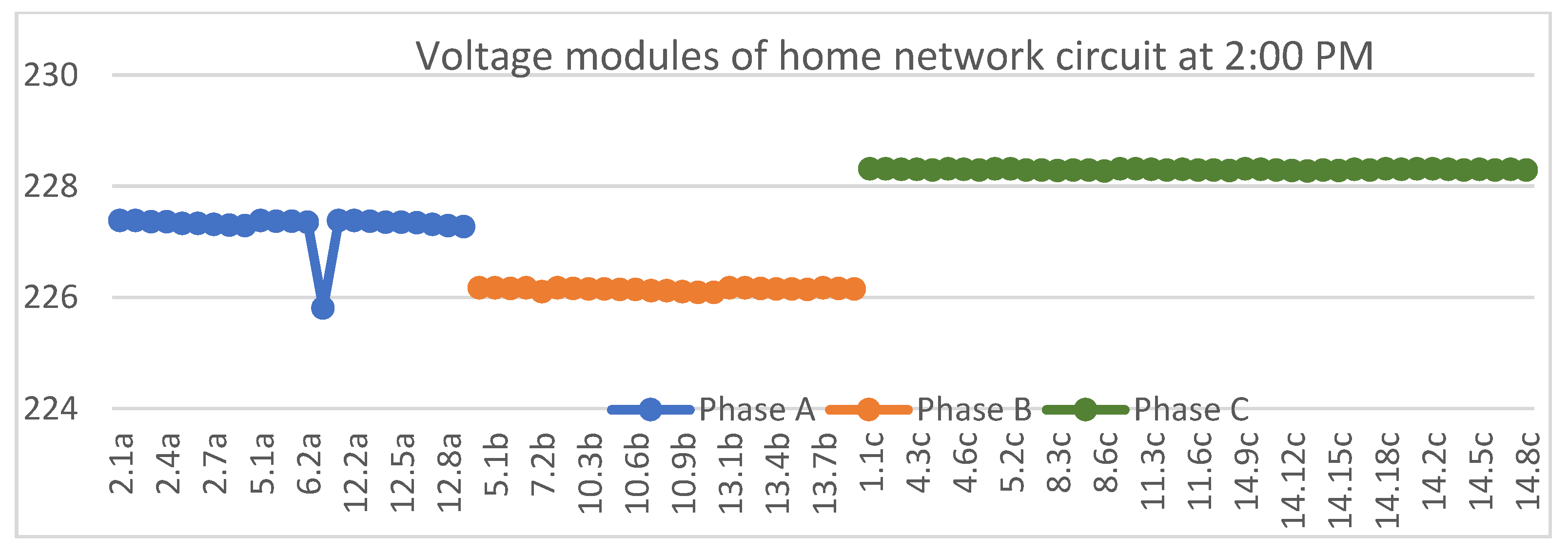


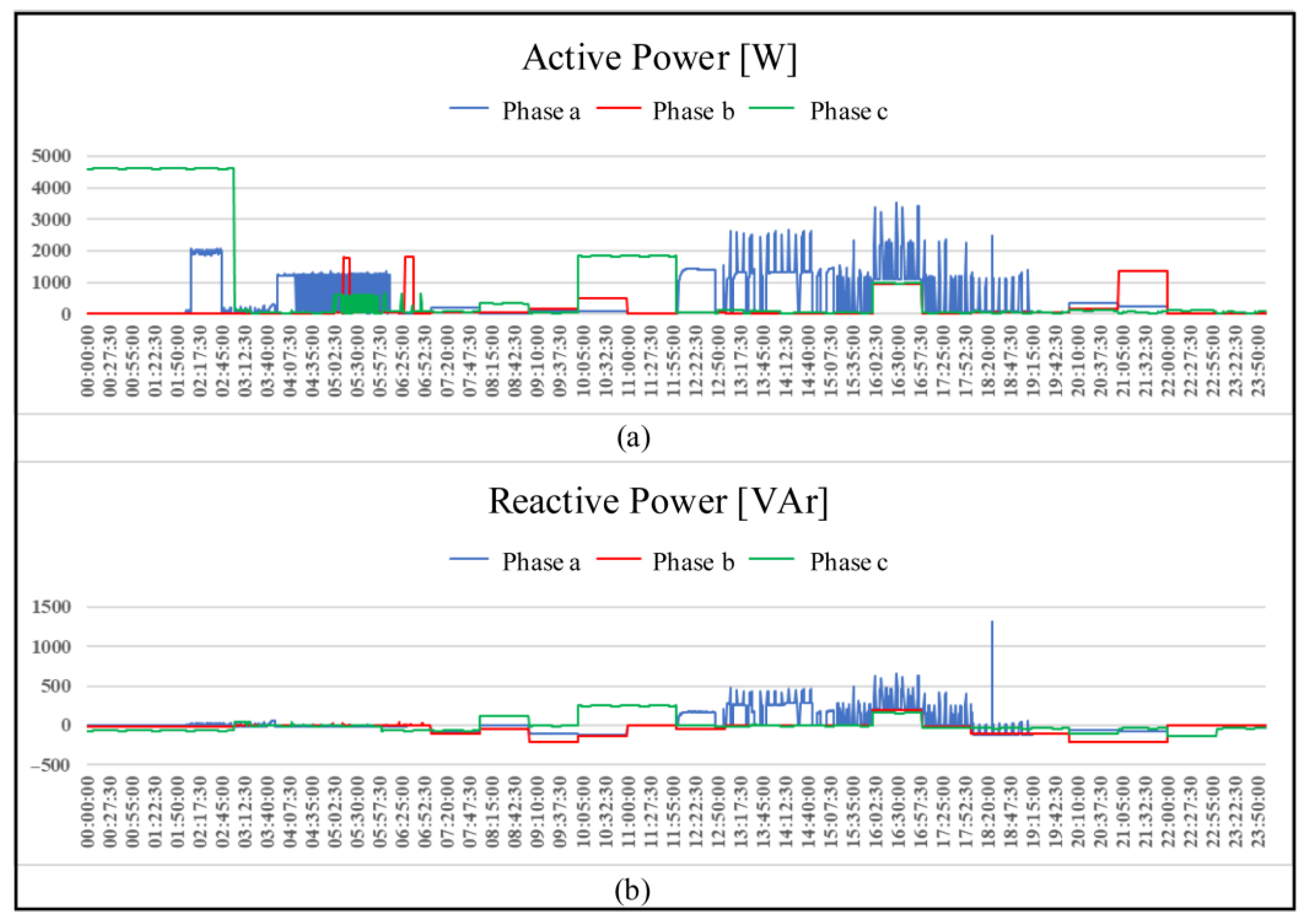
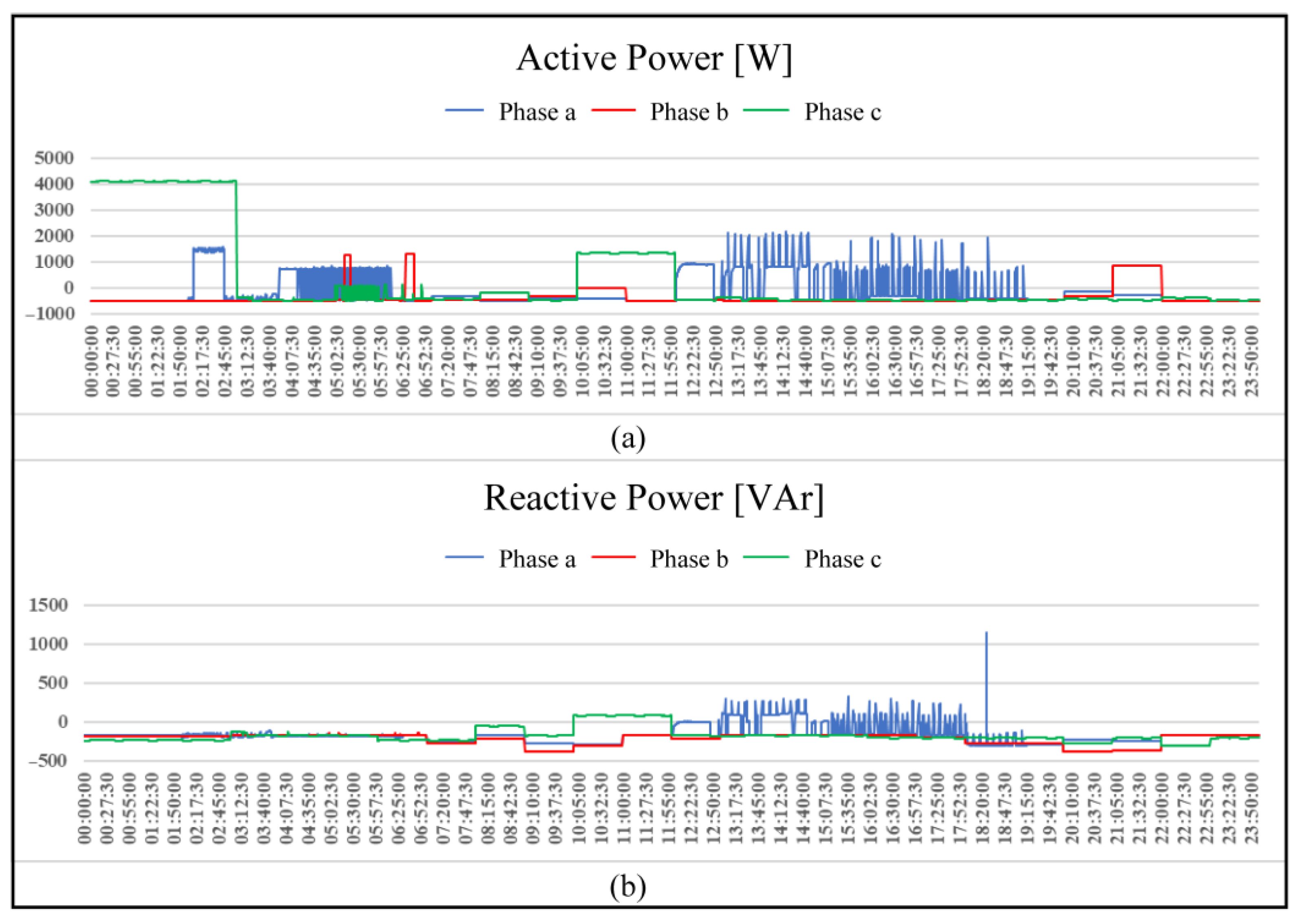
| Ref | Method | Residential Network Included | DG Incorporated into the Residential Network | All Types of Residential Electrical Wiring System Included |
|---|---|---|---|---|
| [4,18,19] | Newton-based approaches | No | No | No |
| [10] | Newton- and BFS-based approach | Yes | No | No |
| [22,23,24] | Implicit Zbus method | No | No | No |
| [25] | Current Injection method | No | No | No |
| [12,13,15,16] | Backward–Forward Sweep | No | No | No |
| [7] | Loop Impedance Matrix-based | Yes | Yes | No |
| [11,21] | Distribution System Load Flow Solution | No | No | No |
| [29] | Implicit Zbus method | Yes | No | No |
| [30] | Newton-based approach | Yes | Yes | No |
| IDs of new generated nodes | A0’, A0”, A9’, A10’, A11’, A12’, A13’, A14’, A15’ | ||||||||
| Node pairs | A0’, A0” | A1, A9’ | A2, A10’ | A11’, A3 | A4, A12’ | A13’, A5 | A14’, A6 | A15’, A7 | A8 |
| Layer-type numeration | 0a, 0b | 1a, 1b | 2a, 2b | 3a, 3b | 4a, 4b | 5a, 5b | 6a, 6b | 7a, 7b | 8a |
| Generator Type | Specified Variables | Unknown State Variables |
|---|---|---|
| DG type 1 | , | , , |
| DG type 2 | , , , | , , |
| Branch | Phase/Neutral | R [Ω/km] | X [Ω/km] | Length [m] |
|---|---|---|---|---|
| A0–A1 | a | 3.62 | 0.11 | 2.5 |
| A1–A2 | a | 3.62 | 0.11 | 2.7 |
| A2–A4 | a | 3.62 | 0.11 | 3.95 |
| A4–A8 | a | 3.62 | 0.11 | 4.45 |
| A0–A3 | b | 3.62 | 0.11 | 8 |
| A3–A5 | b | 3.62 | 0.11 | 1.8 |
| A5–A6 | b | 3.62 | 0.11 | 1.9 |
| A6–A7 | b | 3.62 | 0.11 | 1.5 |
| A0–A9 | n | 10.1 | 0.119 | 2.5 |
| A9–A10 | n | 10.1 | 0.119 | 2.7 |
| A10–A11 | n | 10.1 | 0.119 | 2.8 |
| A11–A12 | n | 10.1 | 0.119 | 1.15 |
| A12–A13 | n | 10.1 | 0.119 | 0.65 |
| A13–A14 | n | 10.1 | 0.119 | 1.9 |
| A14–A15 | n | 10.1 | 0.119 | 1.5 |
| A15–A16 | n | 10.1 | 0.119 | 0.4 |
| Consumer | Original Numeration/(New Numeration) | Phase | Case 1 | Case 2 | ||
|---|---|---|---|---|---|---|
| Active Power [W] | Power Factor | Active Power [W] | Power Factor | |||
| Fluorescent light | A1–A9/L1 | a | 30 | 0.95 | 30 | 0.95 |
| TV | A2–A10/L2 | a | 80 | 0.95 | 160 | 0.9 |
| Other load | A4–A12/L4 | a | 80 | 0.95 | 240 | 0.7 |
| Fluorescent light | A8–A16/L8 | a | 80 | 0.95 | 560 | 0.55 |
| Fluorescent light | A3–A11/L3 | b | 40 | 0.95 | 40 | 0.95 |
| Laptop | A5–A13/L5 | b | 60 | 0.75 | 60 | 0.75 |
| Incandescent lights | A6–A14/L6 | b | 25 | 0.8 | 25 | 0.9 |
| Fan | A7–A15/L7 | b | 30 | 0.95 | 30 | 0.8 |
| Connection Node Point | Load | Active Power [W] | Power Factor | Phase |
|---|---|---|---|---|
| 1.1 | Electric Water Heater E52–50R-045DV | 4500 | 1 | c |
| 2.1 | LG clothes washer F2DV5S7N0E | Figure 20a | Figure 20a | a |
| 2.2 | LED bulb Osram—470 Lm | 5.5 | −0.57 | a |
| 2.3 | Hair dryer | 598 | 0.99 | a |
| 2.4 | Hair dryer | 598 | 0.99 | a |
| 3.1 | Bathroom heater | 1200 | 1 | b |
| 4.1 | LED bulb—Phillips 806 Lm | 16.7 | −0.55 | c |
| 4.2 | LED bulb Osram—470 Lm | 5.5 | −0.57 | c |
| 4.3 | LED bulb—Phillips 806 Lm | 16.7 | −0.55 | c |
| 4.4 | LED bulb Osram—470 Lm | 5.5 | −0.57 | c |
| 5.1 | Electric range/oven Kenmore 790.9131 2013 | 5100 | 0.98 | abc |
| 6.1 | Water Kettle—Anko | 2129.3 | 0.99 | a |
| 7.1 | Dish washer | Figure 20b | Figure 20b | b |
| 8.1 | Moulinex UNO Bread Maker | Figure 20c | Figure 20c | c |
| 8.2 | Microwave—Samsung | 1716.3 | 0.92 | c |
| 8.3 | Refrigerator Maytag, 25.6-cuft side-by-side | Figure 21a | Figure 21a | c |
| 9.1 | Air conditioner LG ES-H123LLA0 | Figure 21b | Figure 21b | a |
| 10.1 | Vacuum—Dyson | 1335.0 | 0.98 | b |
| 10.2 | Mobile phone charger | 10 | −0.47 | b |
| 10.3 | LED—Dick Smith—40” | 64.5 | −0.62 | b |
| 10.4 | Charger Power Tool—Ryobi | 38.2 | −0.62 | b |
| 11.1 | Mobile phone charger | 10 | −0.47 | c |
| 11.2 | Mobile phone charger | 10 | −0.47 | c |
| 11.3 | Mobile phone charger | 10 | −0.47 | c |
| 11.4 | Iron—Kambrook | 1863.7 | 0.99 | c |
| 12.1 | Air conditioner LG ES-H123LLA0 | Figure 21b | Figure 21b | a |
| 12.2 | Laptop Charger—Apple | 58.1 | −0.47 | a |
| 12.3 | Charger Vacuum—Anko | 13.5 | −0.58 | a |
| 12.4 | LED—Dick Smith—40” | 64.5 | −0.62 | a |
| 13.1 | LED bulb—Phillips 806 Lm | 16.7 | −0.55 | b |
| 13.2 | LED—Dick Smith—40” | 64.5 | −0.62 | b |
| 13.3 | Mobile phone charger | 10 | −0.47 | b |
| 13.4 | Laptop Charger—Apple | 58.1 | −0.47 | b |
| 13.5 | USB Adapter Powerbank—Cosmos | 33.2 | −0.54 | b |
| 14.1 | LED bulb Osram—470 Lm | 5.5 | −0.57 | c |
| 14.2 | LED bulb Osram—470 Lm | 5.5 | −0.57 | c |
| 14.3 | LED bulb—Phillips 806 Lm | 16.7 | −0.55 | c |
| 14.4 | LED bulb Osram—470 Lm | 5.5 | −0.57 | c |
| 14.5 | LED bulb Osram—470 Lm | 5.5 | −0.57 | c |
| 14.6 | LED bulb—Phillips 806 Lm | 16.7 | −0.55 | c |
| 14.7 | LED bulb—Phillips 806 Lm | 16.7 | −0.55 | c |
| 14.8 | LED bulb—Phillips 806 Lm | 16.7 | −0.55 | c |
| 14.9 | LED bulb—Phillips 806 Lm | 16.7 | −0.55 | c |
| Case | Voltages [V] | Injected Currents [A] | ||||
|---|---|---|---|---|---|---|
| Ua | Ub | Uc | Ia | Ib | Ic | |
| 1 | 227.502 | 226.337 | 228.480 | 2.163 | 2.441 | 2.362 |
| 2 | 227.547 | 226.315 | 228.460 | 2.317 | 2.317 | 2.317 |
| Total CPU Time [ms] | |
|---|---|
| Proposed load flow | Load flow procedure from [7] |
| 159 | 668 |
| Total CPU Time [ms] | ||
|---|---|---|
| Proposed load flow | Load flow procedure from [29] | Load flow procedure from [30] |
| 432 | 1505 | 2881 |
| Type of Cable | Size of Phase Wires | Size of Neutral Wire | Length |
|---|---|---|---|
| PPY | 2.5 m2 | 2.5 m2 | 35 m |
| Ua | Ub | Uc | ||||||
|---|---|---|---|---|---|---|---|---|
| Calculated [V] | Measured [V] | Mismatch [%] | Calculated [V] | Measured [V] | Mismatch [%] | Calculated [V] | Measured [V] | Mismatch [%] |
| 222.828 | 223.891 | 0.475 | 223.744 | 223.177 | 0.254 | 225.519 | 224.994 | 0.233 |
| θa | θb | θc | ||||||
|---|---|---|---|---|---|---|---|---|
| Calculated [o] | Measured [o] | Mismatch [%] | Calculated [o] | Measured [o] | Mismatch [%] | Calculated [o] | Measured [o] | Mismatch [%] |
| 1.488 | 1.52 | 2.105 | −119.102 | −118.96 | −0.119 | 121.106 | 121.2 | 0.078 |
| θa | Ua | ||||
|---|---|---|---|---|---|
| Calculated [°] | Measured [°] | Mismatch [%] | Calculated [V] | Measured [V] | Mismatch [%] |
| −3.926 | −3.996 | 1.752 | 222.818 | 222.521 | 0.133 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vojnović, N.; Krsman, V.; Vidaković, J.; Vidaković, M.; Popović, Ž.; Pejić, D.; Novaković, Đ. Residential Load Flow Modeling and Simulation. Appl. Syst. Innov. 2025, 8, 130. https://doi.org/10.3390/asi8050130
Vojnović N, Krsman V, Vidaković J, Vidaković M, Popović Ž, Pejić D, Novaković Đ. Residential Load Flow Modeling and Simulation. Applied System Innovation. 2025; 8(5):130. https://doi.org/10.3390/asi8050130
Chicago/Turabian StyleVojnović, Nikola, Vladan Krsman, Jovana Vidaković, Milan Vidaković, Željko Popović, Dragan Pejić, and Đorđe Novaković. 2025. "Residential Load Flow Modeling and Simulation" Applied System Innovation 8, no. 5: 130. https://doi.org/10.3390/asi8050130
APA StyleVojnović, N., Krsman, V., Vidaković, J., Vidaković, M., Popović, Ž., Pejić, D., & Novaković, Đ. (2025). Residential Load Flow Modeling and Simulation. Applied System Innovation, 8(5), 130. https://doi.org/10.3390/asi8050130






