A Privacy-Preserving Record Linkage Method Based on Secret Sharing and Blockchain

Abstract

Privacy-preserving record linkage (PPRL) aims to link records from different data sources while ensuring sensitive information is not disclosed. Utilizing blockchain as a trusted third party is an effective strategy for enhancing transparency and auditability in PPRL. However, to ensure data privacy during computation, such approaches often require computationally intensive cryptographic techniques. This can introduce significant computational overhead, limiting the method’s efficiency and scalability. To address this performance bottleneck, we combine blockchain with the distributed computation of secret sharing to propose a PPRL method based on blockchain-coordinated distributed computation. At its core, the approach utilizes Bloom filters to encode data and employs Boolean and arithmetic secret sharing to decompose the data into secret shares, which are uploaded to the InterPlanetary File System (IPFS). Combined with masking and random permutation mechanisms, it enhances privacy protection. Computing nodes perform similarity calculations locally, interacting with IPFS only a limited number of times, effectively reducing communication overhead. Furthermore, blockchain manages the entire computation process through smart contracts, ensuring transparency and correctness of the computation, achieving efficient and secure record linkage. Experimental results demonstrate that this method effectively safeguards data privacy while exhibiting high linkage quality and scalability.

1. Introduction

In the era of big data, cross-institutional data sharing and integration have become key drivers in advancing fields such as medical research, financial analysis, and government decision-making. Record linkage (RL), as a core technology, aims to identify and match records representing the same entity across multiple data sources, providing critical support for data integration and value extraction [1,2]. However, with the exponential growth of data volumes and increasingly stringent privacy regulations, traditional methods face significant challenges when handling sensitive data. Direct sharing of raw data risks exposing personal information, limiting its widespread use. To address this, privacy-preserving record linkage (PPRL) has emerged, focusing on achieving efficient and accurate record matching without disclosing raw data [3]. For instance, in public health, PPRL can securely link records from different hospitals, transportation systems, or communities for infectious disease contact tracing [4]. While ensuring privacy, it effectively identifies transmission chains and informs containment strategies, complying with relevant data protection regulations.

Researchers have proposed various methods for PPRL, most of which are built on the “honest but curious” model [3,5,6]. This model assumes that participants strictly follow the protocol but may attempt to infer additional information from received data. Such methods typically rely on a semi-trusted third party (STTP) for similarity computation or direct collaborative computation among participants. The former approach risks data privacy leakage due to STTP’s potential untrustworthiness, while the latter incurs significant communication overhead and struggles to prevent malicious collusion among participants, posing threats to data security. Some researchers suggest introducing blockchain technology to record and verify the actions of all participants and third parties in the PPRL process, enhancing overall transparency and traceability [7]. While this strategy improves data security to some extent, it still cannot fully prevent collusion among malicious participants [8]. Therefore, cryptographic techniques such as secure multi-party computation and homomorphic encryption are still needed to achieve higher levels of privacy protection [9]. However, these encryption methods often involve significant communication and computational overhead, presenting a trade-off between efficiency and security in practical deployment. In our prior work, we employed a method based on homomorphic encryption to enhance security, but its high computational cost also confirmed this trade-off between efficiency and security [10].

To specifically address this performance bottleneck, we propose a novel PPRL architecture that deeply integrates blockchain with the distributed computation model of secret sharing, offering a more efficient alternative to computationally intensive homomorphic encryption schemes. In this architecture, we first encode data using Bloom filters, then leverage secret sharing to securely decompose computational tasks across multiple distributed nodes. The blockchain acts as a decentralized coordinator and auditor, managing task allocation, data flow (via IPFS), and result verification through smart contracts, while masking and random permutation mechanisms enhance privacy. This architecture allows most computations to be performed locally on the nodes, thereby minimizing inter-node communication and significantly improving overall efficiency.

The main contributions are as follows:

(1)

We apply secret sharing techniques to data encoded with Bloom filters, introducing masking and random permutation to decompose similarity computations into basic operations that each computation node can independently perform locally. Only a single interaction involving the sharing of masked differences is required between nodes, significantly reducing the communication and computational overhead compared to computationally intensive approaches like those based on homomorphic encryption and effectively enhancing resilience against collusion attacks.

(2)

Addressing the trust issues of third parties and participants in existing PPRL methods, we utilize blockchain smart contracts to manage the entire PPRL process (including verifiable mask generation, task allocation, and node management) and enable trusted auditing. Combined with IPFS for efficient data storage and distribution, the use of tamper-proof records and automated rule execution enhances process transparency and the trustworthiness of computation nodes.

(3)

Through theoretical analysis and experimental validation, we demonstrate that this method ensures data privacy and security while achieving high linkage quality and good scalability, making it suitable for large-scale multi-party collaboration scenarios.

The structure of this paper is organized as follows: Section 2 reviews related work, analyzing existing technologies in the PPRL domain and their limitations. Section 3 introduces the background knowledge and techniques involved in this method. Section 4 elaborates on the proposed PPRL method based on secret sharing and blockchain. Section 5 analyzes the method’s security, computational complexity, and resilience against collusion attacks. Section 6 validates the effectiveness of the method through experiments. Section 7 summarizes the research findings and discusses future directions.

2. Related Works

In recent years, research on PPRL methods has primarily focused on privacy protection while also considering linkage quality and computational efficiency [3,5,6,8]. Among these, Bloom filters have been widely adopted in PPRL due to their excellent space efficiency and fast query capabilities, enabling the encoding of identifiers for similarity matching [11]. However, standard Bloom filters are vulnerable to frequency attacks and cryptanalysis, offering relatively limited privacy protection [6]. To enhance security, researchers have proposed various improved encoding techniques, such as adjacent bit encoding [12], to bolster resistance against attacks. While these encoding methods are generally efficient, they may still leak sensitive information in certain scenarios. In contrast, methods based on secure multi-party computation provide stronger privacy guarantees, allowing matching computations without revealing raw data. Homomorphic encryption enables computations directly on encrypted data, mitigating the risk of plaintext exposure [9]. Laud et al. demonstrated a large-scale PPRL instance using secret sharing on the Sharemind platform [13]. Despite the significant privacy advantages of MPC methods, their high computational and communication overheads pose efficiency bottlenecks for large-scale data applications. To enhance system trustworthiness and auditability, particularly in multi-party collaborative environments lacking trust, blockchain technology has also been applied to PPRL. Nóbrega et al. proposed a blockchain-based PPRL method that leverages smart contracts as a STTP to manage computational tasks during linkage [7]. However, this approach was later criticized for potentially exposing sensitive information during the exchange of Bloom filter segments [8]. To address these security concerns, our prior work [10] explored a different direction, integrating homomorphic encryption with a consortium blockchain framework to enable secure, parallel computation. While this approach successfully enhanced security against malicious adversaries, it also highlighted a critical trade-off: the significant computational overhead inherent to homomorphic encryption remained a primary obstacle to scalability and practical deployment. This challenge underscores a gap in the literature for a solution that can retain the trust and auditability benefits of blockchain while utilizing a more lightweight cryptographic primitive to achieve higher efficiency.

To improve computational efficiency, researchers have explored various optimization techniques, including partitioning, distributed computing, and parallel computing [14]. Partitioning techniques, such as random blocking based on Locality-Sensitive Hashing, can effectively identify similar record pairs while ensuring theoretical correctness, significantly reducing computational load during matching [15,16]. Distributed computing frameworks, such as Apache Flink, support large-scale data processing, enhancing the scalability of PPRL when handling massive datasets [16]. Furthermore, parallel computing methods, by integrating technologies like MapReduce, enable efficient data matching and comparison [10], further improving computational efficiency and reducing processing time. This allows PPRL to operate more effectively in large-scale, multi-party environments.

In terms of linkage quality, researchers have optimized the accuracy and reliability of record linkage from multiple perspectives. For instance, Vaiwsri et al. proposed a novel Bloom filter method for databases with missing values [17]. This approach uses a missing pattern lattice structure to group records and assigns different weights to non-missing attributes to optimize similarity calculations, thereby improving matching accuracy. Additionally, Florens Rohde developed a multi-layer active learning protocol that integrates human review mechanisms to dynamically optimize the matching process [18]. Through iterative learning, this protocol continuously refines matching strategies, minimizing human intervention while maximizing the accuracy and robustness of matches, thus further enhancing linkage quality.

3. Preliminaries and Background

To facilitate understanding of our proposed method, this section provides a detailed explanation of the relevant background knowledge and technical principles.

3.1. Blockchain

Blockchain is a distributed, tamper-resistant ledger technology. In this paper, it serves as a decentralized coordinator, trust anchor, and audit log, leveraging its transparency, immutability, and traceability to provide a highly trusted environment for multi-party collaboration without relying on traditional trusted third parties. The blockchain is primarily responsible for securely storing critical metadata, such as content identifiers (CIDs) for data on IPFS, access rules, task allocation indices, and reputation records of computational nodes [19].

3.2. Smart Contracts

Smart contracts are self-executing code protocols deployed on the blockchain that automatically enforce predefined rules [20]. They are the core mechanism for automating and enforcing the protocol processes of this method, handling specific operational logic, including implementing fine-grained role definitions and data access control policies, coordinating the storage and distribution of secret shares and masked data on IPFS to computational nodes, and managing the audit and verification of final results, as well as dynamically updating the reputation scores of computational nodes.

3.3. InterPlanetary File System

To avoid the high storage costs of blockchain, this method employs IPFS as a distributed file system to store large-scale data, such as Bloom filter shares, masks, and intermediate results. The blockchain only records the unique CIDs of these data. Computational nodes or participants, upon authorization via smart contracts, retrieve the required data directly from IPFS using the CIDs [21]. This strategy of combining on-chain metadata with off-chain data leverages IPFS’s content addressing and distributed storage capabilities, significantly enhancing the system’s scalability [22].

3.4. Bloom Filters

Bloom filters are efficient probabilistic data structures used to represent sets and support membership queries. In privacy-preserving record linkage, they are commonly employed to encode quasi-identifiers (QIDs; such as names or addresses). The specific approach involves decomposing a QID value into q-grams, mapping them to a bit array of length m using k hash functions, and setting the corresponding k bits to 1. This encoding supports approximate matching while providing a degree of privacy protection through the one-way nature of hashing and collision properties.

3.5. Secret Sharing

Secret sharing is a key cryptographic technique for secure multi-party computation, particularly suitable for distributed computing environments [23]. It involves decomposing Bloom filter bits and computational masks into shares and distributing them across multiple computational nodes, ensuring that no single node holds complete information, thereby protecting data privacy in a distributed setting. To support different operations, this method adopts two types of secret sharing schemes:

Boolean Secret Sharing: Primarily based on XOR operations, it is used to securely handle the bits of Bloom filters, enabling computational nodes to compute Boolean shares of the difference between two corresponding bits without revealing the original bit values, denoted as $[d_j{]}_B=[b_{i,j}{]}_B\oplus [b_{j,j}{]}_B$.

Arithmetic Secret Sharing: Based on modular addition, it is used for numerical computations. It securely distributes arithmetic shares of random masks $[r{]}_A$ and constants $[1{]}_A$ required for Boolean-to-arithmetic conversion protocols and supports secure additive aggregation of arithmetic difference shares obtained from Boolean secret sharing, i.e., computing $\sum [d_j{]}_A\left(\mathrm{m}\mathrm{o}\mathrm{d}p\right)$, to derive partial shares of the final Hamming distance [24].

Through the synergistic application of these two secret sharing techniques, this method establishes a foundation for securely and efficiently computing the Hamming distance between records without revealing the specific contents of Bloom filters.

3.6. Hamming Distance

Hamming distance is a metric for measuring the difference between two strings of equal length. For binary strings $A$ and $B$ of length $m$, it is defined as the total number of positions where the corresponding bits differ. Hamming distance can be computed through simple additive aggregation (summing bit differences), which, in a secret sharing framework, is more efficient than computing Dice/Jaccard similarity functions that require secure intersection operations (typically involving complex or high overhead secure multiplications).

4. Methods

The privacy-preserving record linkage method based on secret sharing and blockchain (SSB-PPRL) integrates technologies such as secret sharing, Bloom filters, blockchain, and IPFS to achieve secure matching of multi-party data records. Its core components include the system architecture and three main modules: the data preparation and generation module, the approximate matching module, and the output and audit module. The system architecture leverages the synergy of blockchain and IPFS, using smart contracts to manage data distribution, computation, and verification processes, ensuring both privacy protection and efficiency. The data preparation and generation module are responsible for encoding raw data and decomposing it into distributed shares. The approximate matching module performs secure similarity computations, while the output and audit module verify results and provide traceability.

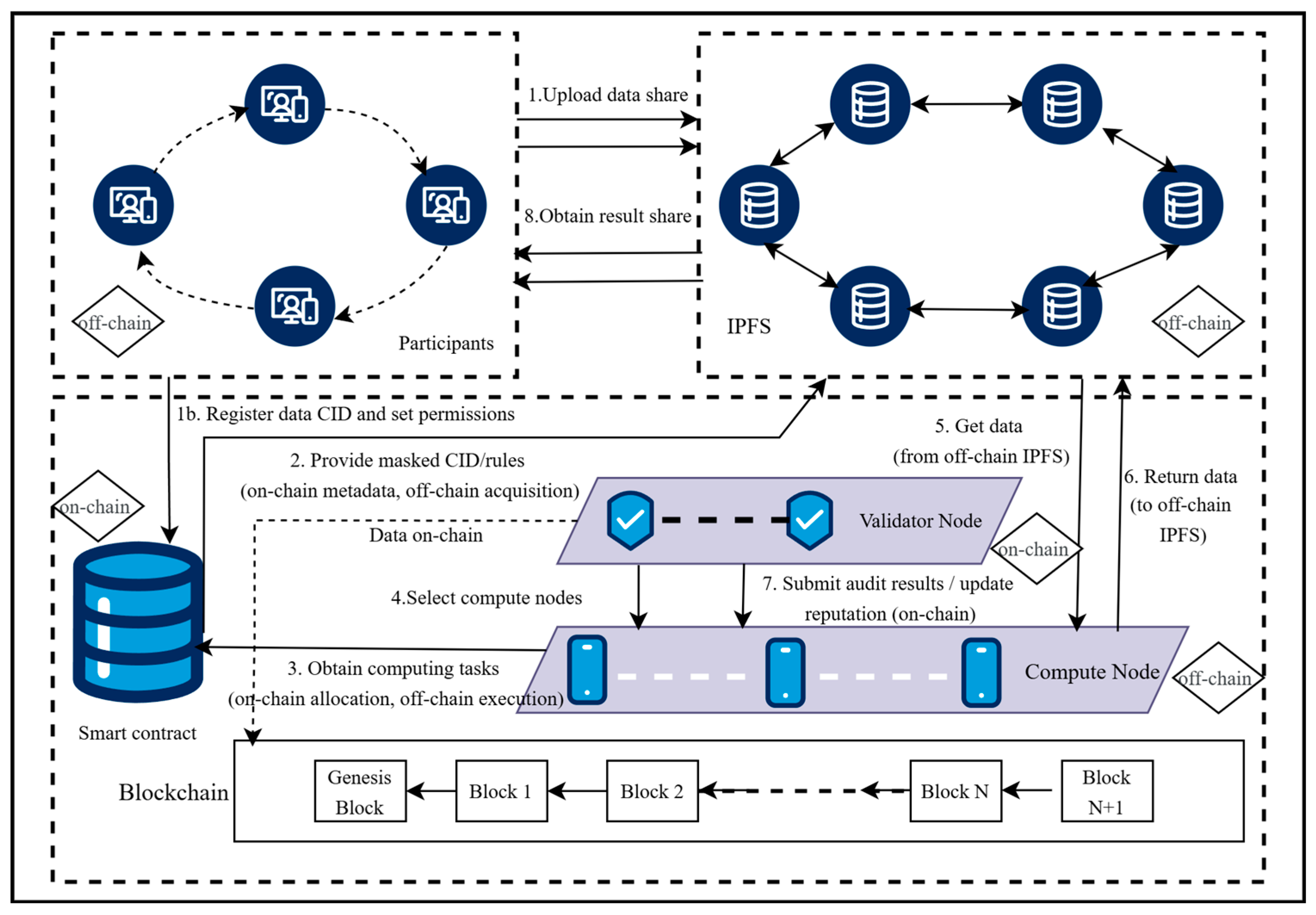
4.1. System Architecture

To implement the SSB-PPRL method, we propose a system architecture integrating blockchain and IPFS. The architecture comprises five components, participants, computational nodes, verification nodes, blockchain, and IPFS, with multiple smart contracts collaboratively managing data distribution, computation, and verification processes [19].

The specific roles in the system are defined as follows:

Participants: Data owners who encode quasi-identifiers into Bloom filters, decompose them into shares using Boolean secret sharing and upload them to IPFS. They only access their own data CIDs and the final results.

Computational Nodes: Off-chain entities that retrieve secret shares and masks from IPFS perform local similarity computations and are restricted to accessing assigned data.

Verification Nodes: On-chain supervisors that audit computation results, update node reputation scores and access output results without interacting with raw data.

Role assignments and data access control are implemented through smart contracts deployed on the blockchain. These contracts define role identities (participants, computational nodes, verification nodes), assign data access permissions, and enforce strict access control logic to ensure sensitive data is only accessed within authorized scopes. The data access control mechanism is designed as follows:

Permission Definition and Negotiation: After participants upload data to IPFS and generate CIDs, they negotiate access permissions with the system through an on-chain mechanism. Metadata associated with each CID is stored in the blockchain’s “data record mapping” in the form of a data structure, including the CID (pointing to Bloom filter shares on IPFS), the data owner’s address, an access permission list (specifying authorized roles or addresses), and an expiration time (defining the validity period of the permission). For example, a participant may propose authorizing a specific computational node to access a particular CID. The system verifies this based on predefined rules (e.g., reputation thresholds) and updates the access permission list upon confirmation.

Access Verification and Time Window: The smart contract provides an access permission verification function. Callers must pass two checks: the current time must be less than or equal to the expiration time, and the caller’s address must be included in the access permission list. Only upon passing these checks can the caller retrieve the CID from the data record mapping and download the data from IPFS. Expired permissions automatically become invalid, preventing unauthorized long-term access.

Dynamic Management and Security: Data owners can revoke or modify permissions at any time. Change requests are validated by the contract for consistency before updating state variables (e.g., the access permission list). To prevent inference attacks, CID distribution is strictly controlled by the contract, ensuring that unauthorized roles cannot directly query the data record mapping. The time window design, combined with on-chain verification, ensures data access remains controllable within the authorized period, enhancing security.

Collaborative Support: The access control contract shares role mappings and reputation information with the computational node selection contract, synchronizes permission states (e.g., expiration) with the audit and verification contract, and provides CIDs and permission rules to the data distribution contract, ensuring compliance in computation and verification processes. Sensitive data is stored on IPFS, with only metadata recorded on the blockchain, making permission negotiation and verification fully transparent and auditable.

The overall system architecture is illustrated in Figure 1.

The system operates in stages: Participants preprocess data, encode it into Bloom filters, split it into secret shares, and upload them to IPFS, generating CIDs. The role and data access control smart contracts negotiate permissions, logging CIDs and permissions on the blockchain. A node selection smart contract chooses computing nodes based on reputation data from an audit verification contract. A data distribution smart contract assigns shares and masks, creating an on-chain index table. Computing nodes download data from IPFS, perform local computations, and upload results to IPFS. The audit verification smart contract inspects results, updates reputation, and syncs permission states. Participants reconstruct the Hamming distance as the outcome. Blockchain records metadata, IPFS stores data, and smart contracts orchestrate the process, ensuring privacy, efficiency, and auditability.

4.2. Data Preparation and Generation Module

The data preparation and generation module is the foundation of the SSB-PPRL method, a privacy-preserving record linkage approach based on secret sharing and blockchain. It transforms raw records into a distributed computing format and generates masks via smart contracts for matching and auditing. The module includes data encoding, Boolean secret sharing generation, mask generation, computing node selection, and data distribution. Data is split into distributed shares and managed by blockchain and IPFS, as shown in Figure 2.

4.2.1. Data Encoding

Participants negotiate preprocessing parameters via smart contracts to standardize data formats and provide initial privacy protection, ensuring consistency for subsequent processing. Quasi-identifier attributes are then encoded into Bloom filters to efficiently match similarity while preserving ambiguity for enhanced privacy protection. Consider a dataset $D=\{r_1,r_2,\dots ,r_N\}$, where each record $r_i$ has a set of quasi-identifier attributes $A=\{a_1,a_2,\dots ,a_p\}$. All participants negotiate Bloom filter parameters—bit length $m$ and number of hash functions $k$—through a blockchain smart contract, with results recorded on-chain to ensure consistency and transparency. For example, Alice maps the quasi-identifiers of record $r_{A_i}$ to a Bloom filter $B{F}_{A_i}=[a_{i1},a_{i2},\dots ,a_{im}]$ ($a_{ij}\in \left\{\mathrm{0,1}\right\}$) using $k$ hash functions. Bob performs the same operation for record $r_{B_i}$, generating $B{F}_{B_i}=[b_{i1},b_{i2},\dots ,b_{im}]$. Parameter selection must balance security and efficiency: a larger $m$ and appropriate $k$ reduce false positives and enhance privacy, but excessively large values decrease the efficiency of Boolean secret sharing decomposition and matching. Thus, parameters are chosen to optimize both aspects.

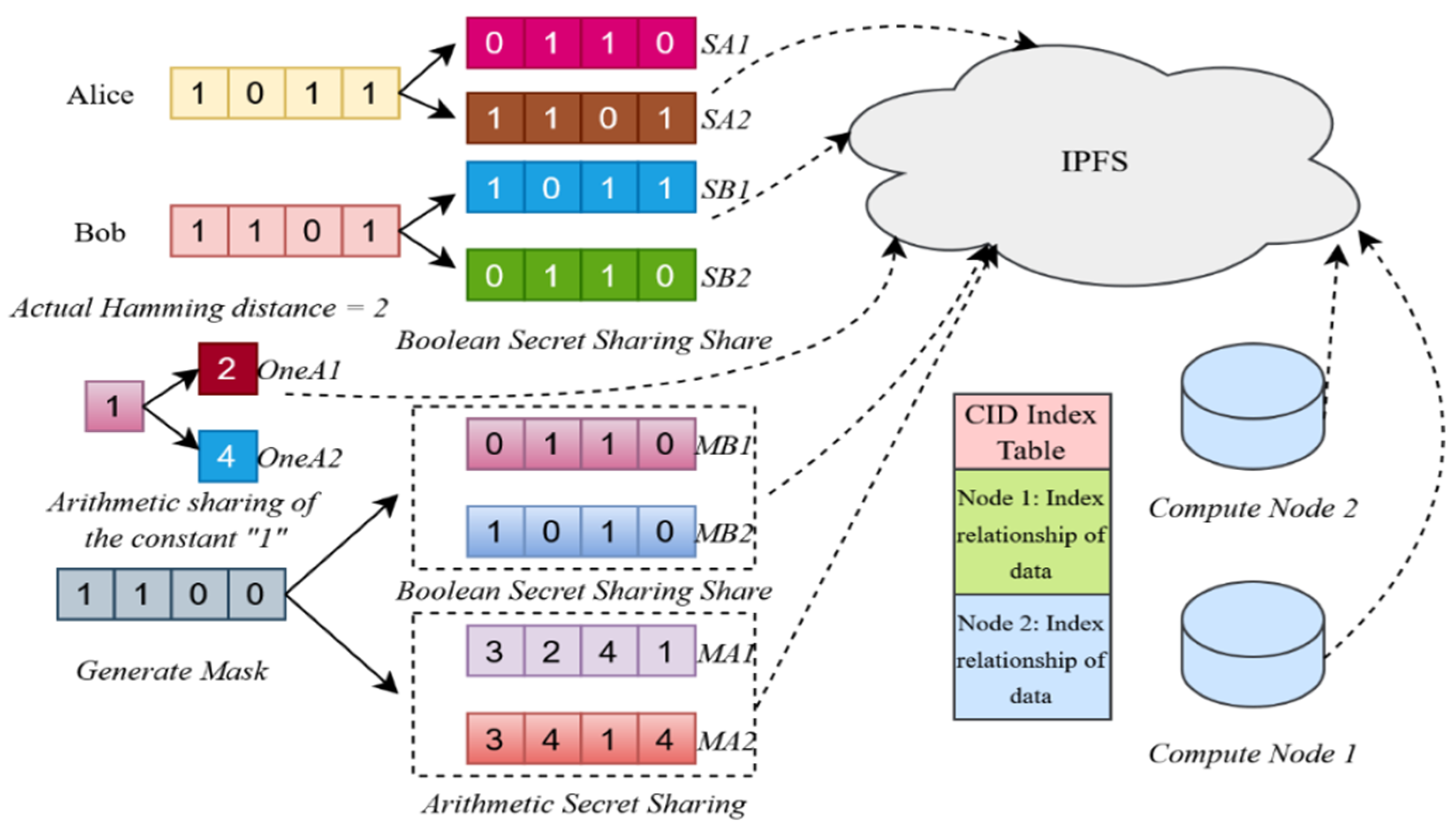
4.2.2. Share Generation of Boolean Secret Sharing

Bloom filters enable fast queries while preserving privacy but are vulnerable to frequency attacks. To mitigate this, participants split each bit into Boolean secret shares and generate masks via smart contracts, distributing them to different computing nodes to ensure no single node accesses complete data, enhancing distributed privacy protection [25].

For the $j$-th bit $a_{ij}\in \left\{\mathrm{0,1}\right\}$ of Alice’s Bloom filter $B{F}_{A,i}$, Boolean secret sharing generates $t$ shares $s_{ij,1},s_{ij,2},\dots ,s_{ij,t}\in \left\{\mathrm{0,1}\right\}$, satisfying

$$a_{ij}=s_{ij,1}\oplus s_{ij,2}\oplus \cdots \oplus s_{ij,t}$$

(1)

Similarly, the $j$-th bit $b_{ij}$ of Bob’s $B{F}_{B,i}$ follows the same condition. Here, $\oplus$ denotes the XOR operation, which ensures that all $t$ shares are required for reconstruction, with fewer than $t$ shares revealing no information about the original value, and randomness obscures frequency patterns.

The generation steps, using Alice’s $a_{ij}$ and Bob’s $b_{ij}$ as examples, are as follows:

• Determine $t$ shares (a system parameter, e.g., $t=3$), randomly generating the first $t-1$ shares and adjusting the last to satisfy the XOR condition.
• For $k=1$ to $t-1$, randomly generate uniformly distributed $s_{ij,k}$, introducing randomness to conceal frequency patterns.
• For Alice, set $s_{ij,t}=a_{ij}\oplus s_{ij,1}\oplus s_{ij,2}\oplus \cdots \oplus s_{ij,t-1}$ (same for Bob), ensuring the XOR result is correct.
• The generated shares form ${\mathrm{shares}}_{A,ij}=\{s_{ij,1},s_{ij,2},\dots ,s_{ij,t}\}$ and ${\mathrm{shares}}_{B,ij}$, which are uploaded to IPFS, with CIDs stored on the blockchain.

4.2.3. Mask Generation and Data Distribution

In distributed computing, nodes compute the difference between two Bloom filters using the XOR operation ($d_i=a_i\oplus b_i$), generating Boolean-shared differences. These are converted to arithmetic shares using masks ($m_i$) to support additive aggregation for Hamming distance, ensuring computational security and privacy of results.

Masks are designed to match the structure of Bloom filters and are generated per quasi-identifier attribute. The dataset contains $n$ attributes, each encoded as a Bloom filter of length $m$, with a corresponding mask $M_j$ (length $m$). Each mask $M_j$ is decomposed into the following: Boolean shares: $M_j[i]$ is split into $t$ Boolean shares, satisfying the following: $m_{j,i,1}\oplus \cdots \oplus m_{j,i,t}=M_j\left[i\right].$ Arithmetic shares: $M_j\left[i\right]$ is split into $t$ arithmetic shares, satisfying

$$s_{j,i,1}+\cdots +s_{j,i,t}\equiv M_j\left[i\right]\left(\mathrm{m}\mathrm{o}\mathrm{d} p\right)$$

(2)

where $p$ is a large prime.

To improve efficiency and reduce the number of masks, record pairs are grouped and $k$ sets of masks are generated. Each set is assigned to a group of record pairs rather than generating unique masks for each pair. The value of $k$ balances efficiency and security: a smaller $k$ reduces computational and storage overhead but increases the risk of collusion inference; a larger $k$ reduces the number of record pairs sharing masks, enhancing resistance to collusion but increasing costs. The value of $k$ can be dynamically adjusted based on the total number of record pairs $N$ and system resources.

Mask Generation Process (Managed by Blockchain Smart Contracts):

• Record Pair Grouping: The total number of record pairs $M$ ($M=\left|D_A\right|\cdot \left|D_B\right|$) is divided into $k$ groups ($k\ll M$, e.g., $k\approx \sqrt{M}$ or a fixed value like $k=10$) using deterministic hashing, balancing security and efficiency.
• Mask Generation: For each group $g$ ($g=\mathrm{1,2},\dots ,k$) and attribute $j$ ($j=\mathrm{1,2},\dots ,n$), a mask $M_{g,j}$ of length $m$ is generated using a Verifiable Random Function (VRF) with $g$ and $j$ as inputs, ensuring randomness and fairness.
• Share Decomposition: Boolean shares: $M_{g,j}\left[i\right]$ is decomposed into $t$ shares. Generate $t-1$ random Boolean shares $m_{g,j,i,1},\dots ,m_{g,j,i,t-1}$, and compute: $m_{g,j,i,t}=M_{g,j}\left[i\right]\oplus m_{g,j,i,1}\oplus \cdots \oplus m_{g,j,i,t-1}.$ Arithmetic shares: $M_{g,j}\left[i\right]$ is decomposed into $t$ shares. Generate $t-1$ random arithmetic shares $s_{g,j,i,1},\dots ,s_{g,j,i,t-1}$, and compute: $s_{g,j,i,t}=\left(M_{g,j}\left[i\right]-\sum _{l=1}^{t-1} s_{g,j,i,l}\right)(\mathrm{m}\mathrm{o}\mathrm{d} p).$ Constant 1 Shares: To support Boolean-to-arithmetic (B2A) conversion, generate $t$ arithmetic shares $[1{]}_{A_1},\dots ,[1{]}_{A_t}$, satisfying $\sum _{l=1}^t [1{]}_{A_l}\equiv 1(\mathrm{m}\mathrm{o}\mathrm{d} p),$ by randomly generating $t-1$ shares and computing $[1{]}_{A_t}$.
• Storage and Management: The generated Boolean shares $m_{g,j,i,l}$, arithmetic shares $s_{g,j,i,l}$, and constant 1 shares $[1{]}_{A_l}$ are uploaded to IPFS, obtaining CIDs. These CIDs, along with the CIDs of secret shares uploaded during the data preparation phase, are recorded and managed by smart contracts (e.g., mask management or data distribution contracts) to ensure efficient and secure data distribution.

4.2.4. Compute Node Selection

After masks and secret shares are uploaded to IPFS, the blockchain triggers the compute node selection smart contract to choose a suitable set of nodes for executing record linkage tasks efficiently and securely [26].

A reputation-based evaluation mechanism is executed by on-chain validation nodes. From $N$ candidate nodes, $k$ nodes ($\{n_1,n_2,\dots ,n_k\}$) are selected, with $k$ determined through negotiation by the task requester. Validation nodes assess each node $i$ based on three key metrics: reputation score $C_i\in [-\mathrm{1,1}]$, indicating trustworthiness; computational power $P_i\in \left[\mathrm{0,1}\right]$, normalized to reflect hardware performance; and task completion rate $R_i\in \left[\mathrm{0,1}\right]$, representing the proportion of successfully completed tasks, measuring execution stability. New nodes, lacking historical data, start with $C_i=0$, $P_i=0$, $R_i=0$. The selection results are synchronized on the blockchain via a consensus mechanism (e.g., PBFT), ensuring consistency and transparency [10].

An audit verification contract dynamically updates and stores node parameters $C_i$, $P_i$, and $R_i$. New nodes begin with $C_i=0$, $P_i=0$, $R_i=0$, and the contract periodically updates these based on task execution logs (e.g., completion time, result accuracy), ensuring parameters accurately reflect node performance and provide a reliable basis for selection.

• Selection Process:

• Weighted Scoring: The task requester specifies the number of nodes $k$ and security level $S\in \{\mathrm{0,1},2\}$ (corresponding to high, medium, or low security requirements). Validation nodes compute each node’s weighted score:

  $$w_i=\alpha C_i+\beta P_i+\gamma R_i$$

  (3)

  where weights are $\alpha =0.5$ (reputation), $\beta =0.3$ (computational power), $\gamma =0.2$ (completion rate), satisfying $\alpha +\beta +\gamma =1$. Weights can be adjusted through participant negotiation.
• Random Adjustment: To ensure new nodes ($w_i=0$) have a chance to participate, a Verifiable Random Function (VRF) adjusts scores:

  $$w_i^{\prime }=w_i+\mathrm{VRF}(\mathrm{seed},i)\cdot \delta ,\delta \in \left[\mathrm{0,0.2}\right]$$

  (4)

  where $\mathrm{seed}$ is collectively generated by validation nodes to ensure fairness, and $\delta$ controls the random offset magnitude.
• Grouping and Selection: Nodes are divided into four groups based on $C_i$:

  ○

  $H=\{i\mid C_i\ge 0.8\}$ (high reputation);

  ○

  $M=\{i\mid 0.5\le C_i<0.8\}$ (medium reputation);

  ○

  $L=\{i\mid 0<C_i<0.5\}$ (low reputation);

  ○

  $Z=\{i\mid C_i=0\}$ (new nodes). Proportions are set based on $S$, e.g., for $S=0$ (high security): $r_H=0.7$, $r_M=0.2$, $r_L=0$, $r_Z=0.1$. Calculate group sizes:

• $n_H=\lfloor k\cdot r_H\rfloor ,n_M=\lfloor k\cdot r_M\rfloor ,n_L=\lfloor k\cdot r_L\rfloor ,n_Z=\lfloor k\cdot r_Z\rfloor .$ If the total is less than $k$, increase $n_H$. After verifying node availability, select nodes from each group in descending order of adjusted scores $w_i^{\prime }$, ensuring the total number of nodes is $k$.

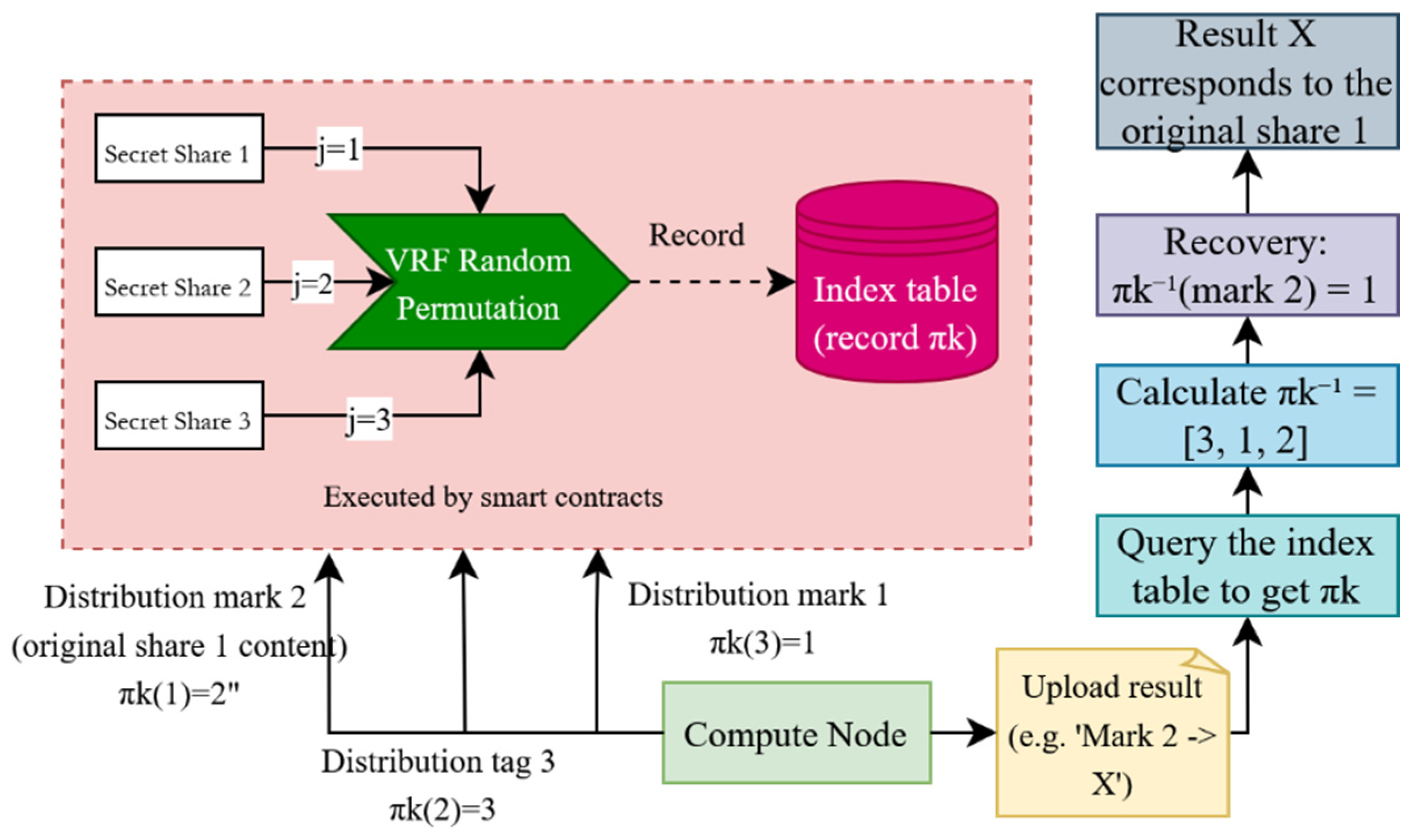
4.2.5. Data Distribution

After compute nodes are selected, the blockchain triggers the data distribution smart contract to coordinate the allocation of data shares stored on IPFS, preparing for approximate matching computations. The core process includes record pair grouping, compute node assignment, random permutation, and data index table generation.

Record Pair Grouping and Input Preparation: The contract retrieves CIDs for task-required data, including Boolean secret shares of Bloom filters uploaded by participants; system-generated mask Boolean shares, mask arithmetic shares, and arithmetic shares of the constant 1; list of selected compute nodes; system parameters: number of mask groups $K$, number of compute nodes/shares per record pair $t$, and total selected nodes $N$. To improve efficiency and enable mask reuse, the contract divides record pairs into $K$ groups using a deterministic hash function, with all pairs in the same group sharing the same mask set.

Compute Node Assignment and Random Permutation: For a record pair $(B_A,B_B)$, assumed to belong to group $g$, the contract assigns $t$ compute nodes to process its $t$ secret shares. Using a Verifiable Random Function (VRF) with seed $\mathrm{s}\mathrm{e}\mathrm{e}\mathrm{d}=\mathrm{concat}(g,A_{\mathrm{id}},B_{\mathrm{id}})$, it randomly selects $t$ nodes from $N$, denoted as $\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{d}\_\mathrm{n}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{s}=\{c_1,c_2,\dots ,c_t\}$. To prevent collusion attacks among nodes, a random permutation mechanism is introduced to obfuscate the logical numbering of shares, breaking their direct association with original data. For each selected node $c_k$ ($k=\mathrm{1,2},\dots ,t$), the contract generates a unique permutation ${\pi }_k$ using VRF with seed $\mathrm{s}\mathrm{e}\mathrm{e}\mathrm{d}=\mathrm{concat}(g,A_{\mathrm{id}},B_{\mathrm{id}},k)$, reordering the set $\{\mathrm{1,2},\dots ,t\}$. For example, when $t=3$, ${\pi }_k$ might be $[2,3,1]$. When node $c_k$ processes logical share $j$ ($j=1,2,\dots ,t$), it retrieves the physical share index:

$${\mathrm{mapped}}_j={\pi }_k\left(j\right).$$

(5)

For instance, if ${\pi }_k=[2,3,1]$, logical share $j=1$ corresponds to physical share 2, $j=2$ to physical share 3, and $j=3$ to physical share 1. Random permutation, by generating a unique mapping for each node, disrupts fixed share assignments, significantly reducing the risk of colluding nodes inferring original data. The permutation process, driven by VRF, ensures randomness and verifiability, guaranteeing fair and auditable allocation while maintaining computational efficiency, as it only involves index remapping without requiring additional cryptographic operations. The random permutation algorithm process is shown in the following Figure 3:

Data Index Table Generation: One of the core tasks of data distribution is generating an index table and storing it on the blockchain. This index table precisely records the allocation details for each computational task, specifying which computing node is responsible for processing which logical share of which record pair, along with the specific data required to complete the task. The index table is typically a key–value store, with keys defined as the tuple $(g,(B_A,B_B),k,j)$, where $g$ is the mask group number for the record pair, $(B_A,B_B)$ is the record pair identifier, $k$ identifies the compute node $c_k$, and $j$ is the logical share index (from 1 to $t$). The value contains the CIDs of all data required to complete task $(k,j)$, along with the node’s permutation information. Specifically, it includes the following: ${\mathrm{CID}}_{s_{A,{\pi }_k\left(j\right)}}$: CID of the ${\pi }_k\left(j\right)$-th Boolean secret share of $B_A$; ${\mathrm{CID}}_{s_{B,{\pi }_k\left(j\right)}}$: CID of the ${\pi }_k\left(j\right)$-th Boolean secret share of $B_B$; ${\mathrm{CID}}_{m_{g,{\pi }_k\left(j\right)}}$: CID of the ${\pi }_k\left(j\right)$-th Boolean share of the $g$-th mask group; ${\mathrm{CID}}_{a_{g,{\pi }_k\left(j\right)}}$: CID of the ${\pi }_k\left(j\right)$-th arithmetic share of the $g$-th mask group; ${\mathrm{CID}}_{[1{]}_{A,{\pi }_k\left(j\right)}}$: CID of the ${\pi }_k\left(j\right)$-th arithmetic share of the constant “1”; ${\pi }_k$: the complete random permutation function corresponding to compute node $c_k$.

The smart contract iterates through all record pairs to be processed, the $t$ compute nodes assigned to each pair, and the $t$ logical share indices $j$ for each node. It computes the mapped physical index ${\mathrm{mapped}}_j={\pi }_k\left(j\right)$, retrieves or combines the corresponding CIDs, and stores this information as key–value pairs in the index table. The algorithm for data distribution is described in pseudocode as Algorithm 1.

Algorithm 1 Data Distribution Algorithm

Input: record_pairs: List of record pairs to be processed; k: Number of mask groups; n: Number of computation nodes per record pair; total_nodes: Total selected computation nodes Output: index_table: Mapping of tasks to computation nodes with CIDs and permutations  1: for each record_pair in record_pairs do  2:   group_id ← DeterministicHash(record_pair) mod k  3:   selected_nodes ← VRFSelectNodes(total_nodes, n)  4:   for each node in selected_nodes do  5:         perm ← VRFGeneratePermutation(n, seed = (record_pair, node))  6:         physical_share ← perm(1)  7:         task_key ← (group_id, record_pair, node, 1)  8:         task_value ← (GetCIDs(record_pair, group_id, physical_share), perm)  9:         index_table[task_key] ← task_value 10:    end for 11: end for 12: StoreIndexTableToBlockchain(index_table) 13: return index_table

In Algorithm 1, lines 1–3 iterate through record pairs, group them via hashing, and randomly select computing nodes for each pair. Lines 4–9 generate a random permutation for each node, compute physical share indices, create task key–value pairs, and populate the index table. Lines 10–13 store the index table on the blockchain and return.

4.3. Approximate Matching Module

The core task of the approximate matching module is to securely and efficiently compute the similarity between records in a distributed environment, using secret shares and masked data generated by the data preparation and generation module, with hamming distance as the metric. The main process includes data acquisition, local difference computation, Boolean-to-arithmetic share conversion, and the generation of partial Hamming distance results. The module relies on local collaboration among multiple computing nodes to perform matching computations, optimizing storage and distribution efficiency through the collaboration of blockchain and IPFS [27]. The data processing of this module is illustrated in Figure 4, taking the processing of a single computing node as an example:

The index table generated by the data distribution smart contract is recorded on the blockchain. This action ensures the transparency, immutability, and auditability of the data distribution process. Based on the assigned task $(g,(B_A,B_B),j)$, computing node $c_k$ queries the index table on the blockchain to obtain the CIDs of the data shares required to complete its task, along with its own random permutation ${\pi }_k$. Subsequently, the computing node can asynchronously download these data shares from IPFS to prepare for approximate matching computations. To enhance security and resistance to collusion, this module adopts a multi-node decentralized strategy, with the number of computing nodes $t$ significantly exceeding the number of shares. The data distribution smart contract randomly allocates data based on participants, records, and attributes, ensuring high data dispersion. Even if some nodes collude, it is difficult to gather enough shares to reconstruct the original information.

The computation process centers on localized operations. After downloading data based on the index table, each computing node independently performs local difference calculations, Boolean-to-arithmetic share conversions, and partial Hamming distance result generation. For a pair of records $(BF{A}_{i,j},BF{B}_{i,j})$, the node processes each bit $l$ ($l$ from 1 to $m$) using obfuscated Boolean shares $[a_{i,j,l}{]}_B^{{\pi }_{\mathrm{gid}}\left(k\right)}$ and $[b_{i,j,l}{]}_B^{{\pi }_{\mathrm{gid}}\left(k\right)}$ to compute the local difference $[d_{i,j,l}{]}_B^k$. Through a modified B2A protocol, $[d_{i,j,l}{]}_B^k$ is converted to an arithmetic share $[d_{i,j,l}{]}_A^k$, which is accumulated to generate the partial Hamming distance share $[D_{i,j}{]}_A^k$. The random permutation mechanism is applied throughout the process to ensure data privacy. The specific steps are as follows.

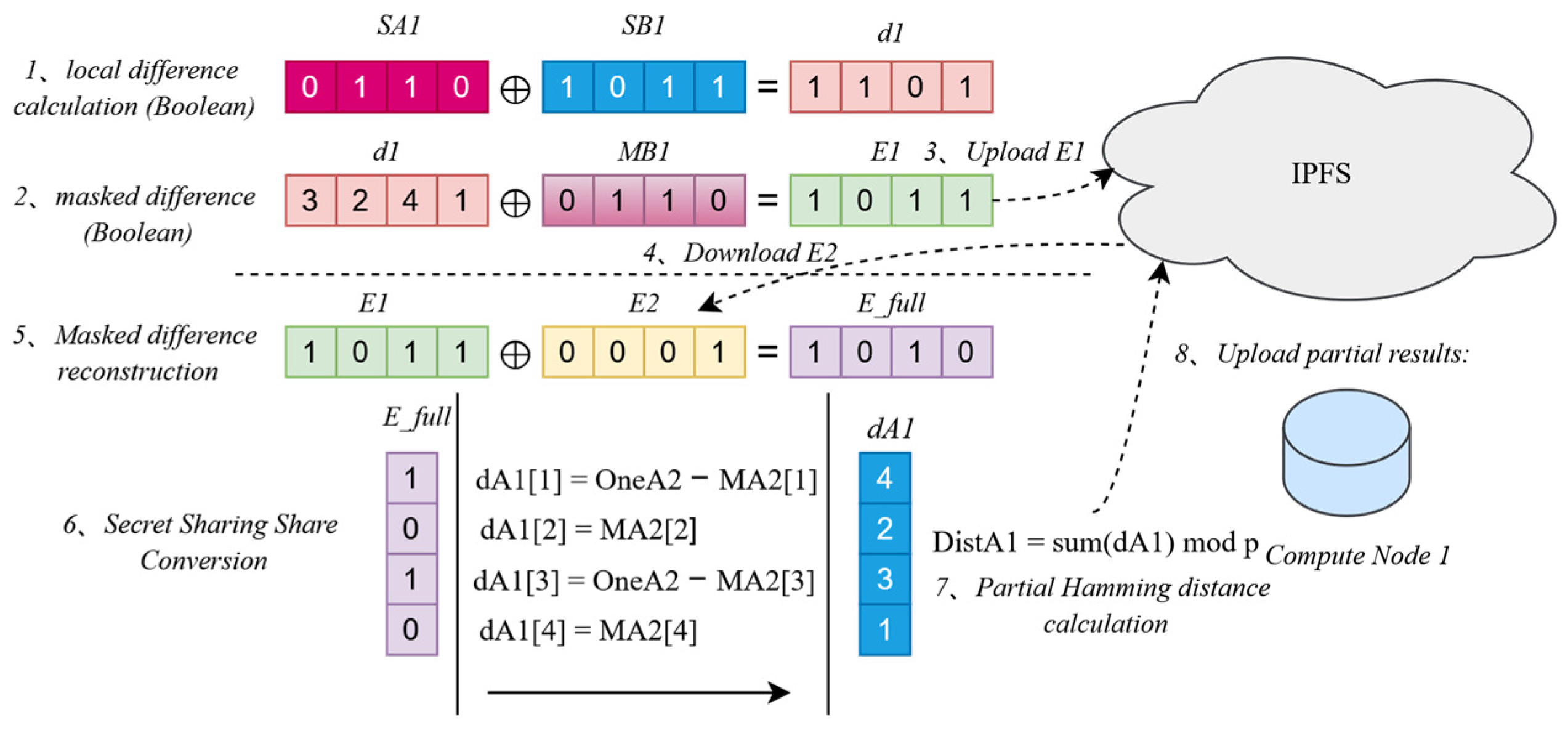
4.3.1. Local Difference Calculation and Masked Difference Vector Generation

The computation of the approximate matching module begins with the Boolean shares of local differences. Each computing node $N_k$ performs an XOR operation for each bit $l$ (where $l$ ranges from 1 to $m$) to calculate the Boolean share of the local difference. The computation formula is as follows:

$$[d_{i,j,l}{]}_B^k=[a_{i,j,l}{]}_B^{{\pi }_{\mathrm{gid}}(k)}\oplus [b_{i,j,l}{]}_B^{{\pi }_{\mathrm{gid}}(k)}$$

(6)

Due to the random permutation ${\pi }_{\mathrm{gid}}$ introduced in data distribution, the node processes obfuscated Boolean shares. However, the properties of the XOR operation ensure that the result is independent of the order, and the shares from all $t$ nodes satisfy

$$d_{i,j,l}=\underset{k=1}{\overset{t}{⨁}} [d_{i,j,l}{]}_B^k$$

(7)

Subsequently, node $N_k$ uses pre-generated Boolean mask shares $[r_{\mathrm{gid},l}{]}_B^{{\pi }_{\mathrm{gid}}\left(k\right)}$ (corresponding to group $\mathrm{g}\mathrm{i}\mathrm{d}$) to compute the masked difference vector $E_k=(e_{1,k},e_{2,k},\dots ,e_{m,k})$ for all $m$ bits. The masked difference for each bit is defined as follows:

$$e_{l,k}=[d_{i,j,l}{]}_B^k\oplus [r_{\mathrm{gid},l}{]}_B^{{\pi }_{\mathrm{gid}}(k)}$$

(8)

The permutation mechanism ensures that the masks correctly correspond to the Boolean shares, thereby guaranteeing the correctness of the computation results while protecting data privacy.

4.3.2. Batch Interaction and Data Sharing

Nodes share masked difference vectors in batches. Node $N_k$ uploads its vector $E_k$ (a Boolean sequence of length $m$) to IPFS, obtaining the content identifier ${\mathrm{cid}}_{E_k}$. It then submits the task identifier and ${\mathrm{cid}}_{E_k}$ to the smart contract to record the upload. The smart contract logs these submissions and, once all $t$ nodes have submitted, notifies relevant nodes by triggering an event (containing the task identifier, node identifiers, and corresponding content identifier list) or updating the task status [28]. Node $N_k$ monitors blockchain events or queries the task status to confirm that all $t$ nodes have completed submissions. Upon confirmation, it retrieves the content identifiers of the other $t-1$ nodes (e.g., ${\mathrm{cid}}_{E_1},\dots ,{\mathrm{cid}}_{E_{k-1}},{\mathrm{cid}}_{E_{k+1}},\dots ,{\mathrm{cid}}_{E_t}$) from the smart contract and downloads the corresponding vectors $E_1,\dots ,E_{k-1},E_{k+1},\dots ,E_t$ via IPFS. The random permutation ${\pi }_{\mathrm{gid}}$, recorded in the index table, allows the node to restore the correct order of downloaded data, ensuring consistency.

4.3.3. Masked Difference Reconstruction and Conversion

After obtaining the masked difference vectors from all nodes, node $N_k$ performs local reconstruction and Boolean-to-arithmetic share conversion. Using its own vector $E_k$ and the $t-1$ downloaded vectors, the node computes the complete masked difference vector $E_{\mathrm{full}}=(e_1,e_2,\dots ,e_m)$, where

$$e_l=e_{l,1}\oplus e_{l,2}\oplus \cdots \oplus e_{l,t}$$

(9)

Based on ${\pi }_{\mathrm{gid}}$, the node ensures that $e_{l,k}$ corresponds to the correct index. The XOR property guarantees the following:

$$e_l=\underset{k=1}{\overset{t}{⨁}} e_{l,k}=d_{i,j,l}\oplus r_{\mathrm{gid},l}$$

(10)

Here, the randomness of $r_{\mathrm{gid},l}$ protects $d_{i,j,l}$ from being exposed. Next, node $N_k$ uses $e_l$, the arithmetic mask share $[r_{\mathrm{gid},l}{]}_A^{{\pi }_{\mathrm{gid}}(k)}$, and the arithmetic share of the constant 1, $[1{]}_A^{{\pi }_{\mathrm{gid}}(k)}$, to compute the arithmetic share for each bit $l$. The results are as follows:

If $e_l=0$ (i.e., $d_{i,j,l}=r_{\mathrm{gid},l}$)

$$[d_{i,j,l}{]}_A^k=[r_{\mathrm{gid},l}{]}_A^{{\pi }_{\mathrm{gid}}(k)}\mathrm{m}\mathrm{o}\mathrm{d} p$$

(11)

If $e_l=1$ (i.e., $d_{i,j,l}=1-r_{\mathrm{gid},l}$)

$$[d_{i,j,l}{]}_A^k=[1{]}_A^{{\pi }_{\mathrm{gid}}(k)}-[r_{\mathrm{gid},l}{]}_A^{{\pi }_{\mathrm{gid}}(k)}\mathrm{m}\mathrm{o}\mathrm{d} p$$

(12)

The permutation mechanism ensures consistency, and the shares from all nodes satisfy

$$\sum _{k=1}^t [d_{i,j,l}{]}_A^k=d_{i,j,l}\mathrm{m}\mathrm{o}\mathrm{d} p$$

(13)

The algorithm for batch interaction and masked difference reconstruction is described in pseudocode as shown in Algorithm 2.

Algorithm 2 Share And Reconstruct Masked Diff Algorithm

Input: masked_diff: Masked difference vector; n: Number of computation nodes; perm: Permutation function for data reordering Output: full_masked_diff: Fully reconstructed masked difference  1: cid_masked_diff ← UploadToIPFS(masked_diff)  2: SubmitToSmartContract(task_id, node_id, cid_masked_diff)  3: WaitForAllNodes(task_id, n)  4: other_cids ← GetOtherNodesCIDs(task_id, n)  5: other_masked_diffs ← [DownloadFromIPFS(cid) for cid in other_cids]  6: Reorder(other_masked_diffs, perm)  7: full_masked_diff ← masked_diff  8: for j ← 1 to n − 1 do  9:        for i ← 1 to m do 10:            full_masked_diff[i] ← full_masked_diff[i] XOR other_masked_diffs[j][i] 11:        end for 12: end for 13: return full_masked_diff

In Algorithm 2, lines 1–6 handle uploading the local masked difference to IPFS and submitting it to the smart contract, then wait for all nodes to submit, download other nodes’ masked differences, and reorder them using the permutation function. Lines 7–13 aggregate the local and other nodes’ masked differences through bitwise XOR operations, generating and returning the complete masked difference vector for subsequent processing.

4.3.4. Hamming Distance Calculation and Result Upload

Finally, node $N_k$ calculates the partial Hamming distance and uploads the result. It locally sums the arithmetic shares for all $m$ bits to generate the partial Hamming distance share:

$$[D_{i,j}{]}_A^k=\left(\sum _{l=1}^m [d_{i,j,l}{]}_A^k\right)\mathrm{m}\mathrm{o}\mathrm{d} p$$

(14)

Subsequently, the node uploads $[D_{i,j}{]}_A^k$ along with the obfuscated index ${\pi }_{\mathrm{gid}}\left(k\right)$ to IPFS, generating a CID and recording it via the smart contract. Batch interaction reduces communication frequency [29], and the random permutation mechanism enhances privacy protection, ensuring the computation process is both efficient and secure.

The algorithm for masked difference conversion and Hamming distance calculation is described in pseudocode as shown in Algorithm 3.

Algorithm 3 B2A conversion And Hamming Distance Algorithm

Input: full_masked_diff: Fully reconstructed masked difference; mask_arith_share: Arithmetic mask share; const_one_share: Arithmetic share of constant one; m: Length of Bloom filter Output: partial_hamming_share: Partial Hamming distance share  1: arith_diff ← []  2: for i ← 1 to m do  3:        if full_masked_diff[i] = 0 then  4:            arith_diff.append(mask_arith_share[i])  5:        else  6:            arith_diff.append(const_one_share[i] - mask_arith_share[i])  7:        end if  8: end for  9: partial_hamming_share ← 0 10: for i ← 1 to m do 11:        partial_hamming_share ← partial_hamming_share + arith_diff[i] 12: end for 13: return partial_hamming_share

In Algorithm 3, lines 1–8 convert each bit of the fully reconstructed masked difference into an arithmetic share vector using the arithmetic mask share and the arithmetic share of constant one, achieving a Boolean-to-arithmetic conversion. Lines 9–13 sum the arithmetic share vector to generate the partial Hamming distance share, which is uploaded to IPFS, submitted to the smart contract, and returned for final result aggregation.

4.4. Output and Audit Module

The output and audit module are the final component of this method, handling the Hamming distance result shares from the approximate matching module, aggregating them to produce the matching results, and ensuring computational correctness and security through audit verification via smart contracts and validation nodes. Blockchain and IPFS are utilized to achieve output and traceability, allowing participants to access only the final results without exposure to masks or intermediate data, with masks generated by the mask distribution contract. Validation nodes randomly sample and recompute results to maintain credibility and node reputation. All actions and data are recorded on the blockchain and stored on IPFS, ensuring security, efficiency, and transparency.

4.4.1. Result Aggregation and Output

After completing the approximate matching tasks, computing nodes upload their partial hamming distance shares to IPFS and record the corresponding CIDs on the blockchain via smart contracts [30]. Participants query the blockchain using the task identifier to obtain the CIDs of the $t$ shares $[D_{i,j}{]}_k^A$ ($k=1,\dots ,t$) for record pair $(i,j)$. They download the shares from IPFS, restore the original order using the index table ${\pi }_{\mathrm{gid}}$ ($[D_{i,j}{]}_A^{{\pi }_{\mathrm{gid}}^{-1}(k)}$), and reconstruct the Hamming distance with the following formula:

$$D_{i,j}=\sum _{k=1}^t [D_{i,j}{]}_A^k\mathrm{m}\mathrm{o}\mathrm{d} p$$

(15)

Participants only obtain $D_{i,j}$, without access to intermediate values or original Bloom filters, ensuring privacy. The Hamming distance can be directly output or further processed, such as applying thresholds to filter similar record pairs.

4.4.2. Audit and Verification

To ensure the integrity and accuracy of computing nodes’ results, the audit verification contract coordinates validation nodes to perform the audit process.

• Trigger and Sampling: Upon activation, validation nodes use a Verifiable Random Function to randomly select a portion of the result shares $[D_{i,j}{]}_k^A$ for verification.
• Data Retrieval: For sampled shares $[D_{i,j}{]}_k^A$, validation nodes query the blockchain’s index table to obtain CIDs and download from IPFS: the sampled share $[D_{i,j}{]}_k^A$, corresponding Bloom filter boolean shares $[a_{i,j,l}{]}_{{\pi }_{\mathrm{gid}}(k)}^B$ and $[b_{i,j,l}{]}_{{\pi }_{\mathrm{gid}}(k)}^B$, mask boolean shares $[r_{\mathrm{gid},l}{]}_{{\pi }_{\mathrm{gid}}(k)}^B$, mask arithmetic shares $[r_{\mathrm{gid},l}{]}_{{\pi }_{\mathrm{gid}}(k)}^A$, constant “1” arithmetic shares $[1{]}_{{\pi }_{\mathrm{gid}}(k)}^A$, and permutation data ${\pi }_{\mathrm{gid}}$.
• Recomputation: Using the retrieved input and mask shares, validation nodes independently recompute the core steps of the approximate matching module to generate a reference value, denoted $[D_{i,j}{]}_{k,\mathrm{ref}}^A$.
• Verification: Validation nodes compare the uploaded share $[D_{i,j}{]}_k^A$ with the recomputed reference $[D_{i,j}{]}_{k,\mathrm{ref}}^A$. If they satisfy $[D_{i,j}{]}_k^A\equiv [D_{i,j}{]}_{k,\mathrm{ref}}^A(\mathrm{m}\mathrm{o}\mathrm{d} p)$, the share passes verification; otherwise, it is marked as incorrect. The trustworthiness of a computing node’s task execution is determined based on the verification results of all sampled shares [31].

4.4.3. Reputation Management

Reputation management, a core function of the audit verification contract, ensures node parameters reflect true performance, guiding the node selection contract.

• Reputation Score $C_i$ Update: $C_i\in [-\mathrm{1,1}]$, initialized at 0, is updated based on task outcomes:
  Correct task: $C_i^{\prime }=\mathrm{m}\mathrm{i}\mathrm{n}(C_i+\mathrm{0.1,1})$. Incorrect task: $C_i^{\prime }=\mathrm{m}\mathrm{a}\mathrm{x}(C_i-0.3,-1)$. Severe malicious behavior (e.g., data tampering): $C_i^{\prime }=-1$. Incentives for consistency: Three consecutive correct tasks: $C_i^{\prime }=\mathrm{m}\mathrm{i}\mathrm{n}(C_i+\mathrm{0.2,1})$; two consecutive incorrect tasks: $C_i^{\prime }=\mathrm{m}\mathrm{a}\mathrm{x}(C_i-0.2,-1)$.
• Computing Power $P_i$ Update: $P_i\in \left[\mathrm{0,1}\right]$, initialized at 0, is periodically updated via off-chain tests (e.g., benchmarks), increasing with hardware performance.
• Task Completion Rate $R_i$ Update: $R_i\in \left[\mathrm{0,1}\right]$, initialized at 0, reflects historical reliability, calculated as follows:

  $$R_i={\displaystyle \frac{\mathrm{Successful}\mathrm{Tasks}}{\mathrm{Total}\mathrm{Tasks}}}$$

  (16)

Updated in real-time by the audit verification contract based on task logs.

New nodes start with $C_i=0$, $P_i=0$, $R_i=0$. The contract optimizes these parameters over time and shares them with the node selection contract. The latter computes a weighted score from $C_i$, $P_i$, and $R_i$, adding a verifiable random offset ${\mathsf{\Delta }}_i$ to yield the final score $S_i^{\prime }=S_i+{\mathsf{\Delta }}_i$. This balances opportunities for new nodes while prioritizing high-reputation ones, ensuring dynamic and accurate node selection.

4.4.4. Record Keeping and Provenance

To ensure traceability and transparency in the audit process, the blockchain records all critical data and computing node actions, including CIDs of Boolean shares $s_{A,l,k}$, $s_{B,l,k}$, masks $r_{l,g}$ and $a_{l,g,k}$ from the data preparation module, and $s_k$ from the approximate matching phase, managed by the data distribution smart contract to maintain clear mappings between matching pairs and masks. Audit verification contract uses on-chain index tables and IPFS data to conduct periodic or on-demand audits, verifying task assignment consistency and ensuring recomputed shares match uploaded ones.

Immutable audit logs on the blockchain capture node reputation changes, anomalies, and verification outcomes, providing a reliable foundation for long-term system operation. If participants question the results, they can request an audit via the verification contract, obtaining a report to confirm result validity. The process operates autonomously, with blockchain and IPFS collaboration ensuring efficient and fair audits.

The algorithm for masked difference conversion and Hamming distance calculation is described in pseudocode as shown in Algorithm 4.

Algorithm 4 Audit And Reputation Management Algorithm

Input: task_id: Task identifier; sample_rate: Proportion of results to audit; index_table: Index table with CIDs; node_performance: Node historical performance data Output: audit_results: Audit results with verification outcomes; updated_reputation: Updated reputation scores; blockchain_records: Stored records on blockchain  1: sampled_shares ← RandomSample(partial_hamming_shares, sample_rate)  2: for each share in sampled_shares do  3:    task_data ← GetTaskData(index_table, share)  4:    reference_share ← RecomputeShare(task_data)  5:    if reference_share == share then  6:         audit_results[share] ← “Verified”  7:         UpdateNodeReputation(node, outcome = “Success”)  8:    else  9:         audit_results[share] ← “Failed” 10:         UpdateNodeReputation(node, outcome = “Failure”) 11:    end if 12: end for 13: cid_audit, cid_reputation ← UploadResultsToIPFS(audit_results, up_reputation) 14: cid_reputation ← UploadToIPFS(updated_reputation) 15: return audit_results, up_reputation, StoreToBlockchain(cid_audit, cid_reputation)

In Algorithm 4, lines 1–4: Randomly sample a portion of the computation result shares and prepare for verification by recalculating. Lines 5–11: Compare the recalculated results with the submitted results, record the audit outcome (“Verified” or “Failed”) accordingly, and update the reputation values of the corresponding computation nodes. Lines 12–15: After the loop, upload the final audit results and updated reputation data to IPFS, store the address (CID) on the blockchain, and return the audit results and reputation data.

5. Method Analysis

5.1. Complexity Analysis

The computational and communication complexity analysis of this method is as follows. Assume there are $P$ participants, each participant $p_i$ possesses $N_i$ records, and let $N=\mathrm{m}\mathrm{a}\mathrm{x}\left(N_i\right)$. The Bloom filter length is $m$, using $k$ hash functions, with quasi-identifier attributes generating an average of $Q$ q-grams. The secret sharing threshold is $t$, meaning each Bloom filter bit is split into $t$ shares processed by $t$ computing nodes. The system selects $N_{\mathrm{nodes}}$ computing nodes to form a node pool. The total number of record pairs to be matched is $M$, distributed across $K$ mask groups, with an audit sampling rate of $s$.

In the data preparation and generation module, parameter negotiation among participants involves on-chain computation and communication costs, with complexity depending on the consensus mechanism and the number of participants $P$, denoted as $O\left({\mathrm{BC}}_{\mathrm{negotiate}}\right(P\left)\right)$ [32]. Data encoding is a local operation, with computational complexity for each participant $p_i$ as $O(N_i\cdot Q\cdot k)$, and the total across all participants is $\sum O(N_i\cdot Q\cdot k)$. Boolean secret share generation is also local, with computational complexity $O(N_i\cdot m\cdot t)$, totaling $\sum O(N_i\cdot m\cdot t)$; this step also involves uploading $N_i\cdot t$ shares to IPFS (communication cost ${\mathrm{Cost}}_{\mathrm{IPFS}}(N_i\cdot t\cdot m)$) and recording CIDs on the blockchain (on-chain write cost ${\mathrm{Cost}}_{{\mathrm{BC}}_{\mathrm{write}}}(N_i\cdot t)$). Mask generation is executed by smart contracts, with on-chain computational complexity approximately $O(K\cdot m\cdot t)$, accompanied by IPFS uploads (cost ${\mathrm{Cost}}_{\mathrm{IPFS}}(2\cdot K\cdot m\cdot t+t)$) and on-chain CID recording (cost ${\mathrm{Cost}}_{{\mathrm{BC}}_{\mathrm{write}}}(2\cdot K\cdot m\cdot t+t)$). The computational complexity of node selection on-chain is denoted as $O\left({\mathrm{BC}}_{\mathrm{select}}\right(N_{\mathrm{nodes}}\left)\right)$. In the data distribution phase, the smart contract processes $M$ record pairs, involving grouping, node selection, permutation generation, and index creation, with on-chain computational complexity approximately $O(M\cdot t\cdot (\mathrm{VRF}+t\left)\right)$, and requires writing $M\cdot t^2$ index records to the blockchain (cost ${\mathrm{Cost}}_{{\mathrm{BC}}_{\mathrm{write}}}(M\cdot t^2)$).

In the approximate matching module, processing is performed for $M$ record pairs, each handled by $t$ computing nodes in parallel. For each pair, data retrieval involves each node querying the blockchain (total cost $O(t^2\cdot {\mathrm{Cost}}_{{\mathrm{BC}}_{\mathrm{read}}}(1\left)\right)$) and downloading data from IPFS (total cost $O(t^2\cdot 5\cdot {\mathrm{Cost}}_{\mathrm{IPFS}}(m\left)\right)$). The total computational complexity for local difference computation and masking is $O(t\cdot m)$. In the batch interaction phase, nodes exchange masked difference vectors via IPFS and blockchain, with total communication cost approximately $O(t^2\cdot {\mathrm{Cost}}_{\mathrm{IPFS}}(m)+t\cdot {\mathrm{Cost}}_{{\mathrm{BC}}_{\mathrm{write}}}(1\left)\right)$. Reconstruction and B2A conversion are computational bottlenecks, with total computational complexity $O(t^2\cdot m)$. The final Hamming distance partial sum has computational complexity $O(t\cdot m)$, requiring result uploads to IPFS (total cost $O(t\cdot {\mathrm{Cost}}_{\mathrm{IPFS}}(\mathrm{scalar}\left)\right)$) and CID submission to the blockchain (total cost $O(t\cdot {\mathrm{Cost}}_{{\mathrm{BC}}_{\mathrm{write}}}(1\left)\right)$). Thus, the total computational complexity for the approximate matching phase across all $M$ pairs is approximately $O(M\cdot t^2\cdot m)$, with IPFS communication complexity approximately $O(M\cdot t^2\cdot {\mathrm{Cost}}_{\mathrm{IPFS}}(m\left)\right)$, and blockchain communication complexity approximately $O(M\cdot t^2\cdot {\mathrm{Cost}}_{{\mathrm{BC}}_{\mathrm{read}}}(1)+M\cdot 2\cdot t\cdot {\mathrm{Cost}}_{{\mathrm{BC}}_{\mathrm{write}}}(1\left)\right)$.

In the output and audit module, the computational complexity for participants aggregating results is $O(M\cdot t)$, with communication costs approximately $O(M\cdot {\mathrm{Cost}}_{{\mathrm{BC}}_{\mathrm{read}}}(t)+M\cdot t\cdot {\mathrm{Cost}}_{\mathrm{IPFS}}(\mathrm{scalar}\left)\right)$. The audit verification process involves recomputing $s\cdot M\cdot t$ shares, with total audit computational complexity approximately $O(s\cdot M\cdot t^3\cdot m)$, and communication complexity approximately $O(s\cdot M\cdot t\cdot ({\mathrm{Cost}}_{{\mathrm{BC}}_{\mathrm{read}}}\left(1\right)+6\cdot {\mathrm{Cost}}_{\mathrm{IPFS}}\left(m\right)\left)\right)$. The on-chain computation and write costs for reputation management are approximately $O(s\cdot M\cdot t)$ and ${\mathrm{Cost}}_{{\mathrm{BC}}_{\mathrm{write}}}(s\cdot M\cdot t)$. Record keeping and provenance involve additional IPFS and blockchain write costs.

The method’s computation is primarily driven by the approximate matching phase’s $O(M\cdot t^2\cdot m)$ and the audit phase’s $O(s\cdot M\cdot t^3\cdot m)$, proportional to the number of record pairs $M$, higher powers of the secret sharing threshold $t$, and Bloom filter length $m$, but the tasks are highly parallelizable. Communication bottlenecks stem mainly from IPFS data transfers (especially $O(M\cdot t^2\cdot {\mathrm{Cost}}_{\mathrm{IPFS}}(m\left)\right)$) and blockchain interactions (where throughput and transaction costs are critical) [33].

5.2. Privacy Analysis

This method establishes multi-layered privacy protection under the “honest-but-curious” model, with considerations extended to stronger malicious models and extreme scenarios such as large-scale node compromise. During the data preparation phase, raw data remains local to participants; only their Bloom filter encodings are processed and decomposed into t Boolean secret shares, which are then distributed to t different computation nodes selected from a larger pool [34]. This highly dispersed sharing ensures that a single computation node (even if malicious and logging/analyzing its shares) can only access 1/t of the fragmented information, making it extremely difficult to infer useful content or launch effective attacks. These shares are stored on IPFS, their CIDs are recorded on the blockchain, and access to data on IPFS is strictly managed by access control smart contracts.

In the approximate matching phase, computation nodes retrieve authorized data from IPFS via CIDs. The core masking technique ensures that nodes operate on obfuscated shares (e.g., shares of d ⊕ r) that are unrelated to the true difference d, meaning that even if t nodes (including Byzantine ones) collude, they cannot recover d. The B2A conversion similarly relies on secret-shared masks and the constant “1” to protect intermediate results. Masked difference vectors $E_k$ exchanged between nodes also do not leak d. Furthermore, the random permutation π mechanism, executed by the data distribution smart contract, further shuffles the logical order of shares, increasing inference difficulty. Malicious nodes submitting tampered data would face verification coordinated by the audit verification smart contract and penalties from the reputation management smart contract.

Regarding potential collusion attacks, an adversary must first identify and organize the specific computation nodes holding all t shares for the same record—a task already made difficult by the fact that the total number of nodes is far greater than t and task assignment is handled by the data distribution smart contract (potentially incorporating randomization and reputation). Even if shares are successfully collected, the random permutation mechanism forces attackers to face t! permutations. Experiments show that even with 80% node collusion, the reconstruction success rate is below ${10}^{-6}$. The entire process is coordinated by multiple smart contracts on the blockchain, ensuring transparency, enforcement, and auditability.

Nevertheless, this method has limitations in certain extreme threat scenarios. Regarding Byzantine behavior, the sampling audit driven by the audit verification smart contract may not capture all malicious acts, and the system relies on the honesty of verification nodes. Concerning DoS attacks, while underlying platforms (blockchain consensus, IPFS distributed nature) offer some protection, large-scale attacks could still impact the system (e.g., if IPFS nodes are attacked, preventing smart contracts from effectively retrieving data via CIDs) or computation nodes (the node selection smart contract filters by reputation, but widespread unavailability remains an issue). As for observable patterns, strong adversaries might still infer information from metadata (like CIDs or task assignment indices on the blockchain), network traffic, or IPFS access timings as side-channels.

Further considering extreme scenarios where a majority of nodes are compromised:

• If a majority of computation nodes are compromised: On the privacy front, an attacker’s chances of collecting all t shares for a record increase, but they still face the t! complexity from random permutation. In terms of result integrity, if most computation nodes in a specific task are malicious, they could collude to submit erroneous results, relying on verification node sampling audit as the main check.
• If a majority of validation nodes are compromised: This would destroy the system’s core trust mechanism, as the audit and reputation systems (maintained by the audit verification and reputation management smart contracts) would fail.
• If both types of nodes are compromised on a large scale: This is a catastrophic scenario. Attackers could submit malicious data and have it “legitimized” by compromised validation nodes, causing the defense system built by various smart contracts and IPFS to face systemic failure. The immutability of the blockchain would only preserve a trace for post-mortem analysis.

Regarding Bloom filters, while they might have risks if used in isolation (especially when facing malicious attackers), in SSB-PPRL, they primarily serve as an encoding tool. Their privacy is ensured by subsequent steps strictly orchestrated and enforced by various smart contracts, such as secret sharing (shares stored on IPFS), mask computation, and random permutation, which largely mitigate their inherent weaknesses. However, to further strengthen against complex malicious attacks that directly analyze or crack Bloom filters encoding themselves, future introduction of techniques like salted hashing or noise injection would be a very valuable supplement.

In the output and audit phase, participants only receive the aggregated Hamming distance $D_{ij}$. Audit verification nodes access data from IPFS as authorized by smart contracts for recomputation. All critical operations and metadata are recorded on the blockchain, ensuring transparency and traceability.

In summary, this method integrates various techniques, including blockchain smart contract-driven access control and process management, alongside IPFS distributed storage. Information available to a single node is limited, and the system is designed to resist collusion by t − 1 nodes. However, primary risks and trust requirements shift to node behavioral security and underlying technology robustness. Therefore, the security and correctness of various smart contracts, the effectiveness of node selection and reputation mechanisms, the secret sharing threshold t, and IPFS data guarantees are crucial for maintaining system privacy and usability in complex adversarial environments.

5.3. Linkage Quality Analysis

This method achieves approximate matching by computing the Hamming distance between Bloom filters, a technique that effectively handles data errors and variations, offering broader applicability compared to methods limited to exact matching. The Hamming distance reflects the similarity of original records based on q-grams. Linkage quality significantly depends on the choice of Bloom filter parameters (length m, number of hash functions k, q-gram length q). These parameters determine the precision of representation and the false positive rate f, directly impacting linkage accuracy. Parameter settings require a trade-off between linkage quality, privacy protection, and system overhead. This method adopts Hamming distance as the similarity metric; it is sensitive to differences in all bit positions, distinguishing it from metrics like the Dice coefficient which focus on shared features. Consequently, its matching performance may vary compared to other metrics under different data characteristics (e.g., sparsity) or application scenarios, necessitating practical evaluation. Subsequent processes, including secret sharing, mask computation, B2A conversion, and final Hamming distance aggregation, are designed to precisely compute the Hamming distance determined by Bloom filter representation, assuming no computational errors or malicious behavior. These cryptographic operations should theoretically not introduce additional loss in linkage quality. Thus, the primary factors affecting linkage quality remain the Bloom filter encoding strategy and its parameter settings in the initial stage.

Beyond the encoding strategy itself, the robustness of the Hamming distance computation process during actual operation critically affects final linkage quality, particularly false positive/negative (FP/FN) rates. Instances where computation nodes fail, do not successfully upload their shares, or (under a malicious model) submit inconsistent or tampered shares, can all impair Hamming distance accuracy.

Partial computation node failure or share loss can lead to inaccurate Hamming distance reconstruction, as aggregating all (t) partial shares submitted by computation nodes is required. This primarily increases False Negatives (reducing recall), as true matches might be missed due to inability to compute an accurate similarity score. While the system’s reputation mechanism penalizes failing nodes, thereby indirectly promoting reliability, unaddressed real-time share loss can still negatively affect judgments for specific linkage pairs.

Similarly, if computation nodes upload inconsistent or erroneous shares (due to unintentional error or Byzantine behavior) that are not captured by the sampling audit mechanism of verification nodes (driven by the audit verification smart contract), the final aggregated Hamming distance will deviate from the true value. An incorrectly calculated Hamming distance might cause dissimilar records to appear similar (leading to false positives, reducing precision) or similar records to appear dissimilar (leading to False Negatives, reducing recall). The current design relies on sampling audits and the reputation system to deter and detect such issues, but the non-comprehensive nature of sampling audits means some erroneous shares might still affect calculations.

In summary, while this method’s cryptographic design aims for accurate Hamming distance computation (making linkage quality primarily dependent on the encoding strategy), practical operational factors like computation node reliability, honesty, and network stability can, if not fully mitigated by existing fault tolerance and error correction mechanisms (e.g., reputation management, sampling audits), indirectly affect Hamming distance accuracy. This, in turn, can adversely impact FP/FN rates. Therefore, further enhancing the fault tolerance of the Hamming distance computation process against such node failures and data inconsistencies is an important aspect for improving overall linkage quality stability.

6. Experimental Results

6.1. Experiment Preparation

In this section, we evaluate the proposed SSB-PPRL method’s performance in three aspects—scalability, linkage quality, and security—through experiments, comparing it with three related methods by Han et al. [10], Vatsalan et al. [35], and Yao et al. [36]. Han et al.’s MP-PPRL-CBT uses a consortium blockchain instead of a semi-trusted third party, integrating homomorphic encryption and MapReduce for secure and efficient multi-party linkage. Vatsalan et al.’s method employs segmented Bloom filters and distributed secure computation for efficient multi-party approximate matching. Yao et al.’s approach introduces twin neural networks to PPRL for adaptive matching via feature learning and proposes a composite Bloom filter to enhance encoding security.

The experimental environment consisted of several high-performance servers, each equipped with an AMD EPYC 7763 CPU (64 cores/128 threads, ~2.45 GHz base frequency), 128 GB DDR4 RAM, high-speed NVMe storage, and Ubuntu 20.04 LTS. The core SSB-PPRL algorithm was implemented in Python 3.8, with cryptographic operations utilizing the PyCryptodome library. Blockchain functionalities were supported by a private Ethereum test network based on Ganache CLI v7.7.0, with smart contracts written in Solidity v0.8.17 and managed by Truffle Suite. For IPFS storage, multiple Kubo v0.18.1 nodes were deployed. These nodes, along with the SSB-PPRL application modules, were containerized using Docker and run in a local high-speed network environment. Interaction with the blockchain was handled via the Web3.py library, and communication with IPFS used the ipfshttpclient library.

The datasets used in this study include the North Carolina Voter Registration List (NCVR), the DBLP-Scholar dataset, and the DBLP-ACM dataset. All three datasets are publicly available and widely used in privacy-preserving record linkage research.

The independent variables in the experiments include the size of the data source, the number of participating parties, and the perturbation ratio. We extracted 5 K, 10 K, 50 K, 100 K, and 500 K records from the datasets. The number of participating parties was set to 3, 5, 7, and 9, respectively.

To more accurately reflect real-world data errors, we applied perturbation processing to the original datasets, generating datasets with different noise levels. Specifically, we created three perturbed versions, introducing spelling errors, semantic changes, and structural adjustments. The perturbation operations included character deletion, random replacement, word order adjustment, and character insertion. To maintain control over the perturbations, we defined three error levels: Mod-1, where each record has at most one error; Mod-2, where each record has at most two errors; and Mod-3, where each record has at most three errors. Through this design, the datasets better align with real-world scenarios, providing effective support for evaluating the robustness and matching capabilities of privacy-preserving record linkage methods under different noise environments.

We adopt five key metrics to evaluate the overall scalability, linkage quality, and security of the proposed method: runtime, precision, recall, F-score, and reconstruction rate. Among them, precision measures the proportion of actual matching record pairs in the total number of candidate record pairs, reflecting the method’s accuracy; recall represents the proportion of actual matching record pairs relative to all true matching record pairs, indicating the method’s coverage capability. The F-score, as a comprehensive metric combining precision and recall, is calculated using the following formula:

$$\mathrm{F}=2 {\displaystyle \frac{Recall\times Precision}{Recall+Precision}}$$

(17)

The reconstruction rate is a metric used to assess an attacker’s ability to recover original data. It measures the extent to which an attacker, by controlling a subset of computation nodes, successfully reconstructs the information in Bloom filters. Suppose there are M Bloom filter pairs, each decomposed into t shares, randomly distributed to t nodes among N nodes [37]. Randomly select c colluding nodes from the N nodes and check how many Bloom filters have all t shares controlled by the colluding nodes.

Theoretically, considering the impact of permutations, the reconstruction rate (i.e., the probability that an attacker successfully obtains all t shares for a specific Bloom filter and guesses its correct permutation) is calculated as follows:

$$Reconstruction Rate={\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{c}{t}\right)}{\left(\genfrac{}{}{0pt}{}{N}{t}\right)}}\times {\displaystyle \frac{1}{t!}}$$

(18)

6.2. Experimental Results and Analysis

6.2.1. Scalability Assessment

In evaluating scalability, we primarily use runtime as the key metric to analyze the system’s performance under different data sizes and computational node configurations.

To ensure security, our method employs secret sharing techniques and smart contract management, which significantly reduce the method’s efficiency. Therefore, we use multi-node distributed computing and attribute-based partitioning methods to accelerate this process. When the number of participating parties is 3, the perturbation ratio is 30%, the number of secret shares is 5, and the number of masks is 5 sets, the runtime of the proposed method (in the approximate matching phase and the audit verification phase) varies with increasing data source size, as shown in Figure 5.

As the dataset size increases, the specific runtime for different numbers of nodes is shown in

Table 1. The runtime performance for varying node counts with growing dataset size.

Dataset Size	Node Count = 64	Node Count = 128	Node Count = 256
5 K	5.73	3.02	1.57
10 K	22.92	12.13	6.28
50 K	572.92	300.00	154.25
100 K	2291.67	1201.00	617.34
500 K	57,291.67	30,120.00	15,480.50

.

When the data size is 50 k, the perturbation ratio is 30%, the number of secret shares is 5, and the number of masks is 5 sets, the running time of the proposed method (for the approximate matching phase and the audit verification phase) varies with the increase in the number of participants, as shown Figure 6.

As the number of participants increases, the specific runtime for different numbers of nodes is shown in

Table 2. The runtime performance for varying node counts with increasing participant numbers.

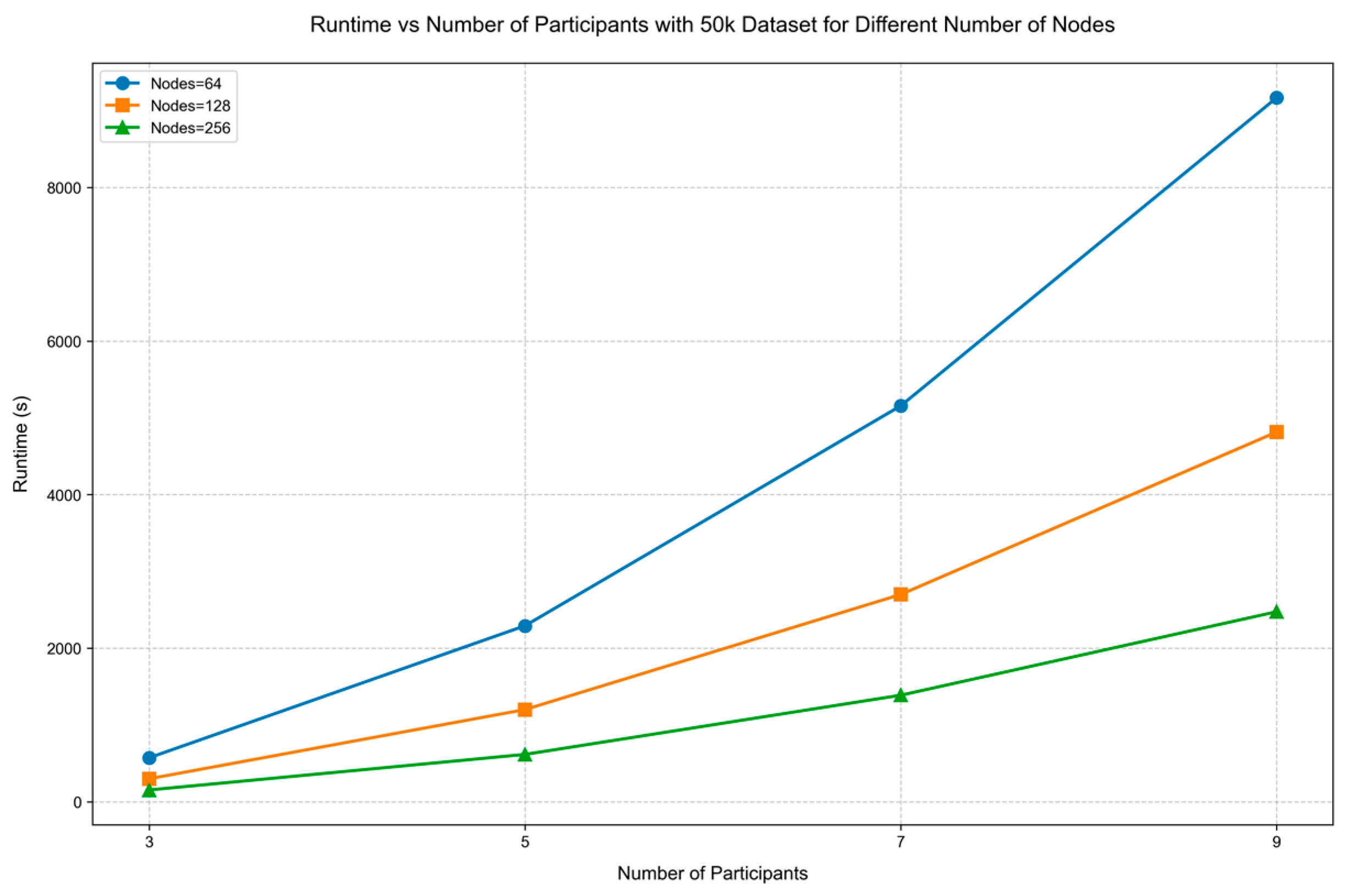
Participants	Node Count = 64	Node Count = 128	Node Count = 256
3	572.92	300	154.25
5	2291.67	1201	617.34
7	5156.25	2700	1388
9	9166.67	4815	2475.3

.

6.2.2. Method Performance Evaluation

To comprehensively evaluate the linkage quality of the proposed method, we assessed the SSB-PPRL method in terms of precision, recall, and F-score. The evaluation examined how these three metrics vary with an increasing number of participants, given a fixed data size, across datasets with three different levels of perturbation.

Under datasets with 20,000 records perturbed to varying degrees (Mod-1 to Mod-3), the precision of all methods decreases as the number of participants and data error rates increase, with the most significant decline observed under high error rates (Mod-3). Benefiting from its neural network matching mechanism, the Yao method achieves the highest prediction precision and robust performance. The Vatsalan method, relying on precise privacy-preserving computation, is primarily constrained by the performance of its Bloom filter and Dice similarity function. Our proposed method, based on accurate secret sharing computation, incurs no additional precision loss and demonstrates precision comparable to the Vatsalan method. Notably, under complex conditions with a high number of participants and elevated error rates, our method outperforms Han, exhibiting a clear advantage in precision. This avoids the potential negative impact of the binary tree structure on matching accuracy observed in the Han method. The precision variation with the number of participants in the three perturbed datasets is shown in Figure 7.

The specific precision values for the three perturbed datasets as the number of participants varies are shown in

Table 3. Precision values for three perturbed datasets changing with participant numbers.

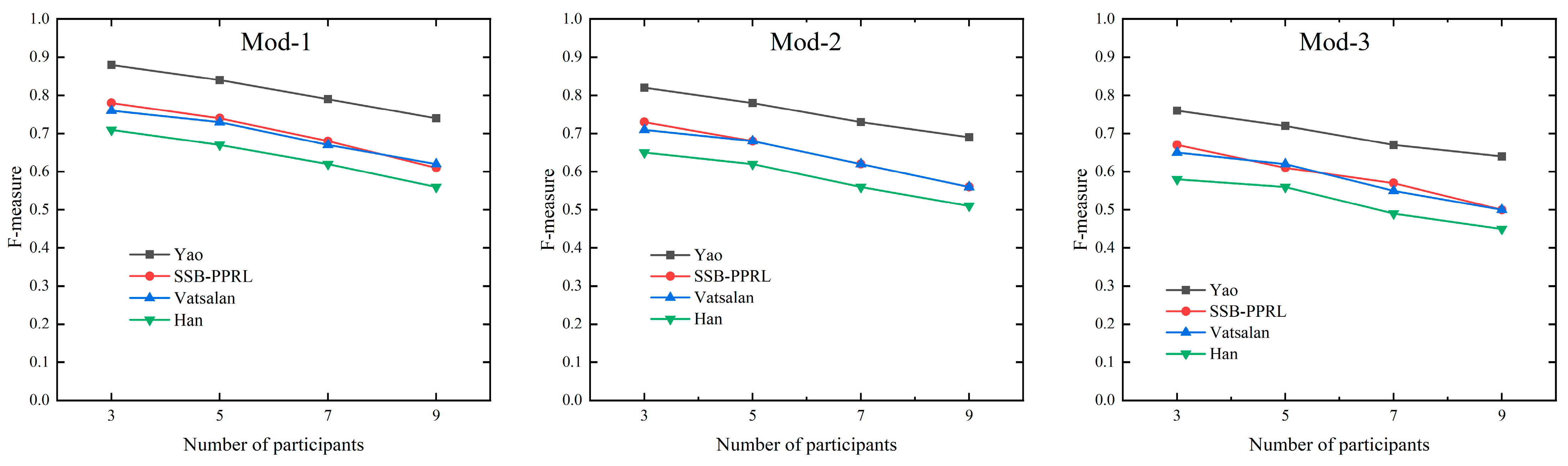
Method	Participants = 3	Participants = 5	Participants = 7	Participants = 9
SSB-PPRL	0.78 (Mod-1)	0.74 (Mod-1)	0.68 (Mod-1)	0.61 (Mod-1)
	0.73 (Mod-2)	0.68 (Mod-2)	0.62 (Mod-2)	0.56 (Mod-2)
	0.67 (Mod-3)	0.61 (Mod-3)	0.57 (Mod-3)	0.5 (Mod-3)
Han	0.71 (Mod-1)	0.67 (Mod-1)	0.62 (Mod-1)	0.56 (Mod-1)
	0.65 (Mod-2)	0.62 (Mod-2)	0.56 (Mod-2)	0.51 (Mod-2)
	0.58 (Mod-3)	0.56 (Mod-3)	0.49 (Mod-3)	0.45 (Mod-3)
Yao	0.88 (Mod-1)	0.84 (Mod-1)	0.79 (Mod-1)	0.74 (Mod-1)
	0.82 (Mod-2)	0.78 (Mod-2)	0.73 (Mod-2)	0.69 (Mod-2)
	0.76 (Mod-3)	0.72 (Mod-3)	0.67 (Mod-3)	0.64 (Mod-3)
Vatsalan	0.76 (Mod-1)	0.73 (Mod-1)	0.67 (Mod-1)	0.62 (Mod-1)
	0.71 (Mod-2)	0.68 (Mod-2)	0.62 (Mod-2)	0.56 (Mod-2)
	0.65 (Mod-3)	0.62 (Mod-3)	0.55 (Mod-3)	0.5 (Mod-3)

.

As the number of participants and perturbation levels increase, the recall rates of all methods show a downward trend. Notably, the decline in recall from Mod-1 to Mod-2 is particularly significant. The Yao method stands out, maintaining the highest recall across all test conditions. Additionally, the Vatsalan method and our proposed SSB-PPRL method also sustain relatively high recall rates, outperforming the Han method, which aligns with their core privacy-preserving mechanisms that theoretically introduce no additional False Negatives. The recall variation with the number of participants in the three perturbed datasets is shown in Figure 8.

The specific recall values for the three perturbed datasets as the number of participants varies are shown in

Table 4. Recalling values for three perturbed datasets changing with participant numbers.

Method	Participants = 3	Participants = 5	Participants = 7	Participants = 9
SSB-PPRL	0.76 (Mod-1)	0.72 (Mod-1)	0.66 (Mod-1)	0.59 (Mod-1)
	0.71 (Mod-2)	0.66 (Mod-2)	0.61 (Mod-2)	0.53 (Mod-2)
	0.65 (Mod-3)	0.59 (Mod-3)	0.56 (Mod-3)	0.47 (Mod-3)
Han	0.69 (Mod-1)	0.65 (Mod-1)	0.6 (Mod-1)	0.54 (Mod-1)
	0.63 (Mod-2)	0.6 (Mod-2)	0.54 (Mod-2)	0.49 (Mod-2)
	0.57 (Mod-3)	0.55 (Mod-3)	0.47 (Mod-3)	0.43 (Mod-3)
Yao	0.86 (Mod-1)	0.83 (Mod-1)	0.78 (Mod-1)	0.73 (Mod-1)
	0.8 (Mod-2)	0.77 (Mod-2)	0.72 (Mod-2)	0.68 (Mod-2)
	0.73 (Mod-3)	0.71 (Mod-3)	0.66 (Mod-3)	0.63 (Mod-3)
Vatsalan	0.75 (Mod-1)	0.73 (Mod-1)	0.65 (Mod-1)	0.6 (Mod-1)
	0.7 (Mod-2)	0.67 (Mod-2)	0.6 (Mod-2)	0.54 (Mod-2)
	0.65 (Mod-3)	0.61 (Mod-3)	0.54 (Mod-3)	0.47 (Mod-3)

.

Under varying numbers of participants and perturbation levels, the Yao method achieves the highest F-score and strong anti-interference capability, benefiting from improvements in its linkage approach. Our proposed method and the Vatsalan method, however, are primarily influenced by the Bloom filter and similarity metric functions in terms of linkage quality. The Han method improves data structure for better efficiency but experiences a slight decline in linkage quality. The F-score variation with the number of participants in the three perturbed datasets is shown in Figure 9.

The specific F-score values for the three perturbed datasets as the number of participants varies are shown in

Table 5. F-score values for three perturbed datasets changing with participant numbers.

Method	Participants = 3	Participants = 5	Participants = 7	Participants = 9
SSB-PPRL	0.77 (Mod-1)	0.73 (Mod-1)	0.67 (Mod-1)	0.61 (Mod-1)
	0.72 (Mod-2)	0.67 (Mod-2)	0.61 (Mod-2)	0.54 (Mod-2)
	0.66 (Mod-3)	0.61 (Mod-3)	0.56 (Mod-3)	0.48 (Mod-3)
Han	0.71 (Mod-1)	0.66 (Mod-1)	0.61 (Mod-1)	0.55 (Mod-1)
	0.64 (Mod-2)	0.61 (Mod-2)	0.56 (Mod-2)	0.51 (Mod-2)
	0.57 (Mod-3)	0.55 (Mod-3)	0.48 (Mod-3)	0.44 (Mod-3)
Yao	0.87 (Mod-1)	0.83 (Mod-1)	0.78 (Mod-1)	0.73 (Mod-1)
	0.81 (Mod-2)	0.77 (Mod-2)	0.72 (Mod-2)	0.68 (Mod-2)
	0.74 (Mod-3)	0.71 (Mod-3)	0.66 (Mod-3)	0.63 (Mod-3)
Vatsalan	0.75 (Mod-1)	0.73 (Mod-1)	0.66 (Mod-1)	0.61 (Mod-1)
	0.71 (Mod-2)	0.67 (Mod-2)	0.61 (Mod-2)	0.55 (Mod-2)
	0.65 (Mod-3)	0.61 (Mod-3)	0.54 (Mod-3)	0.49 (Mod-3)

.

6.2.3. Security Evaluation

In this section, we set the number of secret shares t = 10, meaning each Bloom filter is decomposed into 10 Boolean shares, distributed across 10 computing nodes. We evaluated the ability of colluding nodes to reconstruct the Bloom filter by varying the total number of nodes N (50, 100, 200) and the number of colluding nodes c (starting from 10 and increasing to 0.8 × N). The experimental results are shown in

Table 6. Comparison of theoretical and experimental reconstruction rates under different collusion scenarios.

N	c	Theoretical Reconstruction Rate	Experimental Reconstruction Rate
50	10	$2.683\times {10}^{-17}$	0
50	20	$4.956\times {10}^{-12}$	0
50	40	$2.274\times {10}^{-8}$	0.0000002
100	20	$2.941\times {10}^{-15}$	0
100	40	$1.349\times {10}^{-11}$	0
100	80	$2.621\times {10}^{-8}$	0.0000001
200	40	$1.04\times {10}^{-14}$	0
200	80	$2.021\times {10}^{-11}$	0
200	160	$2.601\times {10}^{-8}$	0.0000001

below.

The experimental results demonstrate how the total number of nodes $N$ and the number of colluding nodes $c$ affect the reconstruction rate under a fixed number of secret shares $t=10$. The reconstruction rate, defined as the probability of colluding nodes recovering a Bloom filter, depends on the likelihood of collecting all $t$ shares and guessing the correct permutation. The theoretical reconstruction rate is given by

$$\mathrm{Reconstruction} \mathrm{rate}={\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{c}{t}\right)}{\left(\genfrac{}{}{0pt}{}{N}{t}\right)}}\times {\displaystyle \frac{1}{t!}}$$

(19)

When c < t, the reconstruction rate is 0, as insufficient shares are collected. In the experiments, t = 10, with permutation possibilities t! = 3,628,800, significantly reducing the attack success rate. When c = t = 10 (i.e., the number of colluding nodes equals the number of secret shares), the theoretical rate is extremely low (e.g., $2.683\times {10}^{-17}$ for N = 50). Experimental values are 0, which is consistent with such a low theoretical probability of successful reconstruction. When c ≥ t, the theoretical reconstruction rate increases with c. However, it remains very small for lower c values and becomes more significant (though still low) for higher c values (e.g., 80% node collusion). For example, for N = 50, c = 40 (80% collusion), the corrected theoretical rate is $2.274\times {10}^{-8}$, with an experimental value of 2 × ${10}^{-7}$. For N = 200, c = 160 (80% collusion), the corrected theoretical rate is $2.601\times {10}^{-8}$, with an experimental value of 1 × ${10}^{-7}$. Permutation difficulty ensures security.

Increasing N (total nodes) reduces the theoretical reconstruction rate, e.g., for c = 40, the rate drops from $2.274\times {10}^{-8}$ at N = 50 to $1.04\times {10}^{-14}$ at N = 200, due to lower collection probability. Increasing c (colluding nodes) raises the theoretical rate. The permutation factor t! ensures these theoretical rates remain very low (e.g., in the order of ${10}^{-8}$ or lower for the parameters tested). The experimental rates observed are in the order of ${10}^{-7}$ for high collusion scenarios.

The experimental reconstruction rates in high collusion scenarios (e.g., 2 × ${10}^{-7}$ for N = 50, c = 40) are observed to be higher than the recalculated theoretical rates (e.g., 2.274 × ${10}^{-8}$ for N = 50, c = 40). This difference might be attributed to factors in the experimental setup or inherent randomness. However, both theoretical (recalculated) and experimental rates are extremely low, and the general trends (effect of N and c) align.

The results show that even with 80% node collusion, the t = 10 configuration results in experimentally observed reconstruction rates around 1–2 × ${10}^{-7}$. This is an extremely low rate. To put this into perspective, a reconstruction rate of 1−2×${10}^{-7}$ signifies approximately one to two successful reconstructions per ten million attempts, making the orders of magnitude rarer than one successful reconstruction per thousand. The dual protection of secret sharing and permutation confirms SBB-PPRL’s strong privacy protection under high collusion scenarios.

7. Conclusions

We propose a privacy-preserving record linkage method based on secret sharing and blockchain (SSB-PPRL), designed for secure and efficient record linkage across multiple data sources. By leveraging secret sharing, blockchain coordination, and IPFS storage, the method enhances privacy, scalability, and fault tolerance. Experimental results demonstrate that it maintains high linkage quality and scalability while ensuring data privacy.

Nevertheless, there is room for improvement in computational efficiency, protocol optimization, and resilience against extreme attack scenarios. Future research will focus on advancing the following key directions: Firstly, efforts will continue to optimize system performance and efficiency, including refining blockchain–IPFS interactions and enhancing node scheduling and core computation strategies managed by smart contracts. Secondly, work will aim to enhance overall system security and robustness, with a focus on researching stronger Byzantine fault-tolerant mechanisms for critical coordination and verification stages (potentially involving new smart contract designs), advanced collusion-resistant techniques, dynamic trust models, and comprehensive defenses and emergency response protocols against various DoS attacks, to effectively address extreme situations of large-scale computation and validation node failures or malicious behavior [38]. Furthermore, attention will be given to ensuring linkage quality under non-ideal conditions, particularly by investigating more fault-tolerant secret sharing aggregation algorithms and computation result consistency verification techniques to stabilize and control false positive/negative rates that may arise from partial node failures or data inconsistencies. Lastly, the integration and advancement of cutting-edge privacy-preserving technologies will be deepened, for instance, by hardening initial encoding stages like Bloom filters through salting or noise injection to defend against direct data analysis attacks [39], and by combining differential privacy and access pattern obfuscation to reduce potential side-channel leakage, ensuring high-level privacy in complex adversarial environments [40].

Through continued exploration in these areas, we expect to further elevate the comprehensive performance of the SSB-PPRL method, enabling it to better serve real-world data sharing requirements.