Complexity of Supply Chains Using Shannon Entropy: Strategic Relationship with Competitive Priorities

Abstract

Entropy is a foundational concept across scientific domains, playing a role in understanding disorder, randomness, and uncertainty within systems. This study applies Shannon’s entropy in information theory to evaluate and manage complexity in industrial supply chain management. The purpose of the study is to propose a quantitative modeling method, employing Shannon’s entropy model as a proxy to assess the complexity in SCs. The underlying assumption is that information entropy serves as a proxy for the complexity of the SC. The research method is quantitative modeling, which is applied to four focal companies from the agrifood and metalworking industries in Southern Brazil. The results showed that companies prioritizing cost and quality exhibit lower complexity compared to those emphasizing flexibility and dependability. Additionally, information flows related to specially engineered products and deliveries show significant differences in average entropies, indicating that organizational complexities vary according to competitive priorities. The implications of this suggest that a focus on cost and quality in SCM may lead to lower complexity, in opposition to a focus on flexibility and dependability, influencing strategic decision making in industrial contexts. This research introduces the novel application of information entropy to assess and control complexity within industrial SCs. Future studies can explore and validate these insights, contributing to the evolving field of supply chain management.

1. Introduction

Entropy serves as a foundational concept in various scientific domains, encompassing fields such as physics, chemistry, computer science, or information theory [1]. In physics, entropy functions as a metric for the degree of disorder or randomness within a system. The second law of thermodynamics posits that the entropy of an isolated system tends to increase over time, ultimately reaching a state of maximal disorder. In chemistry, entropy finds relevance in its association with the distribution of energy among the microscopic states of particles within a system. During a chemical reaction, alterations in entropy can signify a system’s inclination towards either a more disorganized or a more ordered state. In essence, entropy can be seen as intricately linked to the dispersion of energy within a given system [2].

Moving to computer science, particularly information theory, entropy extends beyond its thermodynamic origins, serving as a measure of uncertainty or unpredictability related to a source of information [3]. For instance, measuring the uncertainty of a neural network output is relevant in AI applications such as deep learning-based image classification. In this context, the entropy of the output can serve as a reliable metric for gauging the level of uncertainty in the system [4].

When considering a sequence of symbols in a message, an increase in entropy corresponds to a higher level of unexpectedness for the subsequent symbol. Beyond apparent disorder, entropy reveals the inherent uncertainty in a message represented by a sequence of data, essentially acting as a measure of outcome likelihoods for a random event. Claude Shannon’s seminal 1948 article [5] introduced information entropy, a metric designed to quantify the average information content within a message. A core tenet of Shannon’s theory posits a direct correlation between uncertainty and information: the greater the uncertainty surrounding an event’s outcome, such as the next symbol in a message, the more information it conveys when it occurs [6]. In short, Shannon entropy assigns a value based on the probability of each message outcome. Less probable outcomes contribute more significantly to the overall entropy, as their unexpected nature translates to more informational content [7].

In industrial management, a significant challenge arises from the inherent complexity that emerges when multiple companies collaborate to form a supply chain (SC). At least one prior, recent investigation [8] posits that SCs can be regarded as complex adaptive systems (CASs), often evolving autonomously and independent of a deliberate creation process. Like other types of CASs, it proves beneficial to assess and manage the level of complexity that an SC accrues during its evolution [9], as demonstrated by previous related studies. Among many others, ref. [10] analyzed the underpinning structure of SCs, refs. [11,12] identified drivers that may boost the complexity level in SCs, and refs. [13,14] examined how complexity can influence business performance in SCs, while ref. [15] studied a dedicated tool conceived to measure complexity in SCs. Finally, ref. [16] presents an entropy-based algorithm tailored to measure complexity in SCs. These last two approaches both have a similar gap, which this study aims to bridge.

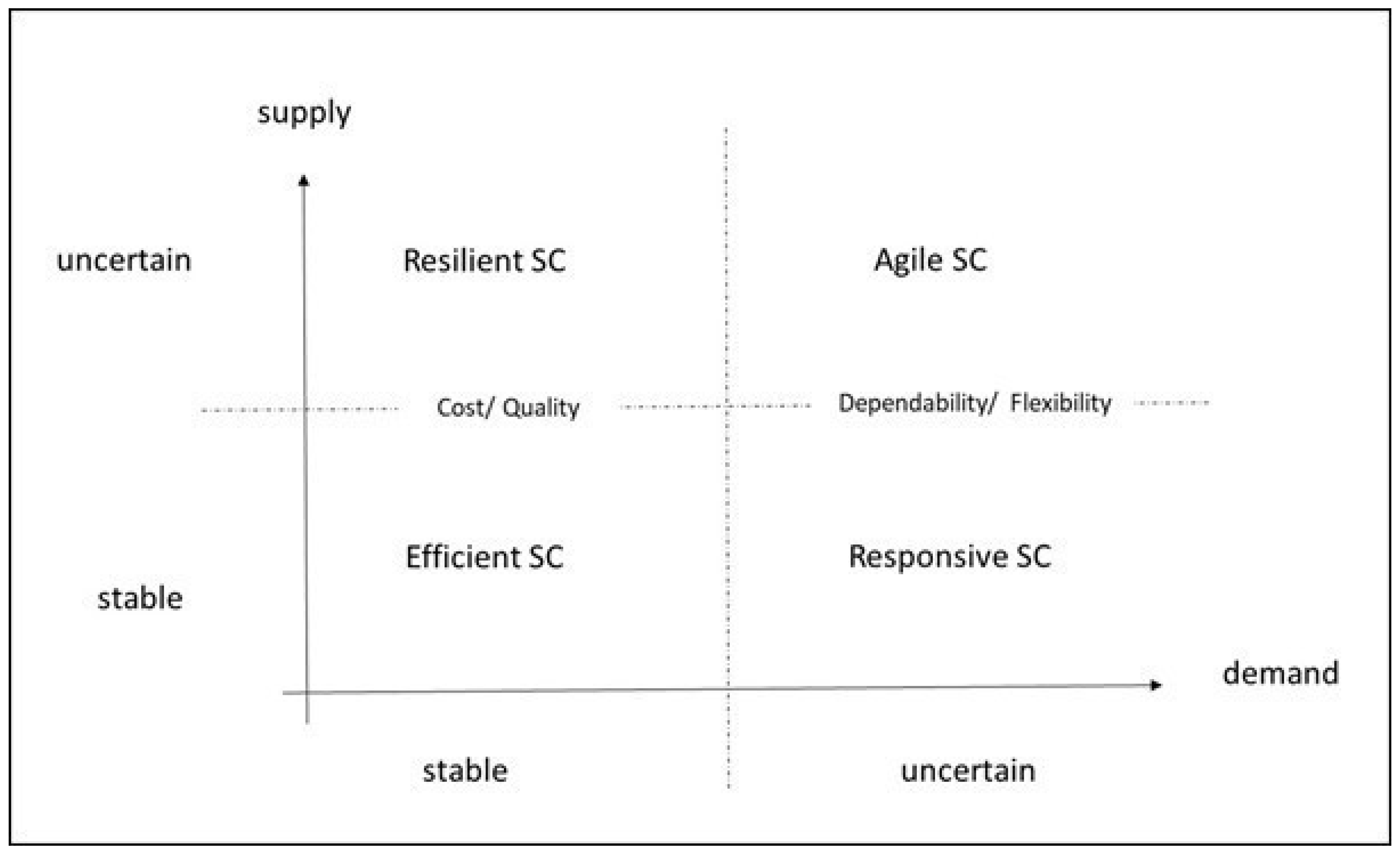
Each company within the collaboration scenario depicted by the SC pursues distinct objectives, spanning areas such as raw material supply, engineering services, transportation, warehousing, manufacturing, and distribution. Despite having individual goals, they all have a shared overarching objective: collectively meeting the requirements of a specific customer type [17]. Beyond their unique operational strategies tailored to meet local objectives, companies operating within an SC must adhere to a meta-strategy that governs the entire system. This meta-strategy outlines global objectives, encompassing the collective goals of all members involved in activities [18]. The success of an SC operation hinges not only on each company achieving its partial or local objectives but on the attainment of global objectives that entail satisfying customer requirements [19]. In short, only the achievement of global objectives ensures the overall success of the SC. This study focuses on applying entropy, as conceived in information theory, to the realm of administrative sciences, more specifically, supply chain management (SCM). It employs Shannon entropy to assess the required information exchanged between agents during SCM. The underlying assumption is that information entropy serves as a proxy measure for the complexity within the SC.

Complexity is not the same as complicatedness [20]. In scientific realms, complexity refers to the inherent nature of a system composed of many interconnected and mutually dependent parts, usually exhibiting emergent, non-linear properties that cannot be explained by individual, isolated components [21]. Replacing even a single component yields sensible variation in outcomes, as the replacement influences internal mutually dependent relationships. Complicatedness refers to a system that is difficult to understand or deal with due to having a high number of parts, but these parts are mutually independent [22]. Replacing one part with another that is similar does not change outcomes. In essence, complexity is inherent to nature, while complicatedness arises from the number of parts. For example, an aircraft engine that entails thousands of parts may be complicated but not complex. A soccer team, even entailing only eleven agents, may be complex but is not complicated. In short, complex systems may show emergent behavior difficult to predict and control, while complicated systems, even when difficult to handle, can be predicted and linearly escalated [23].

Given the uncertainties in SCM, it becomes important to not only assess but also manage the inherent complexity that arises from SC dynamics [24]. Controlling complexity does not solely imply reduction; in some instances, it may imply an increase. For example, in stable environments, reducing complexity can translate to cost reduction, making the SC more efficient. In unstable scenarios, in which innovation and variety are essential, an increase in complexity is often required, making the SC more flexible [25].

This study employs a measure of entropy that connects the concepts of uncertainty and complexity. According to this measure, as a system becomes more uncertain, it also becomes more complex [11]. To describe and monitor a complex system, it is necessary to access a range of information to manage unpredictability, underscoring a fundamental relationship. The greater the complexity, the more information is required to understand the system’s behavior and anticipate possible outcomes presented by complex systems due to their unpredictable nature.

A search on Scopus from 2020 to 2025 using the keywords “Complexity” AND “Supply Chains” yielded 4468 results. In contrast, the search for “Complexity measurement” AND “Supply Chain” returned only three results, and there was just one article found for “Complexity” AND “Supply Chains” AND “Shannon entropy”. This indicates that while the topic of complexity in SCs is significant, there are gaps in the recent, high-impact literature concerning the measurement of complexity and, specifically, the application of Shannon entropy.

Therefore, the purpose of the study is to propose a quantitative modeling method, employing Shannon’s entropy model as a proxy to assess the complexity in SCs. The research method is quantitative modeling. The core principle is to use the theoretical framework of Shannon’s entropy to quantify informational flow entropy as a proxy variable of complexity. The model measures the uncertainty in the flow of information permeating the SC. The underlying assumption is that the complexity of the SC is directly proportional to the amount of information required to manage it effectively [26]. The research subject includes four focal companies of an industrial SC, two from the agrifood industry and two from the metalworking industry, all located in Southern Brazil. This study contributes to SCM studies by encompassing four SC meta-strategies, four competitive priorities, and an entropy-based measure in a single study.

The subsequent sections are structured to provide a comprehensive review of SC complexity, delineate the methodology, present and discuss the results, and draw conclusions from the findings. This systematic approach ensures a thorough exploration and understanding of the intricate dynamics surrounding complexity in industrial SCs.

2. Background Literature

2.1. Complexity and Strategy in Industrial SCs

In industrial SCs, the central entity, often referred to as the focal company, typically is the manufacturing unit. This unit usually is involved in product design and specifying engineering services and has primacy in defining strategic goals and action plans [27]. An illustrative industry exemplifying such dynamics is the automotive sector, in which the car manufacturer usually has the strategic primacy [28].

Manufacturing companies within industrial SCs predominantly concentrate on competitive priorities [29]. These priorities encompass various aspects, such as cost-effectiveness, quality, flexibility, dependability, and innovation. A substantial body of literature has already been developed in this regard, delving into various competitive priorities [30]. Authors and studies have compiled comprehensive sets of priorities, which include subpriorities like environmental concerns or customer satisfaction (a subpriority of quality), lean production (a subpriority of cost-effectiveness), time-to-market and innovation (subpriorities of flexibility), and reliability or timeliness of deliveries (subpriorities of dependability) [31]. This study specifically concentrates on the four primitive competitive priorities outlined in the seminal study [32]: cost, quality, flexibility, and dependability. Cost reduction involves meeting customer requirements in a standardized and competitive market, in which lower prices typically prevail in competition. A focus on quality ensures adherence to standards and minimal variability in product parameters, relevant in standardized markets. Flexibility refers to the company’s capacity to swiftly adjust production parameters, including lot size, production mix, product features, fabrication processes, or delivery points, without compromising other priorities. Dependability signifies the assurance provided by the company to its customers, ensuring high performance in delivery parameters such as speed, reliability, integrity, and punctuality [31].

Industrial SCs also manage overall strategies. This relatively recent area of study has prompted scholars in the literature to highlight well-established meta-strategies within SCs, defined by keywords such as efficient, resilient, responsive, and agile [33]. In brief, an efficient SC is geared towards resolving familiar issues with well-established solutions, aligning with business environments characterized by stable demand and supply. It ensures cost reduction [34]. A resilient SC is designed to address familiar issues with innovative solutions, aligning with business environments in which the demand is stable and supply may be affected by huge or catastrophic situations, such as climate or geopolitical events. It ensures continuous high-quality standards [35]. A responsive SC tackles emerging challenges with well-established solutions, aligning with business environments marked by uncertain demand and stable supply. It ensures a high level of dependability for customers [36]. Lastly, an agile SC is tailored to confront emerging challenges with innovative solutions, aligning with business environments characterized by uncertainty in both demand. It ensures a high level of flexibility [37]. Figure 1, based on the framework proposed by [38], depicts the relationship between SC meta-strategies, competitive priorities, and the levels of uncertainty on both the demand and supply sides.

The meat industry is an example of an activity that relies on efficient SCs due to stable local markets and supply [39]. On the other hand, the renewable energy industry requires resilient SCs since the supply of renewable energy can be disrupted by seasonal and climate events despite high and stable local demand for energy [40]. The fast fashion industry necessitates responsive SCs due to the volatile nature of local demand for trendy clothing, even with a stable supply of raw materials [30]. Lastly, the technology industry typically requires agile SCs due to the highly unpredictable nature of both local markets and the supply of new, fast-evolving technological materials [41].

Several structural factors can contribute to the transformation of an SC from a simple and complicated system to a complex one [42]. This transformation hinges on the creation of interrelationships and mutual dependencies between factors such as, but not limited to the following: (i) The globalization of operations: when international and domestic operations become intertwined, the SC landscape becomes more intricate [43]; (ii) Product variety with shared components: extensive product variety, particularly when leveraging common parts across products, fosters mutual dependencies within the SC [44,45]; (iii) Technological integration: the implementation of shared control systems across diverse operations introduces a layer of complexity, as these systems become interdependent [46]; and (iv) Climate and geopolitical disruptions [47]: events like political instability or climate change have the potential to destabilize SCs. Regarding climate change, the Fukushima disaster in 2011 had a significant impact on Toyota’s operations. An earthquake, followed by a tsunami, damaged the company’s SC infrastructure, disrupting production and delivery schedules [48]. The crisis highlighted the importance of ensuring the resilience of the SC in the face of external disruptions, leading Toyota to re-evaluate its risk mitigation strategies. Ref. [49] explored the disruptions before and after the disaster, with a particular focus on the complex relationship between SC complexity and resilience.

The convergence of such multiple factors creates a more intricate and interdependent array, boosting complexity. Uncertainty emerges as a recurring element in both SC strategies and manufacturing priorities. This recognition underscores the need for adaptive and dynamic approaches within industrial SCM to effectively navigate the complexities posed by fluctuating demand and uncertain supply scenarios [47].

2.2. Related Studies

Previous studies have comprehensively approached the relationship involving strategy and complexity in SCs.

Table 1. Related studies and their contributions, along with the positioning of this study.

Study	Main Features
[9]	Handles resilience and efficiency by managing the number of suppliers, degree of differentiation, and interrelationships in the SC
[10]	Evaluates complexity by theoretically developing an entropy-based measure
[11]	Evaluates complexity by identifying drivers and applying AHP
[12]	Provides an extensive and insightful review of complexity drivers in SC
[13]	Studies drivers that boost complexity in SC and propose mechanisms to overcome their effects and reduce complexity
[14]	Provides a useful methodology to link SC complexity with plant performance, considering plant design and operation strategy, which will be useful in future research
[15]	Manages SC complexity by system dynamics tool, highlighting more effective drivers for complexity level
[16]	Provides a theoretical description of an entropy-based measure as a proxy variable for complexity in SCs and introduces conditional (relative) complexity, which was employed in our study.
Our study	Manages complexity to achieve efficiency, resilience, responsiveness, and agility in SC. The evaluation uses twenty key information elements encompassing five aspects: planning, logistics, workforce, finance, and technology. The study also relates complexity to competitive priorities.

shows related studies and their specific contributions, positioning the current study at the forefront of the relevant literature.

The following analysis reflects the individual and comparative contributions of selected previous studies [9,10,11,12,13,14,15,16].

Study [9] addresses complexity in SCs by mitigating the ripple effects of disruptions. It aims for a balance among robustness, complexity, and efficiency rather than simply minimizing complexity. By strategically managing the number of suppliers, product differentiation, and interrelationships, this study posits that a balanced approach to complexity can lead to broader objectives, such as reduced vulnerability to disruptions. The complexity is examined in a systemic manner, considering its interactions with other performance objectives.

Study [10] introduces a theoretical development of an entropy-based metric to assess the structural complexity of SCs. It lays foundational theoretical and conceptual frameworks for quantifying complexity through information theory, particularly Shannon’s entropy. Prior to this work, complexity was primarily addressed qualitatively or with ad hoc metrics, and this study pioneers a quantitative approach that facilitates comparisons of complexity across different SCs.

Study [11] identifies empirical drivers of complexity within SCs through a methodological framework combining SAP-LAP and AHP, specifically within the context of mining equipment manufacturing in India. This study not only validates existing theoretical perspectives on complexity drivers but also offers empirical evidence and prioritization. By applying structured methodologies to a practical case study, it transitions the discourse on complexity drivers from abstraction to actionable insights, enabling managers in analogous contexts to pinpoint specific sources of complexity.

Study [12] conducts a comprehensive literature review outlining the various drivers of complexity present in SCs. It synthesizes existing knowledge related to operational, structural, and informational complexities, serving as an essential foundation for understanding what contributes to the intricate nature of SCs.

Study [13] illustrates the detrimental impact of complexity on specific SC objectives, such as reducing deforestation in the palm oil SC. It identifies key drivers and demonstrates how multiple actors, geographical factors, and flow dynamics can obstruct crucial sustainability commitments.

Study [14] explores the relationship between complexity and performance, establishing a methodological and empirical linkage between SC complexity and manufacturing operational performance. It quantifies how complexity, influenced by plant design and operational strategy, directly impacts manufacturing outcomes, thereby reinforcing the relevance of complexity management as a vital component of performance improvement.

Study [15] analyzes SC complexity through the lens of performance measurement and system dynamics. This research posits that examining performance indicators can enhance the understanding of complexity while acknowledging that complexity itself significantly influences performance. It identifies impactful complexity drivers that warrant further investigation.

Finally, study [16] expands upon the entropy-based approaches introduced in study [10] by developing an algorithm for assessing SC complexity that incorporates the notion of conditional (relative) complexity. This innovative methodology enables a more focused assessment of specific SC components, enhancing the applicability of complexity metrics for managerial diagnosis and decision making.

In summary, the selected studies can be categorized into four thematic areas:

• Transition from a qualitative understanding of complexity [12] toward quantitative, metric-driven approaches [10,16];
• Identification and analysis of complexity drivers [11,12,15];
• Exploration of performance as a resultant outcome from complexity [13,14,15];
• Conceptualization of complexity as a management variable rather than a static attribute [9], required to achieve other objectives, such as efficiency and agility.

Our study aligns with these thematic groups by offering a quantitative approach, identifying and quantifying drivers of complexity, investigating the performance–complexity relationship as a point for future exploration, and framing complexity as a variable to be optimized rather than merely reduced. Therefore, the research hypothesis is that it is possible to measure complexity in SCs by a quantitative model that identifies drivers and serves as a feedback loop to control complexity according to strategic concerns.

2.3. Employing Shannon’s Entropy as a Proxy to Complexity in SCs

Shannon entropy can be helpful for evaluating complexity by measuring the uncertainty or average unexpectedness associated with a random variable or, in the context of information theory, the amount of information contained in a message [50]. The flow of information exchanged between agents within an SC can be considered as a message, in which the necessity of the next symbol or lack thereof (a piece of managerial information) is the outcome of a random variable. Equation (1) gives Shannon’s entropy H(P), subject to Equation (2), for the discrete outcomes of a random variable that will be employed in this study. The resulting unit is expressed in bits [7].

$$H\left(P\right)=-\sum _{i=1}^n{p_i·log(p}_i)$$

(1)

$$\sum _{i=1}^n{p}_i=1$$

(2)

where:

• H(P) = entropy of a random variable;
• p_i is the probability of the ith outcome;
• n is the number of possible outcomes.

The function H(P) serves as a measure to quantify the level of uncertainty inherent in a probability distribution. This study handles the amount of information necessary to coordinate the actions necessary to meet orders’ requirements within SCs. Higher values of H(P) indicate increased uncertainty or randomness in the distribution, while lower values suggest a higher degree of predictability and reduced uncertainty. This predictability reduces the need for coordination, leading to decreased internal complexity. In simpler terms, a higher H(P) means more information is required to dissipate uncertainty in fulfilling orders, whereas a lower H(P) implies the opposite. When dealing with systems exceeding a single dimension [51], such as the multiple agents actuating in an SC, Shannon’s entropy adopts the multidimensional form presented in Equation (3).

$$H\left(P\right)=-\sum _{k=1}^m\dots \sum _{i=1}^n{p_{i\dots k}·log(p}_{i\dots k})$$

(3)

where:

• n is the number of possible outcomes for each variable;
• m is the number of elements in a given dimension of the problem;
• … are further dimensions of the problem;
• p_i…k are the probabilities of the possible outcomes for the variables.

For a continuous random variable X with a continuous probability distribution p(x), Equation (4) shows the Shannon entropy, subject to Equation (5) [52].

$$H\left(X\right)=-{\int }_{-\infty }^{\infty }p\left(x\right)·logp\left(x\right)dx$$

(4)

$${\int }_{-\infty }^{\infty }p\left(x\right)=1$$

(5)

where:

• x is the continuous random variable whose entropy is being calculated; and
• p(x) is the probability density function of X.

A case of interest for this study occurs when n = 2, which is the so-called binary Shannon entropy, when the maximum entropy occurs when p_i = 0.5. In this case, the Shannon entropy assumes the form shown in Equation (6). Figure 2 showcases the binary H(P), which is a concave function with a maximum at p = 0.5 and an outcome of H_bin(p) = 1 bit [7].

$$H_{bin}\left(p\right)=-p·\mathit{log}\left(p\right)-\left(1-p\right)·\mathit{log}\left(1-p\right)$$

(6)

Entropy is inversely proportional to the diversity of possible outcomes. As the likelihood of a specific group of symbols occurring becomes dominant, the overall entropy of the system decreases [7]. After applying Shannon entropy to a random variable, it is useful to compare the result to the maximum possible entropy, which occurs when the probabilities are uniformly distributed. Taking the derivative of Equation (1) and setting it equal to zero yields the point of maximum entropy. Treating Shannon’s entropy as a relative or percentage rather than an absolute measurement is beneficial, as entropy is influenced not only by the probability distribution but also by the number of possible outcomes and symbols in the message. A system with numerous outcomes and symbols should exhibit a higher absolute value for entropy. Comparing the current entropy to the maximum entropy helps gauge the amount of missing information or the level of uncertainty present in the variable, regardless of the size of the string and the number of possible outcomes [53].

3. Materials and Methods

According to [54], complexity can stem from three distinct sources: materials, finances, and information flows. This study acknowledges that when both material and financial uncertainties arise, it can lead to unanticipated requirements for additional information exchange. Hence, by monitoring the information flow in relevant channels, mainly uncommon requests for further information, all three sources of complexity can be effectively managed. Therefore, the primary research assumption is that to evaluate complexity, the SCM must manage relevant flows of information to fulfill the manufacturing orders received by the focal company. A previous study [55] has established a list of twenty different types of information (j = 1, …, 20) that may or may not be necessary to complete a manufacturing order. Whether or not information j is required to fulfill an order is a binary output for a random event (i = 1 if the information is required; 0 otherwise). Future studies should consider intermediate levels in which information may be partially required (in this case, the outcome would be discrete, not binary). Moreover, the study has identified five relevant paths (k = 1, …, 5) that the 20 pieces of information can follow. For each SC, the study must compute one hundred probabilities of information j being required in path k to fulfill a manufacturing order. Equation (7) uses these probabilities to calculate Shannon entropy.

$$H\left(P\right)=-\sum _{k=1}^5\sum _{j=1}^{20}\sum _{i=1}^2{p_{ijk}·log(p}_{ijk})$$

(7)

where:

• 2 is the number of possible outcomes for a piece of information (required or not); 20 is the number of types of information of interest;
• 5 is the number of agents considered in the SC;
• p_ijk are the probabilities of the information jk (20 pieces and 5 agents) that is required (i = 1) or not (i = 2).

Setting all probabilities to 0.5 results in the maximum possible entropy. Dividing the first result (Equation (7)) by the second provides the percentage entropy, which is more useful in managing the inherent complexity of the SC. Furthermore, given that [p_1jk + p_2jk] = 1, that is, the sum of the probability of the information jk that is required and the probability of the information that is not required must equal 1, it follows that both probabilities cannot exceed or drop below 0.5 at the same time. For example, if p_1jk = 0.25, then it is necessary that p_2jk = 0.75. Since the study must focus only on one value, we chose the lowest one, regardless of whether the character is active or inactive. Switching will not affect the uncertainty.

The study followed a particular methodology, divided into the following steps:

• Four focal companies were selected: two from the agrifood industry and two from the metalworking industry. In each industry, one company prioritizes competition according to cost/quality and the other according to dependability/flexibility;
• At the headquarters of companies, two managers were interviewed together, one responsible for manufacturing and the other for logistics activities. The interviews lasted around two hours. The respondents answered two rounds of questions in consensus. In the first round, they prioritized the four competition objectives. In the second round, they estimated the probabilities. To make the estimate, respondents previously consulted the fifty most important manufacturing orders from the most recent days and counted how many times information j was requested in path k. Further information on orders from all respondents is confidential;
• After the first meeting, managers had enough time to search the orders’ documentation to identify the number of times each piece of information was required. Managers had the chance to contact practitioners to clarify doubts. The number was rounded to facilitate communication. The experience of managers and practitioners, the accuracy of internal documents, and the triangulation during the interviews ensure the reliability of the measurement;
• Equation (7), which expresses the Shannon entropy, was used to calculate maximum entropy and percentage entropy, a proxy variable that describes relative complexity of the SC [16];
• In a final meeting, the results and some avenues for future complexity control were discussed with managers.

Table 2. Information exchanged within the SC.

Group	Tag	Information
Planning and scheduling	I1	Forecasting and sales history
	I2	Manufacturing capacity
	I3	Scheduled maintenance
	I4	Lead times and deadlines
Logistics	I5	Scheduled shipments
	I6	Scheduled arrivals
	I7	Shared inventory situation
	I8	Shared transportation situation
Workforce	I9	Availability of skilled operators
	I10	Availability of skilled designers
Finance	I11	Cash flow situation
	I12	Shared purchases situation
	I13	Credit, payments, and loans
	I14	Shared financing
Technology and innovation	I15	Product development
	I16	Process development
	I17	Shared investments
	I18	Shared machine situation
	I19	Technology transfer
	I20	Technical support

Source: [55].

and Figure 3, respectively, present the twenty pieces of information and the five paths included in the research.

Regarding Table 2, there are five groups responsible for managing twenty pieces of information. These groups include planning and scheduling, which handles manufacturing capacity and deadlines; logistics, which handles raw materials and deliveries; workforce, which handles operators’ skills required to fulfill orders’ requirements; finance, which handles cash flows; and technology and innovation, which handles the technical demands and abilities necessary to satisfy customers’ needs. Figure 3 outlines five essential pathways (R1, R2, R3, R11, and R21) for tracking information exchange. These include the R1 flow of stocked raw materials in continuous demand, the R2 flow of specific engineered materials utilized only as needed, and the R3 flow of engineering and design services engaged on an as-needed basis. Additionally, the manufacturing to distribution pathway R11 encompasses fabrication, maintenance, transportation, and warehousing. Finally, the customer service pathway R21 covers delivery and technical support services. Additional information or pathways should be explored in future studies.

4. Results and Discussion

4.1. The Companies

Company A is an agrifood industry player that specializes in producing soybean meal and oil. The company prioritizes highly standardized products originating from soy cultures. Supplier and customer markets are reasonably stable. Company A relies on large distributors and local distribution channels that serve retailers and companies specializing in agrifood products. Although the company does not frequently modify its product designs, any changes undergo rigorous scrutiny by technical and engineering services for certification before being approved for production and sale.

Company B is an agrifood industry player that specializes in producing fertilizers from the three main mineral groups: nitrogen, phosphate, and potassium, with production capacity across all three. The company incorporates technological advances in processes and products and must rely on specialized technical assistance extended to customers. The company is constantly innovating its product lines to offer its customers, mainly farmers, production enhancements and cost reductions in rural activity. The company operates primarily in markets in which raw material offers and prices are stable, while consumer markets can vary owing to climate events and seasonality. The company sells its products through large distributors and national and international distribution channels that supply large retailers. Any product design changes must undergo technical services that certify their quality before being released for production and sale.

Company C is a metalworking industry player that specializes in producing metallic components for large industrial items, specifically catering to the machinery and equipment industries, as well as the automotive industry. The company uses metallic plates received in large lots for the steelmaking industry, metal closures, safety devices, and, eventually, wood packaging such as pallets. The company operates with stable raw material markets and moderately variable consumer markets. To distribute its products, it uses both local and national logistics operators that store and supply large quantities to buyers.

Company D is a metalworking industry player that specializes in engineered solutions of high complexity to specific markets. The company uses metallic, electric, and electronic parts received in medium and small lots from various suppliers. The raw material markets are somehow unstable, and the consumer markets are highly variable. The company often receives manufacturing orders that require prior engineering designs. The company works with local and national logistics operators who store and transport large parts to buyers with stringent safety requirements. Innovation is continuous, and safety is a requirement, which means that any product design modifications undergo technical services that certify them before their release for production and sale.

Concerning the competitive priorities of focal companies A, B, C, and D, certain patterns emerge in their strategic emphasis.

Focal company A prioritizes compliance with quality standards, primarily driven by stringent food safety requirements. The next is cost reduction, given the intense competition in the sector, in which pricing plays a pivotal role in consumer choices. Flexibility and dependability assume diminished significance for this company, attributed to its management of substantial inventories that promptly cater to unforeseen demands. Among the four SC meta-strategies, the SC is closer to the efficient pattern.

Focal company B prioritizes flexibility due to the changing nature of agrifood activity and the inherent uncertainty in climate conditions. Subsequently, dependability assumes prominence, driven by the temporal commitments of farmers tied to seasonality and prices in the global market. The second is quality, particularly due to the difficulty for customers of handling manufacturing errors. Cost reduction (and consequently price reduction) occupies a relatively lower position on the priority scale, given that the competition in the sector is not too fierce. Among the four SC meta-strategies, the SC is closer to the responsive pattern.

Focal company C prioritizes cost reduction. The standardization of its product influences this strategic choice, its relative ease of production, and the heightened competition within the sector. The second is quality, due to the difficulty for customers of dealing with dimensional, structural, and appearance errors in raw material supplied to other industries. Flexibility and dependability assume less critical roles, given the company’s effective management of substantial inventories to promptly address unexpected demands. Among the four SC meta-strategies, the SC is closer to the efficient pattern.

Finally, focal company D prioritizes dependability. This emphasis is underscored by the industrial market’s stringent deadlines and narrow delivery windows, in which any lapse could result in a loss of business. Flexibility assumes the secondary position, driven by the swift variations in project features and uncertainties surrounding the definition of standardized batches. Quality follows, as manufacturing errors are difficult to amend by the company’s delivery model. Cost reduction, though not irrelevant, takes a less central role, as the packaging cost in industrial deliveries has a less influential role. Among the four SC meta-strategies, the SC is closer to the agile pattern.

4.2. Entropy Calculation

Table 3. Probabilities of information required for SCM.

											Tag
Company	Path	I1	I2	I3	I4	I5	I6	I7	I8	I9	I10	I11	I12	I13	I14	I15	I16	I17	I18	I19	I20
A	R1	40%	10%		50%	30%	30%	30%	10%	10%		30%	30%			30%					10%
	R2	10%			10%							10%				10%					30%
	R3	40%			10%											10%
	R11		10%		10%
	R21	10%	10%		30%	10%	10%	30%	50%
B	R1	10%	25%	25%	30%	10%	10%		10%	5%		30%		30%		10%					20%
	R2	10%	25%	25%	40%				20%	10%		10%		20%		30%	10%				30%
	R3	10%																			30%
	R11	10%	20%	30%	30%	10%	10%		10%	15%		20%		20%
	R21	20%			40%				10%			30%		30%		10%					10%
C	R1		20%		10%			10%									20%				20%
	R2		30%		20%
	R3		20%		10%								20%
	R11	10%		30%						40%					10%
	R21					40%			40%	40%								50%			20%
D	R1	20%			40%			10%				35%		35%		10%	10%
	R2	40%	45%		10%											50%	50%				20%
	R3	45%											20%			20%	20%				45%
	R11	10%	10%	30%	20%					40%		50%		50%	30%	10%	10%				10%
	R21	40%			45%	40%			40%	40%		45%		45%	25%			50%			40%

Source: Authors’ own creation.

and

Table 4. Entropies associated with the probabilities of information required for SCM.

											Tag
Company	Path	I1	I2	I3	I4	I5	I6	I7	I8	I9	I10	I11	I12	I13	I14	I15	I16	I17	I18	I19	I20
A	R1	0.97	0.47		1.00	0.88	0.88	0.88	0.47	0.47		0.88	0.88			0.88					0.47
(19.8%)	R2	0.47			0.47							0.47				0.47					0.88
	R3	0.97			0.47											0.47
	R11		0.47		0.47
	R21	0.47	0.47		0.88	0.47	0.47	0.88	1.00
B	R1	0.47	0.81	0.81	0.88	0.47	0.47		0.47	0.29		0.88		0.88		0.47					0.72
(27.9%)	R2	0.47	0.81	0.81	0.97				0.72	0.47		0.47		0.72		0.88	0.47				0.88
	R3	0.47																			0.88
	R11	0.47	0.72	0.88	0.88	0.47	0.47		0.47	0.61		0.72		0.72
	R21	0.72			0.97				0.47			0.88		0.88		0.47					0.47
C	R1		0.72		0.47			0.47									0.72				0.72
(14.0%)	R2		0.88		0.72
	R3		0.72		0.47								0.72
	R11	0.47		0.88						0.97					0.47
	R21					0.97			0.97	0.97								1.00			0.72
D	R1	0.72			0.97			0.47				0.93		0.93		0.47	0.47
(31.7%)	R2	0.97	0.99		0.47											1.00	1.00				0.72
	R3	0.99											0.72			0.72	0.72				0.99
	R11	0.47	0.47	0.88	0.72					0.97		1.00		1.00	0.88	0.47	0.47				0.47
	R21	0.97			0.99	0.97			0.97	0.97		0.99		0.99	0.81			1.00			0.97

Source: Authors’ own creation.

synthesize the results of the evaluations conducted by managers and the entropies (the sign minus in the entropy was omitted for clarity), respectively. In the first row of Table 4, together with the name of the focal company, it is possible to find the percentage entropy of each SC. The maximum entropy for all applications is 100 bits.

Table 5. Synthesis of the results.

Company	Industry	Competitive Priorities	Percentage Entropy	Empty Cells
A	Agrifood	Cost/quality	19.8%	29
B	Agrifood	Flexibility/dependability	27.9%	42
C	Metalworking	Cost/quality	14.0%	19
D	Metalworking	Flexibility/dependability	31.7%	39

Source: Authors’ own creation.

provides the relationship between the percentage entropy and priorities of the focal company, as well as the number of empty cells in each dashboard. An empty cell means no need to randomly exchange (it is not required or was never required) that kind of information and, consequently, an absence of uncertainty and related complexity.

The cases show that SCs focusing on cost and quality tend to be less complex than those emphasizing flexibility and dependability in the same industry. Companies prioritizing cost and quality have fewer empty cells, indicating fewer complex aspects, than those prioritizing flexibility and dependability.

Table 6. Percentage entropy per group of information and company.

	Group of Information
Company	Planning and Scheduling	Logistics	Workforce	Finance	Technology and Innovation	Total
A	7.6%	5.9%	0.9%	2.2%	3.2%	19.8%
B	11.2%	4.0%	1.4%	6.2%	5.2%	27.9%
C	5.3%	2.4%	1.9%	1.2%	3.2%	14.0%
D	9.6%	2.4%	1.9%	8.3%	9.5%	31.7%
Average	8.4%	3.7%	1.5%	4.5%	5.3%

shows the percentage entropy per group of information per company.

The table reveals that companies that prioritize flexibility and dependability have a greater value in planning and scheduling (company B), finance, and technology and innovation (company D). In contrast, one of the companies (company A) that prioritizes cost and quality has a greater value in logistics. The workforce is a less relevant source of uncertainty in the studied sample of companies. Therefore, company A should care about logistics while companies B and D should focus on planning and scheduling and technology and innovation as the main sources of uncertainty.

Moving to

Table 7. Average entropy per path and company.

Company	R1	R2	R3	R11	R21	Priority
A/C	0.43	0.19	0.18	0.17	0.42	Cost/Quality
B/D	0.51	0.50	0.26	0.50	0.57	Flexibility/Dependability
Δ%	15%	62%	31%	65%	26%

Source: Authors’ own creation.

, the table shows the average entropy per path per company.

The table reveals that the most significant difference between the average entropies is observed in R2 and R11, corresponding to specially engineered products and deliveries from the manufacturer, respectively. In R2 and R11, companies A and C, prioritizing cost and quality, exhibit notably lower average entropies than companies B and D. This suggests that ensuring flexibility and dependability requires greater organizational complexity in SCM in relation to manufactured products and agile deliveries. Such drivers require greater coordination efforts, which increases complexity. Conversely, companies emphasizing cost reduction and quality assurance tend to employ standardized products and larger transfer batches, which reduce concerns regarding project and product development, as well as agile deliveries, variable batches, and changes in the mix. Such drivers require less coordination effort, which decreases complexity.

This may not be a coincidence. Future studies should conduct surveys to test the following hypothesis: Companies that prioritize cost and quality generally exhibit an SCM system with lower relative complexity compared to companies that rely on flexibility and dependability for competition.

5. Final Remarks

The purpose of the study was to propose a quantitative modeling method, employing Shannon’s entropy model as a proxy to assess the complexity in SCs. This study’s object was four SCs in the agrifood and metalworking industries of Southern Brazil. The study’s findings suggest that companies that prioritize cost and quality tend to have lower SCM complexity than those that prioritize flexibility and dependability. The study observed significant differences in the average entropies of specific paths related to engineered products and deliveries. These observations indicate that organizational complexities vary based on competitive priorities.

The findings have implications for industrial practitioners. Companies that prioritize cost and quality may benefit from lower complexity, which leads to streamlined processes. In contrast, those who prioritize flexibility and dependability may need more complex organizational structures to meet dynamic market demands. In summary, the study provided valuable insights for industrial practitioners, including how to align competitive priorities with the inherent complexity of SCs. The study’s findings suggest that prioritizing cost and quality can lead to lower SCM complexity, while flexibility and dependability may lead to higher organizational complexities.

Looking ahead, future research can delve deeper into testing the hypothesis that companies prioritizing cost and quality exhibit lower SCM complexity. The study also suggests exploring the broader applicability of information entropy in assessing and controlling complexity across diverse industries, other types of systems, and global SCs. This exploration would contribute to the evolving field of SCM.

In terms of external validity, the current methodology demonstrates both generalizability and extensibility across various production system typologies. The core principle—quantifying informational flow entropy as an indicator of complexity—remains universally applicable, grounded in Shannon entropy’s theoretical framework for assessing informational complexity. When extending the methodology to other systems, several considerations should be included. (i) Information granularity and diversity: Future models could integrate a wider and more varied array of informational elements, such as sustainability metrics, regulatory compliance parameters, or cybersecurity data. Additionally, incorporating intermediate states (information partially required) could refine entropy measurement and address further nuances of uncertainty. (ii) Multitier interactions: For broader applicability, the mapping scope should include interactions beyond the focal company to encompass second- and third-tier agents. (iii) Large-scale data acquisition: While interview-based methodologies prove effective for detailed case studies, achieving broader generalizability requires collecting transactional data from enterprise resource planning (ERP) and SCM systems. Automated data collection may provide probability calculations with greater statistical significance.

Future research should also include the meta-strategy of the SC. One possibility is to lead four similar surveys, each one focusing on a different meta-strategy to gather enough data to compare outcomes. Another possibility is the use of multicriteria methods to calculate weights in the case of multiple strategies and multiple priorities. At least one study [30] uses confidence intervals to address the inherent uncertainty observed in multicriteria studies focused on investigating the strategic aspects of and preferences in SCs.

One important topic that the study should have addressed, which could be the focus of future research, is the relationship between complexity and performance in SCs. Among other approaches, performance can be measured using the framework provided by the SCOR (Supply Chain Operations Reference) model, as demonstrated in [56]. Among many others, some indicators that can be connected to measure performance are raw material cost, process inventory, and design and sales cost (cost priority); percentage of rework, client satisfaction, and percentage of waste (quality priority); lead time to orders, back orders, and on-time deliveries (dependability priority); and time-to-market, setup time, and average mix of products (flexibility priority).

This study observed that the SCs that prioritize flexibility and dependability generate more uncertainty in planning and scheduling and technology and innovation. On the other hand, one of the SCs that prioritizes cost and quality generates more uncertainty in logistics. These findings can help practitioners identify key areas for future performance improvement actions. Furthermore, it remains to be seen whether there is an analytical relationship between complexity and performance. The need for more information is a result of the need for greater coordination of activities, regardless of the level of complexity. It is also reasonable to assume that too much coordination can lead to reduced performance due to an excess of intermediate activities. At the same time, too little coordination can lead to errors in operations and reduced performance. Therefore, a U-shaped relationship may exist between performance and complexity: an optimal level of complexity maximizes SC performance. This topic is worth exploring further in future research.