Objective Function Formulation to Optimize Control Structure Parameters Using Nature-Inspired Optimization Algorithms
Abstract
1. Introduction
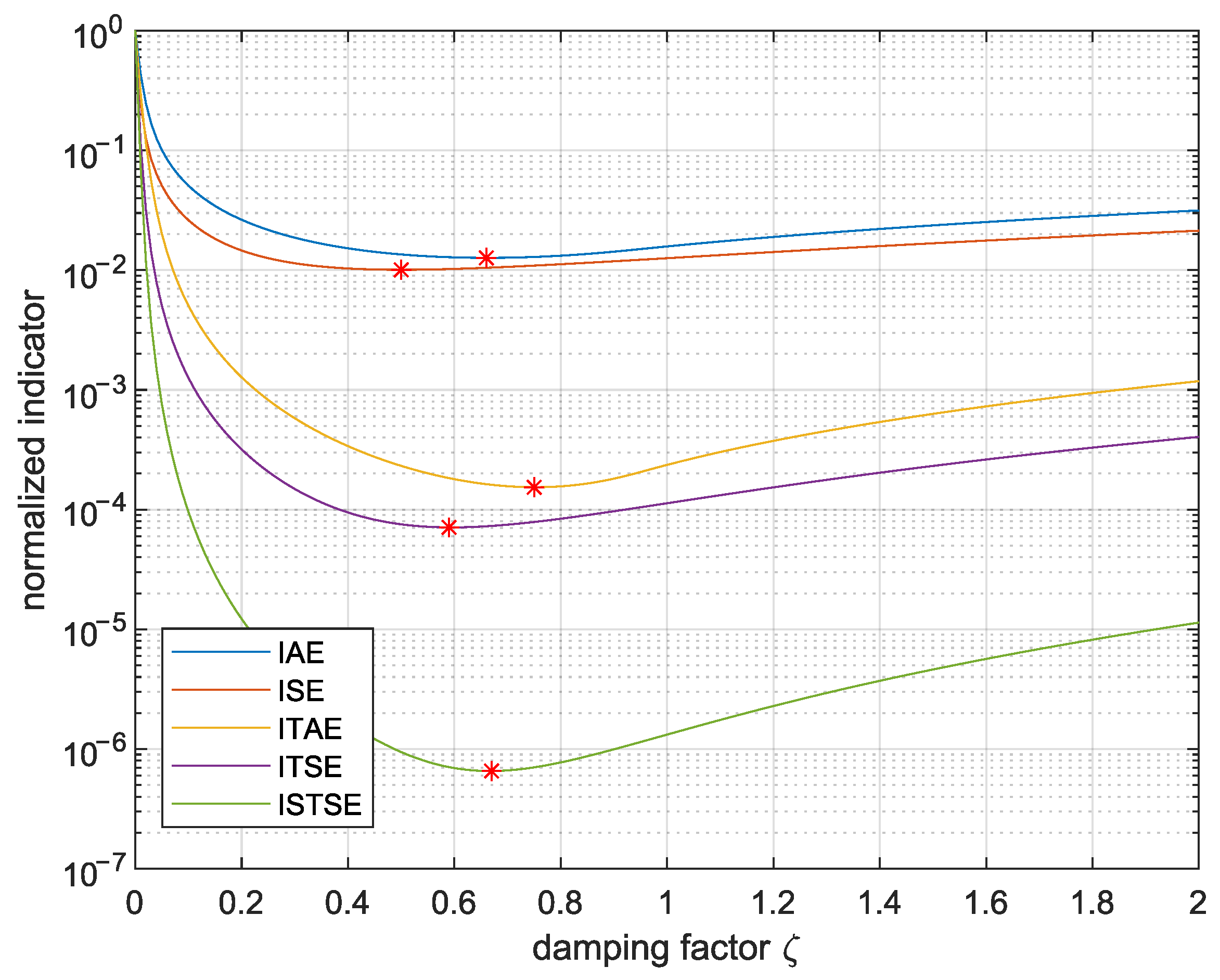
2. Performance Indicators of System Response
2.1. Basic Criteria
- Integral-Squared Error (ISE):
- Integral Absolute Error (IAE):
- Integral Time Squared Error (ITSE):
- Integral Time Absolute Error (ITAE):
- Integral-Squared Time-Squared Error (ISTSE):
2.2. Step Response Indicators
- Percentage Overshot (PO):
- Rising Time (RT):with
- Settling Time (ST):with
- Steady-State Error (SSE):
2.3. Additional Requirements’ Formulation
3. Application of Nature-Inspired Optimization Algorithms for Multi-Objective Constrained Optimization
3.1. Penalties
3.2. Deb’s Rules
- Two feasible solutions: Select the one with better objective function value;
- Feasible and infeasible solutions: Select the feasible solution;
- Two infeasible solutions: Select the one with the lower constant function value.
3.3. Augmented Lagrangian Method
- The initial values of the Lagrange multipliers are set to 0, and the penalty parameter is set to [31]where and are the minimum and maximum values of the penalty factor, respectively, and is the initial guess of the optimization problem.
- Minimize using an unconstrained or box-constrained optimization algorithm.
- While the augmented Lagrangian is minimized, the penalty factor is updated every N iterations:where is the penalty increase factor; ICM is the infeasibility/complementarity measure defined as [30]
- While the augmented Lagrangian is minimized, the Lagrange multipliers are updated every N iterations:where and are the minimum and maximum values of the Lagrange multipliers, respectively.
- If the termination criteria of the optimization algorithm are met, return the results.
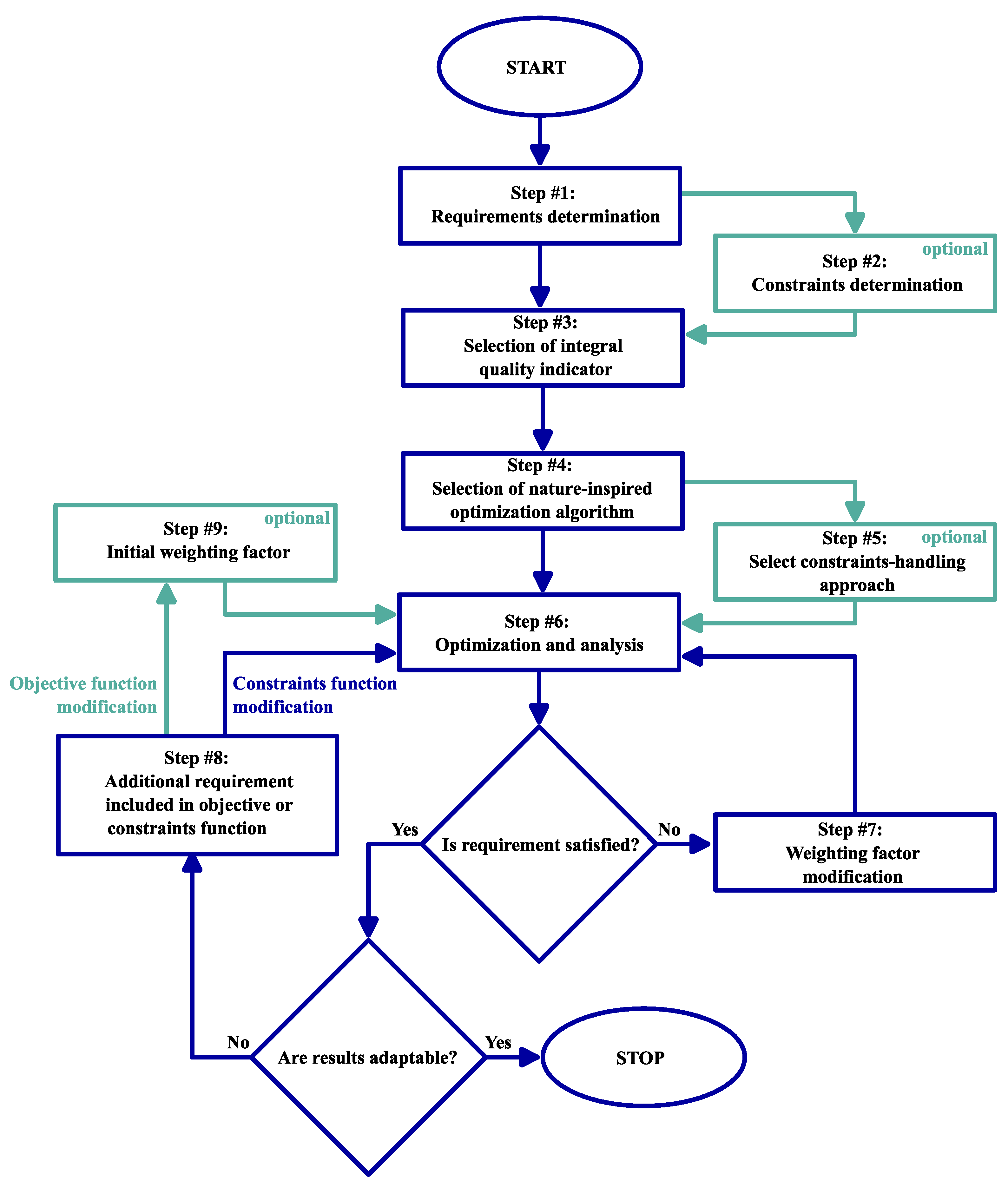
4. The Methodology
- Step #1:
- Determine the requirements of the system response.
- Step #2:
- (optional) Determine the constraints for the control system.
- Step #3:
- Select the basic integral quality indicator, e.g., IAE Equation (2), ITSE Equation (3) (Section 2.1).
- Step #4:
- Select the nature-inspired optimization algorithm.
- Step #5:
- (optional) Select constraint handling approach, e.g., penalties (Section 3.2), Deb’s rules (Section 3.1).
- Step #6:
- Optimize the current objective function and interpret solution. If the solution is satisfactory, the process is finished. Otherwise, continue.
- Step #7:
- (optional) Modify the weighting factor and go to point 6.
- Step #8:
- Include additional requirements, for example, the maximum overshoot value (see Section 2.3).
- Step #9:
- Set the initial guess of the weighting factor of the new requirement and go to point 6.
4.1. An Example
4.1.1. Step #1: Requirement Determination
4.1.2. Step #3: Selection of Integral Quality Indicator
4.1.3. Step #4: Selection of Nature-Inspired Optimization Algorithm
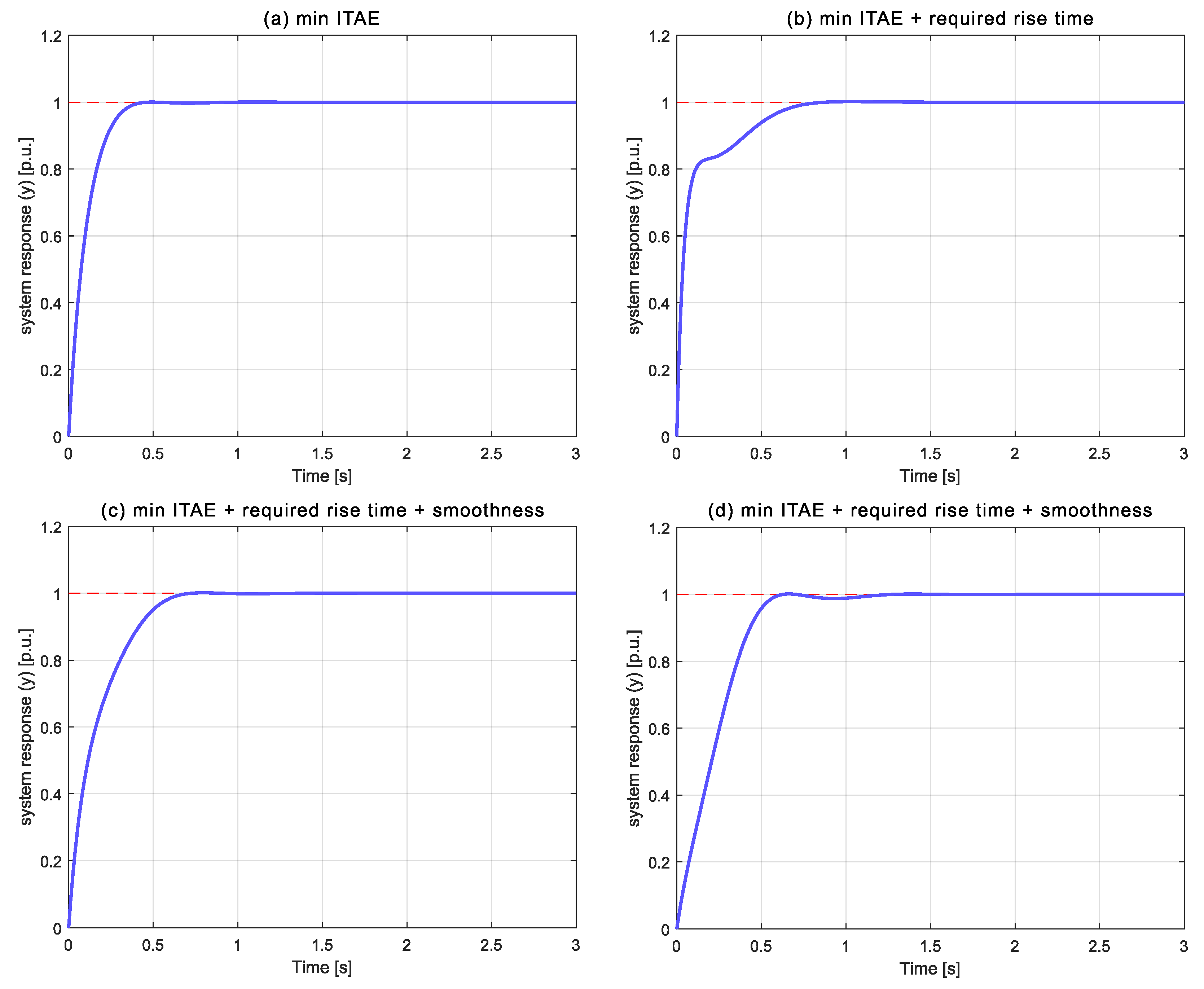
4.1.4. Step #6: Optimization and Analysis
4.1.5. Step #8: Additional Requirement
4.1.6. Step #9: Initial Weighting Factor
4.1.7. Step #6: Optimization and Analysis
4.1.8. Step #7: Weighting Factor Adjustment
4.1.9. Step #6: Optimization and Analysis
4.1.10. Step #8: Additional Requirement
4.1.11. Step #9: Initial Weighting Factor
4.1.12. Step #6: Optimization and Analysis
4.1.13. Step #7: Weighting Factor Adjustment
4.1.14. Step #6: Optimization and Analysis
5. Case Studies
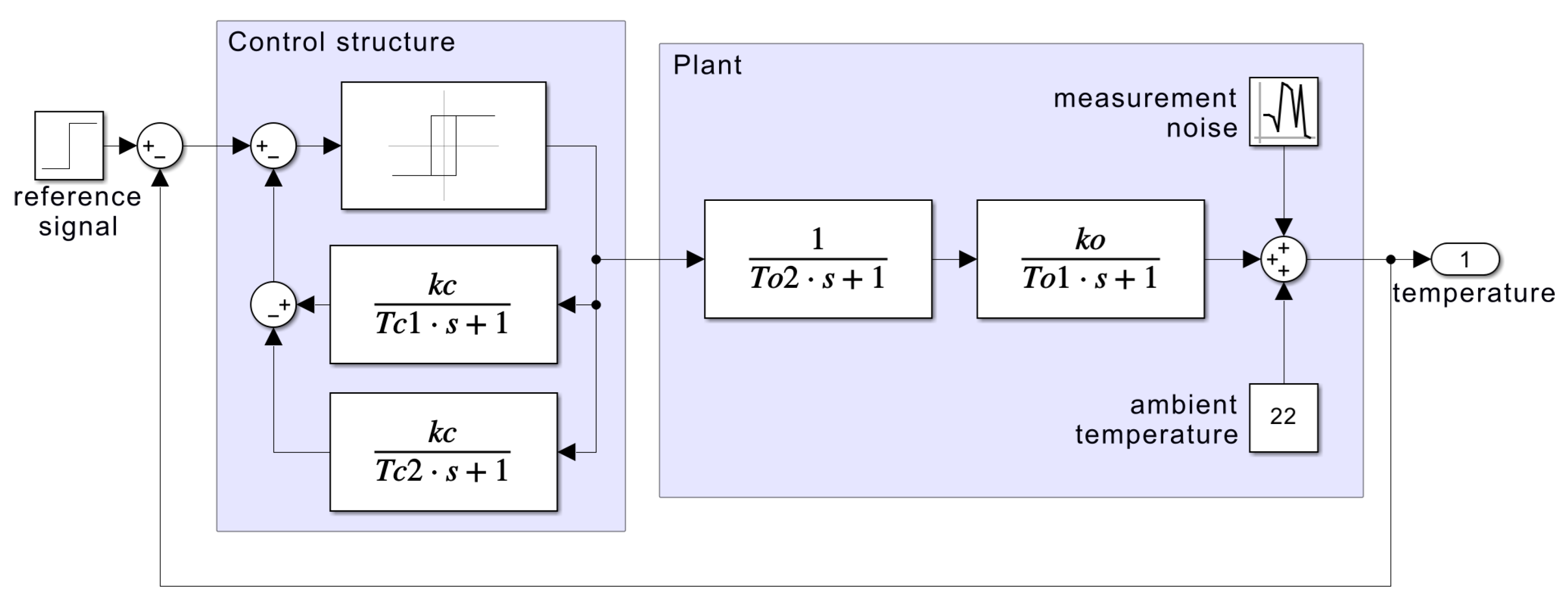
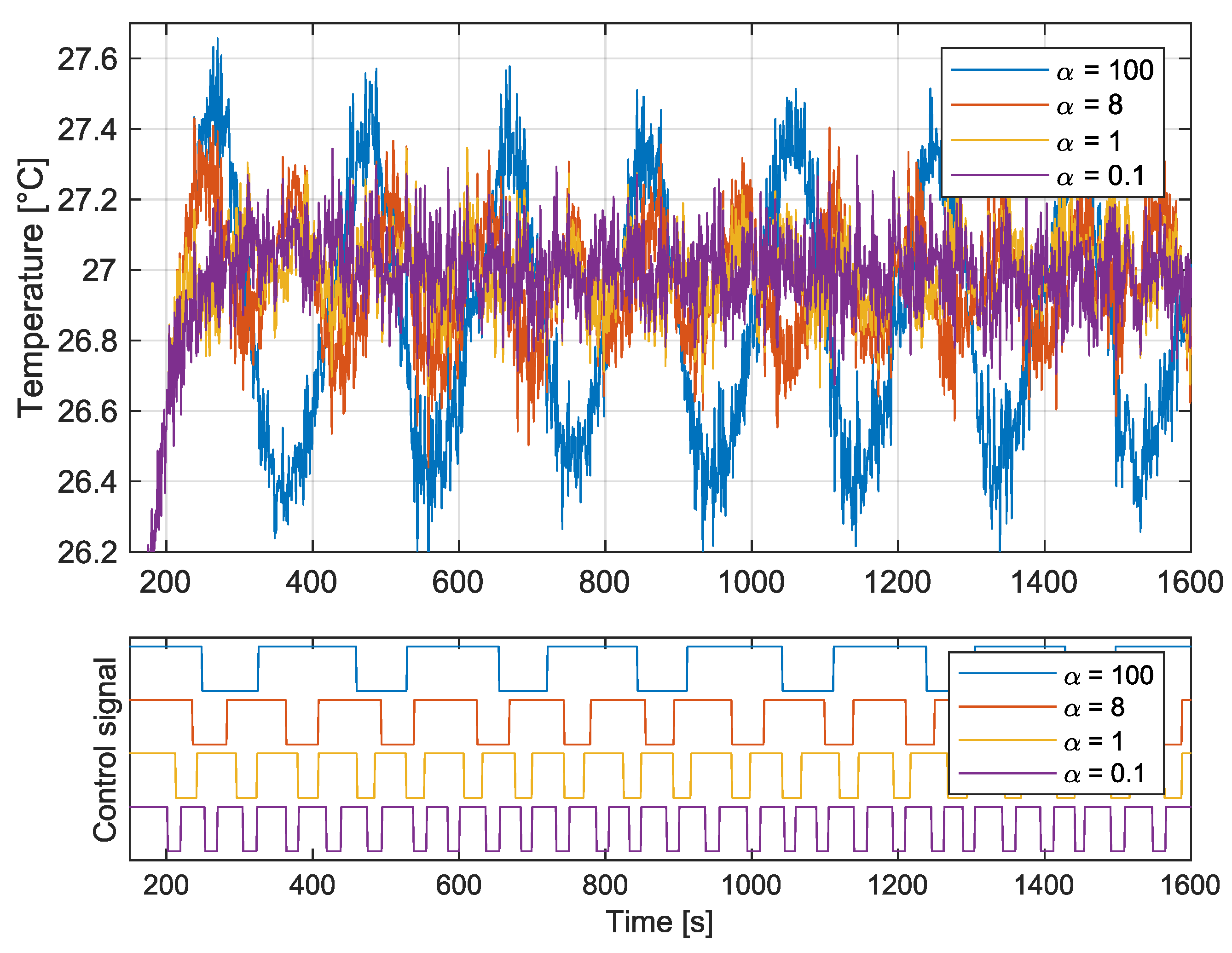
5.1. Hysteresis Control with PID Correction for Temperature Control
5.1.1. Proposed Objective Function
5.1.2. Results
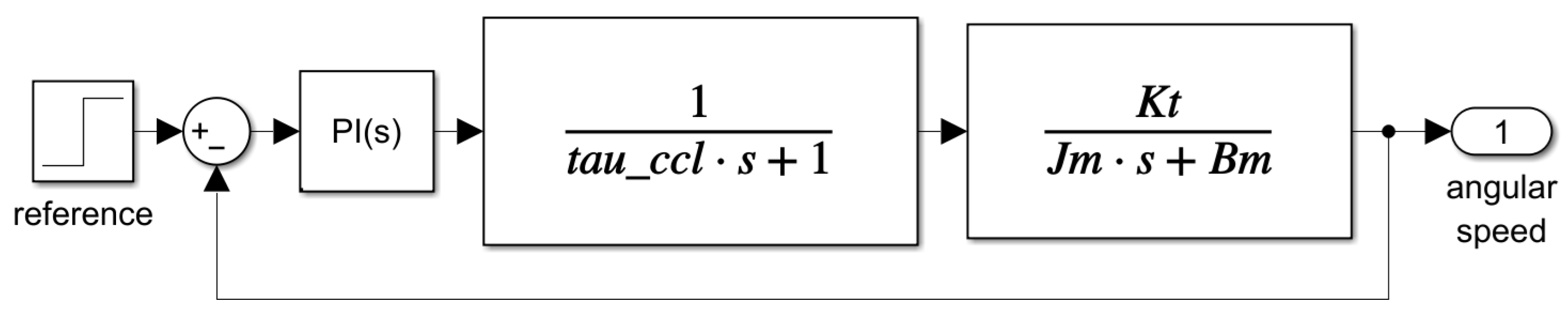
5.2. Proportional–Integral Speed Controller for DC Motor
5.2.1. Mathematical Formulation
5.2.2. Proposed Objective Function
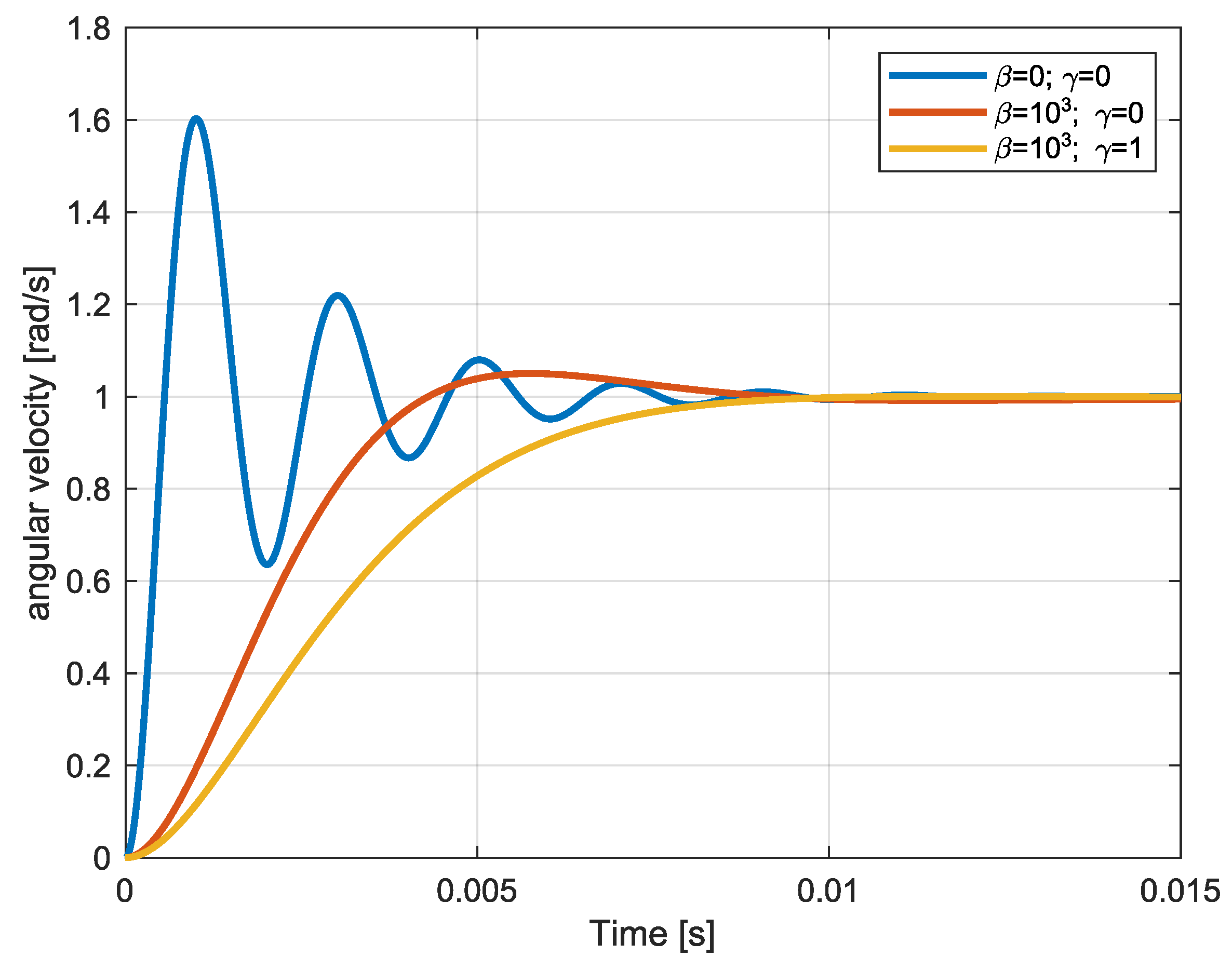
5.2.3. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sahu, B.K.; Pati, S.; Mohanty, P.K.; Panda, S. Teaching–learning based optimization algorithm based fuzzy-PID controller for automatic generation control of multi-area power system. Appl. Soft Comput. 2015, 27, 240–249. [Google Scholar] [CrossRef]
- Solihin, M.I.; Wahyudi; Kamal, M.; Legowo, A. Optimal PID controller tuning of automatic gantry crane using PSO algorithm. In Proceedings of the 2008 5th International Symposium on Mechatronics and Its Applications, Amman, Jordan, 27–29 May 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1–5. [Google Scholar]
- He, Y.; Zhou, Y.; Wei, Y.; Luo, Q.; Deng, W. Wind driven butterfly optimization algorithm with hybrid mechanism avoiding natural enemies for global optimization and PID controller design. J. Bionic Eng. 2023, 20, 2935–2972. [Google Scholar] [CrossRef]
- Patil, R.S.; Jadhav, S.P.; Patil, M.D. Review of Intelligent and Nature-Inspired Algorithms-Based Methods for Tuning PID Controllers in Industrial Applications. J. Robot. Control JRC 2024, 5, 336–358. [Google Scholar] [CrossRef]
- Malarczyk, M.; Katsura, S.; Kaminski, M.; Szabat, K. A Novel Meta-Heuristic Algorithm Based on Birch Succession in the Optimization of an Electric Drive with a Flexible Shaft. Energies 2024, 17, 4104. [Google Scholar] [CrossRef]
- Tarczewski, T.; Stojic, D.; Dzielinski, A. Large Language Model-Based Tuning Assistant for Variable Speed PMSM Drive with Cascade Control Structure. Electronics 2025, 14, 232. [Google Scholar] [CrossRef]
- Sahu, R.K.; Panda, S.; Rout, U.K.; Sahoo, D.K. Teaching learning based optimization algorithm for automatic generation control of power system using 2-DOF PID controller. Int. J. Electr. Power Energy Syst. 2016, 77, 287–301. [Google Scholar] [CrossRef]
- Niewiara, Ł.J.; Szczepański, R.; Tarczewski, T.; Grzesiak, L.M. State feedback speed control with periodic disturbances attenuation for PMSM drive. Energies 2022, 15, 587. [Google Scholar] [CrossRef]
- Tarczewski, T.; Niewiara, Ł.J.; Grzesiak, L.M. Application of artificial bee colony algorithm to auto-tuning of state feedback controller for DC-DC power converter. Power Electron. Drives 2016, 1, 83–96. [Google Scholar]
- Szczepanski, R.; Kaminski, M.; Tarczewski, T. Auto-tuning process of state feedback speed controller applied for two-mass system. Energies 2020, 13, 3067. [Google Scholar] [CrossRef]
- Szczepanski, R.; Tarczewski, T.; Erwinski, K.; Grzesiak, L.M. Comparison of Constraint-handling Techniques Used in Artificial Bee Colony Algorithm for Auto-Tuning of State Feedback Speed Controller for PMSM. In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics, Portu, Portugal, 29–31 July 2018; pp. 279–286. [Google Scholar]
- Tarczewski, T.; Stojic, D.; Szczepanski, R.; Niewiara, L.; Grzesiak, L.M.; Hu, X. Online auto-tuning of multiresonant current controller with nature-inspired optimization algorithms and disturbance in the loop approach. Appl. Soft Comput. 2023, 144, 110512. [Google Scholar] [CrossRef]
- Zychlewicz, M.; Stanislawski, R.; Kaminski, M. Grey wolf optimizer in design process of the recurrent wavelet neural controller applied for two-mass system. Electronics 2022, 11, 177. [Google Scholar] [CrossRef]
- Łapa, K.; Cpałka, K. Flexible fuzzy PID controller (FFPIDC) and a nature-inspired method for its construction. IEEE Trans. Ind. Inform. 2017, 14, 1078–1088. [Google Scholar]
- Benitez-Garcia, S.E.; Villarreal-Cervantes, M.G.; Mezura-Montes, E. Event-triggered control optimal tuning through bio-inspired optimization in robotic manipulators. ISA Trans. 2022, 128, 81–105. [Google Scholar] [CrossRef] [PubMed]
- Du, C.; Yin, Z.; Zhang, Y.; Liu, J.; Sun, X.; Zhong, Y. Research on active disturbance rejection control with parameter autotune mechanism for induction motors based on adaptive particle swarm optimization algorithm with dynamic inertia weight. IEEE Trans. Power Electron. 2018, 34, 2841–2855. [Google Scholar] [CrossRef]
- Bassi, S.; Mishra, M.; Omizegba, E.E. Automatic tuning of proportional-integral-derivative (PID) controller using particle swarm optimization (PSO) algorithm. Int. J. Artif. Intell. Appl. 2011, 2, 25. [Google Scholar] [CrossRef]
- Sun, X.; Hu, C.; Lei, G.; Guo, Y.; Zhu, J. State feedback control for a PM hub motor based on gray wolf optimization algorithm. IEEE Trans. Power Electron. 2019, 35, 1136–1146. [Google Scholar] [CrossRef]
- Kaminski, M. Nature-inspired algorithm implemented for stable radial basis function neural controller of electric drive with induction motor. Energies 2020, 13, 6541. [Google Scholar] [CrossRef]
- Jumani, T.A.; Mustafa, M.W.; Hussain, Z.; Rasid, M.M.; Saeed, M.S.; Memon, M.M.; Khan, I.; Nisar, K.S. Jaya optimization algorithm for transient response and stability enhancement of a fractional-order PID based automatic voltage regulator system. Alex. Eng. J. 2020, 59, 2429–2440. [Google Scholar] [CrossRef]
- Gozde, H. Robust 2DOF state-feedback PI-controller based on meta-heuristic optimization for automatic voltage regulation system. ISA Trans. 2020, 98, 26–36. [Google Scholar] [CrossRef]
- Tarczewski, T.; Grzesiak, L.M. An application of novel nature-inspired optimization algorithms to auto-tuning state feedback speed controller for PMSM. IEEE Trans. Ind. Appl. 2018, 54, 2913–2925. [Google Scholar] [CrossRef]
- Ufnalski, B.; Kaszewski, A.; Grzesiak, L.M. Particle swarm optimization of the multioscillatory LQR for a three-phase four-wire voltage-source inverter with an LC output filter. IEEE Trans. Ind. Electron. 2014, 62, 484–493. [Google Scholar] [CrossRef]
- Fister, D.; Fister, I., Jr.; Fister, I.; Šafarič, R. Parameter tuning of PID controller with reactive nature-inspired algorithms. Robot. Auton. Syst. 2016, 84, 64–75. [Google Scholar] [CrossRef]
- Micev, M.; Ćalasan, M.; Ali, Z.M.; Hasanien, H.M.; Aleem, S.H.A. Optimal design of automatic voltage regulation controller using hybrid simulated annealing–Manta ray foraging optimization algorithm. Ain Shams Eng. J. 2021, 12, 641–657. [Google Scholar] [CrossRef]
- Coutinho, J.P.; Santos, L.O.; Reis, M.S. Bayesian Optimization for automatic tuning of digital multi-loop PID controllers. Comput. Chem. Eng. 2023, 173, 108211. [Google Scholar] [CrossRef]
- Cao, J.; Sun, X.; Tian, X. Optimal control strategy of state feedback control for surface-mounted PMSM drives based on auto-tuning of seeker optimization algorithm. Int. J. Appl. Electromagn. Mech. 2021, 66, 705–725. [Google Scholar] [CrossRef]
- Aguilar-Mejía, O.; Minor-Popocatl, H.; Tapia-Olvera, R. Comparison and Ranking of Metaheuristic Techniques for Optimization of PI Controllers in a Machine Drive System. Appl. Sci. 2020, 10, 6592. [Google Scholar] [CrossRef]
- Eberhard, P.; Sedlaczek, K. Using Augmented Lagrangian Particle Swarm Optimization for Constrained Problems in Engineering. In Advanced Design of Mechanical Systems: From Analysis to Optimization; Springer: Vienna, Austria, 2009; pp. 253–271. [Google Scholar] [CrossRef]
- Birgin, E.G.; Martinez, J.M. Improving ultimate convergence of an augmented Lagrangian method. Optim. Methods Softw. 2008, 23, 177–195. [Google Scholar] [CrossRef]
- Andreani, R.; Birgin, E.G.; Martínez, J.M.; Schuverdt, M.L. On augmented Lagrangian methods with general lower-level constraints. SIAM J. Optim. 2008, 18, 1286–1309. [Google Scholar] [CrossRef]
- Szczepanski, R. An Example of Automatic Tuning of Controller Parameters. MATLAB Central File Exchange. 2025. Available online: https://www.mathworks.com/matlabcentral/fileexchange/181202-an-example-of-automatic-tuning-of-controller-parameters (accessed on 29 May 2025).
- Yang, X.S. Nature-Inspired Optimization Algorithms; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Kumar, A.; Nadeem, M.; Banka, H. Nature inspired optimization algorithms: A comprehensive overview. Evol. Syst. 2023, 14, 141–156. [Google Scholar] [CrossRef]
| IAE | ITAE | ISE | ITSE | ISTSE | |
|---|---|---|---|---|---|
| Rise Time () | |||||
| Settling Time () | |||||
| Percentage Overshoot () |
| Parameter | Value |
|---|---|
| Static gain of the plant () | 7.5 °C/V |
| Time constant of the plant () | 150 s |
| Time constant of the plant () | 50 s |
| Hysteresis value (H) | 1 °C |
| ISE | |||||
|---|---|---|---|---|---|
| 0.1 | 58 | 7.12 | 57.0 | 100 | |
| 1 | 40 | 8.96 | 69.5 | 93.6 | |
| 8 | 25 | 3.29 | 59.6 | 92.5 | |
| 100 | 15 | 0.1 | 100 | 47.2 |
| Parameter | Value |
|---|---|
| Current control loop time constant () | 0.001 s |
| Torque constant () | 1 Nm/A |
| Moment of inertia () | 1 × 10−4 kg·m2 |
| Viscous friction coefficient () | 4 × 10−5 Nm·s/rad |
| ITSE | ||||||
|---|---|---|---|---|---|---|
| 0 | 0 | 60.3% | s | 10 | 10 | |
| 0 | 5.0% | s | 0.546 | 1.748 | ||
| 1 | 0.04% | s | 0.319 | 0.954 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szczepanski, R.; Erwinski, K.; Tarczewski, T. Objective Function Formulation to Optimize Control Structure Parameters Using Nature-Inspired Optimization Algorithms. Appl. Syst. Innov. 2025, 8, 79. https://doi.org/10.3390/asi8030079
Szczepanski R, Erwinski K, Tarczewski T. Objective Function Formulation to Optimize Control Structure Parameters Using Nature-Inspired Optimization Algorithms. Applied System Innovation. 2025; 8(3):79. https://doi.org/10.3390/asi8030079
Chicago/Turabian StyleSzczepanski, Rafal, Krystian Erwinski, and Tomasz Tarczewski. 2025. "Objective Function Formulation to Optimize Control Structure Parameters Using Nature-Inspired Optimization Algorithms" Applied System Innovation 8, no. 3: 79. https://doi.org/10.3390/asi8030079
APA StyleSzczepanski, R., Erwinski, K., & Tarczewski, T. (2025). Objective Function Formulation to Optimize Control Structure Parameters Using Nature-Inspired Optimization Algorithms. Applied System Innovation, 8(3), 79. https://doi.org/10.3390/asi8030079








