An Innovative Applied Control System of Helicopter Turboshaft Engines Based on Neuro-Fuzzy Networks
Abstract
1. Introduction
1.1. The Relevance of the Research
1.2. The State of the Art
1.3. The Main Attributes of the Research
- The development of the proposed neural network system for predicting anomalous data in sensor systems;
- The development of the helicopter TE adaptive control law;
- The development of an intelligent automatic control system for the helicopter TE adaptive control law implementation;
- The development of the fuzzy controller architecture and training algorithm;
- The development of a semi-physical simulation stand for conducting computational experiments;
- Conducting a computational experiment to evaluate helicopter TE control quality under conditions of actuator failure in the fuel flow control mechanism within the gas generator rotor r.p.m. channel.
2. Materials and Methods
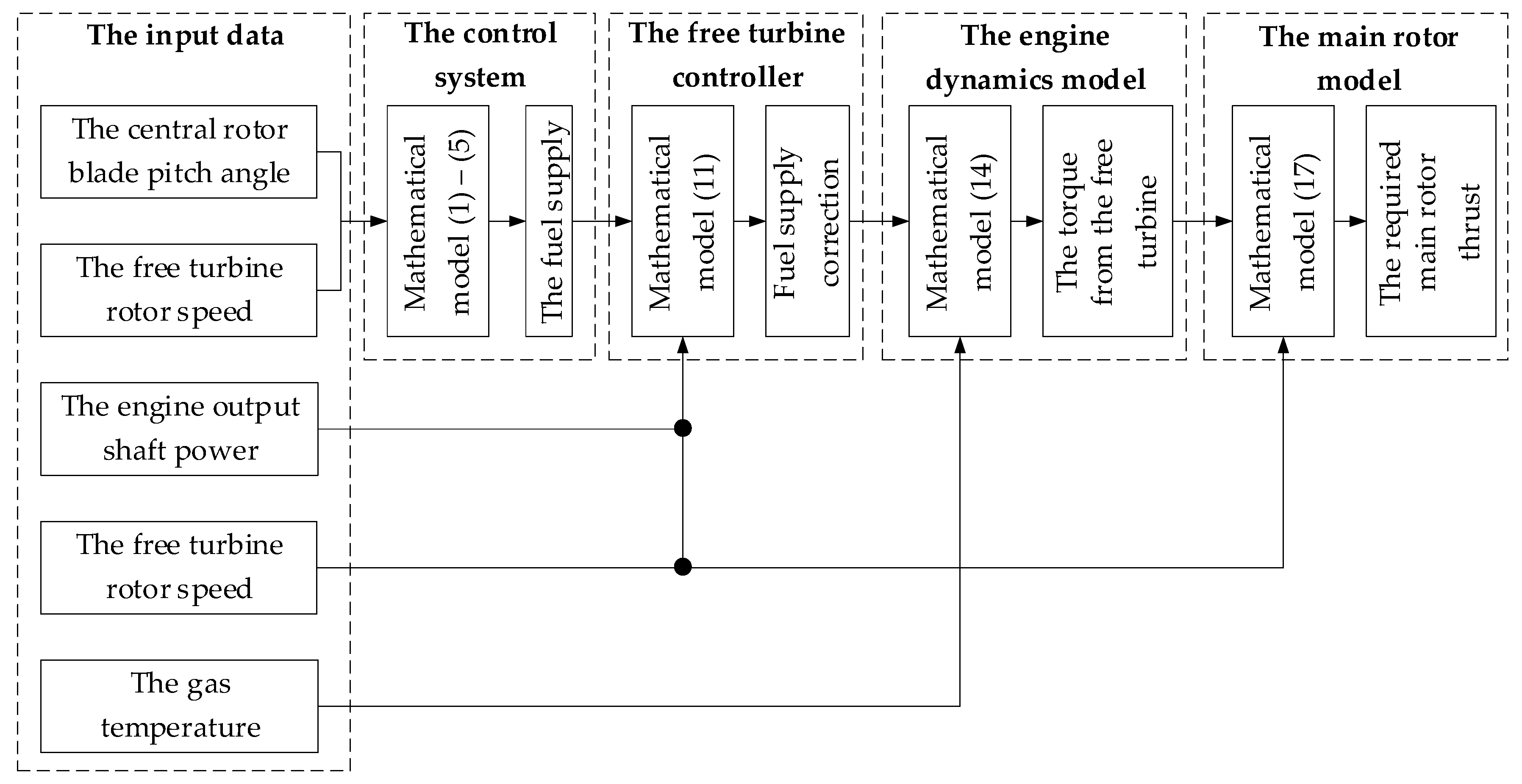
2.1. Development of Helicopter Turboshaft Engine Adaptive Control Law
- Engine (gas generator) operation is controlled by varying the fuel supply GT. It is the sole parameter influencing the gas generator’s operating mode, as the compressor is fixed, and the first stage of the accessible turbine functions as a throttle with a constant cross-section.
- Maintaining constant free turbine speed nFT = const is key for safe helicopter piloting. To meet this condition, the automatic control system (ACS) adjusts GT when the blade pitch angle of the main rotor φm.r. changes.
- The control model is expressed as follows:
- nFT = const, if φm.r. ≤ φm.r.max;
- If φm.r. > φm.r.max, the ACS limits fuel supply, and nFT starts to decrease to constrain one of the limiting parameters (e.g., maximum turbine speed nTCmax or maximum power Ne).
- The free turbine rotor speed regulator central equation when the fuel supply changes is as follows:
- 5.
- The power limitation condition is represented as follows:
- 6.
- Upon reaching the maximum power limit , maintaining nFT = const becomes impossible, and the nFT frequency decreases.
2.2. The Development of the Algorithm for the Discretized Equation for the Main Rotor Thrust Numerical Solution
- Initialization of the initial conditions as follows:
- 2.
- Computation is performed at each time step:
- Fuel flow GT(t) and the blade pitch angle φm.r.(t) are updated according to the “pitch-throttle” system control law based on the specified target parameters and .
- The free turbine rotor speed nFT(t + Δt) is calculated.
- The thrust Tm.r.(t + Δt) is calculated.
- External parameters H(t + Δt), Ta(t + Δt), and Pa(t + Δt) are updated.
- 3.
- Deviations are assessed. Deviations in turbine speed and thrust from target values are calculated according to the following expression:
- 4.
- Control signals are adjusted as follows:
- If , then then fuel flow GT(t) is adjusted.
- If , then the blade pitch angle φm.r.(t) is adjusted.
- 5.
- Transition to the next time step is carried out according to the following expression:t ← t + Δt.
φm.r.(t + Δt) = φm.r.(t) + kφ ⋅ ΔTm.r.(t).
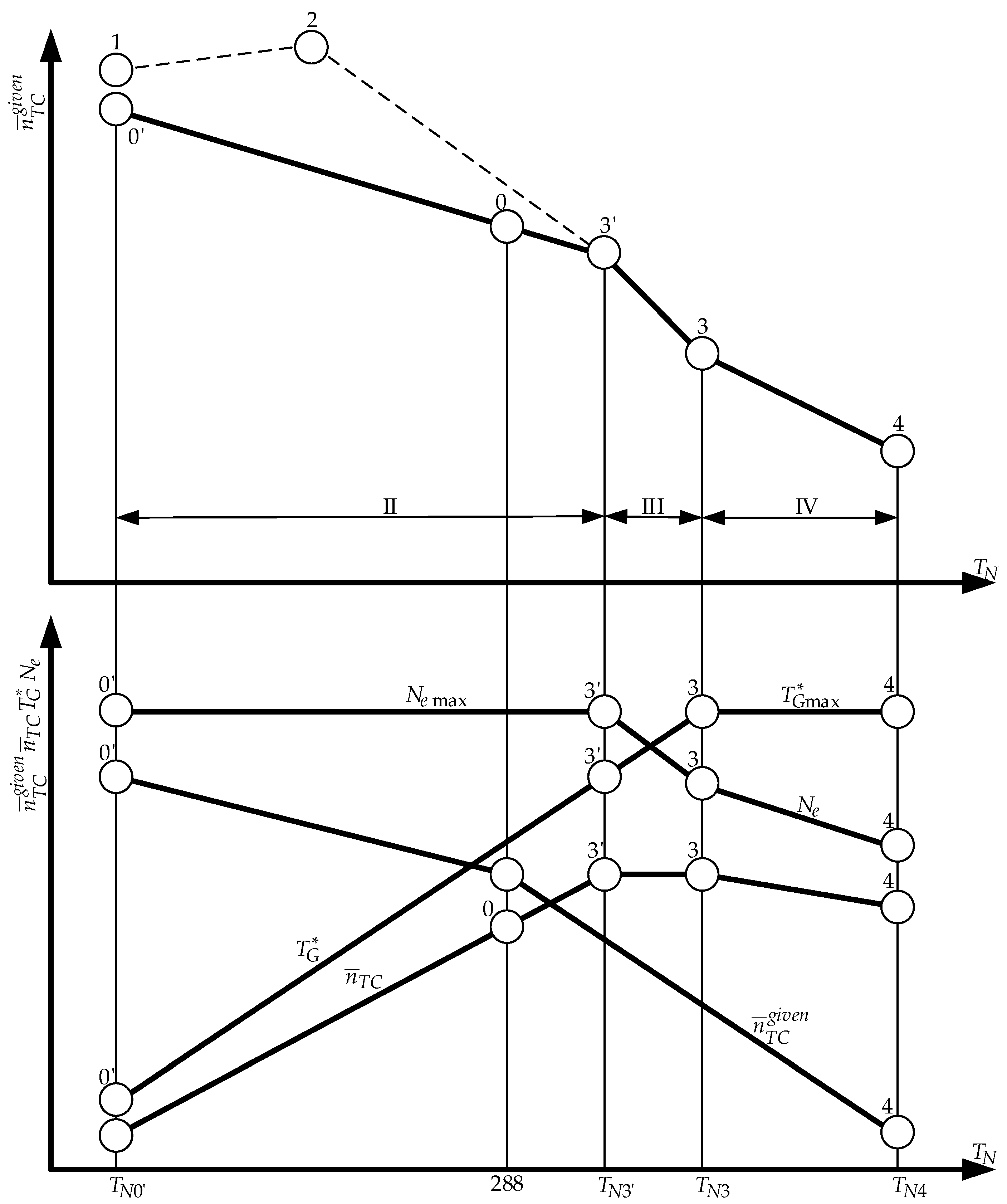
- Determining limiting modes by establishing a limiting-mode line. This is based on the relations between the maximum allowable values for the parameter and temperature at the input to the gas generator (in this case, temperature TN).
- Identifying areas of limitation modes based on changes in temperature TN. In this case, three areas are distinguished (Figure 2) [31]:
- At low values of TN (for example, TN < TN2), a limitation on ΔKymin is observed.
- In the temperature range from TN2 to TN3, a limitation on nTCmax must be maintained.
- When TN > TN3, a limitation on another limiting parameter takes effect.
- Additional limitations involve adding a power limitation line to the limiting-mode line, resulting in a structure consisting of four segments that account for all constraints. In this case, equations describing the relations between power Ne, engine parameters, and temperature are represented by (9).
- Under limitation conditions, the proposed control program forms an equation system linking fuel supply GT, blade pitch angle φm.r., and power parameters, presented in (11).
2.3. The Development of an Intelligent Automatic Control System for the Implementation of the Helicopter Turboshaft Engine Adaptive Control Law
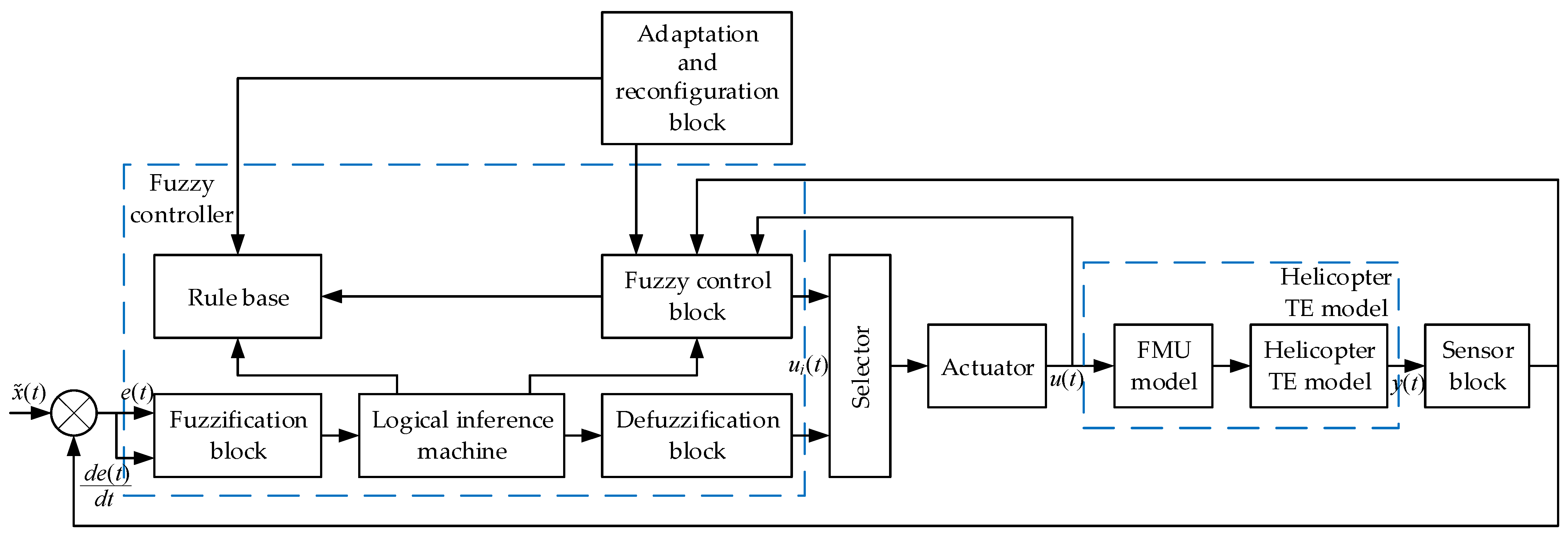
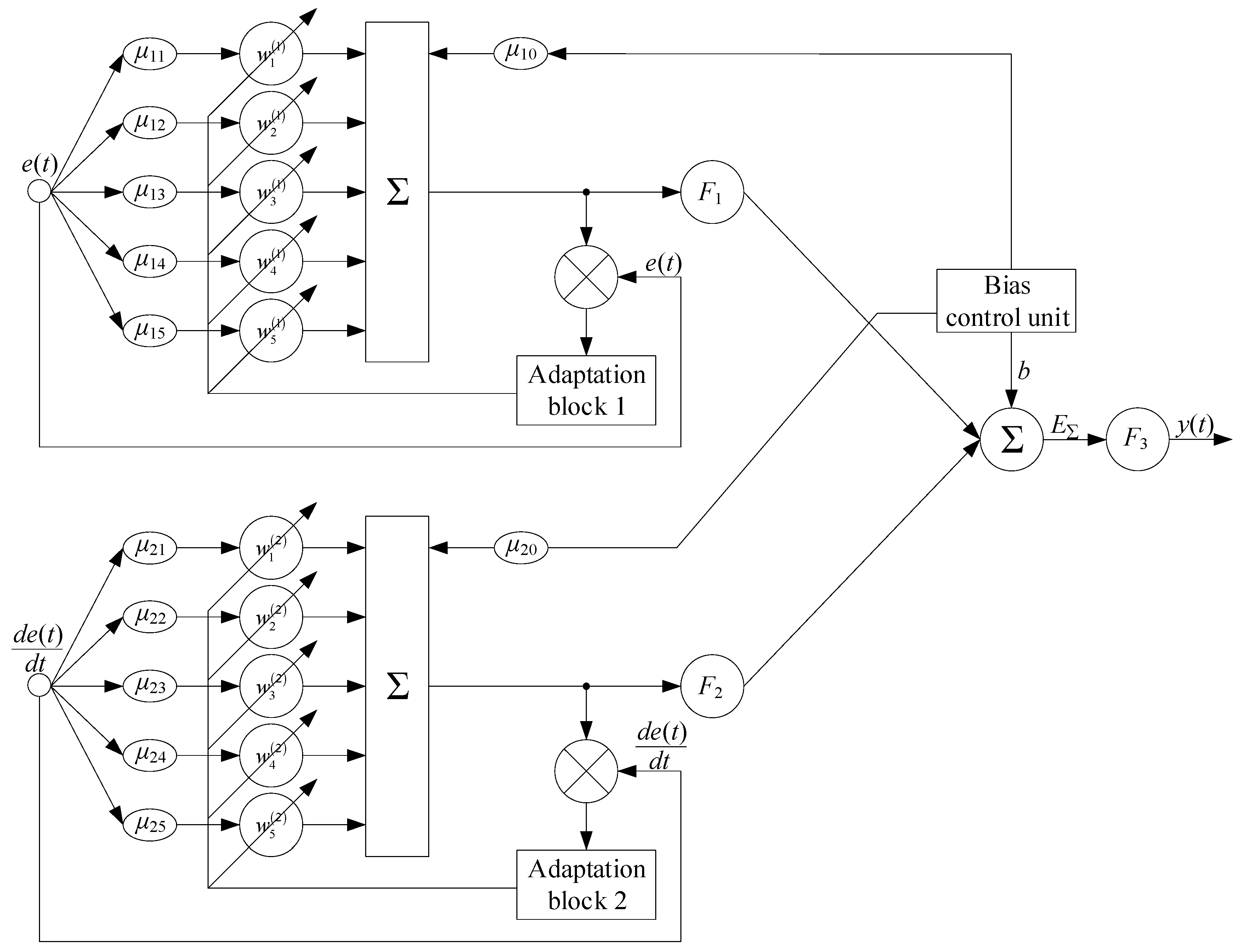
2.4. Development of Fuzzy Controller
- The control error is calculated as
- 2.
- The error change rate .
- . This control law uses the error in gas generator rotor r.p.m. as one of the inputs.
- 2.
- GT = + kG ⋅ ΔnFT(t). It can be controlled based on the fuzzy output u(t), where u(t) affects ΔnFT(t), the change in free turbine speed.
- 3.
- φm.r.(t + Δt) = φm.r.(t) + kφ ⋅ ΔTm.r.(t), where the control action u(t) determines the adjustment to the rotational speed φm.r.(t).
- 4.
- The control actions must also satisfy the constraints given in the system , nTC ≤ nTCmax, .
3. Results
3.1. Input Data Preprocessing
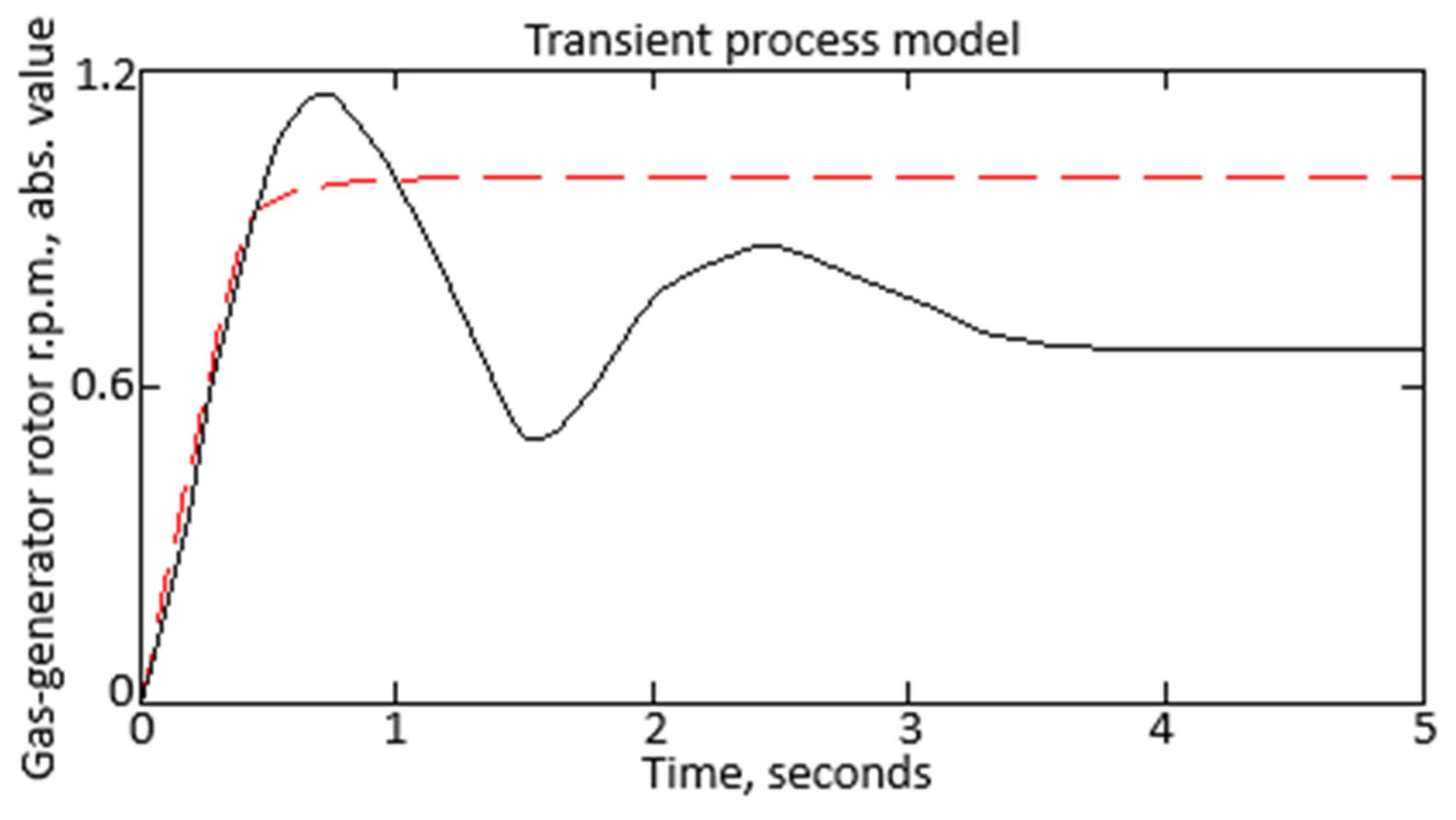
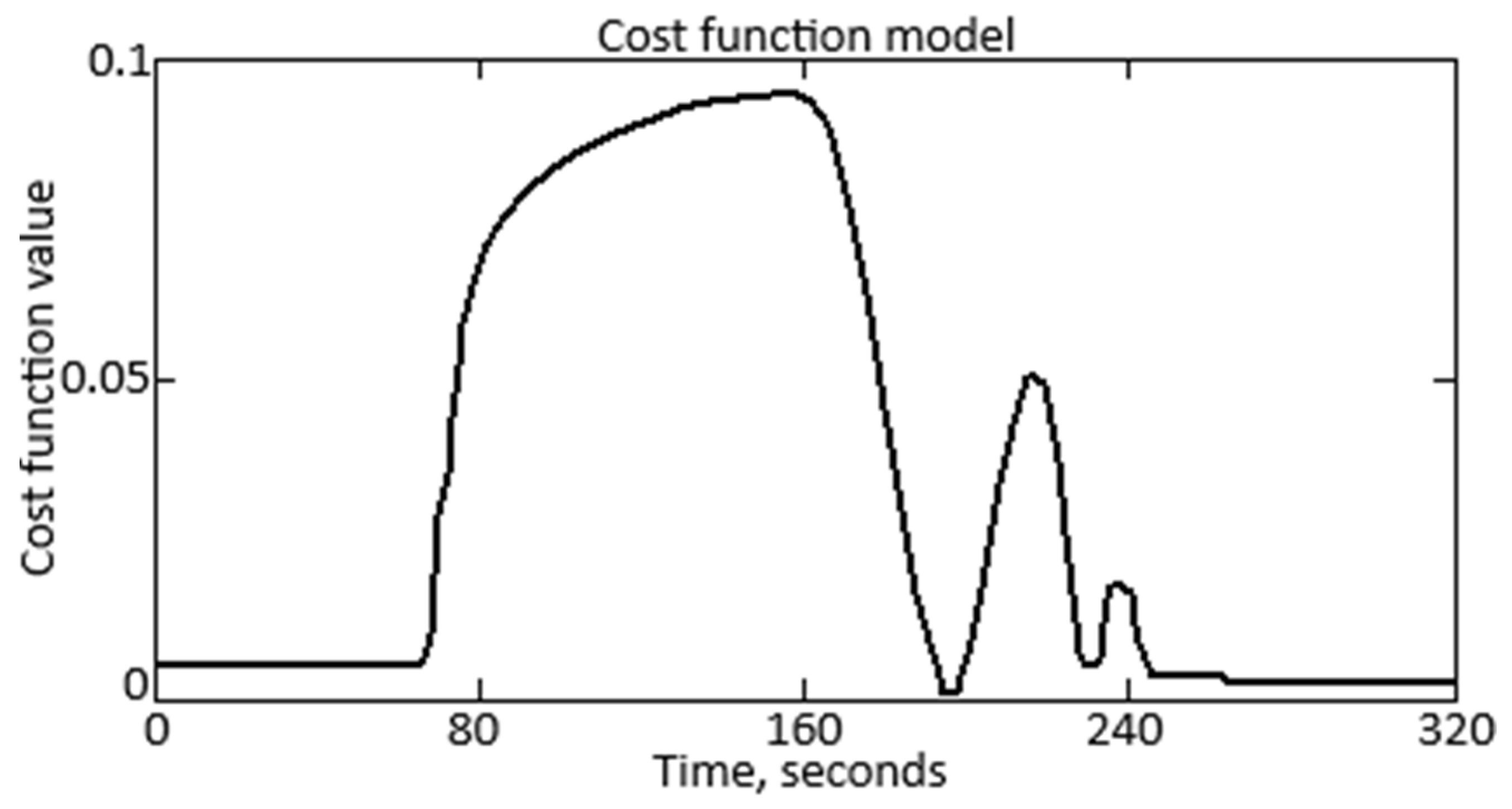
3.2. Results of Computational Experiment
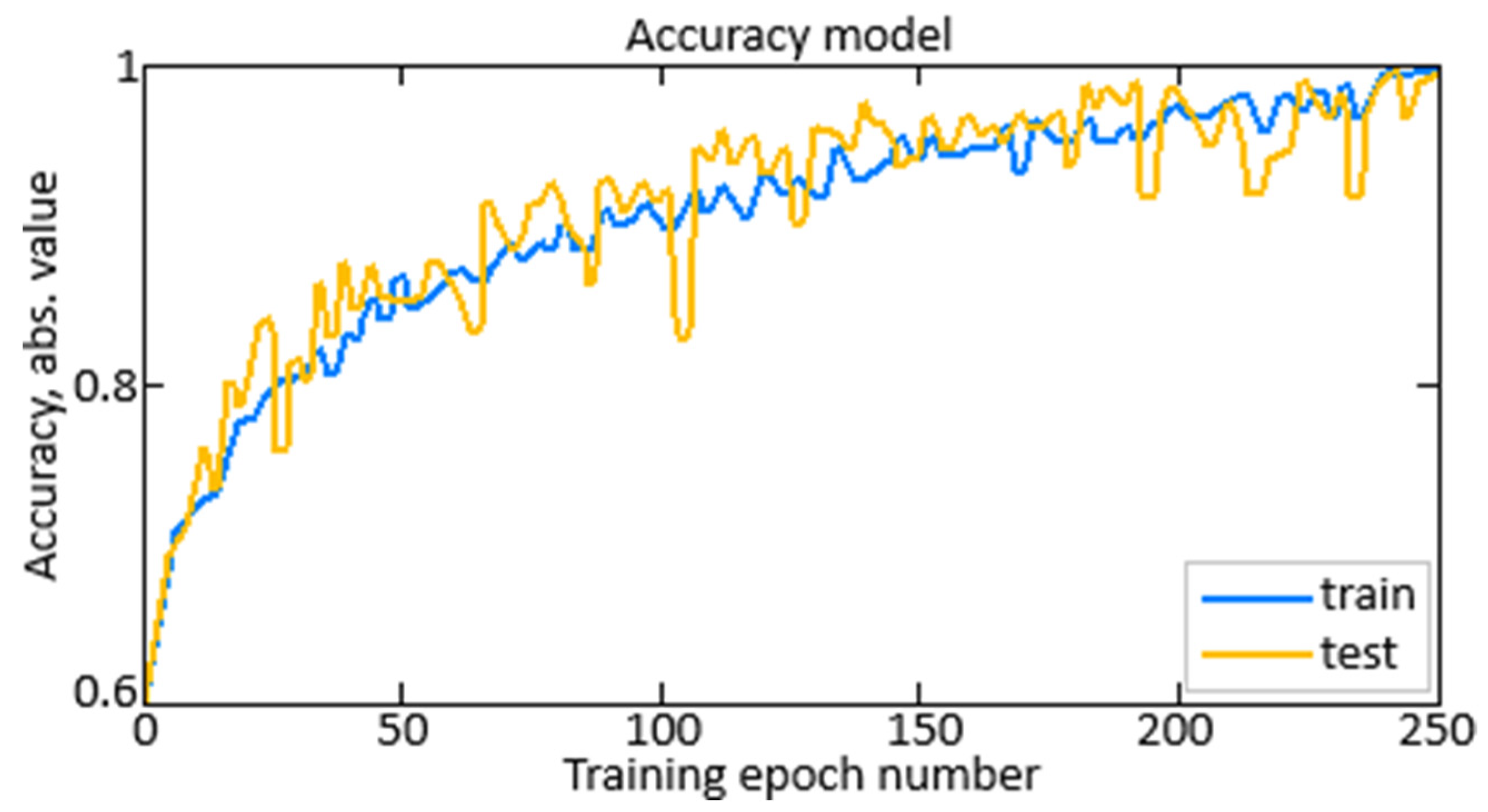
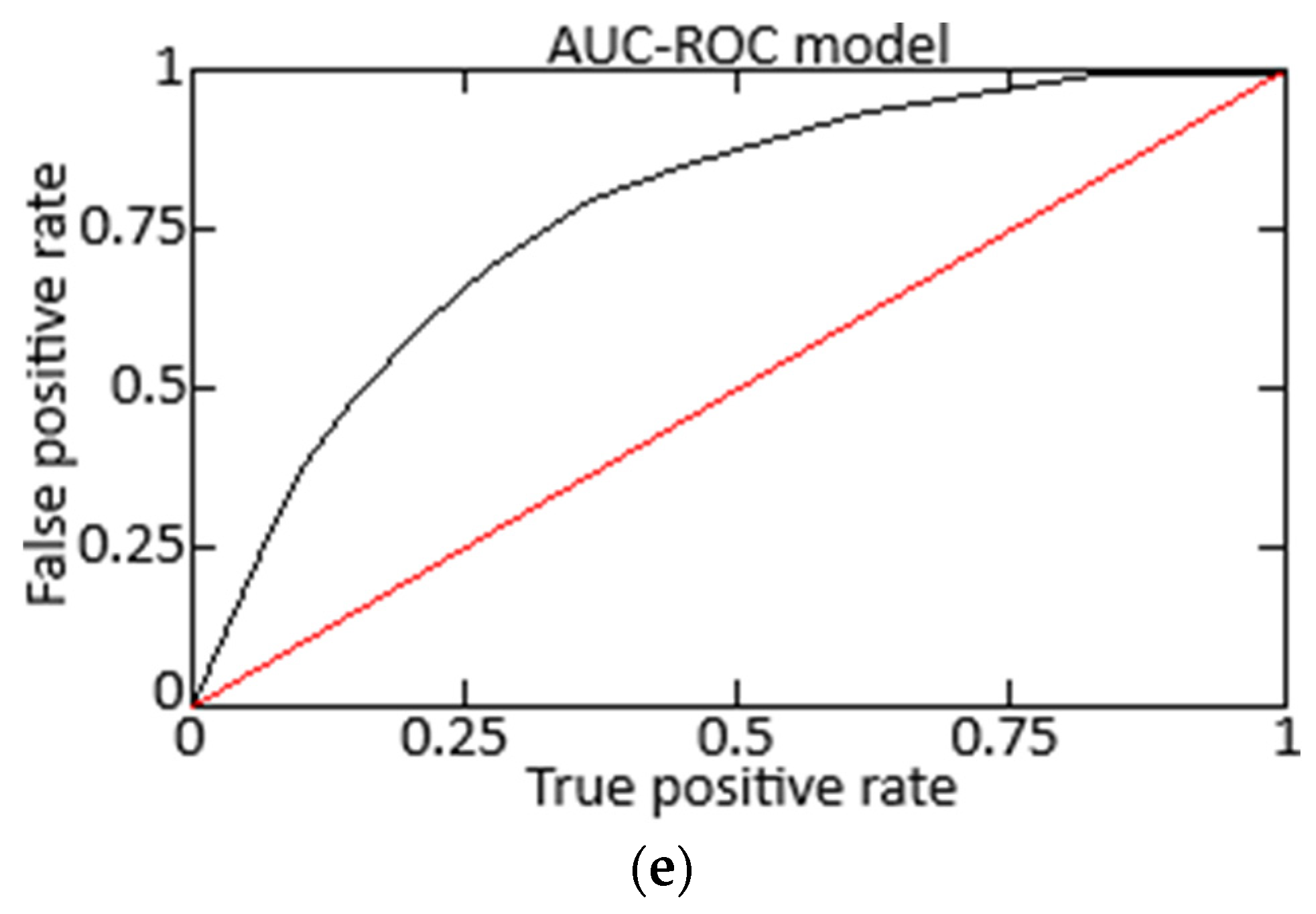
3.3. Neural Network Model Quality Evaluation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| GT | is the fuel supply; |
| φm.r. | is the central rotor blade pitch angle; |
| nFT | is the free turbine rotor speed; |
| nTC | is the gas generator rotor r.p.m.; |
| is the gas temperature in the front of the compressor turbine; | |
| Ne | is the engine output shaft power; |
| H | is the flight altitude; |
| Pα | is the ambient air pressure; |
| Tα | is the ambient air temperature; |
| ηFT | is the free turbine efficiency; |
| is the fuel combustion thermal power; | |
| NFT | is the free turbine power; |
| Nm.r. | is the main rotor power; |
| Npower loss | is the power loss (for transmission and resistance); |
| Hu | is the fuel combustion heat; |
| cp | is the gas specific heat capacity |
| CT(φm.r.) | is the thrust coefficient depending on the blade angle; |
| ρ | is the air density; |
| Am.r. | is the main rotor area; |
| Tm.r. | is the required main rotor thrust; |
| kH | is the coefficient of change in fuel supply with altitude; |
| Hmax | is the maximum design altitude; |
| kT | is the coefficient of dependence of fuel supply on ambient temperature; |
| TN | is the nominal temperature; |
| is the limited fuel supply consistent with safe operating conditions; | |
| is the base fuel supply; | |
| α and β | are the adaptation coefficients for power and rotation speed, respectively; |
| JFT | is the free turbine inertia moment; |
| MFT(t) | is the torque from the free turbine; |
| Mm.r.(t) | is the main rotor resistance moment; |
| kG and kφ | are the gain factors for regulating fuel supply and blade angle; |
| are the fuzzy values; | |
| μA(x) | is the membership function; |
| y | is the output value; |
| θ | are the control parameters; |
| ci | is the membership function center; |
| σi | is the membership function width; |
| γ | is the adaptation rate; |
| ydesired and yactual | are the desired and actual output values; |
| μ | is a factor defining the adaptation degree; |
| δ | is the control parameter; |
| ω | is the disturbance and noise; |
| D | is the fuel metering unit position; |
| k | is the gain coefficient; |
| c | is the damping coefficient; |
| u | is the control action; |
| e | is the control error |
| Kp, Ki, and Kd | are the proportional, integral, and derivative gains, respectively; |
| S | is the measured value; |
| h | is the measurement function; |
| ϵ | is the measurement error; |
| u0(t) | is the control signal under normal operating conditions; |
| uc(t) | is the corrective action dependent on the failure vector; |
| d(t) | is the failure vector; |
| xref(t) | are the target system parameters; |
| γ1 and γ2 | are weights defining the contribution of control actions and failures to the total cost; |
| γ | is the iteration step size. |
References
- Song, J.; Wang, Y.; Ji, C.; Zhang, H. Real-Time Optimization Control of Variable Rotor Speed Based on Helicopter/Turboshaft Engine Onboard Composite System. Energy 2024, 301, 131701. [Google Scholar] [CrossRef]
- Wang, Y.; Ji, C.; Xi, Z.; Zhang, H.; Zhao, Q. An Adaptive Matching Control Method of Multiple Turboshaft Engines. Eng. Appl. Artif. Intell. 2023, 123, 106496. [Google Scholar] [CrossRef]
- Yepifanov, S.; Bondarenko, O. Forming of turboshaft engine mathematical model. Aerosp. Tech. Technol. 2023, 4, 85–94. [Google Scholar] [CrossRef]
- Donateo, T.; Cucciniello, L.; Strafella, L.; Ficarella, A. Control Oriented Modelling of a Turboshaft Engine for Hybrid Electric Urban Air-Mobility. E3S Web Conf. 2020, 197, 05003. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, Q.; Xu, Z.; Zhang, H. A Novel Control Method for Turboshaft Engine with Variable Rotor Speed Based on the Ngdot Estimator Through LQG/LTR and Rotor Predicted Torque Feedforward. Chin. J. Aeronaut. 2020, 33, 1867–1876. [Google Scholar] [CrossRef]
- He, D.; Zhang, R.; Wen, C.; Chen, L. A Control Framework for Turboshaft Engine Based on Thermo-Gas-Dynamic Model. In Proceedings of the Eighth International Conference on Electromechanical Control Technology and Transportation (ICECTT 2023), Hangzhou, China, 19–21 May 2023; Volume 12790. [Google Scholar] [CrossRef]
- Ahmadian, N.; Khosravi, A.; Sarhadi, P. Adaptive Control of a Jet Turboshaft Engine Driving a Variable Pitch Propeller Using Multiple Models. Mech. Syst. Signal Process. 2017, 92, 1–12. [Google Scholar] [CrossRef]
- Sheng, H.; Zhang, T.; Jiang, W. Full-Range Mathematical Modeling of Turboshaft Engine in Aerospace. Int. J. Turbo Jet Engines 2015, 33, 309–317. [Google Scholar] [CrossRef]
- Yepifanov, S.; Bondarenko, O. Development of Turboshaft Engine Adaptive Dynamic Model: Analysis of Estimation Errors. Trans. Aerosp. Res. 2022, 4, 59–71. [Google Scholar] [CrossRef]
- Zou, W.; Song, Z.; Wang, B.; Wen, M.; Zheng, X. An Efficient Multi-Fidelity Simulation Approach for Performance Prediction of Adaptive Cycle Engines. J. Glob. Power Propuls. Soc. 2024, 8, 310–322. [Google Scholar] [CrossRef]
- Lan, J.; Patton, R.J.; Punta, E. Fault-Tolerant Tracking Control for A 3-DOF Helicopter with Actuator Faults and Saturation. IFAC-PapersOnLine 2017, 50, 5250–5255. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, Q.; Du, Z.; Zhang, H. Research on Nonlinear Model Predictive Control for Turboshaft Engines Based on Double Engines Torques Matching. Chin. J. Aeronaut. 2020, 33, 561–571. [Google Scholar] [CrossRef]
- Wang, H.; Wang, D.; Zhang, G. Research of Neural Network PID Control of Aero-Engine; Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2011; Volume 122, pp. 337–343. [Google Scholar] [CrossRef]
- Castiglione, T.; Perrone, D.; Strafella, L.; Ficarella, A.; Bova, S. Linear Model of a Turboshaft Aero-Engine Including Components Degradation for Control-Oriented Applications. Energies 2023, 16, 2634. [Google Scholar] [CrossRef]
- Gu, N.; Wang, X. Model Predictive Controller Design Based on the Linear Parameter Varying Model Method for a Class of Turboshaft Engines. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018. [Google Scholar] [CrossRef]
- Lu, F.; Huang, J.; Xing, Y. Fault Diagnostics for Turbo-Shaft Engine Sensors Based on a Simplified Onboard Model. Sensors 2012, 12, 11061–11076. [Google Scholar] [CrossRef]
- Wu, W.-C.; Meen, T.-H. Use of Sensor Data of Aircraft Turbine Engine for Education of Aircraft Maintenance. Sens. Mater. 2023, 35, 733. [Google Scholar] [CrossRef]
- Ranjbar, A.; Khosravi, A.; Ahmadian, N. Control of a Jet Engine Using Predictor-Based Adaptive Strategy in Different Flight Modes. J. Syst. Control. Eng. 2023, 237, 1349–1364. [Google Scholar] [CrossRef]
- Sheng, H.; Chen, Q.; Li, J.; Jiang, W.; Wang, Z.; Liu, Z.; Zhang, T.; Liu, Y. Research on Dynamic Modeling and Performance Analysis of Helicopter Turboshaft Engine’s Start-Up Process. Aerosp. Sci. Technol. 2020, 106, 106097. [Google Scholar] [CrossRef]
- Cheng, K.; Wang, Y.; Yang, X.; Zhang, K.; Liu, F. An Intelligent Online Fault Diagnosis System for Gas Turbine Sensors Based on Unsupervised Learning Method LOF and KELM. Sens. Actuators A Phys. 2024, 365, 114872. [Google Scholar] [CrossRef]
- Pérez-Ventura, U.; Fridman, L.; Capello, E.; Punta, E. Fault Tolerant Control Based on Continuous Twisting Algorithms of a 3-DoF Helicopter Prototype. Control Eng. Pract. 2020, 101, 104486. [Google Scholar] [CrossRef]
- Bovsunovsky, A.; Nosal, O. Highly Sensitive Methods for Vibration Diagnostics of Fatigue Damage in Structural Elements of Aircraft Gas Turbine Engines. Procedia Struct. Integr. 2022, 35, 74–81. [Google Scholar] [CrossRef]
- Boujamza, A.; Lissane Elhaq, S. Attention-Based LSTM for Remaining Useful Life Estimation of Aircraft Engines. IFAC-PapersOnLine 2022, 55, 450–455. [Google Scholar] [CrossRef]
- Kumar, S.R.; Devakumar, J. Recurrent Neural Network Based Sensor Fault Detection and Isolation for Nonlinear Systems: Application in PWR. Prog. Nucl. Energy 2023, 163, 104836. [Google Scholar] [CrossRef]
- Szrama, S.; Lodygowski, T. Aircraft Engine Remaining Useful Life Prediction Using Neural Networks and Real-Life Engine Operational Data. Adv. Eng. Softw. 2024, 192, 103645. [Google Scholar] [CrossRef]
- Balli, O. Exergetic, sustainability and environmental assessments of a turboshaft engine used on helicopter. Energy 2023, 276, 127593. [Google Scholar] [CrossRef]
- Zheng, X.; Zeng, H.; Wang, B.; Wen, M.; Yang, H.; Sun, Z. Numerical simulation method of surge experiments on gas turbine engines. Chin. J. Aeronaut. 2023, 36, 107–120. [Google Scholar] [CrossRef]
- Lyu, K.; Tan, X.; Liu, G.; Zhao, C. Sensor Selection of Helicopter Transmission Systems Based on Physical Model and Sensitivity Analysis. Chin. J. Aeronaut. 2014, 27, 643–654. [Google Scholar] [CrossRef]
- Aygun, H.; Turan, O. Exergetic sustainability off-design analysis of variable-cycle aero-engine in various bypass modes. Energy 2020, 195, 117008. [Google Scholar] [CrossRef]
- Zhao, Y.-P.; Huang, G.; Hu, Q.-K.; Li, B. An improved weighted one class support vector machine for turboshaft engine fault detection. Eng. Appl. Artif. Intell. 2020, 94, 103796. [Google Scholar] [CrossRef]
- Wang, B.; Wang, F.; Zhang, X.; Wang, J.; Xue, T. Numerical analysis of cooling efficiency for turboshaft engines with converging-diverging film cooling holes. Int. J. Therm. Sci. 2023, 185, 108044. [Google Scholar] [CrossRef]
- Jiang, P.; Xiong, S.; Xu, W.; Du, Z.; He, X. Experimental study on the combustion performance of a turboshaft engine annular combustor. J. Energy Inst. 2023, 111, 101412. [Google Scholar] [CrossRef]
- Han, D.; Pastrikakis, V.; Barakos, G.N. Helicopter performance improvement by variable rotor speed and variable blade twist. Aerosp. Sci. Technol. 2016, 54, 164–173. [Google Scholar] [CrossRef]
- Abdalla, M.S.M.; Balli, O.; Adali, O.H.; Korba, P.; Kale, U. Thermodynamic, sustainability, environmental and damage cost analyses of jet fuel starter gas turbine engine. Energy 2023, 267, 126487. [Google Scholar] [CrossRef]
- Vladov, S.; Banasik, A.; Sachenko, A.; Kempa, W.M.; Sokurenko, V.; Muzychuk, O.; Pikiewicz, P.; Molga, A.; Vysotska, V. Intelligent Method of Identifying the Nonlinear Dynamic Model for Helicopter Turboshaft Engines. Sensors 2024, 24, 6488. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Huang, J.; Zhou, X.; Zou, Z.; Lu, F.; Zhou, W. A Novel, Reduced-Order Optimization Method for Nonlinear Model Correction of Turboshaft Engines. J. Mech. Sci. Technol. 2024, 38, 2103–2122. [Google Scholar] [CrossRef]
- González Castillo, I.; Loboda, I. Analysis of Nonlinear Gas Turbine Models Using Influence Coefficients. Ing. Investig. Y Tecnol. 2021, 22, 1–17. [Google Scholar] [CrossRef]
- Vladov, S.; Shmelov, Y.; Yakovliev, R. Helicopters Aircraft Engines Self-Organizing Neural Network Automatic Control System. CEUR Workshop Proc. 2022, 3137, 28–47. [Google Scholar] [CrossRef]
- Sina Tayarani-Bathaie, S.; Sadough Vanini, Z.N.; Khorasani, K. Dynamic Neural Network-Based Fault Diagnosis of Gas Turbine Engines. Neurocomputing 2014, 125, 153–165. [Google Scholar] [CrossRef]
- Vladov, S.; Shmelov, Y.; Yakovliev, R. Modified Helicopters Turboshaft Engines Neural Network Onboard Automatic Control System Using the Adaptive Control Method. CEUR Workshop Proc. 2022, 3309, 205–224. [Google Scholar]
- Vladov, S.; Shmelov, Y.; Yakovliev, R.; Petchenko, M. Modified Neural Network Fault-Tolerant Closed Onboard Helicopters Turboshaft Engines Automatic Control System. CEUR Workshop Proc. 2023, 3387, 160–179. [Google Scholar]
- Vladov, S.; Shmelov, Y.; Yakovliev, R.; Petchenko, M. Neural Network Method for Parametric Adaptation Helicopters Turboshaft Engines Onboard Automatic Control System Parameters. CEUR Workshop Proc. 2023, 3403, 179–195. [Google Scholar]
- Ibrahem, I.M.A.; Akhrif, O.; Moustapha, H.; Staniszewski, M. Nonlinear Generalized Predictive Controller Based on Ensemble of NARX Models for Industrial Gas Turbine Engine. Energy 2021, 230, 120700. [Google Scholar] [CrossRef]
- Vladov, S.; Shmelov, Y.; Yakovliev, R.; Kozlovskaya, T.; Petchenko, M. Helicopters Turboshaft Engines Intelligent Control Algorithms Synthesis, Taking into Account Required Quality Provision. CEUR Workshop Proc. 2023, 3468, 71–90. [Google Scholar]
- Vladov, S.; Scislo, L.; Sokurenko, V.; Muzychuk, O.; Vysotska, V.; Sachenko, A.; Yurko, A. Helicopter Turboshaft Engines’ Gas Generator Rotor R.P.M. Neuro-Fuzzy Onboard Controller Development. Energies 2024, 17, 4033. [Google Scholar] [CrossRef]
- Vladov, S.; Yakovliev, R.; Hubachov, O.; Rud, J. Neuro-Fuzzy System for Detection Fuel Consumption of Helicopters Turboshaft Engines. CEUR Workshop Proc. 2024, 3628, 55–72. [Google Scholar]
- Vladov, S.; Bulakh, M.; Vysotska, V.; Yakovliev, R. Onboard Neuro-Fuzzy Adaptive Helicopter Turboshaft Engine Automatic Control System. Energies 2024, 17, 4195. [Google Scholar] [CrossRef]
- Vasiliev, V.; Valeev, S. Design of intelligent control systems for gas turbine engines based on the principle of minimum complexity. Bull. USATU 2007, 9, 32–41. [Google Scholar]
- Pogorelov, G.I.; Kulikov, G.G.; Abdulnagimov, A.I.; Badamshin, B.I. Application of Neural Network Technology and High-Performance Computing for Identification and Real-time Hardware-in-the-Loop Simulation of Gas Turbine Engines. Procedia Eng. 2017, 176, 402–408. [Google Scholar] [CrossRef]
- Vladov, S.; Shmelov, Y.; Yakovliev, R.; Petchenko, M.; Drozdova, S. Neural Network Method for Helicopters Turboshaft Engines Working Process Parameters Identification at Flight Modes. In Proceedings of the 2022 IEEE 4th International Conference on Modern Electrical and Energy System (MEES), Kremenchuk, Ukraine, 20–22 October 2022. [Google Scholar] [CrossRef]
- Vladov, S.; Scislo, L.; Sokurenko, V.; Muzychuk, O.; Vysotska, V.; Osadchy, S.; Sachenko, A. Neural Network Signal Integration from Thermogas-Dynamic Parameter Sensors for Helicopters Turboshaft Engines at Flight Operation Conditions. Sensors 2024, 24, 4246. [Google Scholar] [CrossRef]
- Kim, S.; Im, J.H.; Kim, M.; Kim, J.; Kim, Y.I. Diagnostics using a physics-based engine model in aero gas turbine engine verification tests. Aerosp. Sci. Technol. 2023, 133, 108102. [Google Scholar] [CrossRef]
- Vladov, S.; Yakovliev, R.; Hubachov, O.; Rud, J.; Drodova, S.; Perekrest, A. Modified Discrete Neural Network PID Controller for Controlling the Helicopters Turboshaft Engines Free Turbine Speed. In Proceedings of the 2023 IEEE 5th International Conference on Modern Electrical and Energy System (MEES), Kremenchuk, Ukraine, 27–30 September 2023; pp. 797–802. [Google Scholar] [CrossRef]
- Vladov, S.; Shmelov, Y.; Yakovliev, R.; Stushchankyi, Y.; Havryliuk, Y. Neural Network Method for Controlling the Helicopters Turboshaft Engines Free Turbine Speed at Flight Modes. CEUR Workshop Proc. 2023, 3426, 89–108. [Google Scholar]
- Catana, R.M.; Dediu, G. Analytical Calculation Model of the TV3-117 Turboshaft Working Regimes Based on Experimental Data. Appl. Sci. 2023, 13, 10720. [Google Scholar] [CrossRef]
- Gebrehiwet, L.; Nigussei, Y.; Teklehaymanot, T. A Review-Differentiating TV2 and TV3 Series Turbo Shaft Engines. Int. J. Res. Publ. Rev. 2022, 3, 1822–1838. [Google Scholar] [CrossRef]
- Vladov, S.; Sachenko, A.; Sokurenko, V.; Muzychuk, O.; Vysotska, V. Helicopters Turboshaft Engines Neural Network Modeling under Sensor Failure. J. Sens. Actuator Netw. 2024, 13, 66. [Google Scholar] [CrossRef]
- Pasieka, M.; Grzesik, N.; Kuźma, K. Simulation modeling of fuzzy logic controller for aircraft engines. Int. J. Comput. 2017, 16, 27–33. [Google Scholar] [CrossRef]
- Marakhimov, A.R.; Khudaybergenov, K.K. Approach to the synthesis of neural network structure during classification. Int. J. Comput. 2020, 19, 20–26. [Google Scholar] [CrossRef]
- Kim, H.-Y. Statistical Notes for Clinical Researchers: Chi-Squared Test and Fisher’s Exact Test. Restor. Dent. Endod. 2017, 42, 152. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Voinov, V.; Nikulin, M.S. Chapter 2—Pearson’s Sum and Pearson-Fisher Test. In Chi-Squared Goodness of Fit Tests with Applications; Balakrishnan, N., Voinov, V., Nikulin, M.S., Eds.; Academic Press: Waltham, MA, USA, 2013; pp. 11–26. [Google Scholar] [CrossRef]
- Cosenza, P.; Fauchille, A.-L.; Prêt, D.; Hedan, S.; Giraud, A. Statistical Representative Elementary Area of Shale Inferred by Micromechanics. Int. J. Eng. Sci. 2019, 142, 53–73. [Google Scholar] [CrossRef]
- Avram, F.; Leonenko, N.N.; Šuvak, N. Hypothesis testing for Fisher–Snedecor diffusion. J. Stat. Plan. Inference 2012, 142, 2308–2321. [Google Scholar] [CrossRef]
- Stefanovic, C.M.; Armada, A.G.; Costa-Perez, X. Second Order Statistics of -Fisher-Snedecor Distribution and Their Application to Burst Error Rate Analysis of Multi-Hop Communications. IEEE Open J. Commun. Soc. 2022, 3, 2407–2424. [Google Scholar] [CrossRef]
- Benaceur, A.; Verfürth, B. Statistical Variational Data Assimilation. Comput. Methods Appl. Mech. Eng. 2024, 432, 117402. [Google Scholar] [CrossRef]
- Babichev, S.; Krejci, J.; Bicanek, J.; Lytvynenko, V. Gene expression sequences clustering based on the internal and external clustering quality criteria. In Proceedings of the 2017 12th International Scientific and Technical Conference on Computer Sciences and Information Technologies (CSIT), Lviv, Ukraine, 5–8 September 2017. [Google Scholar] [CrossRef]
- Hu, Z.; Kashyap, E.; Tyshchenko, O.K. GEOCLUS: A Fuzzy-Based Learning Algorithm for Clustering Expression Datasets; Lecture Notes on Data Engineering and Communications Technologies; Springer: Cham, Switzerland, 2022; Volume 134, pp. 337–349. [Google Scholar] [CrossRef]
- Altameem, A.; Al-Ma’aitah, M.; Kovtun, V.; Altameem, T. A Computationally Efficient Method for Assessing the Impact of an Active Viral Cyber Threat on a High-Availability Cluster. Egypt. Inform. J. 2023, 24, 61–69. [Google Scholar] [CrossRef]
- Vlasenko, D.; Inkarbaieva, O.; Peretiatko, M.; Kovalchuk, D.; Sereda, O. Helicopter Radio System for Low Altitudes and Flight Speed Measuring with Pulsed Ultra-Wideband Stochastic Sounding Signals and Artificial Intelligence Elements. Radioelectron. Comput. Syst. 2023, 3, 48–59. [Google Scholar] [CrossRef]
- Rusyn, B.; Lutsyk, O.; Kosarevych, R.; Obukh, Y. Application Peculiarities of Deep Learning Methods in the Problem of Big Datasets Classification; Lecture Notes in Electrical Engineering; Springer: Cham, Switzerland, 2021; Volume 831, pp. 493–506. [Google Scholar] [CrossRef]
- Rusyn, B.; Lutsyk, O.; Kosarevych, R.; Kapshii, O.; Karpin, O.; Maksymyuk, T.; Gazda, J. Rethinking Deep CNN Training: A Novel Approach for Quality-Aware Dataset Optimization. IEEE Access 2024, 12, 137427–137438. [Google Scholar] [CrossRef]
- Turchenko, V.; Chalmers, E.; Luczak, A. A deep convolutional auto-encoder with pooling–unpooling layers in caffe. Int. J. Comput. 2019, 1, 8–31. [Google Scholar] [CrossRef]
- Komar, M.; Sachenko, A.; Golovko, V.; Dorosh, V. Compression of network traffic parameters for detecting cyber attacks based on deep learning. In Proceedings of the 2018 IEEE 9th International Conference on Dependable Systems, Services and Technologies (DESSERT), Kyiv, Ukraine, 24–27 May 2018; pp. 43–47. [Google Scholar] [CrossRef]
- Kovtun, V.; Altameem, T.; Al-Maitah, M.; Kempa, W. Entropy-Metric Estimation of the Small Data Models with Stochastic Parameters. Heliyon 2024, 10, e24708. [Google Scholar] [CrossRef]
- Tverdokhlib, O.; Vysotska, V.; Pukach, P.; Vovk, M. Information Technology for Identifying Hate Speech in Online Communication Based on Machine Learning; Lecture Notes on Data Engineering and Communications Technologies; Springer: Cham, Switzerland, 2024; Volume 195, pp. 339–369. [Google Scholar] [CrossRef]
- Lytvyn, V.; Dudyk, D.; Peleshchak, I.; Peleshchak, R.; Pukach, P. Influence of the Number of Neighbours on the Clustering Metric by Oscillatory Chaotic Neural Network with Dipole Synaptic Connections. CEUR Workshop Proc. 2024, 3664, 24–34. [Google Scholar]
- Kovtun, V.; Grochla, K.; Połys, K. Investigation of the Information Interaction of the Sensor Network End IoT Device and the Hub at the Transport Protocol Level. Electronics 2023, 12, 4662. [Google Scholar] [CrossRef]
- Nazarkevych, M.; Kowalska-Styczen, A.; Lytvyn, V. Research of Facial Recognition Systems and Criteria for Identification. In Proceedings of the IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications, IDAACS, Dortmund, Germany, 7–9 September 2023; pp. 555–558. [Google Scholar] [CrossRef]
- Gifalli, A.; Bonini Neto, A.; de Souza, A.N.; de Mello, R.P.; Ikeshoji, M.A.; Garbelini, E.; Neto, F.T. Fault Detection and Normal Operating Condition in Power Transformers via Pattern Recognition Artificial Neural Network. Appl. Syst. Innov. 2024, 7, 41. [Google Scholar] [CrossRef]
- Aliyari, M.; Ayele, Y.Z. Application of Artificial Neural Networks for Power Load Prediction in Critical Infrastructure: A Comparative Case Study. Appl. Syst. Innov. 2023, 6, 115. [Google Scholar] [CrossRef]
- Ale Isaac, M.S.; Flores Peña, P.; Gîfu, D.; Ragab, A.R. Advanced Control Strategies for Securing UAV Systems: A Cyber-Physical Approach. Appl. Syst. Innov. 2024, 7, 83. [Google Scholar] [CrossRef]
- Pang, S.; Jafari, S.; Nikolaidis, T.; Li, Q. A Novel Model-Based Multivariable Framework for Aircraft Gas Turbine Engine Limit Protection Control. Chin. J. Aeronaut. 2021, 34, 57–72. [Google Scholar] [CrossRef]
- Kilic, U.; Villareal-Valderrama, F.; Ayar, M.; Ekici, S.; Amezquita-Brooks, L.; Karakoc, T.H. Deep Learning-Based Forecasting Modeling of Micro Gas Turbine Performance Projection: An Experimental Approach. Eng. Appl. Artif. Intell. 2024, 130, 107769. [Google Scholar] [CrossRef]
- Liu, X.; Song, E.; Zhang, L.; Luan, Y.; Wang, J.; Luo, C.; Xiong, L.; Pan, Q. Design and Implementation for the State Time-Delay and Input Saturation Compensator of Gas Turbine Aero-Engine Control System. Energy 2024, 288, 129934. [Google Scholar] [CrossRef]
- Singh, R.; Maity, A.; Nataraj, P.S.V. Dynamic Modeling and Robust Nonlinear Control of a Laboratory Gas Turbine Engine. Aerosp. Sci. Technol. 2022, 126, 107586. [Google Scholar] [CrossRef]
- Zimbrod, P.; Fleck, M.; Schilp, J. An Application-Driven Method for Assembling Numerical Schemes for the Solution of Complex Multiphysics Problems. Appl. Syst. Innov. 2024, 7, 35. [Google Scholar] [CrossRef]
- de Voogt, A.; Amour, E.S. Safety of Twin-Engine Helicopters: Risks and Operational Specificity. Saf. Sci. 2021, 136, 105169. [Google Scholar] [CrossRef]
- de Voogt, A.; Nero, K. Technical Failures in Helicopters: Non-Powerplant-Related Accidents. Safety 2023, 9, 10. [Google Scholar] [CrossRef]
- Aygun, H.; Caliskan, H. Evaluating and Modelling of Thermodynamic and Environmental Parameters of a Gas Turbine Engine and Its Components. J. Clean. Prod. 2022, 365, 132762. [Google Scholar] [CrossRef]
- Xu, M.; Liu, J.; Li, M.; Geng, J.; Wu, Y.; Song, Z. Improved Hybrid Modeling Method with Input and Output Self-Tuning for Gas Turbine Engine. Energy 2022, 238, 121672. [Google Scholar] [CrossRef]
- Yu, Z.; Yan, X.; Chen, R. Prediction of Pilot Workload in Helicopter Landing after One Engine Failure. Chin. J. Aeronaut. 2020, 33, 3112–3124. [Google Scholar] [CrossRef]
- Chi, C.; Yan, X.; Chen, R.; Li, P. Analysis of Low-Speed Height-Velocity Diagram of a Variable-Speed-Rotor Helicopter in One-Engine-Failure. Aerosp. Sci. Technol. 2019, 91, 310–320. [Google Scholar] [CrossRef]
- Mohammed, M.; Taher, M.K.; khudhair, S. Prediction of Turbojet Performance by Using Artificial Neural Network. Mater. Today Proc. 2022, 60, 1513–1522. [Google Scholar] [CrossRef]
- De Giorgi, M.G.; Quarta, M. Hybrid MultiGene Genetic Programming—Artificial Neural Networks Approach for Dynamic Performance Prediction of an Aeroengine. Aerosp. Sci. Technol. 2020, 103, 105902. [Google Scholar] [CrossRef]
- Ma, Y.; Du, X.; Sun, X. Adaptive Modification of Turbofan Engine Nonlinear Model Based on LSTM Neural Networks and Hybrid Optimization Method. Chin. J. Aeronaut. 2022, 35, 314–332. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, J.; Zhou, W.; Lu, F.; Xu, W. Neural Network-Based Model Predictive Control with Fuzzy-SQP Optimization for Direct Thrust Control of Turbofan Engine. Chin. J. Aeronaut. 2022, 35, 59–71. [Google Scholar] [CrossRef]
- Pu, J.; Zhang, Y.; Guan, Y.; Cui, N. Recurrent Neural Network-Based Predefined Time Control for Morphing Aircraft with Asymmetric Time-Varying Constraints. Appl. Math. Model. 2024, 135, 578–600. [Google Scholar] [CrossRef]
- Song, Z.; Feng, Y.; Lu, C. Superimposable Neural Network for Health Monitoring of Aircraft Hydraulic System. Eng. Fail. Anal. 2024, 160, 108063. [Google Scholar] [CrossRef]
- Xiao, D.; Xiao, H.; Li, R.; Wang, Z. Application of Physical-Structure-Driven Deep Learning and Compensation Methods in Aircraft Engine Health Management. Eng. Appl. Artif. Intell. 2024, 136, 109024. [Google Scholar] [CrossRef]
- Zhao, Y.-P.; Huang, G.; Hu, Q.-K.; Tan, J.-F.; Wang, J.-J.; Yang, Z. Soft Extreme Learning Machine for Fault Detection of Aircraft Engine. Aerosp. Sci. Technol. 2019, 91, 70–81. [Google Scholar] [CrossRef]
- Boujamza, A.; Elhaq, S.L. Optimizing Remaining Useful Life Predictions for Aircraft Engines: A Dilated Recurrent Neural Network Approach. IFAC-PapersOnLine 2024, 58, 811–816. [Google Scholar] [CrossRef]
- Zhou, D.; Zhuang, X.; Zuo, H. A Hybrid Deep Neural Network Based on Multi-Time Window Convolutional Bidirectional LSTM for Civil Aircraft APU Hazard Identification. Chin. J. Aeronaut. 2022, 35, 344–361. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, Z.; Zhou, Z.; Yan, R. Collaborative-Sequential Optimization for Aero-Engine Maintenance Based on Multi-Agent Reinforcement Learning. Expert Syst. Appl. 2024, 247, 123358. [Google Scholar] [CrossRef]
- Razzaghi, P.; Tabrizian, A.; Guo, W.; Chen, S.; Taye, A.; Thompson, E.; Bregeon, A.; Baheri, A.; Wei, P. A Survey on Reinforcement Learning in Aviation Applications. Eng. Appl. Artif. Intell. 2024, 136, 108911. [Google Scholar] [CrossRef]
- Dangut, M.D.; Jennions, I.K.; King, S.; Skaf, Z. Application of Deep Reinforcement Learning for Extremely Rare Failure Prediction in Aircraft Maintenance. Mech. Syst. Signal Process. 2022, 171, 108873. [Google Scholar] [CrossRef]
- Yu, B.; Shen, E.; Huang, Y.; Lu, F. Research on Self-Learning Control Method for Aircraft Engine above Idle State. Adv. Mech. Eng. 2016, 8, 1687814016653888. [Google Scholar] [CrossRef]
- Liu, L.; Song, X.; Zhou, Z. Aircraft Engine Remaining Useful Life Estimation via a Double Attention-Based Data-Driven Architecture. Reliab. Eng. Syst. Saf. 2022, 221, 108330. [Google Scholar] [CrossRef]
- Baranovskyi, D.; Bulakh, M.; Myamlin, S.; Kebal, I. New Design of the Hatch Cover to Increase the Carrying Capacity of the Gondola Car. Adv. Sci. Technol. Res. J. 2022, 16, 186–191. [Google Scholar] [CrossRef]
- Baranovskyi, D.; Myamlin, S.; Bulakh, M.; Podosonov, D.; Muradian, L. Determination of the Filler Concentration of the Composite Tape. Appl. Sci. 2022, 12, 11044. [Google Scholar] [CrossRef]
- Sagin, S.; Madey, V.; Sagin, A.; Stoliaryk, T.; Fomin, O.; Kučera, P. Ensuring Reliable and Safe Operation of Trunk Diesel Engines of Marine Transport Vessels. J. Mar. Sci. Eng. 2022, 10, 1373. [Google Scholar] [CrossRef]
- Sagin, S.V.; Sagin, S.S.; Fomin, O.; Gaichenia, O.; Zablotskyi, Y.; Píštěk, V.; Kučera, P. Use of Biofuels in Marine Diesel Engines for Sustainable and Safe Maritime Transport. Renew. Energy 2024, 224, 120221. [Google Scholar] [CrossRef]

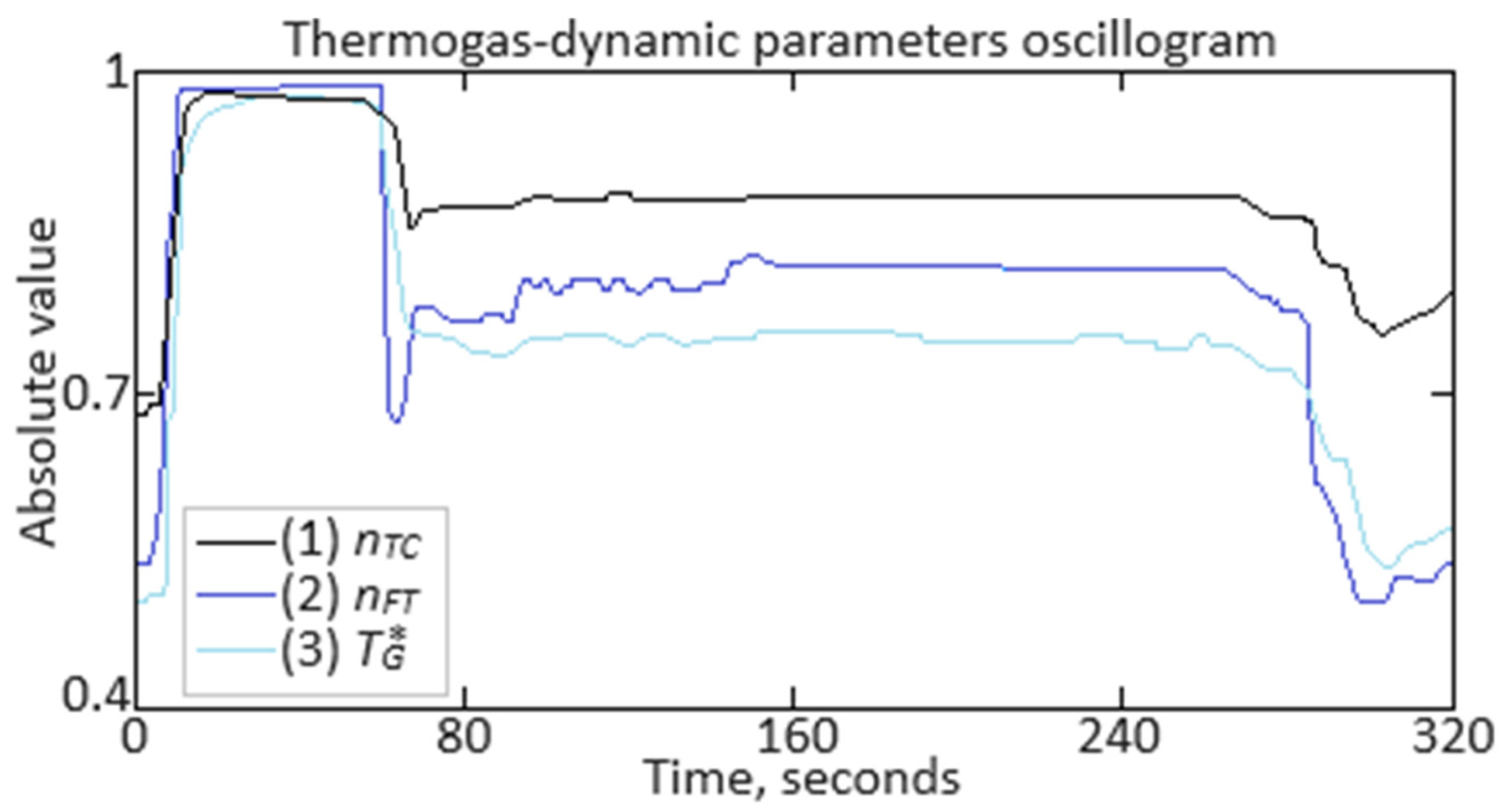
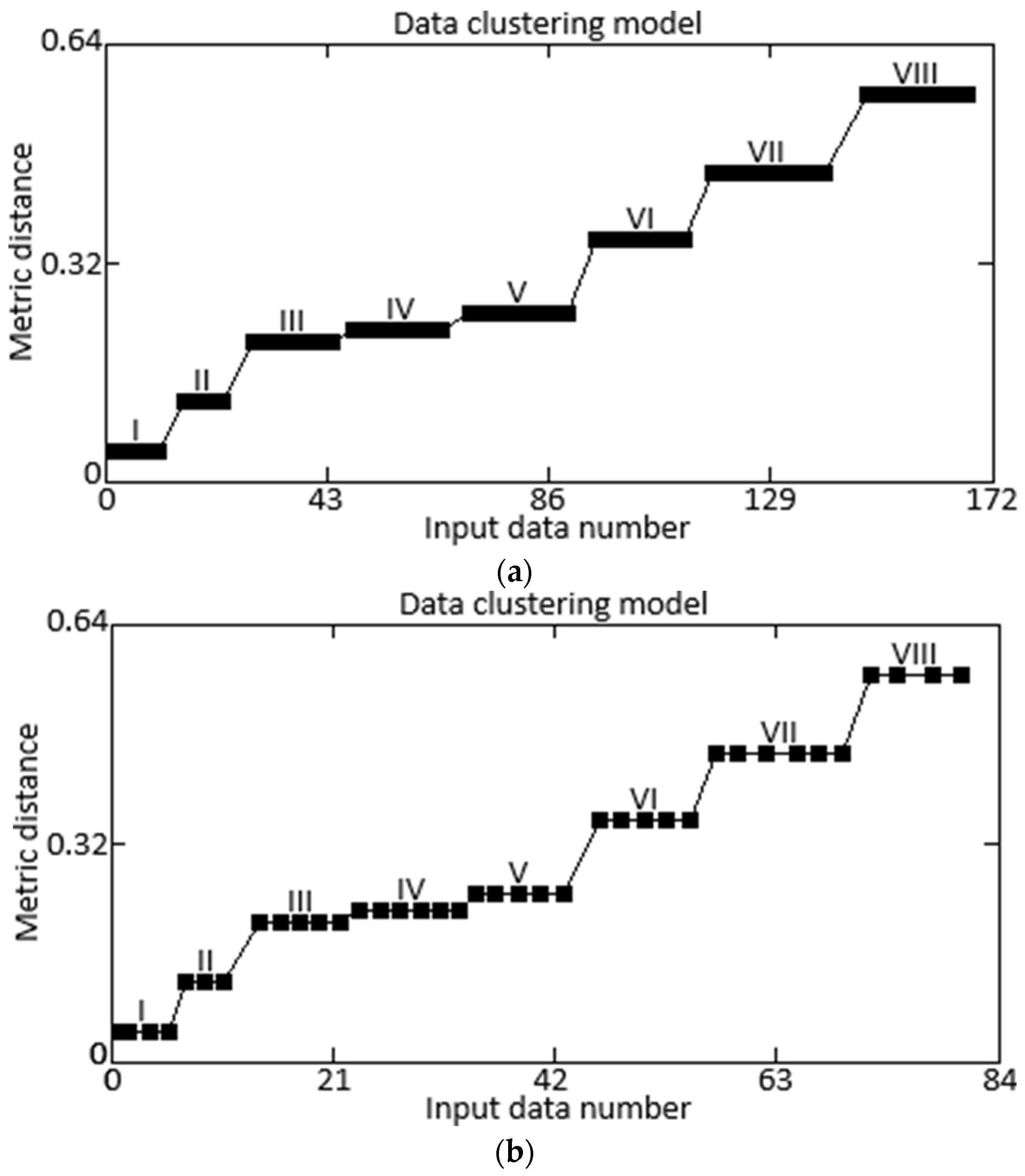
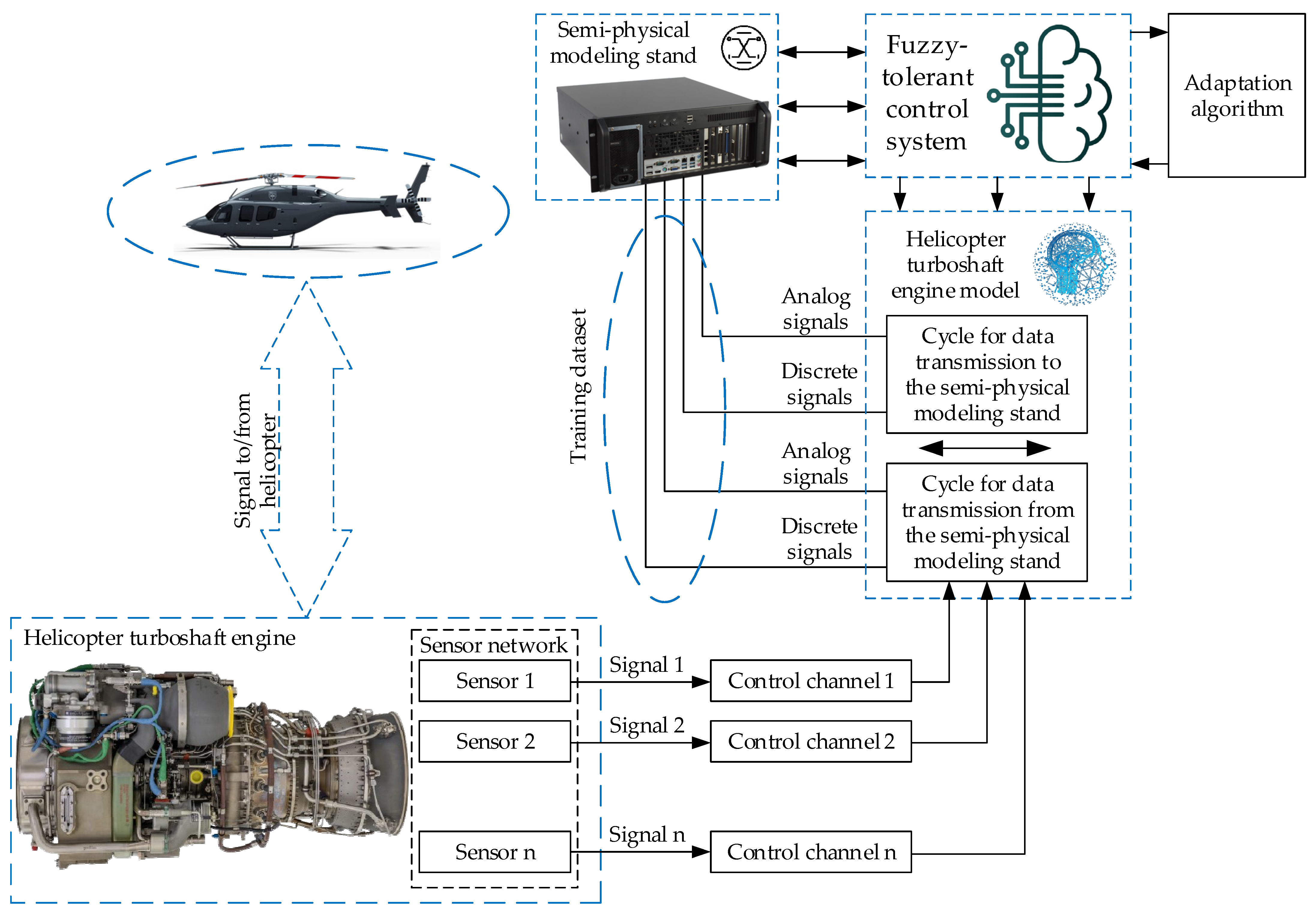
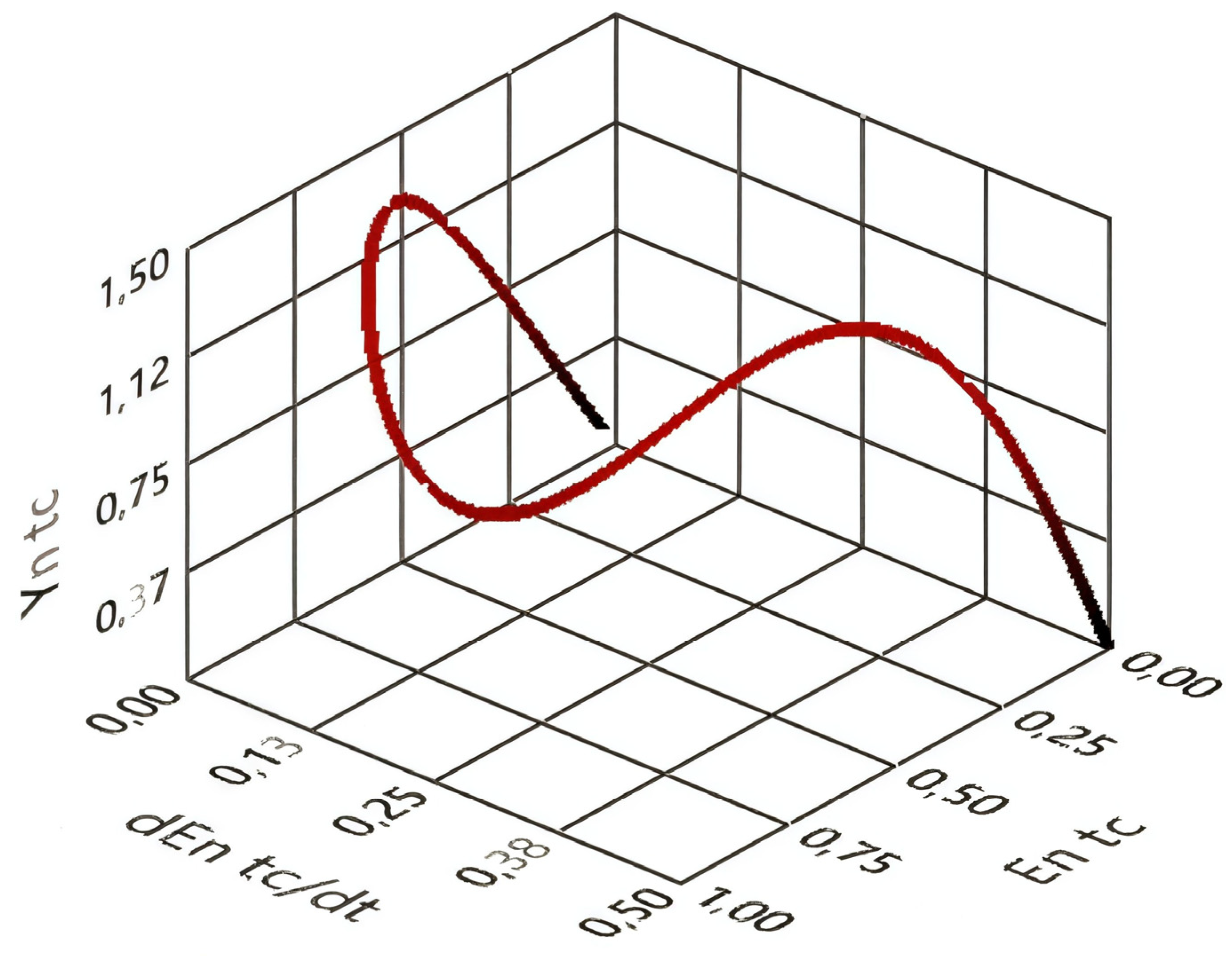


| Number | 1 | … | 38 | … | 84 | … | 127 | … | 181 | … | 219 | … | 256 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| e(t) | 0.008 | … | 0.005 | … | 0.003 | … | 0.007 | … | 0.006 | … | 0.006 | … | 0.006 |
| 0.017 | … | 0.012 | … | 0.013 | … | 0.018 | … | 0.014 | … | 0.014 | … | 0.014 |
| Parameter | Criterion Meaning | Description | |
|---|---|---|---|
| Calculated | Critical | ||
| The Fisher–Pearson criterion | |||
| e(t) | 6.318 | 6.6 | that fell below the critical threshold, signifying homogeneity within the training dataset. |
| 6.327 | |||
| The Fisher–Snedecor criterion | |||
| e(t) | 2.388 | 2.58 | that were below the critical threshold, suggesting homogeneity within the training dataset. |
| 2.394 | |||
| Metric | Proposed Approach | Alternative Approach 1 | Alternative Approach 2 | Alternative Approach 3 | Alternative Approach 4 |
|---|---|---|---|---|---|
| Accuracy | 0.995 (99.5%) | 0.961 (96.1%) | 0.975 (97.5%) | 0.999 (99.9%) | 0.882 (88.2%) |
| Precision | 0.981 (98.1%) | 0.953 (95.3%) | 0.962 (96.2%) | 0.986 (98.6%) | 0.869 (86.9%) |
| Recall | 1.0 | 0.983 | 0.988 | 1.0 | 0.909 |
| F1-score | 0.990 | 0.973 | 0.975 | 0.993 | 0.889 |
| Metric | Proposed Approach | Alternative Approach 1 | Alternative Approach 2 | Alternative Approach 3 | Alternative Approach 4 |
|---|---|---|---|---|---|
| True Positives | 96 | 90 | 92 | 99 | 85 |
| True Negatives | 4 | 10 | 8 | 1 | 15 |
| False Positives | 287 | 282 | 284 | 291 | 277 |
| False Negatives | 14 | 20 | 18 | 11 | 25 |
| True Positive Rate | 0.828 | 0.785 | 0.793 | 0.844 | 0.626 |
| False Positive Rate | 0.0101 | 0.0169 | 0.0152 | 0.0097 | 0.0235 |
| False Negative Rate | 0.0098 | 0.0109 | 0.0103 | 0.0093 | 0.0192 |
| AUC-ROC | 0.831 | 0.773 | 0.791 | 0.848 | 0.651 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Published by MDPI on behalf of the International Institute of Knowledge Innovation and Invention. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vladov, S.; Lytvynov, O.; Vysotska, V.; Vasylenko, V.; Pukach, P.; Vovk, M. An Innovative Applied Control System of Helicopter Turboshaft Engines Based on Neuro-Fuzzy Networks. Appl. Syst. Innov. 2024, 7, 118. https://doi.org/10.3390/asi7060118
Vladov S, Lytvynov O, Vysotska V, Vasylenko V, Pukach P, Vovk M. An Innovative Applied Control System of Helicopter Turboshaft Engines Based on Neuro-Fuzzy Networks. Applied System Innovation. 2024; 7(6):118. https://doi.org/10.3390/asi7060118
Chicago/Turabian StyleVladov, Serhii, Oleksii Lytvynov, Victoria Vysotska, Viktor Vasylenko, Petro Pukach, and Myroslava Vovk. 2024. "An Innovative Applied Control System of Helicopter Turboshaft Engines Based on Neuro-Fuzzy Networks" Applied System Innovation 7, no. 6: 118. https://doi.org/10.3390/asi7060118
APA StyleVladov, S., Lytvynov, O., Vysotska, V., Vasylenko, V., Pukach, P., & Vovk, M. (2024). An Innovative Applied Control System of Helicopter Turboshaft Engines Based on Neuro-Fuzzy Networks. Applied System Innovation, 7(6), 118. https://doi.org/10.3390/asi7060118







