Soft Sensor Technology for the Determination of Mechanical Seal Friction Power Performance
Abstract
1. Introduction
2. Development of Soft Sensor Technology for Determination of Frictional Power Performance of Mechanical Seals
2.1. Derivation of Mechanical Seal Heat Flow Model
2.2. Development of the Soft Sensor for Friction Power Performance Determination
| Algorithm 1: Soft sensor for determining the frictional power of a mechanical seal. |
| define , define |
Calculation of |
3. Evaluation of the Accuracy of the Soft Sensor Determination
3.1. Soft Sensor Validation Test Bench
3.2. Comparison of Equivalent Dimensionless form Coefficient between Numerical and Experimental Results
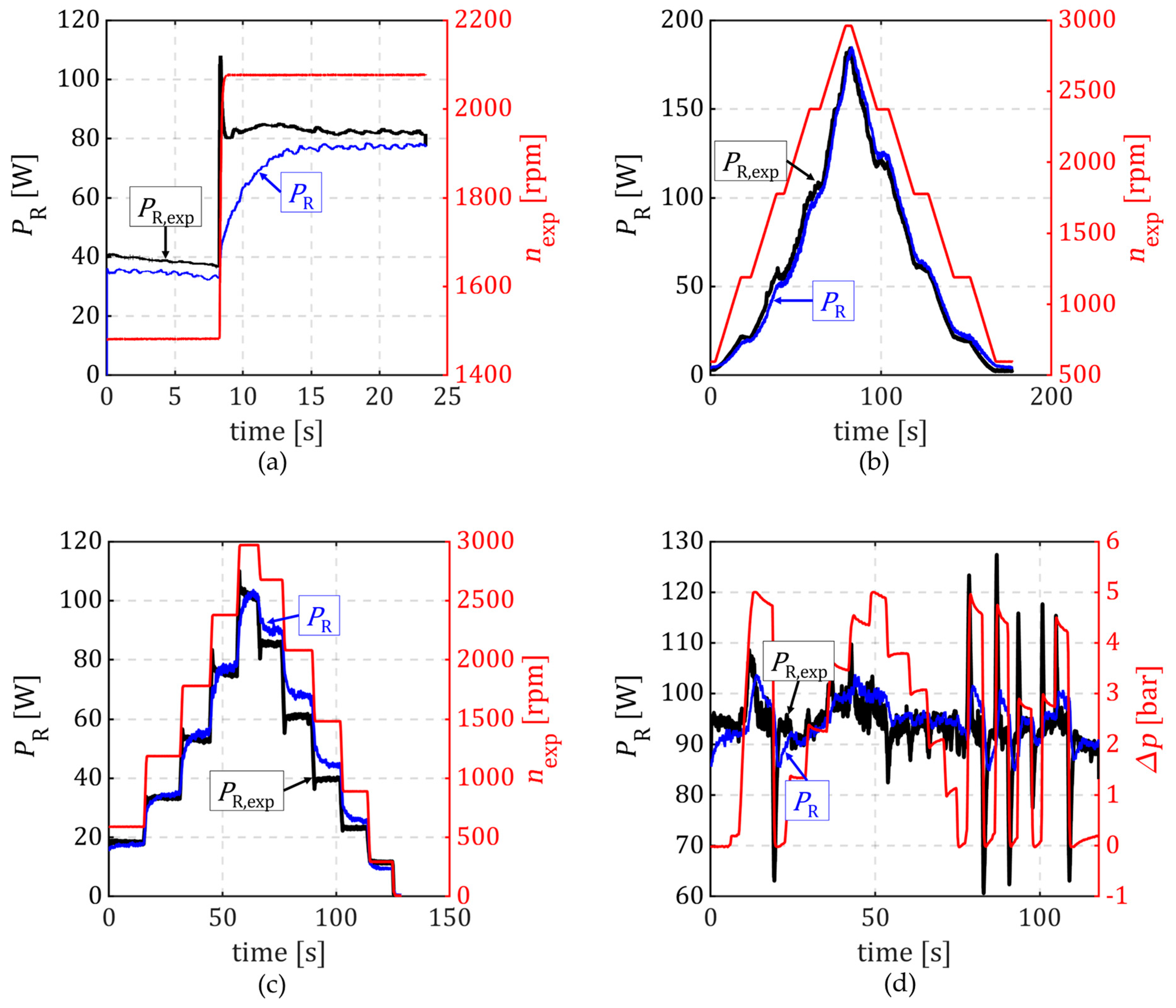
3.3. Quality of Soft Sensor Calculation for Stationary Operation of Mechanical Seals
3.4. Soft Sensor Behaviour with Variation in the Mechanical Seal Stationary Operating Conditions
4. Conclusions
- -
- The calculation of the equivalent dimensionless form coefficient is highly dependent on the model used to determine the averaged Nusselt number. A variety of modelling approaches exist. The heat transfer coefficients determined by the models exhibit considerable variability, which results in discrepancies in the calculation of the dimensionless equivalent mould coefficient.
- -
- By varying the differential pressure across the mechanical seal and the preload on the mechanical seal primary ring, a small deviation between the algorithm and the measurement could be demonstrated.
- -
- Varying the geometry around the mechanical seal affects the heat transfer between the mechanical seal and the fluid. The arrangement of fins around the mechanical seal improves heat transfer and therefore increases the equivalent dimensionless form coefficient.
- -
- The soft sensor heat flow model is based on stationary assumptions. The algorithm reacts slowly to changes in the stationary operating conditions. Rapid changes, e.g., sudden increases in pressure, will not be considered by the algorithm. This significantly increases the errors. The algorithm is not suitable for the representation of dynamic changes in the operating conditions.
- -
- The described algorithm is easy to implement compared with data-based or machine-learning concepts of soft sensors. For this, only the equivalent dimensionless form coefficient characteristics need to be known. It is not necessary to have large amounts of data in order to train a model. There is no need for mechanical machining of the mating ring, as is required when integrating a torque sensor.
5. Patents
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| column matrix of form coefficients | |
| heat transfer area | |
| heat transfer area of the surface | |
| equivalent dimensionless form coefficient | |
| form coefficient of the sliding surface | |
| form coefficient from surface to surface | |
| equivalent form coefficient | |
| exponent Prandl number ratio Nusselt approach | |
| coupling factor temperature sensor | |
| factor Reynolds number Nusselt approach | |
| specific heat capacity of the medium | |
| damping factor low pass filter | |
| inner diameter mechanical seals | |
| outer diameter primary ring | |
| outer diameter mating ring | |
| transmission efficiency | |
| transmission efficiency from surface to surface | |
| frequency | |
| sampling rate | |
| exponent Prandl number Nusselt approach | |
| conventional form factor | |
| characteristic length of the primary ring | |
| characteristic length of the mating ring | |
| exponent Reynolds number Nusselt approach | |
| column matrix of the medium parameter | |
| speed of the primary ring | |
| experimental measured speed of the primary ring | |
| local Nusselt number | |
| averaged Nusselt number | |
| differential pressure above the mechanical seal | |
| friction power | |
| experimental measured friction power | |
| power of the mechanical seal | |
| ventilation power of the mechanical seal | |
| Prandl number of the medium at characteristic temperature of the medium | |
| Prandl number of the medium at temperature of the solid surface | |
| heat flow | |
| convective heat flow | |
| heat flow from surface to surface | |
| characteristic width of the primary ring | |
| characteristic width of the mating ring | |
| radius | |
| Reynolds number | |
| Root Mean Squared Error | |
| preload of the primary ring | |
| axial coordinate of the mechanical seals | |
| heat transfer coefficient | |
| thermal conductivity | |
| thermal conductivity of the primary ring | |
| thermal conductivity of the mating ring | |
| temperature | |
| temperature of the surface | |
| experimental measured temperature at the surface 2 | |
| temperature of the ambient | |
| temperature of the medium | |
| experimental measured temperature of the medium | |
| temperature of the temperature sensor at the mechanical seal | |
| reference temperature | |
| column matrix of the temperatures | |
| Density of the medium | |
| kinematic viscosity of the medium | |
| dynamic viscosity of the medium |
Appendix A
Appendix B
Appendix C
| Measured Quantity | Maximum Relative Error |
| M | 0.054% |
| n | 0.224% |
| Δp | 0.524% |
| s | 1.024% |
| ϑamb | 0.084% |
| ϑM | 0.124% |
| ϑ2 | 0.084% |
| PR | 0.325% |
| Δϑ | 0.149% |
References
- Luo, Y.; Zhang, W.; Fan, Y.; Han, Y.; Li, W.; Acheaw, E. Analysis of Vibration Characteristics of Centrifugal Pump Mechanical Seal under Wear and Damage Degree. Shock Vib. 2021, 2021, 1–9. [Google Scholar] [CrossRef]
- Zou, J.; Luo, Y.; Han, Y.; Fan, Y. Research on Stator Current Characteristics of Centrifugal Pumps under Different Mechanical Seal Failures. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 5748–5762. [Google Scholar] [CrossRef]
- Susan-Resiga, R.F.; Bosioc, A.I.; Stuparu, A.C. Enhanced Affinity Law for Centrifugal Pumps at Variable Speed. IOP Conf. Ser. Earth Environ. Sci. 2023, 1136, 012056. [Google Scholar] [CrossRef]
- Reeh, N.; Manthei, G.; Klar, P.J. Physical Modelling of the Set of Performance Curves for Radial Centrifugal Pumps to Determine the Flow Rate. Appl. Syst. Innov. 2023, 6, 111. [Google Scholar] [CrossRef]
- Wang, X.; Khonsari, M.; Li, S.; Dai, Q.; Wang, X. Experimental Verification of Textured Mechanical Seal Designed Using Multi-Objective Optimization. Ind. Lubr. Tribol. 2019, 71, 766–771. [Google Scholar] [CrossRef]
- Bareis, M.; Berger, W.; Lederer, G.; Otschik, J.; Riedl, M. Gleitringdichtung mit Überwachungsfunktion. International Patent WO2008089800A1, 31 July 2008. [Google Scholar]
- Berger, W.; Bareis, M. Gleitringdichtung mit Reibungsüberwachungseinrichtung. European Patent EP2440816A1, 18 April 2012. [Google Scholar]
- Phillips, R.L.; Jacobs, L.E.; Merati, P. Experimental Determination of the Thermal Characteristics of a Mechanical Seal and Its Operating Environment. Tribol. Trans. 1997, 40, 559–568. [Google Scholar] [CrossRef]
- Jiang, Y.; Yin, S.; Dong, J.; Kaynak, O. A Review on Soft Sensors for Monitoring, Control, and Optimization of Industrial Processes. IEEE Sens. J. 2021, 21, 12868–12881. [Google Scholar] [CrossRef]
- Dai, Y.; Yang, C.; Liu, K.; Liu, A.; Liu, Y. TimeDDPM: Time Series Augmentation Strategy for Industrial Soft Sensing. IEEE Sens. J. 2024, 24, 2145–2153. [Google Scholar] [CrossRef]
- Zhu, W.; Jia, M.; Zhang, Z.; Liu, Y. Dynamic Data Reconciliation for Enhancing the Performance of Kernel Learning Soft Sensor Models Considering Measurement Noise. Chemom. Intell. Lab. Syst. 2024, 246, 105083. [Google Scholar] [CrossRef]
- Frafjord, A.J.; Radicke, J.-P.; Keprate, A.; Komulainen, T.M. Data-Driven Approaches for Deriving a Soft Sensor in a District Heating Network. Energy 2024, 292, 130426. [Google Scholar] [CrossRef]
- Nunes, P.; Santos, J.; Rocha, E. Challenges in Predictive Maintenance—A Review. CIRP J. Manuf. Sci. Technol. 2023, 40, 53–67. [Google Scholar] [CrossRef]
- Shihab, T.A.; Shlapak, L.S.; Namer, N.S.; Prysyazhnyuk, P.M.; Ivanov, O.O.; Burda, M.J. Increasing of Durability of Mechanical Seals of Oil and Gas Centrifugal Pumps Using Tungsten-Free Cermet with Cu-Ni-Mn Binder. J. Phys. Conf. Ser. 2021, 1741, 012031. [Google Scholar] [CrossRef]
- Buck, G.S. Heat Transfer in Mechanical Seals. In International Pump Users Symposium; Texas A&M University: College Station, TX, USA, 1989. [Google Scholar] [CrossRef]
- Holman, J.P. Heat Transfer, 6th ed.; International Student Edition; McGraw-Hill Book Company: New York, NY, USA, 1986; ISBN 0-07-029620-0. [Google Scholar]
- Luan, Z.; Khonsari, M.M. Heat Transfer Analysis in Mechanical Seals Using Fin Theory. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2007, 221, 717–725. [Google Scholar] [CrossRef]
- Brunetière, N.; Modolo, B. Heat Transfer in a Mechanical Face Seal. Int. J. Therm. Sci. 2009, 48, 781–794. [Google Scholar] [CrossRef]
- Mosavat, M.; Moradi, R.; Rahimi Takami, M.; Barzegar Gerdroodbary, M.; Ganji, D.D. Heat Transfer Study of Mechanical Face Seal and Fin by Analytical Method. Eng. Sci. Technol. Int. J. 2018, 21, 380–388. [Google Scholar] [CrossRef]
- Müller, H.K.; Nau, B.S. Fachwissen-Dichtungstechnik; Kapitel 12 Gleitringdichtungen: Grundlagen; Waiblingen. 2021, p. 52. Available online: http://ww3.cad.de/foren/ubb/uploads/Ultimate+AL8.0i/Kapitel12_2007.pdf (accessed on 2 February 2021).
- Glück, B. Berechnung der Stationären, Mehrdimensionalen Wärmeleitung Mittels Formkoeffizienten bei Einer Beliebigen Anzahl von Oberflächen und Unterschiedlichen Randbedingungen; Jößnitz. 2012, p. 15. Available online: https://berndglueck.de/dl/?dl=Waermeleitung+Formkoeffizienten.pdf (accessed on 3 December 2023).
- Baehr, H.D.; Stephan, K. Wärme- Und Stoffübertragung, 9th ed.; Springer Vieweg: Stuttgart, Germany, 2016; ISBN 978-3-662-49677-0. [Google Scholar]
- Schade, H.; Kunz, E.; Kameier, F.; Paschereit, C.O. Strömungslehre, 4th ed.; Walter de Gruyter: Berlin, Germany, 2013; ISBN 978-3-11-029221-3. [Google Scholar]
- Mayer, E. Axiale Gleitringdichtungen, 6th ed.; VDI-Verlag: Lenggries, Germany, 1977; ISBN 3-18-400384-1. [Google Scholar]
- Bernhard, F. Handbuch Der Technischen Temperaturmessung, 2nd ed.; Springer Vieweg: Ilmenau, Germany, 2014; ISBN 978-3-642-24505-3. [Google Scholar]
- Website EagleBurgmann Germany GmbH & Co. KG. Innovativer Gleitwerkstoff eSiC—DE. 2023. Available online: https://www.eagleburgmann.com/de/produkte/emg/innovativer-gleitwerkstoff-esic (accessed on 8 December 2023).
- Ayadi, K.; Brunetière, N.; Tournerie, B.; Maoui, A. Experimental Thermal Analysis of a Mechanical Face Seal. J. Therm. Sci. Eng. Appl. 2016, 8, 031011. [Google Scholar] [CrossRef]
- Becker, K.M. Measurements of Convective Heat Transfer from a Horizontal Cylinder Rotating in a Tank of Water. Int. J. Heat Mass Transf. 1963, 6, 1053–1062. [Google Scholar] [CrossRef]
- Tachibana, F.; Fukui, S. Convective Heat Transfer of the Rotational and Axial Flow between Two Concentric Cylinders. Bull. JSME 1964, 7, 385–391. [Google Scholar] [CrossRef]
- Doane, J.C.; Myrum, T.A.; Beard, J.E. An Experimental-Computational Investigation of the Heat Transfer in Mechanical Face Seals. Int. J. Heat Mass Transf. 1991, 34, 1027–1041. [Google Scholar] [CrossRef]
- Luan, Z.; Khonsari, M.M. Analysis of Conjugate Heat Transfer and Turbulent Flow in Mechanical Seals. Tribol. Int. 2008, 42, 762–769. [Google Scholar] [CrossRef]
- Website Statistics How to RMSE: Root Mean Square Error. 2024. Available online: https://www.statisticshowto.com/probability-and-statistics/regression-analysis/rmse-root-mean-square-error/ (accessed on 4 January 2024).

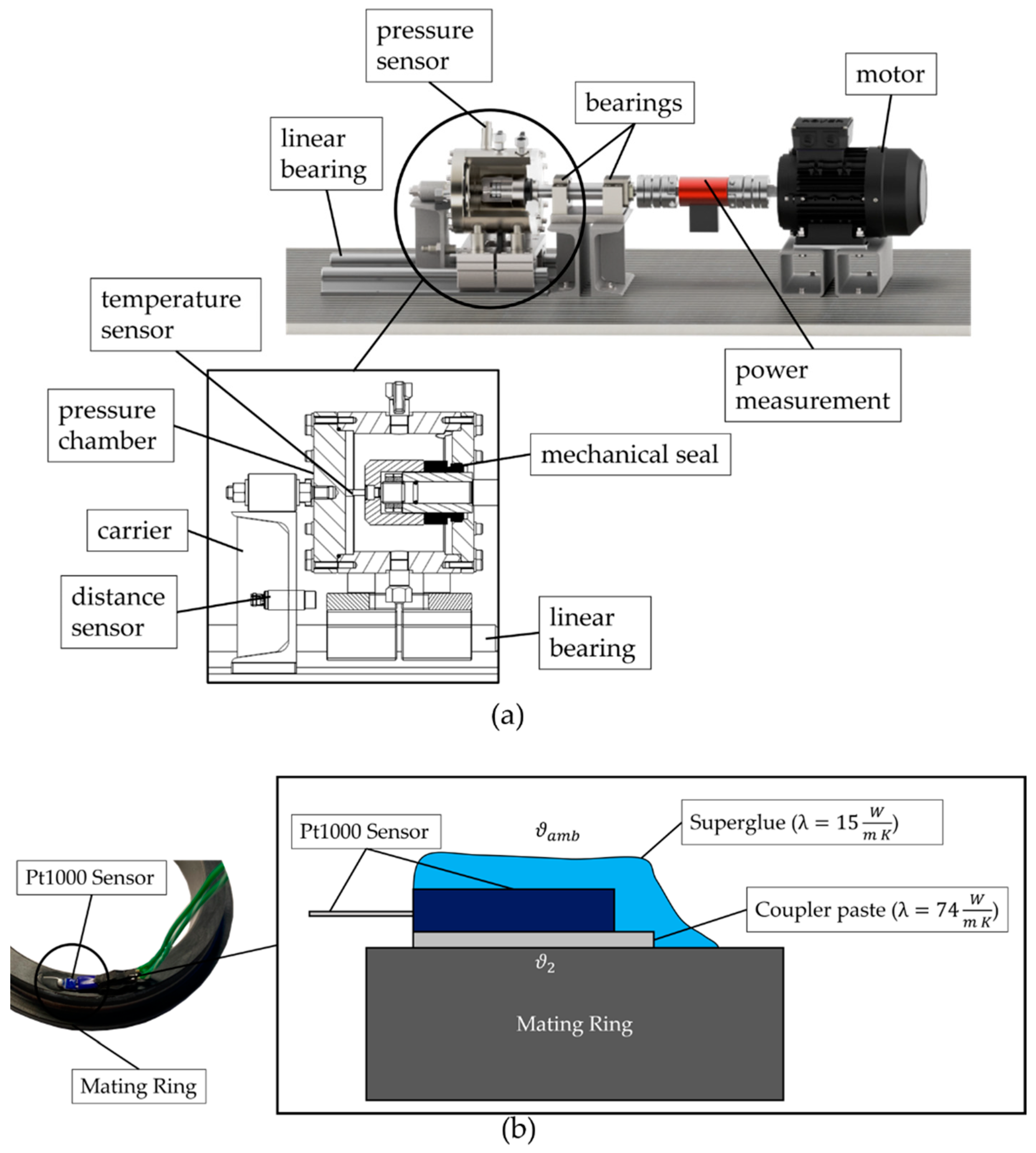

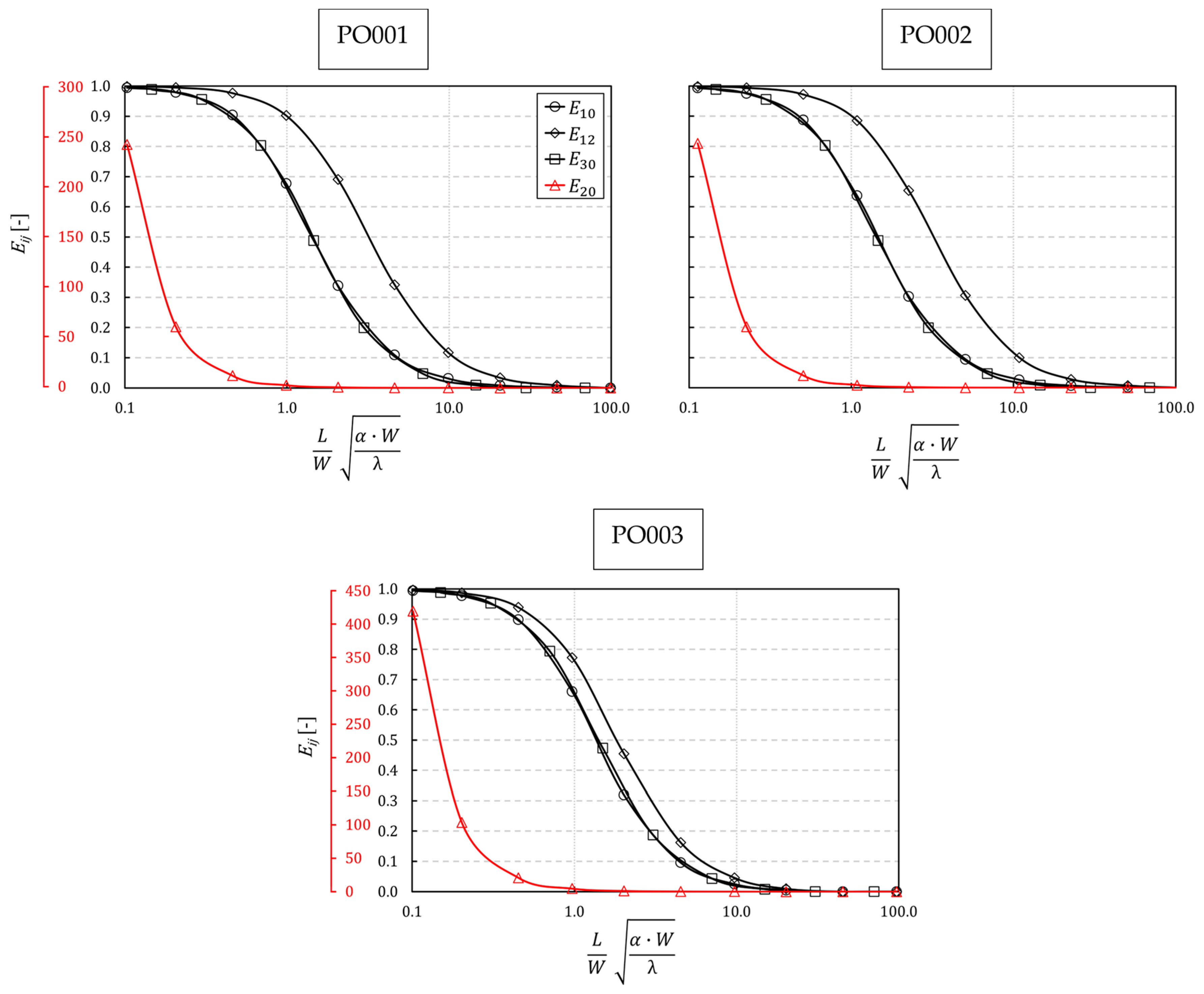
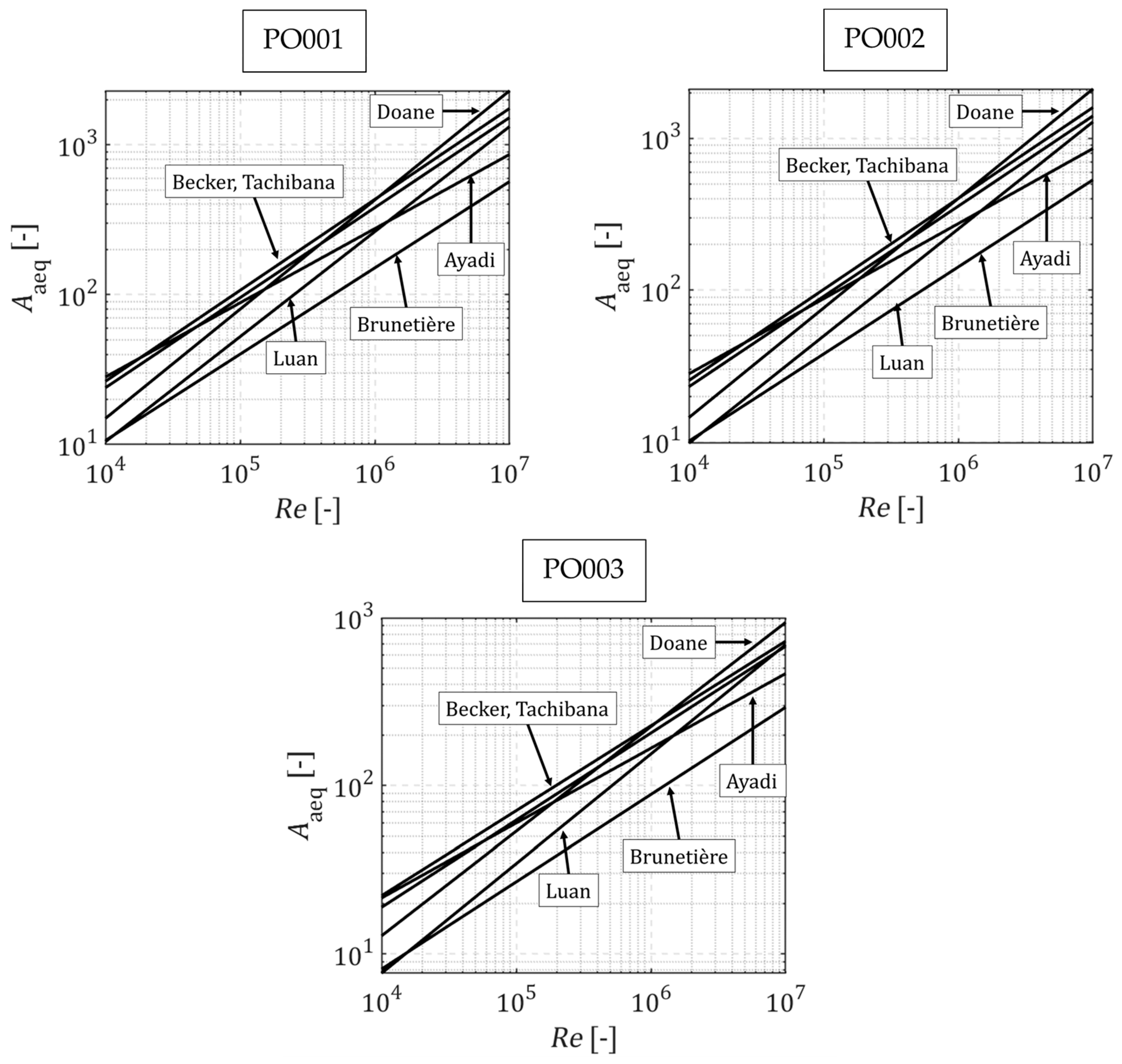
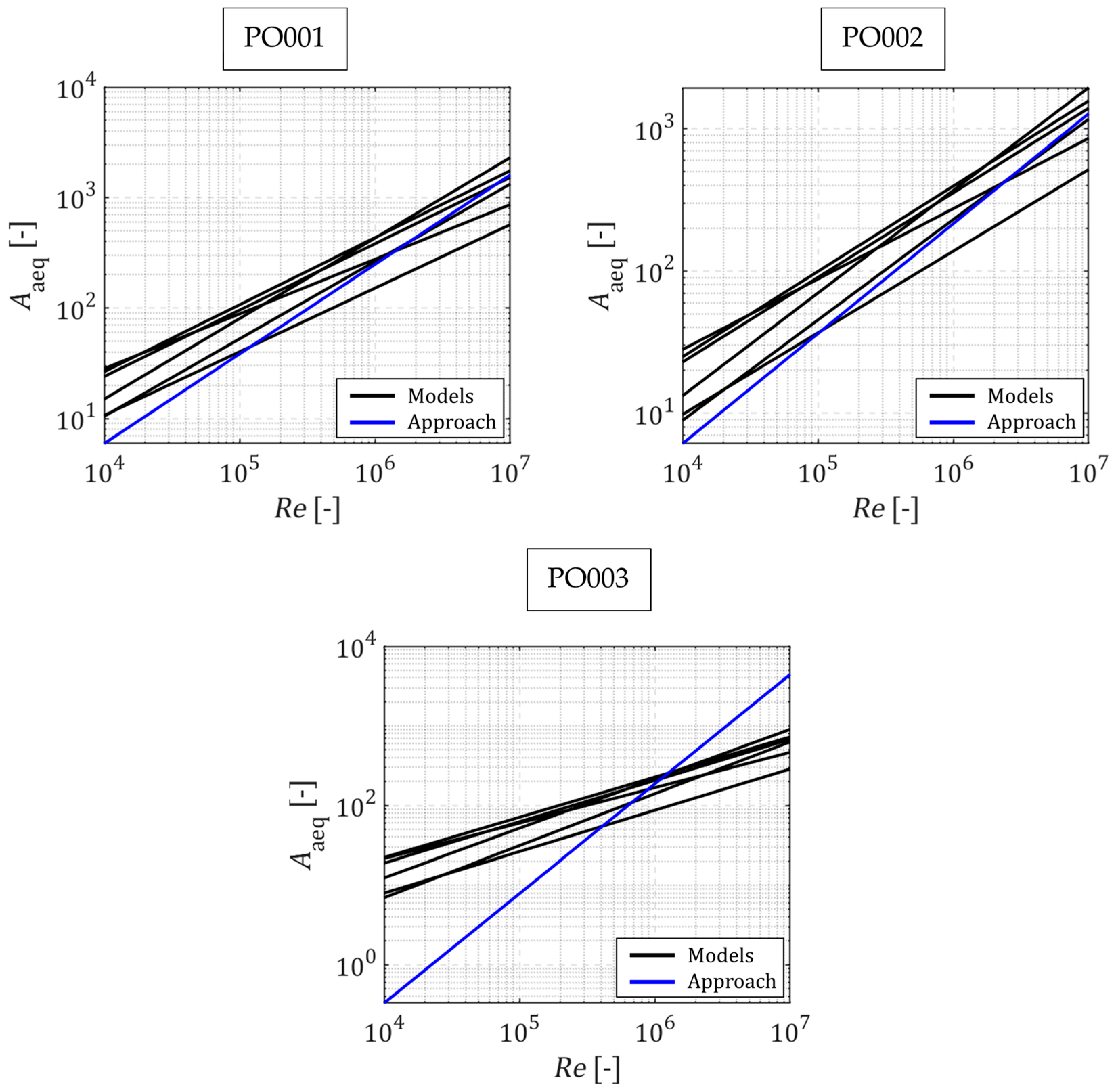

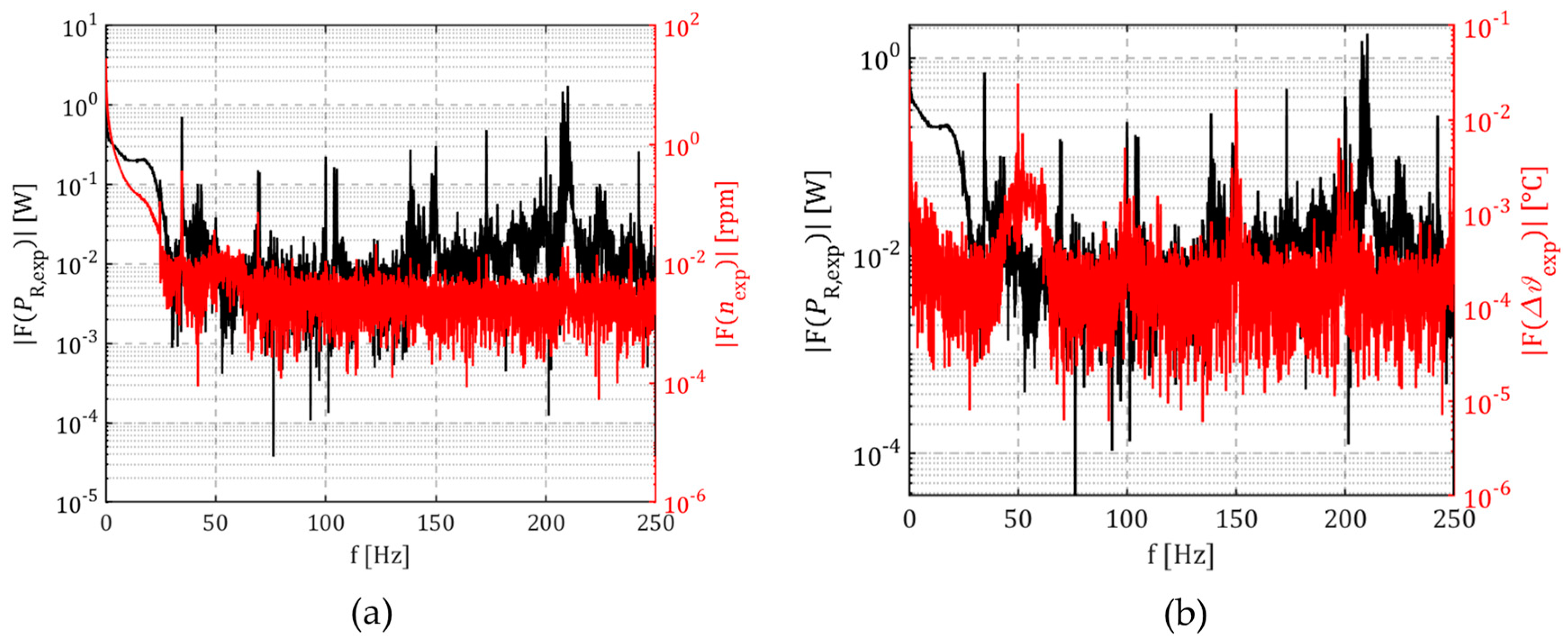
| Parameter | PO001 | PO002 | PO003 |
|---|---|---|---|
| inner diameter () | 38 mm | 38 mm | 50 mm |
| outer diameter mating ring () | 54 mm | 54 mm | 69 mm |
| outer diameter primary ring () | 46 mm | 46 mm | 58 mm |
| characteristic length mating ring () | 11.3 mm | 11.3 mm | 10.5 mm |
| characteristic length primary ring () | 5 mm | 5 mm | 5.4 mm |
| characteristic width mating ring () | 5 mm | 5 mm | 4.5 mm |
| characteristic width primary ring () | 3.5 mm | 3.5 mm | 3.9 mm |
| material mating ring | SiC1 | SiC2 | SiC1 |
| material primary ring | SiC1 | SiC1 | SiC1 |
| heat conductivity mating ring () | |||
| heat conductivity primary ring () |
| Approach Function | PO001 | PO002 | PO003 | |||
|---|---|---|---|---|---|---|
| Ayadi [27] | 0.155 | 0.498 | 0.154 | 0.495 | 0.187 | 0.445 |
| Becker [28] | 0.051 | 0.607 | 0.052 | 0.600 | 0.111 | 0.505 |
| Tachibana [29] | 0.049 | 0.601 | 0.050 | 0.595 | 0.084 | 0.518 |
| Doane [30] | 0.009 | 0.729 | 0.009 | 0.722 | 0.021 | 0.622 |
| Luan [31] | 0.008 | 0.701 | 0.007 | 0.706 | 0.009 | 0.652 |
| Brunetière [18] | 0.027 | 0.576 | 0.026 | 0.574 | 0.035 | 0.519 |
| Approach | 0.810 | 0.773 | 1.376 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reeh, N.; Manthei, G.; Klar, P.J. Soft Sensor Technology for the Determination of Mechanical Seal Friction Power Performance. Appl. Syst. Innov. 2024, 7, 39. https://doi.org/10.3390/asi7030039
Reeh N, Manthei G, Klar PJ. Soft Sensor Technology for the Determination of Mechanical Seal Friction Power Performance. Applied System Innovation. 2024; 7(3):39. https://doi.org/10.3390/asi7030039
Chicago/Turabian StyleReeh, Nils, Gerd Manthei, and Peter J. Klar. 2024. "Soft Sensor Technology for the Determination of Mechanical Seal Friction Power Performance" Applied System Innovation 7, no. 3: 39. https://doi.org/10.3390/asi7030039
APA StyleReeh, N., Manthei, G., & Klar, P. J. (2024). Soft Sensor Technology for the Determination of Mechanical Seal Friction Power Performance. Applied System Innovation, 7(3), 39. https://doi.org/10.3390/asi7030039







