A Study of an EOQ Model of Growing Items with Parabolic Dense Fuzzy Lock Demand Rate
Abstract
:1. Introduction
1.1. Literature Review on Dense Fuzzy Sets
1.2. Literature Review on Inventory Models
1.3. Motivation and Specific Study
2. Preliminaries
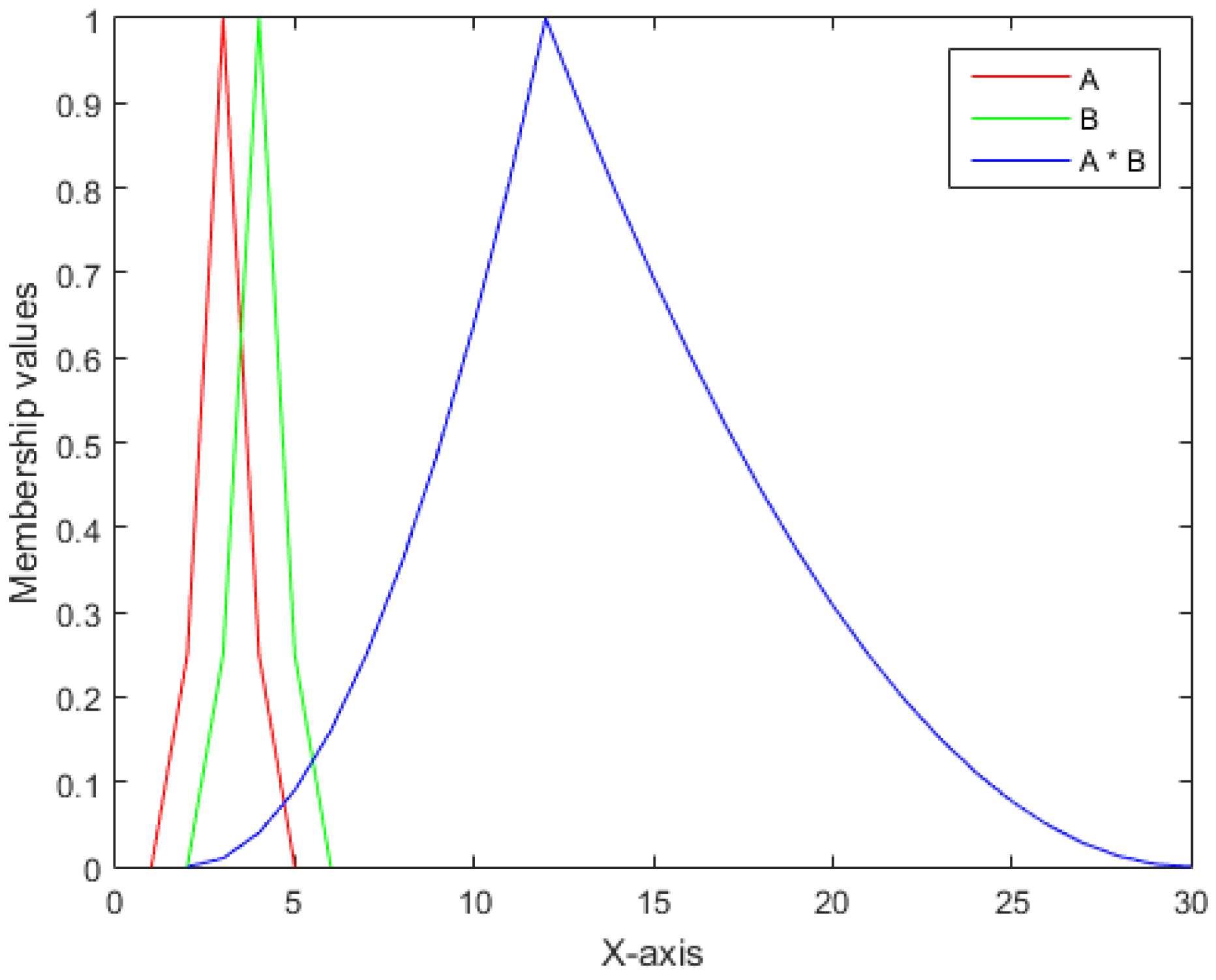
3. Arithmetic Operation over Parabolic Dense Fuzzy Numbers
- (i)
- Addition of Two Parabolic Dense Fuzzy Numbers
- (ii)
- Subtraction of Two Parabolic Dense Fuzzy Numbers
- (iii)
- Scalar multiplication of Parabolic Dense Fuzzy Numbers
- (iv)
- Multiplication of Two Parabolic Dense Fuzzy Numbers
- (v)
- Inverse of a Parabolic Dense Fuzzy Number
4. Formulation of Crisp Model
- (i)
- We considered an additional cost for feeding the growing items.
- (ii)
- Feeding cost depended on the weight of the items.
- (iii)
- The growth function was approximated by a linear function.
- (iv)
- We considered an idle cost for the growth period and cleaning period.
5. Fuzzy Mathematical Model
5.1. Rules of Finding Key Values of the Fuzzy Locks
5.2. Solution Algorithm
6. A Real Case Study
Sensitivity Analysis
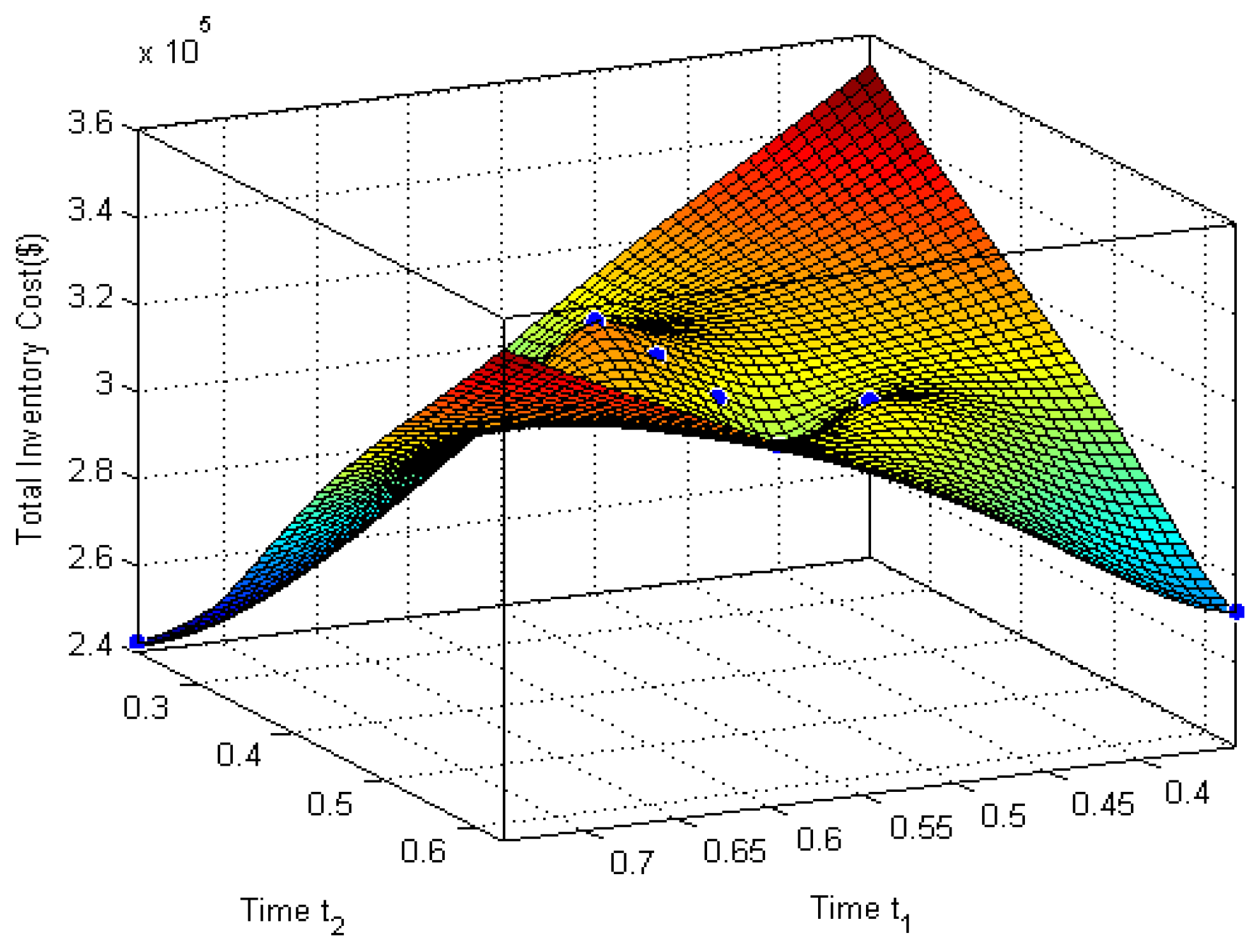
7. Graphical Illustration
8. Managerial Insights
- (i)
- Learning experience is a crucial part of any inventory problem to optimize the inventory cost.
- (ii)
- The decision maker can optimize the inventory cost by utilizing proper key values.
- (iii)
- The less qualified decision maker can also minimize the cost using the PDFLS approach.
- (iv)
- The PDFLS approach gives a finer optimum than the parabolic dense set approach.
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notations
| Demand rate per unit time (g/year) | |
| Growing rate per fish per unit time | |
| Approximated weight of a fingerling (g) | |
| Approximated weight of a fish at the time of selling (g) | |
| Total weight of inventory at time t (g) | |
| The time required to clean the pond for starting a new cycle (years) | |
| Growing period (years) (decision variable) | |
| Selling period (years) (decision variable) | |
| Cycle length (years) | |
| Total number of fish bought in each period (decision variable) | |
| Feeding cost per unit item per unit time ( ) | |
| Holding cost per unit time ($/year) | |
| Setup cost, cost for preparing the environment per period ($) | |
| Price of fingerlings per gram ($/g) | |
| Natural idle cost per unit time ($/year); this cost is considered when the retailer cannot fulfill the customer’s demand | |
| B | Operational cost per cycle ($) |
| Fuzzy deviation parameters |
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–356. [Google Scholar] [CrossRef] [Green Version]
- Bellman, R.E.; Zadeh, L.A. Decision making in a fuzzy environment. Manag. Sci. 1970, 17, 141–164. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Operations on fuzzy numbers. Int. J. Syst. Sci. 1978, 9, 613–626. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. In Proceedings of the VII ITKR’s Session, Sofia, Bulgaria, 20–23 June 1983. [Google Scholar]
- Kaufmann, A.; Gupta, M.M. Introduction of Fuzzy Arithmetic Theory and Applications; Van Nostrand Reinhold: New York, NY, USA, 1985. [Google Scholar]
- Chutia, R.; Mahanta, S.; Baruah, H.K. An Alternative Method of Finding the Membership of a Fuzzy Number. Int. J. Latest Trends Comput. 2010, 1, 69–72. [Google Scholar]
- De, S.K.; Beg, I. Triangular dense fuzzy sets and new defuzzication methods. J. Intell. Fuzzy Syst. 2016, 36, 469–477. [Google Scholar] [CrossRef]
- De, S.K.; Mahata, G.C. Decision of a fuzzy inventory with fuzzy backorder model under cloudy fuzzy demand rate. Int. J. Appl. Comput. Math. 2016, 3, 2593–2609. [Google Scholar] [CrossRef]
- De, S.K. Triangular Dense Fuzzy Lock Set. Soft Comput. 2017, 22, 7243–7254. [Google Scholar] [CrossRef]
- Faritha, A.A.; Priya, G. Optimizing triangular parabolic fuzzy EOQ model with shortage using nearest interval approximation. Int. J. Future Revolut. Comput. Sci. Commun. Eng. 2017, 3, 92–96. [Google Scholar]
- Garg, H.; Ansha. Arithmetic operations on generalized parabolic fuzzy numbers and its application. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2016, 88, 15–26. [Google Scholar] [CrossRef]
- Maity, S.; Chakraborty, A.; De, S.K.; Mondal, S.P.; Alam, S. A comprehensive study of a backlogging EOQ model with non-linear heptagonal dense fuzzy environment. RAIRO-Oper. Res. 2020, 54, 267–286. [Google Scholar] [CrossRef] [Green Version]
- Maity, S.; De, S.K.; Mondal, S.K. A Study of a Backorder EOQ Model for Cloud-Type Intuitionistic Dense Fuzzy Demand Rate. Int. J. Fuzzy Syst. 2019, 22, 201–211. [Google Scholar] [CrossRef]
- Harris, F.W. Operations and Costs (Factory Management Series); A. W. Shaw Co.: Chicago, IL, USA, 1913; pp. 18–52. [Google Scholar]
- Karlin, S. One Stage Inventory Model with Uncertainty, Studies in the Mathematical Theory of Inventory and Production; Stanford University Press: Stanford, CA, USA, 1958. [Google Scholar]
- De, S.K. EOQ model with natural idle time and wrongly measured demand rate. Int. J. Inventory Control Manag. 2013, 3, 329–354. [Google Scholar]
- Das, P.; De, S.K.; Sana, S.S. An EOQ model for time dependent backlogging over idle time: A step order fuzzy approach. Int. J. Appl. Comput. Math. 2014, 1, 171–185. [Google Scholar] [CrossRef] [Green Version]
- De, S.K.; Goswami, A.; Sana, S.S. An interpolating by pass to Pareto optimality in intuitionistic fuzzy technique for an EOQ model with time sensitive backlogging. Appl. Math. Comput. 2014, 230, 664–674. [Google Scholar] [CrossRef]
- Kazemi, N.; Olugu, E.U.; Salwa Hanim, A.-R.; Ghazilla, R.A.B.R. Development of a fuzzy economic order quantity model for imperfect quality items using the learning effect on fuzzy parameters. J. Intell. Fuzzy Syst. 2015, 28, 2377–2389. [Google Scholar] [CrossRef]
- De, S.K.; Sana, S.S. The (p, q, r, l) model for stochastic demand under intuitionistic fuzzy aggregation with Bonferroni mean. J. Intell. Manuf. 2016, 29, 1753–1771. [Google Scholar] [CrossRef]
- Karmakar, S.; De, S.K.; Goswami, A. A pollution sensitive dense fuzzy economic production quantity model with cycle time dependent production rate. J. Clean. Prod. 2017, 154, 139–150. [Google Scholar] [CrossRef]
- Karmakar, S.; De, S.K.; Goswami, A. A pollution sensitive remanufacturing model with waste items: Triangular dense fuzzy lock set approach. J. Clean. Prod. 2018, 187, 789–803. [Google Scholar] [CrossRef]
- Maity, S.; De, S.K.; Pal, M. Two Decision Makers’ Single Decision over a Back Order EOQ Model with Dense Fuzzy Demand Rate. Financ. Mark. 2018, 3, 1–11. [Google Scholar]
- Maity, S.; De, S.K.; Mondal, S.P. A Study of an EOQ Model under Lock Fuzzy Environment. Mathematics 2019, 7, 75. [Google Scholar] [CrossRef] [Green Version]
- De, S.K.; Mahata, G.C. A cloudy fuzzy economic order quantity model for imperfect-quality items with allowable proportionate discounts. J. Ind. Eng. Int. 2019, 15, 571–583. [Google Scholar] [CrossRef] [Green Version]
- Liang, R.; Wang, J.Q. A Linguistic Intuitionistic Cloud Decision Support Model with Sentiment Analysis for Product Selection in E-commerce. Int. J. Fuzzy Syst. 2019, 21, 963–977. [Google Scholar] [CrossRef]
- Nobil, A.H.; Sedigh, A.H.A.; Cárdenas-Barrón, L.E. A Generalized Economic Order Quantity Inventory Model with Shortage: Case Study of a Poultry Farmer. Arab. J. Sci. Eng. 2018, 44, 2653–2663. [Google Scholar] [CrossRef]
- Rezaei, J. Economic order quantity for growing items. Int. J. Prod. Econ. 2014, 155, 109–113. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, L.Y.; Tian, X.Q.; Feng, C. Inventory management research for growing items with carbon-constrained. In Proceedings of the Control Conference (CCC), IEEE 35th Chinese, Chengdu, China, 27–29 July 2016; pp. 9588–9593. [Google Scholar]
- De, S.K.; Mahata, G.C.; Maity, S. Carbon emission sensitive deteriorating inventory model with trade credit under volumetric fuzzy system. Int. J. Intell. Syst. 2021, 1–28. [Google Scholar] [CrossRef]
- Mahata, G.C.; De, S.K.; Maity, S.; Bhattacharya, K. Three-echelon supply chain model in an imperfect production system with inspection error, learning effect, and return policy under fuzzy environment. Int. J. Syst. Sci. Oper. Logist. 2021. [Google Scholar] [CrossRef]
- Salameh, M.K.; Jaber, M.Y. Economic production quantity model for items with imperfect quality. Int. J. Prod. Econ. 2000, 64, 59–64. [Google Scholar] [CrossRef]
- Sebatjane, M.; Adetunji, O. Economic order quantity model for growing items with imperfect quality. Oper. Res. Perspect. 2019, 6, 100088. [Google Scholar] [CrossRef]
- Wee, H.M.; Yu, J.; Chen, M.C. Optimal inventory model for items with imperfect quality and shortage backordering. Omega 2007, 35, 7–11. [Google Scholar] [CrossRef]
- Alfares, H.K.; Afzal, A.R. An Economic Order Quantity Model for Growing Items with Imperfect Quality and Shortages. Arab. J. Sci. Eng. 2021, 46, 1863–1875. [Google Scholar] [CrossRef]
- Rana, K.; Sing, S.R.; Saxena, N.; Sana, S.S. Growing items inventory model for carbon emission under the permissible delay in payment with partially backlogging. Green Financ. 2021, 3, 153–174. [Google Scholar] [CrossRef]
- Choudhury, M.; Mahata, G.C. Sustainable integrated and pricing decisions for two-echelon supplier-retailer supply chain of growing Items. RAIRO-Oper. Res. 2021. [Google Scholar] [CrossRef]
- De-la-Cruz-Márquez, C.G.; Cárdenas-Barrón, L.E.; Mandal, B. An Inventory Model for Growing Items with Imperfect Quality When the Demand Is Price Sensitive under Carbon Emissions and Shortages. Math. Probl. Eng. 2021, 2021, 6649048. [Google Scholar] [CrossRef]
- Gharaei, A.; Almehdawe, E. Optimal sustainable order quantities for growing items. J. Clean. Prod. 2021, 307, 127216. [Google Scholar] [CrossRef]
- Mittal, M.; Sharma, M. Economic Ordering Policies for Growing Items (Poultry) with Trade-Credit Financing. Int. J. Appl. Comput. Math. 2021, 7, 39. [Google Scholar] [CrossRef]











| Authors | Product | Demand | Matter of Growing Items | Solution Approach | |
|---|---|---|---|---|---|
| Conventional Items | Growing Items | ||||
| Harris [14] | ✓ | Crisp | Not included | Convex Optimization | |
| Salameh and Jaber [32] | ✓ | Crisp | Not included | Statistical method | |
| Rezaei [28] | ✓ | Crisp | Non-specific | Convex Optimization | |
| Zhang et al. [29] | ✓ | Crisp | Non-specific | Convex Optimization | |
| Nobil et al. [27] | ✓ | Crisp | Poultry | Convex Optimization | |
| Sebatjane and Adetunji [33] | ✓ | Crisp | Non-specific | Convex Optimization | |
| Wee et al. [34] | ✓ | Crisp | Non-specific | Convex Optimization | |
| Alfares and Afzal [35] | ✓ | Crisp | Non-specific | Convex Optimization | |
| Rana et al. [36] | ✓ | Crisp | Non-specific | Convex Optimization | |
| This Paper | ✓ | Fuzzy (PDFS and PDFLS) | Fishery | New solution algorithm via new defuzzification methods | |
| Approach | ||||||
|---|---|---|---|---|---|---|
| Crisp | - | 0.5479 | 0.4330 | 2887 | 319,476.8 | - |
| General Fuzzy | - | 0.5479 | 0.4330 | 2790 | 308,834.3 | −3.33 |
| Parabolic dense fuzzy | 1 | 0.5479 | 0.4327 | 2838 | 314,155.5 | −1.66 |
| 2 | 0.5479 | 0.4321 | 2846 | 315,042.4 | −1.39 | |
| 3 | 0.5479 | 0.4318 | 2852 | 315,633.7 | −1.20 | |
| PDFLS | 1 | 05479 | 0.4330 | 2740 | 303,233.0 | −5.08 |
| 2 | 0.5479 | 0.4331 | 2724 | 301,459.3 | −5.64 | |
| 3 | 0.5479 | 0.4330 | 2713 | 300,276.8 | −6.00 |
| Parameter | % Change | |||||
|---|---|---|---|---|---|---|
| +30 | 0.5151 | 0.4659 | 2919 | 286,691.8 | −10.26 | |
| +10 | 0.5369 | 0.4440 | 2782 | 296,074.7 | −7.32 | |
| −10 | 0.5589 | 0.4220 | 2644 | 304,128.4 | −4.80 | |
| −30 | 0.5808 | 0.4002 | 2507 | 310,708.3 | −2.74 | |
| +30 | 0.7452 | 0.2358 | 1136 | 231,708.0 | −27.47 | |
| +10 | 0.6137 | 0.3673 | 2092 | 289,909.2 | −9.25 | |
| −10 | 0.4822 | 0.4988 | 3472 | 298,384.2 | −6.60 | |
| −30 | 0.3507 | 0.6303 | 5642 | 259,093.1 | −18.90 | |
| +30 | 0.5479 | 0.4330 | 2713 | 301,090.8 | −5.75 | |
| +10 | 0.5479 | 0.4330 | 2713 | 300,548.1 | −5.92 | |
| −10 | 0.5479 | 0.4330 | 2713 | 300,005.4 | −6.09 | |
| −30 | 0.5479 | 0.4330 | 2713 | 299,462.7 | −6.26 | |
| +30 | 0.5479 | 0.4330 | 2713 | 389,485.0 | +21.91 | |
| +10 | 0.5479 | 0.4330 | 2713 | 330,012.8 | +3.29 | |
| −10 | 0.5479 | 0.4330 | 2713 | 270,540.7 | −15.31 | |
| −30 | 0.5479 | 0.4330 | 2713 | 211,068.6 | −33.93 | |
| +30 | 0.5479 | 0.4330 | 2713 | 300,306.8 | −6.00 | |
| +10 | 0.5479 | 0.4330 | 2713 | 300,286.3 | −6.00 | |
| −10 | 0.5479 | 0.4330 | 2713 | 300,266.8 | −6.01 | |
| −30 | 0.5479 | 0.4330 | 2713 | 300,246.8 | −6.01 | |
| +30 | 0.5479 | 0.4330 | 2713 | 300,283.6 | −6.00 | |
| +10 | 0.5479 | 0.4330 | 2713 | 300,279.0 | −6.00 | |
| −10 | 0.5479 | 0.4330 | 2713 | 300,274.5 | −6.01 | |
| −30 | 0.5479 | 0.4330 | 2713 | 300,270.0 | −6.01 | |
| +30 | 0.5479 | 0.4330 | 2451 | 271,280.7 | −15.08 | |
| +10 | 0.5479 | 0.4330 | 2626 | 290,611.4 | −9.03 | |
| −10 | 0.5479 | 0.4330 | 2800 | 309,942.1 | −2.98 | |
| −30 | 0.5479 | 0.4330 | 2975 | 329,272.8 | +3.06 | |
| +30 | 0.5479 | 0.4330 | 2923 | 323,512.8 | +1.26 | |
| +10 | 0.5479 | 0.4330 | 2783 | 308,022.1 | −3.58 | |
| −10 | 0.5479 | 0.4330 | 2643 | 292,531.4 | −8.43 | |
| −30 | 0.5479 | 0.4330 | 2503 | 277,040.7 | −13.28 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maity, S.; De, S.K.; Pal, M.; Mondal, S.P. A Study of an EOQ Model of Growing Items with Parabolic Dense Fuzzy Lock Demand Rate. Appl. Syst. Innov. 2021, 4, 81. https://doi.org/10.3390/asi4040081
Maity S, De SK, Pal M, Mondal SP. A Study of an EOQ Model of Growing Items with Parabolic Dense Fuzzy Lock Demand Rate. Applied System Innovation. 2021; 4(4):81. https://doi.org/10.3390/asi4040081
Chicago/Turabian StyleMaity, Suman, Sujit Kumar De, Madhumangal Pal, and Sankar Prasad Mondal. 2021. "A Study of an EOQ Model of Growing Items with Parabolic Dense Fuzzy Lock Demand Rate" Applied System Innovation 4, no. 4: 81. https://doi.org/10.3390/asi4040081
APA StyleMaity, S., De, S. K., Pal, M., & Mondal, S. P. (2021). A Study of an EOQ Model of Growing Items with Parabolic Dense Fuzzy Lock Demand Rate. Applied System Innovation, 4(4), 81. https://doi.org/10.3390/asi4040081








