1. Introduction
DC (direct current) motors are widely used components as electrical actuators, in cars, trains and driving high power hoisting machines, milling machines, among others. A field in which DC motors are also widely used is robotics. Whether using these to change the angle of a joint of a robotic manipulator, to drive a vehicle’s traction system, or even to rotate the sensor of a LiDAR (Light Detection and Ranging), there are numerous uses for these in robotics. Another example are the legged-robotic vehicles that can be found in [
1]. However, they have a non-linear behavior that results from the fact that they cannot rotate at any supply voltage, always having a minimum rotation torque (starting torque) that prevents rotation until a when a certain voltage is reached, which is commonly denominated by the motor dead zone. To compensate for these, several control methods can be applied, such as [
2,
3,
4], just to state a few.
Worm gearboxes are typically used when compactness is an important factor, as well as an orthogonal redirectioning is required. Yet, one of the greatest advantage of worm gears is its unique self-locking characteristic. This means that the gear can only rotate by its input side, and cannot be actuated through the load side. As Ye and Wu [
5] state, these features make worm gearboxes useful for multiple types of robotic vehicles and manipulators. However, any gearbox has a main non-linearity, which is it allows some movement of its output shaft without rotating its input, called backlash.
So, using a DC motor with a worm gearbox is a solution that guarantees that, for example in a robotic manipulator, when the arm’s joint reaches the desired angle it does not move until the next required change. It can also be used on vehicles with legged locomotion systems, which can benefit from this type of motors since the joints are blocked in the desired position. Regarding this kind of locomotion, another advantage is that the vehicle can stay immobilized, while guaranteeing the position of the leg, even when the power is down.
To increase safety and robustness in the performance of industrial robots, which otherwise could easily break their joints, or hurt someone, the use of non-rigid joints is increasingly found in the literature and in the industry. These mechanisms contain elastic components (such as springs), which introduce a mechanical energy storage in the system, potentially increasing the maximum output power [
6]. In [
7], Giusti et al. have designed and implemented successfully a controller based on the analysis of the inverse dynamics of the non-rigid joint, and have applied a structured controller. The testbed mixes rigid and elastic joints on an interesting configuration. The usage of non-rigid joints for exoskeletons is also expanding, possibly due to the decrease in the size of the actuators. An example is the work presented in [
8] for a variable viscoelastic joint system. Another interesting application example for non-rigid joints are deployable mechanisms, as the one presented by Zhang et al. [
9], where the singularities of a system like the presented are analyzed and successfully avoided. The Quasi-Direct Drive is also an example of the technology applied to actuate an non-rigid joint, as presented in [
10] for a quadruped.
As it can be easily understood, all the mentioned research has a same primary step—the modeling phase—applied to mathematically translate the behavior of the system. Modeling the system is crucial to understand its behaviour under multiple conditions and also to develop its control. Having the model, one can put a signal in the process input and analyse how the system react, obtaining the system output. The system’s transfer function can be interpreted as the process model. Robotic systems often include DC motors and having a realistic model is crucial to improve the control performance. This is required to be able to design suitable controllers, test them in simulation and obtain relevant results. Thus, the closer to reality the developed model is, the better designed the controller can be in theory and applied in practice. However, all the robotic systems mentioned above include components that adds uncertainties and non-linearities to it, making it more complex to model.
Obtaining a realistic model of the system to be controlled is an advantage when defining and tuning the controller. In addition to being more informative to decide which kind of controller is more appropriate, obtaining the system response to various inputs can be done with increased realism. Obtaining a more realistic model allows to know, as close to reality as possible, how the system will behave after designing and tuning the controllers [
11]. It also allows to theoretically test, as an instance, the system limits, as well as combinations of controllers, or speed profiles. With such a model, the system’s performance also increases significantly. In order to be able to validate the developed approach, PID controllers [
12] will be used. These are relatively easy to implement and provide a realistic use case.
Estimation techniques can be applied to help modeling the system, applied to estimate the unknown or difficult to quantify parameters with precision. These techniques can be applied online or offline, as mentioned by Dupuis et al. [
13], but can, sometimes, result in an inaccurate estimation of the parameters.
Examples of online parameter identification are present in [
14,
15], from evolutionary algorithms, such as Montazeri et al. use in [
16] to recursive methods as Gonzalez et al. [
17] use for their third-order modeling. On offline methods, examples can be [
18,
19,
20]. Multiple techniques can be applied through the use of neural networks, as explained in [
21] or even experimentally, as the authors of [
22,
23] present.
Considering that online estimation methods are relatively more complex, as well as that the conditions associated with the motor presumably will not change when it is actuated and that the essential characteristics of the non-rigid joint developed for this work are not expected to suffer structural changes, the estimation of its dynamic parameters will be carried out with offline techniques, performed through real hardware tests. The assumptions made for the models are set by the authors of [
19].
The process of modeling the subsystems individually and the whole system, as well as controlling the final system will be presented. An introduction to the topic is performed in
Section 1, and the proposed models will be introduced throughout
Section 2.
Section 3 presents the experimental setup specially built to test the obtained models ans in
Section 4 will present the results obtained by the performed experiments. Finally, in
Section 5 are presented the conclusions and future work.
2. Proposed Models
Across this section, the model for the DC motor with worm gearbox will be presented. After that, the model for the non-rigid joint will be introduced. To estimate the parameters of the sub-systems, some experimental tests must be performed. For this, an experimental setup was created, being further presented in Figure 5.
2.1. DC Motor and Worm Gearbox Model
Along this subsection, the generic model for a DC motor will be presented, which is equivalent to the motor-gearbox system. Also, taking into account that some hardware tests must be performed to estimate some parameters, they will also be detailed. Despite what was mentioned in previous paragraph, all the tests were performed with the gearbox coupled to the motor, in order to obtain a reliable model of the motor+gearbox system.
Taking into account the above mentioned considerations, the motor model is further described using the equations associated with it. These are present all over the literature associated with DC motors, so no references will be presented to specific publications. Thus, the general model of a DC motor is as follows:
where
is the voltage applied to the system (V),
i is the electrical current (A),
R the resistance (
),
L the inductance (H), and
the Back Electromotive Force (V). This force is obtained through the second presented equation, where
k is the motor constant, and
the angular speed (rad/s). In Equation (3),
J represents the moment of inertia (kg
),
the motor torque (N·m), obtained by the fourth equation,
the viscous friction coefficient (N·m·s) and
(N·m) the static friction torque. The model used for the static friction
assumes that the
=
while
<
. This explains the existence of the motor dead zone, which is a non-linear element of the model. Despite this, it is neglected, since otherwise it will turn the system into a non-linear one, and as one can see from the first Figure presented in
Section 4, the dead zone is almost nonexistent.
In the Laplace domain, the system can be represented as:
The transfer function of the system will then be:
Adjusting some variables, to facilitate its later use in the estimation of some parameters, it becomes:
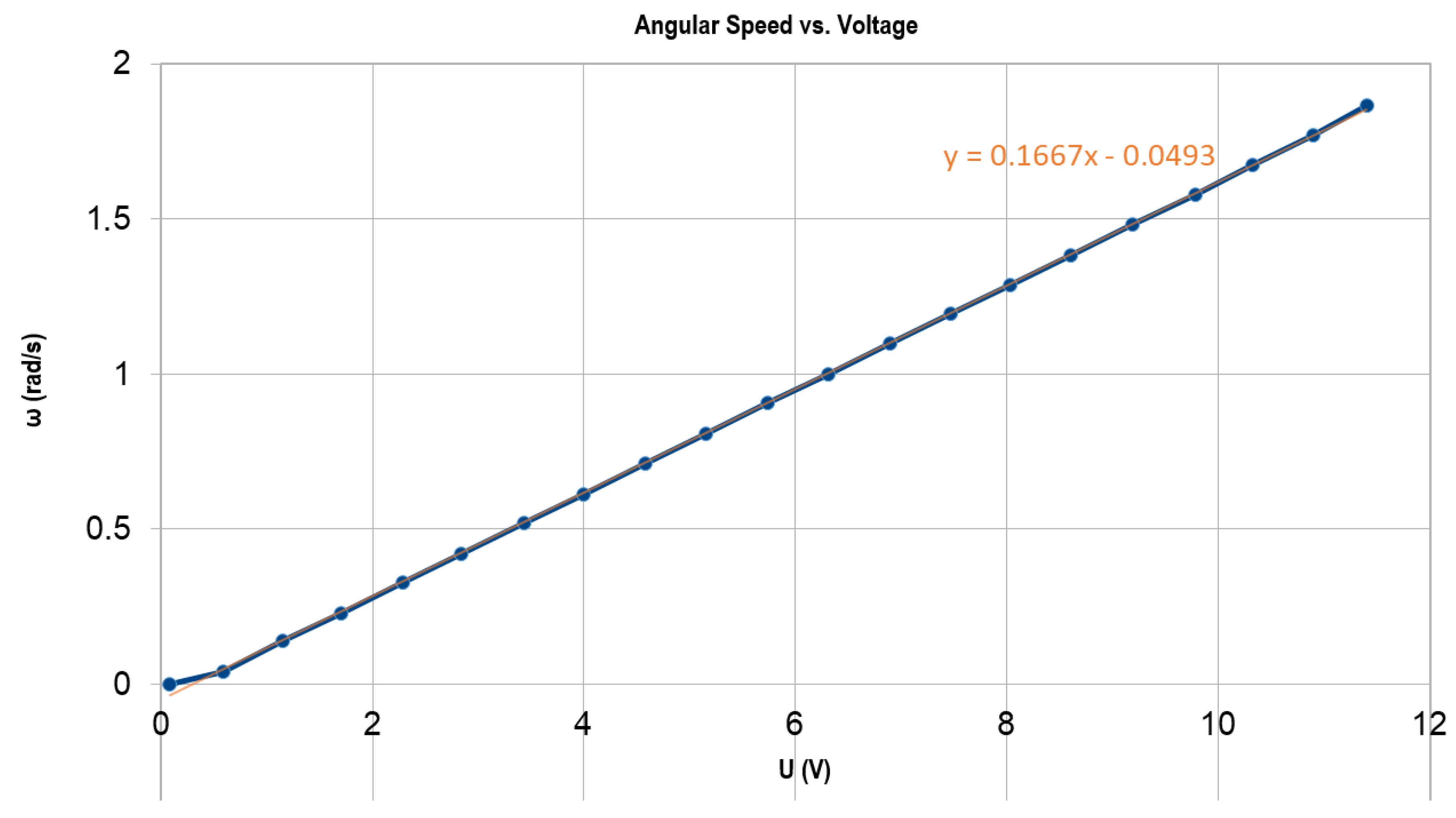
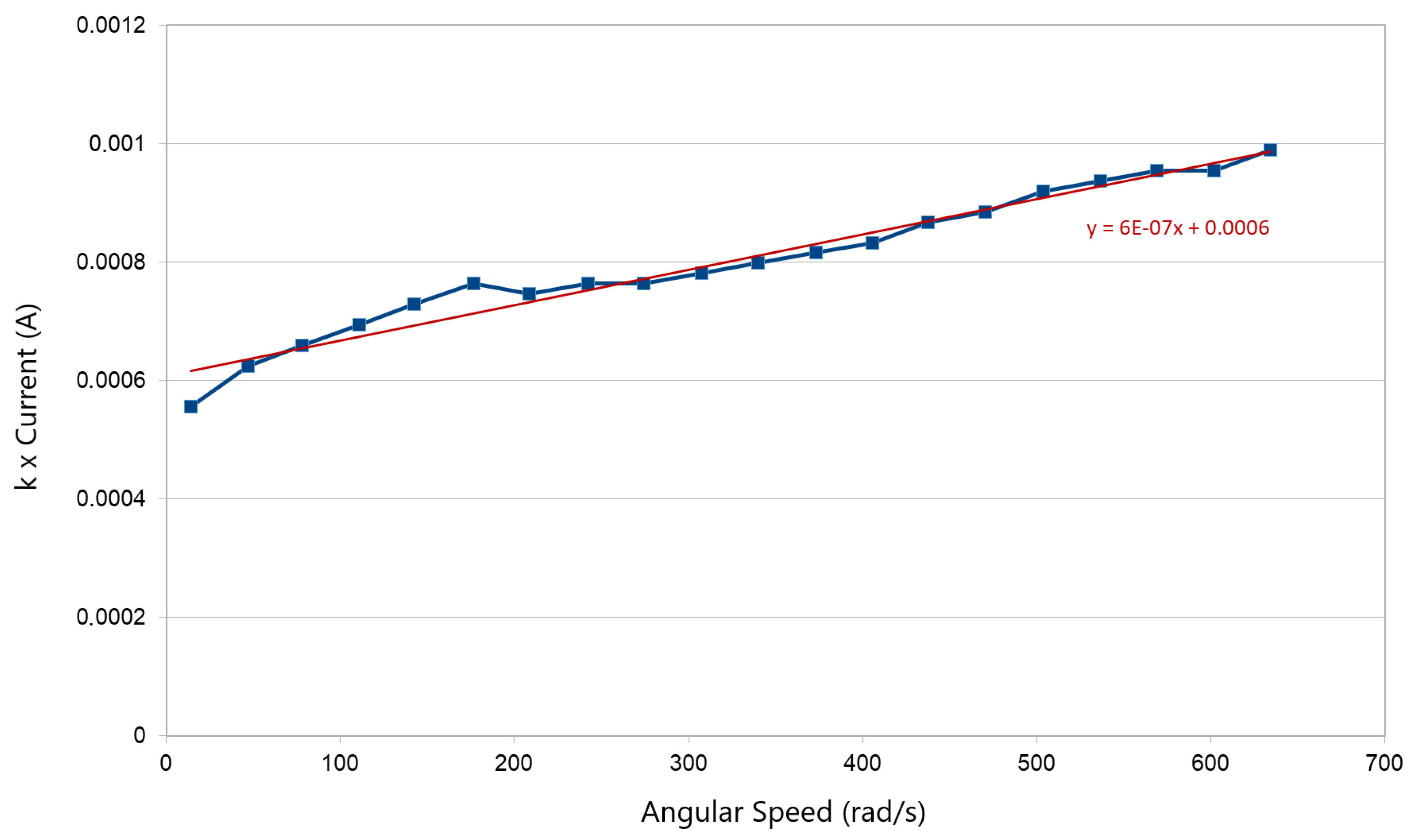
There are some hardware tests that allow to estimate some unknown motor constants, like and . These tests are simple to perform and consist on:
Powering the motor with multiple pre-known values of supply voltage, allowing it to reach the steady-state—This test consists in powering the motor with several different pre-known supply voltages and measure the angular speed at the steady-state throughout the process;
Input a voltage step to the motor terminals—This test consists in powering the motor with a voltage step and obtain its response to this signal, to verify which model suits the best to the tested model.
2.2. Non-Rigid Joint Model
For the non-rigid joint construction, a passive system was designed and developed. Applying 4 springs, attached to a circular support part as further represented in Figure 6, a rotational force is applied in the support’s centre of rotation, is passed to the next link through the springs, providing elasticity and cushioning to the rotational movement. To connect all the parts, as can be noticeable by the mentioned figure, bearings are applied to decrease the rotational friction, as well as to allow a tighter connection between all the parts.
The mathematical/physical representation of the system, with its respective constants, velocities and torques present in
Figure 1.
Given the proposed non-rigid joint, its model will become as follow:
Considering that the initial conditions can be not null, the following variables take values:
Similar to what was described in the above subsection, for modeling the non-rigid joint, as well as for estimating the parameters associated with it, some hardware tests will also be performed, in order to obtain parameters J, K and B, consisting of:
Pulling the link attached to the non-rigid joint to a certain angle - In this test, the link attached to the non-rigid joint is pulled manually for a certain set of increasing angles. For those angles the torque is measured. Then, the link is rotated in the same way to the negative side and the same procedure is applied;
Pulling the link attached to the non-rigid joint and releasing it, capture the angular speed an the angle until it stabilizes - Through this test, the link attached to the non-rigid joint is pulled manually and, after reaching a determined angle, is released and left to stabilize until it reaches the rest angle. The angular speed, the torque and the angle are sampled with a period of 10 ms;
2.3. Control
Taking into account its use for a robotic manipulator joint, it was then decided to use an motor with a worm gearbox, specifically the JGY-371 one. This motor has a rotary encoder, it is powered at 12VDC and it was defined that the motor speed would be 20 rpm, which is the best solution for the purpose defined for the project. With this choice, despite the low maximum angular speed of the motor, the joints can benefit from more torque. The issue of the sudden changes in speed can shorten the life of the motor.
Therefore, the decision of creating an acceleration ramp when the controller activate or deactivate was taken, having the system 3 sub profiles (acceleration, steady state, deceleration). Temporal divisions are called
and
, dividing areas A, B and C of the profiles. To achieve this, there were created functions for the angular acceleration, velocity and position of the motor shaft. To obtain a smoother velocity ramp, it was decided to go with a profile with cubic function. Having decided this, it was necessary to produce a quadratic function for the angular acceleration, which is described below
These acceleration
(
) functions were defined to obtain the desired velocity profile, as mentioned. In the presented equations the term
represent the maximum desired acceleration, while
and
are the time limits for each sub-area. These are more explicit when looking at
Figure 2.
The previous equations represent the intended angular velocity profile. The nomenclature used is also presented in the acceleration equations, with the exception of the
(
), which represents the angular velocity.
Finally, the equations for calculating the angular position of the motor shaft are presented above, with
representing the angle (rad). Since the velocity profile reaches the wanted
when
,
can be obtained through the equation
and the instant
can be calculated through the formula presented next
Based on all the mentioned equations, and to become clearer what, theoretically, must be the motor behaviour, the profiles for angular acceleration, velocity and position are presented in
Figure 2, in a graphical form.
Figure 3 represents the profiles, already after the mentioned functions were implemented in programming, having obtained the graphics that are presented.
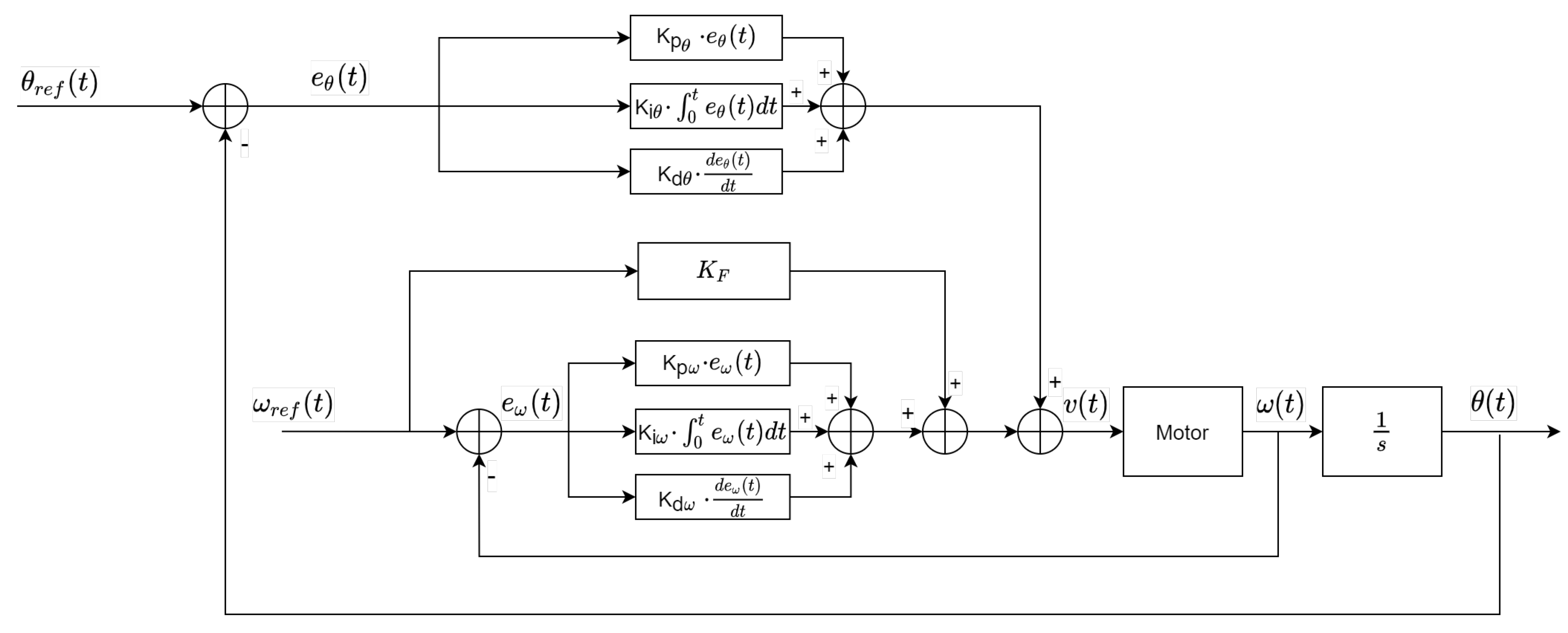
As already mentioned, the controllers to be used will be PID controllers. Thus, in order to validate the developed models, a cascade controller was designed, with the use of a position and a speed controller. It was chosen to only introduce a block of Feed Forward in the latter, and the set was represented in the block diagram in
Figure 4.
3. Experimental Setup Hardware
Throughout this section, the hardware used to create the experimental testbed is detailed. It is worth mentioning that, in order to understand the impact that the gearbox had on the obtained data, it was decoupled from the motor shaft, and the same tests were carried out. The conclusion is that the obtained data are practically the same, only affected by the correction factors related to speed and torque, due to the reduction of the gearbox.
Taking into account the decision of using a motor with a worm gearbox, it was decided to use an off-the-shelf solution, specifically the DC Motor with Permanent Magnets—JGY-371, which is a low cost popular actuator, being a 12 V motor with built-in encoders, attached to a 340:1 reduction worm gearbox. This reduction factor was chosen so that the motor speed would be 20 rpm. With this choice, despite the low maximum angular speed of the motor, the joints can benefit from more torque. In addition to the fact that the incorporated encoder can be applied to collect data in the modeling process, it will also be extremely useful during the motor movement, making it possible to control in closed-loop with access to speed information in real time.
From the motor model point of view, these experiments allow to collect some important variables such as motor speed, motor withdraw current, and applied motor voltage. For the acquisition of the mentioned variables, there were used the following sensors, being the referred acquisition system shown in the right side of
Figure 5:
Built-in encoder—measuring the angular displacement of the motor;
Current sensor—measuring the current that the motor withdraws;
Voltage sensor—measuring the instant and real voltage applied to the motor terminals;
As mentioned, a passive non-rigid joint system was designed and developed, making it possible to test the model and apply the desired controllers. This system is presented in
Figure 6.
For this joint tests, there is the need to know its angular position, as well as the applied torque. So, to obtain the exact angular displacement, an absolute encoder, consisting in a contactless absolute angular position sensor, with 14-bit resolution and immune to external magnetic stray fields, was placed exactly concentrically with the axis of rotation of the joint. Also, to obtain the torque, a straight bar load cell, capable of measuring forces up to 10 kg, was placed in the center of the link to evaluate the exerted force which can, using the distance to the rotational axis, be converted to the applied torque. The left side of
Figure 5 presents the implemented solution, and the interaction between the subsystems. The whole system was powered by a 12VDC power supply to perform the tests. How these values are applied in practice will be detailed in
Section 4.
5. Conclusions and Future Work
Considering the experimental part of the work, the physical implementation of the idealized and modeled prototype of a novel non-rigid joint have met the expectations, adding a damping component to the joint. The addition of the 4 springs allowed the joint to have an non-rigid behavior with only passive components, and consequently without energy consumption. Also, the coupling of a worm gearbox motor to the joint allows to save some energy, since it only consumes when the motor moves, blocking when it is stopped.
Then, it can be concluded that, based on a purely low-cost sensor acquisition system, it is possible to carry out tests and consider measurements that allow to estimate parameters of this complex model. The monitored variables were the force exerted on the link, the angular displacement and the angular position. The angular speed of the motor, as well as its current consumption, and the supply voltage are also variables required to estimate the system parameter.
Regarding the joint, the tests allowed to obtain approximate physical model parameters, like the damping constant and moment of inertia. Comparing the obtained data and the simulated second-order model, it is easily verified that the considered model is suitable. However, differences are effectively noticed, which come from the joint’s dead zone.
For the DC motor subsystem, based on the obtained data, it was possible to obtain a set of measures that allowed, using equations from the physical model of the DC motor, to estimate simpler parameters related to the system, namely its resistance and constant. Then, two models, first and second order, were considered. Using previously obtained data and optimizing to minimize the estimated angular velocity error, it was possible to verify that the second-order model is the one that best reflects the physical behavior of the motor and to model its impedance and moment of inertia parameters.
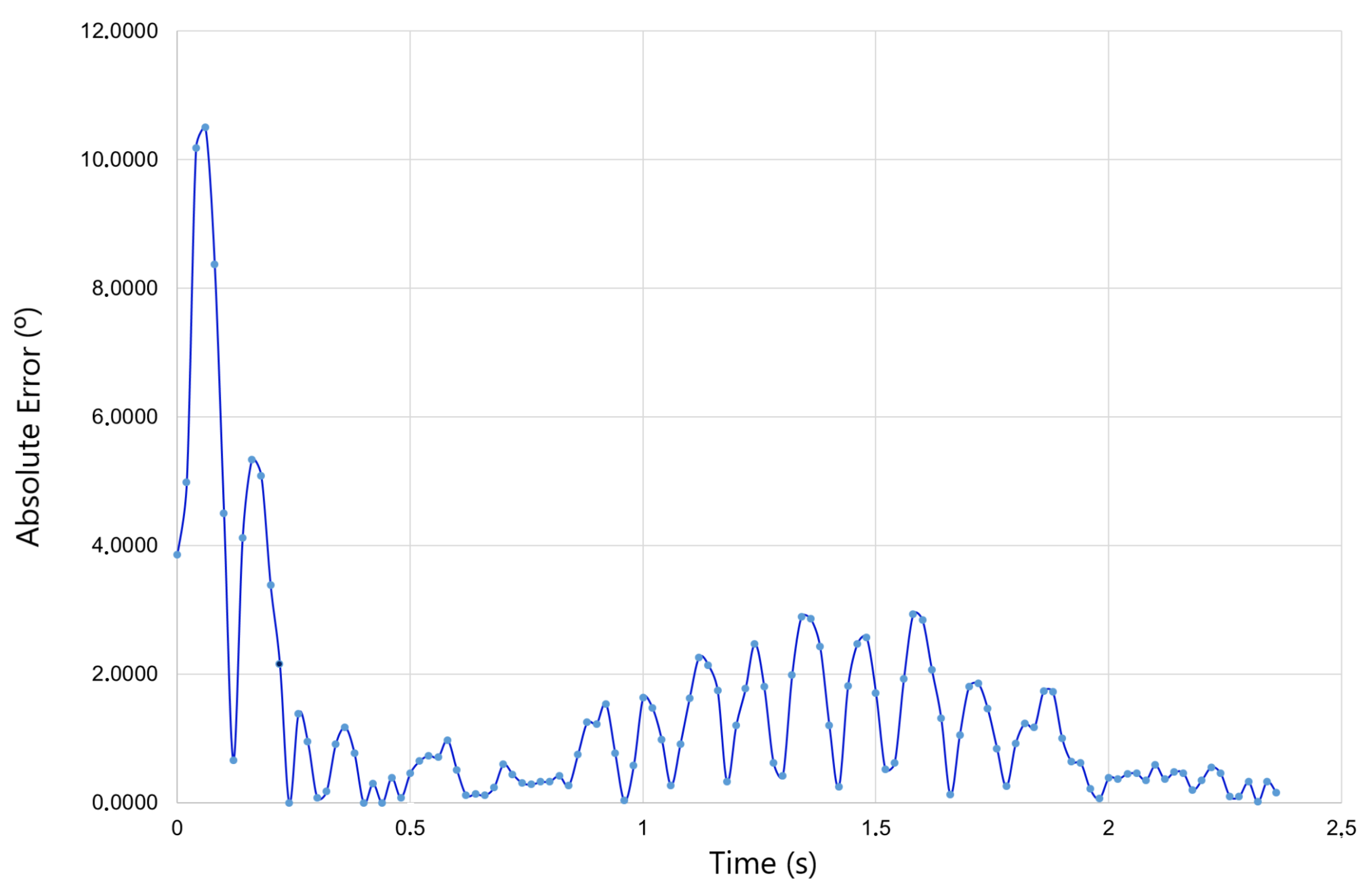
Finally, regarding the developed controller, the obtained experimental results show clearly that it was a good choice, since it can work with the specificities of both the worm gearbox and the non-rigid joint, obtaining minimum overshoot, low settle time and accurate angular positioning.
In terms of future work, it will be interesting to use the developed setup to one of the mentioned applications and evaluate its behaviour. it will also been carried out a study about the behaviour of the system under disturbances. The first one will probably be to use the developed work as a 4DOF manipulator with non-rigid joints, for industrial purposes.