Financial Optimization of a Solar-Driven Organic Rankine Cycle
Abstract
1. Introduction
2. Material and Methods
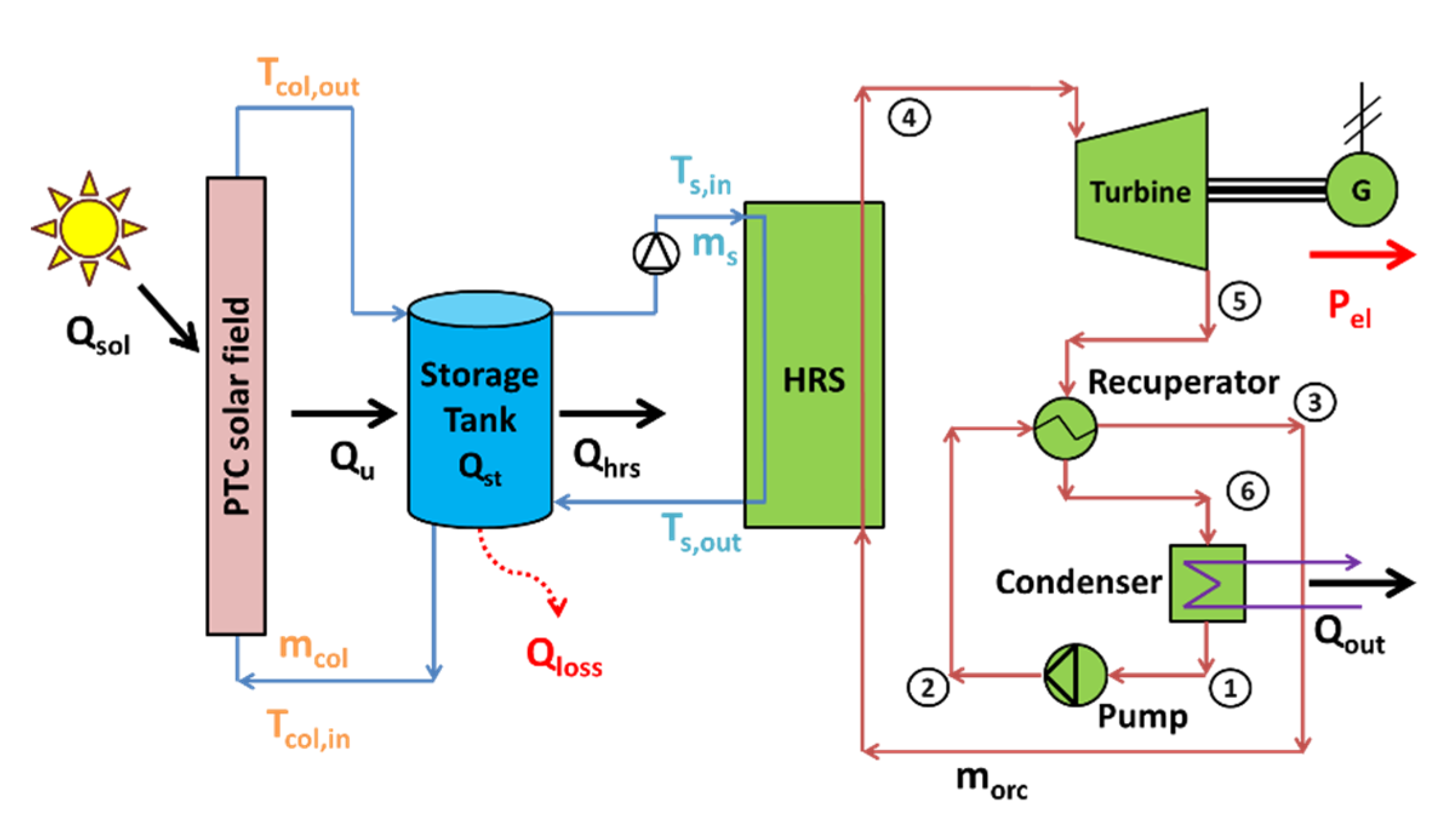
2.1. The Examined System
2.1.1. Solar Field Modeling
2.1.2. Organic Rankine Cycle Modeling
2.1.3. Financial Analysis Formulation
2.2. Procedure Description
3. Results and Discussion
3.1. Parametric Analysis
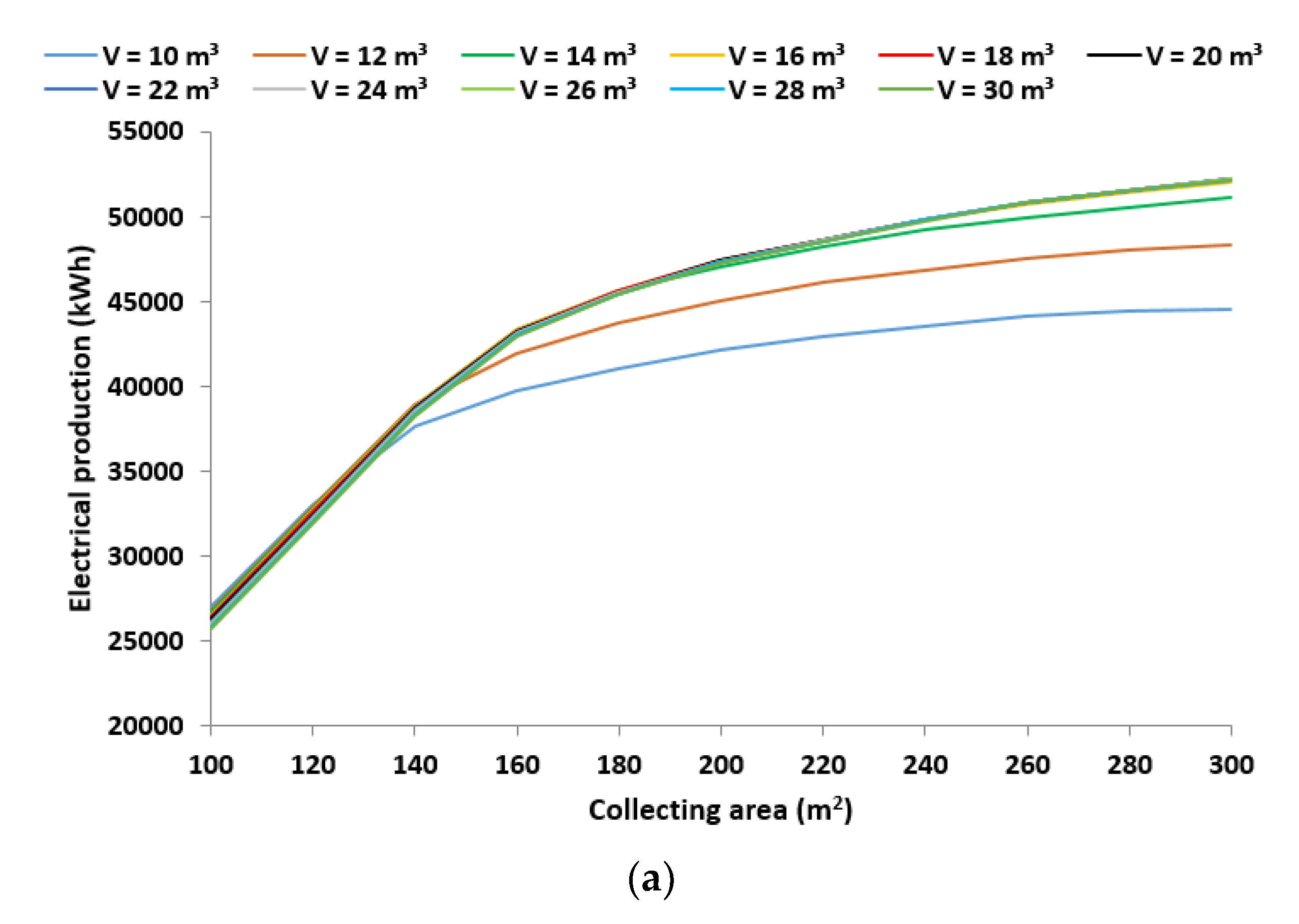
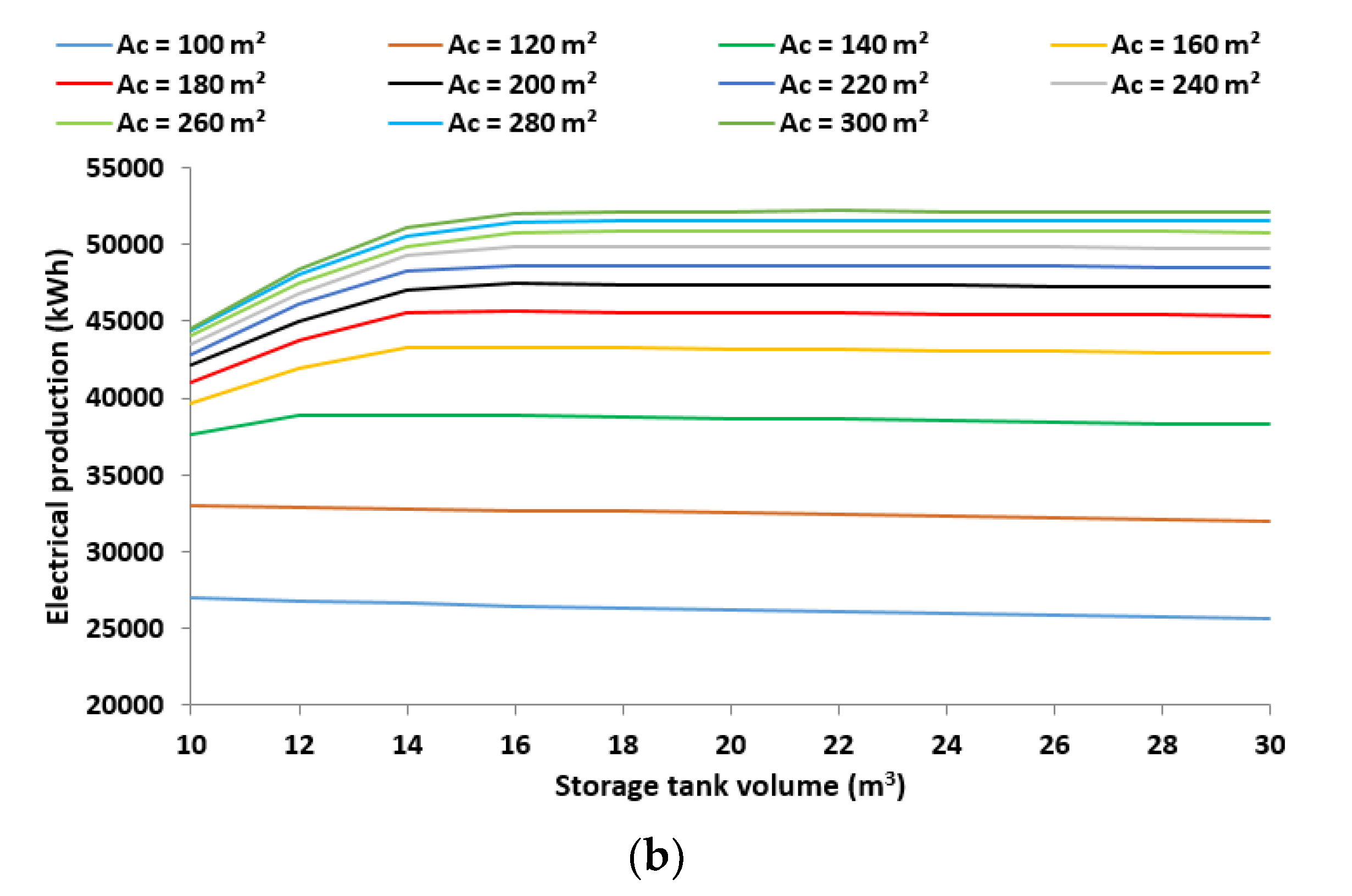
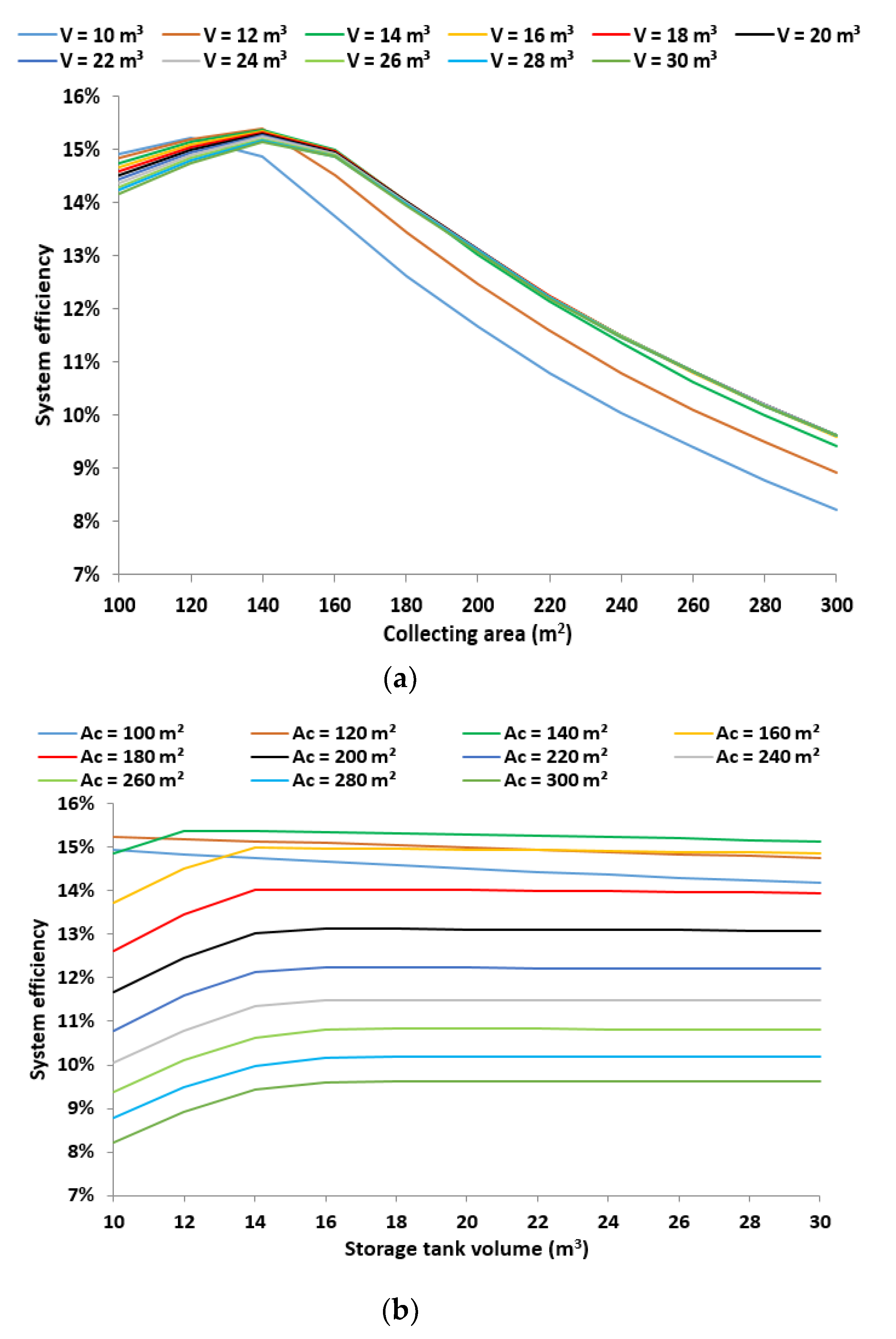
3.1.1. Energy Analysis
3.1.2. Financial Analysis
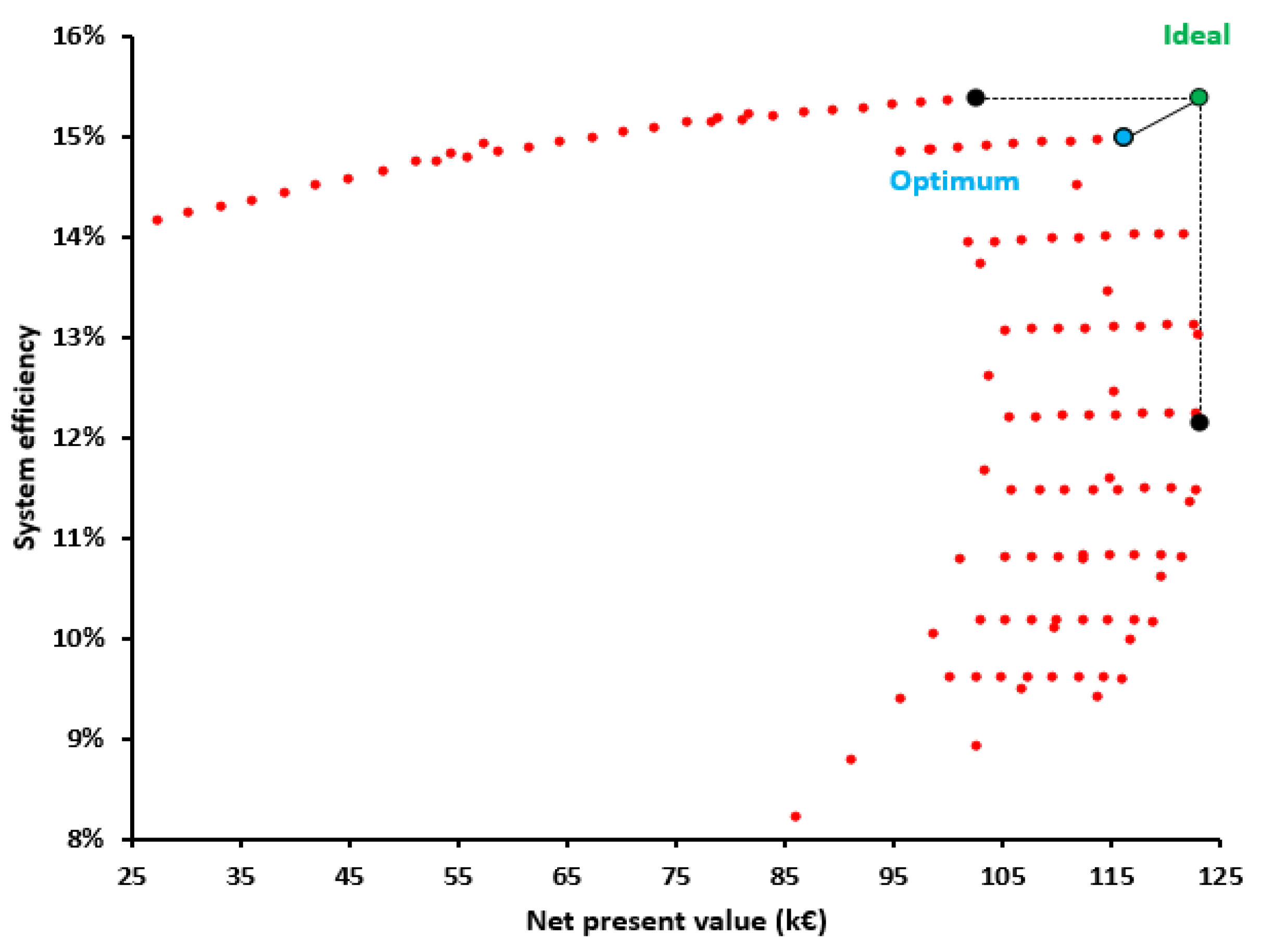
3.2. Optimization Results
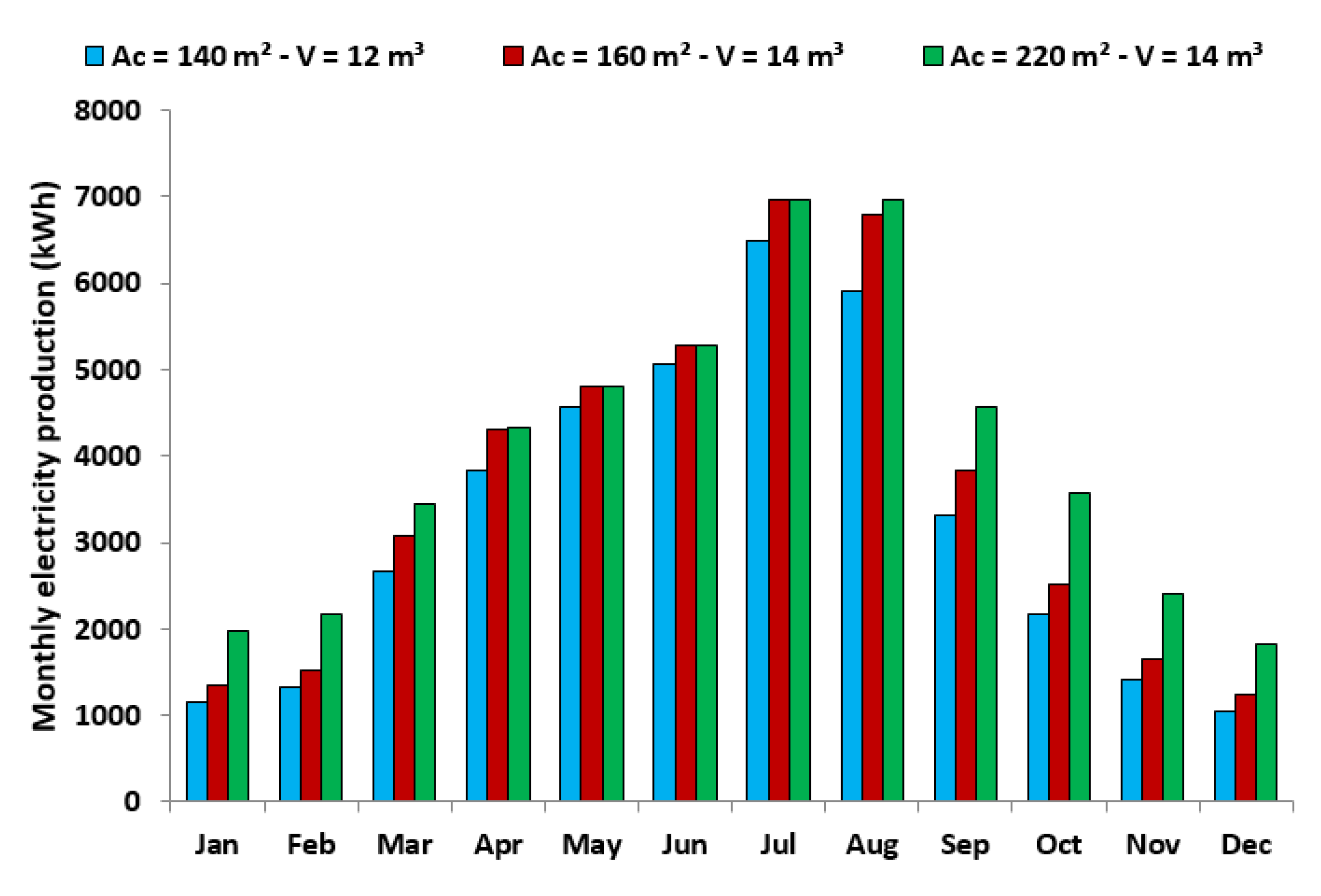
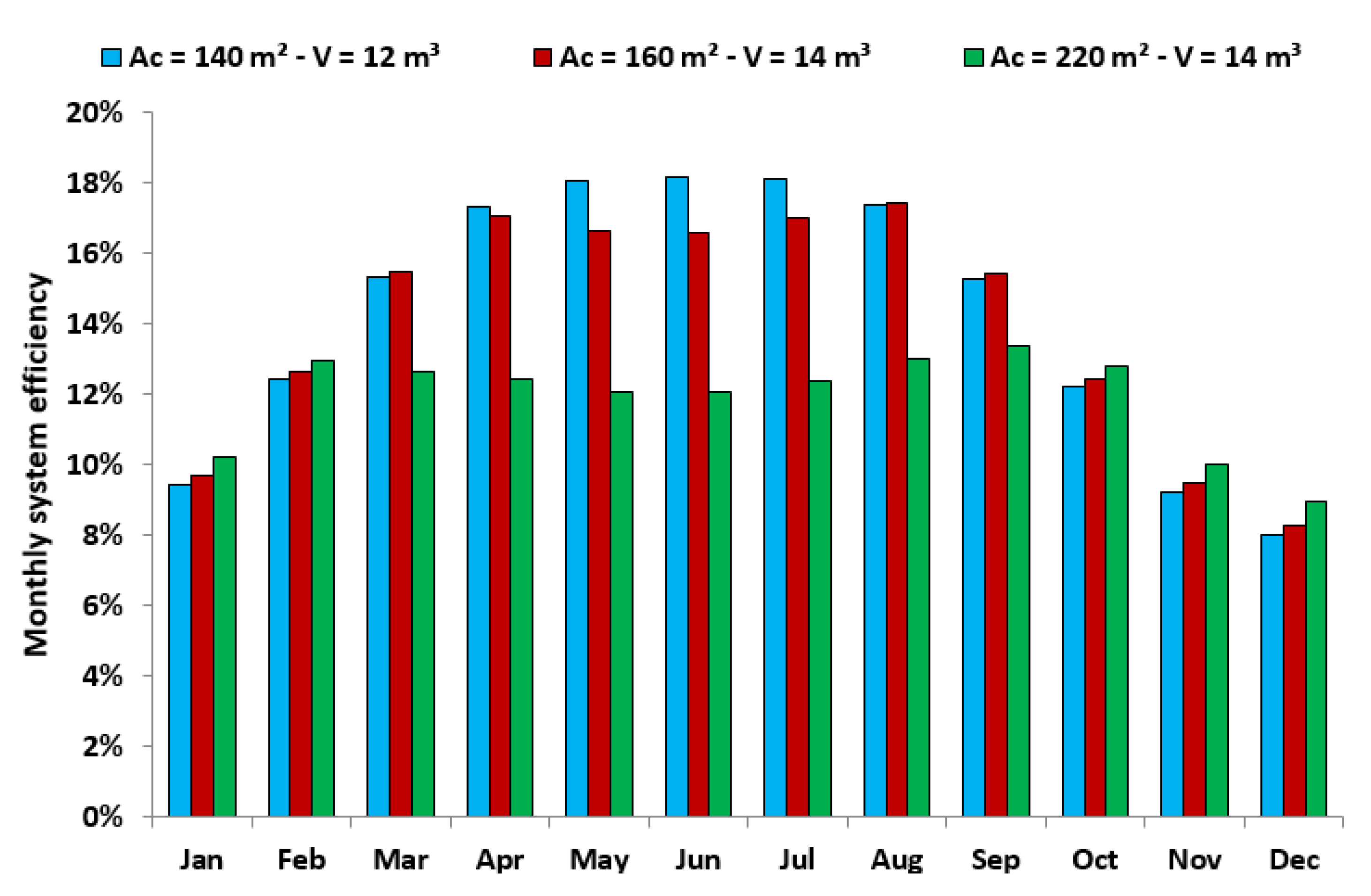
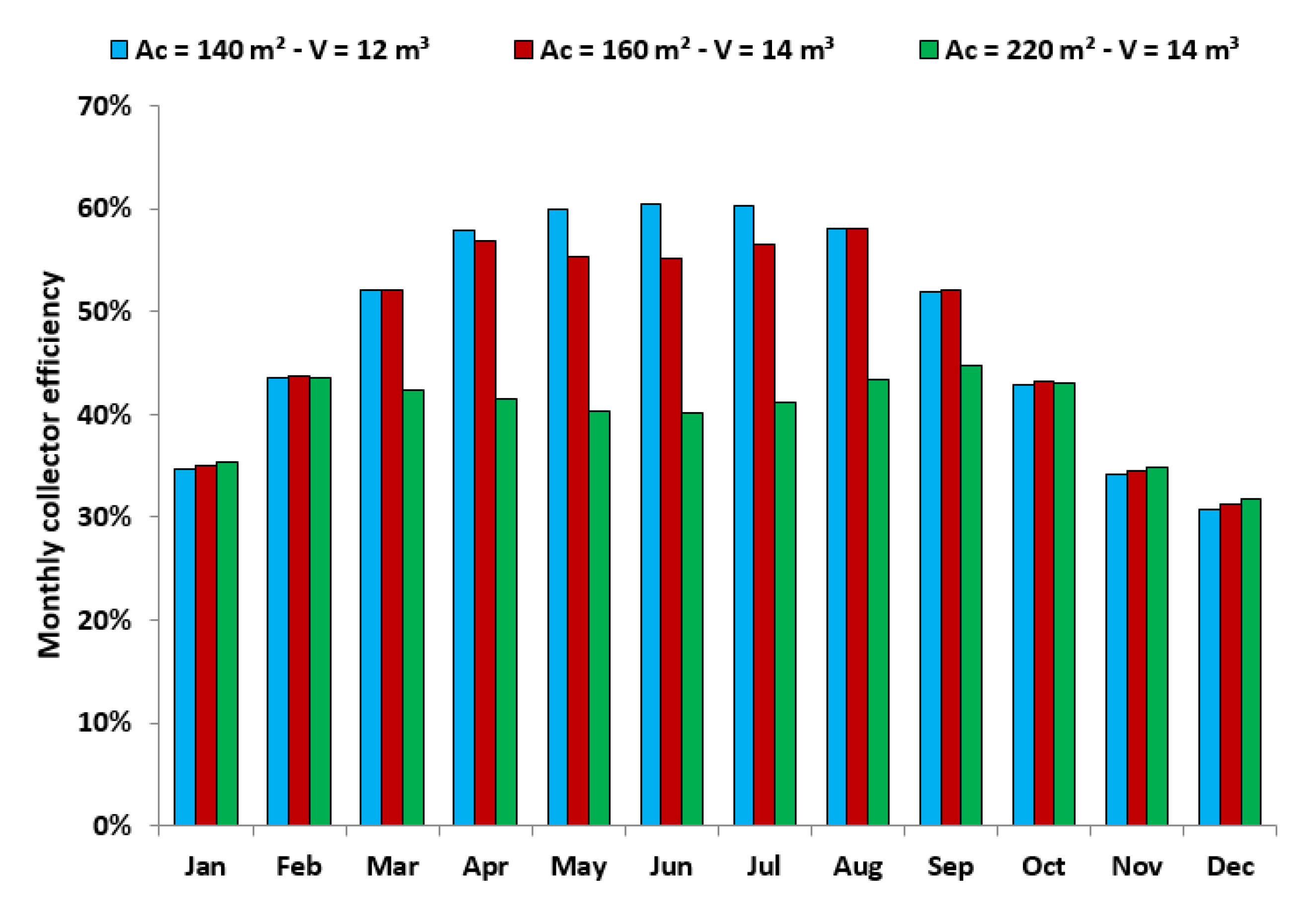
3.3. Monthly Analysis
4. Conclusions
- The maximum system energy efficiency is found at 15.38%, and, in this case, the collecting area is 140 m2 and the storage tank volume is 12 m3.
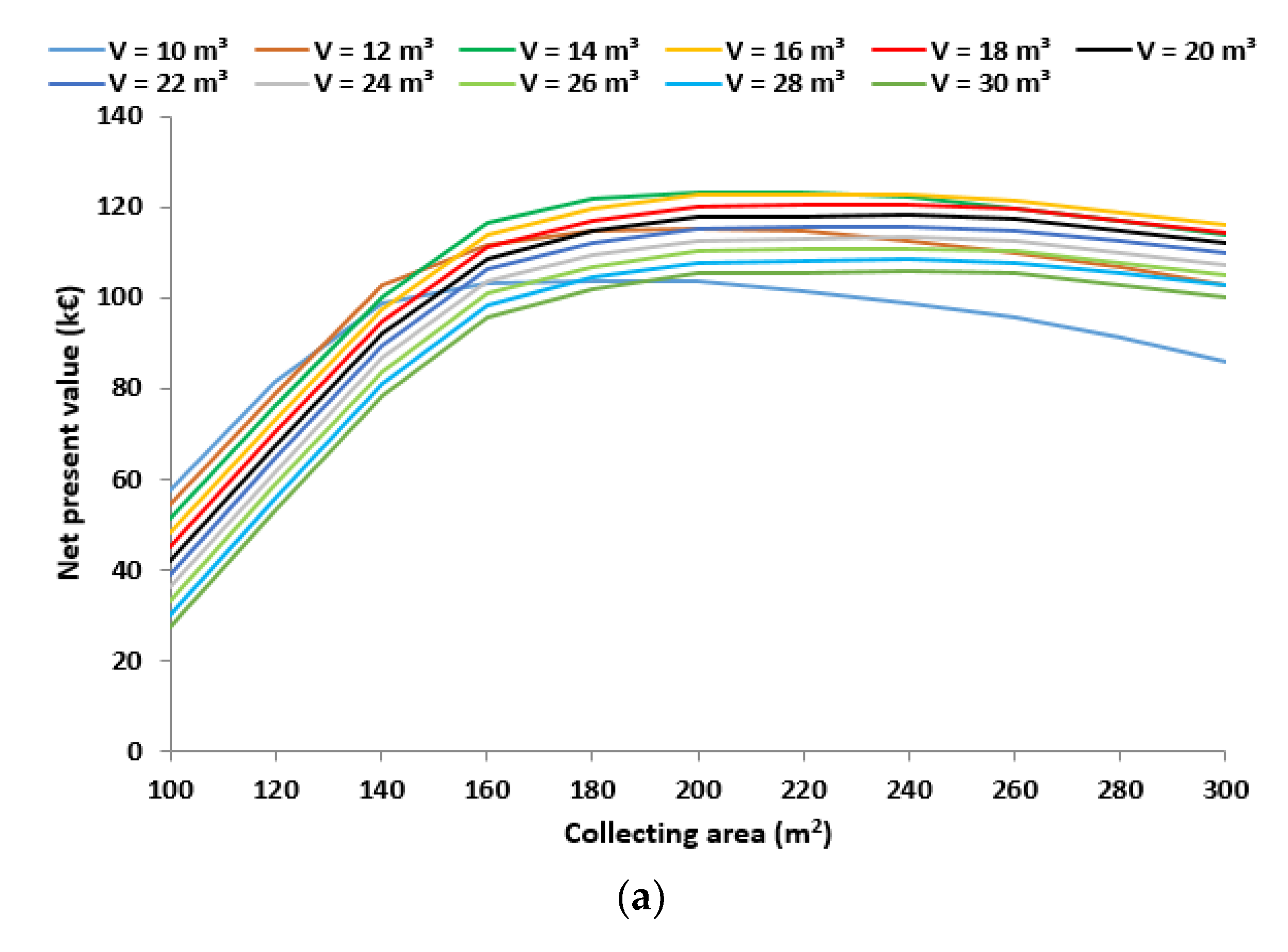
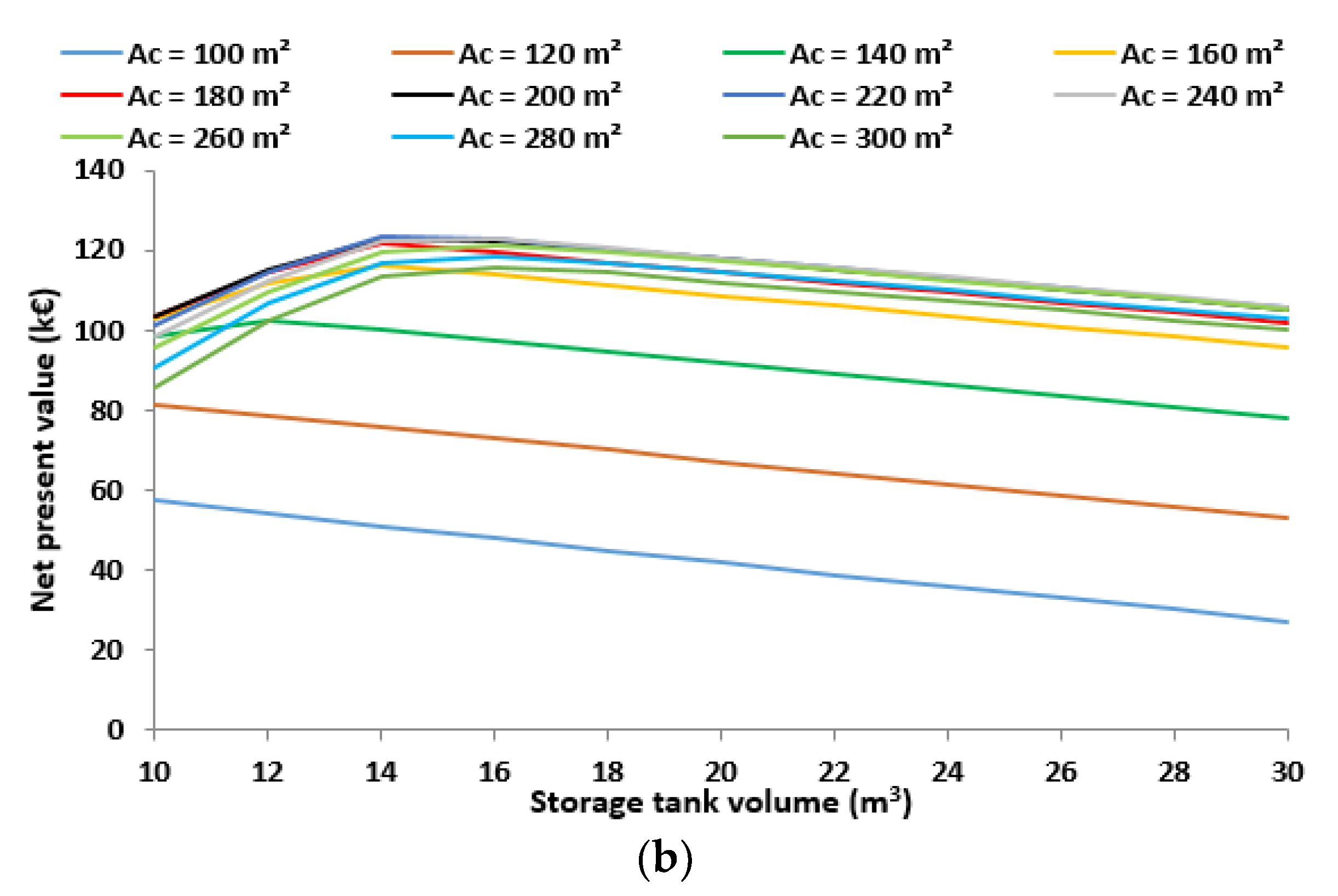
- The maximum net present value is 123 k€ and is found for a 220-m2 collecting area and a 14-m3 storage tank volume.
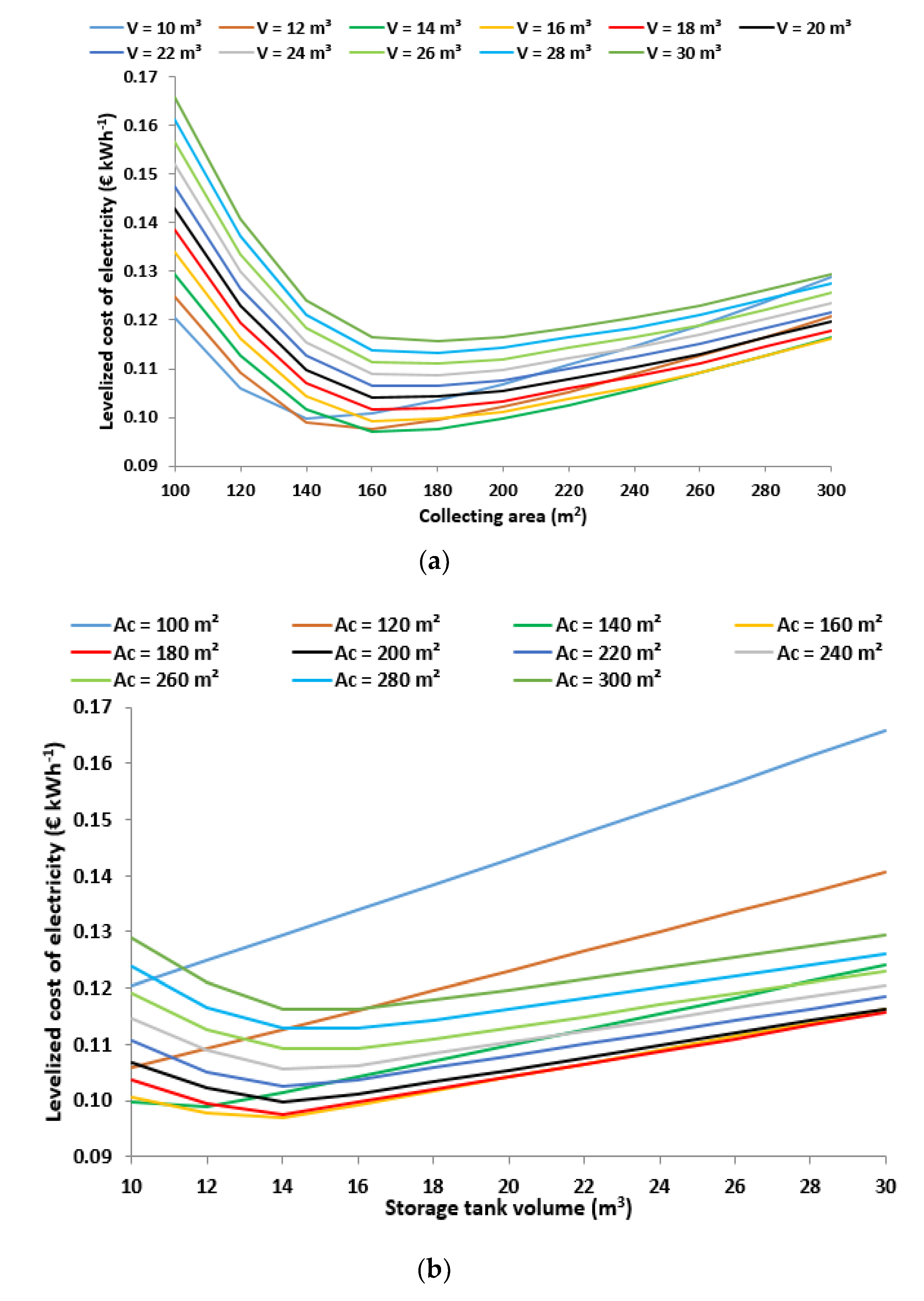
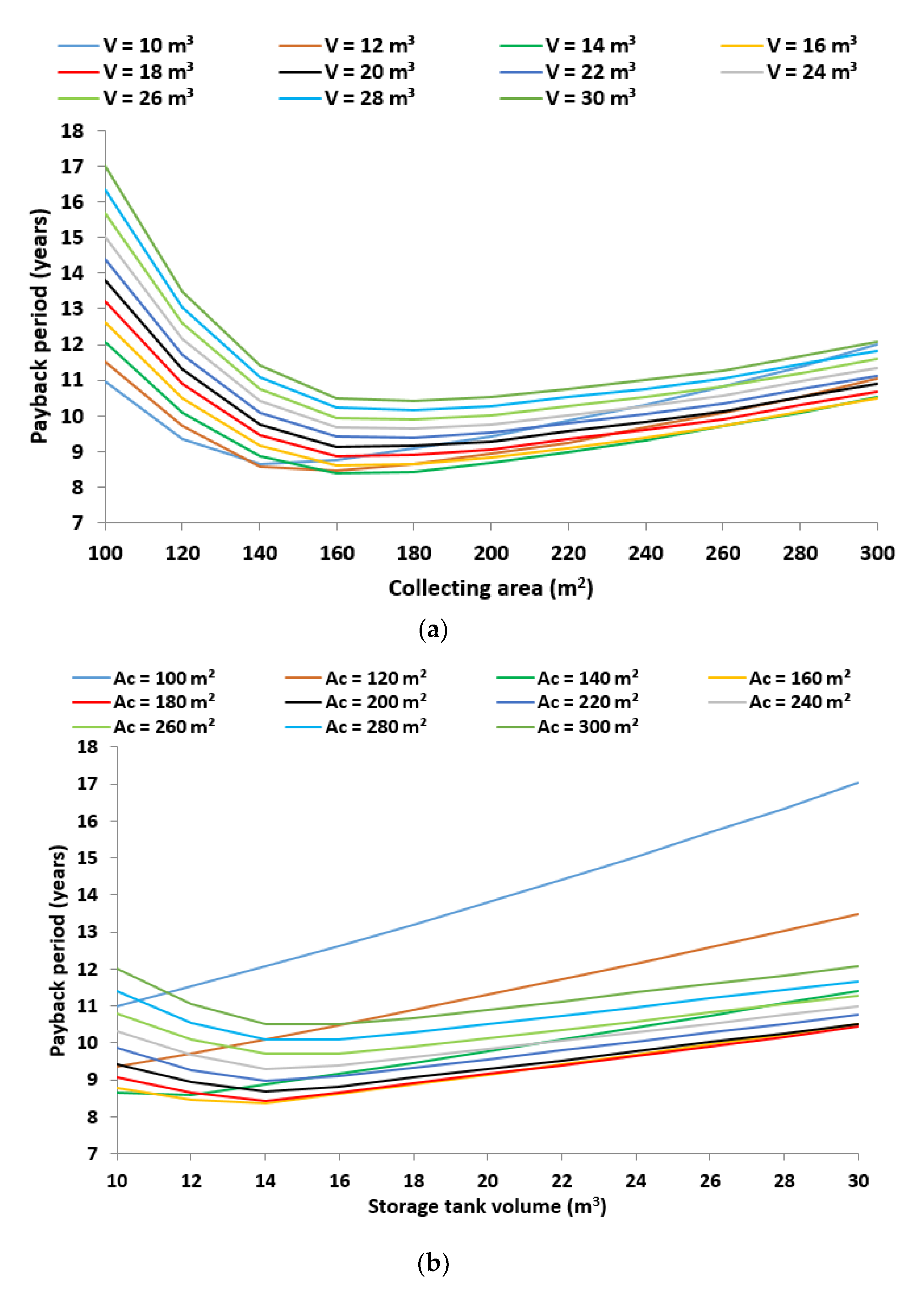
- The minimum payback period is 8.37 years and is found for a 160-m2 collecting area and a 14-m3 storage tank, while, for the same design point, the levelized cost of electricity is minimized at 0.0969 € kWh−1.
- The multi-objective optimization procedure proved that the optimum design is for a 160-m2 collecting area and a 14-m3 storage tank. Moreover, this design point is the optimum according to the payback period minimization and LCOR minimization criteria. Thus, this design is selected as the overall optimum choice.
- The monthly analysis indicates that higher electricity is produced during the summer and especially in July and in August. Moreover, the use of higher collecting areas leads to significant enhancement in electricity production, mainly in the winter period.
Author Contributions
Funding
Acknowledgments

Conflicts of Interest
Nomenclature
| Ac | Collecting area, m2 |
| AT | Storage tank outer area, m3 |
| cp | Specific heat capacity, kJ kg−1 K−1 |
| C0 | Capital cost, € |
| CF | Hourly cash flow, € h−1 |
| E | Yearly energy quantity, kWh |
| F | Objective function of dimensionless distance, - |
| Gb | Solar direct beam irradiation, W·m−2 |
| i | Counter, - |
| h | Specific enthalpy, kJ kg−1 |
| K | Incident angle modifier, - |
| Kcol | Specific collector cost, € m−2 |
| Kel | Electricity cost, € kWhel−1 |
| Korc | Specific cost of the organic Rankine cycle, € kWel−1 |
| KO&M | Yearly operating and maintenance cost, € |
| Ktank | Specific cost of the storage tank, € m−3 |
| LCOE | Levelized cost of electricity, € kWel−1 |
| m | Mass flow rate, kg s−1 |
| N | Project life, years |
| NPV | Net present value, k€ |
| P | Pressure, bar |
| Pel | Net electricity production, kW |
| PPhrs | Pinch Point, °C |
| PP | Payback Period, years |
| Q | Heat rate, kW |
| Qout | Heat rejection to the ambient, kW |
| r | Discount factor, % |
| R | Equivalent investment time, years |
| SD | Sunny days, days |
| SPP | Simple Payback Period, years |
| t | Time, hours |
| T | Temperature, °C |
| Tam | Ambient temperature, °C |
| UT | Thermal loss coefficient of the tank, W m−2·K−1 |
| V | Storage tank volume, m3 |
| Wp | Pumping work, kW |
| WT | Turbine work production, kW |
Greek Symbols
| ΔP | Pressure difference, bar |
| ΔΤsh | Superheating degree in the turbine inlet, °C |
| ΔTrc | Temperature difference in the recuperator, °C |
| ηen | Instantaneous energy efficiency, - |
| ηen-y | Yearly energy efficiency, - |
| ηis,T | Isentropic efficiency of the turbine, - |
| ηg | Generator efficiency, - |
| ηm | Mechanical efficiency, - |
| ηmotor | Motor efficiency, - |
| ηorc | Efficiency of the power block, - |
| ηth,col | Collector thermal efficiency, - |
| θ | Incident solar angle on the collector aperture, ° |
| ρ | Density, kg m−3 |
Subscripts and Superscripts
| col | Collector |
| col,in | Collector inlet |
| col,out | Collector outlet |
| con | Condenser |
| is | Isentropic |
| in | Inlet |
| hrs | Heat recovery system |
| loss | Thermal losses in the tank |
| max | Maximum |
| min | Minimum |
| opt | Optimum |
| orc | Fluid in the organic Rankine cycle |
| out | Outlet |
| s | Heat source |
| s,in | Heat source inlet |
| s,out | Heat source outlet |
| sat | Saturation in the heat recovery system |
| sol | Solar |
| st | Storage tank |
| T | Turbine |
| u | Useful |
Abbreviations
| CSP | Concentrating Solar Power |
| EES | Engineering Equation Solver |
| HRS | Heat Recovery System |
| ORC | Organic Rankine Cycle |
| PTC | Parabolic Trough Collector |
References
- Wang, F.; Cheng, Z.; Tan, J.; Yuan, Y.; Yong, S.; Liu, L. Progress in concentrated solar power technology with parabolic trough collector system: A comprehensive review. Renew. Sustain. Energy Rev. 2017, 79, 1314–1328. [Google Scholar]
- Mehmood, A.; Waqas, A.; Said, Z.; Rahman, S.M.A.; Akram, M. Performance evaluation of solar water heating system with heat pipe evacuated tubes provided with natural gas backup. Energy Rep. 2019, 5, 1432–1444. [Google Scholar] [CrossRef]
- Kasaeian, A.; Bellos, E.; Shamaeizadeh, A.; Tzivanidis, C. Solar-driven polygeneration systems: Recent progress and outlook. Appl. Energy 2020, 264, 114764. [Google Scholar] [CrossRef]
- Islam, M.T.; Huda, N.; Abdullah, A.B.; Saidur, R. A comprehensive review of state-of-the-art concentrating solar power (CSP) technologies: Current status and research trends. Renew. Sustain. Energy Rev. 2018, 91, 87–1018. [Google Scholar] [CrossRef]
- Pelay, U.; Luo, L.; Fan, Y.; Stitou, D.; Rood, M. Thermal energy storage systems for concentrated solar power plants. Renew. Sustain. Energy Rev. 2017, 79, 82–100. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C. Alternative designs of parabolic trough solar collectors. Prog. Energy Combust. Sci. 2019, 71, 81–117. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, G.; Li, L.; Yang, Q.; Tang, B.; Liu, Y. Expansion devices for organic Rankine cycle (ORC) using in low temperature heat recovery: A review. Energy Convers. Manag. 2019, 199, 111944. [Google Scholar] [CrossRef]
- Arabkoohsar, A. Combined steam based high-temperature heat and power storage with an Organic Rankine Cycle, an efficient mechanical electricity storage technology. J. Clean. Prod. 2020, 247, 119098. [Google Scholar] [CrossRef]
- Quoilin, S.; Orosz, M.; Hemond, H.; Lemort, V. Performance and design optimization of a low-cost solar organic Rankine cycle for remote power generation. Sol. Energy 2011, 85, 955–966. [Google Scholar] [CrossRef]
- Astolfi, M.; Xodo, L.; Romano, M.C.; Macchi, E. Technical and economical analysis of a solar–geothermal hybrid plant based on an Organic Rankine Cycle. Geothermics 2011, 40, 58–68. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C. Investigation of a hybrid ORC driven by waste heat and solar energy. Energy Convers. Manag. 2018, 156, 427–439. [Google Scholar] [CrossRef]
- He, Y.-L.; Mei, D.-H.; Tao, W.-Q.; Yang, W.-W.; Liu, H.-L. Simulation of the parabolic trough solar energy generation system with Organic Rankine Cycle. Appl. Energy 2012, 97, 630–641. [Google Scholar] [CrossRef]
- Desai, N.B.; Bandyopadhyay, S. Thermo-economic analysis and selection of working fluid for solar organic Rankine cycle. Appl. Therm. Eng. 2016, 95, 471–481. [Google Scholar] [CrossRef]
- Tzivanidis, C.; Bellos, E.; Antonopoulos, K.A. Energetic and financial investigation of a stand-alone solar-thermal Organic Rankine Cycle power plant. Energy Convers. Manag. 2016, 126, 421–433. [Google Scholar] [CrossRef]
- Askari-Asli Ardeh, E.; Loni, R.; Najafi, G.; Ghobadian, B.; Bellos, E.; Wen, D. Exergy and economic assessments of solar organic Rankine cycle system with linear V-Shape cavity. Energy Convers. Manag. 2019, 199, 111997. [Google Scholar] [CrossRef]
- Chacartegui, R.; Vigna, L.; Becerra, J.A.; Verda, V. Analysis of two heat storage integrations for an Organic Rankine Cycle Parabolic trough solar power plant. Energy Convers. Manag. 2016, 125, 353367. [Google Scholar] [CrossRef]
- Casati, E.; Galli, A.; Colonna, P. Thermal energy storage for solar-powered organic Rankine cycle engines. Sol. Energy 2013, 96, 205–219. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C. Parametric analysis and optimization of an Organic Rankine Cycle with nanofluid based solar parabolic trough collectors. Renew. Energy 2017, 114, 1376–1393. [Google Scholar] [CrossRef]
- F-Chart Software, Engineering Equation Solver (EES). 2015. Available online: http://www.fchart.com/ees (accessed on 12 January 2020).
- Therminol VP-1. Available online: http://twt.mpei.ac.ru/tthb/hedh/htf-vp1.pdf (accessed on 12 January 2020).
- Bellos, E.; Tzivanidis, C.; Belessiotis, V. Daily performance of parabolic trough solar collectors. Sol. Energy 2017, 158, 663–678. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes, 3rd ed.; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Bellos, E.; Tzivanidis, C. Parametric analysis and optimization of a solar driven trigeneration system based on ORC and absorption heat pump. J. Clean. Prod. 2017, 161, 493–509. [Google Scholar] [CrossRef]
- EuroTrough: Development of a Low Cost European Parabolic Trough Collector—EuroTrough; Final Report, Research funded in part by The European Commission in the framework of the Non-Nuclear Energy Programme JOULE III. Contract JOR3-CT98-0231; European Commission: Brussels, Belgium, 2001.
- Geyer, M.; Lüpfert, E.; Osuna, R.; Esteban, A.; Schiel, W.; Schweitzer, A.; Zarza, E.; Nava, P.; Langenkamp, J.; Mandelberg, E. EUROTROUGH—Parabolic Trough Collector Developed for Cost Efficient Solar Power Generation. In Proceedings of the 11th SolarPACES International Symposium on Concentrated Solar Power and Chemical Energy Technologies, Zurich, Switzerland, 4–6 September 2002. [Google Scholar]
- Montes, M.J.; Abánades, A.; Martínez-Val, J.M.; Valdés, M. Solar multiple optimization for a solar-only thermal power plant, using oil as heat transfer fluid in the parabolic trough collectors. Sol. Energy 2009, 83, 2165–2176. [Google Scholar] [CrossRef]
- Mata-Torres, C.; Escobar, R.A.; Cardemil, J.M.; Simsek, Y.; Matute, J.A. Solar polygeneration for electricity production and desalination: Case studies in Venezuela and northern Chile. Renew. Energy 2017, 101, 387–398. [Google Scholar] [CrossRef]
- Bellos, E.; Tzivanidis, C.; Torosian, K. Energetic, exergetic and financial evaluation of a solar driven trigeneration system. Therm. Sci. Eng. Prog. 2018, 7, 99–106. [Google Scholar] [CrossRef]
- World Weather Data Online. Available online: https://www.worldweatheronline.com/v2/weather-averages.aspx?locid=2862396&root_id=882367&wc=local_weather&map=~/athens-weather-averages/attica/gr.aspx (accessed on 12 January 2020).
- Available online: https://www.meteoblue.com/en/weather/historyclimate/climatemodelled/athens_greece_264371 (accessed on 12 January 2020).
- Available online: https://www.holiday-weather.com/athens/averages/ (accessed on 12 January 2020).
- Available online: http://www.lagie.gr/systima-eggyimenon-timon/ape-sithya/adeiodotiki-diadikasia-kodikopoiisi-nomothesias-ape/periechomena/times-energeias-apo-ape-sithya-plin-fb/ (accessed on 12 January 2020).
- Bellos, E.; Tzivanidis, C. Multi-objective optimization of a solar driven trigeneration system. Energy 2018, 149, 47–62. [Google Scholar] [CrossRef]

| Parameters | Symbols | Values |
|---|---|---|
| Electricity cost | (Kel) | 0.28485 € kWhel−1 |
| PTC specific cost | (Kcol) | 250 € m−2 |
| Tank specific cost | (Ktank) | 1000 € m−3 |
| ORC specific cost | (Korc) | 3000 € kWel−1 |
| Project life | (N) | 25 years |
| Discount factor | (r) | 3% |
| Equivalent project years | (R) | 17.41 |
| Operation and maintenance cost | (KO&M) | 1% of the capital cost |
| Parameters | Symbols | Values |
|---|---|---|
| Nominal power production | (Pel) | 10 kW |
| Pressure level in the turbine inlet | (P4) | 37.14 bar |
| Pressure level in the turbine outlet | (P3) | 0.079 bar |
| Superheating in the turbine inlet | (ΔTsh) | 20 °C |
| Condenser temperature level | (Tcon) | 40 °C |
| Saturation temperature in the HRS | (Tsat) | 309.7 °C |
| Motor efficiency | (ηmotor) | 80% |
| Turbine isentropic efficiency | (ηis,T) | 85% |
| Electrical generator efficiency | (ηg) | 98% |
| Mechanical efficiency | (ηm) | 99% |
| Recuperator temperature difference | (ΔTrec) | 10 °C |
| Pinch point in the HRS | (PPhrs) | 5 °C |
| ORC efficiency | (ηorc) | 32.52% |
| Inlet oil temperature in the HRS | (Ts,in) | 334.7 °C |
| Outlet oil temperature in the HRS | (Ts,out) | 204.6 °C |
| Parameters | Symbols | Values | ||
|---|---|---|---|---|
| Minimum | Maximum | Step | ||
| Collecting area | Ac (m2) | 100 | 300 | 20 |
| Storage tank volume | V (m3) | 10 | 30 | 2 |
| V | Ac,opt | Eel | ηen-y | ηth,col | PP | LCOE | NPV |
|---|---|---|---|---|---|---|---|
| (m3) | (m2) | (kWh) | (-) | (-) | (years) | (€ kWh−1) | (k€) |
| 10 | 120 | 33,022 | 15.23% | 52.14% | 9.34 | 0.1060 | 81.61 |
| 12 | 140 | 38,917 | 15.38% | 52.22% | 8.58 | 0.0989 | 102.63 |
| 14 | 140 | 38,888 | 15.37% | 52.41% | 8.86 | 0.1016 | 100.14 |
| 16 | 140 | 38,835 | 15.35% | 52.55% | 9.15 | 0.1043 | 97.52 |
| 18 | 140 | 38,769 | 15.32% | 52.65% | 9.45 | 0.1070 | 94.85 |
| 20 | 140 | 38,694 | 15.29% | 52.74% | 9.76 | 0.1098 | 92.12 |
| 22 | 140 | 38,615 | 15.26% | 52.81% | 10.08 | 0.1126 | 89.39 |
| 24 | 140 | 38,532 | 15.23% | 52.87% | 10.40 | 0.1155 | 86.62 |
| 26 | 140 | 38,447 | 15.20% | 52.92% | 10.73 | 0.1183 | 83.86 |
| 28 | 140 | 38,365 | 15.16% | 52.96% | 11.07 | 0.1212 | 81.10 |
| 30 | 140 | 38,282 | 15.13% | 52.99% | 11.41 | 0.1241 | 78.34 |
| V | Ac,opt | Eel | ηen-y | ηth,col | PP | LCOE | NPV |
|---|---|---|---|---|---|---|---|
| (m3) | (m2) | (kWh) | (-) | (-) | (years) | (€ kWh−1) | (k€) |
| 10 | 140 | 37,620 | 14.87% | 50.38% | 8.66 | 0.0997 | 98.54 |
| 12 | 160 | 41,954 | 14.51% | 48.99% | 8.45 | 0.0977 | 111.82 |
| 14 | 160 | 43,328 | 14.99% | 50.68% | 8.37 | 0.0969 | 116.29 |
| 16 | 160 | 43,306 | 14.98% | 50.92% | 8.62 | 0.0993 | 113.83 |
| 18 | 160 | 43,265 | 14.96% | 51.07% | 8.87 | 0.1017 | 111.28 |
| 20 | 160 | 43,216 | 14.95% | 51.59% | 9.13 | 0.1041 | 108.69 |
| 22 | 180 | 45,537 | 14.00% | 48.02% | 9.39 | 0.1065 | 111.98 |
| 24 | 180 | 45,501 | 13.99% | 48.51% | 9.65 | 0.1088 | 109.45 |
| 26 | 180 | 45,461 | 13.98% | 48.77% | 9.90 | 0.1111 | 106.91 |
| 28 | 180 | 45,423 | 13.96% | 49.17% | 10.16 | 0.1134 | 104.37 |
| 30 | 180 | 45,386 | 13.95% | 49.67% | 10.42 | 0.1157 | 101.83 |
| V | Ac,opt | Eel | ηen-y | ηth,col | PP | LCOE | NPV |
|---|---|---|---|---|---|---|---|
| (m3) | (m2) | (kWh) | (-) | (-) | (years) | (€ kWh−1) | (k€) |
| 10 | 180 | 41,023 | 12.61% | 42.47% | 9.08 | 0.1036 | 103.68 |
| 12 | 200 | 45,022 | 12.46% | 41.86% | 8.92 | 0.1022 | 115.30 |
| 14 | 220 | 48,275 | 12.14% | 40.77% | 8.96 | 0.1025 | 123.21 |
| 16 | 220 | 48,653 | 12.24% | 41.23% | 9.10 | 0.1038 | 122.74 |
| 18 | 240 | 49,851 | 11.49% | 38.81% | 9.60 | 0.1083 | 120.46 |
| 20 | 240 | 49,845 | 11.49% | 38.93% | 9.82 | 0.1103 | 118.09 |
| 22 | 240 | 49,835 | 11.49% | 39.05% | 10.05 | 0.1123 | 115.69 |
| 24 | 240 | 49,822 | 11.49% | 39.15% | 10.28 | 0.1144 | 113.27 |
| 26 | 240 | 49,806 | 11.48% | 39.25% | 10.51 | 0.1164 | 110.85 |
| 28 | 240 | 49,788 | 11.48% | 39.34% | 10.75 | 0.1185 | 108.41 |
| 30 | 240 | 49,770 | 11.48% | 39.43% | 10.99 | 0.1205 | 105.97 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellos, E.; Tzivanidis, C. Financial Optimization of a Solar-Driven Organic Rankine Cycle. Appl. Syst. Innov. 2020, 3, 23. https://doi.org/10.3390/asi3020023
Bellos E, Tzivanidis C. Financial Optimization of a Solar-Driven Organic Rankine Cycle. Applied System Innovation. 2020; 3(2):23. https://doi.org/10.3390/asi3020023
Chicago/Turabian StyleBellos, Evangelos, and Christos Tzivanidis. 2020. "Financial Optimization of a Solar-Driven Organic Rankine Cycle" Applied System Innovation 3, no. 2: 23. https://doi.org/10.3390/asi3020023
APA StyleBellos, E., & Tzivanidis, C. (2020). Financial Optimization of a Solar-Driven Organic Rankine Cycle. Applied System Innovation, 3(2), 23. https://doi.org/10.3390/asi3020023






