Dynamical Networks Modelling Applied to Low Voltage Lines with Nonlinear Filters
Abstract
1. Introduction
1.1. Motivation and Contribution
1.2. Literature Review
1.3. Paper Structure
2. Electromagnetic Interference on Low Voltage Lines—Network Model
2.1. A short on Electromagnetic Interference
- 1)
- Eliminate EMI next to the source. If the source can be accessed, suppressing EMI could be done by, for instance, moving it away, replacement, shielding, using output filters and other suppressor devices, or by altering its internal design of circuits and components. So far, this is the best to do and the source will not be a cause of interference for the whole environment. However, in general, the source is not under control and cannot be accessed.
- 2)
- Eliminate EMI in the path. The second possibility is doing adjustments on the transmitting path. Electromagnetic waves can be transmitted through conductive means, such as cables or “earth”, (conducted EMI) or can be radiated through the environment. The alternatives to prevent the interference are the removal of the recipient equipment, or shielding it against radiated interference, and applying various types of suppressors and filters for undesired conducted disturbances.
- 3)
- Eliminate EMI in the recipient. If it is neither possible to deal with the source nor the path, the last alternative is the elimination of EMI within the recipient. This could be a difficult task and will involve the study of the environment, the existing noise, possible transients, and surges, which will lead to a set of solutions such as physical system layout, distributed filters, suppressors and shielding.
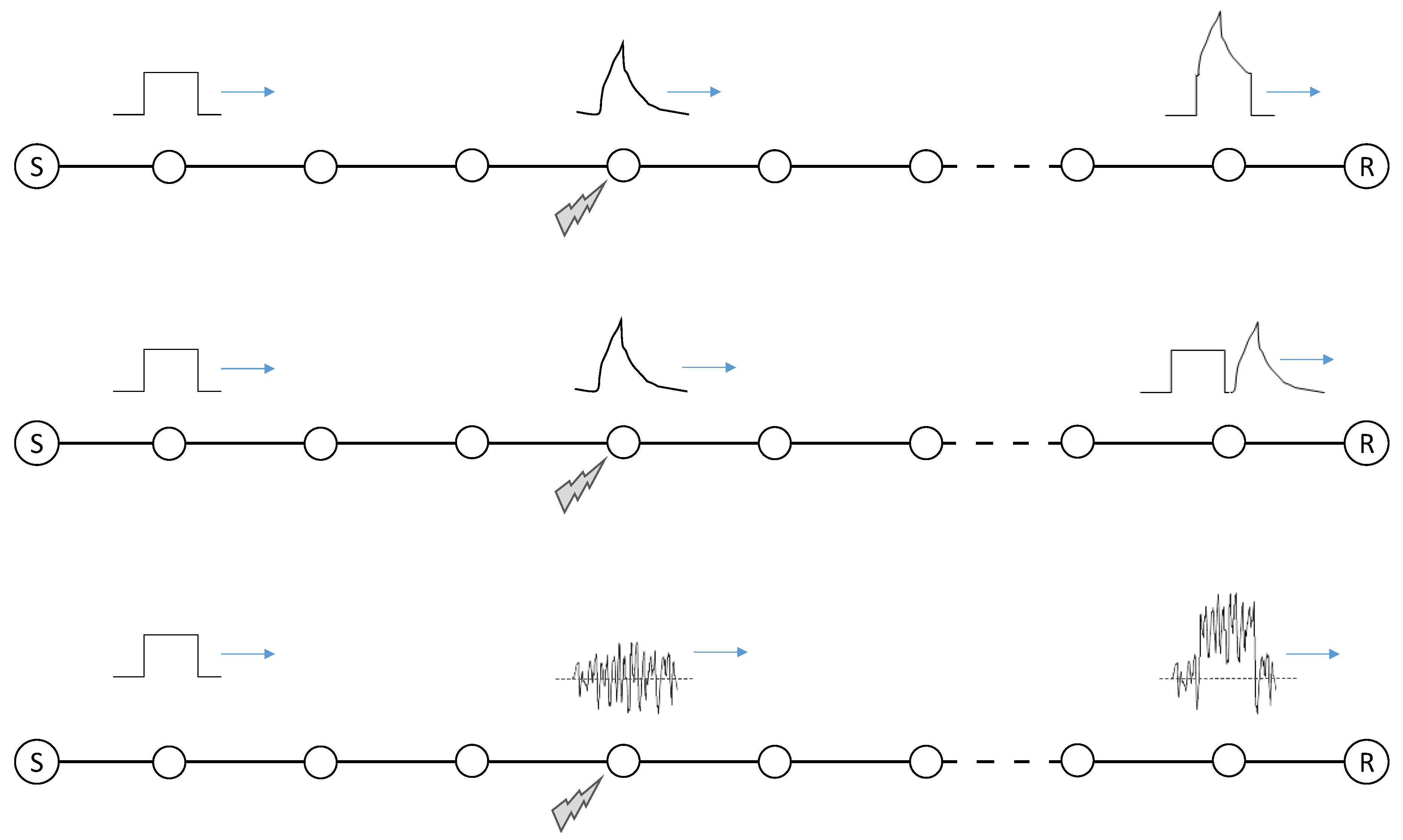
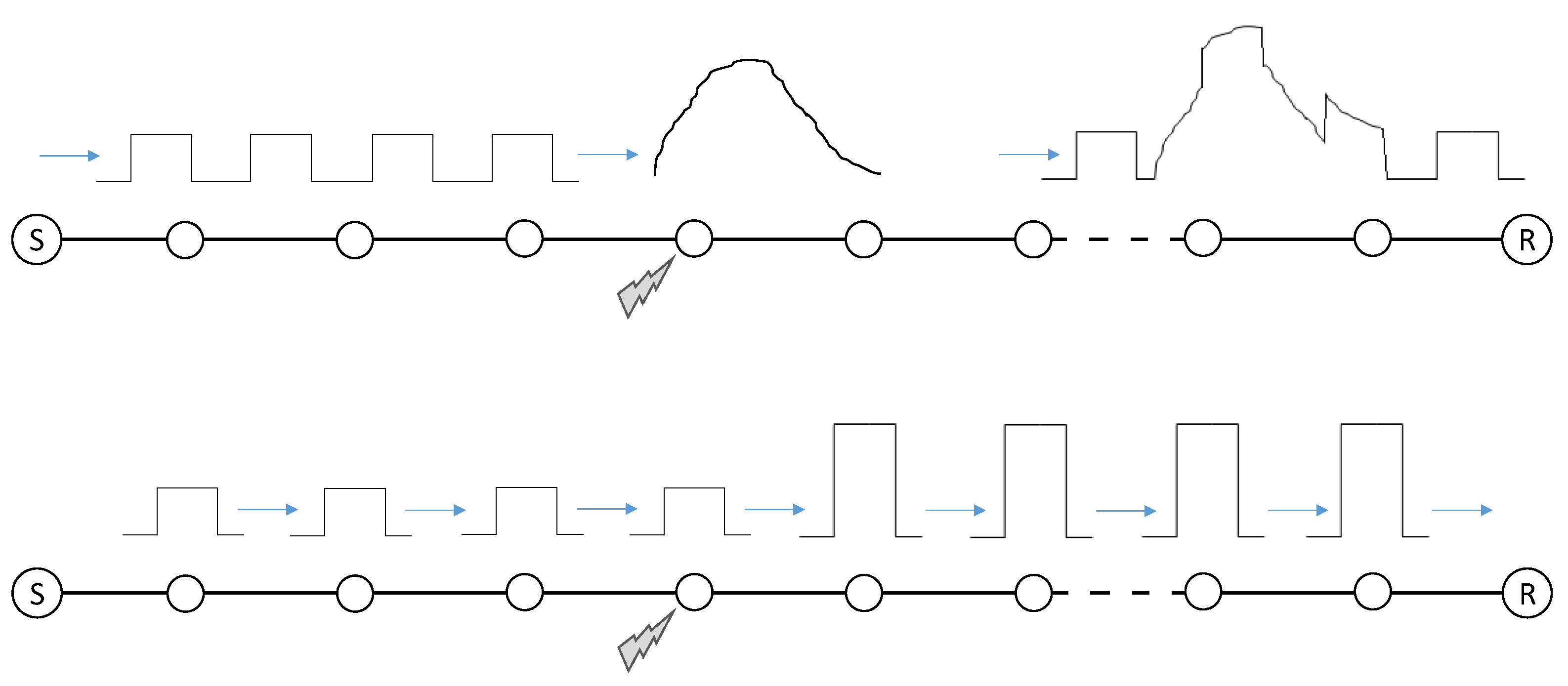
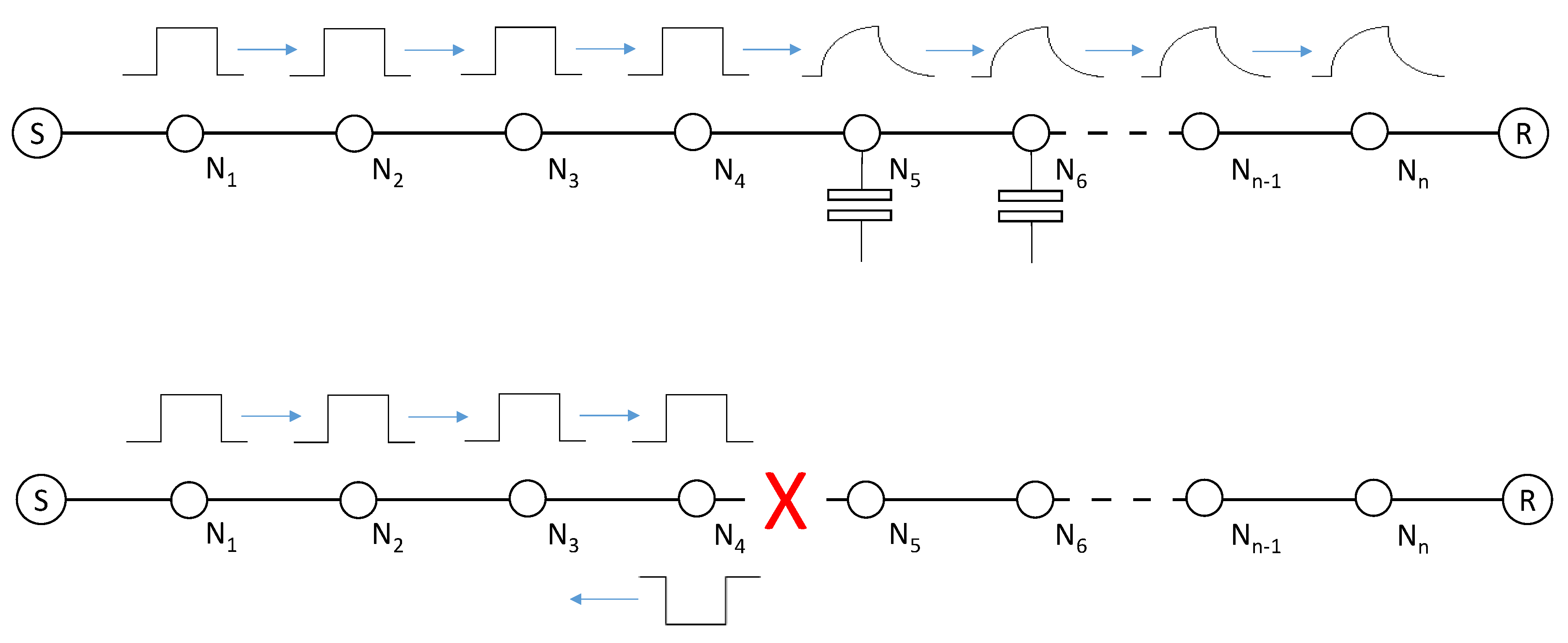
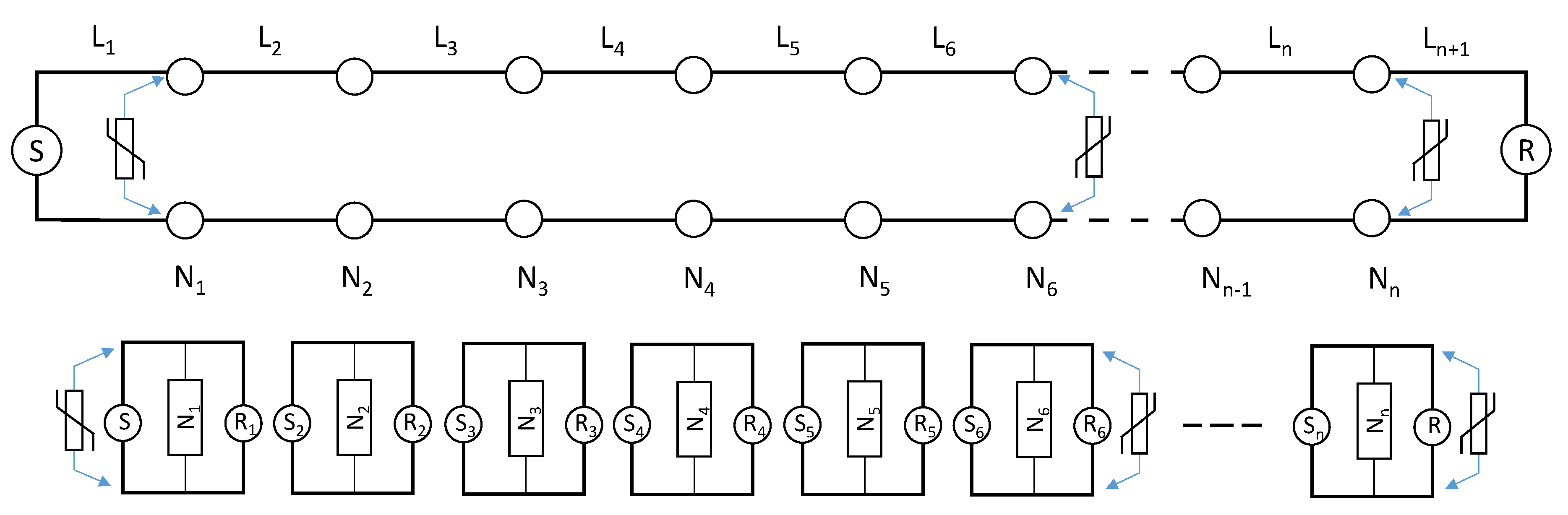
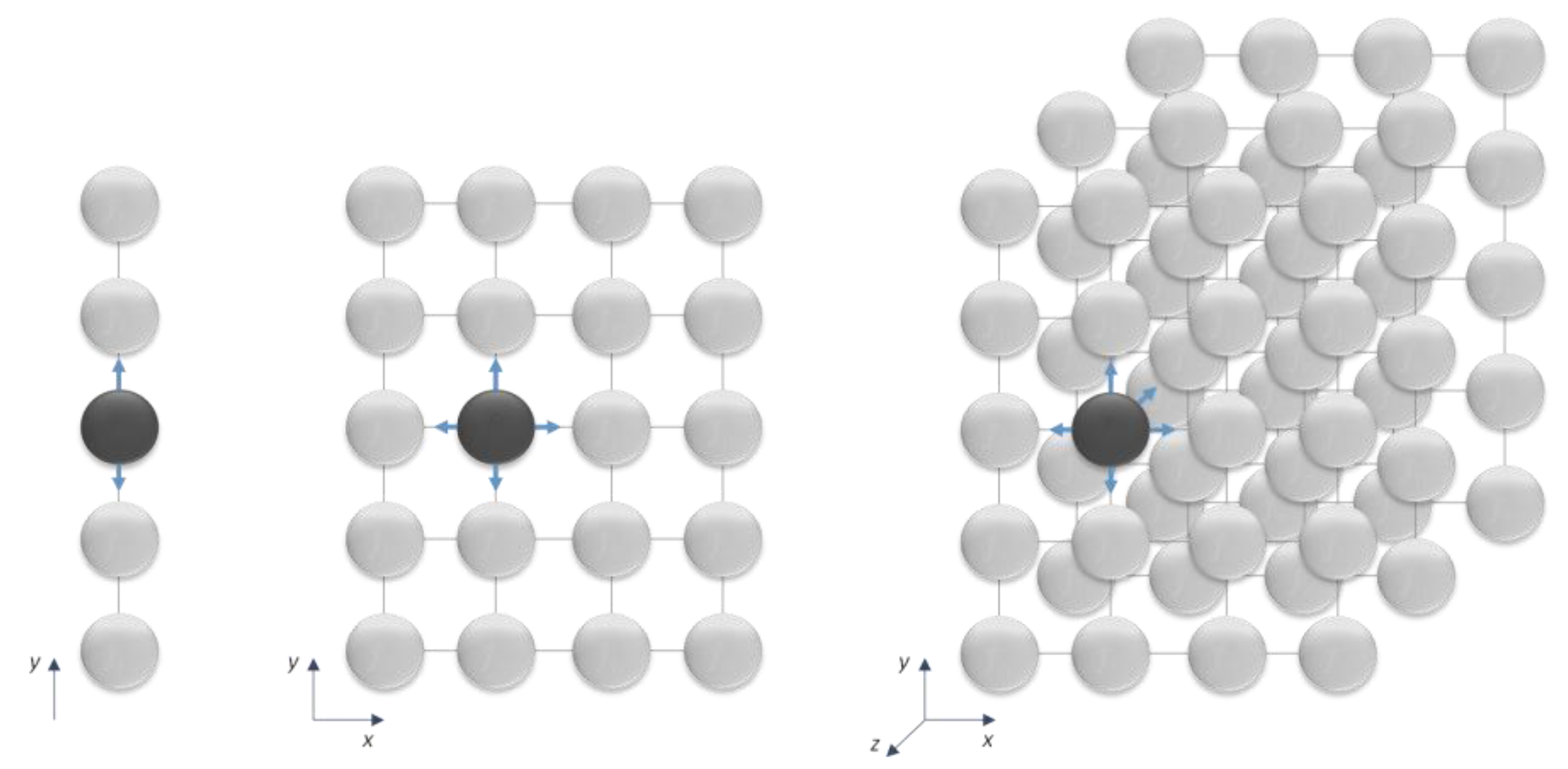
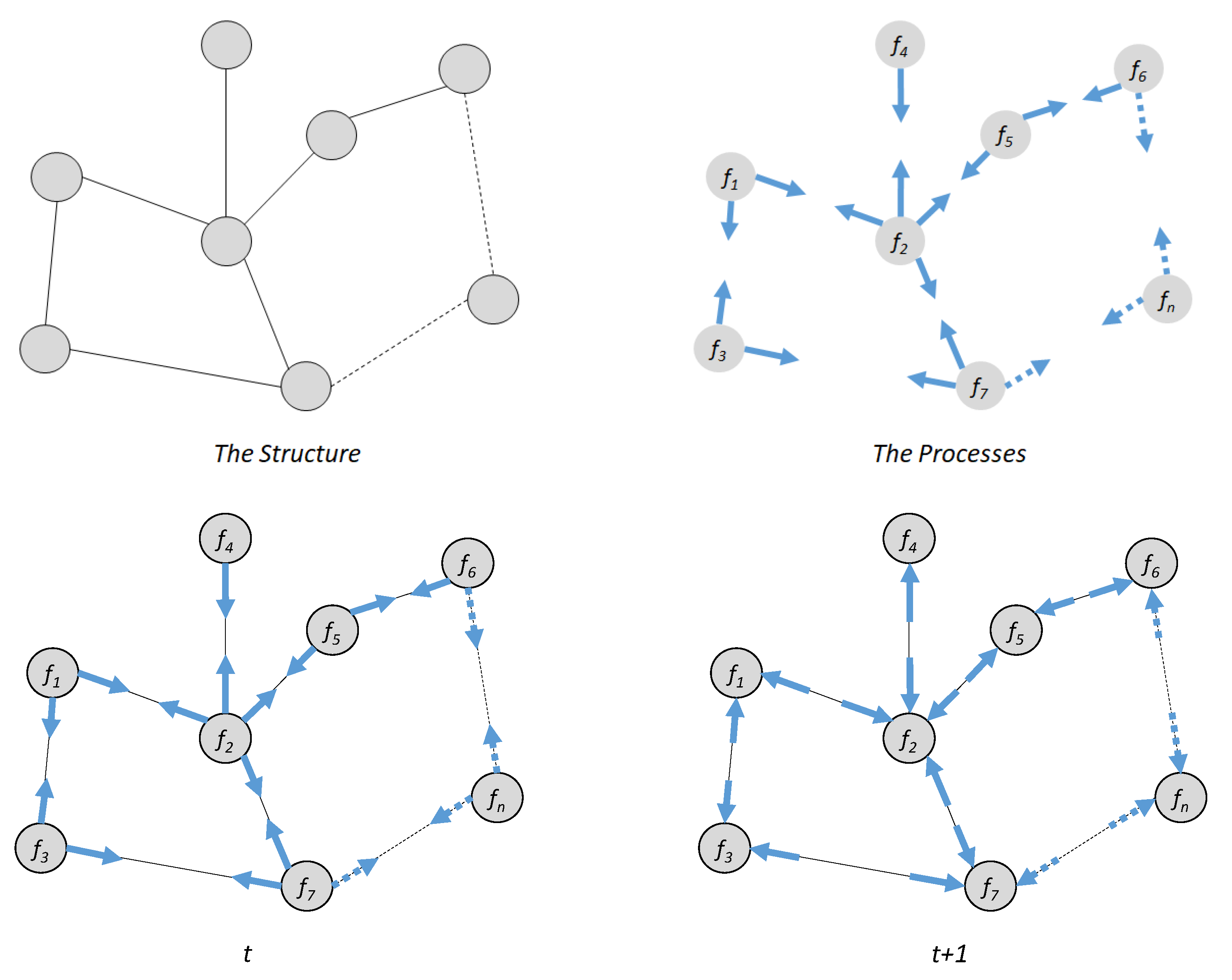
2.2. Robustness of a Simple Communication Network System
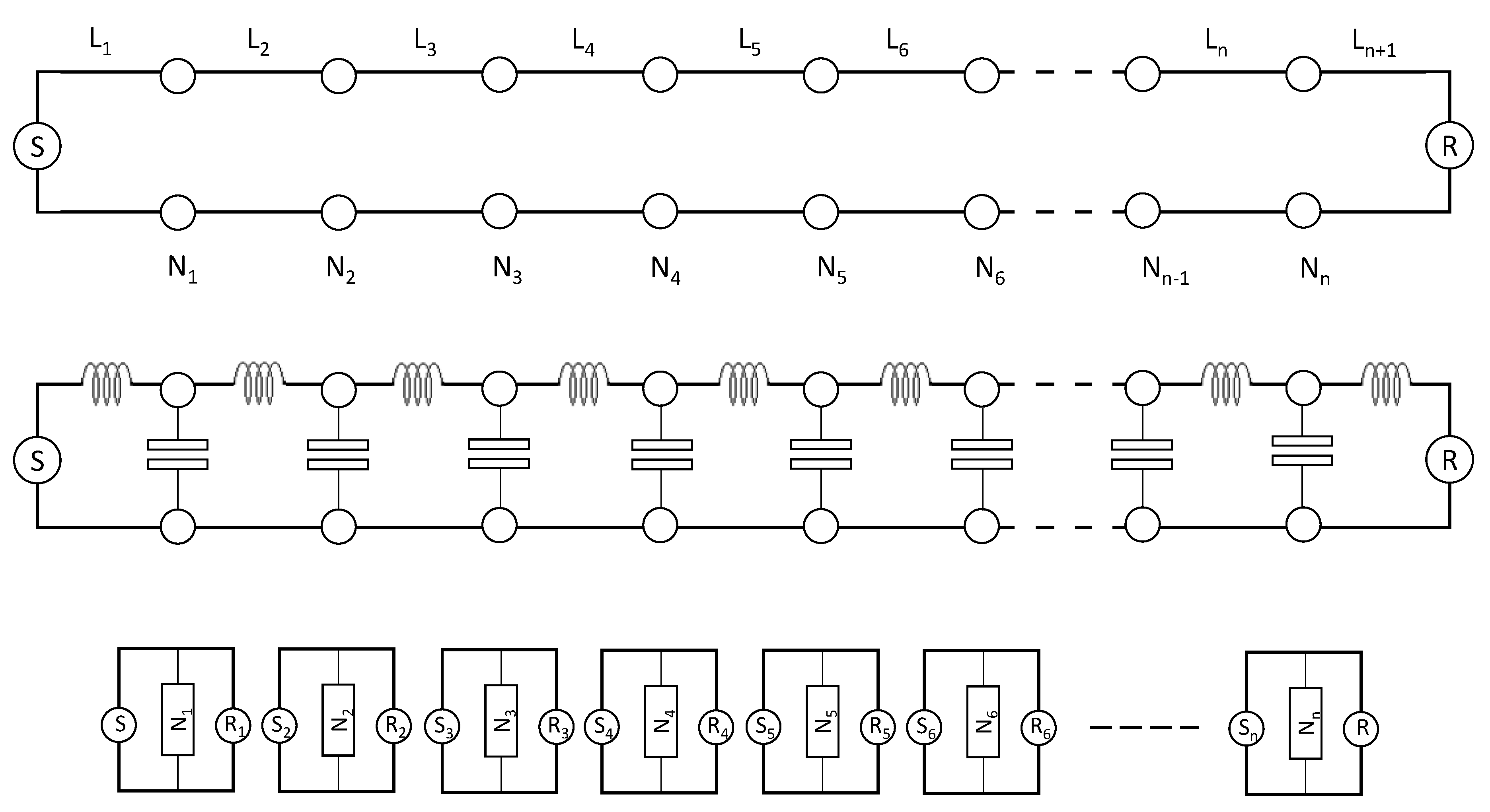
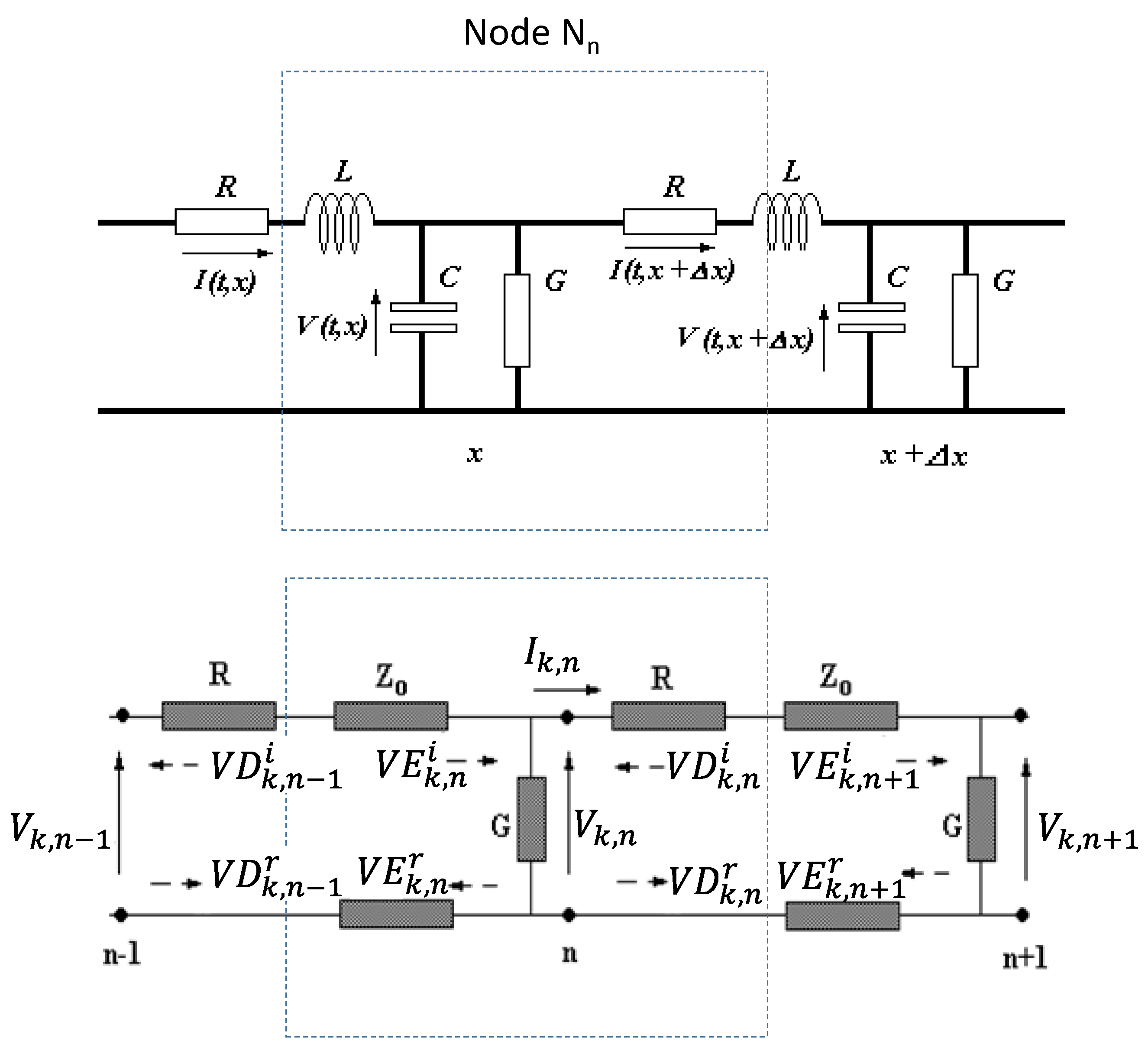
2.3. Low Voltage Lines—Network Model
3. Linear and Nonlinear Filters
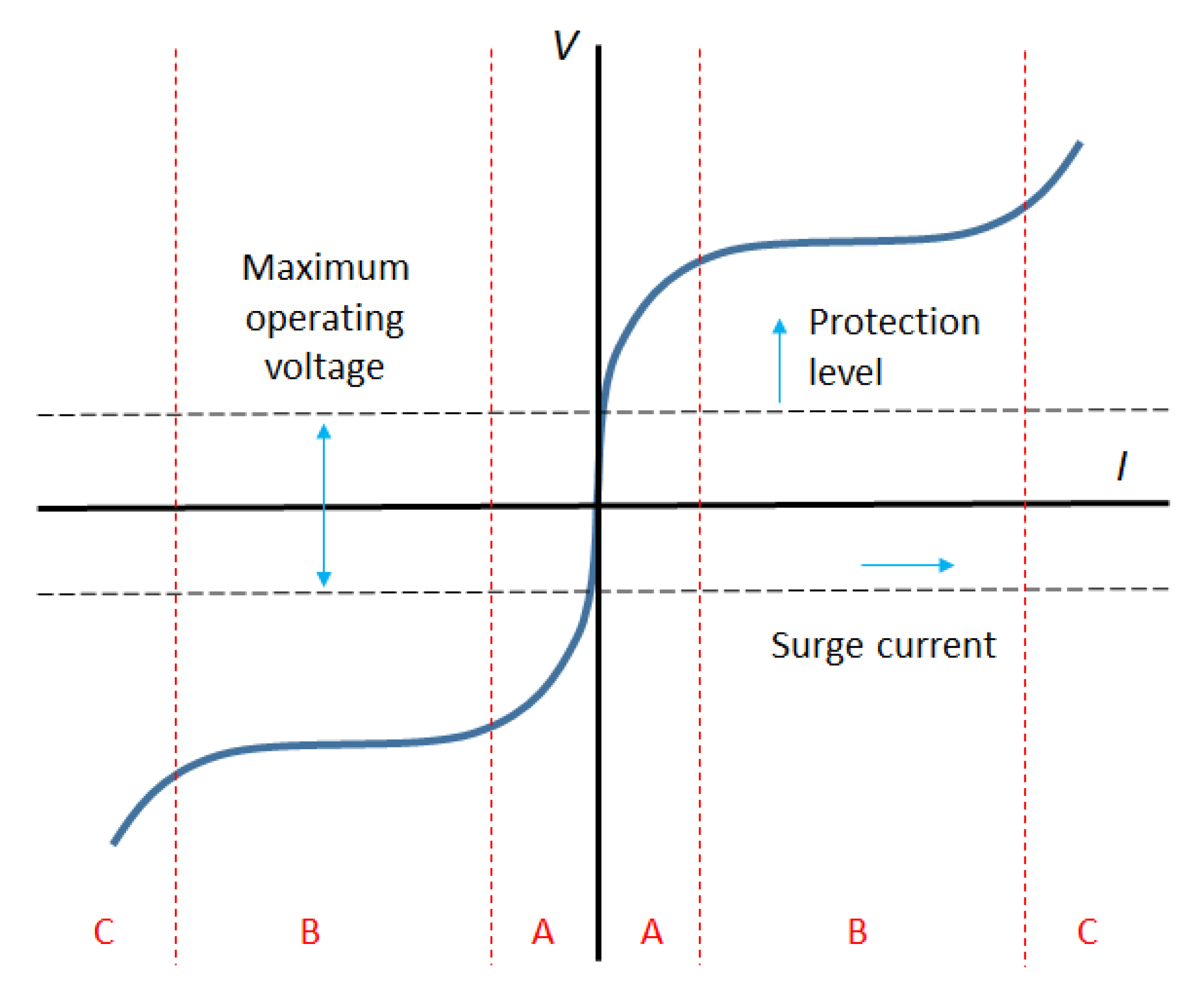
3.1. Overview
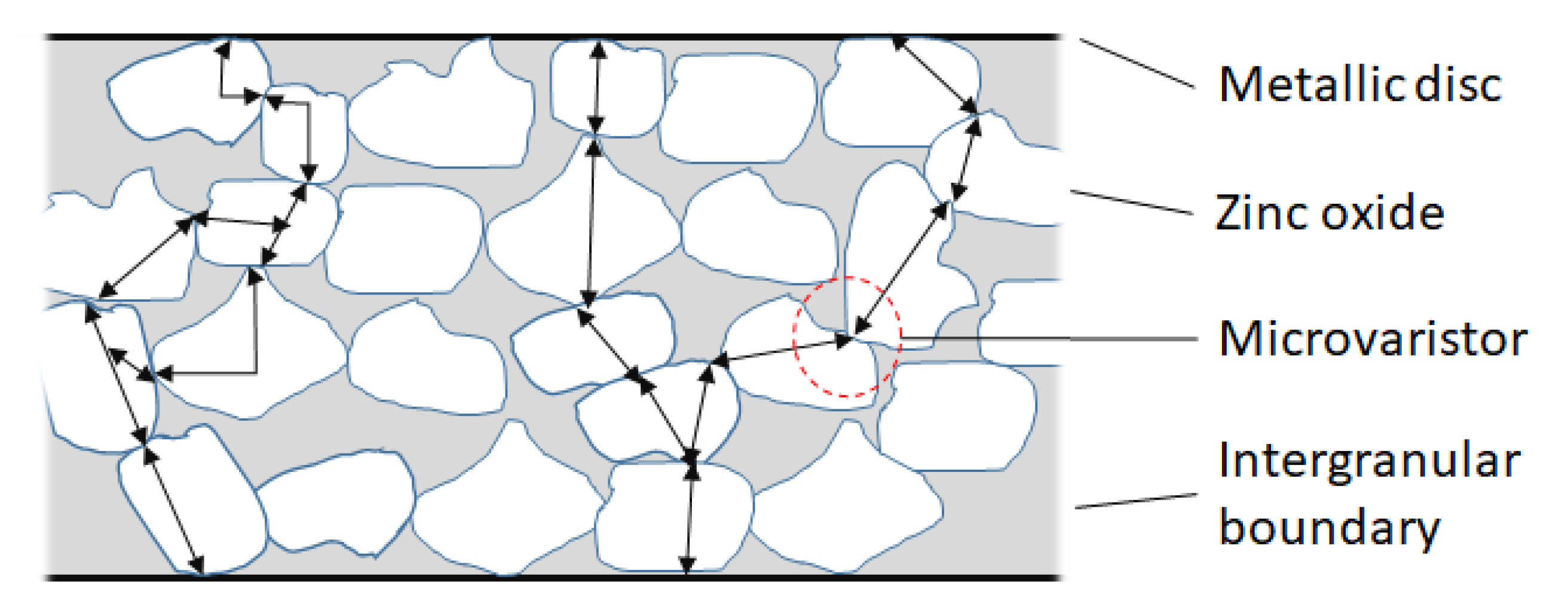
3.2. Metal-Oxide Varistor
3.3. The Dynamic Model of A ZnO Varistor Filter
4. Results, Discussion and Perspectives
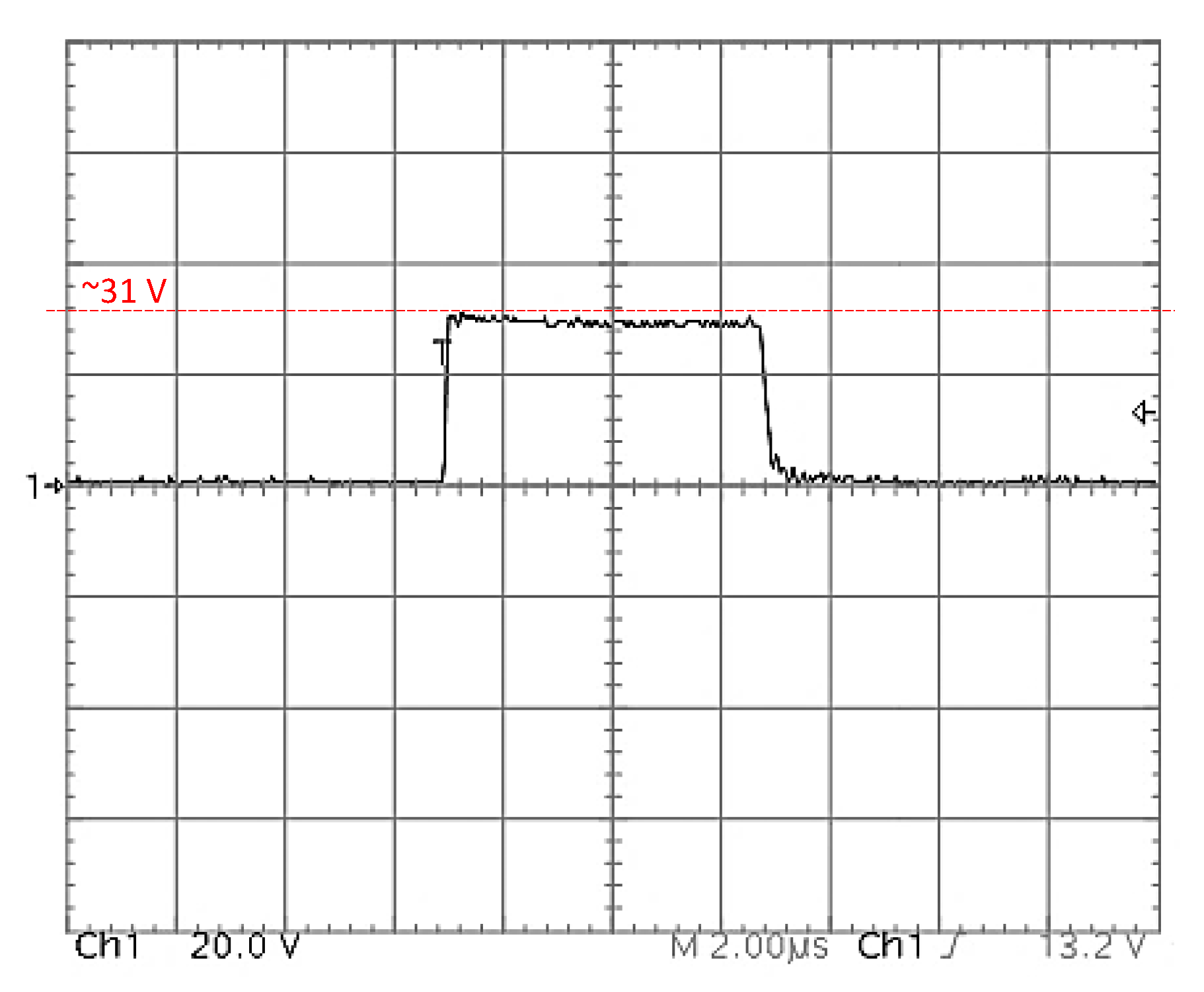
4.1. Results of Practical Experiments and Simulations
4.2. Discussions, Perspectives and Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
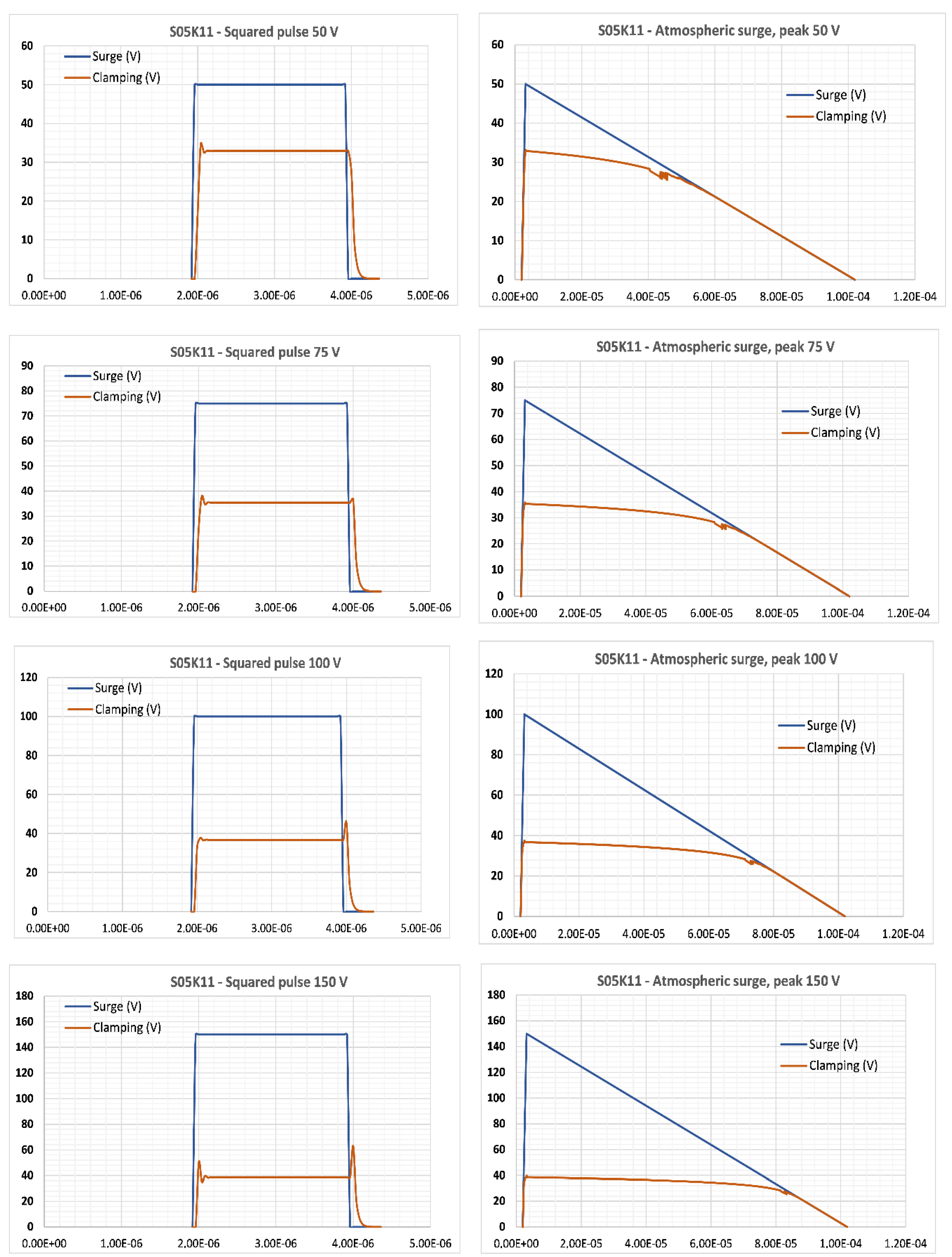
Appendix B
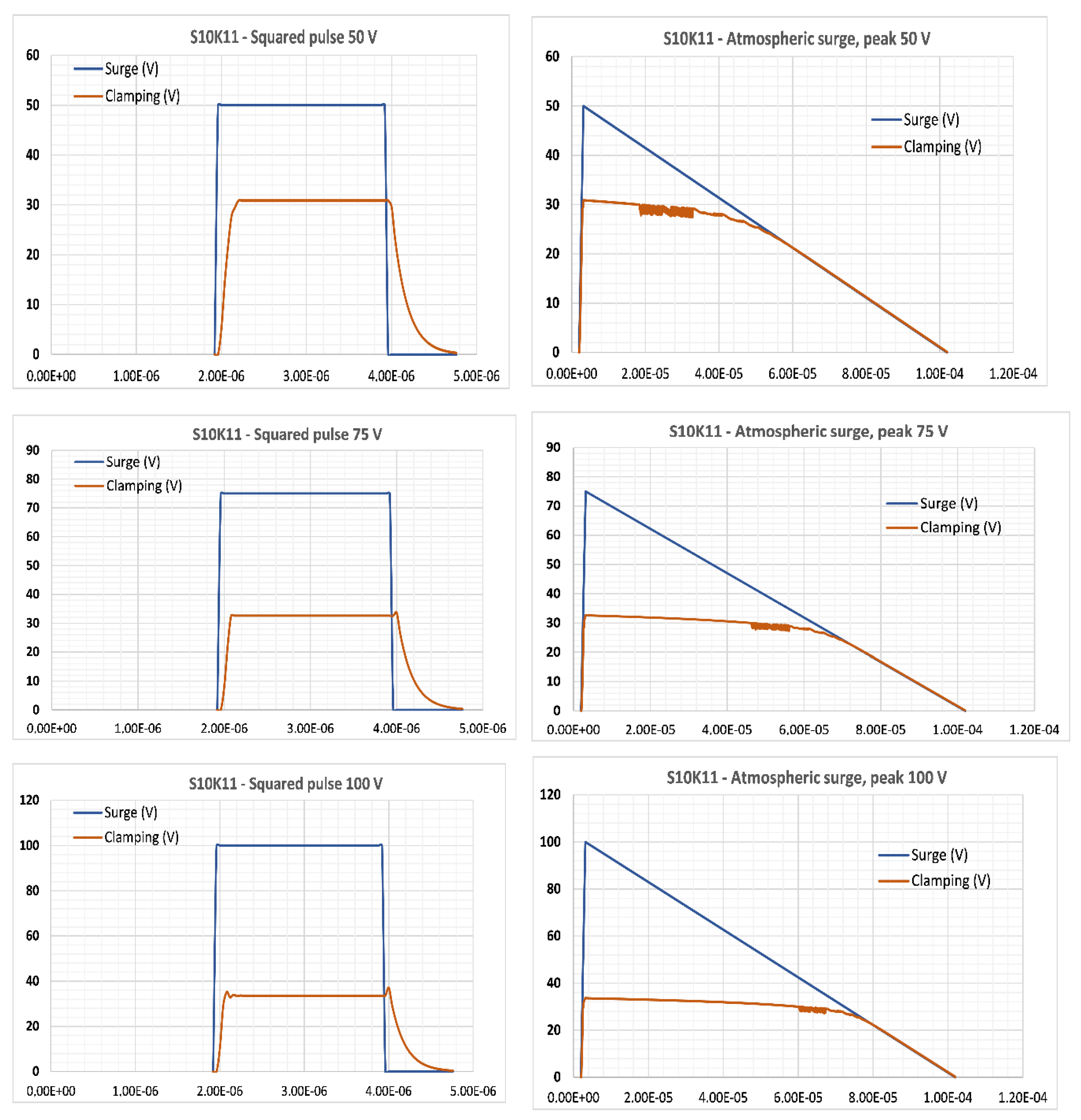
Appendix C
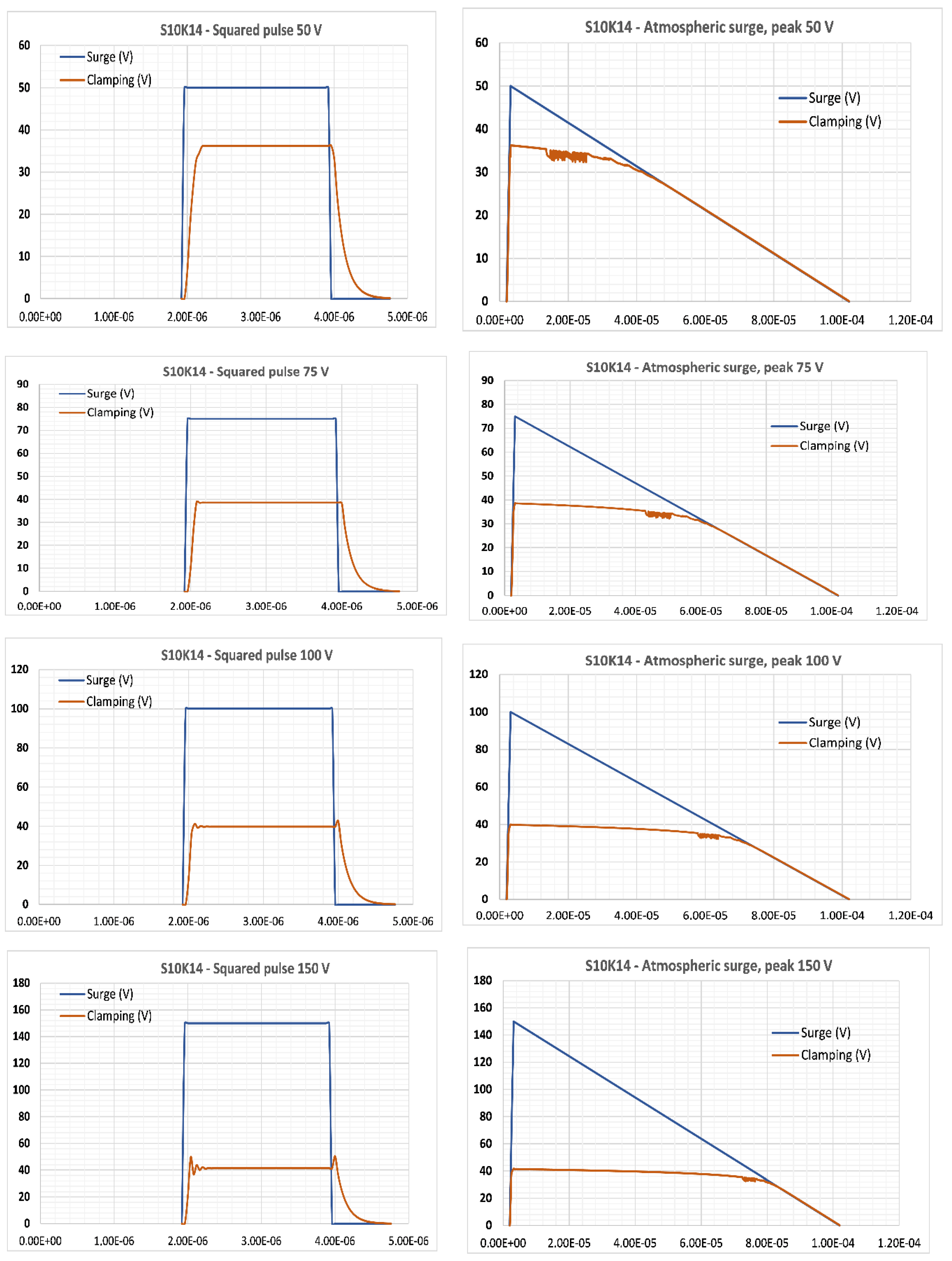
References
- Paul, C.R. Introduction to Electromagnetic Compatibility; John Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]
- Goedbloed, J. Electromagnetic Compatibility; Prentice Hall: New York, NY, USA, 1992. [Google Scholar]
- Christopoulos, C. Principles and Techniques of Electromagnetic Compatibility; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Violette, N. Electromagnetic Compatibility Handbook; Springer: New York, NY, USA, 2013. [Google Scholar]
- Perez, R. Handbook of Electromagnetic Compatibility; Academic Press: San Diego, CA, USA, 2013. [Google Scholar]
- Kaiser, K.L. Electromagnetic Compatibility Handbook; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Ott, H.W. Electromagnetic Compatibility Engineering; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Fazion Filho, M. O Método da Modelagem por Linhas de Transmissão (TLM) e Aplicações em Compatibilidade Eletromagnética (EMC). Master’s Thesis, Federal University of Santa Catarina, Florianopolis, Brazil, 1997. [Google Scholar]
- Christopoulos, C. The Transmission-Line Modeling Method TLM; IEEE Press: New York, NY, USA, 1995. [Google Scholar]
- Johns, P.B.; O’Brien, M. Use of the transmission-line modelling (tlm) method do solve nonlinear lumped networks. Radio Electron. Eng. 1980, 50, 59–70. [Google Scholar] [CrossRef]
- Hoefer, W.J.R. The Transmission Line Matrix (TLM) Method. In Numerical Techniques for Microwave and Millimeter-Wave Passive Structures; Itoh, T., Ed.; Wiley: New York, NY, USA, 1989. [Google Scholar]
- Fazion Filho, M. Estudos de Modelagem Eletromagnética com o Método das Linhas de Transmissão (TLM). Ph.D. Thesis, Federal University of Santa Catarina, Florianopolis, Brazil, 2001. [Google Scholar]
- Grossmann, C.; Roos, H.; Stynes, M. Numerical Treatment of Partial Differential Equations; Springer: Cham, Switzerland, 2005; ISBN 978-3-540-71584-9. [Google Scholar]
- Johns, P.B.; Beurle, R.L. Numerical solution of 2-dimensional scattering problems using a transmission-line matrix. Proc. IEEE 1971, 118, 1203–1208. [Google Scholar] [CrossRef]
- Akhtarzad, S.; Johns, P.B. Solution of Maxwell’s equations in three space dimensions and time by the T.L.M method of numerical analysis. Proc. IEEE 1975, 122, 1344–1348. [Google Scholar] [CrossRef]
- Akhtarzad, S.; Johns, P.B. Generalized elements for T.L.M method of numerical analysis. Proc. IEEE 1975, 122, 1349–1352. [Google Scholar]
- Johns, P.B. A Symmetrical Condensed Node for the TLM Method. IEEE Trans. Microw. Theory Tech. 1987, 35, 370–377. [Google Scholar] [CrossRef]
- Herring, J.L. Developments in the Transmission-Line Modelling Method for Electromagnetic Compatibility Studies. Ph.D. Thesis, University of Nottingham, Nottingham, UK, May 1993. [Google Scholar]
- Trenkic, V. The Development and Characterization of Advanced Nodes for the TLM Method. Ph.D. Thesis, University of Nottingham, Nottingham, England, November 1995. [Google Scholar]
- Righi, M. Diakoptic Solution Techniques for Electromagnetic Fields in Time and Frequency Domain. Ph.D. Thesis, University of Victoria, Victoria, BC, Canada, 1995. [Google Scholar]
- Menezes, L.R.A.X. Modeling of General Medium Constitutive Relationships in the Transmission Line Matrix Method (TLM). Ph.D. Thesis, University of Victoria, Victoria, BC, Canada, 1996. [Google Scholar]
- Johns, D.P. Transmission line matrix method (TLM). In Proceedings of the 2017 IEEE International Symposium on Electromagnetic Compatibility & Signal/Power Integrity (EMCSI), Washington, DC, USA, 7–11 August 2017; pp. 1–34. [Google Scholar]
- Mir, H.; Arya, V.; Höffler, H.; Brand, A. A Novel TLM Analysis for Solar Cells. IEEE J. Photovolt. 2019, 9, 1336–1342. [Google Scholar] [CrossRef]
- SIOV Metal Oxide Varistors; EPCOS AG, TDK Group Company: Munich, Germany. 2018. Available online: https://www.tdk-electronics.tdk.com/download/531268/8954d4a78154a9da5c70a7119fa03e86/siov-general.pdf (accessed on 11 December 2019).
- SIOV Metalloxid-Varistoren, Siemens Matsushita Components; Siemens Matsushita Components GmbH: Dusseldorf, Germany, 1997; pp. 15–50.
- Fazion Filho, M. varistorGeneralModel.py. 2019. Available online: https://github.com/mfaccioni/varistorGeneralModel/blob/master/varistorGeneralModel.py (accessed on 11 December 2019).
- Bley, M., Jr.; Fazion Filho, M.; Raizer, A. Modeling transient discharge suppressors. IEEE Potentials 2004, 23, 43–45. [Google Scholar] [CrossRef]
- Fazion Filho, M.; Ferreira, G.S.; Raizer, A. Nonlinear Device Modeling for Transient Suppression. In Proceedings of the Eighth Biennial IEEE Conference on Electromagnetic Field Computation, Tucson, AZ, USA, 1–3 June 1998. [Google Scholar]
- Fazion Filho, M.; Ferreira, G.S.; Raizer, A. Simulation of Nonlinear Protection Device Using TLM Method. In Proceedings of the EMC’98 International Symposium on Electromagnetic Compatibility Proceedings, Rome, Italy, 14–18 September 1998; pp. 403–407. [Google Scholar]
- Fazion Filho, M.; Ferreira, G.S.; Raizer, A. Modelagem Numérica de Filtros Não-Lineares para Transientes Eletromagnéticos. In Proceedings of the III Congresso Brasileiro de Eletromagnetismo–CBMag’98, São Paulo, Brazil, 28–25 October 1998; pp. 18–21. [Google Scholar]
- Fazion Filho, M.; Bley, M., Jr.; Raizer, A. Modelling nonlinear suppressors using tlm. In Proceedings of the 5th International Workshop on Computational Electromagnetics in Time Domain-TLM, FDTD and Other Techniques (CEM-2003), Halifax, NS, Canada, 17–19 June 2003. [Google Scholar]
- Tektronix Oscilloscope. Available online: https://www.tek.com/oscilloscope (accessed on 11 December 2019).
- Ladyman, J.; Lambert, J.; Wiesner, K. What is a complex system? Eur. J. Philos. Sci. 2013, 3, 33–67. [Google Scholar] [CrossRef]
- Holland, J.H. Emergence: From Chaos to Order; Perseus Books: Cambridge, MA, USA, 1998; ISBN 0-7382-0142-1. [Google Scholar]
- Costa, L.F.; Rodrigues, F.A.; Travieso, G.; Villas Boas, P.R. Characterization of complex networks: A survey of measurements. Adv. Phys. 2007, 56, 167–242. [Google Scholar] [CrossRef]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef]
- Wasserman, S.; Faust, K. Social Network Analysis: Methods and Applications; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]

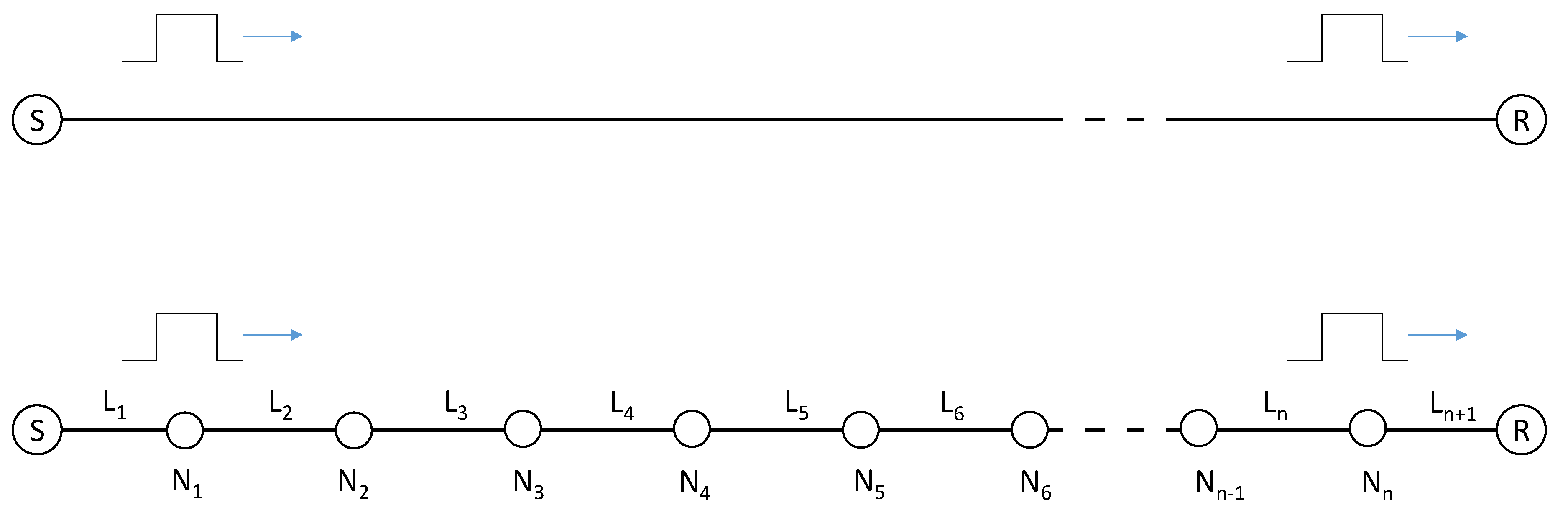


| Line Parameters (Distributed) | ||
|---|---|---|
| R (Ω/m) | C (F/m) | L (H/m) |
| 1.0 × 10−5 | 1.0 × 10−10 | 2.5 × 10−7 |
| Varistor Model [tdk] | Metal Oxide | Disk Diammeter (mm) | C (nF) | Nominal Voltage (V) | Assumed Values According to Technical Specifications | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Va (V) | Ia (A) | Vb (V) | Ib (A) | α | β | |||||
| S05K11 | ZnO | 5 | 1.6 | 11 | 23 | 0.01 | 34 | 1 | 11.78 | 9.04 |
| S10K11 | ZnO | 10 | 6.8 | 11 | 23 | 0.01 | 30 | 0.5 | 14.72 | 8.93 × 10−23 |
| S10K14 | ZnO | 10 | 5.2 | 14 | 28 | 0.01 | 36 | 0.5 | 15.56 | 2.97 × 10−25 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fazion Filho, M. Dynamical Networks Modelling Applied to Low Voltage Lines with Nonlinear Filters. Appl. Syst. Innov. 2020, 3, 18. https://doi.org/10.3390/asi3020018
Fazion Filho M. Dynamical Networks Modelling Applied to Low Voltage Lines with Nonlinear Filters. Applied System Innovation. 2020; 3(2):18. https://doi.org/10.3390/asi3020018
Chicago/Turabian StyleFazion Filho, Mauro. 2020. "Dynamical Networks Modelling Applied to Low Voltage Lines with Nonlinear Filters" Applied System Innovation 3, no. 2: 18. https://doi.org/10.3390/asi3020018
APA StyleFazion Filho, M. (2020). Dynamical Networks Modelling Applied to Low Voltage Lines with Nonlinear Filters. Applied System Innovation, 3(2), 18. https://doi.org/10.3390/asi3020018





