Hamming Code Strategy for Medical Image Sharing
Abstract
1. Introduction
2. Related Works
3. Hamming Codes
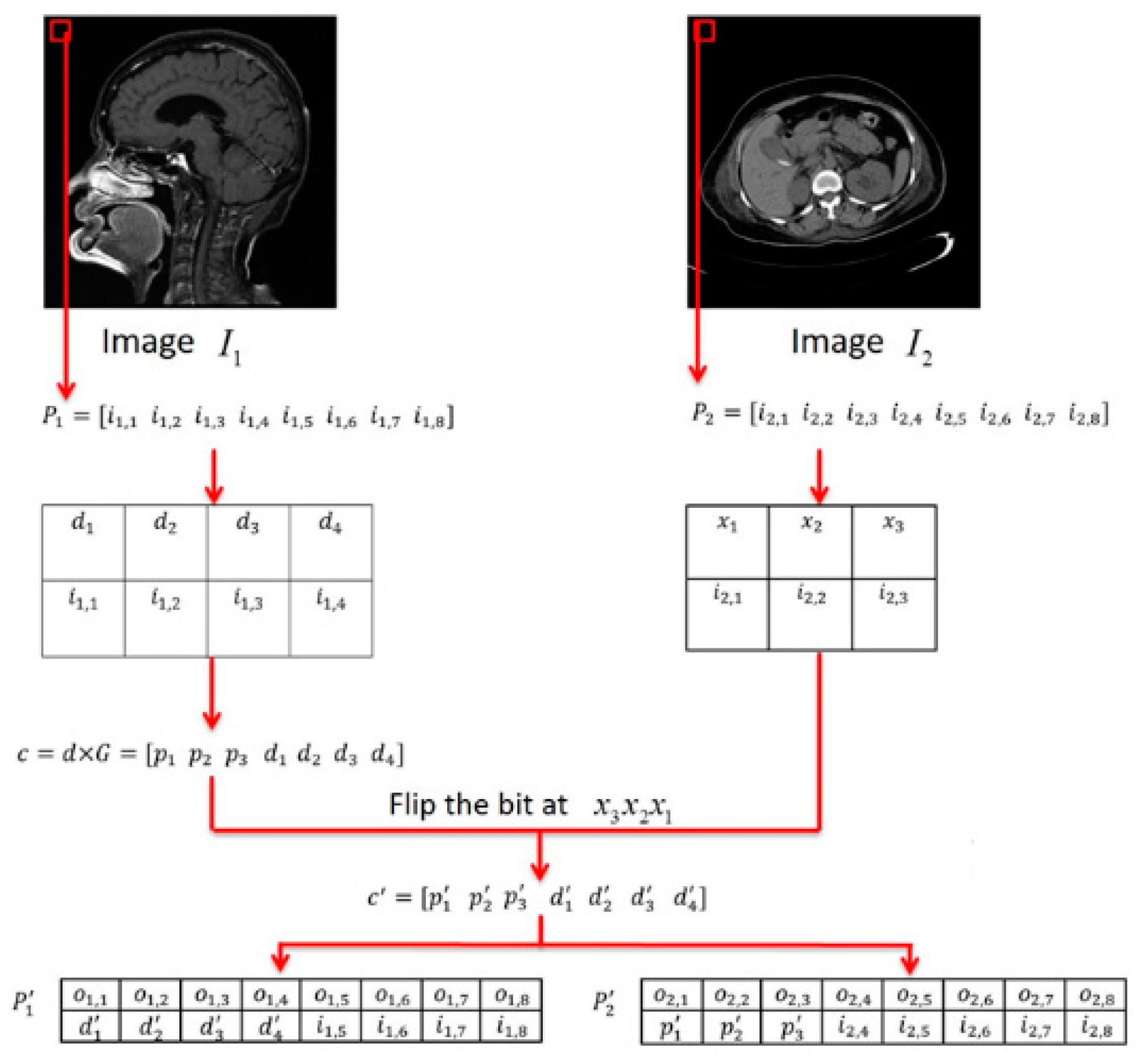
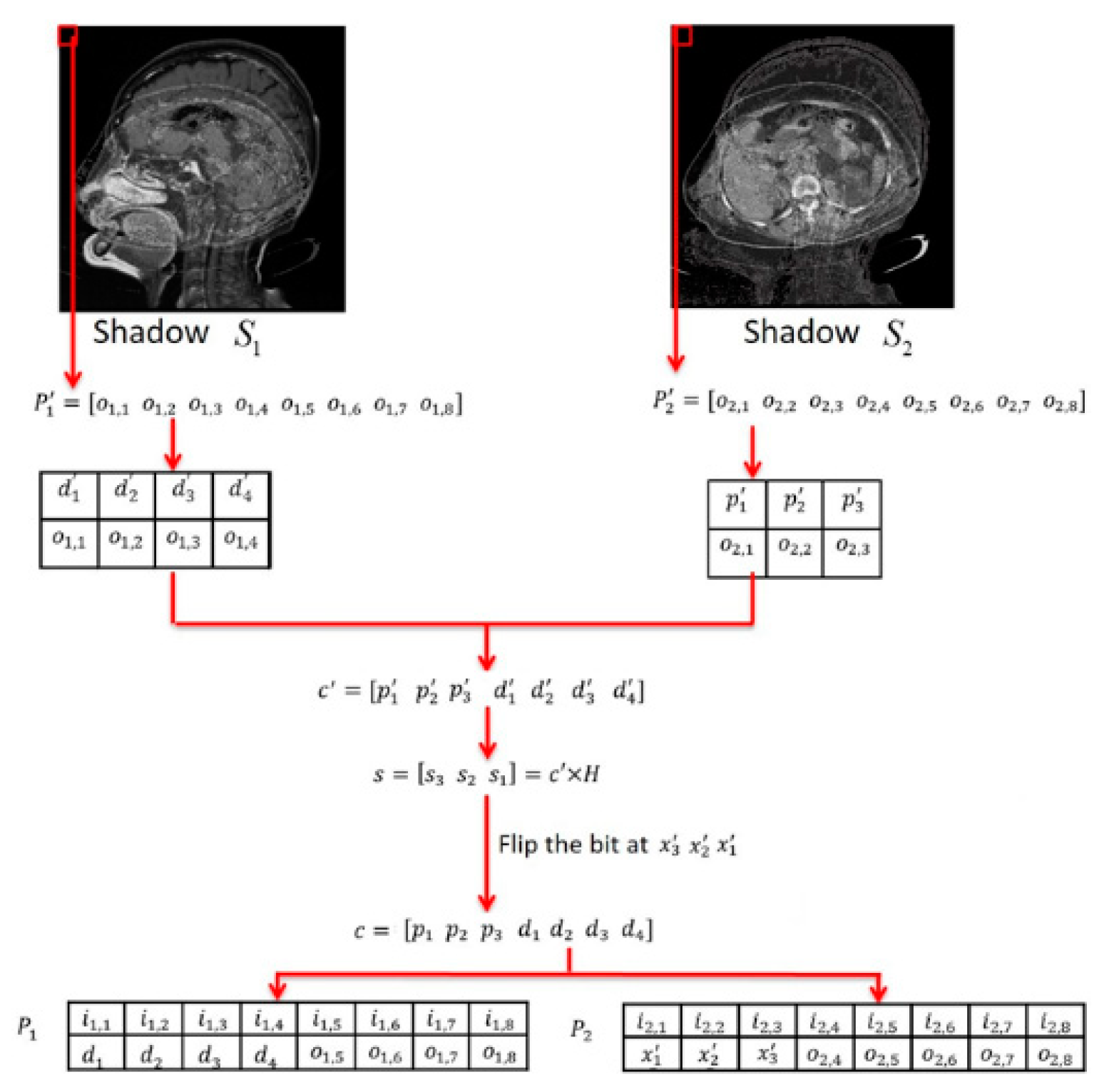
4. The Proposed Scheme
4.1. Using (7,4) Hamming Code
4.2. Using (15,11) Hamming Code
5. Experiments and Discussions
5.1. Experimental Results
5.2. Comparisons
5.3. Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, J.; Zhu, Z.; Fu, C.; Yu, H.; Zhang, L. A fast chaos-based image encryption scheme with a dynamic state variables selection mechanism. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 846–860. [Google Scholar] [CrossRef]
- Dong, C. Asymmetric color image encryption scheme using discrete-time map and hash value. Optik. Int. J. Light Electron. Opt. 2015, 126, 2571–2575. [Google Scholar] [CrossRef]
- Liu, H.; Kadir, A.; Gong, P. A fast color image encryption scheme using one-time S-Boxes based on complex chaotic system and random noise. Opt. Commun. 2015, 338, 340–347. [Google Scholar] [CrossRef]
- Mannai, O.; Bechikh, R.; Hermassi, H.; Rhouma, R.; Belghith, S. A new image encryption scheme based on a simple first-order time-delay system with appropriate nonlinearity. Nonlinear Dyn. 2015, 82, 107–117. [Google Scholar] [CrossRef]
- Bullock, A.; Dimond, R.; Webb, K.; Lovatt, J.; Hardyman, W.; Stacey, M. How a mobile app supports the learning and practice of newly qualified doctors in the UK: An intervention study. BMC Med. Educ. 2015, 15, 71. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, K.; Liang, X.; Su, Z.; Shen, X.; Luo, H.H. Security and privacy for mobile healthcare networks: From a quality of protection perspective. IEEE Wirel. Commun. 2015, 22, 104–112. [Google Scholar] [CrossRef]
- Zhang, L.; Jung, T.; Liu, C.; Ding, X.; Li, X.Y.; Liu, Y. Pop: Privacy-preserving outsourced photo sharing and searching for mobile devices. In Proceedings of the International conference on distributed computing systems, Columbus, OH, USA, 29 June–2 July 2015; pp. 308–317. [Google Scholar]
- Shao, J.; Lu, R.; Lin, X. Fine-grained data sharing in cloud computing for mobile devices. In Proceedings of the 2015 IEEE conference on computer communications (INFOCOM), Kowloon, Hong Kong, China, 26 April–1 May 2015; pp. 2677–2685. [Google Scholar]
- Ibtihal, M.; Hassan, N. Homomorphic encryption as a service for outsourced images in mobile cloud computing environment. In Cryptography: Breakthroughs in Research and Practice; IGI Global: Hershey, PA, USA, 2020; pp. 316–330. [Google Scholar]
- Shankar, T.N.; Sahoo, G.; Niranjan, S. Image encryption for mobile devices. In Proceedings of the International Conference in Communication Control and Computing Technologies, Ramanathapuram, India, 7–9 October 2010; pp. 612–616. [Google Scholar]
- La Rosa, M.; Rabinovich, M.I.; Huerta, R.; Abarbanelac, H.D.I.; Fortuna, L. Slow regularization through chaotic oscillation transfer in an unidirectional chain of Hindmarsh–Rose models. Phys. Lett. A 2000, 266, 88–93. [Google Scholar] [CrossRef]
- Wang, F.; Ding, J.; Dai, Z.; Peng, Y. An application of mobile phone encryption based on Fibonacci structure of chaos. In Proceedings of the 2010 Second World Congress on Software Engineering, Wuhan, China, 19–20 December 2010; Volume 2, pp. 97–100. [Google Scholar]
- Kim, C. Data hiding using improving hamming code. J. Inst. Electron. Inf. Eng. 2013, 50, 180–186. [Google Scholar] [CrossRef]
- Kim, C.; Yang, C.N. Data hiding based on overlapped pixels using hamming code. Multimed. Tools Appl. 2014, 75, 1–13. [Google Scholar]
- Wang, J.T.; Chang, Y.C.; Yu, S.S.; Yu, C.Y. Hamming Code Based Watermarking Scheme for 3D Model Verification. In Proceedings of theInternational Symposium on Computer, Consumer and Control, Taichung, Taiwan, China, 10–12 June 2014; pp. 1095–1098. [Google Scholar]
- Blakley, G.R. Safeguarding cryptographic keys. In Proceedings of the National Computer Conference, New York, NY, USA, 4–7 June 1979; Volume 48, pp. 313–317. [Google Scholar]
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Thien, C.C.; Lin, J.C. Secret image sharing. Comput. Graph. 2002, 26, 765–770. [Google Scholar] [CrossRef]
- Wang, R.Z.; Su, C.H. Secret image sharing with smaller shadow images. Pattern Recognit. Lett. 2006, 27, 551–555. [Google Scholar] [CrossRef]
- Wang, R.Z.; Shyu, S.J. Scalable secret image sharing. Signal Process. Image Commun. 2007, 22, 363–373. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.C.; Lin, C.H.; Chen, Y.H. A novel secret image sharing scheme in color images using small shadow images. Inf. Sci. 2008, 178, 2433–2447. [Google Scholar] [CrossRef]
- Chang, C.C.; Wu, M.N. An algorithm for color image compression base on common bit map block truncation coding. In Proceedings of the 6th Joint Conference on Information Science, Research Triangle Park, NC, USA, 8–13 March 2002; pp. 964–967. [Google Scholar]
- Tsai, D.S.; Horng, G.; Chen, T.H.; Huang, Y.T. A novel secret image sharing scheme for true-color images with size constraint. Inf. Sci. 2009, 179, 3247–3254. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.Y.; Tseng, C.S. Secret image hiding and sharing based on the (t, n)-threshold. Fundam. Inform. 2007, 76, 399–411. [Google Scholar]
- Chang, C.C.; Chen, Y.H.; Wang, H.C. Meaningful secret sharing technique with authentication and remedy abilities. Inf. Sci. 2011, 181, 3073–3084. [Google Scholar] [CrossRef]
- Eslami, Z.; Razzaghi, S.H.; Ahmadabadi, J.Z. Secret image sharing based on cellular automata and steganography. Pattern Recognit. 2010, 43, 397–404. [Google Scholar] [CrossRef]
- Eslami, Z.; Ahmadabadi, J.Z. Secret image sharing with authentication-chaining and dynamic embedding. J. Syst. Softw. 2011, 84, 803–809. [Google Scholar] [CrossRef]
- Lin, P.Y.; Chan, C.S. Invertible secret image sharing with steganography. Pattern Recognit. Lett. 2010, 31, 1887–1893. [Google Scholar] [CrossRef]
- Wu, C.C.; Kao, S.J.; Hwang, M.S. A high quality image sharing with steganography and adaptive authentication scheme. J. Syst. Softw. 2011, 84, 2196–2207. [Google Scholar] [CrossRef]
- Wu, X.; Ou, D.; Ling, Q.; Sun, W. A user-friendly secret image sharing scheme with reversible steganography based on cellular automata. J. Syst. Softw. 2012, 85, 1852–1863. [Google Scholar] [CrossRef]
- Liu, Y.; Chang, C.C. A Turtle Shell-Based Visual Secret Sharing Scheme with Reversibility and Authentication. Multimed. Tools Appl. 2018, 77, 25295–25310. [Google Scholar] [CrossRef]
- Anbarasi, L.J.; Mala, A. EPR hidden medical image secret sharing using DNA cryptography. Int. J. Eng. Technol. 2014, 6, 1346–1356. [Google Scholar]
- Fatma, E.; Hikal, N.A.; Abou-Chadi, F.E.Z. Secret medical image sharing and EPR data embedding scheme over cloud computing environment. Int. J. Comput. Appl. 2013, 69, 19–26. [Google Scholar]
- Tso, H.K.; Lo, T.M.; Chen, W.K. Friendly medical image sharing scheme. J. Inf. Hiding Multimed. Signal Process. 2014, 5, 367–378. [Google Scholar]
- Ulutas, M.; Ulutas, G.; Nabiyev, V.V. Medical image security and EPR hiding using Shamir’s secret sharing scheme. J. Syst. Softw. 2011, 84, 341–353. [Google Scholar] [CrossRef]
- Morelos-Zaragoza, R.H. The Art of Error Correcting Coding, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Yang, C.N.; Yu, K.H.; Lukac, R. User-friendly image sharing using polynomials with different primes. Int. J. Imaging Syst. Technol. 2007, 17, 40–47. [Google Scholar] [CrossRef]
- Thien, C.C.; Lin, J.C. An image-sharing method with user-friendly shadow images. IEEE Trans. Circuits Syst. 2003, 13, 1161–1169. [Google Scholar] [CrossRef]
- Islam, M.S.; Kim, C.H.; Kim, J.M. Computationally efficient implementation of a hamming code decoder using graphics processing unit. J. Commun. Netw. 2014, 17, 198–202. [Google Scholar] [CrossRef]
- Vo, H.P. User-friendly sharing system using polynomials with different primes in two images. Int. J. Comput. Appl. 2014, 86, 40–45. [Google Scholar]
| Comparison of Experiment Results | |||||||
|---|---|---|---|---|---|---|---|
| Pair 1 | Pair 2 | Pair 3 | Pair 4 | ||||
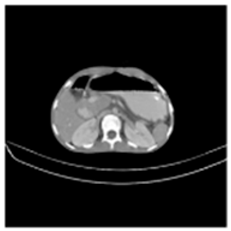 (1-1) | 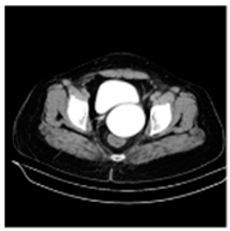 (1-2) | 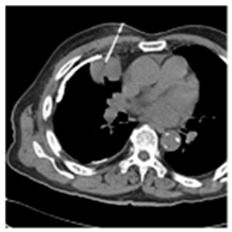 (1-3) | 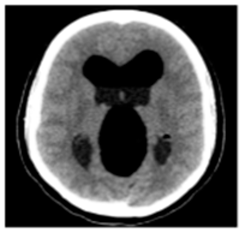 (1-4) | 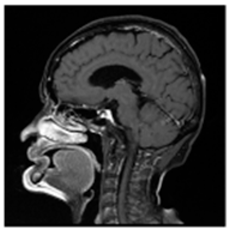 (1-5) | 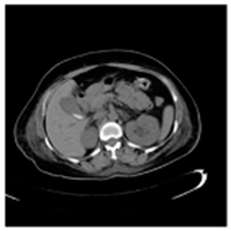 (1-6) | 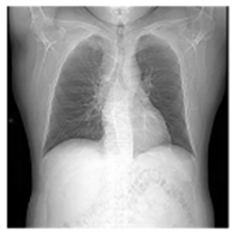 (1-7) | 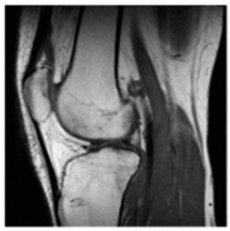 (1-8) |
| Original Medical Images | |||||||
| Pair 1 | Pair 2 | Pair 3 | Pair 4 | ||||
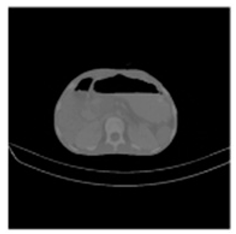 (1-9) PSNR = 44.14 | 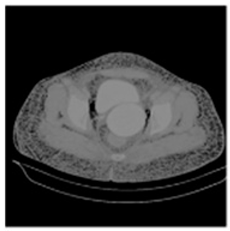 (1-10) PSNR = 41.90 | 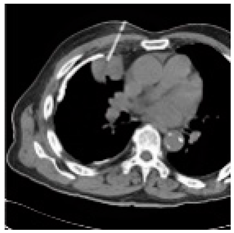 (1-11) PSNR = 40.09 | 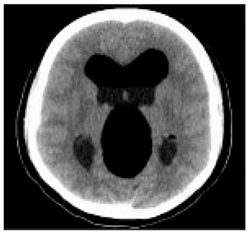 (1-12) PSNR = 41.41 | 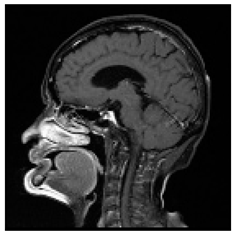 (1-13) PSNR = 42.24 | 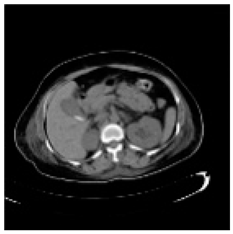 (1-14) PSNR = 40.35 | 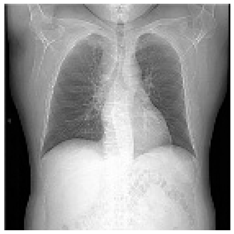 (1-15) PSNR = 40.79 | 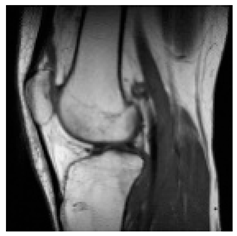 (1-16) PSNR = 40.84 |
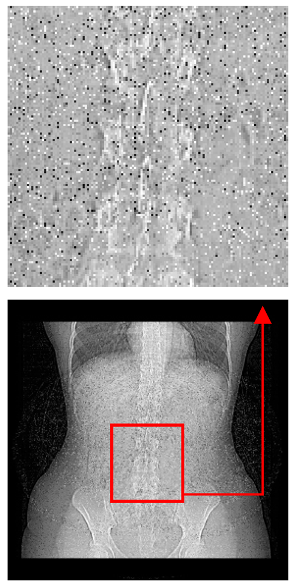
| Shadow Images Produced by Using LSBs | |||||||
| Pair 1 | Pair 2 | Pair 3 | Pair 4 | ||||
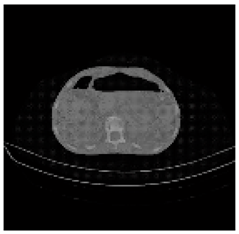 (1-17) PSNR = 26.35 | 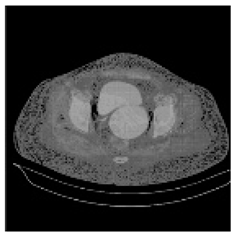 (1-18) PSNR = 25.49 | 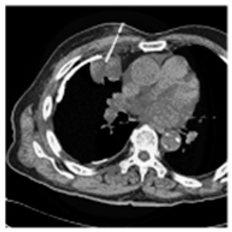 (1-19) PSNR = 23.57 | 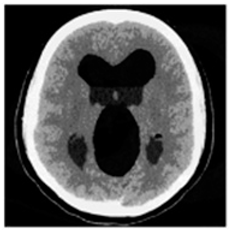 (1-20) PSNR = 24.19 | 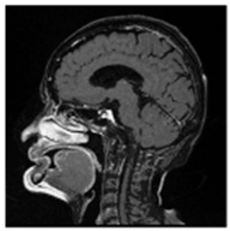 (1-21) PSNR = 24.79 | 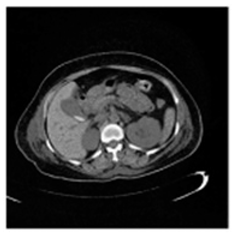 (1-22) PSNR = 24.23 | 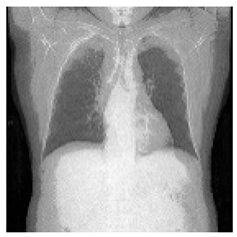 (1-23) PSNR = 23.26 | 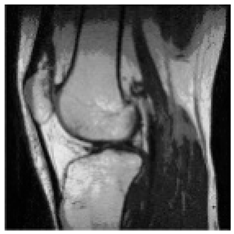 (1-24) PSNR = 24.42 |
| Shadow Images Produced by Using Middle Bits | |||||||
| Pair 1 | Pair 2 | Pair 3 | Pair 4 | ||||
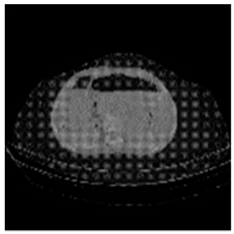 (1-25) PSNR = 18.97 | 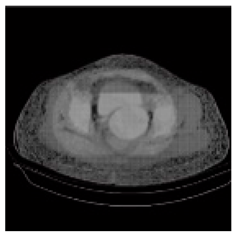 (1-26) PSNR = 19.95 | 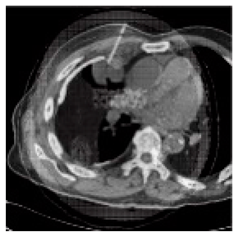 (1-27) PSNR = 14.10 | 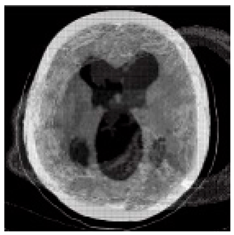 (1-28) PSNR = 13.84 | 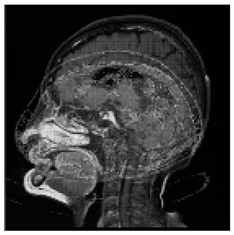 (1-29) PSNR = 16.66 | 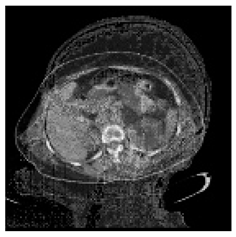 (1-30) PSNR = 13.23 | 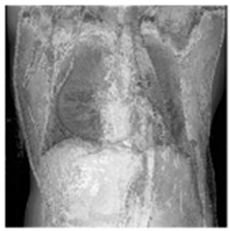 (1-31) PSNR = 13.38 | 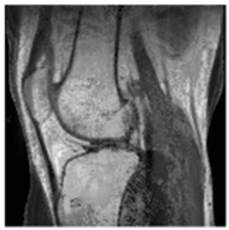 (1-32) PSNR = 14.75 |
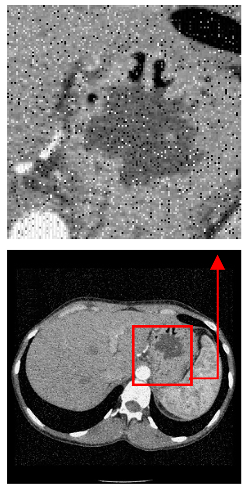
| Shadow Images Produced by Using MSBs | |||||||
| Comparison of Experiment Results | |||||||
|---|---|---|---|---|---|---|---|
| Pair 1 | Pair 2 | Pair 3 | Pair 4 | ||||
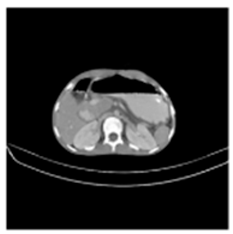 (2-1) | 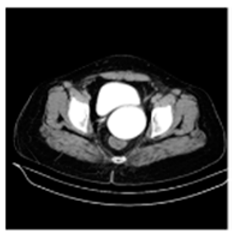 (2-2) | 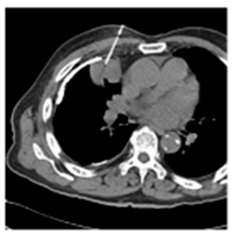 (2-3) | 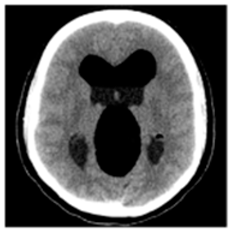 (2-4) | 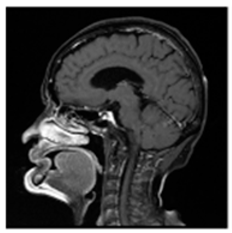 (2-5) | 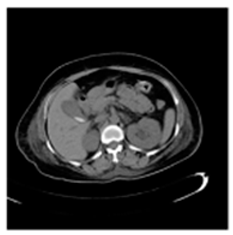 (2-6) | 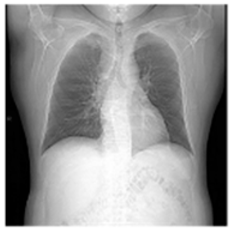 (2-7) | 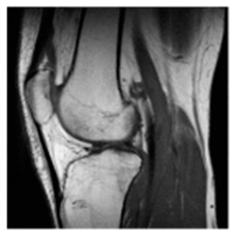 (2-8) |
| Original Medical Images | |||||||
| Pair 1 | Pair 2 | Pair 3 | Pair 4 | ||||
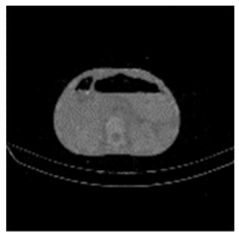 (2-9) PSNR = 28.96 | 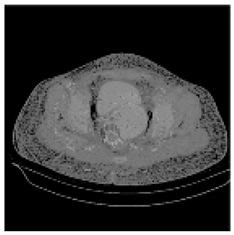 (2-10) PSNR = 27.37 | 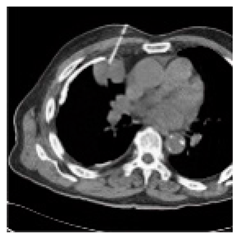 (2-11) PSNR = 26.90 | 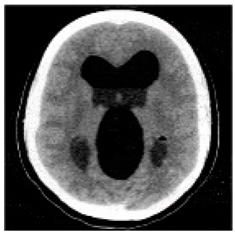 (2-12) PSNR = 23.66 | 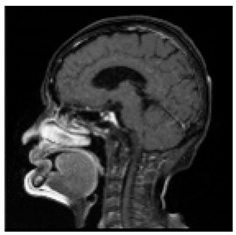 (2-13) PSNR = 25.20 | 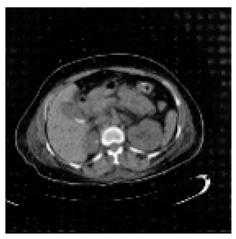 (2-14) PSNR = 21.09 | 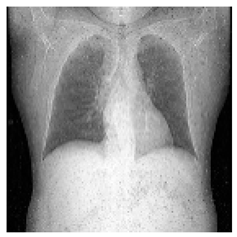 (2-15) PSNR = 21.82 | 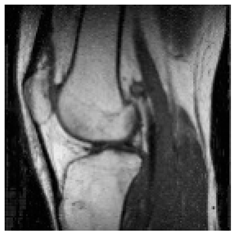 (2-16) PSNR = 21.05 |
| Shadow Images Produced by Using LSBs | |||||||
| Pair 1 | Pair 2 | Pair 3 | Pair 4 | ||||
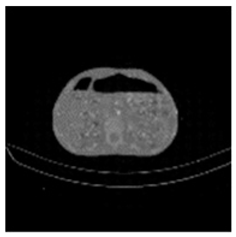 (2-17) PSNR = 26.84 | 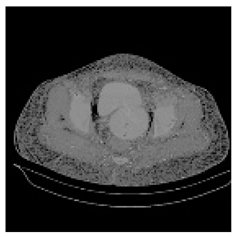 (2-18) PSNR = 27.55 | 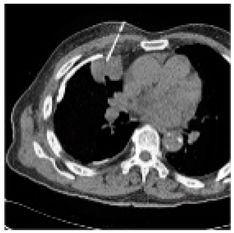 (2-19) PSNR = 22.14 | 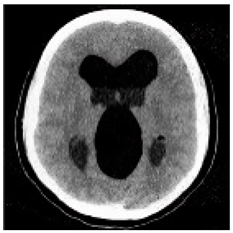 (2-20) PSNR = 21.52 | 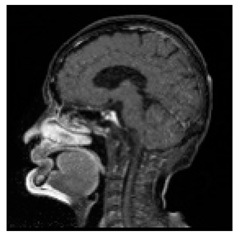 (2-21) PSNR = 21.99 | 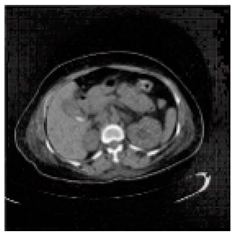 (2-22) PSNR = 17.63 | 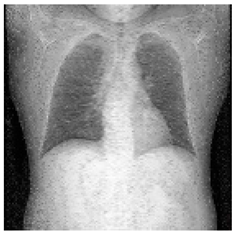 (2-23) PSNR = 19.14 | 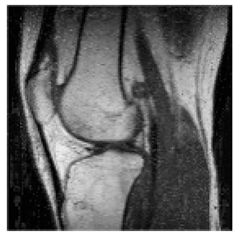 (2-24) PSNR = 19.32 |
| Shadow images produced by using MSBs | |||||||
| Original Medical Images | Shadow Images Produced by Using (7,4) Hamming Code (MSBs) | ||
|---|---|---|---|
| Pair 1 | Pair 2 | ||
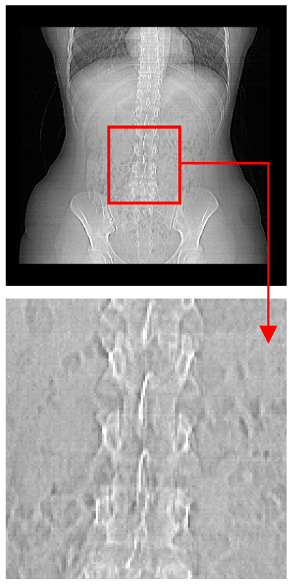 | 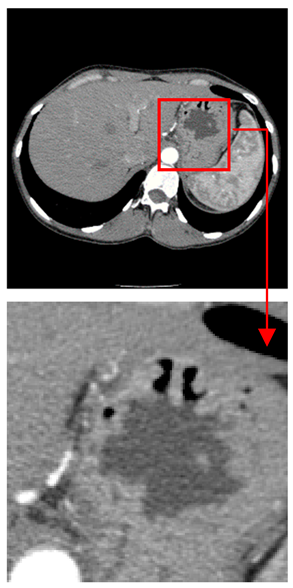 | 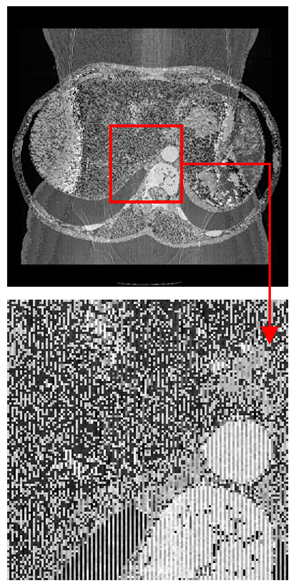 |  |
 |  | 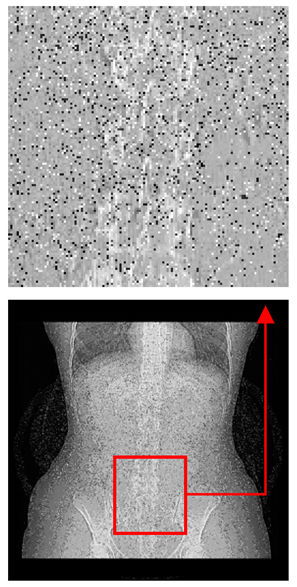 | 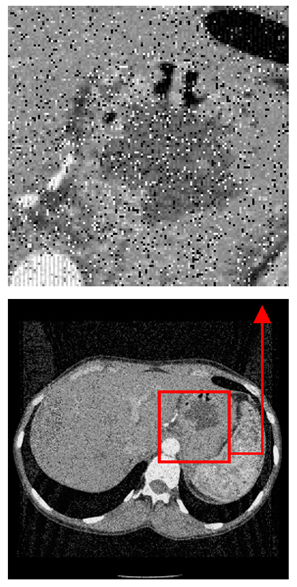 |
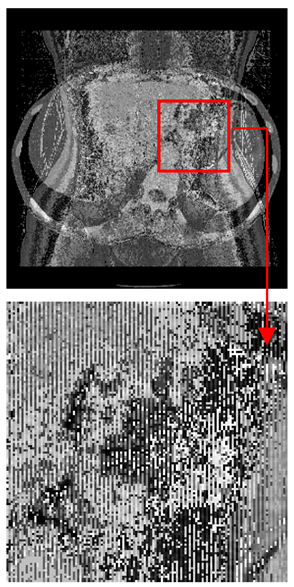
| Pair 3 | Pair 4 | ||
| Shadow images produced by using (15,11) Hamming code (LSBs) | Shadow images produced by using (15,11) Hamming code (MSBs) | ||
| Methods | Time (s) | |||
|---|---|---|---|---|
| (MSBSs) | Creating Shadow (s) | Reconstructing Original Images (s) | Execution Time (s) | |
| (7,4) Hamming code | Pair 1 | 0.6060 | 0.6104 | 1.2164 |
| Pair 2 | 0.6653 | 0.6711 | 1.3364 | |
| Pair 3 | 0.6507 | 0.6576 | 1.3083 | |
| Pair 4 | 0.6344 | 0.6908 | 1.3252 | |
| (15,11) Hamming code | Pair 1 | 0.7054 | 0.8147 | 1.5201 |
| Pair 2 | 0.7534 | 0.8403 | 1.5937 | |
| Pair 3 | 0.6996 | 0.8011 | 1.5007 | |
| Pair 4 | 0.7704 | 0.8715 | 1.6419 | |
| Average | 0.6857 | 0.7447 | 1.4303 | |
| Features | Ref. [31] | Ref. [34] | Ref. [32] | Ref. [37] | Ours (MSBs) |
| Kernel | Magic matrix | Random grid | DNA cryptography | Polynomial | Hamming code |
| Average Execution Time (s) | 1.38 | 0.18 | - | - | 0.69 |
| Visual Perception (PSNR) | 51.72/45.70 | - | 46.8–47 | <30 | 19.15/18.47 |
| Non-Expanded Pixel | Yes | Yes | No | Yes | Yes |
| Lossless Recovery | Yes | Yes | Yes | No | Yes |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Chang, C.-C.; Bai, J.; Le, H.-D.; Chen, C.-C.; Meen, T.-H. Hamming Code Strategy for Medical Image Sharing. Appl. Syst. Innov. 2020, 3, 8. https://doi.org/10.3390/asi3010008
Li L, Chang C-C, Bai J, Le H-D, Chen C-C, Meen T-H. Hamming Code Strategy for Medical Image Sharing. Applied System Innovation. 2020; 3(1):8. https://doi.org/10.3390/asi3010008
Chicago/Turabian StyleLi, Li, Ching-Chun Chang, Junlan Bai, Hai-Duong Le, Chi-Cheng Chen, and Teen-Hang Meen. 2020. "Hamming Code Strategy for Medical Image Sharing" Applied System Innovation 3, no. 1: 8. https://doi.org/10.3390/asi3010008
APA StyleLi, L., Chang, C.-C., Bai, J., Le, H.-D., Chen, C.-C., & Meen, T.-H. (2020). Hamming Code Strategy for Medical Image Sharing. Applied System Innovation, 3(1), 8. https://doi.org/10.3390/asi3010008






