Investigation of a Cross-Section with a Constant Transverse Shear Stress Distribution Using a Numerical Approach
Abstract
1. Introduction
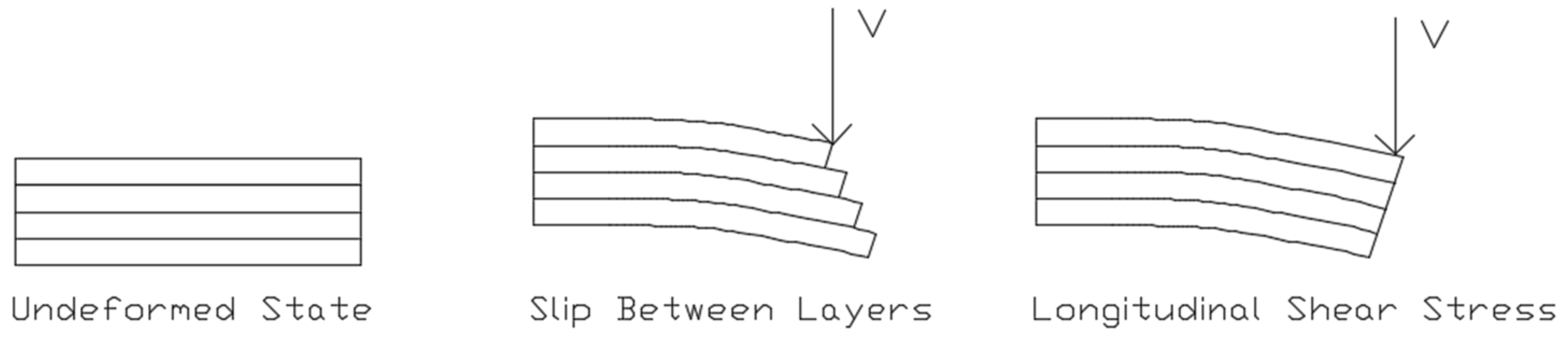
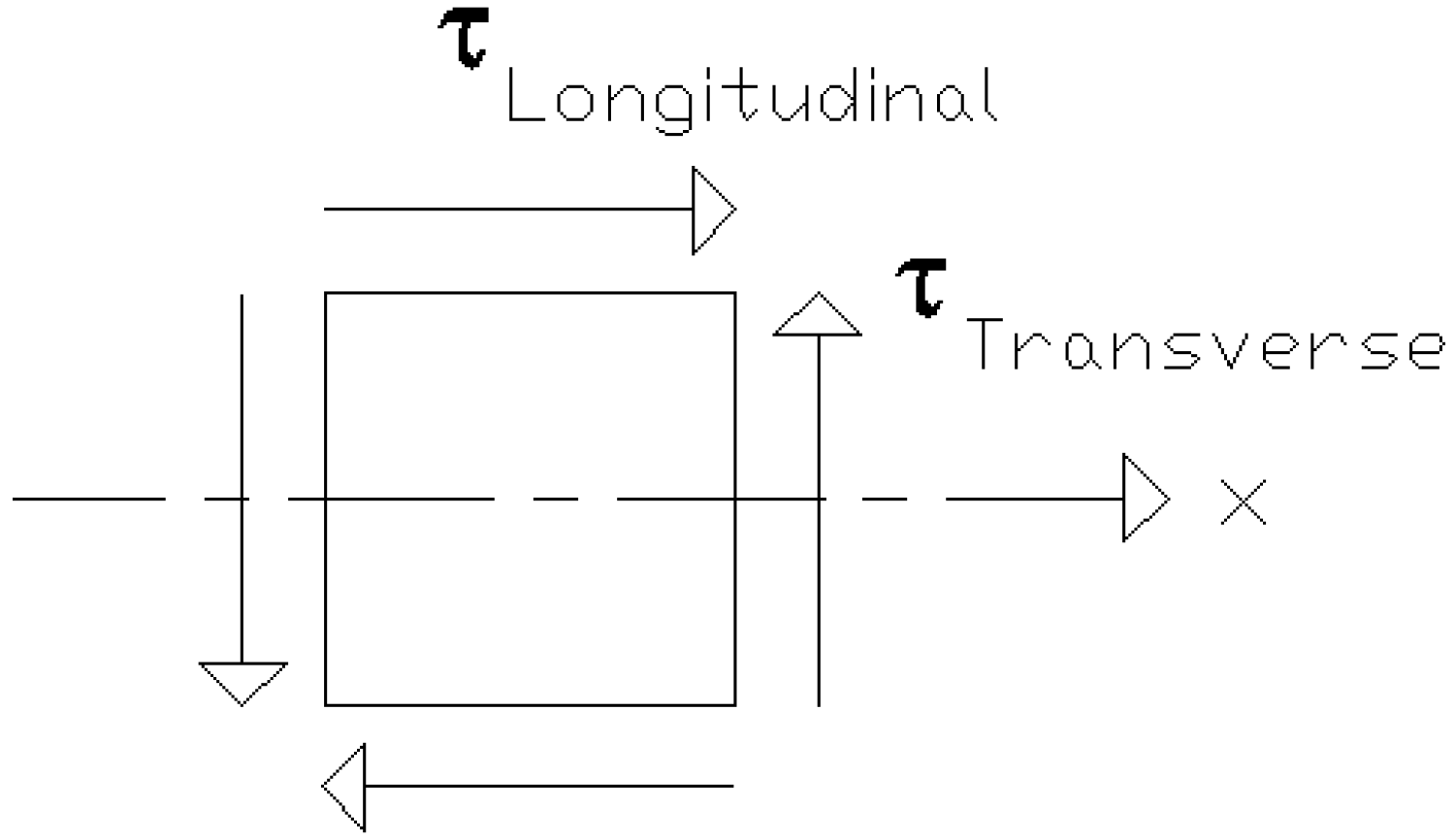
2. Theory
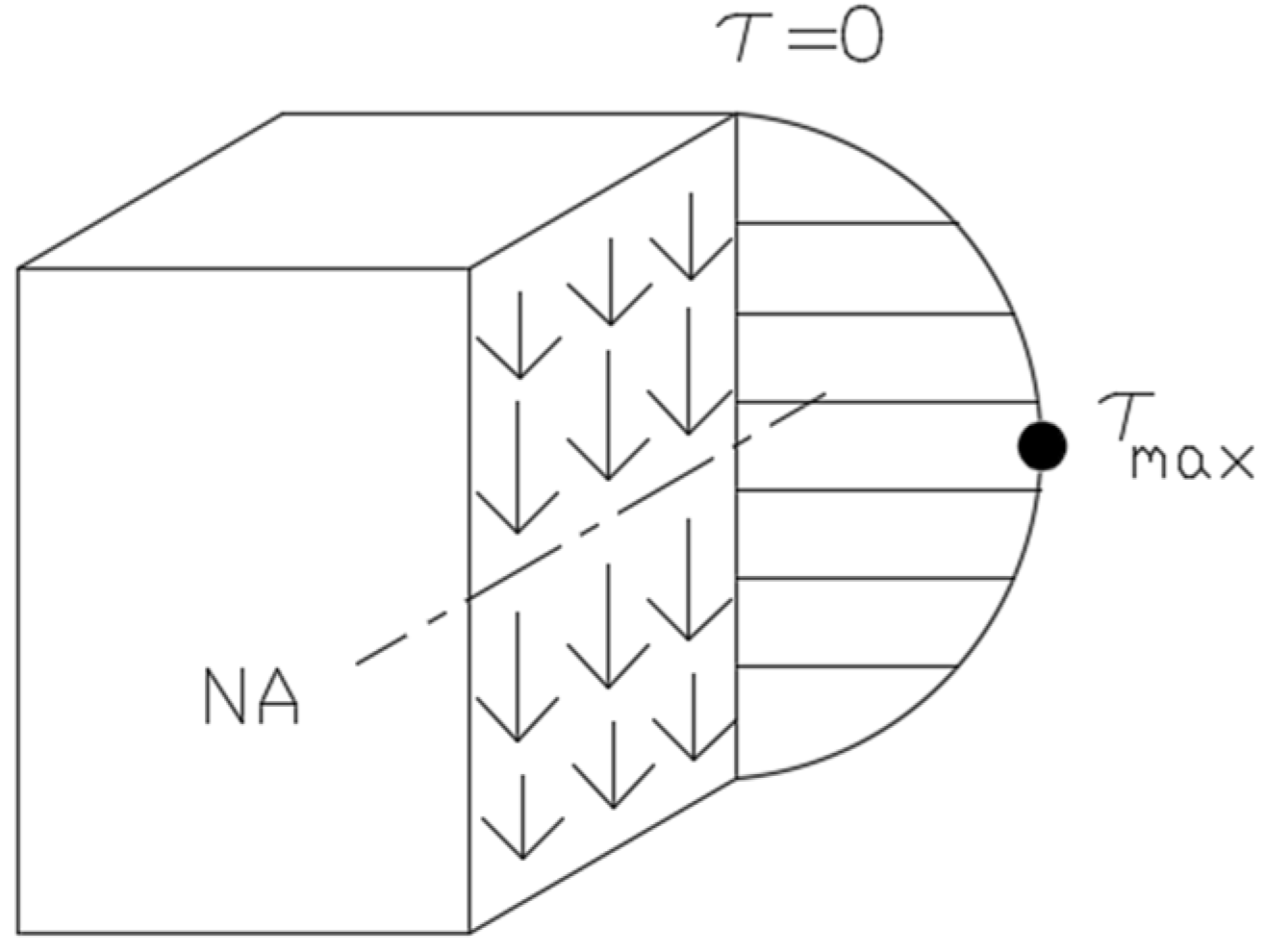
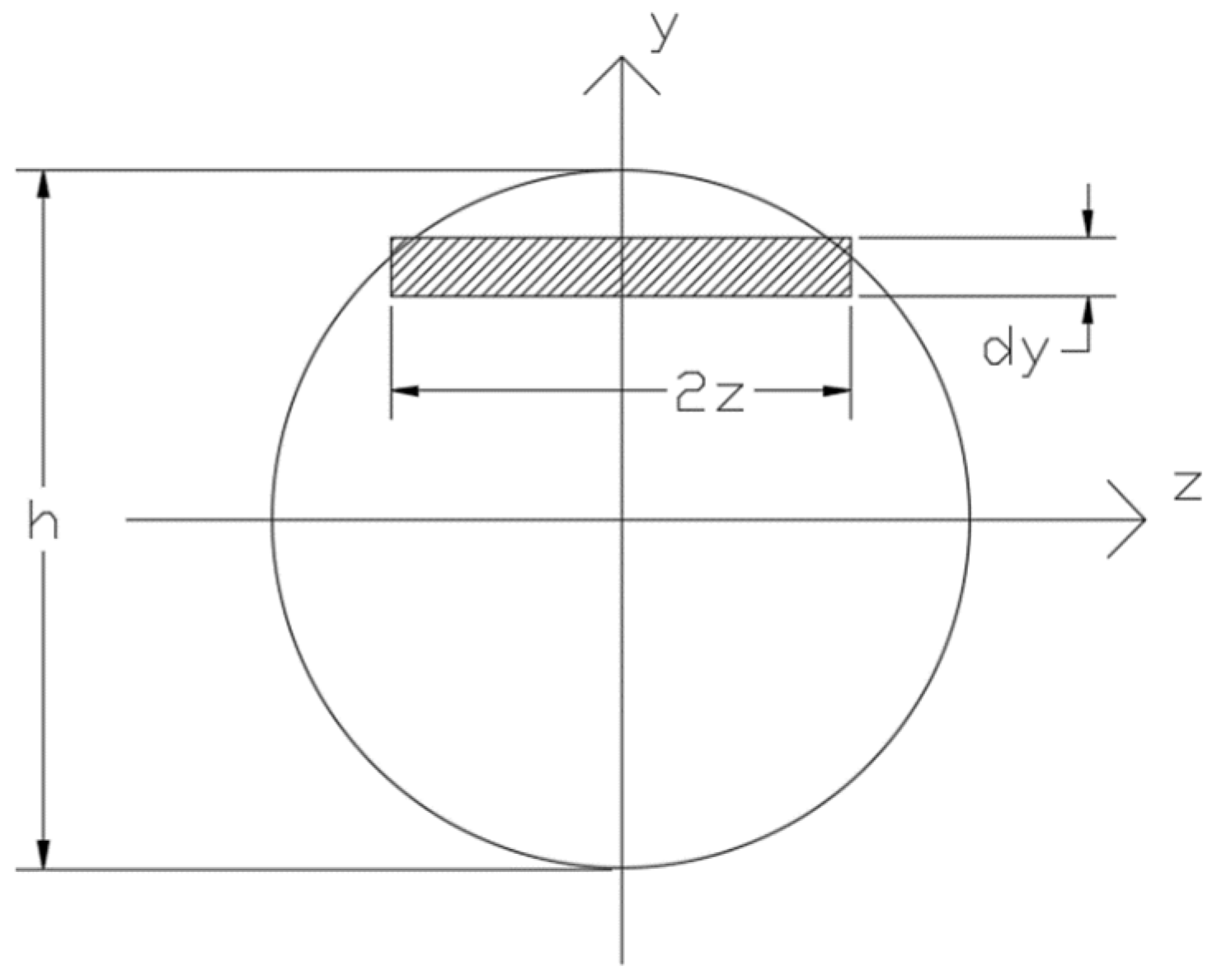
2.1. Transverse Shear Stress Distribution Within a Cross-Section—Analytical Formulation
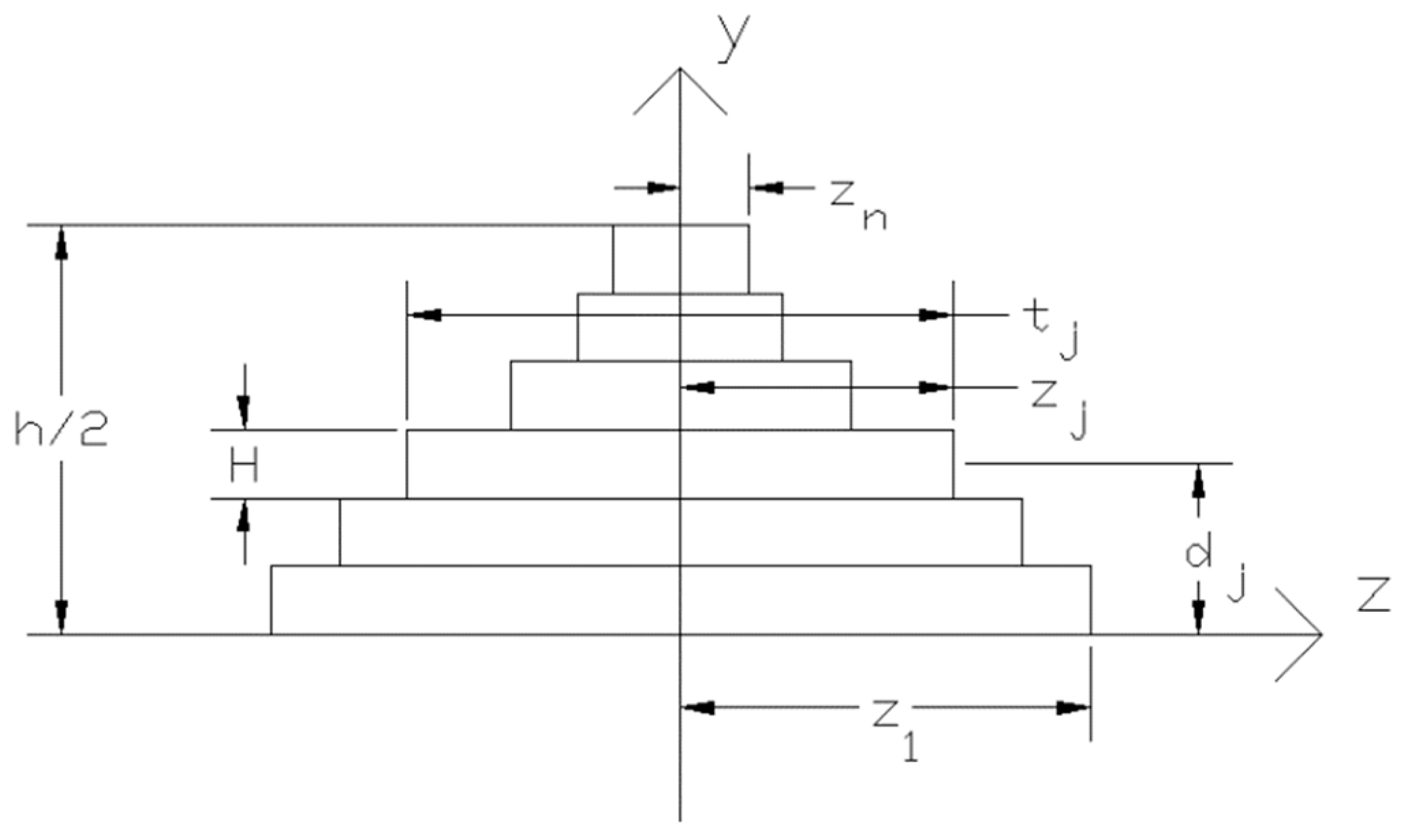
2.2. Transverse Shear Stress Distribution Within a Cross-Section—Numerical Formulation
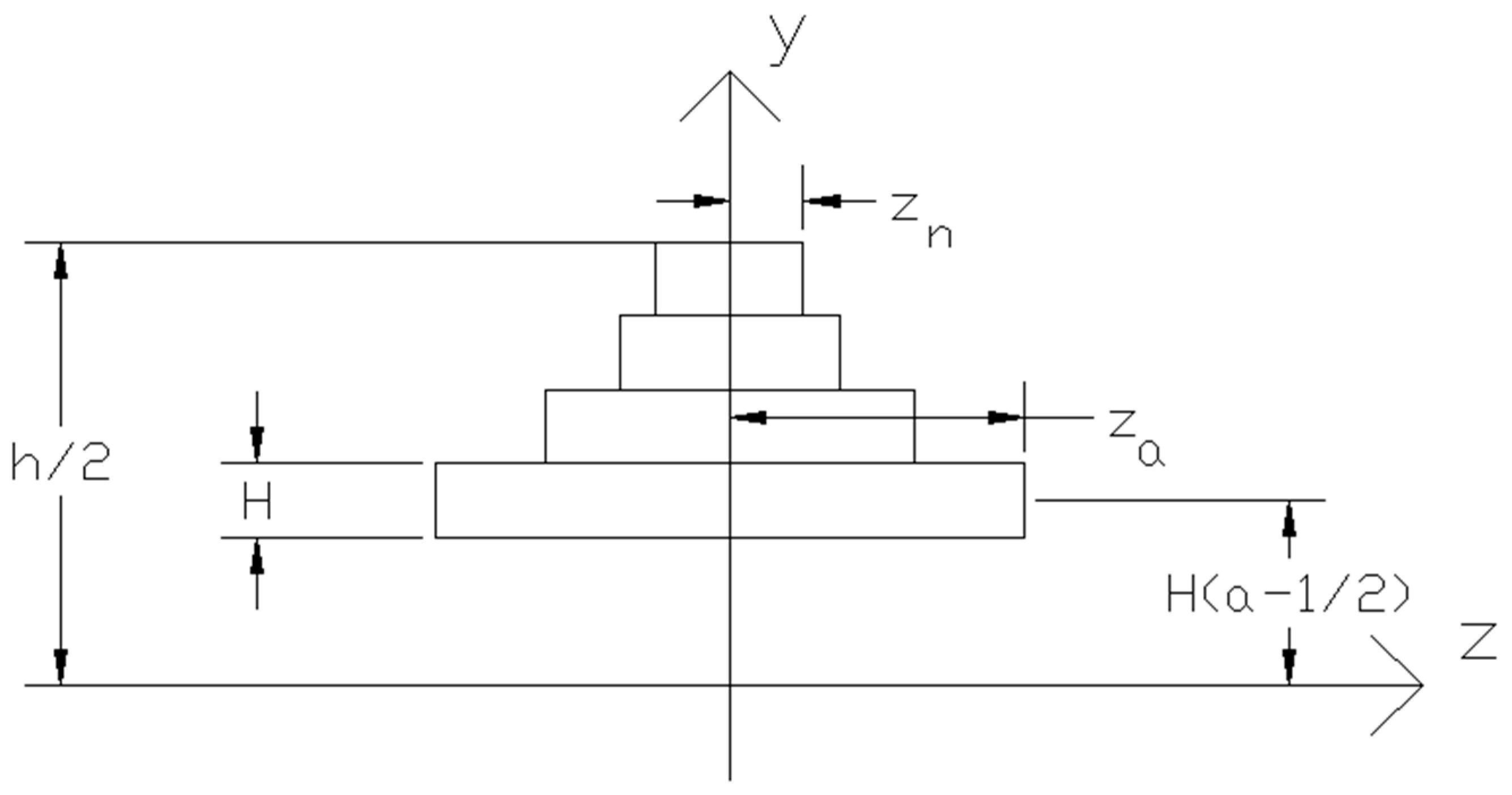
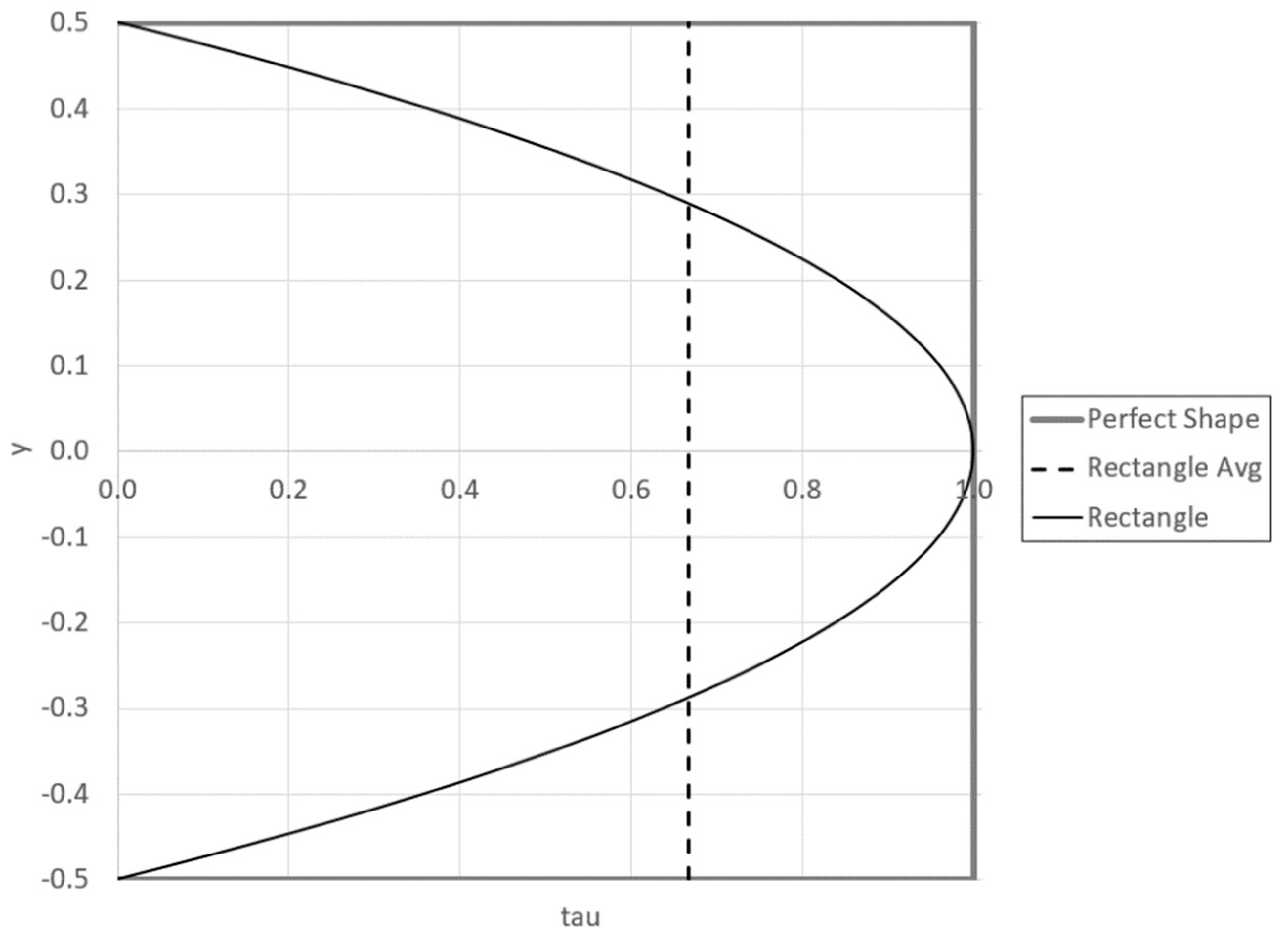
2.3. Constant Transverse Shear Stress Distribution
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Area | |
| Area of Discrete Element | |
| Area Used to Calculate | |
| Numerical Index Where Stress Is Calculated | |
| Constant Relating and | |
| Centroid of Discrete Element | |
| Flare-out Point | |
| Height of Discrete Element | |
| Cross-section Height | |
| Area Moment of Inertia | |
| Area Moment of Inertia of Discrete Element | |
| Element Index | |
| Neutral Axis of Cross-section | |
| Total Number of Discrete Elements for Top Half of Cross-section | |
| First Moment of Area | |
| First Moment of Area Where Transverse Shear Stress is Calculated | |
| Sectional Width of Cross-section Where Transverse Shear Stress is Calculated | |
| Thickness of Discrete Element | |
| Shear Force Carried by the Section, Found from the Shear Force Diagram | |
| Vertical Component of Cross-section | |
| Centroid of Area Used to Calculate | |
| Centroid of Component Area Used to Calculate | |
| Horizontal Component of Cross-section | |
| Half Width of Discrete Element Where Transverse Shear Stress is Calculated | |
| Half Width of Discrete Element | |
| Half Width of Top Discrete Element | |
| Ratio of Widest to Thinnest Discrete Element | |
| Transverse Shear Stress | |
| Average Transverse Shear Stress | |
| Transverse Shear Stress at Discrete Element a | |
| Efficiency of Cross-section | |
| Maximum Transverse Shear Stress |
References
- Ennos, A.R. transverse stresses and modes of failure in tree branches and other beams. Proc. R. Soc. 2009. [Google Scholar] [CrossRef] [PubMed]
- Bardella, L.; Tonelli, D. Explicit analytic solutions for the accurate evaluation of the shear stresses in sandwich beams. J. Eng. Mech. 2012, 138, 502–507. [Google Scholar] [CrossRef]
- Askarinejad, H.; Dhanasekar, M.; Boyd, P.; Taylor, R. Field Measurement of Wheel-Rail Impact Force at Insulated Rail Joint. In Proceedings of the Society for Experimental Mechanics, Brisbane, Australia, 23 September 2012. [Google Scholar]
- Bernardi, P.; Cerioni, R.; Michelini, E.; Sirico, A. Transverse reinforcement optimization of a precast special roof element through an experimental and numerical procedure. Eng. Struct. 2020, 203, 109894. [Google Scholar] [CrossRef]
- Jewett, J.; Carstensen, J. Experimental investigation of strut-and-tie layouts in deep RC beams designed with hybrid bi-linear topology optimization. Eng. Struct. 2019, 197, 109322. [Google Scholar] [CrossRef]
- Liu, S.; An, X.; Jia, H. Topology optimization of beam cross-section considering warping deformation. Struct. Multidiscip. Optim. 2008, 35, 403–411. [Google Scholar] [CrossRef]
- Craig, R. Mechanics of Materials, 3rd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Xia, Y. Transverse Shear in Beams; Lecture Note; The Hong Kong Polytechnic University, Department of Civil Structural Engineering: Hong Kong, China, 2017. [Google Scholar]
- Szaroletta William, K. Utilizing Spreadsheet Solver Methods to Determine Optimal Beam Geometry; Purdue University: West Lafayette, Indiana, 2003. [Google Scholar]
- Mehne, H. On solving constrained shape optimization problems for finding the optimum shape of a bar cross-section. Appl. Numer. Math. 2007, 58, 1129–1141. [Google Scholar] [CrossRef]
- Sapountzakis, E.J.; Mokos, V.G. A BEM solution to transverse shear loading of beams. Comput. Mech. 2005, 36, 384–397. [Google Scholar] [CrossRef]
- Finney, R.L.; Thomas, G.B.; Demana, F.; Waits, B.K. Calculus, 1st ed.; Addison-Wesley Publishing: Boston, MA, USA, 1994. [Google Scholar]
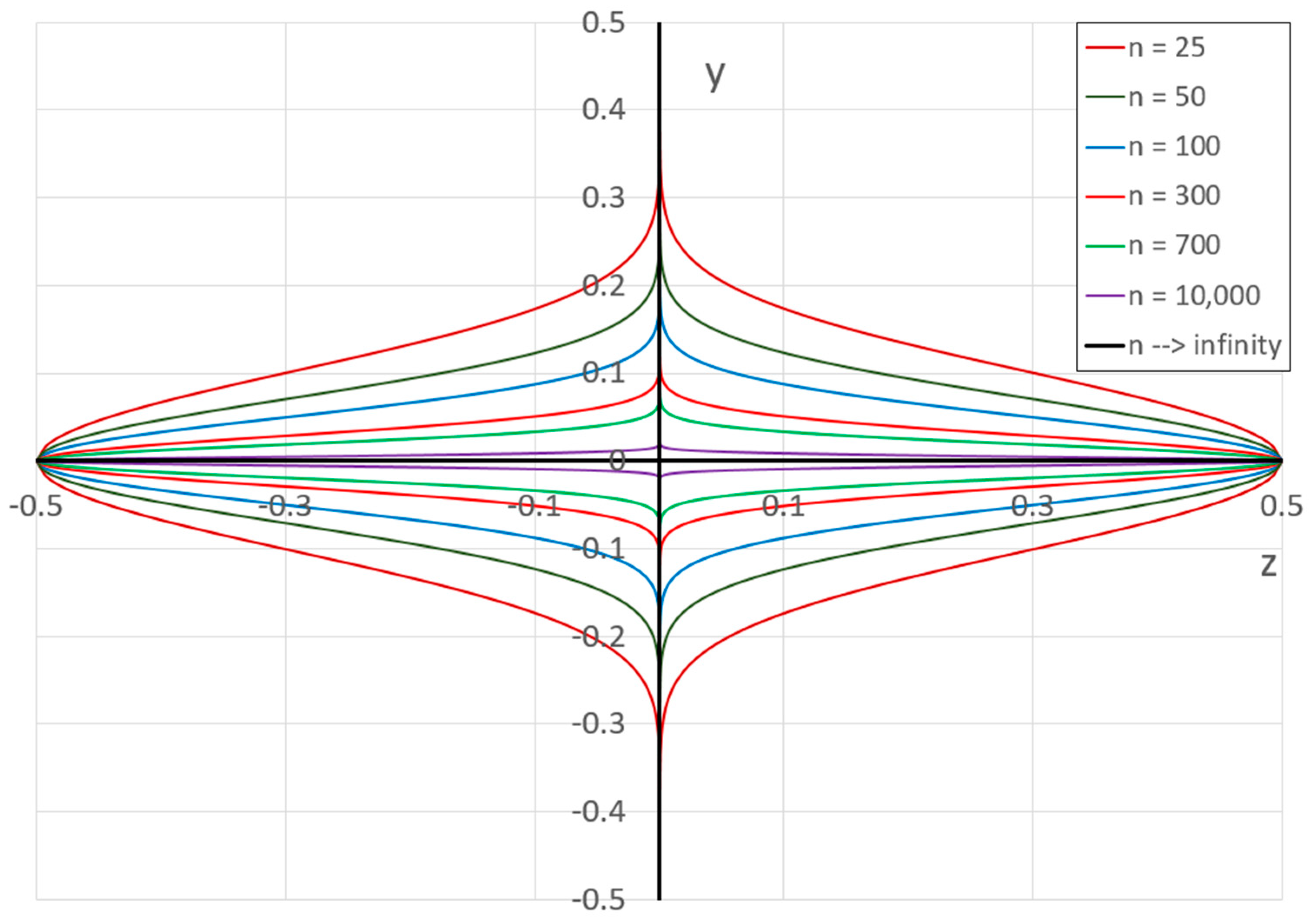
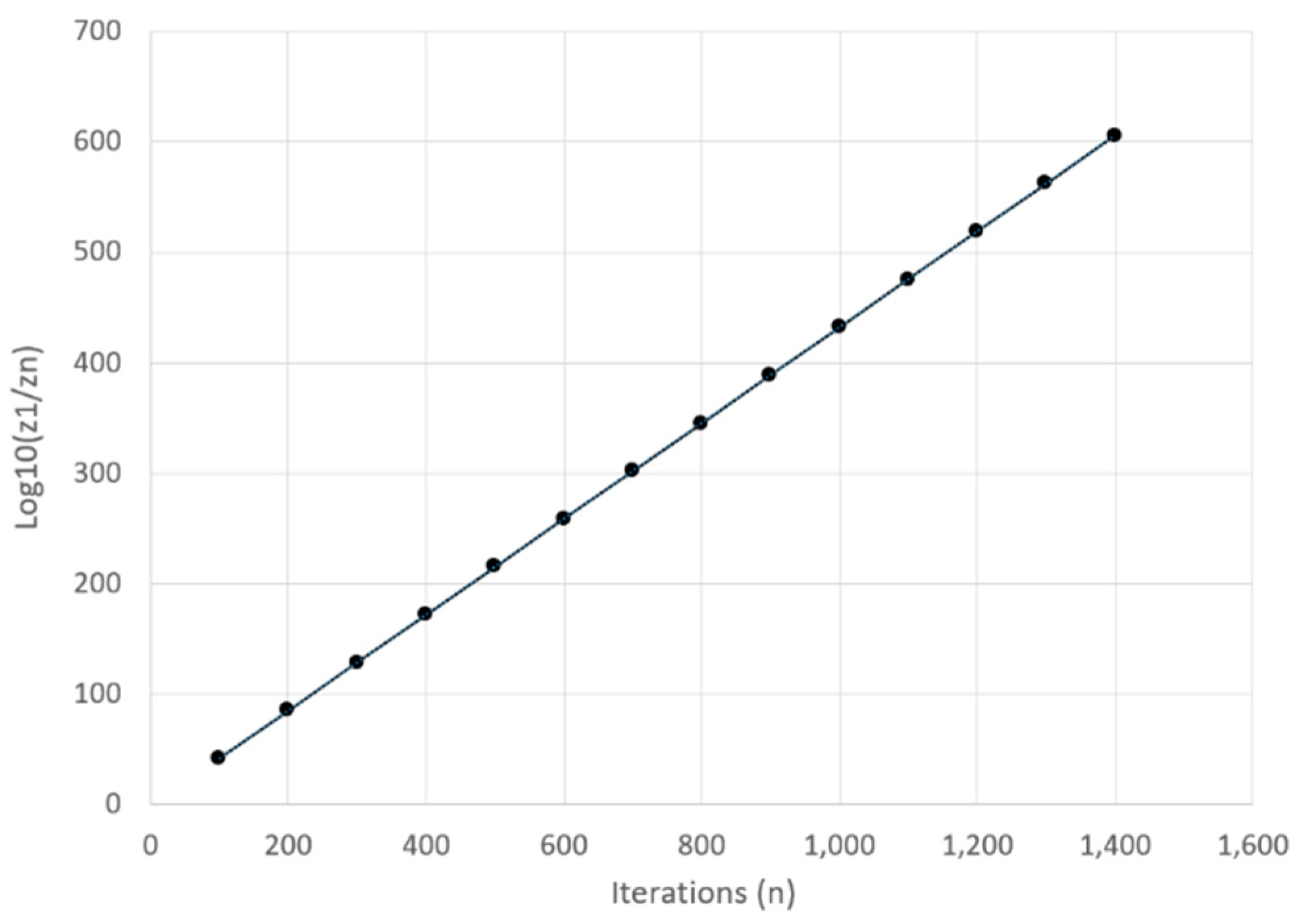
| 100 | 41.81 | 43.21 | 0.1717 | 99.00% |
| 200 | 85.09 | 86.43 | 0.1206 | 99.50% |
| 300 | 128.43 | 129.64 | 0.0987 | 99.67% |
| 400 | 171.80 | 172.85 | 0.0865 | 99.75% |
| 500 | 215.18 | 216.07 | 0.0772 | 99.80% |
| 600 | 258.57 | 259.28 | 0.0710 | 99.83% |
| 700 | 301.97 | 302.49 | 0.0658 | 99.86% |
| 800 | 345.37 | 345.71 | 0.0613 | 99.88% |
| 900 | 388.77 | 388.92 | 0.0578 | 99.89% |
| 1000 | 432.18 | 432.13 | 0.0551 | 99.90% |
| 1100 | 475.59 | 475.35 | 0.0523 | 99.91% |
| 1200 | 519.00 | 518.56 | 0.0505 | 99.92% |
| 1300 | 562.41 | 561.77 | 0.0485 | 99.92% |
| 1400 | 605.82 | 604.99 | 0.0465 | 99.93% |
| n | log(n) | Ratio Name | |||
|---|---|---|---|---|---|
| 7 | 0.84 | 1.0 | 1 | Ten | 85.51706% |
| 9 | 0.96 | 100 | 2 | Hundred | 89.13779% |
| 12 | 1.06 | 1000 | 3 | Thousand | 91.31023% |
| 18 | 1.27 | 1.0 × 106 | 6 | Million | 94.56880% |
| 25 | 1.40 | 1.0 × 109 | 9 | Billion | 96.05011% |
| 32 | 1.51 | 1.0 × 1012 | 12 | Trillion | 96.89651% |
| 235 | 2.37 | 1.0 × 10100 | 100 | Googol | 99.57403% |
| 702 | 2.85 | 1.0 × 10303 | 303 | Centillion | 99.85754% |
| 1400 | 3.15 | 1.0 × 10606 | 606 | 99.92857% | |
| 2319 | 3.37 | 1.0 × 101000 | 1000 | 99.95687% | |
| 2,314,103 | 6.36 | 1.0 × 101,000,000 | 1.0 × 106 | 99.99995% | |
| 2.31 × 109 | 9.36 | 1.0× 101,000,000,000 | 1.0× 109 | 99.99999% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bednarz, E.T.; Mulligan, R.R. Investigation of a Cross-Section with a Constant Transverse Shear Stress Distribution Using a Numerical Approach. Appl. Syst. Innov. 2020, 3, 3. https://doi.org/10.3390/asi3010003
Bednarz ET, Mulligan RR. Investigation of a Cross-Section with a Constant Transverse Shear Stress Distribution Using a Numerical Approach. Applied System Innovation. 2020; 3(1):3. https://doi.org/10.3390/asi3010003
Chicago/Turabian StyleBednarz, Edward T., and Ryan R. Mulligan. 2020. "Investigation of a Cross-Section with a Constant Transverse Shear Stress Distribution Using a Numerical Approach" Applied System Innovation 3, no. 1: 3. https://doi.org/10.3390/asi3010003
APA StyleBednarz, E. T., & Mulligan, R. R. (2020). Investigation of a Cross-Section with a Constant Transverse Shear Stress Distribution Using a Numerical Approach. Applied System Innovation, 3(1), 3. https://doi.org/10.3390/asi3010003





