Surface Aggregation Adsorption of Binary Solutions Between Diiodomethane, Furfural, and N,N-Dimethylformamide
Abstract
1. Introduction
2. Experimental Section and Theoretical Basis
2.1. Chemicals
2.2. Surface Tension Determination
2.3. Theoretical Basis
2.4. Model Fitting
3. Results and Discussion
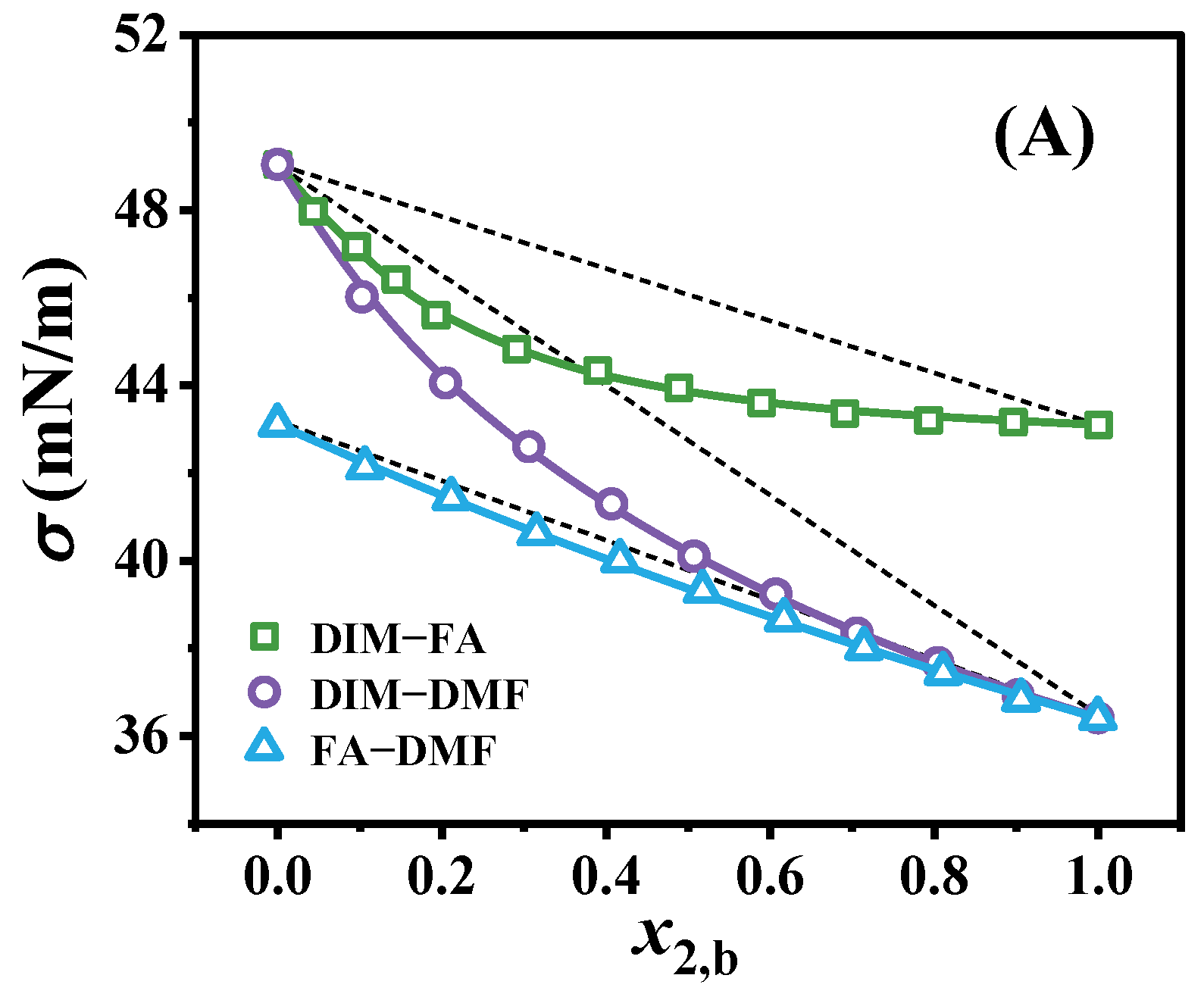
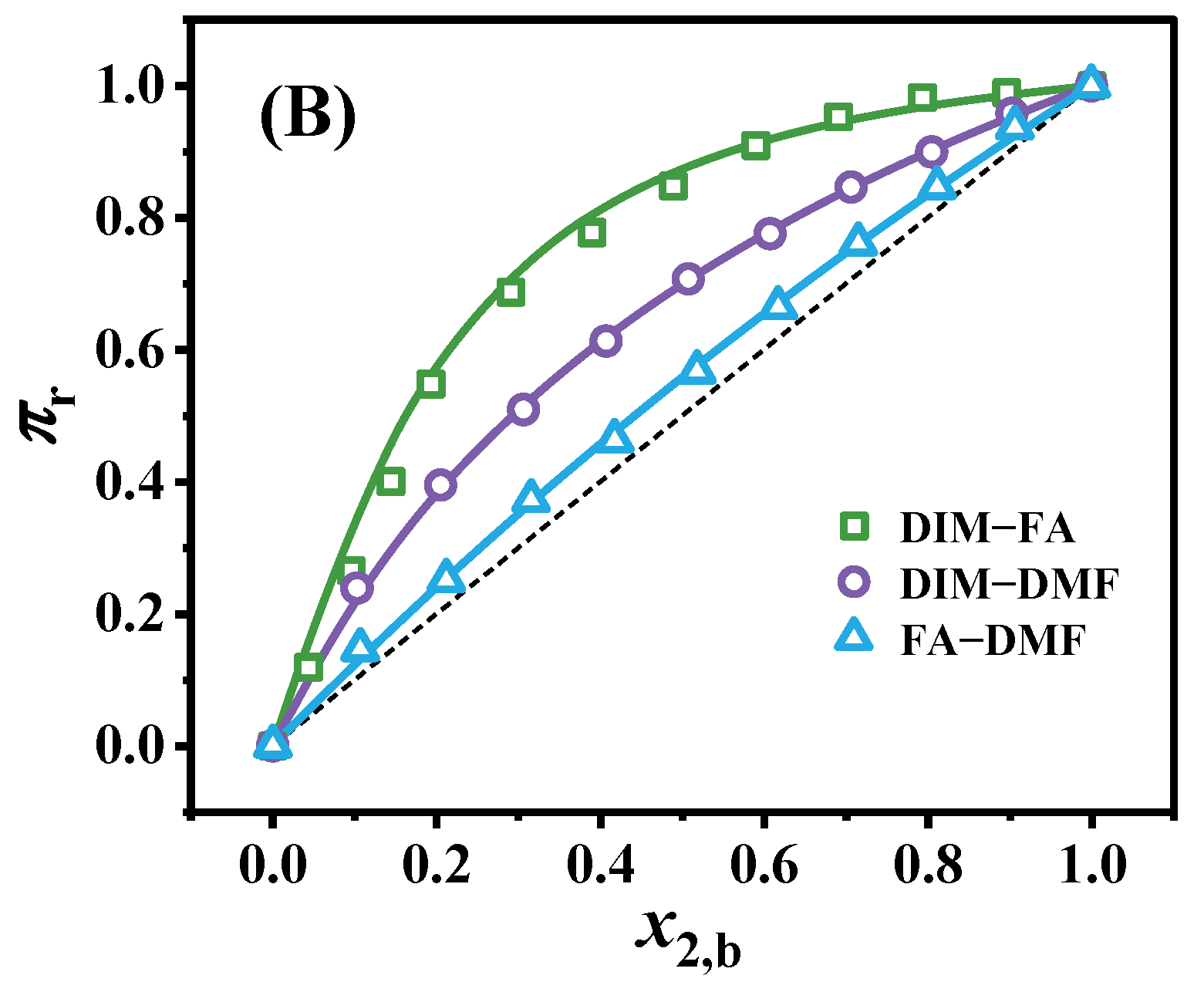
3.1. Surface Aggregation Adsorption
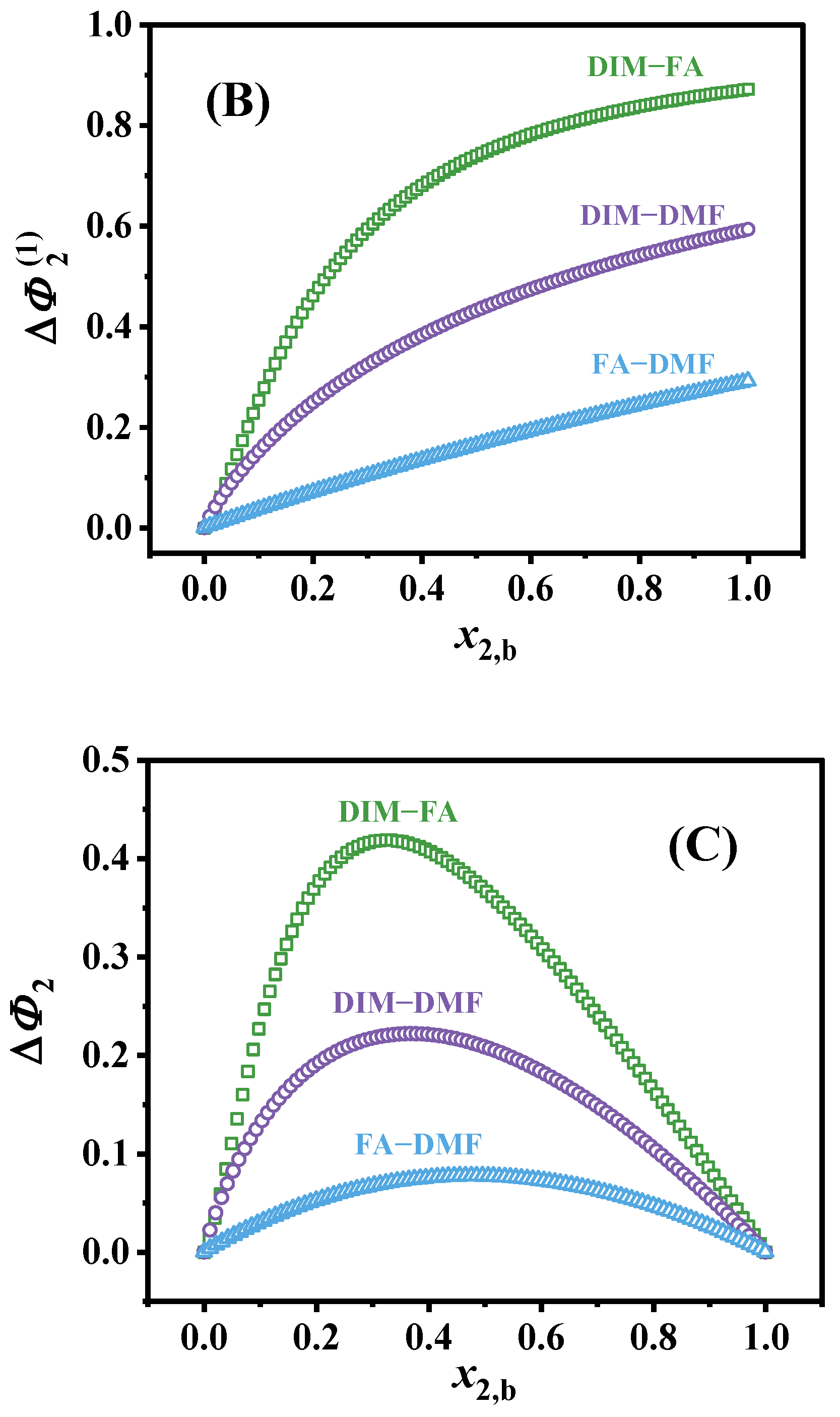
3.2. The Surface Excess
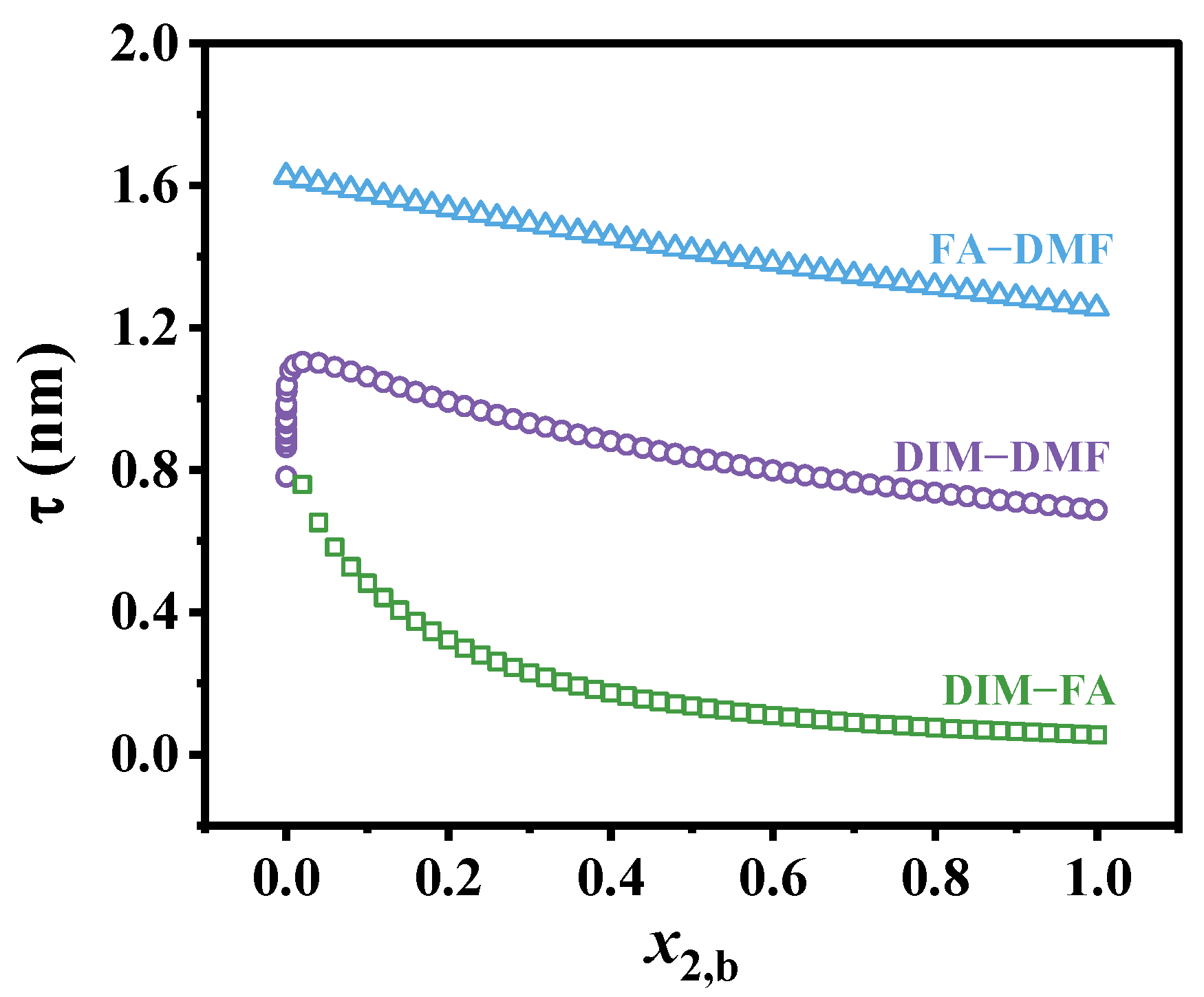
3.3. Adsorption Layer Thickness
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marmur, A. Interfaces at equilibrium: A guide to fundamentals. Adv. Colloid Interface Sci. 2017, 244, 164–173. [Google Scholar] [CrossRef]
- Kaptay, G. The chemical (not mechanical) paradigm of thermodynamics of colloid and interface science. Adv. Colloid Interface Sci. 2018, 256, 163–192. [Google Scholar] [CrossRef]
- Kleinheins, J.; Shardt, N.; Haber, M.E.; Ferronato, C.; Nozière, B.; Peter, T.; Marcolli, C. Surface tension models for binary aqueous solutions: A review and intercomparison. Phys. Chem. Chem. Phys. 2023, 25, 11055–11074. [Google Scholar] [CrossRef] [PubMed]
- Fellows, A.P.; Duque, Á.D.; Balos, V.; Lehmann, L.; Netz, R.R.; Wolf, M.; Thämer, M. Sum-frequency generation spectroscopy of aqueous interfaces: The role of depth and its impact on spectral interpretation. J. Phys. Chem. C 2024, 128, 20733–20750. [Google Scholar] [CrossRef]
- Privat, M.; Bennes, R.; Tronel-Peyroz, E. Ellipsometry and adsorption: The determination of isotherms and the adsorbed layer thickness and fluctuations of the composition in the liquid-vapor interface. J. Colloid Interface Sci. 1988, 121, 198–207. [Google Scholar] [CrossRef]
- Douillard, J.M. Experimental approach of the relation between surface tension and interfacial thickness of simple liquids. J. Colloid Interface Sci. 2009, 337, 307–310. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.X.; Lu, J.R.; Styrkas, D.A.; Thomas, R.K.; Rennie, A.R.; Penfold, J. The structure of the surface of ethanol/water mixtures. Mol. Phys. 1993, 80, 925–939. [Google Scholar] [CrossRef]
- Hyde, A.E.; Ohshio, M.; Nguyen, C.V.; Yusa, S.I.; Yamada, N.L.; Phan, C.M. Surface properties of ethanol/water mixtures: Thickness and composition. J. Mol. Liq. 2019, 290, 111005. [Google Scholar] [CrossRef]
- Raina, G.; Kulkarni, G.U.; Rao, C.N.R. Surface enrichment in alcohol−water mixtures. J. Phys. Chem. A 2001, 105, 10204–10207. [Google Scholar] [CrossRef]
- Chen, H.; Gan, W.; Wu, B.H.; Wu, D.; Guo, Y.; Wang, H.F. Determination of structure and energetics for Gibbs surface adsorption layers of binary liquid mixture 1. Acetone + water. J. Phys. Chem. B 2005, 109, 8053–8063. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Hou, J.; Li, X.; Lu, Z. The influence of sodium iodide salt on the interfacial properties of aqueous methanol solution by a combined molecular simulation and sum frequency generation vibrational spectroscopy study. Langmuir 2019, 35, 7050–7059. [Google Scholar] [CrossRef]
- Kirmse, K.; Morgner, H. Binary liquid mixtures. The relation between surface tension and surface composition as studied by mies (metastable induced electron spectroscopy). Langmuir 2006, 22, 2193–2199. [Google Scholar] [CrossRef]
- Rafati, A.A.; Bagheri, A.; Khanchi, A.R.; Ghasemian, E.; Najafi, M. Application of the UNIFAC model for prediction of surface tension and thickness of the surface layer in the binary mixtures. J. Colloid Interface Sci. 2011, 355, 252–258. [Google Scholar] [CrossRef]
- Azizian, S.; Moghadam, T.F. Derivation of a new equation for prediction of the thin layer depth of the extended-Langmuir model for dilute binary mixtures. Colloids Surfaces A 2011, 378, 67–71. [Google Scholar] [CrossRef]
- Lemraski, E.G.; Pouyanfar, Z. Prediction of surface tension, surface mole fraction and thickness of the surface layer in the ionic liquid binary mixtures. J. Mol. Liq. 2015, 203, 52–58. [Google Scholar] [CrossRef]
- Bermúdez-Salguero, C.; Gracia-Fadrique, J. Gibbs excess and the calculation of the absolute surface composition of liquid binary mixtures. J. Phys. Chem. B 2015, 119, 5598–5608. [Google Scholar] [CrossRef] [PubMed]
- Bagheri, A.; Fazli, M.; Bakhshaei, M. Surface properties and surface thickness of aqueous solutions of alcohols. J. Mol. Liq. 2016, 224, 442–451. [Google Scholar] [CrossRef]
- Santos, M.S.C.S.; Reis, J.C.R. Thermodynamic evaluation of molar surface area and thickness of water + ethanol mixtures. J. Mol. Liq. 2018, 255, 419–428. [Google Scholar] [CrossRef]
- Hernández, A.; Tahery, R. Modeling of surface tension and phase equilibria for water + amine mixtures from (298.15 to 323.15) K using different thermodynamic models. J. Solut. Chem. 2022, 51, 31–57. [Google Scholar] [CrossRef]
- Ma, W.; Du, N.; Hou, W. Predicting surface tension and surface composition of multicomponent liquid mixtures. (I) Ternary mixtures of isopropanol, water, and n-decane or n-tetradecane. Chem. Phys. 2025, 595, 112718. [Google Scholar] [CrossRef]
- Jia, Q.; Du, N.; Deng, Q.; Hou, W. Effect of temperature on the surface aggregation adsorption of water–alcohol binary mixtures. J. Mol. Liq. 2025, 431, 127825. [Google Scholar] [CrossRef]
- Gibbs, J.W. On the equilibrium of heterogeneous substances. Trans. Conn. Acad. Arts Sci. 1878, 3, 441–458. [Google Scholar] [CrossRef]
- Butler, J.A.V. The thermodynamics of the surfaces of solutions. Proc. R. Soc. London Ser. A 1932, 138, 348–375. [Google Scholar]
- Guggenheim, E.A.; Adam, N.K. The thermodynamics of adsorption at the surface of solutions. Proc. R. Soc. London Ser. A 1933, 139, 218–236. [Google Scholar]
- Eberhart, J.G. The surface tension of binary liquid mixtures. J. Phys. Chem. 1966, 70, 1183–1186. [Google Scholar] [CrossRef]
- Shereshefsky, J.L. A theory of surface tension of binary solutions I. Binary liquid mixtures of organic compounds. J. Colloid Interface Sci. 1967, 24, 317–321. [Google Scholar] [CrossRef]
- Connors, K.A.; Wright, J.L. Dependence of surface tension on composition of binary aqueous-organic solutions. Anal. Chem. 1989, 61, 194–198. [Google Scholar] [CrossRef]
- Laaksonen, A.; Kulmala, M. An explicit cluster model for binary nuclei in water–alcohol systems. J. Chem. Phys. 1991, 95, 6745–6748. [Google Scholar] [CrossRef]
- Piñeiro, Á.; Brocos, P.; Amigo, A.; Gracia-Fadrique, J.; Lemus, M.G. Extended Langmuir isotherm for binary liquid mixtures. Langmuir 2001, 17, 4261–4266. [Google Scholar] [CrossRef]
- Bermúdez-Salguero, C.; Clavijo-Penagos, J.A.; Romero, C.M.; Gracia-Fadrique, J. New insight into surface tension inverted curvature for liquid-liquid and solid-liquid binary mixtures: The special case of hexamethylenetetramine in water. Colloid Surf. A 2014, 448, 53–59. [Google Scholar] [CrossRef]
- Phan, C.M. The surface tension and interfacial composition of water–ethanol mixture. J. Mol. Liq. 2021, 342, 117505. [Google Scholar] [CrossRef]
- Phan, C.M. Affinity of amphiphilic molecules to air/water surface. ACS Omega 2023, 8, 47928–47937. [Google Scholar] [CrossRef]
- Qi, W.; Yu, X.; Du, N.; Hou, W. General adsorption model to describe sigmoidal surface tension isotherms of binary liquid mixtures. Langmuir 2023, 39, 507–518. [Google Scholar] [CrossRef]
- Qi, W.; Hou, W. A model for predicting the surface tension and composition of multicomponent liquid mixtures. Sci. Sin. Chim. 2023, 53, 1236–1246. [Google Scholar] [CrossRef]
- Mulero, Á.; Hernández, A.; Vadillo-Rodríguez, V.; Cachadiña, I. Correlations of surface tension for mixtures of n-alkanes as a function of the composition: Applicability and performance analysis of existing models. Phys. Chem. Chem. Phys. 2025, 27, 12812–12836. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.; Qi, W.; Deng, Q.; Hou, W. Surface adsorption of water-alcohol binary solutions. Chem. J. Chin. Univ. 2023, 44, 20230316. [Google Scholar]
- Belton, J.W.; Evans, M.G. Studies in the molecular forces involved in surface formation. II. The surface free energies of simple liquid mixtures. Trans. Faraday Soc. 1945, 41, 1–12. [Google Scholar] [CrossRef]
- Ma, P. Handbook of Basic Data of Petrochemical Industries; Chemical Industry Press: Beijing, China, 1982. [Google Scholar]
- Jańczuk, B.; Wójcik, W.; Zdziennicka, A. Determination of the components of the surface tension of some liquids from interfacial liquid-liquid tension measurements. J. Colloid Interface Sci. 1993, 157, 384–393. [Google Scholar] [CrossRef]
- Balkenende, A.R.; van de Boogaard, H.J.A.P.; Scholten, M.; Willard, N.P. Evaluation of different approaches to assess the surface tension of low-energy solids by means of contact angle measurements. Langmuir 1998, 14, 5907–5912. [Google Scholar] [CrossRef]
- Oosterlaken, B.M.; van den Bruinhorst, A.; de With, G. On the use of probe liquids for surface energy measurements. Langmuir 2023, 39, 16701–16711. [Google Scholar] [CrossRef]
- Michaels, A.; Alexander, R.; Becker, C. Estimation of surface tensions. Ind. Eng. Chem. 1950, 42, 2332–2336. [Google Scholar] [CrossRef]
- Lomba, L.; Giner, B.; Bandrés, I.; Lafuente, C.; Pino, M.R. Physicochemical properties of green solvents derived from biomass. Green Chem. 2011, 13, 2062–2070. [Google Scholar] [CrossRef]
- Lomba, L.; Giner, B.; Lopéz, M.C.; Aldea, L.; Lafuente, C. Thermophysical properties of furfural compounds. Chem. Eng. Data 2014, 59, 329–338. [Google Scholar] [CrossRef]
- Rafati, A.A.; Ghasemian, E.; Iloukhani, H. Surface tension and surface properties of binary mixtures of 1,4-dioxane or N,N-dimethyl formamide with n-alkyl acetates. J. Chem. Eng. Data 2009, 54, 3224–3228. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, L.; Yue, X.; Li, B.; Zhang, J. Density, viscosity, surface tension and spectroscopic studies for the liquid mixture of tetraethylene glycol + N,N-dimethyl formamide at six temperatures. J. Mol. Liq. 2018, 264, 451–457. [Google Scholar] [CrossRef]
- Yano, Y.F. Correlation between surface and bulk structures of alcohol-water mixtures. J. Colloid Interface Sci. 2005, 284, 255–259. [Google Scholar] [CrossRef]
- Goldsack, D.E.; White, B.R. An iterative technique for calculating surface tensions of non-electrolyte solutions. Can. J. Chem. 1983, 61, 1725–1729. [Google Scholar] [CrossRef]
- Tronel-Peyroz, E.; Douillard, J.M.; Tenebre, L.; Bennes, R.; Privat, M. Associated complex formation in the liquid-vapor interface: The water-ethanol and water-tert-butyl alcohol systems. Langmuir 1987, 3, 1027–1034. [Google Scholar] [CrossRef]
- Nath, S. Surface tension of nonideal binary liquid mixtures as a function of composition. J. Colloid Interface Sci. 1999, 209, 116–122. [Google Scholar] [CrossRef] [PubMed]
- Santos, M.S.C.S.; Reis, J.C.R. New thermodynamics for evaluating the surface-phase enrichment in the lower surface tension component. ChemPhysChem 2014, 15, 2834–2843. [Google Scholar] [CrossRef] [PubMed]
- Tahery, R.; Modarress, H.; Satherley, J. Surface tension prediction and thermodynamic analysis of the surface for binary solutions. Chem. Eng. Sci. 2005, 60, 4935–4952. [Google Scholar] [CrossRef]
- Randles, J.E.B.; Behr, B. Adsorption at liquid interfaces. I. Surface tension at the interface between a binary liquid mixture and its vapour. J. Electroanal. Chem. 1972, 35, 389–404. [Google Scholar] [CrossRef]
- Azad, R.; Sharma, T.; Martin, D.; Daschakraborty, S.; Raj, R. Unraveling the surface activity of ethanol–water mixtures through experiments and molecular dynamics simulations. Langmuir 2024, 40, 17577–17589. [Google Scholar] [CrossRef] [PubMed]
- AbouHaidar, R.; Bougueroua, S.; Duflot, D.; Gaigeot, M.-P.; Wyslouzil, B.; Toubin, C. Unraveling aqueous alcohol freezing: New theoretical tools from graph theory to extract molecular processes in MD simulations. Faraday Discuss. 2025, 258, 396–418. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.X.; Lu, J.R.; Thomas, R.K.; Penfold, J. Neutron reflection study of butanol and hexanol adsorbed at the surface of their aqueous solutions. J. Chem. Soc. Faraday Trans. 1996, 92, 565–572. [Google Scholar] [CrossRef]
- Yano, Y.F. Surface structure of aqueous 2-butoxyethanol mixtures studied by x-ray reflection. J. Chem. Phys. 2002, 116, 8093–8096. [Google Scholar] [CrossRef]
- Fellows, A.P.; Duque, Á.D.; Balos, V.; Lehmann, L.; Netz, R.R.; Wolf, M.; Thämer, M. How thick is the air–water interface? A direct experimental measurement of the decay length of the interfacial structural anisotropy. Langmuir 2024, 40, 18760–18772. [Google Scholar] [CrossRef]


| Liquid | Mr (g/mol) | ρ0 (g/cm3) | ρc0 (g/cm3) | vb0 (cm3/mol) | vc0 (cm3/mol) | vs0 (cm3/mol) | ls (nm) |
|---|---|---|---|---|---|---|---|
| DIM | 267.84 | 3.33 | ~0.91 | 80.43 | ~297 | 176.1 | 0.66 |
| FA | 96.09 | 1.16 | 0.359 | 82.84 | 267.6 | 167.4 | 0.65 |
| DMF | 73.10 | 0.94 | 0.267 | 77.77 | 273.7 | 165.5 | 0.65 |
| Binary Solution | n | Kx* | Kx | AAD (mN/m) | ARD (%) | ∆Gad0 (kJ/mol) |
|---|---|---|---|---|---|---|
| DIM (1)–FA (2) | 1.27 | 8.45 | 6.37 | 0.059 | 0.13 | −3.62 |
| DIM (1)–DMF (2) | 0.92 | 2.21 | 2.47 | 0.042 | 0.10 | −2.44 |
| FA (1)–DMF (2) | 1.00 | 1.28 | 1.38 | 0.040 | 0.10 | −0.80 |
| Binary Solution | Γ2(x→1) (μmol/m2) | τx→0 (nm) | τx→1 (nm) | N2(x→0) | |
|---|---|---|---|---|---|
| DIM (1)–FA (2) | 0.29 | 0.88 | ~0.8 | 0.05 | 1.2 |
| DIM (1)–DMF (2) | 2.23 | 0.56 | 0.78 | 0.69 | 1.2 |
| FA (1)–DMF (2) | 2.09 | 0.28 | 1.62 | 1.25 | 2.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Du, N.; Hou, W. Surface Aggregation Adsorption of Binary Solutions Between Diiodomethane, Furfural, and N,N-Dimethylformamide. Colloids Interfaces 2025, 9, 67. https://doi.org/10.3390/colloids9050067
Huang Z, Du N, Hou W. Surface Aggregation Adsorption of Binary Solutions Between Diiodomethane, Furfural, and N,N-Dimethylformamide. Colloids and Interfaces. 2025; 9(5):67. https://doi.org/10.3390/colloids9050067
Chicago/Turabian StyleHuang, Zhongwei, Na Du, and Wanguo Hou. 2025. "Surface Aggregation Adsorption of Binary Solutions Between Diiodomethane, Furfural, and N,N-Dimethylformamide" Colloids and Interfaces 9, no. 5: 67. https://doi.org/10.3390/colloids9050067
APA StyleHuang, Z., Du, N., & Hou, W. (2025). Surface Aggregation Adsorption of Binary Solutions Between Diiodomethane, Furfural, and N,N-Dimethylformamide. Colloids and Interfaces, 9(5), 67. https://doi.org/10.3390/colloids9050067







