Adsorption and Dilational Viscoelasticity of Saponin at the β-Pinene/Water and Air/Water Interfaces
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Measurement of Dynamic Interfacial Tension
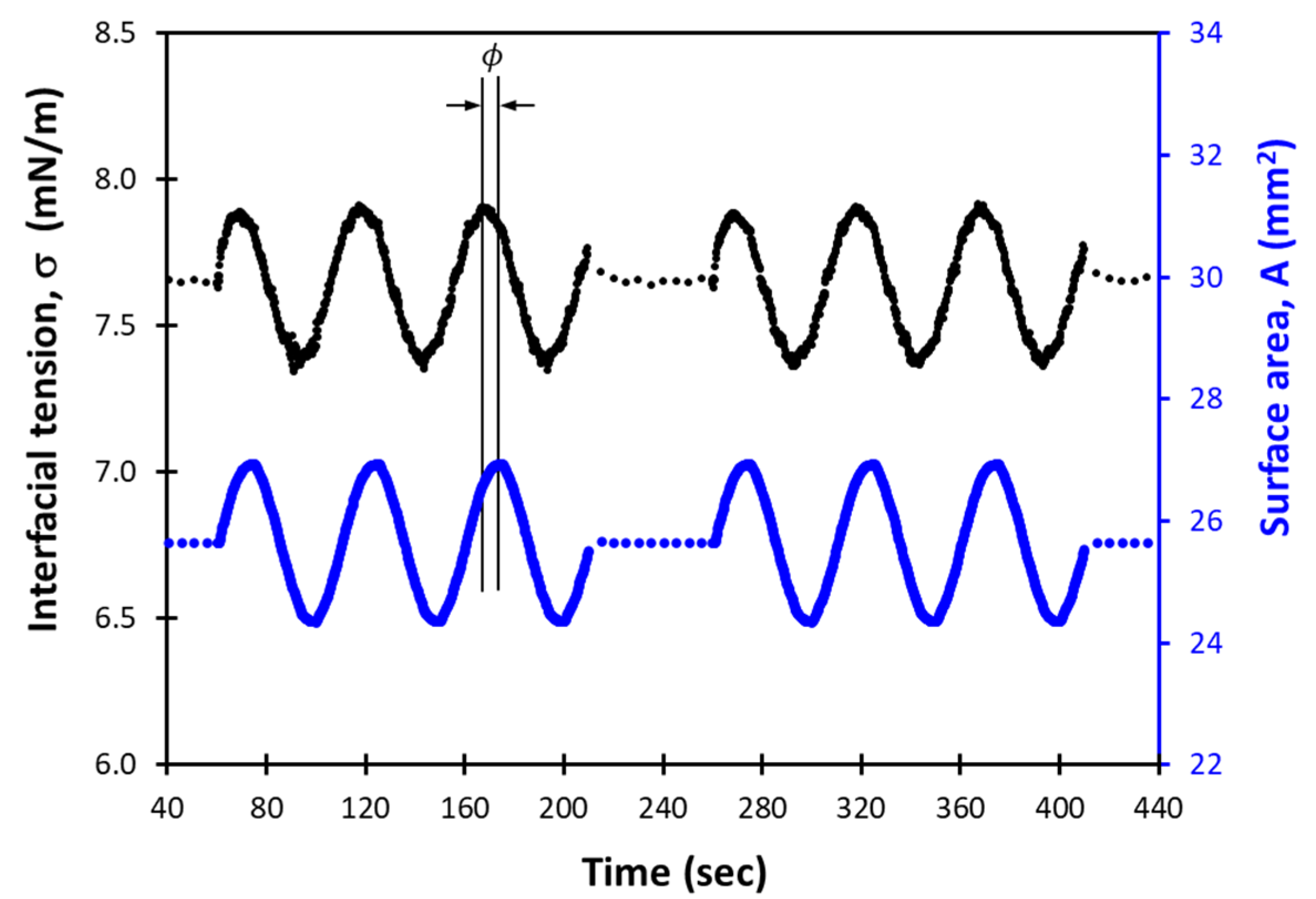
2.3. Measurement of Dilational Viscoelasticity
3. Results and Discussion
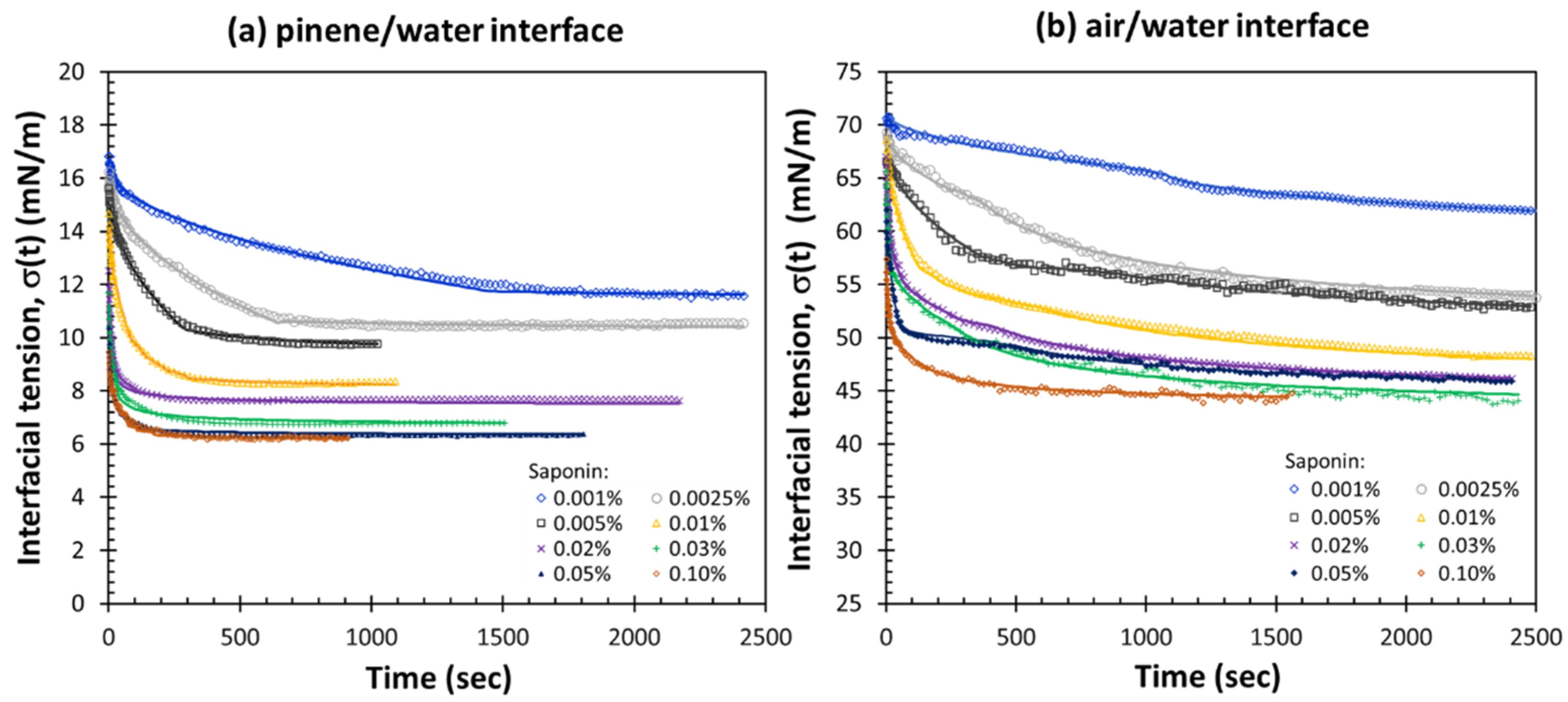
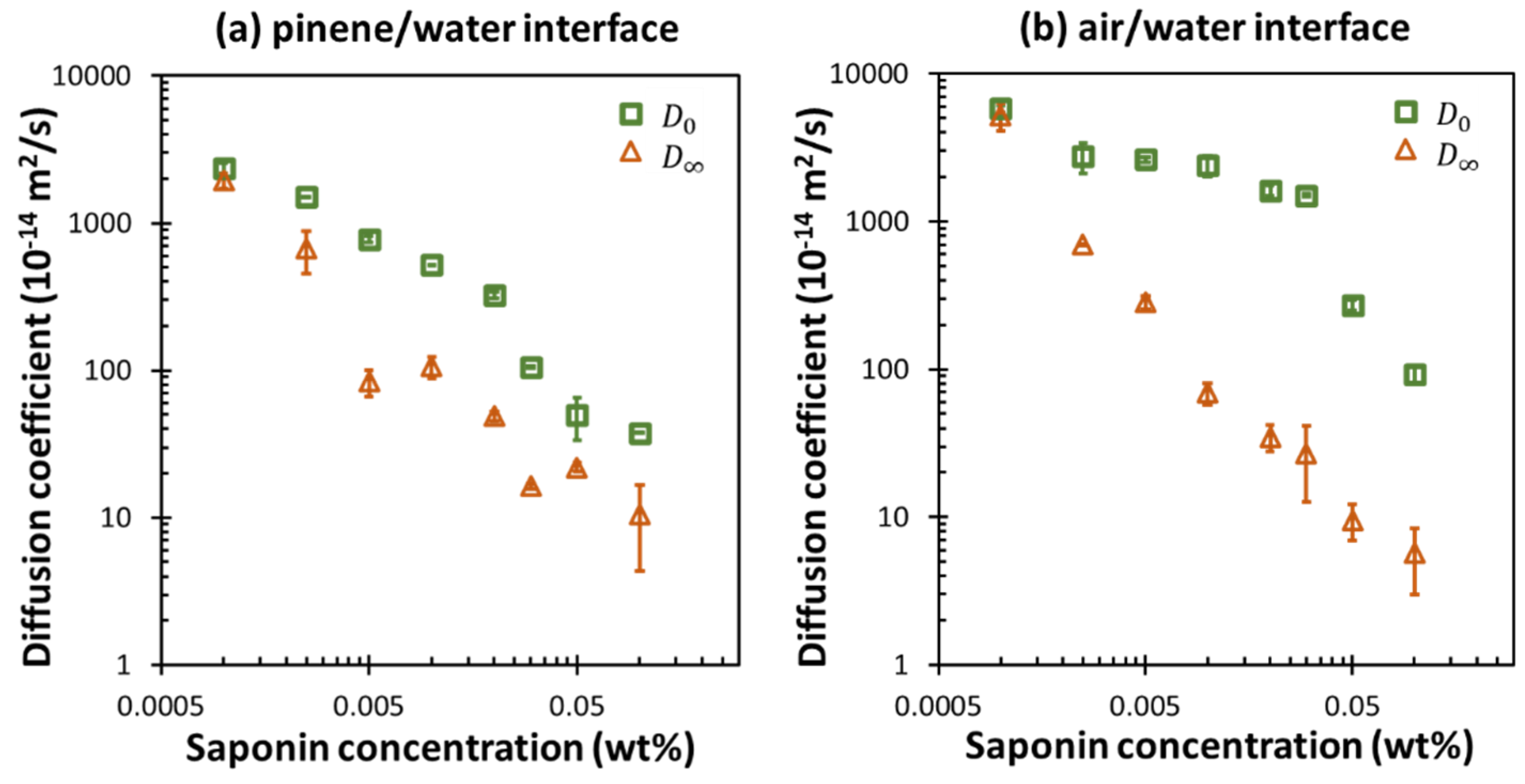
3.1. Adsorption Kinetics
3.2. Adsorption Isotherms
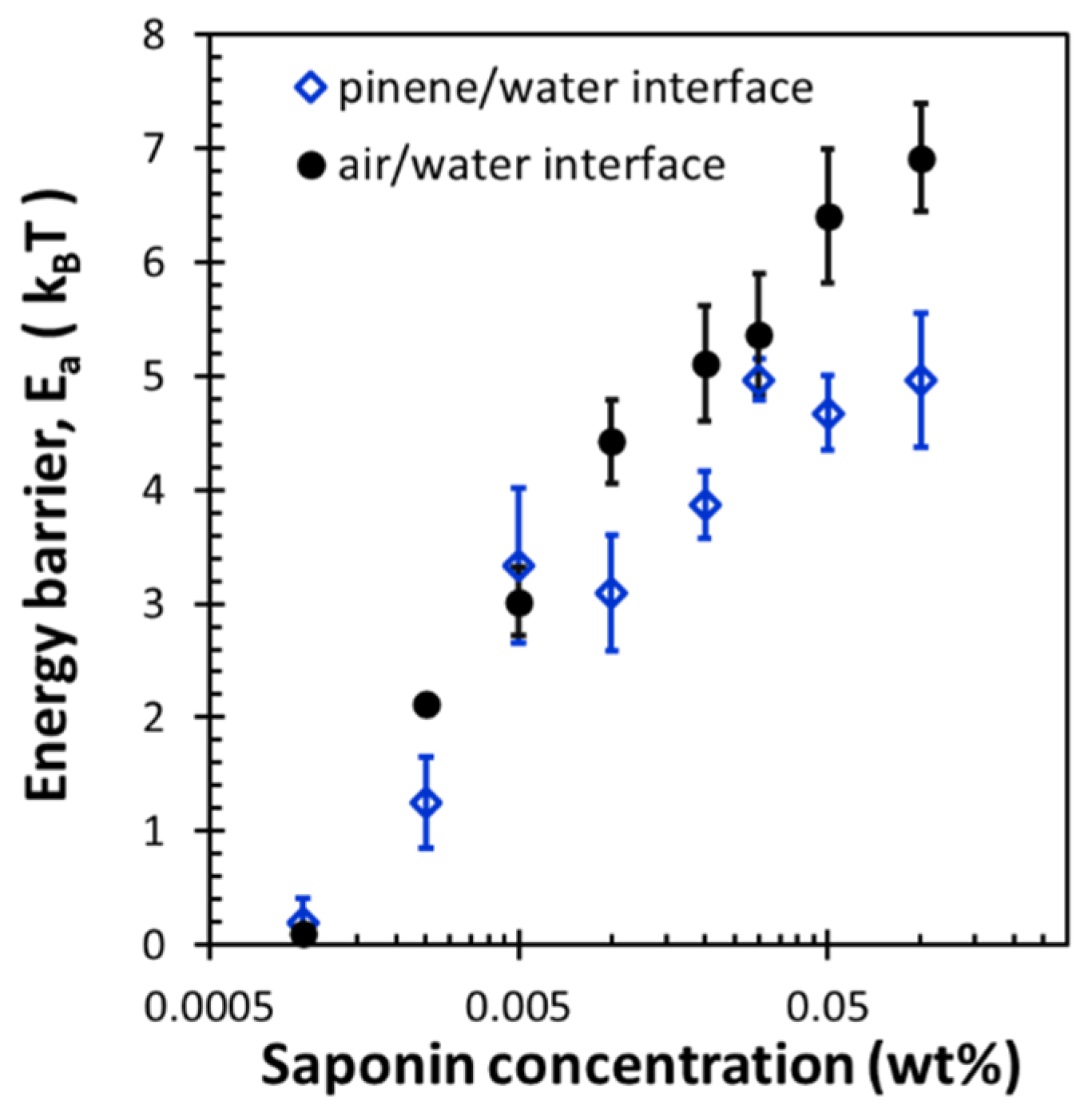
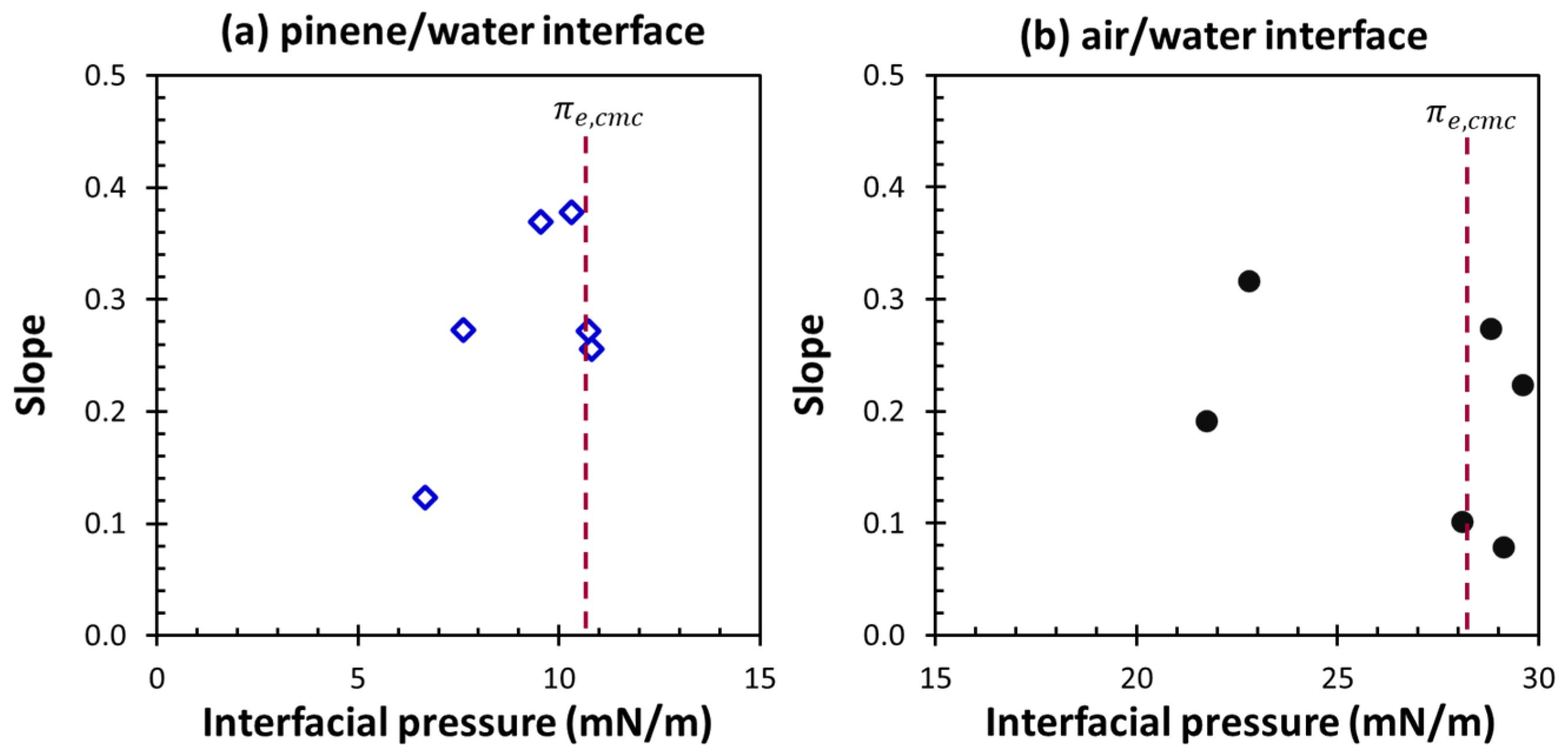
3.3. Dilational Moduli
4. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tsibranska, S.; Tcholakova, S.; Golemanov, K.; Denkov, N.; Pelan, E.; Stoyanov, S.D. Role of interfacial elasticity for the rheological properties of saponin-stabilized emulsions. J. Colloid Interface Sci. 2020, 564, 264–275. [Google Scholar] [CrossRef]
- Stanimirova, R.; Marinova, K.; Tcholakova, S.; Denkov, N.D.; Stoyanov, S.; Pelan, E. Surface rheology of saponin adsorption layers. Langmuir 2011, 27, 12486–12498. [Google Scholar] [CrossRef]
- Golemanov, K.; Tcholakova, S.; Denkov, N.; Pelan, E.; Stoyanov, S.D. Surface shear rheology of saponin adsorption layers. Langmuir 2012, 28, 12071–12084. [Google Scholar] [CrossRef]
- Dziza, K.; Santini, E.; Liggieri, L.; Jarek, E.; Krzan, M.; Fischer, T.; Ravera, F. Interfacial properties and emulsification of biocompatible liquid-liquid systems. Coatings 2020, 10, 397. [Google Scholar] [CrossRef]
- Krzan, M.; Rey, N.G.; Jarek, E.; Czakaj, A.; Santini, E.; Ravera, F.; Liggieri, L.; Warszynski, P.; Braunschweig, B. Surface properties of saponin—chitosan mixtures. Molecules 2022, 27, 7505. [Google Scholar] [CrossRef] [PubMed]
- Akeb, M.; Harrane, A.; Belbachir, M. Polymerization of β-pinene by using natural montmorillonite clay as a green catalyst. Green Materials 2018, 6. [Google Scholar] [CrossRef]
- Prat, D.; Wells, A.; Hayler, J.; Sneddon, H.; McElroy, C.R.; Abou-Shehada, S.; Dunn, P.J. CHEM21 selection guide of classical and less classical solvents. Green Chem. 2016, 18, 288–296. [Google Scholar] [CrossRef]
- Tanzi, C.D.; Vian, M.A.; Ginies, C.; Elmaataoui, M.; Chemat, F. Terpenes as green solvents for extraction of oil from microalgae. Molecules 2012, 17, 8196–8205. [Google Scholar] [CrossRef]
- Salehi, B.; Upadhyay, S.; Orhan, I.E.; Jugran, A.K.; Jayaweera, S.L.; Dias, D.A.; Sharopov, F.; Taheri, Y.; Martins, N.; Baghalpour, N.; et al. Therapeutic potential of α- and β-Pinene: A miracle gift of nature. Biomolecules 2019, 9, 738. [Google Scholar] [CrossRef]
- Üstündağ, G.; Mazza, G. Saponins: Properties, applications and processing. Crit. Rev. Food Sci. Nutr. 2007, 47, 231–258. [Google Scholar] [CrossRef]
- Bombardelli, E.; Morazzoni, P.; Cristoni, A.; Seghizzi, R. Pharmaceutical and cosmetic formulations with antimicrobial activity. U.S. Patent Application 2001/0046525 A1, 31 July 2001. [Google Scholar]
- Cheeke, P.R. Actual and potential applications of yucca Schidigera and Quillaja Saponaria saponins in human and animal nutrition. In Saponins in Food, Feedstuffs and Medicinal Plants; Proceedings of the Phythochemical Society of Europe; Springer: Dordrecht, The Netherlands, 2000; pp. 241–254. [Google Scholar] [CrossRef]
- Jenkins, K.J.; Atwal, A. Effects of dietary saponins on fecal bile acids and neutral sterols, and availability of vitamins A and E in the chick. J. Nutr. Biochem. 1994, 5, 134–137. [Google Scholar] [CrossRef]
- Southon, S.; Wright, A.J.A.; Price, K.R.; Fairweather-Tait, S.J.; Fenwick, G.R. The effect of three types of saponin on iron and zinc absorption from a single meal in the rat. Br. J. Nutr. 1988, 59, 389–396. [Google Scholar] [CrossRef] [PubMed]
- Bomford, R.; Stapleton, M.; Winsor, S.; Beesly, J.E.; Jessup, E.A.; Price, K.R.; Fenwick, G.R. Adjuvancity and ISCOM formation by structurally diverse saponins. Vaccine 1992, 10, 572. [Google Scholar] [CrossRef]
- Oakenfull, D. Soy protein, saponins and plasma cholesterol. J. Nutr. 2001, 131, 2971. [Google Scholar] [CrossRef]
- Herrmann, F.; Wink, M. Synergistic interactions of saponins and monoterpenes in HeLa cells, Cos7 cells and in erythrocytes. Phytomedicine 2011, 18, 1191–1196. [Google Scholar] [CrossRef]
- Yekeen, N.; Malik, A.A.; Idris, A.K.; Reepei, N.I.; Ganie, K. Foaming properties, wettability alteration and interfacial tension reduction by saponin extracted from soapnut (Sapindus Mukorossi) at room and reservoir conditions. J. Pet. Sci. Eng. 2020, 195, 107591. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, P.J.; Sörensen, P.M. Characterization of saponin foam from Saponaria officinalis for food applications. Food Hydrocoll. 2020, 101, 101. [Google Scholar] [CrossRef]
- Santini, E.; Jarek, E.; Ravera, F.; Liggieri, L.; Warszynski, P.; Krzan, M. Surface properties and foamability of saponin and saponin-chitosan systems. Colloids Surf. B Biointerfaces 2019, 181, 198–206. [Google Scholar] [CrossRef]
- Imuetinyan, H.; Agi, A.; Gbadamosi, A.; Junin, R.; Oseh, J. Oil-water interfacial tension, wettability alteration and foaming studies of natural surfactant extracted from Vernonia Amygdalina. Pet. Res. 2022, 7, 350–356. [Google Scholar] [CrossRef]
- Lin, F. Efficient recovery of extra-heavy oil using a naturally abundant green solvent: Toward a more sustainable oil-solid-water separation. Sustain. Mater. Technol. 2020, 25. [Google Scholar] [CrossRef]
- Río, O.; Neumann, A. Axisymmetric drop shape analysis: Computational methods for the measurement of interfacial properties from the shape and dimensions of pendant and sessile drops. J. Colloid Interface Sci. 1997, 196, 136–147. [Google Scholar] [CrossRef]
- Angle, C.W.; Hua, Y. Tailings pond surfactant analogues: Effects on toluene-diluted bitumen drops in NaHCO3/K2CO3 solution Part 1: Dynamic interfacial tension. Energy Fuels 2013, 27, 3603–3612. [Google Scholar] [CrossRef]
- Alexandrov, N.; Marinova, K.G.; Danov, K.D.; Ivanov, I.B. Surface dilational rheology measurements for oil/water systems with viscous oils. J. Colloid Interface Sci. 2009, 339, 545–550. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Li, Y.; Wang, J.; Zhang, Y. Interfacial behavior of alkaline protease at the air-water and oil-water interfaces. Appl. Surf. Sci. 2018, 433, 1128–1136. [Google Scholar] [CrossRef]
- Díez-Pascual, A.M.; Monroy, F.; Ortega, F.; Rubio, R.G.; Miller, R.; Noskov, B.A. Adsorption of water-soluble polymers with surfactant character: Dilational viscoelasticity. Langmuir 2007, 23, 3802–3808. [Google Scholar] [CrossRef]
- Sheu, E.Y.; De Tar, M.M.; Storm, D.A. Interfacial properties of asphaltenes. Fuel 1992, 71, 1277–1281. [Google Scholar] [CrossRef]
- Vogler, E.A.J. A Simple mathematical model of time-dependent interfacial tension. Colloid Interf. Sci. 1989, 133, 228–236. [Google Scholar] [CrossRef]
- Ward, A.F.H.; Tordai, L. Time-dependence of boundary tensions of solutions I. The role of diffusion in time-effects. J. Chem. Phys. 1946, 14, 453–461. [Google Scholar] [CrossRef]
- Fainerman, V.; Makievski, A.; Miller, R. The analysis of dynamic surface tension of sodium alkyl sulphate solutions, based on asymptotic equations of adsorption kinetic theory. Colloids Surfaces A Physicochem. Eng. Asp. 1994, 87, 61–75. [Google Scholar] [CrossRef]
- Lin, S.Y.; Tsay, R.Y.; Lin, L.W.; Chen, S. Adsorption kinetics of C12E8 at the air-water interface: Adsorption onto a clean interface. Langmuir 1996, 12, 6530–6536. [Google Scholar] [CrossRef]
- Chang, C.-H.; Franses, E.I. Adsorption dynamics of surfactants at the air/water interface: A critical review of mathematical models, data, and mechanisms. Colloids Surf. A Physicochem. Eng. Asp. 1995, 100, 1–45. [Google Scholar] [CrossRef]
- Kutuzov, S.; He, J.; Tangirala, R.; Emrick, T.; Russell, T.P.; Böker, A. On the kinetics of nanoparticle self-assembly at liquid/liquid interfaces. Phys. Chem. Chem. Phys. 2007, 9, 6351–6358. [Google Scholar] [CrossRef]
- Ferdous, S.; Ioannidis, M.A.; Henneke, D. Adsorption kinetics of alkanethiol-capped gold nanoparticles at the hexane–water interface. J. Nanoparticle Res. 2011, 13, 6579–6589. [Google Scholar] [CrossRef]
- Fang, S.; Chena, T.; Chena, B.; Xiong, Y.; Zhu, Y.; Duan, M. Graphene oxide at oil-water interfaces: Adsorption, assembly and demulsification. Colloids Surf. A Physicochem. Eng. Aspects 2016, 511, 47–54. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Wang, X.; Wang, Y.; Yan, Y.; Zhang, Y.; Li, H.; Zhao, Y. Adsorption kinetics and interfacial dilational properties of fluorinated hyperbranched polymer at n-decane/water interface. J. Dispers. Sci. Technol. 2014, 36, 343–350. [Google Scholar] [CrossRef]
- Liggieri, L.; Ravera, F.; Passerone, A. A diffusion-based approach to mixed adsorption kinetics. Colloids Surf. A Physicochem. Eng. Asp. 1996, 114, 351–359. [Google Scholar] [CrossRef]
- Ravera, F.; Liggieri, L.; Steinchen, A. Sorption kinetics considered as a renormalized diffusion process. J. Colloid Interface Sci. 1993, 156, 109–116. [Google Scholar] [CrossRef]
- Eastoe, J.; Dalton, J.S.; Rogueda, P.G.A.; Crooks, E.R.; Pitt, A.R.; Simister, E.A. Dynamic surface tensions of nonionic surfactant solutions. J. Colloid Interface Sci. 1997, 188, 423–430. [Google Scholar] [CrossRef]
- Miller, R.; Aksenenko, E.; Fainerman, V. Dynamic interfacial tension of surfactant solutions. Adv. Colloid Interface Sci. 2017, 247, 115–129. [Google Scholar] [CrossRef]
- Bizmark, N.; Ioannidis, M.A.; Henneke, D.E. Irreversible adsorption-driven assembly of nanoparticles at fluid interfaces revealed by a dynamic surface tension probe. Langmuir 2014, 30, 710–717. [Google Scholar] [CrossRef] [PubMed]
- Joos, P.; Van Hunsel, J. Adsorption kinetics of micellar Brij 58 solutions. Colloids Surfaces 1988, 33, 99–108. [Google Scholar] [CrossRef]
- Noskov, B. Kinetics of adsorption from micellar solutions. Adv. Colloid Interface Sci. 2002, 95, 237–293. [Google Scholar] [CrossRef]
- Liggieri, L.; Ferrari, M.; Massa, A.; Ravera, F. Molecular reorientation in the adsorption of some CiEj at the water-air interface. Colloids Surf. A. Physicochem. Eng. Aspects 1999, 156, 455–463. [Google Scholar] [CrossRef]
- Fainerman, V.B.; Miller, R.; Wüstneck, R.; Makievski, A.V. Adsorption isotherm and surface tension equation for a surfactant with changing partial molar area. 1. Ideal surface layer. J. Phys. Chem. 1996, 100, 7669–7675. [Google Scholar] [CrossRef]
- Penfold, J.; Thomas, R.K.; Tucker, I.M.; Petkov, J.T.; Stoyanov, S.D.; Denkov, N.D.; Golemanov, K.; Tcholakova, S.; Webster, J.R.P. Saponin adsorption at the air–water Interface—Neutron reflectivity and surface tension study. Langmuir 2018, 34, 9540–9547. [Google Scholar] [CrossRef]
- Pagureva, N.; Tcholakova, S.; Golemanov, K.; Denkov, N.; Pelan, E.; Stoyanov, S.D. Surface properties of adsorption layers formed from triterpenoid and steroid saponins. Colloids Surf. A Physicochem. Eng. Aspects 2016, 491, 18–28. [Google Scholar] [CrossRef]
- Wojciechowski, K. Surface activity of saponin from Quillaja bark at the air/water and oil/water interfaces. Colloids Surf. B Biointerfaces 2013, 108, 95–102. [Google Scholar] [CrossRef] [PubMed]
- Wojciechowski, K.; Orczyk, M.; Marcinkowski, K.; Kobiela, T.; Trapp, M.; Gutberlet, T.; Geue, T. Effect of hydration of sugar groups on adsorption of Quillaja bark saponin at air/water and Si/water interfaces. Colloids Surf. B Biointerfaces 2014, 117, 60–67. [Google Scholar] [CrossRef] [PubMed]
- Tempel, M.v.D.; Lucassen-Reynders, E. Relaxation processes at fluid interfaces. Adv. Colloid Interface Sci. 1983, 18, 281–301. [Google Scholar] [CrossRef]
- Noskov, B. Fast adsorption at the liquid-gas interface. Adv. Colloid Interface Sci. 1996, 69, 63–129. [Google Scholar] [CrossRef]
- Ravera, F.; Ferrari, M.; Liggieri, L. Adsorption and partitioning of surfactants in liquid–liquid systems. Adv. Colloid Interface Sci. 2000, 88, 129–177. [Google Scholar] [CrossRef]
- Lucassen, J.; Van Den Tempel, M. Dynamic measurements of dilational properties of a liquid interface. Chem. Eng. Sci. 1972, 27, 1283–1291. [Google Scholar] [CrossRef]
- van Kempen, S.E.H.J.; Schols, H.A.; van der Linden, E.; Sagis, L.M.C. Non-linear surface dilatational rheology as a tool for understanding microstructures of air/water interfaces stabilized by oligofructose fatty acid esters. Soft Matter 2013, 9, 9579–9592. [Google Scholar] [CrossRef] [PubMed]
- Gochev, G.G.; Schneck, E.; Miller, R. Effects of aqueous isotopic substitution on the adsorption dynamics and dilational rheology of β-lactoglobulin layers at the water/air interface. J. Phys. Chem. B 2024, 128, 2821–2830. [Google Scholar] [CrossRef]
- Cao, C.; Lei, J.; Zhang, L.; Du, F.-P. Equilibrium and dynamic interfacial properties of protein/ionic liquid type surfactant solutions at the decane/water interface. Langmuir 2014, 30, 13744–13753. [Google Scholar] [CrossRef]
- Wang, C.; Cao, X.L.; Guo, L.L.; Xu, Z.C.; Zhang, L.; Gong, Q.T.; Zhang, L.; Zhao, S. Effect of molecular structure of catanionic surfactant mixtures on their interfacial properties. Colloids Surf. A Physicochem. Eng. Aspects 2016, 509, 601–612. [Google Scholar] [CrossRef]
- Liggieri, L.; Ravera, F.; Ferrari, M. Surface rheology investigation of the 2-D phase transition in n-dodecanol monolayers at the water−air interface. Langmuir 2003, 19, 10233–10240. [Google Scholar] [CrossRef]
- Ferri, J.K.; Stebe, K.J. Soluble surfactants undergoing surface phase transitions: A Maxwell construction and the dynamic surface tension. J. Colloid Interface Sci. 1999, 209, 1–9. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, X.-C.; Gong, Q.-T.; Zhang, L.; Luo, L.; Zhao, S.; Yu, J.-Y. Interfacial dilational properties of tri-substituted alkyl benzene sulfonates at air/water and decane/water interfaces. J. Colloid Interface Sci. 2008, 327, 451–458. [Google Scholar] [CrossRef] [PubMed]
- Jayalakshmi, Y.; Ozanne, L.; Langevin, D. Viscoelasticity of surfactant monolayers. J. Colloid Interface Sci. 1995, 170, 358–366. [Google Scholar] [CrossRef]





| Interface | cmc | Γ | As | |
|---|---|---|---|---|
| wt% | mM | μmol/m2 | nm2/molecule | |
| pinene/water | 0.050 | 0.41 | 0.57 | 2.93 |
| air/water | 0.015 | 0.12 | 2.64 | 0.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, F. Adsorption and Dilational Viscoelasticity of Saponin at the β-Pinene/Water and Air/Water Interfaces. Colloids Interfaces 2025, 9, 68. https://doi.org/10.3390/colloids9050068
Lin F. Adsorption and Dilational Viscoelasticity of Saponin at the β-Pinene/Water and Air/Water Interfaces. Colloids and Interfaces. 2025; 9(5):68. https://doi.org/10.3390/colloids9050068
Chicago/Turabian StyleLin, Feng. 2025. "Adsorption and Dilational Viscoelasticity of Saponin at the β-Pinene/Water and Air/Water Interfaces" Colloids and Interfaces 9, no. 5: 68. https://doi.org/10.3390/colloids9050068
APA StyleLin, F. (2025). Adsorption and Dilational Viscoelasticity of Saponin at the β-Pinene/Water and Air/Water Interfaces. Colloids and Interfaces, 9(5), 68. https://doi.org/10.3390/colloids9050068







