Abstract
The quasi-steady diffusiophoresis of a soft particle composed of an uncharged hard sphere core and a uniformly charged porous surface layer in a concentric charged spherical cavity full of a symmetric electrolyte solution with a concentration gradient is analyzed. By using a regular perturbation method with small fixed charge densities of the soft particle and cavity wall, the linearized electrokinetic equations relevant to the fluid velocity field, electric potential profile, and ionic concentration distributions are solved. A closed-form formula for the diffusiophoretic (electrophoretic and chemiphoretic) velocity of the soft particle is obtained as a function of the ratios of the core-to-particle radii, particle-to-cavity radii, particle radius to the Debye screening length, and particle radius to the permeation length in the porous layer. In typical cases, the confining charged cavity wall significantly influences the diffusiophoresis of the soft particle. The fluid flow caused by the diffusioosmosis (electroosmosis and chemiosmosis) along the cavity wall can considerably change the diffusiophoretic velocity of the particle and even reverse its direction. In general, the diffusiophoretic velocity decreases with increasing core-to-particle radius ratios, particle-to-cavity radius ratios, and the ratio of the particle radius to the permeation length in the porous layer, but increases with increasing ratios of the particle radius to the Debye length.
1. Introduction
Diffusiophoresis refers to the motion of colloid particles under imposed solute concentration gradients [1,2,3,4,5,6,7,8] and provides the mechanisms for numerous applications in the characterization, separation, transport, and manipulation of particles in microfluidics [9,10,11,12,13,14] and layered two-dimensional nanocolloid/liquid crystals [15,16], as well as in the autonomous motion of micromotors [17,18,19]. In a nonionic solution, the particle interacts with solute molecules via the Van der Waals and dipole attractive forces, and diffusiophoresis proceeds toward the regions where there is a higher solute concentration [20]. For the diffusiophoresis of a charged particle in an electrolyte solution, the particle–ion interaction is dominated by electrostatics and the range of its electric double layer with a thickness of the order of the Debye screening length [21]. In the past, the diffusiophoretic motion of a hard particle (which is impermeable to ionic fluids) [22,23], a porous particle (which is permeable) [24], and a soft particle (which has a hard core covered by a porous layer) [25,26,27,28] with an arbitrary electric double layer thickness were studied analytically (by assuming a weak applied electrolyte concentration gradient) and experimentally.
In various applications of diffusiophoresis, the colloid particles are rarely unbounded, and it is important to understand whether boundaries significantly affect the particle mobility [5,29]. In the limiting case of a very thin double layer, the normalized fluid velocity field around a hard sphere undergoing diffusiophoresis is identical to that of one undergoing electrophoresis, and the already extensively studied boundary effect on electrophoretic motion can be used to explain the effect on diffusiophoretic motion [10]. On the other hand, the boundary effect of diffusiophoresis is different from that of electrophoresis when a double layer polarization is incorporated. By using a boundary collocation technique, the diffusiophoretic motion of a hard sphere with a thin polarized double layer near one or two plates [30] and along the axis of a microtube [31,32] was examined.
The diffusiophoresis of a charged sphere in a charged spherical cavity can be used to model diffusiophoretic motions in lab-on-a-chip devices and dead-end pores involving self-regulated drug delivery [33,34]. In fact, the diffusiophoresis of a charged hard or porous sphere with a thin polarized or an arbitrary double layer situated at the center of a charged spherical cavity [35,36] and the diffusiophoresis of a charged soft sphere with an arbitrary double layer inside a nonconcentric uncharged spherical cavity [37] have been studied theoretically. However, the effect of a charged boundary on the diffusiophoretic motion of a soft particle has not been investigated. In this paper, the diffusiophoresis of a charged soft spherical particle inside a concentric charged spherical cavity with an arbitrary electric double layer thickness is analyzed. The fluid velocity field, electric potential profile, and ionic concentration distributions are determined as the power series of the small fixed charge densities of the soft sphere and cavity wall. An explicit formula for the diffusiophoretic mobility of the soft sphere is obtained as a function of the relevant parameters.
2. Electrokinetic Equations and Boundary Conditions
As shown in Figure 1, we consider the diffusiophoresis of a soft spherical particle of radius , consisting of an uncharged hard sphere core of radius and a charged porous surface layer of thickness , situated at the center of a charged spherical cavity of radius occupied by a symmetric electrolyte solution in a quasi-steady state. A linear electrolyte concentration profile is imposed along the cavity wall with a constant gradient in the direction, and the induced particle velocity in this direction needing to be determined. The origin of the spherical coordinates is attached to the particle center (at ), and the problem is independent of (symmetric about the axis).

Figure 1.
Geometric sketch for the diffusiophoresis of a charged soft sphere in a concentric charged spherical cavity.
The normalized electrolyte concentration gradient is taken to be positive but small, so that the system deviates slightly from equilibrium. Therefore, the cationic and anionic concentration profiles and , respectively; the dynamic pressure distribution ; and the electrical potential distribution can be decomposed into the following:
where , , and are the equilibrium profiles of the ionic concentrations, dynamic pressure, and electrical potential, respectively, and , , and are the pertinent small perturbations.
The small perturbed quantities, , , and , and the fluid velocity are governed by the linearized ionic continuity equations, modified Stokes–Brinkman equations, and Poisson–Boltzmann equation, respectively, as follows [25]:
In the previous equations, the ionic electrochemical potential energy perturbations are as follows:
Furthermore, is the flow penetration length or the square root of the permeability in the porous surface layer of the soft sphere; are the ionic diffusivities in the fluid; is the valence of the symmetric electrolyte (which is positive); and are the viscosity and dielectric permittivity, respectively, of the fluid; and equals unity if and zero otherwise. The pressure term in Equation (5) disappears owing to the application of a curl to the momentum equation; the fluid velocity also satisfies the continuity equation; and the constants , , and inside and outside the porous layer are considered to be the same.
The boundary conditions of the small perturbed quantities along the interface between the hard sphere core and the porous surface layer and at the particle surface are as follows [25]:
where is the hydrodynamic stress tensor of the fluid, is the unit vector in the direction, and Equation (8) takes a reference frame traveling with the soft particle.
The boundary conditions at the cavity wall are as follows [35]:
where , , and is the unit vector in the direction. Equations (10) and (11) for the induced perturbed electrical potential and the ionic electrochemical potential energies result from the electrolyte concentration gradient imposed along the cavity wall and the equality of the anion and cation fluxes in the particle-free fluid. Equation (10c) for the stationary cavity also takes the same reference frame as Equation (8).
3. Solution of the Diffusiophoretic Velocity
The equilibrium electrical potential profile of a soft spherical particle, whose porous surface layer has a constant space charge density , situated at the center of a spherical cavity, having a constant surface charge density , satisfying the continuity of electrical potential and current at the particle surface () and the Gauss condition at the hard core surface () and cavity wall (), can be obtained as follows [38]
where
Both and are dimensionless, and is the Debye screening parameter. For the case of a symmetric electrolyte, the second-order terms in Equation (11) disappear.
The substitution of Equations (11)–(13) into the Gauss condition at yields a relation between the surface charge density and the zeta potential of the cavity wall:
where
Namely, after the substitution of Equation (15), Equation (11) is also valid for the solution of in the case of a cavity wall with a constant zeta potential.
When the parameters and are small, in order to solve for the perturbed quantities , , , , and with the diffusiophoretic velocity of the soft spherical particle, these variables can be expressed as power expansions of and , such as the following:
where the to-be-determined coefficients , , , , , etc. do not depend on and but are dependent on the core-to-particle radius ratio , the particle-to-cavity radius ratio , the ratio of the particle radius to the permeation length in the porous layer , and the electrokinetic particle radius . There are zeroth-order terms of and in the expansions of and , as shown in Equations (10a) and (10b). The substitution of these expansions and Equation (11) into Equations (4)–(10) yields results for , (to the orders and ), , , and (to the orders , , and ) as follows:
where the dimensionless functions , , , and with i and j equal to 0, 1, and 2 are given by Equations (A1)–(A4) and (A9)–(A11) in Appendix A.
The electrical force acting on the soft spherical particle can be expressed as follows [38]
The substitution of Equations (11) and (18) into the previous equation results in this force to the second orders,
The drag force exerted by the fluid on the soft spherical particle can be expressed as follows:
where is the unit dyadic. Substituting Equation (20) into the previous equation, we obtain the following:
where the dimensionless coefficients , , , , , and are given by Equations (A1)–(A4).
Applying the constraint that the total force on the diffusiophoretic soft sphere is zero to the summation of Equations (22) and (24), we obtain the following:
where
which is a characteristic particle velocity. After the substitution of Equation (15), Equation (17) is also valid for the diffusiophoretic velocity of the particle in the case of a cavity wall with a constant zeta potential. Equations (25) and (26) for the limit reduce to the diffusiophoretic velocity of a charged porous spherical particle within a charged spherical cavity obtained earlier, and analytical expressions are available in some limiting cases [36].
In Equation (17) for the diffusiophoretic velocity of the soft spherical particle within the spherical cavity, the first-order terms and second-order terms denote the contributions from electrophoresis that are caused by the induced electric field in Equation (10) and chemiphoresis, respectively. The fixed charge at the cavity wall changes the particle motion through the wall-corrected electrical potential distribution and diffusioosmosis-induced (electroosmosis-induced and chemiosmosis-induced) recirculating flows generated by the interaction of the imposed electrolyte concentration gradient with the electrical double layer adjacent to the wall. The terms and are the diffusiophoretic velocity of a charged soft particle in an uncharged cavity () and the translational velocity of an uncharged soft particle () in a charged cavity induced by diffusioosmosis, respectively. Equation (25) agrees with the electrophoretic velocity of a soft spherical particle within a charged cavity available in the literature [38].
4. Results and Discussion
The analytical formulae for the diffusiophoretic velocity of a charged soft spherical particle within a concentric charged spherical cavity are obtained in Equations (17) and (25)–(27), and the graphical results will be given here. The normalized first-order (electrophoretic) velocities and for the special case of a porous spherical particle () within a concentric charged cavity as calculated from Equation (25) are plotted in Figure 2 and Figure 3, respectively, as functions of the hydrodynamic resistance parameter , the particle-to-cavity radius ratio , and the electrokinetic particle radius . These normalized velocities are always positive; therefore, the sign of the product determines the direction of the electrophoresis and the sign of determines the direction of the contribution from the electroosmosis at the cavity wall to the particle velocity. For the fixed values of and , both and are the monotonically increasing functions of from zero at . For the specified values of and , both and are the monotonically decreasing functions of as expected, but may strongly depend on , while is only weakly dependent on . For fixed and , both and are the monotonically decreasing functions of as expected, and equals 1 and 0 if equals 0 and 1, respectively.
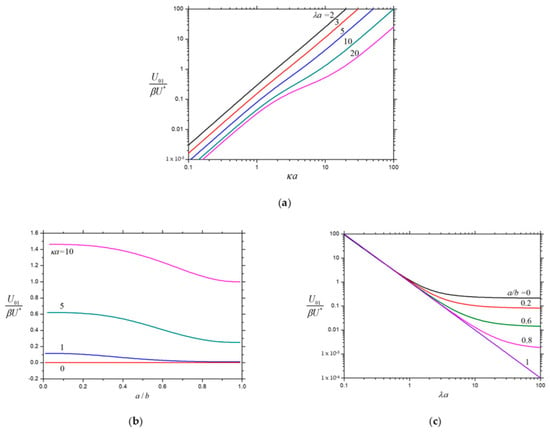
Figure 2.
Normalized velocity for the electrophoresis of a charged porous sphere () in a spherical cavity: (a) ; (b) ; and (c) .

Figure 3.
Normalized velocity for a porous sphere () in a charged spherical cavity with electroosmosis: (a) ; (b) ; and (c) .
The normalized net first-order velocity (with ) of a charged porous particle inside a charged cavity is plotted versus the fixed charge density ratio (equaling ) in Figure 4 (in straight lines with the slope ) for different values of , , and . The electroosmotic flow at the cavity wall enhances/reduces this electrophoretic velocity if the fixed charge densities and are in the same/opposite signs. If the magnitude of is large, the wall effect can be significant. When the value of is negative and the magnitude is great, the velocity direction of the confined particle may be opposite to the direction of the electrophoresis in an unbounded fluid. The magnitude of in general decreases with the increases in and , but increases with an increase in .

Figure 4.
Normalized velocity for the electrophoresis of a charged porous sphere () in a charged spherical cavity versus the fixed charge density ratio : (a) and ; (b) and ; and (c) and .
The normalized second-order velocities , , and of a charged porous sphere inside a charged cavity caused by the chemiphoretic and wall-induced chemiosmotic effects as calculated from Equation (26) are plotted in Figure 5, Figure 6 and Figure 7, respectively, as functions of the parameters , , and . All these second-order velocities are monotonically decreasing functions of as expected, but none of them is a monotonic function of (local extrema appear at moderate values of ), keeping the other parameters unchanged. For the specified values of and , the value of increases monotonically with an increase in , whereas and may not be monotonic functions of . As expected, in the limits and , while in the limit . For the given values of and , both and are strongly dependent on (inversely proportional to if is smaller than about 10), while only weakly depend on .
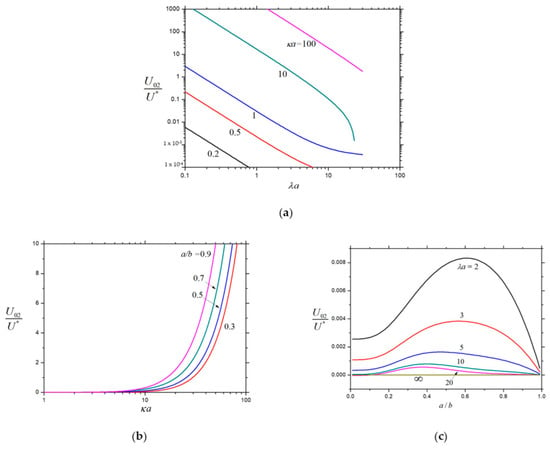
Figure 5.
Normalized velocity for the chemiphoresis of a charged porous sphere () in a spherical cavity: (a) ; (b) ; and (c) .
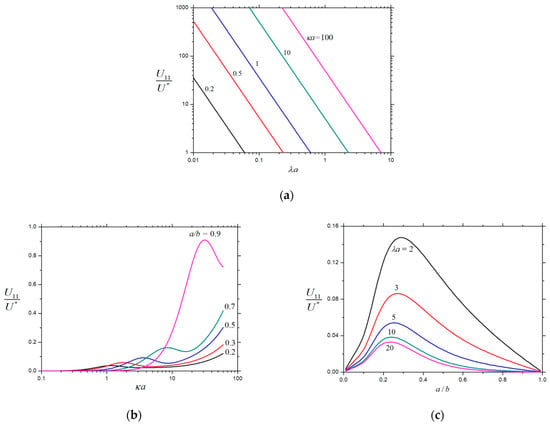
Figure 6.
Normalized velocity for a charged porous sphere () in a charged spherical cavity: (a) ; (b) ; and (c) .
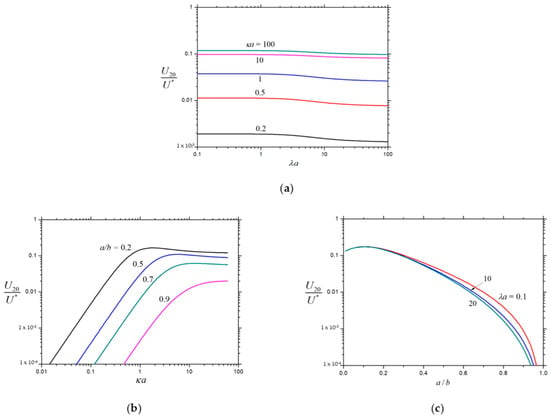
Figure 7.
Normalized velocity for a porous sphere () in a charged spherical cavity with chemiosmosis: (a) ; (b) ; and (c) .
The normalized net second-order velocity (with ) of a charged porous particle inside a charged cavity is plotted versus the fixed charge density ratio in Figure 8 (in parabolic curves that concave upward) for various values of the parameters , , and . For the given values of , , and , this velocity may reverse its direction twice as changes, due to the combined effects of chemiphoresis and wall-induced chemiosmosis. If the magnitude of is large, the cavity wall effect on the motion of the porous sphere is substantial. The magnitude of generally diminishes when and increase, but increases with an increasing .
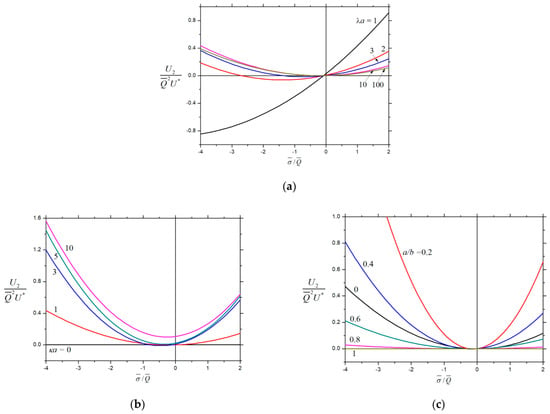
Figure 8.
Normalized velocity for the chemiphoresis of a charged porous sphere () in a charged spherical cavity versus the fixed charge density ratio : (a) and ; (b) and ; and (c) and .
Figure 8 shows the various values of the parameters , , and , as well as the fixed charge densities and . For the diffusiophoresis of a porous particle in a symmetric electrolyte whose cation and anion have different diffusivities (, like the aqueous solution of NaCl), the plots of against with and the different values of , , and are given in Figure 9 (a combination of Figure 4 and Figure 8), where the contributions from electrophoresis and chemiphoresis, as well as from wall-induced electroosmosis and chemiosmosis, are included. Furthermore, for the fixed values of , , and , the cavity wall effect is significant as the magnitude of is large, and the particle velocity may reverse twice in its direction when changes.
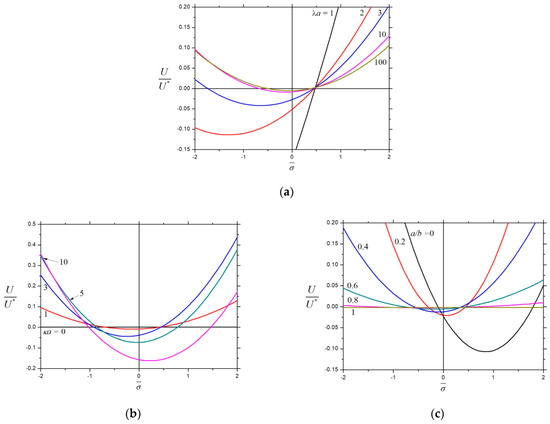
Figure 9.
Normalized velocity for the diffusiophoresis of a charged porous sphere () in a charged spherical cavity with and versus the charge density : (a) and ; (b) and ; and (c) and .
Having understood the effect of a concentric charged cavity on the diffusiophoretic velocity of a charged porous particle, we can examine the general case of a diffusiophoretic soft particle. The normalized first-order velocities and for a soft spherical particle within a concentric charged cavity as calculated from Equation (25) are plotted versus the core-to-particle radius ratio for different values of the hydrodynamic resistance parameter , the particle-to-cavity radius ratio , and the electrokinetic particle radius in Figure 10 and Figure 11, respectively. Likewise, these normalized velocities are always positive; the sign of the product determines the direction of the electrophoresis; and the sign of determines the direction of the wall-induced electroosmotic effect on the particle. Both and are monotonically increasing functions of from zero at , monotonically decreasing functions of , and monotonically decreasing functions of to zero at , keeping the other parameters unchanged. For the specified values of , , and , the normalized electrophoretic velocity monotonically decreases with a rise in the radius ratio , as expected, from the value for a charged porous sphere at to zero for an uncharged rigid (impermeable) sphere at . On the other hand, the normalized velocity of the soft particle caused by the electroosmotic effect of the charged cavity wall for the given values of , , and is generally not a monotonic function of and has a maximum at a relatively large value of .
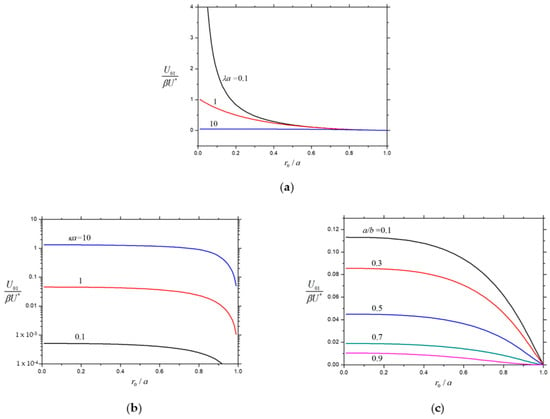
Figure 10.
Normalized velocity for the electrophoresis of a charged soft sphere in a spherical cavity versus : (a) and ; (b) and ; and (c) and .
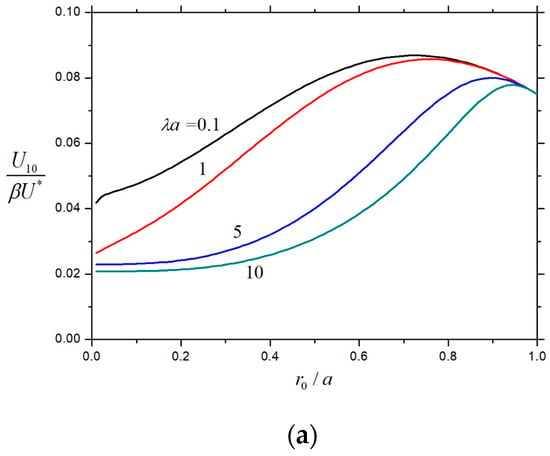

Figure 11.
Normalized velocity for a soft sphere in a charged spherical cavity with electroosmosis versus : (a) and ; (b) and ; and (c) and .
In Figure 12, the normalized net first-order velocity (with ) of a charged soft particle inside a charged cavity is plotted versus the fixed charge density ratio for the different values of . Again, the electroosmotic effect of the cavity wall enhances/reduces this particle velocity if the fixed charge densities and are in the same/opposite signs. When the value of is negative and the magnitude is great, the velocity direction of the particle may be opposite to the direction of the electrophoresis in an unbounded fluid. The value of decreases with an increase in , mainly due to the effect of on the electrophoretic velocity .

Figure 12.
Normalized velocity for the electrophoresis of a charged soft sphere in a charged spherical cavity with , , and versus the fixed charge density ratio .
The normalized second-order velocities , , and of a charged soft sphere inside a charged cavity caused by the chemiphoretic and wall-induced chemiosmotic effects as calculated from Equation (26) are plotted versus the core-to-particle radius ratio in Figure 13, Figure 14 and Figure 15, respectively, for the different values of , , and . Likewise, all these velocities are monotonically decreasing functions of that generally increase with an increasing , but none of them depends monotonically on (local extrema appear at moderate values of ), keeping the other parameters unchanged. For the specified values of , , and , the normalized velocities and generally decreases with a rise in the radius ratio from their values for a charged porous sphere at to zero for an uncharged rigid sphere at . However, the normalized velocity of the soft particle caused by the chemiosmotic effect of the charged cavity wall for the given values of , , and is generally not a monotonic function of .
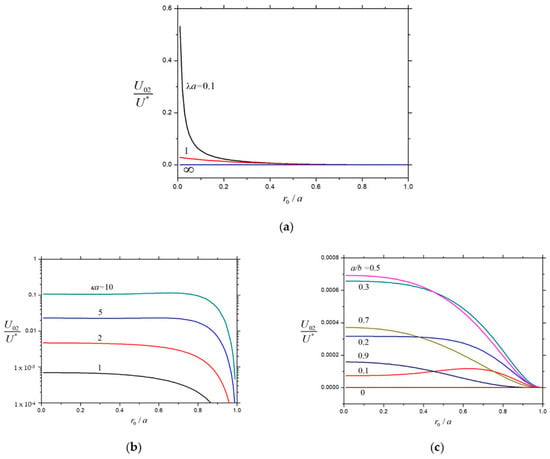
Figure 13.
Normalized velocity for the chemiphoresis of a charged soft sphere in a spherical cavity versus : (a) and ; (b) and ; and (c) and .
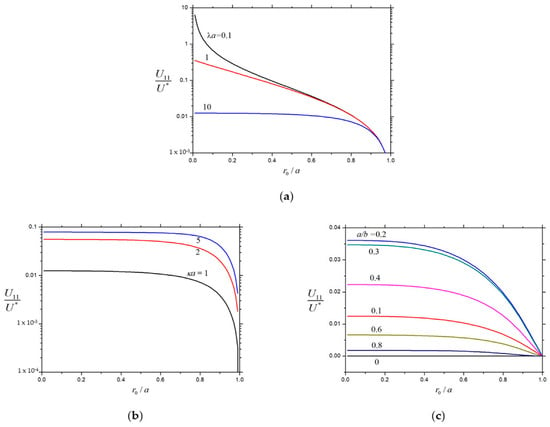
Figure 14.
Normalized velocity for a charged soft sphere in a charged spherical cavity versus : (a) and ; (b) and ; and (c) and .

Figure 15.
Normalized velocity for a soft sphere in a charged spherical cavity with chemiosmosis versus : (a) and ; (b) and ; and (c) and .
In Figure 16, the normalized net second-order velocity (with ) of a charged soft particle inside a charged cavity is plotted versus the fixed charge density ratio for the various values of . Furthermore, for the given values of , , and , this velocity may reverse its direction twice as changes, due to the combined effects of chemiphoresis and wall-induced chemiosmosis. In general, the value of decreases with an increasing if is positive, but it is not a monotonic function of if is negative.
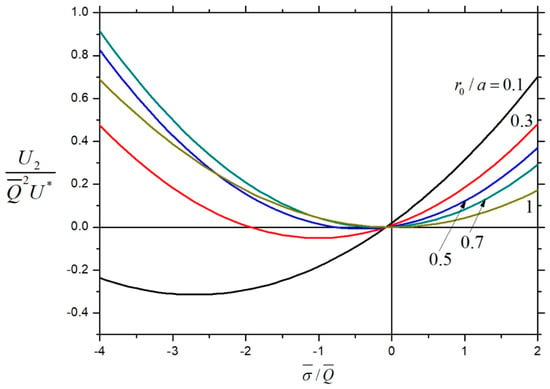
Figure 16.
Normalized velocity for the chemiphoresis of a charged soft sphere in a charged spherical cavity with , , and versus the fixed charge density ratio .
5. Conclusions
The quasi-steady diffusiophoresis of a charged soft spherical particle at the center of a charged spherical cavity under an applied concentration gradient of a symmetric electrolyte is analyzed for the arbitrary values of the core-to-particle radius ratio , the particle-to-cavity radius ratio , the ratio of the particle radius to the permeation length in the porous surface layer , and the ratio of the particle radius to the Debye length . By using a regular perturbation method with small dimensionless fixed charge densities and of the porous surface layer and cavity wall, respectively, the linearized electrokinetic differential equations relevant to the fluid velocity field, electric potential profile, and ionic concentration distributions are solved. The balance of the electrostatic and hydrodynamic forces acting on the soft sphere results in an explicit formula, Equation (17) with Equations (25)–(27), for the diffusiophoretic velocity of the particle in terms of , , , and up to the second orders of and . The diffusioosmotic flow at the cavity wall can substantially change the particle velocity and even reverse its direction. The normalized electrophoretic and chemiphoretic velocity components and (and also ) depend strongly on , while the normalized electroosmosis-induced and chemiosmosis-induced velocity components and are weak functions of . The diffusiophoretic velocity generally decreases when , , and increase, but increases with an increasing . The contributions to the particle velocity from the diffusioosmotic flow taking place along the charged cavity wall and from the wall-corrected diffusiophoretic force are equivalently important, and this diffusioosmotic flow can reverse the direction of the particle velocity.
Author Contributions
Conceptualization, H.-J.K.; methodology, H.-J.K. and W.-Z.C.; investigation, H.-J.K. and W.-Z.C.; writing—original draft preparation, H.-J.K. and W.-Z.C.; writing—review and editing, H.-J.K.; supervision, H.-J.K.; and funding acquisition, H.-J.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science and Technology council Taiwan: grant number MOST 110-2221-E-002-017-MY3.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of this study; in the collection, analyses, or interpretation of the data; in the writing of the manuscript; or in the decision to publish these results.
Appendix A. Functions in Equations (18)–(20)
In Equation (20),
where , (for the first-order fluid velocity field), , , and (for the second-order fluid velocity field),
The functions and defined by Equations (A9) and (A10) have no relation to the parameters and in the main text.
In Equations (21) and (22)
where and ,
where and .
References
- Dukhin, S.S.; Derjaguin, B.V. Surface and Colloid Science; Matijevic, E., Ed.; Wiley: New York, NY, USA, 1974; Volume 7. [Google Scholar]
- Prieve, D.C.; Anderson, J.L.; Ebel, J.P.; Lowell, M.E. Motion of a particle generated by chemical gradients. Part 2. Electrolytes. J. Fluid Mech. 1984, 148, 247–269. [Google Scholar] [CrossRef]
- Pawar, Y.; Solomentsev, Y.E.; Anderson, J.L. Polarization effects on diffusiophoresis in electrolyte gradients. J. Colloid Interface Sci. 1993, 155, 488–498. [Google Scholar] [CrossRef]
- Khair, A.S. Diffusiophoresis of colloidal particles in neutral solute gradients at finite Péclet number. J. Fluid Mech. 2013, 731, 64–94. [Google Scholar] [CrossRef]
- Keh, H.J. Diffusiophoresis of charged particles and diffusioosmosis of electrolyte solutions. Curr. Opin. Colloid Interface Sci. 2016, 24, 13–22. [Google Scholar] [CrossRef]
- Prieve, D.C.; Malone, S.M.; Khair, A.S.; Stout, R.F.; Kanj, M.Y. Diffusiophoresis of charged colloidal particles in the limit of very high salinity. Proc. Natl. Acad. Sci. USA 2019, 116, 18257–18262. [Google Scholar] [CrossRef] [PubMed]
- Shin, S. Diffusiophoretic separation of colloids in microfluidic flows. Phys. Fluids 2020, 32, 101302. [Google Scholar] [CrossRef]
- Lee, S.; Lee, J.; Ault, J.T. The role of variable zeta potential on diffusiophoretic and diffusioosmotic transport. Colloids Surf. A 2023, 659, 130775. [Google Scholar] [CrossRef]
- Smith, R.E.; Prieve, D.C. Accelerated deposition of latex particles onto a rapidly dissolving steel surface. Chem. Eng. Sci. 1982, 37, 1213–1223. [Google Scholar] [CrossRef]
- Anderson, J.L. Colloid transport by interfacial forces. Annu. Rev. Fluid Mech. 1989, 21, 61–99. [Google Scholar] [CrossRef]
- Abecassis, B.; Cottin-Bizonne, C.; Ybert, C.; Ajdari, A.; Bocquet, L. Osmotic manipulation of particles for microfluidic applications. New J. Phys. 2009, 11, 075022. [Google Scholar] [CrossRef]
- Wanunu, M.; Morrison, W.; Rabin, Y.; Grosberg, A.Y.; Meller, A. Electrostatic focusing of unlabeled DNA into nanoscale pores using a salt gradient. Nat. Nanotechnol. 2010, 5, 160–165. [Google Scholar] [CrossRef] [PubMed]
- Hatlo, M.M.; Panja, D.; van Roij, R. Translocation of DNA molecules through nanopores with salt gradients: The role of osmotic flow. Phys. Rev. Lett. 2011, 107, 68101. [Google Scholar] [CrossRef] [PubMed]
- Velegol, D.; Garg, A.; Guha, R.; Kar, A.; Kumar, M. Origins of concentration gradients for diffusiophoresis. Soft Matter 2016, 12, 4686–4703. [Google Scholar] [CrossRef] [PubMed]
- Shen, T.Z.; Hong, S.H.; Song, J.K. Electro-optical switching of graphene-oxide liquid crystals with an extremely large Kerr coefficient. Nat. Mater. 2014, 13, 394–399. [Google Scholar] [CrossRef] [PubMed]
- Shen, T.Z.; Perera, K.N.A.; Masud, A.R.; Priyadharshana, P.A.N.S.; Park, J.-Y.; Wang, Q.-H.; Hong, S.H.; Song, J.K. A dual-frequency photonic crystal nanocolloid with hue- and brightness-tunable structural colors. Cell Rep. Phys. Sci. 2023, 4, 101343. [Google Scholar] [CrossRef]
- Sen, A.; Ibele, M.; Hong, Y.; Velegol, D. Chemo and phototactic nano/microbots. Faraday Discuss. 2009, 143, 15–27. [Google Scholar] [CrossRef] [PubMed]
- Brown, A.; Poon, W. Ionic effects in self-propelled Pt-coated Janus swimmers. Soft Matter. 2014, 10, 4016–4027. [Google Scholar] [CrossRef] [PubMed]
- Oshanin, G.; Popescu, M.N.; Dietrich, S. Active colloids in the context of chemical kinetics. J. Phys. A Math. Theor. 2017, 50, 134001. [Google Scholar] [CrossRef]
- Staffeld, P.O.; Quinn, J.A. Diffusion-induced banding of colloid particles via diffusiophoresis 2. Non-electrolytes. J. Colloid Interface Sci. 1989, 130, 88–100. [Google Scholar] [CrossRef]
- Bohinc, K.; Bossa, G.V.; May, S. Incorporation of ion and solvent structure into mean-field modeling of the electric double layer. Adv. Colloid Interface Sci. 2017, 249, 220–233. [Google Scholar] [CrossRef] [PubMed]
- Prieve, D.C.; Roman, R. Diffusiophoresis of a rigid sphere through a viscous electrolyte solution. J. Chem. Soc. Faraday Trans. 2 1987, 83, 1287–1306. [Google Scholar] [CrossRef]
- Keh, H.J.; Wei, Y.K. Diffusiophoretic mobility of spherical particles at low potential and arbitrary double-layer thickness. Langmuir 2000, 16, 5289–5294. [Google Scholar] [CrossRef]
- Wei, Y.K.; Keh, H.J. Diffusiophoretic mobility of charged porous spheres in electrolyte gradients. J. Colloid Interface Sci. 2004, 269, 240–250. [Google Scholar] [CrossRef] [PubMed]
- Huang, P.Y.; Keh, H.J. Diffusiophoresis of a spherical soft particle in electrolyte gradients. J. Phys. Chem. B 2012, 116, 7575–7589. [Google Scholar] [CrossRef] [PubMed]
- Ohshima, H. Diffusiophoretic velocity of a spherical soft particle. Colloid Polym. Sci. 2022, 300, 153–157. [Google Scholar] [CrossRef]
- Ohshima, H. Diffusiophoresis of a soft particle as a model for biological cells. Colloids Interfaces 2022, 6, 24. [Google Scholar] [CrossRef]
- Akdeniz, B.; Wood, J.A.; Lammertink, R.G.H. Diffusiophoretic behavior of polyelectrolyte-coated particles. Langmuir 2024, 40, 5934–5944. [Google Scholar] [CrossRef] [PubMed]
- Joo, S.W.; Lee, S.Y.; Liu, J.; Qian, S. Diffusiophoresis of an elongated cylindrical nanoparticle along the axis of a nanopore. ChemPhysChem 2010, 11, 3281–3290. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.C.; Keh, H.J. Diffusiophoresis and electrophoresis of a charged sphere perpendicular to one or two plane walls. J. Colloid Interface Sci. 2008, 322, 634–653. [Google Scholar] [CrossRef]
- Lee, S.Y.; Yalcin, S.E.; Joo, S.W.; Sharma, A.; Baysal, O.; Qian, S. The effect of axial concentration gradient on electrophoretic motion of a charged spherical particle in a nanopore. Microgravity Sci. Technol. 2010, 22, 329–338. [Google Scholar] [CrossRef]
- Chiu, H.C.; Keh, H.J. Diffusiophoresis of a charged particle in a microtube. Electrophoresis 2017, 38, 2468–2478. [Google Scholar] [CrossRef] [PubMed]
- Kar, A.; Chiang, T.-S.; Rivera, I.O.; Sen, A.; Velegol, D. Enhanced transport into and out of dead-end pores. ACS Nano 2015, 9, 746–753. [Google Scholar] [CrossRef] [PubMed]
- Shin, S.; Um, E.; Sabass, B.; Ault, J.T.; Rahimi, M.; Warren, P.B.; Stone, H.A. Size-dependent control of colloid transport via solute gradients in dead-end channels. Proc. Natl. Acad. Sci. USA 2016, 113, 257–261. [Google Scholar] [CrossRef] [PubMed]
- Chiu, Y.C.; Keh, H.J. Diffusiophoresis of a charged particle in a charged cavity with arbitrary electric-double-layer thickness. Microfluid. Nanofluid. 2018, 22, 84. [Google Scholar] [CrossRef]
- Chiu, Y.C.; Keh, H.J. Diffusiophoresis of a charged porous particle in a charged cavity. J. Phys. Chem. B 2018, 122, 9803–9814. [Google Scholar] [CrossRef] [PubMed]
- Chang, X.; Hsu, W.-L.; Hsu, J.-P.; Tseng, S. Diffusiophoresis of a soft spherical particle in a spherical cavity. J. Phys. Chem. B 2009, 113, 8646–8656. [Google Scholar]
- Chen, W.J.; Keh, H.J. Electrophoresis of a charged soft particle in a charged cavity with arbitrary double-layer thickness. J. Phys. Chem. B 2013, 117, 9757–9767. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).